Enhanced Arithmetic Optimization Algorithm Guided by a Local Search for the Feature Selection Problem

1  Introduction

Feature selection is one of the fundamental and essential processes when implementing machine learning methods due to the increasing number of features in datasets. The presence of numerous features can hinder the classifier’s effectiveness in solving classification problems and diminish its overall performance. Moreover, an abundance of features can lead to overfitting, typically resulting in degraded performance. In single-objective feature selection, the goal is to identify a reduced subset of features that maintains low prediction error while minimizing the number of selected features [1,2]. By utilizing fewer features and training examples, the two primary objectives of feature selection can be achieved, leading to a reduction in computational complexity and an increase in generalization performance and model accuracy.

Three categories of evolutionary feature selection techniques exist filter, hybrid, and wrapper techniques. In comparison to wrapper algorithms, filters are computationally more efficient because they employ metrics like mutual information [3–5], fisher score [6], correlation [7], ReliefF [8], inconsistency rate [9], or even an ensemble of such metrics [10], filter approaches have the drawback of not being biased toward the Machine Learning (ML) algorithm [11], according to an evaluation of 22 distinct filtering techniques by [12], there is no filter approach consistently outperforms all other methods. While wrapper algorithms examine the efficacy of the feature subsets depending on the effectiveness of the prediction model [13], which frequently yields higher performance [14–18].

A filter and a wrapper are combined in a two-stage process to implement the hybrid approaches. With the intention of narrowing the search space, a filter is initially applied to the features of a hybrid approach. The meta-second heuristic’s step only employs the highest-ranking characteristics. Researchers have employed this strategy of removing characteristics of low rank [19,20]. Two significant limitations plague such methods. First, only features are affected by the decreased search space, thus, this strategy would not be very useful for data with a large number of samples. Second, the features with low rank when paired with other features, might become significant. Furthermore, all possible feature interactions are missed by this filter-based methodology, some hybrid methods have overcome this problem by combining local search with optimization methods [21,22].

The computing problems associated with employing Genetic Algorithms for feature selection in a wrapper scenario for big datasets were addressed by proposing a two-stage surrogate-assisted evolutionary strategy [23]. Pashaei et al. developed a hybrid wrapper feature selection technique that combines Simulated Annealing (SA), a crossover operator, and the Binary Arithmetic Optimization Algorithm (BAO) to find the lowest collection of informative genes for classification [24]. Ewees et al. [25] proposed a method that combines the standard BAO with the Genetic Algorithm (GA) operators.

Feature selection is a challenging task due to its intractable nature. To address this challenge, a new meta-heuristic optimization algorithm called the Arithmetic Optimization Algorithm (AOA) has been proposed. AOA has been modified to specifically address the feature selection problem, and it considers two objectives: maximizing prediction accuracy and minimizing the size of the selected subset.

A local search with neighborhood search strategies (NBH) has been introduced within the AOA algorithm to search effectively among large search spaces, namely, the AOA_NBH algorithm. The proposed AOA_NBH algorithm was compared with the original AOA algorithm and with other state-of-the-art methods. The following summarizes the main contributions of this paper:

•   A recently proposed AOA algorithm for continuous optimization problems has been modified to deal with discrete optimization problems by investigating the S-shaped transfer function to be applied to feature selection problems.

•   Two objectives are considered in the formulation of the feature selection problem, i.e., minimizing both the error rate and the size of the selected feature subset.

•   A Tournament selection method has been proposed to maintain the diversity of the AOA population.

•   A new local search method is proposed to improve the local intensification of AOA, with two neighborhood methods.

The organization of this paper is as follows: the Arithmetic Optimization Algorithm with selection method and local search method are represented in Section 2, Section 3 represents the experiential results with some discussions on the results, and Section 4 presents the comparison of the proposed algorithm with three population-based algorithms, finally, the conclusion and future works are presented in Section 5.

2  The Proposed Arithmetic Optimization Algorithm

AOA is a population-based stochastic algorithm based on a mathematical foundation [26]. The AOA typically consists of two phases of search, referred to as exploration and exploitation, which are patterned after mathematical operations. The exploration phase employs multiplication (×) and division (÷) operators, while the exploitation phase uses addition (+) and subtraction (−) operators. The AOA first generates search agents at random. Each one is a solution to a problem. The best solution is determined by calculating the fitness function for each solution. The Math Accelerated Function (MAF) value is then used to determine whether AOA should perform exploration or exploitation procedures, where the Math Accelerated Function is a tool used to guide decision-making between exploration and exploitation procedures. Its relevance lies in its ability to provide a quantitative measure that informs the system about the most appropriate strategy at a given point in time. Finally, the MAF value is adjusted using the following Eq. (1):

 MAF(Citr)=min+Citr(max−mintotal_Itr)(1)

where total_Itr denotes the total number of iterations. The minimum and maximum values of the accelerated function are referred to as Min and Max, respectively. As can be observed in the following Eq. (2), the AOA’s exploration phase mainly uses multiplication (×) and division (÷).

Pi,j(Citr +1)={bstj÷(Opt+ϵ)×((UBj−LBj)×μ+LBj),r<0.5bstj×Opt×((UBj−LBj)×μ+LBj),otherwise(2)

Opt(Citr)=1−Citr1αtotal_Itr1α(3)

The parameter α controls the execution of the exploitation phase. Where the addition (+) and subtraction (−) are used in the exploitation phase by means of Eq. (4).

Pi,j(Citr +1)={bstj−(Opt+ϵ)×((UBj−LBj)×μ+LBj),r<0.5bstj+Opt×((UBj−LBj)×μ+LBj),otherwise(4)

2.1 AOA for Feature Selection Problem

Feature selection can be considered as a binary problem, where the solution is a list of zeros and ones, zero for the removed selected features and one for the selected features. Thus, a binary algorithm should be implemented to solve the problem of feature selection. In AOA, the transfer function is used to obtain the binary solutions after computing the new solution. AOA was first presented in continuous problem space; therefore, we developed a transfer function for AOA known as an S-shaped transfer function (TransFunc) [27] to address the binary problem space as shown in Eq. (5).

TransFunc(Pij(Citr))=11+exp⁡(−Pij(Citr))(5)

where Citr is the number of iterations currently being performed. Eq. (6) is used to update the solution in AOA for S-shaped transfer functions to produce the subset of features.

Pij(Citr+1)={0,r>TransFunc(Pij(Citr))1,r≤TransFunc(Pij(Citr))(6)

The minimization of the number of selected features and the minimization of the classification error rate can be seen as two opposing objectives in the multi-objective optimization problem of feature selection. Each solution is assessed in accordance with the suggested fitness function, which is based on the KNN classifier to determine the classification error rate as well as the number of features of the solution that were specifically chosen for the solution. The original version of AOA and the updated AOA (AOA_NBH) algorithms assess the solution quality using the fitness function in Eq. (7).

fitnessFun=∂×et+(1−∂)×SelectedFeaturesTotalFeatures(7)

where fitnessFun is the fitness function to be minimized, ∂ is a parameter between zero and one, which denotes the weight of the error rate and the number of features being selected in the function, and et is the error rate given by the classifier [26]. The overall AOA for feature selection is represented in Algorithm 1.

2.2 Selecting the Solutions for Exploitation: AOA

Considered all solutions to be exploited which resulted in a slowdown of the algorithm speed and delayed convergence, thus the idea of choosing only the promising areas of the search space is suggested in order to speed up the algorithm and make the algorithm converge toward the optimal solution faster. According to Goldberg et al. [28], a tournament selection approach is a straightforward and easy-to-use selection mechanism.

One of the known selection methods in evolutionary algorithms is the tournament selection [29], n solutions are chosen at random from the population during the tournament selection procedure. These solutions are contrasted with one another, and then a tournament is held to choose the winner. The selection pressure is then adjusted by comparing a generated random number between 0 and 1 with a selection probability that acts as a convenient mechanism which is 0.5. If the generated random number is greater than 0.5, the highest fitness solution be chosen; otherwise, the weakest solution will be selected. Tournament selection allows most solutions a chance to be chosen while maintaining the diversity of the chosen solutions [29].

2.3 AOA with Local Search (AOA_NBH)

AOA is a new optimization technique that showed good performance in several optimization problems. AOA uses the addition and subtraction operators to perform the exploitation regardless of the fitness values of the newly produced solution. The proposed method replaces the exploitation operators with a local search with neighborhood methods. It treats a solution as its starting point, improves it, and then replaces the original solution with the improved one. The working solution will be selected by tournament selection, then change neighborhood operators (0 becomes 1 and one becomes 0) are applied including changing random one, two, or three features. The pseudocode of the proposed local search method is illustrated in Algorithm 2.

The suggested local search is implemented in Algorithm 1, by replacing the exploitation phase. The local search is applied after the exploitation of the AOA algorithm, the process of local search starts with a given population P, and then the tournament selection selects a solution to be improved. The process of the local search is performed until the maximum number of iterations is exceeded or the solution is not improved after performing 50% of the local search’s iterations. The fitness function is then performed to check the quality of the new solution, the solution is accepted if its quality is better than the original one, otherwise, the counter of unimproved moves will be increased by 1, and finally, the improved solution will be replaced by the new solution in the population. This method provides a fast improvement of the selected solutions in population which speed up convergence speed.

This approach gives a fast improvement of the chosen solutions within the population, which in turn speeds up the rate at which the optimization process converges. In other words, it quickly enhances the quality of alternative solutions that the algorithm is taking into account. This quick advancement speeds up the algorithm’s convergence to the ideal or nearly optimal solution, requiring less time and computer resources to get a successful result. Essentially, it accelerates the convergence of the algorithm by concentrating on the most promising options early on in the search process.

3  Experiential Results and Discussions

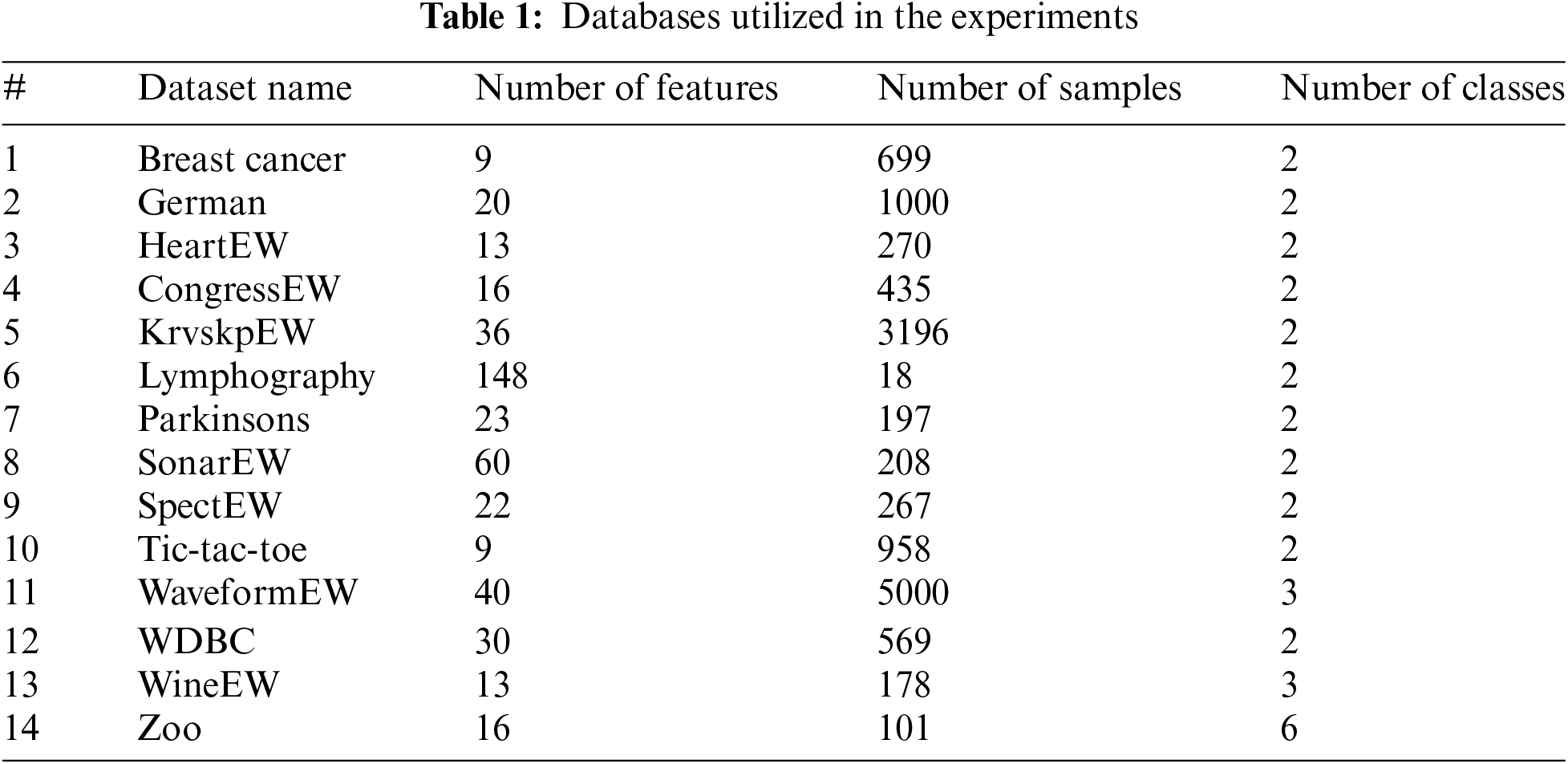
In this part, the effectiveness of this work is evaluated using 14 UCI datasets that have been utilized in several reliable studies. Table 1 [30] has a presentation of these datasets. The results of this study have been carried out utilizing a personal computer with an Intel i5-2.30 GHz processor and 8.0 GB of RAM. Ten runs are used in this experiment. Moreover, each considered dataset for experiments is split into 80% for training and 20% for testing [31].

The algorithms under examination employed the same number of iterations and population size, the final parameter settings for the AOA, and the proposed local search based on experimental findings using various parameter values as follows:

•   The population size is set to 20.

•   The number of iterations of 500 was used in all algorithms.

•   α equals to 5.

•   μ equals to 0.5.

•   min is set to 0.2.

•   max is set to 0.9.

•   The number of local search iterations (itrls) is set to 50.

Table 2 compares AOA and AOA_NBH in terms of accuracy and the number of selected features.

Several important criteria and performance comparisons were used to assess the feature selection methods. A 5-fold cross-validation approach was used to generate these measures, The findings in Table 2, summarize the results of 10 separate runs for each method, where the worst, average (avg), and best accuracy for each run were presented. The number of selected features that produced the best accuracy is denoted by NSF and the results in boldface illustrate the best performance for each instance.

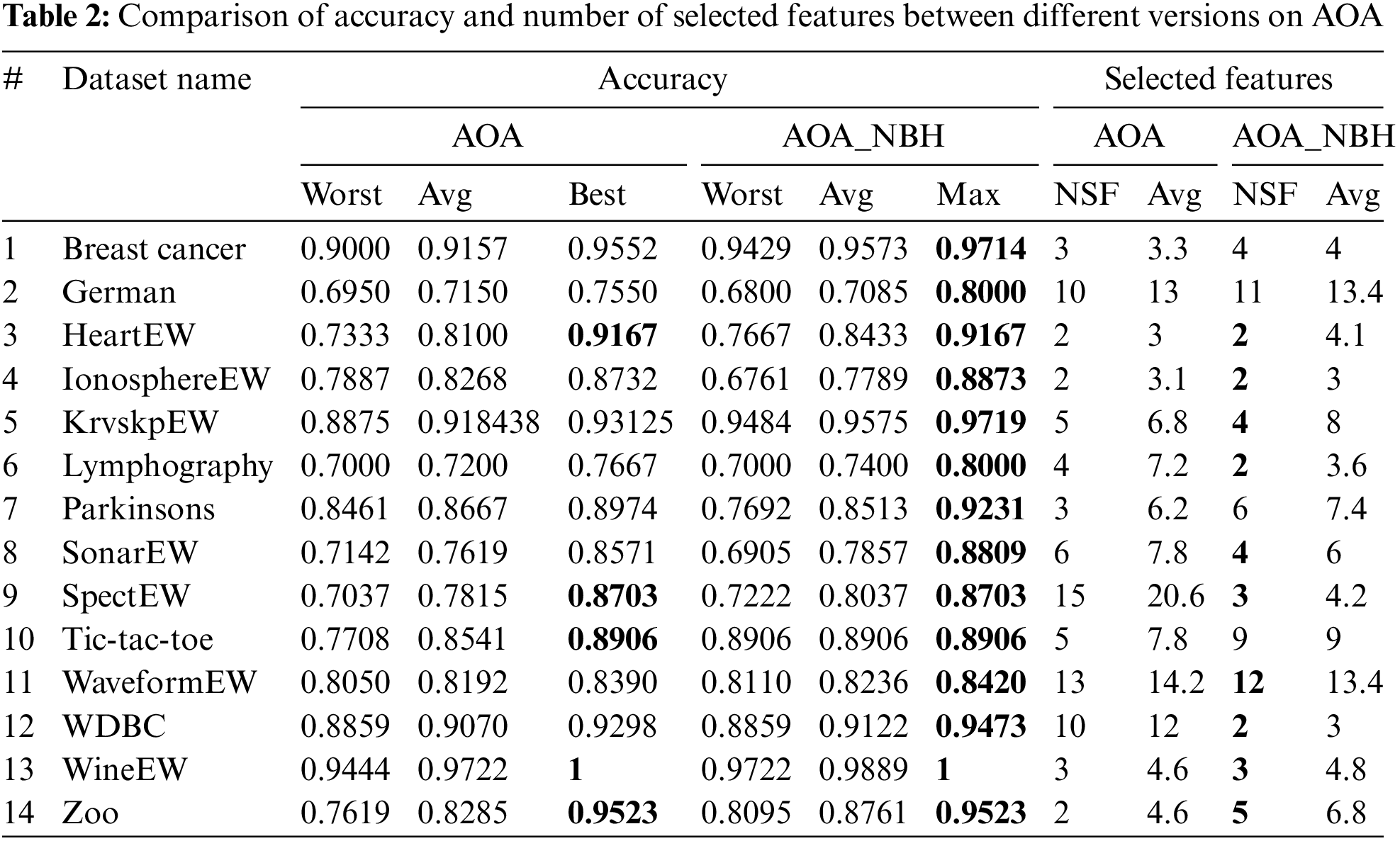
In general, most of the maximum achieved accuracies by AOA_NBH outperformed those achieved by AOA algorithm, except 5 datasets achieved exactly the same best accuracies, but they achieved better average accuracies over 10 runs as can be observed in Fig. 1. Where the x-axis shows the names of the datasets and y-axis show the accuracy value.

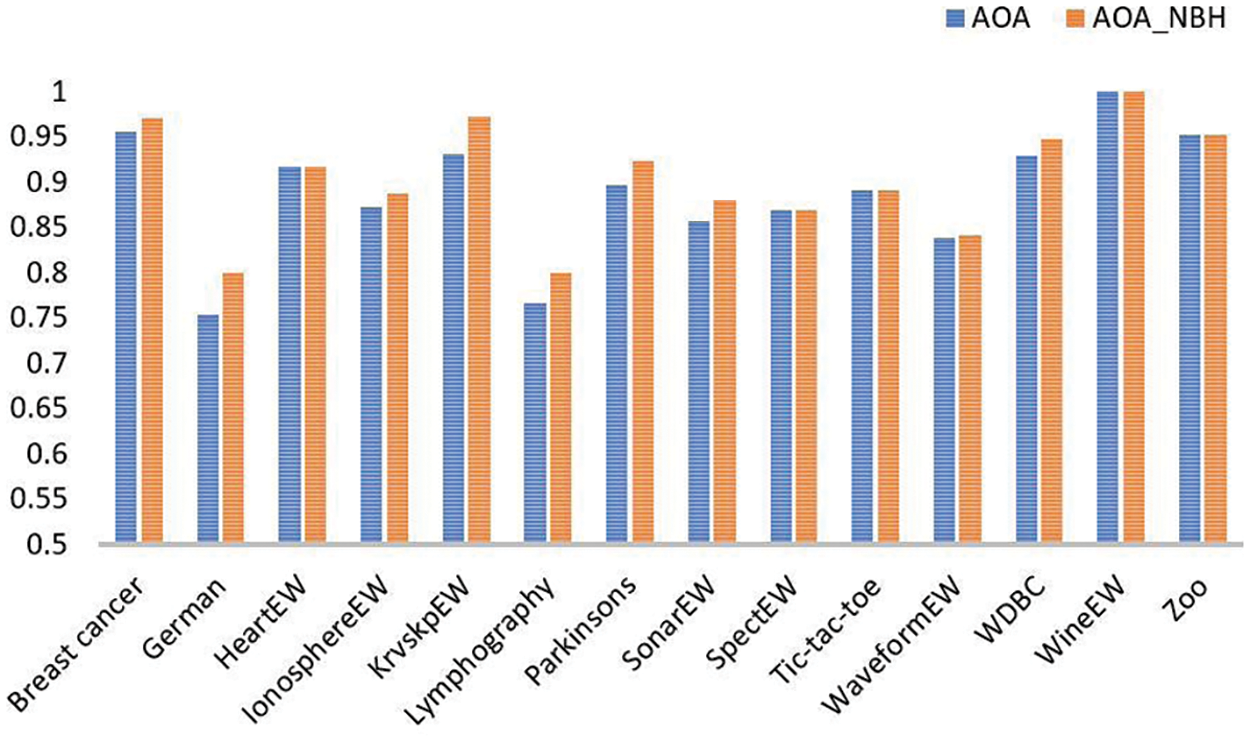
Figure 1: Comparing AOA and AOA_NBH in terms of accuracy

When considering the number of selected features in comparison, the AOA_NBH algorithm outperforms the AOA in 10 out of 14 datasets as can be observed in Fig. 2. Where the x-axis shows the names of the datasets and y-axis show the number of features.

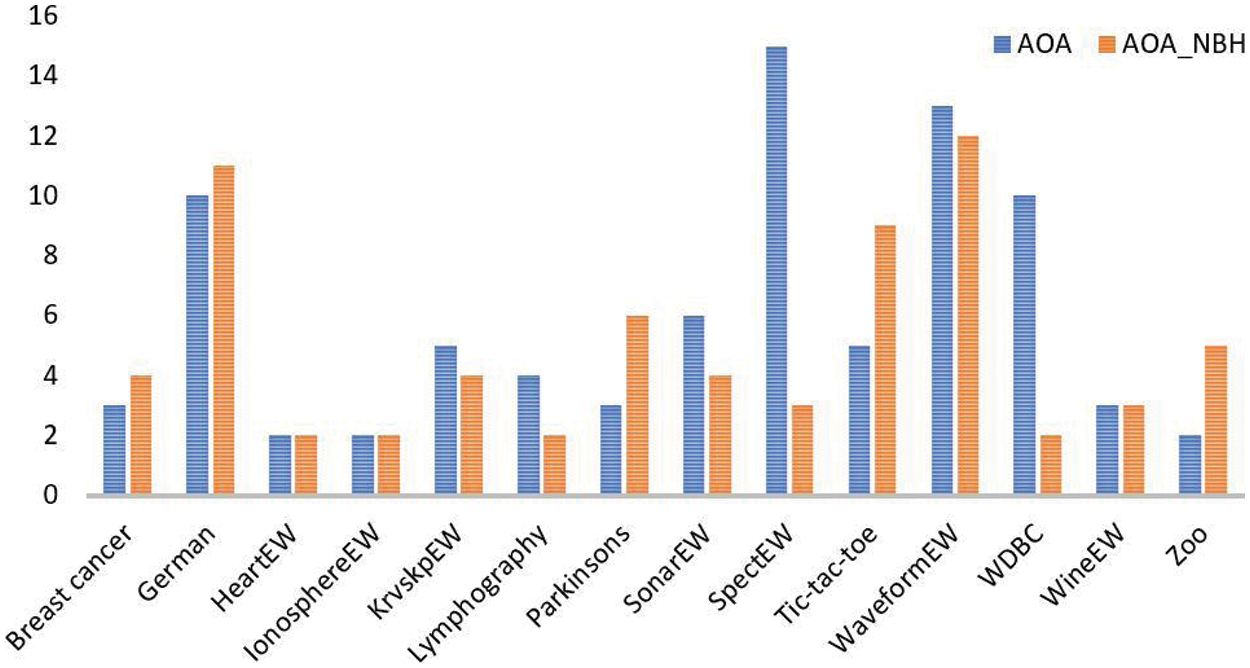
Figure 2: Comparing AOA and AOA_NBH in terms of number of selected features

This behavior may be explained by the improvement of exploitation behavior, which is improved by the local search method. This strategy focuses search efforts on promising areas in the search space rather than randomly exploiting a large and ineffective area. This local search method enables the algorithm to effectively focus on regions where substantial improvements in accuracy or feature selection may be made, leading to a more successful optimization process. The convergence behavior of both algorithms is shown in Fig. 3, which demonstrates how AOA_NBH and AOA algorithms improved in optimizing the fitness function over iterations, four dataset’s convergence curves demonstrate that AOA_NBH exhibits faster convergence than AOA in the tested datasets. We can observe that AOA_NBH was able to get the best results across the tested datasets.

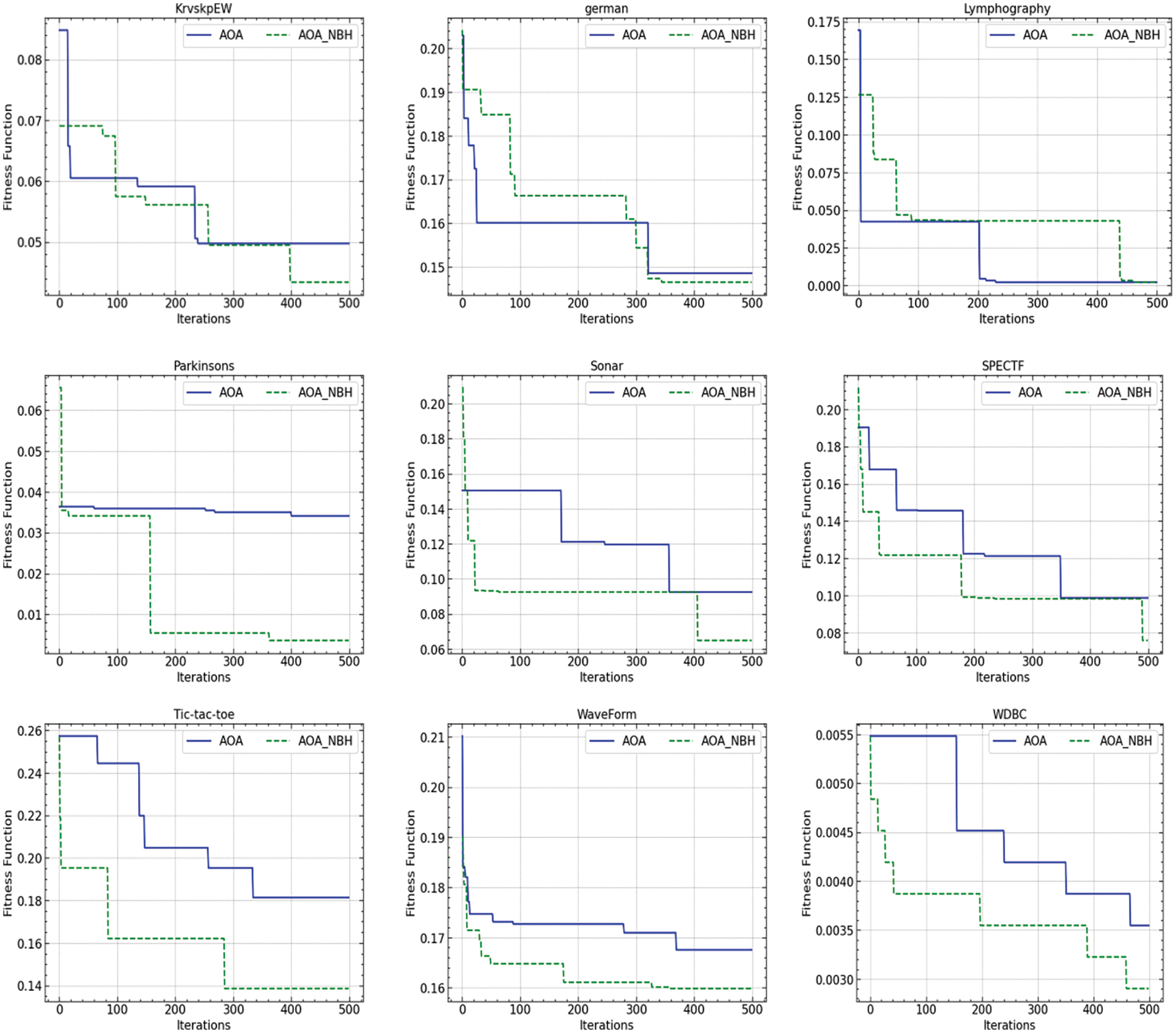
Figure 3: Convergence behavior of the AOA and the AOA_NBH algorithms

These convergence curves showed an interesting trend: across most datasets, AOA_NBH consistently showed faster convergence than the AOA method. Examining different performance metrics, including classification accuracy, fitness values, and the number of chosen features, which all continually preferred the AOA_NBH method, helped to support this acceleration in convergence.

4  Comparison with Population-Based Algorithms

From the previous section, we discovered that the AOA_NBH method outperforms the AOA in terms of the number of selected features and accuracy across all datasets. In this part, we contrast the performance of the best strategy provided with the approaches from the feature selection literature that are most closely related. The outcomes of AOA_NBH, Moth-Flame Optimization (MFO) algorithm, Whale Optimization Algorithm (WOA), particle swarm optimization (PSO) and Binary Whale Optimization Algorithm (BWOA) [32] in terms of accuracy are shown in Table 3, but the BWOA does not apply for all the mentioned datasets, so the symbol (−) means no results for these datasets.

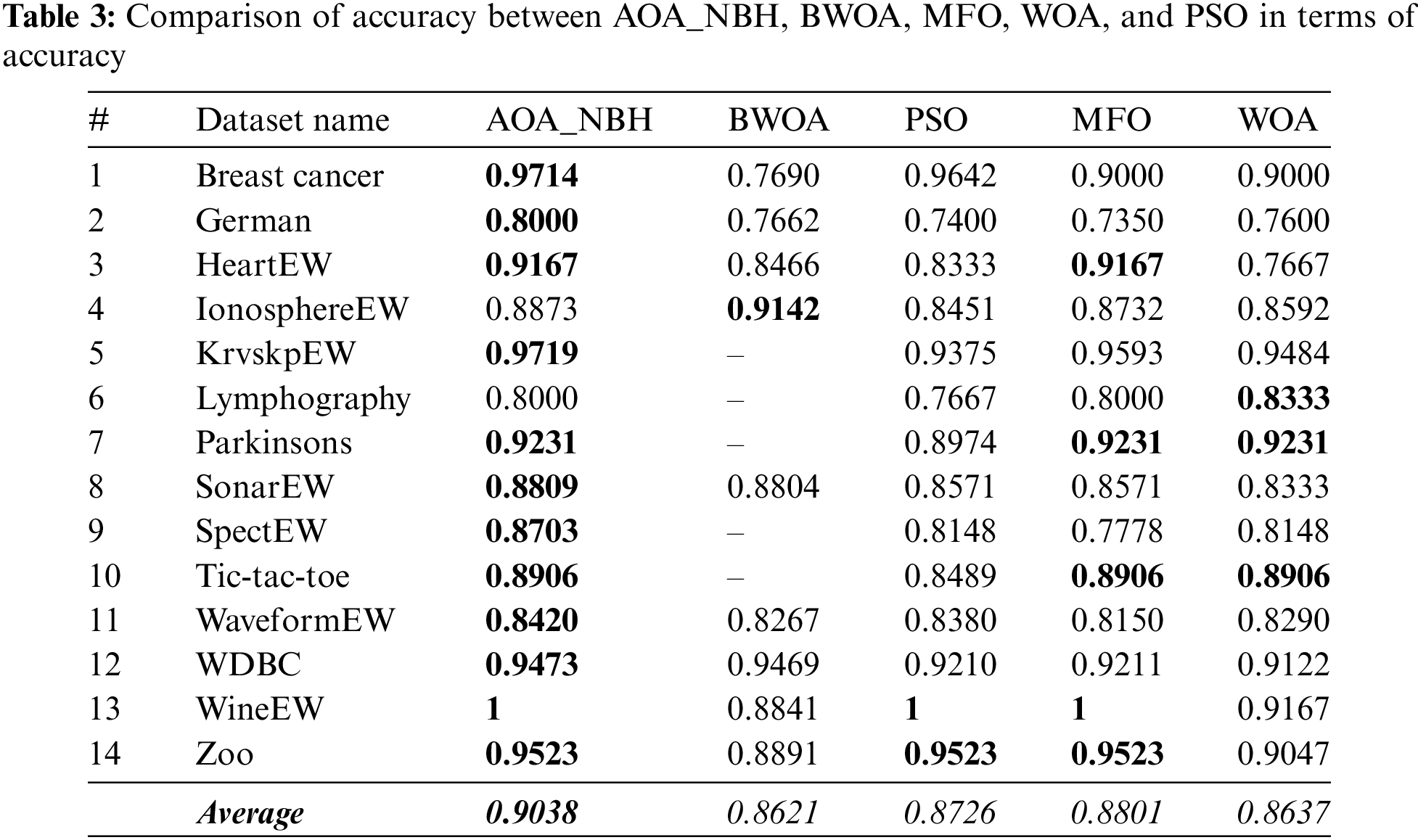
AOA_NBH performs better than other algorithms on all datasets except for two, on which WOA and BWOA perform somewhat better than other approaches while still falling short of AOA_NBH and placing second, whereas, on 86% of the datasets, AOA_NBH performs significantly better than other techniques, with an average accuracy of 90% compared to the closest approach’s accuracy of 88% for the MFO algorithm followed by PSO, WOA and BWOA algorithms with 87%, 86.37% and 86.21% average accuracy, respectively. This may be recognized by the fact that the improvement in the exploration and exploitation of AOA can explore the promising areas of the feature space.

Fig. 4 shows clearly that the AOA_NBH performs more effectively than the other algorithms (PSO, MFO, and WOA) in the majority of the datasets, however, in some datasets, similar results are obtained. Where the x-axis shows the names of the datasets and y-axis show the accuracy value.

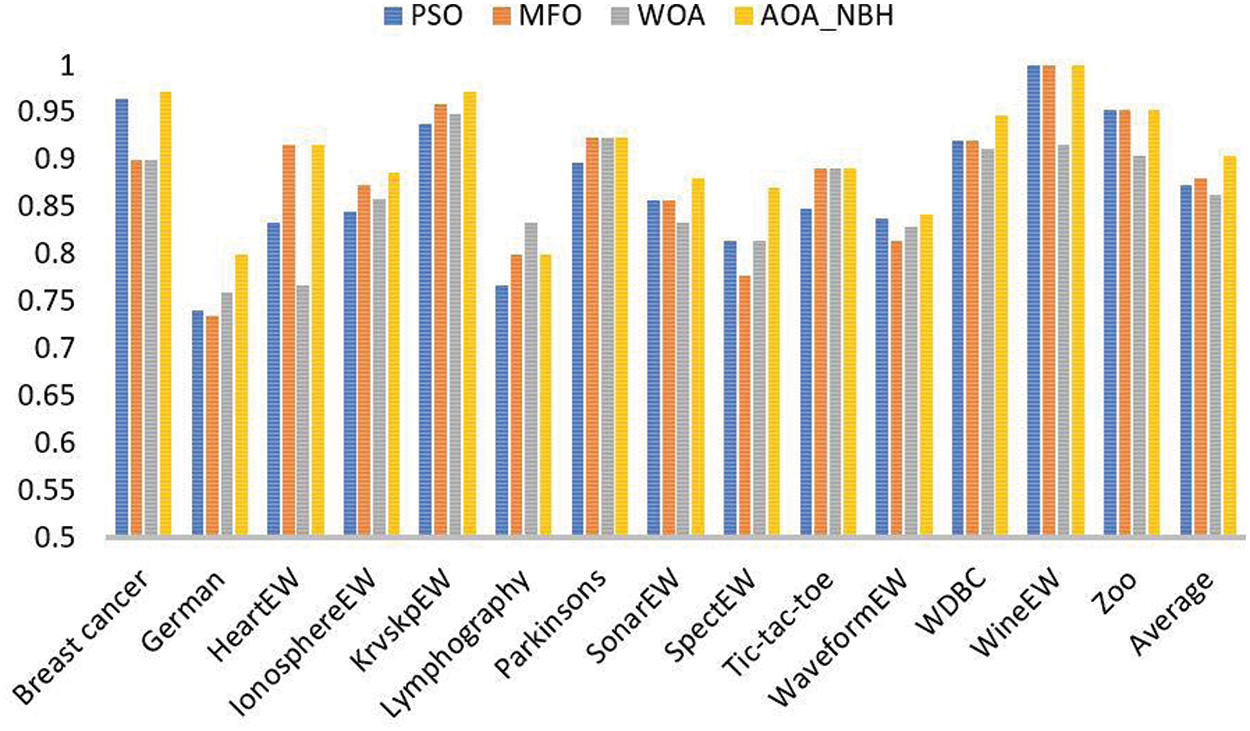
Figure 4: Comparing AOA_NBH, MFO, WOA, and PSO in terms of accuracy

As the efficiency of the proposed algorithm is shown through the results, it is useful to express the results in the form of boxes to show the capability of the proposed AOA_NBH in producing stable solutions by measuring the variation in the results on four databases. Fig. 5 represents the box plot of all algorithms using four datasets, where each algorithm has performed 10 different runs.

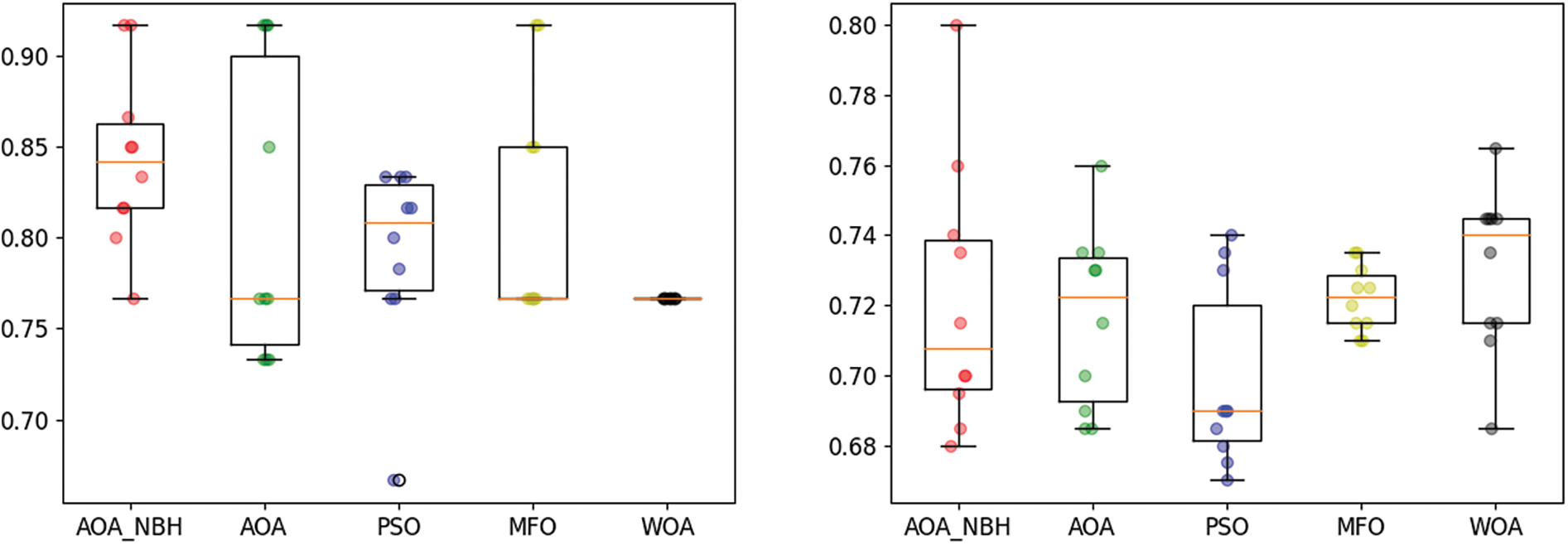
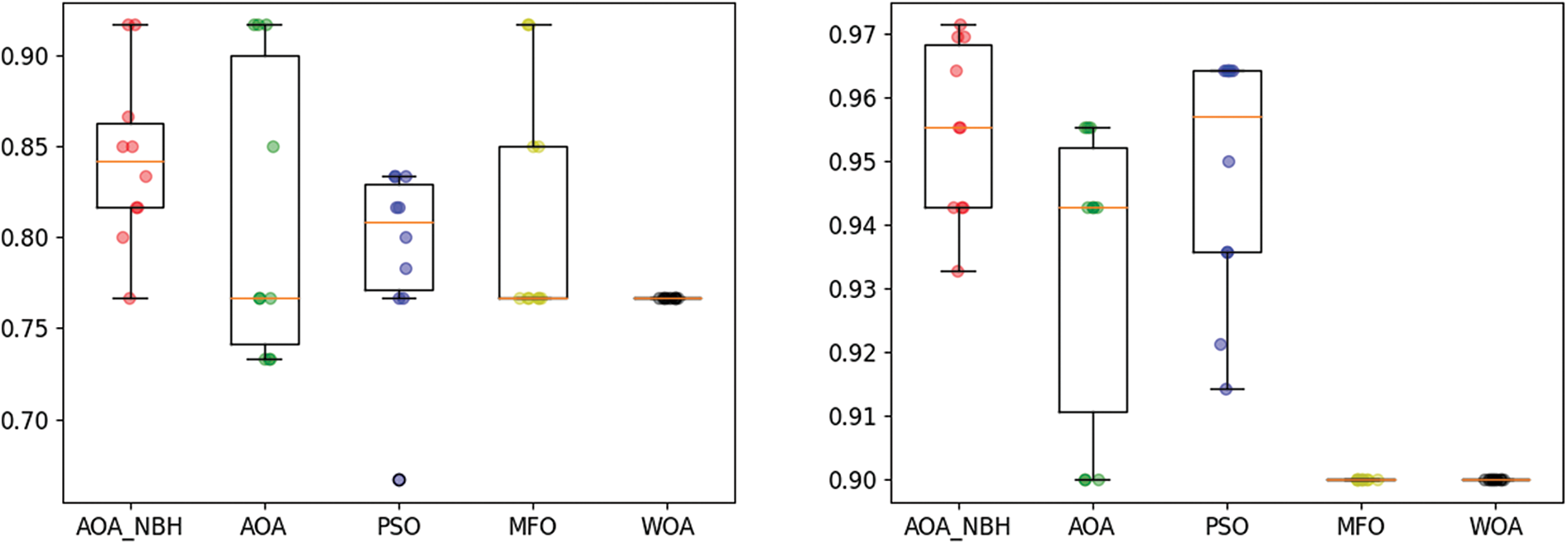
Figure 5: Boxplot of AOA_NBH, AOA, PSO, MFO, and WOA algorithms when applied on the German, Breast cancer, HeartEW, and IonosphereEW datasets

Fig. 5 shows that the median accuracies (represented by the horizontal lines inside the boxes) of the AOA_NBH algorithm when using the Breast cancer, HeartEW, and IonosphereEW datasets are greater than that of those AOA, PSO, MFO and WOA algorithms, but AOA_NBH algorithm only produced higher median accuracy than PSO when using German dataset. Also, when comparing the dispersion of the results, the interquartile ranges are reasonably small (as shown by the lengths of the boxes). In this case, the middle half of the data has little variability, though the overall range of the data set is greater for the AOA_NBH algorithm (as shown by the distances between the ends of the two whiskers for each boxplot).

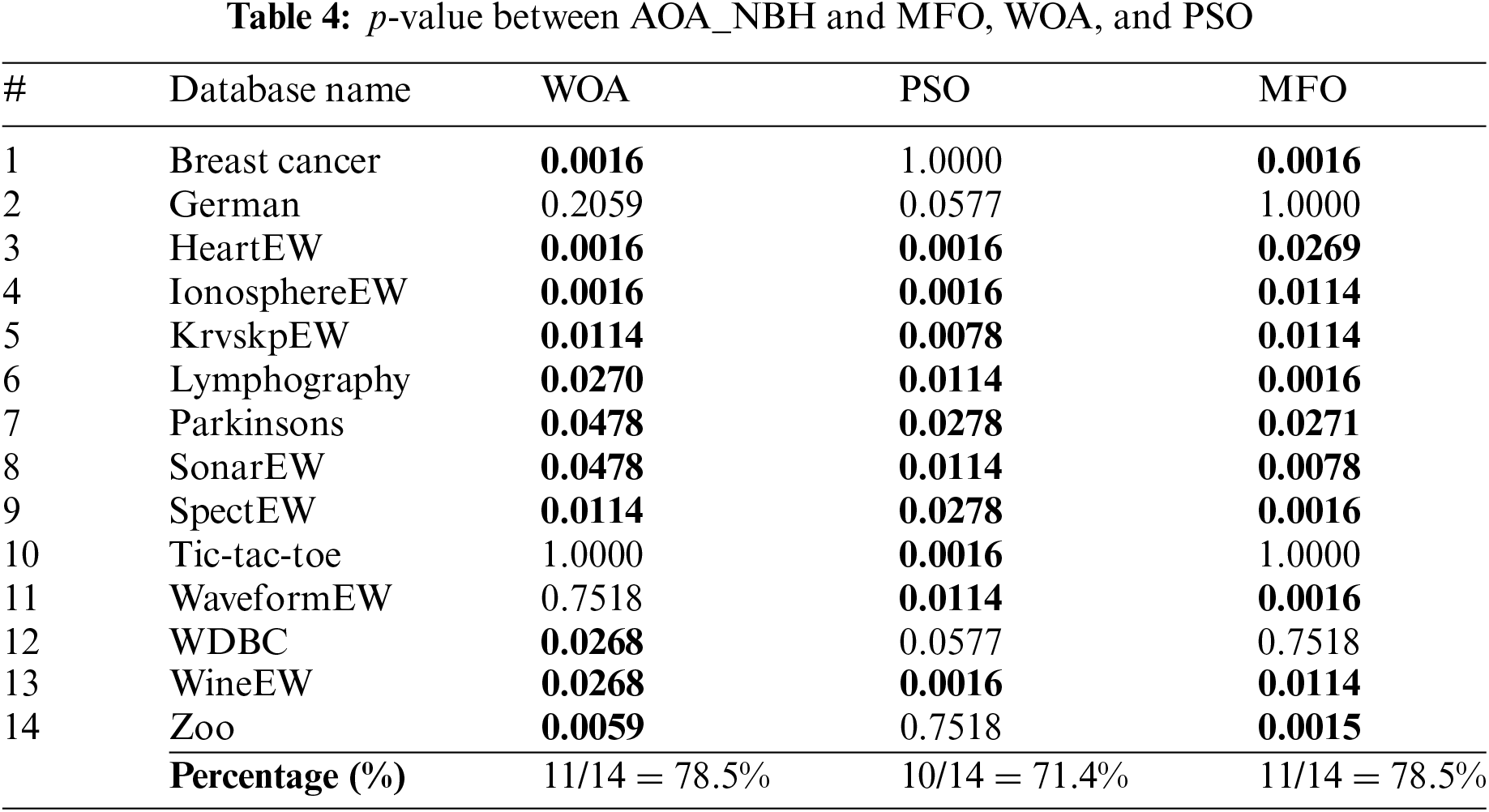
To show the significance of the results, the p-value has been frequently employed, where p-value is a numerical value obtained from a statistical test that indicates how probable it is that you would have discovered a certain collection of observations if the null hypothesis were true. To determine whether to reject the null hypothesis in hypothesis testing, p-values are employed.

In Table 4, the p-value test is applied between the AOA_NBH and WOA, AOA_NBH and PSO, and AOA_NBH and MFO, in this work, we specify significance levels based on standard thresholds which using the alpha significance level of 0.05. Statistically the results with p-values less than 0.05 are considered significant, then it can be seen clearly that the percent of the significant values are acceptable, where the significant percentage between the AOA_NBH and WOA is 78.5%, AOA_NBH and PSO is 71.4% and AOA_NBH and MFO is 78.5%. This indicates that the local neighborhood search is a significant modification on AOA algorithm, where the exploitation of AOA improved by searching effectively on the neighborhood of the best solutions in the population.

5  Conclusion and Future Works

This study presents the Arithmetic Optimization Algorithm (AOA) as a method for identifying the optimal feature subset. To address binary optimization problems, AOA is modified using a transfer function. Additionally, the feature selection problem is tackled by modifying AOA to consider two objectives: increasing prediction accuracy and reducing the number of selected features. To achieve successful searching within a large space, a local search using neighborhood search methods (NBH) is incorporated into the AOA algorithm, resulting in the AOA_NBH algorithm. The performance of the proposed methods applied to AOA is investigated using 14 common UCI benchmark datasets. Three population-based methods are compared with the results of the proposed techniques, demonstrating their superiority. The findings reveal that the suggested method converges quickly, leading to the identification of effective feature sets for most datasets. Future research could explore the effectiveness of these strategies with various real-world problems and evaluate their performance using additional classifiers.

Acknowledgement: Not applicable.

Funding Statement: No funding statement.

Availability of Data and Materials: The datasets generated and/or analysed during the current study are available: http://archive.ics.uci.edu/ml (accessed on 01/03/2024).

Conflicts of Interest: The author declares that they have no conflicts of interest to report regarding the present study.

References

1. M. Abedi and F. S. Gharehchopogh, “An improved opposition-based, learning firefly algorithm with dragonfly algorithm for solving continuous optimization problems,” Intell. Data Anal., vol. 24, no. 2, pp. 309–338, 2020. doi: 10.3233/IDA-194485. [Google Scholar] [CrossRef]

2. A. Benyamin, S. G. Farhad, and B. Saeid, “Discrete farmland fertility optimization algorithm with metropolis acceptance criterion for traveling salesman problems,” Int. J. Intell. Syst., vol. 36, no. 3, pp. 1270–1303, 2021. doi: 10.1002/int.22342. [Google Scholar] [CrossRef]

3. R. Tanabe and H. Ishibuchi, “A review of evolutionary multimodal multiobjective optimization,” IEEE Trans. Evol. Comput., vol. 24, no. 1, pp. 193–200, 2019. doi: 10.1109/TEVC.2019.2909744. [Google Scholar] [CrossRef]

4. H. Zhou, X. Wang, and R. Zhu, “Feature selection based on mutual information with correlation coefficient,” Appl. Intell., vol. 52, no. 5, pp. 1–18, 2022. doi: 10.1007/s10489-021-02524-x. [Google Scholar] [CrossRef]

5. T. Saw and W. M. Oo, “Ranking-based feature selection with wrapper PSO search in high-dimensional data classification,” IAENG Int. J. Comput. Sci., vol. 50, pp. 1, 2023. [Google Scholar]

6. Q. Gu, Z. Li, and J. Han, “Generalized fisher score for feature selection,” in 27th Conf. Uncertainty Artif. Intell., Barcelona, Spain, UAI, 2011. [Google Scholar]

7. H. F. Eid, A. E. Hassanien, T. H. Kim, and S. Banerjee, “Linear correlation-based feature selection for network intrusion detection model,” in Adv. Secur. Inf. Commun. Netw.: First Int. Conf. Cairo, Egypt, Springer, 2013, pp. 3–5. [Google Scholar]

8. L. Sun, T. Yin, W. Ding, Y. Qian, and J. Xu, “Multilabel feature selection using ML-relieff and neighborhood mutual information for multilabel neighborhood decision systems,” Inf. Sci., vol. 537, no. 4, pp. 401–424, 2020. doi: 10.1016/j.ins.2020.05.102. [Google Scholar] [CrossRef]

9. R. Leardi, R. Boggia, and M. Terrile, “Genetic algorithms as a strategy for feature selection,” J. Chemom., vol. 6, no. 5, pp. 267–281, 1992. doi: 10.1002/cem.1180060506. [Google Scholar] [CrossRef]

10. N. Alrefai et al., “An integrated framework based deep learning for cancer classification using microarray datasets,” J. Ambient Intell. Humaniz. Comput., pp. 1–12, 2022. [Google Scholar]

11. Y. Zhang, S. Li, T. Wang, and Z. Zhang, “Divergence-based feature selection for separate classes,” Neurocomputing, vol. 101, no. 4, pp. 32–42, 2013. doi: 10.1016/j.neucom.2012.06.036. [Google Scholar] [CrossRef]

12. A. Bommert, X. Sun, B. Bischl, J. Rahnenführer, and M. Lang, “Benchmark for filter methods for feature selection in highdimensional classification data,” Comput. Stat. Data Anal., vol. 143, no. 10683, pp. 9, 2020. doi: 10.1016/j.csda.2019.106839. [Google Scholar] [CrossRef]

13. J. Maldonado, M. C. Riff, and B. Neveu, “A review of recent approaches on wrapper feature selection for intrusion detection,” Expert. Syst. Appl., vol. 116822, no. 2, pp. 116822, 2022. doi: 10.1016/j.eswa.2022.116822. [Google Scholar] [CrossRef]

14. M. Alwohaibi, M. Alzaqebah, N. M. Alotaibi, A. M. Alzahrani, and M. Zouch, “A hybrid multi-stage learning technique based on brainstorming optimization algorithm for breast cancer recurrence prediction,” J. King Saud Univ.-Comput. Inf. Sci., vol. 34, no. 8, pp. 5192–5203, 2022. [Google Scholar]

15. E. A. N. Benhlima, “Review on wrapper feature selection approaches,” in Int. Conf. Eng. MIS (ICEMIS), IEEE, 2016, pp. 1–5. [Google Scholar]

16. M. K. Alsmadi et al., “Cuckoo algorithm with great deluge local-search for feature selection problems,” Int. J. Electr. Comput. Eng., vol. 12, no. 4, pp. 2088–8708, 2022. [Google Scholar]

17. M. Alzaqebah, S. Jawarneh, R. M. A. Mohammad, M. K. Alsmadi, and I. Almarashdeh, “Improved multi-verse optimizer feature selection technique with application to phishing, spam, and denial of service attacks,” Int. J. Commun. Netw. Inf. Secur., vol. 13, no. 1, pp. 76–81, 2021. [Google Scholar]

18. Y. C. Wang, J. S. Wang, J. N. Hou, and Y. X. Xing, “Natural heuristic algorithms to solve feature selection problem,” Eng. Letters, vol. 31, pp. 1, 2023. [Google Scholar]

19. X. F. Song, Y. Zhang, D. W. Gong, and X. Z. Gao, “A fast hybrid feature selection based on correlation-guided clustering and particle swarm optimization for high-dimensional data,” IEEE Trans. Cybern., vol. 52, no. 9, pp. 9573–9586, 2021. doi: 10.1109/TCYB.2021.3061152. [Google Scholar] [PubMed] [CrossRef]

20. P. Rani, R. Kumar, A. Jain, and S. K. Chawla, “A hybrid approach for feature selection based on genetic algorithm and recursive feature elimination,” Int. J. Inf. Syst. Model. Design (IJISMD), vol. 12, no. 2, pp. 17–38, 2021. doi: 10.4018/IJISMD. [Google Scholar] [CrossRef]

21. S. Chattopadhyay, R. Kundu, P. K. Singh, S. Mirjalili, and R. Sarkar, “Pneumonia detection from lung x-ray images using local search aided sine cosine algorithm based deep feature selection method,” Int. J. Intell. Syst., vol. 37, no. 7, pp. 3777–3814, 2022. doi: 10.1002/int.22703. [Google Scholar] [CrossRef]

22. M. Ghosh, S. Malakar, S. Bhowmik, R. Sarkar, and M. Nasipuri, “Memetic algorithm-based feature selection for handwritten city name recognition,” in Comput. Intell. Commun., Bus. Anal.: First Int. Conf., Kolkata, India, 2017, pp. 24–25. [Google Scholar]

23. M. G. Altarabichi, S. Nowaczyk, S. Pashami, and P. S. Mashhadi, “Fast genetic algorithm for feature selection—a qualitative approximation approach,” Expert. Syst. Appl., vol. 211, no. 11852, pp. 8, 2023. doi: 10.1145/3583133. [Google Scholar] [CrossRef]

24. E. Pashaei and E. Pashaei, “Hybrid binary arithmetic optimization algorithm with simulated annealing for feature selection in highdimensional biomedical data,” J. Supercomput., vol. 78, no. 13, pp. 15598–15637, 2022. doi: 10.1007/s11227-022-04507-2. [Google Scholar] [CrossRef]

25. A. A. Ewees et al., “Boosting arithmetic optimization algorithm with genetic algorithm operators for feature selection: Case study on cox proportional hazards model,” Mathematics, vol. 9, no. 18, pp. 2321, 2021. doi: 10.3390/math9182321. [Google Scholar] [CrossRef]

26. E. Emary, H. M. Zawbaa, and A. E. Hassanien, “Binary ant lion approaches for feature selection,” Neurocomputing, vol. 213, no. 6, pp. 54–65, 2016. doi: 10.1016/j.neucom.2016.03.101. [Google Scholar] [CrossRef]

27. A. W. Mohamed and H. Z. Sabry, “Constrained optimization based on modified differential evolution algorithm,” Inf. Sci., vol. 194, no. 6, pp. 171–208, 2012. doi: 10.1016/j.ins.2012.01.008. [Google Scholar] [CrossRef]

28. D. E. Goldberg, B. Korb, and K. Deb, “Messy genetic algorithms: Motivation, analysis, and first results,” Complex Syst., vol. 3, no. 5, pp. 493–530, 1989. [Google Scholar]

29. G. Sanchita and D. Anindita, “Evolutionary algorithm-based techniques to handle big data,” in Techniques and Environments for Big Data Analysis, 2016, vol. 17, pp. 113–158. [Google Scholar]

30. D. Dua and C. Graff, UCI Machine Learning Repository. University of California, School of Information and Computer Science, 2019. Accessed: Jun. 2, 2023. [Online]. Available: http://archive.ics.uci.edu/ml. [Google Scholar]

31. J. Friedman, T. Hastie, and R. Tibshirani, “Additive logistic regression: A statistical view of boosting (with discussion and a rejoinder by the authors),” Annals Stat., vol. 28, no. 2, pp. 337–407, 2000. doi: 10.1214/aos/1016218223. [Google Scholar] [CrossRef]

32. A. G. Hussien, A. E. Hassanien, E. H. Houssein, M. Amin, and A. T. Azar, “New binary whale optimization algorithm for discrete optimization problems,” Eng. Optim., vol. 52, no. 6, pp. 945–959, 2020. doi: 10.1080/0305215X.2019.1624740. [Google Scholar] [CrossRef]