Performance Evaluation of Multi-Agent Reinforcement Learning Algorithms

1  Introduction

The collaborative Multi-agent Reinforcement Learning (MARL) approach has been seen to be highly applicable in a range of domains in Reinforcement Learning (RL), such as self-driving cars [1], sensor networks [2], robot swarms [3,4], and video games [5,6]. RL is a form of machine learning in which an individual or a group of individuals perform a repeated action in a given setting. Agents acquire knowledge of the behavior through experimentation and trial. The agent must decide if they should take the greatest reward immediately or search for states that may generate larger rewards, despite the delayed outcome. Agents learn through obtaining rewards for desirable behaviors and punishments for undesirable ones, which are referred to as collisions. The RL applies the Markov Decision Process (MDP) framework [7] to solve a decision-making problem and discover the optimal policy through the Q-learning function [8] to estimate the value function and pick an action that gives the highest expected rewards. The unique architecture of the deep Q-learning Network (DQN) was defined, which is a different kind of deep neural network (DNN) for dynamic programming functions [9]. The latest successful autonomous agent algorithms that have been used for controlling the single agent like the Proximal Policy Optimizer (PPO) algorithm [10] have been extended to the Multi-agents PPO (MAPPO) [11] algorithm for controlling the MARL in a specific environment.

A MARL system is multiple distributed entities called agents that make decisions autonomously and communicate within a shared environment [12]. Every agent is trying to search to reach an assigned goal for which a broad set of skills might be required to build intelligent behavior. For that, RL has been adapted as a learning framework to provide the required skills for the agents. All agents seek to fulfill their designated objective, requiring an extensive range of abilities to form intelligent behavior. RL has adapted as an educational structure to give the agents the abilities. Depending on the task, a complex interaction between agents may occur, which could result in agents working together or competing against each other to outperform other competitors. Various MARL algorithms have been used to solve multi-agent cooperative problems in the StarCraft Multi-Agent Challenge (SMAC) platform, like the MAPPO algorithm, and the two popular Centralized Training with Decentralized Execution algorithms, the Value-Decomposition Network (VDN) algorithm [13], Q-learning with Mixtures of Experts (QMIX) [14], and Multi-agent Actor Attention Critic (MAA2C) algorithm [15]. Creating a strong MARL system is possible by making use of neural network functions. It is essential to have a reliable environment to train our agents. Training multiple agents can be conducted through the use of various MARL environments. Various MARL environments can be used for training the multiple agents: The Hanabi Challenge [16], OpenAIGym [17], and the most challenging environment SMAC environment [18]. To Build a strong MARL system using neural network function approximations, such as QMIX, VDN, MAA2C, and MAPPO algorithms, we need a strong environment to train our agents in. The SMAC environment has been noted as the optimal context for the MARL system [19].

In this paper, we will use the SMAC environment to train the four MARL algorithms: QMIX, VDN, MAA2C, and MAPPO. The multiple agents will be trained in defending and attacking scenarios in two different SMAC MAPs. The agents will learn how to cooperate to win the match with minimum damage. The performance of the four chosen algorithms was compared to decide which one does better in the chosen environment. The rest of the paper is organized as follows. In Section 2, we discuss the related research and relevant work. In Section 3, we present the proposed method. In Section 4, we present the results, discussion, and limitations. The conclusion is presented in Section 5.

2  Related Works

2.1 Single-Agent Reinforcement Learning

The MDP is one of the most well-known single-agent RL methods, which follows a sequence of decision-making under uncertain conditions that depicts the relationship between an agent and its environment. The second single-agent is the value-based approach, which uses value functions; these functions comprise the state-value function and the action-value function, also known as the Q-function [20]. A popular network that uses this method is DQN. The third method is the model‑based method. Model-based approaches learn a model of the environment that captures the transition and reward function. The agent can then use planning to construct the trajectories and use the model to find the optimal policy [21]. In our recent work, we employed the PPO algorithm to train a single agent to explore the environment and avoid obstacles with minimal collisions [22,23].

2.2 Centralized Training with Decentralized Execution

The Centralized Training with Decentralized Execution (CTDE) paradigm presents the state-of-the-art practice MARL [24]. Agents in the CTDE may communicate and access global information with each other while being trained; however, this is not allowed during execution. Recently, the use of CTDE for training and execution has become more common. There has been a growing interest in the CTDE paradigm in recent years. Some popular algorithms that use the CTDE paradigm are the Counterfactual Multi-Agent (COMA) algorithm [25], the VDN algorithm, and the QMIX algorithm. All these algorithms used the CTDE paradigm that was introduced in 2018. The VDN algorithm was the first to attempt in this field, adopting the summation operation, and the QMIX algorithm uses the Q-values with a non-linear function of the global state. In MARL, multiple agents interact with a specific environment and try to reach the destination autonomously. The popular CTDE algorithm that has been used for solving MARL problems is the QMIX and VDN algorithms. The VDN algorithm was the first attempt to allow for centralized value-function learning with decentralized execution [26].

2.3 MARL Algorithms

In MARL, multiple agents interact with a specific environment and try to reach the destination autonomously. Various algorithms can be used for training multiple agents like QMIX, VDN, MAA2C, and MAPPO. The recommended function that has been used in RL algorithms is the Q-learning function. Q-learning is used to learn the optimal action-selection policy for an agent in the MDP environment. The Q-learning function is a value-based method that learns the optimal action-value function by iteratively updating the Q-values of state-action pairs using the Bellman equation. QMIX is a MARL algorithm that was proposed in 2018. QMIX is a value-based approach that extends the regular Q-learning algorithm to handle multi-agent systems of a large scale with non-linear interactions and intricate coordination problems. In QMIX, each agent keeps a record of its Q-value function, which depends on its state and action, as well as the joint state of all agents that is summarized by the global state. The global state is represented as a combination of local states with each weight being gained by a distinct expert network. The expert networks are used to connect the local states of each agent to a global state representation, which is then employed to compute the Q-values. The major advantage of QMIX is that it can handle large-scale multi-agent systems and complex coordination problems. Additionally, QMIX can learn successful coordination approaches that are not restricted to predefined communication or coordination protocols. QMIX outperforms several state-of-the-art MARL algorithms, especially in SMAC environments. In [27], QMIX algorithms were used to address the problem of multiple agents’ cooperative control in complex scenarios.

VDN is also a MARL algorithm that was proposed in 2018. VDN is an approach that takes advantage of the traditional Q-learning algorithm and makes use of value-based principles to handle multi-agent systems. It does this by breaking down the global Q-value function into individual Q-value functions. Every agent in VDN upholds its Q-value function, which is conditional on its state, action, and joint state that captures the state of all agents. The global Q-value function is then computed as the sum of the local Q-value functions of all agents. The major advantage of VDN is that it can process large multi-agent systems in a decentralized way, without needing any interaction or coordination between agents. This allows VDN to scale large numbers of agents and effectively learn coordination strategies in complex environments. VDN has achieved excellent performance on several benchmark tasks, including the SMAC environment. It has achieved competitive results compared with other state-of-the-art algorithms. In [28], the VDN algorithm was employed to accomplish a multi-agent task in a set of decomposable games, to reach an optimal Q-function value.

MAPPO algorithm is a MARL algorithm that was proposed in 2019. It assigns each agent their policy network, which is responsible for transforming the agent’s observations into a probability distribution regarding the actions they will take. All agents’ policies are trained together using a centralized critical network, which evaluates the value of the combined state and action space. One of the major benefits of MAPPO is that it can manage large-scale multi-agent systems independently, with no need for agents to communicate or coordinate with each other. This enables MAPPO to accommodate a high number of agents and effectively comprehend coordination strategies in intricate surroundings. MAPPO has proven to be successful on a variety of benchmark tasks, including the SMAC environment, and it has achieved competitive results with other state-of-the-art MARL algorithms. In [11], MAPPO achieves high performance in the popular multi-agent environment StarCraft II.

The MAA2C is a reinforcement learning algorithm used for training multiple agents to perform a specific task. The MAA2C algorithm is an extension of the Advantage Actor-Critic (A2C) [29] reinforcement learning algorithm that works to handle multiple agents’ tasks, optimize the policy for all agents, and learn the policies that maximize the expected reward. MAA2C agents receive their observations from the environment and can use this information to update their policy and decide an action. The agents’ policies are updated in parallel, using the A2C algorithm to maximize the expected reward. The algorithm has a shared value function, which computes the predicted reward for all the agents and is used to determine the advantage values for each agent. The MAA2C approach has been employed in cooperative activity for multi-agent games like SMACLite [30]. It has shown promising results in improving the coordination and performance of multiple agents working together to achieve a common goal. In [31], the MAA2C algorithm showed an outstanding performance in terms of the total throughput in a multi-device-to-device (D2D) cellular communication system as an environment for multi-agent.

2.4 MARL Virtual Reality Environments

Different MARL environments have been created to support research and the development of new technologies, offering a wide range of options such as the Hanabi Challenge, OpenAI Gym, and SMAC. Hanabi Challenge is a multi-agent environment for evaluating the ability of agents to learn to communicate and collaborate effectively. It was introduced in 2018 and has become a popular benchmark environment for MARL research. In the game Hanabi Challenge, players collaborate to arrange cards into colorful ``fireworks" by following a specific order. Each player has cards in their hand that they can see, while the cards held by the other players remain unseen. Players should interact with each other to give a hint about the cards they hold and what actions they should take, at the same time being aware of the cards that have already been played. The game aims to acquire the highest score possible by playing as many cards as possible and to avoid any missteps that would cause the game to finish. The game is hard to master due to the requirement of players to combine playing cards with giving accurate hints while avoiding errors, which requires effective communication and cooperation.

The OpenAI Gym is a popular open-source toolkit for developing and comparing RL algorithms. It has a set of environments for testing and assessing reinforcement learning algorithms, including classic control tasks, Atari games, robotics tasks, and the most recent multi-agent environments. The OpenAI Gym has been constructed to give RL algorithms a consistent interface to access. Every environment has defined observation and action spaces, a reward function, and an ending condition. OpenAI Gym offers convenient compatibility with many reinforcement learning frameworks and algorithms. It also offers a unified approach to evaluate the proficiency of multiple RL algorithms across a broad array of tasks. The multi-agent environments in OpenAI Gym provide a challenging platform for evaluating the performance of MARL algorithms in complex and dynamic environments.

SMAC is a virtual environment used for training and testing the MARL algorithms in a strategy game known as StarCraft II. SMAC is an expansion of the StarCraft II Learning Environment (SC2LE) and presents multiple challenging exercises that require sophisticated coordination and strategic skills. Agents in SMAC must move through a complex landscape and constructions and join forces to reach a shared goal. This landscape shows a variety of activities, such as safeguarding a base from enemy action and attacking the enemy base. Agents need to understand and utilize successful communication as well as collaboration procedures and show adept planning and decision-making capabilities. SMAC offers a testing environment that is both realistically demanding and challenging for the assessment of MARL algorithms because it requires that agents learn to communicate and cooperate in a complicated environment. It also provides a flexible platform for developing and testing new MARL algorithms.

The above-mentioned Virtual Reality (VR) environment is an example but not limited number of the available testing and training environments in VR form.

3  Methodology

This section will discuss the tool that has been used for the training, the four MARL algorithms, and the SMAC training environment. The method that we will explain in this section can be used to design multi-agent systems, such as drones [32].

3.1 Training Platform (Epymarl)

In this work, the Epymarl tool [33] has been used to train four algorithms VDN, QMIX, MAA2C, and MAPPO in the SMAC environment. Epymarl has almost all the MARL algorithms available to use and is compatible with many MARL environments, especially the SMAC environment. Epymaral is stable because it is PyTorch base and gives more reasonable metrics for any scenarios like a battle won mean, dead allies mean and dead enemies mean. For the software components that have been used in this work, we use Ubuntu 20.04 Python 3.8, with PyTorch 1.7.1 [34], and the CUDA Toolkit 11.7.1 [35]. The hardware that we used for the training in this work is CPU Cor i7 11800H, with 32 GB RAM and RTX 3080 laptop GPU, with CUDA Toolkit 11.7.1, and PyTorch 1.7.1.

3.2 Algorithms

In this work, VDN, QMIX, MAA2C, and MAPPO algorithms have been used to train multiple agents in the SMAC environment. We have chosen two scenarios from the SMAC environment (attacking and defending) to train. All the agents learn how to work with other agents in a specific scenario and every algorithm gives a different result. All the algorithms have been trained for two million iterations in the two scenarios, and at the end, a comparison was made to choose the best-performing algorithm for each scenario.

3.3 Training Environment (SMAC)

We have chosen the SMAC environment as a training environment for training VDN, QMIX, MAA2C, and MAPPO algorithms. This environment contains a lot of different maps. We have chosen two maps: The first one represents the attacking scenario called SMAC_MAP_3M, and the second is named SMAC_MAP_Corridor, which represents the defending scenario. In the attacking scenario, the agent learned how to cooperate with the other agent and attack the enemies to win with less damage, while in the defending scenario, the agents learned how to stay alive as much as possible and assist the other agents to win the game. Reinforcement learning agents are trained to perform specific actions in a particular environment, and those actions can be repeated in different scenarios in another environment. The idea of attack and defense could potentially apply to the study of mobile attacks in cooperative learning as well [36]. Fig. 1 shows the initial status of each environment, where Fig. 1A illustrates the attacking scenario environment, and Fig. 1B illustrates the defending scenario environment. For The SMAC_MAP_3M, the four algorithms trained 3 agents against 3 enemies, and we call this the simple scenario because we have three vs. three agents. While in the defending scenario map (Corridor), is a complex scenario because we have 6 trained agents against a huge wave of enemies. We had trained agents to perform a cooperative strategy for attacking or defending and winning the match with less damage. In the first scenario, multiple agents were trained to learn the art of attacking and the second scenario trained them on defending tactics. The agents were instructed to attack and defend to achieve success with minimal harm. VDN, QMIX, MAA2C, and MAPPO algorithms were employed to train the multiple agents in the SMAC environment. Attaching and defending scenarios were chosen to examine the performance of the four algorithms in the SMAC environment. The two scenarios utilized the same algorithms, but they were trained with different concepts. This enables a better evaluation of the performance of each algorithm in guiding and accomplishing tasks with two types of performing teams, attacking team, and defending team. The attacking environment method is illustrated in Fig. 2A and the defending procedure is outlined in Fig. 2B. The amount of reward each agent obtains depends on their survival and if their team has won. Finally, the most successful action was considered for agents in the next rounds.

Figure 1: Shows the initial status for the two environments used in this work, where (A) represents the SMAC map that has been used for the attacking scenario named MAP_3M, and (B) SMAC_MAP_Corridor represents the environment that was used for the defending scenario

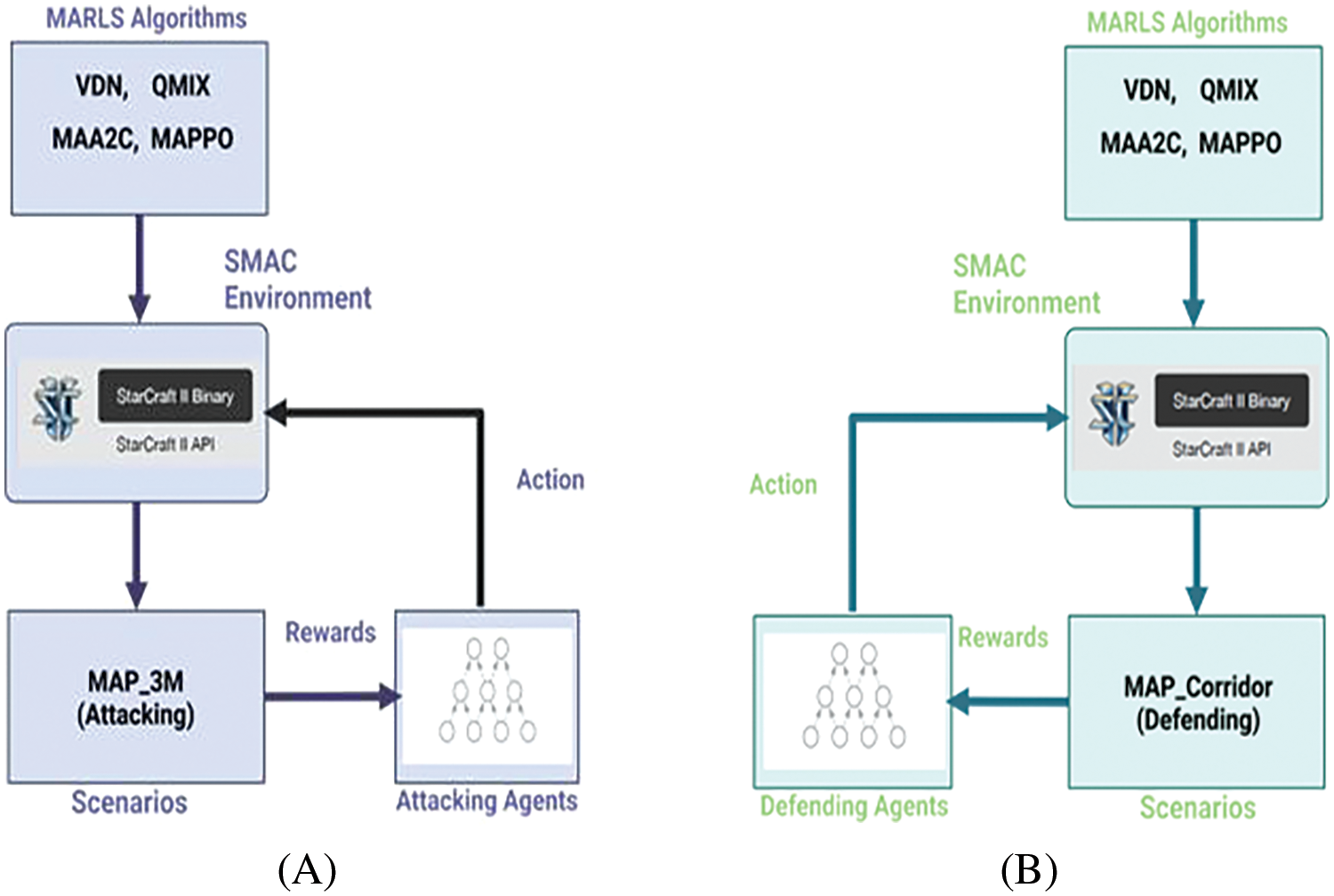
Figure 2: The method of this work, where (A) represents the structure of training multiple agents in the attacking scenario, and (B) represents the structure of training multiple agents in the defending scenario

In Table 1, we summarize our method of this work; we have trained MARL algorithms like VDN, QMIX, MAA2C, and MAPPO, to design multiple agents’ systems, and every agent was trained for two in two scenarios attacking and defending. We have classified the 3M map as a simple task for the agents because it is only 3 trained agents attacking 3 enemies. The Corridor map has been classified as a complex task because 6 trained agents defended their position against 24 enemies, and held their position as much as they could to win the match. Later, the algorithm that gives the highest result is chosen as the best one.

4  Results

In this section, we will review the research results for our algorithms, and compare them. We have trained the four algorithms in the SMAC environment.

4.1 The Attack Scenario Results

SMAC map 3M has been used as a training environment to train our algorithms and construct an agent that can work together with other agents to win the game. The win in this scenario is not the only factor in judging the algorithms. It is necessary to analyze which algorithm achieved the highest result and the rate at which the algorithms operated. Fig. 3 shows a screenshot from the simple task environment MAP_3M, the green lines represent the agent’s attacking direction. During the training process with this map, the three agents begin their search for the target, as shown in Fig. 3A. Some of these agents were able to find the target and initiate the cooperative attack, as shown in Fig. 3B. Finally, the three agents attack the enemy together, as shown in Fig. 3C.

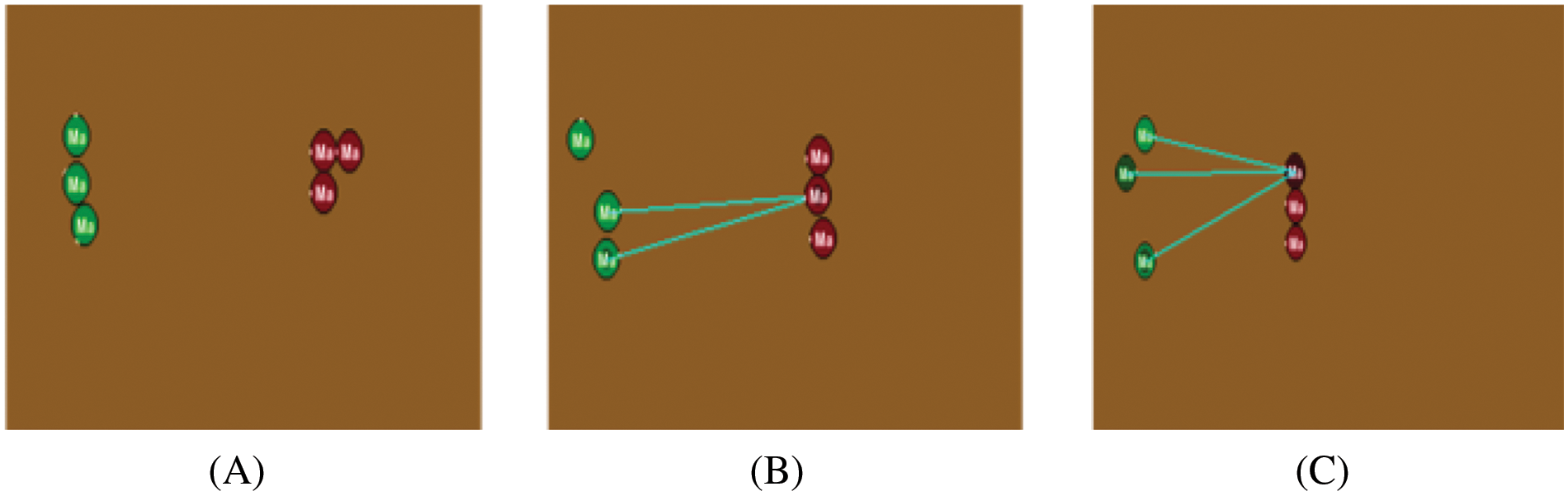
Figure 3: Screenshot from the training of the attacking scenario SMAC map 3M (Simple task), the three green circles represent the training agent, and the three red circles represent the enemies, (A) the agents start to search for the target. (B) Two of the agents could find the target and start the cooperative attack. (C) All three agents attack the target

We created one model for each algorithm to evaluate which algorithm offers the best performance for the Simple attacking scenario. The four algorithms (MAA2C, MAPPO, QMIX, and VDN) were trained with two million iterations of training. The performance and speed of our algorithms were evaluated by considering the value of battle won mean, dead allies mean, and dead enemies mean metrics in this situation. These metrics represent the amount of victory achieved by each agent for each algorithm in each match. The QMIX algorithm was identified as producing the highest value, with a reliable increase compared to other algorithms. The VDN algorithm provides the second greatest value for the battle Won mean, and this increase is more reliable than what was seen in the MAA2C and MAPPO algorithms.

This work reported that MAPPO and MAA2C algorithms had the poorest performance, but MAA2C outperformed MAPPO, with MAPPO’s result dropping from 0.6 to 0.1 while MAA2C held on 0.5 at the latter stages of training. According to the battle-won mean value comparison, the QMIX and VDN algorithms give the best results, while the MAA2C was more effective than MAPPO. Fig. 4 shows the value of the battle won mean for each algorithm.

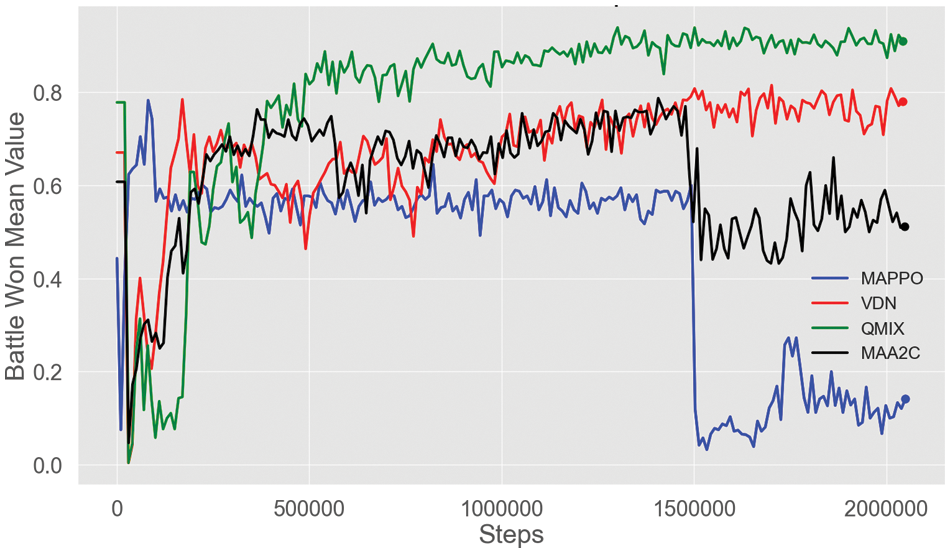
Figure 4: The battle won means comparison for the four algorithms in SMAC map 3M MAPPO with blue, VDN with red color, QMIX with green color, and MAA2C with black color

We employed the Max function to identify the maximum value of the battle won mean achieved for every algorithm and at which iteration. At iteration number 1,301,528, the QMIX algorithm achieved the highest battle-won mean of 0.939 in the training, while the VDN algorithm got the second highest value of the battle-won mean of 0.815 at iteration number 1,701,973. The MAA2C and MAPPO algorithms produced nearly identical outcomes, the MAA2C achieving the third greatest value for the battle won mean at iteration number 1,407,231 with a value of 0.787, and the MAPPO algorithm achieving the weakest result of 0.782 at iteration 81,193. The QMIX algorithm was the best one and the MAPPO was the worst one. During the initial stages of training any machine learning algorithm, it is not in a stable state. Our selected algorithms (MAPPO, VDN, QMIX, MAA2C) achieve stability after 500,000 iterations. The long-term stability of the algorithm is important to demonstrate its performance and accuracy. However, neither MAPPO nor MAA2C exhibit such stability.

The results of the battle won demonstrate that the QMIX and VDN algorithms provide the highest performance in this scenario. The meaning of the dead allies means metric gives how many trained agents have been killed in one iteration, while the meaning of the dead enemies means gives how many enemies have been killed in each iteration. Fig. 4 illustrates a comparison of the mean values of dead allies and dead enemies for the four algorithms over two million iterations. The highest performing algorithm produces the lowest value of dead allies mean and should generate the highest value of dead enemies mean too. Our investigation demonstrated that the QMIX algorithm had the lowest value of dead allies mean and the highest value of dead enemies mean, while the VDN algorithm provided the second lowest value for the dead allies and the second highest value for the dead enemies. For the MAA2C and MAPPO algorithm, MAA2C got third place for both dead allies and dead enemies, while the result of the MAPPO was the worst in this work for the attacking scenario. QMIX and VDN algorithms were given the best result for both dead allies and dead enemies in this scenario.

The Min function was employed to identify the minimum value of dead allies mean and the number of iterations that occurred, while the Max function was employed to identify the maximum value of dead enemies mean. QMIX algorithm got the lowest value in Fig. 4A with value 0.593 and got the maximum value in Fig. 4B with value 2.923, both at iteration number 1,902,029, and the VDN algorithm got the second lowest value in Fig. 5A with value 1.117 and achieved the second biggest value in Fig. 5B with value 2.754 at iteration number 1,501,765. while the MAA2C and MAPPO algorithms’ results were the worst in this work, the MAA2C got the third lowest value in Fig. 5A with a value of 1.917 and the third highest value in Fig. 5B with value equal to 2.785 at iteration number 1,245,522, while the MAPPO algorithm got a value equal to 1.982 in Fig. 5A and in Fig. 5B 2.768 both at iteration 81,193. According to the results of Figs. 5A and 5B, the QMIX and VDN algorithms give the best value, making them the best algorithms in this work for the attacking scenario with SMAC map_3M.

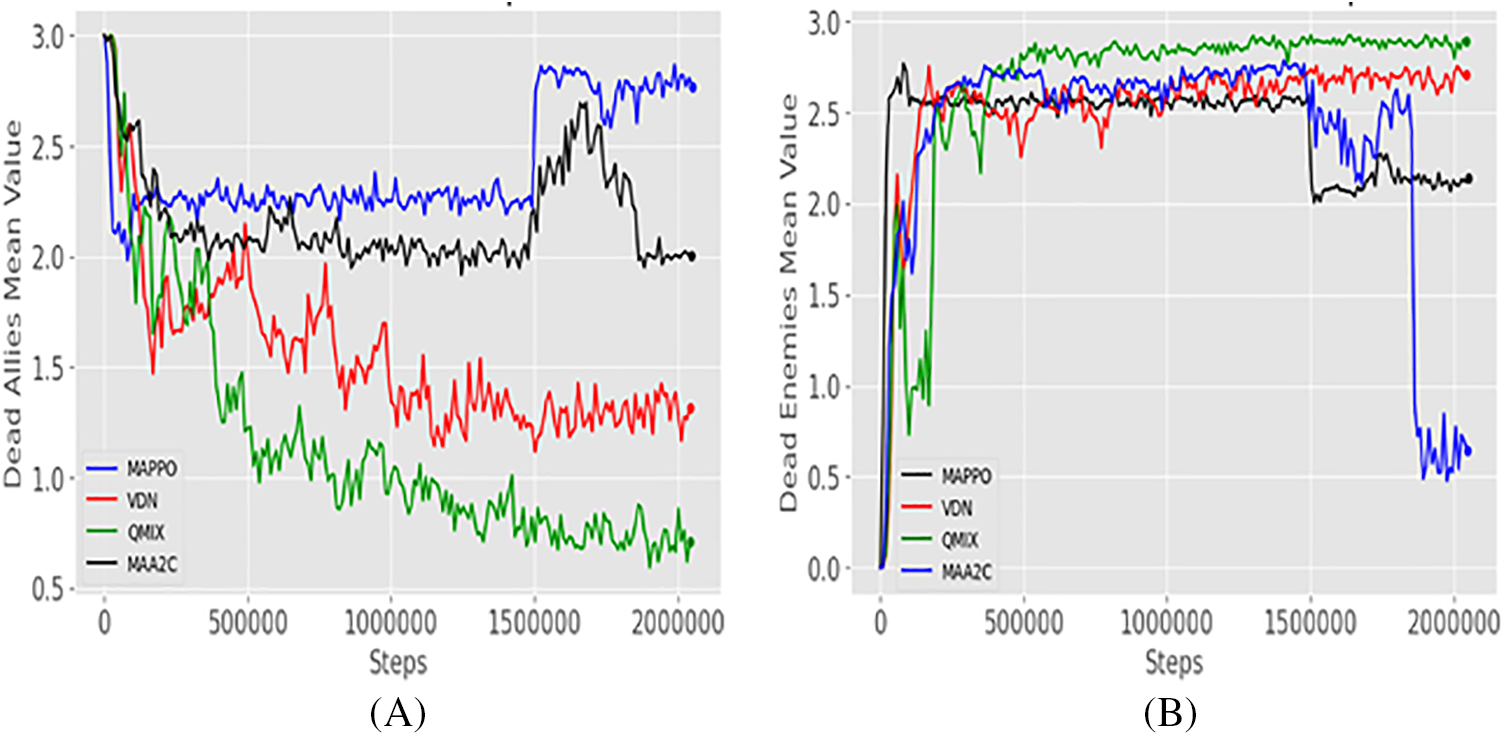
Figure 5: (A) Dead allies mean, and (B) Dead enemies mean, the comparison for the four algorithms in SMAC map 3M, MAPPO with blue color, VDN with red color, QMIX with green color and MAA2C with black color

4.2 The Defending Scenario Results

This scenario is considered more challenging because the agent is required to master survival strategies and collaborate with other agents to achieve victory in the game. The results were analyzed to check which algorithm worked faster and could reach the highest value with the three metrics: Battle won mean, dead allies mean and dead enemies mean. Fig. 6 shows a screenshot from the complex task environment MAP Corridor, the green lines represent the agent’s attacking direction. At the beginning of the training process, the agents start searching for the target, as seen in Fig. 6A. Then, a few of these agents discovered the target and started the cooperative attack, like the agents shown in Fig. 6B. Finally, all the agents collaborate and launch an assault attack on the enemies, as illustrated in Fig. 6C.

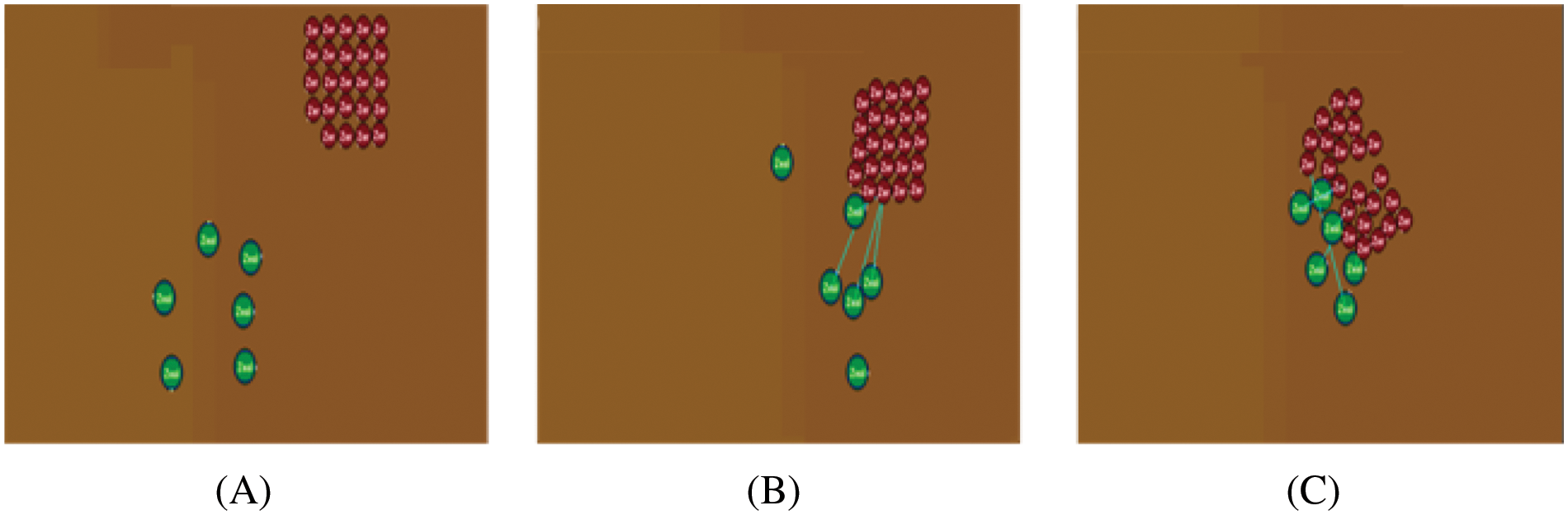
Figure 6: Screenshot from the training of the defending scenario SMAC map Corridor (Complex task), the six green circles represent the training agent, and the 24 red circles represent the enemies, (A) the agents searching for the target. (B) Two of the trained agents could find the target and start the cooperative attack. (C) All three agents attack the target

We evaluated the four algorithms (MAA2C, MAPPO, QMIX, and VDN) to evaluate which algorithm produced a successful result for the defending scenario. We have chosen the SMAC map Corridor as our training environment to check the performance and speed of every algorithm to see which agent succeeded in the defending scenario and kill more enemies faster to win the match without losing allies. The battle won means representing the successfully won value for the multiple agents for every algorithm in every match. We can pick the algorithm that gives us the best outcome in terms of the battle won mean. Fig. 7 shows a comparison of the highest value of the battle-won mean reached by every algorithm. The VDN algorithm generated the highest value with a rapid rise at the first million iterations, while the QMIX algorithm created the second highest value for the battle won mean at the end of training. The MAPPO and MAA2C algorithms gave the poorest results in this work, however, MAA2C could not produce a result and stayed at zero, while the MAPPO eventually attained 0.01. In the defending scenario, VDN had the best performance compared to the other algorithms. Its values started increasing earlier during the training process and eventually reached the highest value of all. The high performance of VDN and QMIX algorithms reflects the proper mechanism those algorithms work on. The VDN performs to reach the goal that the total reward has an additivity property, while QMIX always assumes that the overall reward should be in line with the monotonic constraint. Our results showed that the VDN and QMIX can observe a higher level of state information during the training stage and a much deeper class of action-value functions.

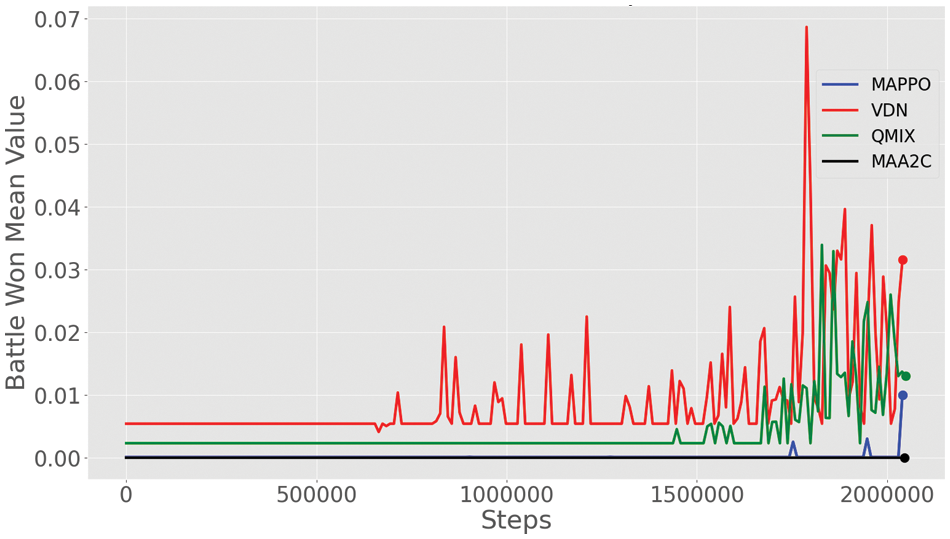
Figure 7: The battle won means comparison for the four algorithms in SMAC map Corridor MAPPO with blue, VDN with red color, QMIX with green color, and MAA2C with black color

By employing the Max function, we could determine the highest value of battle won mean value achieved by the four algorithms in a specific number of iterations. The VDN algorithm had the greatest battle-won mean score of 0.068 at iteration 1,788,419 of the training, and the QMIX algorithm followed with a score of 0.033 at 1,828,764 iterations. The outcomes of MAA2C and MAPPO were near zero, where MAPPO got 0.01 at iteration 2,040,165, achieving the third highest value, while the result of MAA2C achieved was zero. In this scenario, the VDN algorithm was the best one, and the MAA2C was the worst one. The defending scenario has revealed that the QMIX and VDN algorithms have the highest mean value of the battle won.

The dead allies and dead enemies mean are the next metrics used to verify the performance of our algorithms; the dead allies mean metric indicates the number of trained agents killed in a single iteration, while the dead enemies mean indicates the number of enemies killed at every iteration. According to the available performance evaluation metrics in the chosen environment, the dead enemies refer to the accuracy and dead allies refer to loss. Fig. 8 shows a comparison of the highest value of the dead allies and dead enemies mean reached by the four algorithms that were trained for two million iterations. The best algorithm must give the smallest value of dead allies mean and the biggest value of dead enemies means. The results indicated that the VDN algorithm achieved the minimum value of dead allies mean and the second highest value of dead enemies mean, while the QMIX algorithm got the second smallest value of the dead allies mean and the greatest value of dead enemies mean. The worst result in this work was achieved by the MAA2C and MAPPO algorithms, where the value of these algorithms was almost zero. QMIX and VDN algorithms were given the best result for the dead allies and dead enemies in this scenario.

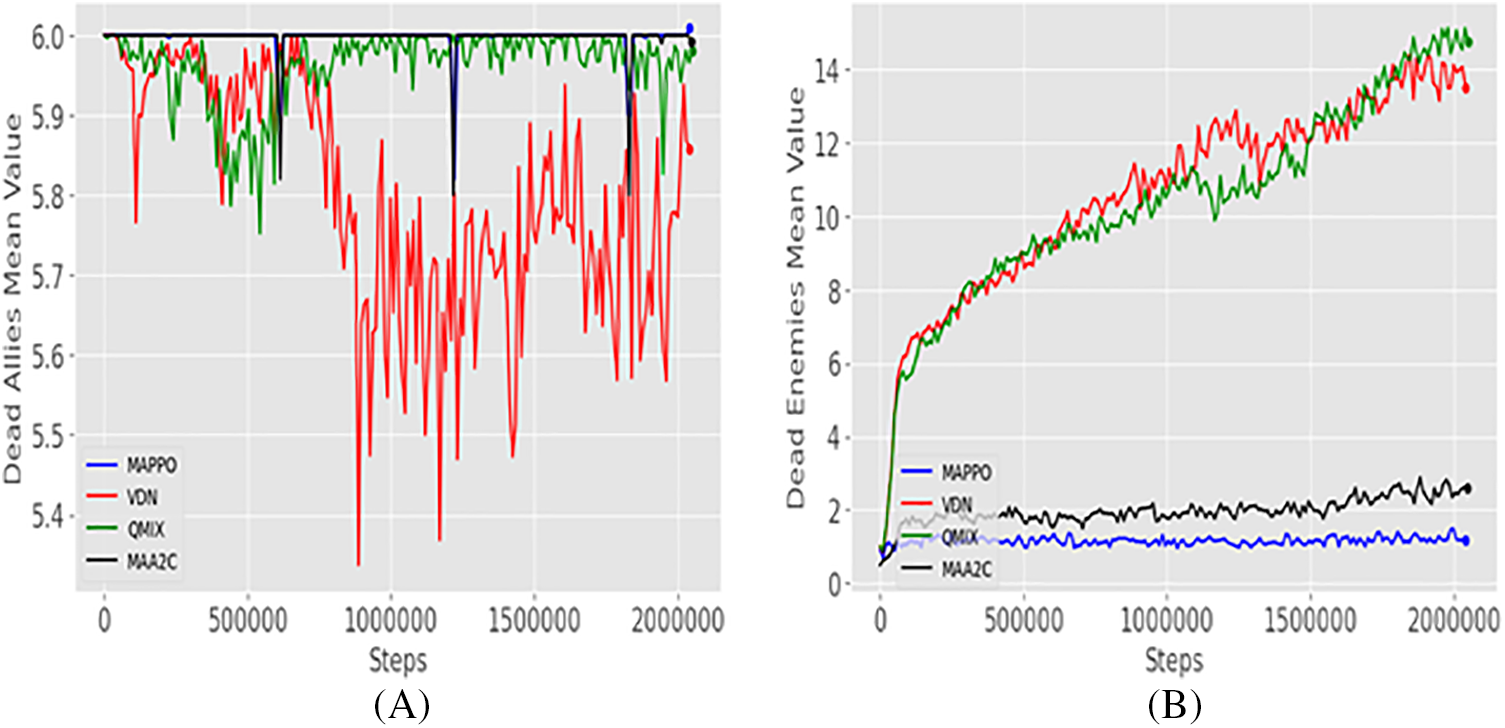
Figure 8: (A) Dead allies mean, and (B) Dead enemies mean comparison for the four algorithms in SMAC map 3M, MAPPO with blue color, VDN with red color, QMIX with green color, and MAA2C with black color

The VDN algorithm had the lowest recorded mean value in Fig. 8A with 5.337 and had the second highest mean value in Fig. 8B with 14.421, both were achieved at iteration 86,4360. At iteration number 2,134,850, the QMIX algorithm achieved the second smallest value in Fig. 8A with 5.752 and the first highest value in Fig. 8B with 15.137. Additionally, the results of the MAA2C and MAPPO algorithms were the poorest in this scenario. The MAA2C had the third smallest value in Fig. 8A at 5.800 and the third greatest value in Fig. 8B at 1.480, both at iteration 1,217,486. The MAPPO algorithm had the poorest results for both Figs. 8A and 8B in this scenario. The results in Figs. 8A and 8B, indicate that the QMIX and VDN algorithms have the highest performance in the defending scenario; therefore, these are the most suitable algorithms for this scenario.

To summarize the outcomes of the four algorithms across two scenarios, this work implemented four algorithms, QMIX, VDN, MAA2C, and MAPPO, in two various scenarios, attacking and defending. Four algorithms were tested on two scenarios, with some providing excellent results and others giving poor results. We examined the outcomes of the algorithms in the SMAC MAP_3M the simple task, where QMIX produced exceptional results, achieving the highest battle won mean, dead enemies mean, and the lowest dead allies mean. In the same scenario, the VDN algorithm gives the second highest value for the battle won mean, dead enemies mean, and the lowest value in dead allies mean. The other two algorithms, MAA2C ranked third and MAPPO, yielded the lowest results. During the complex task scenario SMAC MAP Corridor, both QMIX and VDN demonstrated impressive results. Specifically, the VDN algorithm demonstrated the best performance in terms of the battle-won mean and dead allies mean, while QMIX excelled in dead enemies mean. The results of MAA2C and MAPPO in this Complex scenario were poor and nearly equal to zero. Table 2 shows the highest values achieved by the four algorithms MAPPO, VDN, QMIX, and MAA2C for the metrics battle won mean, dead allies mean and dead enemies mean in the two scenarios (3M, Corridor).

4.3 Discussion

The results of this work showed that the four MARL algorithms, namely QMIX, VDN, MAPPO, and MAA2C algorithms were successful in both attacking and defending scenarios in the SMAC environment. The trained algorithms provide us with a different result in every scenario. Examination of this work revealed that the QMIX algorithm was the most successful in the attacking scenario. The QMIX achieved the greatest success in terms of the three metrics battle won mean, dead allies mean and dead enemies mean, while the VDN algorithm was the most effective in the defending scenario, with battle won mean increasing from the start of the training and yielding the greatest value of battle won mean dead allies mean. Moreover, QMIX generated the largest dead enemies mean in the defending scenario and achieved the second smallest value of dead allies mean of 5.752 and the first highest value of dead enemies mean of 15.137. The comparison we made for the four chosen algorithms was based on the performance of the four algorithms in the chosen environments. This performance can be affected by the type of the chosen environment to train each algorithm. For instance, Yu et al. [11] compared the performance of different MARL algorithms including MAPPO and QMIX in 22 different environments and scenarios. In some of the chosen scenarios in [11], MAPPO did better than QMIX, especially in terms of the number of wins in each scenario. In [14], four MARL algorithms including QMIX and VDN were compared in the SMAC environment with eight different scenarios and the results showed that QMIX was the best algorithm in all the chosen scenarios as we confirmed in this work. In this work, we were able to run a comparison in the SMAC environment between four MARL algorithms in two different scenarios (defending and attacking) which are the most commonly used in terms of battles. Our research demonstrates the effectiveness of MARL algorithms in cooperative assignments and highlights their potential applications in real-world scenarios. The SMAC environment provides a valuable tool for testing and evaluating these algorithms, and our results show that they can be used to achieve victory with minimal damage. The implications of our findings are significant, and we believe that our research has the potential to make a meaningful impact in a variety of fields.

4.4 Limitations

The first limitation of this work is that we cannot link these Epymarl algorithms with a separate environment designed by any graphics application to train or design a personal multi-agent system. The second limitation is in the defending scenario of SMAC MAP_Corridor. We trained multiple agents to protect their spot and maintain it as much as possible, but we could not get to a satisfying value with any algorithm. This is normal since there were six agents up against twenty-four competitors, making victory almost impossible; thus, we consider the defending scenario a complex mission.

5  Conclusion

This paper has applied four algorithms: VDN, QMIX, MAA2C, and MAPPO in two SMAC environments to evaluate their performance in attacking and defending tasks to determine the most successful. Through training in the SMAC environment, the multiple agents gain the knowledge of how to collaborate with other agents to attack their enemies or guard their position to come out victorious with minimal damage. To evaluate the algorithm’s success in the attacking and defending scenarios, three metrics have been considered: Battle won mean, dead allies mean, and dead enemies mean. To test the performing algorithm, it must have the maximum value of battles won mean, enemies dead mean, and the minimal value of allies’ dead mean. Results showed that QMIX had the highest value in battle won mean, dead enemies mean, and the lowest value in dead allies mean for the attacking scenario. Consequently, the QMIX algorithm is considered the best algorithm in the attacking scenario in this work. The VDN algorithm achieved the second-best results in this work. The MAA2C was third and MAPPO had the lowest performance for the attacking scenario. In the defending scenario, the VDN algorithm was the most successful due to achieving the highest battle-won mean and the lowest dead enemies mean. The QMIX algorithm had the highest dead enemies mean and was the second-best performing. For both the MAPPO and MAA2C algorithms, MAPPO showed the third-highest performance, but the MAA2C had the poorest outcome in this scenario. To sum up, the QMIX is the most successful algorithm in the attacking scenario, and the VDN is best in the defending scenario. Reinforcement learning agents are trained to perform specific actions in a particular environment, and those actions can be repeated in different scenarios in another environment. As we mentioned earlier, the idea of attack and defense could potentially apply to the study of mobile attacks in cooperative learning, and we are planning for future work to implement this work on multi-cooperative drone tasks in a similar environment.

Acknowledgement: The authors acknowledge the contribution and the support of the Department of Electrical & Computer Engineering and Computer Science at Jackson State University (JSU).

Funding Statement: This work was supported in part by United States Air Force Research Institute for Tactical Autonomy (RITA) University Affiliated Research Center (UARC), and in part by the United States Air Force Office of Scientific Research (AFOSR) Contract FA9550-22-1-0268 awarded to KHA, https://www.afrl.af.mil/AFOSR/. The contract is entitled: “Investigating Improving Safety of Autonomous Exploring Intelligent Agents with Human-in-the-Loop Reinforcement Learning,” and in part by Jackson State University.

Author Contributions: The authors confirm contribution to the paper as follows: Study conception and design: A. Abdulghani, M. Abdulghani, W. Walters, K. Abed; data collection: A. Abdulghani; analysis and interpretation of results: A. Abdulghani, M. Abdulghani, W. Walters, K. Abed; draft manuscript preparation: A. Abdulghani, M. Abdulghani, K. Abed. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data openly available in a public repository. The data that support the findings of this study are openly available in SMAC2 at https://github.com/oxwhirl/smacv2.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Y. Cao, W. Yu, W. Ren, and G. Chen, “An overview of recent progress in the study of distributed multi-agent coordination,” IEEE Trans. Ind. Inform., vol. 9, no. 1, pp. 427–438, 2012. [Google Scholar]

2. C. Zhang and V. Lesser, “Coordinated multi-agent reinforcement learning in networked distributed pomdps,” in AAAI Conf. Artif. Intell. (AAAI), 2011, vol. 25, no. 1. [Google Scholar]

3. M. Hüttenrauch, A. Šošić1, and G. Neumann, “Guided deep reinforcement learning for swarm systems,” University of Lincoln, Sep. 18, 2017. arXiv:1709.06011. [Google Scholar]

4. L. Busoniu, R. Babuska, and B. D. Schutter, “A comprehensive survey of multiagent reinforcement learning,” IEEE Trans. Syst., Man, Cybern., Part C (Appl. and Rev.), vol. 38, no. 2, pp. 156–172, 2008. [Google Scholar]

5. S. Chen, M. Zhu, D. Ye, W. Zhang, Q. Fu, and W. Yang, “Which heroes to pick? Learning to draft in moba games with neural networks and tree search,” IEEE Trans. Games, vol. 13, no. 4, pp. 410–421, 2021. [Google Scholar]

6. C. Hong, I. Jeong, L. F. Vecchietti, D. Har, and J. H. Kim, “AI world cup: Robot-soccer-based competitions,” IEEE Trans. Games, vol. 13, no. 4, pp. 330–341, 2021. [Google Scholar]

7. R. Bellman, “A markovian decision process,” Indiana Univ. Math. J., vol. 6, no. 4, pp. 679–684, Jan. 1957. doi: 10.1512/iumj.1957.6.56038. [Google Scholar] [CrossRef]

8. C. B. Watkins and P. Dayan, “Q-learning,” Mach. Learn., vol. 6, no. 4, pp. 679–684, May 1992. doi: 10.1007/bf00992698. [Google Scholar] [CrossRef]

9. M. Roderick, J. MacGlashan, and S. Tellex, “Implementing the deep Q-network,” in 30th Conf. Neural Inf. Process. Syst. (NIPS 2016), Barcelona, Spain, Nov. 20, 2017. [Google Scholar]

10. J. Schulman, F. Wolski, P. Dhariwal, A. Radford, and O. Klimov, “Proximal policy optimization algorithms,” Aug. 28, 2017. doi: 10.48550/arXiv.1707.06347. [Google Scholar] [CrossRef]

11. C. Yu, A. Velu, E. Vinitsky, Y. Wang, A. M. Bayen, and Y. Wu, “The surprising effectiveness of MAPPO in cooperative, multi-agent games,” Cornell University, Mar. 2021. doi: 10.48550/arxiv.2103.01955. [Google Scholar] [CrossRef]

12. G. Weiss, “Multiagent systems and societies of agents,” in Multiagent Systems: A Modern Approach to Distributed Artificial Intelligence, MIT Press, Liverpool, UK, 2000, pp. 79–120. [Google Scholar]

13. P. Sunehag et al., “Value-decomposition networks for cooperative multi-agent learning based on team reward. adaptive agents and multi-agent systems,” DeepMind & Unive. Liverpool, pp. 2085–2087, 2017. [Google Scholar]

14. T. Rashid, M. Samvelyan, C. Schroeder, G. Farquhar, J. Foerster and S. Whiteson, “QMIX: Monotonic value function factorisation for deep multi-agent reinforcement learning,” Cornell University, Mar. 2018. doi: 10.48550/arxiv.1803.11485. [Google Scholar] [CrossRef]

15. M. S. Stanković, M. Beko, N. Ilic, and S. S. Stanković, “Multi-agent off-policy actor-critic algorithm for distributed multi-task reinforcement learning,” Eur. J. Control, vol. 100853, Jun. 2023. doi: 10.1016/j.ejcon.2023.100853. [Google Scholar] [CrossRef]

16. N. Bard et al., “The hanabi challenge: A new frontier for AI research,” Artif. Intell., vol. 280, pp. 103216, Mar. 2020. doi: 10.1016/j.artint.2019.103216. [Google Scholar] [CrossRef]

17. G. Brockman et al., “OpenAI gym,” Brockman2016OpenAIG arXiv:1606.01540. [Google Scholar]

18. M. Samvelyan et al., “The starcraft multi-agent challenge,” in Deep Reinf. Learn. 33rd Conf. Neural Inf. Process. Syst. (NeurIPS 2019), Vancouver, Canada, pp. 2186–2188. [Google Scholar]

19. O. Vinyals et al., “Grandmaster level in starCraft II using multi-agent reinforcement learning,” Nature, vol. 575, no. 7782, pp. 350–354, Oct. 2019. doi: 10.1038/s41586-019-1724-z [Google Scholar] [PubMed] [CrossRef]

20. A. Wong, T. Bäck, A. V. Kononova, and A. Plaat, “Deep multiagent reinforcement learning: Challenges and directions,” Artif. Intell. Rev., vol. 56, no. 6, pp. 5023–5056, Oct. 2022. doi: 10.1007/s10462-022-10299-x. [Google Scholar] [CrossRef]

21. J. B. Hamrick et al., “On the role of planning in model-based deep reinforcement learning,” arXiv:2011.04021, 2021. [Google Scholar]

22. A. M. Abdulghani, M. M. Abdulghani, W. L. Walters, and K. H. Abed, “AI safety approach for minimizing collisions in autonomous navigation,” J. Artif. Intell., vol. 5, pp. 1–14, 2023. doi: 10.32604/jai.2023.039786. [Google Scholar] [CrossRef]

23. C. C. Rosser, W. L. Walters, A. M. Abdulghani, M. M. Abdulghani, and K. H. Abed, “Implementation of strangely behaving intelligent agents to determine human intervention during reinforcement learning,” J. Artif. Intell., vol. 4, no. 4, pp. 261–277, 2022. [Google Scholar]

24. L. Kraemer and B. Banerjee, “Multi-agent reinforcement learning as a rehearsal for decentralized planning,” Neurocomput., vol. 190, pp. 82–94, May 2016. doi: 10.1016/j.neucom.2016.01.031. [Google Scholar] [CrossRef]

25. J. Foerster, G. Farquhar, T. Afouras, N. Nardelli, and S. Whiteson, “Counterfactual multi-agent policy gradients,” in Proc. AAAI Conf. Artif. Intell., vol. 32, no. 1, Apr. 2018. doi: 10.1609/aaai.v32i1.11794. [Google Scholar] [CrossRef]

26. J. Zhao, X. Hu, M. Yang, W. Zhou, J. Zhu, and H. Li, “CTDS: Centralized teacher with decentralized student for multi-agent reinforcement learning,” IEEE Trans. Games, 2022. doi: 10.1109/TG.2022.3232390. [Google Scholar] [CrossRef]

27. X. Fang, P. Cui, and Q. Wang, “Multiple agents cooperative control based on QMIX algorithm in SC2LE environment,” in 2020 7th Int. Conf. Inf., Cybern., Comput. Soc. Syst. (ICCSS), Guangzhou, China, 2020, pp. 435–439. doi: 10.1109/ICCSS52145.2020.9336865. [Google Scholar] [CrossRef]

28. Z. Dou, J. G. kuba, and Y. Yang, “Understanding value decomposition algorithms in deep cooperative multi-agent reinforcement learning,” arXiv:2202.04868, 2022. [Google Scholar]

29. Y. Wang, C. Zhang, T. Yu, and M. Ma, “Recursive least squares advantage actor-critic algorithms,” IEEE Trans. Syst., Man, Cyber.: Syst., 2022. doi: 10.48550/arxiv.2201.05918. [Google Scholar] [CrossRef]

30. A. Michalski, F. Christianos, and V. S.Albrecht, “SMAClite: A lightweight environment for multi-agent reinforcement learning,” Cornell University, May 2023. doi: 10.48550/arxiv.2305.05566. [Google Scholar] [CrossRef]

31. X. Li, G. Chen, G. Wu, Z. Sun, and G. Chen, “Research on multi-agent D2D communication resource allocation algorithm based on A2C,” Electron., vol. 12, no. 2, pp. 360, 2023. doi: 10.3390/electronics12020360. [Google Scholar] [CrossRef]

32. M. M. Abdulghani, A. A. Harden, and K. H. Abed, “A drone flight control using brain-computer interface and artificial intelligence,” in 2022 Int. Conf. Comput. Sci. Comput. Intell.–Artif. Intell. (CSCI’22-AIIEEE Comput. Soc. Conf. Publ. Serv. (CPS), Las Vegas, Nevada, Dec. 14–16, 2022. [Google Scholar]

33. G. Papoudakis, F. Christianos, L. Schafer, and S. V. Albrecht, “Benchmarking multi-agent deep reinforcement learning algorithms in cooperative tasks,” in 35th Conf. Neural Inf. Process. Syst. (NeurIPS 2021) Track Datasets Benchmarks, University of Edinburgh, 2020. [Google Scholar]

34. A. Paszke et al., PyTorch: An Imperative Style, High-Performance Deep Learning Library. Cornell Un., 2019, vol. 32, pp. 8026–8037. doi: 10.48550/arXiv.1912.01703. [Google Scholar] [CrossRef]

35. R. S. Dehal, C. Munjal, A. A. Ansari, and A. S. Kushwaha, “GPU computing revolution: CUDA,” in 2018 Int. Conf. Adv. Comput., Commun. Control Netw. (ICACCCN), Greater Noida, India, 2018, pp. 197–201. doi: 10.1109/ICACCCN.2018.8748495. [Google Scholar] [CrossRef]

36. Y. Shang, “Resilient vector consensus over random dynamic networks under momalicious bile attacks,” Comput. J., 2023. doi: 10.1093/comjnl/bxad043. [Google Scholar] [CrossRef]