 Open Access
Open Access
ARTICLE
A Reference Vector-Assisted Many-Objective Optimization Algorithm with Adaptive Niche Dominance Relation
1 School of Computer Science and Technology, Huaibei Normal University, Huaibei, 340604, China
2 School of Physic and Electronic Information, Huaibei Normal University, Huaibei, 340604, China
3 Anhui Engineering Research Center for Intelligent Computing and Application on Cognitive Behavior (ICACB), Huaibei Normal University, Huaibei, 340604, China
4 Anhui Province Key Laboratory of Intelligent Computing and Applications, Huaibei Normal University, Huaibei, 340604, China
5 Institute of Artificial Intelligence, Hefei Comprehensive National Science Center, Hefei, 230000, China
* Corresponding Author: Yating Wu. Email:
(This article belongs to the Special Issue: Artificial Intelligence Algorithm for Industrial Operation Application)
Intelligent Automation & Soft Computing 2024, 39(2), 189-211. https://doi.org/10.32604/iasc.2024.042841
Received 14 June 2023; Accepted 31 January 2024; Issue published 21 May 2024
Abstract
It is still a huge challenge for traditional Pareto-dominated many-objective optimization algorithms to solve many-objective optimization problems because these algorithms hardly maintain the balance between convergence and diversity and can only find a group of solutions focused on a small area on the Pareto front, resulting in poor performance of those algorithms. For this reason, we propose a reference vector-assisted algorithm with an adaptive niche dominance relation, for short MaOEA-AR. The new dominance relation forms a niche based on the angle between candidate solutions. By comparing these solutions, the solution with the best convergence is found to be the non-dominated solution to improve the selection pressure. In reproduction, a mutation strategy of -bit crossover and hybrid mutation is used to generate high-quality offspring. On 23 test problems with up to 15-objective, we compared the proposed algorithm with five state-of-the-art algorithms. The experimental results verified that the proposed algorithm is competitive.Keywords
Supplementary Material
Supplementary Material FileMany problems in practical applications can be seen as multi-objective optimization problems (MOPs), such as cloud computing [1], industrial copper burdening system [2], and engineering design [3,4]. Many-objective optimization problem (MaOP) [5] is a task that needs to simultaneously optimize m (m > 3) conflicting objectives. The mathematical form of MaOP is represented by Eq. (1).
{F(x)=(f1(x),f2(x),…,fm(x))Ts.t.x∈Ω(1)
where Ω∈Rn is the feasible search region of the decision vector x=(x1,x2,…,xn)T, f(x)∈Rm is the objective vector, and n is the number of decision variables. Generally, we assume that f(x) is a minimization problem. Due to the duality principle, the maximization problem can be transformed into the minimization problem. Unlike single-objective optimization, due to the conflicting nature of multi-objective functions, multi-objective optimization problems cannot obtain a single optimal solution, but a group of compromise solutions. These compromise solutions form Pareto set (PS) in the decision space and map to the corresponding Pareto front (PF) in the objective space.
Owing to the strong population-based search properties of multi-objective evolutionary algorithms (MOEAs), they can be solved efficiently for MOPs. However, when encountering MaOPs, the performance of MOEA will deteriorate rapidly due to the curse of dimensional [6]. Researchers have developed new algorithms to solve MaOPs. It can be classified into four types: Convergence enhancement, Decomposition-based, Indicator-based and Secondary selection criteria.
The first category includes various convergence enhancement methods. The convergence pressure loss of most traditional MOEAs is the direct result of the inability to distinguish the traditional dominance relation. The most direct convergence enhancement method is to modify the dominance relation to improve the selection pressure. For example, ϵ-dominance [7] compares the dominance relation between solutions using relaxation factors; Yang et al. [8] proposed a grid-based method to choose solutions with a greater dominance priority and control the percentage of Pareto optimal solutions by changing the grid size.
The second category refers to Decomposition-based algorithms that decompose the MOP into multiple single-objective optimization problems. For example, the Multi-objective evolutionary algorithm based on decomposition (MOEA/D) [9] proposed by Zhang and Li decomposes m-objective MOP/MaOP into m single-objective problems for simultaneous optimization. Then, each sub-problem is then handled in a surrounding region that is bound by its associated reference vector. Another decomposition method involves decomposing the complicated MOP/MaOP into multiple simpler MOPs. For example, MOEA/D based on MOP to MOP (MOEA/D-M2M) [10] divides the entire PF into a set of segments, and each of which can be regarded as a separate issue. And many algorithms have been proposed based on the decomposition [11].
The third category is indicator-based methods [12], which proposes a number of MOEAs based on hypervolume (HV). Their main disadvantage is the high computational complexity of HV, especially when solving the MaOP. Sun et al. [13] introduced an Inverse Generation Distance (IGD) indicator in MOEA to solve the MaOP with up to 20-objective. An evolutionary algorithm (IGD+EMOA) based on inverse generation distance plus (IGD+) indicator was proposed [14] to solve the MaOP with up to 8-objective. The IGD+ indicator is a variant of the IGD.
The fourth category is characterized by a combination of Pareto dominance and other selection criteria. These methods choose high ranking non-dominated solutions based on Pareto dominance first, and then use the secondary selection criterion to distinguish non-comparable candidates. Existing methods in this genre mainly employ three typical ideas. The first is to develop new criteria to support methods with good convergence and diversity in non-comparable candidate solutions, such as Promising-region based EMO algorithm (PREA) [15]. The second idea is to use performance indicators to distinguish the quality of non-comparable candidate solutions by selecting those with great contributions, such as the Kriging-assisted Two_Arch2 (KTA-2) [16]. The typical algorithm of the third idea is Many-objective evolutionary algorithm based on dominance and decomposition (MOEA/DD) [17], which combines Pareto dominance with decomposition-based algorithms.
The existing four classes of methods have been able to solve many-objective optimization problems well, but there are still various shortcomings. Decomposition-based algorithms are seriously affected by the weight vector setting, and the computational complexity of indicator-based algorithms is high. Most MaOEAs mainly improve the performance of the algorithm from the perspective of environmental selection, and little attention has been paid to offspring generation. In addition, as far as most dominance relations are concerned, some methods can easily generate the solution set concentrated in a small region of the Pareto front. Considering these issues, in this paper, we propose a reference vector-assisted many-objective optimization algorithm with adaptive niche dominance relations (MaOEA-AR). First using k-bit crossover [18] and hybrid mutation in the mating strategy to generate high-quality offspring. Using a new dominance relation to select non-dominated solutions in environmental selection, and then using angle penalized distance (APD) [19] to further balance convergence and diversity. The contributions of this study are summarized as follows:
1. A new dominance relation, called the adaptive niche dominance relation (A-NDR), is proposed for many-objective optimization. By developing niche techniques based on the angle between candidate solutions and having just one candidate solution with the best convergence in each niche, A-NDR balances convergence and diversity, where convergence is calculated in terms of the PF shape adaptively by selecting the convergence indicator. The proposed A-NDR is parameter-free since the size of the niche is determined adaptively by the distribution of candidate solutions.
2. Mating selection also uses the niche mating method to select neighbor solutions in the objective space, the k-bit crossover to avoid the generation of the identical offspring to the parents and to improve the quality of the parents, and hybrid mutation to produce high-quality offspring.
The rest of this paper is structured as follows. The proposed algorithm is further explained in Section 2. The experimental design and some of the data analysis are presented in Section 3. Finally, Section 4 presents the conclusions and outlook for the future. The related works, motivation, some of the experimental results and analyses of this paper are given in the Supplementary Material.
This section describes the proposed algorithm MaOEA-AR in detail. First, the general framework of the algorithm is given. The reproduction strategy was then discussed. Subsequently, we describe the environment selection, as well as the adaptive niche dominance relation and angle penalty distance used in the environment selection.
The details of the general framework of the proposed MaOEA-AR are presented in Algorithm 1. First, initialize (lines 1–3) to generate a set of uniformly distributed reference vectors, initial populations, and train the initial improved growing neural gas (iGNG) net [20] using reference vectors with associated solutions. Copy the non-dominant solution from the initial population into archive A. Then, k-bit crossover and hybrid mutation are used to generate high-quality parent and offspring (lines 5–6, Algorithm 2 and Algorithm 3) individuals and update archive A. The solution in archive A and the solution in the current population are used as input data to train the iGNG network and set the weights of nodes. Finally, in the environment selection (Algorithm 4), N solutions are selected from the joint population of the current and its offspring using adaptive niche dominance relation and angle penalty distance.

As shown in Algorithm 2, in lines 1–12, the niche mating randomly selects 80% or 20% of the parent individuals from local neighbors or whole populations, which is similar to the traditional setting [21], to avoid reproducing the same offspring as the parents. Niche is a more stable and effect way to exchange evolutionary information between two solutions with similar objective vectors. In line 3, the solution is selected by normalizing the objective values to the same range to ensure fairness. In lines 13–20, k-bit crossover randomly modifies at least one but not more than (|j|−1) decision variables between one or two parent individuals. Then, we perform mutation operation (Algorithm 3).


Algorithm 3 describes the hybrid mutation method in detail, in which the mutation and the traditional mutation are randomly applied at a set ratio of 20% and 80%, respectively. We have no attempt to find the best ratio, but the probability of using the traditional bit-wise mutation method should be set relatively larger, because it provides a more general and stable variation. It is worth noting that c1 and c0 in line 3 and line 9 are not indicator of candidate solutions but indicator of genes with values of 1 or 0 in the decision vector of a solution. Furthermore, the specific mutation in Algorithm 3 is very simple. The index only needs to be flipped, and the specific gene represented by c1(k) in line 6 or t in line 15 changes from 1 to 0 or 0 to 1.
The environmental selection process is presented in Algorithm 4. The environmental selection consisted of three main parts. The first part combined the populations and archives for selection. The second is to perform an adaptive niche dominance relation ranking to locate key layers. The third is the APD selection, which is the same as in [19]. Here, we use the adaptive niche dominance relation to identify non-dominated solutions in the population and remove extreme solutions with a large Euclidean distances from the ideal point. The number of solutions in the population after APD selection may be greater than N. Therefore, we will remove the crowded solutions to improve the diversity of the population. Finally, the solutions with the smallest Euclidean distance to their neighbors are removed individually until the number of solutions equals N.

2.3.1 Adaptive Niche Dominance Relation
Inspired by the literature [22], we propose an adaptive niche dominance relation (A-NDR) to balance the convergence and diversity of non-dominated solutions using the niche technique in this study. Specifically, in the A-NDR, if and only if
{Con(x)<Con(y),αxy<¯αCon(x)⋅αxy¯α<Con(y),αxy>¯α(2)
where αxy denotes the acute angle between the objective values of the two candidate solutions, namely,
αxy=arccos(f(x),f(y))(3)
and ¯α is the size of the niche in which each candidate solution is located, which can be adjusted to the size of the niche adaptive, so that the candidate solutions concentrate on non-dominated solutions at a rate of approximately 50%, ¯α is set to the ⌊|P|2⌋-th smallest element of {mini∈P∖{j}αij|i∈P}, αij denotes the acute angle between any pair of candidate solutions. Eq. (2) shows that, each candidate solution x in the population has a niche with size ¯α, and the dominance relationship related to the candidate solution x is determined by mainly considering the candidate solutions in its niche. According to the first formula in (2), if the angle between any x and a candidate solution y is smaller than ¯α, x is said to dominate y once the convergence degree of x is smaller than that of y. It means that, inside each niche, since there do not exist two non-dominated solutions having a smaller angle than ¯α, the diversity of the non-dominated solution set is naturally preserved. Because the PF is unknown prior, and the PF shape will seriously affect the performance of the algorithm, the ratio q=d/¯d of the distance from the ideal point to the solution and the distance from the ideal point to the hyperplane is used to determine the shape of the PF [23], where
{d=||x||¯d=|∑mi=1f′′i(x)−1|√m(4)
f′′i(x) is the objective function after normalization using the standardized method in [24]. According to the different PF shapes, q values can be taken as >1, =1 and <1, as shown in Fig. 1, and different convergence indicators are selected according to q values.
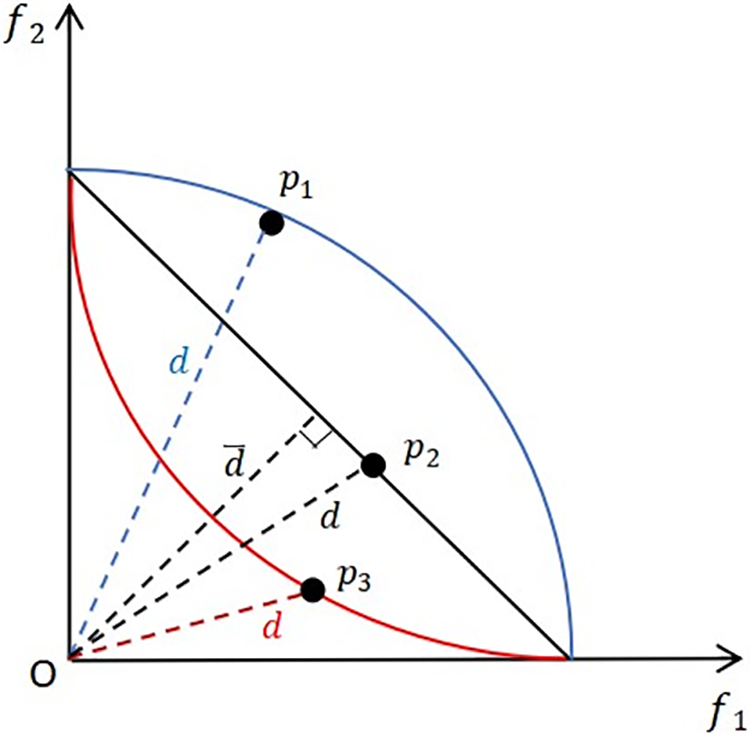
Figure 1: Describes an example of PF shape estimation. Given three solutions p1, p2 and p3 in the bi-objective space, respectively, denote the solutions under different shapes of PF
con(x)={∑mi=1|fi(x)−z∗i|,q>1max1<i<m|fi(x)−z∗i|,q<1∑mi=1fi(x),q=1(5)
It can be seen from Eq. (5) that each solution in the population has a niche of size ¯α, and the dominance relation associated with candidate solution x is determined mainly by considering the candidate solution in their niche. If the angle between any x and y is less than ¯α, then x is considered to dominate y when c(x)<c(y). If two solutions are not in the same niche, i.e., αxy>¯α, and if y converges much worse than x, then it is considered that x can still dominate y. The probability that x dominates y is negatively correlated with αxy. This can guarantee a better convergence of non-dominated solutions. Fig. 2 shows the dominant region obtained by A-NDR in the bi-objective space. There are two different cases: One is that y1 is in the x dominant region, and the convergence degree is worse than x, x is better than y1; the other is that y2 is outside the niche, but its convergence is worse than x, so x still dominates y2.
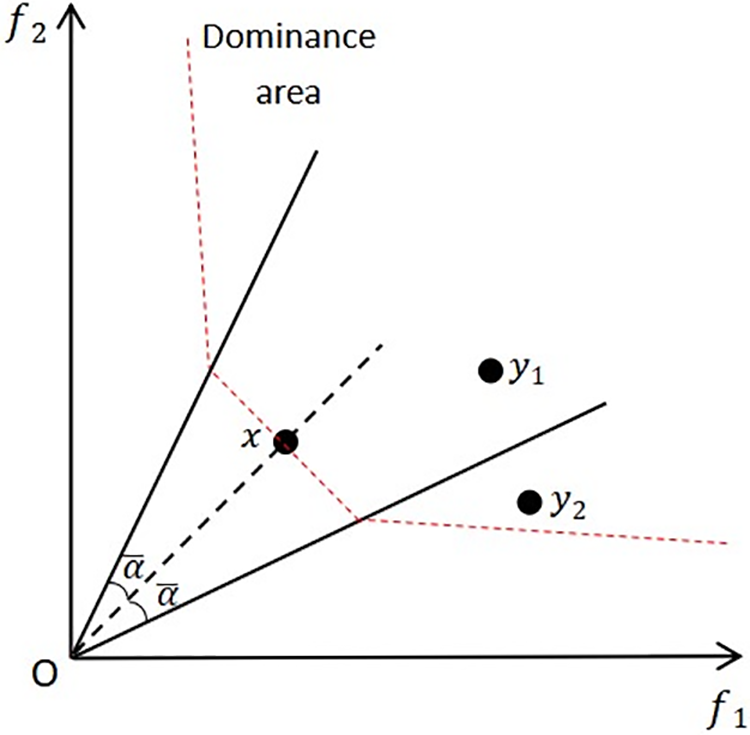
Figure 2: Dominant region of the solution obtained by A-NDR in bi-objective spaces
2.3.2 Angle Penalized Distance
The objective function is converted to the same range by using Eq. (6).
f′i(x)=fi(x)−znadi(6)
divide population P into N sub-populations P1,P2,P3,...,PN associating each individual with its nearest reference vector. As shown in Fig. 3, the angle between an individual and vector v2 is smaller, associating the individual with v2.
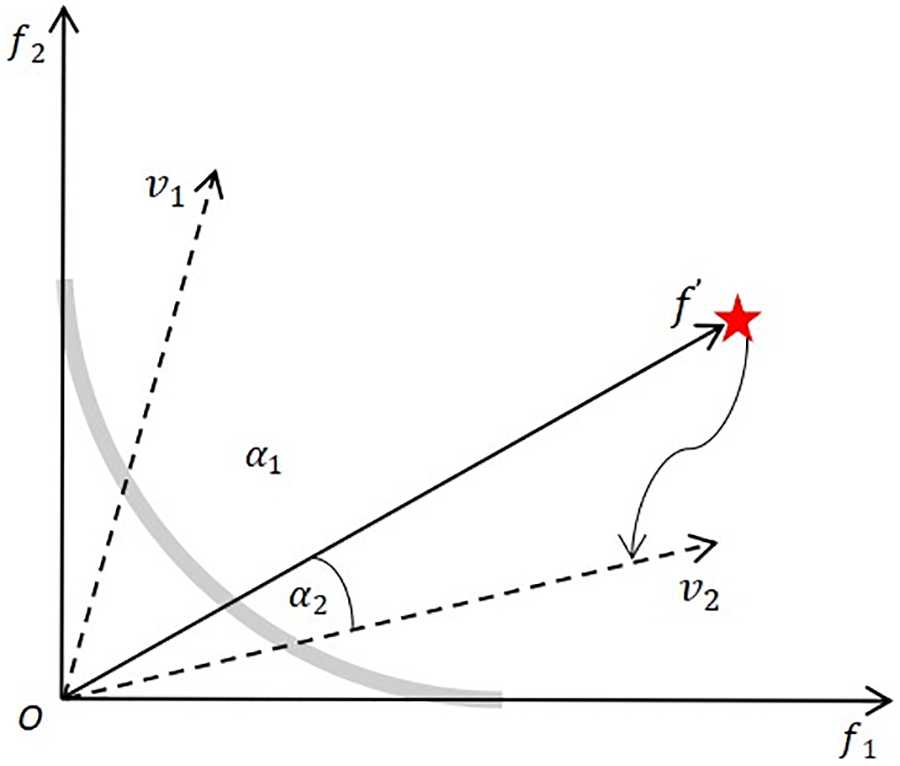
Figure 3: Individual and reference vector association diagram
The relation between the two sub-spaces is measured by the cosine value of the acute angle.
cosαi,j=f′i(x)−vj||f′i(x)||(7)
where cosαi,j is the angle between f′i(x) and vj. If and only if the angle between them is the smallest among all the reference vectors, that is, when the cosine value is the largest, the individual is assigned to the sub-population where vector vj is located. After dividing the population, an elite individual from each sub-population is selected to continue participating in the next generation. We used the APD [19] to select elite individuals.
di,j=(1+P(αi,j))⋅||f′i(x)||(8)
where P(αi,j) is the αi,j correlated penalty function.
P(αi,j)=m⋅(ttmax)θ⋅αi,jφvj(9)
and
φvj=mini={1,…,N},i≠j<vi, vj>(10)
where tmax denotes the predefined maximum number of iterations. φvj is the minimum angle value between the reference vector vi and other vectors in the current generation. θ is a user-defined control P(αi,j) parameter. Consistent with the setting in [19], θ = 2. In the early stage of evolution, P(αi,j) is close to 0, and convergence is emphasized, whereas in the late stage of evolution, the effect of P(αi,j) on di,j gradually increases, and the distribution of the solution is emphasized.
MaOEA-AR consists of three main components: (1) Reproduction (k-bit crossover), (2) Hybrid mutation, and (3) Environmental selection. Details of the complexity analysis of these three components are given below. The complexity of reproduction (Algorithm 3) is concentrated in lines 6–20 of Algorithm 2, which has a complexity of O(N), since each execution requires the selection of an excellent parent individual from a population of N, where N is the size of the population. Hybrid mutation requires the selection of a proportion of parents from local neighbour or from the whole population to be mutated, and therefore requires O(|Q|∗|c1|∗D), where |Q| is the size of the offspring, |c1| is the gene that has been mutated, and D is the size of the offspring that has been mutated. The complexity of the environment selection depends on both A-NDR (line 2 of Algorithm 4) and APD (lines 3–7 of Algorithm 4). The complexity of A-NDR is determined by the PF estimation, which has a computational complexity of O(mN2), where m is the number of objectives. APD hold a computational complexity of O(mN2) in the worst case. Therefore, the complexity of environment selection is O(mN2). In summary, the overall computational complexity of MaOEA-AR is O(mN2).
In this section, we experiments on 23 benchmark test problems from three widely used test suites (i.e., Benchmark MOP proposed by Deb, Thiele, Laumanns, and Zitzler (DTLZ) [25], MaF [26] and Benchmark MOP proposed by Walking Fish Group (WFG) [27]) to compare MaOEA-AR with five state-of-the-art algorithms (i.e., Many-objective evolutionary algorithms based on an independent two-stage (MaOEA-IT) [28], IGD based many-objective evolutionary algorithm (MaOEA-IGD) [13], Many-objective evolutionary algorithm based on objective space reduction (MaOEA-RD) [29], MOEA/D with update when required (MOEA/D-UR) [30] and MOEA/D [9]). We chose the commonly used comprehensive evaluation indicators HV [31] and IGD [32]. The experiments were conducted on Evolutionary multi-objective optimization platform (PlatEMO) [33], and the comparison algorithm was obtained from the platform.
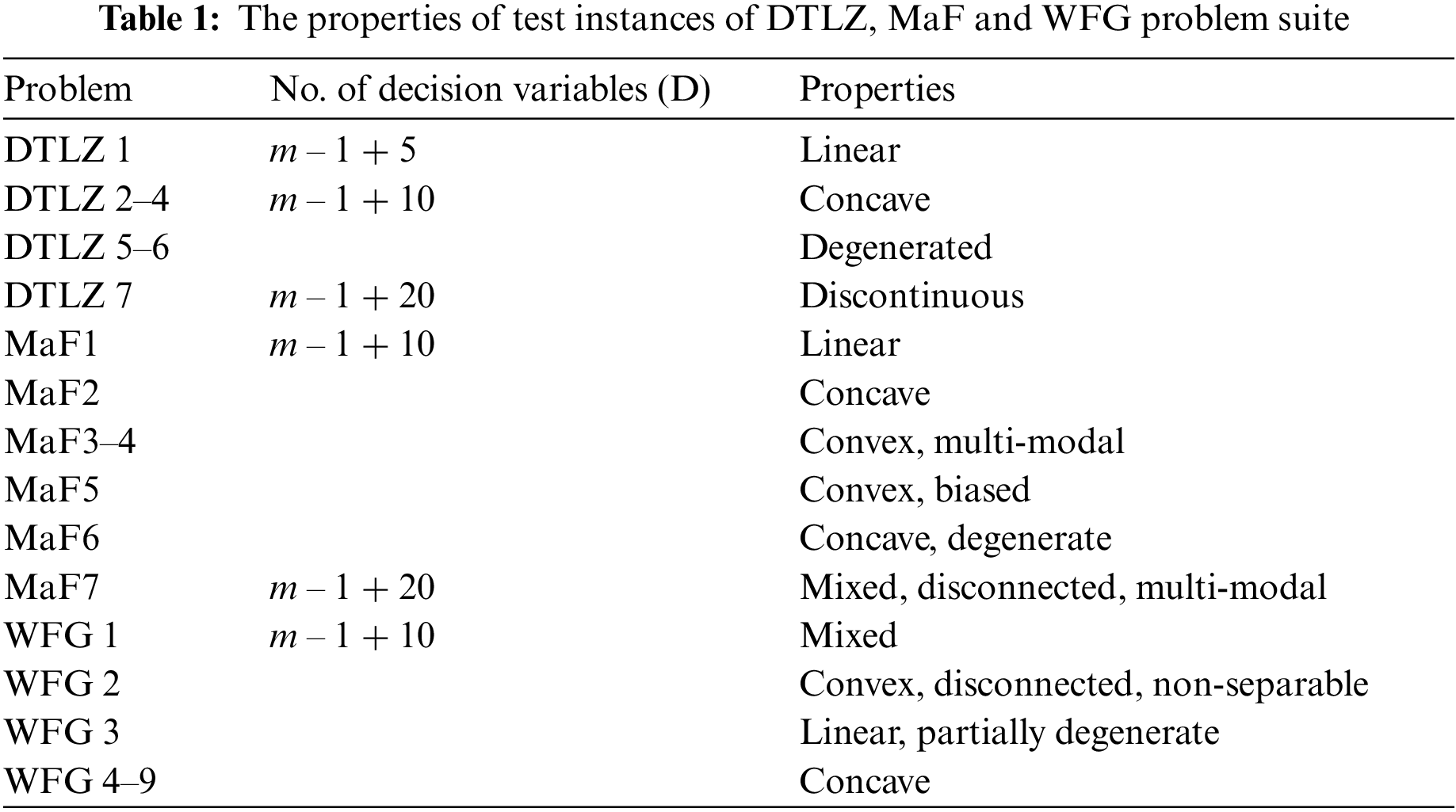
On the 23 benchmark problems of DTLZ, MaF and WFG test suite, we compared the proposed algorithm with the five state-of-the-art algorithms. All problems in the DTLZ and WFG test suites can have any set of decision variable dimensions and objective numbers. MaF was proposed by Cheng et al. [26] in 2017 and includes various representative problems in the real-world. Its test suite contains 15 multi-objective optimization problems chosen by MaF 1–7 to evaluate the algorithm’s performance in solving complex problems. Some properties of these benchmark function suites are listed in Table 1.
With the continuous proposal of MaOEAs, evaluating the performance of MaOEA has also become an important research direction. When the algorithms solve MaOPs, it is necessary to quantify the performance of the algorithm through performance indicators, and to quantify the performance of one algorithm in comparison with the performance of other algorithms. The comprehensive indicators HV and IGD are the most often utilized indicators. Based on the magnitude of the range covered by the PS computed by the algorithm in the objective space, HV is used to evaluate convergence and diversity. By evaluating the similarity between the true PF and the PF generated by the algorithm, the IGD evaluates convergence and diversity. In general, the algorithm performs better the lower the IGD value, whereas the opposite is true for HV. In this study, we use these two indicators to evaluate the performance of the proposed MaOEA-AR, as shown in Eqs. (11) and (12).
HV=volume(∪|PF|i=1vi)(11)
IGD(PF∗,PF)=∑i∈PF∗d(i,PF)|PF∗|(12)
where PF is obtained by algorithm, PF∗ is the standard Pareto front, vi is the hypervolume formed by the reference points and the individuals, d(i,PF) is the Euclidean distance between the individual i on the PF and the nearest individual i, and |PF∗| denotes the total number of points on the true Pareto front.
Population size N: In algorithms for reference vector or point generation, a two-layer strategy is usually used to generate uniformly distributed reference points N to avoid generating too many reference points, which is determined by N=Cm−1h1+m−1+Cm−1h2+m−1, where h1 and h2 are the partition parameters of the inner and outer layers, respectively. As in [33], we set the population size equal to the number N of reference points. In this study, we set the objectives as m = 5, 8, 10 and 15. Table 2 provides the details of the corresponding population size and partition parameters.

Numbers of run and stop conditions: To obtain reliable experimental results, we ran each algorithm 20 times independently on each test instance. This end when the maximum number of function evaluations (maxFEs) is reached. To ensure that each algorithm converges, we uniformly set the maxFEs at 100,000 for each test instance.
Operator parameter settings: The crossover probability pc and mutation probability pm are set to 1.0 and 1/n, respectively, and n is the number of decision variables. The distribution indicator of crossover operator ηc and mutation operator ηm is set to 20. To achieve the best performance of the comparison algorithm, we set the crossover probability pc of MaOEA-IGD to 0.9.
Two parameters in MaOEA-AR require to be predefined, i.e., the user-defined parameter θ that controls the rate of change of the penalty function in Eq. (9), and the parameters fr controlling the frequency of reference vector updates in Algorithm 1. In this paper, θ=2 makes APD work well on a variety of problems with different numbers of objectives without changing the settings. fr=0.1 is used to deal with different target scales, and we adjust the reference vector after fr∗Gmax each generation. Detailed parametric sensitivity analyses for θ and fr are provided in Supplementary Materials III of [20].
3.4 Experimental Results Analysis
In this section, we analyze and evaluate the MaOEA-AR based on the statistical results of 20 independent runs of each algorithm on 16 benchmark problems (92 test instances). Wilcoxon rank sum test is used to compare the difference between the average value obtained by MaOEA-AR and the other five algorithms. The significance level was 0.05, and the ‘+’, ‘−’ and ‘=’ in the table indicate that the performance of other algorithms is significantly better, significantly lower, and no different than MaOEA-AR. Table 3 exhibits the performance of MaOEA-AR on 23 benchmark problems with five comparison algorithms, and the Wilcoxon rank-sum test of MaOEA-AR on the test instances is shown in Fig. 4. It can be seen that MaOEA-AR has strong competitiveness for both HV and IGD.
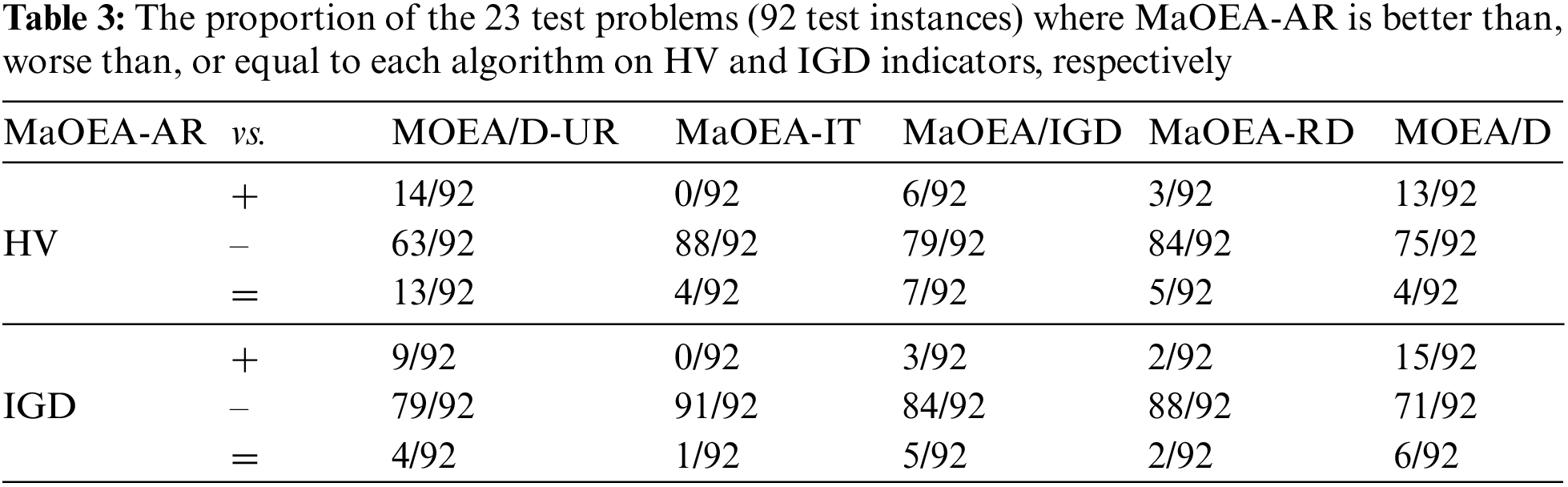
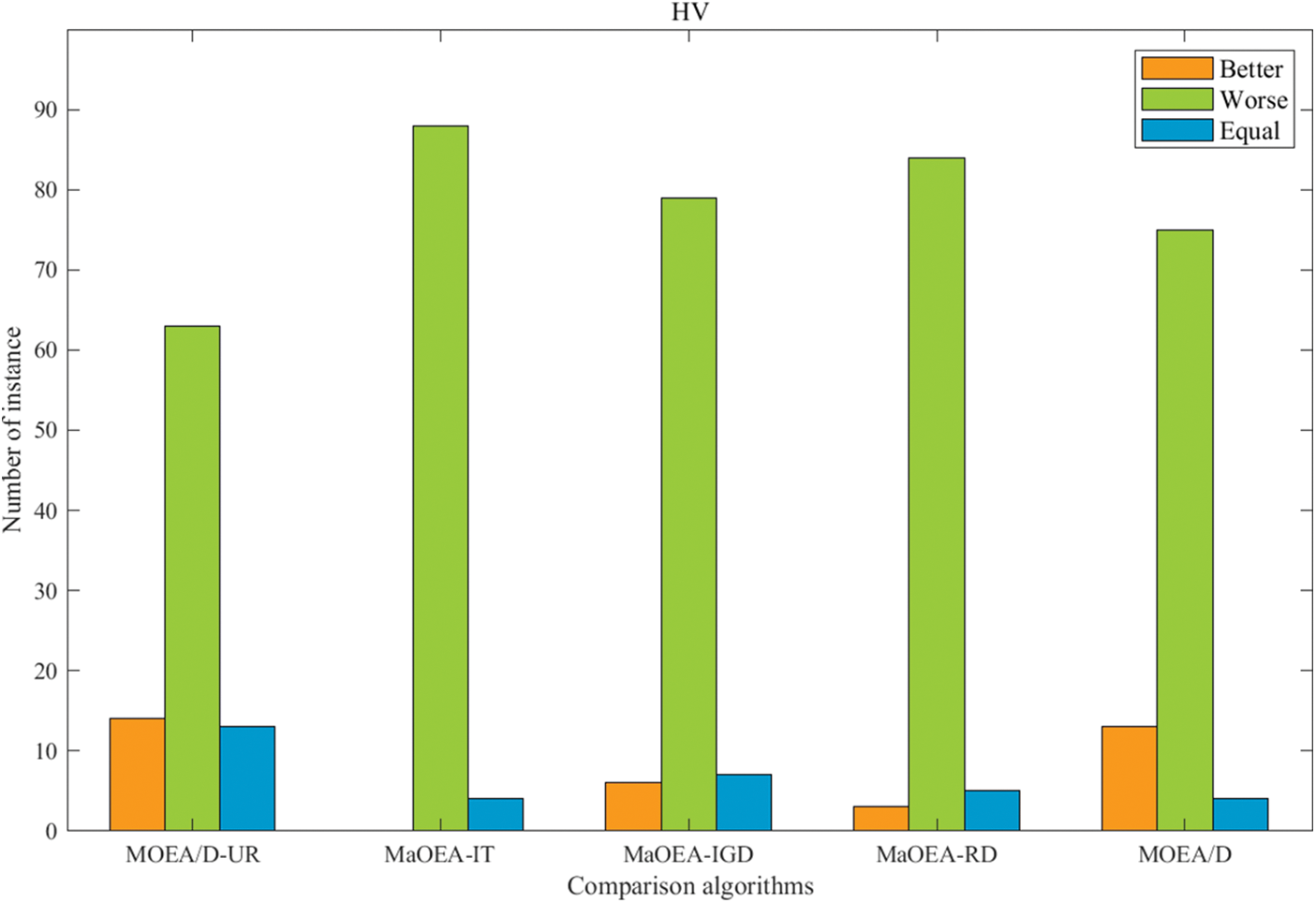
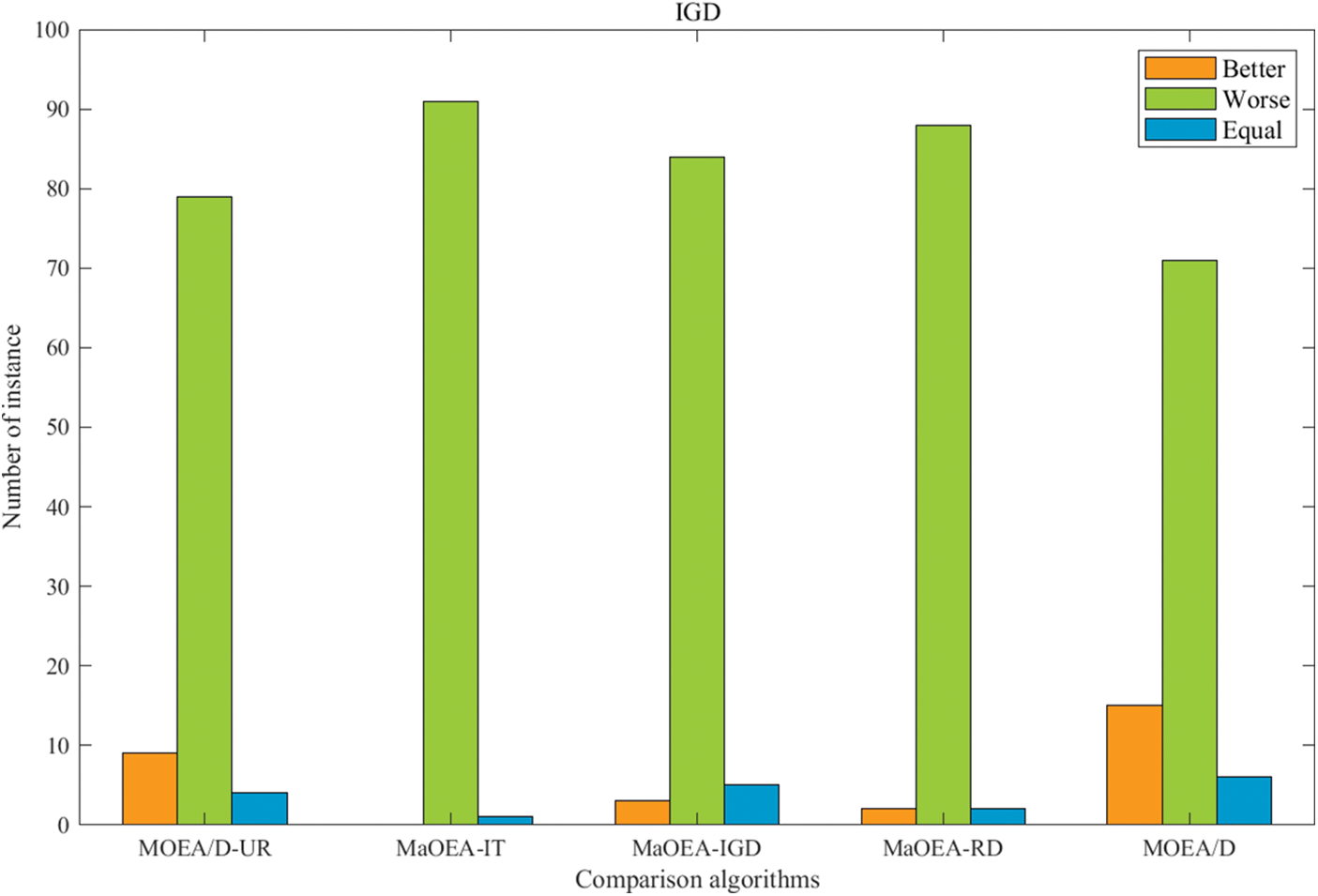
Figure 4: Wilcoxon rank sum test of MaOEA-AR on test instances in terms of HV and IGD
In this paper we conducted 5 groups of experiments to verify the performance of the algorithm and the effectiveness of each strategy. We conducted experiments on all three benchmark test suites, DTLZ, MaF and WFG. The results and analyses of the first group of DTLZ benchmark experiments and the second group of MaF benchmark experiments are given in the Supplementary Material, and the results and analyses of the third group of WFG benchmark experiments are given below. The 4th group of experiments are ablation experiments to validate the performance of the A-NDR and k-bit crossover strategies and the analysis of their results are also given in the Supplementary Material. The fifth group of experiments was designed to validate the algorithm’s ability to solve real-world problems, and in the following we give the results and analyses of the experiments that dealt with three real-world problems.
The experimental statistics of the six algorithms on the WFG test problem are given in Tables 4 and 5. MaOEA-AR has performed very competitively on most problems. In Table 4, we can see that WFG2 is a difficult problem, where PF is disconnected. Similar to other algorithms, MaOEA-AR does not handle this problem well, but MOEA/D-UR can solve the WFG2 problem well and obtain the best performance on its objectives in any dimension. This is because the decomposition-based algorithm predefines a set of well-distributed weight vectors that improve the diversity of the solutions obtained, in addition, the algorithm uses a specific mechanism to maintain a good balance between diversity and convergence. MaOEA-AR obtained 23 optimal values on 36 test problems, and optimal values on any dimension of the objective in WFG4, WFG5, WFG7 and WFG9. MOEA/D-UR followed closely behind, obtaining 11 optimal values. Only two optimal values were obtained for MaOEA-IGD. MaOEA-IT, MaOEA-RD and MOEA/D did not obtain optimal values. There are several reasons for this phenomenon: First, at mating selection, k-bit crossover was used to select excellent paternal individuals and a hybrid mutation strategy was used to generate high-quality offspring individuals; Secondly, the proposed A-NDR improves the selection pressure of the algorithm and ensures that the population can converge. Table 5 lists the IGD values for the six algorithms on the WFG problem. MaOEA-AR can handle all WFG problems except WFG3 very well. WFG3 is a difficult problem in which the PF is degenerate and the decision variables are non-separable. Similar to other algorithms, MaOEA-AR does not handle this problem well, but MOEA/D-UR can solve the WFG3 problem well and obtain the best performance on its objectives in any dimension. To better observe the performance of the six algorithms on the WFG problem, we chose to plot the PF obtained by each algorithm on a WFG9 of 15-objective. The PF of WFG9 is biased, multi-modal, deceptive and in-separable. It can be seen that MaOEA-AR, MOEA/D-UR and MaOEA-IGD have similar distributions, but MaOEA-AR has better performance. It not only converges to the true PF, but covers the true PF more extensively, indicating that it has better diversity. The second best is MOEA/D-UR, which also converges well to true PF, but does not cover 1-3-objective well and does not fully converge on 13-objective. This is followed by MaOEA-IGD, which also converges well to true PF but does not have good coverage on 5-15-objective. However, the PFs obtained by MaOEA-IT, MaOEA-RD and MOEA/D hardly cover the true PF. In addition, in Figs. 4 and 5, we can see that the visualization in the high-dimensional objective space is very poor, so we show in Fig. 6 the performance of each algorithm on the 3-objective problem, where the more complex WFG9 is still chosen for the test problem. Compared to other algorithms, the solutions obtained by MaOEA-AR in the figure cover the entire PF with a wide and uniform coverage. MOEA/D-UR, MaOEA-RD and MOEA/D can also cover the entire PF, but not uniformly. The solutions of MOEA/-UR and MOEA/D are concentrated around the second objective. The MaOEA-IT solution, on the other hand, is concentrated in the middle region and is less diverse. The solutions of MaOEA-IGD are distributed at the vertices of the three objectives.
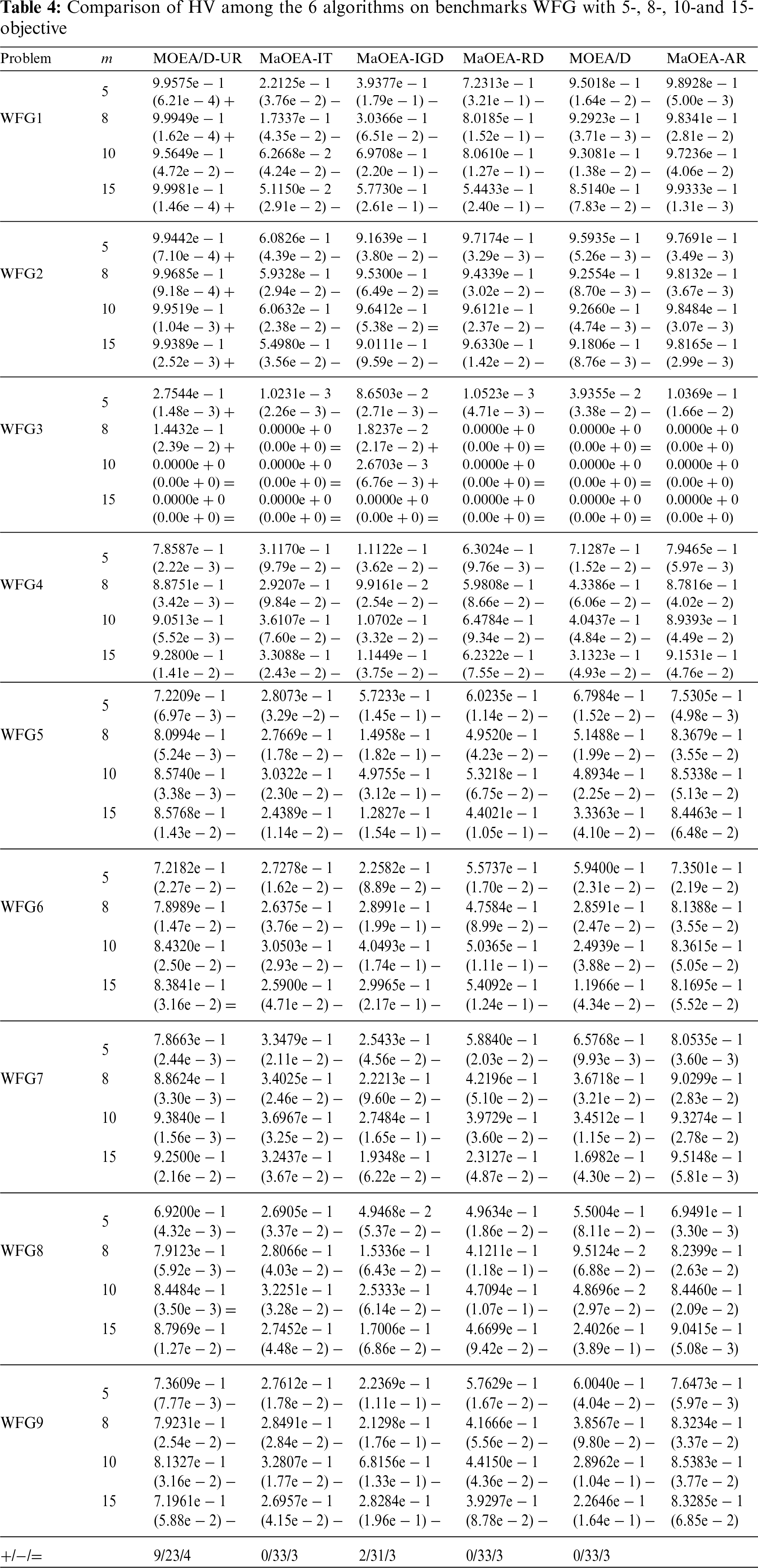
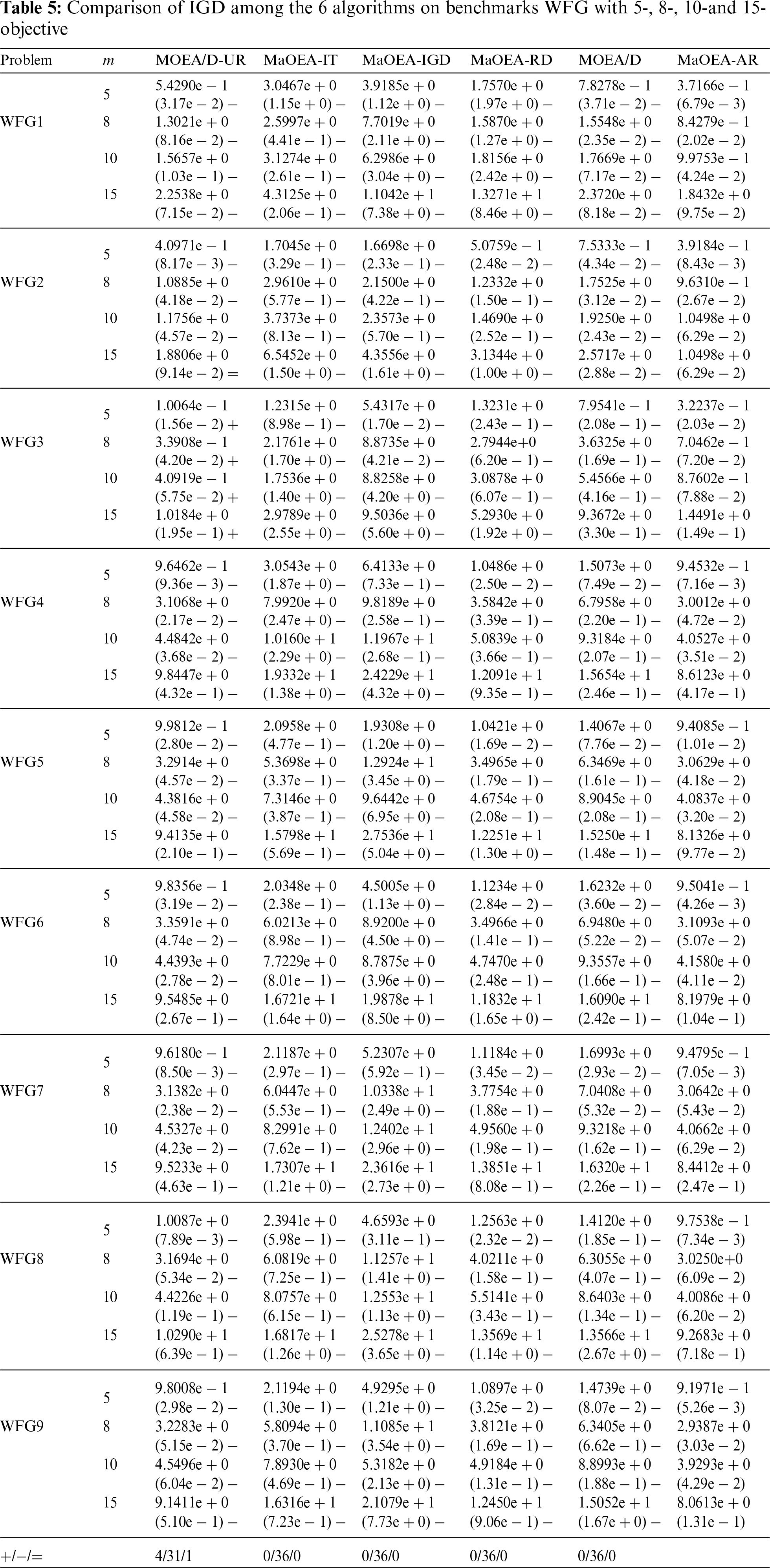
Figure 5: Distribution of solutions on WFG9 with 15-objective
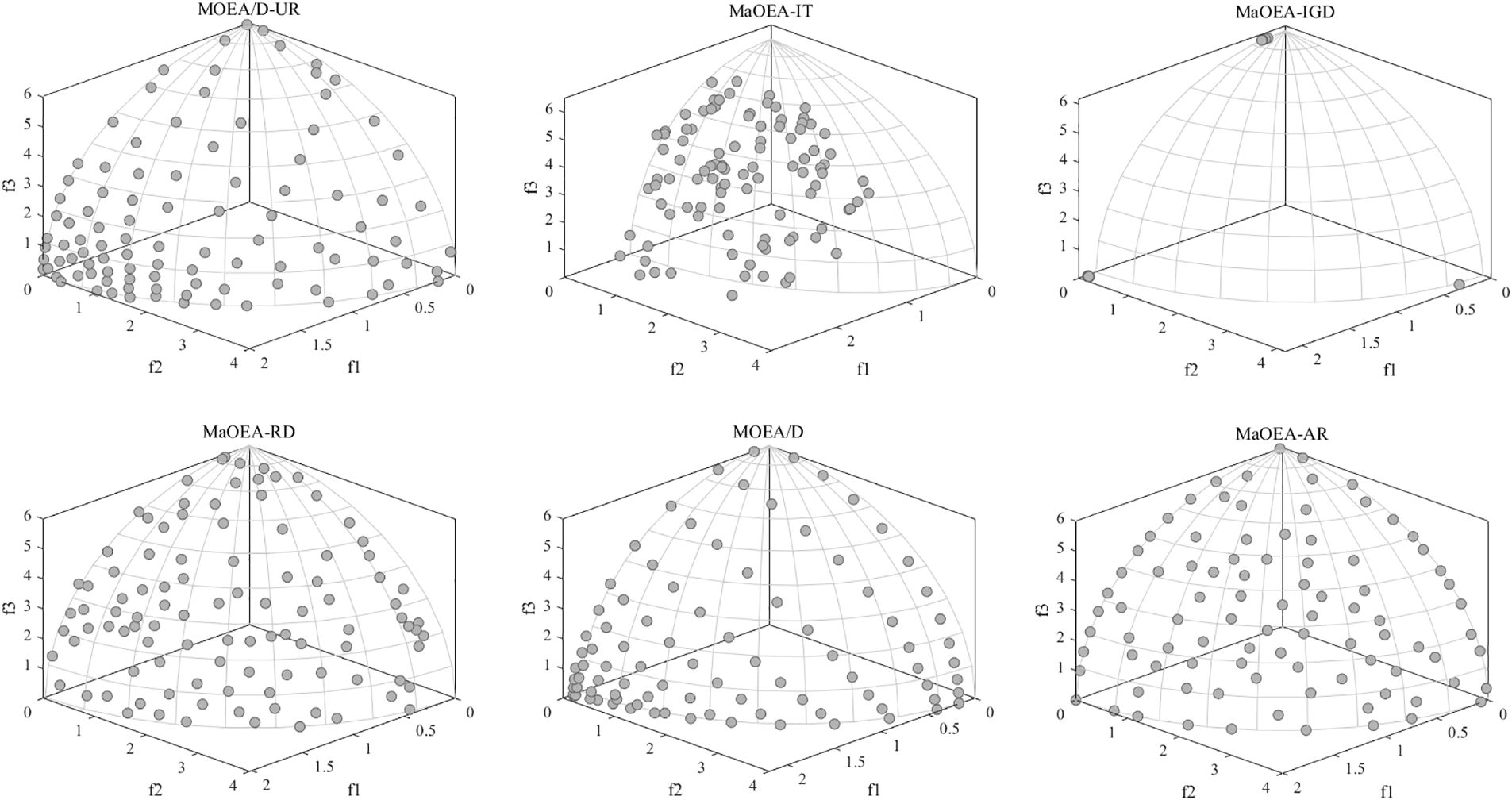
Figure 6: Distribution of solutions on WFG9 with 3-objective
To observe the evolution of the algorithms, the evolutionary trajectory of the IGD values of the experimental results obtained using the five state-of-the-art algorithms and MaOEA-AR on the 10-objectives DTLZ4, WFG4 and WFG9 are shown in Fig. 7. In these plots, the X-axis denotes the number of functional assessments, and the Y-axis denotes the value of the IGD indicator, with the data used for plotting obtained from the data closest to the average IGD value. Throughout the evolutionary process, MaOEA-AR significantly outperformed other algorithms on the DTLZ4, WFG4 and WFG9 problems, which makes it competitive in terms of the balance between convergence and diversity. It is clear from Fig. 7 that MaOEA-AR all converge very quickly and are more robust than the other five algorithms. MaOEA-AR converges steadily and rapidly during the evolution. This is because the population itself dynamically guides its evolution towards PF, and A-NDR accelerates its convergence.
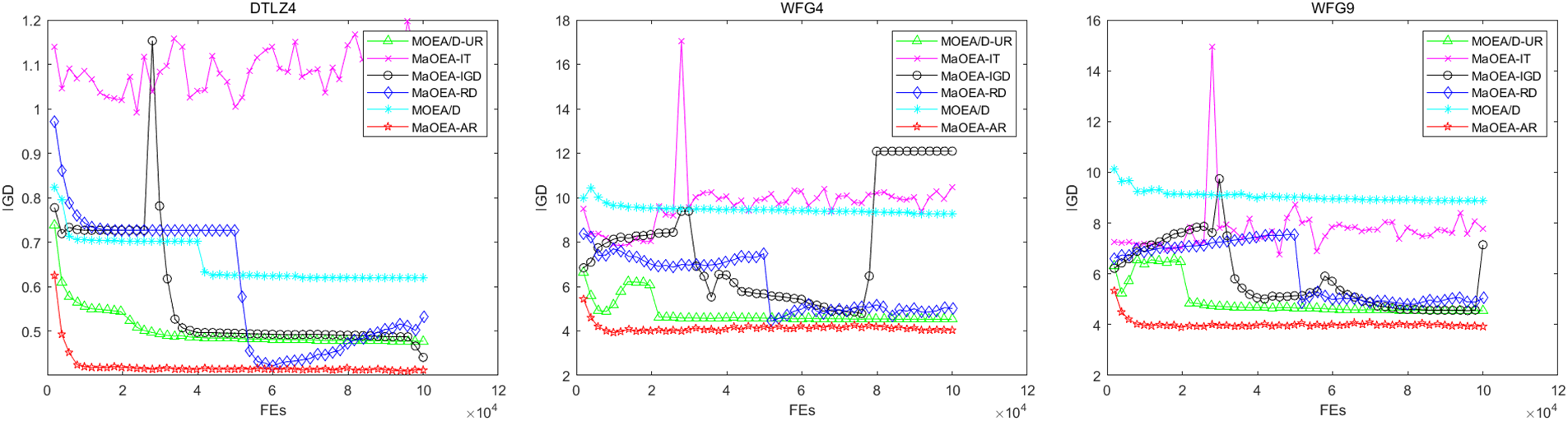
Figure 7: Convergence curves of the algorithms IGD on DTLZ4, WFG4 and WFG9 with 10-objective
3.4.2 Performance on Real-World Applications
To verify the algorithm’s ability to solve real-world optimization problems, three of the many-objective test problems from the RE test suite were selected to validate MaOEA-AR’s ability to solve real-world problems. The RE test suite consists of 16 real-world problems with bounded constraints, we have chosen among them RE4-7-1, RE4-6-2 and RE6-3-1 for experiments, whose corresponding real-world problems and their characteristics are given in Table 6. We refer to the settings in [34], where the population size is 120 when m = 4, and when m = 6, the population size is 182. The other parameters for each algorithm are set as shown in Section 3.3. In [35], it was noted that setting maxFEs to a small value estimates the performance of the algorithm on expensive problems. We referenced this study and also set the maxFEs to 10,000 in our experiments. Table 7 lists the HV averages obtained from 20 independent runs of the six algorithms on three real-world problems. The MaOEA-IGD solution on the RE4-6-2 problem deviates from the true PF and obtains a HV value of NaN. The experimental results show that MaOEA-AR significantly outperforms the other five algorithms.
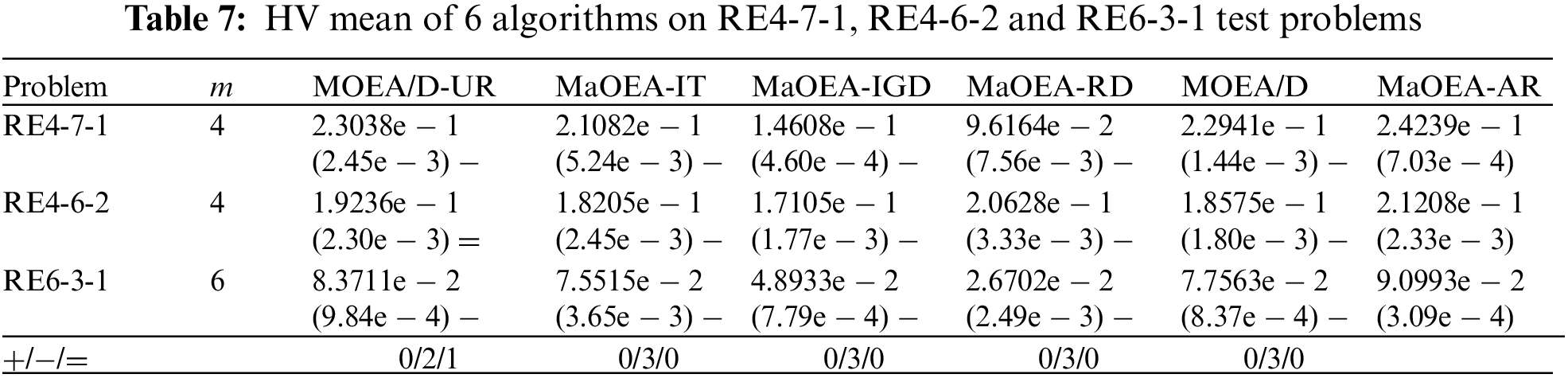
The above experimental results show that MaOEA-AR has strong competitiveness in these conventional problems and some real-world representative problems. This can be explained by the fact that our adaptive niche dominance relation is different from the traditional Pareto dominance relations and the existing improved dominance. Most dominance relations can only find a set of solutions concentrated in a small area on the Pareto front. In this study, we used a customized niche technique to balance the diversity of non-dominated convergence, which generates selection pressure even in the high-dimensional objective space, and comparability between non-dominated solutions, alleviating the dominance resistance phenomenon. In the process of generating offspring, we used k-bit crossover and hybrid mutation instead of traditional mutation operators to generate high-quality offspring, which further improves the selection pressure of the algorithm. In addition, we used the APD to dynamically balance the convergence and diversity of the algorithm during environment selection. However, MaOEA-AR is less effective at dealing with degenerate and irregular problems.
In this study, we proposed a reference vector-assisted algorithm MaOEA-AR with an adaptive niche dominance relation to solve MaOPs. We balance the convergence and diversity of the non-dominated solution set by a customized niche technique, where the convergence indicator is determined by the ratio of the distance from the ideal point to the solution and the distance from the ideal point to the hyperplane to select the appropriate convergence indicator by determining the PF shape to maximize the selection pressure of the algorithm. When reproducing offspring are generated, k-bit crossover and hybrid mutations are selected to generate high-quality offspring. Finally, in environment selection, the APD is used to sample solutions with good convergence and diversity. MaOEA-AR was tested with five state-of-the-art algorithms with up to 15-objective on 23 test problems in the DTLZ, MaF and WFG benchmark test suites, as well as on three test problems from the real-world test set RE. The experimental results show that the performance of MaOEA-AR is significantly better than the other five algorithms and has strong competitiveness. In the future, we will optimize the performance of the algorithm to solve degenerate and discontinuous problems, and apply the algorithm to more practical applications.
Acknowledgement: We thank PlatEMO, an evolutionary multi-objective optimization platform developed by BIMK group at Anhui University, for providing us with a good experimental environment.
Funding Statement: This research is supported by the National Natural Science Foundation of China (Grant No. 61976101), the University Natural Science Research Project of Anhui Province (Grant No. 2023AH040056), the Natural Science Research Project of Anhui Province (Graduate Research Project, Grant No. YJS20210463), the Funding Plan for Scientic Research Activities of Academic and Technical Leaders and Reserve Candidates in Anhui Province (Grant No. 2021H264), the Top Talent Project of Disciplines (Majors) in Colleges and Universities in Anhui Province (Grant No. gxbjZD2022021), the University Synergy Innovation Program of Anhui Province, China (GXXT-2022-033) and supported by the Innovation Fund for Postgraduates of Huaibei Normal University (Grant Nos. cx2022041, yx2021023, CX2023043). We would like to thank Editage (www.editage.cn) for English language editing.
Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization of this study, Methodology, Software, Writing: Yating Wu; Supervision, Writing-review & editing, Funding acquisition: Fangzhen Ge; Visualization, Investigation: Debao Chen; Supervision: Longfeng Shen. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The experiment in this paper is a simulation experiment, which is completed on the evolutionary multi-objective optimization platform PlatEMO. The comparison algorithm and test function are all from this platform. The experimental data can be found in this paper and Supplementary Material.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
Supplementary Materials: The supplementary material is available online at https://doi.org/10.32604/iasc.2024.042841.
References
1. J. L. Xu, Z. X. Zhang, Z. M. Hu, L. Du, and X. J. Cai, “A many-objective optimized task allocation scheduling model in cloud computing,” Appl. Intell., vol. 51, no. 6, pp. 3293–3310, 2021. doi: 10.1007/s10489-022-03963-w. [Google Scholar] [CrossRef]
2. L. B. Ma et al., “Learning to optimize: Reference vector reinforcement learning adaption to constrained many-objective optimization of industrial copper burdening system,” IEEE Trans. Cybern., vol. 52, no. 12, pp. 12698–12711, Dec. 2022. doi: 10.1109/TCYB.2021.3086501 [Google Scholar] [PubMed] [CrossRef]
3. Z. Y. Hu, Z. H. Wei, H. Sun, J. M. Yang, and L. X. Wei, “Optimization of metal rolling control using soft computing approaches: A review,” Arch. Comput. Method Eng., vol. 28, no. 2, pp. 405–421, 2021. doi: 10.1007/s11831-018-9250-y. [Google Scholar] [CrossRef]
4. X. F. Liu, Z. H. Zhan, and J. Zhang, “Resource-aware distributed differential evolution for training expensive neural-network-based controller in power electronic circuit,” IEEE Trans. Neural Netw. Learn. Syst., vol. 33, no. 11, pp. 6286–6296, 2022. doi: 10.1109/TNNLS.2021.3075205 [Google Scholar] [PubMed] [CrossRef]
5. M. Farina and P. Amato, “On the optimal solution definition for many-criteria optimization problems,” in 2002 Annu. Meet. North Am. Fuzzy Inf. Process. Soc. Proc. NAFIPS-FLINT 2002 (Cat. No. 02TH8622), New Orleans, LA, USA, 2002, pp. 233–238. [Google Scholar]
6. R. C. Purshouse and P. J. Fleming, “On the evolutionary optimization of many conflicting objectives,” IEEE Trans. Evolut. Comput., vol. 11, no. 6, pp. 770–784, 2007. doi: 10.1109/TEVC.2007.910138. [Google Scholar] [CrossRef]
7. M. Laumanns, L. Thiele, K. Deb, and E. Zitzler, “Combining convergence and diversity in evolutionary multi-objective optimization,” Evol. Comput., vol. 10, no. 3, pp. 263–282, 2002. doi: 10.1162/106365602760234108 [Google Scholar] [PubMed] [CrossRef]
8. S. X. Yang, M. Q. Li, X. H. Liu, and J. H. Zheng, “A grid-based evolutionary algorithm for many-objective optimization,” IEEE Trans. Evolut. Comput., vol. 17, no. 5, pp. 721–736, 2013. doi: 10.1109/TEVC.2012.2227145. [Google Scholar] [CrossRef]
9. Q. F. Zhang and H. Li, “MOEA/D: A multi-objective evolutionary algorithm based on decomposition,” IEEE Trans. Evolut. Comput., vol. 11, no. 6, pp. 712–731, 2007. doi: 10.1109/TEVC.2007.892759. [Google Scholar] [CrossRef]
10. H. L. Liu, F. Q. Gu, and Q. F. Zhang, “Decomposition of a multi-objective optimization problem into a number of simple multi-objective sub-problems,” IEEE Trans. Evolut. Comput., vol. 18, no. 3, pp. 450–455, 2014. doi: 10.1109/TEVC.2013.2281533. [Google Scholar] [CrossRef]
11. L. B. Ma, M. Huang, S. X. Yang, R. Wang, and X. W. Wang, “An adaptive localized decision variable analysis approach to large-scale multi-objective and many-objective optimization,” IEEE Trans. Cybern., vol. 52, no. 7, pp. 6684–6696, Jul. 2022. doi: 10.1109/TCYB.2020.3041212 [Google Scholar] [PubMed] [CrossRef]
12. D. Brockhoff and E. Zitzler, “Improving hypervolume-based multi-objective evolutionary algorithms by using objective reduction methods,” in 2007 IEEE Congr. Evol. Comput., Singapore, 2007, pp. 2086–2093. [Google Scholar]
13. Y. N. Sun, G. G. Yen, and Y. Zhang, “IGD indicator-based evolutionary algorithm for many-objective optimization problems,” IEEE Trans. Evolut. Comput., vol. 23, no. 2, pp. 173–187, 2019. doi: 10.1109/TEVC.2018.2791283. [Google Scholar] [CrossRef]
14. E. M. Lopez and C. A. C. Coello, “IGD+-EMOA: A multi-objective evolutionary algorithm based on IGD+,” in 2016 IEEE Congr. Evol. Comput., Vancouver, BC, Canada, 2016, pp. 999–1006. [Google Scholar]
15. J. W. Yuan, H. L. Liu, F. Q. Gu, Q. F. Zhang, and Z. S. He, “Investigating the properties of indicators and an evolutionary many-objective algorithm using promising regions,” IEEE Trans. Evolut. Comput., vol. 25, no. 1, pp. 75–86, 2021. doi: 10.1109/TEVC.2020.2999100. [Google Scholar] [CrossRef]
16. Z. S. Song, H. D. Wang, C. He, and Y. C. Jin, “A kriging-assisted two-archive evolutionary algorithm for expensive many-objective optimization,” IEEE Trans. Evolut. Comput., vol. 25, no. 6, pp. 1013–1027, 2021. doi: 10.1109/TEVC.2021.3073648. [Google Scholar] [CrossRef]
17. K. Li, K. Deb, Q. F. Zhang, and S. Kwong, “An evolutionary many-objective optimization algorithm based on dominance and decomposition,” IEEE Trans. Evolut. Comput., vol. 19, no. 5, pp. 694–716, 2015. doi: 10.1016/j.knosys.2021.107392. [Google Scholar] [CrossRef]
18. H. Xu, B. Xue, and M. J. Zhang, “A duplication analysis-based evolutionary algorithm for bi-objective feature selection,” IEEE Trans. Evolut. Comput., vol. 2, no. 2, pp. 205–218, 2021. doi: 10.1109/TEVC.2020.3016049. [Google Scholar] [CrossRef]
19. R. Cheng, Y. C. Jin, M. Olhofer, and B. Sendhoff, “A reference vector guided evolutionary algorithm for many-objective optimization,” IEEE Trans. Evolut. Comput., vol. 20, no. 5, pp. 773–791, 2016. doi: 10.1109/TEVC.2016.2519378. [Google Scholar] [CrossRef]
20. Q. Q. Liu, Y. C. Jin, M. Heiderich, T. Rodemann, and Y. Guo, “An adaptive reference vector-guided evolutionary algorithm using growing neural gas for many-objective optimization of irregular problems,” IEEE Trans. Cybern., vol. 52, no. 5, pp. 2698–2711, 2022. doi: 10.1109/TCYB.2020.3020630 [Google Scholar] [PubMed] [CrossRef]
21. B. H. Nguyen, B. Xue, P. Andreae, H. Ishibuchi, and M. J. Zhang, “Multiple reference points-based decomposition for multi-objective feature selection in classification: Static and dynamic mechanisms,” IEEE Trans. Evolut. Comput., vol. 24, no. 1, pp. 170–184, 2020. doi: 10.1109/TEVC.2019.2913831. [Google Scholar] [CrossRef]
22. Y. Tian, R. Cheng, X. Y. Zhang, Y. S. Su, and Y. C. Jin, “A strengthened dominance relation considering convergence and diversity for evolutionary many-objective optimization,” IEEE Trans. Evolut. Comput., vol. 23, no. 2, pp. 331–345, 2019. doi: 10.1109/TEVC.2018.2866854. [Google Scholar] [CrossRef]
23. L. Li, G. G. Yen, A. Sahoo, L. Chang, and T. Gu, “On the estimation of pareto front and dimensional similarity in many-objective evolutionary algorithm,” Inform. Sci., vol. 563, pp. 375–400, 2021. doi: 10.1016/j.ins.2021.03.008. [Google Scholar] [CrossRef]
24. K. Deb and H. Jain, “An evolutionary many-objective optimization algorithm using reference-point-based non-dominated sorting approach, part I: Solving problems with box constraints,” IEEE Trans. Evolut. Comput., vol. 18, no. 4, pp. 577–601, 2014. doi: 10.1109/TEVC.2013.2281535. [Google Scholar] [CrossRef]
25. K. Deb, L. Thiele, M. Laumanns, and E. Zitzler, “Scalable test problems for evolutionary multi-objective optimization,” in Proc. 2002 Congr. Evol. Comput. (Cat. No.02TH8600), Singapore, 2002, pp. 105–145. [Google Scholar]
26. R. Cheng et al., “A benchmark test suite for evolutionary many-objective optimization,” Complex Intell. Syst., vol. 3, no. 1, pp. 67–81, 2017. [Google Scholar]
27. S. Huband, P. Hingston, L. Barone, and L. While, “A review of multi-objective test problems and a scalable test problem toolkit,” IEEE Trans. Evolut. Comput., vol. 10, no. 5, pp. 477–506, 2006. doi: 10.1109/TEVC.2005.861417. [Google Scholar] [CrossRef]
28. Y. N. Sun, B. Xue, M. J. Zhang, and G. G. Yen, “A new two-stage evolutionary algorithm for many-objective optimization,” IEEE Trans. Evolut. Comput., vol. 23, no. 5, pp. 748–761, 2019. doi: 10.1109/TEVC.2018.2882166. [Google Scholar] [CrossRef]
29. Z. He and G. G. Yen, “Many-objective evolutionary algorithm: Objective space reduction and diversity improvement,” IEEE Trans. Evolut. Comput., vol. 20, no. 1, pp. 145–160, 2016. doi: 10.1109/TEVC.2015.2433266. [Google Scholar] [CrossRef]
30. L. R. C. de Farias and A. F. R. Araujo, “A decomposition-based many-objective evolutionary algorithm updating weights when required,” Swarm and Evolutionary Computation. vol. 68. pp. 100980, Feb. 2022. [Google Scholar]
31. L. While, P. Hingston, L. Barone, and S. Huband, “A faster algorithm for calculating hypervolume,” IEEE Trans. Evolut. Comput., vol. 10, no. 1, pp. 29–38, 2006. doi: 10.1109/TEVC.2005.851275. [Google Scholar] [CrossRef]
32. E. Zitzler, L. Thiele, and M. Laumanns, “Performance assessment of multi-objective optimizers: An analysis and review,” IEEE Trans. Evolut. Comput., vol. 7, no. 2, pp. 117–132, 2003. doi: 10.1109/TEVC.2003.810758. [Google Scholar] [CrossRef]
33. Y. Tian, R. Cheng, X. Y. Zhang, and Y. C. Jin, “PlatEMO: A MATLAB platform for evolutionary multi-objective optimization [educational forum],” IEEE Comput. Intell. Mag., vol. 12, no. 4, pp. 73–87, 2017. doi: 10.1109/MCI.2017.2742868. [Google Scholar] [CrossRef]
34. R. Tanabe and H. Ishibuchi, “An easy-to-use real-world multi-objective optimization problem suite,” Appl. Soft. Comput., vol. 89, pp. 106078, Apr. 2020. doi: 10.1016/j.asoc.2020.106078. [Google Scholar] [CrossRef]
35. Q. L. Zhu et al., “An elite gene guided reproduction operator for many-objective optimization,” IEEE Trans. Cybern., vol. 51, no. 2, pp. 765–778, 2021. doi: 10.1109/TCYB.2019.2932451 [Google Scholar] [PubMed] [CrossRef]
36. H. Jain and K. Deb, “An evolutionary many-objective optimization algorithm using reference-point based non-dominated sorting approach, part II: Handling constraints and extending to an adaptive approach,” IEEE Trans. Evolut. Comput., vol. 18, no. 4, pp. 602–622, 2013. doi: 10.1109/TEVC.2013.2281534. [Google Scholar] [CrossRef]
37. M. G. Parsons and R. L. Scott, “Formulation of multi-criterion design optimization problems for solution with scalar numerical optimization methods,” J. Ship. Res., vol. 48, no. 1, pp. 61–76, 2004. doi: 10.5957/jsr.2004.48.1.61. [Google Scholar] [CrossRef]
38. T. Ray, K. Tai, and K. C. Seow, “Multi-objective design optimization by an evolutionary algorithm,” Eng. Optimiz., vol. 33, no. 4, pp. 399–424, 2001. [Google Scholar]
Supplementary Materials
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF
 Downloads
Downloads
 Citation Tools
Citation Tools
