Trading in Fast-Changing Markets with Meta-Reinforcement Learning

1  Introduction

Algorithmic trading, using mathematical models and computers to automate the buying and selling of financial securities, has created new opportunities as well as new challenges for the financial industry over the last few decades [1]. A variety of trading strategies, such as statistical arbitrage [2], momentum trading [3] and mean regression trading [4], have been proposed by applying mathematical and statistical methods. Due to the low signal-to-noise ratio of financial data and the non-linear nature of markets, the design of trading strategies for algorithmic trading systems is non-trivial [5].

The goal of trading strategies is to maximize the wealth accumulation during a trading period. The final wealth depends upon the sequences of interdependent trading actions in which optimal trading decisions do not just decide immediate trade returns but also affect subsequent future returns. The trading problem fits exactly with the framework of reinforcement learning (RL). Deep reinforcement learning (DRL), which effectively combines deep learning and reinforcement learning, has recently witnessed significant advances in various domains. Peters et al. [6] applied vanilla policy gradient (VPG) to robotics and evaluated its performance in hitting a baseball with an anthropomorphic arm. Schulman et al. [7] proposed a new family of policy gradient methods called proximal policy optimization (PPO) for robotic locomotion and Atari game playing.

Deep learning can automatically extract complex and implicit features from large amounts of data [8]. DRL combines the feature extraction capabilities of deep learning and the decision-making abilities of reinforcement learning, hence adapting for developing trading strategies in a highly noisy financial market with nonlinear dynamics. Andrew et al. [9] developed a paired trading strategy in the stock market that can be effectively learned and executed using a double deep Q-network. Lee et al. [10] presented a trading strategy that leverages wavelet transform and deep reinforcement learning, through decomposing input data within wavelet transformation and utilizing high-frequency data to perform deep reinforcement learning with a long short-term memory network.

Challenges remain in developing effective trading policies using DRL due to a combination of nonlinear and non-stationary dynamic behaviors exhibited within financial markets. The non-stationary behavior refers to the time-varying nature of the underlying distributions, which is marked by variations in the first, second, or higher moments shown in stochastic processes over time, and this is especially true in financial markets [11,12]. However, it is difficult for DRL to deal with non-stationary financial markets since it is notably sample inefficient. An optimal trading model can only be learned slowly through many iterative steps over many samples. Therefore, it is hard for DRL to keep pace with the time-varying nature of financial markets.

Meta-reinforcement learning (Meta-RL) can quickly adapt to new environment tasks by parameter updates using a small number of samples [13–16]. It has been used to tackle the control problem in a dynamic environment. Finn et al. [13] developed a model agnostic meta-learning (MAML) method and applied it in simulated continuous control environments. Maruan et al. [14] proposed a Meta-RL method for adaption in non-stationary locomotion and competitive multi-agent settings. Liaw et al. [15] put forward a meta-policy learning method which can realize efficient task executions in an autonomous driving simulator. Huang et al. [16] applied a meta-reinforcement learning method to grid emergency control, demonstrating its capability to quickly adapt to new power flow conditions and system dynamic parameters. To the best of our knowledge, there is no work that has investigated the realistic trading conditions and studied the possibility for trading in fast-changing financial markets using Meta-RL.

As aforementioned, RL methods may fail to adapt rapidly enough in highly dynamic financial environments because only a limited number of interactions are permitted before the market starts changing. This paper proposes a MAML-based trading method, which consists of a PPO meta-learner and a VPG learner, to deal with trading challenges encountered by traditional RL in a non-stationary financial market. Firstly, the training data is divided into multiple task data for fixed periods, so the market represented by each task data is relatively stationary during such a small period. Secondly, an easily adaptable trading policy is learned across the multiple task data by the PPO meta-learner. Finally, when trading in a new market task, the learned policy is updated by the VPG learner through the data available from the new task, and then the updated policy is used to trade in the rest part of the market task. Moreover, to improve the adaptability of the MAML-based trading method in fast-changing market conditions, an ordered multiple-step updating mechanism is introduced in the MAML-based trading method.

The rest of this article is organized as follows. In Section 2, the proposed trading method based on MAML and its improvement are described in detail. The experimental results of different trading methods on IF300, CSI500, and Dow Jones index and the investigation on the effectiveness of mechanism updating are presented in Section 3. Section 4 delivers the conclusion of this study.

2  Methodology

In this section, we model the trading problem as a Markov decision process, introduce a traditional RL-based trading method, and propose the Meta-RL-based trading method and its improved version.

2.1 Markov Decision Process Formalization for Trading

The trading problem can be modeled as a Markov decision process, where a trading agent interacts with the market environment at discrete time steps. At each time step t, the agent receives a state st as a representation of the market, then chooses a trading action at and executes it on the market, and finally calculates the immediate profit as a reward Rt+1 according to the new market state st+1 at the next time step.

State space: Since the market state is partially observed, this paper uses the past price spreads of securities, technical indicators including MACD and RSI, and the last trading action to represent the market state.

The MACD index can be calculated as follows (Baz et al. [17]):

MACDt=DEAt−DIFtDIFt=m(pt−12:t)−m(pt−26:t)DEAt=m(DIFt−9:t)(1)

m(pt−n:t) denotes the exponentially weighted moving average of prices over a time horizon n.

The RSI index (Wilder [18]) is

RSI=AULAUL+ADL⋅(2)

AUL and ADL represent the average upward price movements and downward price movements over a period of time, respectively.

Action space: A discrete action space {−1, 0, +1} is used for trading, where −1 corresponds to a maximal short position, 0 to no holdings, and +1 to a maximal long position.

Reward function: The value of the reward function at time t can be evaluated as follows, where bp represents the transaction cost rate.

Rt=at(pt−pt−1)−bp⋅pt|at−at−1|(3)

The trading goal is to maximize the expected cumulative discounted rewards, where γ is the discounting factor.

G=∑t=1Hrt−1Rt(4)

2.2 Trading Method Based on VPG

For simplicity of calculation, the Vanilla Policy Gradients (VPG)-based method is taken as a baseline in this paper. In VPG, the trading policy πθ, which takes the market state as the input and outputs the trading action, is parameterized using a neural network with parameters θ. The VPG learns an optimal policy by the stochastic gradient descent algorithm to minimize the loss, which is a negative expected cumulative reward defined in (4).

θ=θ−α∇θL(θ)(5)

According to the policy gradient theorem [19], the gradient can be calculated with the surrogate loss

L(θ)=−Eτ∼πθ[∑t=1Hlogπθ(at|st)A^t](6)

τ=[s0,a0,r1,s1,a1,r2,…] is a trajectory sampled by policy πθ. A^t represents an advantage value over the trajectory assessing the good of action at at state st, which can be estimated by the generalized advantage function

A^t=δt+γλδt+1+…+(γλ)H−t−1δH−1(7)

λ is the hyperparameter. δt is the temporal difference error, which can be calculated based on the parameterized value function as follows:

δt=Rt+1+γV(st+1,w)−V(st,w)(8)

The least squares method is used to estimate the value function

w∗=argminw⁡Eπθ[(G−V(s,w))2](9)

where the linear value function estimation is used to directly obtain the least squares solution of the value function weights.

An optimal trading policy is learned using VPG on the history trading data of a financial market, then the policy is used to trade in the market in the future. The learned trading policy will degenerate over time if the market is non-stationary and the market dynamic will go differently from that of the training market.

2.3 Trading Method Based on MAML

To deal with the trading challenges encountered by traditional RL, such as VPG, in a non-stationary financial market, this paper applies meta-reinforcement learning to seek trading policies with quick adaption to new environment tasks. Specifically, this paper proposes a MAML-based trading method consisting of a PPO meta-learner and a VPG learner.

The history trading data is firstly divided into a number of episodes with a fixed length H. A task data contains Ns+1 consecutive episodes, where the first Ns episodes compose the support part and the last episode is the query part.

M task data are randomly sampled for each iteration during training. For task i, policy πθi′ can be achieved from an initial policy πθ by the VPG learner with one step update on its support part.

θi′=θ−α∇θ1Ns∑j=1NsLi,j(τθ1:K)(10)

where α is the step size. Li,j(τθ1:K) indicates the surrogate loss on K trajectories produced by policy πθ from the j-th episode of the support part of task i, which is calculated according to (6). The obtained policy can be used on the query part of the same task market since the market condition represented by one task data is relatively stationary for a short period.

A good initial policy πθ is learned by the PPO meta-learner across multiple tasks from a random policy, which can quickly adapt to a new task market with one or a few update steps on a small number of samples. The parameter update of the initial policy on the query part of randomly sampled M tasks is

θ=θ−β∇θ1M∑i=1MLi;q(πθi′)(11)

where β is the step size for meta updates. The loss on the query part of task i, Li;q(πθi′), to be minimized is defined as

Li;q(πθi′)=−Est,at∼πθi′[min(rt(θi′)A^t, clip(rt(θi′),ε)A^t)](12)

rt(θi′)=πθi′(at|st)πθold,i′(at|st)(13)

For each iteration of the meta-update process, πθold is the initial policy without being optimized and πθ is the recently optimized initial policy. The meta loss is computed in (12) and optimized with respect to θ for T steps, with each step being updated according to (11). πθold,i′ and πθi′ are achieved from πθold and πθ by the VPG learner with one step update on the support part of task i as given in (10), respectively.

The PPO is used as a meta-learner here since it can reuse the generated trajectories and prevent destructively large policy updates. Therefore, a good initial policy can be learned stably by the PPO meta-learner with a small number of tasks. The framework of the MAML-based trading method is shown in Fig. 1.

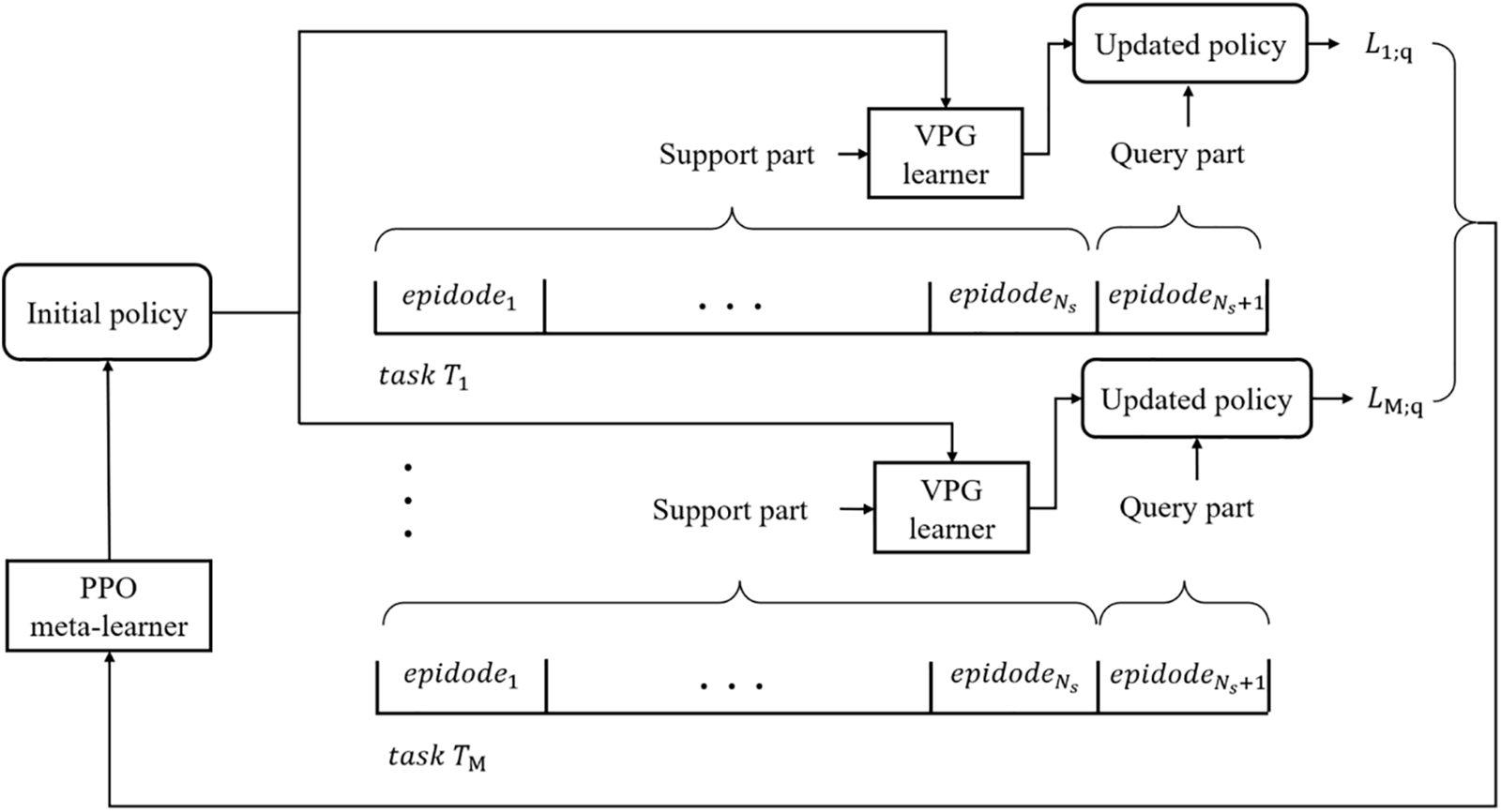
Figure 1: Framework of the MAML-based trading method

2.4 MAML-Based Trading Method with Ordered Multiple-Step Updating

To improve the adaptability of the MAML-based trading method in fast-changing markets, an ordered multiple-step updating mechanism is proposed to couple with the MAML framework. The dynamically changing market within a task is explored by updating the learned initial trading policy through sequential updates on the episodes of the support part data before being applied to trade in the query part of the task market. The ordered multiple-step updating mechanism is formulated as

θij+1=θij−α∇θijLi,j(τθij1:K),j=1,2,…,Ns(14)

where θi1=θ are the parameters of the common initial policy for every task market learned by the PPO meta-learner. The equation describes that the latest policy parameters θij after j-1 steps update from initial policy parameters are updated to θij+1 with K trajectories on the j-th episode of the support part produced by πθij, which will in turn be updated on the (j+1)-th episode. The final policy πθiNs+1=πθi′ updated on the last episode of the support part will be used to trade in the query part of the same task market.

3  Experimental Results and Evaluation

The experimental results of different trading methods used on IF300, CSI500, and DJI are presented and analyzed in this section. The results of different updating mechanisms applied in the MAML method are also provided and evaluated.

3.1 Experimental Setup

This paper conducts experiments on the stock index futures of China IF300, CSI500, and the US Dow Jones stock index (DJI). The daily closing price data are used as shown in Fig. 2. The training period is from January 04, 2013 to November 26, 2020, and the testing period is from November 27, 2020 to November 25, 2022.

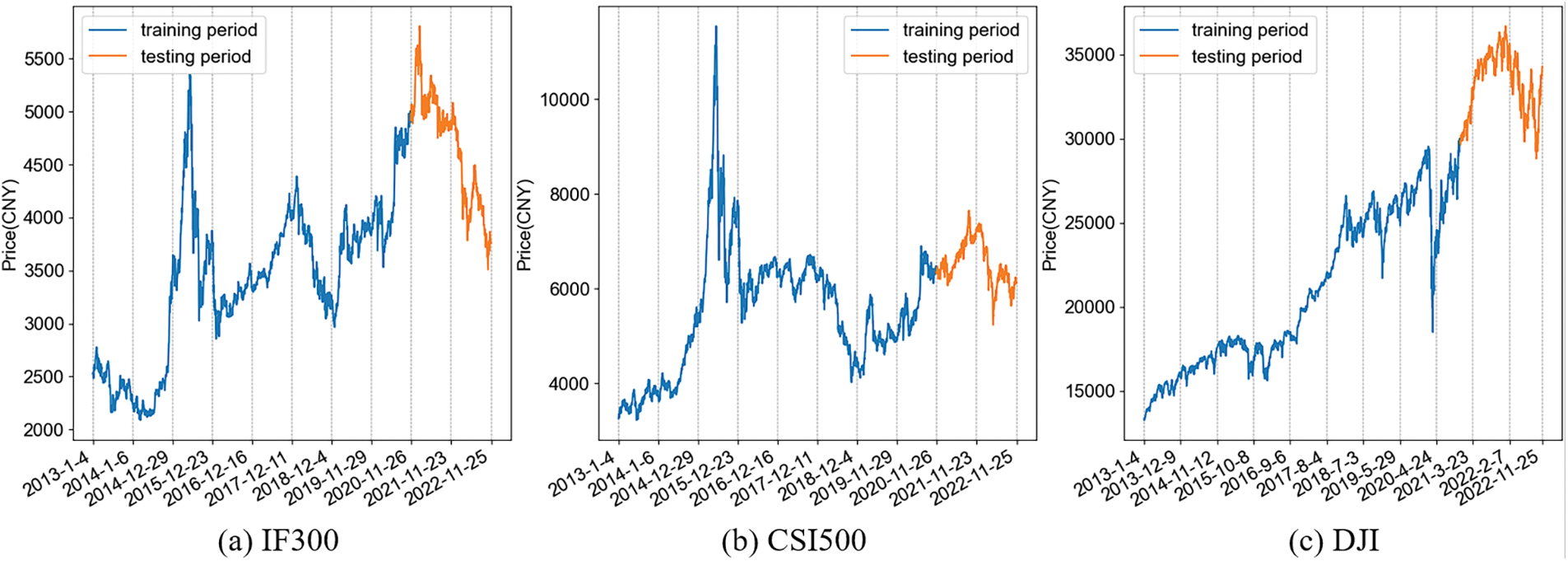
Figure 2: Daily closing price of IF300, CSI500, and DJI

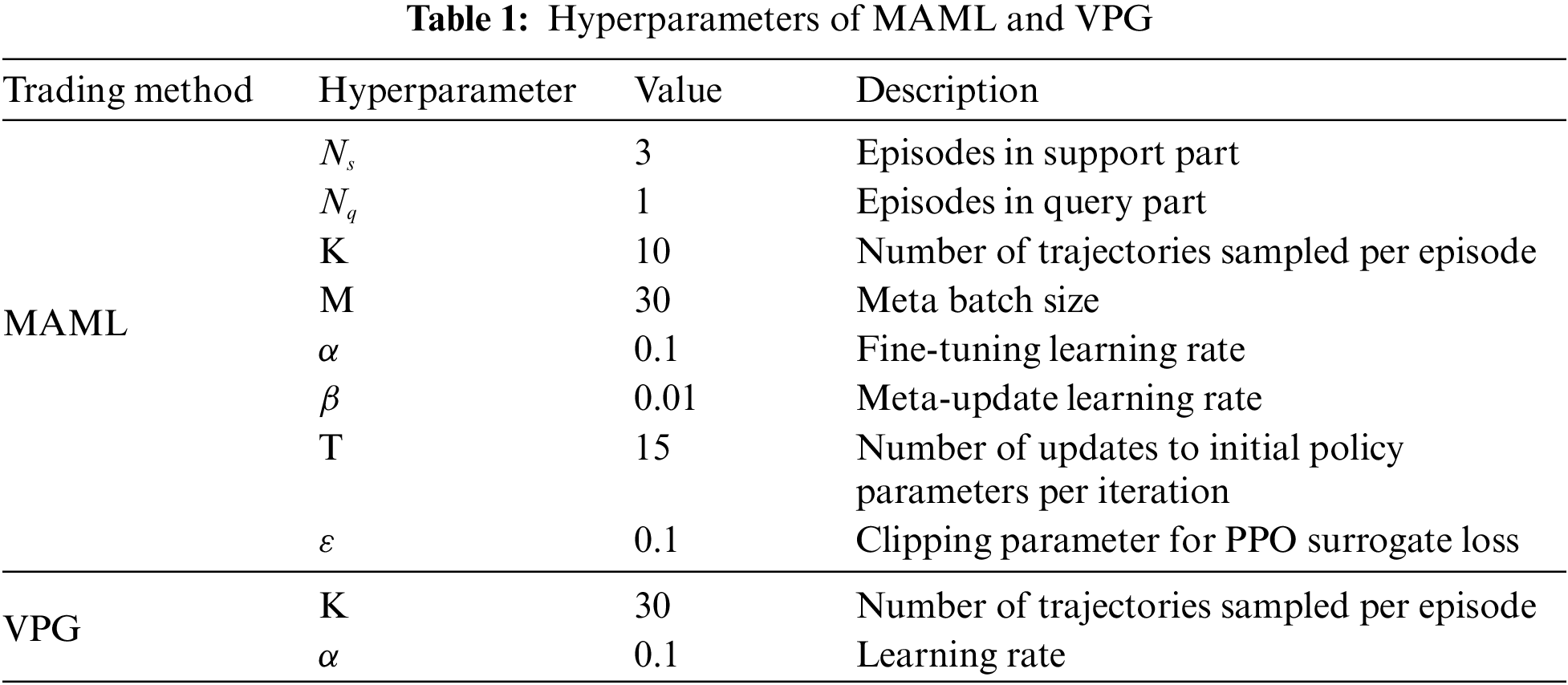
A Multi-Layer Perceptron with two hidden layers is used as the policy network, which takes the market state as input. The first and second hidden layers have 128 and 32 neurons, respectively. Both use a leaky ReLu activation function. The policy network outputs logits for each trading action, which are then input to the categorical distribution function to obtain the softmax-normalized trading action probabilities. During trading policy training the discount factor is set to 0.99 and the GAE parameter 0.9. The horizon of the episode is 20 days. Other specific hyperparameter settings for MAML and VPG are shown in Table 1. The MAML model and the VPG model are trained for 12000 iterations and 1200 iterations, respectively, when they converge.

The proposed model is built and run on Pytorch 1.8.1, a machine learning platform. The programming language is Python 3.6.3. Both the MAML-based trading model and the VPG-based trading model are trained and evaluated on a server with two Intel Golden 6240 CPUs, two NVIDIA RTX 2080 Ti GPUs and 128 GB RAM.

3.2 Evaluation Metrics

This paper quantitatively assesses the trading models’ performance by employing the following metrics:

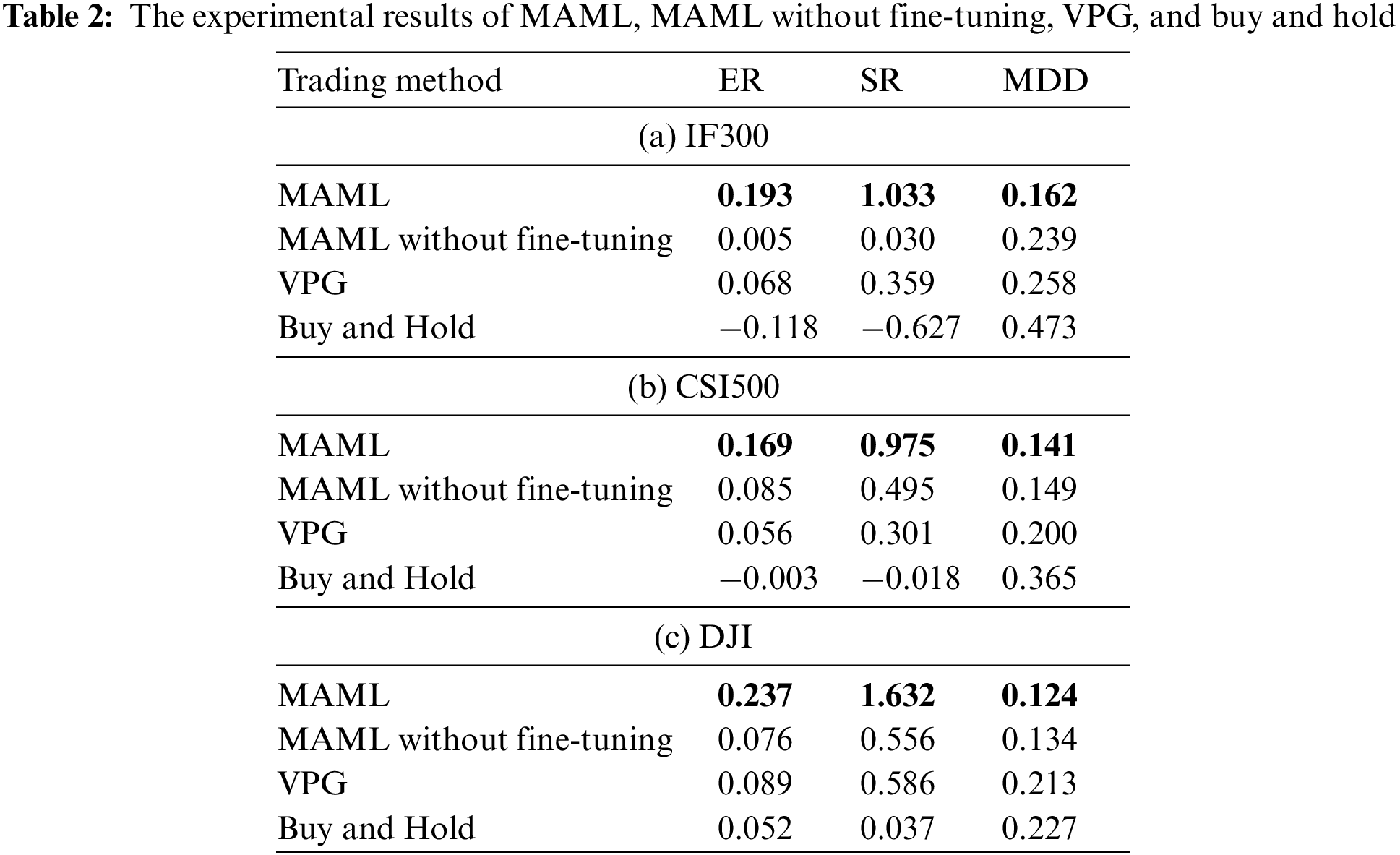
ER (Annualized Expected Return Rate): This metric gauges the annualized rate of expected return.

SR (Annualized Sharpe Ratio): The Sharpe ratio, calculated as the ratio of the annualized expected return (ER) to the annualized standard deviation (STD) of trade returns, serves as an indicator of risk-adjusted performance.

MDD (Maximum Drawdown): MDD is defined as the most significant loss experienced during a trading period, measured from the highest peak to the subsequent lowest trough in the profit curve.

These quantitative metrics provide a comprehensive evaluation of the models’ effectiveness in terms of returns, risk management, and potential downturns in the trading strategies.

3.3 Performance Comparison of MAML and VPG for Different Markets and Different Market Phases

The cumulative profit curves of MAML, VPG, and Buy and Hold methods in the testing period of IF300, CSI 500, and DJI are shown in Fig. 3. The curve of MAML without fine-tuning is also represented in the figure, in which the initial policy trained by the meta-learner of MAML is applied for trading directly without fine-tuning. Buy and Hold builds a long position at the beginning of the testing period and holds it until the end, reflecting the market itself. From the figure we can see that the curves of the MAML model are above for most time period in different markets. This demonstrates that the proposed Meta-RL-based trading method can perform better than the RL-based method. We can also see that MAML without fine-tuning and VPG have similar performances.

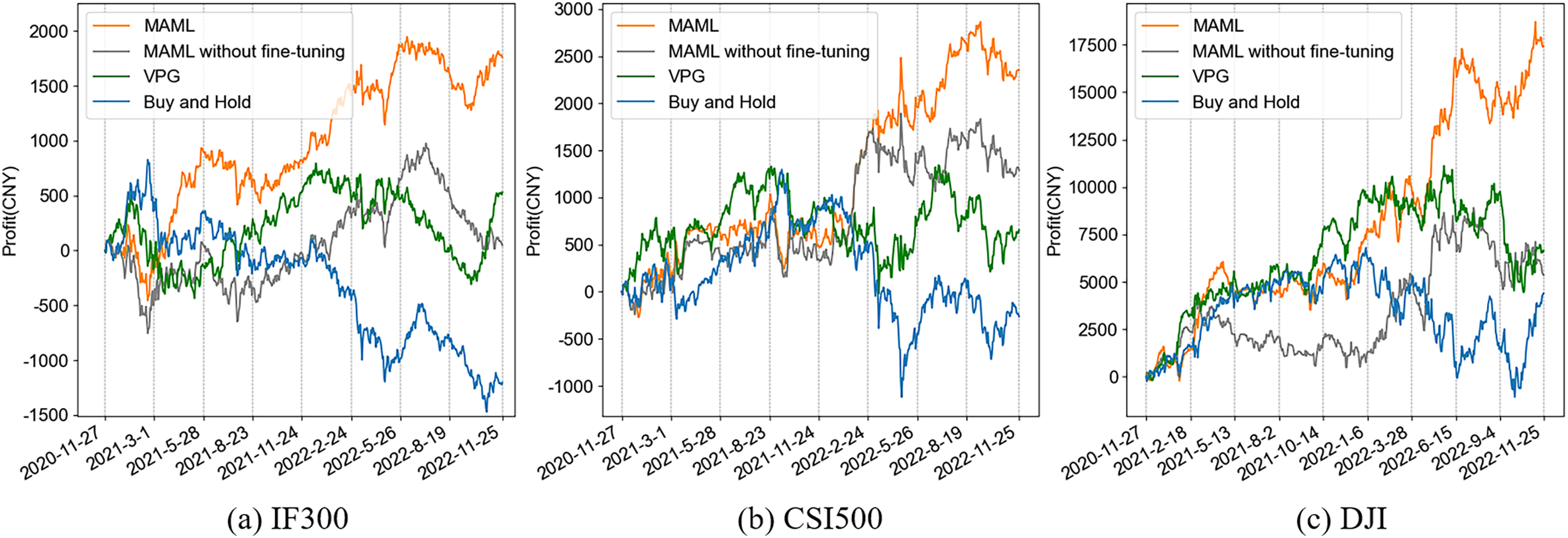
Figure 3: The cumulative profit of MAML, MAML without fine-tuning, VPG, and buy and hold

The quantitative performance comparisons of different trading methods are shown in Table 2. We can see that MAML has the highest annualized return and Sharpe ratio and the lowest maximum drawdown. Therefore, the MAML-based trading method can achieve higher profit and lower risk than other methods.

This paper also investigates the performance of trading policies learned by MAML and VPG across market phases with different changing speeds. The price standard deviation is used to characterize the changing speed. The market with a higher standard deviation fluctuates faster over time. We divide the testing period into multiple market phases. Each phase has a fixed length of three months and the division operates with a step length of one month.

Fig. 4 represents the profit of the VPG model and the profit gap between the MAML model and the VPG model on the market phases with different standard deviations. We can see from the figure that the profit of the VPG model decreases with the increment of the standard deviation. The trading method based on the traditional RL method is hard to keep pace with the time-varying financial market. We can also see from the figure that the profit gap between the MAML model and the VPG model increases with the increment of the standard deviation. This again demonstrates that the proposed meta-RL-based trading method can effectively tackle the challenges encountered by the traditional RL-based method in a fast-changing financial market.

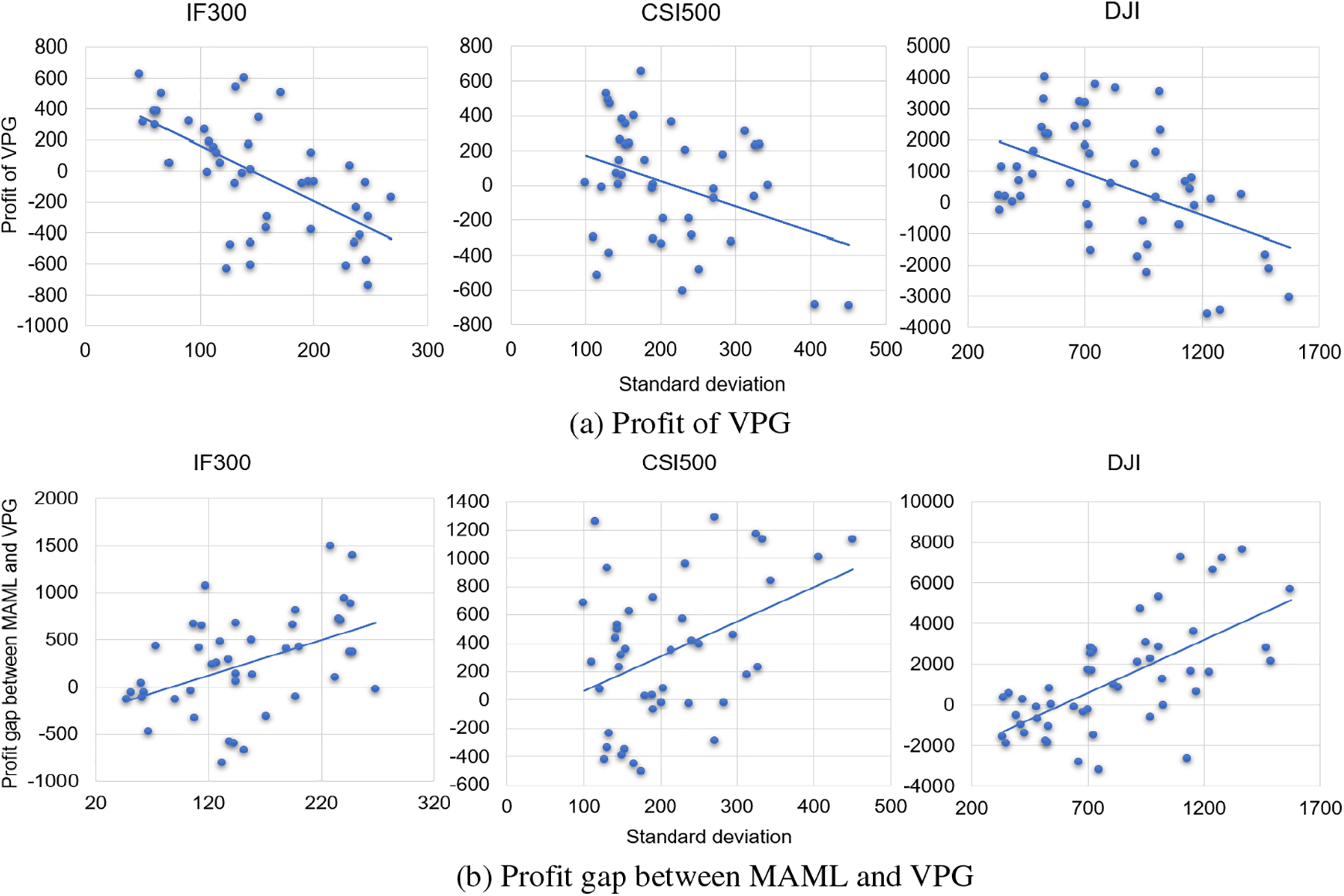
Figure 4: The profit of the VPG model and the profit gap between the MAML model and the VPG model on the market phases with different standard deviations

3.4 Effectiveness of Fine-Tuning Mechanisms in MAML

When testing the MAML model on part of a testing period (the query part of a task), a good initial policy learned from the training period is first fine-tuned on the adjacent prior part (the corresponding support part), and the tuned policy is fixed and applied to the query part. The fine-tuning mechanism plays an important role for MAML to adapt to market changes.

This paper presents three metrics to measure the market change between a query part and the corresponding support part.

The difference of mean prices (MD), which is the first-order moment change, is defined by

MD=|Meanpriceofquerypart−Meanpriceofcorrespondingsupportpart|

The difference of standard deviations (SD), which is the second-order moment change is defined by

SD=|Standarddeviationofquerypart−Standarddeviationofcorrespondingsupportpart|

The overlap ratio of price range (RO), which is the proportion of a query part contained in the corresponding support part is given by

RO=pricerangeofquerypart∩pricerangeofcorrespondingsupportpartpricerangeofquerypart

Fig. 5 represents the profit gap of the MAML models with and without fine-tuning for different market changes between the query part and the support part in a testing period on IF300, CSI500, and DJI. We can see from the figure that the profit gap between different MAML models increases with the increment of MD and SD, and decreases as RO increases. It means that the fine-tuning mechanism is more effective for MAML in a faster-changing market. We can also see that when RO is close to 1 or MD and SD are close to 0, the performances of fine-tuned and non-fine-tuned trading policies converge. The fine-tuning mechanism no longer works in a stable market environment.

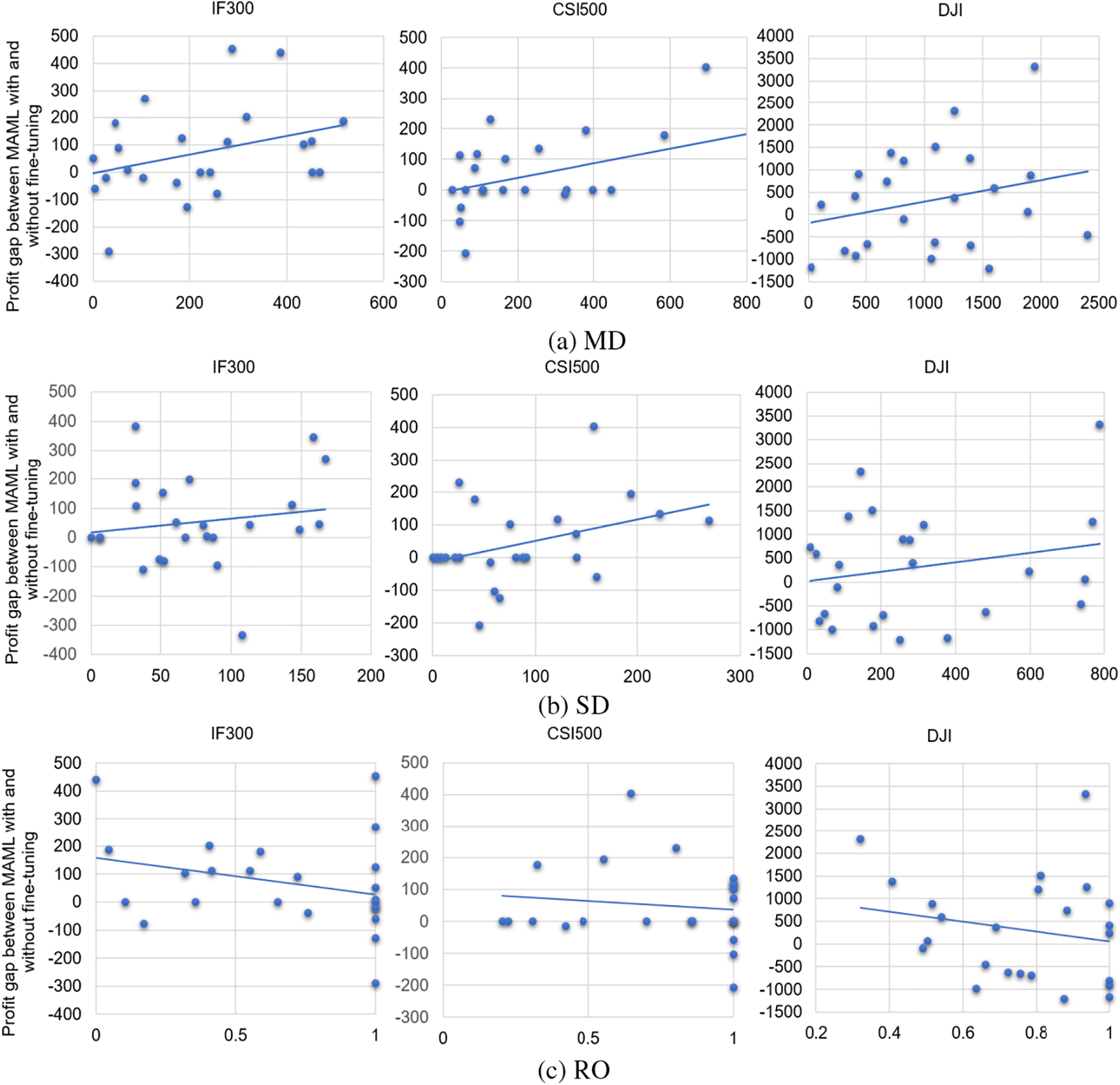
Figure 5: The profit gap of the MAML models with and without fine-tuning for different market changes between query part and support part

3.5 Performance Comparison of MAML with Different Updating Mechanisms

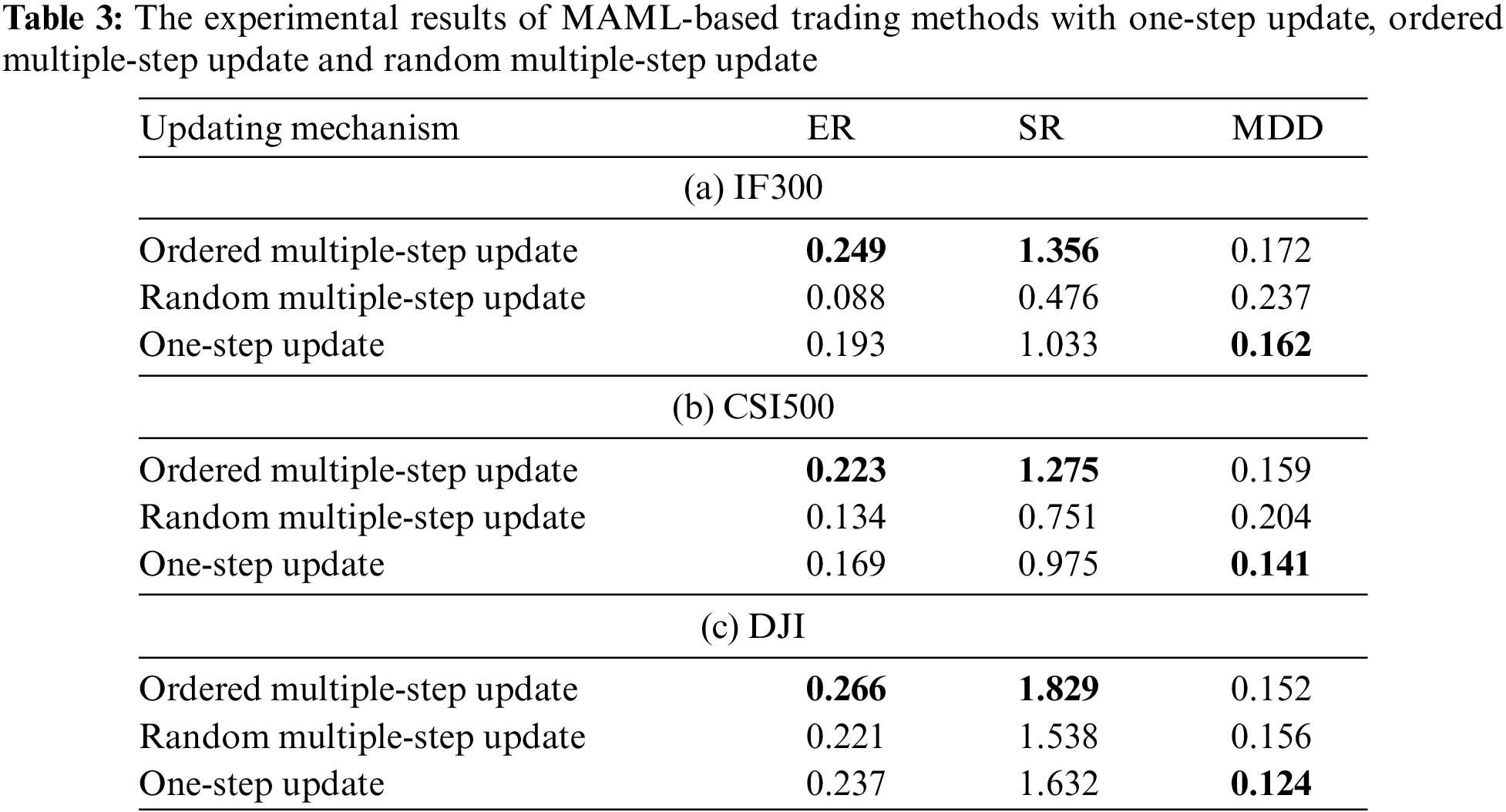
In this subsection, we compare the profit and risk performances of the MAML method with different updating mechanisms, i.e.: ordered multiple-step updating, random multiple-step updating and one-step updating for IF300, CSI500, and DJI. The one-step updating mechanism introduced in Subsection 2.3 and the ordered multiple-step updating mechanism in Subsection 2.4 are proposed to deal with the dynamic changes within a task. In the random multiple-step updating mechanism, the episodes of the support part in a task data are selected randomly to update the initial policy.

From the results as shown in Fig. 6, we can see that the profit generated by the ordered multiple-step updating mechanism is greater than the others for most of the testing periods in all different markets examined. This demonstrates that the ordered multiple-step updating can better adapt to fast-changing market than other updating mechanisms. We can also see from Table 3 that even though the one-step updating mechanism of MAML has the smallest MDD, the ordered multiple-step updating mechanism achieves the largest ER and SR. In other words, the proposed MAML-based trading method with ordered multiple-step updating can earn the highest total profit or profit per risk.

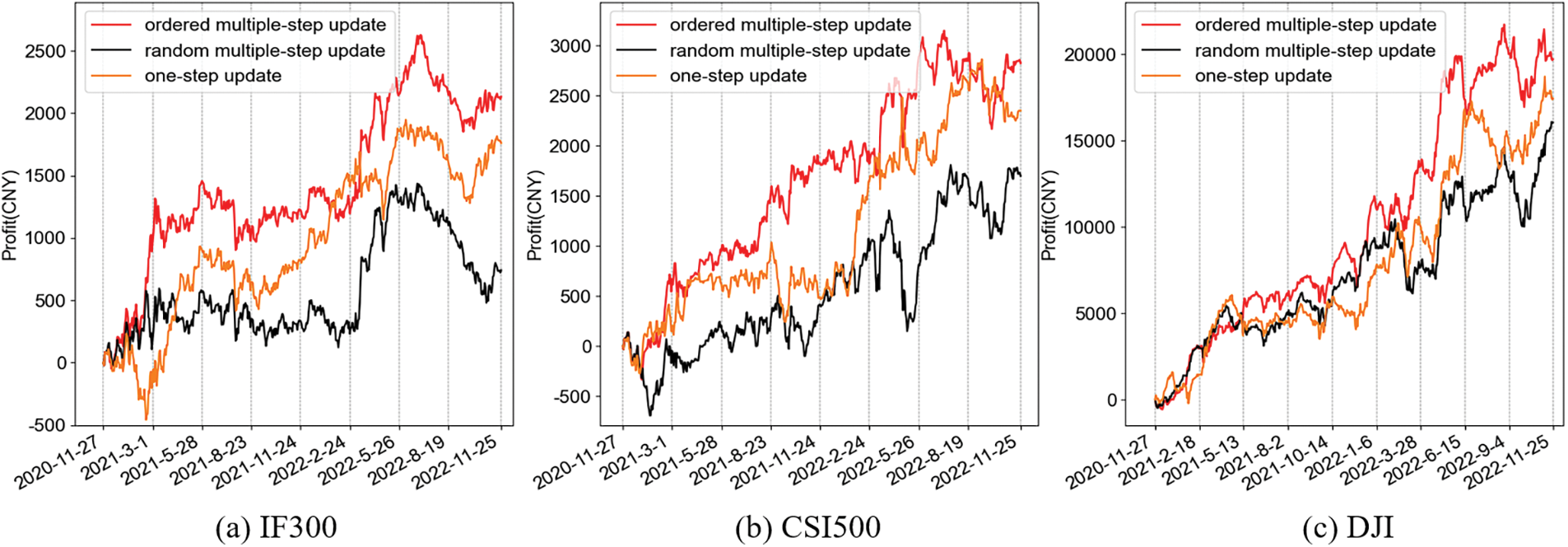
Figure 6: The cumulative profit of MAML-based trading methods with one-step update, ordered multiple-step update and random multiple-step update

4  Conclusions

This paper proposes a MAML-based trading method consisting of a PPO meta-learner and a VPG learner, to develop a trading policy capable of quickly adapting to market environments exhibiting non-stationary characteristics. In this method, training data is divided into multiple task data with each over an equal and small time period. This division ensures that each task data experiences a relatively stationary market environment. This new trading method can effectively address the challenges faced by traditional reinforcement learning-based trading methods. It achieves this by generating a good initial policy through the PPO meta-learner and subsequently fine-tuning the initial policy using the VPG learner when trading in new market tasks.

The experimental results based on IF300, CSI500, and DJI demonstrate that the MAML-based trading method outperforms the traditional reinforcement learning-based method in terms of profit and risk in a fast-changing market. Especially, the fine-tuning mechanism plays an important role that makes MAML a promising candidate for supporting adaptive and sustainable trading in such an environment. Moreover, an ordered multiple-step updating mechanism is also proposed to further improve the adaptability of the MAML-based method by exploring the changing dynamic within a task market. Looking forward, utilizing the temporal relationship between tasks to enhance our model’s adaptation to fast-changing markets is a direction for achieving further performance improvements.

Acknowledgement: We would like to extend our sincere gratitude to those who provided support throughout this work, as well as to the reviewers who offered valuable comments that significantly contributed to the improvement of this paper.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Q.G., X.P. and Y.T.; data collection: M.G. and Y.T.; analysis and interpretation of results: M.G. and Y.T.; draft manuscript preparation: Y.T. and Q.G. supervision: Q.G. and X.P. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. A. A. Kirilenko and A. W. Lo, “Moore’s law vs. Murphy’s law: Algorithmic trading and its discontents,” Soc. Sci. Electron. Publ., vol. 27, no. 2, pp. 51–72, 2013. doi: 10.2139/ssrn.2235963. [Google Scholar] [CrossRef]

2. M. Avellaneda and J. H. Lee, “Statistical arbitrage in the U.S. equities market,” Quant. Financ., vol. 10, no. 7, pp. 761–782, 2008. doi: 10.1080/14697680903124632. [Google Scholar] [CrossRef]

3. T. A. Darden, M. E. Ferrenz, C. C. Klann, M. J. Ledwith, and G. M. Davis, “Modified momentum strategies in commodity futures markets,” Syst. Inf. Eng. Design Symp., vol. 31, pp. 218–222, 2009. [Google Scholar]

4. T. Lubnau and N. Todorova, “Trading on mean-reversion in energy futures markets,” Energy Econ., vol. 51, pp. 312–319, 2015. doi: 10.1016/j.eneco.2015.06.018. [Google Scholar] [CrossRef]

5. Z. Zhang, S. Zohren, and S. Roberts, “Deep reinforcement learning for trading,” J. Finan. Data Sci., vol. 2, pp. 25–40, 2020. [Google Scholar]

6. J. Peters and S. Schaal, “Policy gradient methods for robotics,” in Proc. IROS, Beijing, China, 2006, pp. 2219–2225. [Google Scholar]

7. J. Schulman, F. Wolski, and P. Dhariwal, “Proximal policy optimization algorithms,” in Proc. ICML, Sydney, Australia, 2017, pp. 2931–2940. [Google Scholar]

8. X. Xu et al., “A group-wise feature enhancement-and-fusion network with dual-polarization feature enrichment for SAR ship detection,” Remote Sens., vol. 14, pp. 5276, 2022. [Google Scholar]

9. B. Andrew, “Deep reinforcement learning pairs trading with a double deep Q-network,” in Proc. CCWC, Las Vegas, USA, 2020, pp. 222–227. [Google Scholar]

10. J. Lee, H. Koh, and H. J. Choe, “Learning to trade in financial time series using high-frequency through wavelet transformation and deep reinforcement learning,” Appl. Intell., vol. 51, pp. 6202–6223, 2021. doi: 10.1007/s10489-021-02218-4. [Google Scholar] [CrossRef]

11. A. Hong, M. Gao, and Q. Gao, “Non-stationary financial time series forecasting based on meta-learning,” Electron. Lett., vol. 59, no. 1, pp. e12681, 2023. doi: 10.1049/ell2.12681. [Google Scholar] [CrossRef]

12. N. E. Huang, M. L. Wu, W. Qu, S. R. Long, and S. Shen, “Applications of hilbert-huang transform to non-stationary financial time series analysis,” Appl. Stoch. Models Bus. Indust., vol. 19, pp. 245–268, 2003. doi: 10.1002/asmb.501. [Google Scholar] [CrossRef]

13. C. Finn, P. Abbeel, and S. Levine, “Model-agnostic meta-learning for fast adaptation of deep networks,” in Proc. ICML, Sydney, Australia, 2017, pp. 1126–1135. [Google Scholar]

14. A. Maruan, B. Trapit, Y. Baram, I. Sutskever, I. Mordatch and P. Abbeel, “Continuous adaptation via meta-learning in non-stationary and competitive environments,” in Proc. ICLR, Vancouver, Canada, 2018. [Google Scholar]

15. R. Liaw, S. Krishnan, A. Garg, D. Crankshaw, J. E. Gonzalez and K. Goldberg, “Composing meta-policies for autonomous driving using hierarchical deep reinforcement learning,” in Proc. ICRA, Singapore, 2017. [Google Scholar]

16. R. Huang et al., “Learning and fast adaptation for grid emergency control via deep meta reinforcement learning,” IEEE Trans. Power Syst., vol. 37, pp. 4168–4178, 2022. doi: 10.1109/tpwrs.2022.3155117. [Google Scholar] [CrossRef]

17. J. Baz, N. Granger, C. R. Harvey, N. L. Roux, and S. Rattray, “Dissecting investment strategies in the cross section and time series,” Soc. Sci. Electron. Publ., vol. 22, 2015. [Google Scholar]

18. J. W. Wilder, “New concepts in technical trading systems,” Trend Res., pp. 63–70, 1978. [Google Scholar]

19. R. Sutton, D. A. McAllester, and S. Singh, “Policy gradient methods for reinforcement learning with function approximation,” in Proc. NIPS, Denver, USA, 1999, pp. 1057–1063. [Google Scholar]