A Deep Reinforcement Learning-Based Technique for Optimal Power Allocation in Multiple Access Communications

1  Introduction

Nowadays, due to the explosive demand for using wireless applications with higher data rates by users, the next generation of wireless communication networks (6G) should be designed to guarantee successful data transmission [1–4]. On the other hand, in multi-user wireless communication systems such as multiple access channels (MAC), where users send their independent data to the common receiver, more capacity and spectral efficiency are required than the single-user point-to-point (P2P) communications. One promising approach to meet these challenges is to more effectively allocate network resources with interference management. Generally speaking, power allocation (PA) is an effective technique that can improve the performance of wireless networks by delivering the source information to the destination efficiently. In addition, by allocating the appropriate source power to each user, the quality of service (QoS) and fairness for all mobile users, especially the edge users, in multiple access communications can be guaranteed. However, the lack of flexible guidelines for providing fair resource allocation to users and significant interference caused by the unplanned deployment of other nodes are momentous issues that should be modified to make wireless multi-user networks work perfectly. To this end, in this paper, we investigate the PA problem by exploiting machine learning (ML) methods to maximize the sumrate of wireless multiple access communications [5,6]. However, this optimization problem is non-convex and NP-hard [7–10] PA so it cannot be solved efficiently [11–14]. NP-hard problems are difficult to solve efficiently, and finding an optimal solution typically requires exploring a large number of possibilities. While no known efficient algorithm exists for solving NP-hard problems in the general case, various approximation algorithms and heuristics can be employed to find good solutions or approximate solutions within a reasonable amount of time [15–17].

In recent years, several algorithms have been proposed for the PA problem such as fractional programming (FP) and weighted minimum mean squared error (WMMSE) [18–21]. Although these methods have excellent performances in both theoretical analysis and numerical simulation, they are not appropriate enough for implementation in real wireless communication systems [22]. In other words, these algorithms highly depend on tractable mathematical models, and the computational complexities are too high, so they are not suitable for practical usage where the user distribution, propagation environment, geographical location of nodes, etc., are considered as main factors. Therefore, the need for novel approaches to the PA problem in practical wireless communications feels more than ever. In this regard, ML-based methods have been rapidly developed in wireless communications over the last few years. The ML-based algorithms are often model-free and can be efficiently used for optimization problems over feasible wireless communication scenarios. In addition, regarding the advancements of the graphic processing unit (GPU), the implementation and performance of them can be affordable and fast, which provides a better condition for network operators.

There are several branches of the ML method, where supervised learning and reinforcement learning (RL) are the most popular ones [23]. Within supervised learning, a deep neural network (DNN) undergoes training to approximate certain optimal or suboptimal objective algorithms. Nevertheless, the target algorithm is often inaccessible, and the effectiveness of the DNN is constrained by the supervisor [24–27]. Conversely, Reinforcement Learning (RL) has found extensive application in optimizing systems of unknown nature through interaction. The adaptable nature of RL makes it a versatile solution for models where the statistical features of the system undergo continuous changes. The most well-known RL algorithm is the Q learning approach which has been recently studied for the PA problem in [28–30]. The trained DNN with Q learning is known deep Q learning network (DQN), which is proposed to resolve the PA problem in the single-user P2P communication system [31,32]. However, to the best of the authors’ knowledge, the PA problem over wireless multi-user communication systems such as fading MAC has not been investigated by exploiting the DQN model. Generally speaking, MAC is a fundamental channel model for uplink communications from an information-theoretic perspective in multi-user wireless networks, which has recently attracted significant attention in performance analysis of emerging technologies for 6G wireless communications [33–37]. Thus, analyzing the PA problem under wireless k-user MAC can be of great interest [38–42].

1.1 Related Works

Given the efficiency of deep learning (DL)-based methods in optimization problems, many contributions have been carried out for analyzing wireless communication networks from various aspects by exploiting DL algorithms. In [4], the authors discussed several novel applications of DL in physical layer security, where they showed how their ideas can be extended to multi-user secure communication systems. They also introduced radio transformer networks (RTNs) as a flexible approach to integrating expert knowledge into the DL model. The PA problem for a downlink massive multiple-input multiple-output (MIMO) system by exploiting DL methods was studied in [43]. In this work, the authors trained a deep neural network to teach the relationship between user positions and optimal PA policies. Subsequently, they endeavored to anticipate PA profiles for a novel set of user positions. The findings indicated that the utilization of DL in MIMO systems can markedly enhance the trade-off between complexity and performance in PA, as opposed to conventional optimization-centric approaches. Due to the lack of celebrated algorithms like water-filling and max-min fairness for analyzing the PA problem in wireless type-machine communication (MTC), the authors in [44] introduced the learning centric power allocation (LCPA) method, offering a fresh perspective on radio resource allocation in a learning-driven scenario. This approach involves the use of an empirical classification error model supported by learning theory and an uncertainty sampling method that considers diverse distributions among users, the authors formulated the LCPA as a non-convex non-smooth optimization problem and they indicated that their proposed LCPA algorithms outperform traditional PA algorithms. In [45], the authors executed a dynamic PA scheme by applying model-free deep reinforcement learning (DRL), where each user can collect the channel state information (CSI) and quality of service (QoS) information from several nodes and adopt its own transmit power accordingly. With the goal of optimizing a utility function based on the weighted sum rate, the study utilized DQN to analyze both random variations and delays in CSI. The findings demonstrated that the suggested framework is particularly suitable for practical scenarios characterized by inaccuracies in the system model and non-negligible delays in CSI. The authors in [46] introduced a distributed reinforcement learning approach known as distributed power control using Q-learning (DPC-Q). This method was designed to manage interference generated by femtocells on users in downlink cellular networks. The authors explored two distinct approaches for DPC-Q, namely, independent and cognitive scenarios. By considering the heterogeneous cellular networks (HetNets), the authors in [47] employed a machine learning approach based on Q-learning to address the resource allocation challenge in intricate networks. They defined each base station as an agent, and in the context of multi-agent cellular networks, cooperative Q-learning was utilized as an effective method for resource management in such multi-agent network scenarios. The results in [47] illustrated that using the Q-learning approach can offer more than a four-fold increase in the number of supported femtocells compared with previous works. In [48], a strategy for optimizing energy consumption was introduced, employing techniques from DRL and transfer learning (TL). The authors incorporated an adaptive reward system to autonomously modify parameters within a reward function, aiming to strike a balance between users’ energy consumption and QoS requirements throughout the learning process. Furthermore, the authors in [49] focused on optimizing the ON/OFF strategy of small base stations by leveraging DQN to improve energy efficiency. Subsequently, they suggested a user-specific cell activation approach to address the challenge of allocating users with diverse requirements. Furthermore, in [50,51], a framework employing the DRL method was introduced to achieve the optimal solution for power-efficient resource allocation in beamforming problems.

1.2 Paper Contributions

Motivated by the above-mentioned observations, we investigate the PA problem in the multi-user communication system, exploiting the DQN model, where the simulation results show our proposed DQN model provides better performance as compared with benchmark algorithms. The main contributions of our work are summarized as follows:

•   First, we propose a model-free two-step training structure, wherein the DQN is firstly trained offline with the DRL algorithm within simulated environments, and then the learned DQN is used for optimization problems in real multi-user communications through transfer learning.

•   We also discuss the PA problem of exploiting deep Q learning (DQL). In this regard, we propose a DQN-enabled method and train it with the current sumrate as the reward function, lacking prospective rewards to aid the DQN in approaching the optimal solution.

•   Finally, the suggested DQN is evaluated by distributed performance, and the results show that the average sumrate of DQN surpasses model-driven algorithms.

1.3 Paper Organization

The remaining sections of this paper are structured as follows. Section 2 describes the system model and the PA problem in the considered wireless fading MAC. The details of our proposed DQN model are presented in Section 3. In Section 4, the efficiency of proposed DQN in comparison with benchmarks algorithms is illustrated by simulation results. Finally, Section 5 presents the conclusions and discussions.

2  System Model

Consider the wireless multiple-access communication system model depicted in Fig. 1, where transmitters ti wish to send an independent message reliably Xi, i∈{1,2,…,k} to the common receiver r, respectively. The inputs Xi sent by i-th user over the considered fading channels are restricted to the average power as E[|Xi|2]≤Pmax, where E[.] is the expectation operator. At time slot T, by assuming that the transmitters and the receiver are equipped with single antenna, the received signal at the receiver r is defined as follows:

Y=∑i=1kgiTXi+Z,i∈{1,2,…,k}(1)

where giT=|hiT|2βi, i∈{1,2,…,k} are the independent channel coefficients between the i-th transmitter and the common receiver r. The terms hi and βi denote the small-scale fading and large-scale shadowing, respectively. Z defines the additive white Gaussian noise (AWGN) with zero mean and variance N (i.e., Z∼N(0,N)) at the receiver r. Thus, the instantaneous signal-to-noise ratios (SNRs) γi for the considered k-user MAC can be defined as:

γiT=PiTgiT∑i≠jPjTgjT+N(2)

where PiT denotes the transmitting power of the i-th user.

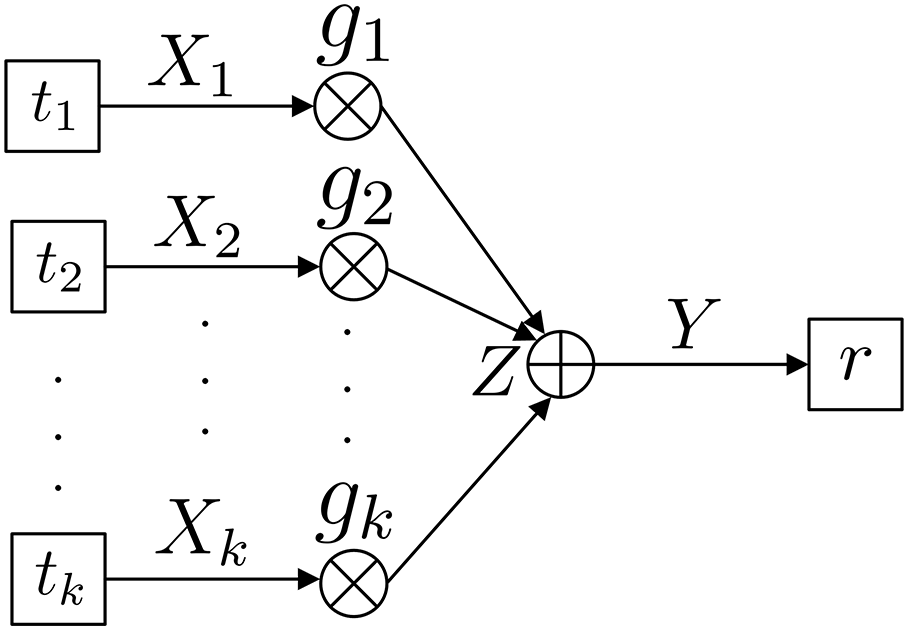
Figure 1: System model depicting the k-user MAC

The sumrate of the considered k-user MAC with coherent receiver (i.e., the channel coefficients gi are known at the receiver r) was determined in [52] as:

CT=12log2(1+∑i=1kγiT).(3)

We now formulate the optimization problem to maximize the generic sumrate objective function of the considered MAC under maximum power constraint as follows:

maximaizePTCT(4)

subject to 0≤PiT≤Pmax,i=1,2,…,k(5)

CiT≤RiT,i=1,2,…,k(6)

where PT={P1T,P2T,…,PkT} is the transmitting power vector. The objective of (4) is to maximize the sumrate of users, ensuring that each user attains the specified information rate RiT as state in (5). The term CiT=12log2(1+γiT) refers to the capacity of i-th link. The problem that represented in (4) is non-convex and NP-hard. For this purpose, we utilize a data-driven learning algorithm, employing the DQN method to address it.

3  Problem Formulation and Proposed Solution

3.1 Deep Q Network

Q learning is a flexible model-free RL approach which widely used in dealing with the Markov decision process (MDP) problems [53]. Q learning is regarded as a function approximator with the value of Q, which depends on the state sT∈S and the action aT∈A at time instant T. The terms S and A denote the action and state sets, respectively. To obtain the next state sT+1, the agent first performs the action aT, engages with the environment, and subsequently receives the reward rT at time step T. In order to settle infinite state space, the DQN is introduced to merge Q learning with a pliable DNN by considering the fact that the state s can be continuous. Thus, the cumulative discounted reward function is defined as:

RT=∑τ∞γτrt+τ+1(7)

where the discount factor γϵ[0,1) represents the balancing factor determining the significance of immediate vs. future rewards. So, the Q function of the agent with an action a and DQN parameter θ over state s for a specific policy π is determined as:

Qπ(s,a;θ)=Eπ[RT|sT=s,aT=a](8)

The primary objective of Q-learning is to identify the optimal behavior for agents operating in an unknown environment, with the goal of maximizing the Q function. To this end, the dynamic programming equation used to calculate a function approximator Q, commonly known as the Bellman equation, is employed to maximize Eq. (4). Thus, Bellman equation is defined as [54,55]:

wT=rT+γmaxa′Q(sT+1,a′;θT)(9)

where wT is the optimal value of Q. The unique strictly concave solution provided by Eq. (9) will be reached by applying limit as T→∞.

The main novelty of Q learning is to utilize temporal-difference (TD) in order to approximate the Q function. To this end, the DQN is trained with the standard Q learning update of the parameters θ as follows:

θT+1=θT+η(wT−Q(sT,aT;θT))∇Q(sT,aT;θT)(10)

where η defines the learning rate. The expression in (10) is similar to the stochastic gradient descent which gently updates the current value of Q(sT,aT;θT) to the object wT. The agent experience data is also loaded as (sT,aT,rT,ST+1). As a result, the DQN undergoes training using batch data retrieved randomly from the experience replay memory.

3.2 Deep Reinforcement Learning

In most applications in which the current strategy has enduring impacts on the cumulative reward like playing video games, the DQN gains significant outputs and defeats players. However, for the PA problem in this scenario, the discount factor γ should be assumed zero. Given the aim of DQL which is to maximize the Q function, we assume γ=0. Thus, Eq. (8) can be written as:

maxQ=maxEπ[rT|sT=s,aT=a](11)

Now, for our considered PA problem, we set s=gT and a=PT, where gT={g1T,g2T,…,gkT} is the channel state information (CSI) set. Then, by assuming rT=CT, we have:

maxQ=maxEπ[CT|gT,PT](12)

0≼PT≼Pmax

Since during the execution period the policy is deterministic, (12) can be expressed as:

maxQ=maxCT(gT,PT)(13)

0≼PT≼Pmax

which is an equivalent form of the maximization problem mentioned in (4). This result shows that the optimal solution for maximization problem in (4) is identical to that of (8), under the assumptions of γ=0 and rT=CT.

The optimal out for the maximization problem in (4) is just depends on the instantaneous wireless channel conditions, meaning that the ideal solution PT∗ of (4) is just specified by the current CSI gT (see Fig. 2). Thus, the channel CiT is computed by (gT,PT). Although the optimal power solution PT∗ can be determined by exploiting a DQN with only input gT, the performance of this specific DQN is suboptimal due to the non-convex nature of the problem, making it challenging to reach the optimal point. Hence, we exploit two auxiliary aspects as CT−1 and PT−1 for this problem. As the channel can be described as a first-order Markov process, leveraging the solution from the previous time period assists the DQN in achieving the optimal power level. So, (13) can be expressed as:

maxQ=maxCT(gT,PT,CT−1,PT−1)(14)

0≼PT≼Pmax

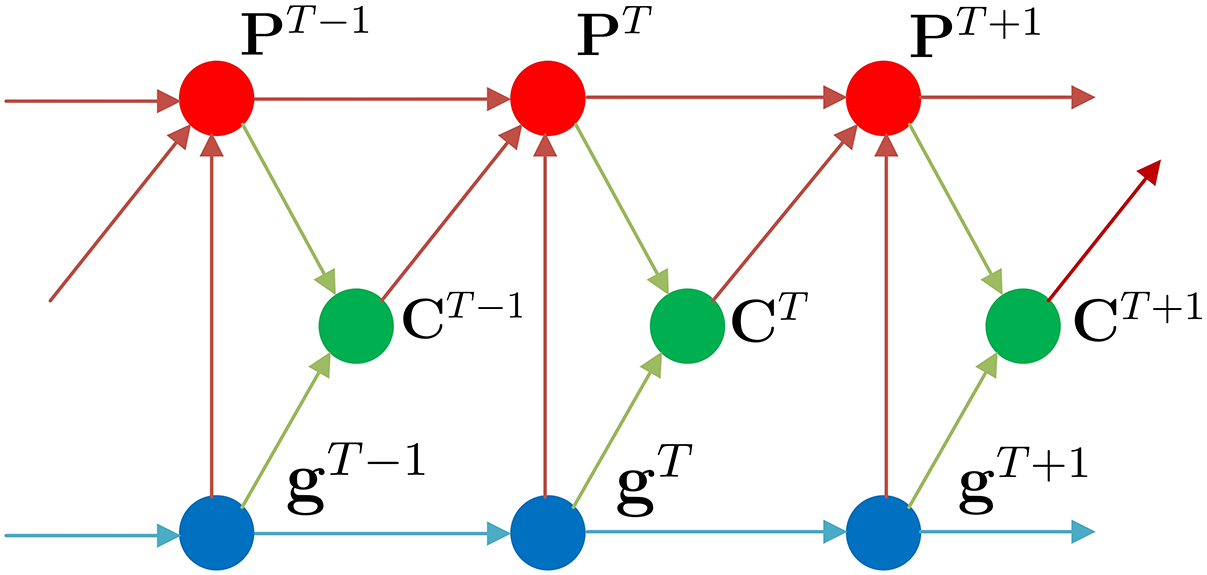
Figure 2: The DQN solution is achieved through CSI gT, conjunction with rate CT−1 and transmitting power PT−1

By assuming γ=0 and rT=CT, (9) is reduced to be wT=CT and the replay memory is streamlined to (sT,aT,rT). So, the current sumrate of the corresponding power levels with a specific CSI can be predicted by considering DQN as an estimator.

3.3 DQN Design in MAC

To alleviate the burden of online training caused by the inherent need for a substantial amount of data in the data-driven algorithm, in our proposed model, we first offline pre-train the DQN with the DRL algorithm over simulated wireless fading channels. Then, we dynamically set the learned DQN in real scenarios by exploiting the transfer learning. Due to the fact that the practical wireless fading channels are dynamic and also affected by the random factors in the propagation environment, the data-driven algorithm can be a promising approach to analyze such communication networks. Regarding the above-mentioned, we present our two-step framework in the following scenarios.

In the proposed wireless fading MAC, each transmitter-receiver link is considered as an agent; so, a multi-agent system model is analyzed. However, training the multi-agent model proves challenging as it demands an increased amount of learning data, training duration, and DNN parameters. Hence, we opt for centralized training and exclusively train a single agent, utilizing the experience replay memory from all agents. Consequently, we share the learned strategy of the considered agent over the distributed execution period. Therefore, we define the components of the replay memory for our designed DQN as follows:

3.3.1 State

Given that the full environment information is redundant, and the irrelevant elements should be eliminated, creating the accurate state of the agent is momentous. We assume that the agent includes the corresponding perfect instantaneous CSI in (2). Thus, the logarithmic normalized interferer set ℐiT can be defined as follows:

ℐiT={1,…,1⏟i−1,{log2⁡(1+giTgjT)|i≠j}}.(15)

We also normalize the channel amplitudes of interferes with that of the required link, and since the channel amplitudes are often modified by magnitude orders, we prefer the logarithmic format for them. To mitigate computational complexities and reduce input dimensionality, the elements in ℐiT are arranged in descending order, ensuring that only the initial C elements are retained. As we mentioned in 3.2, the remaining elements, specifically the downlink rate CT−1, and transmitting power PT−1 at last time slot T, constitute parts of the input to our proposed DQN. Thus, we define the state as:

siT={ℐiT,CiT−1,PiT−1}(16)

3.3.2 Reward

The power considered in the maximization problem of (4) is a continuous variable which is only subjected to the maximum power limitation. Considering that the action space of the DQN needs to be finite, the available transmitting power is discretized into |A| levels. Thus, we define the allowed power set as:

|A|={0,Pmin,(PmaxPmin)1A−2,…,Pmax}.(17)

where Pmin>0 is the transmitting power.

3.3.3 Action

In some previous works, the authors designed the reward function to improve the transmitting rate of the agent and also mitigate the interference influence, while this modeling is a suboptimal method to the target function of (4). In order to gain an optimal target for our considered problem, in this paper, we directly treat CT as the reward function so that its universality among all agents. We prove that this assumption is feasible in the training simulations under the small or medium scale of multi-user communications.

In order to gain more insights into the DQL process for the considered PA problem over MAC, we provide Algorithm 1 which indicates the step-by-step description of this process.

4  Simulation Results

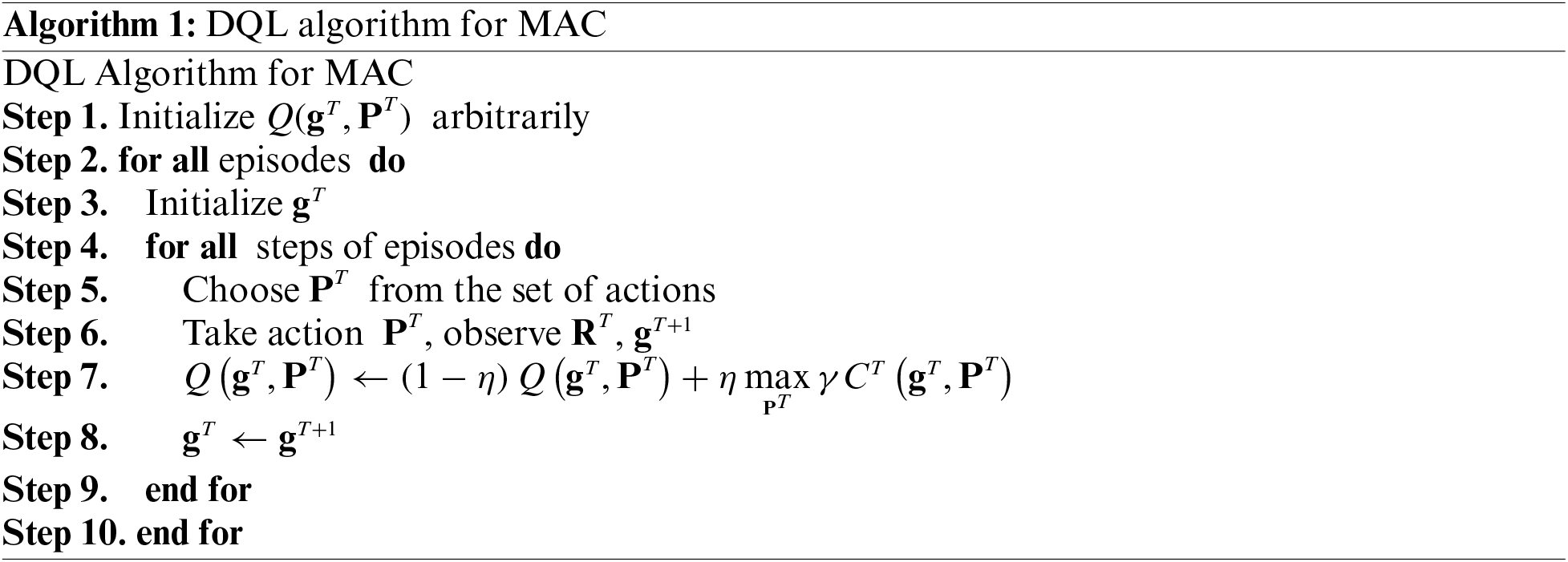
In this section, we showcase the simulation outcomes for the given PA problem under the k-user fading MAC. We first provide the simulation configuration, then the performance of the discount factor is analyzed, and finally, the proposed algorithm efficiency is evaluated.

4.1 Simulation Configuration

Specifically, we simulate the proposed model for k=2,4,6,8 users assuming the Rayleigh fading for each channel from the transmitter to receiver and the Jack’s model with Doppler frequency fd=10 Hz and period τd=20 ms. The large-scale fading is modeled as β=120.9+37.6log10⁡(d)+10log10⁡(ζ) according to the LTE standard, where ζ is a log-normal random variable with the standard deviation of 8 dB, and d denotes the distance between each transmitter to the common receiver. We set the AWGN power as N=−114 dBm, and the transmitting power constraints as Pmin=5 dBm, Pmin38 dBm. We consider a four-layer feed-forward neural network (FNN) as DQN, where the neuron numbers of two hidden layers are assumed to be 128 and 64, respectively. We assume a linear activation function of the output layer and also consider the ReLU is adopted in the hidden layers. The dimension of the input and output are assumed to be 50 and 10, respectively.

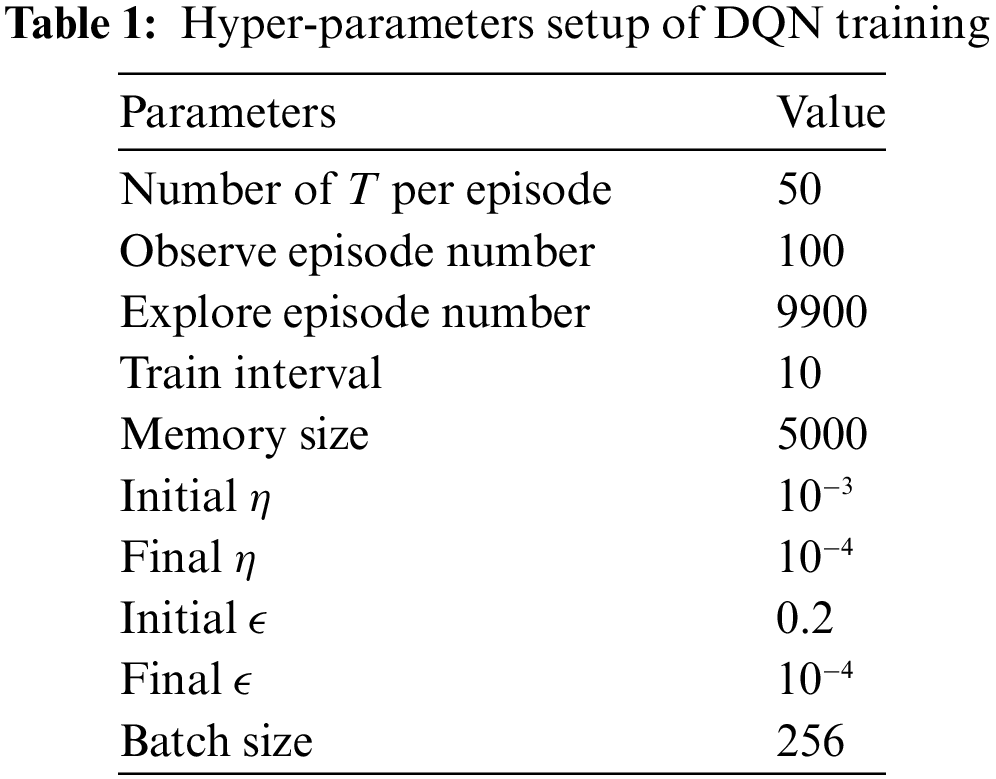
Utilizing pre-existing interaction data can be efficiently accomplished through offline RL, which operates in a fully off-policy RL setting. In this setup, the agent is trained using a static dataset of recorded experiences, without engaging in further interactions with the environment. Offline RL serves various purposes, including (i) pretraining an RL agent with existing data, (ii) empirically assessing RL algorithms based on their capacity to leverage a fixed dataset of interactions, and (iii) generating real-world impact. In online RL, actions with high rewards are chosen by an agent and then the corresponding agent receives corrective feedback. In contrast, since additional data cannot be collected in offline RL, it becomes essential to contemplate generalization using a fixed dataset. Therefore, utilizing techniques from supervised learning that employ an ensemble of models to enhance generalization, we employ random initialization as a straightforward method to extend the capabilities of DQN. The agents take actions randomly over the first 100 episodes, and then they track the adaptive ϵ-greedy learning method, provided in [43], in order to enter the next tracking epoch. We assume the large-scale fading is constant during each episode, so, we need to consider the number of training episodes enough large in order to dominate the generalization issue. Each episode consists of 50 time slots, and the DQN is trained with 256 random samples from the experience replay memory every 10 time slots. We utilize the Adam algorithm [44] as the optimizer in our proposed model, with the learning rate η decreasing exponentially from 10−3 to 10−4. To gain more insights, we provide all training parameters used for simulation in Table 1. We consider the FP algorithm, WMMSE algorithm, maximum PA, and random PA schemes as benchmarks in order to appraise our proposed DQN-based algorithm. Moreover, we assume that the CSI is known for all schemes.

4.2 Discount Factor

Here, we analyze the performance of the discount factor γ for the considered model. For this purpose, Fig. 3 shows the behavior of the average rate C¯ for the selected values of γ. It can be seen that the average rate C¯ reaches lower values under higher discount factor values (i.e., γ=0.7,0.9) compared with the rest of γ values at the same time slot. As shown in Fig. 4, we can clearly see that the highest (lowest) value of C¯ is achieved under the lowest (highest) values of γ. The simulation result indicates that the non-zero values of γ have a destructive effect on the performance of DQN, which is consistent with the analytical results discussed in 3.2. Therefore, it is found that setting the discount factor with zero value or with the lowest non-zero values, provides the best performance for the proposed multi-user system model.

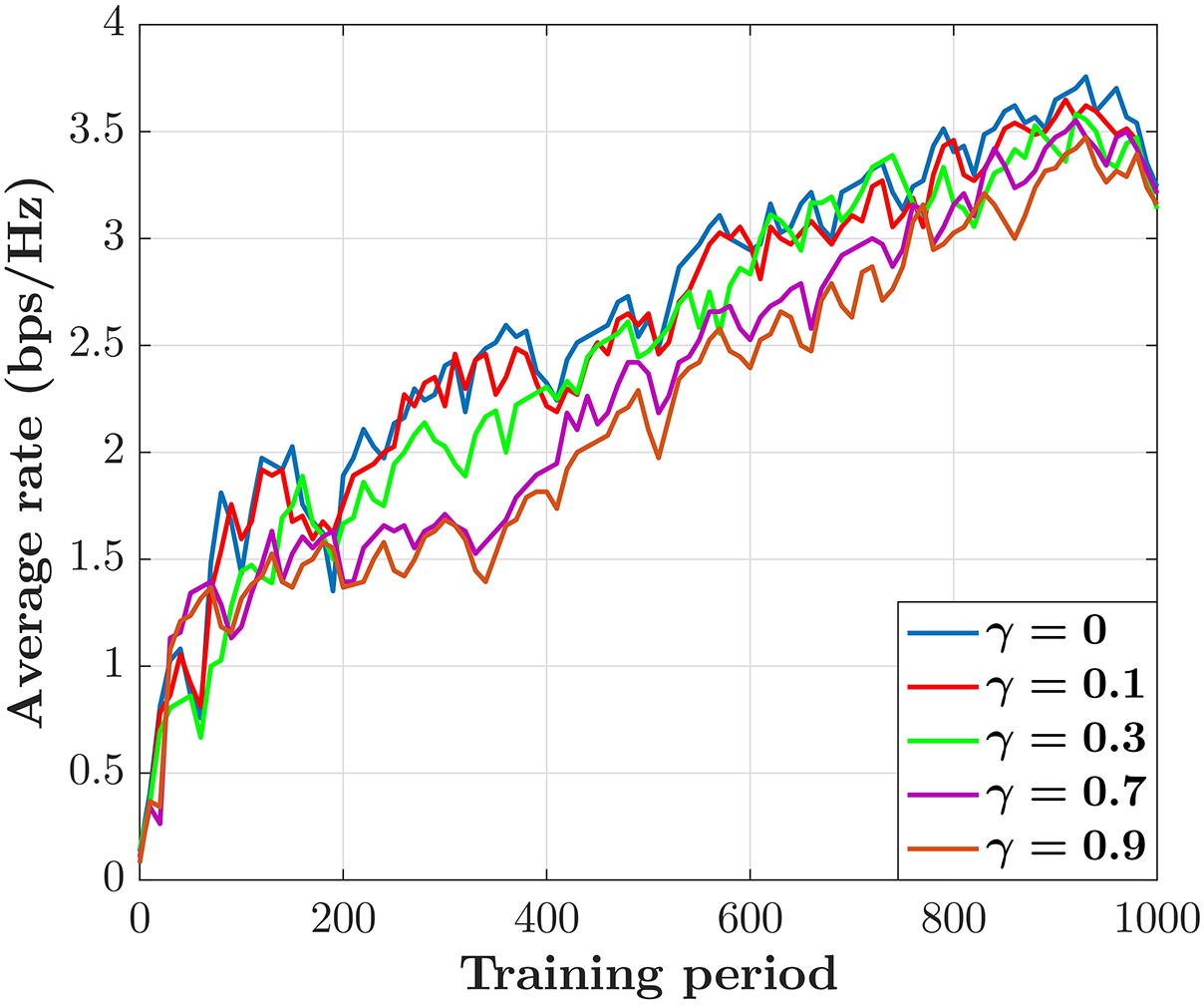
Figure 3: The average rate C¯ vs. distance factor γ under 4-user wireless fading MAC

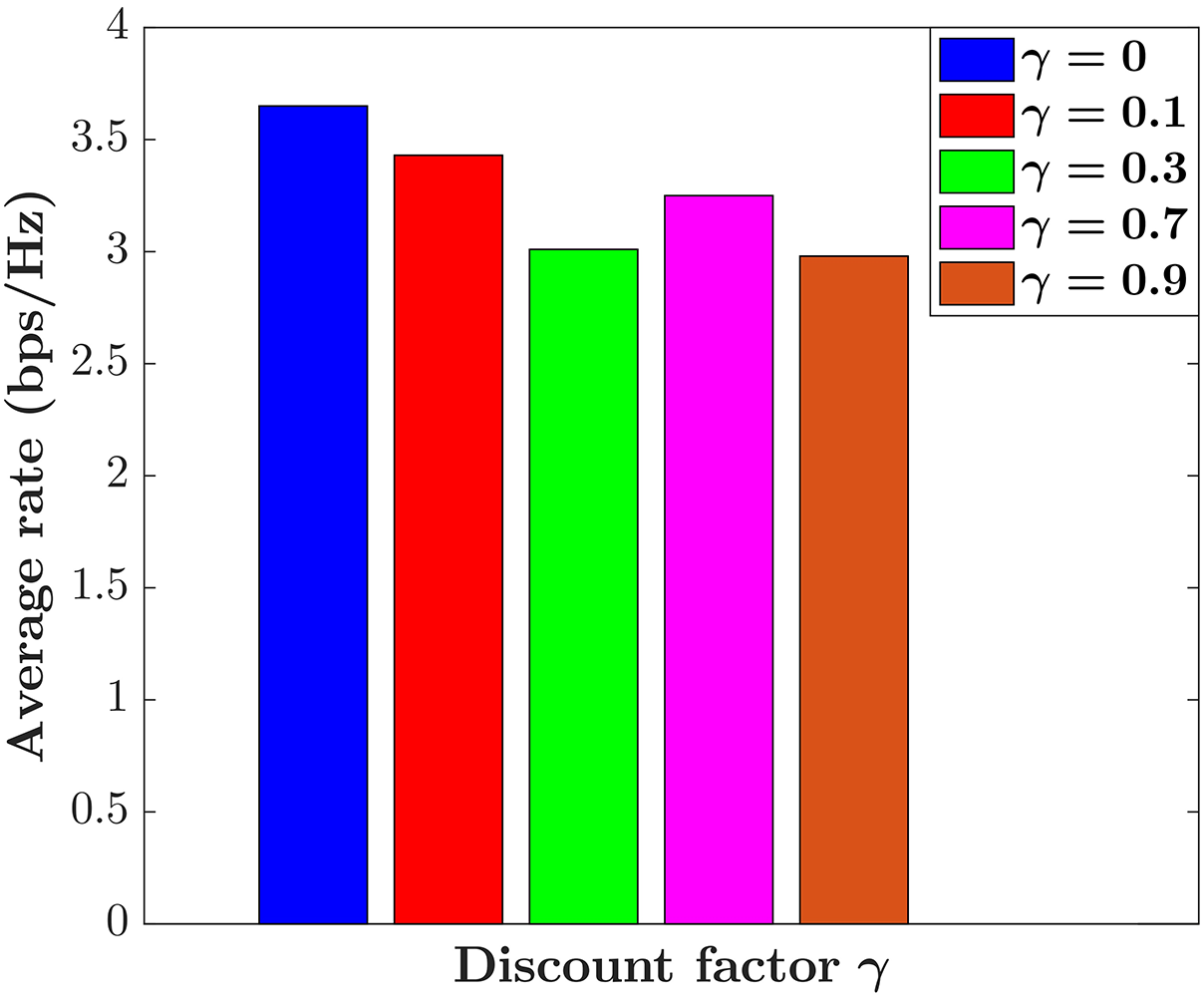
Figure 4: The average rate C¯ vs. distance factor γ under 4-user wireless fading MAC

4.3 Algorithm Comparison

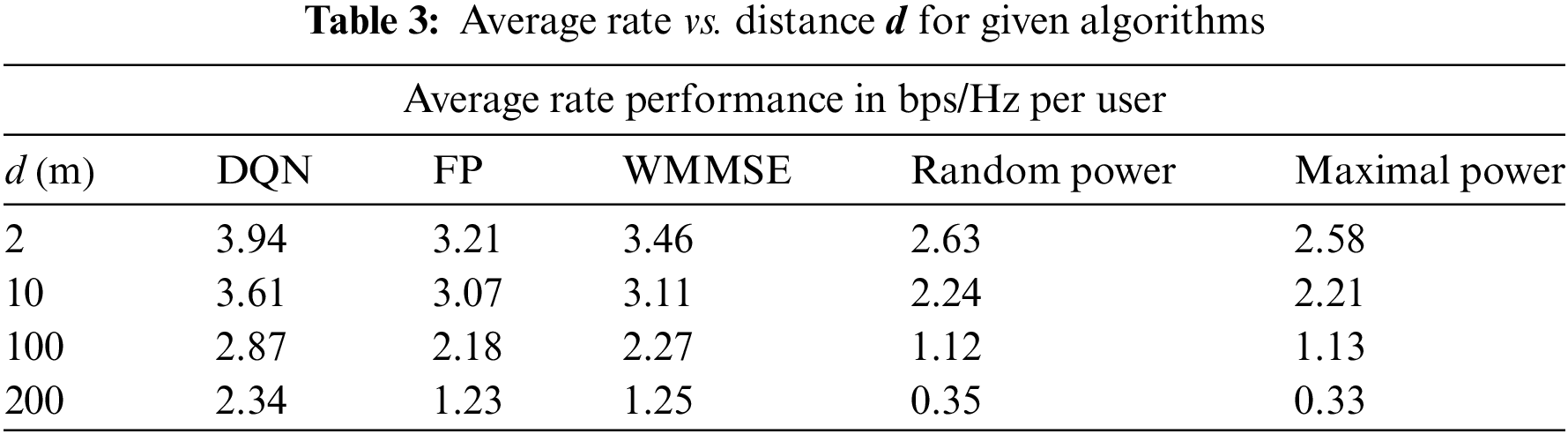
In this subsection, we compare the trained DQN under γ=0 with the four benchmark schemes which are previously introduced. Given that the user density is variable over time in real wireless communication networks, the DQN has to be designed in a way that provides good generalization capability against this matter. To this end, the performance of the average capacity C¯ vs. the number of users k under selected algorithms is illustrated in Fig. 5. We can see that the proposed DQN method provides the best performance in terms of C¯ in all experiment scenarios. It should be noted the difference between the random/maximum PA algorithms and the rest optimization schemes is raised as the user number k become larger. The main reason for this issue is that as the number of users increases the interference becomes stronger. Thus, the optimization of PA is a momentous issue in designing wireless communication networks with ultra-dense users. Moreover, Fig. 6 shows an example result of one testing episode for k=4 users. It can be seen that the performance of considered algorithms (i.e., DQN, FP, and WMMSE) is unstable and especially depending on the specific large-scale fading effects. In addition, we can observe that the WMMSE cannot always provide a better average rate compared with the FP method over time. However, as expected, we can see that the proposed DQN algorithm offers the best performance in terms of average rate during the time for a fixed number of users. In Fig. 7, we represent the behavior of the average rate in terms of the average SNR of a random user when k=2 under Rayleigh fading multiple access channels. We can observe as the average SNR increases, the average rate grows under all algorithms since increasing the average SNR provides a better channel condition between users and the common receiver. Additionally, it can be seen that our proposed DQN algorithm offers a higher average rate compared with other scenarios over average SNR changes, however, the average SNR values become similar for all algorithms at high SNR regimes.

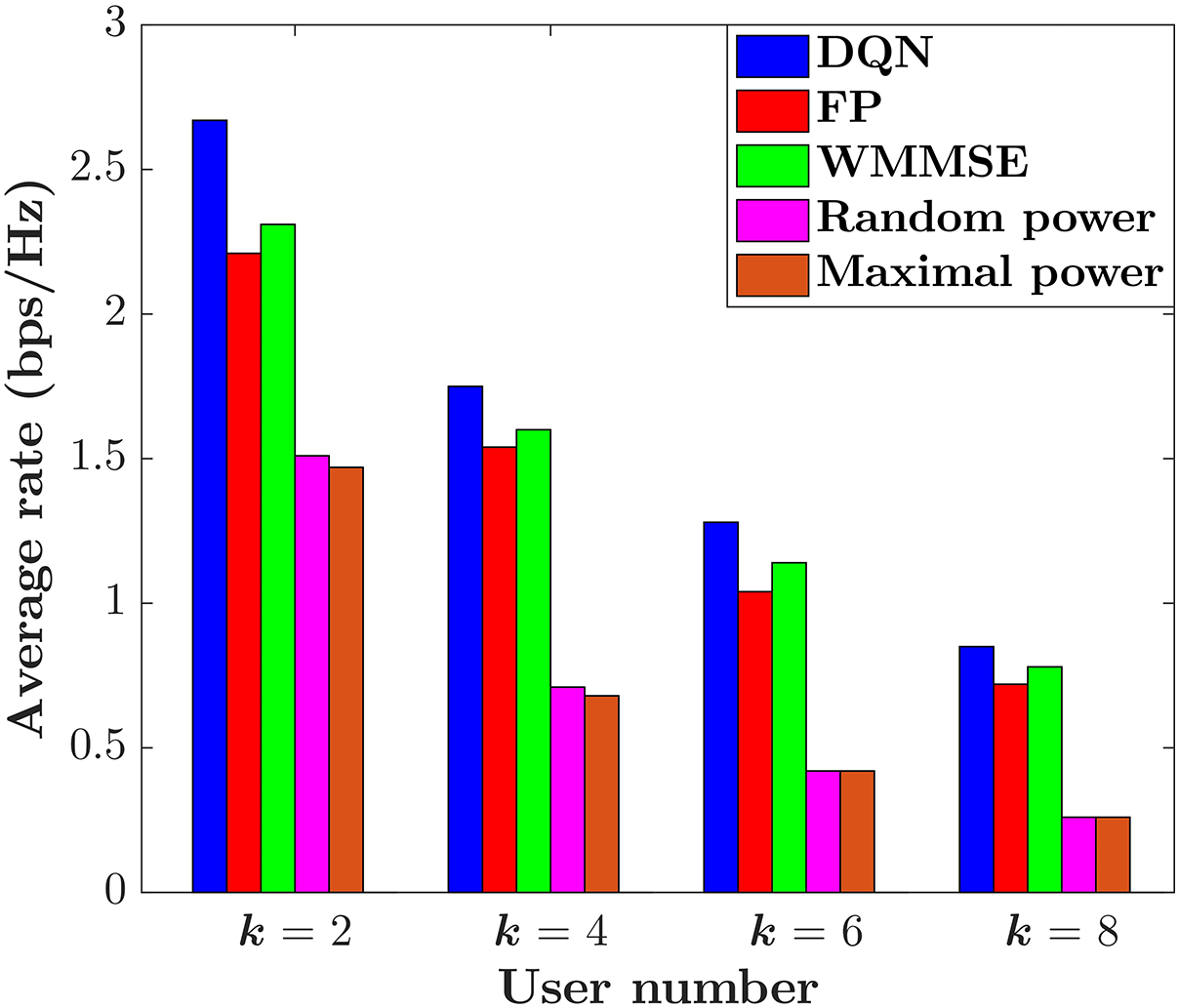
Figure 5: The average rate C¯ vs. user number k for five power allocation schemes: (1) DQN; (2) FP; (3) WMMSE; (4) Random power; (5) Maximal power

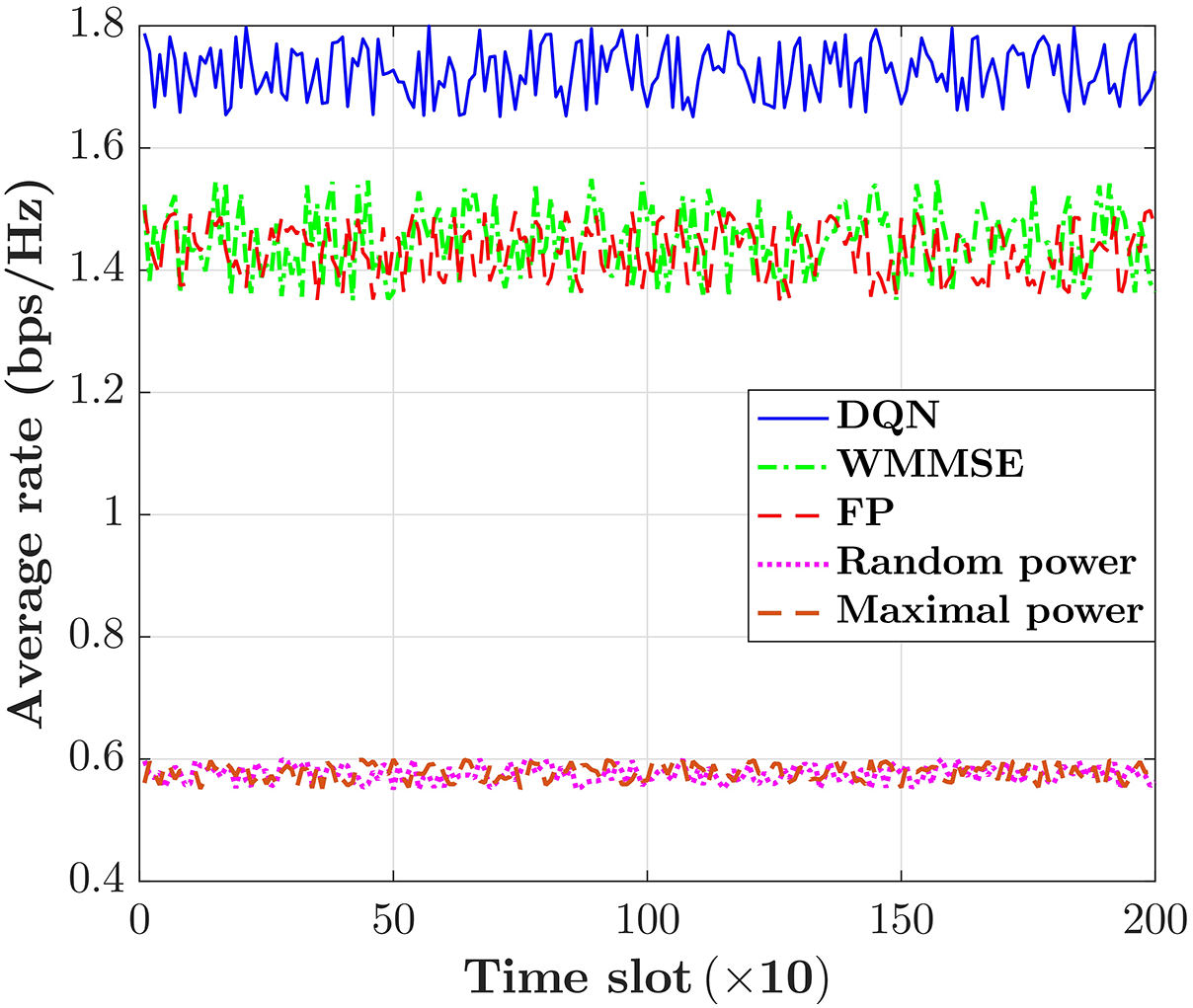
Figure 6: The average rate C¯ vs. distance factor γ under 4-user wireless fading MAC

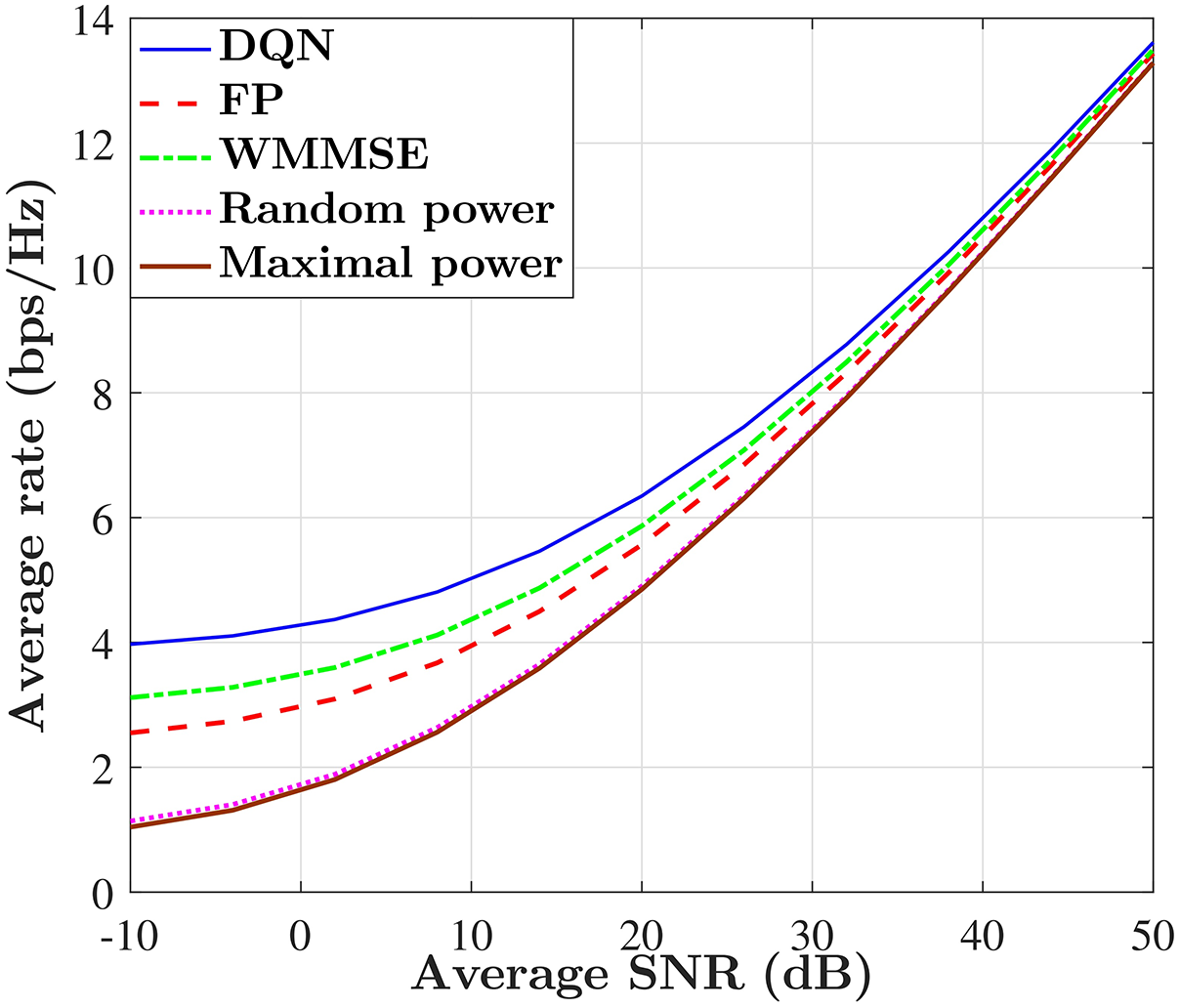
Figure 7: The average rate C¯ vs. average SNR under 2-user wireless fading MAC

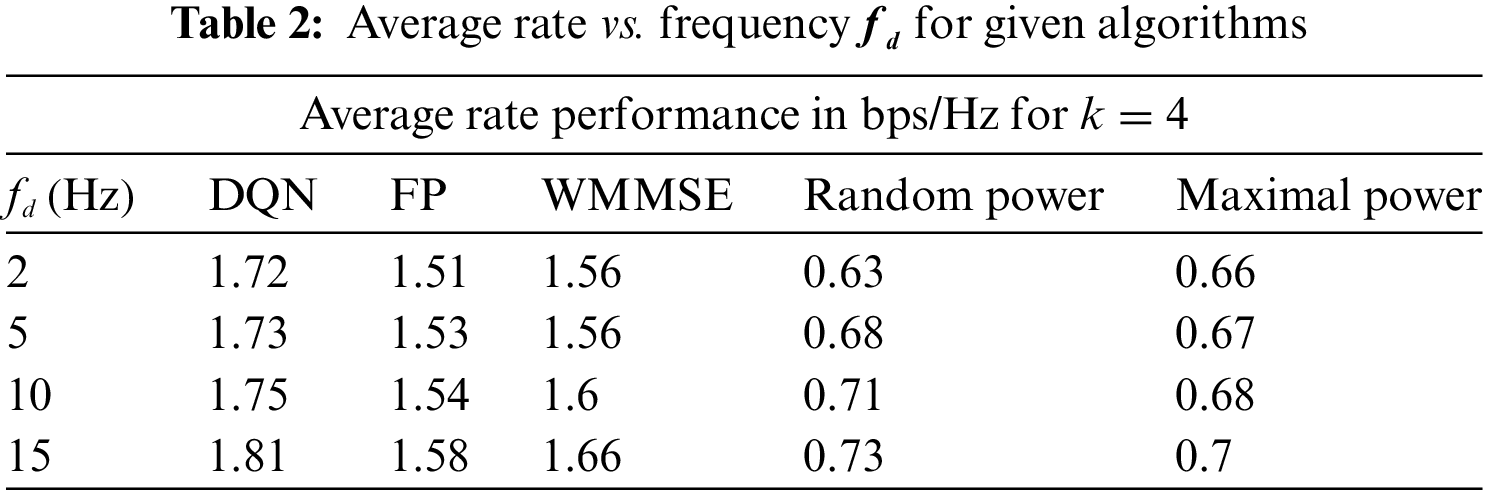
Table 2 compares the performance of the average rate in terms of frequency fd for k=4 under five different algorithms. It can be observed as frequency grows; the average rate slightly increases for all algorithms. Furthermore, by comparing the DQN method with other algorithms, we can witness the resilience of our proposed algorithm in the face of alterations in interference conditions and the fading characteristics of the environment. The impact of the distance between each transmitter to the common receiver on the average rate performance is illustrated in Table 3. It is clearly seen as the users are located at a farther distance from the common receiver, the less average rate is achieved for all algorithms. We can also see that our proposed technique is less sensitive to distance changes compared with other algorithms, where it still provides the highest average rate. From the computation complexity viewpoint, the DQN has a linear relationship with the number of layers in terms of time cost, while the time cost is not steady for the iterative algorithms such as FP and WMMSE. For these iterative methods, the time cost is highly dependent on the criterion condition, initialization, and CSI.

5  Conclusions

In this paper, we studied the PA problem for wireless multiple-access communication, exploiting the data-driven model-free DQL. In this scenario, we employed the current sumrate as the reward function to align with the power allocation optimization objective. In our proposed DQL algorithm, we elegantly used is as an estimator for the prediction of the current sumrate under all power levels with a specific CSI. The simulation results showed that the trained DQN with zero discount factor provides the highest value of the average sumrate. In addition, it was shown that the proposed DQN has a better performance compared with benchmarks algorithms in terms of the average sumrate, which indicates the designed DQN has proper generalization capabilities. We also introduced offline centralized learning using simulated wireless multi-user communication networks, wherein the acquired knowledge from the trained DQN is assessed through distributed executions. In future research, we plan to explore online learning to align with real-world scenarios involving particular user distributions and propagation environments.

Acknowledgement: The work described in this paper has been developed within the project PRESECREL. We would like to acknowledge the financial support of the Ministerio de Ciencia e Investigación (Spain), in relation to the Plan Estatal de Investigación Científica y Técnica y de Innovación 2017–2020.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: Study conception and design: S. Soltani, E. Ghafourian, R. Salehi; data collection: S. Soltani, D. Martín, M. Vahidi; analysis and interpretation of results: E. Ghafourian, R. Salehi, D. Martín, M. Vahidi; draft manuscript preparation: S. Soltani, E. Ghafourian, R. Salehi, D. Martín. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. K. David and H. Berndt, “6G vision and requirements: Is there any need for beyond 5G?” IEEE Veh. Technol. Mag., vol. 13, no. 3, pp. 72–80, 2018. [Google Scholar]

2. M. Z. Chowdhury, M. Shahjalal, S. Ahmed, and Y. M. Jang, “6G wireless communication systems: Applications, requirements, technologies, challenges, and research directions,” IEEE Open J. Commun. Soc., vol. 1, pp. 957–975, 2020. [Google Scholar]

3. S. Miri, M. Kaveh, H. S. Shahhoseini, M. R. Mosavi, and S. Aghapour, “On the security of ‘an ultra-lightweight and secure scheme for communications of smart metres and neighbourhood gateways by utilisation of an ARM Cortex-M microcontroller’,” IET Inform. Secur., vol. 13, no. 3, pp. 544–551, 2023. [Google Scholar]

4. I. F. Akyildiz, A. Kak, and S. Nie, “6G and beyond: The future of wireless communications systems,” IEEE Access, vol. 8, pp. 133995–134030, 2020. [Google Scholar]

5. T. O’shea and J. Hoydis, “An introduction to deep learning for the physical layer,” IEEE Trans. Cogn. Commun. Netw., vol. 3, no. 4, pp. 563–575, 2017. [Google Scholar]

6. M. B. Shahab, M. F. Kader, and S. Y. Shin, “On the power allocation of non-orthogonal multiple access for 5G wireless networks,” in 2016 Int. Conf. on Open Source Systems & Technologies (ICOSST), Lahore, Pakistan, 2016, pp. 89–94. [Google Scholar]

7. M. Kaveh, M. S. Mesgari, and B. Saeidian, “Orchard algorithm (OAA new meta-heuristic algorithm for solving discrete and continuous optimization problems,” Math. Comput. Simulat., vol. 208, pp. 95–135, 2023. [Google Scholar]

8. P. Afrasyabi, M. S. Mesgari, M. Razban, and M. Kaveh, “Multi-modal routing using NSGA-II algorithm considering COVID-19 protocols: A case study in Tehran,” Earth Observ. Geomat. Eng., vol. 6, no. 1, pp. 1–14, 2022. [Google Scholar]

9. M. Kaveh, M. S. Mesgari, D. Martín, and M. Kaveh, “TDMBBO: A novel three-dimensional migration model of biogeography-based optimization (case study: Facility planning and benchmark problems),” J. Supercomput., vol. 2023, pp. 1–56, 2023. [Google Scholar]

10. M. Kaveh and M. S. Mesgari, “Hospital site selection using hybrid PSO algorithm-case study: District 2 of Tehran,” Scienti.-Res. Quart. Geo. Data (SEPEHR), vol. 28, no. 111, pp. 7–22, 2019. [Google Scholar]

11. C. Li, Q. Zhang, Q. Li, and J. Qin, “Price-based power allocation for non-orthogonal multiple access systems,” IEEE Wirel. Commun. Le., vol. 5, no. 6, pp. 664–667, 2016. [Google Scholar]

12. J. Zhu, J. Wang, Y. Huang, S. He, X. You and L. Yang, “On optimal power allocation for downlink non-orthogonal multiple access systems,” IEEE J. Sel. Area. Comm., vol. 35, no. 12, pp. 2744–2757, 2017. [Google Scholar]

13. Z. Xiao, L. Zhu, J. Choi, P. Xia, and X. G. Xia, “Joint power allocation and beamforming for non-orthogonal multiple access (NOMA) in 5G millimeter wave communications,” IEEE T. Wirel. Commun., vol. 17, no. 5, pp. 2961–2974, 2018. [Google Scholar]

14. W. U. Khan, F. Jameel, T. Ristaniemi, B. M. Elhalawany, and J. Liu, “Efficient power allocation for multi-cell uplink noma network,” in 2019 IEEE 89th Veh. Technol. Conf. (VTC2019-Spring), Kuala Lumpur, Malaysia, 2019, pp. 1–5. [Google Scholar]

15. N. Najafi, M. Kaveh, D. Martín, and M. R. Mosavi, “Deep PUF: A highly reliable DRAM PUF-based authentication for IoT networks using deep convolutional neural networks,” Sens., vol. 21, no. 9, pp. 2009, 2021. [Google Scholar]

16. S. S. Fard, M. Kaveh, M. R. Mosavi, and S. B. Ko, “An efficient modeling attack for breaking the security of XOR-arbiter PUFs by using the fully connected and long-short term memory,” Microprocess. Microsy., vol. 94, pp. 104667, 2022. [Google Scholar]

17. M. Kaveh, M. S. Mesgari, and A. Khosravi, “Solving the local positioning problem using a four-layer artificial neural network,” Eng. J. Geospatial Inf. Tech., vol. 7, no. 4, pp. 21–40, 2020. [Google Scholar]

18. K. Shen and W. Yu, “Fractional programming for communication systems—Part I: Power control and beamforming,” IEEE T. Signal Proces., vol. 66, no. 10, pp. 2616–2630, 2018. [Google Scholar]

19. Q. Shi, M. Razaviyayn, Z. Q. Luo, and C. He, “An iteratively weighted MMSE approach to distributed sum-utility maximization for a MIMO interfering broadcast channel,” IEEE T. Signal Proces., vol. 59, no. 9, pp. 4331–4340, 2011. [Google Scholar]

20. M. Kaveh, Z. Yan, and R. Jäntti, “Secrecy performance analysis of RIS-aided smart grid communications,” IEEE T. Ind. Inform., 2023. doi: 10.1109/TII.2023.3333842. [Google Scholar] [CrossRef]

21. H. Zhang, L. Venturino, N. Prasad, P. Li, S. Rangarajan and X. Wang, “Weighted sum-rate maximization in multi-cell networks via coordinated scheduling and discrete power control,” IEEE J. Sel. Area Comm., vol. 29, no. 6, pp. 1214–1224, 2011. [Google Scholar]

22. Z. Qin, H. Ye, G. Y. Li, and B. H. F. Juang, “Deep learning in physical layer communications,” IEEE Wirel. Commun., vol. 26, no. 2, pp. 93–99, 2019. [Google Scholar]

23. Y. LeCun, Y. Bengio, and G. Hinton, “Deep learning,” Nature, vol. 521, no. 7553, pp. 436–444, 2015. [Google Scholar] [PubMed]

24. S. Aghapour, M. Kaveh, M. R. Mosavi, and D. Martín, “An ultra-lightweight mutual authentication scheme for smart grid two-way communications,” IEEE Access, vol. 9, pp. 74562–74573, 2021. [Google Scholar]

25. H. Sun, X. Chen, Q. Shi, M. Hong, X. Fu and N. D. Sidiropoulos, “Learning to optimize: Training deep neural networks for interference management,” IEEE T. Signal Proces., vol. 66, no. 20, pp. 5438–5453, 2018. [Google Scholar]

26. F. Meng, P. Chen, L. Wu, and X. Wang, “Automatic modulation classification: A deep learning enabled approach,” IEEE T. Veh. Technol., vol. 67, no. 11, pp. 10 760–10 772, 2018. [Google Scholar]

27. H. Ye, G. Y. Li, and B. H. Juang, “Power of deep learning for channel estimation and signal detection in OFDM systems,” IEEE Wirel. Commun. Le., vol. 7, no. 1, pp. 114–117, 2017. [Google Scholar]

28. R. Amiri, H. Mehrpouyan, L. Fridman, R. K. Mallik, A. Nallanathan and D. Matolak, “A machine learning approach for power allocation in HetNets considering QoS,” in 2018 IEEE Int. Conf. on Communications (ICC), Kansas City, MO, USA, 2018, pp. 1–7. [Google Scholar]

29. H. Rabiei, M. Kaveh, M. R. Mosavi, and D. Martín, “MCRO-PUF: A novel modified crossover RO-PUF with an ultra-expanded CRP space,” Comp. Mater. Contin., vol. 74, no. 3, pp. 4831–4845, 2023. [Google Scholar]

30. F. D. Calabrese, L. Wang, E. Ghadimi, G. Peters, L. Hanzo and P. Soldati, “Learning radio resource management in RANs: Framework, opportunities, and challenges,” IEEE Commun. Mag., vol. 56, no. 9, pp. 138–145, 2018. [Google Scholar]

31. M. Kaveh, S. Aghapour, D. Martín, and M. R. Mosavi, “A secure lightweight signcryption scheme for smart grid communications using reliable physically unclonable function,” in 2020 IEEE Int. Conf. on Environ. and Electr. Eng. and 2020 IEEE Ind. and Commer. Power Syst. Eur. (EEEIC/I&CPS Europe), Madrid, Spain, 2020, pp. 1–6. [Google Scholar]

32. Y. S. Nasir and D. Guo, “Deep reinforcement learning for distributed dynamic power allocation in wireless networks,” arXiv preprint arXiv:1808.00490, 2018. [Google Scholar]

33. Y. Cheng, K. H. Li, Y. Liu, K. C. Teh, and H. V. Poor, “Downlink and uplink intelligent reflecting surface aided networks: NOMA and OMA,” IEEE T. Wirel. Commun., vol. 20, no. 6, pp. 3988–4000, 2021. [Google Scholar]

34. B. Zheng, Q. Wu, and R. Zhang, “Intelligent reflecting surface assisted multiple access with user pairing: NOMA or OMA?” IEEE Commun. Lett., vol. 24, no. 4, pp. 753–757, 2020. [Google Scholar]

35. F. R. Ghadi, G. A. Hodtani, and F. J. Lopez-Martinez, “The role of correlation in the doubly dirty fading MAC with side information at the transmitters,” IEEE Wirel. Commun. Lett., vol. 10, no. 9, pp. 2070–2074, 2021. [Google Scholar]

36. J. Ghosh, V. Sharma, H. Haci, S. Singh, and I. H. Ra, “Performance investigation of NOMA versus OMA techniques for mmWave massive MIMO communications,” IEEE Access, vol. 9, pp. 125300–125308, 2021. [Google Scholar]

37. C. Wu, X. Mu, Y. Liu, X. Gu, and X. Wang, “Resource allocation in STAR-RIS-aided networks: OMA and NOMA,” IEEE T. Wirel. Commun., vol. 21, no. 9, pp. 7653–7667, 2022. [Google Scholar]

38. F. R. Ghadi and F. J. Lopez-Martinez, “RIS-aided communications over dirty MAC: Capacity region and outage probability,” arXiv preprint arXiv:2208.07026, 2022. [Google Scholar]

39. F. R. Ghadi and W. P. Zhu, “Performance analysis over correlated/independent Fisher-Snedecor F fading multiple access channels,” IEEE T. Veh. Technol., vol. 71, no. 7, pp. 7561–7571, 2022. [Google Scholar]

40. Q. Wang, H. Chen, C. Zhao, Y. Li, P. Popovski and B. Vucetic, “Optimizing information freshness via multiuser scheduling with adaptive NOMA/OMA,” IEEE T. Wirel. Commun., vol. 21, no. 3, pp. 1766–1778, 2021. [Google Scholar]

41. X. Mu, Y. Liu, L. Guo, J. Lin, and Z. Ding, “Energy-constrained UAV data collection systems: NOMA and OMA,” IEEE T. Veh. Technol., vol. 70, no. 7, pp. 6898–6912, 2021. [Google Scholar]

42. F. R. Ghadi and G. A. Hodtani, “Copula function-based analysis of outage probability and coverage region for wireless multiple access communications with correlated fading channels,” IET Commun., vol. 14, no. 11, pp. 1804–1810, 2020. [Google Scholar]

43. L. Sanguinetti, A. Zappone, and M. Debbah, “Deep learning power allocation in massive MIMO,” in 2018 52nd Asilomar Conf. on Signals, Systems, and Computers, Pacific Grove, USA, IEEE, 2018, pp. 1257–1261. [Google Scholar]

44. S. Wang, Y. C. Wu, M. Xia, R. Wang, and H. V. Poor, “Machine intelligence at the edge with learning centric power allocation,” IEEE T. Wirel. Commun., vol. 19, no. 11, pp. 7293–7308, 2020. [Google Scholar]

45. Y. S. Nasir and D. Guo, “Multi-agent deep reinforcement learning for dynamic power allocation in wireless networks,” IEEE J. Sel. Area Comm., vol. 37, no. 10, pp. 2239–2250, 2019. [Google Scholar]

46. H. Saad, A. Mohamed, and T. ElBatt, “Distributed cooperative Q-learning for power allocation in cognitive femtocell networks,” in 2012 IEEE Vehicular Technology Conf. (VTC Fall), Quebec City, QC, Canada, 2012, pp. 1–5. [Google Scholar]

47. R. Amiri, H. Mehrpouyan, L. Fridman, R. K. Mallik, A. Nallanathan and D. Matolak, “Matolak A machine learning approach for power allocation in HetNets considering QoS,” in 2018 IEEE Int. Conf. on Communications (ICC), Pacific Grove, CA, USA, 2018, pp. 1–7. [Google Scholar]

48. G. Sun, D. Ayepah-Mensah, R. Xu, V. K. Agbesi, G. Liu and W. Jiang, “Transfer learning for autonomous cell activation based on relational reinforcement learning with adaptive reward,” IEEE Syst. J., vol. 16, no. 1, pp. 1044–1055, Mar. 2022. [Google Scholar]

49. H. Li, H. Gao, T. Lv, and Y. Lu, “Deep Q-learning based dynamic resource allocation for self-powered ultra-dense networks,” in 2018 IEEE Int. Conf. on Communications Workshops (ICC Workshops), Kansas City, MO, USA, 2018, pp. 1–6. [Google Scholar]

50. Z. Xu, Y. Wang, J. Tang, J. Wang, and M. C. Gursoy, “A deep reinforcement learning based framework for power-efficient resource allocation in cloud RANs,” in 2017 IEEE Int. Conf. on Communications (ICC), Paris, France, 2017, pp. 1–6. [Google Scholar]

51. J. Liu, B. Krishnamachari, S. Zhou, and Z. Niu, “DeepNap: Data-driven base station sleeping operations through deep reinforcement learning,” IEEE Inter. Things J., vol. 5, no. 6, pp. 4273–4282, Dec. 2018. [Google Scholar]

52. A. El Gamal and Y. H. Kim, Network Information Theory. Cambridge, UK: Cambridge University Press, 2011. [Google Scholar]

53. F. R. Ghadi, M. Kaveh, and D. Martín, “Performance analysis of RIS/STAR-IOS-aided V2V NOMA/OMA communications over composite fading channels,” IEEE Transactions on Intelligent Vehicles, 2023. doi: 10.1109/TIV.2023.3337898. [Google Scholar] [CrossRef]

54. R. S. Sutton and A. G. Barto, Reinforcement Learning: An Introduction. vol. 22447. Cambridge, MA: MIT Press, 1998. [Google Scholar]

55. D. P. Kingma and J. Ba, “Adam: A method for stochastic optimization,” arXiv preprint arXiv:1412.6980. 2014. [Google Scholar]