Optimal Scheduling of Multiple Rail Cranes in Rail Stations with Interference Crane Areas

1  Introduction

Currently, air pollution is becoming more critical than ever. Rail transportation is an environmentally friendly solution because of low CO2 emission, and will be further developed in the near future. In a rail transportation system, the main facility is the rail station. It is the place for trains to be discharged/loaded with outbound/inbound containers by rail cranes (RMGC, RTGC), forklifts and reach stackers. Fig. 1 shows the general layout of a rail station. In this paper, we consider the scheduling of the rail cranes because their operations directly influence the throughput of the rail stations. We not only assigned the job to cranes but also gave the job sequencing for each crane in order to minimize the makespan (the maximum completion time) of cranes. A dual cycle of crane is selected to minimize the number of crane working cycles.

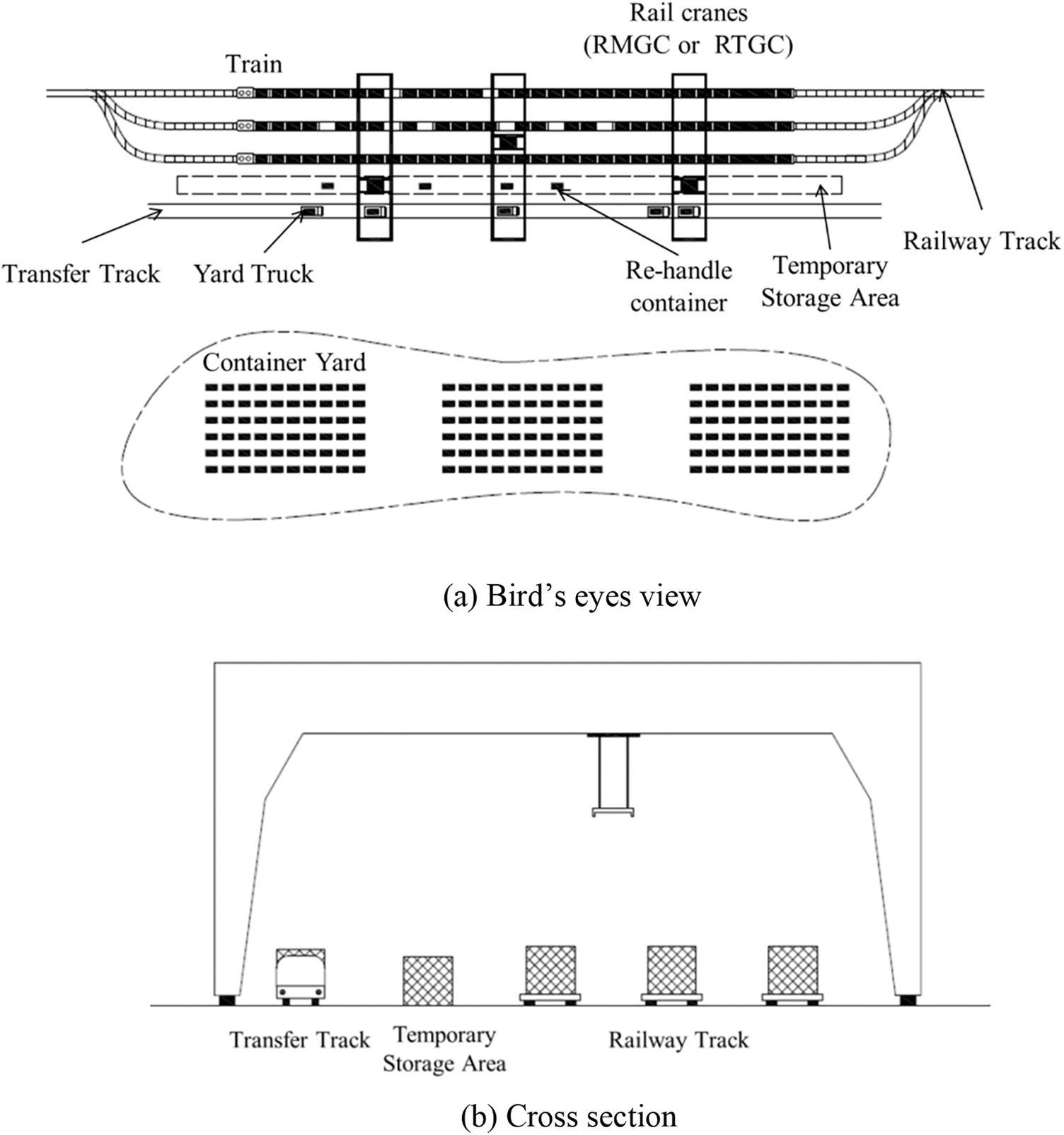
Figure 1: Layout of a rail station

In a working cycle, a crane simultaneously loads and discharges inbound container and outbound container on the trains, respectively. First, the crane moves to the transfer track, picks up the inbound container from the truck and loads it on to the train. Then, the crane moves to the outbound container position, discharges it from the train and loads it on to the truck. The re-handling of container (double handling) happened when an inbound container needs loading on the train but the outbound container at that position has not been unloaded. In that case, the inbound container needs to be loaded to a temporary storage area and be loaded on the train immediately after the outbound container is unloaded.

One difficulty of this problem is re-handling. An inbound container is directly loaded onto a train if the wagon is empty; otherwise, the inbound container needs to be re-handled. In that instance, the inbound container is unloaded from a truck and stacked in a temporary storage area. The inbound container that is stacked in the temporary storage area will be loaded onto the train after the wagon is empty (or the outbound container is discharged). In that case, we say that the outbound needs re-handling. Obviously, the re-handling operations of containers (inbound containers or outbound containers) depend on the point of time that the containers are transferred by cranes. In the simplest case, the re-handling case is caused by the operation of a crane, or may unfortunately be caused by two cranes being operated. A crane loads an inbound container on a wagon but that wagon has yet to be discharged, meaning the inbound container needs to be stored in a temporary storage area. Later, another crane unloads the wagon, and it should load the inbound container onto the wagon.

This paper is organized as follows. Section 2 presents the literature review while Section 3 explains the mathematical model. In Section 4, the Simulated Annealing algorithms are developed to get near optimal solutions. Section 5 presents the performance validation of the algorithms and finally, Section 6 presents the conclusions of this study.

2  Literature Review

There are numerous studies related to the operations in rail terminals. Research related to the operation problems in a rail station can be classified into three sub-problems of layout design, load planning, and rail crane scheduling. There are some studies related to the layout design of a rail terminal. Kozan [1] determined the crane split and assignment of trains to rail way tracks by a simple heuristic decision rule and a simple dispatching rule. In addition, a simulation was applied based on these heuristic rules to compare different yard layouts. Ballis et al. [2] identified the main design parameters of a railroad transport terminal such as the length and utilization of trans-shipment tracks, the mean stacking height in a storage area, and the type and amount of handling equipment by an analysis tool consisting of three modules comprising of an expert system, a simulation model, and a cost calculation module. Abacoumkin et al. [3] have proposed a similar approach to Ballis et al. [2], where they developed an expert system to define the terminal parameters such as cargo volume, loading unit mixture, equipment, layout characteristic, and operation conditions. Kozan [4] used a simulation model to compare different combinations of handling equipment to determine the most efficient set of handling equipment which is balanced between investigation cost and performance. Benna et al. [5] presented a simulation tool to plan and to design for the infrastructure, capacity, layout, and strategies of railroad container terminals.

There are several papers on the load planning on trains. For instance, Feo et al. [6] optimized the assignments of highway trailer to wagon in a piggyback (trailer on flatcar) system. Bostel et al. [7] were interested in the loading of containers on trains at a rail transfer terminal. Their aim was to minimize the displacement of containers. In contrast to Bostel et al. [7], Corry et al. [8] considered a different terminal system, different objectives and constraints. Their study proposes several techniques for determining an appropriate balance between container handling and weight distribution at a railroad transfer terminal. In Bruns et al. [9], their objective was to assign containers to the wagon of a train to maximize the weight of load units and minimize the travelling cost of load units from their current storage location to the assigned location.

Similarly, there are several papers related to the rail crane scheduling problem. For instance, Alicke [10] delved into logistical issues in container transfer at a theoretical intermodal terminal “Mega Hub” based on constraint satisfaction modeling and heuristics to minimize the maximum lateness of all trains. Boysen et al. [11] investigated the static crane areas in rail—road transshipment yards. In contrast, Boysen et al. [12] focused on the optimization of static crane areas in rail—rail transshipment contexts, using dynamic programming for optimal work area allocation. However, the optimal job sequencing of rail cranes remained unaddressed. Interestingly, none of these studies considered the efficiency-enhancing dual-cycle operation for rail cranes. Jeong et al. [13] demonstrated the application of dual-cycle operations for sequencing rail crane jobs and truck positions, but limited their model to unidirectional crane movement. Pap et al. [14] proposed a branch-and-bound algorithm for optimized dual-cycle job sequencing of a rail cranes, but their work excluded container re-handling scenarios. Guo et al. [15] tackled container loading/unloading scheduling with multiple gantry crane constraints, addressing safety clearance and non-crossing constraints. Their work, however, assumed one-dimensional crane travel and neglected dual-cycle operations or container re-handling. In contrast to these approaches, Nguyen et al. [16] studied rail crane job scheduling specifically in the context of container transfers between trains and trucks, incorporating both re-handling and dual-cycle operations into their model.

Scheduling problems of rail cranes in a rail station are similar to the scheduling problems of quay cranes at sea port container terminals. Many researchers have studied quay crane scheduling problems (QCSP) at port container terminals. In the quay crane scheduling problem, there are several factors which must be considered which are the bays, stacks, groups of containers and containers. However, the majority of studies have focused on the QCSP of container groups or vessel bays. Kim et al. [17] considered the sequence problem of discharging and loading groups of containers of quay cranes in order to minimize the completion time of a ship operation with the interference constraints of cranes. They proposed a branch-and-bound algorithm, and a greedy randomized adaptive search procedure (GRASP) to solve the problem. Moccia et al. [18] revised the formulation in Kim et al. [17], and obtained the optimal solution of the QCSP in small and medium sized instances. A branch-and-cut algorithm was developed to achieve the solutions of larger-sized instances. Moreover, some later studies including those of (Kaveshgar et al. [19]; Lee et al. [20]; Sammarra et al. [21]) tried to revise several issues in the formulation of Kim et al. [17] and applied novel approaches towards problem solving. Ng et al. [22] formulated the quay crane scheduling problem through integer programming. They developed an algorithm to obtain the lower bound of the problem based on the job scheduling problem for parallel machines with sequence independent processing time and LPT (largest processing time) rule. In order to find near optimal solutions, they developed a scheduling heuristic by decomposing the original problem into a number of independent quay crane scheduling sub-problems. The ship was partitioned into zones, with each crane operating within an individual zone. Dynamic programming was used to determine the optimal partition. Meisel [23] considered the QCSP with the inclusion of another aspect, in which a crane at a vessel is only available within certain time windows. A mixed integer programming model as well as a lower bound was developed. A heuristic approach was proposed to minimize the makespan of the cranes. Chen et al. [24] proposed a multi-commodity network flow model with two sets of flow trade-off constraints for multiple cranes and automated guide vehicles. Their constraints were used to solve inter-robot constraints to show the complicated interactions among agents accurately. Yang et al. [25] presented an integrated optimization method to manage the multi-devices integrated scheduling and storage space assignment issue in an energy-efficient manner. A bi-objective model is suggested to minimize the whole operating time and energy consumption, in which the transporting operations of imported and exported intermodal containers were solved simultaneously. Similarly, Li et al. [26] conducted a simulation-based solution for a multiple cranes scheduling issue in a steelmaking shop. Crane scheduling issues for a novel kind of automated container terminal system based on multi-storey frame bridges were explored by Zhen et al. [27]. Schulz et al. [28] depicted the planning situation encountered at a large rail-road terminal in Germany and presented a mixed-integer model capturing the core of the decision-making. They carried out a complicated analysis of issue’s variants and developed a heuristic method in a simulated annealing framework based on these structural insights. Moreover, recent studies on railway container terminal have shown the ongoing interests of various researchers for allocation, planning and scheduling problems [29,30].

In summary, the rail crane scheduling problems in this study are based on the movement of containers. We consider not only the gantry moves, but also the trolley moves. Moreover, the re-handle cases are also considered. In contrast, many studies of QCSP have focused on the operation of quay cranes based on the groups or bays of containers. The movements of containers are usually decided by the crane drivers’ experiences, and hence, reports on QCSP usually only focus on the movement of the gantry. The multi-crane scheduling problem in rail stations is NP-hard, so it is meaningful to propose intelligent optimization algorithm to solve this problem based on parallel simulated annealing.

3  Mathematical Model

In this section, the mathematical model is developed.

Notation

Decision variable

Derived variable

Min[Cmax](1)

Subject to

Ci−Ck≤(1−XiEkk)M∀k∈K,i∈I(2)

Ci+Ri×dix,T+2ix,iy−Ck≤(1−XiEkk)M∀k∈K,i∈O(3)

Cmax≥Ck+∑i∈ITIik+∑i∈OTOik∀k∈K(4)

pi={ty(Tr+2−iy)+Rity(Tr+2−iy)∀i∈ORity+(1−Ri)ty(Tr+2−iy)∀i∈I(5)

−MZij≤Ci−Cj+pj<M(1−Zij)∀i,j∈I∪O(6)

∑v=1k∑u∈I∪OXujv−∑v=1k∑u∈I∪OXuiv≤M(Zij+Zji)∀i,j∈I∪O,ix<jx,k∈K(7)

∑k∈K∑i∈I∪OXijk=1∀j∈I∪O(8)

∑i∈I∪OXijk−∑i∈I∪OXjik=0∀k∈K,j∈I∪O(9)

∑i∈I∪OX0kik=1∀k∈K(10)

∑i∈I∪OXiEkk=1∀k∈K(11)

Cj−Ci≤RiM+|x(i)−x(j)|M+|y(i)−y(j)|M∀i∈I′,j∈O′(12)

|Ri−Rj|≤|x(i)−x(j)|M+|y(i)−y(j)|M∀i∈I′,j∈O′(13)

Ri=0∀i∈I∖I′(14)

Dij+Ci−Cj≤(1−Xijk)M∀k∈K(15)

∑j∈OXijk(djx,jyix,T+1−djx,jyix,iy−dix,iyix,T+2+dix,T+1ix,T+2)+∑j∈IXijk(djx,T+2ix,T+1−djx,T+2ix,iy−dix,iyix,T+2+dix,T+1ix,T+2)−TIik≤(1−Ri)M∀k∈K,i∈I(16)

∑j∈OXijk(djx,jyix,iy−djx,jyix,T+2+dix,T+2ix,iy)+∑j∈IXijk(djx,T+2ix,iy−djx,T+2ix,T+2+dix,T+2ix,iy)−TOik≤(1−Ri)M∀k∈K,i∈O(17)

TIik≥(0−Ri)M∀k∈K,i∈I(18)

T0ik≥(0−Ri)M∀k∈K,i∈O(19)

dix,T+20kx,0ky+dix,iyix,T+2−Ci<(1−X0ik)M∀k∈K,i∈I(20)

dix,iy0kx,0ky+dix,T+2ix,iy−Ci<(1−X0ik)M∀k∈K,i∈O(21)

Xijk,Ri,Zij=0 or 1∀k∈K,i,j∈I∪O(22)

The mathematical model is defined in the objective function as Eq. (1). The makespan is the maximum completion time of all cranes, as described in Eq. (4). The completion time of a crane is the completion time of the last container in its container sequence, as in Eqs. (2) and (3). Eq. (5) is the processing time of a container. Eq. (6) defines the variable Zij if container j is handled after the operation of container i is completed, Zij=1; otherwise, Zij=0. Eq. (7) is noninterference constraint. Eq. (8) ensures that a container is assigned to only one crane. Eq. (9) is the flow balance constraint. Eqs. (10) and (11) select the initial and final containers of a crane, respectively. Eqs. (12) to (14) evaluate the re-handling cases. Eq. (12) denotes that if an inbound container i i∈I′ is loaded onto a wagon before the unloading of the outbound container j, Ci≤Cj, j∈O′ and ix=jx and iy=jy, the container i needs to be loaded to the temporary storage area, Ri=1. If the inbound container i and the outbound container have the same position on a train, Ri=Rj (Eq. (13)). If the inbound container i is loaded into temporary storage area, after unloading the outbound container j, the crane should load the inbound container i onto the wagon. Eq. (14) guarantees that the inbound container, which is not occupied by an outbound container, is not loaded into the temporary storage area. Eq. (15) determines the finishing time of a container. Eqs. (16) to (19) define the additional time if a container needs to be re-handled. Eqs. (20) and (21) determine the completion time of the first container in the schedule of a crane. The value of Dij is calculated by Eq. (23).

Dij={djx,T+2ix,iy+djx,jyjx,T+2∀i,j∈Idjx,jyix,T+2+djx,T+2jx,jy∀i,j∈Odjx,jyix,iy+djx,T+2jx,jy∀i∈I,j∈Odjx,T+2ix,T+2+djx,jyjx,T+2∀i∈O,j∈I(23)

4  Simulated Annealing Algorithms

The meta-heuristic simulated annealing algorithm is used to solve the problem of multiple rail cranes scheduling.

4.1 The Traditional SA

4.1.1 Initial Solution

A solution to the scheduling problem is a permutation representation of the job sequence of each crane. The initial solution of the SA is obtained by assigning containers to cranes based on the balancing workload among cranes. The “workload” is the total of all the travelling times to unload outbound containers or to load inbound containers [11]. One time unit is applied for the travelling time between the two closest railway tracks. The temporary storage area serves as a buffer zone between the transfer track and the railway track. Table 1 presents examples of containers. The table also includes the total crane travel time required to load or unload these containers. In the table, the train and wagon columns show the positions of containers. The total workload requires 41 units of time. Hence, the first crane is assigned wagons 1 to 5. The second crane is assigned wagons 6 to 10. The first crane has a total workload of 20 units. The workload of the second crane is 21 units.

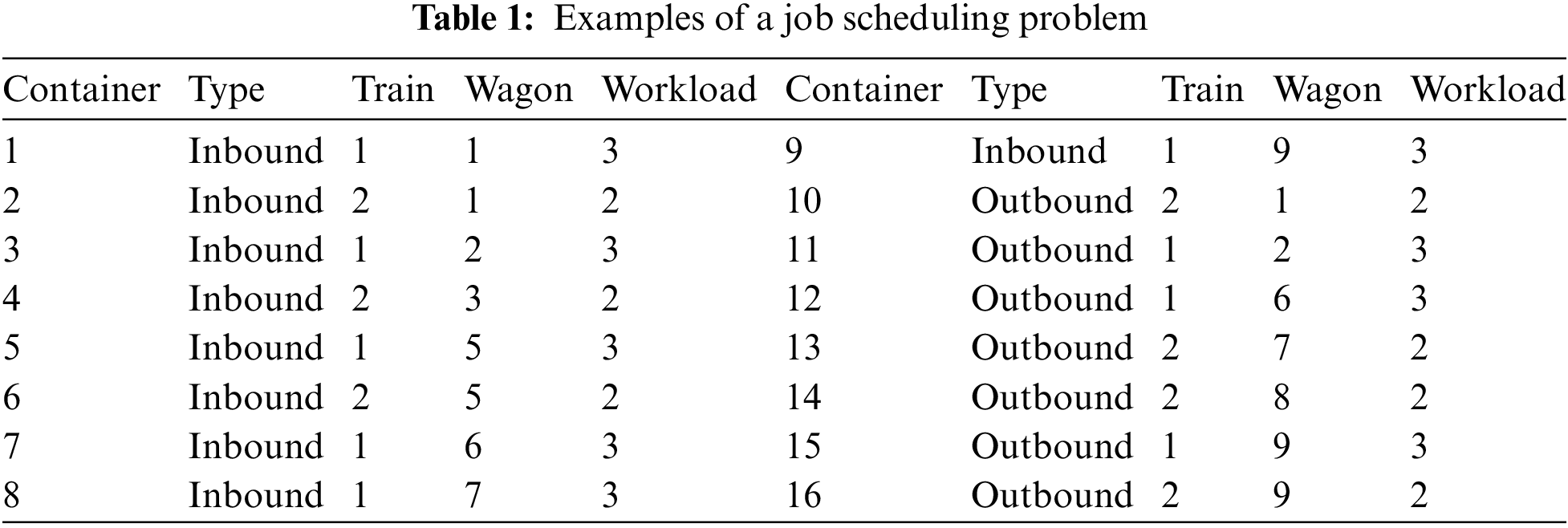
The job sequence comes from a simple heuristic, called “unidirectional” operating, in which a crane will handle its job in a single direction.

4.1.2 Neighborhood Solution

Two methods are used to generate the neighborhood solutions in this simulated annealing algorithm. The first method is pairwise interchange two containers that are assigned to the same crane. The second method is to exchange the assignment of a container. In the second method, two adjacent cranes are selected randomly, assume that two cranes kn and kn+1 are selected. Crane kn has a job sequence {s1n,s2n,…,smn} and crane kn+1 has a job sequence {s1n+1,s2n+1,…,sm′n+1}. There are two cases of the exchange of assignment of containers. Case 1: The last task in the job sequence of crane kn is assigned to crane kn+1 as the first task, {smn,s1n+1,s2n+1,…,sm′n+1}. Case 2: The first task in the job sequence of crane kn+1 is assigned to crane kn as the last task, {s1n,s2n,…,smn,s1n+1}. These two cases are applied with probability 0.5. Overall, the first method and the second method are selected with probability α, if rand(0,1)≤α the first method is used, otherwise the second method are applied, where rand(0,1)is random number between 0 and 1.

4.1.3 The Acceptance Criterion

The neighbor solution is accepted if Q(R)≤Q(C) or rand(0,1)<eQ(C)−Q(R)Ti, where Q(*) is the completion time of crane k in solution (*), Ti is the current temperature of iteration i.

4.1.4 The Cooling Down Function

In this SA, the geometric update scheme of (Lundy et al. [31]) is referred.

Ti=Ti−1×π(24)

and the algorithm stops when the computation exceeds an expected time.

4.2 The Parallel SA

Parallel computing is a technique to increase computation speed of a computer. In this algorithm the searching neighborhood solutions is separated into many threads of the CPU, which search the solution simultaneously. Hence it can search more solution candidates than the traditional SA wihthin a similar time frame. All operators in this algorithm are the same as those of the traditional SA. Fig. 2 shows the flowchart of the algorithm. In the parallel SA, the neighborhood solutions are generated from the same current solution by many threads simultaneously. If a thread can achieve a new current solution or a new best solution, it will update to the current solution or the global best solution. All the operators of the parallel SA are the same as the operators of the SA.

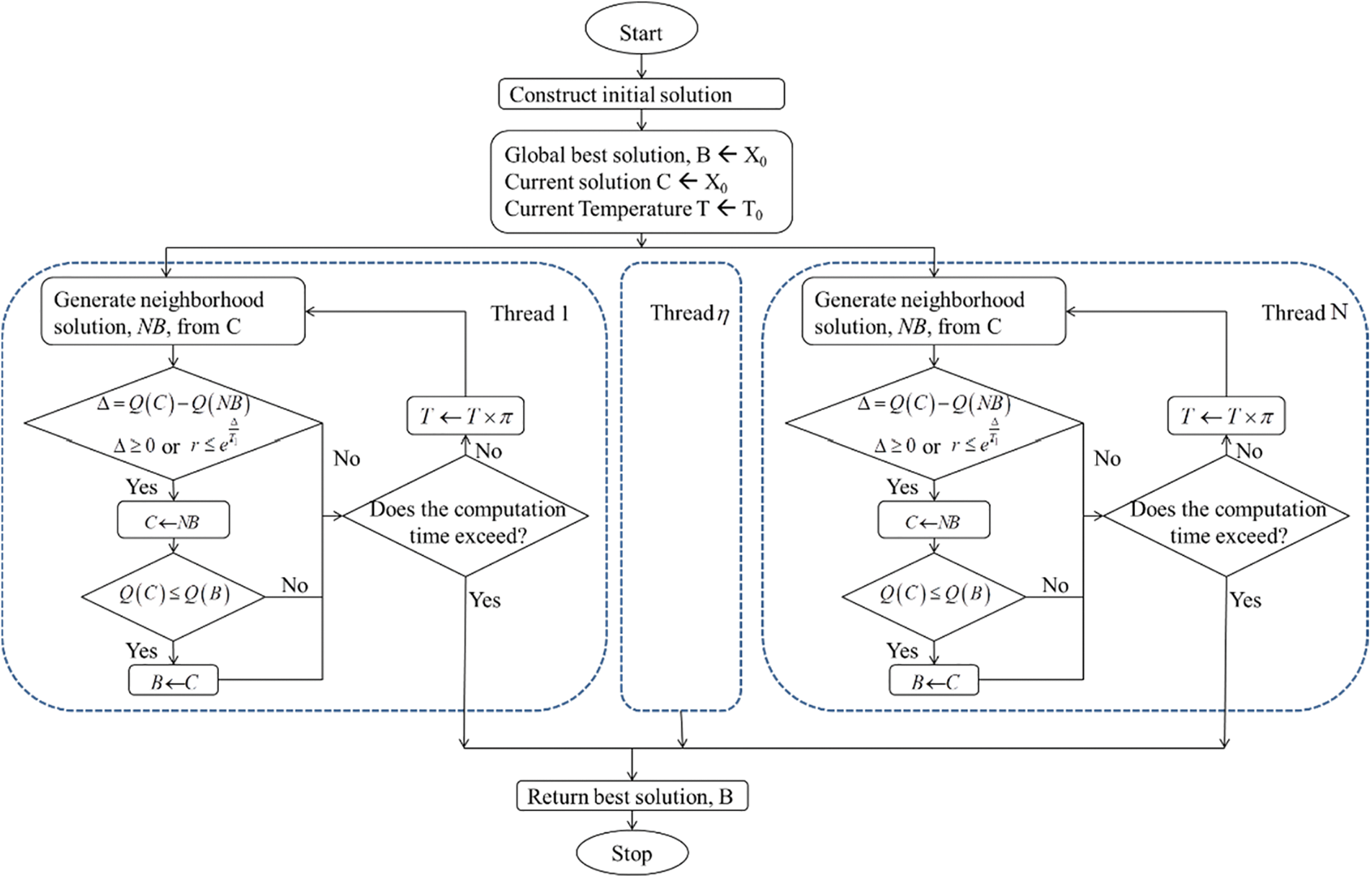
Figure 2: Parallel SA flowchart

5  Numerical Examples

It is very difficult to obtain the optimal solutions from the mathematical model. Fig. 3 shows the computation of CPLEX 12.6 on Windows 10 64 bits, Intel core i7, RAM 24 GB, SSD 512 GB to get the optimal solution from the mathematical model. From Fig. 3, the computation time increases rapidly when the number of containers increases. The computation time is very long because CPLEX used an exact algorithm and the multi-crane scheduling problem in rail stations is NP-hard. Sometimes it is difficult to find the optimum solution with large problem size. For instance, when the number of containers is 10, we cannot achieve the optimal solution within 12 h. With the case of 10 containers and 2 cranes, it takes a very long computational time (more than 16 h) to find the optimal solution.

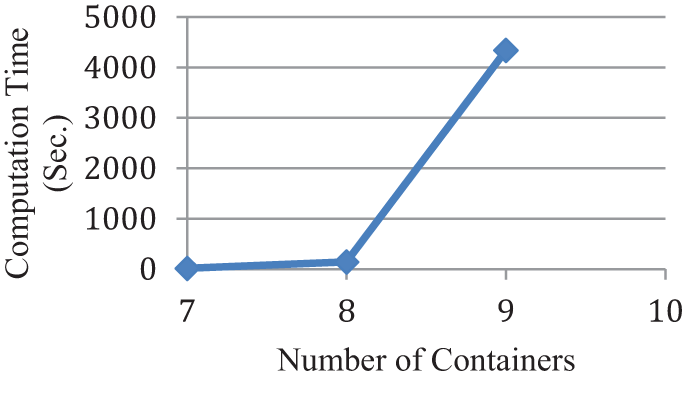
Figure 3: Computation time of mathematical model

5.1 Determine Parameter of the Simulated Annealing Algorithm

In this Section, we use the method of Ruiz et al. [32] to determine the parameters of these algorithms. The simulated annealing algorithms in this research have three parameters, α, T and π. We set four values for α, {0.2,0.4,0.6,0.8}, seven values for T, {1,5,10,20,40,80,160} and four values for π, {0.9999000,0.9999900,0.9999990,0.9999999}.

There are 112 combinations of three parameters. The algorithm is tested with 24 problems, which are generated randomly by Bernoulli distribution. The probabilities that a wagon carries a container are {0.25,0.50,0.75,0.95}. The number of the trains are {1,2,3} and the number of the rail cranes are {2,3}. A problem is generated twice for the inbound containers and outbound containers. The response variable is calculated by relative percentage deviation (RPD) (Ruiz et al. [32]).

RPD=Msol−BestsolBestsol×100(25)

where, Msol is the objective value of a given problem obtained by a combination of the three parameters, Bestsol is the best solution returned by all combinations of all parameters for the same problem. The algorithms are run by setting the computation time:

CpuTime = NumberOfInbounds × NumberOfOutbounds × NumberOfCranes ×20 (Milliseconds)

5.2 Determine Parameter of the SA

Table 2 shows the ANOVA table of RPD vs. all the parameters. The result in Table 2 shows that all parameters are very significant. In Fig. 4, the mean plot of the three parameters is presented. From this figure, the set of parameters giving the best performance is α=0.2,T=5 and π=0.999999.

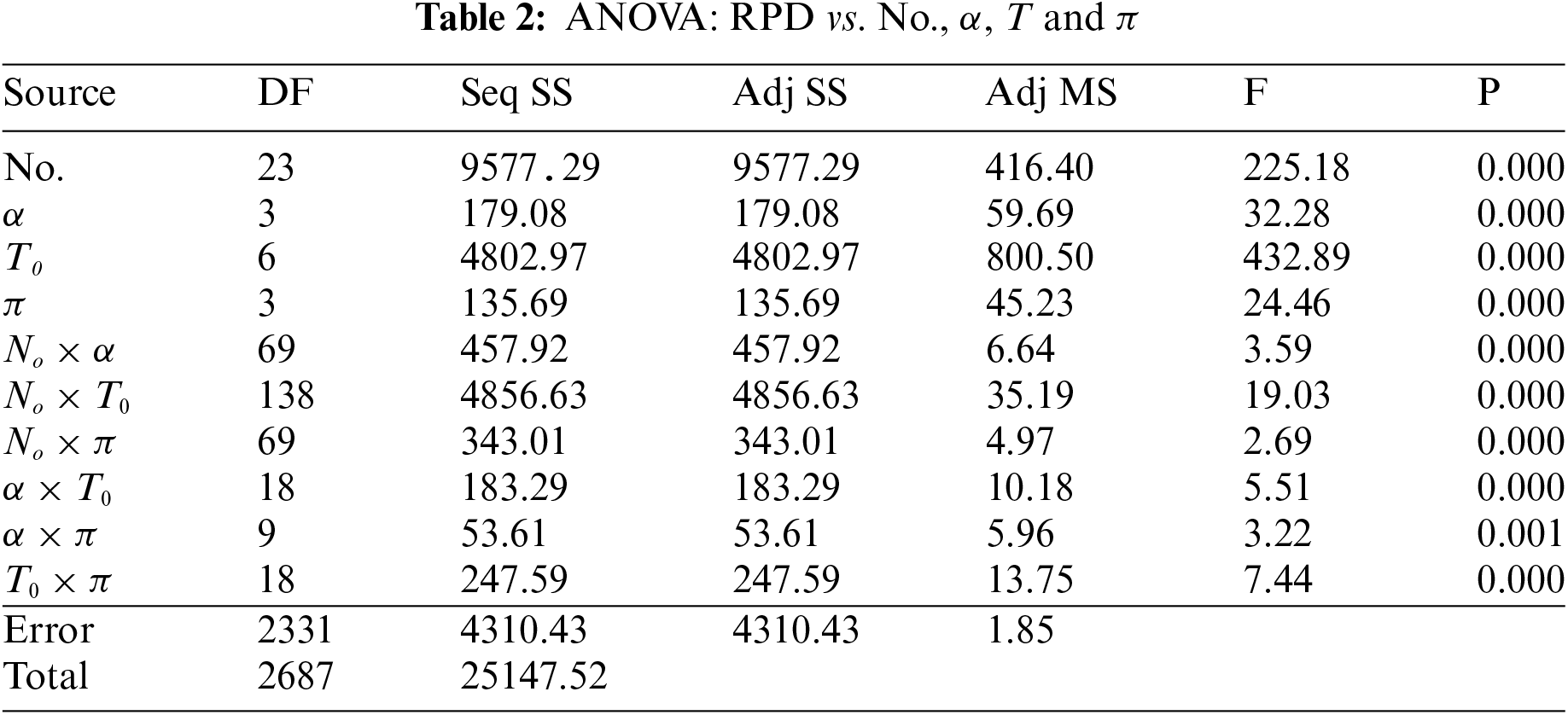
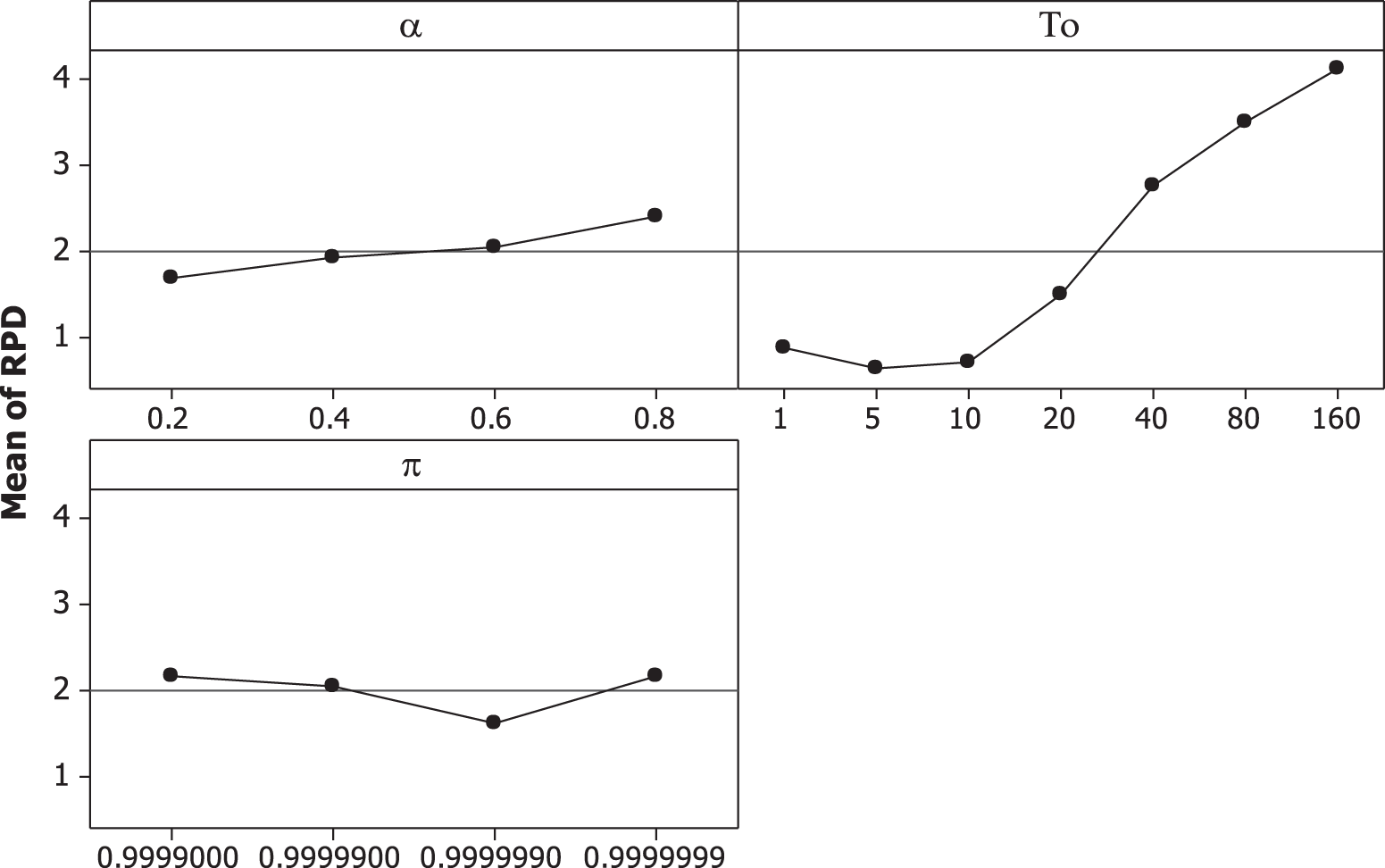
Figure 4: Mean of RPD of the SA

5.3 Determine Parameter of the PSA

Table 3 shows the ANOVA results of three parameters, showing all the factors are significant. From the Fig. 5, the set of parameters giving the best results is α=0.2,T=10 and π=0.999999.

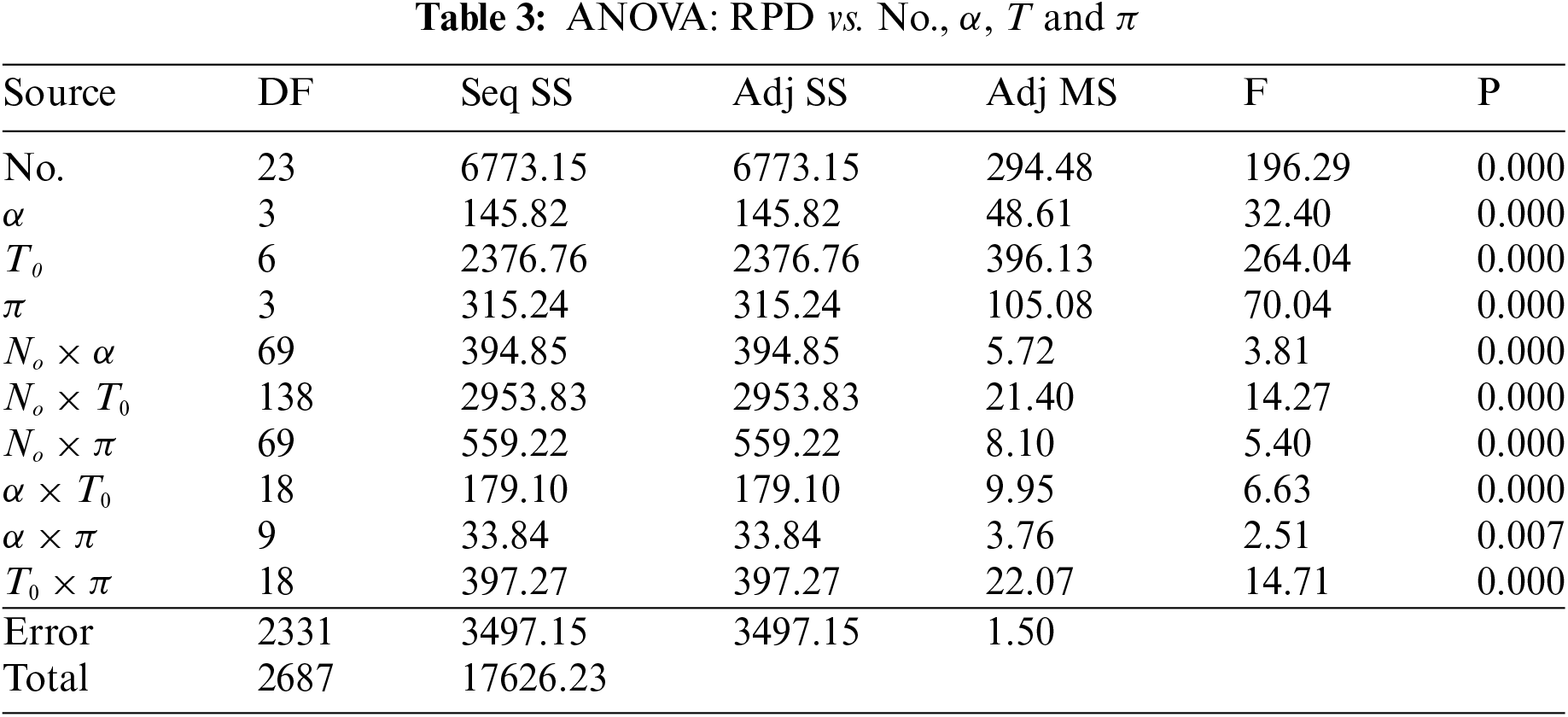
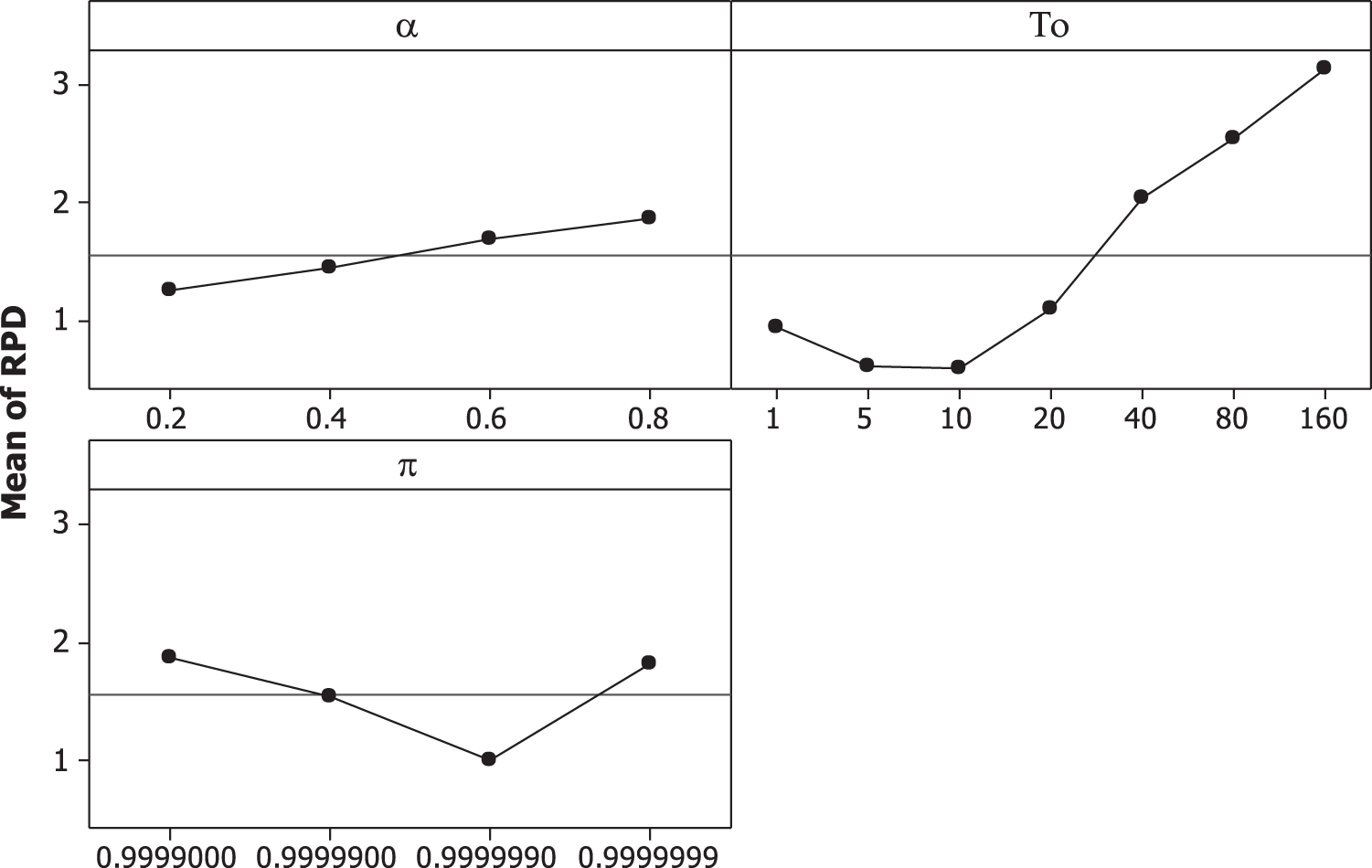
Figure 5: Mean of RPD of the PSA

5.4 Performances of the Algorithms

Table 4 shows the results of the SA and PSA. 24 problems are used to test the algorithms. Each problem is executed 10 times to obtain the mean and standard deviation. The Discrete Artificial Bee Colony algorithm (DABC) in Guo et al. [15] and the Greedy Randomized Adaptive Search Procedure (GRASP) in Kim et al. [17] are developed to compare to our proposed algorithms. All the algorithms are coded in JAVA programming language. From Table 4, the SA and PSA outperform the DABC and GRASP. In the small size problem, the gap between our algorithms and the other algorithms is small. When the sizes of the problems increase, the gaps among the algorithms are increased. The PSA outperforms the SA because the PSA can search for more solution candidates than the SA for a given time period.

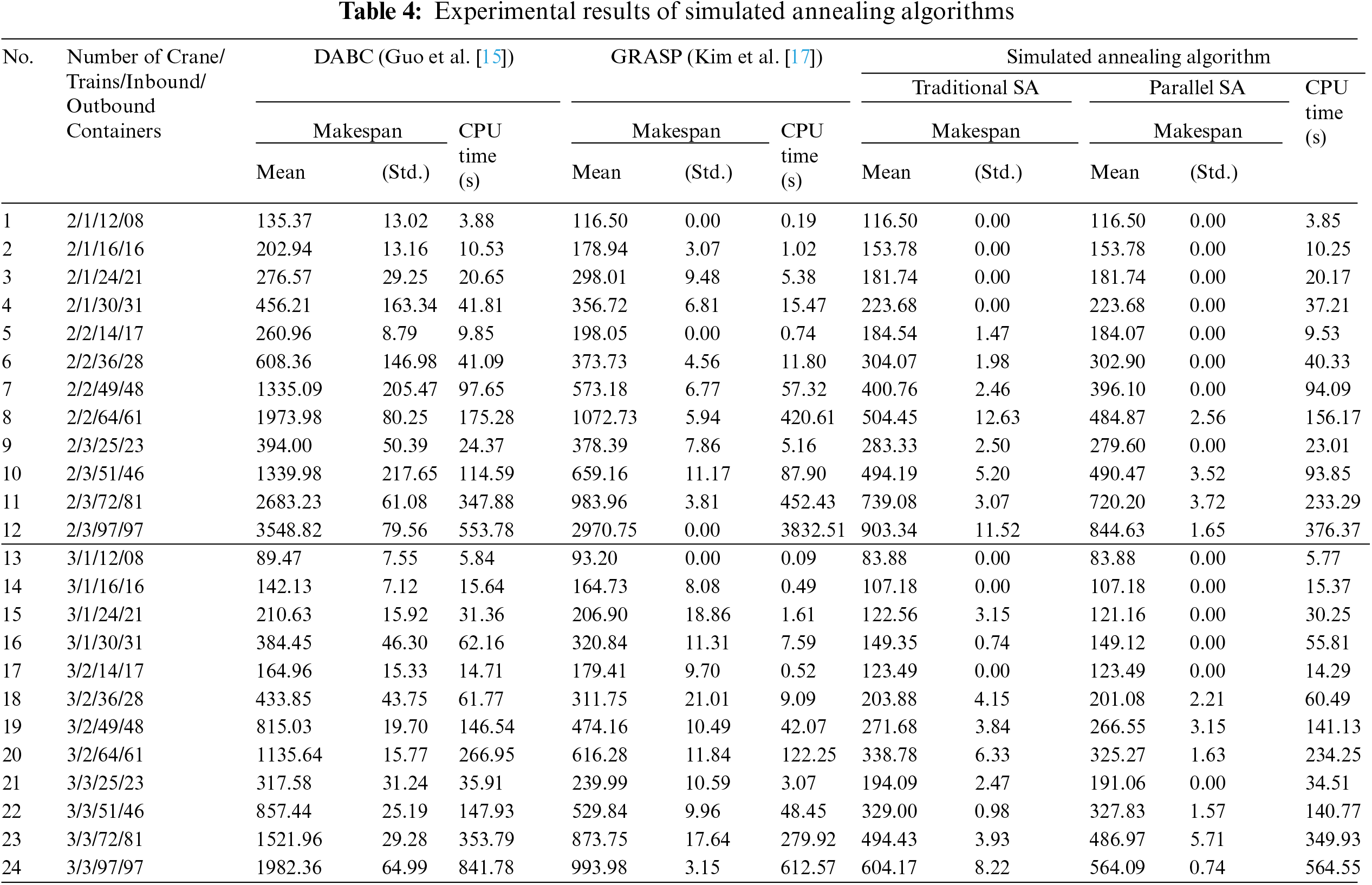
Table 5 and Fig. 6 show the makespan obtained from the parallel SA with 24 problems which are generated with unbalanced rate of inbound and outbound containers. If the problems have similar total number of containers, the problem which have more outbound containers than inbound containers will lead to higher makespan value. The balance rate of inbound and outbound containers gives smaller makespan than the unbalance case.

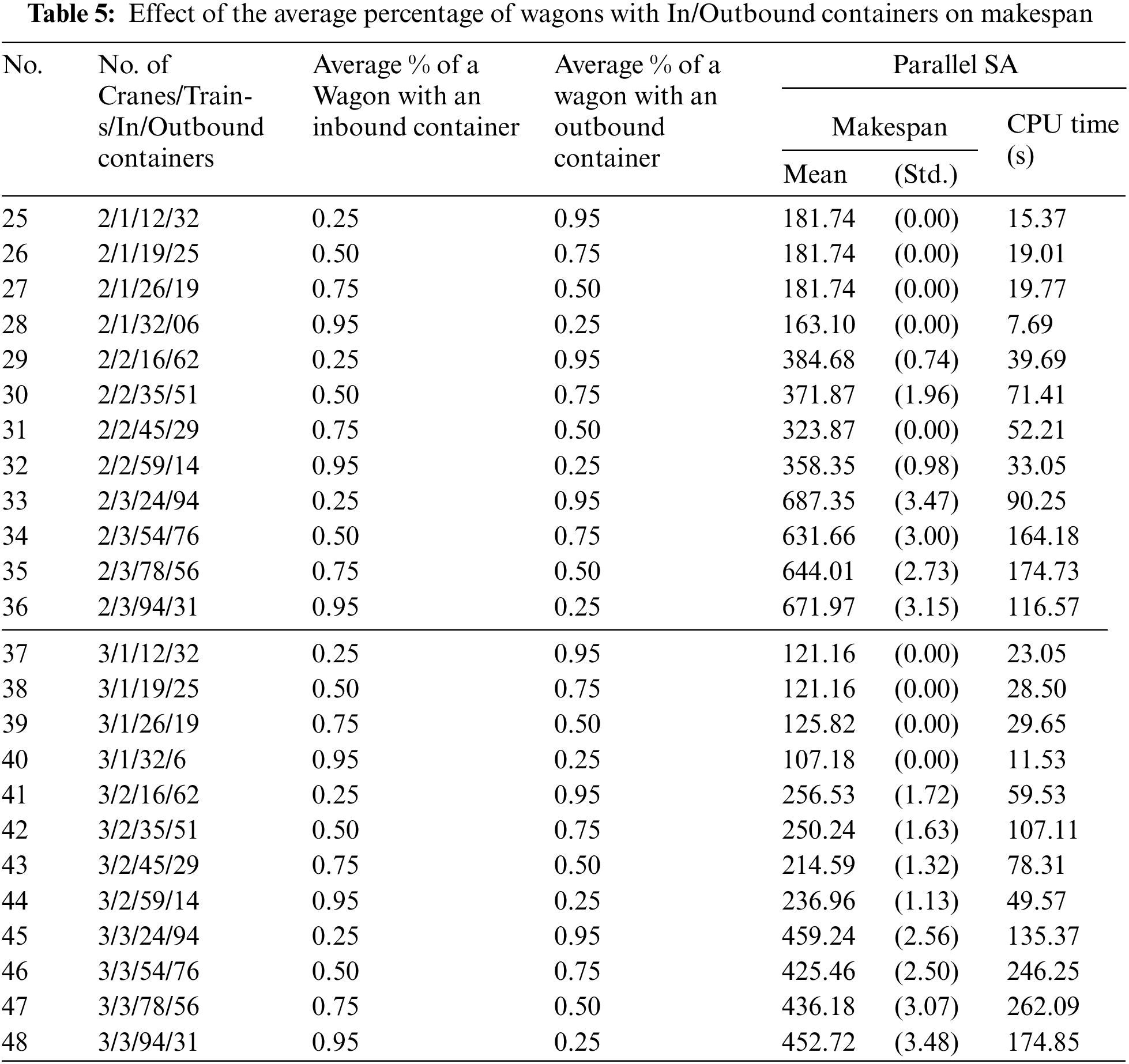
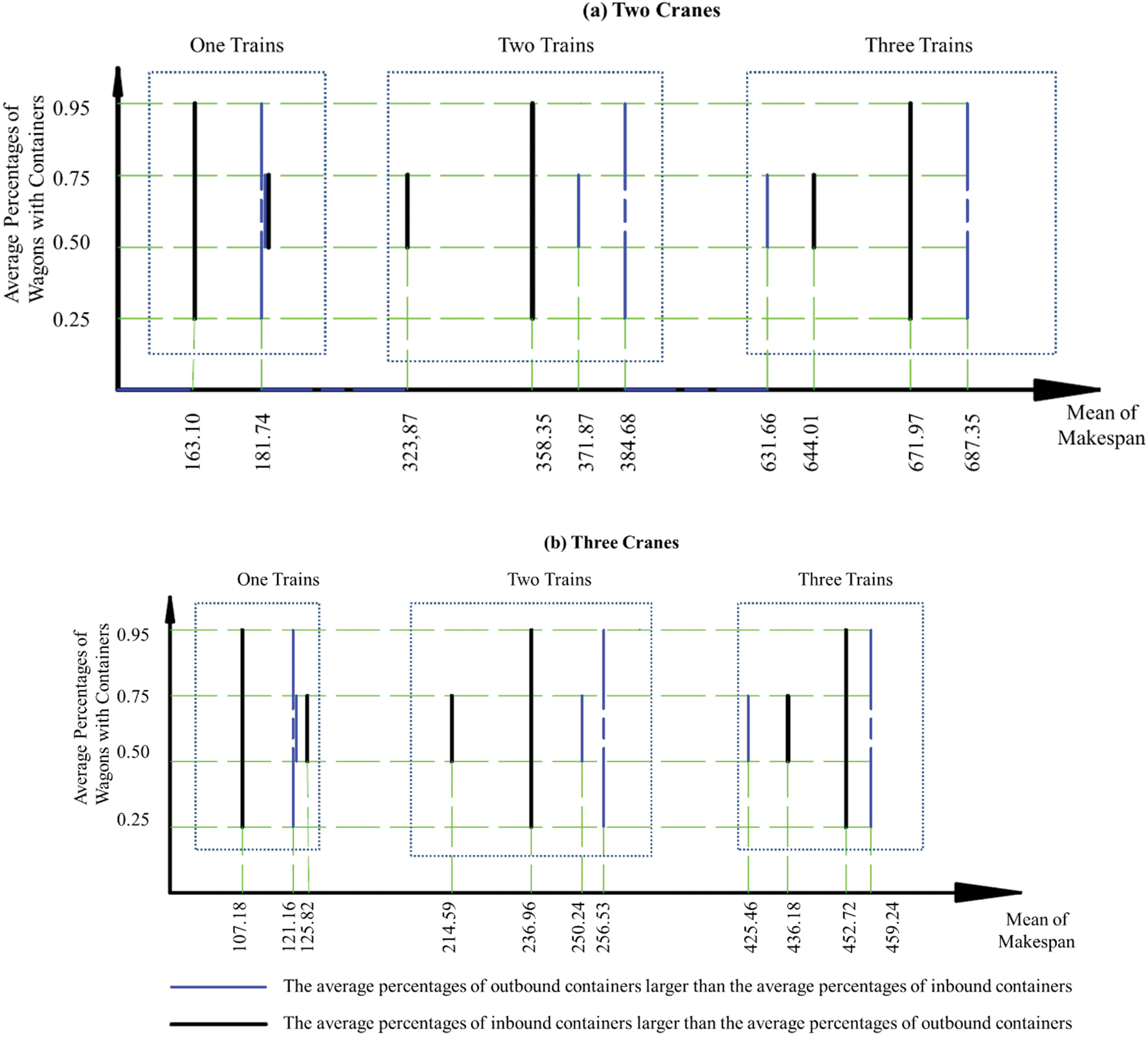
Figure 6: The average of percentages of wagon with containers vs. the mean of makespan

6  Conclusions

In this paper, we considered a multi-crane scheduling problem in rail stations. We not only assigned the job tasks to cranes in the dynamic boundary of cranes but also determined the sequence scheduling of each crane. The makespan of cranes was used as an optimization criterion and a Simulated Annealing (SA) and a parallel SA algorithm were proposed to find the solutions. We investigated the performance of algorithms by numerical examples. In general, the parallel SA algorithm outperformed the SA. Furthermore, the algorithms proposed in this paper gave better solutions than other considered algorithms. Moreover, we considered problems with balanced and unbalanced rates of inbound and outbound containers. The problems which had a balance rate of inbound and outbound containers gave smaller makespan, because cranes can perform more dual-cycle operations. When the rate of the outbound container is bigger than the rate of the inbound container, it usually leads to a higher makespan, because of the occurrence of re-handling cases.

Acknowledgement: None.

Funding Statement: The authors received no funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: Study conception and design: NVAD, NHT; data collection: NVAD, NLT; analysis and interpretation of results: NVAD, NLT, NHT; draft manuscript preparation: NVAD, NHT. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. E. Kozan, “Increasing the operational efficiency of container terminals in Australia,” J. Oper Res Soc, vol. 48, no. 2, pp. 151–161, 1997. [Google Scholar]

2. A. Ballis and J. Golias, “Comparative evaluation of existing and innovative rail-road freight transport terminals,” Transp. Res. Part A: Policy Pract., vol. 36, no. 7, pp. 593–611, 2002. [Google Scholar]

3. C. Abacoumkin and A. Ballis, “Development of an expert system for the evaluation of conventional and innovative technologies in the intermodal transport area,” Eur. J. Oper. Res., vol. 152, no. 2, pp. 410–419, 2004. [Google Scholar]

4. E. Kozan, “Optimum capacity for intermodal container terminals,” Transp. Plan. Technol., vol. 29, no. 6, pp. 471–482, 2006. [Google Scholar]

5. T. Benna and M. Gronalt, “Generic simulation for rail-road container terminals,” in Proc. 40th Winter Simul. Conf. 2008, Miami, FL, USA, Dec. 6–12, 2008, pp. 2656–2660. [Google Scholar]

6. T. A. Feo and J. L. González-Velarde, “The intermodal trailer assignment problem,” Transport. Sci., vol. 29, no. 4, pp. 330–341, 1995. [Google Scholar]

7. N. Bostel and P. Dejax, “Models and algorithms for container allocation problems on trains in a rapid transshipment shunting yard,” Transport. Sci., vol. 32, no. 4, pp. 370–379, 1998. [Google Scholar]

8. P. Corry and E. Kozan, “An assignment model for dynamic load planning of intermodal trains,” Comput. Oper. Res., vol. 33, no. 1, pp. 1–17, 2006. [Google Scholar]

9. F. Bruns and S. Knust, “Optimized load planning of trains in intermodal transportation,” OR Spectrum, vol. 34, no. 3, pp. 511–533, 2012. [Google Scholar]

10. K. Alicke, “Modeling and optimization of the intermodal terminal Mega Hub,” in H. O. Günther, K. H. Kim (Eds.Container Terminals and Automated Transport Systems: Logistics Control Issues and Quantitative Decision Support, Berlin Heidelberg: Springer Berlin Heidelberg, 2005, pp. 307–323. [Google Scholar]

11. N. Boysen and M. Fliedner, “Determining crane areas in intermodal transshipment yards: The yard partition problem,” Eur. J. Oper. Res., vol. 204, no. 2, pp. 336–342, 2010. [Google Scholar]

12. N. Boysen, M. Fliedner, and M. Kellner, “Determining fixed crane areas in rail-rail transshipment yards,” Transp. Res. Part E: Logist. Transp. Rev., vol. 46, no. 6, pp. 1005–1016, 2010. [Google Scholar]

13. B. J. Jeong and K. H. Kim, “Scheduling operations of a rail crane and container deliveries between rail and port terminals,” Eng. Optimiz., vol. 43, no. 6, pp. 597–613, 2011. [Google Scholar]

14. E. Pap, G. Bojanic, N. Ralevic, M. Georgijevic, and V. Bojanic, “Crane scheduling method for train reloading at inland intermodal container terminal,” in Proc. 2012 IEEE 10th Jubilee Int. Symp. Intell. Syst. Inf., 2012, pp. 189–192. [Google Scholar]

15. P. Guo, W. Cheng, Z. Zhang, M. Zhang, and J. Liang, “Gantry crane scheduling with interference constraints in railway container terminals,” Int. J. Comput. Int. Syst., vol. 6, no. 2, pp. 244–260, 2013. [Google Scholar]

16. V. A. D. Nguyen and W. Y. Yun, “Optimal job scheduling of a rail crane in rail terminals,” Int. J. Ind. Eng., vol. 21, no. 3, pp. 129–140, 2014. [Google Scholar]

17. K. H. Kim and Y. M. Park, “A crane scheduling method for port container terminals,” Eur J. Oper. Res., vol. 156, no. 3, pp. 752–768, 2004. [Google Scholar]

18. L. Moccia, J. F. Cordeau, M. Gaudioso, and G. Laporte, “A branch-and-cut algorithm for the quay crane scheduling problem in a container terminal,” Nav. Res. Log., vol. 53, no. 1, pp. 45–59, 2006. [Google Scholar]

19. N. Kaveshgar, N. Huynh, and S. K. Rahimian, “An efficient genetic algorithm for solving the quay crane scheduling problem,” Expert Syst. Appl., vol. 39, no. 18, pp. 13108–13117, 2012. [Google Scholar]

20. D. H. Lee and J. H. Chen, “An improved approach for quay crane scheduling with non-crossing constraints,” Eng. Optimiz., vol. 42, no. 1, pp. 1–15, 2010. [Google Scholar]

21. M. Sammarra, J. F. Cordeau, G. Laporte, and M. F. Monaco, “A tabu search heuristic for the quay crane scheduling problem,” J. Sched., vol. 10, no. 4–5, pp. 327–336, 2007. [Google Scholar]

22. W. C. Ng and K. L. Mak, “Quay crane scheduling in container terminals,” Eng. Optimiz., vol. 38, no. 6, pp. 723–737, 2006. [Google Scholar]

23. F. Meisel, “The quay crane scheduling problem with time windows,” Nav. Res. Logist., vol. 58, no. 7, pp. 619–636, 2011. [Google Scholar]

24. X. Chen, S. He, Y. Zhang, L. Tong, P. Shang and X. Zhou, “Yard crane and AGV scheduling in automated container terminal: A multi-robot task allocation framework,” Transp. Res. Part C: Emerg. Technol., vol. 114, pp. 241–271, 2020. [Google Scholar]

25. Y. Yang, X. Zhu, and A. Haghani, “Multiple equipment integrated scheduling and storage space allocation in Rail-Water intermodal container terminals considering energy efficiency,” Transp. Res. Record., vol. 2673, pp. 199–209, 2019. [Google Scholar]

26. J. Li, A. Xu, and X. Zang, “Simulation-based solution for a dynamic multi-crane-scheduling problem in a steelmaking shop,” Int. J. Prod. Res., vol. 58, pp. 6970–6984, 2020. [Google Scholar]

27. L. Zhen, H. Hu, W. Wang, X. Shi, and C. Ma, “Cranes scheduling in frame bridges based automated container terminals,” Transp. Res. Part C: Emerg. Technol., vol. 97, pp. 369–384, 2018. [Google Scholar]

28. A. Schulz, M. Fliedner, B. Fiedrich, and C. Pfeiffer, “Levelling crane workload in multi-yard rail-road container terminals,” Eur. J. Oper. Res., vol. 293, pp. 941–954, 2021. [Google Scholar]

29. G. Ren, X. Wang, J. Cai, and S. Guo, “Allocation and scheduling of handling resources in the railway container terminal based on crossing crane area,” Sustain., vol. 13, no. 3, pp. 1190, 2021. doi: 10.3390/su13031190. [Google Scholar] [CrossRef]

30. J. Li et al., “A flexible scheduling for twin yard cranes at container terminals considering dynamic cut-off time,” J. Mar. Sci. Eng., vol. 10, no. 5, pp. 675, 2022. doi: 10.3390/jmse10050675. [Google Scholar] [CrossRef]

31. M. Lundy and A. Mees, “Convergence of an annealing algorithm,” Math. Program., vol. 34, pp. 111–124, 1986. [Google Scholar]

32. R. Ruiz and T. Stützle, “A simple and effective iterated greedy algorithm for the permutation flowshop scheduling problem,” Eur. J. Oper. Res., vol. 177, pp. 2033–2049, 2007. [Google Scholar]