A New Flower Pollination Algorithm Strategy for MPPT of Partially Shaded Photovoltaic Arrays

1  Introduction

Because of the unpredictable variations in weather, the non-linear electrical properties of PV systems make it challenging to ensure optimal performance. Hence, MPPT controllers are commonly applied in PV systems to enhance and optimize PV output under varying weather conditions. The research question is how the PV array can operate at GMPP in partial shading conditions.

Several MPPT approaches have been introduced in efforts to capture the maximum power point (GMPP), including traditional MPPT methods (online and offline techniques) and Al-based MPPT methods (fuzzy logic control, artificial neural network, and metaheuristic methods (MHAs)) [1,2].

However, each of the aforementioned methods has at least one disadvantage, such as failing to track global maximum power point (GMPP) completely, having slow tracking speed, low accuracy, increasing computation burden, or being caught occasionally in local maximum power point (LMPP).

To address the aforementioned shortcomings, a novel modified flower pollination algorithm (MFPA) is developed here, which is an improved version of the flower pollination algorithm (FPA) that generates the required control variable randomization and successfully tracks the GMPP with a short tracking time under various partial shading conditions.

Hill climbing (HC) [3] and perturb and observe (P&O) [4] are two widely used online techniques due to their ease of implementation and straightforward control methods. The MPP was achieved similarly by these two algorithms.

The HC algorithm performs by continuously perturbing a power converter’s duty cycle, while the P&O algorithm performs by perturbation of the PV system’s operating voltage. Although these algorithms are simple to use, their operating points suffer from constant oscillation around the MPP. Even though the choice of a small step size for the perturbation may enhance the oscillations, it reduces the PV system tracking speed. Hence, in [5,6], an improved version of the P&O algorithm was developed with variable perturbation step-size as a way of overcoming the above shortcomings.

Nevertheless, under partial shading conditions (PSC), these methods failed to locate the GMPP.

Offline techniques for tracking the MPP of a PV system have been developed, such as, fractional short-circuit current (FSCC) [7] and fractional open-circuit voltage (FOCV) [8]. FOCV and FSCC are offline techniques that isolate the PV module to find the MPP.

Both offline MPPT methods have the basic advantages of implementing and convergence quickly towards the estimated MPP. The FOCV calculates the MPP voltage by utilizing a fractional portion of the open-circuit voltage. Similarly, the FSCC is represented as a percentage of the short-circuit current compared to the MPP current. The PV system is unable to locate a true MPP due to the aforementioned approximate relationships.

It is noteworthy that, AI-based MPPT is considered to be a promised technique to achieve GMPP for a P-V curve of a PV system, where its P-V curve has numerous peaks. AI-based MPPT can be categorized as fuzzy logic (FL) [9–11], artificial neural network (ANN) methods [12–14], and metaheuristic methods (MHAs) [15–17]. In [18], the FL controller was applied in conjunction with the INC method to determine the output duty cycle. A new hybrid technique based on an artificial neural network (ANN) and fractional-order PID (FOPID) controller was proposed in [12]. The sanitized teacher learning-based optimization algorithm is utilized for training the feed-forward ANN using the experimental data. Then, the water cycle algorithm is employed to tune the parameters of the FOPID controller.

The MHA was designed to address an optimization problem that tailors its approach to each specific situation [15–17]. Given that advance knowledge of P-V curves is seldom available, employing an MHA is a suitable option for GMPP tracking in the presence of partial shading conditions [19]. All MHAs have two characteristics in common: They are nature-inspired (based on biological, ethological, or physics concepts), and they exploit random features to escape from local optimal points. Due to its straightforward implementation, particle swarm optimization (PSO) is a widely favored choice among MHAs for MPPT [20,21]. PSO, on the other hand, suffers from a long tracking time for wide search spaces. One of the major issues with the traditional PSO method is its delayed convergence to MPP.

In [22] ant colony optimization (ACO) technique was developed and was used in MPPT. When evaluated in both uniform and shading pattern conditions, ACO performs similarly to PSO. In [23], a modified differential evolution technique was designed to determine the GMPP in scenarios involving partial shading. This approach offers swift convergence and a straightforward implementation thanks to its limited number of control parameters. However, there is, no mechanism in place to keep track of the particle’s prior movements and locations throughout the program. Consequently, it has a proclivity to become caught in the local MPP. The flower pollination algorithm (FPA) is presented in [24] in an attempt to address the abovementioned disadvantages. In [25], the bio-inspired hybrid two-stage MPPT technique involves a flower pollination algorithm (FPA). In the first stage, this moves the pollen toward the GMPP, while in the second stage, the P&O algorithm is employed to enhance acceleration when the pollen approaches the GMPP.

In this research, a modified flower pollination algorithm (MFPA) was developed to determine the GMPP for a PV system under different environmental conditions.

The following are the key features that the proposed method can successfully employ to realize MPPT:

(1) The ability of the proposed MFPA method to identify the approximate best duty ratio value at every peak by reinitializing the pollen to the duty ratios associated with these peaks. This capability is aimed at reducing the time required for the algorithm to converge towards the GMPP. The use of the computed duty ratios, as proposed MFPA starting points lowers the time taken to find the GMPP, increasing the PV system’s generated energy and efficiency.

(2) In the procedure of dual-mode optimization, appropriate randomness for the control variable is produced.

(3) Transition between two modes is influenced both by population fitness and switch probability values. The proposed method overcomes the shortcomings of the standard flower pollination algorithm (FPA), which has a slow convergence rate at the latter stages.

The following is how the reminder of the paper is organized:

Section 2 outlines PV modeling, and Section 3 describes the principle of flower pollination control structure. Sections 4 and 5 respectively, cover the proposed MFPA methodology’s control structure, as well as detailed steps for FPA–MPPT implementation. The simulation results are presented in Section 6. In Section 7, the study’s conclusions are presented.

2  Modeling of PV System

Fig. 1 illustrates the control arrangement of the PV system, consisting of three sets of PV modules connected in series and a boost converter linked to a battery. The primary objective of the proposed FPA algorithm is to optimize the PV system’s operation to achieve its maximum power output. The battery serves the function of maintaining a stable load voltage. In [26], the paper delves into the models describing the performance of the PV system when subjected to partial shading conditions (PSC). Multiple peaks appear on the PV array’s Power-Voltage (P-V) and PV array’s power-duty (P-D) curve as a consequence of shading on the PV system, which are depicted in Figs. 2 and 3, respectively. When the level of irradiance varies among the PV modules connected in series, the number of peaks observed in the P-V curve corresponds to the number of these modules, as discussed in [27]. In the control configuration depicted in Fig. 1 for the PV system, three sets of PV modules are interconnected in a series arrangement. This arrangement results in the emergence of three distinct peaks when each group is subjected to varying levels of irradiance. Moreover, SP1, SP2, SP3, SP4, and SP5 (from Eqs. (1) to (5)) are the shading patterns (SPs) used in Fig. 3’s P-D curves. The irradiances for these shading patterns are as follows:

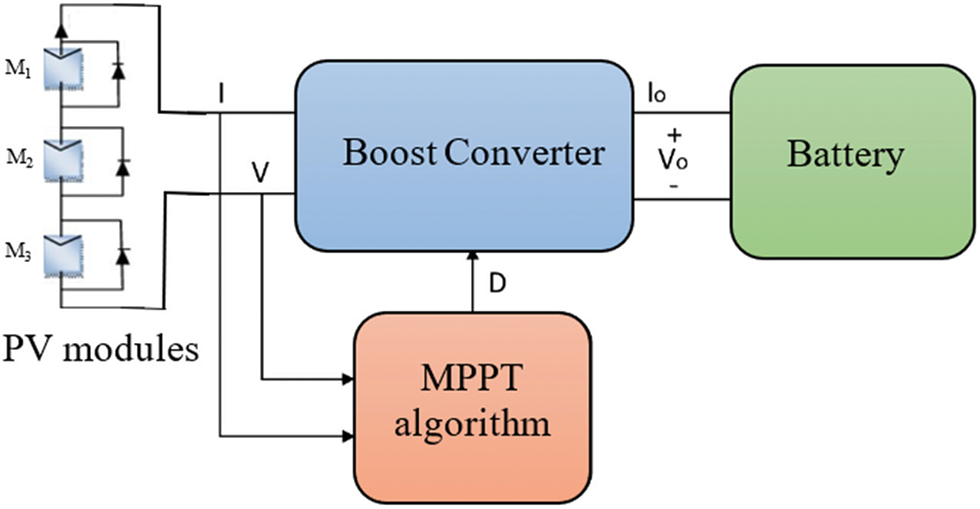
Figure 1: A diagram illustrating the PV system

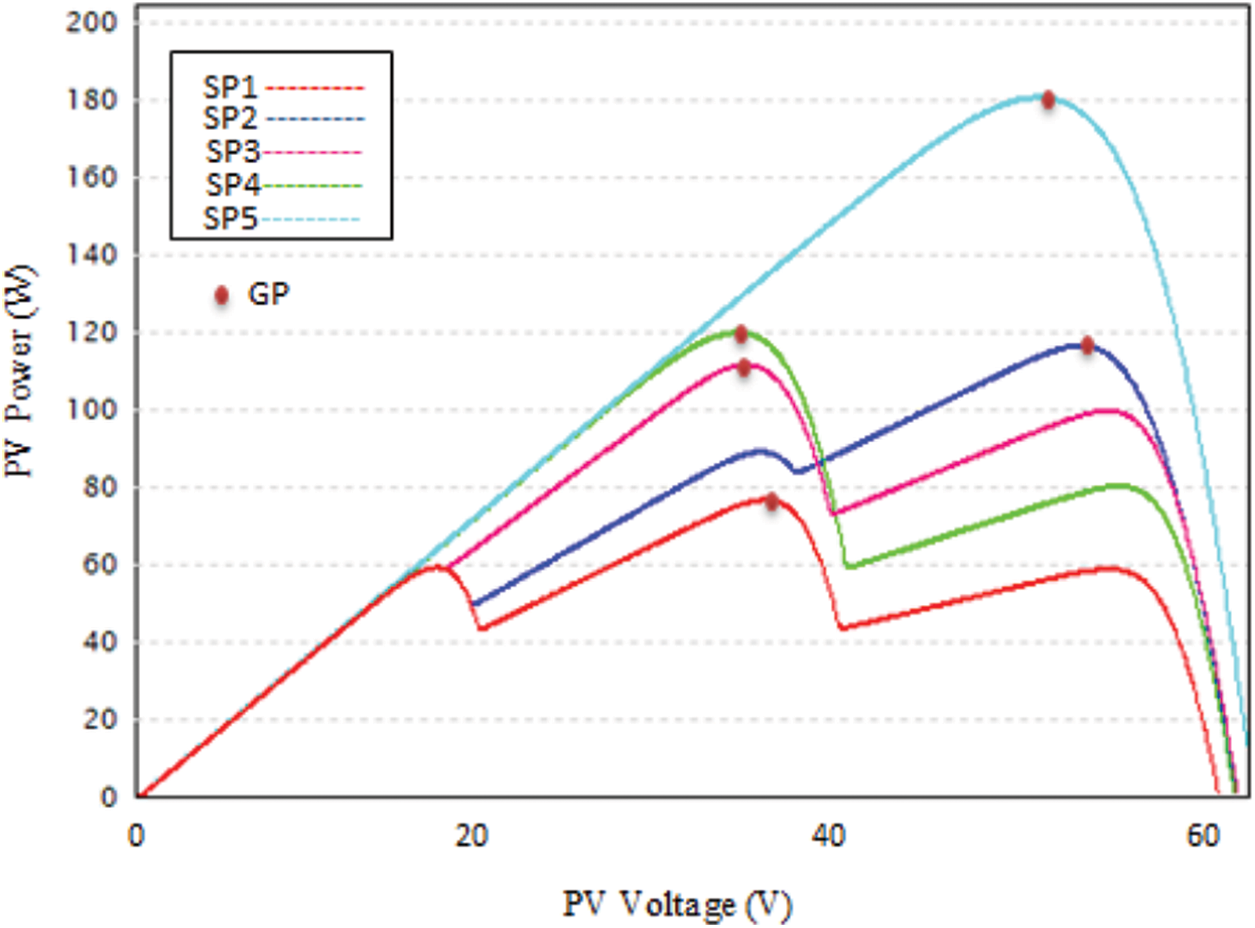
Figure 2: Power-Voltage curve under different shading patterns

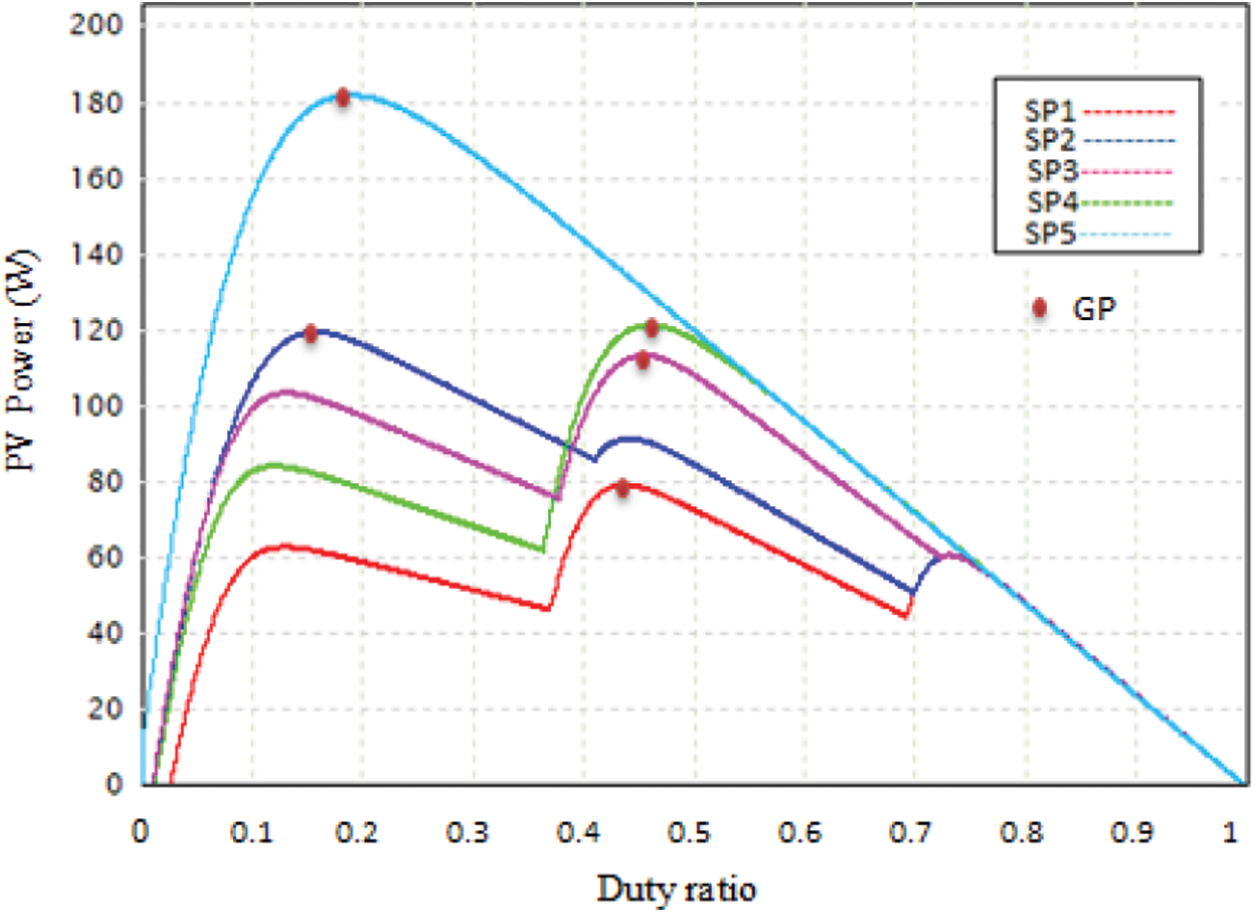
Figure 3: Power-duty ratio curve under different shading patterns

SP1=[300,1000,600]W/m2(1)

SP2=[1000,700,600]W/m2(2)

SP3=[500,900,1000]W/m2(3)

SP4=[100,1000,400]W/m2(4)

SP5=[1000,1000,1000]W/m2(5)

The numbers enclosed in brackets correspond to the three components of irradiance within each shading pattern and align with the irradiance levels experienced by each of the three PV modules, as illustrated in Fig. 1. It is important to note that, as seen in Figs. 2 and 3, SP5 corresponds to a uniform distribution at each module, and its P-D curve has only one peak, allowing conventional MPPT approaches to detect the GMPP efficiently.

Shading patterns (SP1, SP2, and SP3) correspond to partial shading conditions, with one global point (GP) and several local points (LPs) displayed in various locations. GPs are found in the second, third, and second locations of the P-D curves in SP1, SP2, and SP3. The shading pattern SP4 has one GP in the first place on the P-D curve and one LP in the second place. The crucial observation from Fig. 3 is that, the duty ratios of the peaks shown in the same location are similar. To expedite the convergence rate, it is advantageous to reset the pollen at the duty ratio allied with these peaks, as was practiced in this study, as was undertaken in this paper.

The author in [28] took a similar approach, but used a bat algorithm to initialize bat values so that they were close to the expected positions of peaks.

The following equation approximates the relationship at each peak between duty ratios, open circuit voltage and DC link voltage:

d(k)=1−(n−k+1)×kVn×VOCVDC(6)

where Voc represents the open circuit voltage, VDC is the DC-link voltage, k is a counter used to indicate duty ratio’s order, n is the peaks’ number, KV is a constant with a value ranging from 0.76 to 0.82 [29]. Eq. (6) can be employed to derive the initial duty ratio values at the initial locations, ensuring their proximity to all LPs, which helps expedite the convergence process. The time taken to find the GP is reduced when the computed duty ratios are used as starting points for pollen, which increases the PV system’s generated power and efficiency. In the simulation results section, these benefits are presented, analyzed, and assessed.

3  Flower Pollination Algorithm

In 2014, Yang et al. [30] pioneered the development of FPA, which draws inspiration from the natural pollination mechanism observed in flowers. Pollination, a process involving the transfer of pollen from one species to another, can occur either through self-pollination or cross-pollination. This process facilitates the generation of new flower species. Pollination occurs in two ways based on pollens: 1) biotic process—cross-pollination—where pollens are transferred between two distinct species by pollinators such as bees, bats, and birds; 2) abiotic process—self-pollination—where pollen from the same plants fertilize, resulting in the emergence of a new species. The only pollination agent here is the wind.

It is important to highlight that within the FPA, cross-pollination accounts for 90% of the pollination process, while self-pollination makes up only 10% [30]. A probability switch denoted as P, with values ranging from 0 to 1, regulates the balance between cross-pollination and self-pollination. Flower constancy is established based on the reproduction probability, which is linked to the quantity of flowers involved in the pollination process. Below are the fundamental design principles for applying FPA:

Rule 1: Cross-pollination is a global pollination mechanism that occurs after pollen transmission by levy flight. The specified equation for global pollination can be written as:

xik+1=xik+L(G−xik)(7)

where G denotes the global optimal solution attained by using a group of pollens (xik). L is the levy factor which controls the pollen movement. As pollen movement follows the levy distribution, the pollen flight in the levy distribution shown in [30] is expressed by:

L=λΓ(λ)sin⁡(πλ2)π×1S1+λ(S≫SO>0)(8)

where Γ(λ) represents the standard gamma function, which is appropriate for large step sizes (S > 0). The researchers determined a value of λ = 1.5 through a trial-and-error approach to attain faster convergence.

Rule 2: The second rule is that the local pollination process distinguishes self-pollination. The formula designated for local pollination can be represented as:

xik+1=xik+ε(xmk−xjk)(9)

Pollen from different flowers of identical plant species is represented as the xm and xj, whereas the local search conducted within the interval [0,1] is indicated by ɛ. Local pollination takes place within the vicinity of closely spaced flowers, whereas global pollination happens between plants that are more distant from each other. Consequently, a probability switch denoted as P within the range of [0,1] is utilized to regulate the transition between these pollination processes. Typically, the probability switch P is set to an optimal value of 0.8. This is because the FPA technique relies on only two pollination processes, local and global, making it highly suitable for tackling non-linear optimization problems, as noted in [30]. Additionally, since the algorithm is structured to conduct both search processes within a single iteration, it is deemed well-suited for applications in MPPT.

The most distinctive aspect of this algorithm, as compared to other bio-inspired algorithms, is its incorporation of self-pollination to introduce randomization into each iteration. Soft computing approaches in the literature frequently search globally or locally within an iteration. Moreover, the integration of both local and global searches in FPA has dual advantages: it simplifies the coding process and expedites the identification of the GMPP region. Additionally, tuning FPA settings is more flexible, making the approach even more suitable for MPPT applications.

4  Modified Pollination Algorithm

The development of a modified flower pollination algorithm (MFPA) aims to improve the convergence performance of the FPA technique The initial modification to the conventional FPA is discussed in Section 2, which pertains to resetting the pollen at the duty ratios associated with peaks in partial shading. This adjustment is made to shorten the convergence time.

This section gives a detailed analysis of the second FPA modification:

According to the populations individual fitness, the flower populations in MFPA are classified into three categories [31]. Individuals who are far from the global maximum have adapted their behavior on a global scale to prevent early convergence. Those individuals in proximity to the global maximum have undergone local optimization to facilitate a seamless convergence process. Furthermore, individuals at intermediate stages toward the global maximum are managed using dual-mode optimization, where the switch probability p, typically set at 0.8 to signify the optimal value. The following is a full description of the implementation process: Set n is the population size; N is the iterations number; xi denotes the population, with i ranging from 1 to n; f(xi) is signifies the fitness function of the population xi, while fm represents the optimum fitness; f1 is the average fitness; f2 is the average fitness of the population of f(xi) > f1.

(1) f(xi) > f2

These individuals are already approaching the global maximum and are fairly excellent in population. As a result, to accelerate the convergence, local pollination will be used. Eq. (9) can be used to update the individual rule.

(2) f1≤f(xi)≤f2

These individuals are considered to be part of the common population. They will be pollinated both globally and locally, with a switch probability of 0.8, likewise to the conventional FPA method.

(3) f(xi)<f1

Individuals who are far from the global maximum are generally poor in population. Therefore, to prevent premature convergence, global pollination will be undertaken. Eq. (7) is used for updating the rule of these poor individuals. proposed MFPA can offer the control variables with the required randomness, making it ideal for studying MPPT issues in PV systems with changeable irradiance conditions. Furthermore, the decision as to whether to execute local or global pollination is based on the population fitness value; hence, enhancing the algorithm’s convergence.

Speed and the PV system’s efficiency. It is worth noting that the authors in [31] used a similar strategy but without determining the approximate best duty ratio value at each peak by reinitializing the pollen at these peaks’ duty ratios.

5  MFPA Implemented for MPPT Application

Generally, the MPPT is accomplished by controlling the PV system’s DC/DC converter. The study proposes an MFPA-based MPPT controller that adjusts the duty cycle regularly until the PV system output reaches the GMPP. The proposed FPA method introduced here employs the duty cycle d of the PV power converter’s pulse width modulation (PWM) to represent the position of the population, and the fitness of the population is determined by the output power of the PV array.

To obtain the corresponding power P, the PV system can be injected by new duty ratios d one by one.

The following procedures are developed and described to implement the MFPA method in an MPPT application:

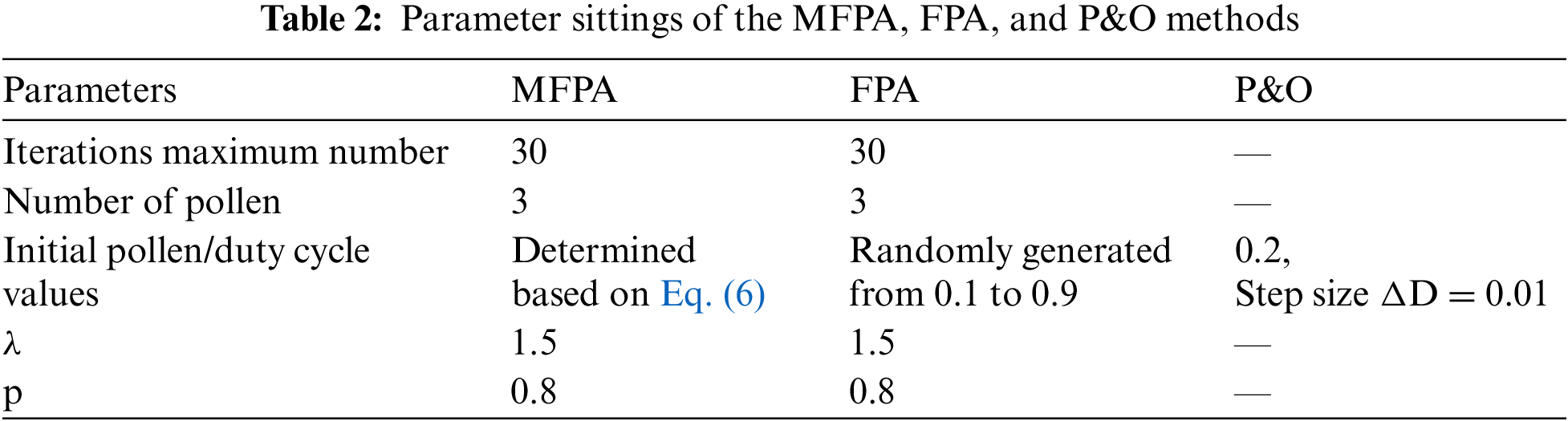
Step 1: Initialization parameters: In contrast to the FPA technique, where the duty cycle (xi, i = 1,2,,n) is randomly generated from 0.1 to 0.9 over the P-V curve, the initialization of the duty cycle value in MFPA method is performed based on Eq. (6), iterations maximum number (N = 30) and switch probability (p = 0.8).

Step 2: Fitness evaluation: The duty cycle xi is suitably evaluated using fitness function P, and finds the duty cycle d capturing the optimum power G.

Step 3: Determine the f1 and f2 values: Compute f1 of duty cycles which acquire output power values, as well as the average f2 of output power values which are greater than f1.

Step 4: Duty cycle updating value: Local pollination is conducted to acquire the subsequent duty cycle if the power P linked to duty cycle xi is higher than f2. If the duty cycle xi’s corresponding power P is lessthan f1, the next duty cycle can be obtained by global pollination. Moreover switch probability control is used to perform global or local pollination when the P value is between the f1 and f2. The duty cycle utilizes updating rules which are either cross-pollination or self-pollination.

Step 5: Termination conditions: Continue the process from steps 2 to 4 until all pollens have reached convergence at the GMPP within the specified maximum iteration limit, which in this case is N = 30.

Step 6: Re-initialization: The position of the GMPP varies when the change in the partial shading condition occurs. This requires re-initializing the MFP algorithm and searching for a new GMPP. In this study, In this study, Eq. (10) is applied to detect occurrences of partial shading or irradiance change, which triggers the reinitialization of the MFPA.

PPV(k)−PPV(k−1)PPV(k)>ΔP(%)(10)

where PPV (k−1) corresponds to the PV output power measured in the preceding iteration, PPV (k) stands for the PV output power during the kth iteration, and ΔP signifies the threshold limit. Fig. 4 illustrates a flowchart representing the MPFA for the application of MPPT in a PV system.

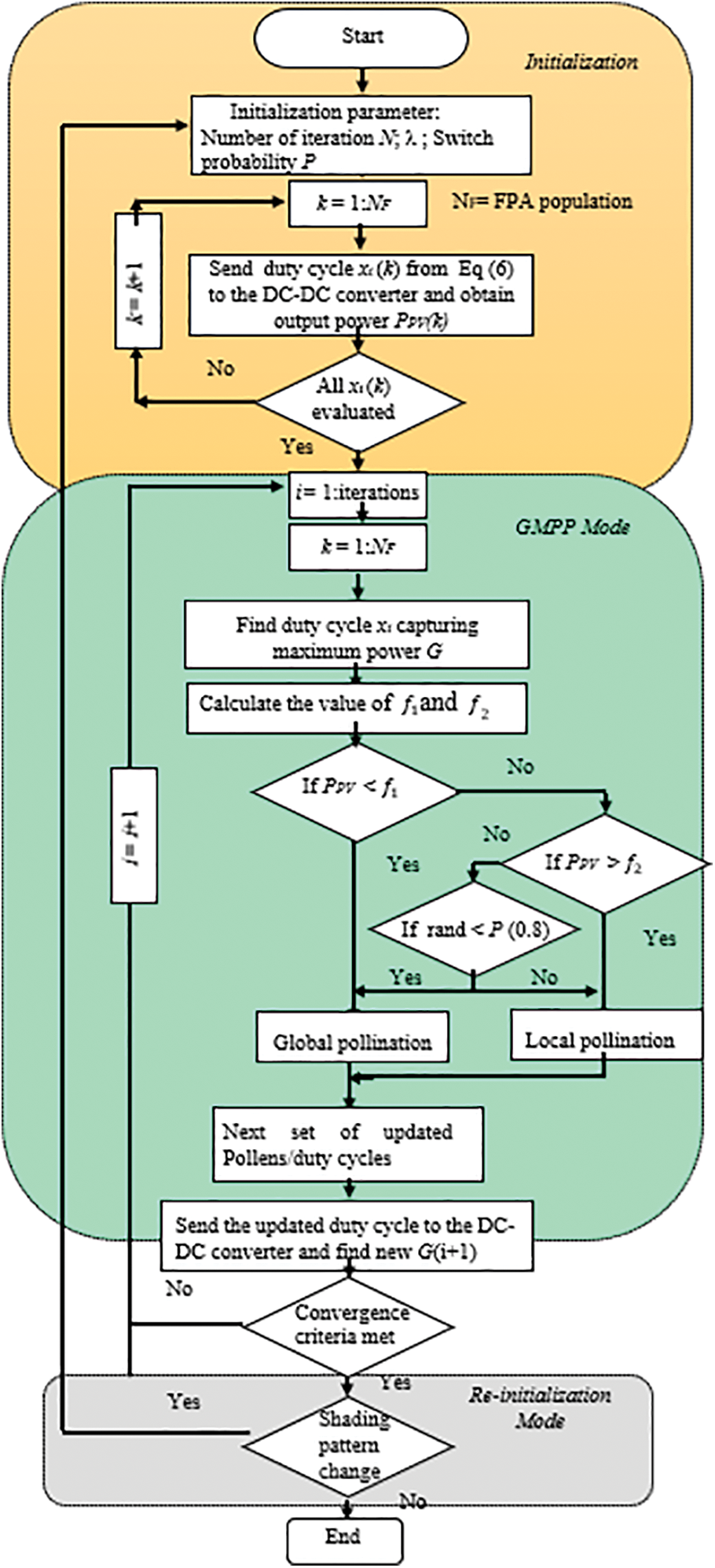
Figure 4: The flow chart of the modified flower pollination algorithm

6  Simulation Results and Comparison

Four distinct shade patterns, as stated in Section 2, are evaluated with three PV panels connected in a string to assess the modified FPA performance for MPPT application. Furthermore, Fig. 1 presents the configuration of the PV system employed during the simulation. The simulated results were then subjected to a quantitative comparison of efficiency and convergence speed among the MFPA, FPA, and P&O methods. The PSIM software was used in this research to develop the algorithms. The algorithms used in the study (MFPA, FPA, and P&O) were meticulously coded, and their parameters were fine-tuned to have fair comparison. It is worth noting that the FPA technique follows the random duty cycle initialization process. The sample time of 0.01 s is used between duty cycles. Typically, one of the fundamental factors for evaluating the effectiveness of bio-inspired algorithms is the adjustment of parameters.

Furthermore, this is a critical aspect in obtaining faster GMPP convergence. Consequently, two FPA parameters, which are the probability switch P and scaling factor λ, and two P&O parameters, which are the primary duty cycle D and the change in the duty cycle ΔD, are adjusted with utmost care in this paper for optimal performance. Table 1 shows the PV module specification. Table 2 shows the parameter sittings of the MFPA, FPA, and P&O methods.

6.1 Case 1: Test the MFPA into MPP Problems

6.1.1 Simulation Discussion of Pattern 1

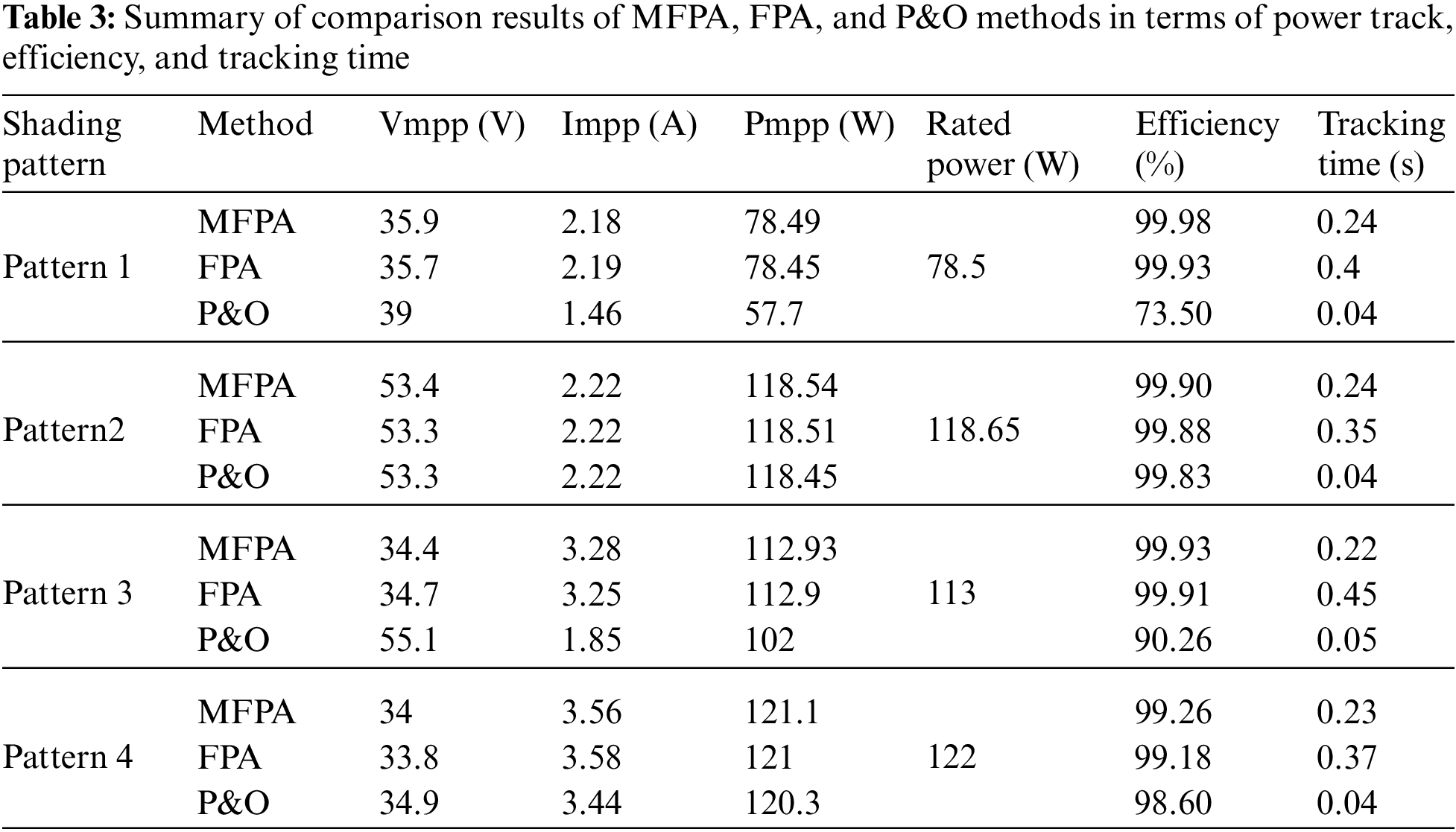
In Pattern 1, the P-V curve exhibits three MPPs, and the GMPP is located at V = 36 V, as illustrated in Fig. 2. The proposed MFPA method quickly identifies the GMPP in under 0.24 s, with a 78.49 W output power (Fig. 5a). In comparison to the proposed method, the FPA method also attains the GMPP within 0.4 s of tracking time, resulting in a PV output power of 78.45 W (Fig. 5b), but it generates a large number of oscillations in the present waveform, delaying power convergence. However, the Perturb and Observe (P&O) method becomes confined to one of the local MPPs, resulting in a PV output power of 57.4 W (Fig. 5c). Based on the simulation results, the proposed MFPA method, with its distinctive initialization characteristic of duty cycles close to the Maximum Power Points (MPPs), unquestionably exhibits a quicker convergence rate when contrasted with the traditional FPA method.

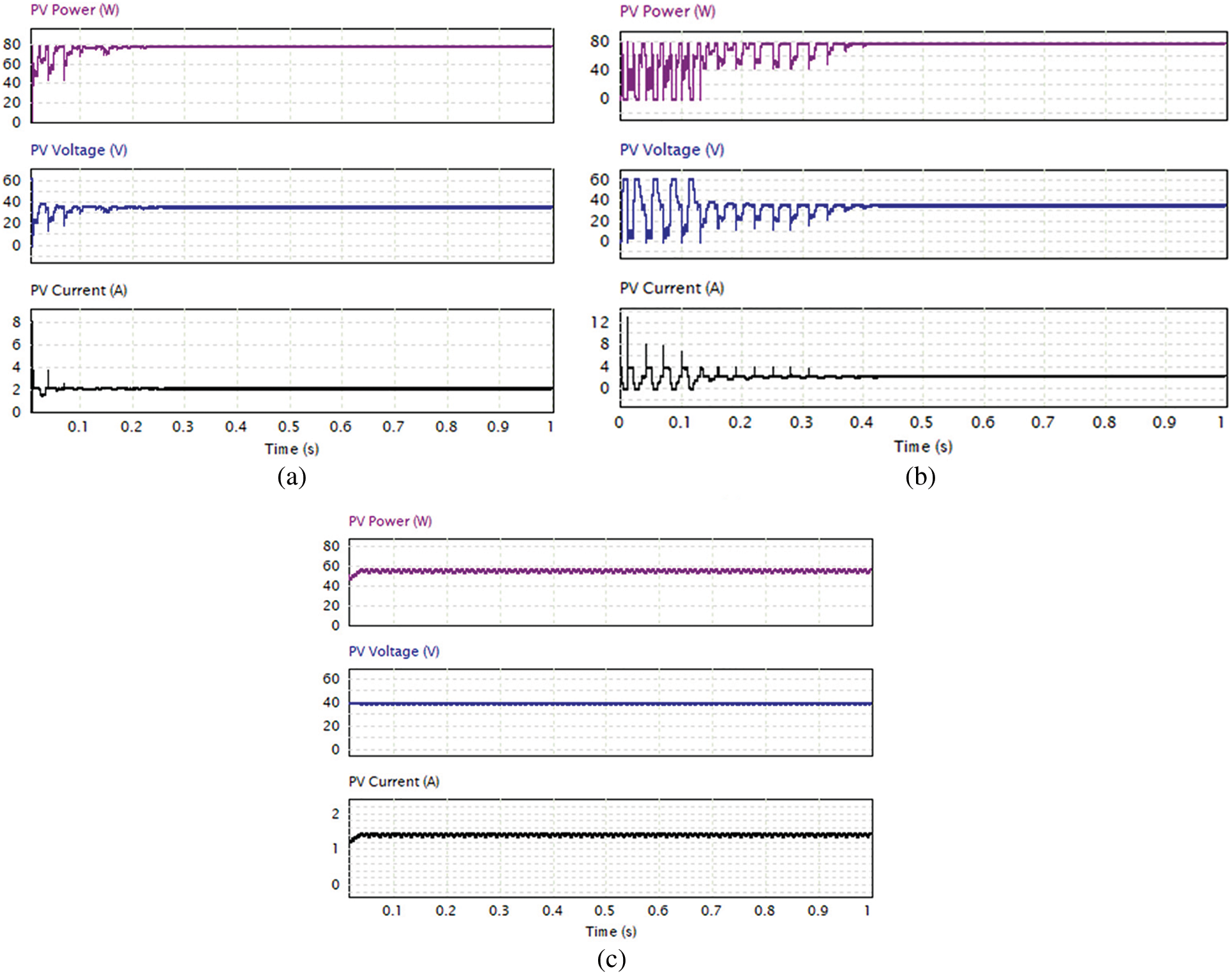
Figure 5: Simulation results of PV power, PV voltage and PV current using (a) proposed MFPA, (b) FPA, and (c) P&O under Pattern 1

6.1.2 Simulation Discussion for Pattern 2

In Pattern 1, the P-V curve exhibits three MPPs, and the GMPP is located at V = 54 V, as illustrated in Fig. 2. The proposed MFPA method successfully reached GMPP in 0.24 s with minimum oscillations and a PV output power of 118.54 W (Fig. 6a). The power oscillation in the MFPA method demonstrates the algorithm’s ability to operate at GMPP.

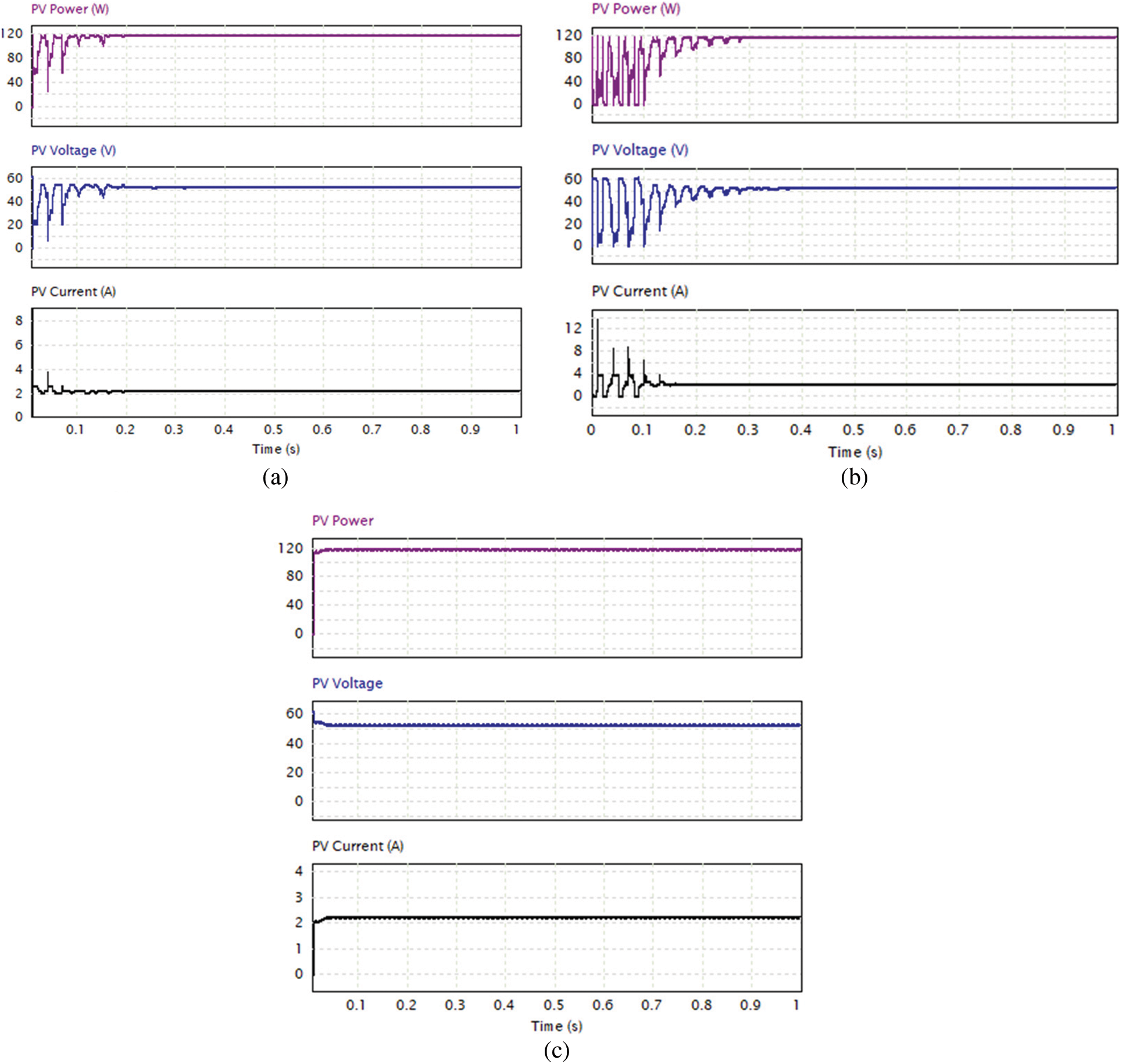
Figure 6: Simulation results of PV power, PV voltage and PV current using (a) proposed MFPA, (b) FPA, and (c) P&O under Pattern 2

However, the FPA method is affected by its reliance on switching between global pollination and local pollination, which is controlled by a switch probability and suffers from suboptimal randomness generation, the FPA created oscillation and took 0.35 s before settling at GMPP with a PV output power of 118.51 W (Fig. 6b), In contrast, the P&O method can effectively trace the GMPP when the initial duty cycle value is set to 0.2, resulting in output power of 118.45 W (Fig. 6c). The P&O method’s capability for tracking GMPP is dependent on the search starting point. For example, when the search commences with a duty cycle of 0.6, the P&O method might face difficulty in locating the GMPP in this particular scenario.

Overall, the proposed MFPA method has successfully settled to GMPP with minor oscillations and faster convergence speed. Table 3 summarizes the comparison findings of the MFPA, FPA, and P&O methods in terms of power track, efficiency, and tracking time.

6.2 Case 2: Test the MFPA with Benchmark Functions

To compare the effectiveness of MFPA in comparison to other methods, thirteen standard benchmark functions are utilized to evaluate their searching capacity and convergence stability. The benchmark function utilized in this work was described in [32], containing details such as the objective function, search range, and global minimum. For simulation, the particle size is set to N = 25, the dimension to D = 5, and the iteration number to 100. Fig. 7 shows the convergence curves obtained by two different algorithms, the FPA and MFPA algorithms, when six different benchmark functions were used. In all six benchmark functions, MFPA’s searching capability outperforms that of FPA.

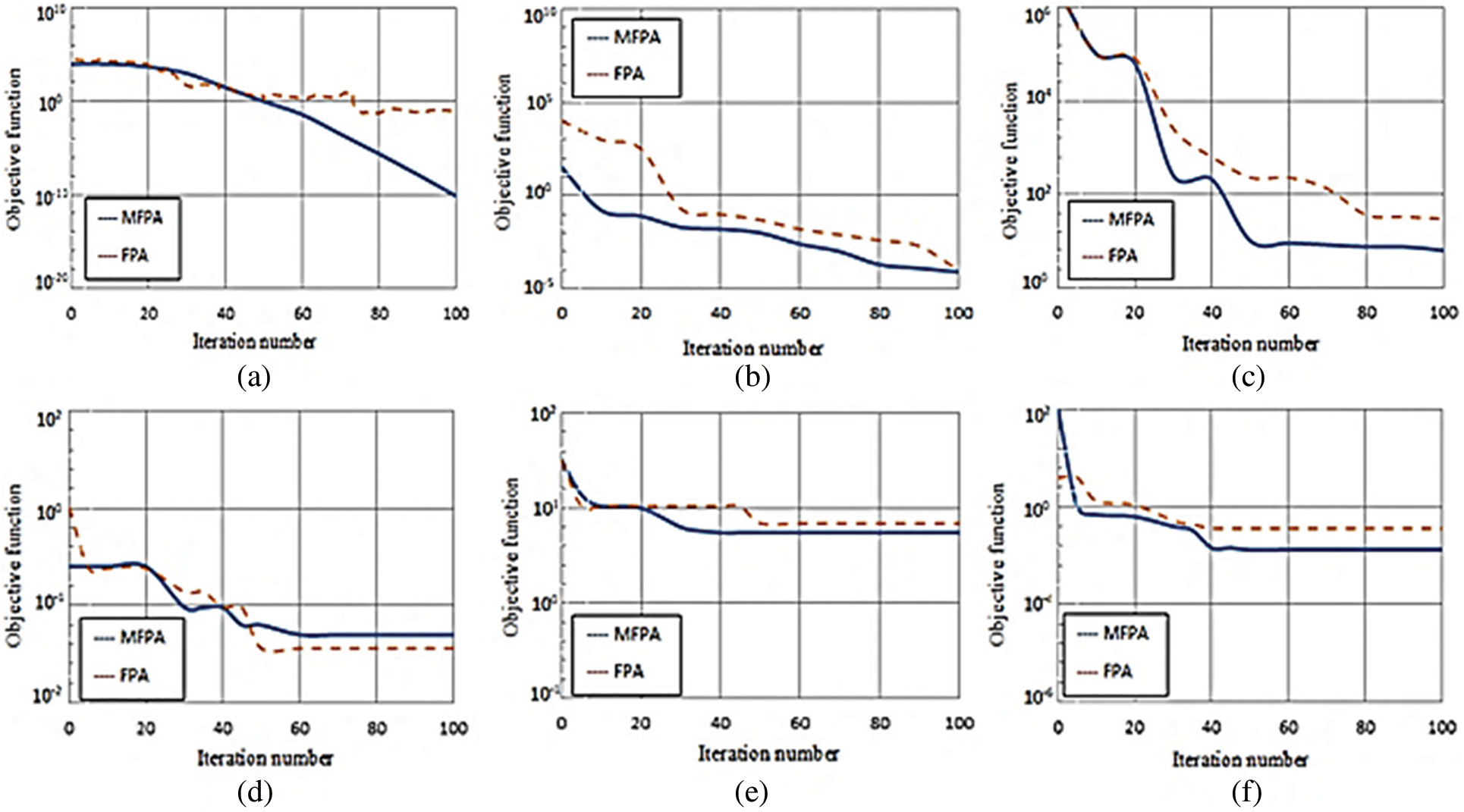
Figure 7: Convergence of FPA and MFPA algorithms for various benchmark functions. (a) F1, (b) F3, (c) F5, (d) F7, (e) F9, and (f) F11

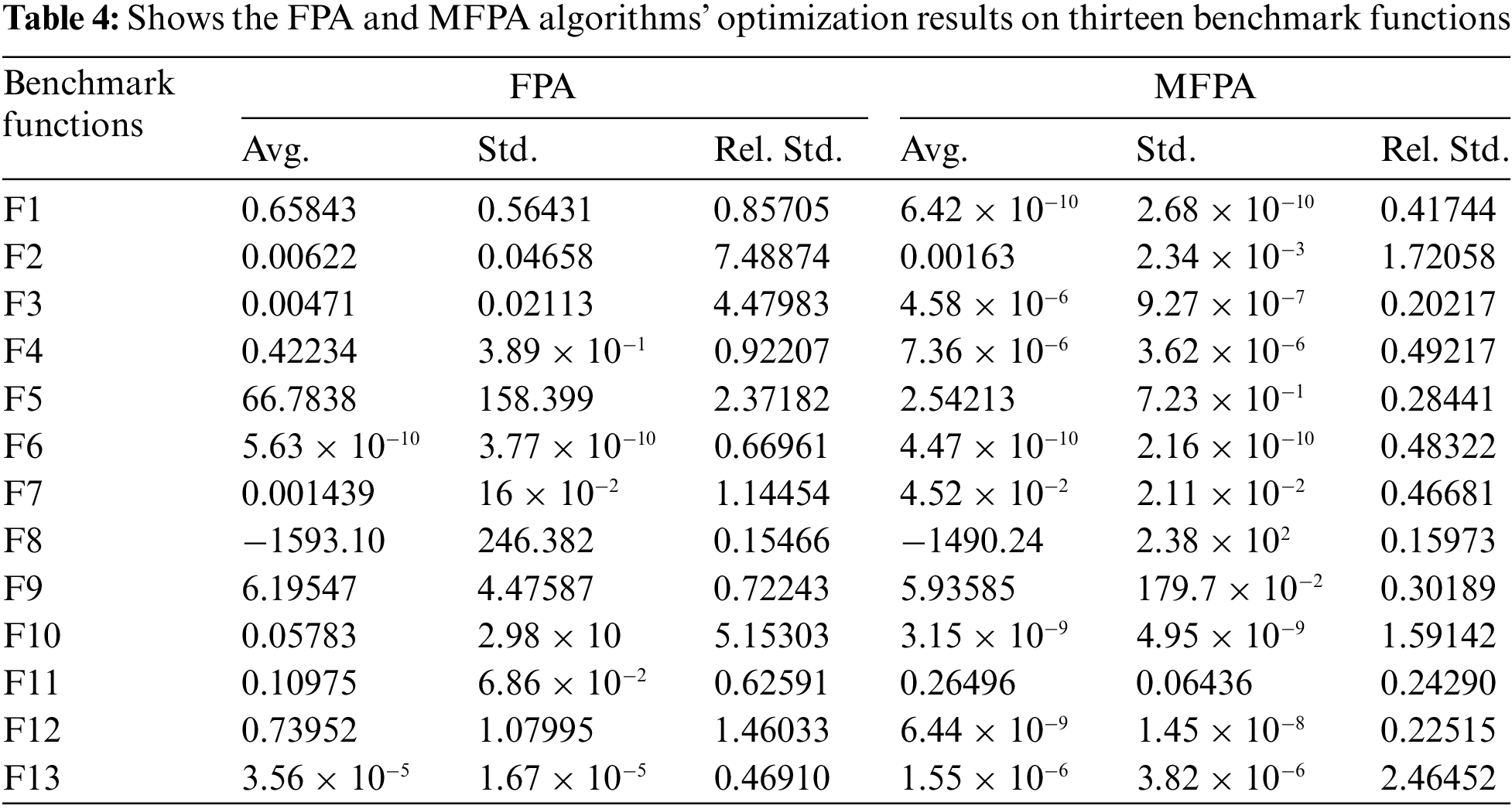
To more thoroughly investigate optimization performance Table 4 shows the FPA and MFPA algorithms’ optimization results on thirteen benchmark functions over the course of 30 independent runs. The average value, standard deviation, and relative standard deviation of the achieved objective values are represented as Avg., Std., and Rel. Std., respectively. The MFPA algorithm has a better searching ability than that of the FPA algorithm because it obtains lower average values for all thirteen benchmark functions. Furthermore, the MFPA method achieves lower relative standard deviations than that of FPA algorithm for all of the benchmark functions, demonstrating its good convergence stability.

7  Conclusion

This paper introduces a novel bio-inspired modified flower pollination algorithm (MFPA) for GMPP tracking in PV systems.

In contrast to random initializations, establishing the duty ratios of the pollen at the anticipated peaks of the P-V curve substantially decreased the convergence time. The presented method preserves the unique randomness of the FPA while incorporating a dual-mode optimization influenced by population fitness and switch probability values, indicating that it is not constrained by only controlling the switch probability. The FPA’s outstanding performance as an MPPT for PV systems was dramatically improved as a result of these adjustments to the FPA method.

Furthermore, due to its straightforward design and simplicity of implementation, the proposed approach is highly suitable for application in a PV system. Extensive case studies are conducted to confirm the effectiveness and advantages of MFPA in comparison to other techniques. Simulation outcomes demonstrate that the proposed MFPA method efficiently identifies the GMPP more quickly than the standard FPA method across various partial shading scenarios.

Acknowledgement: None.

Funding Statement: The author received no specific funding for this study.

Author Contributions: The author confirms contribution to the paper as follows: conceptualization: M. J. Alshareef, methodology: M. J. Alshareef, simulation validation: M. J. Alshareef, writing—original draft preparation: M. J. Alshareef, writing—review and editing: M. J. Alshareef, funding acquisition: M. J. Alshareef.

Availability of Data and Materials: Not applicable.

Conflicts of Interest: The author declares that they have no conflicts of interest to report regarding the present study.

References

1. S. H. Hanzaei, S. A. Gorji and M. Ektesabi, “A scheme-based review of MPPT techniques with respect to input variables including solar irradiance and PV arrays’ temperature,” IEEE Access, vol. 8, pp. 182229–182239, 2020. [Google Scholar]

2. M. J. Alshareef, “An effective falcon optimization algorithm based MPPT under partial shaded photovoltaic systems,” IEEE Access, vol. 10, pp. 131345–131360, 2022. [Google Scholar]

3. V. Jately, B. Azzopardi, J. Joshi, B. Venkateswaran V, A. Sharma et al., “Experimental analysis of hill-climbing MPPT algorithms under low irradiance levels,” Renewable and Sustainable Energy Reviews, vol. 150, pp. 111467, 2021. [Google Scholar]

4. M. Alsumiri, “Residual incremental conductance based nonparametric MPPT control for solar photovoltaic energy conversion system,” IEEE Access, vol. 7, pp. 87901–87906, 2019. [Google Scholar]

5. M. J. Alshareef, “A novel auto-scaling variable step-size maximum power point tracking (MPPT) method for photovoltaic system under changing environmental conditions,” Umm Al-Qura University Journal of Engineering & Architecture, vol. 12, pp. 7–13, 2021. [Google Scholar]

6. Y. Ji, B. Wu, Y. Hou and A. Ding, “A MZ modulator bias control system based on variable step P&O algorithm,” IEEE Photonics Technology Letters, vol. 32, no. 23, pp. 1473–1476, 2020. [Google Scholar]

7. H. Ahmed Sher, A. Faisal Murtaza, A. Noman, K. E. Addoweesh, K. Al-Haddad et al., “A new sensorless hybrid MPPT algorithm based on fractional short-circuit current measurement and P&O MPPT,” IEEE Transactions on Sustainable Energy, vol. 6, no. 4, pp. 1426–1434, 2015. [Google Scholar]

8. D. Baimel, S. Tapuchi, Y. Levron and J. Belikov, “Improved fractional open circuit voltage MPPT methods for PV Systems,” Electronics, vol. 8, no. 3, pp. 321, 2019. [Google Scholar]

9. M. Alshareef, “An improved MPPT method based on fuzzy logic controller for a PV system,” Studies in Informatics and Control, vol. 30, no. 1, pp. 89–98, 2021. [Google Scholar]

10. H. Rezk, M. Aly, M. Al-Dhaifallah and M. Shoyama, “Design and hardware implementation of new adaptive fuzzy logic-based mppt control method for photovoltaic applications,” IEEE Access, vol. 7, pp. 106427–106438, 2019. [Google Scholar]

11. A. Messai, A. Mellit, A. Guessoum and S. A. Kalogirou, “Maximum power point tracking using a GA optimized fuzzy logic controller and its FPGA implementation,” Solar Energy, vol. 85, no. 2, pp. 265–277, 2011. [Google Scholar]

12. R. Bisht and A. Sikande, “A novel hybrid architecture for MPPT of PV array under partial shading conditions,” Soft Computing, 2023. https://doi.org/10.1007/s00500-023-08323-5 [Google Scholar] [CrossRef]

13. S. R. Kiran, C. H. H. Basha, V. P. Singh, C. Dhanamjayulu, B. R. Prusty et al., “Reduced simulative performance analysis of variable step size ANN based MPPT techniques for partially shaded solar PV systems,” IEEE Access, vol. 10, pp. 48875–48889, 2022. [Google Scholar]

14. L. M. Elobaid, A. K. Abdelsalam and E. E. Zakzouk, “Artificial neural network-based photovoltaic maximum power point tracking techniques: A survey,” IET Renewable Power Generation, vol. 9, no. 8, pp. 1043–1063, 2015. [Google Scholar]

15. P. Savsani, R. L. Jhala and V. J. Savsani, “Comparative study of different metaheuristics for the trajectory planning of a robotic arm,” IEEE Systems Journal, vol. 10, no. 2, pp. 697–708, 2016. [Google Scholar]

16. E. G. Talbi, Metaheuristics: From Design to Implementation. Hoboken, NJ, USA: Wiley, 2009. [Google Scholar]

17. X. S. Yang, “Metaheuristic optimization: Algorithm analysis and open problems,” In: P. M. Pardalos, S. Rebennack (Eds.Experimental Algorithms, pp. 21–32, Berlin, Germany: Springer, 2011. [Google Scholar]

18. T. Radjai, L. Rahmani, S. Mekhilef and J. P. Gaubert, “Implementation of a modified incremental conductance MPPT algorithm with direct control based on a fuzzy duty cycle change estimator using dSPACE,” Solar Energy, vol. 110, pp. 325–337, 2014. [Google Scholar]

19. N. Singh, K. K. Gupta, S. K. Jain, N. K. Dewangan and P. Bhatnagar, “A flying squirrel search optimization for MPPT under partial shaded photovoltaic system,” IEEE Journal of Emerging and Selected Topics in Power Electronics, vol. 9, no. 4, pp. 4963–4978, 2021. [Google Scholar]

20. H. Li, D. Yang, W. Su, J. Lü and X. Yu, “An overall distribution particle swarm optimization mppt algorithm for photovoltaic system under partial shading,” IEEE Transactions on Industrial Electronics, vol. 66, no. 1, pp. 265–275, 2019. [Google Scholar]

21. M. Alshareef, Z. Lin, M. Ma and W. Cao, “Accelerated particle swarm optimization for photovoltaic maximum power point tracking under partial shading conditions,” Energies, vol. 12, no. 4, pp. 623, 2019. [Google Scholar]

22. L. L. Jiang and D. L. Maskell, “A uniform implementation scheme for evolutionary optimization algorithms and the experimental implementation of an ACO based MPPT for PV systems under partial shading,” in IEEE Symp. on Computational Intelligence Applications in Smart Grid (CIASG), Orlando, FL, USA, pp. 1–8, 2014. [Google Scholar]

23. K. S. Tey, S. Mekhilef, M. Seyedmahmoudian, B. Horan, A. M. T. Oo et al., “Improved differential evolution-based MPPT algorithm using SEPIC for PV systems under partial shading conditions and load variation,” IEEE Transactions on Industrial Informatics, vol. 14, no. 10, pp. 4322–4333, 2018. [Google Scholar]

24. J. Prasanth Ram and N. Rajasekar, “A novel flower pollination based global maximum power point method for solar maximum power point tracking,” IEEE Transactions on Power Electronics, vol. 32, no. 11, pp. 8486–8499, 2017. [Google Scholar]

25. J. Ram, D. Pillai, A. Ghias and N. Rajasekar, “Performance enhancement of solar PV systems applying P&O assisted flower pollination algorithm (FPA),” Solar Energy, vol. 199, pp. 214–229, 2020. [Google Scholar]

26. E. Avila, N. Pozo, M. Pozo, G. Salazar and X. Domínguez, “Improved particle swarm optimization based MPPT for PV systems under partial shading conditions,” in Proc. of IEEE Southern Power Electron. Conf. (SPEC), Chile, Puerto Varas, pp. 1–6, 2017. [Google Scholar]

27. N. Priyadarshi, S. Padmanaban, P. Kiran Maroti and A. Sharma, “An extensive practical investigation of FPSO-based MPPT for grid integrated PV system under variable operating conditions with anti-islanding protection,” IEEE Systems Journal, vol. 13, no. 2, pp. 1861–1871, 2019. [Google Scholar]

28. A. M. Eltamaly, M. S. Al-Saud and A. G. Abokhalil, “A novel bat algorithm strategy for maximum power point tracker of photovoltaic energy systems under dynamic partial shading,” IEEE Access, vol. 8, pp. 10048–10060, 2020. [Google Scholar]

29. M. A. Husain, A. Jain and A. Tariq, “A novel fast mutable duty (FMD) MPPT technique for solar PV system with reduced searching area,” Journal of Renewable and Sustainable Energy, vol. 8, no. 5, pp. 054703, 2016. [Google Scholar]

30. X. S. Yang and M. Karamanoglu, “Multi-objective flower algorithm for optimization,” Procedia Computing Science, vol. 18, pp. 861–868, 2014. [Google Scholar]

31. T. Pei, X. Hao and Q. Gu, “A novel global maximum power point tracking strategy based on modified flower pollination algorithm for photovoltaic systems under non-uniform irradiation and temperature conditions,” Energies, vol. 11, no. 10, pp. 2708, 2018. [Google Scholar]

32. M. Mohamed, A. Zaki Diab and H. Rezk, “Partial shading mitigation of PV systems via different meta-heuristic techniques,” Renewable Energy, vol. 130, pp. 1159–1175, 2019. [Google Scholar]