Modified Elite Opposition-Based Artificial Hummingbird Algorithm for Designing FOPID Controlled Cruise Control System

1  Introduction

Control engineering is a field that focuses on designing systems to maintain the desired performance of a process or a device. One of the most widely used systems in control engineering is the proportional-integral-derivative (PID) controller, which is used to control the output of a process based on its error signal. However, recent research has shown that fractional-order PID (FOPID) controllers offer improved performance over conventional PID controllers, especially in systems with nonlinear dynamics or time-varying parameters. The design of a FOPID controller involves the use of fractional calculus, which is an extension of classical calculus that deals with integrals and derivatives of non-integer orders. FOPID controllers offer greater flexibility in terms of tuning and can provide better control performance.

Control engineering is a field that deals with designing systems to regulate the behavior of a process or a device. One of the most commonly used systems in control engineering is the proportional-integral-derivative (PID) controller, which is used to maintain the desired output of a process based on its error signal. However, recent research has shown optimized FOPID (fractional-order PID) controllers, which offer improved control performance over conventional PID controllers. Optimized FOPID controllers involve the use of advanced algorithms and optimization techniques to tune the controller parameters and achieve desired control objectives. These controllers provide greater flexibility and can improve the control performance of complex systems with nonlinear dynamics or time-varying parameters.

Reducing fuel consumption and emissions, like carbon dioxide and air pollutants, is a pressing challenge for the transportation sector, particularly the automobile industry, which is grappling with oil scarcity and environmental concerns [1]. To address this, policymakers and car manufacturers are exploring a range of strategies and products, such as advanced engines, intelligent vehicles, and new energy technologies [2]. One technology that has gained attention is the cruise control system [3], a new technology with the potential to reduce fuel consumption (at both the local and global level), driver fatigue, risk of collisions, and traffic congestion [4].

The cruise control system aims to offer drivers a comfortable driving experience and improve fuel economy while meeting driving time and the desired speed limit [5]. Research on cruise control system has focused on controlling the vehicle speed at a desired velocity with more convenient control strategies in order to design a system that balances the fuel efficiency, driving safety and comfort [6]. Many control strategies have been proposed, including classic proportional-integral-derivative (PID) control [7] and its fractional counterpart (FOPID) [8], PID control with reference model [9], fuzzy logic control [10], and model predictive control [11]. Of the many controllers proposed, the PID framework has been favored for designing cruise control systems due to its simplicity [12]. On the other hand, the FOPID controllers can boast a greater capability as the use of fractional terms gives them more flexibility in design, making them a more suitable option for dynamic systems [13]. This has been confirmed by various applications that demonstrate the enhanced ability of FOPID controllers [14,15].

A proper tuning method is necessary to make the most of the benefits offered by FOPID controllers. In this regard, the metaheuristic algorithms have demonstrated significant capabilities as artificial intelligence optimization techniques [16–19]. Recently, researchers have utilized various artificial intelligence techniques to tune different controllers for cruise control systems, such as the enhanced reptile search algorithm [20], global neighborhood algorithm [21], modified version of Aquila optimizer [22], Harris hawks optimization [23], arithmetic optimization algorithm [24], antlion optimizer [25], genetic algorithm [17], and atom search optimization with Nelder-Mead method [3]. These methods have been shown to result in improved performance. Despite the advancements in optimization frameworks, there’s still ample room for improvement, as evidenced by the “no free lunch” theorem [26] as it highlights that there’s no one-size-fits-all solution, leaving the door wide open for further enhancement and development [27–29].

In this study, therefore, the authors aimed to apply a new intelligent optimization approach to design a FOPID controller in a cruise control system such that a more capable method can be developed. To this end, the artificial hummingbird algorithm [30] was adopted as a novel efficient optimization technique and its capability was further boosted with the aid of a modified version of the elite opposition-based learning scheme [31]. The modified elite opposition-based artificial hummingbird algorithm was initially tested on some of the widely used benchmark functions in order to show its superiority over the basic form of the artificial hummingbird algorithm. Then, it was utilized to appropriately tune the FOPID controller used in a cruise control system. The performance of the proposed method was tested against existing best and recent artificial intelligence-based methods used to tune FOPID controlled cruise control system. For this purpose, Harris hawks optimization [23] based FOPID, arithmetic optimization algorithm [24] and antlion optimizer [25] based integer order PID (IOPID) controllers were adopted alongside the basic and modified forms of the artificial hummingbird algorithms-based FOPID controllers. Transient response, frequency response and robustness analyses have shown that the proposed method based FOPID controller can perform more efficiently compared to the reported best approaches in the literature, making the proposed method in this study more favorable for the cruise control system.

The remainder of this paper is organized as follows: Section 2 shows the main procedure of the Artificial hummingbird algorithm. Section 3 shows the proposed modified elite opposition-based artificial hummingbird algorithm. Section 4 shows the experimental results on benchmark functions. This is followed by Section 5, which shows the simulation results on vehicle cruise control system. Finally, Section 6, the conclusion and future works directions.

2  Artificial Hummingbird Algorithm

Memory capacity, foraging strategies and flight skills of hummingbirds have inspired the construction of the artificial hummingbird algorithm (AHA) as an efficient optimization technique [30]. In this optimization technique, three models (guided foraging, territorial foraging, migrating foraging) are used for mimicking the foraging behaviors. A population of n hummingbirds is randomly initialized and located on n food sources using xi=L+r⋅(U−L), where xi is the position of the ith food source, L and U are respectively the lower and upper limits of a d-dimensional problem, i=1,…,n, and r is a random vector within [0, 1]. The following definition is used to create a visit table:

VTi,j={0,i≠jnull,i=j(1)

where i=1,…,n and j=1,…,n. In the visit table defined by Eq. (1), null indicates a specific food source where a hummingbird takes the food whereas 0 means that the ith hummingbird has just visited the jth food source in the current iteration.

In guided foraging, the behavior of the hummingbird visiting the food source with the highest nectar refilling rate is modeled. A hummingbird flies towards the determined food source by performing omnidirectional, diagonal, and axial flight skills [30]. The mathematical model of the guided foraging is defined as:

vi(t+1)=xi,trg(t)+α⋅D⋅(xi(t)−xi,trg(t))(2)

where vi(t+1) represents the candidate food source position, α is the guided factor subjecting to the normal distribution with mean 0 and deviation 1, xi(t) is the ith food source position at time t, xi,trg(t) is the targeted food source that the ith hummingbird aims to visit. The position of the ith food source is updated as follows where f is the fitness function value.

xi(t+1)={xi(t), f(xi(t))≤f(vi(t+1))vi(t+1), f(xi(t))>f(vi(t+1))(3)

A hummingbird is likely to look for a new food source after visiting the target food source. This is described as territorial foraging which is explained as:

vi(t+1)=xi(t)+b⋅D⋅xi(t)(4)

where b is a territorial factor which is subjected to the normal distribution with mean 0 and deviation 1. After performing the territorial foraging behavior, the visit table is updated. A hummingbird may also migrate to a food source, which is far away if a commonly visited region suffers from enough food supply. This behavior is described with the migration foraging behavior which is described as:

xwrst(t+1)=L+r⋅(U−L)(5)

where xwrst stands for the food source with the worst nectar refilling rate. The migration strategy helps the AHA to avoid local stagnation. More detailed explanation of the AHA can be found from [30].

3  Proposed Modified Elite Opposition-Based Artificial Hummingbird Algorithm

In the field of control engineering, the design of efficient and robust control systems is a critical task. One of the key challenges in this area is to develop controllers that can provide stable and accurate control of complex systems with nonlinear dynamics or time-varying parameters. One promising approach for addressing this challenge is the use of advanced optimization techniques to design controllers that can achieve optimal control performance.

One such optimization technique is the elite opposition-based artificial hummingbird algorithm, which is a metaheuristic algorithm inspired by the foraging behavior of hummingbirds. This algorithm has been modified and used in conjunction with fractional-order PID (FOPID) controllers to improve the control performance of cruise control systems.

The modified elite opposition-based artificial hummingbird algorithm for designing FOPID controlled cruise control systems involves the use of a population of hummingbirds that forage for food in an environment. The hummingbirds update their position based on their own experience and the experience of the best hummingbirds in the population. The algorithm also employs an opposition-based learning strategy to further enhance its performance.

The use of this modified algorithm has shown promising results in improving the control performance of cruise control systems by effectively tuning the parameters of the FOPID controller. This approach can potentially be extended to other control problems and applications, providing a novel and effective means of designing advanced control systems.

The proposed modified elite opposition-based AHA (m-AHA) optimization technique employs a novel modified version of the elite opposition-based learning technique to increase the performance of the original AHA optimization technique. The opposition-based learning (OBL) technique [32] has been a staple among researchers looking to enhance optimization algorithms [33]. Within the realm of OBL, the elite opposition-based learning (EOBL) is a unique approach that considers the best and current agents to generate opposite solutions of those agents [31]. Due to its promising capability, the EOBL has already been adopted for different applications as an aiding structure [34,35].

To define EOBL, Xo=⟨x1o, x2o,…,xko⟩ can be used by considering X=⟨x1, x2,…,xk⟩ to be an elite candidate solution with k decision variables where xio=δ(dai+dbi)−xi, δ is a parameter within (0, 1), dai and dbi are the dynamic boundaries. In this study, three random variables of a, b and c, all of which within [0, 1], are adopted to redefine the the EOBL as xio=δ(a⋅dai+b⋅dbi)−c⋅xi. The solution in basic EOBL is kept within boundaries (lower, Lbi and upper, Ubi) by using the definition of xio=rand(Lbi, Ubi). In here, xio<Lbi or xio>Ubi and rand(Lbi, Ubi) is a random number within (Lbi, Ubi). In this study, however, the solution is set to the upper boundary when it exceeds the upper level; otherwise, it is set to the lower boundary. As illustrated in the detailed flowchart given in Fig. 1, the proposed m-AHA optimization technique firstly initializes its parameters, and then applies three foraging behaviors of the basic AHA. Simultaneously, it evaluates the current and elite candidate solutions and choses the best N solutions. This procedure continues for total iterations (T).

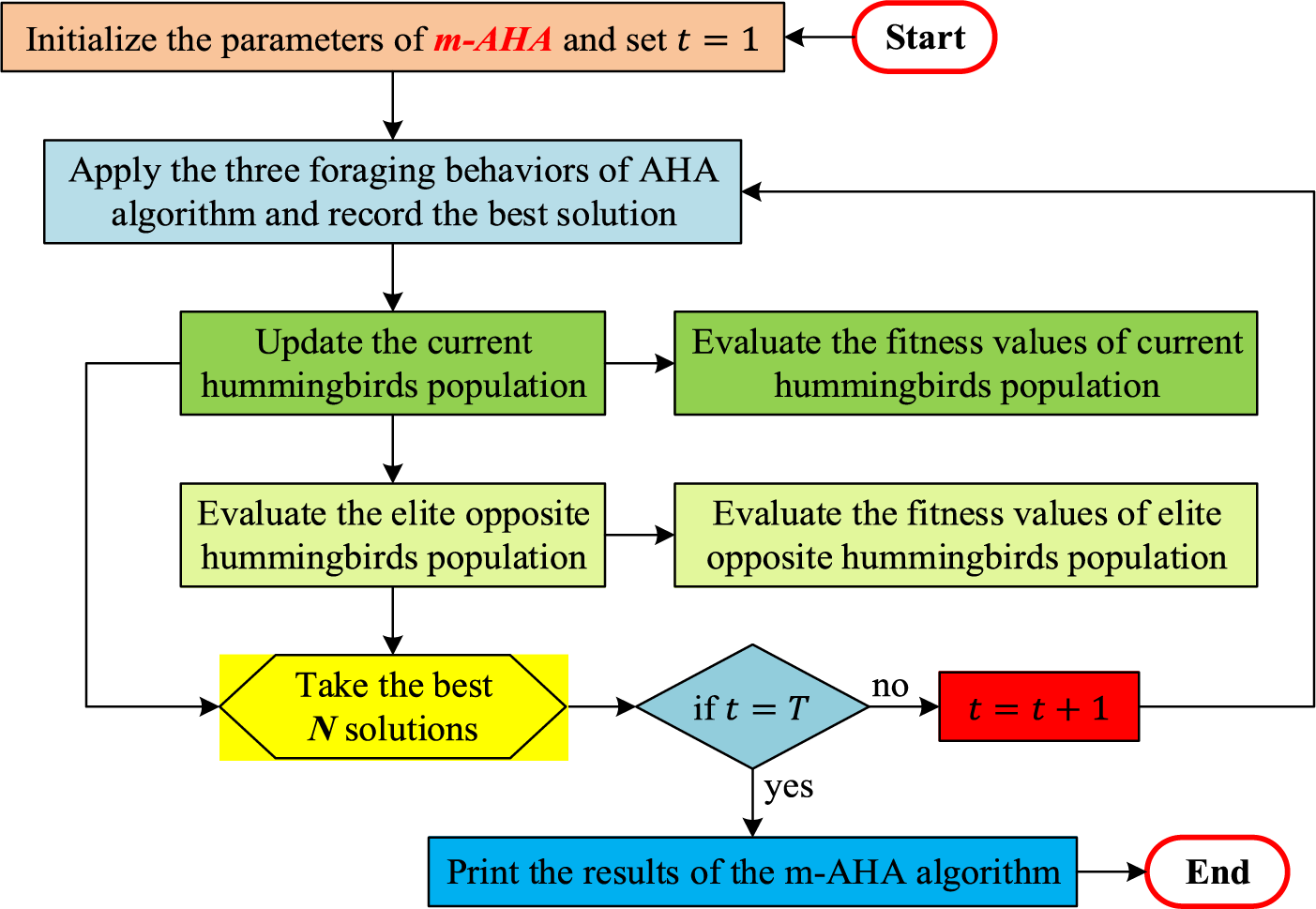
Figure 1: Flowchart of m-AHA

4  Experimental Results on Benchmark Functions

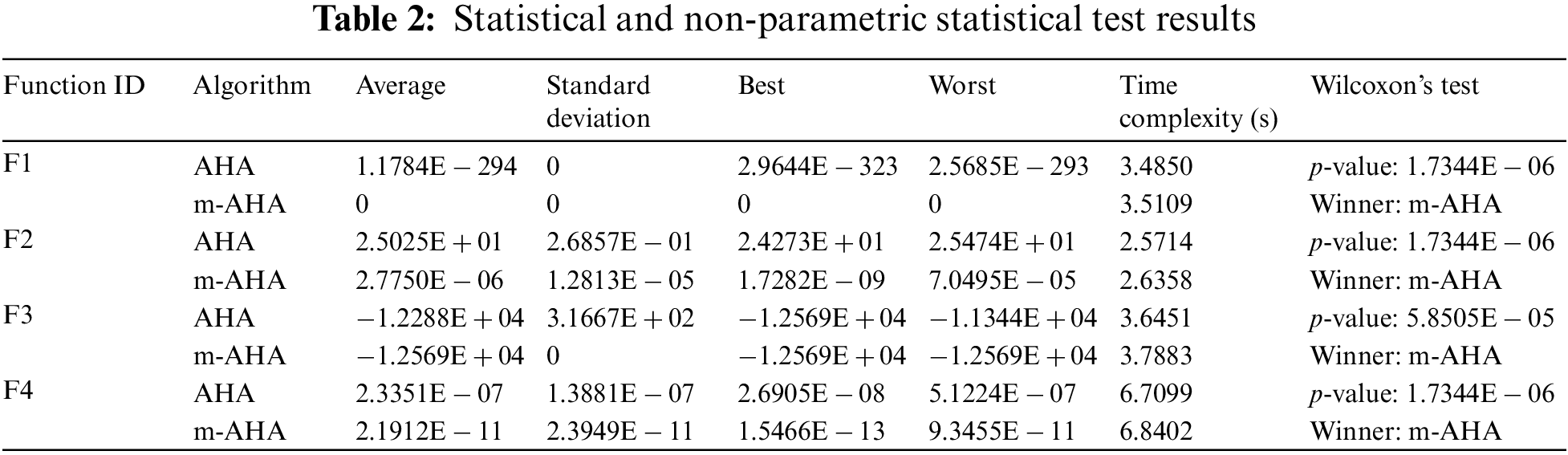
For an initial evaluation, the widely adopted test functions provided in Table 1 were used in this study. The definitions and other related details of the used benchmark functions are also provided in the respective table. For the fairness in the evaluation, the following parameters were used for the basic AHA and proposed m-AHA optimization techniques: Population size n=50, maximum number of iterations T=1000, migration coefficient 2×n. The statistical and non-parametric statistical (Wilcoxon signed rank test) obtained from those test functions are presented in Table 2. As presented, the proposed m-AHA optimization technique reaches far better results for F1, F3 and F4 when compared to the basic AHA and it also achieves the optimal value for F2 indicating its superior performance. This is further supported via Wilcoxon’s test as the m-AHA is the winner for all test functions.

5  Simulation Results on Vehicle Cruise Control System

In this section, the focus is on the cruise control system’s linearized model and the steps involved in its implementation. The results obtained are compared and presented in order to showcase the proposed method’s superiority for the cruise control system.

5.1 Linearized Model

The engine throttle angle (u) is adjusted by the cruise control system in order to maintain the actual speed (v) of a vehicle. This is performed based on the reference speed. The longitudinal dynamics of the vehicle can be represented as the combination of engine’s climbing resistance (Fg), drive force (Fd) and aerodynamic drag (Fa) as well as the inertia force M(dv/dt) using the following expression [36].

Fd=Mdvdt+Fa+Fg(6)

The cruise control system’s dynamic model is illustrated in Fig. 2 which represents the effects of the total mass (M), wind gust speed (vw), road angle (θ) and aerodynamic drag coefficient (Ca).

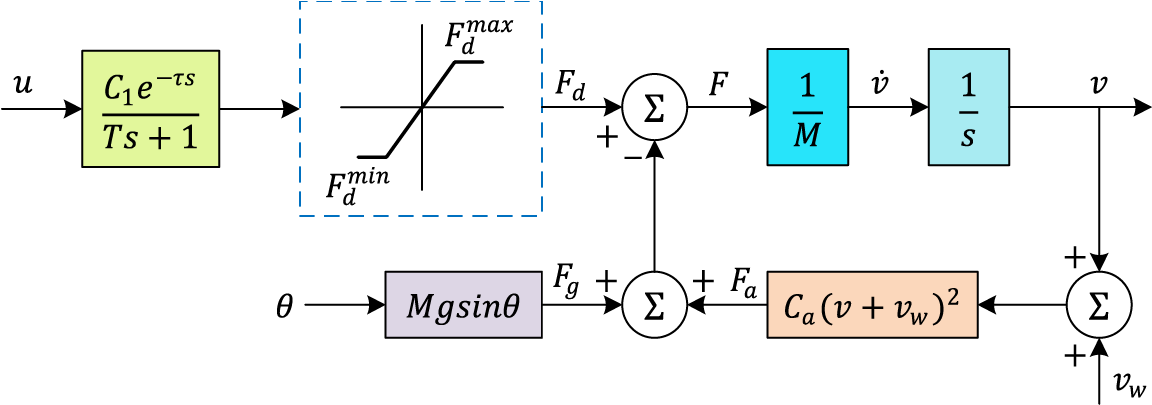
Figure 2: Cruise control system’s dynamic model

Assuming the vehicle operates at a constant speed of 30 km/h without wind gust or climbing resistance, the state model of the system can be characterized as outlined in the following definitions [22]:

v˙=1M(Fd−Cav2)(7)

F˙d=1T(C1u(t−τ)−Fd)(8)

A nominal drive force and throttle position are required to maintain an equilibrium state, which can be obtained via linearization around the set points using the following definitions:

δv˙=−2Cav0Mδv+1MδFd(9)

δF˙d=−1TδFd+C1Tδu(t−τ)(10)

The transfer function of the linearized model can then be represented as a ratio of the following polynomials where C=C1/(MTτ), p1=−2(Cav0/M), p2=−1/T and p3=−1/τ:

G(s)=ΔV(s)ΔU(s)=C(s−p1)(s−p2)(s−p3)(11)

5.2 FOPID Controlled System

A more flexible controller is desirable for cruise control system like dynamic systems. To this end, the idea of using a fractional order controller for dynamic systems was proposed. Based on this idea, a generalized version of the PID controller named the FOPID controller was introduced as an improved version that incorporates fractional orders (λ and μ) [37]. FOPID controller’s transfer function is defined as follows:

CFOPID(s)=Kp+Kisλ+Kdsμ(12)

where Kp, Ki, and Kd are proportional, integral, and derivative gains, while λ and μ stand for fractional integral and derivative orders, respectively. Fig. 3 presents the block diagram of a cruise control system that is controlled with a FOPID controller.

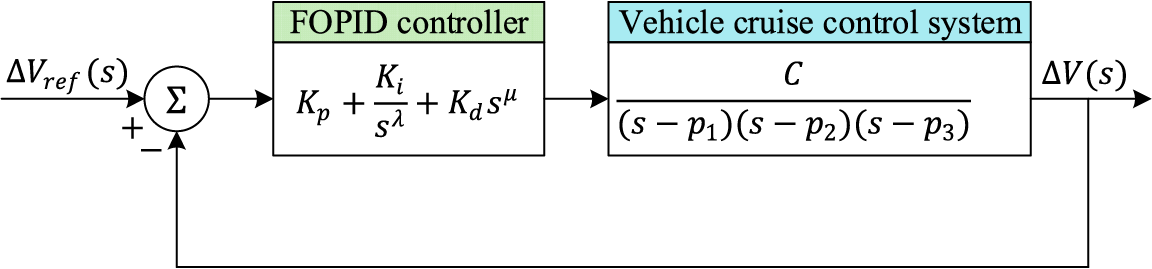
Figure 3: A cruise control system with FOPID controller

In this study, the following boundaries of 3≤Kp≤5, 0.10≤Ki≤0.25, 3≤Kd≤5, 0<λ<2 and 0<μ<2 are considered for the parameters of the FOPID controller [24].

5.3 Test System and Objective Function

For this study, we utilized comparable values found in previous research for the cruise control system in order to maintain fairness in comparison. The parameters given in Table 3 were used by setting the nominal operating speed to 30 km/h [9]. The performance of the cruise control system can be improved by minimizing its maximum overshoot percentage, steady-state error, settling time and rise time through the use of an objective function.

In this study, we adopted the F objective function given in the following expression [38]:

F=(1−e−ρ)(%OS100+Ess)+e−ρ(Ts−Tr)(13)

This function balances the maximum overshoot percentage (%OS), steady-state error (Ess), settling time (Ts), and rise time (Tr), with a weighting coefficient (ρ). Our simulations have determined that the best results are obtained when the weighting coefficient is set to ρ=1.5.

5.4 Implementation Stage of Proposed m-AHA Algorithm

The procedure for implementing the m-AHA method to the cruise control system is outlined in Fig. 4. The m-AHA algorithm uses the F objective function to determine the optimal parameters for the FOPID controller. The study used the following parameters: population size n=30, maximum number of iterations T=50, migration coefficient 2×n.

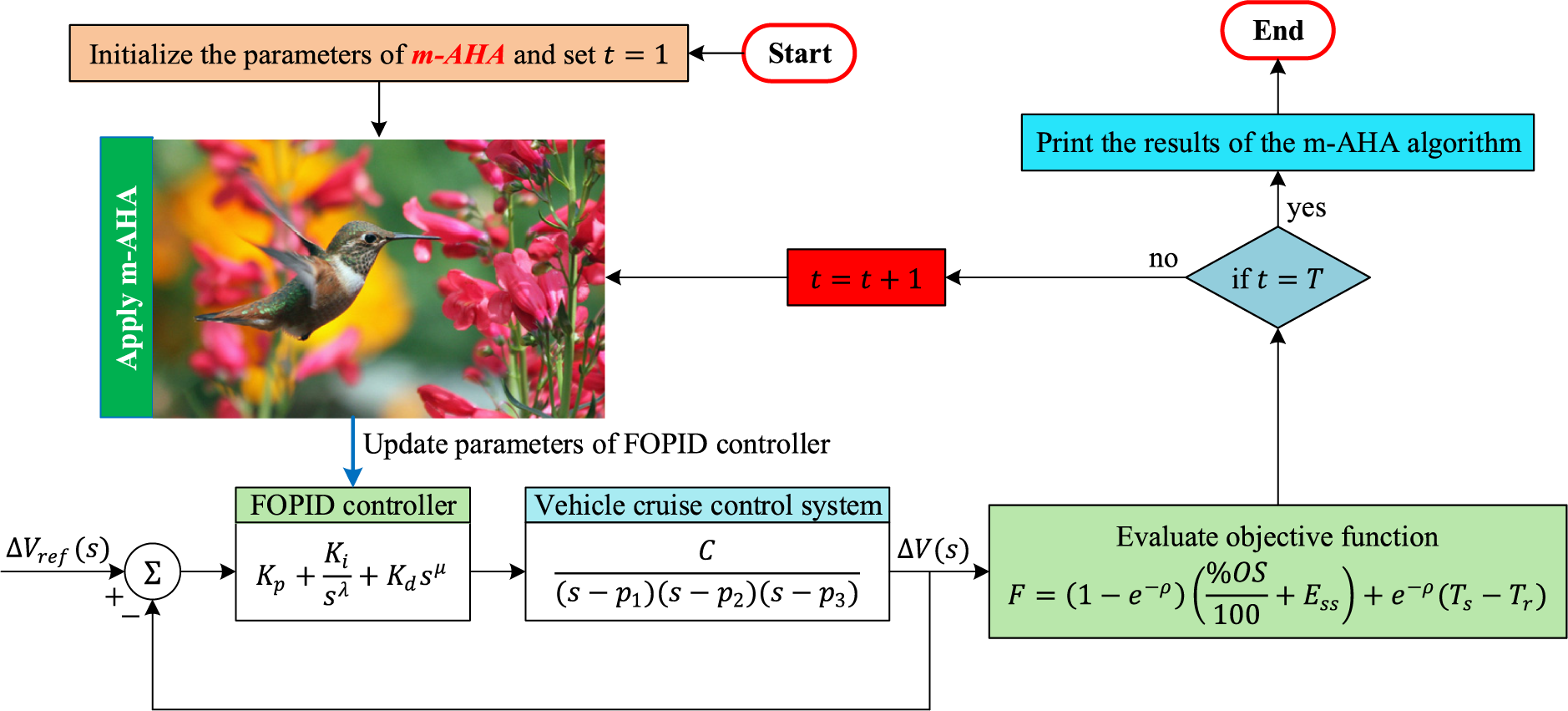
Figure 4: Block diagram detailing the implementation procedure of the proposed method to the cruise control system

The results of the objective function for each run of the AHA and m-AHA optimization techniques are displayed in Fig. 5. The figure clearly demonstrates that the proposed m-AHA optimization method consistently outperforms the original AHA technique, reaching the lowest values for each run. The more promising capacity of the m-AHA optimization technique is further validated with the statistical and non-parametric (Wilcoxon’s test) tests presented in Table 4.

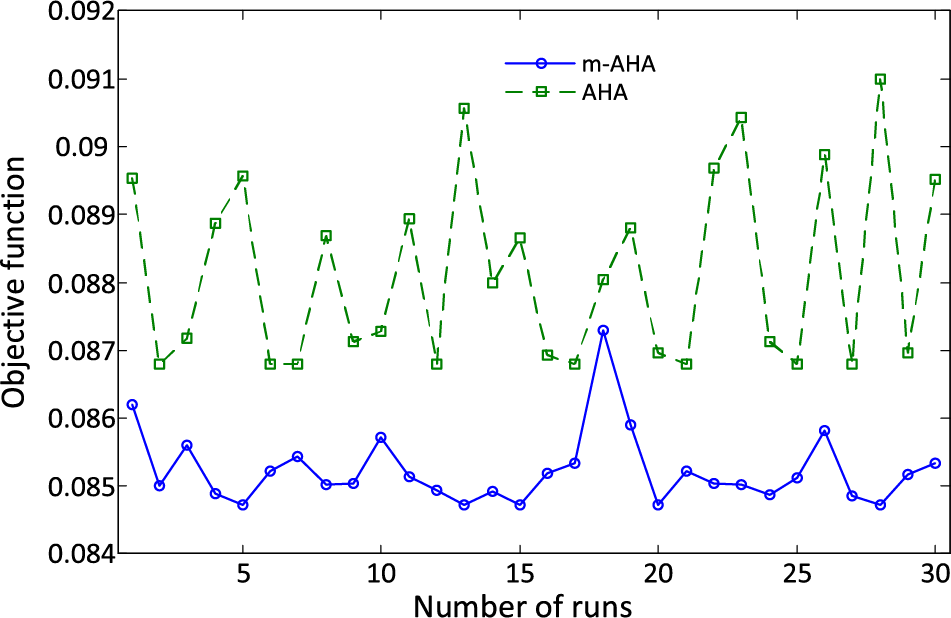
Figure 5: Objective function values for each run

5.5 Comparison with Existing Best and Recent Approaches

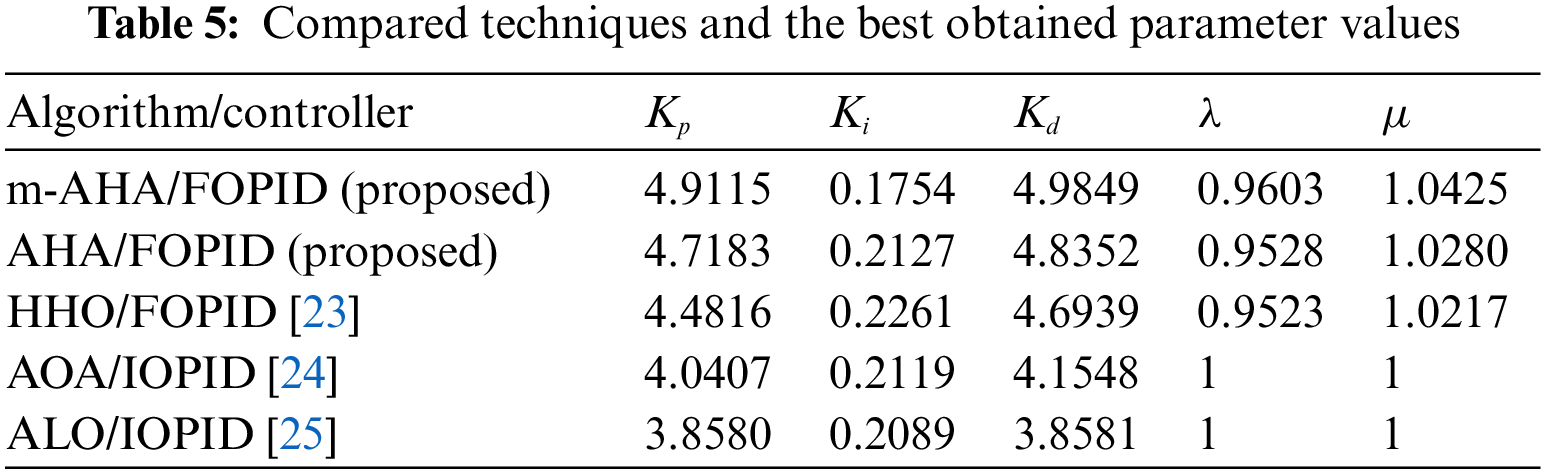
For this study, we adopted the existing best approaches reported in the literature in order to show the excellent capability of the proposed m-AHA optimization technique for the cruise control system. In that sense, we adopted the Harris hawks optimization (HHO) [23] based FOPID controllers, arithmetic optimization algorithm (AOA) [24] and antlion optimizer (ALO) [25] based IOPID controllers alongside the m-AHA and AHA optimization based FOPID controllers. Those approaches and the related best parameters obtained with each technique are listed in Table 5.

5.5.1 Transient Response Analysis

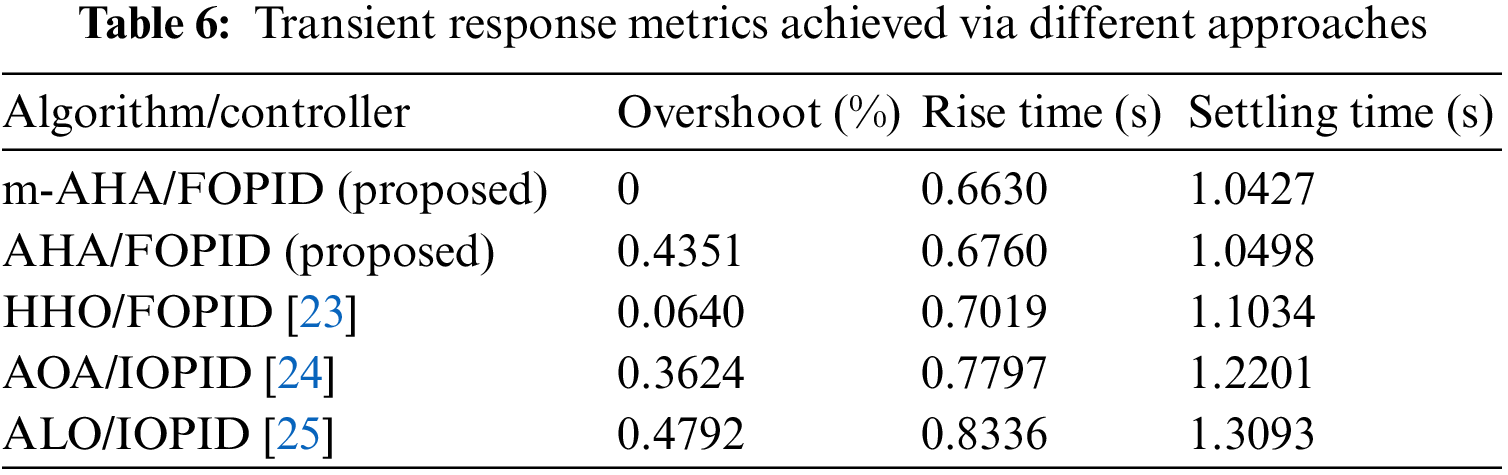
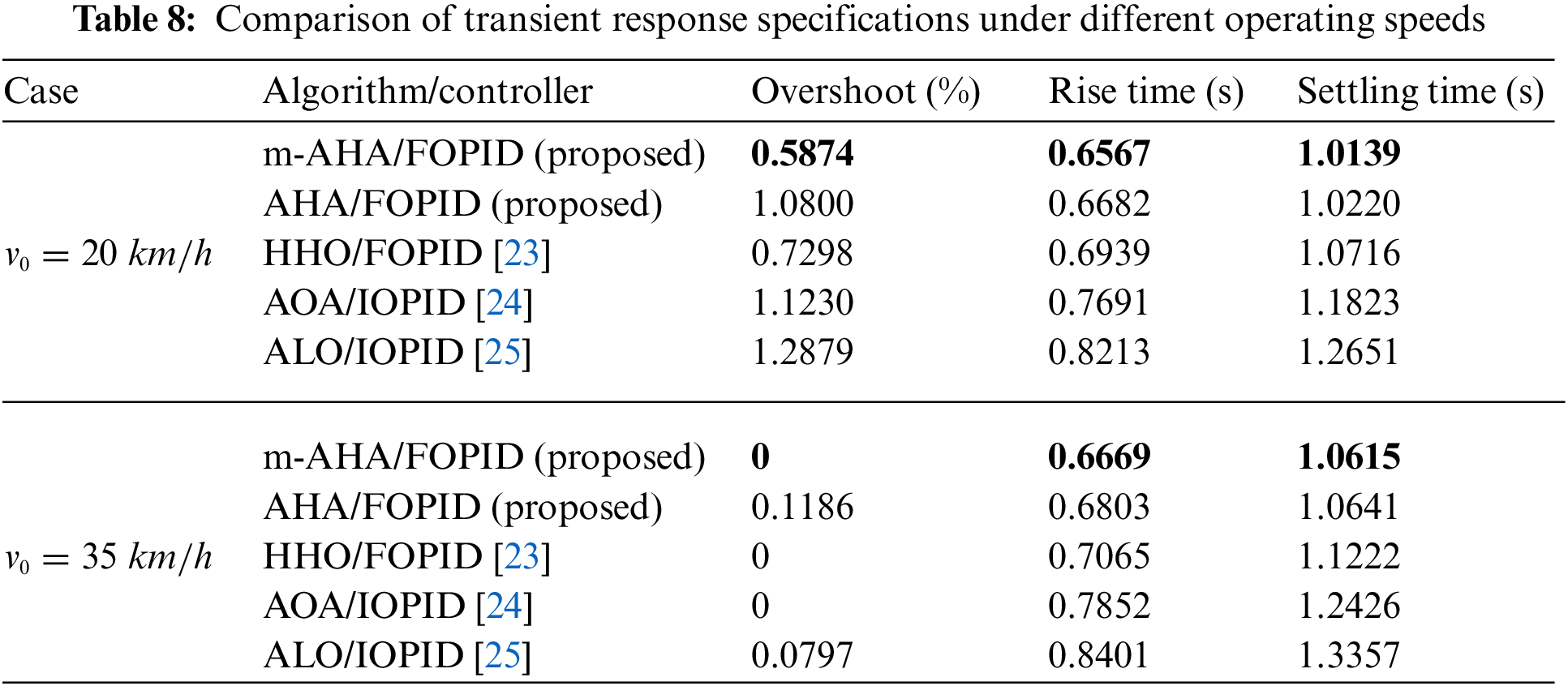
The velocity step responses for of the m-AHA/FOPID, AHA/FOPID, HHO/FOPID, AOA/FOPID and ALO/FOPID approaches are illustrated in Fig. 6. One can easily observe the capability of the proposed m-AHA/FOPID approach in terms of reaching better transient response. This can also be further verified from the presented values in Table 6, which also shows zero overshoot, less rise and settling time values achieved via the proposed m-AHA algorithm.

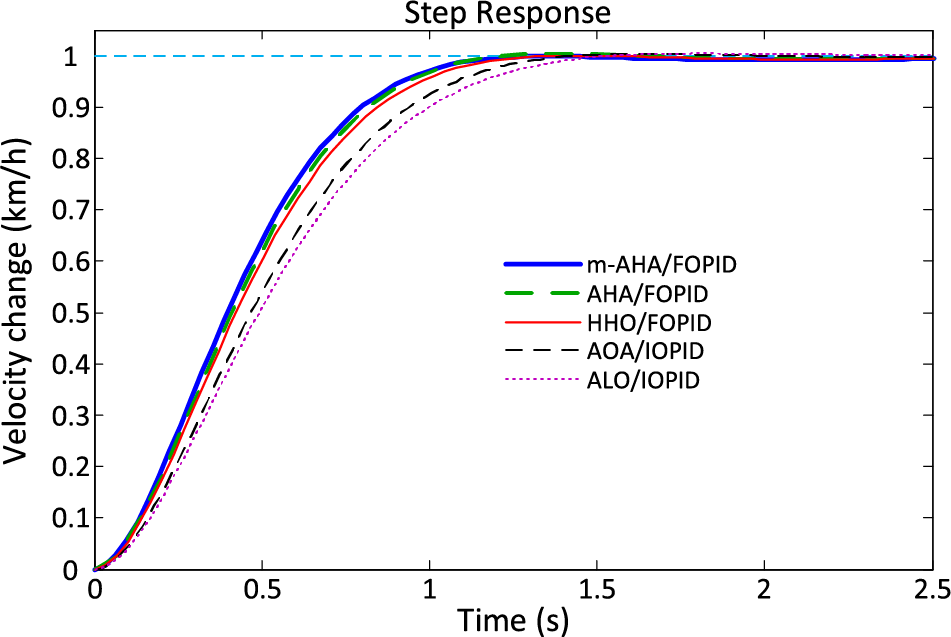
Figure 6: Velocity step responses

5.5.2 Frequency Response Analysis

The importance of assessing the frequency response of the system cannot be overstated when it comes to determining the effectiveness of the FOPID controller that has been optimized using the proposed m-AHA technique in a cruise control system. To evaluate the system’s performance, crucial parameters in the frequency domain such as bandwidth, gain and phase margins are employed. Fig. 7 displays the Bode plot of the cruise control system with the FOPID controller that has been optimized using the m-AHA technique.

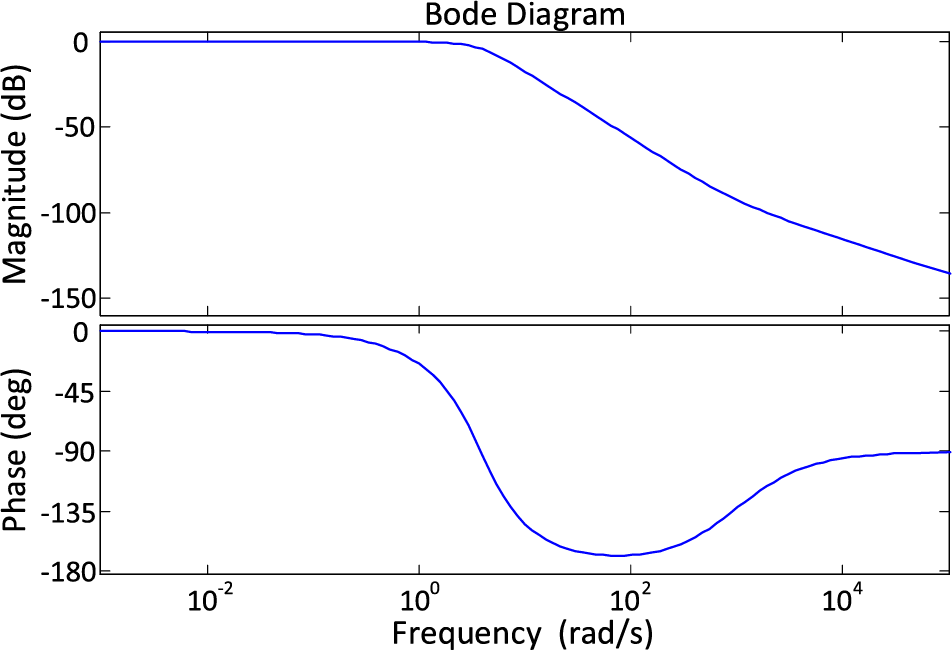
Figure 7: Bode diagram of m-AHA/FOPID-based system

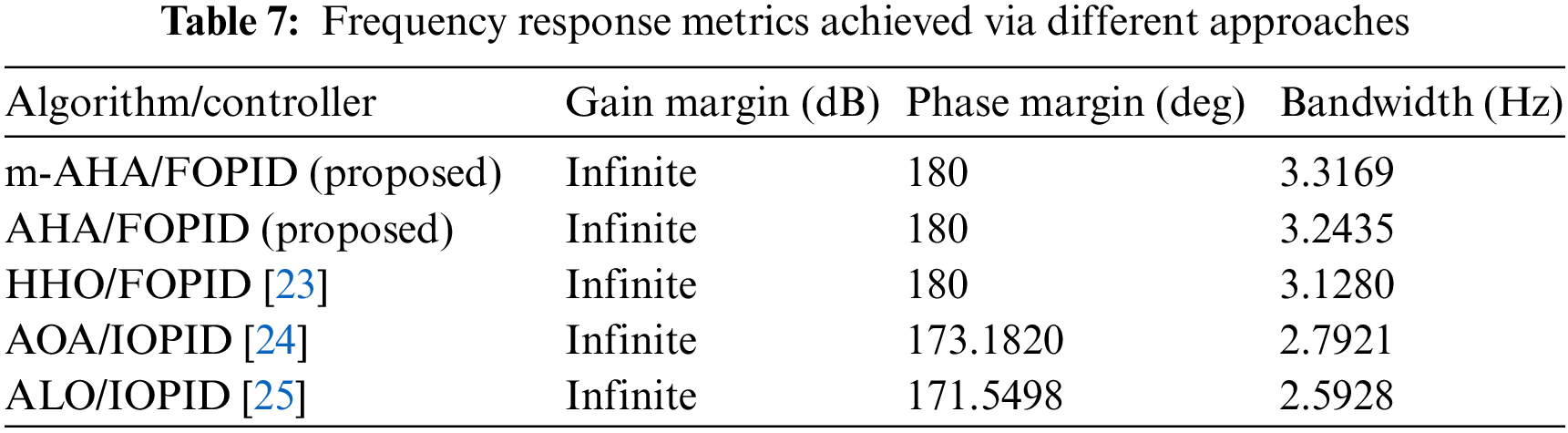
Table 7 compares the performance of the basic AHA and the proposed m-AHA optimization techniques in terms of the frequency domain parameters, and it is evident that the proposed m-AHA/FOPID controlled cruise control system exhibits the most stability and is a testament to the superior capability of the proposed optimization approach.

5.5.3 Robustness Analysis under Different Operating Speeds

The proposed m-AHA optimization technique was evaluated for its robustness in a FOPID-controlled cruise control system, considering two different scenarios that took into account changes in the reference speed. In that sense, velocity step responses for 20 km/h and 35 km/h were investigated. Figs. 8 and 9 respectively illustrate the velocity step responses for 20 km/h and 35 km/h reference speeds. The superiority and stability of the proposed method for various speeds is evident from the figures, showcasing its outstanding ability to regulate the cruise control system. This case is further numerically verified with the presented values in Table 8 as more desirable results (highlighted in bold) were achieved with the proposed m-AHA optimization technique.

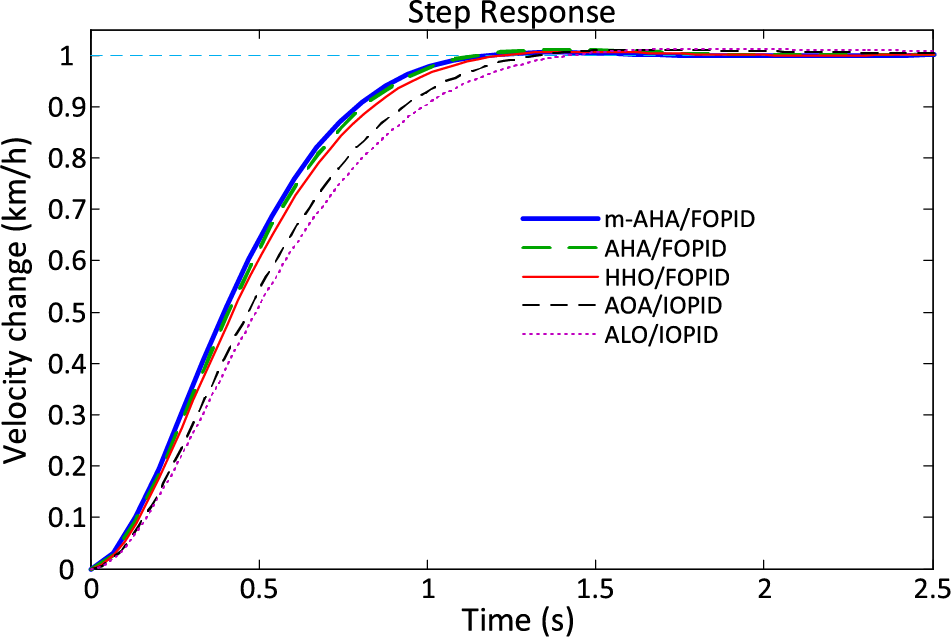
Figure 8: Velocity step responses for v0=20 km/h

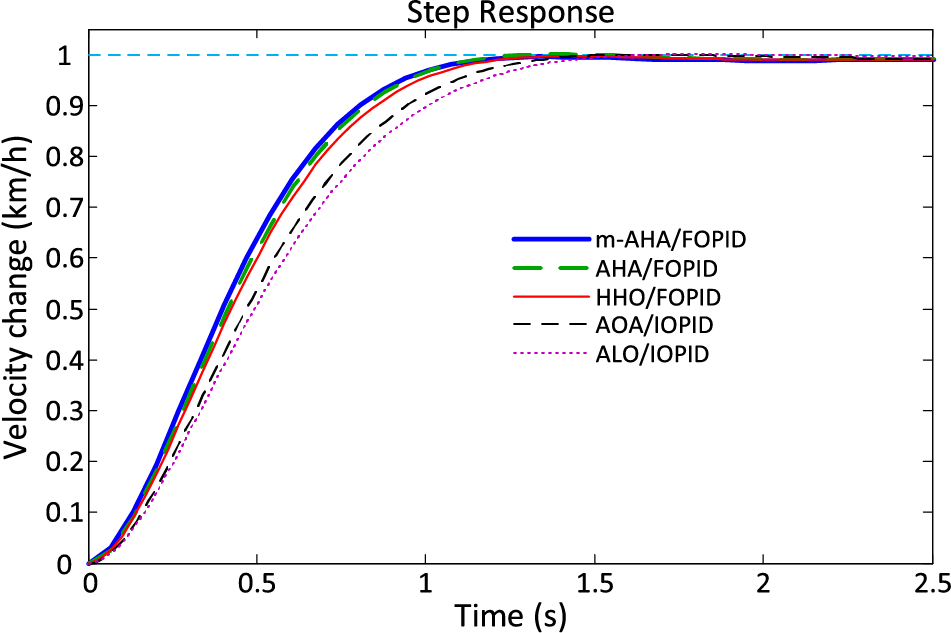
Figure 9: Velocity step responses for v0=35 km/h

6  Conclusion

The present study delves into exploring the potential of the m-AHA optimization technique in fine-tuning the parameters of a FOPID controller for regulating the speed of an autonomous vehicle that is equipped with a cruise control system. The m-AHA was constructed based on the convenient integration of the basic form of the AHA optimization technique and a newly modified EOBL mechanism. The more promising performance of the m-AHA optimization technique is shown on widely adopted and well-known benchmark functions through the evaluation of statistical and non-parametric statistical analyses. More excellent capability of the proposed m-AHA optimization technique for tuning the FOPID controller in a cruise control system is also comparatively demonstrated by using more recent and best performing approaches that employ the FOPID controller for the same purpose. The evaluations through transient, frequency and robustness characteristics have confirmed the proposed method’s more effective capacity for the cruise control system that is controlled with a FOPID controller.

In conclusion, the use of FOPID controllers has shown promise for improving the performance of control systems, especially in systems with nonlinear dynamics or time-varying parameters. The design of FOPID controllers involves the use of fractional calculus, which provides greater flexibility in tuning the controller parameters. Future research in this area may focus on the development of novel optimization techniques for designing FOPID controllers that can achieve better control performance in various applications. Additionally, the application of FOPID controllers could be applied to other control problems beyond cruise control, such as robotics, renewable energy systems, and industrial processes. Overall, the use of FOPID controllers has the potential to significantly advance the field of control engineering and improve the performance of complex systems in various applications.

Acknowledgement: Not applicable.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: Study conception and design: L. Abualigah, S. Ekinic, D. Izci, and R. Abu Zitar; data collection: S. Ekinic; analysis and interpretation of results: S. Ekinic; draft manuscript preparation: L. Abualigah, S. Ekinic, D. Izci, and R. Abu Zitar. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data is available from the authors upon reasonable request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Z. Nie and H. Farzaneh, “Adaptive cruise control for eco-driving based on model predictive control algorithm,” Applied Sciences, vol. 10, no. 15, pp. 5271, 2020. [Google Scholar]

2. Z. Chen, S. Xiong, Q. Chen, Y. Zhang, J. Yu et al., “Eco-Driving: A scientometric and bibliometric analysis,” IEEE Transactions on Intelligent Transportation Systems, vol. 23, no. 12, pp. 22716–22736, 2022. [Google Scholar]

3. D. Izci and S. Ekinci, “A novel hybrid ASO-NM algorithm and its application to automobile cruise control system,” in 2nd Int. Conf. on Artificial Intelligence: Advances and Applications, Singapore, pp. 333–343, 2022. [Google Scholar]

4. K. Osman, M. F. Rahmat and M. A. Ahmad, “Modelling and controller design for a cruise control system,” in 2009 5th Int. Colloquium on Signal Processing & its Applications, Kuala Lumpur, Malaysia, pp. 254–258, 2009. [Google Scholar]

5. M. A. S. Zainuddin, M. Abdullah, S. Ahmad and K. A. Tofrowaih, “Performance comparison between predictive functional control and PID algorithms for automobile cruise control system,” International Journal of Automotive and Mechanical Engineering, vol. 19, no. 1, pp. 9460–9468, 2022. [Google Scholar]

6. M. M. Gulzar, B. Sharif, D. Sibtain, L. Akbar and A. Akhtar, “Modelling and controller design of automotive cruise control system using hybrid model predictive controller,” in 2019 15th Int. Conf. on Emerging Technologies (ICET), Peshawar, Pakistan, pp. 1–5, 2019. [Google Scholar]

7. M. K. Rout, D. Sain, S. K. Swain and S. K. Mishra, “PID controller design for cruise control system using genetic algorithm,” in 2016 Int. Conf. on Electrical, Electronics, and Optimization Techniques (ICEEOT), Chennai, India, pp. 4170–4174, 2016. [Google Scholar]

8. R. Pradhan and B. B. Pati, “Optimal FOPID controller for an automobile cruise control system,” in 2018 Int. Conf. on Recent Innovations in Electrical, Electronics & Communication Engineering (ICRIEECE), Bhubaneswar, India, pp. 1436–1440, 2018. [Google Scholar]

9. D. Izci, S. Ekinci, M. Kayri and E. Eker, “A novel improved arithmetic optimization algorithm for optimal design of PID controlled and Bode’s ideal transfer function based automobile cruise control system,” Evolving Systems, vol. 13, no. 3, pp. 453–468, 2022. [Google Scholar]

10. E. Onieva, J. Godoy, J. Villagrá, V. Milanés and J. Pérez, “On-line learning of a fuzzy controller for a precise vehicle cruise control system,” Expert Systems with Applications, vol. 40, no. 4, pp. 1046–1053, 2013. [Google Scholar]

11. W. Wu, D. Zou, J. Ou and L. Hu, “Adaptive cruise control strategy design with optimized active braking control algorithm,” Mathematical Problems in Engineering, vol. 2020, pp. 1–10, 2020. [Google Scholar]

12. S. Chaturvedi and N. Kumar, “Design and implementation of an optimized PID controller for the adaptive cruise control system,” IETE Journal of Research, pp. 1–8, 2021. https://doi.org/10.1080/03772063.2021.2012282 [Google Scholar] [CrossRef]

13. D. Izci and S. Ekinci, “A novel-enhanced metaheuristic algorithm for FOPID-controlled and Bode’s ideal transfer function–based buck converter system,” Transactions of the Institute of Measurement and Control, 2023. https://doi.org/10.1177/01423312221140671 [Google Scholar] [CrossRef]

14. M. A. George, D. V. Kamat and C. P. Kurian, “Electric vehicle speed tracking control using an ANFIS-based fractional order PID controller,” Journal of King Saud University–Engineering Sciences, 2022. https://doi.org/10.1016/j.jksues.2022.01.001 [Google Scholar] [CrossRef]

15. O. Can, S. Ekinci and D. Izci, “Honey badger algorithm for adjustment of FOPID controller adopted in an automatic voltage regulator system,” in 2022 Global Energy Conf. (GEC), Batman, Turkey, pp. 262–265, 2022. [Google Scholar]

16. M. J. Blondin and J. P. Trovão, “Soft-computing techniques for cruise controller tuning for an off-road electric vehicle,” IET Electrical Systems in Transportation, vol. 9, no. 4, pp. 196–205, 2019. [Google Scholar]

17. J. E. Naranjo, F. Serradilla and F. Nashashibi, “Speed control optimization for autonomous vehicles with metaheuristics,” Electronics, vol. 9, no. 4, pp. 551, 2020. [Google Scholar]

18. L. YiFei, H. L. Minh, S. Khatir, T. Sang-To, T. Cuong-Le et al., “Structure damage identification in dams using sparse polynomial chaos expansion combined with hybrid K-means clustering optimizer and genetic algorithm,” Engineering Structures, vol. 283, pp. 115891, 2023. [Google Scholar]

19. H. L. Minh, T. Sang-To, S. Khatir, M. Abdel Wahab and T. Cuong-Le, “Damage identification in high-rise concrete structures using a bio-inspired meta-heuristic optimization algorithm,” Advances in Engineering Software, vol. 176, pp. 103399, 2023. [Google Scholar]

20. S. Ekinci and D. Izci, “Enhanced reptile search algorithm with Lévy flight for vehicle cruise control system design,” Evolutionary Intelligence, 2022. https://doi.org/10.1007/s12065-022-00745-8 [Google Scholar] [CrossRef]

21. A. Singhal, R. Roy, D. Mittal and P. Dahiya, “Optimal tuning using global neighborhood algorithm for cruise control system,” in 2021 7th Int. Conf. on Advanced Computing and Communication Systems (ICACCS), Coimbatore, India, pp. 336–339, 2021. [Google Scholar]

22. S. Ekinci, D. Izci, L. Abualigah and R. A. Zitar, “A modified oppositional chaotic local search strategy based Aquila optimizer to design an effective controller for vehicle cruise control system,” Journal of Bionic Engineering, 2023. https://doi.org/10.1007/s42235-023-00336-y [Google Scholar] [CrossRef]

23. D. Izci and S. Ekinci, “An efficient FOPID controller design for vehicle cruise control system using HHO algorithm,” in 2021 3rd Int. Cong. on Human-Computer Interaction, Optimization and Robotic Applications (HORA), Ankara, Turkey, pp. 1–5, 2021. [Google Scholar]

24. D. Izci, S. Ekinci, M. Kayri and E. Eker, “A novel enhanced metaheuristic algorithm for automobile cruise control system,” Electrica, vol. 21, no. 3, pp. 283–297, 2021. [Google Scholar]

25. R. Pradhan, S. K. Majhi, J. K. Pradhan and B. B. Pati, “Antlion optimizer tuned PID controller based on Bode ideal transfer function for automobile cruise control system,” Journal of Industrial Information Integration, vol. 9, pp. 45–52, 2018. [Google Scholar]

26. D. H. Wolpert and W. G. Macready, “No free lunch theorems for optimization,” IEEE Transactions on Evolutionary Computation, vol. 1, no. 1, pp. 67–82, 1997. [Google Scholar]

27. A. awad Mohamed, L. Abualigah, A. Alburaikan and H. A. E. W. Khalifa, “AOEHO: A new hybrid data replication method in fog computing for IoT application,” Sensors, vol. 23, no. 4, pp. 2189, 2023. [Google Scholar]

28. R. A. Zitar, L. Abualigah, F. Barbaresco and A. E. Seghrouchni, “Modified arithmetic optimization algorithm for drones measurements and tracks assignment problem,” Neural Computing and Applications, vol. 35, pp. 10421–10447, 2023. [Google Scholar]

29. F. Gul, A. Mir, I. Mir, S. Mir, T. U. Islaam et al., “A centralized strategy for multi-agent exploration,” IEEE Access, vol. 10, pp. 126871–126884, 2022. [Google Scholar]

30. W. Zhao, L. Wang and S. Mirjalili, “Artificial hummingbird algorithm: A new bio-inspired optimizer with its engineering applications,” Computer Methods in Applied Mechanics and Engineering Methods, vol. 388, pp. 114194, 2022. [Google Scholar]

31. D. Izci, S. Ekinci, E. Eker and A. Demirören, “Biomedical application of a random learning and elite opposition-based weighted mean of vectors algorithm with pattern search mechanism,” Journal of Control, Automation and Electrical Systems, vol. 34, no. 2, pp. 333–343, 2023. [Google Scholar]

32. H. R. Tizhoosh, “Opposition-based learning: A new scheme for machine intelligence,” in Int. Conf. on Computational Intelligence for Modelling, Control and Automation and Int. Conf. on Intelligent Agents, Web Technologies and Internet Commerce (CIMCA-IAWTIC’06), Vienna, Austria, pp. 695–701, 2005. [Google Scholar]

33. D. Izci, S. Ekinci, E. Eker and M. Kayri, “Augmented hunger games search algorithm using logarithmic spiral opposition-based learning for function optimization and controller design,” Journal of King Saud University-Engineering Sciences, 2022. https://doi.org/10.1016/j.jksues.2022.03.001 [Google Scholar] [CrossRef]

34. B. H. Abed-alguni and D. Paul, “Island-based cuckoo search with elite opposition-based learning and multiple mutation methods for solving optimization problems,” Soft Computing, vol. 26, no. 7, pp. 3293–3312, 2022. [Google Scholar]

35. L. Wang and C. Huang, “A novel elite opposition-based jaya algorithm for parameter estimation of photovoltaic cell models,” Optik, vol. 155, pp. 351–356, 2018. [Google Scholar]

36. A. A. Frank, S. J. Liu and S. C. Liang, “Longitudinal control concepts for automated automobiles and trucks operating on a cooperative highway,” SAE Transactions, vol. 98, pp. 1308–1315, 1989. [Google Scholar]

37. S. Das, I. Pan, S. Das and A. Gupta, “Improved model reduction and tuning of fractional-order PIλDμ controllers for analytical rule extraction with genetic programming,” ISA Transactions, vol. 51, no. 2, pp. 237–261, 2012. [Google Scholar] [PubMed]

38. D. Izci, B. Hekimoğlu and S. Ekinci, “A new artificial ecosystem-based optimization integrated with Nelder-Mead method for PID controller design of buck converter,” Alexandria Engineering Journal, vol. 61, no. 3, pp. 2030–2044, 2022. [Google Scholar]