Interval Type-2 Fuzzy Model for Intelligent Fire Intensity Detection Algorithm with Decision Making in Low-Power Devices

Abbreviations and Mathematical Symbols

1  Introduction

Fire disasters are the most common occurrences in East Africa’s densely populated local urban markets. For instance, Gisozi, Rwanda; Gikomba, Kenya; and Owino, Uganda, are constantly threatened by rampant fire accidents, which have caused severe loss of life and property (ref. Fig. 1). These markets, provide income for small-scale vendor communities by selling their daily wares. According to Uganda police investigative reports, the major causes of fires include; electrical short circuits, negligence, and neglected charcoal stoves [1–4]. The current vendor communities heavily rely on human patrol and observation methods. However, they are quite inefficient and may cause extensive damage to vendors’ property due to unnecessary delays [2,3]. Also, unit–smoke detectors have a high rate of false alerts due to their high sensitivity calibration to their surrounding environment [5–7]. Ruchkin et al. [8–10] proposed satellite–based systems that are prohibitively expensive to acquire and maintain for developing countries. Camera systems are also incapable of monitoring the initial ignition of surface fires as well as the level of fire danger [11]. Related works are discussed in Table 1. This study therefore, presents an Interval Type-2 Tang Sugeno Kang fuzzy model for an intelligent fire intensity detection algorithm with decision making in low-power devices. The performance of the proposed model was investigated using a free open-source fuzzy toolbox integrated into MATLAB2018a. Two secondary input parameters, namely; fire intensity due temperature change (FIT~) and fire intensity due to gases dissipated (FIG~) are considered.

Figure 1: Percentage (%) of victims (injured, fatal) affected by fire accidents in the period (2012–2020), a case of Uganda [2]

Results show that the proposed Interval Type-2 TSK fuzzy model outperformed Mamdani’s Type-1 by an accuracy of 98.2%, compared to 95.8% in Lule et al. [1]. The footprint of uncertainty (FOU) in the Interval Type-2 fuzzy sets provides additional degrees of freedom, allowing for the modelling of uncertainties to improve efficiency. Secondly, Type-2 systems outperformed Type-1 fuzzy systems in overcoming the dimensionality problem, which leads to the high computational overload associated with rule-based systems [12,13]. Thus, the model’s efficiency significantly improved because the Interval Type-2 (IT2) TSK fuzzy model minimized the uncertainty errors inherent in Type-1 fuzzy systems [14].

Hence, a lightweight fire intensity detection algorithm based on the Interval Type-2 TSK fuzzy model for decision-making in low-power fire devices is presented. When compared to Mamdani’s Type-1 systems, the Interval Type-2 TSK fuzzy method improved the model’s accuracy to 98.2%, MAE = 1.3010, MSE = 1.6938, and RMSE = 1.3015 for effective fire detection. Thus, the proposed solution can be implemented in low-cost, low-power fire detection systems to improve the accuracy of monitoring the current state of fire. This shall assist the firefighting personnel in fully monitoring, understanding, and mitigating any level of the state of fire danger in order to make an appropriate decision. Early warning notifications can also be provided to aid in the rapid evaluation of persons, thereby improving fire safety surveillance, management, and protection for the market community through informed decision-making in low-cost fire devices. The remainder of the paper includes; Related Works, Materials and Methods, Second Order FAM, Algorithm Design Procedure, Relational Mathematical Operations Theory and Notations in Type-2 Fuzzy Systems, Simulation Experimental Setup, Results and Discussion, Conclusion, and Future Works.

2  Related Works

In the Table 1, we show a detailed discussion of the proposed solutions and their limitations for the related works.

3  Materials and Methods

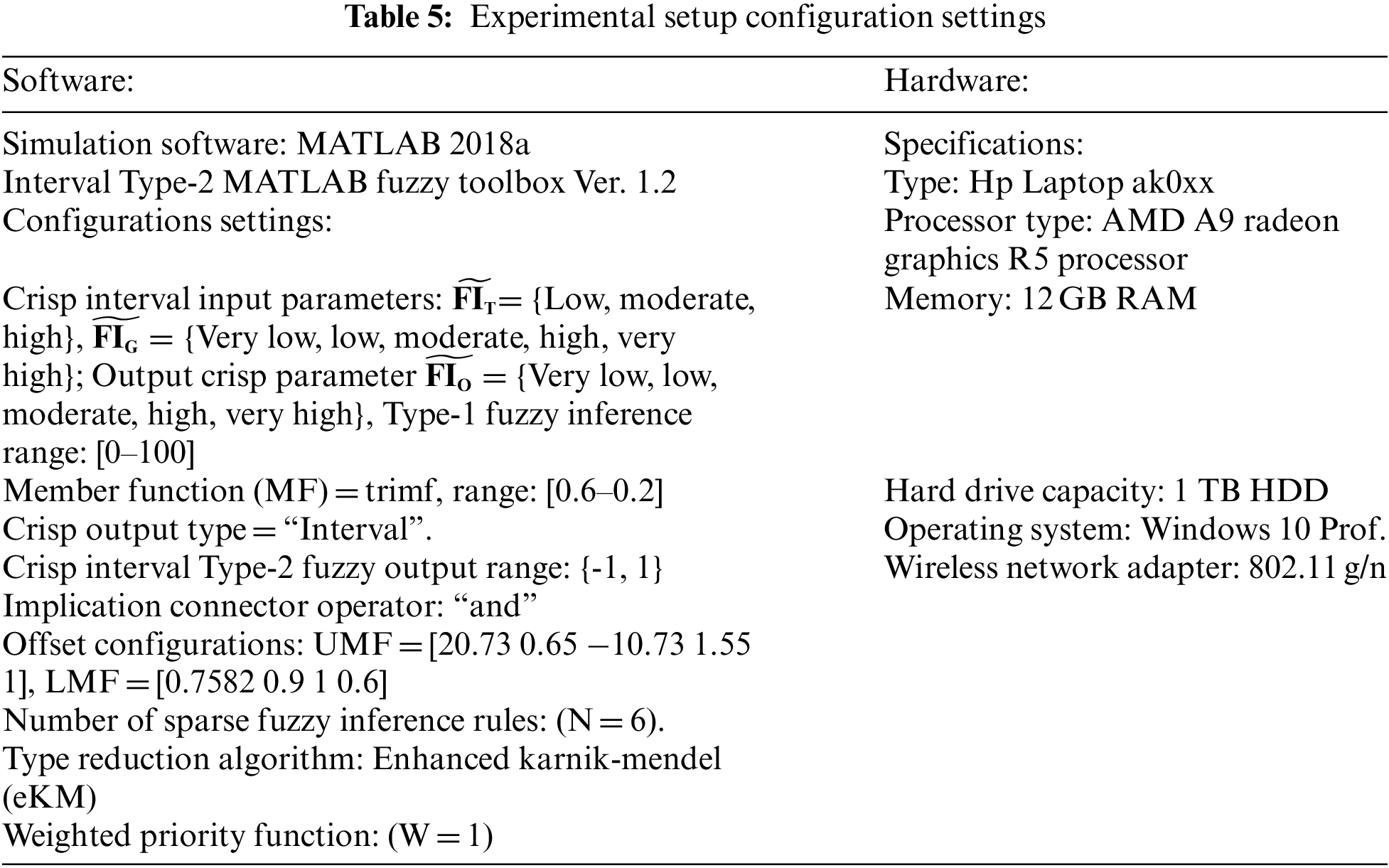
The study employs a free open-source MATLAB/Simulink fuzzy toolbox integrated with Interval Type-2 fuzzy logic system. Because it is widely available to the users of Type-2 fuzzy systems community. The simulink library connects the fuzzy logic system and the fuzzy toolbox. To study the performance of the IT2 TSK fuzzy model, the tool is configured in MATLAB2018a [26]. MATLAB [1,27], is a multi–paradigm computing tool, that enables the modelling of real-time complex engineering solutions. Two secondary Interval Type-2 input parameters are used; i.e., Fire intensity due to temperature change  FIT~, and Fire intensity due to dissipated gases (CO2, CO), FIG~. The fire intensity interval output value FIO ~ of the IT2 TSK model is proposed to minimize the inherent errors of Type-1 (T1) fuzzy systems using a type reduction method, called the enhanced Karnik-Mendel (eKM) in range of [−1, 1]. Because eKM reduces the computational overload associated with fuzzy system design. The model was designed using the trim member function (trimf) using six sparse inference rules. NB: Flame presence = “True” for all fuzzy inference rules, else = “False”. To determine the best-fit dataset of the IT2 TSK fuzzy model, a linear regression method is used to evaluate the datasets for improved accuracy. To compute the accuracy, error metric parameters, namely; the mean absolute error (MAE), mean square error (MSE), root mean square error (RMSE), and the coefficient of determination (R2), are used to determine the quality of the best choice of fit data to the model. For N = 17; N denotes the number of Interval Type-2 rule outcomes being sampled. The obtained dataset with the lowest RMSE value, is identified as the best fit dataset for the model in order to determine the operating efficiency and accuracy of the proposed Interval Type-2 fuzzy model.

3.1 Second Order Fuzzy Associative Matrix (2FAM)

The fuzzy associative matrix (FAM) is a content addressable memory for storing the fuzzy inference rules of a particular associated fuzzy model [28,29]. The study used the 2FAM method, with the Interval Type-2 fuzzy input sets as crisp input values for the proposed TSK model. With the second-order derivatives, the output fuzzy values of Type-1 (T1) fuzzy sets are converted into Type-2 (T2) input values. Note that, Type-2 fuzzy systems have gained popularity due to the fact that inherent errors created by Type-1 (T1) systems can be minimized by Type-2 fuzzy systems [27,30]. This improves the models’ accuracy, by allowing them to create flawlessly functioning fuzzy systems in real time. Type-1 systems are denoted by A, and the Type-2 fuzzy associative members or elements are denoted by A^ [28,31] of comparable second order as per Dr. Loft Zadeh. For n = 1, 2, 3, …, N, then the associated order n can be explicitly defined. Thus, the Interval Type-2 TSK fuzzy control model’s corresponding 2FAM sparse inference rules are then defined in Table 2. NB: The model utilizes six sparse rules to reduce the high computational overloads associated with Type-2 fuzzy system design.

3.2 Proposed Interval Type-2 TSK Sparse Fuzzy Inference Rules (FIR) Design

Using the FAM method, as discussed in Section 3.1 above, we can further derive six (6) corresponding Interval Type-2 TSK sparse fuzzy inference rules for the proposed model.

3.3 Interval Type-2 TSK Decision Parameters for Inputs and Outputs of the Proposed Fuzzy Model

The proposed IT2 TSK model utilizes two inputs FIT~,FIG~ and output FIO~ parameters to investigate the performance behaviour of the proposed Interval Type-2 TSK model. The universe of discourse for the various crisp interval inputs and output parameters is defined in Tables 3 and 4, respectively.

4  Algorithm Design Procedure

In Fig. 2, a schematic design of Mamdani’s Type-1 fuzzy-based algorithms is defined by Lule et al. [1]. The fire intensity due to temperature change (EFIP1) and fire intensity due to the dissipated gases, i.e., (CO2, CO), (EFIP2), are Mamdani’s Type-1 fuzzy outputs. For effective fire detection, the fire detection algorithms consider temperature, humidity, CO2, CO, and flame parameters. Through the process of oxidation, oxygen reacts with carbon present in any burning material to give two dissipated gases, namely; CO2 and CO. The fuzzy algorithms’ schematics assume the threshold values Th and Thg to determine the minimal values of temperature rise and, gases dissipated, respectively, due to combustion. FI is the optimal fire intensity detection value of (FIO~) obtained by the proposed Interval Type-2 TSK algorithm.

Figure 2: Mamdani’s Type-1 fuzzy algorithms for fire intensity due temperature change (EFIP1) and dissipated gas (EFIP2), respectively [1]

4.1 Algorithm Assumptions Considered

Several assumptions are made by the proposed algorithm to ensure an optimal fire intensity detection value (FIO~), realized:

     i.  Three key parameters for fire combustion are considered, namely; temperature (ΔT), and two by-products of dissipated gases; carbon dioxide (ΔCO2), and carbon monoxide (ΔCO).

    ii.  To reduce the computational overload associated with Type-2 fuzzy systems, six sparse inference fuzzy rules are used to optimize the performance of the overall fire intensity detection value of (FIO ~).

   iii.  Note that humidity (ΔH) is not a key parameter for combustion due to its high dependency on temperature change and pressure within the surrounding environment. Note that for each inference rule, flame presence is a boolean probability equal to “True” or “False”. Because of the high computational cost overheads associated with Type-2 fuzzy systems, output processing with centroid type reduction and defuzzification methods may cause unnecessary bottlenecks on Interval Type-2 fuzzy systems. Hence, alternative approaches, such as the Nie-Tan method [32,33], can be suggested.

4.2 Proposed Fire Intensity Detection Algorithm Procedure Based on IT2 TSK Fuzzy Approach

4.3 Fire Intensity Detection Model Using Interval Type 2 TSK Fuzzy Approach

In Fig. 3, the framework of the fire intensity detection model is made up of temperature, humidity, CO2, and CO as data acquisition units, an optimized IT2 TSK model training unit, and a fire status decision-making unit. The obtained dataset is then trained using the IT2 TSK fuzzy model which is integrated with an intelligent fire intensity detection algorithm to determine an informed “fire status” decision due to the surrounding environment.

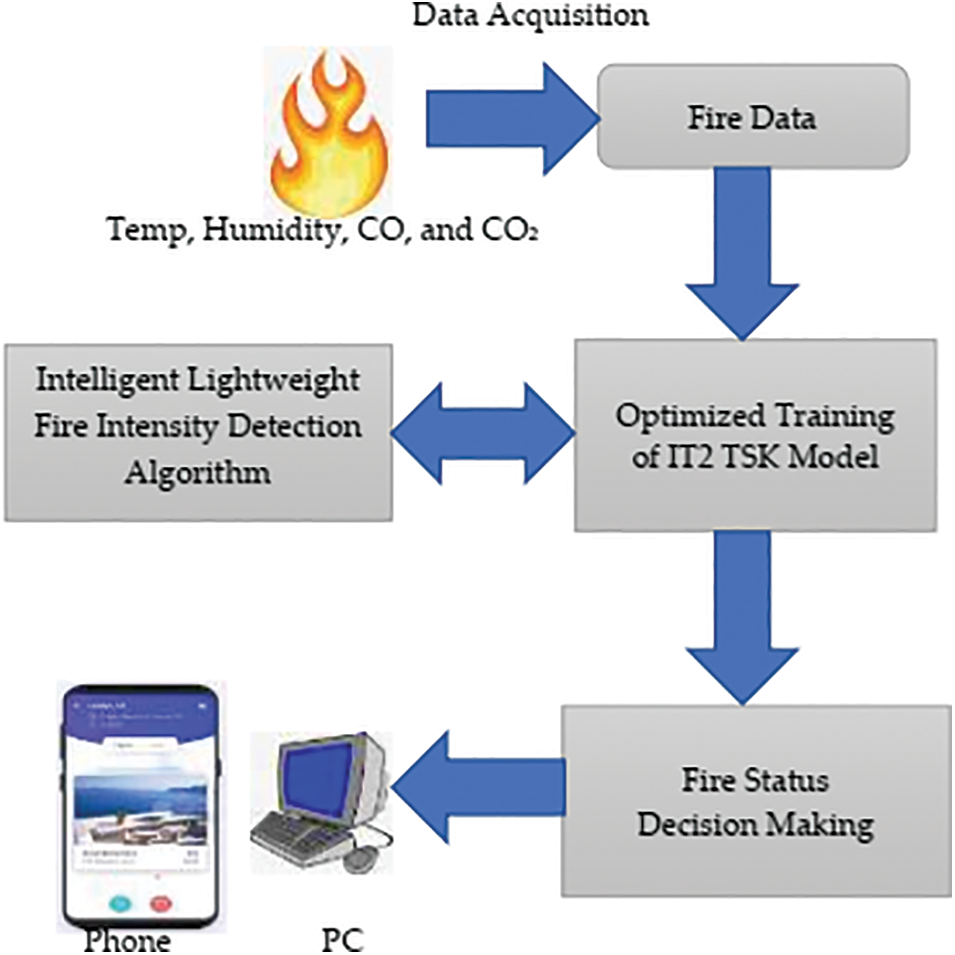
Figure 3: Proposed breakdown of the IT2 TSK fuzzy detection model with “fire status” decision making

5  Relational Mathematical Operations Theory and Notations in Type-2 Fuzzy Systems

A non-deterministic truth degree with imprecision and uncertainty for each set of elements is defined in Type-2 fuzzy set. Fuzzy inference systems utilize fuzzy reasoning and a set of principles to map fuzzy inputs to outputs. This method applies in a variety of application domains, like computer vision, pattern recognition, and intrusion detection. T1 systems represent the membership, as the membership of each element in a fuzzy set, whereas Interval Type-2 fuzzy sets represent the membership as crisp intervals bound by the range of [−1, 1] [34–36]. Type-1 fuzzy systems have been used in a variety of fields, but they are most commonly associated with noisy data and extremely large uncertainty error limits as represented in their inference rule consequents [37,38]. Thus, from the principle of fuzzy set theory, the application of Interval Type-2 TSK fuzzy inference systems can be correlated using relational mathematical theoretical representations.

Let U, be the initial universe of objects, EU, the set of parameters about the objects, P(U), the power set of U such that: A⊆E. Molodtsv [39] defined a set of the pair (F, A) called, the soft set over U, where F is a mapping given by: F: A → P(U). For ε Є A, F(ε) is defined as a set of ε-approximate elements of the soft set (F, A). Type-2 fuzzy sets denoted by Ã, are also characterized by a general Type-2 membership function for which, μà (x, U), such that: U defines a finite and non-empty set, which is referred to as a universe of discourse [40]. The membership function associates each element x Є U, with a value in the interval [0, 1].

Hence; UxI→I where; xЄ, I = [ 0,1 ] and µЄx⊆I

A~={(x,  u), μA~(x, u)|xЄu, uЄ Jx⊆I }for:0≤μA~ (x,u) ≤1

A~=∫x∈μ ∫μ∈Jx μA~(x,u)(x, u)=∫x∈μ ∫μ∈Jxfx (u)/ux Jx⊆1(1)

where fx(u)=µA~(x, u)

Hence, for the class of Type-2 fuzzy sets of the Universe U is denoted by FT2(U) [41].

5.1 Operations of General Type-2 Fuzzy Sets

If U is to be a nonempty universe such that A~,B~Є FT2(U): then,

A~=∫x∈u μA~(x)x∫x∈u [∫x∈Jxufx (u)/u]x , Jxu⊆IB~=∫x∈u μB~(x)x∫x∈u [∫γ∈Jxγgx (γ)/γ]x, Jxγ⊆I(2)

Hence, applying the general type-2 fuzzy operations to the aforementioned fuzzy sets, defined by Eq. (2), i.e., union, intersection, and complement, yields Eqs. (3)–(5), respectively, which can be explicitly reduced as follows:

μA~uB~(x)=∫u∈jxu ∫γ∈jxγ [fx(u)∧gx(u)]u∨γ=UA~(x)⊔UB~(x), x∈U(3)

μA~nB~(x)=∫u∈jxu ∫γ∈jxγ [fx(u)∧gx(u)]u∧x=UA~(x)UB~(x), x∈U(4)

μ∼A~(x)=μA~(x)=∫u∈jxu fx (u)1−μ(5)

where ∧ is the t-norm minimum operator, ∨ is the maximum operator, and ⊔ the joint operation, μA~uB~(x),μA~(x),μB~(x) are the secondary membership functions, and for all belonging to Mamdani’s Type-1 fuzzy sets [39,41].

5.2 IT2 TSK Fuzzy Inference Systems vis-à-vis Decision Making

An Interval Type-2 fuzzy set (FS) can be characterized by the Eq. (6) below:

A~=∫x∈X {∫μϵJx 1/μ}/x,Jx⊆ [0 1](6)

The secondary grades of A~ is equal to 1: X is the primary domain with input x and primary degree membership μ. Jx, is the secondary domain with values varying from [0–1]. The Interval Type-2 fuzzy set can therefore be best described by having the lower (LMF) or u_A~(x) and the upper membership functions (UMF) or u¯A~(x). Therefore, the given shaded region (ref. Fig. 4), between the LMF and UMF is called the “Footprint of Uncertainty (FOU)”. Thus, FOU represents a third-dimensional value of the membership function (MF) at each point on its two-dimensional domain such that [42]:

FOU(A~)=Ux Є X[u_A~(x),u¯A~(x)](7)

Figure 4: Shows the interval Type-2 fuzzy set with a shaded region known as the FOU [42]

From Eq. (6), using the Interval Type-2 TSK fuzzy systems rules approach, the firing strength, determines the minimal probability for a given fire status. Thus, the fire status can be determined using the IF … THEN structure for the fuzzy inference consequent decision evaluation. Upon this background, consider a typical Type-1 TSK sparse rules-based approach comprised of n fuzzy inference rules [43]:

R1: IFx1isA11and…xkisAk1and…xqisAq1 THENy=f1x11(…xq1,),⋯

Rn:IFx1isA1nand…xkisAknand…xqisAqn THENy=fn(x1n…,xqn),

where Aji (i ∈{1,2…n} and j∈{1,2…q}).

Alternatively, assuming the IT2 TSK sparse rules are comprised of n rules, then a zero or first-order polynomial function can be derived such that:

R1:IFx1isA~11and…xkisA~k1and…THENy=p~01+p~11x11+…p~k1xk1

Ri:IFx1isA~1iand…xkisA~kiand…THENy=p~0ip~1ix11+…p~kixki⋯

Rn:IFx1isA~1nand…xkisA~knand…THENy=p~0n+p~1ix1n+…p~knxkn

where A~ji(j∈{1, …,k}and i∈{1, …,n}) is defined as an Interval Type-2 fuzzy set having an input variable xj in the ith rule, giving a consequent in the crisp polynomial function as:

y= fi(xj, …,xk)=p~0n+p~iix1n…p~knxkn where p~ji are crisp intervals or consequent parameters for a given universe of discourse such that; O(A~1∗…A~k∗), A~ji, the antecedent value of the rule Ri. Using the related IT2 TSK fuzzy model approach of Jie Li et al. [44] the approximate firing strength (α¯i), of matching degree s and antecedent variable xj, using a t-norm operator * can be deduced to the Eq. (8):

f_=u_ A~1(x1)∗u_ A~2(x2)∗…∗A~n(xn);

f¯=u¯A~1(x1)∗u¯A~2(x2)∗…∗u¯A~n(xn), then the firing strength (α¯i) can be deduced as follows:

(α¯i)=s( A~1i¯, A~1¯)∧…∧s( A~ki¯, A~k¯)(8)

Applying, the type reduction (TR) and defuzzification methods, using the center of sets to compute the centroid of every consequent set. Then the weighted average of each consequent is determined as follows:

Y=[y1, yr]∫y1…∫ym  ⋅∫f1  …∫fm 1∑i=1mfiyi∑i=1mfi(9)

Y is the interval set, determined by the constants yiandyr⋅fi is[f_i, f¯i].

yi=[yii, yri] is the centroid of the Type-2 interval fuzzy set in the consequent part. Karnik et al. [45] showed that two endpoints are dependent on the mixture of fi and f¯i values can be determined as:

yr=yr(f_1,…,f_R,f¯R+1…f¯m,yr1,yrm)

yi=yi(f¯1,…,f¯m,f_I+1 …f_m,yi1,yim )(10)

NB: (yr,yi) are determined by using Eq. (10). A special iterative formula was then developed by Mendel et al. [46] to produce the computational values of yr(max) and yi(min) as:

yr=∑i=1Rf_iyir+∑i=R+1mf¯iyir∑i=1Rf−i+∑i=R+1mf¯i

yi=∑i=1Lf¯iyi1+∑i=L+1mf¯iyi1∑i=1Lf¯i+∑i=L+1mf_i(11)

Thus, the switch points can be determined by using Karnik-Mendel’s (KM) algorithm [45,46]. Therefore, the crisp outputs in the defuzzification layer can then be computed as follows:

y=yr+yi2(12)

5.3 Type Reduction

Type Reduction (TR) is a phase used to defuzzify the Type-2 fuzzy sets that transform Type-2 into Type-1 fuzzy systems. T1 and IT2 fuzzy systems differ in that IT2 fuzzy systems employ an extra TR procedure to process Interval Type-2 systems. The KM TR method is widely used to calculate the type-reduced sets iteratively [47]. Other methods include; Iterative Algorithm with Stop Condition (IASC), Enhanced IASC, Enhanced Opposite Direction Searching Algorithm (EODS), Wu-Mendel Uncertainty Bound Method (WM), Nie-Tan (NT) and Begian-Melek-Mendel(BMM) [26]. The enhanced KM algorithm is used in the study to reduce computational overload and significantly captures most features of the IT2 fuzzy model, such as adaptability and stability. The major bottleneck of Type-2 fuzzy systems is output processing using the centroid TR and defuzzification method. Since KM algorithms are associated with high computational costs, this may hinder their real-time application [48]. Thus, to compromise between the speed, computational overload, and complexity, other methods were proposed, i.e., the Nie-Tan method, to compute the output of the IT2 TSK fuzzy system [33,49]. N refers to the number of system inputs, such that: N = 1, 2, 3, …, n.

Then, the Nie-Tan method can therefore be mathematically defined using the Eq. (13) below:

y=∑n=1N yn(f_n+f¯n)∑nN(f_n+f¯n)(13)

6  Simulation Experiment Setup

Fig. 5 shows an Interval Type-2 Takagi Sugeno Kang (TSK) fuzzy design view of the model editor using MATLAB. A free open–source MATLAB fuzzy logic toolbox is carefully configured with varying parameter settings as defined in Table 5 and successfully integrated into the MATLAB2018a environment for proper functioning. The tool is widely used in the modeling and simulation of Type-2 fuzzy systems [47]. The model uses a TSK inference system to ensure higher performance is realized for the proposed fire detection algorithm [50]. Through “fuzzification”, crisp inputs are defined in Table 3. The Enhanced Karnik–Mendel algorithm is used to minimize the computational overload in Type-2 systems [45]. Through the “defuzzification” process, the performance outcome of the proposed IT2 fuzzy model can be obtained.

Figure 5: Main model editor of IT2 TSK with crisp interval inputs: (FIT~), (FIG~) and crisp output parameter: (FIO~), the optimized fire intensity value

7  Results and Discussion

In Figs. 6a–6d, results were obtained by integrating a free open-source fuzzy toolbox of Interval Type-2 within the MATLAB 2018a environment [27]. The tool was used to investigate the IT2 TSK model’s performance behaviour. Two input parameters are used; fire intensity due to gases dissipated FIG~ and fire intensity due to temperature change FIT~. The optimized fire intensity output FIO~ is determined by the correlation between FIG~ vis a vis FIT~. Based on six significant IT2 TSK sparse rules defined in Table 1, the eKM type reduction algorithm was used to reduce the computational complexity associated with Type-2 fuzzy systems.

Figure 6: (a–d) show a 2D, 3D surfaces control view outputs for the IT2 TSK fuzzy model with continuous discrete color pattern separations using MATLAB 2018a

Several insights can be drawn:

     i.  The fire intensity surface control results of the Interval Type-2 TSK fuzzy model range from [−1, 1]. The obtained linear discrete model pattern (ref. Fig. 6a) shows changes in FIG~ or FIT~ gradually influence the output value of FIO~. E.g., an increase in both FIG~ and FIT~ significantly increases FIO~. Thus, higher changes in FIG~ or FIT~ increase the risk of fire intensity due to combustion. Also, Figs. 6b–6d show a higher FIT~ with increasing temperature change, results in a higher risk of dissipated gases of FIG~. Hence, the increased output performance of FIO~ vis-à-vis increased FIT~ and FIG~.

    ii.  In Fig. 6c, an increase in fire intensity due to dissipated gasses FIG~, raises the output value of FIO~ due to increased gas combustion. Similarly, in Fig. 6d, an increase in temperature change FIT~ increases the value of FIO~. Hence, general Type-2 fuzzy systems significantly improve the output design of the Interval Type-2 TSK model. In Figs. 6b–6d, increased temperature yields higher FIO~ due to an increased fire intensity risk associated with temperature change. Likewise, Fig. 6c shows increased gases dissipated, yields higher FIO~ (Greater fire intensity from blue to dark red region).

Table 6 and Fig. 7 depict a graphical representation of a set of absolute values taken to study the correlation between FIT~, FIG~ against values of (FIO~), for the Interval Type-2 TSK fuzzy model. The firing strength is computed using the sparse inference rules approach. The Enhanced Karnik-Mendel (eKM) algorithm gives a smooth, stable curve (dashed line) of the output fire intensity  FIO~, with an accuracy rate of 98.2%. Thus, the heat transferred during combustion increases (FIO~) with the proposed IT2 TSK model. With regression analysis, an accuracy rate of 98.2% is determined as the best-fit data for the model. Hence, a significant improvement of  (FIO~) is realized using the IT2 TSK inference system compared to Mamdani’s Type-1 fuzzy model in Lule et al. [1]. Also, a sudden drop or (unstable state) in temperature change is observed through  FIT~=0.7959 to 0.02041, FIG~=1 to 0.1429. Because of the inherent error uncertainties associated with the rule-based consequents in the fuzzy model. Secondly, the reduced levels of oxygen depleted due to combustion, reflect a decrease in the overall output performance of the fuzzy model. Thus, results show a subsequent drop in both temperatures and CO2 concentration levels in the surrounding environment.

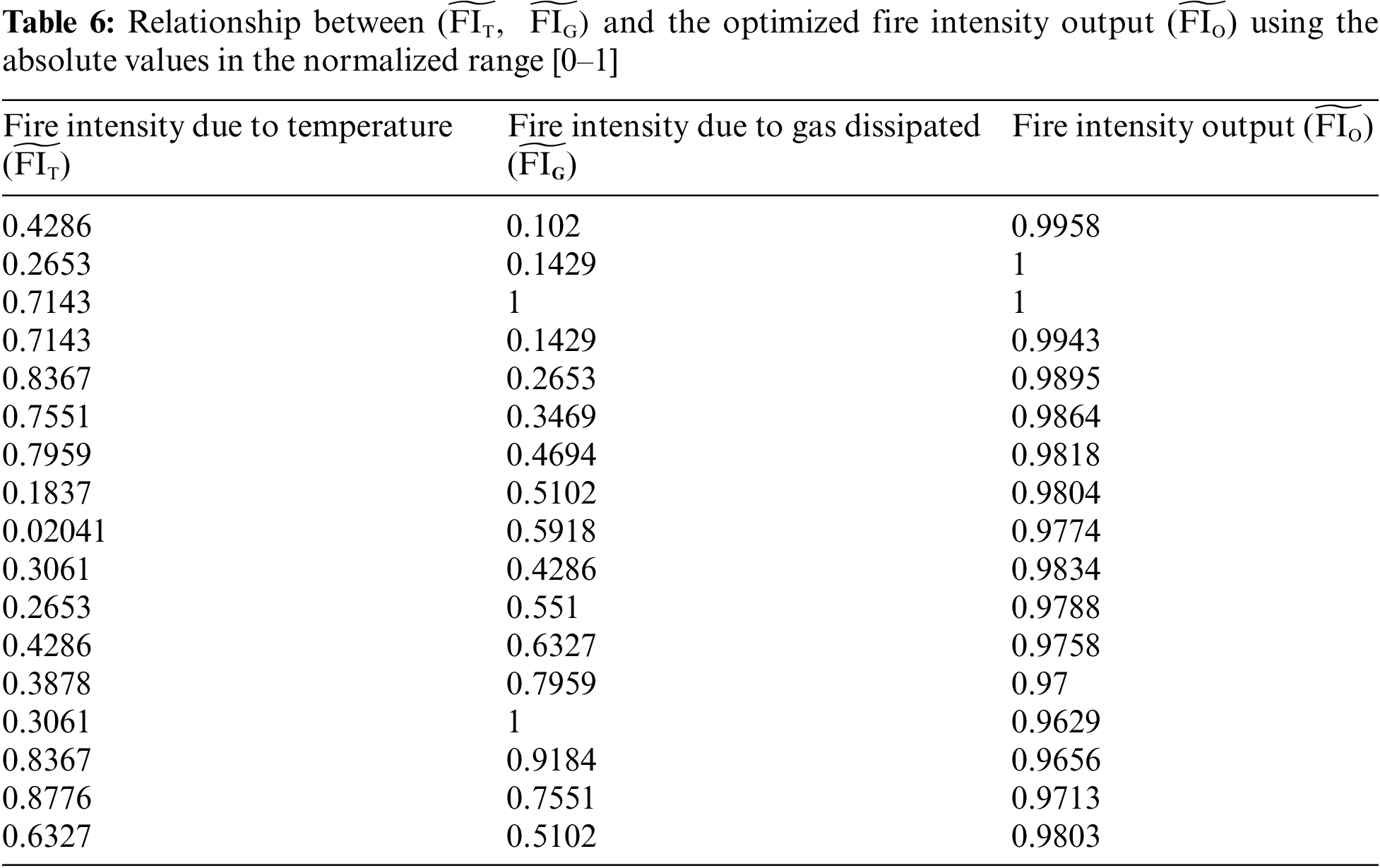
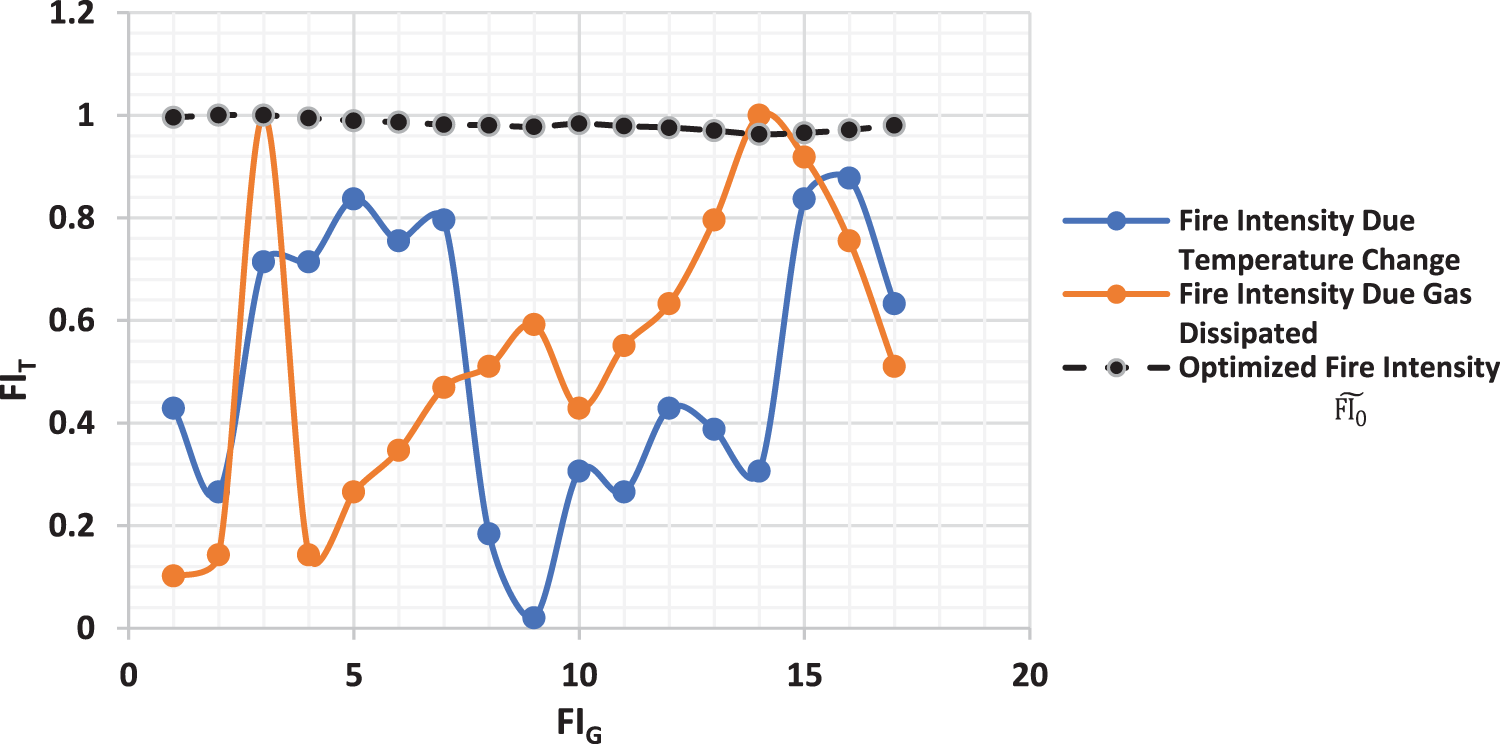
Figure 7: Evaluation of IT2 TSK fuzzy model with absolute values of FIT~, FIG~ vs. FIO~ in the normalized range of [0–1]

In Table 7 and Fig. 8, useful insights are derived by plotting EFIP1, EFIP2 against values of FIO~;

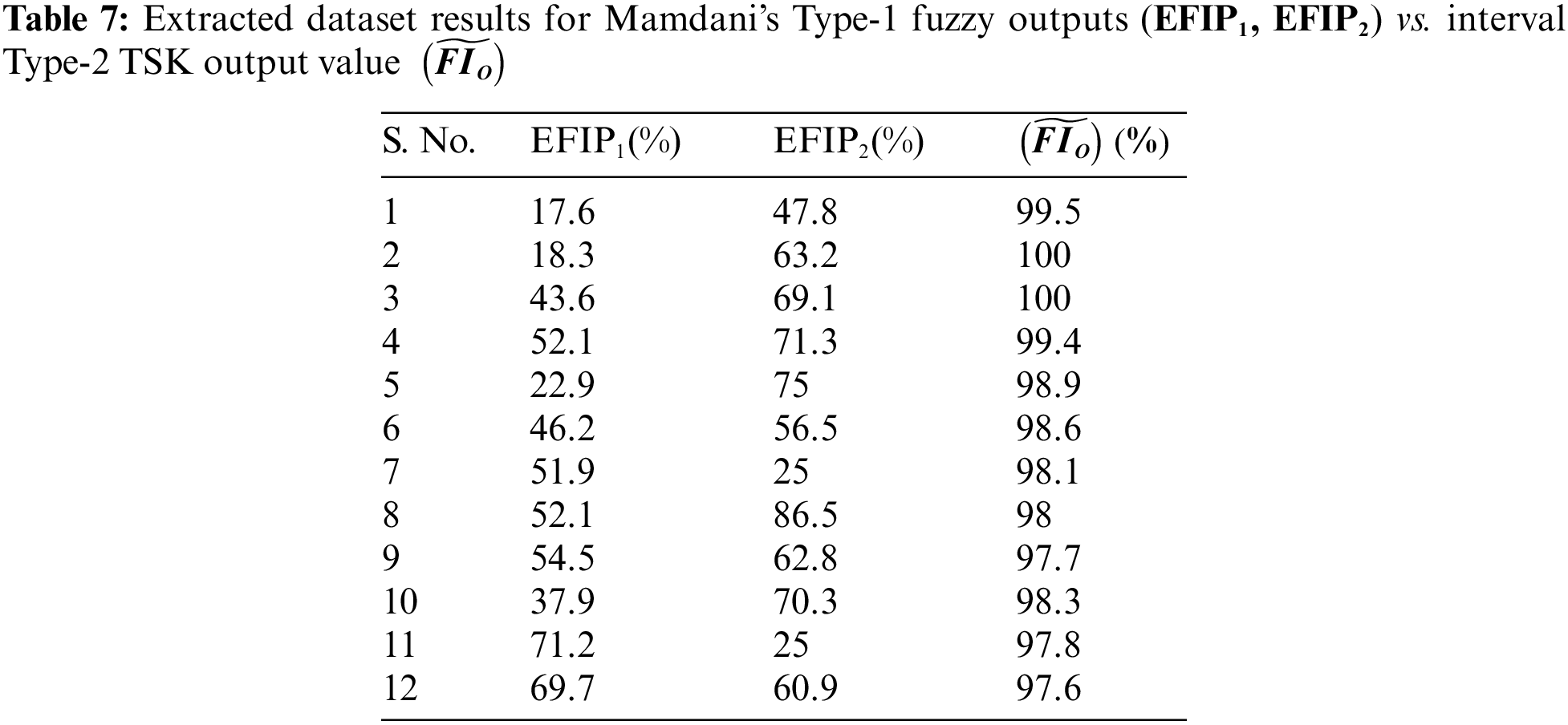
Figure 8: Mamdani’s Type-1 fuzzy models (EFIP1, EFIP2) vs. the proposed interval Type-2 TSK Output (FIO~)

Compared to the Interval Type-2 TSK output FIO~, the EFIP1 and EFIP2 in Mamdani’s Type-1 fuzzy systems yielded a lower (unstable) performance outcome. Mamdani’s TI fuzzy systems have high uncertainty error bounds despite using a dense network of fuzzy inference rules. Therefore, the Interval Type-2 fuzzy model reduced the error bounds caused by the Type-1 fuzzy systems. Thus, the performance outcome of the model was significantly improved.

Therefore, the IT2 TSK fuzzy model value of  FIO~, greatly outperformed Mamdani’s Type-1 inference models of (EFIP1) and (EFIP2) [1]. Mandani’s Type-1 systems contain associated error uncertainties leading to low operating outcomes. The datasets presented in Expt. X–Z, generally show an improved accuracy output value of the IT2 TSK model equivalent to 98.2% for N = 17 sampled fuzzy rule outcomes.

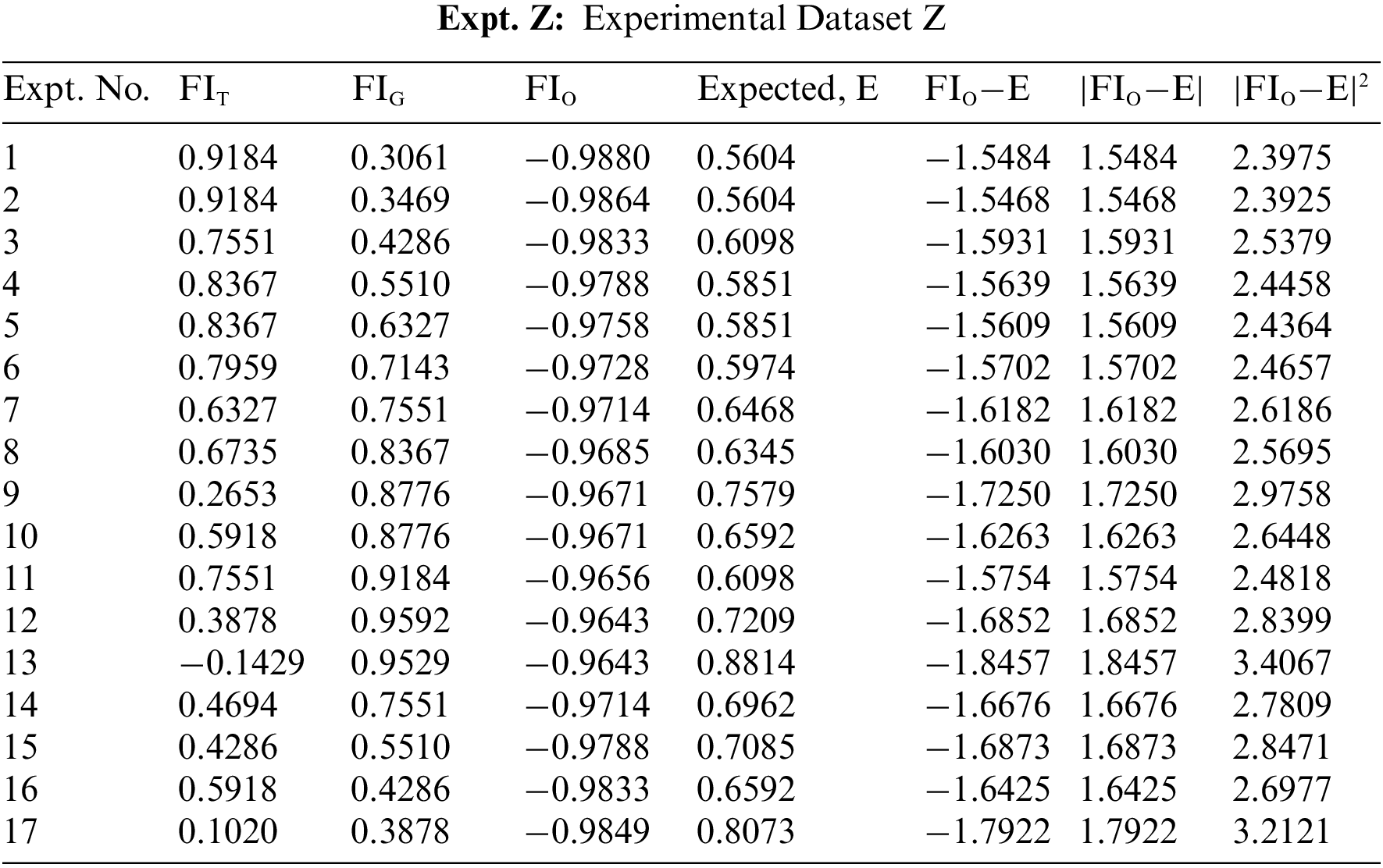
7.1 Performance Evaluation of the Proposed IT2 TSK Fuzzy Model Using Regression Analysis

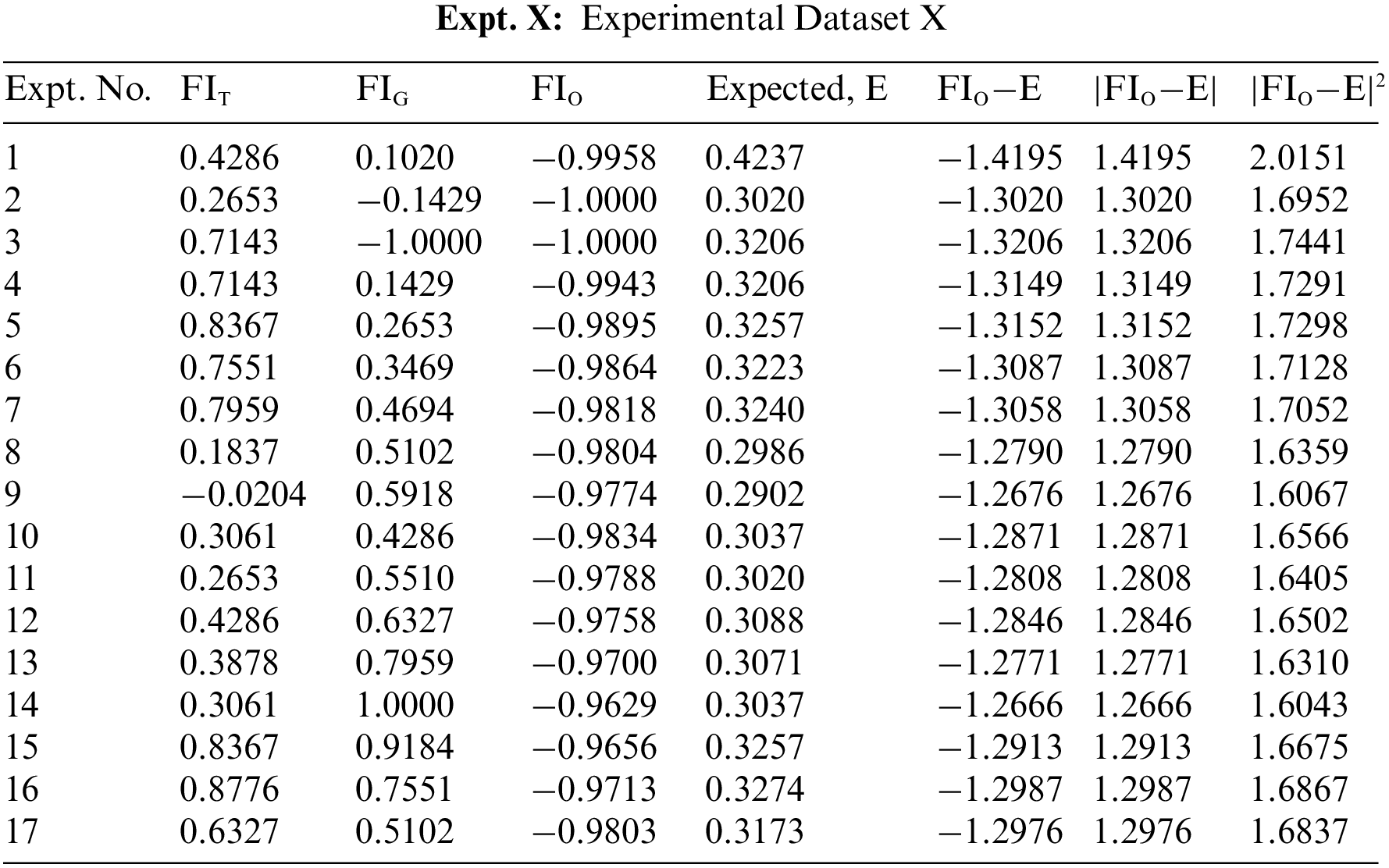
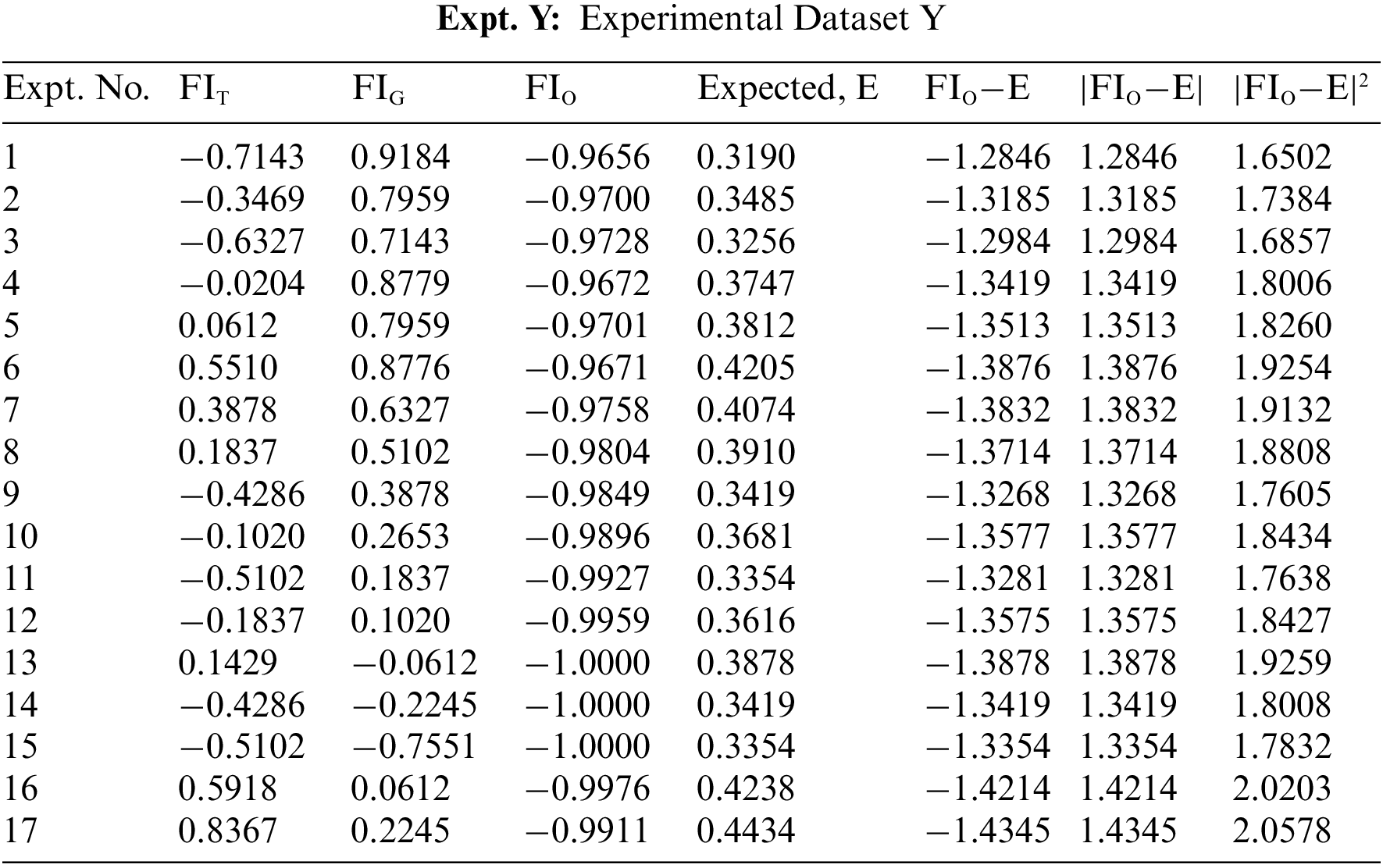
Table 8 provides a detailed summary of the statistical metric parameters, i.e., MAE, MSE, RMSE, and R2, used in the study to compare the performance outcome of each dataset for the model. Three experimental (Expt.) datasets, X, Y, and Z, are extracted from the IT2 TSK fuzzy model bound in the range of [1, −1]. With regression analysis, the best-fit dataset of the model is determined. Regression analysis is used in identifying the data with the greatest influence. A correlation is established between independent input variables of FIT~ and, FIG~, the dependent output (FIO~), the expected outcome (E). The linear regression equations are then determined for various Expt. datasets (X, Y, and Z), as; y= −0.2281x+0.5215; y= 0.0802x+0.3763; and y= −0.3025+0.8382, respectively. Error metric parameters are used to compute the error deviations of the datasets to assess the accuracy of the predictions, defined; i.e., Mean Absolute Error (MAE) = ∑|FI0−E|N; Mean Square Error (MSE) = ∑|FI0−E|N2; and Root Mean Square Error (RMSE) = ∑|FI0−E|N2 or MSE, For N = 17, sampled fuzzy-based inference rule outcomes for the proposed Interval Type-2 TSK fuzzy model.

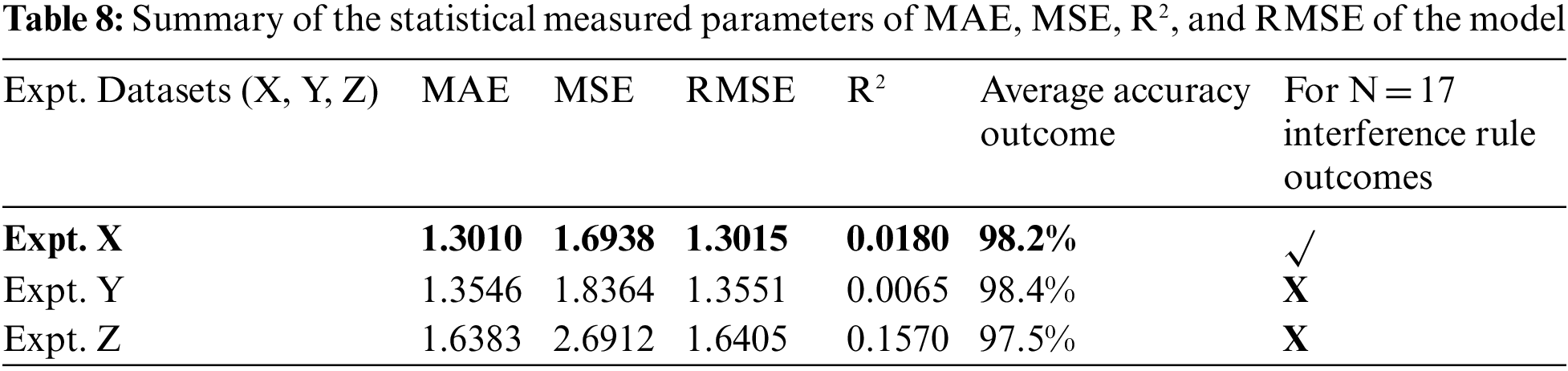
7.2 Comparison between the Previous Works Done and the Proposed Solution

Table 9 provides a detailed comparison between the related works and the proposed IT2 TSK fuzzy model.

8  Limitations

Because of the inherent uncertainty errors present in fuzzy-based systems, Interval Type-2 fuzzy systems reduce the degree of membership and change the meaning of fuzzy words, which may have a significant impact on the model’s overall decision-making and performance efficiency of the output value.

9  Conclusion and Future Works

In this paper, an Interval Type-2 TSK fuzzy model for an intelligent lightweight fire intensity detection algorithm with decision-making in low-power fire detection devices is presented. Using a multisensory design approach, the proposed method increased the model’s accuracy rate to 98.2% while minimizing false alarms in fire detection systems or devices. Besides, Interval Type-2 fuzzy systems have a footprint of uncertainty (FOU) in their fuzzy sets, allowing them to further minimize the inherent errors associated with fuzzy system designs [27]. Hence, this solution can also be implemented in low-cost, low-power fire detection systems to notify the state or level of fire danger. Thus, the study shall assist the firefighting personnel in fully monitoring, comprehending, and mitigating any level of fire danger, allowing them to make informed and appropriate decisions about the fire suppression mechanisms to be used. Future work plans to implement a hardware-based solution for a low-cost fire detection system using an Adaptive Neural Fuzzy Inference System (ANFIS), which develops more accurate models combined with computational intelligence and fuzzy logic to provide more precise learning capabilities for effective fire detection, improving fire safety monitoring and protection of the market community by leveraging early warning alerts for safe evacuations. Thus, a foundation has been laid for the development of inbuilt low-power fire detection systems that are cost-effective and easily deployable by firefighters in developing countries to protect against fire accidents in marketplaces or public gathering areas.

Acknowledgement: Special thanks to Prof. Chomora Mikeka for providing all the valuable technical information leading to the initial drafting of the article. Also, thanks to Dr. Alexander Ngenzi and Dr. Didacienne Mukanyiligira for contributing to the knowledge in drafting & conceptualization of the research article.

Funding Statement: Funding is provided by the African Center of Excellence in Internet of Things (ACEIoT), College of Science & Technology (CST), University of Rwanda.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: C. Mikeka, A. Ngenzi; data collection: E. Lule; analysis and interpretation of results: E. Lule, D. Mukanyiligira, A. Ngenzi; draft manuscript preparation: E. Lule. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: All the data concerning fire outbreaks in Uganda can be obtained in published reports of the Uganda Police Force (UPF): https://www.upf.go.ug/publications/. All simulated datasets used have been extracted from the MATLAB 2018a modeling and simulation Experiments, all included in the manuscript.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. E. Lule, C. Mikeka, A. Ngenzi and D. Mukanyiligira, “Design of an IoT-based fuzzy approximation prediction model for early fire detection to aid public safety and control in the local urban markets,” Symmetry, vol. 12, no. 9, pp. 1391, 2020. [Google Scholar]

2. Uganda Police, “Annual crime report 2019,” Uganda Crime Annual Report, 2020. [Google Scholar]

3. UPF, Uganda Police Annual Crime Report, Kampala, 2021. [Google Scholar]

4. E. Lule and T. Eddie Bulega, “A scalable wireless sensor network (WSN) based architecture for fire disaster monitoring in the developing world,” International Journal of Computer Networks and Information Security (IJCNIS), vol. 7, no. 2, pp. 40–49, 2015. [Google Scholar]

5. A. Muralidharan and S. Shakthi, “Fire detection system using fuzzy logic,” International Journal of Engineering Sciences and Research Technology (IJESRT), vol. 3, no. 4, pp. 1–4, 2014. [Google Scholar]

6. A. Labellapansa, N. Syafitri, E. Kadir, R. Saian, A. Saibah et al., “Prototype for early detection of fire hazards using fuzzy logic approach and Arduino microcontroller,” International Journal of Advanced Computer Research (IJACR), vol. 9, no. 44, pp. 276–282, 2019. [Google Scholar]

7. S. S. A. Vidya and P. Malini, “IOT based forest fire detection and early warning system using raspberry Pi and GSM,” International Journal of Future Generation Communications and Networking, vol. 13, no. 1, pp. 1430–1435, 2020. [Google Scholar]

8. V. Ruchkin, A. Kolesenkov, B. Kostrov and E. Ruchkina, “Algorithms of fire seat detection, modeling their dynamics and observation of forest fires via communication technologies,” in Proc. of Fourth Mediterranean Conf. on Embedded Computing (MECO), Budva, Montenegro, pp. 254–257, 2015. [Google Scholar]

9. S. Yan, K. Shi, Y. Li, J. Liu and H. Zhao, “Integration of satellite remote sensing data in underground coal fire detection: A case study of the Fukang region, Xinjiang, China,” Frontiers of Earth Sciences, vol. 14, no. 1, pp. 1–12, 2020. [Google Scholar]

10. K. Liolis, S. Pantazis, V. Gennatos, S. Costicoglou and I. Andrikopoulos, “An automated fire detection and alerting application based on satellite and wireless communications,” in Proc. of Fifth Advanced Satellite Multimedia Systems and the Eleventh Conf. on Signal Processing for Space Communications Workshop, Cagliari, Italy, pp. 270–277, 2010. [Google Scholar]

11. A. AA Alkhatib, “Smart and low-cost technique for forest fire detection using wireless sensor networks,” International Journal of Computer Applications, vol. 81, no. 11, pp. 12–18, 2013. [Google Scholar]

12. Q. F. Fan, T. Wang, Y. Chen and Z. F. Zhang, “Design and application of interval type-2 TSK fuzzy logic system based on QPSO algorithm,” International Journal of Fuzzy Systems, vol. 20, no. 3, pp. 835–846, 2018. [Google Scholar]

13. N. Boumella, K. Djouani and M. Boulemden, “A robust interval type-2 TSK fuzzy logic system design based on chebyshev fitting,” International Journal of Control Automation and Systems, vol. 10, no. 4, pp. 727–736, 2012. [Google Scholar]

14. M. Almaraashi, R. John, A. Hopgood and S. Ahmadi, “Learning of interval and general type-2 fuzzy logic systems using simulated annealing: Theory and practice,” Information Sciences, vol. 360, no. 2016, pp. 21–42, 2016. [Google Scholar]

15. S. Sendra, L. García, J. Lloret, I. Bosch and R. Vega-Rodríguez, “LoRaWAN network for fire monitoring in rural environments,” Electronics, vol. 9, no. 3, pp. 531, 2020. [Google Scholar]

16. P. Li and W. Zhao, “Image fire detection algorithms based on convolutional neural networks,” Case Studies in Thermal Engineering, vol. 19, no. 2020, pp. 100625, 2020. [Google Scholar]

17. A. A. P. B. Devi and N. Karna, “Design and implementation of a fire detection system using a fuzzy logic algorithm,” in Proc. of IEEE Asia Pacific Conf. on Wireless and Mobile Applications, Bali, Indonesia, pp. 99–104, 2019. [Google Scholar]

18. B. Sarwar, I. S. Bajwa, N. Jamil, S. Ramzan and N. Sarwar, “An intelligent fire warning application using IoT and an adaptive neuro-fuzzy inference system,” Sensors, vol. 19, no. 14, pp. 3150, 2019 [Google Scholar] [PubMed]

19. B. Sarwar, I. S. Bajwa, S. Ramzan, B. Ramzan and M. Kausar, “Design and application of fuzzy logic based fire monitoring and warning systems for smart buildings,” Symmetry, vol. 10, no. 11, pp. 615, 2018. [Google Scholar]

20. R. L. Z. Pacori and J. H. A. Alcantara, “Identification of internal failure in power transformers using fuzzy logic through the dissolved gas analysis in mineral insulating oil,” in Proc. of Twenty Seventh IEEE Int. Conf. Electronics, Electrical Engineering and Computing (INTERCON), Lima, Peru, pp. 20–23, 2020. [Google Scholar]

21. V. Khule, M. D. Dhagate and M. R. Kadam, “Design and implementation of a fire detection and control system for automobiles using fuzzy logic,” International Journal of Engineering Sciences and Research Technology, vol. 6, no. 4, pp. 112–119, 2017. [Google Scholar]

22. S. H. Park, D. H. Kim and S. C. Kim, “Recognition of IoT-based fire-detection system fire signal patterns applying fuzzy logic,” Heliyon, vol. 9, no. 2, pp. e12964, 2023 [Google Scholar] [PubMed]

23. T. Listyorini and R. Rahim, “A prototype fire detection implemented using the internet of things and fuzzy logic,” World Transactions on Engineering and Technology Education, vol. 16, no. 1, pp. 42–46, 2018. [Google Scholar]

24. A. A. Rafiq, E. Alimudin, A. F. Pratiwi and E. D. P. Sari, “The application of fuzzy logic to identify the room on navigation map of fire extinguisher robot,” in Proc. of Fourth EAI Int. Conf. on Vocational Education and Technology (IConVET2021), Singaraja, Bali, Indonesia, pp. 270, 2021. [Google Scholar]

25. R. K. Ikbar, E. Mulyana, R. Madiati and R. Nurmalasari, “Fire fighting robot using a flame detector and ultrasonic based on fuzzy logic control,” in Proc. of Sixteenth Int. Conf. on Telecommunication Services and Applications(TSSA), Lombok, Indonesia, pp. 1–6, 2022. [Google Scholar]

26. A. Taskin and T. Kumbasar, “An open-source matlab/simulink toolbox for interval type-2 fuzzy logic systems,” in Proc. of IEEE Symp. Series on Computational Intelligence, Cape Town, South Africa, pp. 1561–1568, 2015. [Google Scholar]

27. D. Wu and J. M. Mendel, “Recommendations on designing practical interval type-2 fuzzy systems,” Engineering Applications of Artificial Intelligence, vol. 85, pp. 182–193, 2019. [Google Scholar]

28. L. A. Zadeh, “The concept of a linguistic variable and its application to approximate reasoning-I,” Information Sciences, vol. 8, no. 3, pp. 199–249, 1975. [Google Scholar]

29. T. Djatna and A. Ginantaka, “Traceability of information routing based on fuzzy associative memory modeling in fisheries supply chain,” International Journal of Fuzzy Systems, vol. 22, no. 2, pp. 724–734, 2020. [Google Scholar]

30. A. Hailemichael, S. M. Salaken, A. Karimoddini, A. Homaifar, K. Abbas et al., “Developing a computationally effective interval type-2 TSK fuzzy logic controller,” Journal of Intelligent and Fuzzy Systems, vol. 38, no. 2, pp. 1915–1928, 2019. [Google Scholar]

31. J. M. Mendel, “Type-2 fuzzy sets and systems: A retrospective,” Informatik-Spektrum, vol. 38, no. 6, pp. 523–532, 2015. [Google Scholar]

32. S. Greenfield and F. Chiclana, “Accuracy and complexity evaluation of defuzzification strategies for the discretized interval type-2 fuzzy sets,” International Journal of Approximate. Reasoning, vol. 54, no. 8, pp. 1013–1033, 2013. [Google Scholar]

33. O. Salazar, J. D. Rojas and H. Serrano, “Nie-Tan method and its improved version: A counter example,” Ingeniería, vol. 21, no. 2, pp. 138–153, 2016. [Google Scholar]

34. P. Killeen and S. Behavior, “Introduction to type-2 fuzzy logic systems,” in Proc. of IEEE Int. Conf. on Fuzzy Systems. IEEE World Congress on Computational Intelligence, Anchroge, AK, USA, vol. 2, pp. 915–920, 1998. [Google Scholar]

35. J. Li, L. Yang, X. Fu, F. Chao and Y. Qu, “Interval type-2 TSK+ fuzzy inference system,” in Proc. of IEEE Int. Conf. on Fuzzy Systems, Rio, de Janeiro, Brazil, pp. 1–8, 2018. [Google Scholar]

36. N. Caǧman, S. Enginoǧlu and F. Citak, “Fuzzy soft set theory and its applications,” Iranian Journal of Fuzzy Systems, vol. 8, no. 3, pp. 137–147, 2011. [Google Scholar]

37. M. Suhail, I. Akhtar, S. Kirmani and M. Jameel, “Development of progressive fuzzy logic and ANFIS control for energy management of the plug-in hybrid electric vehicle,” IEEE Access, vol. 9, pp. 62219–622231, 2021. [Google Scholar]

38. I. M. Alhamad and A. M. Hamdan, “A Fuzzy-based smart HVAC controller for mosque buildings: A design procedure under Dubai climate,” in Proc. of Sixth Int. Conf. on Renewable Energy: Generation and Applications (ICREGA), Al Ain, United Arab Emirates, pp. 119–124, 2021. [Google Scholar]

39. D. Molodtsov, “Soft set theory-first results,” International Journal of Computer and Mathematics with Applications, vol. 37, pp. 19–31, 1999. [Google Scholar]

40. I. Maalej, C. Rekik, D. B. H. Abid and N. Derbel, “Interval type-2 takagi-sugeno-kang fuzzy logic approach for three-tank system modeling,” in Proc. of Twenty Third IEEE Int. Symp. on Industrial Electronics, Istanbul, Turkey, pp. 144–149, 2014. [Google Scholar]

41. C. Li, J. Yi, M. Wang and G. Zhang, “Uncertainty degree of interval type-2 fuzzy sets and its application to thermal comfort modeling,” in Proc. of Nineth Int. Conf. in Fuzzy Systems and Knowledge Discovery, (FSKD), Chongqing, China, pp. 206–210, 2012. [Google Scholar]

42. J. R. Castro, O. Castillo and P. Melin, “An interval type-2 fuzzy logic toolbox for control applications,” in Proc. IEEE Int. Conf. on Fuzzy Systems, London, UK, pp. 1–6, 2007. [Google Scholar]

43. Q. Ren, M. Balazinski and L. Baron, “High-order interval type-2 takagi-sugeno-kang fuzzy logic system and its application in acoustic emission signal modeling in turning process,” International Journal of Advanced Manufacturing Technology, vol. 63, no. 9–12, pp. 1057–1063, 2012. [Google Scholar]

44. J. Li, L. Yang, Y. Qu and G. Sexton, “An extended takagi–sugeno–kang inference system (TSK+) with fuzzy interpolation and its rule base generation,” Soft Computing, vol. 22, no. 10, pp. 3155–3170, 2018. [Google Scholar]

45. N. N. Karnik, J. M. Mendel and Q. Liang, “Type-2 fuzzy logic systems,” IEEE Transactions on Fuzzy Systems, vol. 7, no. 6, pp. 643–658, 1999. [Google Scholar]

46. J. M. Mendel, R. I. John and F. Liu, “Interval type-2 fuzzy logic systems made simple,” IEEE Transactions on Fuzzy Systems, vol. 14, no. 6, pp. 808–821, 2006. [Google Scholar]

47. D. Wu and J. M. Mendel, “Designing practical interval type-2 fuzzy logic systems made simple,” in Proc. of IEEE Int. Conf. on Fuzzy Systems, Beijing, China, pp. 800–807, 2014. [Google Scholar]

48. Y. Chen, “Study on centroid type-reduction of interval type-2 fuzzy logic systems based on noniterative algorithms,” Complexity, vol. 2019, pp. 7325053, 2019. [Google Scholar]

49. J. Li, R. John, S. Coupland and G. Kendall, “On Nie-Tan operator and type-reduction of interval type-2 fuzzy sets,” IEEE Transactions on Fuzzy Systems, vol. 26, no. 2, pp. 1036–1039, 2018. [Google Scholar]

50. Z. Ashraf, M. L. Roy, P. K. Muhuri and Q. M. D. Lohani, “Interval type-2 fuzzy logic system based similarity evaluation for image steganography,” Heliyon, vol. 6, no. 5, pp. e03771, 2020 [Google Scholar] [PubMed]

51. A. F. Zulkarnain, Y. Sari and R. Rakhmadani, “Monitoring system for early detection of fire in wetlands based Internet of Things (IoT) using fuzzy methods,” IOP Conf. Series Material Science Engineering, West Java, Indonesia, vol. 1115, no. 1, pp. 012007, 2021. [Google Scholar]

52. R. L. Z. Pacori and J. H. A. Alcantara, “Identification of internal failure in power transformers using fuzzy logic through the dissolved gas analysis in mineral insulating oil,” in Proc. IEEE 27th Int. Conf. Electronics, Electrical Engineering and Computing (INTERCON), Lima, Peru, pp. 20–23, 2020. [Google Scholar]

53. P. Li and W. Zhao, “Image fire detection algorithms based on Convolutional Neural Networks,” Case Studies Thermal Engineering, vol. 19, 2020. [Google Scholar]