Distributed Active Partial Label Learning

1  Introduction

Traditional supervised learning methods depend on collecting a sufficient number of labeled data, in order to achieve good learning results. However, in many practical applications, it is easy to obtain a massive number of unlabeled data is simple and inexpensive, but manually labeling each data sample is time-consuming and laborious [1]. To reduce the labeling effort and cost, active learning (AL), which can iteratively assign a class label to the valuable sample selected from an unlabeled data pool, has been developed [2–12]. Extensive experiments in [2–12] have shown AL can efficiently reduce the cost of label acquisition for training a high-precision model.

Most studies on AL [2–12] utilized the representativeness criterion [4] and uncertainty criterion [2,5,12] as their selection criteria. For the former one, the samples that can effectively represent the whole dataset are preferentially selected. For the latter one, the samples whose predicted class labels have the highest level of uncertainty are given preference for selection. The simulation results in [3,10] suggested that combining the two criteria in a selection strategy can achieve superior performance.

Nevertheless, most current AL methods suppose that the labels queried at AL rounds must be free of ambiguity, which may be unrealistic in many practical cases where only weakly supervised information can be accessed during the label acquisition process. To successfully exploit the weakly supervised information for predictor model induction, partial label learning (PLL), which can deal with the training data annotated with a candidate label set, has been proposed. Owing to its good performance, the PLL has received much attention and has recently risen to prominence in the area of machine learning [13–26]. It is acknowledged that the main difficulty for PLL lies in the fact that the ground-truth label is mixed into the candidate label set and cannot be directly accessible to the learning process. To extract valuable information from candidate labels and reduce the detrimental effects of false positive labels, some disambiguation strategies are employed [13–20]. Specifically, they construct a parametric model for each candidate label, and then recover the ground-truth label by optimizing a specific objective in a competitive [17,20] or collaborative manner [16,18,19]. Lately, a PLL algorithm without any disambiguation strategy has been developed to transform a PPL problem into several binary classification problems via a coding procedure, and then determine the label for unseen data based on the outputs of binary classifiers via a decoding procedure [22]. Lately, an active PLL (APLL) algorithm has been proposed based on an adaptive selection strategy [25], which induces the classifier by utilizing label propagation to recover the ground truth label from the candidate labels queried in the AL rounds. Nevertheless, the learning performance of this algorithm relies on the accuracy of label propagation. In the case that a large number of addition false positive labels are randomly mixed in the candidate label set, the negative effect of false positive labels can diffuse over the entire dataset through label propagation, which may diminish the effectiveness of the classifier.

Besides, it is important to point out that most previous AL or PLL algorithms only consider the situation of centralized processing, in which all the training data need to be centrally processed by a single fusion node. Nevertheless, in some practical applications like wireless sensor networks [27,28] and distributed computing systems [29–32], all the training data are collected/stored in a decentralized manner [26–32]. In such a case, due to the privacy protection requirement of the original data, and the limited transmission capacity of the network, centralizing all the training data into one fusion node for processing is impractical. So, jointly considering the AL, PLL, and distributed processing, developing the distributed active partial label learning (dAPLL) algorithm where all nodes in the considered network collaboratively select the valuable unlabeled data to query labels and train a PLL classifier based on the exploitation of its own partially labeled (PL) data and the information cooperation among its neighbors, is preferred.

In this paper, the issue of distributed classification of PL data selected in AL rounds over a network is addressed, and the dAPLL algorithm is proposed. The proposed algorithm is a distributed PLL algorithm with a fully decentralized sample selection strategy. A brief overview of the paper’s highlights is presented as follows:

•   A fully decentralized sample selection strategy is proposed by taking the uncertain criterion and representative criterion into account. Here, a distributed clustering method is developed to obtain several global cluster centers. Then, on the basis of the values of representativeness and uncertainty of the training data measured by these centers, the valuable samples are selected in turn at each individual node to query the labels.

•   A distributed PLL algorithm is proposed based on a coding-decoding procedure. Using the disambiguation-free strategy, several binary classification problems are constructed. Besides, in order to deal with the issue of imbalanced class distribution in multiple binary classification problems, the cost-sensitive loss function is employed. Then, the random feature map is exploited to construct the model parameter, so that the global estimation of the model parameter can be performed in a decentralized manner without sharing any original data with other nodes.

The remaining parts of this paper are structured as follows. In Section 2, to offer preliminary knowledge, some typical related works on PLL, AL and distributed processing are briefly reviewed. In Section 3, the details of the dAPLL algorithm are presented. In Section 4, we conduct numerical simulations to demonstrate the effectiveness of the proposed algorithms. In Section 5, we draw some conclusions and plan for future work.

2  Related Works

In this section, some typical related works about AL, PLL and distributed processing are briefly reviewed.

To the best of our knowledge, the problem of fully decentralized AL has not been addressed. So, here, we only introduce several centralized AL methods [2,3,6] and distributed-like AL methods [7,9,10,11]. In recent years, several centralized AL methods have been proposed [2,3,6], including single-mode AL methods [3,6] and batch-mode methods [2]. In these methods, both the uncertainty sampling and representative sampling criteria are considered, and then the labels of several selected samples are queried at each AL round. In the literature [7,9,11], several distributed-like AL methods have been developed for image recognition or automatic hyper-parameter selection. Here, there exists a powerful fusion center in the network to centrally select the valuable sample from dispersedly stored unlabeled data to query its label. The slave nodes can only independently utilize the computation capacity to measure the importance of their own local data samples, but cannot exchange any information with each other. Besides, another distributed-like AL method was proposed [10]. In this algorithm, all the unlabeled training data are randomly distributed at multiple nodes. In each AL round, each node independently selects the most valuable data from its own local dataset, and then adopts the diffusion cooperative strategy to collaboratively train the multi-class classifier. In other words, there is no information cooperation among the neighbors in the sample selection process. So, these distributed AL methods are not yet fully decentralized. Besides, it is worth pointing out that the aforementioned approaches cannot be directly used to handle the PL data. Lately, a centralized PLL algorithm has been proposed based on the AL mechanism [25]. In this APLL algorithm, the most important data can be chosen to be annotated with a set of candidate labels based on the combination of multiple measures, and then the classifiers can be learned by using label propagation to resolve the ambiguities of the candidate labels. But, as mentioned above, the effectiveness of this method is limited by the poor accuracy of label propagation.

Generally speaking, in most PLL algorithms, there exist two main distinct categories of disambiguation strategies to learn the ground-truth label, i.e., identification-based disambiguation [17,20] and average-based disambiguation [16,18]. The former strategy assumes the ground-truth label is a hidden variable, and disambiguates the candidate labels based on an iterative optimization procedure [17,20]. The latter strategy considers the candidate labels to be of equal importance, and recovers the ground truth label by differentiating the output results obtained from each candidate label [16,18]. Besides, lately, a PLL algorithm without any disambiguation strategy has been proposed in [22]. By employing an error-correcting output code (ECOC), several binary training datasets can be generated. Then, several binary classifiers are trained, and the true label of the testing data can be determined by the decoding of the output of the binary classifiers. Nevertheless, these PLL methods require that all the PL data must be gathered together in one node, which is unavailable for a distributed network. Also, the difficulty of label acquisition cannot be taken into consideration. Lately, a distributed PLL algorithm has been proposed using semi-supervised learning [26], in which an average-based disambiguation method is developed to exploit the information of both PL and unlabeled data. But, according to the analysis presented in [26], due to the common failing of average-based disambiguation methods, this method may be inefficient in the case that false positive labels co-occur with the ground-truth label.

Recently, owing to the rapid growth of wireless sensor networks [27,28] and distributed computing systems [29–32], distributed processing has attracted much research attention. A large number of distributed learning algorithms have been proposed, which cover a wide range of problems in signal processing [27,28] and machine learning [29,30,32]. However, most of the existing distributed algorithms belong to supervised learning, which requires a substantial quantity of precisely and unambiguously labeled data for good learning performance. Thus, these approaches are impractical in the case that there exist only a few precisely labeled data.

3  Distributed APLL Algorithm

In this part, the issue of distributed classification of PL data selected in AL rounds is first formulated in Section 3.1. Then, a fully decentralized sample selection strategy is developed in Section 3.2 and a distributed PLL algorithm is proposed in Section 3.3. The computational complexity of the proposed algorithm is analyzed in Section 3.4.

3.1 Problem Formulation

Here, we focus on the problem of APLL over a connected network with J nodes distributed over a geographic region. We represent this network as a connected graph G(J,E) with a set of nodes J and a set of edges E. For each node j∈J, let the neighbor set be Bj={i|(j,i)∈E}, which contains all of its one-hop neighbors and itself.

At initial state, each node j in this network is allowed to access only a small amount of labeled data denoted by XjL={(xj,n,sj,n)|1≤j≤J} and Nj unlabeled data denoted by XjU={xj,n|1≤j≤J}, where xj,n∈Rd denotes the attributes of the data, and sj,n denotes the set of candidate labels. Let {Y=1,2,…,K} denote the output space with K class labels, and the candidate label set sj,n⊆Y. Then, at each iteration, since the number of labeled data is too small to train a classifier with high precision, each node j first adopts a fully decentralized sample selection strategy to annotate the most valuable sample from XjU with a series of candidate labels. Correspondingly, the labeled training dataset XjL is expanded with the new selected data. After that, each node j trains the multi-class classifier based on its new local dataset and the local estimates of the model parameters exchanged with its neighboring nodes. These two update steps are alternatively iterated until convergence.

3.2 Fully Decentralized Sample Selection Strategy

In the distributed network, all the training data are randomly distributed at multiple nodes. To avoid the disclosure of data privacy, each node is only able to access its own data, but not exchange the private original data with other nodes. Considering this, it is preferable to develop a fully decentralized sample selection strategy, in which the most valuable unlabeled data can be automatically selected to query its label at each individual node without sharing the original data among neighbors. The details of the decentralized sample selection strategy are presented in this subsection.

The core concept of representativeness is to preferentially choose the data samples that can accurately represent the whole dataset. Assuming that the distribution of the data samples is not excessively dispersed, it is intuitive that the data sample near the cluster center can be considered a highly representative sample. To be specific, the whole unlabeled training data are clustered into C classes at first, and the Euclidean distance between the training data and its nearest cluster center is exploited to measure the representativeness. Considering that the data are distributed over a network, a distributed clustering method is proposed to estimate the locations of the cluster centers. The main steps are summarized in Algorithm 1.

Here, to perform the distributed cluster algorithm, each node j clusters the training data into the nearest partition, and obtains the corresponding partition count. Then, each node j exchanges its cluster centers and partition counts with its one-hop neighbors, and updates the locations of the cluster centers based on the new exchanged information. Although direct information fusion is constrained within neighboring nodes, each node can also access information shared by other nodes in a connected network after sufficient cooperation. Finally, the locations of C cluster centers {cm}m=1C at different nodes reach a consensus.

Then, the Representativeness (Rep) of data samples can be quantified by the distance between the local data sample xj,n and its closest cluster center c1, i.e.,

Rep(xj,n)=||xj,n−c1||22.(1)

So, the sample with a small Rep value can be regarded as a good representative sample of the cluster.

Meanwhile, the core principle of uncertain selection is to choose the samples with the greatest uncertainty first. Here, the First best vs. Second best (FS) is adopted to measure the degree of uncertainty,

FS(xj,n)=y^j,n1−y^j,n2,(2)

where y^j,n1 and y^j,n2 denote the highest and second highest values of the predicted soft label of xj,n.

The FS value is used to measure the difference between the two highest values of the predicted soft labels. A small value of FS indicates that the predicted soft labels of the two most possible classes are very close to each other for the current classifier. Exploiting the supervised information from this data sample can provide more valuable information to the classifier.

Hence, how to obtain the predicted soft labels of the unlabeled data becomes an important issue. The weighted voting method is an easy and typical method to solve this problem. Specifically, the predicted soft labels of each unlabeled data are determined by the cluster centers obtained in the distributed clustering, which can be expressed as

y^j,nk=1C∑m=1Cωj,mnyc,mk,k=1,…,K,(3)

where ωj,mn denotes the similarity between the cluster center cm and the local unlabeled data xj,n, and it is usually calculated by the Gaussian kernel function. Besides, yc,mk denotes the k-th label of the cluster center cm.

Nevertheless, according to the basic settings of distributed clustering, each node j can access the attributes of the cluster centers, but cannot obtain the labels. So, before calculating the predicted soft labels of the unlabeled training data via (3), the global consistent estimates of soft labels of the cluster centers should be obtained. To achieve this, a distributed estimation algorithm is developed.

Here, a small loop with in each AL round indexed by τ2 is set. In the initial state of the small loop, each node j estimates the soft labels of the cluster centers based on its local labeled dataset. Then, each node j updates the estimates of {y^c,mk}m=1C by fusing its local estimates with those of its one-hop neighbors. The combination cooperative coefficient vji is usually designed based on the Metropolis rule [26,31]. The theoretical analysis given in [33] proved that in a connected network, the difference among the local estimates can rapidly converge to zero after a predetermined number of iterations. The maximum number of small loop executions can be limited to a fixed number T2. Exceeding this number, the final predicted soft labels and the FS value of each unlabeled data can be computed via (3) and (2).

For clarity, the essential steps of the uncertainty evaluation are summarized in Algorithm 2.

Next, a score is defined to combine these two measures, which is given by

Score(xj,n)=−γRep(xj,n)−FS(xj,n),(4)

where γ∈[0,1] is a weight coefficient to make a trade-off between uncertainty and representativeness. A higher score implies that the unlabeled data is more valuable.

3.3 Distributed Partial Label Learning Algorithm

To train a multi-class classifier with high accuracy under the supervision of PL data, a binary decomposition based on ECOC is employed [22]. In the coding procedure, a K×Pcoding matrix M∈{+1,−1}K×P is constructed. Here, each row of the coding matrix M(k,:)represents a P element codeword for each class label. Each column of the coding matrix M(:,p) represents one binary classification dataset, which can divide the label space into two disjoint classes. Specifically, if the candidate label set of a PL data sample entirely falls into a dichotomy, then this sample can be transformed into a binary classification sample, i.e.,

yp+={yk|M(k,p)=+1,1≤k≤K},yp−={yk|M(k,p)=−1,1≤k≤K}.(5)

For clarity, an illustrative example of ECOC coding is shown in Fig. 1.

Figure 1: The illustrative example of ECOC coding

Based on ECOC, the PL dataset is split up into P different binary classification datasets. Then, the distributed classification method is exploited to train P binary classifiers, so that the training samples can be classified into the corresponding binary classes.

Assuming that the discriminant functions of P binary classifiers are non-linear, we have

fp=wpTϕ(x),p=1,…,P,(6)

where ϕ is an unknown non-linear kernel map. Besides, the model parameter wp is usually calculated by the combination of the kernel map ϕ(xn) and the weight coefficient apn, i.e., wp=∑napnϕ(xn).

Based on the above settings, the global optimization problem can be formulated as follows:

minwpF=∑p=1P∑n=1Npδpn||ypn−fpn||22,(7)

where ypn stands for the labels of xn obtained via ECOC, fpn denotes the p-th output of the discriminant function of xn, and Np denotes the size of the training dataset that belongs to the p-th class. Besides, to deal with the issue of an imbalanced distribution of positive and negative samples for the binary classification problem, we design the penalty scalar δpn to be cost-sensitive.

The decentralization of the global optimization problem can be performed as follows:

minwj,p⁡F=∑j=1J⁡Fj=∑j=1J⁡(∑p=1P⁡∑n=1Nj,p⁡δj,pn||yj,pn−fj,pn||22),s.t.wj,p=wi,p,p=1,…,P,j∈J,i∈Bj,(8)

where wj,p denotes the local estimate of the model parameter wp.

To solve this decentralized optimization problem, we set a small loop within each AL round indexed by τ3, and set the maximum iteration of the small loop as T3. Here, we would like to use the descent gradient method together with the diffusion cooperation strategy [27,28] to obtain the optimal solution. To be specific, we reconstruct the objective function as a combination of the local cost function Fj and the difference between the local estimates wj,p at the node j and the instantaneous estimates wi,p′ exchanged from the node i, i.e.,

minwj,pF=∑j=1JFj+∑i∈Bjzji||wj,p−wi,p′||22,(9)

where the combination coefficient ∑i∈Bjzji=1, zji=0 if i∉Bj.

To obtain the global optimal solution, the gradient descent method is utilized to optimize the objective function, which is given by

wj,p(τ3+1)=wj,p(τ3)−μ(τ3)∇wj,pFj(τ3)−ξ∑i∈Bj∖jzji(wj,p(τ3)−wi,p′),(10)

where μ(τ3) denotes a time-varying step size, and ξ denotes a positive constant. By introducing the instantaneous variable wj,p′(τ3+1), the above equation can be rewritten as

wj,p′(τ3+1)=wj,p(τ3)−μ(τ3)∇wj,pFj(τ3),(11a)

wj,p(τ3+1)=wj,p′(τ3+1)−ξ∑i∈Bj∖jzji(wj,p(τ3)−wi,p′).(11b)

We can find that after the update in (11a), wj,p′(τ3+1) becomes the latest estimate for the model parameter. So, we would like to use wj,p′(τ3+1) to replace the wj,p(τ3) in (11b). In addition,wi,p′ also can be replaced by wi,p′(τ3+1). Then, we have

wj,p(τ3+1)=wj,p′(τ3+1)−ξ∑i∈Bj∖jzji(wj,p′(τ3+1)−wi,p′(τ3+1))=(1−ξ∑i∈Bj∖j⁡zji)wj,p′(τ3+1)+ξ∑i∈Bj∖j⁡zjiwi,p′(τ3+1)=∑i∈Bjvjiwi,p′(τ3+1),(12)

where vji=ξzji and vjj=1−ξ∑i∈Bj∖jzji for i∈Bj.

Here, the gradients ∇wj,pFj(τ3) can be computed by ∇wj,pFj(τ3)=∑nδj,pn(yj,pn−fj,pn(τ3))⋅ϕ(xj,n).

From (12), it is noticed that the fundamental step in the distributed classification method is the exchange and combination of weight vectors {wj,p}p=1P. However, in the non-linear classification, the gradient ∇wj,pFj(τ3) is a linear combination of a series of kernel feature maps. Since the non-linear kernel feature map is unknown, ∇wj,pFj(τ3) cannot be explicitly expressed.

To solve this problem, a finite-dimensional random feature map is exploited to replacethe infinite-dimensional kernel feature map for the construction of the kernel function, i.e., k(xk,xn)≈<ϕ^(xk),ϕ^(xn)>. Specifically, the random feature map of the considered Gaussian kernel can be explicitly expressed as a D dimensional vector, which is given by [32]

[ϕ^(xn)]l={1Dcos⁡(θl+12Txn),0<l<D, odd,1Dsin⁡(θl2Txn),0<l<D, even,(13)

where θl is obtained by randomly sampling the probability distribution [34,35].

Using the random feature map, the gradient ∇wj,pFj(τ3) can be computed by

∇wj,pFj(τ3)=∑nδj,pn(yj,pn−fj,pn(τ3))ϕ^(xj,n).(14)

Correspondingly, an explicit expression for wj,p can be obtained, i.e., wj,p=∑naj,pnϕ^(xj,n).

By alternatively updating two equations in (11a) and (12), the P binary classifiers can be trained in a global sense. In the decoding procedure, given a testing sample x∗, the signed outputs of the P binary classifiers can be obtained, and then a P×1 output vector ψp(x∗) is constructed by stacking the P outputs one by one. Finally, the predicted label of x∗ can be determined by the codeword closest to the output vector, i.e.,

h(x∗)=arg⁡minyk(1≤k≤K)dist(ψP(x∗),M(k,:)).(15)

For clarity, the main steps of the proposed distributed PLL algorithm are summarized in Algorithm 3.

Combining the fully decentralized sample selection strategy and the dPLL algorithm, the dAPLL algorithm is obtained. The procedures of these two parts are respectively shown in Figs. 2 and 3, and the main steps are summarized as follows:

Figure 2: The produce diagram of the fully decentralized sample selection strategy

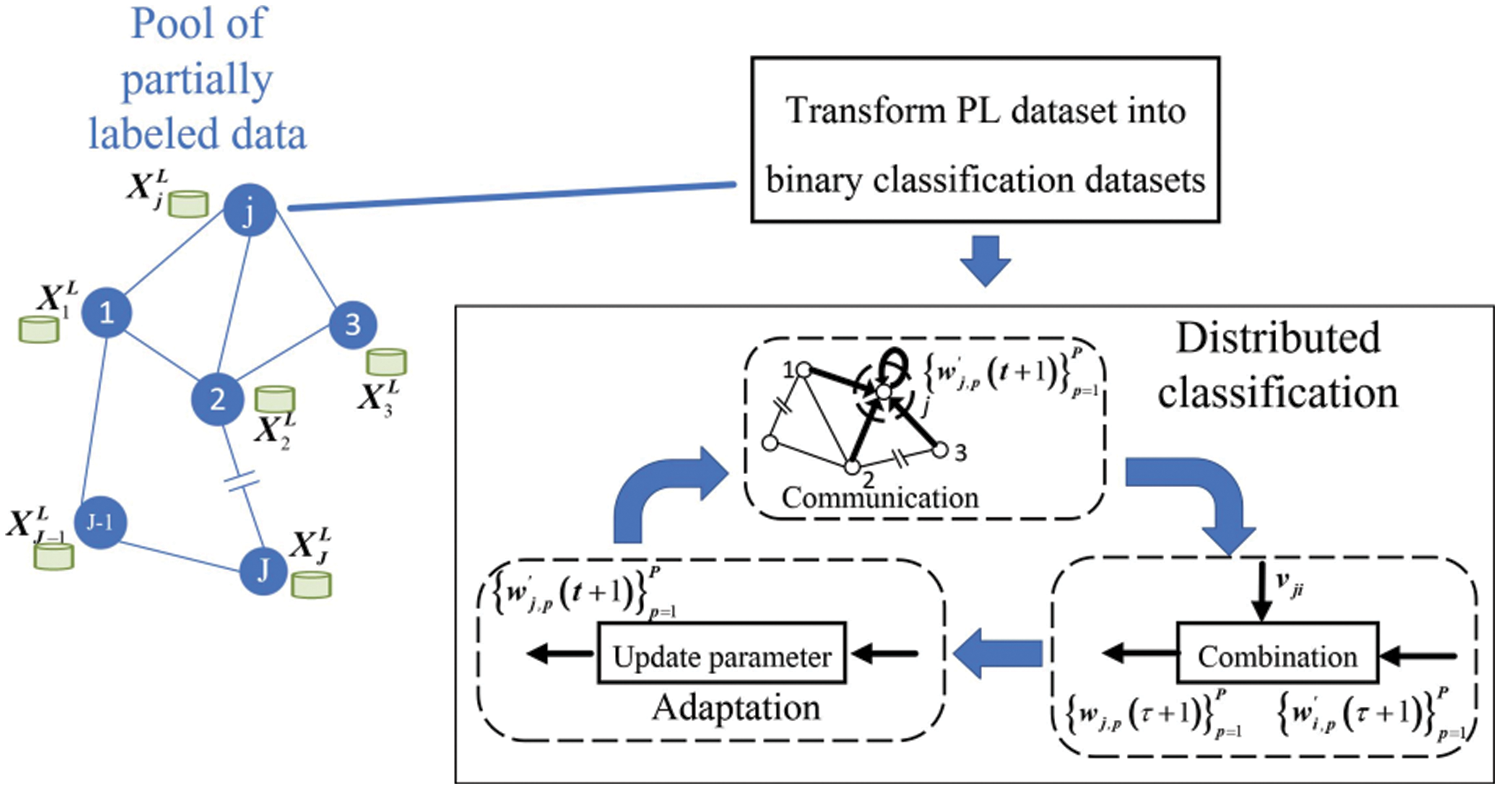
Figure 3: The produce diagram of dPLL algorithm

1.    Fully decentralized sample selection strategy: At initial state, each node j cooperatively clusters its local data into C partitions, and calculates the Rep value for each unlabeled data sample. Under the sample selection strategy, in each AL round, each node j first performs the global prediction for the class labels of the cluster centers, and then obtains the FS value of each unlabeled data via weighted voting. Finally, for each node j, the sample with the highest score combined by Rep and FS values is selected to be partially labeled.

2.    dPLL algorithm: At each AL round, for each node j, the selected PL dataset is transformed into P binary classification datasets via a coding procedure, and then P binary cost-sensitive classification problems can be constructed. By using the descent gradient method together with the diffusion cooperative strategy, the model parameters of the P binary classifiers can be collaboratively estimated. Given the testing data, the true label can be determined through the decoding of the signed outputs of P binary classifiers.

3.4 Computational Complexity Analysis

Next, the computational complexity of the proposed algorithm with respect to the number of multiplication and addition operations is analyzed. At each AL round, for each node j, the complexities of the selection of the valuable sample for manual labeling and the training of the classifier are summarized in Table 1. According to our analysis in Table 1, when the number of clustering centers, the set cardinality |Bj|, the maximum iteration of the small loop T2 are controlled into a suitable region, the computation complexity is only related to the number of classes and the total number of labeled and unlabeled data used for training. Besides, in the distributed PLL algorithm, its computation complexity depends on the number of training data for each binary classification problem, if the dimension of the random feature map, the number of binary classifiers and the maximum iteration of the small loop T3 remain invariant. So, the computation complexity of the dAPLL algorithm is moderate, provided that the size of the training data set is not too large.

4  Experiments

To test the effectiveness of the dAPLL algorithm, numeral simulations on both artificially generated and real-world PL datasets are performed. All the simulations are run on the same computer using MATLAB 2018a. This computer has a four-core (2.20-GHz) CPU, 16.0-GB RAM, and the Windows 10 operation system.

In this experiment, we run 50 separate Monte Carlo cross-validation simulations, and report on the average results. During each Monte Carlo simulation, all the used datasets are randomly split into 10 equal-size folds, where 8 folds are supposed to be unlabeled for manual labeling during the training process and the remaining 2 are used for testing. Here, we simulate distributed cases by distributing all the unlabeled training data over different nodes in a randomly generated connected network composed of 10 nodes and 23 edges [32]. To generate artificial PL datasets, three common controlling parameters in PLL, q, r and ε are chosen to control the artificially generated multi-class datasets under different configurations [22]. To be specific, q denotes the proportion of the labeled data samples selected in AL rounds that are partially labeled, r denotes the amount of additional false positive labels that are included in the candidate label set for each PL data, and ε denotes the probability with which a specific noisy label and the ground-truth label occur together. Besides, to investigate the performance of different algorithms with varying numbers of labeled data, we define the Ratio of Labeled data gained by Manual labeling compared to Total amount of training data collected over a network (RLMT).

4.1 Classification of the “Double-Moon” Dataset

In this experiment, 4000 data samples with zero-mean Gaussian white noise (signal-to-noise ratio equals to 20 dB) are generated. Then, the number of label classes is set as 4, and a certain number of false positive candidate labels are assigned to partial training data, so that the PL dataset can be obtained under a specific configuration [26].

At each trail of this experiment, we choose 3500 unlabeled data as training data, and then use the remaining 500 data as testing data. Besides, the weighting coefficient γ, the number of binary classifiers P, the number of labeled data |XjL| at initial state, the number of clusters C, the step size μ(τ3) and the dimension D are set to be 0.4, 6, 2, 10, 0.5/τ30.8 and 150, respectively. Moreover, the maximum numbers of three small loops T1,T2 and T3 are set as 20, 10 and 20.

The effectiveness of the dAPLL algorithm in classifying data samples is investigated using different configurations. To show the superiority of our proposed dAPLL algorithm, the simulation results of other comparison algorithms are also presented. (1) dAPLL random: During each AL round, each node selects the unlabeled data at random to query its label. (2) non-cooperation APLL (ncAPLL): Each node selects the most valuable data from its own local dataset independently in each AL round, and then trains the multi-class classifier without transmitting any information among nodes. (3) centralized APLL (cAPLL): A single fusion node is responsible to centrally select J valuable data to query the labels in each AL round.

The classification accuracies of four comparison algorithms with varying numbers of AL rounds are illustrated in Fig. 4. It is plain to see that the performances of different algorithms improve as the number of AL rounds increases. The performance of the proposed dAPLL algorithm is quite comparable to that of the cAPLL algorithm, and both of these algorithms show vast performance improvements over the ncAPLL algorithm, indicating the effectiveness of the distributed processing. Besides, it is easy to notice that the dAPLL algorithm outperforms the dAPLL random algorithm. So, the proposed selection strategy has the potential to effectively reduce the amount of labeled data required to train a classifier with a high level of accuracy.

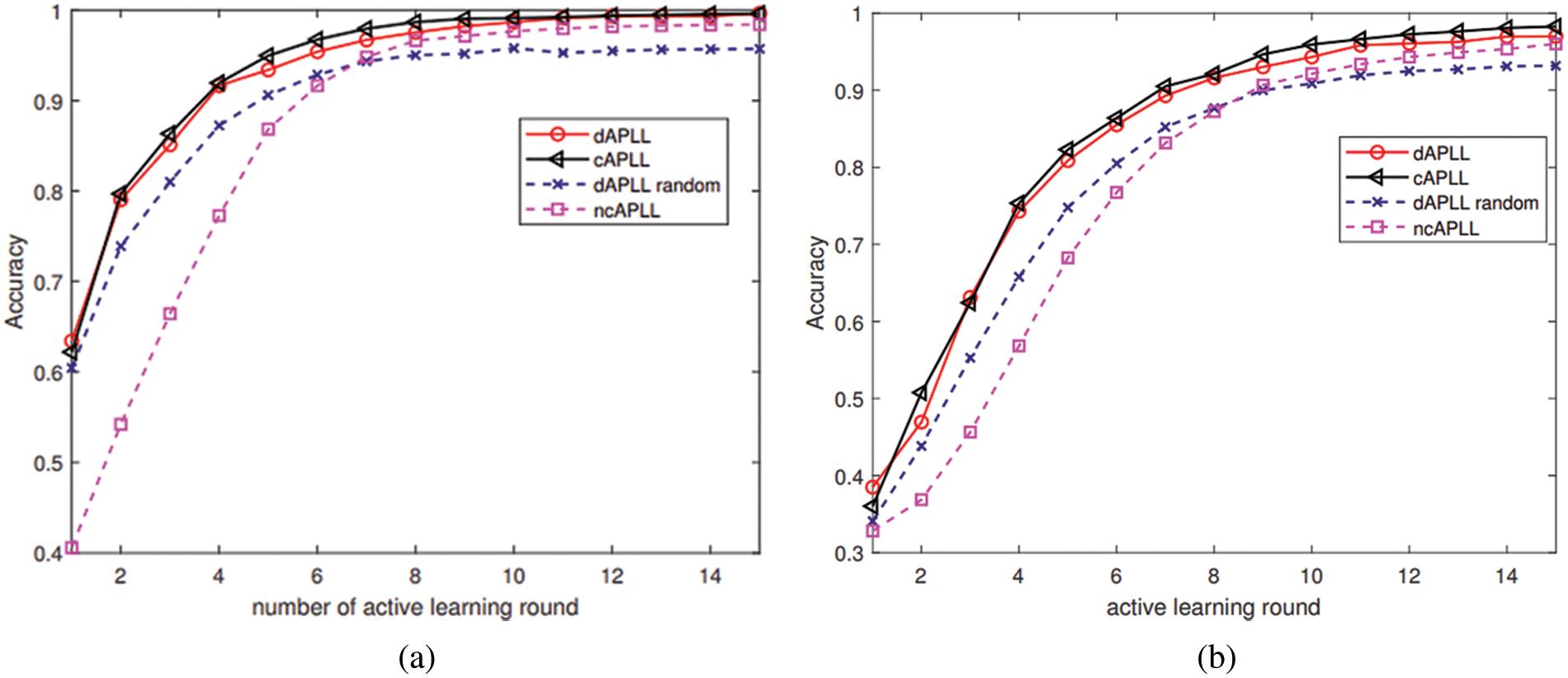
Figure 4: Learning performance of four comparison algorithms vs. AL rounds with different configurations on the “Double-Moon” dataset. (a) Simulation results with q=0.4 and r=1. (b) Simulation results with ε=0.3, q=1 and r=1

Two 3D-plots are depicted to investigate the classification accuracy of the proposed algorithm against the number of AL rounds and the values of q or ε. The simulation results in Fig. 5 show that the classification accuracy of the proposed algorithm improves with the number of AL rounds. The value of q can significantly affect the classification accuracy of the dAPLL algorithm. As q gradually increases, the classification accuracy of the dAPLL rapidly decreases. In addition, the classification accuracy is insensitive to the value of ε, indicating that a small proportion of co-occurring false positive labels does not greatly affect the learning performance.

Figure 5: Learning performance of the dAPLL algorithm vs. different control parameters on the “Double-Moon” dataset. (a) Simulation results vs. AL rounds and q (with r=1). (b) Simulation results vs. AL rounds and ε (with q=1 and r=1)

The impact of the dimension D and the number of binary classifiers P on the learning performance of the dAPLL algorithm is investigated in Fig. 6. According to the simulation results, it is recommended that the appropriate values of D and P should be set to 150 and 6, respectively.

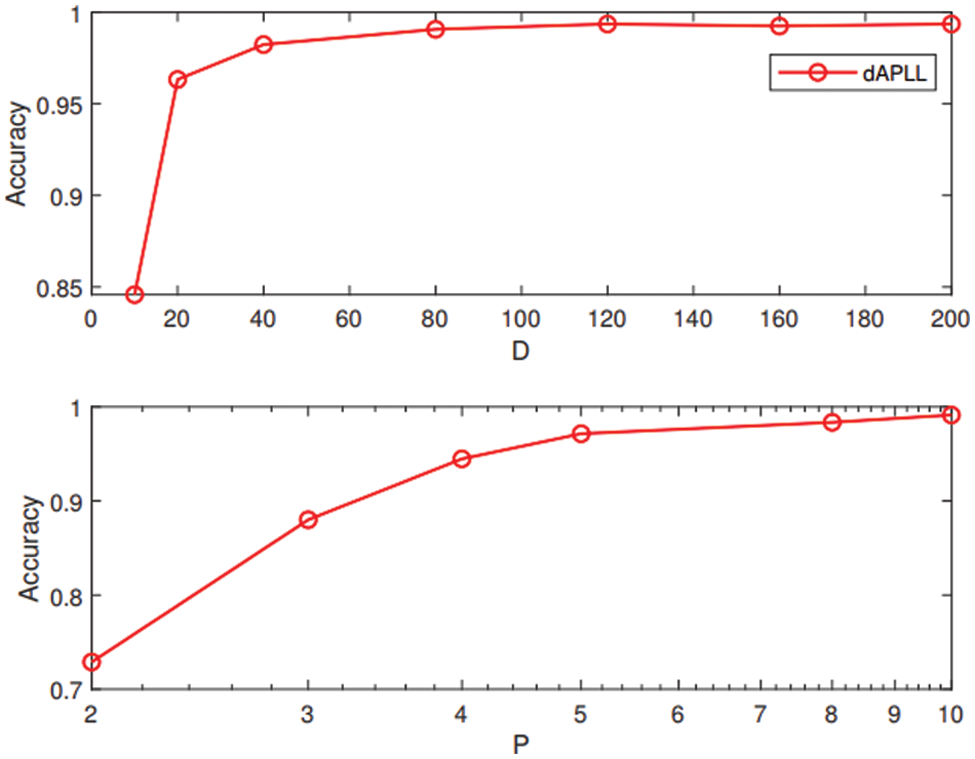
Figure 6: Learning performance of the dAPLL algorithm vs. dimension of random feature map D and number of binary classifier P on the “Double-Moon” dataset

4.2 Classification of the “Vertebral Column” Dataset

In this experiment, a collaborative classification of vertebral column data is considered [36]. Here, a total of 310 vertebral column data for patients are collected by medical institutions. Each data sample captures six different biomechanical characteristics that are derived from the structure of the lumbar spine and pelvis. Our target is to analyze the condition of the vertebral column, and classify these data into three classes: normal, disk hernia and spondylolisthesis. But, since the diagnosis of disease requires much professional knowledge, it is difficult to assign a precise label to each data item. So, it is preferable to utilize the dAPLL to train a high-precision multi-class classifier based on only a few PL data.

Here, we set the number of training data and testing data as 250 and 60, respectively. The other settings remain the same as those set in the previous experiment.

The learning curves of four comparison algorithms with varying numbers of AL rounds on the vertebral column dataset are given in Fig. 7. The classification accuracy of different algorithms significantly increases as the number of AL rounds increases. There is a very small difference in classification accuracy between the proposed dAPLL algorithm and the cAPLL algorithm, and both of them are superior to ncAPLL and dAPLL random, indicating the effectiveness of the proposed algorithm.

Figure 7: Learning performance of four comparison algorithms vs. AL rounds with different configurations on the “Vertebral Column” dataset. (a) Simulation results with q=0.4 and r=1.(b) Simulation results with ε=0.3, q=1 and r=1

The learning performance of dAPLL algorithm with varying numbers of AL rounds and different values of q are also tested. By observing the simulation results shown in Fig. 8a, we are able to notice that as the AL round increases, more and more supervised information is exploited from PL data, and thus the learning performance of the proposed algorithm gradually improves. Besides, as the probability of PL data in the labeled data pool q increases, the classification accuracy of the dAPLL rapidly decreases, indicating that the false positive labels have a significant effect on the learning performance.

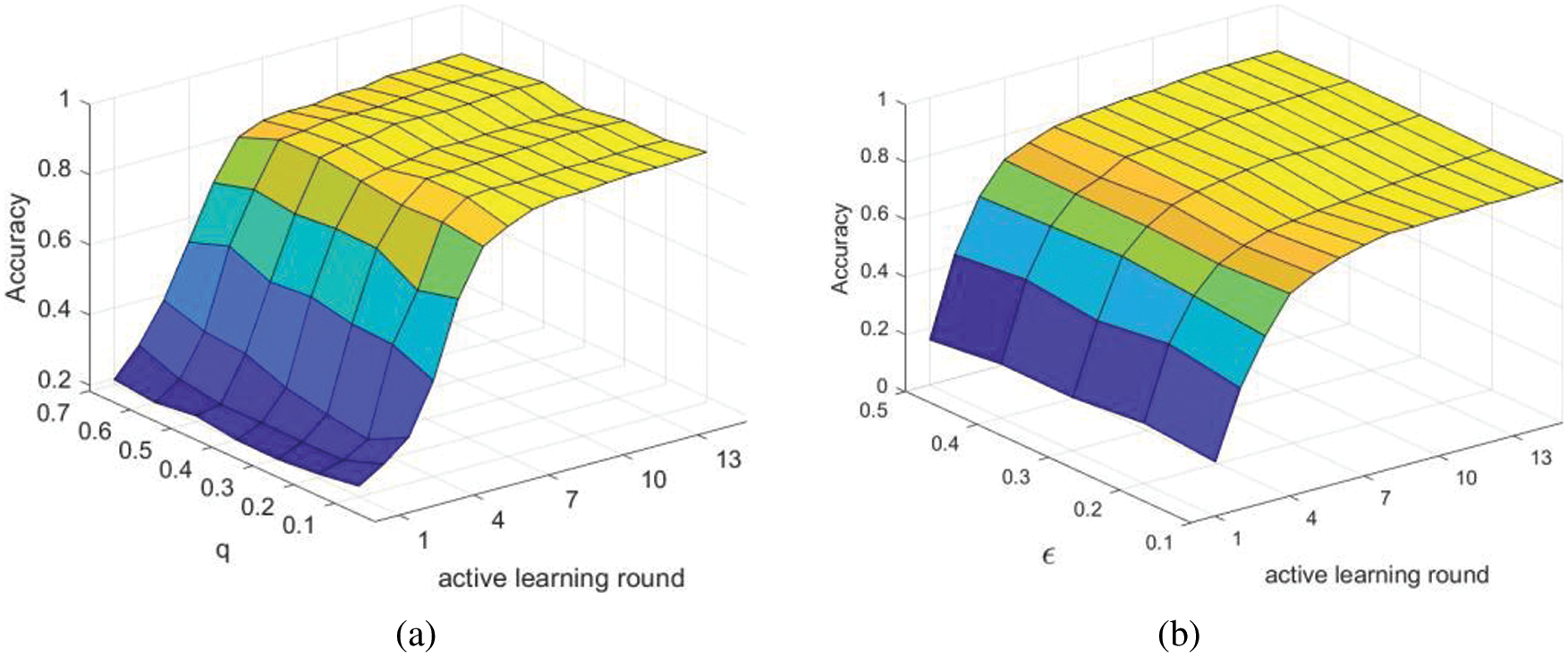
Figure 8: Learning performance of dAPLL algorithm vs. different control parameters on the “Vertebral Column” dataset. (a) Simulation results vs. AL rounds and q (with r=1). (b) Simulation results vs. AL rounds and ε (with q=1 and r=1)

In addition, the joint influence of varying numbers of AL rounds and different values of ε on the classification accuracy is also investigated. By observing Fig. 8b, we can notice that as the value of ε increases, the classification accuracy of the proposed algorithm slightly decreases, which verifies the effectiveness of our proposed method for dealing with the coupling false positive label.

4.3 Classification of Some Other Artificial and Real PL Datasets

In this subsection, we further show the generality of the proposed algorithm via numerical simulations on four artificial PL datasets [36] and two real PL datasets [13,37]:

Pendigits dataset [36]: This dataset contains the recognition results of pen-based handwriting digits. Each data contains 16 written characters of digits from 0 to 9.

Wine dataset [36]: These data are obtained by a chemical component analysis of the wine derived from different cultivars, which records the quantities of 13 constituents found in three types of wines.

mHealth dataset [36]: This dataset contains a total of 23 features of body motion and vital signs recorded by volunteers.

Ecoli dataset [36]: This dataset is about the protein localization sites in cells. These data record 8 features of different proteins.

Lost dataset [37]: This dataset is about the classification of the characters derived from the screenplay. Here, 108 features of an ambiguously labeled face are extracted from the video.

Birdsong dataset [13]: This dataset is about the classification of birdsong. Each data contains 548 features of the singing syllables in a 10-s period. The full characteristics of the datasets are presented in Table 2.

As far as we know, distributed active partial label learning is a new topic that has not been addressed before. So, the performances of one active partial label learning algorithm with adaptive selection strategy (APLL-AS) [25] and the other four centralized supervised partial label learning algorithms, including the Partial Label k-Nearest Neighbor (PL-kNN) [38], the Partial Label Support Vector Machine (PL-SVM) [19], the COnfidence-Rated Discriminative partial label learning (CORD) [18], the Error-Correcting Output Code (ECOC) [22], and the Self-Paced Partial Label Learning (SP-PLL) [21], are evaluated for comparison. Additionally, the results of the cAPLL and dAPLL random are also provided, which act as a benchmark.

To investigate the performance of different algorithms with varying numbers of false positive labels, we depict the changing curves of classification accuracies vs. different values of q with fixed r and RLMT on four artificial PL datasets in Figs. 9 and 10. It is noted that since the number of classes in the Wine dataset is only 3, the configuration r=2 cannot be tested.

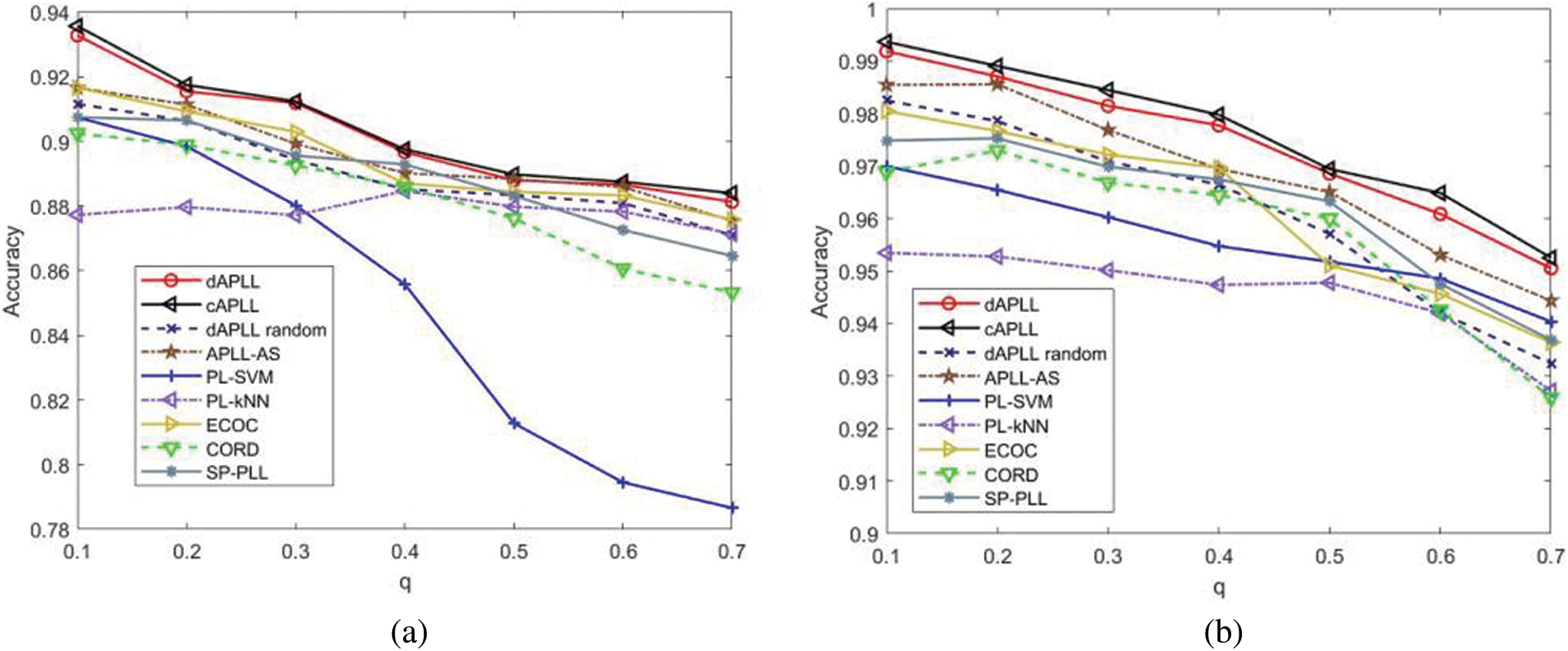
Figure 9: Learning performance of all the considered algorithms vs. q with r=1and specific value of RLMT on four artificial PL datasets. (a) Simulation results on the “Pendigits” dataset using RLMT = 180/2800. (b) Simulation results on the “Wine” dataset using RLMT = 140/1420. (c) Simulation results on the “mHealth” dataset using RLMT = 140/4910. (d) Simulation results on the “Ecoli” dataset using RLMT = 140/270

Figure 10: Learning performance of all the considered algorithms vs. q with r=2 and specific value of RLMT on four artificial PL datasets. (a) Simulation results on the “Pendigits” dataset using RLMT = 180/2800. (b) Simulation results on the “mHealth” dataset using RLMT = 140/4910. (c) Simulation results on the “Ecoli” dataset using RLMT = 140/270

From the simulation results, we can see that when r and RLMT keep invariant, with increasing of q, higher proportion of labeled data are associated with a set of candidate labels rather than a single true label, which can have a greatly negative influence on the learning performance. So, there is a significant decline in classification accuracy across all the comparison methods.

Comparing the simulation results between Figs. 9 and 10, it is easy to notice that with a fixed q and RLMT, as the number of false positive labels r increases, more additional labels are randomly added to the candidate label set, which may hurt the learning performance. So, the performances of different algorithms become poor.

Besides, we also test the performance of different algorithms vs. different values of ε on four artificial PL datasets. The detailed simulation results are presented in Fig. 11. Given a fixed q, r and RLMT, as the value the ε increases, the probability of the coupling false positive label also increases, which brings many troubles to the classifier induction with high-precision. So, the classification accuracies of different algorithms decrease in varying degrees.

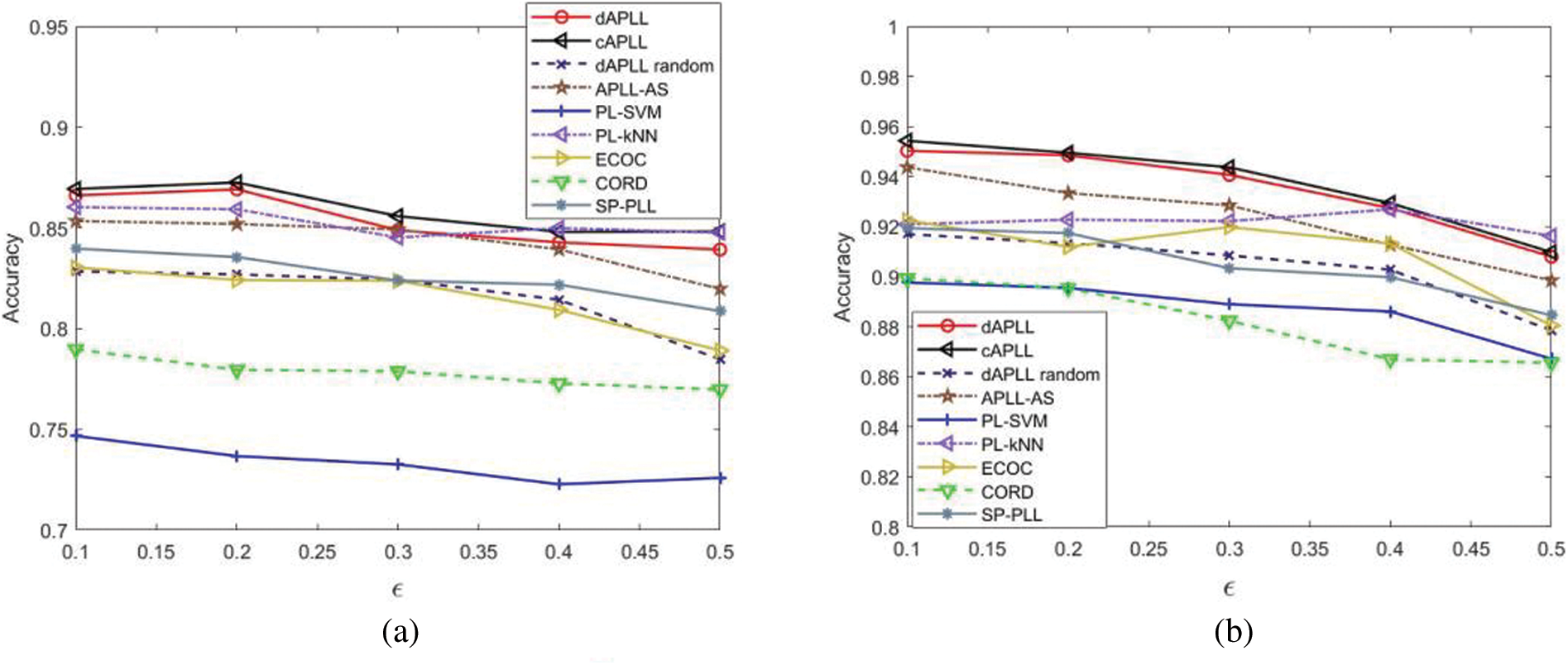
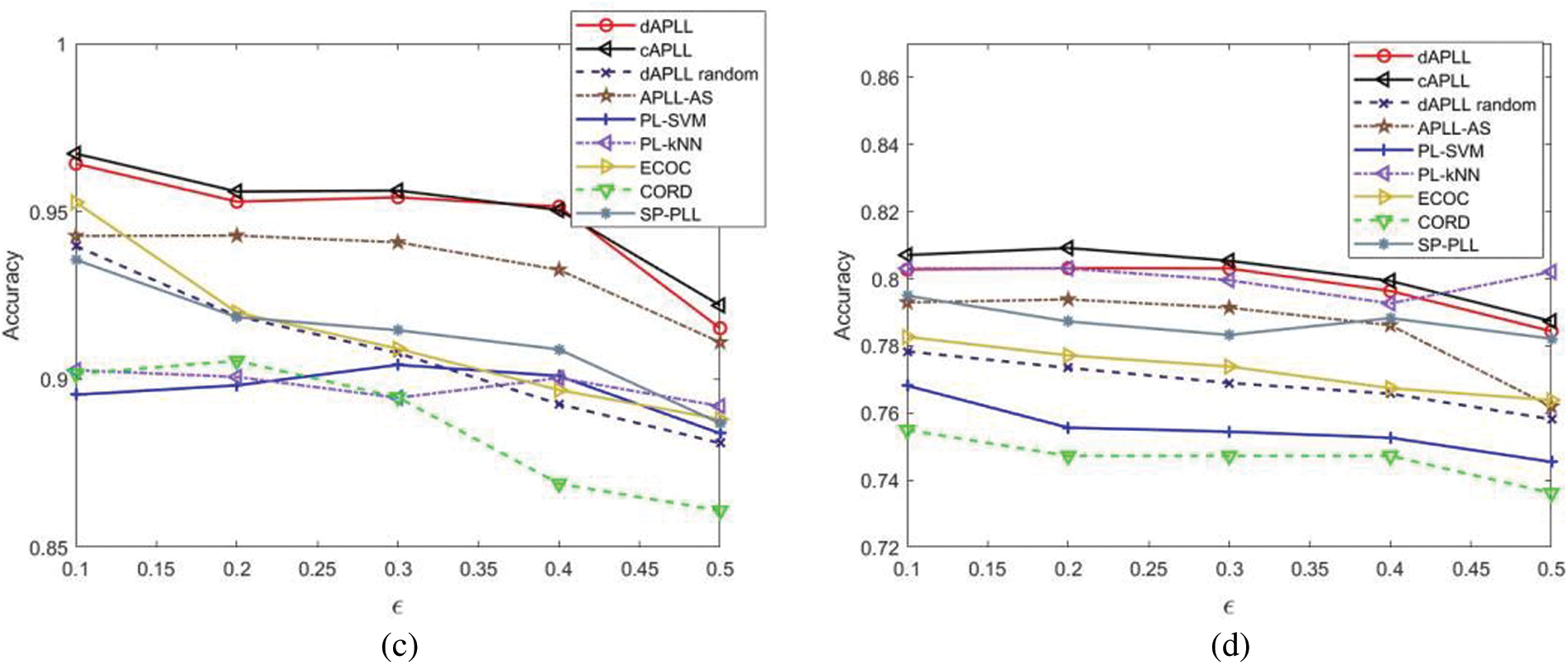
Figure 11: Learning performance of all the considered algorithms vs. ε with q=1, r=1 and specific value of RLMT on four artificial PL datasets. (a) Simulation results on the “Pendigits” dataset using RLMT = 180/2800. (b) Simulation results on the “Wine” dataset using RLMT = 140/1420. (c) Simulation results on the “mHealth” dataset using RLMT = 140/4910. (d) Simulation results on the “Ecoli” dataset using RLMT = 140/270

Furthermore, we compare the learning performance of different algorithms vs. the number of RLMT with different parameter configurations. As shown in Fig. 12, with the increasing of the RLMT, more and more weakly supervised information can be exploited for the training of predictor models. The learning performance of different algorithms gradually improves.

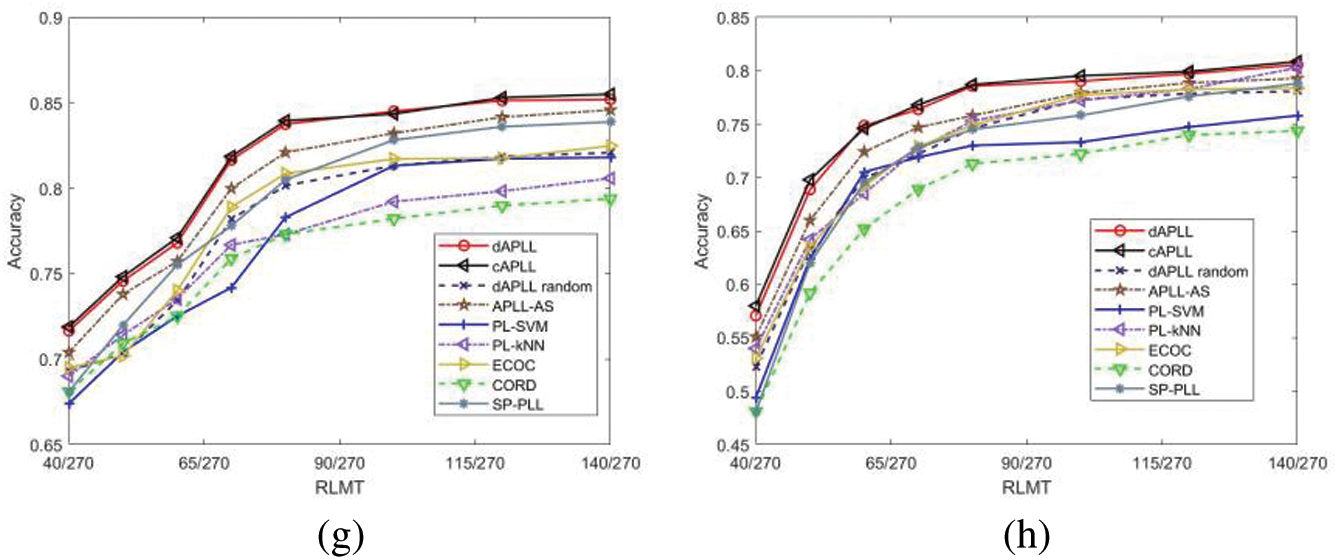
Figure 12: Learning performance of all the considered algorithms vs. RLMT with different parameters on four artificial PL datasets. (a) Simulation results on the “Pendigits” dataset with q=0.2 and r=1. (b) Simulation results on the “Pendigits” dataset with ε=0.2, q=1 and r=1. (c) Simulation results on the “Wine” dataset with q=0.3 and r=1. (d) Simulation results on the “Wine” dataset with ε=0.2, q=1 and r=1. (e) Simulation results on the “mHealth” dataset with q=0.3 and r=1. (f) Simulation results on the “mHealth” dataset with ε=0.2, q=1 and r=1. (g) Simulation results on the “mHealth” dataset with q=0.3 and r=1. (h) Simulation results on the “Ecoli” dataset with ε=0.3, q=1 and r=1

Across all the configurations on different datasets, our proposed algorithm and the corresponding centralized algorithm show similar learning performance, which verifies the generality of distributed learning. Besides, our proposed algorithm outperforms the APLL-AS method in almost all the configurations, which demonstrates that our proposed method is more effective to deal with data with ambiguous labels. Moreover, the proposed dAPLL algorithm performs better than dAPLL random and the other PLL algorithms using a random sample selection strategy by a wide margin in almost all cases, especially when only small amounts of data are selected to be assigned with the candidate labels. The results from these simulations indicate that our proposed method is capable of achieving good learning performance with a small amount of PL data.

To further verify the effectiveness of our proposed algorithm, two real-world datasets (Lost [37] and Birdsong [13]) are adopted. The simulation results of all the used algorithms are presented in Fig. 13. From Fig. 13, we can find that the classification accuracy of dAPLL is extremely close to that of cAPLL, which indicates that the proposed distributed method can achieve good learning performance in the classification of data samples with ambiguity. Besides, due to the performance improvement caused by the fully decentralized sample selection strategy and the disambiguation-free strategy, the proposed dAPLL significantly outperforms the dAPLL random and the other comparison algorithms.

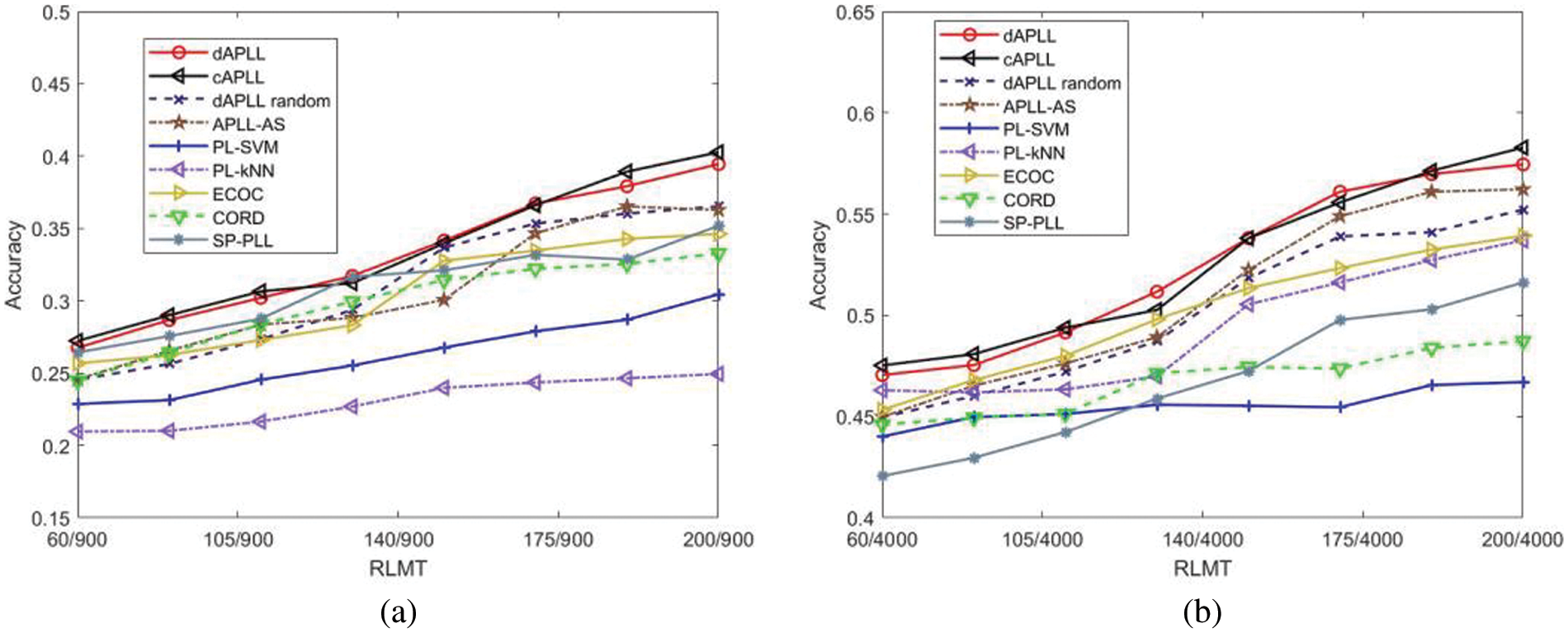
Figure 13: Learning performance of all the considered algorithms vs. RLMT on two real PL datasets. (a) Simulation results on the “Lost” dataset. (b) Simulation results on the “Birdsong” dataset

To provide more evidence on the effectiveness of the proposed algorithm, we rank all considered algorithms in terms of their classification accuracies on different controlled parameter configurations in Table 3. By observing Table 3, it is clear that the average rank of the proposed algorithm is greater than that of the other comparison algorithms, and is only surpassed by the corresponding centralized algorithm, verifying the generality of our proposed dAPLL algorithm.

5  Conclusion

To handle the issue of distributed classification of PL data selected by AL rounds over a network, the dAPLL algorithm has been developed. The proposed algorithm is a distributed PLL algorithm together with a fully decentralized sample selection strategy. As for a fully decentralized sample selection strategy, both representativeness and uncertainty criteria are considered. To be specific, following a distributed clustering method, a certain number of cluster centers are first selected as the representative data of the whole dataset at the initialized state. Then, the Rep and FS are chosen to evaluate the degree of representativeness and uncertainty of the data samples. Meanwhile, based on the disambiguation-free strategy, a distributed PLL algorithm is proposed. Using the coding matrix, the labeled/PL dataset is transformed into several binary classification training datasets. In order to deal with the issue of imbalanced class distribution in multiple binary classification problems, the loss function is designed to be cost-sensitive. To collaboratively estimate the model parameters of binary classifiers without disclosing data privacy, the kernel feature map is approximated by the random feature map. Based on this, several binary classifiers are trained in a global sense, and the label of testing data can be obtained based on the decoding of the signed outputs of the binary classifiers. Simulations on several datasets are conducted, and the results show that our proposed dAPLL approach outperforms the other comparison algorithms, and achieves near-optimal performance compared to the cAPLL. In addition, our proposed algorithm consistently achieves better results than the other existing APLL/PLL algorithms, indicating the effectiveness of APLL.

In the future, we would like to extend the distributed processing algorithm to solve the problem of multi-dimension classification. This is because in some real-world applications, the training data may be simultaneously assigned with multiple labels from different dimensions. In these cases, distributed multi-dimension classification, in which a series of inter-connected nodes train the multi-label classifier in a collaborative manner, is preferred.

Funding Statement: This work was financially supported by the National Natural Science Foundation of China (62201398), Natural Science Foundation of Zhejiang Province (LY21F020001), Science and Technology Plan Project of Wenzhou (ZG2020026).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Y. Leng, X. Xu and G. Qi, “Combining active learning and semi-supervised learning to construct SVM classifier,” Knowledge-Based Systems, vol. 44, pp. 121–131, 2013. [Google Scholar]

2. B. Demir, C. Persello and L. Bruzzone, “Batch-mode active-learning methods for the interactive classification of remote sensing images,” IEEE Transactions on Geoscience and Remote Sensing, vol. 49, no. 3, pp. 1014–1031, 2011. [Google Scholar]

3. M. Wang and X. S. Hua, “Active learning in multimedia annotation and retrieval: A survey,” ACM Transactions on Intelligent Systems and Technology, vol. 2, no. 2, pp. 1–21, 2011. [Google Scholar]

4. S. J. Huang, R. Jin and Z. H. Zhou, “Active learning by querying informative and representative examples,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 36, no. 10, pp. 1936–1949, 2014. [Google Scholar] [PubMed]

5. A. J. Joshi, F. Porikli and N. Papanikolopoulos, “Multi-class active learning for image classification,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition (CVPR’09), Miami, FL, USA, pp. 2372–2379, 2009. [Google Scholar]

6. A. J. Joshi, F. Porikli and N. Papanikolopoulos, “Scalable active learning for multiclass image classification,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 34, no. 11, pp. 2259–2273, 2012. [Google Scholar] [PubMed]

7. X. Chen and B. Wujek, “AutoDAL: Distributed active learning with automatic hyperparameter selection,” in Proc. of the 34th AAAI Conf. on Artificial Intelligence (AAAI’20), New York, NY, USA, pp. 3537–3544, 2020. [Google Scholar]

8. H. Sun and R. Grishman, “Employing lexicalized dependency paths for active learning of relation extraction,” Intelligent Automation & Soft Computing, vol. 34, no. 3, pp. 1415–1423, 2022. [Google Scholar]

9. X. Chen and B. Wujek, “A unified framework for automatic distributed active learning,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 44, no. 12, pp. 9774–9786, 2022. [Google Scholar] [PubMed]

10. P. Shen, C. Li and Z. Zhang, “Distributed active learning,” IEEE Access, vol. 4, pp. 2572–2579, 2016. [Google Scholar]

11. S. Chakraborty, “Distributed active learning for image recognition,” in Proc. of the IEEE Winter Conf. on Applications of Computer Vision (WACV’18), Lake Tahoe, NV, USA, pp. 1833–1841, 2018. [Google Scholar]

12. L. Shi, Y. Zhao and J. Tang, “Batch mode active learning for networked data,” ACM Transactions on Intelligent Systems and Technology, vol. 3, no. 2, pp. 1–25, 2012. [Google Scholar]

13. T. Cour, B. Sapp, C. Jordan and B. Taskar, “Learning from ambiguously labeled images,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition (CVPR’09), Miami, FL, USA, pp. 919–926, 2009. [Google Scholar]

14. T. Cour, B. Sapp and B. Taskar, “Learning from partial labels,” Journal of Machine Learning Research, vol. 12, pp. 1501–1536, 2011. [Google Scholar]

15. E. Hüllermeier and J. Beringer, “Learning from ambiguously labeled examples,” Intelligent Data Analysis, vol. 10, no. 5, pp. 419–439, 2006. [Google Scholar]

16. L. Feng, J. Lv, B. Han, M. Xu, G. Niu et al., “Provably consistent partial-label learning,” in Proc. of the 33rd Int. Conf. on Neural Information Processing Systems (NeurIPS’20), Virtual Conference, pp. 10948–10960, 2020. [Google Scholar]

17. J. Lv, M. Xu, L. Feng, G. Niu, X. Geng et al., “Progressive identification of true labels for partial-label learning,” in Proc. of the 37th Int. Conf. on Machine Learning (ICML’20), Virtual Conference, pp. 6500–6510, 2020. [Google Scholar]

18. C. Tang and M. L. Zhang, “Confidence-rated discriminative partial label learning,” in Proc. of the 31st AAAI Conf. on Artificial Intelligence (AAAI’17), San Francisco, CA, USA, pp. 2611–2617, 2017. [Google Scholar]

19. F. Yu and M. L. Zhang, “Maximum margin partial label learning,” Machine Learning, vol. 106, no. 4, pp. 573–593, 2017. [Google Scholar]

20. Y. Zhou, J. He and H. Gu, “Partial label learning via Gaussian processes,” IEEE Transactions on Cybernetics, vol. 47, no. 12, pp. 4443–4450, 2017. [Google Scholar] [PubMed]

21. G. Lyu, S. Feng, T. Wang and C. Lang, “A self-paced regularization framework for partial-label learning,” IEEE Transactions on Cybernetics, vol. 52, no. 2, pp. 899–911, 2022. [Google Scholar] [PubMed]

22. M. L. Zhang, F. Yu and C. Z. Tang, “Disambiguation-free partial label learning,” IEEE Transactions on Knowledge and Data Engineering, vol. 29, no. 10, pp. 2155–2167, 2017. [Google Scholar]

23. Y. Zhou and H. Gu, “Geometric mean metric learning for partial label data,” Neurocomputing, vol. 275, pp. 394–402, 2018. [Google Scholar]

24. D. B. Wang, M. L. Zhang and L. Li, “Adaptive graph guided disambiguation for partial label learning,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 44, no. 12, pp. 8796–8811, 2022. [Google Scholar] [PubMed]

25. Y. Li, C. Liu, S. Zhao and Q. Hua, “Active partial label learning based on adaptive sample selection,” International Journal of Machine Learning and Cybernetics, vol. 13, pp. 1603–1617, 2022. [Google Scholar]

26. Y. Liu, Z. Xu and C. Zhang, “Distributed semi-supervised partial label learning over networks,” IEEE Transactions on Artificial Intelligence, vol. 3, no. 3, pp. 414–425, 2022. [Google Scholar]

27. F. S. Cattivelli and A. H. Sayed, “Diffusion LMS strategies for distributed estimation,” IEEE Transactions on Signal Processing, vol. 58, no. 3, pp. 1035–1048, 2010. [Google Scholar]

28. J. Chen and A. H. Sayed, “Diffusion adaptation strategies for distributed optimization and learning over networks,” IEEE Transactions on Signal Processing, vol. 60, no. 8, pp. 4289–4305, 2012. [Google Scholar]

29. P. A. Forero, A. Cano and G. B. Giannakis, “Consensus-based distributed support vector machines,” Journal of Machine Learning Research, vol. 11, pp. 1663–1707, 2010. [Google Scholar]

30. L. Georgopoulos and M. Hasler, “Distributed machine learning in networks by consensus,” Neurocomputing, vol. 124, pp. 2–12, 2014. [Google Scholar]

31. S. Huang and C. Li, “Distributed extreme learning machine for nonlinear learning over network,” Entropy, vol. 17, no. 2, pp. 818–840, 2015. [Google Scholar]

32. Y. Liu, Z. Xu and C. Li, “Distributed online semi-supervised support vector machine,” Information Sciences, vol. 466, pp. 236–257, 2018. [Google Scholar]

33. S. Wang and C. Li, “Distributed stochastic algorithm for global optimization in networked system,” Journal of Optimization Theory and Applications, vol. 179, pp. 1001–1007, 2018. [Google Scholar]

34. A. Rahimi and B. Recht, “Random features for large-scale kernel machines,” in Proc. of the 20th Int. Conf. on Neural Information Processing Systems (NeurIPS’07), Vancouver, BC, Canada, pp. 1177–1184, 2007. [Google Scholar]

35. S. Vempati, A. Vedaldi, A. Zisserman and C. Jawahar, “Generalized RBF feature maps for efficient detection,” in Proc. of the British Machine Vision Conf. (BMVC’10), Aberystwyth, UK, pp. 1–11, 2010. [Google Scholar]

36. C. Blake and C. Merz, “UCI repository of machine learning databases,” 1998. Available: https://archive.ics.uci.edu/ [Google Scholar]

37. F. Briggs, X. Z. Fern and R. Raich, “Rank-loss support instance machines for MIML instance annotation,” in Proc. of the 18th ACM SIGKDD Int. Conf. on Knowledge Discovery and Data Mining (KDD’12), Beijing, China, pp. 534–542, 2012. [Google Scholar]

38. N. Nguyen and R. Caruana, “Classification with partial labels,” in Proc. of the 14th ACM SIGKDD Int. Conf. on Knowledge Discovery and Data Mining (KDD’08), Las Vegas, Nevada, USA, pp. 551–559, 2008. [Google Scholar]