Research on Freezing of Gait Recognition Method Based on Variational Mode Decomposition

1  Introduction

PD is a highly prevalent neurodegenerative disease, and FOG is the most common and disabling pathological gait in Parkinson’s patients [1]. From the perspective of the pathogenesis of PD, FOG cannot be cured entirely [2]. Currently, the treatment of FOG is mainly based on levodopa-based drugs [3]. Due to the limited therapeutic effect of dopamine drugs and surgery on FOG [4,5], non-drug therapy has become a hot research direction for FOG intervention. Human gait recognition (HGR) technology as the basis of non-drug therapy has attracted scholars of attention. The main challenges of gait recognition are complex environmental changes and high costs [6]. In the field of gait recognition, instrumental gait analysis is now widely used [7]. The first method is a comprehensive analysis of patients’ movements in a gait laboratory; the second method is to identify FOG through wearable sensors and long-term detection systems. Due to the high cost and complex operation of the first laboratory analysis method, the automated FOG monitoring technology based on wearable sensors has gradually become the basis for the non-drug treatment of FOG. The advent of new technologies such as machine learning, wearable sensors, and portable neurostimulation devices has paved the way for non-drug treatments for FOG [8].

A large number of scholars have researched FOG recognition. Moore et al. [9] first tried to detect FOG based on inertial sensors, which can detect 78% of FOG events. Hausdorff et al. [10] introduced a new feature index based on the research of Moore et al. and used the threshold method to identify FOG with the freezing index. Djuric-Jovicic et al. [11] processed the data obtained by an inertial sensor mounted on the handle and used the Pearson correlation coefficient method for gait recognition classification. Mazilu et al. [12] used power index and freezing index as features, and used machine learning methods for FOG recognition. The method of machine learning mainly uses decision trees, random forests and naive Bayes algorithms, etc. In 2017, Rodriguez et al. [13] and others proposed a machine-learning algorithm based on SVM. This new algorithm has significantly improved specificity and sensitivity, and it can detect FOG in the daily life of Parkinson’s patients. Rodríguez-Molinero et al. [14] later proposed an accelerometer-based FOG detection algorithm, which used the Spearman correlation coefficient to evaluate the convergence of the algorithm and the scale. The correlation between the algorithm and the UPDRS-III scale confirms the feasibility of the algorithm for detecting FOG. In 2018, Handojoseno et al. [15] proposed Electroencephalogram (EEG) as an innovative technology that can effectively predict the imminent FOG. In addition, with the in-depth exploration of neural networks, more and more hybrid identification algorithms combined with them are developed. For example, neural network models such as ANN [16], DAN2 [17], ANNs [18], and CNN [19] have shown well in the hybrid algorithm performance. However, there are still some limitations to the existing characteristics of identification: 1. FOG detection methods based on inertial sensors will decline in global performance. 2. The identification method based on the acceleration meter has high requirements for the measurement environment, which cannot achieve daily accurate real-time monitoring, and the calculation cost is too high. 3. FOG prediction method based on EEG depends on precision professional equipment.

In response to the above issues, this article proposes a Parkinson’s FOG recognition algorithm based on the decomposition of differential modulus. As the base classifier of the integrated classifier, the RUSBoost integrated algorithm is designed for unbalanced data sets and single classifiers performance, and the super-added optimization is performed to achieve the more accurate and efficient goals of the FOG recognition algorithm.

2  Feature Extraction of FOG Based on Variational Mode Decomposition

VMD is an entirely non-recursive modal variational and signal processing method [20]. Compared with the Empirical Mode Decomposition (EMD) and the improved algorithm of the EMD [21], VMD can solve the adverse effects brought by modulus and endpoint effects and can show excellent noise robustness in practical applications. So this article used VMD to decompose the signal. Assume that the acceleration signal collected by the patient’s rear sensor is , s(t) is decomposed into k finite bandwidth intrinsic mode component functions BIMFk(t) through VMD. The goal of decomposition is to minimize the sum of the estimated bandwidths of all modal components, and the sum of all modal components BIMFk(t) is equal to the acceleration signal s(t).

The construction process of the variational problem is as follows:

We use the Hilbert transform to obtain the analytical signal of each modal component function BIMFk(t) and obtain the corresponding unilateral frequency spectrum as (1).

(δ(t)+jπt)∗BIMFk(t)(1)

The multiplier e−jwkt is introduced to the unilateral spectrum of each BIMFk(t) to adjust the s(t) center frequency wk(t) corresponding to each mode, then modulate the unilateral spectrum of each BIMFk(t) into the corresponding base band as (2).

[(δ(t)+jπt)∗BIMFk(t)]e−jwk(t)(2)

Then use the L2 norm to perform Gaussian smoothing on the demodulated signal, and estimate the bandwidth of each BIMFk(t), and a constrained variational model of the signal s(t) to be decomposed is constructed in formula (3).

{min{BIMFk},{wk}{∑k‖∂t[(δ(t)+jπt)∗BIMFk(t)]e−jwk(t)‖22}s.t.∑kBIMFk(t)=s(t)(3)

Introduce the Lagrangian operator λ(t) and the secondary penalty factor α, transform the constrained variational model into an unconstrained variational model, and construct the Lagrangian function of the following formula (4).

L(BIMFk,wk,λ)=α∑k‖∂t[(δ(t)+jπt)∗BIMFk(t)]e−jwk(t)‖22+‖s(t)−∑kBIMFk(t)‖22+⟨λ(t),s(t)−∑kBIMFk(t)⟩(4)

Solve the transformed unconstrained variational model using the alternating direction multiplier method, getting the following formula (5).

BIMFkn+1=arg⁡min{α‖∂t[(δ(t)+jπt)∗BIMFk(t)]e−jwk(t)‖22+‖s(t)−∑BIMFk(t)+λ(t)2‖22}(5)

Convert the above equation into the frequency domain through the Parseval’s theorem. Therefore (5) can be written as formula (6).

BIMFkn+1=arg min{α‖jw[(1+sgn(w+wk))∗BIM^Fk(w)(w+wk)]‖22+‖s^(w)−∑BIM^Fk(t)+λ(t)2‖22}(6)

Replace w in the first term of the above formula with w−wk as formula (7).

BIM^Fkn+1=arg⁡min{α‖j(w−wk)[(1+sgn(w))BIM^Fk(w)]‖22+‖s^(w)−∑BIM^Fk(w)+λ(w)2‖22}(7)

Since the actual signal has Hermitian symmetry, the form of the integral of the interval containing zero positive frequency can be obtained.

BIM^Fkn+1=arg⁡min{∫0∞4α(w−wk)2|BIM^Fk(w)|2+2|s^(w)−∑BIMFk(w)+λ^(w)2|2dw}(8)

Let the first term of the above formula be zero. The optimal solution of the modal component function BIMFk(t) can be obtained as (9).

BIM^Fkn+1(w)=s^(w)−∑BIMFk(w)+λ^(w)21+2α(w−wk)2(9)

BIM^Fkn+1(w) is equivalent to the Wiener filter of residual s^(w)−∑BIM^Fk(w), through the Fourier transform, the modal component function group BIM^Fkn+1(t) in the frequency domain can be obtained.

The center frequency wk as (10).

wkn+1(t)=arg⁡min{‖∂t[(δ(t)+jπt)∗BIMFk(t)]e−jwk(t)‖22}(10)

Convert the above formula to the frequency domain as (11).

wkn+1=arg⁡min{∫0∞(w−wk)2|BIM^Fk(w)|2dw}(11)

Solve the above formula can obtain the final solution wkn+1 as (12).

wkn+1=∫0∞w|BIM^Fk(w)|2dw∫0∞|BIM^Fk(w)|2dw(12)

In this paper, through the average instant frequency method and signal decomposition experiment, it is determined that when the number of decomposition layers is k = 3, the VMD can be adapted to the FOG signal well.

Figs. 1 and 2 are the results of VMD decomposition of a particular segment of the acceleration signal on the x-axis of the patient’s rear according to K = 3. We can see that VMD can complete the FOG adaptive decomposition well when the decomposition layer number K = 3.

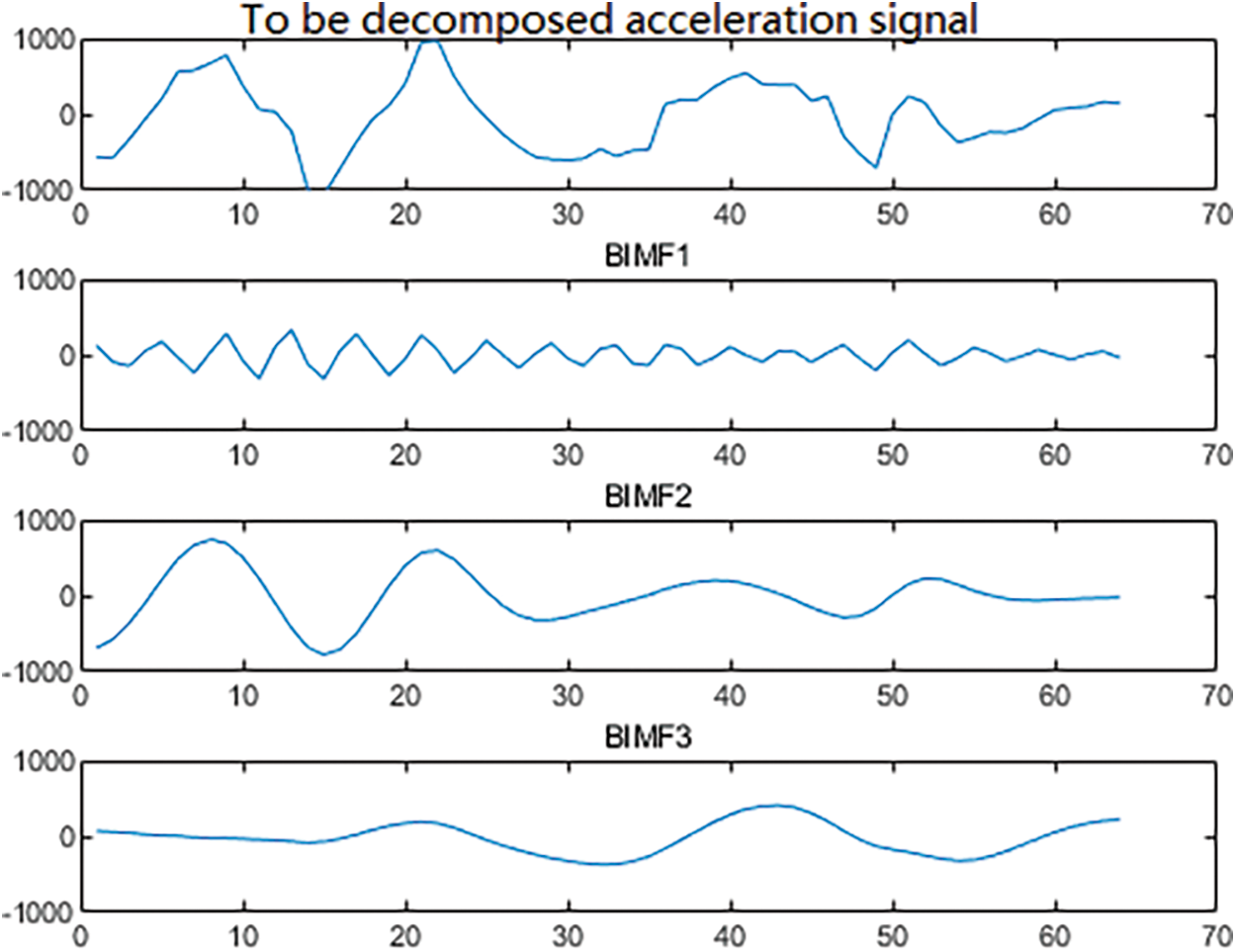
Figure 1: Time domain diagram of each BIMF

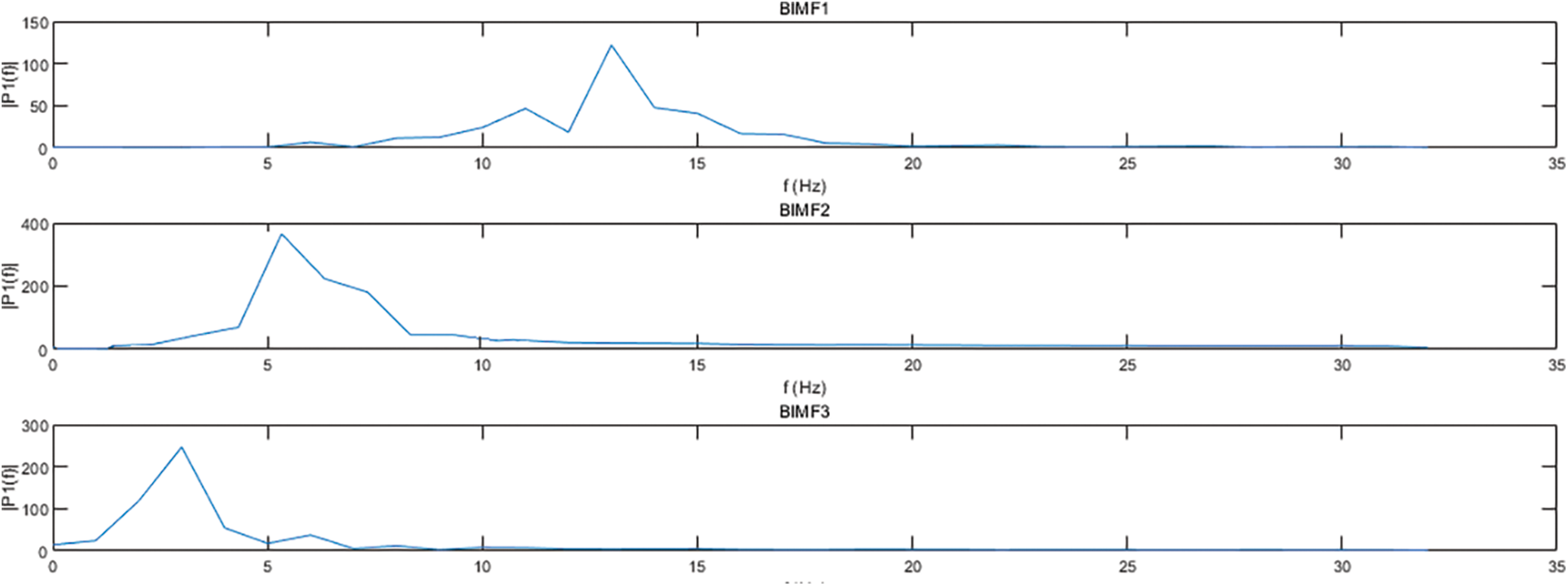
Figure 2: Frequency domain diagram of each BIMF

The specific implementation process of the algorithm is as shown in Fig. 3.

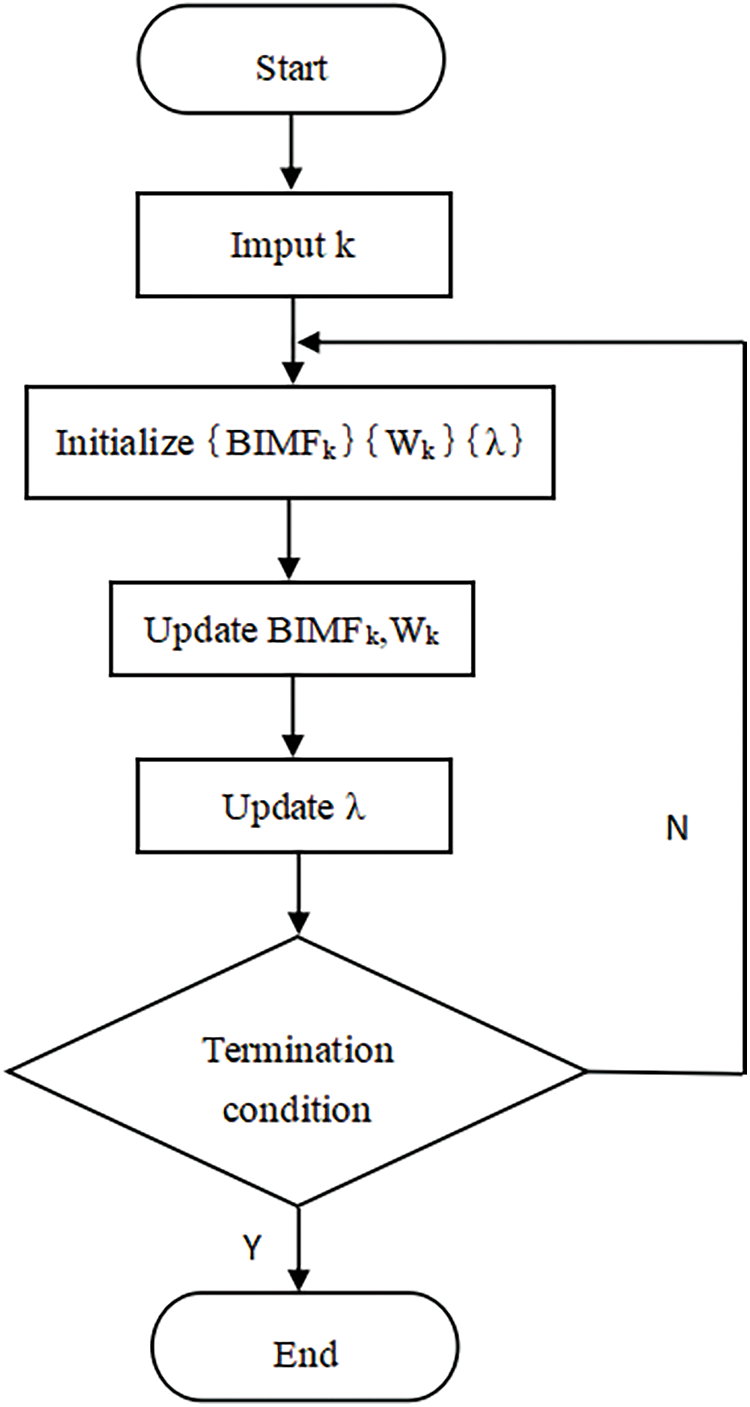
Figure 3: VMD process of gait signal

3  Design and Processing of FOG Characteristics Based on VMD

The characteristics of the BIMF group obtained by the decomposition of the acceleration signal of the patient’s rear by VMD can describe the gait information relatively finely. In addition to using statistics that represent time domain characteristics to describe each BIMF, to describe the energy distribution state of gait information, this paper also uses energy entropy as a new statistic, which can replace power index and freezing index. Energy entropy is expressed by the following formulas (13)–(16):

He=−∑i=1npi×lg⁡pi(13)

pi represents the proportion of energy in the total energy as (15).

E=∑i=1nEi(14)

pi=EiE(15)

E=∫−∞+∞s2(t)dt(16)

In practical applications, due to the existence of redundant features, the overall performance of the algorithm will be affected to a certain extent, such as increased computation, decreased real-time performance, decreased recognition accuracy, etc. Therefore, feature dimensionality reduction is required. We used the CART model to realize the feature selection of the embedding method. The feature selection basis is the feature importance of the CART model, and its expression is shown in formula (17).

imp=Ls×Lgini−ls×lg⁡ini−rs×rginits(17)

imp represents the importance of each feature, Ls represents the number of samples included in the decision node that uses the feature as the basis for selection, ls is the number of samples in the left subtree after the decision, rs is the number of samples in the right subtree after the decision, and Lgini Represents the Gini coefficient of the current decision node, lg⁡ini is the Gini coefficient of the left subtree, rgini is the Gini coefficient of the right subtree, and ts represents the total number of samples in the training set.

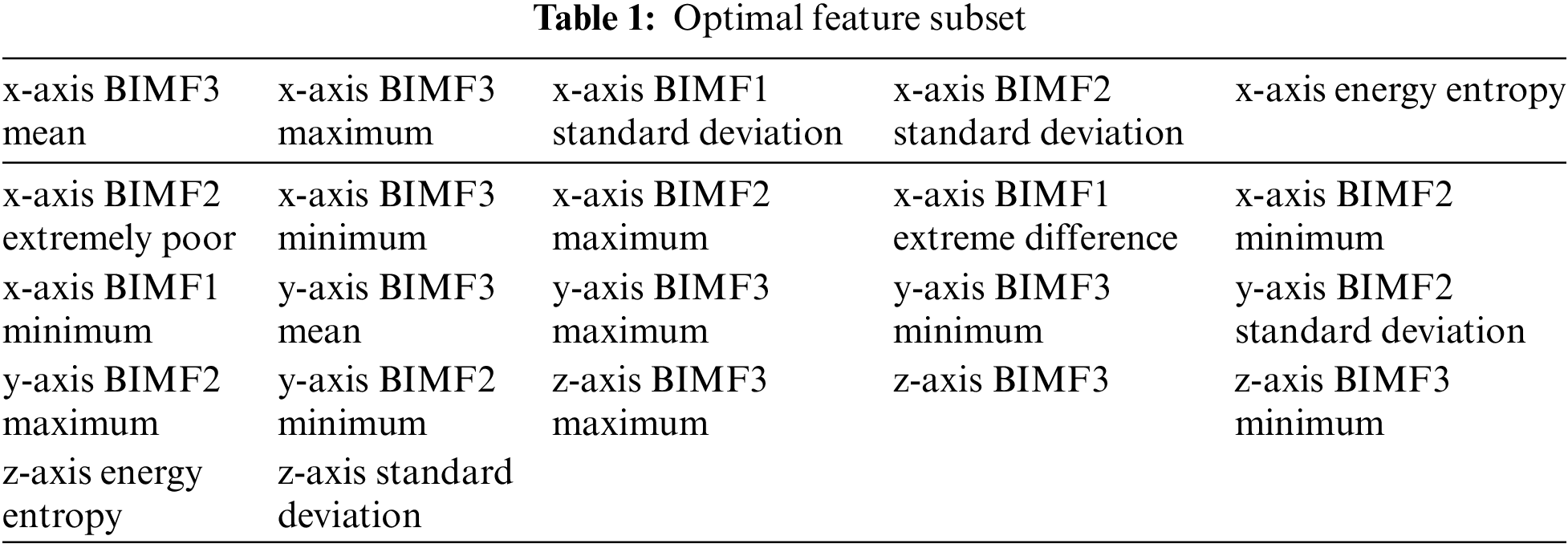
After the patient’s rear three-axis acceleration signal decomposed by VMD, a total of 9 BIMF corresponds. The seven statistics of these 9 BIMF plus the energy entropy of the three-axis, with a total of 66 characteristic values. These characteristics may have redundant, which affects the overall performance of the algorithm in the actual application, so dimension reduction is needed. We used the forward search method to determine the optimal feature subset. By analyzing the number of features and the performance curve of the CART classification model, we can know that the following 22 features can achieve performance similar to the complete feature classification. These 22 features are as Table 1.

4  RUSBoost Algorithm and Its Bayesian Optimization

In this paper, the CART ensemble model is used to avoid the occurrence of overfitting. Due to the limited classification ability of a single CART model and the imbalance in the number of positive and negative samples in the sample, the RUSBoost ensemble algorithm is selected to solve the above problems.

Suppose the training set is S={(x1,y1),(x2,y2),⋯,(xm,ym)}, where xi represents a particular sample and yi is used to represent the category label. The base classifier is WeakerLearner, and the number of iterations is denoted as T. The steps of the RUSBoost algorithm as Table 2.

From the rough grid search and simple experiments, the number of iterations nc and the maximum number of splits of the CART model mns are the parameters that have the most significant impact on the FOG recognition algorithm in this paper. Therefore, nc and mns are set as the optimization targets.

Maximize the arithmetic mean of the sensitivity (sen) and specificity (spe) of the validation set according to the classification requirements of the imbalanced data set as (18).

When performing Bayesian optimization, the optimization goal used in this article as (19).

AM=sen+spec2(18)

F(AM)=1−AM(19)

Let the integrated algorithm be EC. The optimal feature subset of gait is D, after inputting the parameters nc and mns to EC, and the output of EC is the value of the verification set AM, as formula (20).

AM=EC(D,nc,mns)(20)

Finally, the optimization problem is determined as (21).

{Obj:minF(AM)s.t.:10≤nc≤200,nc∈N100≤mns≤2000,mns∈NAM=Classifier(mns,nc)(21)

The Gaussian process is determined by the mean value function m and the covariance matrix function k. The mean value function is a vector, and the mean value of the covariance matrix function in this paper is zero. The Gaussian process is as (22).

f∼gp(m,k)(22)

If the known information of the objective function deduced from the model is D1:x={x1:x,f1:t}, where ft=f(xt), the value of the following search is planned to be xt+1.

K=[k(x1,x1)⋯k(x1,xt)⋮⋱⋮k(xt,x1)⋯k(xt,xt)](23)

Both ft and ft+1 obey the joint Gaussian distribution. When the expectation is zero, the joint distribution of ft and ft+1 is shown as (24).

where k is (25).

ft+1 is the edge density function of the joint distribution, expressed by the following formula (26).

[f1:tft+1]∼N(0,[kkkTk(xt+1,xt+1)])(24)

k=[k(xt+1,x1)⋅k(xt+1,x2)⋯k(xt+1,xt)](25)

P(ft+1|D1:t,xt+1)=N(mt(xt+1),δ2(xt+1))(26)

The mean of the sampling points is expressed by (27).

mt(xt+1)=kTK−1f1:t(27)

The variance of xt+1 is (28).

δ2(xt+1)=k(xt+1,xt+1)−kTK−1k(28)

Thus, we can estimate the probability distribution of the sampling point xt+1 at any place.

This article chooses the sampling function EI function as (29).

EI(x)={(m(x)−f(x+))ϕ(Z)+σ(x)φ(Z)σ(x)>00σ(x)=0(29)

where ϕ(⋅) is the probability density function of the standard Gaussian distribution, and φ(⋅) is the standard Gaussian distribution function where Z means as (30).

Z=m(x)−f(x+)σ(x)(30)

Introduce a scalar ε into the EI function, ε>0, at this time, the EI function and Z are (31) and (32).

EI(x)={(m(x)−f(x+)−ε)ϕ(Z)+σ(x)φ(Z)σ(x)>00σ(x)>0(31)

Z=m(x)−f(x+)−εσ(x)(32)

In each iteration, the next set of mns and nc can be selected by the maximized EI function objective. If the current iteration number reaches the maximum, the iteration will stop. At this time, the mns and nc corresponding to the smallest objective function value all seek the optimal value.

5  Bayesian Optimization Experiment

To verify the performance effect of the FOG recognition algorithm proposed in this paper, the recognition algorithms based on Adaboost [22], Tomeklinks-Adaboost [23], RUSBoost and ROS-Adaboost [24] integration framework are respectively tested for the FOG recognition effect. To exclude the interference of hyperparameters, the learning rate is set to 0.1, the number of iterations is set to 30, the CART model is selected as the base classifier for all frameworks. The maximum number of splits of the CART model is 127. The effect of each integrated framework for verification on the optimal feature subset is shown in Table 3.

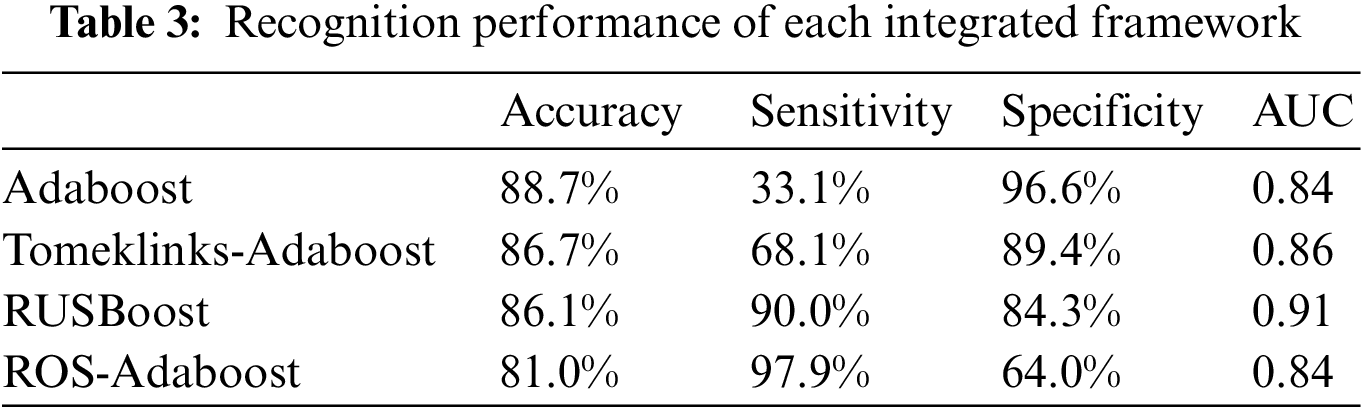
From the experimental results, we can find that RUSBoost has high accuracy, sensitivity and specificity, which can effectively solve the impact of unbalanced data sets.

We used the feature set collected by the patients’ rear acceleration sensor with a time window of 1s after feature selection. The Bayesian optimization process of RUSBoost on the training set and validation sets are shown in Figs. 4 and 5.

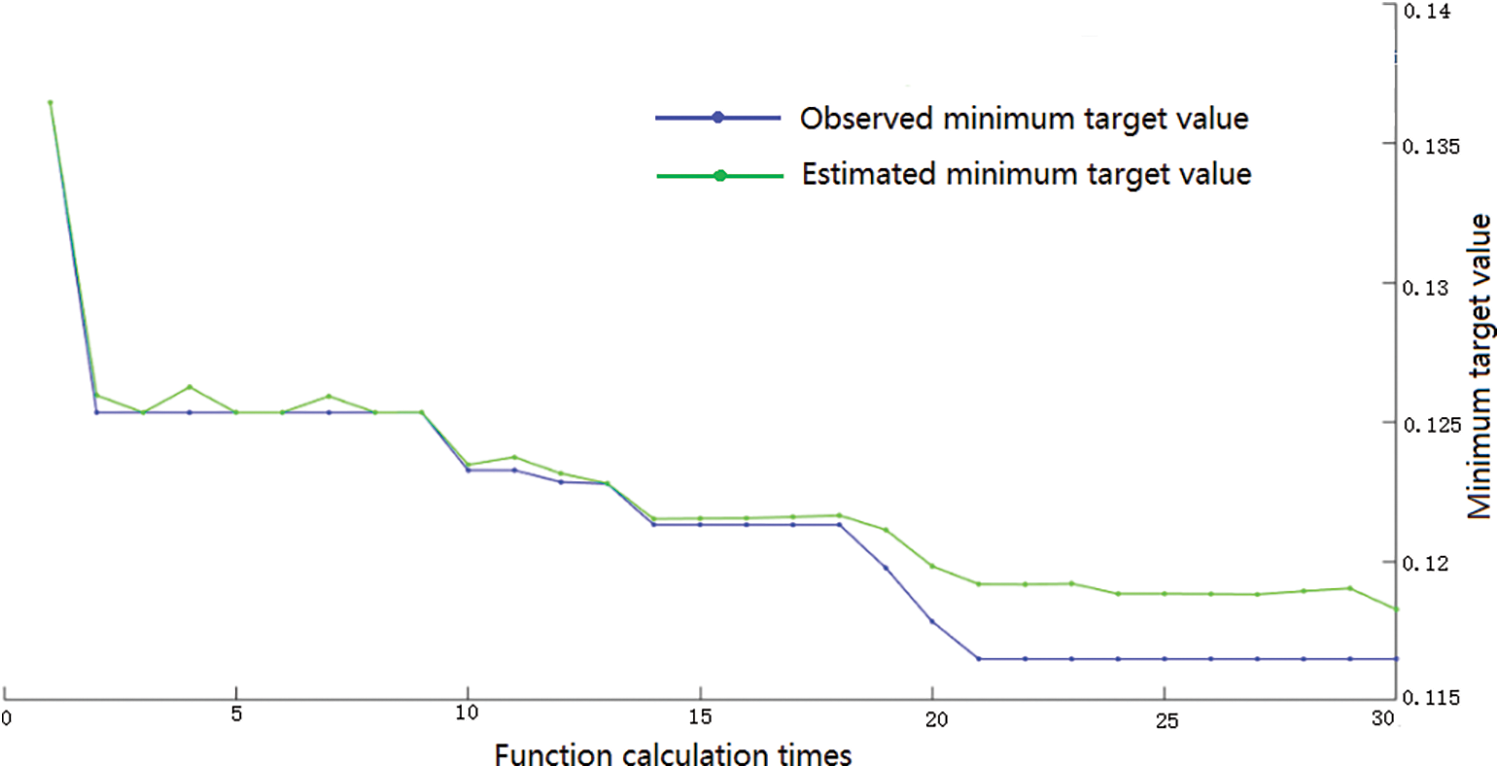
Figure 4: RUSBoost framework hyperparameter optimization process

Figure 5: RUSBoost objective function model estimation

The contour map is shown in Fig. 6.

Figure 6: RUSBoost model estimated contour map

According to the results of Bayesian optimization, the objective function can be minimized when mns = 413 and nc = 89. Use this set of values as hyperparameters to train the RUSBoost model again. After testing on the test set, we can obtain the accuracy of the RUSBoost framework. It is 87.8%, the sensitivity is 89.7%, and the specificity is 87.5%. The ROC curve at this time is as Fig. 7.

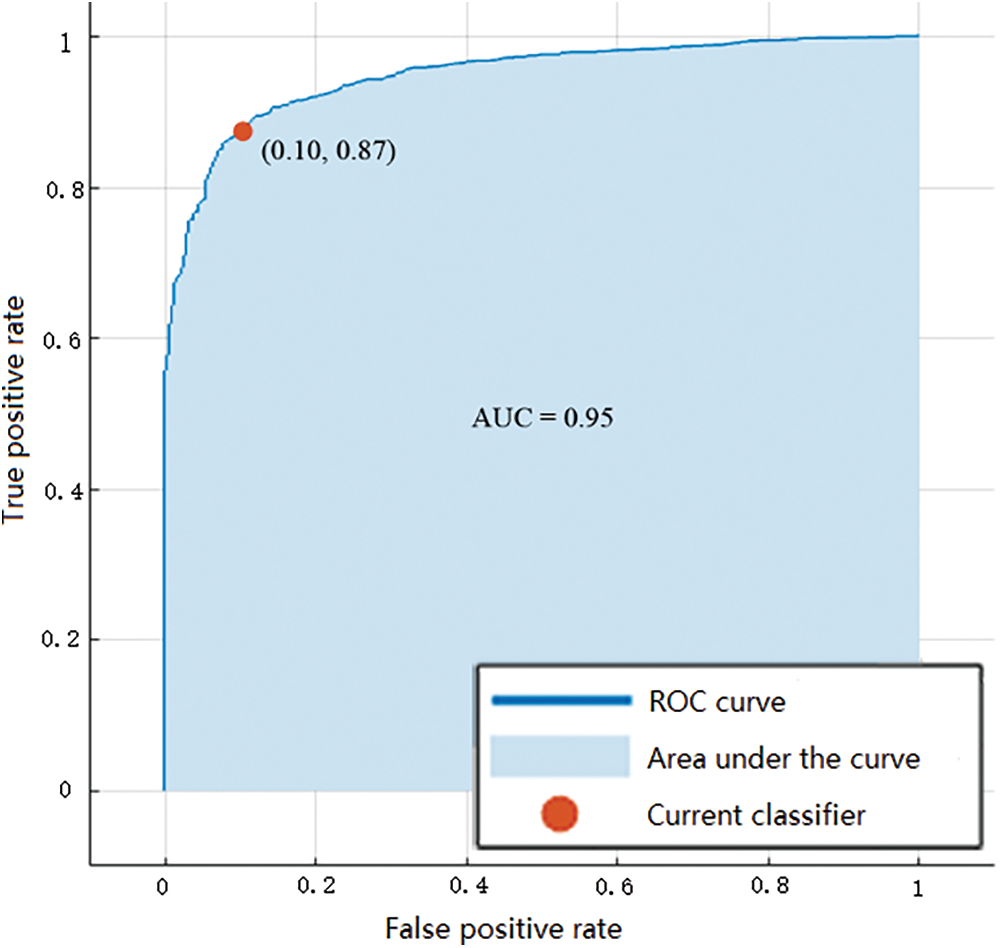
Figure 7: ROC curve and AUC value after RUSBoost Bayesian optimization

From the results of Bayesian optimization experiments, the complexity and recognition speed of the RUSBoost framework is moderate, and the recognition accuracy is similar to the optimal accuracy of the verification set in the hyperparameter optimization process.

6  Conclusion

This work proposed a method of FOG recognition. First, the signal analysis is performed through the modular modulus decomposition. The signal decomposition experiment has proved that the VMD can effectively suppress the mixing and endpoint effects of the modulus and endpoints. Subsequently, the CART model was selected as the base classifier of the integrated algorithm and made a feature reduction. The experiment proved that the optimal feature could effectively save storage overhead and time costs without affecting the algorithm’s accuracy. Finally, the performance comparison experiments of the performance of the unbalanced data set and the single classifier were performed. The results showed that the RUSBoost integrated algorithm could more effectively complete the FOG recognition task and determine the top division of the maximum split through Bayesian optimization 1023 The performance of the identification algorithm when the number of base classifiers is 100. The learning efficiency is 0.1. At this time, the accuracy rate of the algorithm is 91.9%, the sensitivity is 92.3%, the specificity is 91.5%, and the AM value is 0.919.

Acknowledgement: Thanks to Mr. Yan Huanguang from Beijing Yili Tiancheng Technology Company and Ms. Wang Chunjing from Deyu Robotics Company for their help in system design and testing.

Funding Statement: This journal was supported by the Jilin Provincial Science and Technology Department Natural Fund under Grant (20190201099JC) and State Key Laboratory of Control and Simulation of Power System and Generation Equipment (CN) (ascl-zytsxm-202022).

Author Contributions: Shoutao Li: Conceptualization, Methodology, Supervision, Funding acquisition. Ruyi Qu: Data curation, Software, Formal analysis, Writing-original draft preparation. Yu Zhang: Software, Formal analysis. Dingli Yu: Supervision.

Availability of Data and Materials: All the datasets used or analyzed during the current study are included in this published article.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. S. J. Chang, I. Cajigas and J. D. Guest, “Deep brain stimulation of the Cuneiform nucleus for levodopa-resistant freezing of gait in Parkinson’s disease: Study protocol for a prospective, pilot trial,” Pilot and Feasibility Studies, vol. 7, no. 1, pp. 906274, 2021. [Google Scholar]

2. V. Rodrigo, S. Samuel and M. Martina, “Executive control of walking in people with Parkinson’s disease with freezing of gait,” Neurorehabilitation and Neural Repair, vol. 34, no. 12, pp. 1138–1149, 2020. [Google Scholar]

3. R. L. White, M. C. Campbell, D. K. Yang, W. Shannon, A. Z. Snyder et al., “Little change in functional brain networks following acute levodopa in drug-naive parkinson’s disease,” Movement Disorders, vol. 35, no. 3, pp. 499–503, 2020. [Google Scholar] [PubMed]

4. H. Wood, “Gene therapy boosts response to levodopa in patients with Pakinson disease,” Nature Reviews Neurology, vol. 16, no. 5, pp. 242, 2020. [Google Scholar]

5. A. Bougea, N. Spantideas, A. Katoulis and L. Stefanis, “Levodopa-induced skin disorders in patients with Parkinson disease: A systematic literature review approach,” Acta Neurologica Belgica, vol. 119, no. 3, pp. 325–336, 2019. [Google Scholar] [PubMed]

6. A. Mehmood, M. A. khan, U. Tariq, C. W. Jeong, Y. Nam et al., “Human gait recognition: A deep learning and best feature selection framework,” Computers, Materials & Continua, vol. 70, no. 1, pp. 343–360, 2022. [Google Scholar]

7. P. H. Chen, R. L. Wang, D. J. Liou and J. S. Shaw, “Gait disorders in Parkinson’s disease: Assessment and management,” International Journal of Gerontology, vol. 7, no. 4, pp. 189–193, 2013. [Google Scholar]

8. C. Cosentino, M. Baccini, M. Putzolu, D. Ristori, L. Avanzino et al., “Effectiveness of physiotherapy on Freezing of Gait in Parkinson’s disease: A systematic review and meta-analyses,” Movement Disorders, vol. 35, no. 4, pp. 523–536, 2020. [Google Scholar] [PubMed]

9. S. T. Moore, H. G. MacDougall and W. G. Ondo, “Ambulatory monitoring of freezing of gait in Parkinson’s disease,” Movement Disorders, vol. 22, pp. S79, 2007. [Google Scholar]

10. J. M. Hausdorff, L. Gruendlinger and L. Scollins, “Deep brain stimulation effects on gait variability in Parkinson’s disease,” Movement Disorders, vol. 24, no. 11, pp. 1688–1692, 2009. [Google Scholar] [PubMed]

11. M. D. Djuric-Jovicic, N. S. Jovicic, S. M. Radovanovic, I. D. Stankovic, M. B. Popović et al., “Automatic identification and classification of freezing of gait episodes in Parkinson’s disease patients,” IEEE Transactions on Neural Systems and Rehabilitation Engineering, vol. 22, no. 3, pp. 685–694, 2014. [Google Scholar] [PubMed]

12. S. Mazilu, M. Hardegger, Z. Zhu, D. Roggen, G. Troster et al., “Online detection of freezing of gait with smartphones and machine learning techniques,” in Int. Conf. on Pervasive Computing Technologies for Healthcare (PervasiveHealth 2012) and Workshops, San Diego, CA, United states, USA, 2012. [Google Scholar]

13. D. M. Rodriguez, A. Sama, A. Catala, A. Bayes, S. Alcaine et al., “Home detection of freezing of gait using support vector machines through a single waist-worn triaxial accelerometer,” PLoS One, vol. 12, no. 2, pp. 1764, 2017. [Google Scholar]

14. A. Rodríguez-Molinero, A. Sama, C. Perez-Lopez, D. Rodriguez-Martin, L. R. Quinel et al., “Analysis of correlation between an accelerometer-based algorithm for detecting parkinsonian gait and UPDRS subscales,” Frontiers in Neurology, vol. 8, pp. 431, 2017. [Google Scholar]

15. A. M. Handojoseno, G. R. Naik, M. Gilat, J. M.Shine, N. N. Tuan et al., “Prediction of Freezing of Gait in patients with Parkinson’s Disease using EEG signals,” Studies in Health Technology and Informatics, vol. 246, pp. 124–131, 2018. [Google Scholar] [PubMed]

16. R. Adhikari and R. Agrawal, “A combination of artificial neural network and random walk models for financial time series forecasting,” Neural Computing and Applications, vol. 24, no. 6, pp. 1441–1449, 2014. [Google Scholar]

17. E. Guresen, G. Kayakutlu and T. U. Daim, “Using artificial neural network models in stock market index prediction,” Expert Systems with Applications, vol. 38, no. 8, pp. 10389–10397, 2011. [Google Scholar]

18. M. Khashei and M. Bijari, “Fuzzy artificial neural network model for incomplete financial time series forecasting,” Journal of Intelligent & Fuzzy Systems, vol. 26, no. 2, pp. 831–845, 2014. [Google Scholar]

19. Y. Lin, K. C. Chen, X. Zhang, B. Tan and Q. Lu, “Forecasting crude oil futures prices using BiLSTM-Attention-CNN model with Wavelet transform,” Applied Soft Computing, vol. 130, no. 2, pp. 109723, 2022. [Google Scholar]

20. Y. Lin, Q. Lu, B. Tan and Y. Y. Yu, “Forecasting energy prices using a novel hybrid model with variational mode decomposition,” Energy, vol. 246, no. 2, pp. 123366, 2022. [Google Scholar]

21. Y. H. Liang, Y. Lin and Q. Lu, “Forecasting gold price using a novel hybrid model with ICEEMDAN and LSTM-CNN-CBAM,” Expert Systems with Applications, vol. 206, no. 10, pp. 117847, 2022. [Google Scholar]

22. Y. Wang, B. Zheng, M. Xu, S. Cai, J. Younseo et al., “Prediction and analysis of hub genes in renal cell carcinoma based on CFS gene selection method combined with Adaboost algorithm,” Medicinal Chemistry, vol. 16, no. 5, pp. 1573–4064, 2020. [Google Scholar]

23. Z. Min, B. Zou, F. Wei, X. Liu and W. Lei, “Effective prediction of three common diseases by combining SMOTE with Tomek links technique for imbalanced medical data,” in Proc. of IEEE Int. Conf. of Online Analysis and Computing Science (ICOACS), Chongqing, China, pp. 225–228, 2016. [Google Scholar]

24. D. Quan, F. Wei, D. Gabriel, X. Wang, W. Huang et al., “A novel double ensemble algorithm for the classification of multi-class imbalanced hyperspectral data,” Remote Sensing, vol. 14, no. 15, pp. 3765, 2022. [Google Scholar]