A Multi-Object Genetic Algorithm for the Assembly Line Balance Optimization in Garment Flexible Job Shop Scheduling

1  Introduction

With the increasing demand from consumers for personalized and diversified clothing products, garment enterprises must respond quickly to market changes and provide personalized customization services to meet their needs [1]. Compared to traditional mass production, personalized customization tends to be a small-batch multi-variety (SBMV) production mode and requires the full utilization of process flexibility and machine flexibility in garment production [2]. Clothing intelligent hanging systems have flexible workstation combination abilities and information collaboration capabilities, which can effectively meet the requirements of this mode in a flexible garment assembly line. However, the hanging assembly line faces the assembly line balancing (ALB) problem and the machine allocation problem during clothing changes due to the SBMV production mode. The process route optimization problem involved in ALB is at the core of pre-production scheduling and belongs to the flexible shop scheduling problem [3]. The machine allocation impacts the downtime in the production line for retooling during product changeovers. By optimizing the assembly line process allocation and machine allocation schemes, the efficiency and flexibility of the entire assembly line can be maximized.

In this paper, a multi-object genetic algorithm (MOGA) is proposed for the balance optimization problem of garment assembly lines to achieve the goals of maximizing the efficiency of assembly line sequencing and minimizing the adjustment path for machines. In MOGA, the population is initialized by topological sorting to coincide with the process constraints. During the iteration process, a joint fitness function based on machine adjustment path and assembly line efficiency is used as a criterion. A constraint adjustment method based on related processes is introduced into crossover and mutation operations to ensure the generation of effective offspring. Machine constraints are considered in the process of decoding chromosomes and process allocation. The resulting preparation plan is in line with the limitations of station space and worker operability in actual production. Process allocation mechanism splits some processes into two stations in batches to make the bottleneck station not fixed at a specific position and improves the compilation efficiency. Through the production examples of the garment workshop, the effectiveness of the MOGA formulation scheme is verified. MOGA achieves the routine optimization objectives of assembly line balancing while meeting the optimization requirement of minimizing the machine adjustment path for rapid changeover under the small-batch multi-variety production mode. MOGA provides a reference for the enterprise to design the man-machine scheduling scheme of the actual production line.

The structure of the paper is given here: Section 2 introduces the related research on assembly line balancing in traditional manufacturing and garment manufacturing industries. Section 3 describes the scheduling problem in the flexible garment assembly line and establishes the corresponding mathematical model with constraints. Section 4 introduces the fusion methods of the multi-objective algorithm with other algorithms and mechanisms in various stages or links. Section 5 validates the feasibility and effectiveness of using the multi-objective algorithm for scheme planning in garment production through specific case studies, and Section 6 draws the conclusion.

2  Related Works

The traditional exact algorithm is suitable for solving small-scale and simple optimization problems accurately [4]. For the flexible shop scheduling problem, various heuristic algorithms can obtain an approximate optimal solution in a short time [5,6]. In [7], Deng et al. proposed an optimized algorithm called ICMPACO to solve large-scale optimization problems that balances convergence speed and solution diversity. The experimental results demonstrate that the ICMPACO algorithm effectively obtains a better assignment result and optimization value when solving TSP and actual gate assignment problems. In [8], Chen et al. used staff assignments to simulate assembly line balancing to achieve more balanced production and reduced cycle time. By conducting a comparative case study and implementing simulation, Chen found that the tabu search algorithm outperforms simulated annealing in the staff assignment problem. In [9], Goli et al. introduced the method to optimize the energy consumption of non-permutation flow shop scheduling and batch size simultaneously, using multiple improved metaheuristic algorithms, including MOALO, MOKA, MOKSEA, etc. The results showed that the proposed hybrid algorithm provided high-quality Pareto solutions in a shorter time and had greater advantages than traditional algorithms, and there was a linear relationship between processing time and objective function. In [10], Chica et al. proposed using robust multi-objective optimization and simulation techniques to solve assembly line balancing problems and demonstrated the advantages of using a robust production line in a Nissan case. Decision-makers are encouraged to adopt robust multi-objective optimization methods to make the most flexible decision. In [11], Wang et al. optimized U-shaped production lines by developing a mixed-integer nonlinear programming model and optimizing it with an improved genetic algorithm. The model was successfully applied to Company X, resulting in improved load balancing, production rhythm, and reduced time fluctuations at workstations.

In the garment production process, there are a lot of serial and parallel constraints between garment processes, so it is necessary to conform to the constraints to ensure the generation of feasible solutions when using various heuristic algorithms to solve the assembly line balancing problem in the garment workshop. In [12], Yan et al. developed an intelligent assembly line system that utilizes an improved particle swarm optimization algorithm to enhance the balance index of the garment production line and improve the lean production level of enterprises. In [13], Zhang et al. employed the genetic algorithm to optimize a garment assembly line with three different working layouts. The optimized layouts effectively reduced the balance loss rate of the assembly line. In [14], Qian et al. proposed an adaptive genetic algorithm to ensure the balance of working time at each station. The algorithm allocated processes and matched workers to maximize adaptability to mixed assembly line production. In the existing research on workshop scheduling, most studies focus on the production mode of large-scale manufacturing or processing multiple orders on the same production line, with the main goal of optimizing assembly line balance and minimizing maximum completion time. However, there are relatively few studies on optimizing assembly line efficiency and machine adjustment path in the context of the small-batch multi-variety production mode in garment assembly line pre-scheduling. It is necessary for clothing enterprises to carry out relevant research and apply it to practice in order to improve productivity.

3  Mathematical Model

The problem of single-piece flow garment assembly line planning belongs to the multi-process route flexible workshop scheduling problem, which can be described as: each workpiece has multiple process routes. Each workpiece contains n processes that must pass through m stations in turn to complete the garment sewing task. In order to describe the mathematical model of the assembly line better, the relevant parameters are defined in Table 1.

Considering the limitations of station number and machine number, the constraints of the assembly line problem in a single-piece garment workshop are as follows:

∑j=1m⁡yjmji≤2,∀i=1,2,…,n(1)

∑k=1p⁡∑i=1n⁡xijk≤yj,∀j=1,2,…,m(2)

∑k=1p⁡(xijk−xi+1,j,k)≥0,∀i=1,2,…,n−1,j=1,2,…,m(3)

∑j=1m⁡xijkmji,∀i=1,2,…,n,k=1,2,…,p(4)

∑k=1p⁡xijk=1,∀i=1,2,…,n(5)

xijk≥0,∀i=1,2,…,n,j=1,2,…,m,k=1,2,…,p(6)

Eq. (1) means that each workstation contains at most two types of machines. Eq. (2) means that only one workpiece can be processed at a workstation at the same time. Eq. (3) means that an operation can only be partially processed at most once. Eq. (4) means that an operation can be processed on only one machine at one workstation. Eq. (5) means that all operations of each job must be completed. Eq. (6) means that processing time is always non-negative.

In the production process, indexes of the assembly line evaluate the balance state of the assembly line and judge whether the plan can guarantee on-time delivery. Aiming at solving FCALBP with a multi-objective algorithm, we adopt the optimization objectives of maximizing the assembly line balancing rate and minimizing the machine adjustment path during changeovers and establish the following mathematical model:

The first optimization objective is to maximize the assembly line balancing rate after process and machine allocation. The calculation method for this objective is to take the average of the efficiency of each station in the plan.

E=∑j=1mEejm,∀j=1,2,…,m(7)

Eej represents the production efficiency of each station, which is calculated as the ratio of the total process time at a station to the bottleneck station’s process time in the plan.

Eej=TjTbs×100%,∀j=1,2,…,m(8)

Tbs refers to the processing time of the station with the maximum total processing time in the plan.

Tbs=max{Tj},∀j=1,2,…,m(9)

The second optimization objective is to find the minimum machine adjustment path. In the small-batch multi-variety apparel production mode, in order to achieve rapid changeover production, the assembly line needs to be able to switch production processes quickly and effectively. The objective function calculates the sum of adjustment distances for all machines on the assembly line.

R=∑|Sk−Sk'|+∑Sk'(10)

4  Multi-Objective Genetic Algorithm

4.1 Coding and Population Initialization

4.1.1 Coding Method

In the research on traditional assembly line balancing problem with genetic algorithms, binary encoding is commonly used for coding and decoding. In the FCALBP, the usage of binary coding may give rise to infeasible solutions by causing disruption to the precedence relationships between garment processes. Alternatively, the object-oriented coding method effectively represents the feasible scheme of such problems as chromosomes and makes the offspring chromosomes inherit the characteristics of the parents. Therefore, MOGA uses the path representation method to encode cloth processes and generate process chromosomes. The length of the process chromosome is equal to the total number of processes of a garment. Each process gene carries related process information such as subsequent procedures, standard working hours, and machine models. MOGA comprises two chromosome populations, namely process chromosomes and schedule chromosomes. The number of chromosomes in both populations is always the same, and a one-to-one mapping relationship is established between them. The process chromosome population considers the constraint relationships between processes and undergoes genetic algorithm operations such as selection, crossover, and mutation. The schedule chromosome population is generated from the process chromosome population through the process allocation mechanism and is used to calculate the fitness value of MOGA, which is then fed back to the process chromosome selection phase.

The process allocation mechanism considers the number of stations and the assignable operation time of a single workpiece at each station based on the process chromosome and performs process allocation accordingly. Bottleneck working hours that always exist in the same station will cause congestion of the hanging line. In the allocation process, some processes are batch-split to allow for periodic processing at two different stations, thereby optimizing the bottleneck station of the assembly line. After the process allocation mechanism is applied, a schedule chromosome is generated that corresponds uniquely to the process chromosome. The chromosome carries information about the processes and split processes at each station and can be further decoded to obtain a scheduling plan that includes information about the processes and machine assignments.

4.1.2 Population Initialization

The garment process chart has the same structure as a directed acyclic graph. The scheduling of all garment processes and the traversal of a directed acyclic graph share common characteristics: All vertices appear and only appear once (uniqueness of processing). If there is a path from vertex 1 to vertex 2, then vertex 1 must be in front of vertex 2 in the sort (process constraints). A vertex can point to multiple vertices or be pointed by multiple vertices (process flexibility).

MOGA utilizes random topological sorting for population initialization [15,16]. Topological sorting ensures the sorting of garment processes and the generation of process chromosomes without violating garment process constraints. In this study, a random operator was introduced into the topological sorting process to ensure that the initial population is generated within the entire feasible solution space, thereby enhancing the global search capability of MOGA. The Fig. 1 is the process chromosome generation flowchart, and the specific steps are as follows:

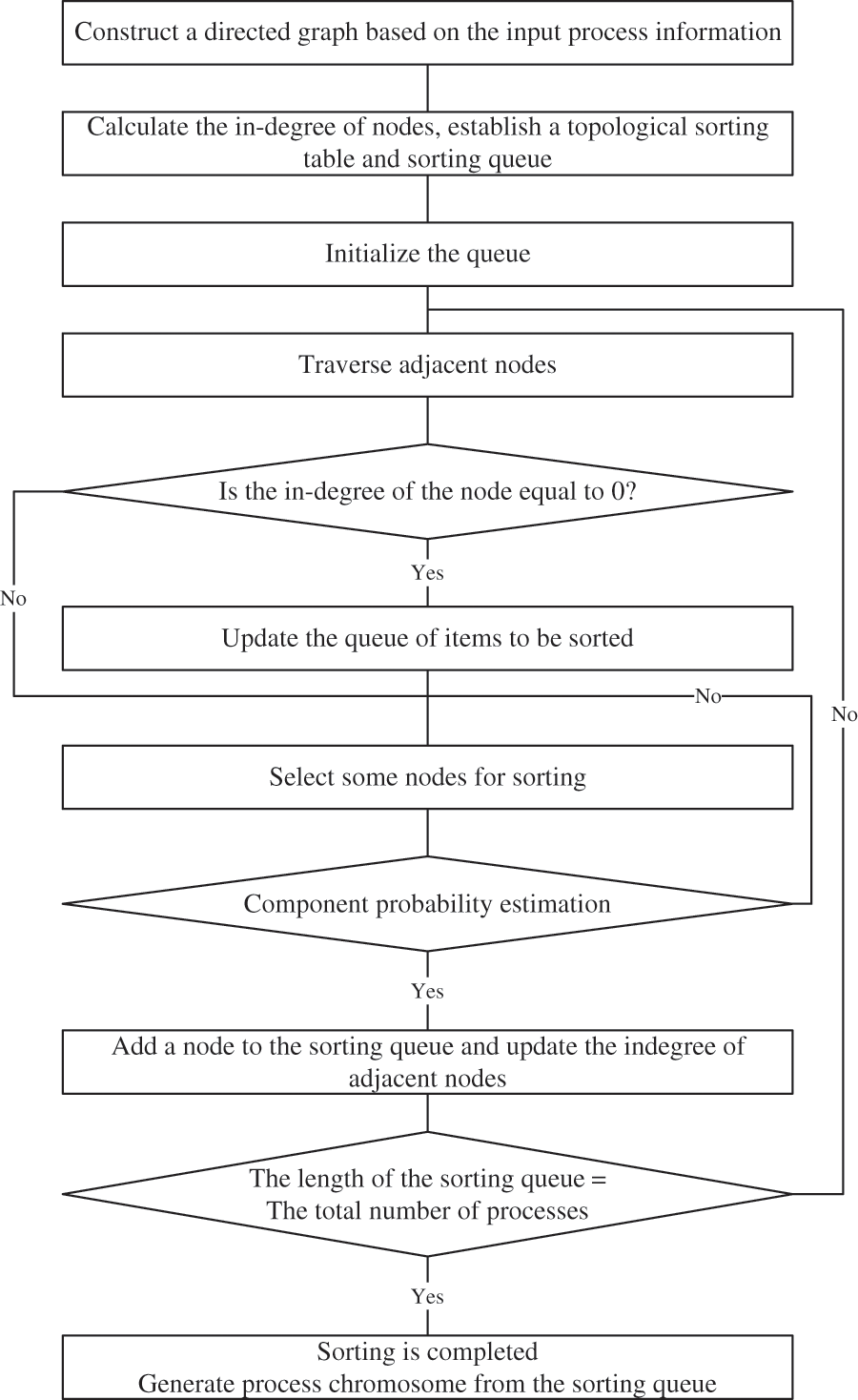
Figure 1: Flow chart of process chromosome generation

Step 1: Define the constraint relationship. According to the process flow and process information, define the order constraints.

Step 2: Generate the process dependency graph. Construct a directed acyclic graph (DAG) by arranging all processes based on their order constraints. Each node in the graph represents a process, and the edges represent the dependencies between them.

Step 3: Topological sorting. Use the random topological sorting algorithm to sort the nodes in the process dependency graph. Select a node with an indegree of 0 as the starting point and start traversing the adjacent nodes. When a node is visited, if its indegree is 0, decide whether to add an element to the result list based on the random operator. If yes, remove all the edges it points to. Otherwise, continue traversing other nodes. Repeat Step 3 until all nodes have been visited.

Step 4: Generate the process chromosome population. The list of nodes is the process chromosome. Initialize the population according to the size of the population.

The generation of programming chromosomes in MOGA includes the following steps:

Step 1: Process positioning: Except for the first process, when other processes are treated as pending processes to be assigned, the workstations allocated by all previous processes are first determined. The process is positioned at the last workstation and undergoes an incoming station judgment.

Step 2: Incoming station judgment: In the process allocation mechanism, the incoming station judgment includes machine type judgment and station working time judgment. When the number of machine types in the station is 0 or 1, the working time is directly measured. If the working time meets the requirements, the process can enter the station, and the station machine type and working time will be updated. If the working time does not meet the requirements, proceed to step 3. When the number of station machines is 2, the machine corresponding to the pending process is consistent with the current machine at the station for working time judgment. If it is inconsistent, proceed to the next station in order to perform step 2.

Step 3: Batch process allocation: When the working time does not meet the requirements, splitting is carried out according to the constraints described in Eq. (1). The split ratio is determined based on the ratio of remaining working time to the current process time and is taken as a value close to 1/n or (n − 1)/n:

Rp=(Tj−Tj′Tj)Ti, ∀j=1,2,…,m,i=1,2,…,n(11)

In the Eq. (11), Tj represents the actual production pace of the station, T′j represents the total working time of the processes that have entered the station, and Ti represents the processing time for the divisible process. Batch splitting allocates the i-th process of the entire batch of workpieces to be processed periodically between two stations according to the proportion of Rp, and a single workpiece process cannot be split to be processed at two stations.

Step 4: Repeat steps 1 to 3 until all process genes of the process chromosome have entered the station.

4.2 Select Operation

The joint fitness value of the chromosome for planning is utilized as the assessment criteria for chromosomes throughout the MOGA iteration process. The efficient fitness value of the assembly line and the fitness value of the machine adjustment path are given various weights. By normalizing the results of minimizing the machine adjustment path, the fitness value of the machine adjustment path is generated. The available calculation process is as follows:

fitness=w1∙E+w2∙normalize_route(12)

The optimal staffing plan involves achieving efficient production while maintaining the original machine layout of the assembly line. However, in practical implementation, some machines may require adjustments to improve assembly line change efficiency. The machine adjustment path is processed using a maximum-minimum normalization method to scale the path features within the range of 0–1 [17].

normalize_route=(1−R−min_Rmax_R−min_R)(13)

In the iteration process of the multi-objective genetic algorithm, an elite preservation strategy is used to preserve individuals with superior performance to accelerate algorithm convergence and improve the quality of solutions. Specifically, in each generation of the population, the top 40% of chromosomes based on fitness value (rank-based) are selected as the elite group in the current population, which will produce offspring for the next generation.

Moreover, selecting chromosomes from a solution set is also an important method to enhance search performance. For individuals in the solution set, the top 20% of chromosomes based on joint fitness values are reserved. Then, according to other criteria such as assembly line efficiency and machine adjustment path, two sub-sets are selected from the solution set, each accounting for 10% of the total population size, and combined with the previous elite group to form a new generation of offspring. Such an operation can consider multiple criteria comprehensively and help find better solutions.

4.3 Improve Crossover and Mutation Operations

4.3.1 Cross Operation

Crossover operations play a key role in the genetic algorithm [18]. The constraint relationship between garment processes is complex. Directly performing crossover operations will destroy the constraint relationship between offspring chromosome process genes. In this paper, the crossover operation is improved by the constraint adjustment method to ensure the effectiveness of the offspring chromosomes. The front endpoint g1 and the back endpoint g2 of the cross-gene segment are randomly generated. The substrings before the endpoint g1 and the substrings after the endpoint g2 of the two parental process chromosomes (P1, P2) are retained. The cross-gene segments between g1 and g2 are exchanged. The same gene in the gene segment retains the original order for interchange. After verifying the constraint relationship, the differential genes are inserted at the appropriate position according to the gene position of the subsequent procedure.

Fig. 2 is a process roadmap containing 10 processes. The parent (P1, P2) chromosomes that satisfy the constraint relationship are shown in Fig. 3. In the two-point crossover operation, the breakpoints g1 and g2 are first selected. Interchange the same processes 3, 4, 6, and 7 in the intermediate substring and retain the gene order in the respective parent to cross. The differential gene in the P1 substring is 8, and the insertion point of its offspring is between the process genes 7 and 9. The differential gene in the P2 substring is 2, and the insertion point of its offspring is between process genes 1 and 3. There are currently two optional points, and the optional points are randomly selected to perform the insertion operation. The intersection eventually produced offspring S1 and S2.

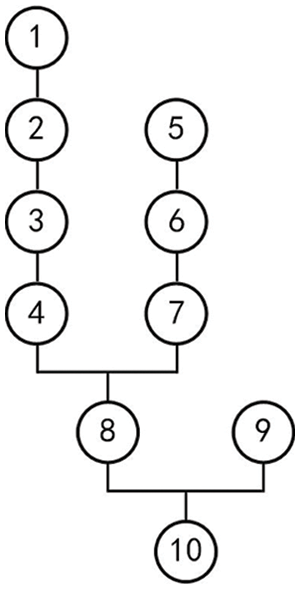
Figure 2: Process directed acyclic graph

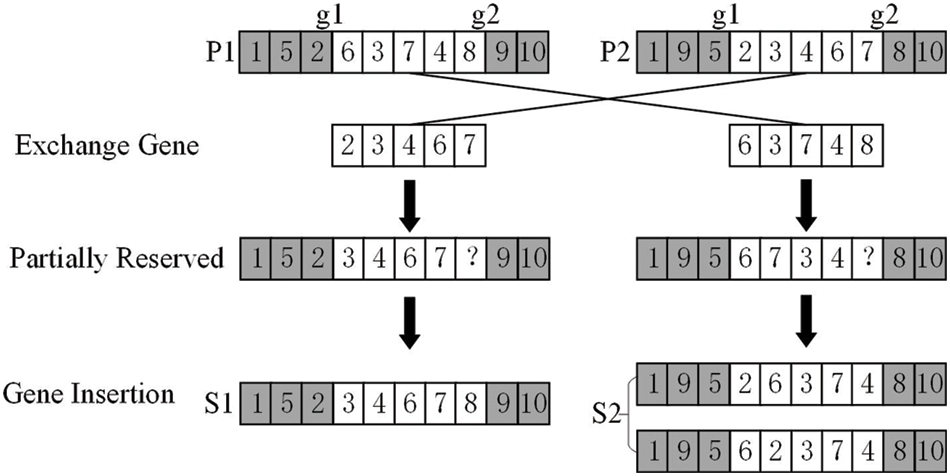
Figure 3: Schematic diagram of two-point intersection

4.3.2 Mutation Operation

In the genetic algorithm, the chromosome gene is disturbed by mutation operations to ensure the ability to jump out of the local optimal solution. In this paper, the mutation operation is carried out by improving the two-point exchange method. Two points are randomly selected on the parent chromosome, and the genes at these two positions are exchanged with the offspring. The mutation operation also adjusts the location of the mutant gene on the infeasible solution using the constraint adjustment method to ensure the effectiveness of the offspring chromosome. Based on the process route of Fig. 2, the parent chromosome is generated, and the two-point exchange mutation operation is performed as shown in Fig. 4.

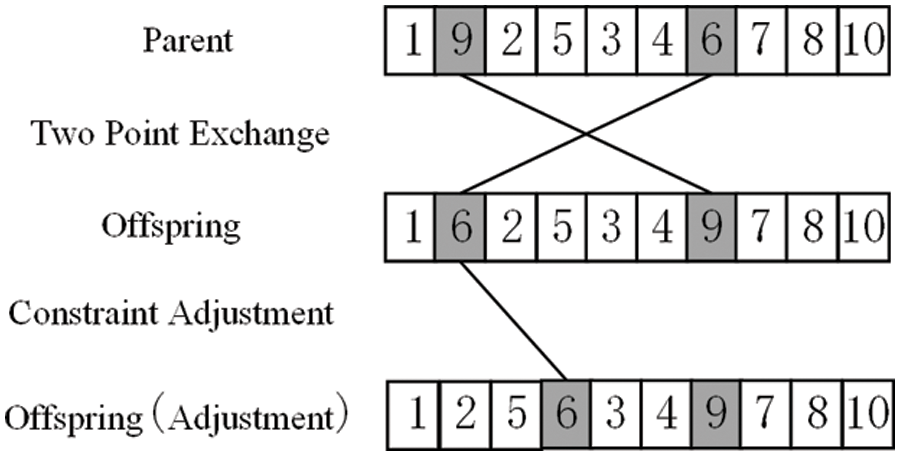
Figure 4: Schematic diagram of two-point exchange

4.4 Algorithm Framework

The flow chart of MOGA is shown in Fig. 5, and the specific execution steps of MOGA are as follows:

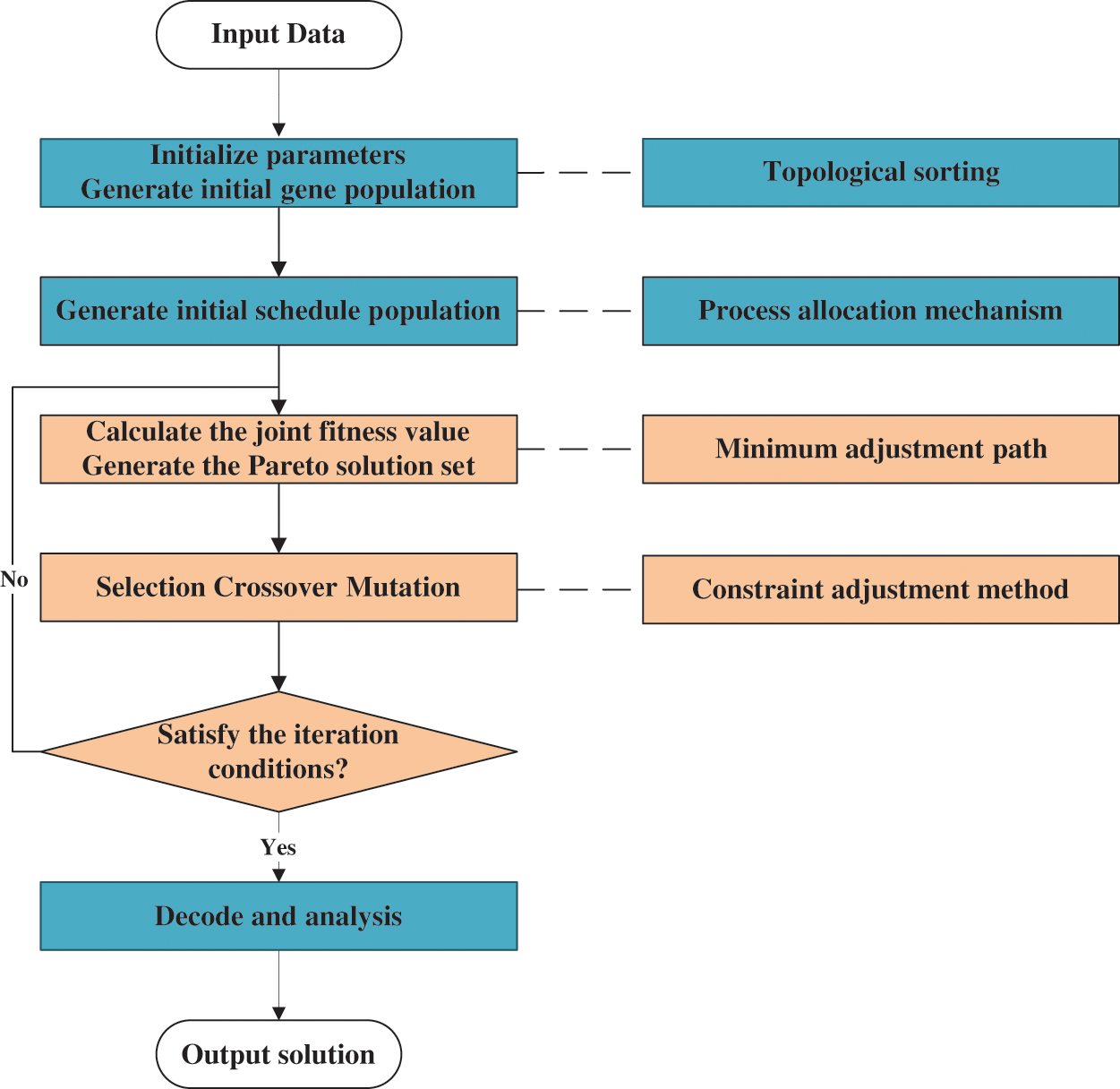
Figure 5: Flow chart of MOGA

Step 1: Obtain order and process information in the standard time database. Set the initial parameters of the multi-object genetic algorithm. The initial process chromosome population is generated by random topological sorting. The scheme chromosome is generated by the initial process chromosome population through the process allocation mechanism.

Step 2: Calculate the population fitness value and select the dual mechanism. Perform improved crossover and mutation operations.

Step 3: Judge whether the iteration termination condition is satisfied according to fitness and the maximum number of iterations.

Step 4: If the iteration termination condition is not satisfied, go to step 2 and repeat the above steps until the termination condition is satisfied. If the iteration termination condition is satisfied, decode the optimal solution and generate the assembly line scheme.

5  Experiments and Computational Results

This paper takes the workwear shirt production order of a garment company in Hangzhou as an example. This shirt contains 64 basic processes, which can be divided into 5 garment modules according to the parts of the garment pieces. Process constraints are shown in Fig. 6. The related processes of each process involve seven types of machines, such as flat cars, knife cars, computer flat cars, and four-line overlaid cars. Artificial operation does not require additional station space, so it is not included in the calculation of the number of station machine types. Process-related information is shown in Table 2. The process number corresponds to the process roadmap in Fig. 6.

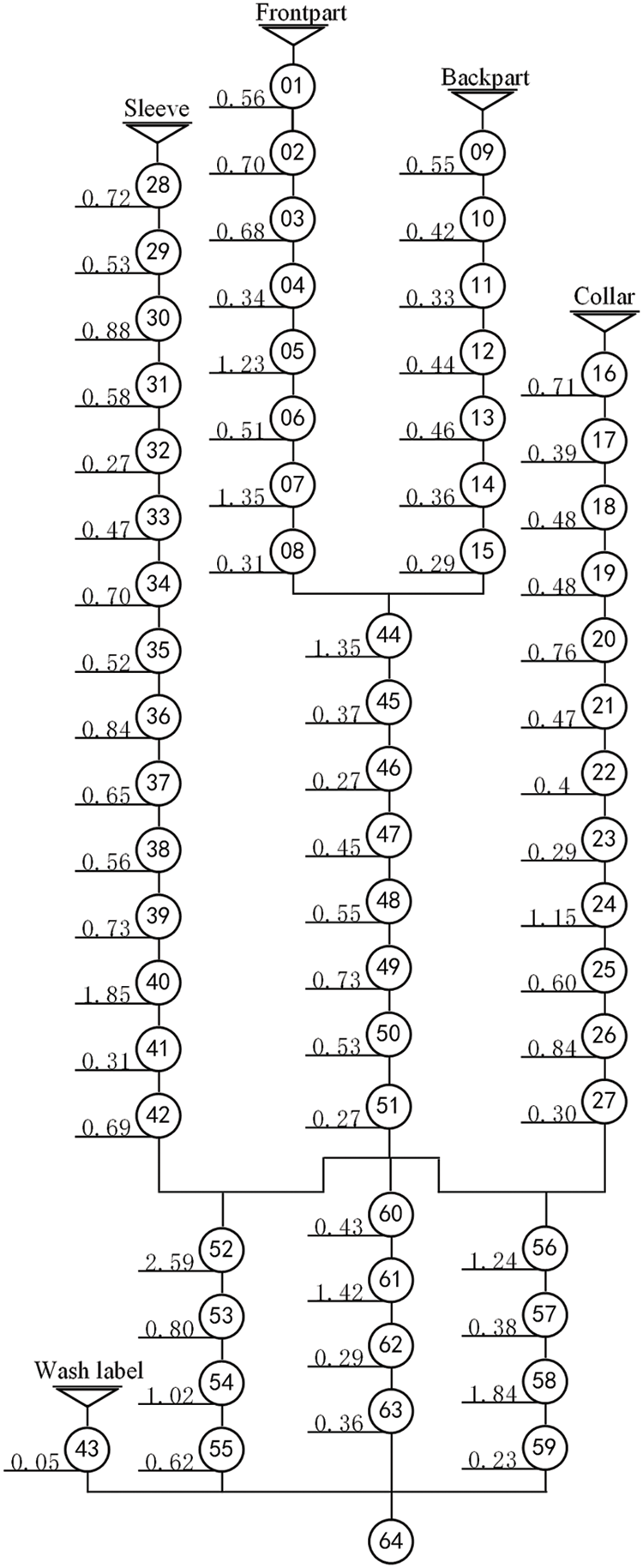
Figure 6: Shirt process roadmap

The assembly line scheme of the tooling shirt in this example is based on the artificial scheme of the garment workshop. According to the delivery requirements, there is a daily output of 200 shirts. The daily operation time of workers is 9 h. The example beat is 2.7 min. The standard working time for single-shirt sewing is 41.49 min. The theoretical minimum number of stations is 16. The population size is set to 50 in the hanging assembly line compilation scheme generation program. Then the topological sort selection probability is 0.5. The crossover probability is 0.6. The mutation probability is 0.05. The station’s production beat is 2.7. The maximum number of iterations is 200.

According to various methods of assembly line process allocation, the processing time and number of machine types for each station are shown in Table 3. In the artificial compilation scheme, the process time at the bottleneck station is 3.66 mins. The assembly line compilation efficiency is 70.93%, and the proportion of stations containing three types of machines is 43.75%. Compared to the artificial scheme compilation, MOGA and GA algorithms impose stricter control over station processing time and limit the number of machines used. The efficiency of traditional GA for assembly line configuration is 85.05%, with a bottleneck station processing time of 2.71 min. Compared to artificial scheme compilation, the assembly line efficiency has been improved by nearly 15%. The number of stations in the garment production line is usually 16, 18, 20, and 22. Due to the limitation of the number of station machine types, the number of stations in MOGA and GA has increased. The 18 stations of the final scheme are still of common scale.

Fig. 7 shows the joint fitness value iteration curve of the MOGA. In the production process, bottleneck process time that always exists at the same station will cause congestion in the hanging line. In order to improve the bottleneck station, some processes will be split into batches when the process inbound operation is carried out in programming. The corresponding process is periodically assigned to two fixed stations for the sewing operation. The bottleneck station will not be fixed in the same position. The efficiency of the assembly line will fluctuate within a certain range throughout the sewing stage. Compared to traditional genetic algorithms, MOGA further improves assembly line efficiency from 85.05% to 88.33% by integrating the mechanism of batch splitting of processes in the chromosome generation stage for scheme compilation. Fig. 8 shows the assembly line efficiency iteration curves of MOGA and GA.

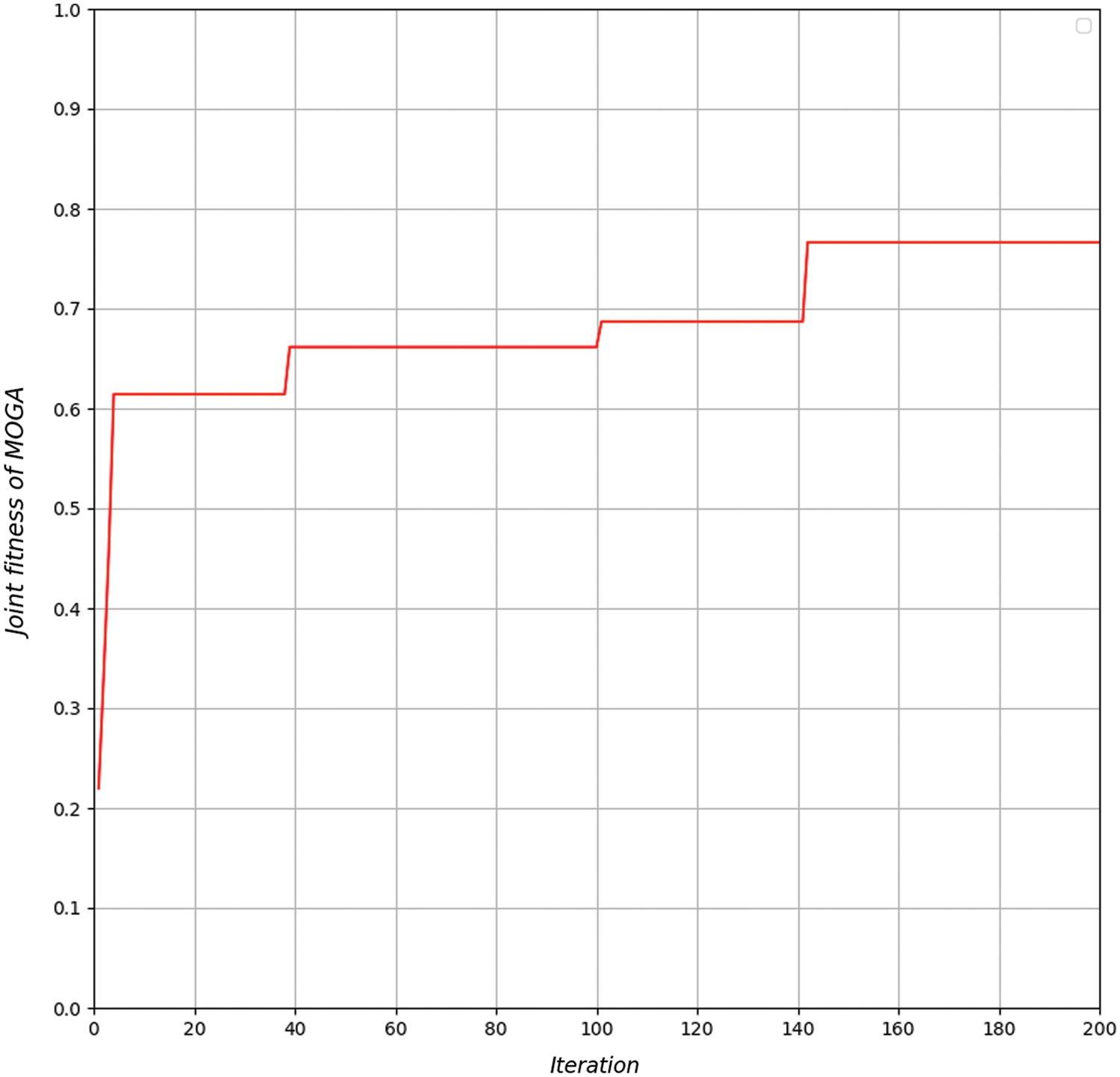
Figure 7: Joint fitness curve

Figure 8: Efficiency curve

Fig. 9 shows the machine adjustment path iteration curves. Observing the change curve during the iteration process reveals that, despite some instability, the machine adjustment path can converge. The assembly line efficiency of traditional genetic algorithms converges to the optimal value, but the corresponding machine adjustment path fluctuates dramatically. In MOGA, machine adjustment path is assigned weights and optimized. MOGA minimizes the machine adjustment path as one of its optimization objectives. Although there is a certain fluctuation due to the optimization of assembly line efficiency during the iteration process, the overall convergence can be effectively achieved. In this example, the final machine adjustment path of MOGA is 123.

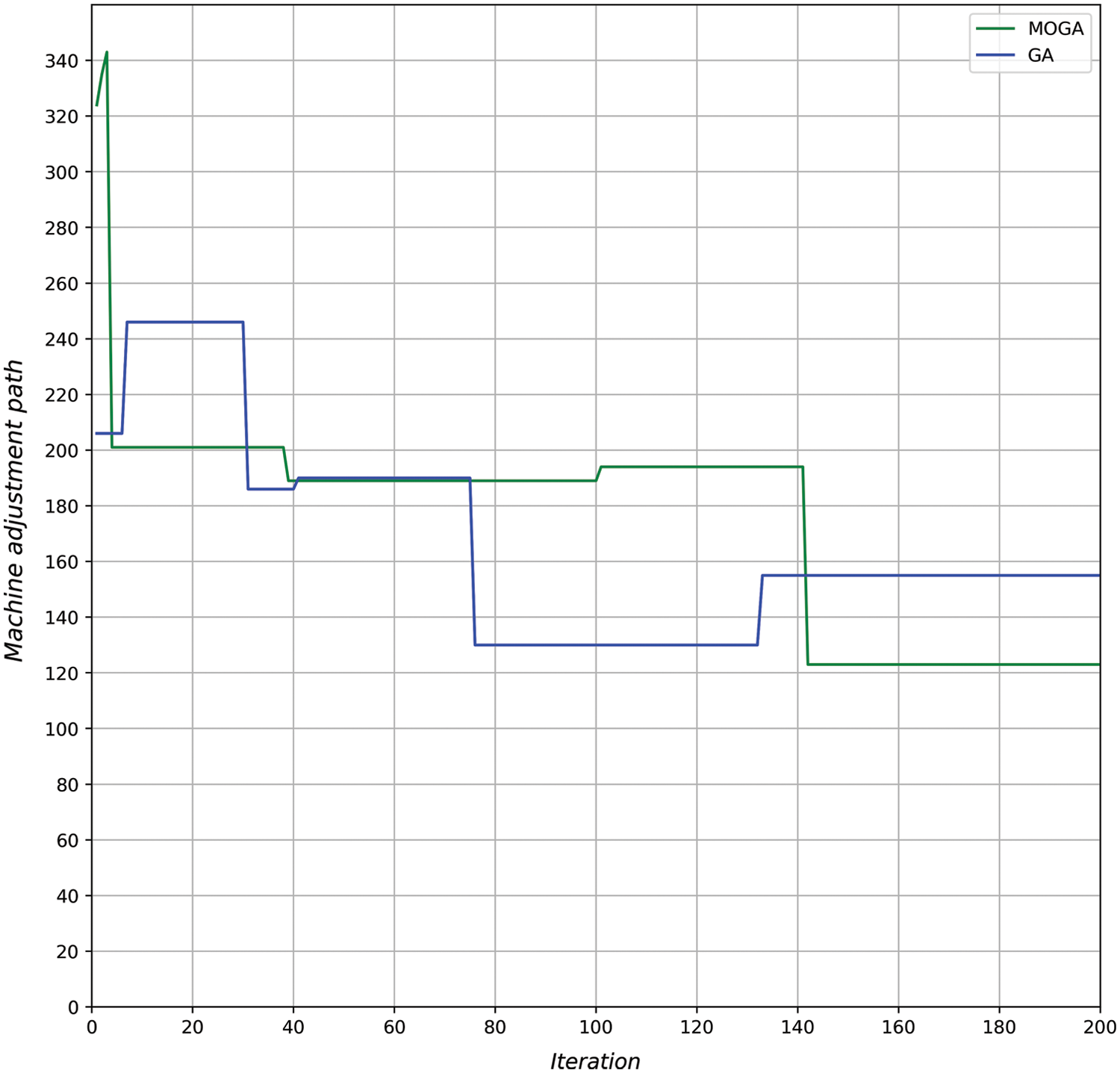
Figure 9: Machine adjustment path curve

Except for the shirt sample, this paper automatically compiles the orders of the leopard head single-collar shirt and horn pants of the garment company. The effectiveness of the multi-object genetic algorithm is further verified by comparing the compilation effects of artificial compilation schemes. Some process information and compilation efficiency of the two garments are shown in Table 4.

6  Conclusion

In this paper, we propose a solution to the scheduling problem in flexible garment workshops with the small-batch multiple-variety production mode. The proposed approach formulates a mathematical model that maximizes assembly line efficiency and minimizes the machine adjustment path based on the constraints of actual production. Further, a multi-objective genetic algorithm (MOGA) is developed by enhancing the population initialization, crossover, and mutation processes of traditional genetic algorithms. The MOGA-based scheduling approach has been empirically verified, utilizing real-life enterprise orders. The results suggest that MOGA is efficient in optimizing the processing sequences of garment hanging lines while complying with the requirements of flexibility and equipment constraints in garment manufacturing. Notably, MOGA generates a higher assembly line compilation efficiency (more than 10%) compared to artificial arrangement methods in multiple clothing scenarios. Importantly, MOGA considers machine adjustment paths as one of its optimization objectives to ensure minimum value convergence during iterations. As a result, the final production scheme can effectively accelerate the speed of assembly line machine adjustments for new orders and reduce downtime, thereby meeting the demand for the small-batch multi-variety production mode. These findings demonstrate the potential of MOGA-based approaches for designing multi-objective and multi-priority combinatorial optimization algorithms to help businesses achieve lean production goals.

During the MOGA solving process, various parameters, including fitness value weighting, crossover, and mutation probabilities, can significantly impact the final solution. To further optimize AI-based intelligent decision-making systems for flexible manufacturing pre-scheduling, we will focus on enabling autonomous learning, adaptation, and parameter adjustment during production. In this paper, we primarily design MOGA to perform pre-scheduling tasks for garment assembly lines. However, actual production processes are subject to real-time constraints, such as worker absence or machine failure, which require immediate adjustments to workflow allocation. Thus, in our future research, we plan to investigate real-time scheduling for garment job shops to handle unexpected events adequately.

Acknowledgement: We appreciate information such as garment process data in the article instance verification provided by Hangzhou Maidi Intelligence Technology Co. during the preparation of this manuscript (http://www.madest.com/service.html).

Funding Statement: This research was partly supported by Key R&D project of Zhejiang Province (2018C01005), http://kjt.zj.gov.cn/.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. M. Kim, J. Ahn, J. Kang and S. Kim, “A systematic review on smart manufacturing in the garment industry,” Fashion & Textile Research Journal, vol. 22, no. 5, pp. 660–675, 2020. [Google Scholar]

2. Z. P. Li, “Management decisions in multi-variety small-batch product manufacturing process,” International Journal of Simulation Modelling, vol. 21, no. 3, pp. 537–547, 2022. [Google Scholar]

3. K. Gao, Z. Cao, L. Zhang, Z. Chen, Y. Han et al., “A review on swarm intelligence and evolutionary algorithms for solving flexible job shop scheduling problems,” IEEE/CAA Journal of Automatica Sinica, vol. 6, no. 4, pp. 904–916, 2019. [Google Scholar]

4. L. Gao, Q. H. Liu, X. Y. Li and Q. J. Li, “A review of integrated process planning and workshop scheduling,” Industrial Engineering, vol. 25, no. 3, pp. 1–9, 2022. [Google Scholar]

5. A. Ala, A. Mahmoudi, S. Mirjalili, V. Simic and D. Pamucar, “Evaluating the performance of various algorithms for wind energy optimization: A hybrid decision-making model,” Expert Systems with Applications, vol. 221, no. 14, pp. 119731, 2023. [Google Scholar]

6. A. J. Radhia, “Review of artificial intelligence applications in garment manufacturing,” Artificial Intelligence for Fashion Industry in the Big Data Era, pp. 97–123, 2018. [Google Scholar]

7. W. Deng, J. Xu and H. Zhao, “An improved ant colony optimization algorithm based on hybrid strategies for scheduling problem,” IEEE Access, vol. 7, pp. 20281–20292, 2019. [Google Scholar]

8. G. Y. H. Chen, P. S. Chen, J. F. Dang, S. L. Kang and L. J. Cheng, “Applying meta-heuristics algorithm to solve assembly line balancing problem with labor skill level in garment industry,” International Journal of Computational Intelligence Systems, vol. 14, no. 1, pp. 1438–1450, 2021. [Google Scholar]

9. A. Goli, A. Ala and M. H. Keshteli, “Efficient multi-objective meta-heuristic algorithms for energy-aware non-permutation flow-shop scheduling problem,” Expert Systems with Applications, vol. 213, no. 8, pp. 119077, 2023. [Google Scholar]

10. M. Chica, J. Bautista and J. Armas, “Benefits of robust multi-objective optimization for flexible automotive assembly line balancing,” Flexible Services and Manufacturing Journal, vol. 31, no. 1, pp. 75–103, 2019. [Google Scholar]

11. T. Wang, R. Fan, Y. Peng and X. Wang, “Optimization on mixed-flow assembly U-line balancing problem,” Cluster Computing, vol. 22, no. S4, pp. 8249–8257, 2019. [Google Scholar]

12. Y. N. Yan, L. Z. Liu, B. Y. Luo and H. R. Cui, “Clothing production line compilation based on particle swarm optimization,” Textile Journal, vol. 3, no. 10, pp. 120–124, 2018. [Google Scholar]

13. X. J. Zhang, L. C. Wang and Y. Chen, “Balance optimization of garment sewing production line based on genetic algorithm,” Textile Journal, vol. 41, no. 2, pp. 125–129, 2020. [Google Scholar]

14. C. H. Qian and Y. B. Huang, “Balance design of clothing production mixed assembly line based on genetic algorithm,” Wool Textile Science and Technology, vol. 49, no. 5, pp. 75–79, 2021. [Google Scholar]

15. D. Agdas, D. J. Warne, J. O. Norgaard and F. G. Masters, “Utility of genetic algorithms for solving large-scale construction time-cost trade-off problems,” Journal of Computing in Civil Engineering, vol. 32, no. 1, pp. 4017072, 2018. [Google Scholar]

16. Z. Li, F. Xiong, L. Wang and H. Chen, “Research on prefabricated production scheduling based on hybrid algorithm of genetic and taboo search,” Computer Measurement and Control, vol. 28, no. 10, pp. 211–215, 2020. [Google Scholar]

17. H. Henderi, T. Wahyuningsih and E. Rahwanto, “Comparison of min-max normalization and Z-score normalization in the K-nearest neighbor (kNN) algorithm to test the accuracy of types of breast cancer,” International Journal of Informatics and Information Systems, vol. 4, no. 1, pp. 13–20, 2021. [Google Scholar]

18. Q. Liu, N. Wang, J. Li, T. Ma, F. Li et al., “Research on flexible job shop scheduling optimization based on segmented AGV,” CMES-Computer Modeling in Engineering & Sciences, vol. 134, no. 3, pp. 2073–2091, 2023. [Google Scholar]