Competitive and Cooperative-Based Strength Pareto Evolutionary Algorithm for Green Distributed Heterogeneous Flow Shop Scheduling

1  Introduction

With the development of international trade and the global economy, enterprises receive more and more orders. However, the traditional centralized manufacturing model cannot meet the fast-producing requirement of the market [1]. Because to occupy more parts of the market, the enterprises reduce the production due date in succession but the total processing time cannot be changed. Thus, the enterprise will open multiple factories to finish orders and this mode is called distributed manufacturing. Flow shop scheduling problems [2] are one of the most classical combinational optimization problems which have been deeply researched. As its extension problem, the distributed heterogeneous permutation flow shop scheduling problem (DHPFSP) has attracted more and more attention in recent years [3]. In DHPFSP, the processing time, machine number, machine type, worker number or et al. is different which makes DHPFSP has factory flexibility. Meanwhile, the DHPFSP is harder to solve than traditional distributed identical permutation flow shop scheduling problems. Thus, studying DHPFSP can provide theoretical guidance to practical manufacturing. With the growing global temperature, green scheduling gets more and more attention [4]. Moreover, total energy consumption (TEC) is the critical indicator that reflects carbon emissions. Thus, to ensure sustainable and green manufacturing, this work aims to minimize makespan and TEC in DHPFSP.

The main methods for DHPFSP include the iterative greedy algorithm [5], memetic algorithm [6], cooperative algorithm [7], Pareto-based genetic algorithm [8], and decomposition-based algorithm [9]. Moreover, Huang et al. [3] proposed a bi-roles co-evolutionary (BRCE) framework which can greatly balance computation resources between global and local searches. However, BRCE and previous works are hard to explore during the global search for the following reasons: i) They ignore the heuristic information of each solution. ii) The fast no-dominated sorting environment selection strategy can not balance convergence and diversity well.

Strength Pareto evolutionary algorithm (SPEA2) gets many concerns in multi-objective optimization problems due to its special fitness representation and good performance [10]. Thus, adopting SPEA2 for DHPFSP can balance convergence and diversity. Competitive swarm optimization (CSO) is also popular because CSO uses the heuristic information of each solution and lets the loser swarm learn from the winner swarm which accelerates the converging of global search [11]. So combining CSO and SPEA2 can improve the convergence of global search which is never proposed for DHPFSP before.

This study aims to resolve the green DHPFSP (GDHPFSP) by minimizing makespan and TEC. To solve GDHPFSP, a competitive and cooperative strength Pareto evolutionary algorithm (CCSPEA) is proposed for GDHPFSP. The main contributions are summarized as follows: 1) An improved fitness function from SPEA2 is used to represent the heuristic information of each solution. By combining the convergence metric and diversity metric, the comprehensive performance of each solution can be represented. 2) A competitive and cooperative genetic operator is proposed to rapidly converge. According to the heuristic information, the population can be divided into winner and loser swarms. Then, a cooperative genetic operator is designed for each swarm to accelerate converging. Finally, a separation experiment is designed on 22 DHPFSP instances. The results demonstrate the effectiveness of each improvement. Moreover, CCSPEA is compared to five state-of-arts and the results state the superiority of CCSPEA.

The rest of this manuscript is organized as follows: The literature review is introduced in Section 2. The description of DHPFSP are introduced in Section 3. Section 4 illustrates the proposed CCSPEA. The detailed results of the experiments are explained and discussed in Section 5. Finally, Section 6 concludes this work and discusses future directions.

2  Literature Review

2.1 Related Work of SPEA2

SPEA2 [10] has attracted much attention for multi-objective optimization problems due to its convergence speed and performance. Sahoo et al. [12] combined SPEA2 and particle swarm optimizer for electrical distribution systems optimization problems. Li et al. [13] applied the deep-q-learning algorithm to improve the performance of shift-based density estimation SPEA2 (SPEA2 + SDE). Xu et al. [14,15] applied SPEA2 in edge computing to optimize the Internet of Things. Liu et al. [16] adopted SPEA2 + SDE for the STATCOM allocation problem and got good results. Biswas et al. [17,18] adopted SPEA2 to charge transportation problems and get better performance than state-of-arts. Maurya et al. [19] used SPEA2 to smart home appliances scheduling problems and got the best results. Luo et al. [20] improved SPEA2 to find top-k solutions in preference-based multi-objective optimization problems and obtained great performance. Cao et al. [21] designed an improved SPEA2 based on the relationship propagation chain for iron-steel scheduling. Amin-Tahmasbi used to apply SPEA2 to solve flow shop problems and got good results [22]. Based on the introductions above, it is obvious that SPEA2 is an effective algorithm for the discrete multi-objective optimization problem.

2.2 Related Work of CSO

Instead of the traditional partial swarm optimizer (PSO) algorithm, a novel pairwise competitive schema-based swarm optimizer was proposed, which is called the competitive swarm optimizer (CSO) [11]. Unlike the classical PSO [23,24], CSO divides the population of each generation into a winner group and a loser group. Then, the winner only executes mutation to improve itself and the loser learns critical knowledge from the selected winner to generate a new solution.

{vl(t+1)=r0vl(t)+r1(xw(t)′−xl(t)′),xl(t+1)=xl(t)+vl(t+1),xw(t)′=xw(t)+r0vw(t),xl(t)′=xl(t)+r0vl(t),(1)

The CSO is proposed for the continuous optimization problem and the main learning schema is vector difference which is shown in Eq. (1). Due to its fast-learning feature, the CSO is usually used to solve multi/many-objective optimization problems (MOP) [25,26]. Gu et al. improved the initialization and learning strategies of CSO which can get better balance convergence and diversity [27]. Huang et al. considered parameter adaptive CSO to improve its intelligence [28]. Large-scale MOP is the main research field of CSO [29] and many improved CSO has been proposed. Mohapatra et al. designed a tri-competitive schema-based CSO to improve exploration [30–32]. Ge et al. proposed inverse modeling to update the winners to accelerate the convergence of CSO [33]. Liu et al. designed three different competitive schemas to improve the diversity of CSO [34]. Qi et al. designed the neighborhood search strategy to enhance CSO [35]. Chen et al. divided CSO into three phases and got better results than state-of-arts. Moreover, CSO also can be applied to constrained MOP [36], many-objective optimization problems [37], feature selection [38], and wireless sensor networks [39].

2.3 Related Work of DHPFSP

DHPFSP has attracted more and more attention in recent years. Chen et al. solved DHPFSP with the content machine speed by an improved estimation distribution algorithm which got better performance than state-of-arts [6]. Shao et al. designed several strategies of local search for DHPFSP to improve the convergence of the algorithm [40]. To balance the convergence and diversity, Li et al. improved the MOEA/D with the behavior of bee swarm for DHPFSP which enhances the convergence [9]. Zhao et al. developed a self-learning framework for operator selection that enhances the convergence of local search [41]. Mao et al. proposed the hash map to store the candidate solution which improves the ability of global search for DHPFSP [8]. Meng et al. considered DHPFSP with lot-streaming and sequence-dependent set-up time and proposed an algorithm of artificial bee colony to solve it [42]. Lu et al. combined hybrid flow shop and flow shop as DHPFSP [43]. Huang et al. proposed the BRCE algorithm for DHPFSP which divided global and local search into two populations and balanced convergence and diversity [3].

2.4 Research Gap and Motivation

The previous algorithm BRCE [3] gets the best performance on DHPFSP. However, there are some disadvantages to BRCE which are stated as follows: 1) The BRCE randomly selects a parent from the mating pool to generate offspring but does not use the heuristic information of population. However, CSO [11] can divide the population into a winner swarm and a loser swarm which can enhance global search by using the heuristic information of the population. 2) The BRCE adopts environment selection by fast non-dominated sorting which keeps convergence first and diversity later. This strategy always focuses on the last front of all fronts but considers little about crowded solutions in the former fronts. However, SPEA2 [10] can measure convergence and diversity by a comprehensive metric that can better balance the convergence and diversity of the whole population. Thus, SPEA2 is applied to better represent the heuristic information of each solution. 3) The BRCE executes crossover by particle match crossover (PMX) [3] to generate offspring. However, the decision space of DHPFSP is so large and PMX is too weak to sufficiently search the potential solutions.

Thus, based on the discussion above, this work proposed a competitive and cooperative strength Pareto evolutionary algorithm (CCSPEA) for DHPFSP to overcome the disadvantages of BRCE.

3  Problem Statement

In DHPFSP, there are total nf heterogeneous factories and n jobs. Each job needs to be processed by m stage in each factory and each stage has only one machine to process. Each machine Mf,k can adjust processing speed vf,i,k from {v1, …, v5} when processing job Ii. The every job’s original processing time on every stage in each factory is pof,i,j and the real processing time is pof,i,j/vf,i,k. Meanwhile, pof,i,j is different at the same stage in each factory. There are three sub-problems in DHPFSP: i) determine the factory assignment of each job; ii) ensure the processing sequence of all jobs in every heterogeneous factory; and iii) assign a processing speed for each job on each stage of the machine. The objectives are to minimize makespan and TEC. It is worth noting that the machine work power is prf,i,j * vf,i,k2.

DHPFSP’s assumptions of in this work are described in following parts: i) At time zero, every job starts being processed at stage one. ii) All machines are not allowed to process other jobs when it is processing one job. iii) Each job can only be assigned to single factory. Meanwhile, every job is not permitted to be processed on two different machines at the same time. iv) Every machine’s energy consumption of and processing times of each job is certain. v) Transportation and setup constraints are not studied. Furthermore, dynamic events are not studied. vi) Every job’s processing time of on the same stage in different heterogeneous factories is different.

The MILP model is the same as reference [3]. Thus, the notations and model are not introduced in this work.

4  Our Approach: CCSPEA

4.1 Framework of CCSPEA

Algorithm 1 states the framework of CCSPEA. First, CCSPEA is an improvement of BRCE [3], and CCSPEA also divides global and local searches into two swarms P and C. Meanwhile, P is initialized by three heuristic rules to permit great convergence and diversity. Second, P will be divided into winner W and loser L by competitive strategy. Next, the cooperative evolution is adopted to let L learn from W and accelerate converging. Then, W executes self-evolution to search for potential non-dominated solutions. Moreover, after the environmental selection, multiple neighborhood structure search and energy-saving strategies are adopted to enhance convergence. In the end, the ultimate non-dominated solutions set is got from consumer swarm C.

4.2 Encoding and Decoding

Encoding schema: In proposed approach CCSPEA, job sequence (JS), factory assignment (FA), and speed selection (SS) are represented by two vectors and a matrix. Fig. 1 shows the encoding schema for DHPFSP. In FA and SS, the job order is from J1 to Jn and the correspondence is unchangeable. Nevertheless, the job processing order in JS needs to be permuted. The jobs reflection sequence for FA and SS is always from I1 to In which is unchangeable and the job sequence for JS can be changed.

Figure 1: The solution representation of DHPFSP

Decoding schema: First, according to the FA vector, each job is assigned to the selected heterogeneous factories. Second, the processing sequences of all jobs in each factory are got from the JS vector. Then, all jobs are processed from stage one to m. Meanwhile, the actual processing time is calculated by the original processing time divided by speed vi,k in SS. Definitively, after all jobs are processed through all stages, the TEC and the maximum finish time (makespan) are able to be obtained.

4.3 Initialization

Initialization is a critical step for shop scheduling problems [4]. By high-quality initialization, the algorithm only pays little computation resource, and an initialization population with great convergence and diversity can be got. Algorithm 2 illustrates the detailed procedure of heuristic initialization. First, randomly generate part of JS, FA, and SS. Then, generate ps/10 SS with maximum speed and generate ps/10 SS with minimum speed. Finally, generate ps/5 FA by selecting a factory with the minimum workload. If several factories have the same workload, choose the factory with the minimum T. The rest of ps*3/5 is supplemented by a random rule. Initializing part of solutions with min or max speed can rapidly get close to the bounds of makespan and TEC. Because the processing time of each job is the smallest when the speed selection is the max and the makespan of a solution converge to the lower bound. Similarly, the TEC converges rapidly when the speeds of all jobs are the smallest. Moreover, applying the workload balance rule can efficiently reduce makespan and makes solutions converge. Thus, those solutions initialized by heuristic rules have great convergence. Meanwhile, the rest solutions of the population are initialized by the random rule and they bring great diversity to the initialization population.

4.4 Competitive Selection

Inspired by CSO [11] and SPEA2 [10], this work proposed a competitive selection strategy to accelerate converging. The original competitive strategy of CSO is one-to-one competition and a loser solution learns from the winner solution by differential operator shown in Eq. (1). However,

DHPFSP is a discrete optimization problem and this strategy is not suitable. Thus, we designed an implicit competition according to comprehensive performance. Different from NSGA-II [44], SPEA2 has a more efficient comprehensive evaluation strategy. Thus, producer population P is divided into winner and loser swarms by fitness of SPEA2. Algorithm 3 shows the detailed procedure. First, count the domination relationship between all solutions. Then, add up the number of being dominated of each solution as its convergence point. Next, calculate the closest Euclidean distance of each solution to others and use Di in line 20 as the diversity point of each solution. Finally, add Ri and Di as comprehensive fitness, and sort it by ascending. The lower SF, the better performance. Thus, the first half of the sorted population is regarded as the winner swarm and the other half of the population is the loser swarm.

This strategy can rapidly assign different roles to all solutions by using its heuristic information (i.e., comprehensive fitness). After competitive selection, we design different evolutionary operators to faster converging of winner and loser swarms.

4.5 Cooperative Evolution and Self-Evolution

According to CSO [11], the loser needs to learn from the winner to accelerate convergence. In DHPFSP, the crossover operator can maximize the exchange of valid information. Thus, the quality of crossover is critical to exploration. In our approach CCSPEA, the universal crossover (UX) [45] and precedence operation crossover (POX) [1] are applied as learning operators which are shown in Fig. 2. As for POX, the job set I is randomly divided into two sets A = {1, 4} and B = {2, 3, 5}. Then, move the jobs belonging to set A from JS1 to the new empty solution JS3 and move jobs from B in JS2 to JS4. Next, fill the empty spaces in JS3/JS4 by jobs of set B/A from JS2/JS1 in the same order. As for UX, a random 0–1 vector R size n is generated. Exchange the genes of FA1 and FA2 when the value of the same position Ri = 1, i = 1,…,n. Moreover, the procedures of cooperative evolution and self-evolution are shown in Fig. 3.

Figure 2: POX for JS, and UX for FA and SS

Figure 3: Cooperative evolution and self-evolution

Cooperative evolution: To accelerate loser swarm converging, each loser will randomly select a solution from the winner swarm and execute the crossover operator.

Self-evolution: In the original CSO [11], the winner only adopts a mutation operator to update itself. However, due to the complexity of DHPFSP, each winner will execute the crossover operator by randomly selecting another winner. Moreover, each offspring will adopt three mutation operators with probability Pm to enhance diversity. As for JS, randomly select two jobs and exchange their positions. For FA, randomly select a job and move it to another factory. For SS, randomly select a stage of a random job and change its speed selection.

Environmental selection: To enhance convergence, the child solutions obtained from the evolution operators are combined with the population P. Then, select the new population from the combined population by fast non-dominated sorting and crowding distance strategy [44].

4.6 Local Search

In DHPFSP, designing neighborhood sturctures referring to problem knowledge could enhance convergence better. According to DHPFSP’s features mentioned in [3]. A variable neighborhood search strategy is proposed to enhance the convergence of the consumer population. Algorithm 4 states its procedure. Firstly, search the critical path of a solution Ci. Next, randomly choose a neighborhood structure to generate offspring S. Finally, if the child solutions can not be dominated by the original solution, it would be added to the consumer population to improve diversity.

4.7 Energy-Saving Strategy

For green shop scheduling, the energy-saving strategy is the key procedure to lower TEC [4]. BRCE [3] has stated the problem features. This work proposed an energy-saving strategy by adjusting the speed of a solution. Algorithm 5 describes the detailed procedure of the energy-saving strategy. First, the processing flow on the first machine is determined. Second, compare Fi,k − 1 and Fi − 1,k to judgment whether the idle time is generated by operation Ii,k − 1 or Ii − 1,k. Then, decrease the speed of the former speed to reduce energy consumption. After traversing all operations, the TEC can be decreased.

Fig. 4 shows an example of how the energy-saving strategy reduces TEC. As for O22, comparing finish time F1,2 of O12 and finish time F2,1 of O21 can find there is an idle gap between O22 and O12. Thus, this is the type one that the finish time of the adjacent process on the same machine is less than the finish time of the previous operation of the same job. Moreover, reduce the speed of O12 and the idle time is reduced. So TEC is reduced. As for O32, comparing finish time F3,1 of O31 and finish time F2,2 of O22 can find there is a gap that can be increased to reduce TEC and not increase the makespan. Thus, this is type two and reduce the speed of O31 to reduce the TEC.

Figure 4: An example of energy-saving strategy

5  Results of Numerical Experiment

Our approach CCSPEA is detailedly introduced in Section 4. To test the effectiveness of CCSPEA, the parameter, ablation, and comparison experiments are adopted. All algorithms are coded in MATLAB2020 and the experimental environments are on an Intel(R) Xeon(R) Gold 6246R CPU @ 3.4 GHz with 384G RAM.

5.1 Instances and Metrics

The dataset used in this work is from [3] which contains 22 different scales of instances. The number of jobs is from 20 to 200. Moreover, the amount of factories is from two to three. The machine number is from five to 20. There are totally five levels for speed selection which are vf,i,k∈{1, 2, 3, 4, 5}. Moreover, the processing time of each job on the same stage is disparate in each factory. The processing power WO = 2.0kWh and the idle power WI = 1.0kWh. Moreover, each instance is defined by n_m_nf. The stop criteria are MaxNEFs = 400 * n ≥ 2 * 104.

To measure the performance of each algorithm, three types of metrics in multi-objective optimization problem are used, which are generation distance (GD) [44], Spread [44] and hypervolume (HV) [46]. The higher HV, the better the comprehensive performance. If a algorithm gets smaller GD and Spread, it has the better convergence and diversity.

5.2 Parameter Analysis Experiment

The parameter setting seriously affects an algorithm’s performance for solving DHPFSP. The CCSPEA has three parameters including population size ps, mutation rate Pm of the new solution, and the starting threshold Et of energy-saving. To simplify the parameter experiment, a design-of-experiment (DOE) Taguchi method [47] is adopted to adjust the parameter of CCSPEA. Moreover, the parameters’ levels are designed following: Et = {0, 0.5, 0.9}; ps = {100, 150, 200}; Pm = {0.1, 0.15, 0.2}. An orthogonal table L9 (33) is used for parameter experiment. For a fair comparison, every parameter variant algorithm independently runs ten times under stop criteria (MaxNFEs = 400 * n). Moreover, the average values of HV, GD and Spread metrics for each run are recorded. Figs. 5 and 6 show three main effects plots and interaction plots of all parameters on HV, GD, and Spread metrics. Based on comprehensive observation, the best parameter configuration of CCSPEA is that ps = 150, Pm = 0.15, and Et = 0.9.

Figure 5: Main effects plots of HV, GD, and spread metrics

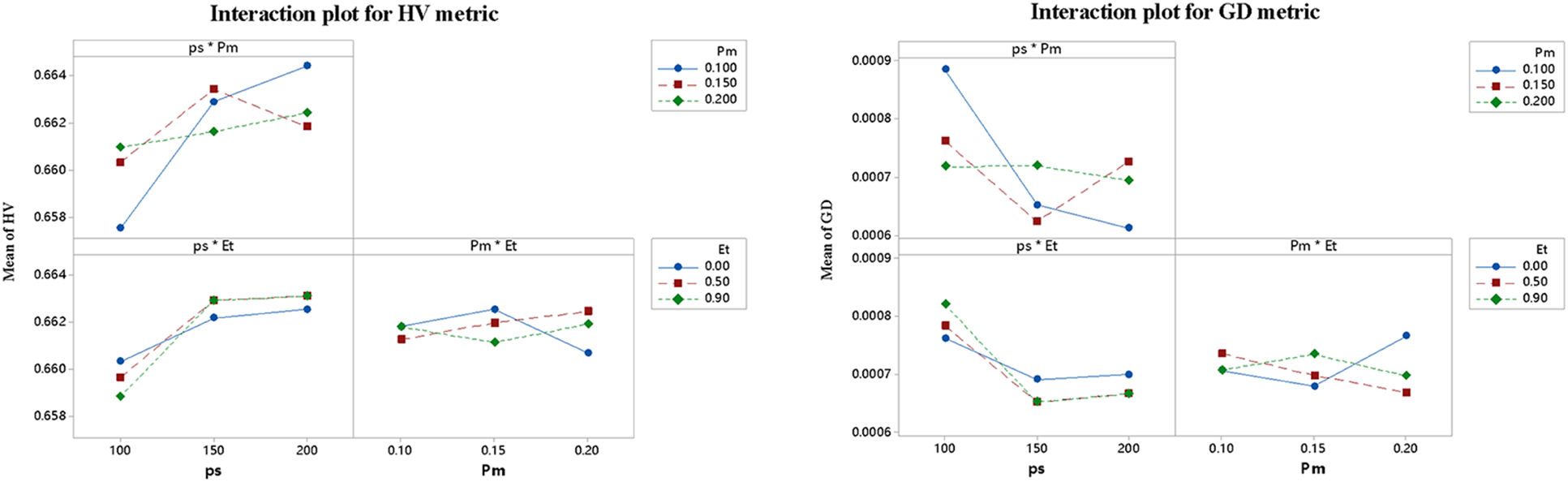
Figure 6: Interaction plots of HV, GD, and spread metrics

5.3 Components Separation Experiment

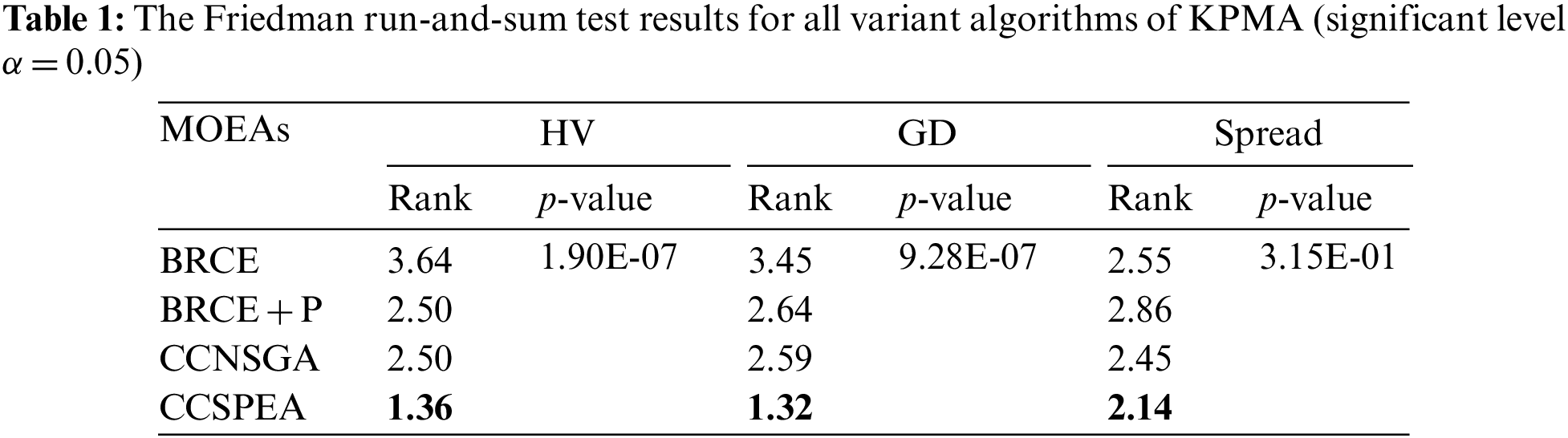
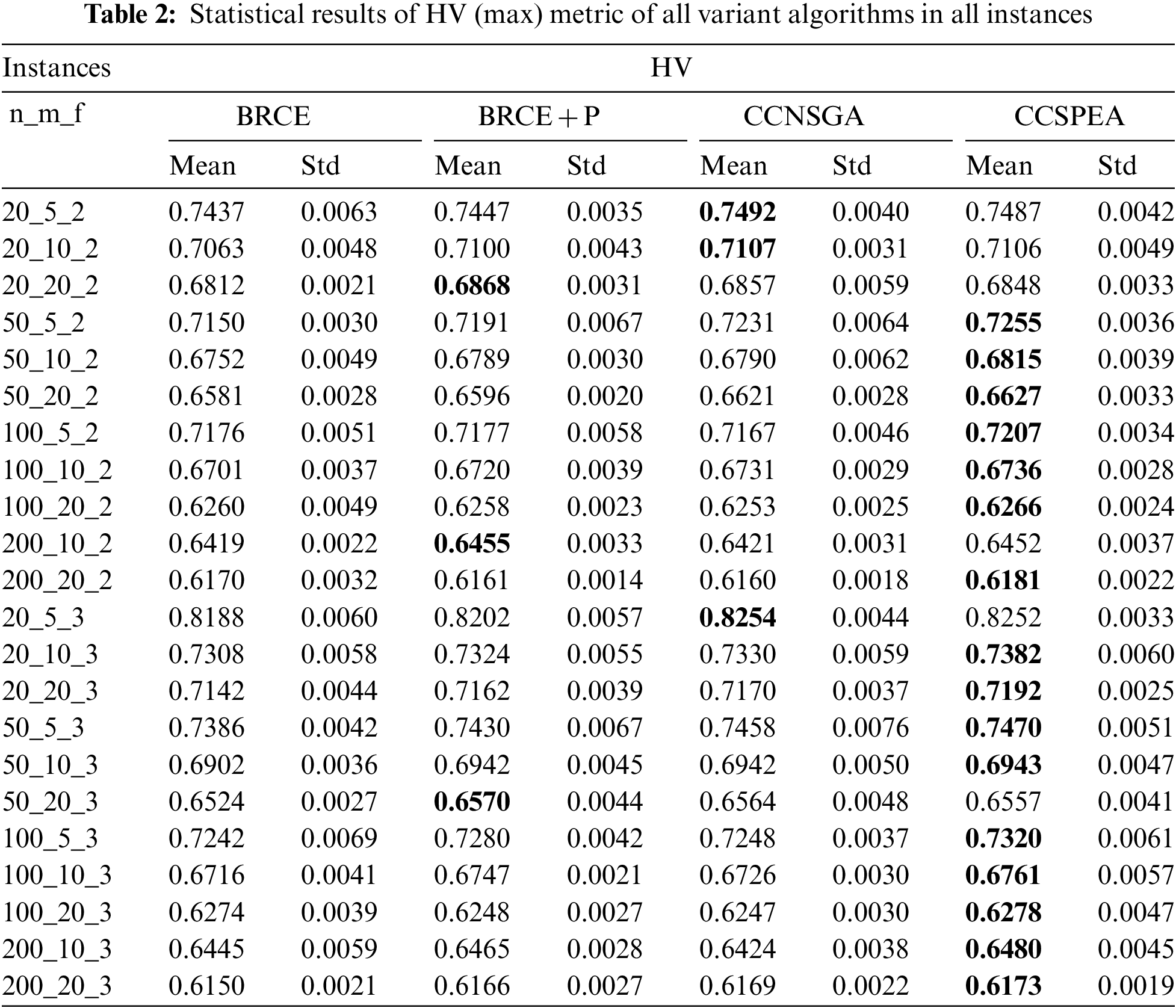
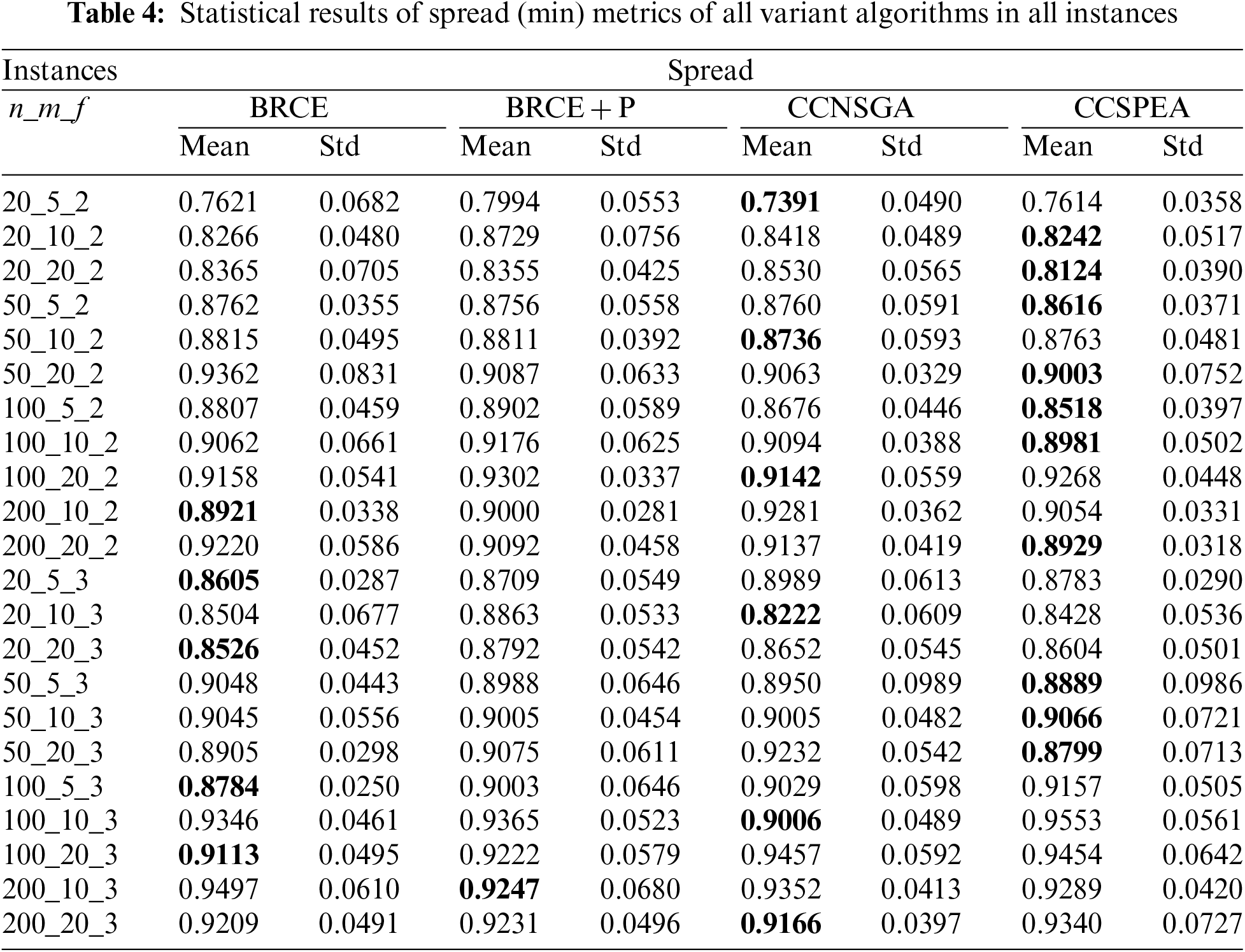
To evaluate the effectiveness of each improvement proposed in this work, four variant algorithms are created which are: i) BRCE is the original algorithm with heuristic initialization, local search, and energy-saving strategies whose effectiveness has been evaluated in [3]; ii) BRCE + P is BRCE with POX which replaces the original particle match crossover; iii) CCNSGA is BRCE + P with competitive selection and cooperative evolution. But the competitive strategy is based on fast non-dominated sorting which does not use the heuristic information of solution; vi) CCSPEA uses SPEA2 fitness to measure the comprehensive performance in CCNSGA. For a fair comparison, every variant algorithm independently executes ten times under stop criteria (MaxNFEs = 400 * n ≥ 2 * 104).

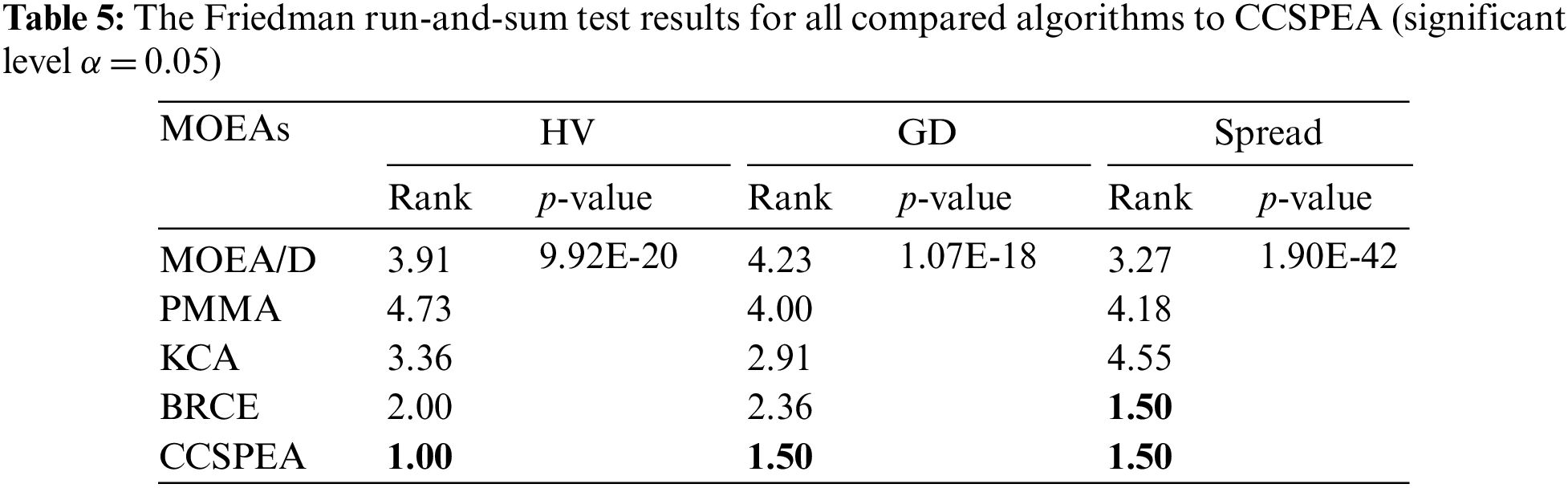
Tables 2–4 state the statistical results of HV, GD, and Spread metrics of all variant algorithms. The best values of each metric are marked by bold. Furthermore, Table 1 shows the Friedman rank-and-sum test results with confidence level α = 0.05. Based on the results, several conclusions are got: 1) By comparing BRCE + P and BRCE, the BRCE + P has higher rank representing that the POX crossover operator can effectively improve the convergence. 2) By comparing CCNSGA with BRCE + P, CCNSGA has higher GD and Spread rank which states that the proposed cooperative evolution can effectively improve diversity and convergence. 3) Comparing CCSPEA and CCNSGA can prove the effectiveness of the proposed competitive selection based on SPEA2 fitness. 4) The p-value is less than 0.05, which means a significant difference between all variants.

5.4 Comparison Experiment and Discussions

A comparison experiment is designed to further test the performance of CCSPEA, CCSPEA is compared to four state-of-arts: MOEA/D [48], PMMA [6], KCA [7], and BRCE [3]. The parameter of each comparison algorithm is set with the best parameters according to their references. As for PMMA [6], the elite rate β = 0.2, update rate α = 0.1, and population size ps = 40. For MOEA/D, BRCE, and CCSPEA, the crossover rate Pc = 1.0, mutation rate Pm = 0.15, and population size ps = 100. For KCA [7], the population size ps = 10, energy-efficient rate PE = 0.6, and local search times LS = 100. The neighborhoods updating range for MOEA/D T = 10. For a fair test, all MOEAs have the same stop criteria (MaxNFEs = 400 * n ≥ 2 * 104) and all MOEAs run 20 independent times on 22 instances.

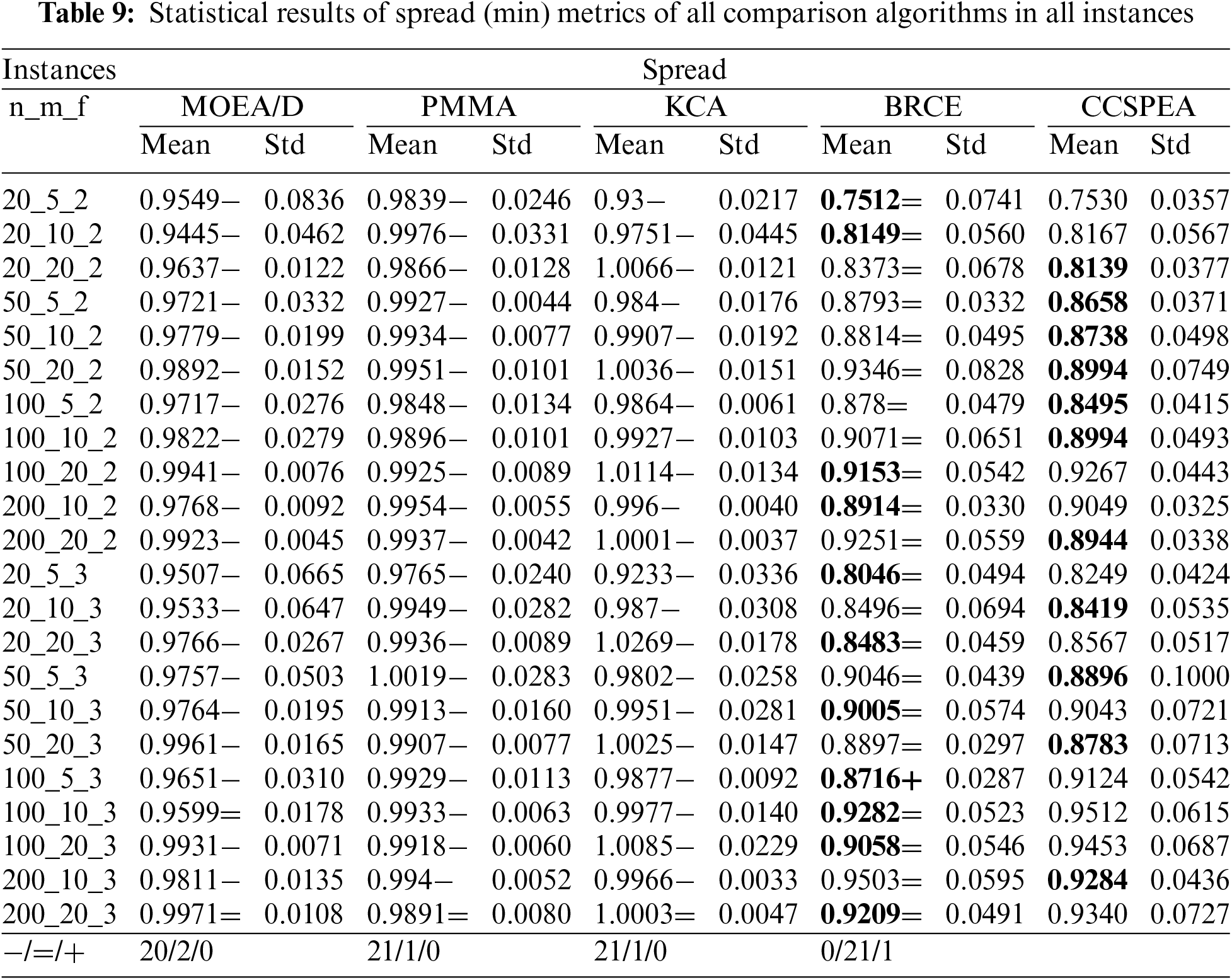
Tables 7–9 show the statistical results of HV, GD, and Spread metrics for all MOEAs. Furthermore, the notations “−” and “+” represent that the compared algorithms are significantly worse or better than CCSPEA. Notation “=” states that there is no significant difference between compared algorithm and CCSPEA. In addition, the optimal values are marked in bold. Based on the results of Tables 7–9, as for HV and GD metrics, CCSPEA is significantly superior to all comparison algorithms, which means CCSPEA has better convergence and comprehensive performance than others. About the Spread metric, CCSPEA is significantly better than KCA, PMMA, and MOEA/D over twenty test problems due to its design. However, the CCSPEA has no significant difference from BRCE because the bi-roles co-evolutionary framework in BRCE can vastly improve diversity. Table 5 shows the results of Friedman rank-and-sum test of all compared MOEAs on all test problems with a confidence level α = 0.05. CCSPEA ranks the best for HV, GD and Spread metrics and the p-value ≤ 0.05, stating that CCSPEA is significantly superior to the compared MOEAs. Table 6 shows the results of the Wilcoxon test for comparing CCSPEA to other algorithms on all metrics which are one-to-one statistical tests. The R+/R− means CCSPEA is better/worse than the compared algorithm. The gap between R+ and R− is bigger, the CCSPEA is significantly better than compared algorithm where the p-value is smaller than 0.05. Based on observation, CCSPEA is significantly superior to all MOEAs on HV metric which means CCSPEA has the best comprehensive performance. As for GD metric, CCSPEA is significantly superior to all algorithms except KCA. Because KCA has only 10 solutions and converges to the middle part of all non-dominated solutions. Thus, KCA has better convergence than CCSPEA on large-scale instances. As for Spread, CCSPEA is significantly better than all algorithms except BRCE. Because BRCE also applies the co-evolutionary framework which brings great diversity.

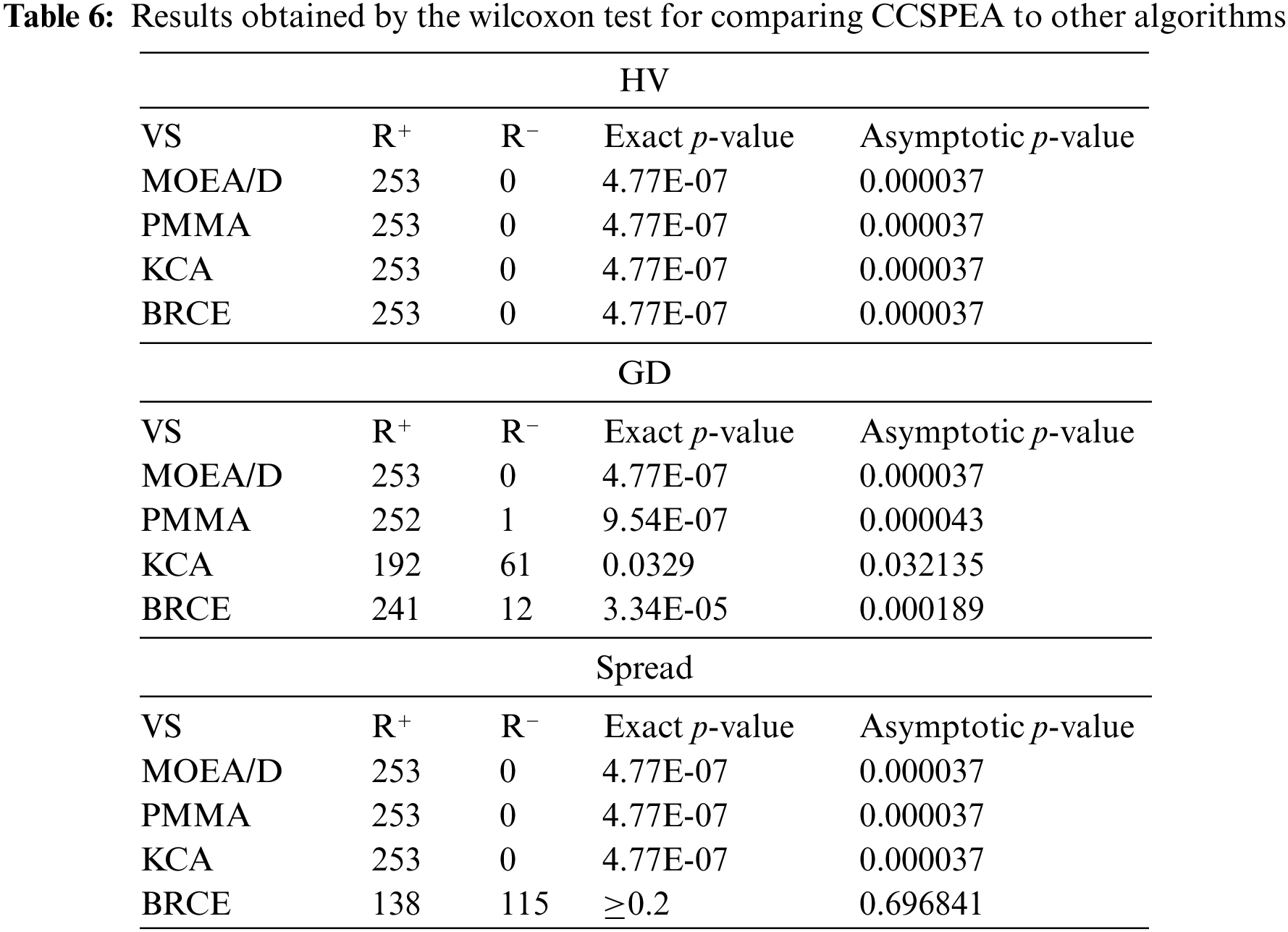
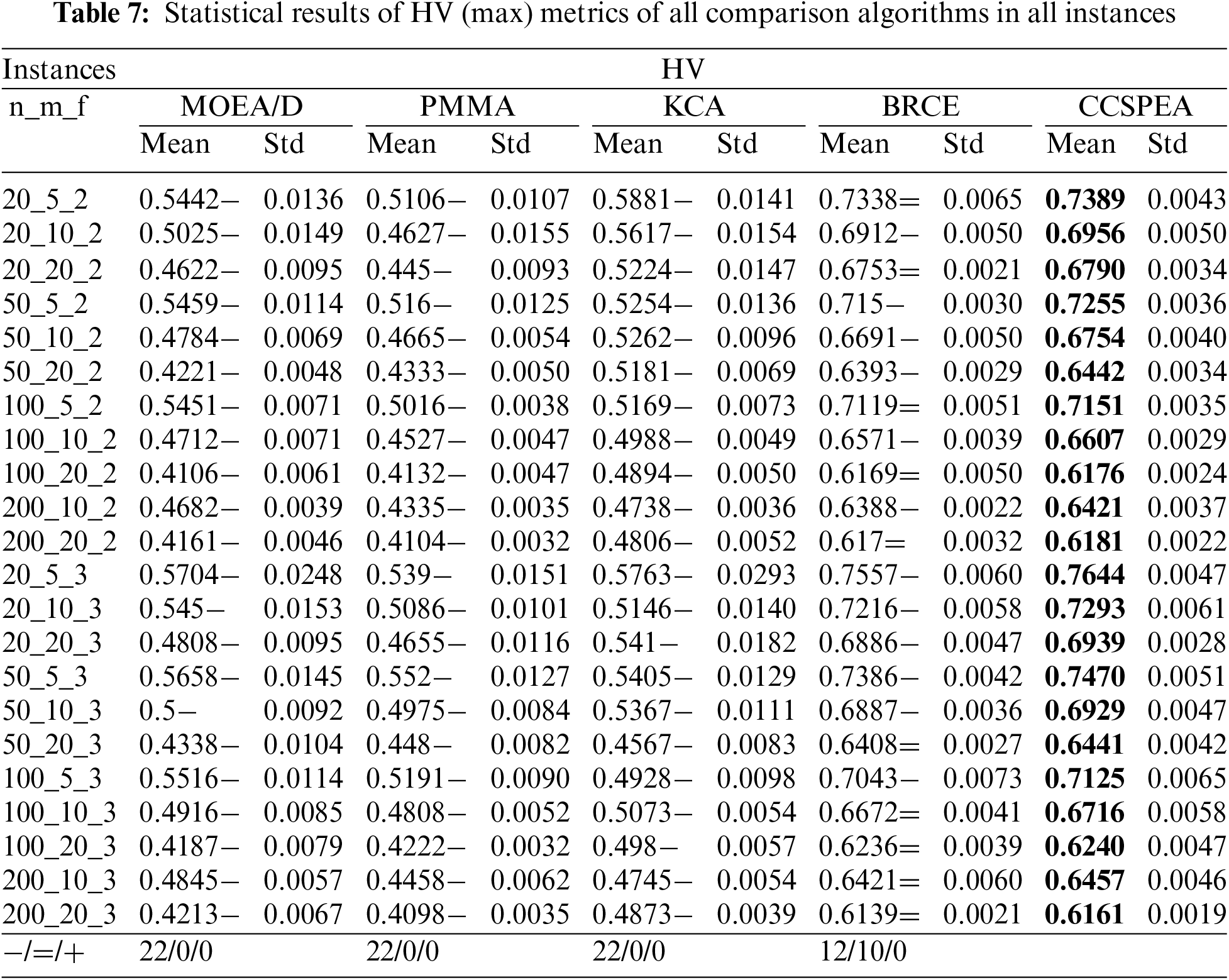
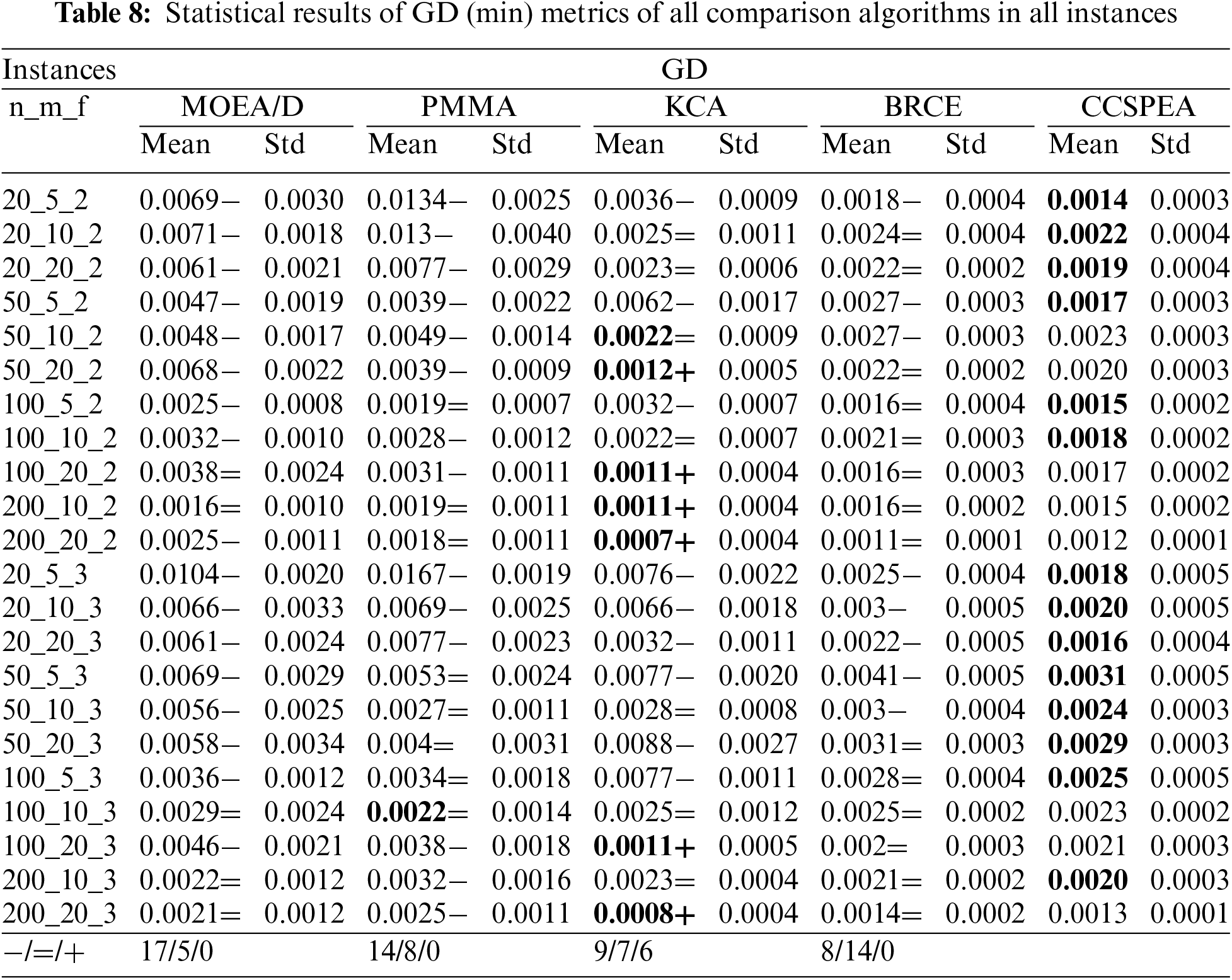
The success of CCSPEA is because of its design. First, the proposed POX operator has a larger step that can search more space than BRCE. Second, the designed competitive selection sufficiently uses the heuristic information (i.e., convergence, diversity, and rank) to help the solution select the crossover parent. Next, the cooperative evolution and self-evolution accelerate losers converging and let the winner further explore objective space. Finally, several efficient problem-based strategies such as heuristic initialization, VNS, and energy-saving improve the convergence. Furthermore, Fig. 7 displays the PF comparison results. Each MOEA selects the PF result with the best HV metric from 20 runs. As for the diversity and convergence of PF, CCSPEA has better Pareto solutions results than all comparison MEOAs, representing that CCSPEA has stronger ability to search Pareto solutions and get closer to practical PF.

Figure 7: PF comparison results of all algorithms on 20_5_2

6  Conclusions

This work proposed a competitive and cooperative strength Pareto evolutionary algorithm for GDHPFSP. First, a competitive selection is proposed to divide the population into two swarms according to heuristic information. Second, cooperative evolution and self-evolution are designed for winner and loser swarms to accelerate convergence. Next, POX is adopted to generate a larger step to search objective space. Then, several problem-based strategies such as heuristic initialization, VNS, and energy-saving strategy are proposed to enhance exploitation. In the end, the results of detailed experiments show that CCSPEA is significantly superior to four comparison MOEAs in terms of finding PF with better diversity and convergence.

Some future tasks are discussed following: i) apply competitive strategy to other shop scheduling problems; ii) design a more efficient environmental selection strategy; and iii) consider the reinforcement learning in CCSPEA.

Funding Statement: This work was partly supported by the National Natural Science Foundation of China under Grant Nos. 62076225 and 62122093, and the Open Project of Xiangjiang Laboratory under Grant No 22XJ02003.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. R. Li, W. Gong, L. Wang, C. Lu and S. Jiang, “Two-stage knowledge-driven evolutionary algorithm for distributed green flexible job shop scheduling with type-2 fuzzy processing time,” Swarm and Evolutionary Computation, vol. 74, pp. 101139, 2022. [Google Scholar]

2. Y. Pan, K. Gao, Z. Li and N. Wu, “Improved meta-heuristics for solving distributed lot-streaming permutation flow shop scheduling problems,” IEEE Transactions on Automation Science and Engineering, pp. 1–11, 2022. [Google Scholar]

3. K. Huang, R. Li, W. Gong, R. Wang and H. Wei, “BRCE: Bi-roles co-evolution for energy-efficient distributed heterogeneous permutation flow shop scheduling with flexible machine speed,” Complex & Intelligent Systems, 2023. [Online]. Available: https://doi.org/10.1007/s40747-023-00984-x [Google Scholar] [CrossRef]

4. R. Li, W. Gong, C. Lu and L. Wang, “A Learning-based memetic algorithm for energy-efficient flexible job shop scheduling with type-2 fuzzy processing time,” IEEE Transactions on Evolutionary Computation, pp. 1–1, 2022. [Google Scholar]

5. C. Lu, L. Gao, J. Yi and X. Li, “Energy-efficient scheduling of distributed flow shop with heterogeneous factories: A real-world case from automobile industry in China,” IEEE Transactions on Industrial Informatics, vol. 17, no. 10, pp. 6687–6696, 2021. [Google Scholar]

6. J. Chen, L. Wang, X. He and D. Huang, “A probability model-based memetic algorithm for distributed heterogeneous flow-shop scheduling,” in IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, pp. 411–418, 2019. [Google Scholar]

7. J. -J. Wang and L. Wang, “A Knowledge-based cooperative algorithm for energy-efficient scheduling of distributed flow-shop,” IEEE Transactions on Systems, Man, and Cybernetics: Systems, vol. 50, no. 5, pp. 1805–1819, 2020. [Google Scholar]

8. J. -Y. Mao, Q. -K. Pan, Z. -H. Miao, L. Gao and S. Chen, “A hash map-based memetic algorithm for the distributed permutation flowshop scheduling problem with preventive maintenance to minimize total flowtime,” Knowledge-Based Systems, vol. 242, pp. 108413, 2022. [Google Scholar]

9. H. Li, X. Li and L. Gao, “A discrete artificial bee colony algorithm for the distributed heterogeneous no-wait flowshop scheduling problem,” Applied Soft Computing, vol. 100, pp. 106946, 2021. [Google Scholar]

10. E. Zitzler, M. Laumanns and L. Thiele, “Spea2: Improving the strength pareto evolutionary algorithm,” Tech. Rep., 2001. [Google Scholar]

11. X. Zhang, X. Zheng, R. Cheng, J. Qiu and Y. Jin, “A competitive mechanism based multi-objective particle swarm optimizer with fast convergence,” Information Sciences, vol. 427, pp. 63–76, 2018. [Google Scholar]

12. N. C. Sahoo, S. Ganguly and D. Das, “Multi-objective planning of electrical distribution systems incorporating sectionalizing switches and tie-lines using particle swarm optimization,” Swarm and Evolutionary Computation, vol. 3, pp. 15–32, 2012. [Google Scholar]

13. M. Li, Z. Wang, K. Li, X. Liao, K. Hone et al., “Task allocation on layered multiagent systems: When evolutionary many-objective optimization meets deep q-learning,” IEEE Transactions on Evolutionary Computation, vol. 25, no. 5, pp. 842–855, 2021. [Google Scholar]

14. X. Xu, X. Liu, Z. Xu, F. Dai, X. Zhang et al., “Trust-oriented IoT service placement for smart cities in edge computing,” IEEE Internet of Things Journal, vol. 7, no. 5, pp. 4084–4091, 2020. [Google Scholar]

15. X. Xu, Q. Wu, L. Qi, W. Dou, S. B. Tsai et al., “Trust-aware service offloading for video surveillance in edge computing enabled internet of vehicles,” IEEE Transactions on Intelligent Transportation Systems, vol. 22, no. 3, pp. 1787–1796, 2021. [Google Scholar]

16. Y. Liu, X. Y. Xiao, X. P. Zhang and Y. Wang, “Multi-objective optimal STATCOM allocation for voltage sag mitigation,” IEEE Transactions on Power Delivery, vol. 35, no. 3, pp. 1410–1422, 2020. [Google Scholar]

17. A. Biswas and T. Pal, “A comparison between metaheuristics for solving a capacitated fixed charge transportation problem with multiple objectives,” Expert Systems with Applications, vol. 170, pp. 114491, 2021. [Google Scholar]

18. A. Biswas, L. E. Crdenas-Barrn, A. A. Shaikh, A. Duary and A. Cspedes-Mota, “A study of multi-objective restricted multi-item fixed charge transportation problem considering different types of demands,” Applied Soft Computing, vol. 118, pp. 108501, 2022. [Google Scholar]

19. V. K. Maurya and S. J. Nanda, “Time-varying multi-objective smart home appliances scheduling using fuzzy adaptive dynamic spea2 algorithm,” Engineering Applications of Artificial Intelligence, vol. 121, pp. 105944, 2023. [Google Scholar]

20. W. Luo, L. Shi, X. Lin, J. Zhang, M. Li et al., “Finding top-k solutions for the decision-maker in multiobjective optimization,” Information Sciences, vol. 613, pp. 204–227, 2022. [Google Scholar]

21. J. Cao, R. Pan, X. Xia, X. Shao and X. Wang, “An efficient scheduling approach for an iron-steel plant equipped with self-generation equipment under time-of-use electricity tariffs,” Swarm and Evolutionary Computation, vol. 60, pp. 100764, 2021. [Google Scholar]

22. H. Amin-Tahmasbi and R. Tavakkoli-Moghaddam, “Solving a bi-objective flowshop scheduling problem by a multi-objective immune system and comparing with SPEA2+ and SPGA,” Advances in Engineering Software, vol. 42, no. 10, pp. 772–779, 2011. [Google Scholar]

23. F. Wang, H. Zhang and A. Zhou, “A particle swarm optimization algorithm for mixed-variable optimization problems,” Swarm and Evolutionary Computation, vol. 60, pp. 100808, 2021. [Google Scholar]

24. F. Wang, X. Wang and S. Sun, “A reinforcement learning level-based particle swarm optimization algorithm for large-scale optimization,” Information Sciences, vol. 602, pp. 298–312, 2022. [Google Scholar]

25. Y. Tian, X. Zheng, X. Zhang and Y. Jin, “Efficient large-scale multi-objective optimization based on a competitive swarm optimizer,” IEEE Transactions on Cybernetics, vol. 50, no. 8, pp. 3696–3708, 2020. [Google Scholar] [PubMed]

26. X. Wang, B. Zhang, J. Wang, K. Zhang and Y. Jin, “A Cluster-based competitive particle swarm optimizer with a sparse truncation operator for multi-objective optimization,” Swarm and Evolutionary Computation, vol. 71, pp. 101083, 2022. [Google Scholar]

27. Q. Gu, Y. Liu, L. Chen and N. Xiong, “An improved competitive particle swarm optimization for many-objective optimization problems,” Expert Systems with Applications, vol. 189, pp. 116118, 2022. [Google Scholar]

28. W. Huang and W. Zhang, “Multi-objective optimization based on an adaptive competitive swarm optimizer,” Information Sciences, vol. 583, pp. 266–287, 2022. [Google Scholar]

29. R. Cheng and Y. Jin, “A competitive swarm optimizer for large scale optimization,” IEEE Transactions on Cybernetics, vol. 45, no. 2, pp. 191–204, 2015. [Google Scholar] [PubMed]

30. P. Mohapatra, K. Nath Das and S. Roy, “A modified competitive swarm optimizer for large scale optimization problems,” Applied Soft Computing, vol. 59, pp. 340–362, 2017. [Google Scholar]

31. X. Wang, K. Zhang, J. Wang and Y. Jin, “An enhanced competitive swarm optimizer with strongly convex sparse operator for large-scale multiobjective optimization,” IEEE Transactions on Evolutionary Computation, vol. 26, no. 5, pp. 859–871, 2022. [Google Scholar]

32. C. Huang, X. Zhou, X. Ran, Y. Liu, W. Deng et al., “Co-evolutionary competitive swarm optimizer with three-phase for large-scale complex optimization problem,” Information Sciences, vol. 619, pp. 2–18, 2023. [Google Scholar]

33. Y. Ge, D. Chen, F. Zou, M. Fu and F. Ge, “Large-scale multiobjective optimization with adaptive competitive swarm optimizer and inverse modeling,” Information Sciences, vol. 608, pp. 1441–1463, 2022. [Google Scholar]

34. S. Liu, Q. Lin, Q. Li and K. C. Tan, “A comprehensive competitive swarm optimizer for large-scale multiobjective optimization,” IEEE Transactions on Systems, Man, and Cybernetics: Systems, vol. 52, no. 9, pp. 5829–5842, 2022. [Google Scholar]

35. S. Qi, J. Zou, S. Yang, Y. Jin, J. Zheng et al., “A Self-exploratory competitive swarm optimization algorithm for large-scale multiobjective optimization,” Information Sciences, vol. 609, pp. 1601–1620, 2022. [Google Scholar]

36. X. Chen and G. Tang, “Solving static and dynamic multi-area economic dispatch problems using an improved competitive swarm optimization algorithm,” Energy, vol. 238, pp. 122035, 2022. [Google Scholar]

37. C. He, M. Li, C. Zhang, H. Chen, X. Li et al., “A competitive swarm optimizer with probabilistic criteria for many-objective optimization problems,” Complex & Intelligent Systems, vol. 8, no. 6, pp. 4697–4725, 2022. [Google Scholar]

38. B. H. Nguyen, B. Xue and M. Zhang, “A constrained competitive swarm optimizer with an SVM-based surrogate model for feature selection,” IEEE Transactions on Evolutionary Computation, pp. 1, 2022. [Google Scholar]

39. P. Musikawan, Y. Kongsorot, P. Muneesawang and C. So-In, “An enhanced obstacle-aware deployment scheme with an opposition-based competitive swarm optimizer for mobile WSNs,” Expert Systems with Applications, vol. 189, pp. 116035, 2022. [Google Scholar]

40. W. Shao, Z. Shao and D. Pi, “Multi-local search-based general variable neighborhood search for distributed flow shop scheduling in heterogeneous multi-factories,” Applied Soft Computing, vol. 125, pp. 109138, 2022. [Google Scholar]

41. F. Zhao, R. Ma and L. Wang, “A self-learning discrete jaya algorithm for multiobjective energy-efficient distributed no-idle flow-shop scheduling problem in heterogeneous factory system,” IEEE Transactions on Cybernetics, pp. 1–12, 2021. [Google Scholar]

42. T. Meng and Q. -K. Pan, “A distributed heterogeneous permutation flow-shop scheduling problem with lot-streaming and carryover sequence-dependent setup time,” Swarm and Evolutionary Computation, vol. 60, pp. 100804, 2021. [Google Scholar]

43. C. Lu, L. Gao, J. Yi and X. Li, “Energy-efficient scheduling of distributed flow shop with heterogeneous factories: A real-world case from automobile industry in China,” IEEE Transactions on Industrial Informatics, vol. 17, no. 10, pp. 6687–6696, 2021. [Google Scholar]

44. K. Deb, A. Pratap, S. Agarwal and T. Meyarivan, “A fast and elitist multiobjective genetic algorithm: NSGA-II,” IEEE Transactions on Evolutionary Computation, vol. 6, no. 2, pp. 182–197, 2002. [Google Scholar]

45. R. Li, W. Gong and C. Lu, “A reinforcement learning based RMOEA/D for bi-objective fuzzy flexible job shop scheduling,” Expert Systems with Applications, vol. 203, pp. 117380, 2022. [Google Scholar]

46. L. While, P. Hingston, L. Barone and S. Huband, “A faster algorithm for calculating hypervolume,” IEEE Transactions on Evolutionary Computation, vol. 10, no. 1, pp. 29–38, 2006. [Google Scholar]

47. R. C. Van Nostrand, “Design of experiments using the taguchi approach: 16 steps to product and process improvement,” Technometrics, vol. 44, no. 3, pp. 289–289, 2002. [Google Scholar]

48. Q. Zhang and L. Hui, “MOEA/D: A multiobjective evolutionary algorithm based on decomposition,” IEEE Transactions on Evolutionary Computation, vol. 11, no. 6, pp. 712–731, 2007. [Google Scholar]