 Open Access
Open Access
ARTICLE
Attentive Neighborhood Feature Augmentation for Semi-supervised Learning
1 School of Computer Science and Cyber Engineering, Guangzhou University, Guangzhou, 510002, China
2 Fujian Provincial Key Laboratory of Information Processing and Intelligent Control, Minjiang University, Fuzhou, 350121, China
* Corresponding Authors: Jing Li. Email: ; Xianmin Wang. Email:
(This article belongs to the Special Issue: AI Powered Human-centric Computing with Cloud/Fog/Edge)
Intelligent Automation & Soft Computing 2023, 37(2), 1753-1771. https://doi.org/10.32604/iasc.2023.039600
Received 07 February 2023; Accepted 14 April 2023; Issue published 21 June 2023
Abstract
Recent state-of-the-art semi-supervised learning (SSL) methods usually use data augmentations as core components. Such methods, however, are limited to simple transformations such as the augmentations under the instance’s naive representations or the augmentations under the instance’s semantic representations. To tackle this problem, we offer a unique insight into data augmentations and propose a novel data-augmentation-based semi-supervised learning method, called Attentive Neighborhood Feature Augmentation (ANFA). The motivation of our method lies in the observation that the relationship between the given feature and its neighborhood may contribute to constructing more reliable transformations for the data, and further facilitating the classifier to distinguish the ambiguous features from the low-dense regions. Specially, we first project the labeled and unlabeled data points into an embedding space and then construct a neighbor graph that serves as a similarity measure based on the similar representations in the embedding space. Then, we employ an attention mechanism to transform the target features into augmented ones based on the neighbor graph. Finally, we formulate a novel semi-supervised loss by encouraging the predictions of the interpolations of augmented features to be consistent with the corresponding interpolations of the predictions of the target features. We carried out experiments on SVHN and CIFAR-10 benchmark datasets and the experimental results demonstrate that our method outperforms the state-of-the-art methods when the number of labeled examples is limited.Keywords
Deep neural networks have achieved favorable performance on a wide variety of tasks [1–5]. Training deep neural networks commonly requires a large amount of labeled training data. However, since collecting labeled data necessarily involves expert knowledge, labeled data is usually unavailable for many learning tasks. To address this problem, numerous semi-supervised learning (SSL) methods have been developed, which exploit abundant unlabeled data effectively to improve the performance of deep models and relieve the pressure brought by the lack of labeled data.
Existing SSL methods are mainly based on a low-density separation assumption, that is, the decision boundary learned by the model is supported to lie in low-density regions of the instances. Consistency regularization is a typical measure to implement the low-density separation assumption, which has been widely used on many benchmarks. The main idea of consistency regularization is to enforce the model to produce the same output distribution for an input instance and its perturbed version. The conventional consistency-regularization-based methods mainly focus on how to construct effective perturbations. For instance, Laine et al. [6] generated different perturbations by two network models to make them predict agreement. Miyato et al. [7] produced the worst perturbations according to the adversarial direction when adversarial training [8,9], and then enforced the outputs from the original example and its perturbed version to be consistent.
Recently, data augmentation has quickly turned into the mainstream technique of consistency regularization in SSL due to its powerful capability of expanding the examples’ feature representations. The essence of data augmentation is to expand the feature representations from the given training dataset. To this end, numerous data-augmentation-based SSL methods are developed. For instance, Verma et al. [10] proposed an interpolation consistency training (ICT) algorithm to train deep neural networks in the semi-supervised learning paradigm. This algorithm enforced the prediction at an interpolation of unlabeled points to be consistent with the interpolation of the predictions at those points. Xie et al. [11] presented a new perspective on how to effectively noise unlabeled examples. This work verifies that the quality of noising produced by advanced data augmentation methods is very important for semi-supervised learning. Berthelot et al. [12] presented a MixMatch approach to guess the low-entropy labels for data-augmented unlabeled examples and mixes labeled and unlabeled data using the MixUp strategy. Sohn et al. [13] presented the FixMatch algorithm to simplify existing SSL approaches. The model’s predictions on weakly-augmented unlabeled pictures are used to construct pseudo-labels, which are then trained to predict the pseudo-label when fed a strongly-augmented version of the same image.
The aforementioned methods commonly generate augmented instances on their naive representations, which are unable to derive abstract semantic representations for the learning of semi-supervised models. Accordingly, inspired by the idea of feature fusion [14–18], several works focus on augmenting data by merging the feature representations of the instances from the semantic layer. Verma et al. [19] proposed a manifold mixup method to encourage neural networks to predict less confidently on interpolations of hidden representations. This method leveraged semantic interpolations as an additional training signal, obtaining neural networks with smoother decision boundaries at multiple levels of representation. Upchurch et al. [20] proposed a deep feature interpolation (DFI) method for automatic high-resolution image transformation. DFI can be used as a new baseline to evaluate more complex algorithms and provides a practical answer to the question of which image transformation tasks are still challenging after the advent of deep learning. Kuo et al. [21] proposed a novel learned feature-based refinement and augmentation method which produces a varied set of complex transformations. The transformations, combined with traditional image-based augmentation, can be used as part of the consistency-based regularization loss.
The existing feature fusion methods boost the capability of the feature representations to some extent [22]. However, they only consider the information of a single given example when merging the features. The overlooking of the relationship between the given feature and its neighborhood may lead to false predictions for the unlabeled examples and further limit the performance of SSL. To clarify this phenomenon and put forward our motivation, we take a simple example as shown in Fig. 1. As shown in Fig. 1a, we can see that in low-density feature embedding regions, it is difficult for the classifier to distinguish the ambiguous unlabeled features. Here, the ambiguous unlabeled features are the features that are derived from the unlabeled examples and have approximately identical margins to the boundaries in the embedding spaces. The ambiguous unlabeled features have similar representations, thus they may yield similar outputs from the SSL model and then generate unreliable pseudo labels for the unlabeled examples. This fact leads to false decision boundaries during the training process. Whereas, as shown in Fig. 1b, if the neighborhood of the given feature is considered, the representation of the feature can be strengthened and refined. Based on the cluster characteristics of the neighborhood, the ambiguous unlabeled features have discriminative representations, which contributes to yielding more reliable pseudo labels for the training. Therefore, it is reasonable to generate diverse and abstract transformations by exploiting the neighborhood information of examples on their semantic feature spaces. To this end, we use the self-attention [23] mechanism to aggregate the neighbor features, and then apply a neighbor graph to refine and augment the target features. By creating such a neighborhood graph, it is possible to obtain more discriminative feature representations, which help to produce more trustworthy decision boundaries for the SSL model and more private pseudo labels (as shown in Fig. 1c).

Figure 1: A simple case to clarity the motivation of our method. The blue and red circles represent represents unlabeled samples that have been divided into different clusters by the SSL model. Triangles represent labeled samples. The gray circles represent feature representations that are difficult to be discriminated by the classifier. (a) illustrates that the ambiguous unlabeled samples are difficult to be classified by their representations. (b) indicates the use of ANFA to aggregate neighboring samples, the thicker the line, the greater the attention weight. (c) shows that the SSL model can correctly classify unlabeled samples with refined features
According to the foregoing analysis, this paper proposes a novel feature augmentation framework called Attentive Neighborhood Feature Augmentation (ANFA) for SSL. First, given labeled and unlabeled data examples, we project them to an embedding space and construct a neighborhood graph based on the similarity of representations on their embedding spaces. Second, we refined the features via weighting the neighbor representations of the target features, where the weights are adaptively acquired relying upon the similarity between the target features and the neighborhood graph. Finally, we mix up the target and refined features to obtain the interpolated features and then propose a novel consistency regularization loss that encourages the predictions of the interpolated features to be consistent with their corresponding interpolated pseudo-labels. Moreover, we test our method on standard SSL datasets such as SVHN [24] and CIFAR-10 [25] and neural network architectures CNN-13 and WRN28-2 [26], and the experimental results demonstrate that our approach outperforms the baseline methods.
This paper is organized as follows. First, we survey the related work and analyze their advantage and disadvantage in Section 2. Then, we elaborate the proposed method in Section 3. Next, we conduct experiments and analyze the results in Section 5.
In the past, many semi-supervised deep learning methods have been developed. In this section, we focus on some related works, including the consistency regularization methods, augmentation methods, and the attention scheme.
2.1 Consistency Regularization Methods
Current state-of-the-art SSL methods mostly use this technique. The key idea of consistent regularization methods is that the model should be robust to local perturbations in the input space, which requires the deep neural network to be consistent with the original samples and the prediction results after adding small perturbations. In image classification tasks, the approach is to make the model’s predictions invariant to texture or geometric changes in the image.
Different consistency regularization techniques differ in how they choose perturbations
Recently, a series of methods that combine consistent regularization techniques with other semi-supervised learning methods have achieved the best performance, such as MixMatch [12], ReMixMatch [34], and FixMacth [13], using strong data augmentation to create perturbations, while also using pseudo-labels, entropy Minimization, sharpening, and other techniques improve the confidence of the model. At the same time, several works have improved some graph-based methods to better extract intrinsic features from raw data. Yang et al. [35] used self-paced regularization to better factorize matrices and introduced adaptive graphs using dynamic neighbor assignment to find low-dimensional manifolds. Chen et al. [36] improved the Graph non-negative matrix factorization (GNMF) method, introduced the
We summarize the advantages and disadvantages of some consistency regularization methods shown in Table 1.

For SSL with the deep model, most recent works incorporate different data augmentation methods into their baseline models to achieve higher performance. Data augmentation alleviates the problem of limited data by performing diverse but reasonable transformations on the data and has been widely used in the training of deep models [37]. Data augmentation increases data diversity and prevents overfitting in the training of deep models. Simple data augmentation methods include random flips, blurs, transitions, geometric transformations, changing the contrast and color of images, and so on. In addition, complex augmentation operations also exist. Mixup enforces interpolation smoothness between every two training samples by generating new training samples through a convex combination of two images and their corresponding labels. It has been shown that models trained with Mixup are robust to out-of-distribution data and facilitate the uncertainty calibration of the network. In recent years, an SSL data augmentation strategy for strong image processing has attracted attention. In image classification, unsupervised data Augmentation (UDA) [11] uses AutoAugment [38], which uses reinforcement learning [39,40] to search for the best combination of different image augmentation operations based on the confidence of a validated model. In addition, the CTAugment proposed by Remixmatch [34] and the RandAugment [41] used in Fixmatch [13] use different strategies to maximize the effect of data enhancement.
We summarize the key findings and limitations of some data augmentation methods shown in Table 2.

Vaswani et al. [23] define scaled dot-product attention as an operation that maps a query and a set of key-value pairs to an output that computes a dot product of the query and key and scales it, using a softmax function for normalization and computing attention weights. It can be expressed as follows:
where
In recent years, attention mechanisms have been successfully applied to various computer vision tasks [42,43]. SENet [44] obtains the weight of each channel of the input feature layer and uses its weight to make the network focus on more important information [45]. Residual attention networks [46] are built by stacking attention modules that generate attention-aware features. As the modules go deeper, the attention-aware functions from different modules change adaptively. CBAM [47] sequentially infers the attention map along two independent dimensions of channel and space and then multiplies the attention map with the input feature map for adaptive feature refinement [48].
We summarize the key findings and limitations of some attention methods shown in Table 3.

In this section, we present our work for semi-supervised deep learning. A glimpse of our approach is shown in Fig. 2. Our approach consists of three parts, namely neighbor graph representation, feature augmentation, and consistency regularization. We first construct a neighborhood feature graph that represents the relationship between the target feature and its neighbors. Then, based on the neighborhood feature graph, we augment the features by attention mechanism. Finally, we propose a new loss that encourages the prediction at an interpolation of features to be consistent with the interpolation of the predictions at those features.

Figure 2: The pipeline of attentive neighborhood feature augmentation for semi-supervised learning
In SSL tasks, we given a labeled dataset
3.2 Neighborhood Feature Graph
In order to efficiently leverage the knowledge of neighbors for regularization, we propose to construct a graph among the samples and their neighborhoods in the feature semantic space. To select suitable neighbors from the dataset, we propose to use
we first extract the feature
where
where
With a neighborhood feature graph built by the process described above, we propose a learned feature augmentation module via self-attention to improve target feature embedding by aggregating the neighborhood features. The proposed module refines input image features in the feature space by leveraging important neighborhood information.
Formally, Given a neighborhood feature graph
where
In detail, we first compute the dot product similarity between
where

Figure 3: Illustration of the proposed attentive neighborhood feature augmentation module
3.4 Consistency Regularization
We obtain refined features by aggregating neighborhood information via the module described above. To relate refined features containing knowledge of neighbors to each other, we employ the Mixup strategy, which encourages predictions based on linear combinations of two features to approximate linear combinations of their pseudo-labels.
Formally, given two random refined features
where
The goal of Feature Mixup Model is minimizing the divergence between the model prediction on the interpolated feature
Given a labeled data minibatch
where y is the label of x and
Therefore, the total loss can be written as:
where
Our propose method for SSL is summarized in Algorithm 1.

Algorithm 1: The proposed Attentive Neighborhood Feature Augmentation (ANFA) Algorithm for semi-supervised learning
Because we need to build a global neighborhood graph, the computational complexity and memory overhead for our proposed method will unavoidably rise. We must specifically pre-train the feature extractor on labeled data before calculating the similarity matrix. We retrieve the neighborhood of each test sample from the memory bank created in the training phase and directly construct the neighborhood subgraph in the test phase. Although additional calculations are required, the convergence rate of our proposed method is much quicker than that of strong enhancement-based methods such as FixMatch and ReMixMatch, which typically require thousands of training epochs, whereas our method only requires 500 training epochs to converge.
In this section, we evaluate the proposed framework on commonly used SSL benchmark datasets, CIFAR-10 [25] and SVHN [24], and discuss the experimental results. We report the error rates are averaged over 5 runs with different seeds for data splitting. Specifically, we first briefly introduce the SSL benchmark datasets. Then, we show the implementation details of our proposed framework. In the end, we conduct ablation studies to validate the effectiveness of our proposed framework for SSL.
SVHN is a street view house numbers dataset, which has 73,257 training samples and 26,032 test samples from 10 number classes. The samples are
CIFAR10 is a natural image dataset, which has 50,000 training samples and 10,000 test samples belonging to 10 natural classes. The samples are RGB images of
Data Augmentation. We adopt standard data augmentation and data normalization in the preprocessing phase following our baselines. On the CIFAR10 dataset, we first augment the training data by random horizontal flipping and random translation (in the range of [−2, 2] pixels), and then apply global contrast normalization and ZCA normalization based on statistics of all training samples. On the SVHN dataset, we first augment the training data with random translations. Inspired by [11,13], we also employ RandAugment [41] strategy to augment the training samples, which gives us a strong baseline.
Model Architecture. We conduct our experiments using a 13-layer CNN network and Wide-Resnet-28-2 architectures. For CNN-13, we adopt the exactly same 13-layer convolution neural network architecture as in [10], which eliminates the dropout layers compared to the variants in other SSL methods. The Wide-Resnet-28-2 architecture [51] is a specific residual network architecture, with extensive hyperparameter search to compare the performance of various consistency-based semi-supervised algorithms, which has been adopted as the standard benchmark architecture in recent state-of-the-art SSL methods.
Training. We use an SGD optimizer with a momentum of 0.9 and a weight decay factor
We show our results on the CIFAR10 and SVHN datasets in Tables 4 and 5 and we have the following observations.
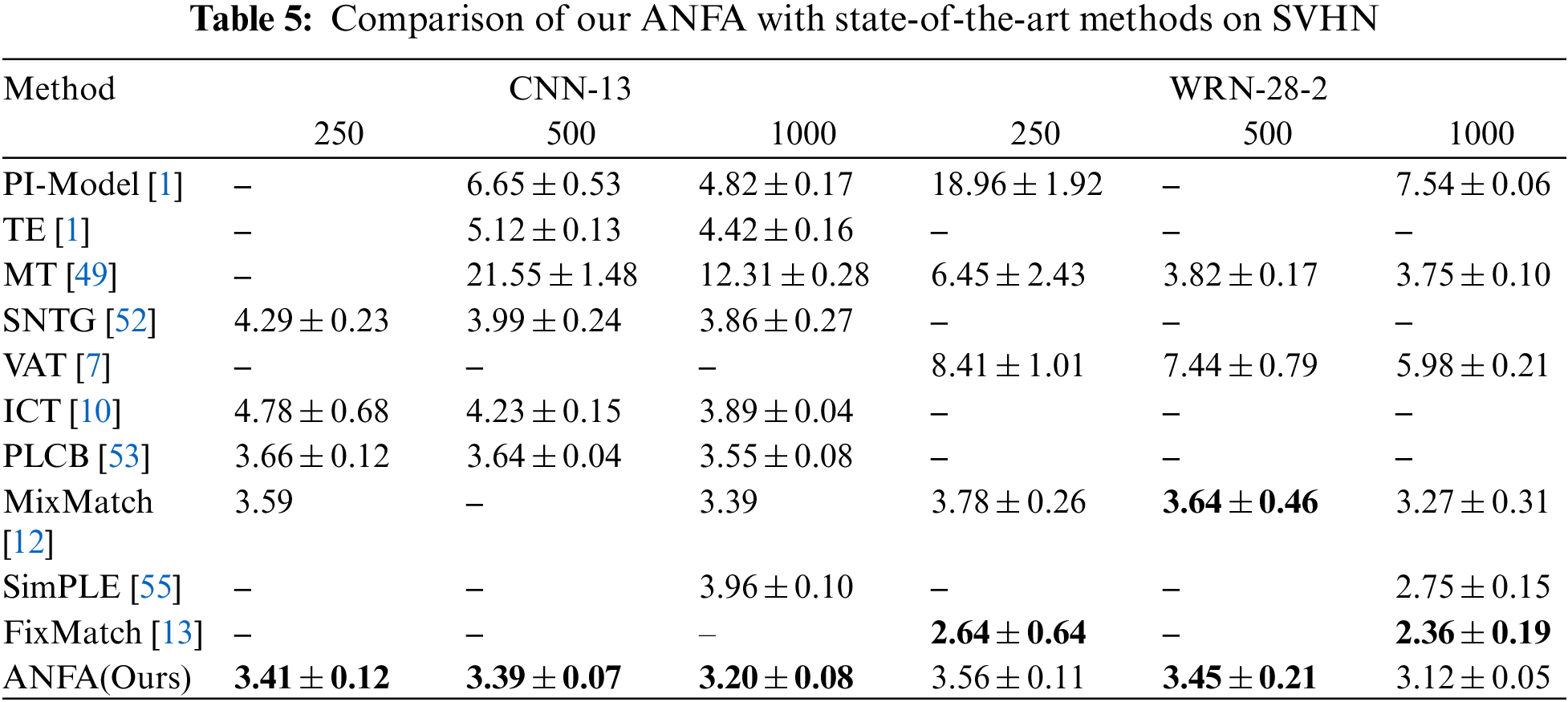
For CIFAR10, our method achieves comparable results with state-of-the-art methods. It is worth mentioning that current methods with leading performance methods on the CIFAR-10 need require thousands of training epochs. In contrast, our approach converges more easily. Meanwhile, our method outperforms all the baselines under the CNN-13 architecture with 1 and 4 k labeled training samples.
For SVHN, this is much easier than the task on CIFAR-10 and the baselines already achieve a quite high accuracy. Nonetheless, our method still demonstrates a clear improvement over all the baselines across different numbers of labeled data. In particular, our method outperforms all of the baselines under the CNN-13 architecture with 250, 500, and 1 K labeled training data, which already beats the results of all baselines with 500 labeled samples.
Comparison with other attention functions. In the proposed method, we investigate the impact of various attention functions, and we choose classical attention functions for the experiments: dot-product attention, additive attention, hard attention, and multi-head attention. The experimental findings on the CIFAR-10 dataset are shown in Fig. 4. We can see that the proposed method has the same performance when using the additive attention function as when using the dot product attention function, but the calculation is faster when using the dot product attention function because it can be computed using highly optimized matrix multiplication. At the same time, when using the hard attention function, performance is slightly lower because using the one-hot weight loses some local information. Multi-head attention performs slightly better than dot-product attention, but it requires more memory and calculations. In conclusion, we employ dot-product attention, which has slightly lower performance but lower computational overhead.

Figure 4: Comparison with other attention functions on CIFAR-10
Effectiveness of Attentive Aggregation. We propose an attention-based feature augmentation module that aggregates the neighboring features to enhance the features of the target instance, which improves the performance of the model. To show the effectiveness of attention-based aggregation, we compare the proposed attentive aggregation with the average feature aggregate method, which is the most straightforward strategy for summarizing features. We adopt ICT as the baseline model and conduct experiments on the CIFAR10 dataset with 4000 labeled samples. We conduct a baseline experiment providing the comparison results in Fig. 5. We can observe that the attention-based neighborhood feature augmentation module improves the performances of the ICT model (from 91.4% to 93.2%), and the neighborhood information helps the model to learn discriminative feature embeddings. Meanwhile, attention-based aggregation performs better than average aggregation and attentive aggregation converges faster because the adaptive weight learned by attention fully captures the neighborhood information.

Figure 5: Test classification accuracy on CIFAR-10
Evaluation of the Neighborhood Feature Graph Size. We find that different numbers of neighbors affect the performance of the experiment. Our previous experiments on CIFAR10 fixed the size of the neighbor graph to 16. Here we explore different neighbor graph sizes for our attentive neighborhood feature augmentation. Specifically, we conduct experiments with different neighbor graph sizes on the CIFAR10 and SVHN datasets, respectively, and present the results in Fig. 6. It can be seen from the figure that the final performance will be reduced if the number of neighbors is too large or too small. This may be explained by the fact that a too-small number of neighbors will not obtain sufficient neighbor information, while a too-large number of neighbors will introduce irrelevant neighbors, which may weaken the effectiveness of neighborhood aggregation and thus impair the target features [57].
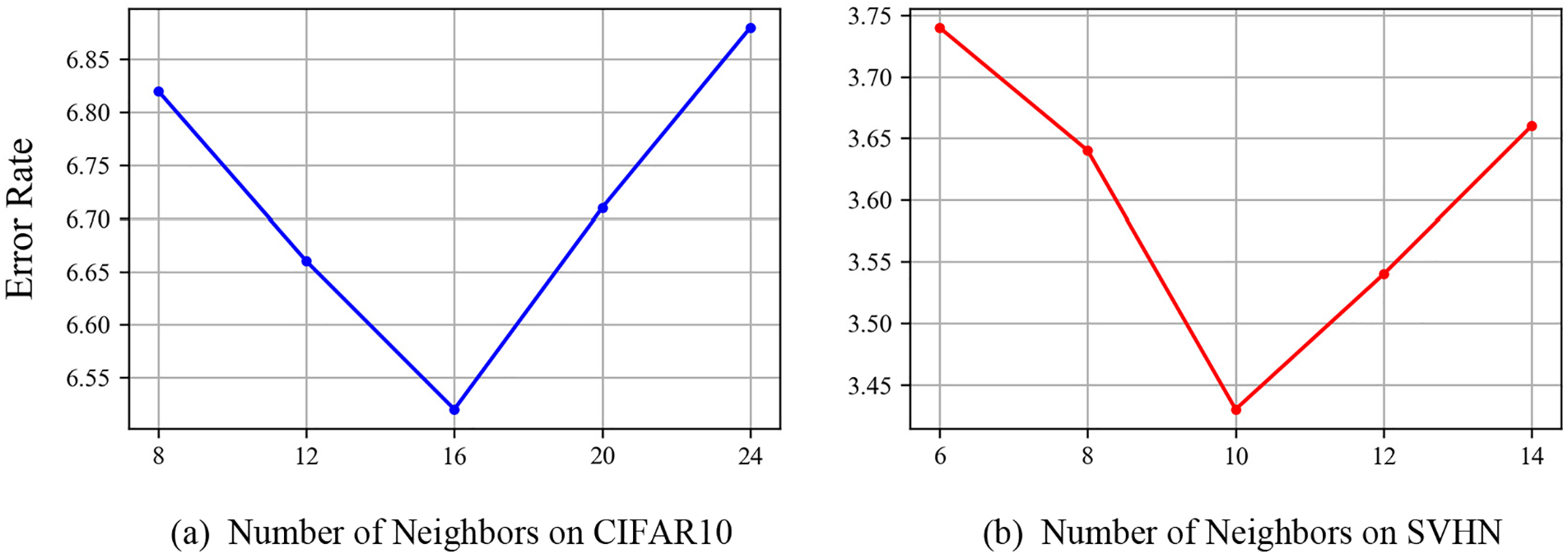
Figure 6: Evaluation of number of neighbor graph size on CIFAR-10(a) and SVHN(b)
Combination of Augmentation Strategy. Since our method employs a data augmentation strategy, we will further investigate the impact of commonly used pixel-based data augmentation strategies on the performance of the proposed method. We conduct ablation experiments on CIFAR10 datasets with WRN-28-2 architecture to study the influence of strong augmentation policies (RandAugment) and Mixup on experimental performance. The results are shown in Table 6. As we can see, excellent data augmentation techniques give a boost to our approach. Our method can be well combined with other pixel-based augmentation strategies, as various transpositions can provide richer neighborhood information and drive our model to learn better feature representations for refinement.

In this paper, we propose a novel data augmentation method for semi-supervised learning by exploiting neighborhood information of a given instance in its semantic feature. First, for the target instance, we construct a neighbor graph based on a similarity matrix calculated by its neighbor features in the semantic layer. Second, we refine the target features with an attention-based module according to the neighbor graph. Finally, we mix up the target features and their corresponding predictions and promote a novel consistency loss as the consistency regularization. We conducted experiments on SVHN and CIFAR10 datasets. The experimental results demonstrate that our proposal is superior to the state-of-the-art SSL methods under CNN-13 neural architecture when the number of label examples is small. Moreover, the attention-based module in our method can be combined with some mainstream semi-supervised learning methods to further improve the SSL performance. Note that it might be time-consuming to create the neighborhood graph in our method when the number of training examples is large. Thus, for future work, we will focus on reducing the time complexity of constructing the neighborhood graph by exploring a parallel computation strategy. In addition, we will consider the scenario where the training dataset is unbalanced.
Funding Statement: This work was supported by the National Natural Science Foundation of China (Nos. 62072127, 62002076, 61906049), Natural Science Foundation of Guangdong Province (Nos. 2023A1515011774, 2020A1515010423), Project 6142111180404 supported by CNKLSTISS, Science and Technology Program of Guangzhou, China (No. 202002030131), Guangdong basic and applied basic research fund joint fund Youth Fund (No. 2019A1515110213), Open Fund Project of Fujian Provincial Key Laboratory of Information Processing and Intelligent Control (Minjiang University) (No. MJUKF-IPIC202101), Natural Science Foundation of Guangdong Province No. 2020A1515010423), Scientific research project for Guangzhou University (No. RP2022003).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Z. Zhou, C. Ding, J. Li, E. Mohammadi, G. Liu et al., “Sequential order-aware coding-based robust subspace clustering for human action recognition in untrimmed videos,” IEEE Transactions on Image Processing, vol. 32, pp. 13–28, 2023. [Google Scholar] [PubMed]
2. J. Li, J. Wu, L. Chen, J. Li and S. Lam, “Blockchain-based secure key management for mobile edge computing,” IEEE Transactions on Mobile Computing, vol. 22, no. 1, pp. 100–114, 2023. [Google Scholar]
3. W. Wang, X. Wang, M. Zhou, X. Wei, J. Li et al., “A spatiotemporal and motion information extraction network for action recognition,” Wireless Networks, vol. 29, pp. 1–17, 2023. [Google Scholar]
4. X. Wei, J. Li, M. Zhou and X. Wang, “Contrastive distortion-level learning-based no-reference image-quality assessment,” International Journal of Intelligent Systems, vol. 37, no. 11, pp. 8730–8746, 2022. [Google Scholar]
5. W. Li, Y. Wang and J. Li, “Enhancing blockchain-based filtration mechanism via IPFS for collaborative intrusion detection in IoT networks,” Journal of Systems Architecture, vol. 127, pp. 102510, 2022. [Google Scholar]
6. S. Laine and T. Aila, “Temporal ensembling for semi-supervised learning,” arXiv preprint arXiv:1610.02242, 2017. [Google Scholar]
7. T. Miyato, S. Maeda, M. Koyama and S. Ishii, “Virtual adversarial training: A regularization method for supervised and semi-supervised learning,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 41, no. 8, pp. 1979–1993, 2018. [Google Scholar] [PubMed]
8. X. Wang, J. Li, Q. Liu, W. Zhao, Z. Li et al., “Generative adversarial training for supervised and semi-supervised learning,” Frontiers Neurorobotics, vol. 16, pp. 859610, 2022. [Google Scholar]
9. Z. Luo, C. Zhu, L. Fang, G. Kou, R. Hou et al., “An effective and practical gradient inversion attack,” International Journal of Intelligent Systems, vol. 37, no. 11, pp. 9373–9389, 2022. [Google Scholar]
10. V. Verma, K. Kawaguchi, A. Lamb, J. Kannala, Y. Bengio et al., “Interpolation consistency training for semi-supervised learning,” Neural Networks, vol. 145, pp. 90–106, 2022. [Google Scholar] [PubMed]
11. Q. Xie, Z. Dai, E. Hovy, T. Luong and Q. V. Le, “Unsupervised data augmentation for consistency training,” Advances in Neural Information Processing Systems, vol. 33, pp. 6256–6268, 2020. [Google Scholar]
12. D. Berthelot, N. Carlini, I. Goodfellow, A. Oliver, N. Papernot et al., “Mixmatch: A holistic approach to semi-supervised learning,” Advances in Neural Information Processing Systems, vol. 32, pp. 1–11, 2019. [Google Scholar]
13. K. Sohn, D. Berthelot, C. Li, Z. Zhang, N. Carlini et al., “Fixmatch: Simplifying semi-supervised learning with consistency and confidence,” Advances in Neural Information Processing Systems, vol. 33, pp. 596–608, 2020. [Google Scholar]
14. Y. Chen, R. Xia, K. Zou and K. Yang, “FFTI: Image inpainting algorithm via features fusion and Two-steps inpainting,” Journal of Visual Communication and Image Representation, vol. 93, pp. 103776, 2023. [Google Scholar]
15. R. Xia, Y. Chen and B. Ren, “Improved anti-occlusion object tracking algorithm using unscented rauch-tung-striebel smoother and kernel correlation filter,” Journal of King Saud University-Computer and Information Sciences, vol. 34, no. 8, pp. 6008–6018, 2022. [Google Scholar]
16. Y. Chen, R. Xia, K. Yang and K. Zou, “MFFN: Image super-resolution via multi-level features fusion network,” The Visual Computer, vol. 39, pp. 1–16, 2023. [Google Scholar]
17. Y. Chen, L. Liu, V. Phonevilay, K. Gu, R. Xia et al., “Image super-resolution reconstruction based on feature map attention mechanism,” Applied Intelligence, vol. 51, pp. 4367–4380, 2021. [Google Scholar]
18. X. Wang, X. Kuang, J. Li, J. Li, X. Chen et al., “Oblivious transfer for privacy-preserving in VANET’s feature matching,” IEEE Transactions on Intelligent Transportation Systems, vol. 22, no. 7, pp. 4359–4366, 2021. [Google Scholar]
19. V. Verma, A. Lamb, C. Beckham, A. Najafi, I. Mitilagkas et al., “Manifold mixup: Better representations by interpolating hidden states,” in Int. Conf. on Machine Learning, Long Beach, CA, USA, pp. 6438–6447, 2019. [Google Scholar]
20. P. Upchurch, J. Gardner, G. Pleiss, R. Pless, N. Snavely et al., “Deep feature interpolation for image content changes,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition, Honolulu, HI, USA, pp. 7064–7073, 2017. [Google Scholar]
21. C. Kuo, C. Ma, J. Huang, Z. Kira, G. Tech et al., “Featmatch: Feature-based augmentation for semi-supervised learning,” in Computer Vision–ECCV 2020: 16th European Conf., Glasgow, UK, August 23–28, 2020, Proc., Part XVIII 16, Springer Int. Publishing, pp. 479–495, 2020. [Google Scholar]
22. X. Liu, J. Yin, J. Li, P. Ding, J. Liu et al., “TrajectoryCNN: A new spatio-temporal feature learning network for human motion prediction,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 31, no. 6, pp. 2133–2146, 2020. [Google Scholar]
23. A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones et al., “Attention is all you need,” Advances in Neural Information Processing Systems, vol. 30, pp. 5998–6008, 2017. [Google Scholar]
24. Y. Netzer, T. Wang, A. Coates, A. Bissacco, B. Wu et al., “Reading digits in natural images with unsupervised feature learning,” 2011. [Google Scholar]
25. A. Krizhevsky and G. Hinton, “Learning multiple layers of features from tiny images,” Master’s Thesis, University of Tront, pp. 32–33, 2009. [Google Scholar]
26. S. Zagoruyko and N. Komodakis, “Wide residual networks,” arXiv preprint arXiv:1605.07146, 2016. [Google Scholar]
27. X. Wang, J. Li, X. Kuang, Y. Tan and J. Li, “The security of machine learning in an adversarial setting: A survey,” Journal of Parallel and Distributed Computing, vol. 130, pp. 12–23, 2019. [Google Scholar]
28. T. Huang, Q. Zhang, J. Liu, R. Hou, X. Wang et al., “Adversarial attacks on deep-learning-based SAR image target recognition,” Journal of Network and Computer Applications, vol. 162, no. 12, pp. 102632. 2020. [Google Scholar]
29. J. Lai, Y. Huo, R. Hou and X. Wang, “A universal detection method for adversarial examples and fake images,” Sensors, vol. 22, no. 9, pp. 3445, 2022. [Google Scholar] [PubMed]
30. N. Srivastava, G. Hinton, A. Krizhevsky, I. Sutskever and R. Salakhutdinov, “Dropout: A simple way to prevent neural networks from overfitting,” The Journal of Machine Learning Research, vol. 15, no. 1, pp. 1929–1958, 2014. [Google Scholar]
31. H. Zhang, M. Cisse, Y. N. Dauphin and D. Lopez-Paz, “Mixup: Beyond empirical risk minimization,” arXiv preprint arXiv:1710.09412, 2017. [Google Scholar]
32. X. Wei, X. Wei, X. Kong, S. Lu, W. Xing et al., “FMixcutmatch for semi-supervised deep learning,” Neural Networks, vol. 133, pp. 166–176, 2021. [Google Scholar] [PubMed]
33. J. Chen, M. Yang and J. Ling, “Attention-based label consistency for semi-supervised deep learning based image classification,” Neurocomputing, vol. 453, pp. 731–741, 2021. [Google Scholar]
34. D. Berthelot, N. Carlini, E. D. Cubuk, A. Kurakin, H. Zhang et al., “Remixmatch: Semi-supervised learning with distribution alignment and augmentation anchoring,” arXiv preprint arXiv:1911.09785, 2019. [Google Scholar]
35. X. Yang, H. Che, M. F. Leung and C. Liu, “Adaptive graph nonnegative matrix factorization with the self-paced regularization,” Applied Intelligence, vol. 52, pp. 1–18, 2022. [Google Scholar]
36. K. Chen, H. Che, X. Li and M. F. Leung, “Graph non-negative matrix factorization with alternative smoothed L 0 regularizations,” Neural Computing and Applications, vol. 34, pp. 1–15, 2022. [Google Scholar]
37. F. Ou, Y. Wang, J. Li, G. Zhu and S. Kwong, “A novel rank learning based no-reference image quality assessment method,” IEEE Transactions on Multimedia, vol. 24, pp. 4197–4211, 2021. [Google Scholar]
38. E. D. Cubuk, B. Zoph, D. Mane, V. Vasudevan, Q. V. Le et al., “Autoaugment: Learning augmentation strategies from data,” in Proc. of the IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Long Beach, CA, USA, pp. 113–123, 2019. [Google Scholar]
39. X. Lu, J. Jie, Z. Lin, L. Xiao, J. Li et al., “Reinforcement learning based energy efficient robot relay for unmanned aerial vehicles against smart jamming,” Science China Information Sciences, vol. 65, no. 1, pp. 112304, 2022. [Google Scholar]
40. B. Zoph and Q. V. Le, “Neural architecture search with reinforcement learning,” in Proc. of Int. Conf. on Learning Representations, Toulon, France, pp. 1–16, 2017. [Google Scholar]
41. E. D. Cubuk, B. Zoph, J. Shlens and Q. V. Le, “Randaugment: Practical automated data augmentation with a reduced search space,” in Proc. of the IEEE/CVF Conf. on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, pp. 702–703, 2020. [Google Scholar]
42. C. Ji, Z. Zhu, X. Wang, W. Zhai, X. Zong et al., “Task-aware swapping for efficient DNN inference on DRAM-constrained edge systems,” International Journal of Intelligent Systems, vol. 37, no. 11, pp. 8155–8169, 2022. [Google Scholar]
43. N. Jiang, W. Jie, J. Li, X. Liu and D. Jin, “GATrust: A multi-aspect graph attention network model for trust assessment in OSNs,” IEEE Transactions on Knowledge and Data Engineering, vol. 32, pp. 1, 2022. [Google Scholar]
44. J. Hu, S. Li and G. Sun, “Squeeze-and-excitation networks,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, pp. 7132–7141, 2018. [Google Scholar]
45. X. Li, Z. Zheng, P. Cheng, J. Li and L. You, “MACT: A multi-channel anonymous consensus based on Tor,” World Wide Web, vol. 25, pp. 1–25, 2022. [Google Scholar]
46. F. Wang, M. Jiang, C. Qian, S. Yang, C. Li et al., “Residual attention network for image classification,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition, Honolulu, HI, USA, pp. 3156–3164, 2017. [Google Scholar]
47. S. Woo, J. Park, J. Lee and I. Kweon, “Cbam: Convolutional block attention module,” in Proc. of the European Conf. on Computer Vision (ECCV), Munich, Germany, pp. 3–19, 2018. [Google Scholar]
48. Y. Chen, Y. Li, Q. Chen, X. Wang, T. Li et al., “Energy trading scheme based on consortium blockchain and game theory,” Computer Standards & Interfaces, vol. 84, pp. 103699, 2023. [Google Scholar]
49. A. Tarvainen and H. Valpola, “Mean teachers are better role models: Weight-averaged consistency targets improve semi-supervised deep learning results,” Advances in Neural Information Processing Systems, vol. 30, pp. 1–10, 2017. [Google Scholar]
50. Y. Chen, J. Ma, X. Wang, X. Zhang and H. Zhou, “DE-RSTC: A rational secure two-party computation protocol based on direction entropy,” Int. J. International Journal of Intelligent Systems, vol. 37, no. 11, pp. 8947–8967, 2022. [Google Scholar]
51. A. Oliver, A. Odena, C. Raffel, E. D. Cubuk and I. J. Goodfellow, “Realistic evaluation of deep semi-supervised learning algorithms,” Advances in Neural Information Processing Systems, vol. 31, pp. 1–12, 2018. [Google Scholar]
52. Y. Luo, J. Zhu, M. Li, Y. Ren and B. Zhang, “Smooth neighbors on teacher graphs for semi-supervised learning,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, pp. 8896–8905, 2018. [Google Scholar]
53. E. Arazo, D. Ortego, P. Albert, N. E. O’ Connor and K. McGuinness, “Pseudo-labeling and confirmation bias in deep semi-supervised learning,” Int. Joint Conf. on Neural Networks, Glasgow, United Kingdom, pp. 1–8, 2020. [Google Scholar]
54. Z. Feng, Q. Zhou, Q. Gu, X. Tan, G. Cheng et al., “Dmt: Dynamic mutual training for semi-supervised learning,” Pattern Recognition, vol. 30, pp. 108777, 2022. [Google Scholar]
55. Z. Hu, Z. Yang, X. Hu and R. Nevatia, “Simple: Similar pseudo label exploitation for semi-supervised classification,” in Proc. of the IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Nashville, TN, USA, pp. 15099–15108, 2021. [Google Scholar]
56. H. Xu, H. Xiao, H. Hao, L. Dong, X. Qiu et al., “Semi-supervised learning with pseudo-negative labels for image classification,” Knowledge-Based Systems, vol. 260, pp. 110166, 2023. [Google Scholar]
57. W. Tang, B. Li, M. Barni, J. Li and J. Huang, “Improving cost learning for JPEG steganography by exploiting JPEG domain knowledge,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 32, no. 6, pp. 4081–4095, 2021. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF
 Downloads
Downloads
 Citation Tools
Citation Tools