SFSDA: Secure and Flexible Subset Data Aggregation with Fault Tolerance for Smart Grid

1  Introduction

As technologies such as artificial intelligence, 5G communications, big data, and more become widely available in various fields [1], the smart grid is gradually replacing traditional grids to provide efficient and reliable uninterrupted energy supply to households and businesses, with advantages such as dynamic electricity distribution, automatic pricing, and automatic troubleshooting [2].

In SG, device entities can interconnect and communicate with each other, which greatly increases productivity and automation [3–5]. However, many security issues in SGs pose a potential threat to personal privacy as well [6–8]. In smart grid, smart meters (SMs) installed in homes collect electricity consumption data from users in real-time and periodically submit this data to a control server (CS). CS collects and analyzes electricity consumption data from all users so that it can forecast electricity demand and adjust prices. While real-time individual electricity consumption can improve the quality of CS and user services, it is also capable of being used by malicious entities and inferring the user’s privacy. For example, analyzing many intimate details of users’ daily life through electricity consumption, such as the time of departure and return of the occupants, used appliances, and the use time of appliances [9], seriously threatens personal privacy. Therefore, it requires challenging efforts to balance the tradeoff between data sharing and data privacy to enable the convenience advantages brought by smart grid [10].

Privacy-Preserving Data Aggregation (PPDA) introduces the concept of edge computing to reduce data latency and communication bandwidth between edge devices [11]. To effectively protect personal privacy, it aggregates all the electricity consumption transmitted by SMs and then transmits the aggregated data to CS. As a result, CS no longer collects a single user’s electricity consumption, but the sum of all users’ consumption. This allows CS to analyze and process data without knowing individual data, taking full advantage of the convenience of smart grid. In recent years, the fog computing architecture is used in various data aggregation schemes to further improve aggregation efficiency while protecting personal privacy due to the powerful computing and storage capabilities of the Fog node (FN) [12]. Researchers use a variety of techniques for data aggregation that preserve privacy, such as homomorphic encryption, differential privacy, and blind factor. Although existing data aggregation schemes [13–15] are able to guarantee users’ privacy, most do not consider fine-grained requirements. In practical applications, CS needs not only to collect and analyze the total electricity consumption from all customers, but also to get more detailed and rich statistical characteristics through more detailed electricity consumption. To better determine generating capacity and pricing, for example, CS requires the total electricity consumption and the total number of customers within a given data range. As a result, the utility of the data will be greatly enhanced if the aggregation scheme meets the fine-grained requirements.

Various multi-subset data aggregation schemes [16–18] have been proposed for the past few years to achieve fine-grained requirements. Zhang et al. [19] found that proper subset adjustment allowed CS to gather data in a more focused way. For instance, during the day of the working day, the subset ought to be focused on a low-power interval range. Whereas, they found that existing multi-subset aggregation schemes cannot meet the requirement of dynamically adjusting the subset. If the subset is adjusted, the system parameters need to be updated again in their schemes. To address the shortcomings of the above multi-subset aggregation scheme, Zhang et al. [19] first proposed a novel flexible subset data aggregation (FSDA) scheme. In their scheme, The total interval (0,R] is divided into k consecutive intervals [0,R1),[R1,R2),…,[Rk−1,Rk), and CS is able to dynamically change the value of k and Rj (1≤j≤k) according to the requirements. Specifically, firstly, the electricity meter SMi of the i-th (1≤i≤n) user constructs k data slots and fills the slots in the corresponding range with electricity data. The filled data Mi is sent to FN as plaintext after encryption. Secondly, FN aggregates the encrypted data. Finally, CS decrypts the aggregated data to get the total electricity consumption of the interval corresponding to k slots. As a result, the scheme can display the extent of dense data distribution in more detail while coarsely displaying the extent of sparse data distribution with higher data utility. However, we launched an effective attack on FSDA. When SMi needs more than one Paillier ciphertext to accommodate k slots (for example, k>15 in FSDA scheme), only one of Paillier ciphertexts will be filled with the electricity data, while others are the Paillier ciphertext of 0. Then, the malicious FN can decrypt the Paillier ciphertext filled with electricity data by using the Paillier ciphertext without data filling, thus completely obtaining individual electricity consumption. In addition, FSDA has not considered the issues of fault tolerance. Some SMs may inevitably fail due to limited-service life, network failure, or natural hazard. Thus, a data aggregation scheme must be fault-tolerant if it is to be applied in practice, meaning that even if some SMs fail, it will still work. Therefore, it remains challenging to design a secure and fault-tolerant data aggregation scheme. We aim at solving this challenge.

Contributions: The first flexible multi-subset aggregation scheme with both security and fault tolerance is proposed. The main contributions are summarized as follows:

(1) We find a potential security flaw in FSDA [19] scheme for personal privacy disclosure. Specifically, when the SM submits more than one Paillier ciphertext (for example, when k>15 in FSDA scheme), the attacker can use the Paillier ciphertext itself to recover the plaintext, that is, the user’s electricity consumption. Our proposed attack to recover the single electricity consumption is feasible from the theoretical proof and experimental results.

(2) A secure and flexible multi-subset aggregation improvement scheme is proposed. Based on FSDA scheme, different hash functions for different Paillier ciphertexts of a single SM are introduced to avoid the correlation between different ciphertexts of the SM, so even if the SM generates more than one Paillier ciphertext, revealing Paillier ciphertexts will not result in a single electricity consumption. Experiments show that the improved scheme enhances privacy while maintaining computational efficiency.

(3) A first flexible subset data aggregation scheme with fault tolerance was constructed. We combine the fault tolerance method proposed in [14] with the flexible multi-subset aggregation improvement scheme to improve application capability in real-world scenarios. Experimental results show that our scheme is computationally efficient for multi-subset aggregation with fault tolerance.

The rest of this paper is organized as follows. Section 2 discusses related works. Section 3 briefly reviews the FSDA scheme and introduces the extended Shamir’s threshold secret-sharing scheme (tSSS). Section 4 shows the security flaws of FSDA, and then presents an attack method and experimentative verification. Section 5 describes the improved SFSDA in detail, followed by security analysis and performance evaluation in Sections 6 and 7, respectively. Finally, a conclusion is drawn in Section 8.

2  Related Works

Data aggregation in the smart grid not only protects data privacy, but also provides useful electricity consumption information for CS, which has become a research hotspot for privacy protection in smart grid in recent years. There are many techniques for achieving data aggregation to protect data privacy, such as homomorphic encryption [20,21] and differential privacy [22,23].

Homomorphic encryption allows data to be computed on the ciphertext, and the result of the additive operation on the ciphertext is equal to the result of adding plaintext and then encrypting it. Therefore, the aggregator can directly aggregate all the encrypted electricity consumption data submitted by SMs without knowing the raw electricity consumption data [24]. In recent years, Liu et al. [25], Ding et al. [26], Zhao et al. [27], Gope et al. [28], Li et al. [29], and Zhang et al. [30] have used homomorphic encryption for data aggregation to protect data privacy. In [29] and [30], aggregators use homomorphic encryption technology to achieve efficient privacy-preserving data aggregation, but the drawback of this scheme is that malicious aggregators have access to raw data. To prevent internal attacks, researchers typically combine homomorphic encryption technology with blind factors for data aggregation. Fan et al. [31] proposed the first data aggregation scheme for internal attackers by using homomorphic encryption and blind factor. However, the scheme only works in the case of short plaintext data, and Bao et al. [32] found that the scheme was not resistant to the public key replacement attack, because both public/private key pairs are generated by users themselves. In addition, differential privacy is often used for data aggregation. Liu et al. [33] protected the raw data by adding random noise, but the aggregation result obtained by this scheme is not accurate enough. Song et al. [34] propose a DMDA scheme. In their scheme, a set of known sum random numbers is used instead of random noise to obtain accurate aggregated data.

However, none of the above schemes is fault tolerant. To improve robustness and practicability, researchers have done in-depth research on fault-tolerant data aggregation. Xue et al. [15] proposed a fault-tolerant data aggregation scheme that does not rely on trusted authority (TA). However, once the failed SM returns to normal, its original secret key, including shares, must also be changed via the secure channel, which will lead to serious communication overload and high delay. Lyu et al. [35] proposed a data aggregation scheme with fault tolerance that requires the support of TA, which has low computational overhead. However, the fault tolerance of the scheme requires the protocol participants (FN, TA, and the cloud) to carry out an extra round of communication, resulting in a large communication cost. Saleem et al. [36] proposed a FESDA scheme with non-interactive fault-tolerant methods. In their scheme, CS prepares the equivalent ciphertext of all SMs in advance. If the SM fails, CS can decrypt aggregated data using the equivalent ciphertext of the failed SM. However, Wu et al. [14] found a security defect in FESDA scheme and demonstrated that CS can abuse equivalent ciphertexts of SMs to recover any SM’s reading. To remedy this defect, they introduced an extended Shamir’s threshold secret-sharing scheme (tSSS) and constructed FPDA, which is an improvement on FESDA scheme, and demonstrated its computational efficiency.

In addition to adding fault tolerance to improve the practicability of the scheme, the multi-subset aggregation has been extensively studied for the past few years as a means to enhance the functionality of aggregation schemes. In 2015, Lu et al. [17] realized two-subset aggregation for the first time based on Paillier homomorphic encryption. In the same year, Erikin [37] realized multi-subset data aggregation using Chinese remainder theorem and homomorphic encryption. To support users to join and quit dynamically, Liu et al. [38] constructed 3PDA scheme, in which, users can dynamically join the virtual aggregation domain of data aggregation. In [16] and [39], their proposed schemes are TA-independent that support users to join and exit dynamically without complicated initialization.

To obtain more detailed and targeted data with better statistical characteristics, Zhang et al. [19] recently proposed the first flexible subset aggregation scheme FSDA. In some situations, however, their scheme may reveal personal information.

The flexibility and fault tolerance described above are both important in multi-subset aggregation. To the best of our knowledge, there is no multi-subset aggregation both supports fault tolerance and flexible subset data aggregation. Our goal is to construct a secure flexible subset data aggregation with fault tolerance for smart grid.

3  Preliminaries

Some preliminaries required for SFSDA scheme are introduced in this section including FSDA scheme and extended Shamir’s tSSS.

3.1 Brief Review of FSDA Scheme

As shown in Fig. 1, the system model consists four entity types: (1) TA: it is responsible for generating parameters for the system and sending private keys to CS and SMs respectively. TA will remain offline once the system is up and running. (2) SMs: each SM collects the multi-dimensional data, performs cryptographic operations, and then sends a report to FN. (3) FN: it uses the property of additive homomorphism to aggregate all reports submitted by SMs. (4) CS: it performs decryption using its private key. The dynamic subset adjustment aggregation reduces the computational consumption of encryption by adjusting subsets, and obtains better data acquisition results. Figs. 2a and 2b show the aggregation results of other subset aggregation schemes and the aggregation results of FSDA scheme after dynamically adjusting subsets, respectively. As can be seen from Fig. 2, FSDA scheme can optimize the distribution of electricity consumption according to real-time electricity consumption. The scheme consists of the following five main phases.

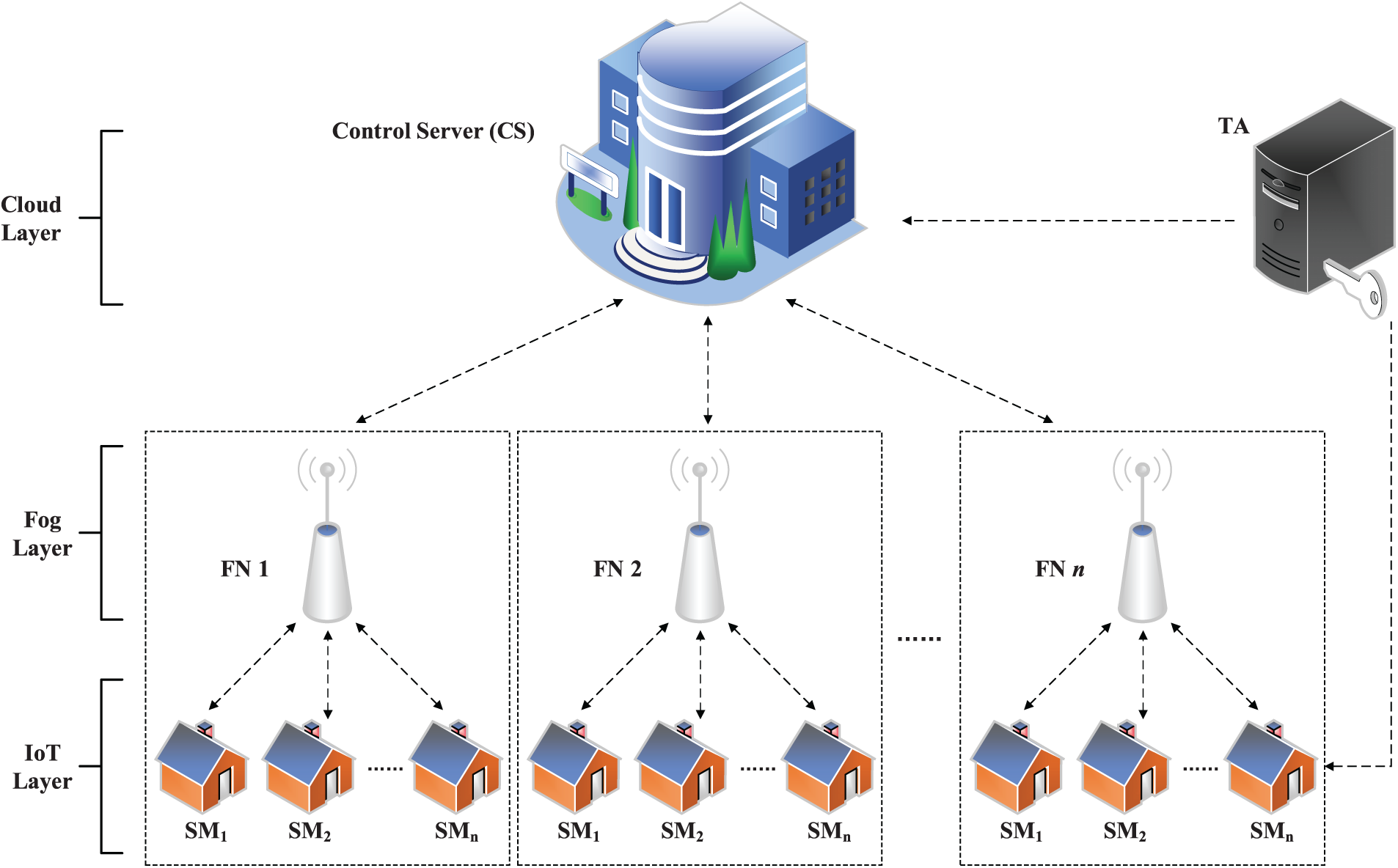
Figure 1: System model from FSDA scheme

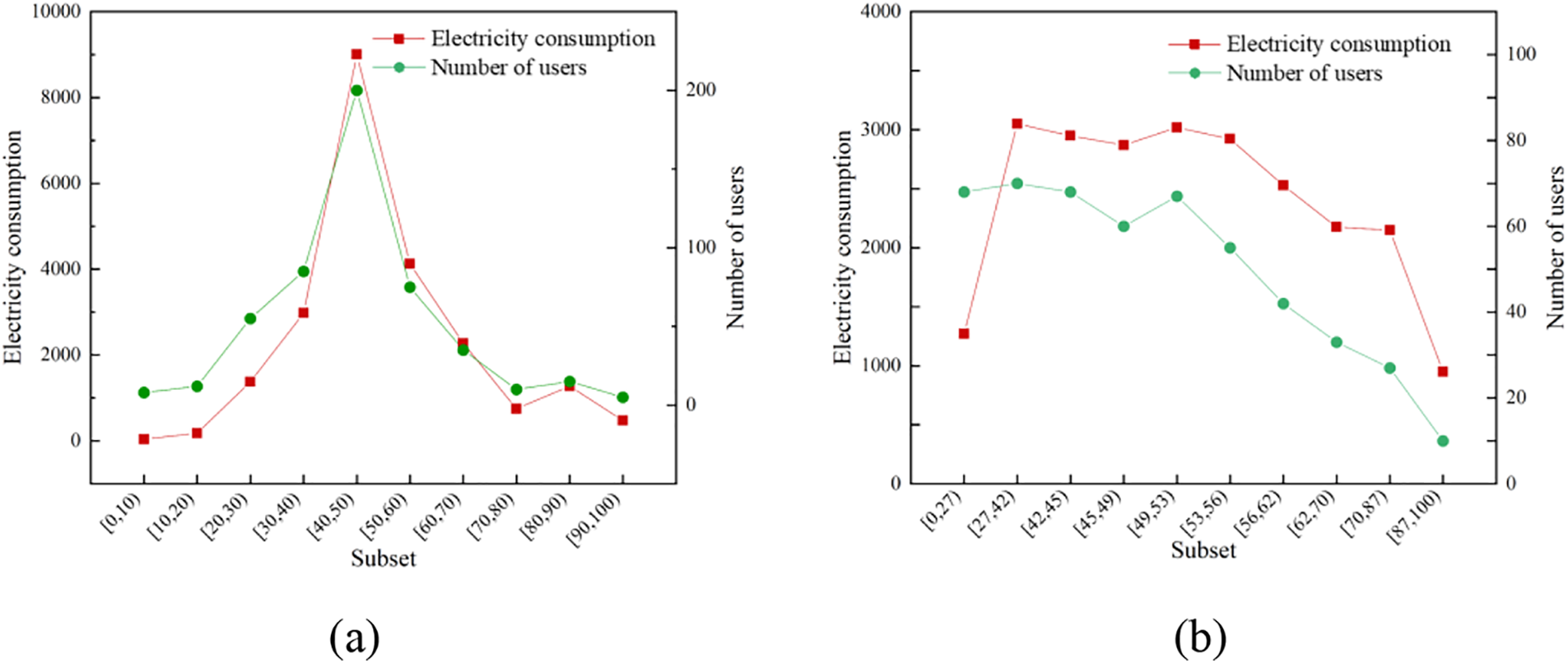
Figure 2: Examples of aggregation result. (a) Other schemes. (b) FSDA scheme

3.1.1 Initialization

TA generates a public key Kpub=(N;g) and a private key Kpri=(λ;μ), where g=N+1. Then, TA selects (n+1) large numbers s0,s1,…,sn as blind factors, satisfying ∑i=0nsi=0modλ. TA sends s0 to CS, s1 to SM1, s2 to SM2, …, sn to SMn through a secure channel.

CS divides [0,R) into k continuous intervals [0,R1), [R1,R2),…,[Rk−1,Rk), where R is the upper limit of electricity consumption and Rk=R. CS then sends (ΔR1,…,ΔRk,Δt) to FN, where ΔRj=(Rj−Rj−1) (where 1≤j≤k) and Δt is defined as the submission time interval.

FN calculates the size of each slot data lj+d, where lj=|ΔRj⋅n|, d=|n|. FN then sends (ΔRj, Δt, lj+d) to each SMi.

3.1.2 Individual Data Encryption

SMi constructs a data slot, where the size of a slot (j) is lj+d, and each bit of slot data is set to 0 by default. Then, “1” and data (Di−Rj−1) are filled in the first and second part of slot (j), respectively, where Di∈[Rj−1,Rj) is the reading of SMi. The data structure of plaintext Mi used for encryption is shown in Fig. 3. Finally, SMi uses the private key si to calculate

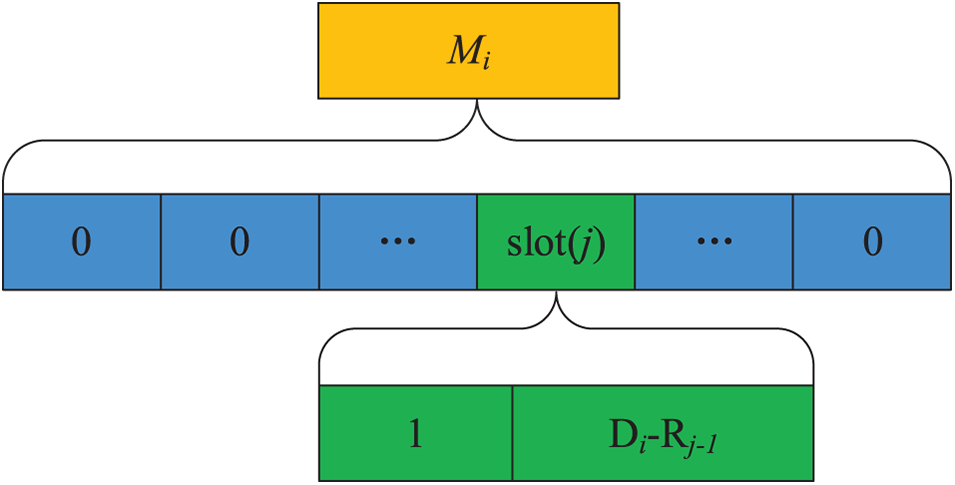
Figure 3: Data format of Mi

ci=(1+NMi)⋅H(T)N⋅simodN2,(1)

where H is the SHA-256 hash function.

Remark: A ciphertext ci is originally computed by ci=gMi⋅H(T)N⋅si modN2, and the author of FSDA proves by reasoning that due to the element g=N+1, the calculation of ci can be transformed into Eq. (1). This method can reduce the calculation time, and has also been adopted in PPSO [40] and PPMA [18].

3.1.3 Data Aggregation

After receiving all ciphertexts ci from the connected SMs, FN performs aggregation

C=∏i=1ncimodN2.(2)

Then, FN sends C to CS.

3.1.4 Decryption

CS calculates

V=C⋅H(T)N⋅s0modN2=(1+N∑i=1nMi)∑i=0nsimodN2=1+N∑i=1nMimodN2.(3)

And CS gets M=∑i=1nMi by computing (V−1)/N. Then, CS splits M to M1||M2||…||Mk. Dj1=Mj1 is the number of households in the j-th subset, Dj2=Mj2+Rj−1⋅Mj1 is the corresponding total consumption date in the j-th subset.

3.1.5 Subset Adjustment Phase

CS resets the submission setting when a subset or interval time needs to be adjusted. First, CS redistributes [0,R) into k′ new continuous intervals, resets the submission setting (ΔRj′,Δt′), and sends it to FN. Then, FN updates the (ΔRj′Δt′,lj′+d) and sends it to the SMi. Finally, SMi reconstructs the data Mi′.

3.2 Extended Shamir’s tSSS

Shamir’s (k¯,n¯) tSSS refers to sharing secrets among n¯ participants, in which any k¯ or more participants can reconstruct secrets, on the contrary, less than k¯ participants cannot reconstruct secrets. In this section, we first introduce the original Shamir’s tSSS [41], and later the extended Shamir’s (k¯,n¯) tSSS for our scheme.

3.2.1 Shamir’s tSSS

Step 1: Share distribution. Given that P is a large prime number. We usually call a person who needs to share a secret S∈ZP the dealer. First, randomly selects k¯−1 elements and makes a0=S. The dealer then builds a polynomial

F(x)=ao+a1⋅x1+a2⋅x2+…ak¯−1⋅xk¯−1modP.(4)

Given that xi is the serial number of participants γi, where 1≤i≤n¯. Take each xi into F(x) to get a share yi=F(xi), and calculate to get n¯ groups (xi,yi). Participants γi secretly keep their respective (xi,yi).

Step 2: Secret recovery. Take k¯ shares into the following equation:

F(x)=∑i=0k¯yi⋅LimodP,(5)

where Li=∏j=1,j≠ik¯([−xj]/[xi−xj])modP. Then restore secret S by S=F(0).

3.2.2 Extended Shamir’s tSSS

To achieve fault tolerance for flexible subset data aggregation, we use extended Shamir’s (k¯,n¯) tSSS, and it works by three steps, as described below.

Step1: Setup. Choose a large prime number P, thus the corresponding finite field is GF(P). Let N=p⋅q, where p and q are two large prime factors of P−1. Let g be a generator of order N in GF(P).

Step2: Share distribution. The dealer calculates the share yi of the secret S under the module N, and assigns yi to the participant Υi. And then, let the new secret that the dealer wants to share at time T be S′ and h=H(T)∈Z is a blind factor about time. Compute ΔT=S′−gh⋅SmodP and make it public.

Step 3: Secret recovery. Our goal is to recover S′ at time T. First, the collector obtains the blind share Yi=gyi⋅hmodP of k¯ or more participants and calculates

S¯′=∏i=1k¯(Yi)LimodP=∏i=1k¯(gyi⋅h)LimodP=gh⋅∑i=1k¯(yi⋅Li)modP=gh⋅(S+kN)modP=gh⋅SmodP.(6)

where k∈Z. Since gNmodP=1, the final equation of Eq. (6) holds. Then, the collector computes S′=S¯′+ΔT to restore the secret S′ at time T.

It is worth noting that the extended (k¯,n¯) tSSS scheme is master key secure and reusable. There’s no way for the collector to get any information on the initial secret S due to the difficulty of recovering S is equivalent to the difficulty of solving the discrete logarithm problem. And due to the constant updating of time T, the share provided by each participant is different in the relevant interval of time series. Therefore, the extended (k¯,n¯) tSSS scheme is reusable.

4  Attack on FSDA Scheme in a Specific Scenario

In this section, the attack method in a specific scenario for FSDA is designed and verified by experiments.

4.1 Design of Attack Method

In FSDA scheme, to realize flexible multi-subset aggregation, SMi constructs data Mi according to the requirements of CS, and then fills the electricity consumption data into a slot of Mi. If one Mi is not enough to divide the number of slots to meet the requirements of CS, then SMi will construct additional data to divide more slots, in this case, the constructed data is Mi=(Mi1,Mi2). Take the parameter values set by the author of FSDA scheme as an example, where |p|=|q|=512, the maximum electricity consumption is limited to 100 Wh, and the maximum total number of users is not more than 5000. Then, at this time, a Paillier ciphertext can accommodate up to 15 subsets. If 16 or more subsets need to be set, SMi constructs multiple data, taking the construction of Mi=(Mi1,Mi2) as an example, and then fills electricity consumption Di into one of the constructed data. Suppose Di is filled in Mi1, then Mi2=0, and ci=(ci1,ci2)=((1+NMi1)⋅H(T)N⋅simodN2,H(T)N⋅simodN2) can be obtained from Eq. (1). It is not difficult to find that two parts of data in the ciphertext ci contain H(T)N⋅si at the same time, and our attack finds the potential security flaw of FSDA scheme from this correlation in the ciphertext.

In the particular case described above, suppose that the goal of FN is to obtain a single electricity consumption Di∗ from a user ui∗ at time T∗. Our attack works by the following steps.

Step 1: Malicious FN receives the ciphertext ci∗ submitted by ui∗.

Step 2: FN extracts ci1∗=(1+NMi1∗)⋅H(T∗)N⋅simodN2 and ci2∗=H(T∗)N⋅simodN2 from the acquired ci∗, calculates (ci2∗)−1, meaning a multiplicative inverse for ci2∗ under the modulus N2, i.e., (ci2∗)−1⋅ci2∗=1modN2. Theorem 1 shows that the multiplicative inverse element of ci2∗ always exists under given parameters.

Theorem 1: Assume N=p⋅q where p and q are secure primes with |p|=|q|=512 bits, and H is the SHA-256 hash function with 256-bit output, a multiplicative inverse (ci2∗)−1modN2 exists where ci2∗=H(T∗)N⋅simodN2.

Proof: Given the ring (Z/mZ,+,×), where m>1. A congruence class β mod m has a multiplicative inverse in Z/mZ if and only if gcd(β,m)=1. Thus, it is sufficient to prove gcd(ci2∗,N2)=1. ■

Since H(T∗) is less than p and q, we can easily get gcd(H(T*), pq) = 1 and gcd(H(T∗)Nsi,N2)=1.

Let H(T∗)N⋅si=k0⋅N2+ci2∗ where k3∈Z. So H(T∗)N⋅si=k0⋅(p⋅q)2+k1⋅k3⋅p. Therefore, we can conclude that H(T∗)N⋅si contains at least one factor p, which contradicts the conclusion gcd(H(T∗)N⋅si,N2)=1. Thus, gcd(ci2∗,N2)=1.

Step 3: Compute V=ci1∗(ci2∗)−1 modN2=(1+NMi1∗)modN2.

Step 4: FN gets Mi1∗ by Mi1∗=(V−1)/N, thus obtaining the electricity consumption Di∗ in Mi1∗.

Our attack on FSDA is shown in Fig. 4.

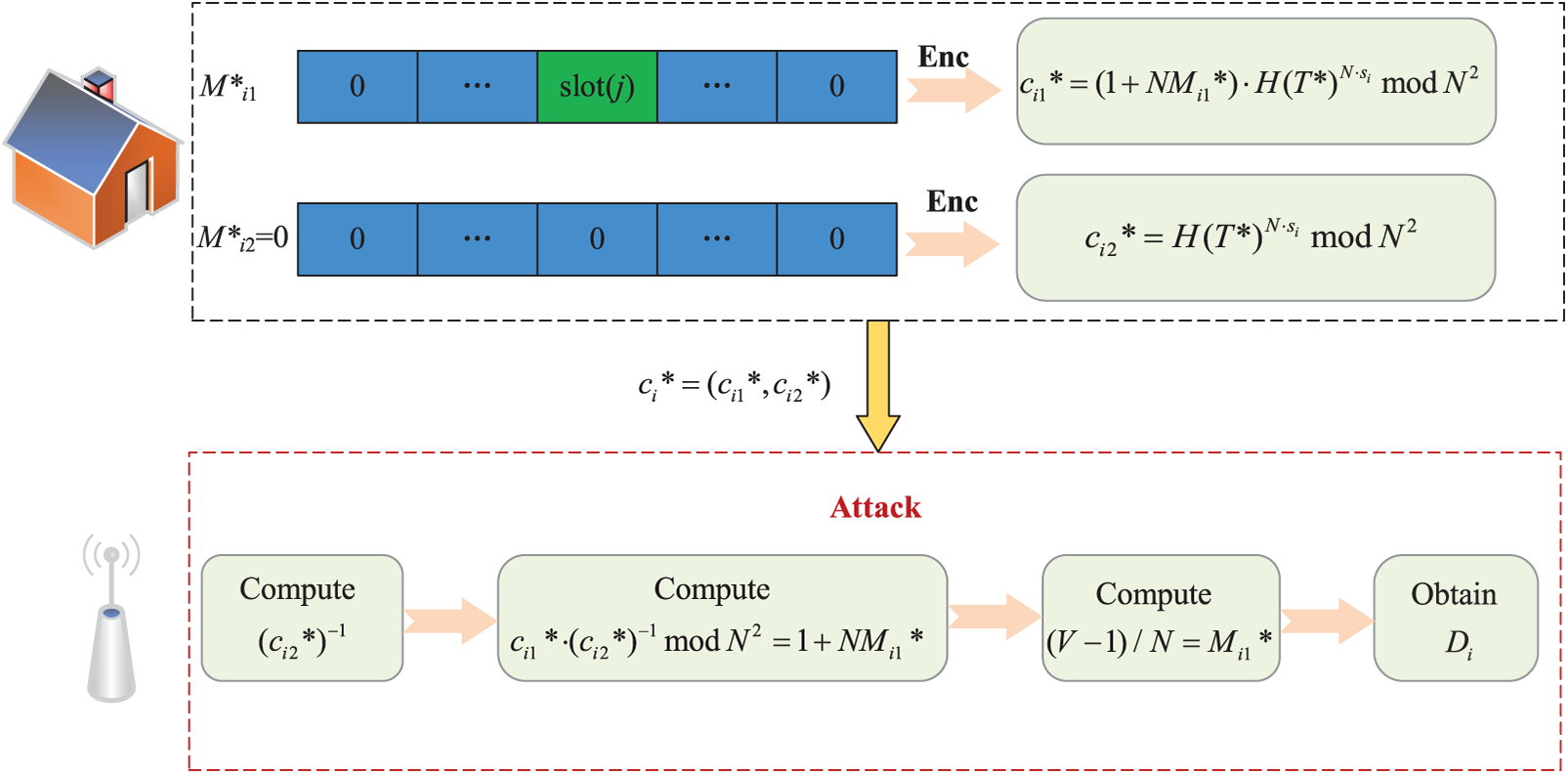
Figure 4: Flowchart of the attack method

4.2 Experimentative Verification

We implemented FSDA scheme in java and attacked it. The experimentation is performed on a computer with an Intel core i7 CPU (2.8 GHz) running Windows 10 and 16-GB RAM. In our experiment, the number of users is set to 10000, and SMs encrypts the data with their respective private keys and transmits it to FN. After FN gets the ci of all users, it executes our proposed attack method. Experiments show that the electricity consumption of all users can be restored correctly, and the average recovery time is 372 us. Therefore, our proposed attack method is feasible and efficient.

5  Our SFSDA Scheme

An improved scheme SFSDA based on FSDA is proposed to improve the safety of the original scheme while adding fault tolerance features. The flow chart of the SFSDA scheme is shown in Fig. 5, where the additional fault-tolerant method is described in the red dotted line box.

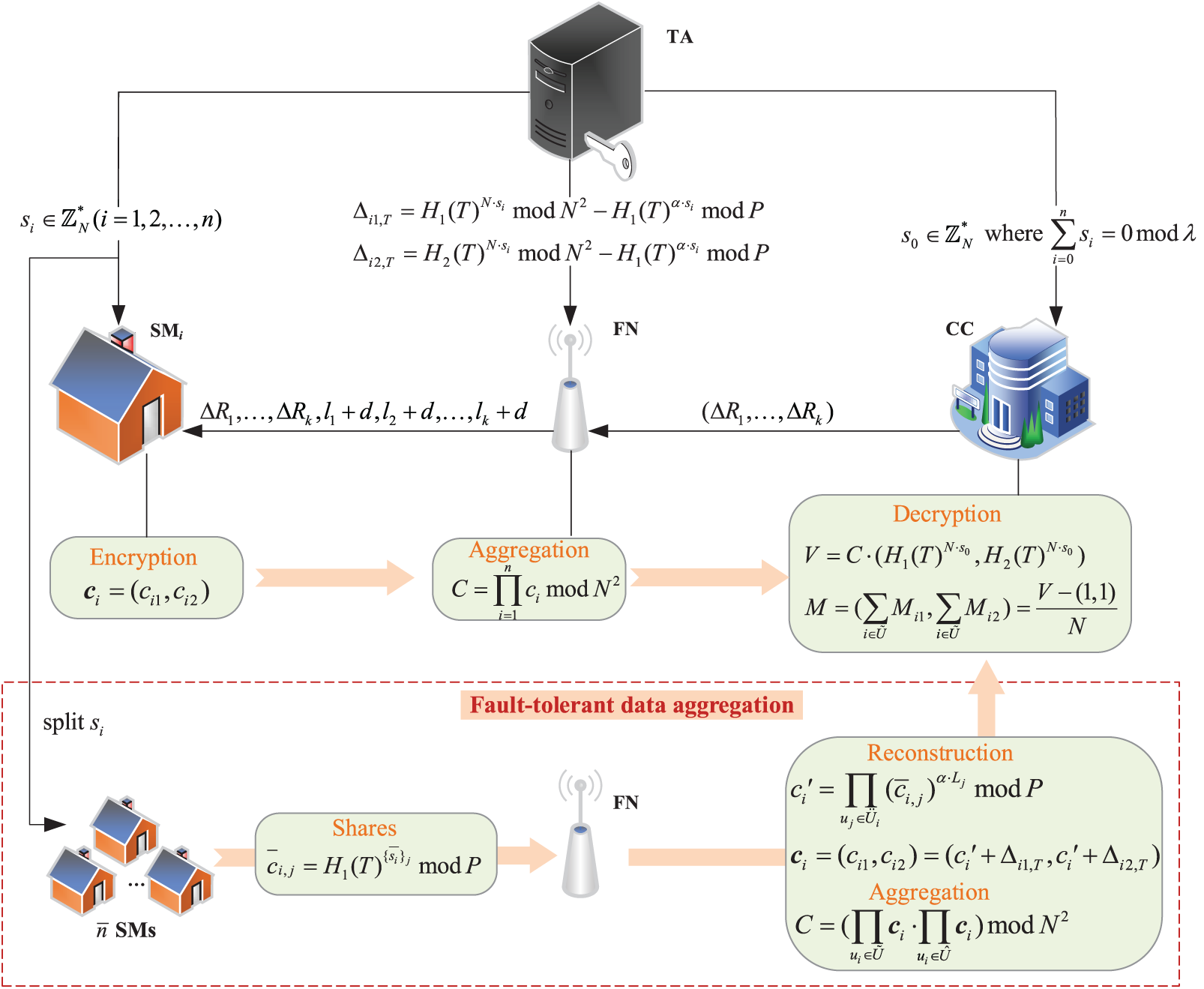
Figure 5: Schematic diagram of SFSDA scheme

5.1 System Model and Design Goal

The system model we consider is the same as FSDA scheme, as described in Section 3.1, which consists primarily of four entity types: Offline TA, CS, FNs, and SMs.

In the attacker model, FNs and CS are honest-but-curious. These entities will faithfully implement the protocol, but they are curious about the private information contained in the reports. Moreover, SMs are honest and tamper-resistant. However, there exists an external adversary 𝒜 that may compromise the SMs, FN, and CS. The adversary goals may include knowing the aggregated and individual SM readings. There are also some considerations for adversary 𝒜: Offline TA is thought to be invulnerable and a collusion attack can be initiated by at most any (n−1) SMs.

Our design goal of the improved scheme is mainly to provide privacy preservation, practicability, and the utility of data in smart grid. Specifically, it includes the following three aspects.

(1) Privacy: All electricity consumption information in smart grid should be protected. The adversary 𝒜 cannot access the user’s data, even if the attacker intercepts the communication data transmitted on an insecure channel. To protect the consumer’s personal electricity consumption data, no entity other than the consumer himself can obtain the consumer’s electricity consumption data. To protect aggregated data results, no entity other than CS can obtain aggregated data results.

(2) Flexible: Our scheme can achieve the same function of flexibly adjusting subsets as FSDA scheme. Compared with the traditional multi-subset aggregation scheme, our scheme can provide more targeted aggregation data for CS.

(3) Fault tolerance: Compared with FSDA scheme, our scheme can decrypt the data correctly when a user fails to submit the data. In practical applications, the user’s electric meter will often malfunction, and fault tolerance is the key to the application of the aggregation scheme in real life.

5.2 Overview

As mentioned above, FSDA scheme has the risk of disclosing personal privacy. Therefore, we add extra secure hash functions to the encryption phase of FSDA scheme, and introduce an extended Shamir’s (k¯,n¯) tSSS to make the scheme fault-tolerant.

(1) Security enhancement. In the individual data encryption phase, SFSDA differs from the original scheme in that if the ciphertext ci exceeds one Paillier ciphertext (i.e., ci=(ci1,ci2)), ci1 and ci2 contain two different hash functions, H1 and H2, respectively. Therefore, our SFSDA scheme does not make ci1 and ci2 contain the same as the FSDA scheme as described in Section 4.1. This improved method can effectively resist the proposed attacks and prevent personal privacy from leaking.

(2) Fault tolerance. When some faulty SMs cannot submit the ciphertext, In Eq. (3) of the decryption process in the FSDA scheme, ∑i=1nsimodλ≠0, hence, CS cannot obtain aggregated data results by decryption. To support the correct decryption, an extended Shamir’s (k¯,n¯) tSSS is performed to reconstruct the equivalent ciphertext H(T)N⋅si of malfunctioning SMi.

5.3 Detailed SFSDA Scheme

Without loss of generality, we describe SFSDA scheme in detail, taking the case where SMi needs to construct two pieces of data (i.e., Mi=(Mi1,Mi2)) to store subsets as an example.

5.3.1 Initialization

In the initialization phase, TA is mainly responsible for generating system parameters, CS transfers data-related settings to FN, and FN assigns settings to SMs. It is divided into the following three steps.

Step 1: Given the system parameter κ. Set N=p⋅q and a generator g=1+N, where p and q are two large prime numbers satisfying |p|=|q|=κ. And let P=αN+1 be a large prime number, where α is a small integer. Defines H1 and H2 as hash functions SHA-256. TA publishes the public key Kpub=(H1,H2,N,g,α) and holds the private key Kpri(λ,μ).

Step 2: Given the upper limit R of electricity consumption, CS divides [0,R) into k continuous intervals [0,R1), [R1,R2),...,[Rk−1,Rk), where Rk=R. CS then sends (ΔR1,...,ΔRk) to FN, where ΔRj=(Rj−Rj−1), j=1,2,…,k.

Step 3: FN calculates the size lj+d for slot (j), where lj=|ΔRj⋅n| and d=|n|. FN sends (ΔRj,lj+d) to each SMi.

5.3.2 Entity Registration

The registration of SMs and CS is completed by TA, which includes the following three steps.

Step 1: TA randomly selects (n+1) numbers s0,s1,…,sn∈ZN∗ satisfying ∑i=0nsi=0modλ, and sends s0 and si(i=1,2,...,n) to CS and SMi as their private keys respectively through the secure channel.

Step 2: TA randomly selects n¯ users (defined as U¯i) in the residential area. By applying extended Shamir’s (k¯,n¯) tSSS with modulus N, TA calculates share {s¯i}j (uj∈U¯i,1≤j≤n¯) of si, then sends all shares {s¯∗}j (uj∈U, and * is a universal symbol) to the corresponding user uj and sends all (ui,U¯i) to FN.

Step 3: For each time T and user ui, TA calculates Δi1,T=H1(T)N⋅simodN2−H1(T)α⋅simodP and Δi2,T=H2(T)N⋅si modN2−H1(T)α⋅simodP and sends them to FN.

5.3.3 Individual Data Encryption

SMi needs to construct data Mi=(Mi1,Mi2) at each time T, then fill the electricity data into the corresponding data slot, and finally encrypt the data and transmit it to FN.

Step 1: SM constructs a data slot, where the size of slot (j) is lj+d, and each bit of slot data is set to 0 by default.

Step 2: SMi detects reading Di for each time interval Δt. If Di∈[Rj−1,Rj), the “1” and the data Di−Rj−1 are filled in the first and second parts of the slot, respectively.

Step 3: SMi encrypts data Mi with its private key si:

ci1=(1+NMi1)⋅H1(T)N⋅simodN2,ci2=(1+NMi2)⋅H2(T)N⋅simodN2,(7)

and pass ci=(ci1,ci2) to FN.

5.3.4 Data Aggregation

FN checks all received ci and marks the lost user set U^. If U^ is not empty, for each ui∈U^, FN acquires the (ui,U¯) and sends a request for the share to uj∈U¯ (1≤j≤n¯). After receiving the request, uj acknowledges the malfunction of SMi and returns c¯i,j=H1(T){s¯i}j. FN receives k¯ shares from uj (denoted as U¨i), and it then calculates Lj=∏uw∈U¨i,uw≠uj([−uw]/[uj−uw])modN, ci′=∏uj∈U¨i(c¯i,j)α⋅LjmodP. The equivalent ciphertext can be obtained by computing

ci=(ci1,ci2)=(ci′+Δi1,T,ci′+Δi2,T).(8)

FN aggregates all equivalent ciphertexts and accepted ciphertexts

C=(∏ui∈U~ci⋅∏ui∈U^ci)modN2,(9)

and pass C and U^ to CS.

5.3.5 Decryption

After obtaining the aggregated data, CS first decrypts the data, and then splits the decrypted data to obtain the aggregation results of each subset. It includes the following two steps.

Step 1: CS performs the following calculations with its private key s0:

V=C⋅(H1(T)N⋅s0,H2(T)N⋅s0)=(1+N∑i∈U~Mi1,1+N∑i∈U~Mi2)modN2.(10)

CS obtains M by calculating

M=(∑i∈U~Mi1,∑i∈U~Mi2)=V−(1,1)N.(11)

Step 2: CS splits M into M1||M2||…||Mk. Mj (1≤j≤k) can be split into Mj1||Mj2. Finally, CS gets the number of users Dj1=Mj1 and the corresponding total consumption Dj2=Mj2+Rj−1⋅Mj1 of the j-th subset.

5.3.6 Subset Adjustment Phase

When CS wants to adjust the subset according to the specific situation, it only needs to reset the related settings of the subset.

Step 1: As in the initialization phase, CS divides [0,R) into k′ continuous intervals [0,R1′), [R1′,R2′), …,[Rk−1′,Rk′), where Rk′=R. CS then sends (ΔR1′,…,ΔRk′) to FN.

Step 2: FN recalculates the size lj′+d′. FN then sends (ΔRj′,lj′+d′) to each SMi.

Step 3: SMi constructs new data Mi′ containing k′ slots, and the size of slot (j) is lj′+d′ (1≤j≤k′).

5.4 Correction

The correctness evaluation of SFSDA mainly includes the reconstruction of equivalent ciphertext and the decryption of aggregated ciphertext.

5.4.1 Reconstruction of Equivalent Ciphertext

After FN receives k¯ shares from uj (denoted as U¨i), it reconstructs the equivalent ciphertext using extended Shamir’s (k¯,n¯) tSSS according to Eq. (6):

ci′=∏uj∈U¨i(c¯i,j)α⋅LjmodP=H1(T)α⋅(si+k⋅N)modP,(12)

where k∈Z. Since |H1(T)|=256 and |p|=|q|=512, thus gcd(H1(T),P)=1 and H1(T)αmodP is a generator with order N. So, there is H1(T)α⋅k⋅NmodP=1 and ci′=H1(T)α⋅si modP. From Eq. (8), the equivalent ciphertext can be obtained by computing

ci=(ci1,ci2)=(ci′+Δi1,T,ci′+Δi2,T)=(H1(T)N⋅simodN2,H2(T)N⋅simodN2).(13)

5.4.2 Decryption of Aggregated Ciphertext

V=C⋅(H1(T)N⋅s0,H2(T)N⋅s0)modN2=(∏ui∈U~ci⋅∏ui∈U^ci)⋅(H1(T)N⋅s0,H2(T)N⋅s0)modN2=(1+N∑ui∈U~Mi1,1+N∑ui∈U~Mi2)⋅(H1(T)N⋅(∑ui∈U~si+∑ui∈U^si+s0),H2(T)N⋅(∑ui∈U~si+∑ui∈U^si+s0))modN2=(1+N∑i∈U~Mi1,1+N∑i∈U~Mi2)modN2(14)

The last equation holds since U~∪U^=U and ∑i=1nsi+s0modλ=0. Finally, M=(∑i∈U~Mi1,∑i∈U~Mi2) is obtained.

6  Security Analysis

The security of the scheme is mainly analyzed through the following scenarios.

Scenario 1: The scenario described in Section 5 is semantically secure.

Proof: Both the single ciphertext submitted by SM and the aggregated ciphertext generated by FN calculation are valid ciphertexts of Paillier cryptosystem [42]. Because the security of the public key cryptosystem is based on solving Composite Residuosity Class Problem over ZN2∗, it has been proven to be semantically safe. Therefore, a plaintext is protected by the corresponding ciphertext. ■

Scenario 2: Even if a malicious CS colludes with SMs and FN, it would not be computationally possible to gain privacy.

Proof: CS can decrypt aggregated data with its private key s0 because s0+∑i=1nsi=0modλ and H(T)s0+∑i=1nsi=1modN2, but s0 cannot be used to decrypt any individual data Mi. If CS wants to obtain Mi, the first method is to decrypt an aggregated ciphertext with λ or si to obtain Mi, the second method is to obtain H1(T)N⋅simodN2 and H2(T)N⋅simodN2, then calculate their multiplication inverse, and then use the methods of steps 3 and 4 in the designed attack to obtain plaintext.

For the first method, on the one hand, λ is saved by TA, and no other entity can get it. On the other hand, even if the CS colludes with n−1 users ui (i=1,2,…,n−1), it is not computationally feasible to recover the sn from s1,s2,…,sn−1 obtained from the user ui and its own sn.

For the second method, extended Shamir’s (k¯,n¯) tSSS can be used to recover H1(T)N⋅simodN2 and H2(T)N⋅simodN2. If CS wants to reconstruct them, it needs to collude with at least k¯ out of n¯ users. However, as described in the system model, SMs are honest, so this method is not feasible. ■

Scenario 3: Malicious FN cannot obtain individual data and aggregate data results.

Proof: FN will receive all ciphertexts submitted from ui and perform an addition homomorphic operation. If FN wants to obtain individual data or aggregated data after the homomorphic operation, there are two methods: one is to obtain λ or si, and the other is to obtain H1(T)N⋅simodN2 and H1(T)N⋅simodN2. Since FN does not have λ or the private key si of ui and CS, it cannot get the corresponding plaintext of ciphertext. In the worst case, like CS, even if FN colludes with n SMs and CS, it cannot recover sn through si (i=0,1,…,n−1). In addition, FN can use secret reconstruction to obtain equivalent ciphertexts H1(T)N⋅simodN2 and H2(T)N⋅simodN2. However, if FN wants to reconstruct equivalent ciphertexts, at least k¯ users must honestly confirm the malfunction of ui. Therefore, based on the honest condition of user SMs, FN has no authority to reconstruct the equivalent ciphertext of normal users.

In the case of user failure, the user ui cannot submit encrypted data normally, and FN will perform the secret reconstruction. After at least k¯ users honestly confirm the ui failure and submit shares, FN can successfully reconstruct the equivalent ciphertext. Since the extended Shamir’s (k¯,n¯) tSSS method used is master key secured, FN cannot get any information about the user’s private key. In addition, the equivalent ciphertext of the FN reconstruction is not reusable, i.e., H1(T)N⋅simodN2 and H2(T)N⋅simodN2 reconstructed at the user ui failure moment T cannot be used to forge the H1(T′)N⋅simodN2 and H2(T′)N⋅simodN2 at the normal moment T′. That prevents FN from reusing the equivalent ciphertext to recover the electricity consumption information in the ciphertext submitted by the user. ■

Scenario 4: Our scheme can effectively resist the attacks proposed in this paper.

Proof: Different from the FSDA scheme, our scheme uses different hash functions H1 and H2 in the two Paillier ciphertexts submitted by the user. Therefore, it is not feasible for an attacker to obtain (1+NMi)modN2 by calculating the multiplication inverse of H1(T)N⋅simodN2 (or H2(T)N⋅si modN2) and multiplying it with (1+NMi)⋅H2(T)N⋅simodN2 (or (1+NMi)⋅H1(T)N⋅simodN2). ■

7  Performance Analysis

In this section, we evaluate the performance of the proposed SFSDA scheme and compare it with FSDA [19], MSDA [39] and FPDA [14] in terms of computation overhead, communication overhead and storage overhead. It is worth noting that fault-tolerant data aggregation will incur additional overhead due to the addition of fault-tolerant functionality in our scheme. Therefore, the performance evaluation of the scheme will evaluate normal data aggregation and fault-tolerant data aggregation respectively.

Two evaluation environments are used. We evaluate computation costs for data aggregation and decryption on the first platform consisting of a computer with an Intel Core i7 CPU (2.8 GHz) and 16 GB of memory running on Ubuntu 18.04. Computation costs are evaluated for all encryption of SMs on the second platform with a Raspberry Pi (RasPi). The RasPi 3 Model B is installed Ubuntu MATE 21.04 operating system with 1.2-GHz quad-core 64-bit ARM Cortex-A53 CPU and 1 GB of memory. In our implementation, the basic security parameters are the same as described FSDA, where the size of p and q are set to 512 bits. To facilitate the comparison with the original scheme, the maximum electricity consumption and the number of users of our scheme are also consistent with FSDA scheme. The maximum electricity consumption is set to 100 Wh and the total number of users is less than 5000. We choose a random integer value from 0 to 100 as each SM’s reading. Thus, a Paillier ciphertext may contain at most 15 subsets.

7.1 Computation Overhead

To facilitate the evaluation, some notations are defined. Exponentiation operation is denoted as Oe, point multiplication operation is denoted as Om, hash operation is denoted as OH, and point addition operation is denoted as Oa.

For normal data aggregation, our scheme and FSDA scheme work in the same way. Therefore, their computation overhead is the same. In SFSDA and FSDA, when SMi produces its report, it requires ⌈k/15⌉Oe and ⌈k/15⌉Om to generate the ciphertext. In MSDA, SMi requires ⌈k/10⌉Oe and ⌈k/10⌉Om to generate ciphertext, and also requires one OH and two Oa to update secret key. In FPDA, SMi requires kOe and kOm. Fig. 6a shows that when transmitting multiple subsets, the computation overhead of our scheme is consistent with FSDA, lower than the others. When FN aggregates ciphertext, in SFSDA, FSDA, MSDA and FPDA, it requires ⌈k/15⌉(n−1)Om, ⌈k/15⌉(n−1)Om, ⌈k/10⌉(n−1)Om and k(n−1)Om respectively. Fig. 6b shows that the computation costs of FN in our scheme and FSDA are the lowest compared with the other two schemes. In addition, when CS decrypts the aggregated message, in SFSDA, FSDA, MSDA and FPDA, it requires ⌈k/15⌉Oe, ⌈k/15⌉Oe, ⌈k/10⌉Oe and kOe respectively. Fig. 6c shows that the cost of CS in our scheme is still the lowest compared with the other three schemes, and the costs of CS of all schemes fluctuate a little.

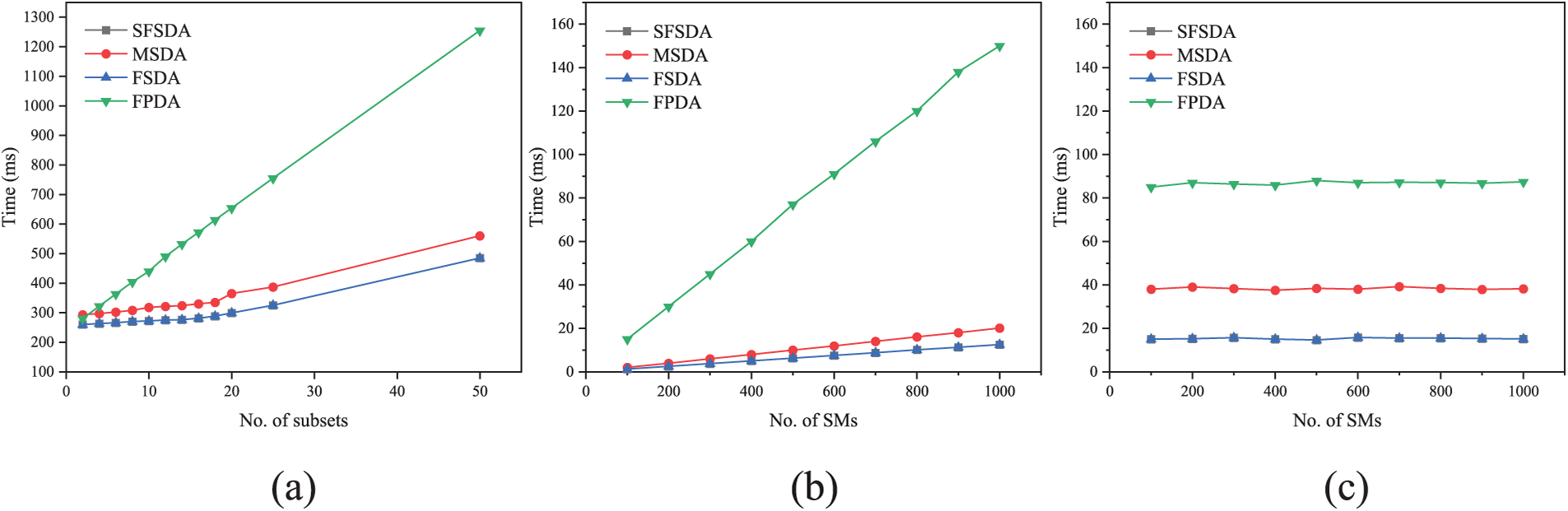
Figure 6: Normal data aggregation. (a) Computation overhead of SM (b) Computation overhead of FN with k = 15 (c) Computation overhead of CS with k = 15

For fault-tolerant data aggregation, our scheme generates extra computation overhead as shown in Fig. 7. Since CS is not involved in fault-tolerant data aggregation, Fig. 7 only gives the total time to generate shares for all SMs with different failure probabilities and different thresholds, and the time for FN to perform reconfiguration and aggregation. Figs. 7a and 7b show that under the same threshold, with the increase of failure probability, the total time for SMs to generate shares and the time for FN to perform reconstruction and aggregation increase approximately linearly with the increase of failure probabilities. As can be seen from Figs. 7a and 7b, the extra computation overhead incurred by SMs and FN would increase significantly if the thresholds were increased.

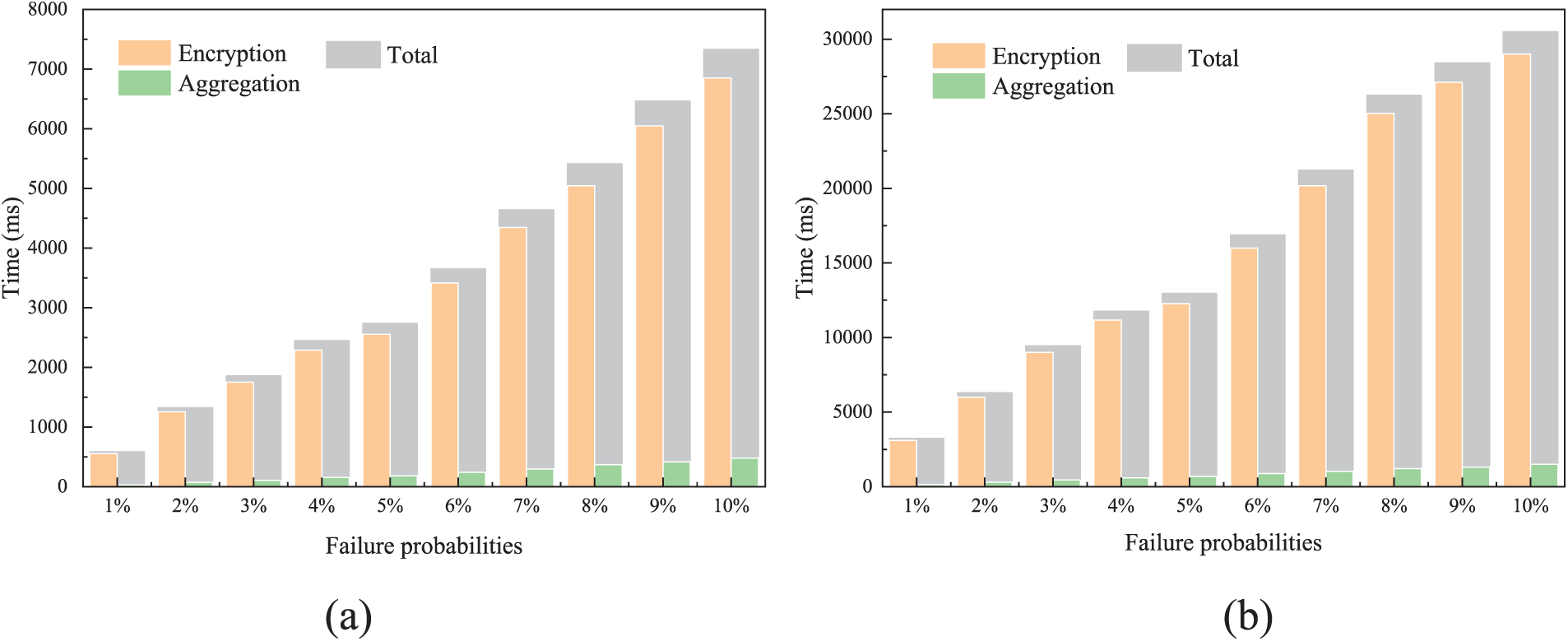
Figure 7: Fault-tolerant data aggregation. (a) Computation overhead under different failure probabilities with (3, 5), n=500 (b) Computation overhead under different failure probabilities with (13, 20), n=500

7.2 Communication Overhead

In our scheme, the failure probability is defined as β, and the maximum sequence number length of users is defined as l. Since the size of p and q is 512 bits, the size of N is 1024 bits. Hence, the size of N2 is 2048 bits. We also assume the share reported by SMs to FN is about 1024 bits under modulus P=αN+1, where α is a small integer. Besides, by instantiating our SFSDA scheme with β=5%, l=20, n=500, k¯=13, n¯=20 and k=15, detailed communication overheads are shown in Table 1. During normal data aggregation, each SM transmits ciphertext of size ⌈k/15⌉|ZN2∗| to FN in our scheme, which should be ⌈k/15⌉|ZN2∗| in FSDA, ⌈k/10⌉|ZN2∗| in MSDA, and k|ZN2∗| in FPDA. Besides, in MSDA, each SM needs to send additional |Zp∗| to each other to update secret key. Therefore, the overheads of all SMs in SFSDA, FSDA, MSDA, and FPDA are 1000, 1000, 127000, and 15000 kb respectively. Since the length of the aggregated ciphertext is the same as the ciphertext uploaded by SM, the communication cost between FN and CS is the same as the communication cost between SM and FN, which is 2, 2, 4 and 30 kb in SFSDA, FSDA, MSDA, and FPDA respectively. When the user fails to submit data, in our scheme, FN transmits a sequence number of size l to SM to send a request for reconstruction, resulting in a total additional communication overhead of l⋅(β⋅n)⋅n¯≈10 kb from FN to SMs. SM transmits a share of size |Zp∗| to FN, resulting in a total communication overhead of |Zp∗|⋅(β⋅n)⋅n¯≈500 kb from SMs to FN. FN transmits to the CS the serial number of the failed user of size l, resulting in a total communication overhead of l⋅(β⋅n)≈0.5 kb from FN to CS. While in FPDA, the extra communication overhead is k times that of our scheme. As can be seen from Table 1, for normal data aggregation, the communication overhead of our scheme is consistent with that of the FSDA and lower than that of the other two schemes. For fault-tolerant data aggregation, our scheme can achieve a low communication overhead.

7.3 Storage Overhead

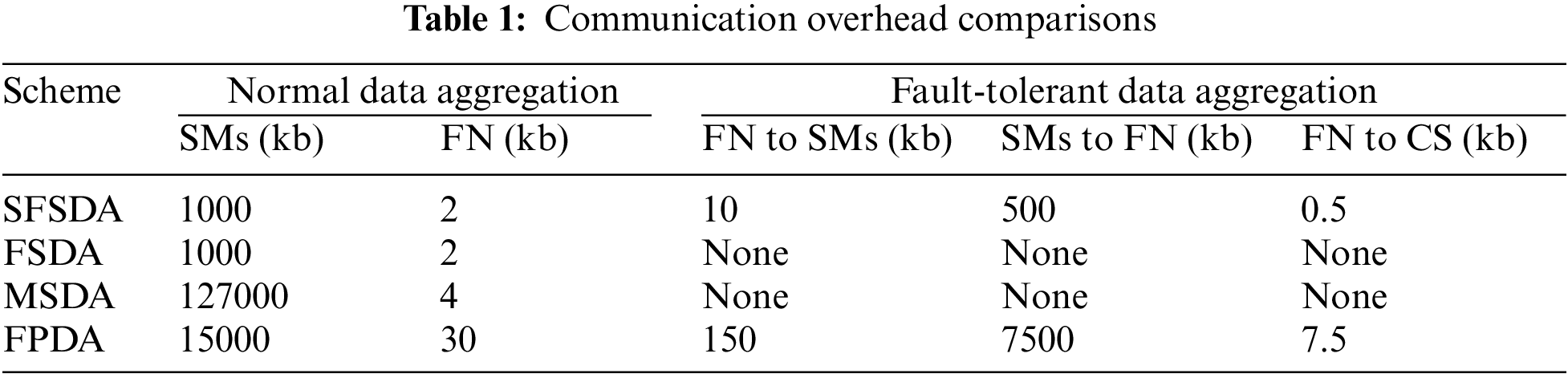
In SFSDA and FPDA schemes, to achieve fault tolerance, SM and FN need to store the original share {s¯i} in addition to their private keys, and FN needs to store the index with the size l⋅n⋅n¯ for finding the private key and Δi,T sent by TA in advance. Let SM submit electricity consumption every 15 min, then each SM will submit its electricity consumption at 96 different times a day. Set Δi,T to be updated daily, then Δi,T=96⋅n⋅|ZN2∗|. Table 2 shows the storage overhead for each entity. For normal data aggregation, the storage overhead of our scheme is consistent with that of FSDA and FPDA, and the storage overhead of SM is less than that of MSDA. For fault-tolerant data aggregation, SM only stores a small amount of extra data, and most of the storage overhead for handling user failures is borne by FN.

8  Conclusion

In this article, we identified the potential security flaw of personal privacy disclosure in the FSDA scheme. Once the ciphertext sent by SM to FN contains two or more Paillier ciphertexts, the ciphertext itself will reveal the encrypted personal electricity consumption, resulting in personal privacy infringement. In addition, the FSDA scheme lacks fault tolerance. Once SM cannot submit data, CS will not get the correct decryption results. To solve the above-mentioned security issues and hold the fault-tolerant property, a secure flexible subset data aggregation with fault tolerance SFSDA is proposed. On the one hand, our scheme allows for flexible subset aggregation, where the subset can be flexibly adjusted to the needs of CS without compromising user privacy. On the other hand, when the encrypted data of a faulty user cannot be obtained, the CS can still obtain the correct aggregation result by reconstructing the equivalent ciphertext in our scheme. The experimental results show that our scheme is efficient, flexible, and practical. For future work, as the existing data aggregation schemes for smart grids only perform sum operations on the data, some important operations, such as linear operations, are ignored. Therefore, maintaining linear homomorphism of data aggregation for smart grids is an important direction for our future research.

Funding Statement: This work was supported by National Natural Science Foundation of China (Grant Nos. 62102452, 62172436), Natural Science Foundation of Shaanxi Province (No. 2023-JC-YB-584), Innovative Research Team in Engineering University of PAP (KYTD201805), Engineering University of PAP’s Funding for Key Researcher (No. KYGG202011).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. H. Xu, M. Guo, N. Nedjah, J. Zhang and P. Li, “Vehicle and pedestrian detection algorithm based on lightweight YOLOv3-promote and semi-precision acceleration,” IEEE Transactions on Intelligent Transportation Systems, vol. 23, no. 10, pp. 19760–19771, 2022. [Google Scholar]

2. P. Kumar, Y. Lin, G. Bai, A. Paverd, J. S. Dong et al., “Smart grid metering networks: A survey on security, privacy and open research issues,” IEEE Communications Surveys & Tutorials, vol. 21, no. 3, pp. 2886–2927, 2019. [Google Scholar]

3. Y. Yang, X. Yang, M. Heidari, M. A. Khan, G. Srivastava et al., “Astream: Data-stream-driven scalable anomaly detection with accuracy guarantee in IIoT environment,” IEEE Transactions on Network Science and Engineering, 2022. [Google Scholar]

4. L. Qi, Y. Yang, X. Zhou, W. Rafique and J. Ma, “Fast anomaly identification based on multi-aspect data streams for intelligent intrusion detection toward secure industry 4.0,” IEEE Transactions on Industrial Informatics, vol. 18, no. 9, pp. 6503–6511, 2021. [Google Scholar]

5. Z. G. Al-Mekhlafi, M. A. Al-Shareeda, S. Manickam, B. A. Mohammed and A. Qtaish, “Lattice-based lightweight quantum resistant scheme in 5g-enabled vehicular networks,” Mathematics, vol. 11, no. 2, pp. 399, 2023. [Google Scholar]

6. M. A. Al-Shareeda, S. Manickam, S. A. Laghari and A. Jaisan, “Replay-attack detection and prevention mechanism in industry 4.0 landscape for secure secs/gem communications,” Sustainability, vol. 14, no. 23, pp. 15900, 2022. [Google Scholar]

7. M. A. Al-Shareeda and S. Manickam, “Msr-dos: Modular square root-based scheme to resist denial of service (dos) attacks in 5g-enabled vehicular networks,” IEEE Access, vol. 10, pp. 120606–120615, 2022. [Google Scholar]

8. M. A. Al-Shareeda, S. Manickam, B. A. Mohammed, Z. G. Al-Mekhlafi, A. Qtaish et al., “Provably secure with efficient data sharing scheme for fifth-generation (5G)-enabled vehicular networks without road-side unit (RSU),” Sustainability, vol. 14, no. 16, pp. 9961, 2022. [Google Scholar]

9. E. L. Quinn, “Privacy and the new energy infrastructure,” Available at SSRN 1370731, 2009. [Google Scholar]

10. F. Wang, G. Li, Y. Wang, W. Rafique, M. R. Khosravi et al., “Privacy-aware traffic flow prediction based on multi-party sensor data with zero trust in smart city,” ACM Transactions on Internet Technology (TOIT), 2022. [Google Scholar]

11. X. Zhou, X. Yang, J. Ma, I. Kevin and K. Wang, “Energy efficient smart routing based on link correlation mining for wireless edge computing in IoT,” IEEE Internet of Things Journal, vol. 9, no. 16, pp. 14988–14997, 2021. [Google Scholar]

12. M. A. Al-Shareeda and S. Manickam, “Covid-19 vehicle based on an efficient mutual authentication scheme for 5g-enabled vehicular fog computing,” International Journal of Environmental Research and Public Health, vol. 19, no. 23, pp. 15618, 2022. [Google Scholar] [PubMed]

13. H. Bao and R. Lu, “A new differentially private data aggregation with fault tolerance for smart grid communications,” IEEE Internet of Things Journal, vol. 2, no. 3, pp. 248–258, 2015. [Google Scholar]

14. L. Wu, M. Xu, S. Fu, Y. Luo and Y. Wei, “FPDA: Fault-tolerant and privacy-enhanced data aggregation scheme in fog-assisted smart grid,” IEEE Internet of Things Journal, vol. 9, no. 7, pp. 5254–5265, 2021. [Google Scholar]

15. K. Xue, B. Zhu, Q. Yang, D. S. Wei and M. Guizani, “An efficient and robust data aggregation scheme without a trusted authority for smart grid,” IEEE Internet of Things Journal, vol. 7, no. 3, pp. 1949–1959, 2019. [Google Scholar]

16. X. Wang, Y. Liu and K. K. R. Choo, “Fault-tolerant multisubset aggregation scheme for smart grid,” IEEE Transactions on Industrial Informatics, vol. 17, no. 6, pp. 4065–4072, 2020. [Google Scholar]

17. R. Lu, K. Alharbi, X. Lin and C. Huang, “A novel privacy-preserving set aggregation scheme for smart grid communications,” in 2015 IEEE Global Communications Conf. (GLOBECOM), San Diego, CA, USA, pp. 1–6, 2015. [Google Scholar]

18. S. Li, K. Xue, Q. Yang and P. Hong, “PPMA: Privacy-preserving multisubset data aggregation in smart grid,” IEEE Transactions on Industrial Informatics, vol. 14, no. 2, pp. 462–471, 2017. [Google Scholar]

19. L. Zhang and Y. Liu, “FSDA: Flexible subset data aggregation for smart grid,” IEEE Systems Journal, vol. 17, no. 1, pp. 569–578, 2023. [Google Scholar]

20. T. ElGamal, “A public key cryptosystem and a signature scheme based on discrete logarithms,” IEEE Transactions on Information Theory, vol. 31, no. 4, pp. 469–472, 1985. [Google Scholar]

21. P. Paillier, “Public-key cryptosystems based on composite degree residuosity classes,” in Int. Conf. on the Theory and Applications of Cryptographic Techniques, Berlin, Heidelberg, Springer, pp. 223–238, 1999. [Google Scholar]

22. C. Dwork, “Differential privacy: A survey of results,” in Int. Conf. on Theory and Applications of Models of Computation, Berlin, Heidelberg, Springer, pp. 1–19, 2008. [Google Scholar]

23. C. Dwork and A. Roth, “The algorithmic foundations of differential privacy,” Foundations and Trends® in Theoretical Computer Science, vol. 9, no. 3–4, pp. 211–407, 2014. [Google Scholar]

24. Z. Song, W. Zhong, T. Zhou, D. Chen, Y. Ding et al., “SEMDA: Secure and efficient multidimensional data aggregation in smart grid without a trusted third party,” Security and Communication Networks, 2023. [Google Scholar]

25. J. N. Liu, J. Weng, A. Yang, Y. Chen and X. Lin, “Enabling efficient and privacy-preserving aggregation communication and function query for fog computing-based smart grid,” IEEE Transactions on Smart Grid, vol. 11, no. 1, pp. 247–257, 2019. [Google Scholar]

26. Y. Ding, B. Wang, Y. Wang, K. Zhang and H. Wang, “Secure metering data aggregation with batch verification in industrial smart grid,” IEEE Transactions on Industrial Informatics, vol. 16, no. 10, pp. 6607–6616, 2020. [Google Scholar]

27. S. Zhao, F. Li, H. Li, R. Lu, S. Ren et al., “Smart and practical privacy-preserving data aggregation for fog-based smart grids,” IEEE Transactions on Information Forensics and Security, vol. 16, pp. 521–536, 2020. [Google Scholar]

28. P. Gope and B. Sikdar, “Lightweight and privacy-friendly spatial data aggregation for secure power supply and demand management in smart grids,” IEEE Transactions on Information Forensics and Security, vol. 14, no. 6, pp. 1554–1566, 2018. [Google Scholar]

29. H. Li, X. Lin, H. Yang, X. Liang, R. Lu et al., “EPPDR: An efficient privacy-preserving demand response scheme with adaptive key evolution in smart grid,” IEEE Transactions on Parallel and Distributed Systems, vol. 25, no. 8, pp. 2053–2064, 2013. [Google Scholar]

30. K. Zhang, X. Liang, M. Baura, R. Lu and X. S. Shen, “PHDA: A priority based health data aggregation with privacy preservation for cloud assisted WBANs,” Information Sciences, vol. 284, pp. 130–141, 2014. [Google Scholar]

31. C. I. Fan, S. Y. Huang and Y. L. Lai, “Privacy-enhanced data aggregation scheme against internal attackers in smart grid,” IEEE Transactions on Industrial Informatics, vol. 10, no. 1, pp. 666–675, 2013. [Google Scholar]

32. H. Bao and R. Lu, “Comment on privacy-enhanced data aggregation scheme against internal attackers in smart grid,” IEEE Transactions on Industrial Informatics, vol. 12, no. 1, pp. 2–5, 2015. [Google Scholar]

33. Y. Liu, G. Liu, C. Cheng, Z. Xia and J. Shen, “A privacy-preserving health data aggregation scheme,” KSII Transactions on Internet and Information Systems (TIIS), vol. 10, no. 8, pp. 3852–3864, 2016. [Google Scholar]

34. J. Song, Y. Liu, J. Shao and C. Tang, “A dynamic membership data aggregation (DMDA) protocol for smart grid,” IEEE Systems Journal, vol. 14, no. 1, pp. 900–908, 2019. [Google Scholar]

35. L. Lyu, K. Nandakumar, B. Rubinstein, J. Jin, J. Bedo et al., “PPFA: Privacy preserving fog-enabled aggregation in smart grid,” IEEE Transactions on Industrial Informatics, vol. 14, no. 8, pp. 3733–3744, 2018. [Google Scholar]

36. A. Saleem, A. Khan, S. U. R. Malik, H. Pervaiz, H. Malik et al., “FESDA: Fog-enabled secure data aggregation in smart grid IoT network,” IEEE Internet of Things Journal, vol. 7, no. 7, pp. 6132–6142, 2019. [Google Scholar]

37. Z. Erkin, “Private data aggregation with groups for smart grids in a dynamic setting using CRT,” in 2015 IEEE Int. Workshop on Information Forensics and Security (WIFS), Rome, Italy, pp. 1–6, 2015. [Google Scholar]

38. Y. Liu, W. Guo, C. I. Fan, L. Chang and C. Cheng, “A practical privacy-preserving data aggregation (3PDA) scheme for smart grid,” IEEE Transactions on Industrial Informatics, vol. 15, no. 3, pp. 1767–1774, 2018. [Google Scholar]

39. Z. Zeng, X. Wang, Y. Liu and L. Chang, “MSDA: Multi-subset data aggregation scheme without trusted third party,” Frontiers of Computer Science, vol. 16, no. 1, pp. 1–7, 2022. [Google Scholar]

40. K. Xue, Q. Yang, S. Li, D. S. Wei, M. Peng et al., “PPSO: A privacy-preserving service outsourcing scheme for real-time pricing demand response in smart grid,” IEEE Internet of Things Journal, vol. 6, no. 2, pp. 2486–2496, 2018. [Google Scholar]

41. A. Shamir, “How to share a secret,” Communications of the ACM, vol. 22, no. 11, pp. 612–613, 1979. [Google Scholar]

42. D. Boneh, E. J. Goh and K. Nissim, “Evaluating 2-DNF formulas on ciphertexts,” TCC, vol. 3378, pp. 325–341, 2005. [Google Scholar]