Forecasting Energy Consumption Using a Novel Hybrid Dipper Throated Optimization and Stochastic Fractal Search Algorithm

1  Introduction

The consumption of energy is increased over time and thus increases the consumption of fossil fuels, which might lead to the destruction of our ecosystem irreversibly. Therefore, we need to find efficient and more innovative technological methods for decreasing energy consumption in all sectors to protect our environment and ensure future energy supply. Furthermore, these technologies may assist in making more intelligent decisions about the energy consumption of all types of equipment more effectively.

The development of smart households is a cost-effective approach that can help in saving energy. Smart households are usually based on a set of relays, controllers, sensors, and meters, in addition to a control system to manage the full operation and interaction between them. The main goal of a smart household is to collect relevant information about the environment and behavior of residents along with their habits, to make efficient decisions regarding the reduction of energy consumption. A smart household can learn the routines and lifestyles of its residents using machine learning techniques, allowing activities and operations to be automated. Based on the absence and presence of residents, temperature, and light, for example, can be automatically regulated. In addition, the systems of smart households can be connected with switchboards and other traditional systems to optimize energy consumption [1]. For linking virtual and physical devices in a smart household to the Internet, the Internet of Things (IoT) can be utilized. The main advantage of IoT is that it enables users to automate the functioning of their devices, collect information and remotely manage them. The scales of applicability of IoT are various, starting from simple appliances, such as washing machines and refrigerators in a household, on a small scale, to the transportation system of a city in complex infrastructure, on a large scale.

A significant reduction of environmental effects due to saving can be achieved by predicting the potential energy consumption of a household [2–4]. Consequently, a lot of time and effort has been invested in developing solutions to energy consumption optimization in a smart household. The most essential of these solutions is to use the least amount of energy possible while retaining customer satisfaction [5]. Several machine learning (ML) techniques for energy prediction of appliances in smart households have been suggested for this purpose [6,7]. Traditional machine learning methods such as super vector machines, k-nearest neighbor, neural networks, multi-layer perceptron, decision trees, deep learning, and ensemble approaches are extensively used to provide efficient solutions to this problem of accurate energy consumption prediction.

In this paper, a novel approach is proposed for predicting energy consumption using recent advances in machine learning. The prediction of the energy consumption is performed using a new LSTM-based model. To improve the performance of the proposed LSTM-based model, we developed a new optimization algorithm based on the DTO and SFS optimization algorithms to adjust the parameters of the LSTM-based model. To show the effectiveness of the proposed approach, we employed a publicly available dataset that contains 121273 measurements gathered over ten years in the United States. The experiments based on the given dataset show that the proposed approach outperforms the other forecasting approaches considered in this work.

The following organization is followed in presenting the contents of this work. The relevant related works are presented in Section 2. The proposed methodology for energy consumption is explained in Section 3. The results of the conducted experiments are discussed in Section 4. The conclusion is then presented in Section 5.

2  Related Works

In recent research, a variety of techniques to energy consumption prediction have been developed, with the goal of developing effective energy consumption prediction systems to enhance energy savings and lessen environmental consequences. Most of these methods start with historical energy usage time series data and use machine learning techniques to create a forecast model. Authors in [6] used artificial neural network (ANN), linear regression (LR), and decision tree (DT) to forecast energy consumption in cottages, dwellings, and government buildings. They also looked at the impact of the number of people, family size, building time, house style, and electrical equipment. Summer and winter results were obtained. In comparison to ANN and LR, their findings demonstrate that DT has higher accuracy.

In the same way, the authors in [8] present three models for predicting energy consumption based on linear regression multiple layers (LRML) and simple linear regression (SLR). They also took into account three distinct scenarios. The training dataset for energy consumption was divided into three groups: annually, daily, and hourly peak hours. In comparison to the LRML, their findings reveal that the SLR-based algorithm is better at forecasting yearly and hourly-based forecasts.

In [9], the authors suggested using a graphical energy consumption prediction model. They target figuring out how energy consumption is related to human behaviors and routines, specifically the rate and duration of use of electronic household devices. Temperature differences between the outdoor and indoor environments and the energy required utilities such as heating are among the model factors.

The study’s objective was to foretell energy usage patterns for the coming week and month. The extreme learning machine (ELM), the adaptive neuro-fuzzy inference system (ANFIS), and the ANN are usually introduced as methods for predicting residential energy usage. In addition, they experimented with a wide range of membership functions, both in terms of quantity and variety, to determine what made for the most effective ANFIS architecture. They have also tried out their method with different ANN architectures and levels of hidden complexity. In [10], researchers report the success of using a recurrent neural network trained on hourly energy consumption data to predict the cooling and heating energy needs of a building based on the current weather and the present time.

For estimating the yearly energy consumption of households, authors in [11] used SVM, general regression neural network (GRNN), radial basis function neural network (RBFNN), and backpropagation ANN. These models were developed using real-world data from 59 households and tested on nine others. In comparison to other models, their findings reveal that GRNN and SVM are better suited to this problem. However, a test of all approaches revealed that SVM predicted the potential consumption with more accuracy and was superior to the others.

The authors used SVM and MLP in [12] to solve the problem of predicting energy consumption. In addition, they improved the predictions of district consumption by grouping households according to their consumption patterns. Moreover, they illustrated how the normalized root mean squared error diminishes as the number of clients increases in an empirical plot. Up to 782 households are included in this research. SVM was also used to forecast monthly energy consumption in tropical regions by the authors of [13]. According to their findings based on three years of power usage data, SVM has a strong prediction performance.

The authors in [14] used clustering-based Short-Term Load prediction. The prediction is carried out for the next day’s 48 half-hourly loads. The daily average load of all training and testing patterns is determined for each day, and the patterns are grouped using a threshold value between the testing pattern’s daily average load and the training pattern’s daily average load. Their findings reveal that the SVM clustering-based strategy is more accurate than the results produced without clustering the input patterns. The SVM outcome for predicting was better than the Auto Regressive modeling for the same sort of forecasting, according to the authors in [15]. SVM had a root means square error (RMSE) of 0.0215 while testing data, whereas LR had an RMSE of 0.0376. The research revealed that the prediction was more accurate since the RMSE was lower.

Deep learning is a very appealing alternative for longer-term predictions because it can represent expressive functions through numerous layers of abstraction [16]. In [17], the authors used a deep recurrent neural network to predict the energy consumption needed for heating in a commercial building in the United States. They looked at the deep model’s performance across a horizon of long-to-medium-term prediction.

3  The Proposed Methodology

This section discusses the overall methodology proposed to forecast energy consumption. In addition, the proposed optimization algorithm is explained.

3.1 General Scheme

The study’s overarching design is shown in Fig. 1. After preparing and preprocessing the dataset, six optimization algorithms are employed to optimize the parameters of a new LSTM-based model to improve the prediction accuracy of the energy consumption. These optimization algorithms include the proposed hybrid optimization algorithm (dynamic DTO and SFS algorithms and is called DDTOSFS), the standard DTO algorithm, the standard SFS algorithm, the standard particle swarm optimization (PSO) algorithm, the standard grey wolf optimization (GWO) algorithm, and the standard whale optimization algorithm (WOA). The optimized LSTM models are: DDTOSFS + LSTM, PSO + LSTM, DTO + LSTM, SFS + LSTM, GWO + LSTM, and WOA + LSTM). The forecasting of energy consumption is made in terms of these optimized models, and the accuracy of those predictions is measured using statistical metrics.

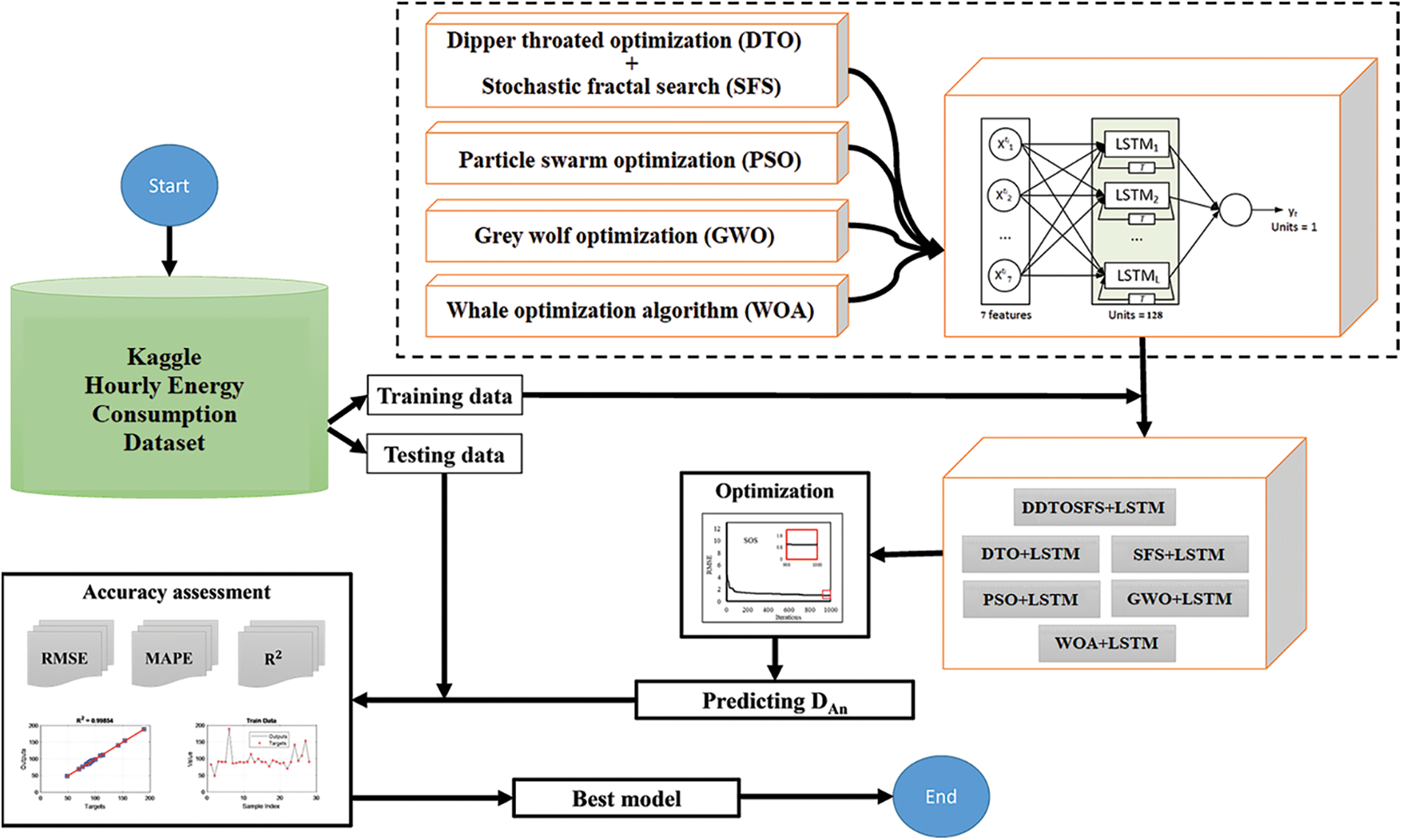
Figure 1: The overall steps of the approach proposed for forecasting energy consumption

3.2 Long Short-Term Memory (LSTM)

The LSTM model is an enhancement of the traditional neural network model that gained the capability of solving a variety of problems. Long-term memory retention is one of LSTM’s key advantages that makes it suitable for modeling temporal dependencies and time sequence predictions, such as the case of IoT energy consumption prediction. Fig. 2 depicts the structure of the proposed energy consumption prediction model based on LSTM units. Each LSTM unit consists of three gates: output o, forget f, and input i. The cell state is referred to as c. The information flow in this model is usually controlled by the three gates [18]. The input at time t, is denoted by Xt. The output of the hidden layer is ht, and its previous output is denoted by ht−1. The cell input and output are referred to as c~t, ct, respectively, and the previous state is denoted by ct−1. The measurement of ct and ht can be performed by calculating the following equations first.

it=σ(Wi Xt+Uiht−1+bi)(1)

ft=σ(Wf Xt+Ufht−1+bf)(2)

ot=σ(Wo Xt+Uoht−1+bo)(3)

c~t=tanh(Wc Xt+Ucht−1+bc)(4)

where Wi, Wf, and Wo refer to matrices of weights used to connect Xt with the input cell and the three gates. On the other hand, Ui, Uf, who are matrices of weights used to connect ht−1 with the input cell and the three gates. The bias terms are denoted by bi, bf, bo, and bc, tanh and σ refer to the tangent and sigmoid functions, respectively. Moreover, the measurement of the cell output state is calculated as follows.

ct=it⊙c~t+ft⊙ct−1(5)

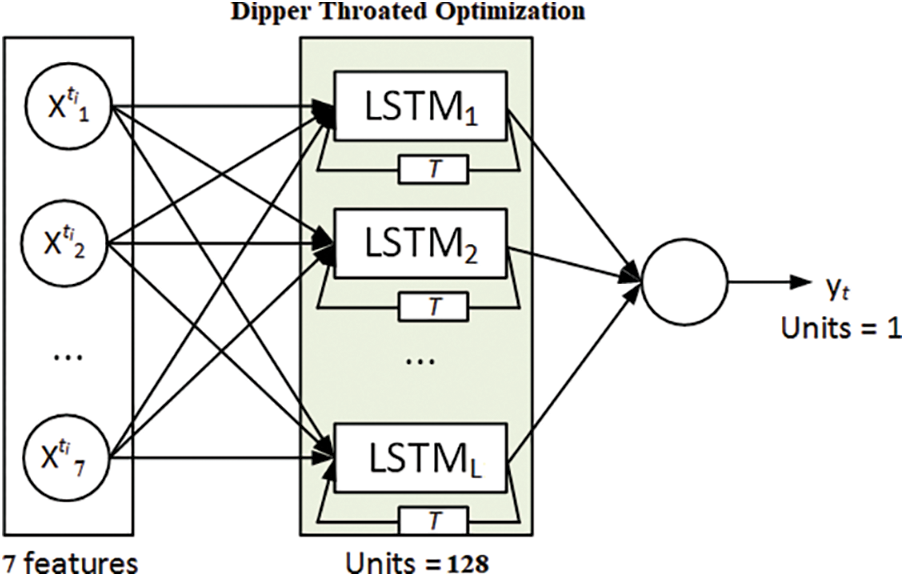
Figure 2: The structure of the proposed LSTM-based forecasting model

The final output of the LSTM cell is measured using the following equation.

ht=ot ⊙tanhtanh (ct)(6)

3.3 Dipper Throated Optimization (DTO)

The DTO algorithm assumes that there are swimming and flying folks of birds looking for food. The ability of these birds to find food depends of their locations and speed while search for food. The following matrices are used to depict the birds’ locations (L) and speeds (S).

L=[L1,1L1,2L1,3…L1,dL2,1L2,2L2,3…L2,dL3,1L3,2L3,3…L3,d……………Lm,1Lm,2Lm,3…Lm,d](7)

S=[S1,1S1,2S1,3…S1,dS2,1S2,2S2,3…S2,dS3,1S3,2S3,3…S3,d……………Sm,1Sm,2Sm,3…Sm,d](8)

where Li,j refers to the ith bird in the jth dimension for i Є 1, 2, 3, …, m and j Є 1, 2, 3, …, d, and its speed is indicated by Si,j for the jth dimension. For each bird, the following matrix represents the values of the fitness functions h = h1, h2, h3, …, hn.

h=[h1(L1,1,L1,2,L1,3,…,L1,d)h2(L2,1,L2,2,L2,3,…,L2,d)h3(L3,1,L3,2,L3,3,…,L3,d)…hm(Lm,1,Lm,2,Lm,3,…,Lm,d)](9)

Finally, the location of swimming birds can be updated using the following formulas.

L(i+1)={Lbest(i)−K1.|K2.Lbest(i)−L(i)|if R<0.5L(i)+S(i+1)otherwise(10)

S(i+1)=K3S(i)+K4r1(Lbest(i) −L(i))+K5r2(LGbest −L(i))(11)

where K1, … K5, r1, and r2, are adaptive variables whose values are changed during the optimization process based on a selection of random values. The DTO algorithm detailed steps are depicted in Fig. 3a [19].

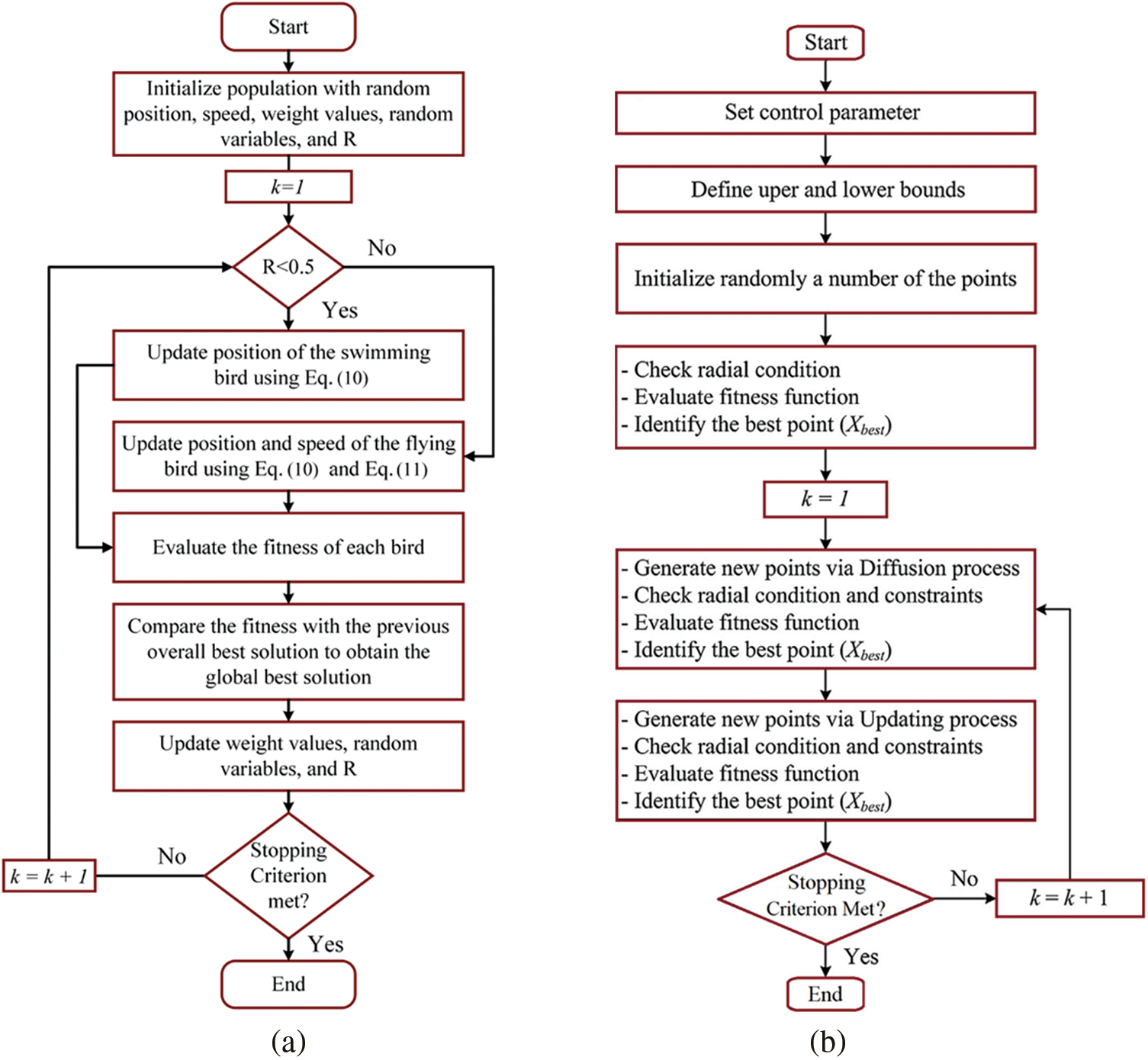
Figure 3: Flowcharts of the employed optimization algorithms (a) DTO algorithm and (b) SFS algorithm

3.4 Stochastic Fractal Search Algorithm

The natural phenomena of growth served as inspiration for the development of the powerful meta-heuristic algorithm known as stochastic fractal search (SFS). For optimality, this method mimics fractal characteristics. Here we discuss the Diffusion and the Update processes, the two key components of SFS’s search for an optimal solution. To maximize the likelihood of discovering a better solution and to avoid local minima, the diffusion process involves each point diffusing around its present position to use the search space. By using a Gaussian walk, this method may produce an infinite number of new points. Two statistical approaches are used in the updating process to efficiently probe the search space. The initial statistical process involves ordering all the points according to their fitness values and assigning each rank a probability value. The steps of the SFS algorithm are depicted in the flowchart shown in Fig. 3b.

3.5 The Proposed DDTOSFS Optimization Algorithm

The proposed optimization algorithm is based on exploring the search space using the DTO and SFS algorithms interchangeably. The interchange between the two algorithms is based on an iteration number (k); where the DTO algorithm works with the even iterations and the SFS algorithm works with the odd iterations. The steps of the proposed dynamic DTOSFS algorithm are shown in the flowchart depicted in Fig. 4.

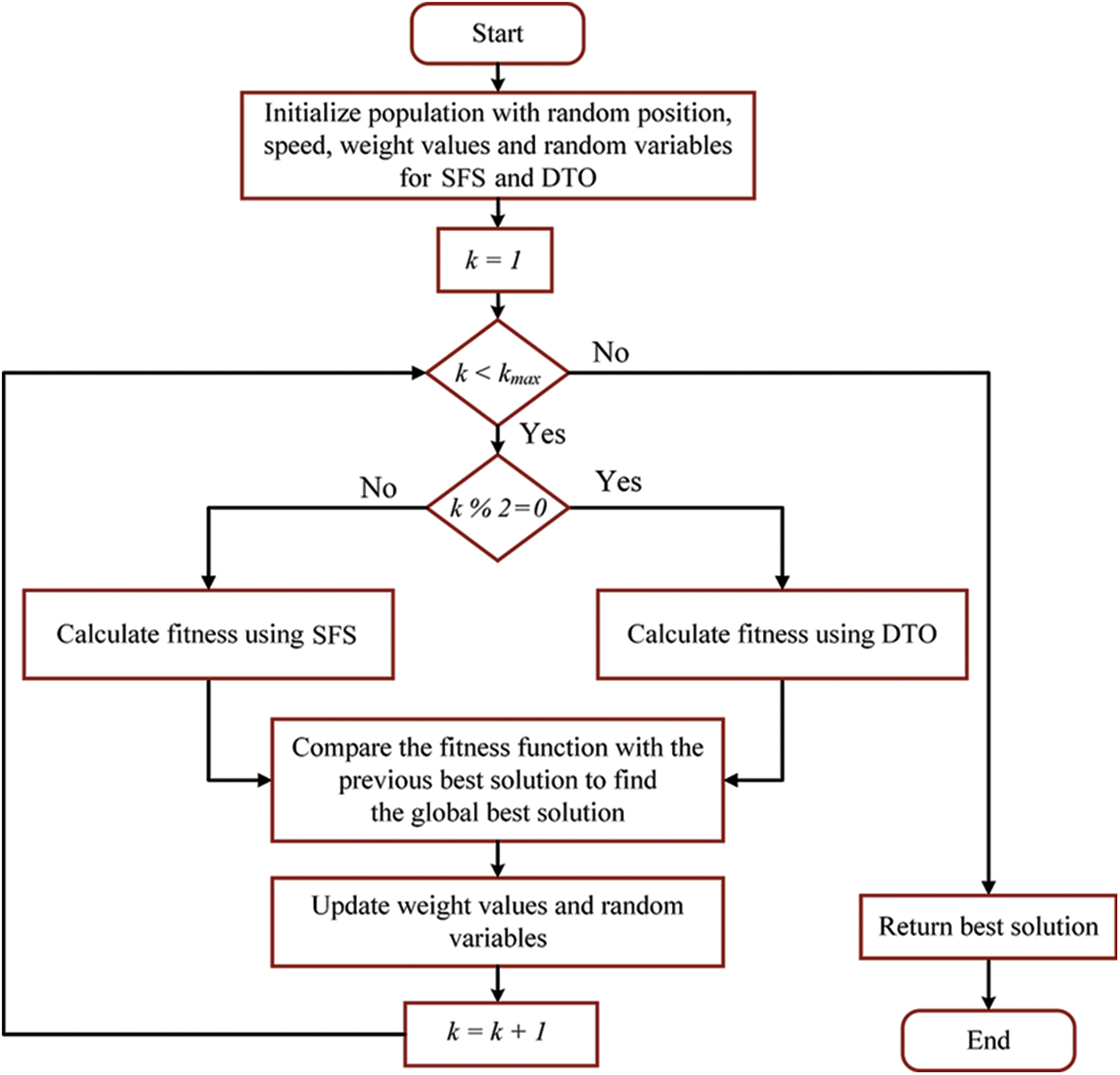
Figure 4: Flowcharts of the proposed dynamic DTOSFS algorithm

4  Experimental Results

The publicly available hourly energy consumption dataset [20] is employed to validate the proposed method’s effectiveness. This dataset consists of 121273 measurements gathered over more than 10 years. To use this dataset, a set of preprocessing steps are performed to ensure the integrity and consistency of the dataset samples. These preprocessing steps include (Data resampling using various parameter optimization methods and various base models, Data normalization, Scaling the values between [0, 1], Handling outliers (using standard deviation), Handling missing values, and Data Smoothing (exponential smoothing)). Fig. 5 shows the visualization of the energy consumption distribution during over 24 h/day of a sample day in the dataset as shown in Fig. 5a, over 12 months of a sample year as shown in Fig. 5b, over the full set of years as shown in Fig. 5c, and the histogram of the energy consumption values as shown in Fig. 5d.

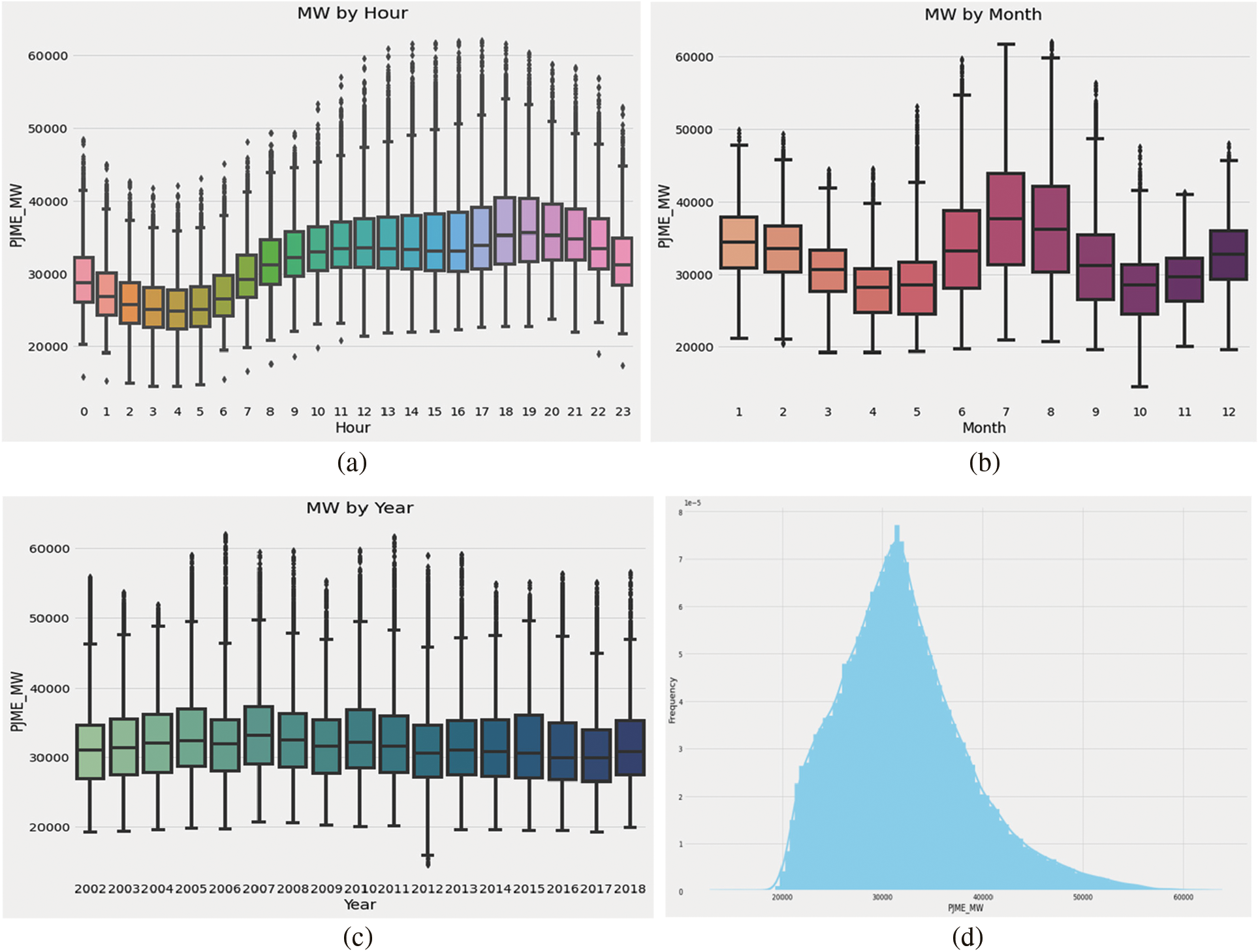
Figure 5: Visualizing the dataset features

After data preprocessing, the dataset is divided into testing (20%) and training (80%). The LSTM’s parameters are optimized using the proposed DDTOSFS algorithm, which is trained using the data from the training set. The following conditions are chosen for the training procedure. A total of 30 populations will be used, with a maximum of 20 iterations, and 20 runs will be performed. Additionally, five basic models are trained using the same training data to determine which model will benefit most from optimization. Multi-layer perceptron (MLP), Support vector regression (SVR), K-nearest neighbor (KNN), random forest (RF), and the regular LSTM are all examples of such benchmark forecasting models [21,22]. The eight evaluation metrics used to measure the performance of these models are presented in Table 1.

The evaluation of these criteria based on the achieved results using the proposed model and other prediction models is presented in Table 2. As shown in this table, the proposed approach achieves better values than the other prediction models for all types of evaluation criteria, which proves the superiority of the proposed model in predicting the energy consumption accurately.

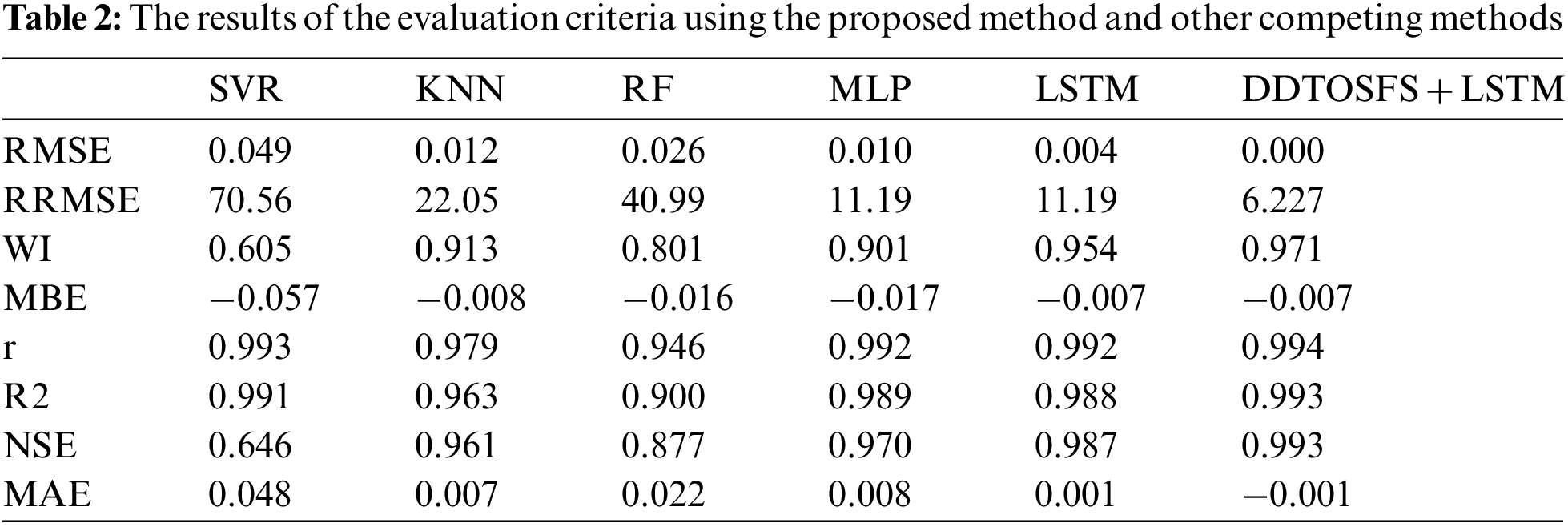
Five other optimization algorithms are incorporated in the experiments to prove the superiority of the proposed optimized LSTM. These algorithms are GWO [23], PSO [24], WOA [25], SFS [26], and DTO [27]. These algorithms are used to optimize the LSTM-based model parameters. The recorded evaluation results are presented in Table 3 in terms of the prediction results statistical analysis. As represented by the results in the table, the proposed approach is shown superior when compared to other optimization algorithms.

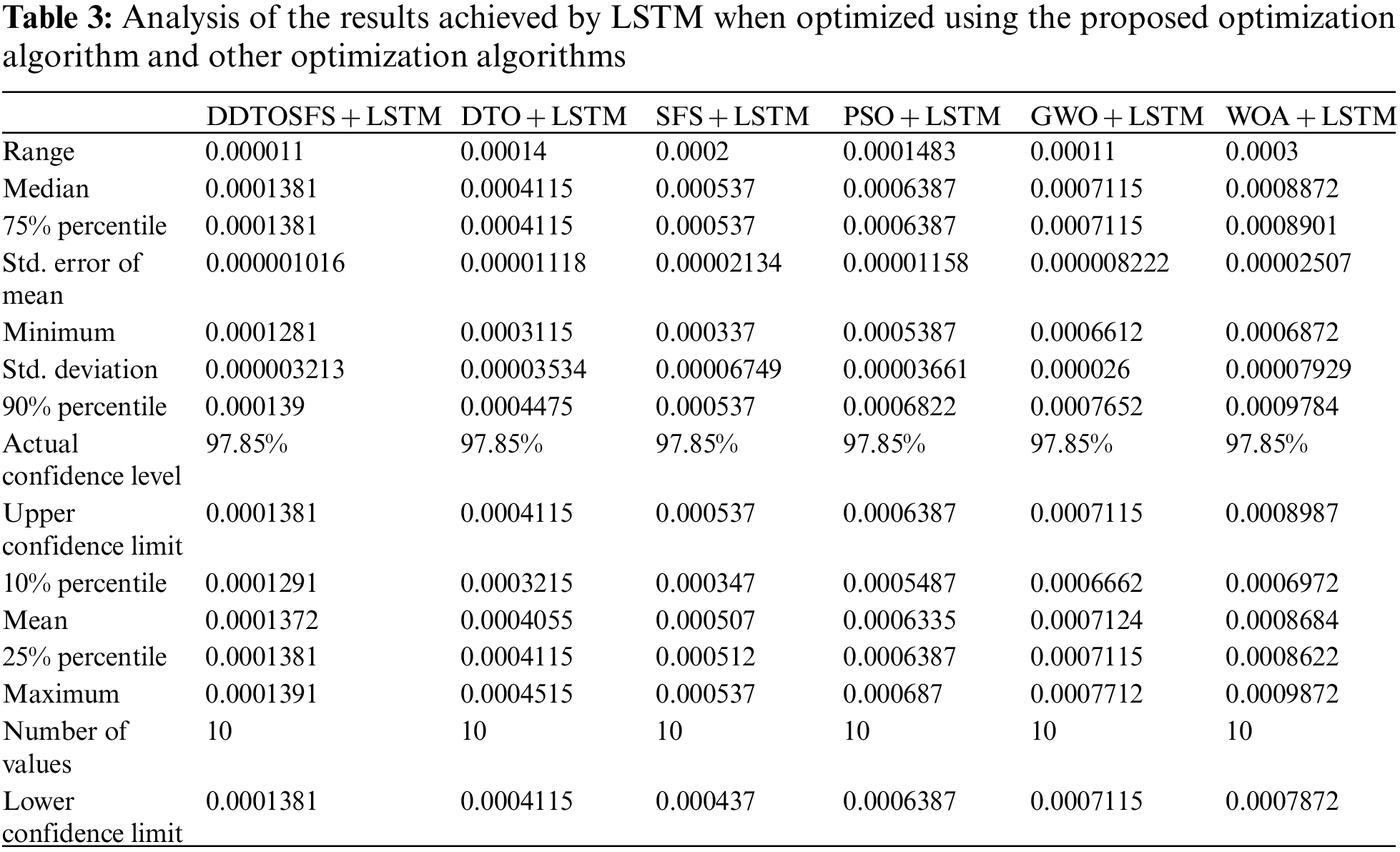
Fig. 6 displays four plots to illustrate the model performance from the point of view of a visual representation of the prediction results achieved by the proposed approach. The predicted energy consumption is mapped against the residual error plot shown in Fig. 6a, and the homoscedasticity plot shown in Fig. 6b. The small size of the residual errors in these plots is an indication of the reliability of the projected values. Fig. 6c is a quartile-quartile (QQ) plot comparing the predicted and observed values, illustrating how well they match up [28–35]. To see that the results closely follow a straight line, as shown in the figure, is conclusive evidence for the validity of the suggested model. Prediction errors are visualized using the heatmap as in Fig. 6d. From these plots, the proposed DDTOSFS + LSTM approach is proven to provide the least amount of inaccuracy in forecasting energy consumption.

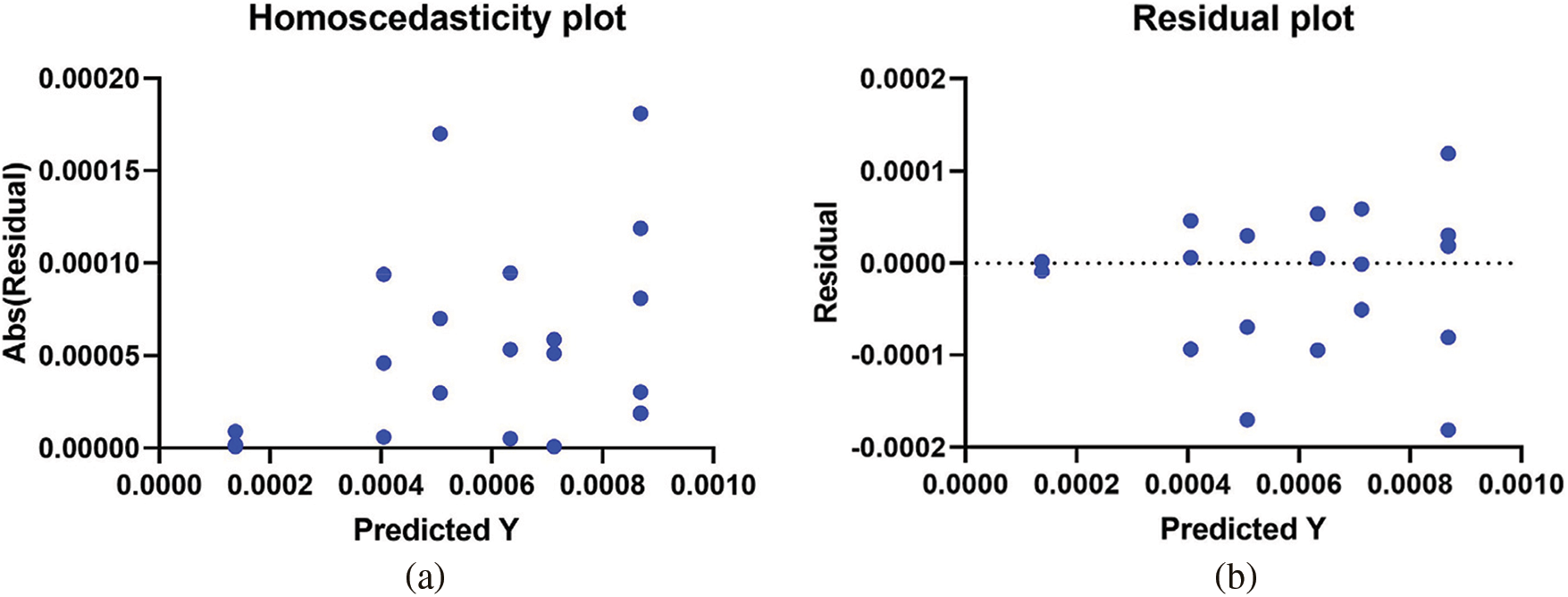
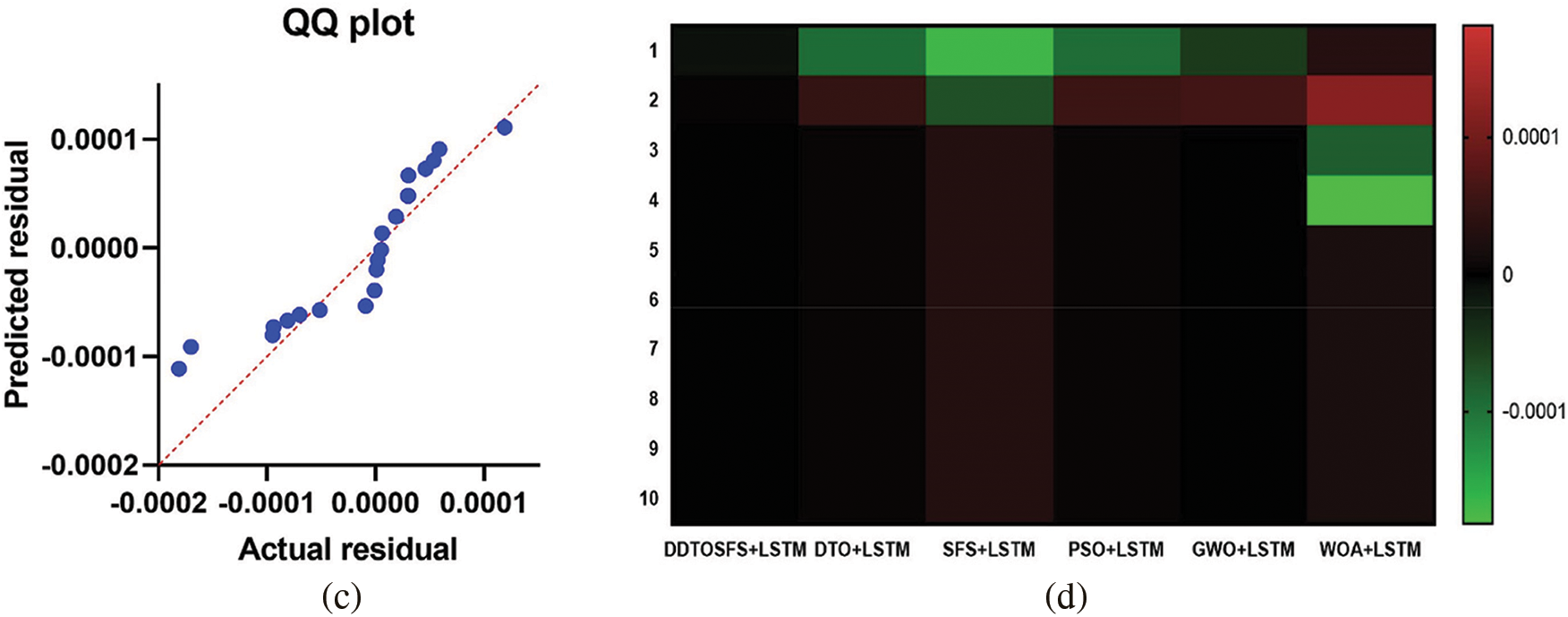
Figure 6: Representation of the results achieved using the proposed method

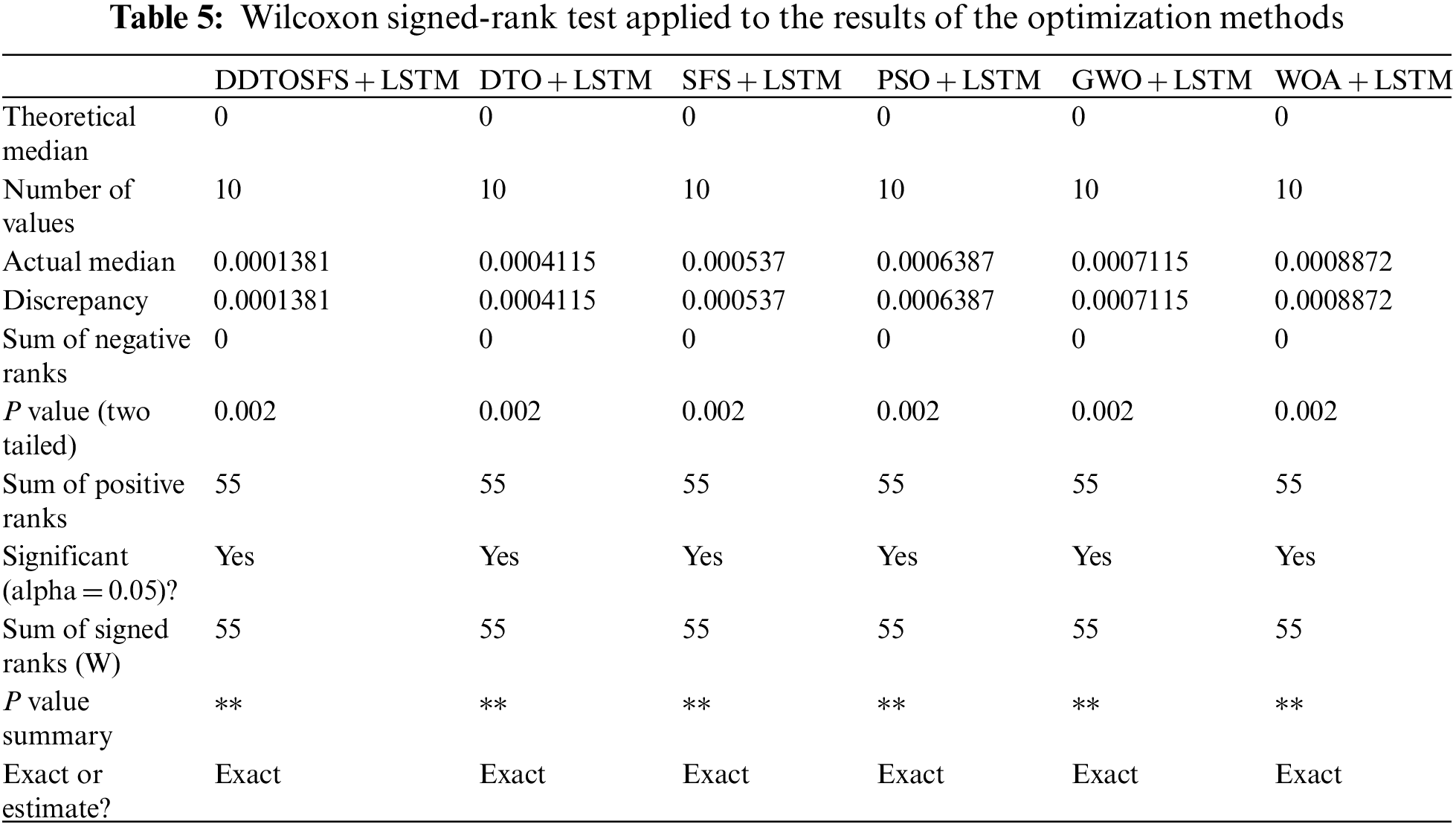
In addition, the suggested DDTOSFS + LSTM approach is compared to the other method using a statistical difference to determine the p-values, demonstrating the substantial difference between the two methods. Wilcoxon’s rank-sum test is used to carry out this analysis. Both null and alternative hypotheses are posited before the test is run. Average algorithmic parameters are equalized under the null hypothesis H0 (DDTOSFS + LSTM = DTO + LSTM, SFS + LSTM = PSO + LSTM, GWO + LSTM = WOA + LSTM). Alternatively, H1 proposes that the algorithms’ means are not comparable. Table 5 displays the results of the Wilcoxon rank-sum test. The table shows a statistically significant difference between the suggested DDTOSFS + LSTM algorithm and the other algorithms, with p-values of less than 0.05.

The ANOVA test is also used to further investigate the method’s efficacy. In this analysis, two basic hypotheses are posed: the alternative and null hypotheses. Mean values of the algorithm are equalized, DDTOSFS + LSTM = DTO + LSTM = SFS + LSTM = PSO + LSTM = GWO + LSTM = WOA + LSTM, for the null hypothesis denoted by H0. Whereas, under the alternative hypothesis H1, the means of the algorithms are not comparable. Table 4 displays the findings of the analysis of variance. The table shows that the suggested algorithm performs as predicted when compared with alternative feature selection techniques. The root-mean-squared error (RMSE) between the proposed technique and the other methods’ predictions is displayed in Fig. 7. You can see that the proposed model has the lowest RMSE values in this graph. The prediction error histogram is displayed in Fig. 8. As can be seen in the image, the suggested model yields the lowest error values in its predictions compared to the other techniques. These figures underline the efficacy of the proposed strategy for estimating energy needs. The comparison between actual and expected energy use is also displayed in Fig. 9. To illustrate the reliability of the proposed strategy, the picture above superimposes projected and observed energy consumption.

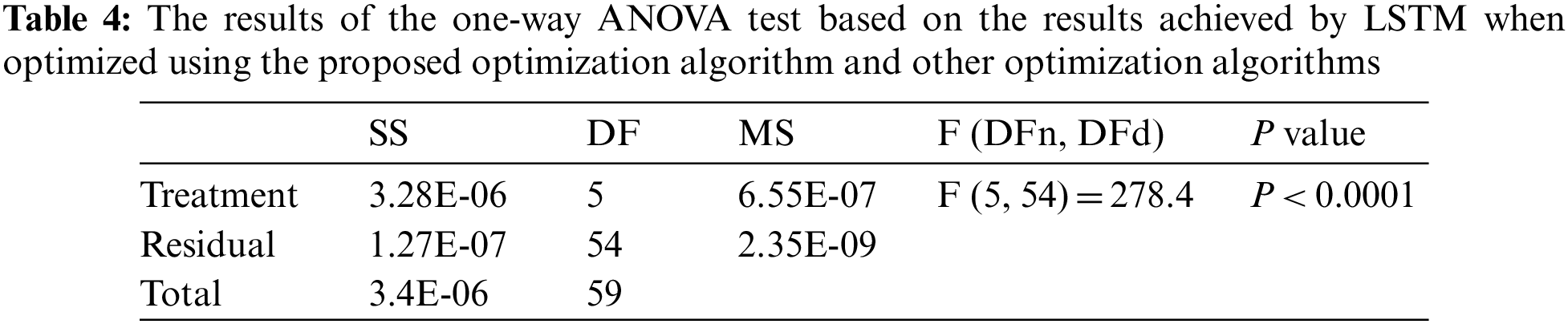
Figure 7: RMSE values achieved by LSTM when optimized using different algorithms

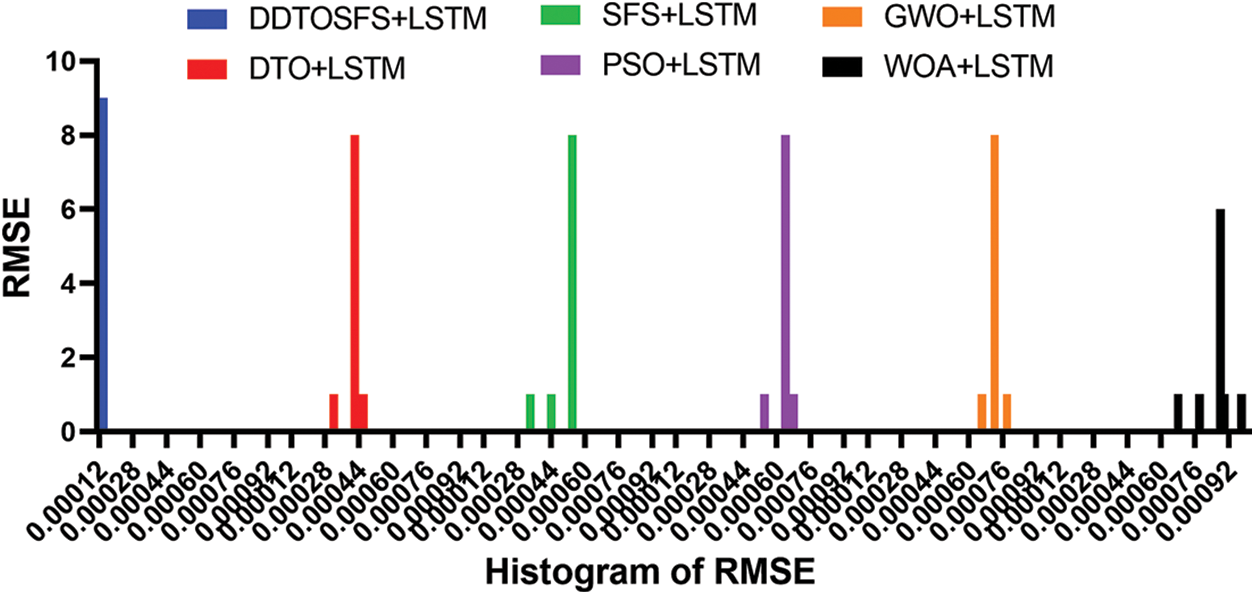
Figure 8: Histogram of RMSE values achieved by LSTM model optimized using optimization algorithms

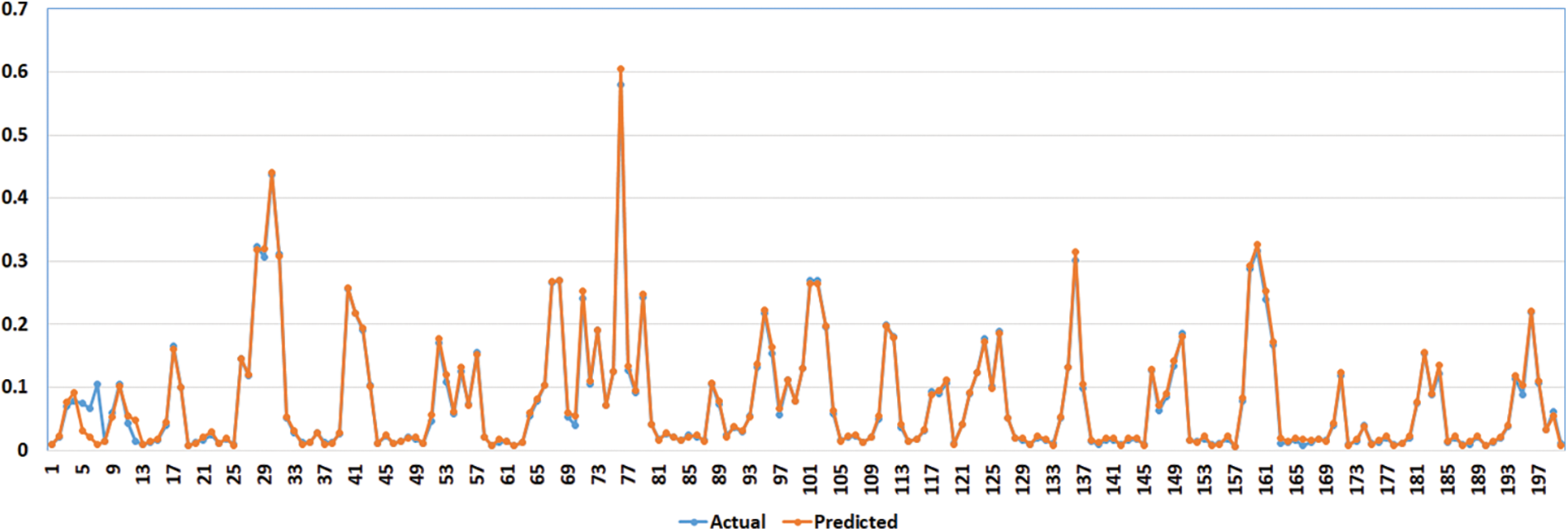
Figure 9: The predicted vs. actual energy consumptions resulting using the proposed model

5  Conclusion

In this work, we proposed a new strategy for forecasting energy consumption. The proposed approach relies on improving the performance of LSTM by adjusting its parameters, which allows for precise prediction results. Multiple optimization strategies and machine learning models are used to evaluate the proposed technique against a vast group of methods. Statistical analysis is used to demonstrate the reliability and validity of the suggested approach, which is validated by the findings. Additionally, a series of plots, including QQ, residual, homoscedasticity, and histograms, are used to conduct an in-depth study of the final results. This evaluation verified the efficiency and excellence of the suggested approach to precisely forecasting energy usage. The findings of this research can help in decision making and risk management considered by the governing authorities.

Funding Statement: This research project was funded by the Deanship of Scientific Research, Princess Nourah bint Abdulrahman University, through the Program of Research Project Funding After Publication, Grant No (43- PRFA-P-52).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. S. Das, T. Choudhury and S. Mohapatra, “Data analytics to increase efficiency of the AI based energy consumption predictor,” in Int. Conf. on Computational Intelligence for Smart Power System and Sustainable Energy (CISPSSE), Keonjhar, India, pp. 1–4, 2020. [Google Scholar]

2. S. Jia, W. Yao and Z. Wang, “Accurate prediction method for energy consumption in automatic tool changing process of computer numerical control lathe,” in World Conf. on Mechanical Engineering and Intelligent Manufacturing (WCMEIM), Shanghai, China, pp. 241–244, 2019. [Google Scholar]

3. G. Sha and Q. Qian, “Prediction of commercial building lighting energy consumption based on EPSO-BP,” in Int. Conf. on Control, Automation and Systems (ICCAS), PyeongChang, Korea (Southpp. 1035–1040, 2018. [Google Scholar]

4. P. Schirmer, I. Mporas and I. Potamitis, “Evaluation of regression algorithms in residential energy consumption prediction,” in European Conf. on Electrical Engineering and Computer Science (EECS), Athens, Greece, pp. 22–25, 2019. [Google Scholar]

5. X. Wang, X. Li, D. Qin, Y. Wang, L. Liu et al., “Prediction of industrial power consumption and air pollutant emission in energy internet,” in Asia Energy and Electrical Engineering Symp. (AEEES), Chengdu, China, pp. 1155–1159, 2021. [Google Scholar]

6. Z. Wu and W. Chu, “Sampling strategy analysis of machine learning models for energy consumption prediction,” in Int. Conf. on Smart Energy Grid Engineering (SEGE), Oshawa, Canada, pp. 77–81, 2021. [Google Scholar]

7. M. Fayaz and D. Kim, “A prediction methodology of energy consumption based on deep extreme learning machine and comparative analysis in residential buildings,” Electronics, vol. 7, no. 10, pp. 222, 2018. [Google Scholar]

8. R. Akter, J. -M. Lee and D. -S. Kim, “Analysis and prediction of hourly energy consumption based on long short-term memory neural network,” in Int. Conf. on Information Networking (ICOIN), Jeju Island, Korea (Southpp. 732–734, 2021. [Google Scholar]

9. J. Li, “Evolutionary modeling of factors affecting energy consumption of urban residential buildings and prediction models,” in Int. Conf. on Electronics, Communication and Aerospace Technology (ICECA), Coimbatore, India, pp. 1333–1336, 2021. [Google Scholar]

10. Z. Qiuhong, Z. Zhan and W. Jiayi, “Application of regional building energy consumption prediction model in building construction,” in Int. Conf. on Intelligent Transportation, Big Data & Smart City (ICITBS), Vientiane, Laos, pp. 92–94, 2020. [Google Scholar]

11. Y. Liang and Z. Hu, “Prediction method of energy consumption based on multiple energy-related features in data center,” in Int. Conf. on Parallel & Distributed Processing with Applications, Big Data & Cloud Computing, Sustainable Computing & Communications, Social Computing & Networking, Xiamen, China, pp. 140–146, 2019. [Google Scholar]

12. M. Chuang, W. Yikuai, Z. Junda, C. Ke, G. Feixiang et al., “Research on user electricity consumption behavior and energy consumption modeling in big data environment,” in Int. Conf. on Big Data, Artificial Intelligence and Internet of Things Engineering (ICBAIE), Nanchang, China, pp. 220–224, 2021. [Google Scholar]

13. X. Zhao, “Energy saving prediction method for public buildings based on data mining,” in Int. Conf. on Measuring Technology and Mechatronics Automation (ICMTMA), Beihai, China, pp. 484–487, 2021. [Google Scholar]

14. M. Babaoğlu and B. Haznedar, “Turkey long-term energy consumption prediction using whale optimization algorithm,” in Signal Processing and Communications Applications Conf. (SIU), Istanbul, Turkey, pp. 1–4, 2021. [Google Scholar]

15. F. Janković, L. Šćekić and S. Mujović, “Matlab/Simulink based energy consumption prediction of electric vehicles,” in Int. Symp. on Power Electronics, Novi Sad, Serbia, pp. 1–5, 2021. [Google Scholar]

16. A. Rahman and A. Smith, “Predicting heating demand and sizing a stratified thermal storage tank using deep learning algorithms,” Applied Energy, vol. 228, no. 1, pp. 108–121, 2018. [Google Scholar]

17. I. Goodfellow, Y. Bengio and A. Courville, “Deep Learning,” in MIT Press, Cambridge, 2016. [Google Scholar]

18. S. Hochreiter and J. Schmidhuber, “Long short-term memory,” Neural Computing, vol. 9, no. 8, pp. 1735–1780, 1997. [Google Scholar]

19. A. Takieldeen, E. -S. M. El-kenawy, E. Hadwan and M. Zaki, “Dipper throated optimization algorithm for unconstrained function and feature selection,” CMC-Computers, Materials & Continua, vol. 72, no. 1, pp. 1465–1481, 2022. [Google Scholar]

20. R. Mulla, K. Banachewicz and A. Dahesh “Hourly Energy Consumption,” 2018, Accessed: December 20, 2022. [Online]. Available: https://www.kaggle.com/datasets/robikscube/hourly-energy-consumption [Google Scholar]

21. E.-S. M. El-Kenawy, S. Mirjalili, S. Ghoneim, M. Eid, M. El-Said et al., “Advanced ensemble model for solar radiation forecasting using sine cosine algorithm and newton’s laws,” IEEE Access, vol. 9, no. 1, pp. 115750–115765, 2021. [Google Scholar]

22. A. Abdelhamid and S. Alotaibi, “Robust prediction of the bandwidth of metamaterial antenna using deep learning,” Computers, Materials & Continua, vol. 72, no. 2, pp. 2305–2321, 2022. [Google Scholar]

23. H. R. Hussien, E. -S. M. El-Kenawy and A. El-Desouky, “EEG channel selection using a modified grey wolf optimizer,” European Journal of Electrical Engineering and Computer Science, vol. 5, no. 1, pp. 17–24, 2021. [Google Scholar]

24. E. -S. M. El-kenawy and M. Eid, “Hybrid gray wolf and particle swarm optimization for feature selection,” International Journal of Innovative Computing, Information & Control, vol. 16, no. 1, pp. 831–844, 2020. [Google Scholar]

25. M. M. Eid, E. -S. M. El-kenawy and A. Ibrahim, “A binary sine cosine-modified whale optimization algorithm for feature selection,” in National Computing Colleges Conf., Taif, Saudi Arabia, pp. 1–6, 2021. [Google Scholar]

26. N. Gorgolis, I. Hatzilygeroudis, Z. Istenes and L. Gyenne, “Hyperparameter optimization of LSTM network models through genetic algorithm,” in Int. Conf. on Information, Intelligence, Systems and Applications (IISA), Patras, Greece, pp. 1–4, 2019. [Google Scholar]

27. T. Tran, K. Teuong and D. Vo, “Stochastic fractal search algorithm for reconfiguration of distribution networks with distributed generations.” Ain Shams Engineering Journal, vol. 11, no. 2, pp. 389–407, 2020. [Google Scholar]

28. E. M. El-Kenawy, M. M. Eid, M. Saber and A. Ibrahim, “MbGWO-SFS: Modified binary grey wolf optimizer based on stochastic fractal search for feature selection,” IEEE Access, vol. 8, pp. 107635–107649, 2020. [Google Scholar]

29. N. Abdel Samee, E. M. El-Kenawy, G. Atteia, M. M. Jamjoom, A. Ibrahim et al., “Metaheuristic optimization through deep learning classification of covid-19 in chest x-ray images,” Computers, Materials & Continua, vol. 73, no. 2, pp. 4193–4210, 2022. [Google Scholar]

30. E. -S. M. El-Kenawy, S. Mirjalili, A. Ibrahim, M. Alrahmawy, M. El-Said et al., “Advanced meta-heuristics, convolutional neural networks, and feature selectors for efficient COVID-19 X-ray chest image classification,” IEEE Access, vol. 9, no. 1, pp. 36019–36037, 2021. [Google Scholar] [PubMed]

31. A. Abdelhamid and S. Alotaibi, “Optimized two-level ensemble model for predicting the parameters of metamaterial antenna,” Computers, Materials & Continua, vol. 73, no. 1, pp. 917–933, 2022. [Google Scholar]

32. D. Sami Khafaga, A. Ali Alhussan, E. M. El-kenawy, A. E. Takieldeen, T. M. Hassan et al., “Meta-heuristics for feature selection and classification in diagnostic breast cancer,” Computers, Materials & Continua, vol. 73, no. 1, pp. 749–765, 2022. [Google Scholar]

33. D. Sami Khafaga, A. Ali Alhussan, E. M. El-kenawy, A. Ibrahim, S. H. Abd Elkhalik et al., “Improved prediction of metamaterial antenna bandwidth using adaptive optimization of LSTM,” Computers, Materials & Continua, vol. 73, no. 1, pp. 865–881, 2022. [Google Scholar]

34. E. -S. M. El-Kenawy, S. Mirjalili, F. Alassery, Y. Zhang, M. Eid et al., “Novel meta-heuristic algorithm for feature selection, unconstrained functions and engineering problems,” IEEE Access, vol. 10, pp. 40536–40555, 2022. [Google Scholar]

35. A. Abdelhamid, E. -S. M. El-kenawy, B. Alotaibi, M. Abdelkader, A. Ibrahim et al., “Robust speech emotion recognition using CNN + LSTM based on stochastic fractal search optimization algorithm,” IEEE Access, vol. 10, pp. 49265–49284, 2022. [Google Scholar]