A Single Image Derain Method Based on Residue Channel Decomposition in Edge Computing

1  Introduction

With the development of Internet technologies and service-oriented applications, IoT is increasingly used in various fields of Industry 4.0, Image processing is the primary research direction in IoT applications (such as intelligent transportation [1,2], smart city [3,4] etc.). Researchers have obtained a vast number of photographs from various sensors, but generally these photographs from different devices are inevitably affected by a complex set of meteorological factors. Significantly, the rainfall patterns or streaks captured by the visual system (e.g., still images or dynamic video sequences) usually result in sharp fluctuations in the intensity of the image, and always severely affect the performance of outdoor computer vision tasks. In addition, the refraction and reflection of light by rain lines leads to a degree of degradation of the content in the optical image, such as blurring, deformation, etc., therefore, image deraining is a crucial pre-processing step for subsequent tasks. Rainfall streaks and rainfall accumulation are probably entangled, which creates difficulty for modeling with simple physical models, hence, developing an efficient derain network structure with low hardware cost and slight computational complexity is significantly important.

Restoring a rainfall-contaminated image to a clear one is called “image derain”. Compared with video images, single images lack time series information and the spatio-temporal characteristics of rain pattern or raindrop changes are hard to capture, making the process of single image derain more challenging. Most of the traditional methods assume that rain patterns appearing in an image have local similarities, so they focus on studying the rain pattern and the physical model of the background layer. For example, rain pattern removal is achieved by exploiting the local similarity pattern of rain patterns across the image, forcing a predetermined prior on the rain and background layers, and then constructing a loss function for optimization [5,6]. There are different prior approaches such as: layer prior [5], sparse representation [7], rainfall dominated region prior [8], and frequency prior [9,10]. More specifically, Li et al. [5] proposed a prior method based on a Gaussian mixture model that accommodate multiple directions and scales of rain patterns. Luo et al. [7] proposed a method to sparsely approximate the patches of two layers by very high discriminative codes over a learned dictionary with strong mutual exclusivity property. Zhu et al. [8] enforced a specific rainfall direction based on the area where rainfall dominates specific rainfall directions to distinguish the background texture from the rainfall streaks. However, the soundness of these conventional rain removal methods depends on the reliability of the manually designed prior assumptions under unknown backgrounds and rain streaks.

As artificial intelligence has developed rapidly in recent years, machine learning methods are also gradually applied to image derain. In these methods, pairs of rainfall/no-rainfall data are used for training to obtain a mapping function from a rainfall background to a no-rainfall background. These approaches involve simple Convolutional Neural Network [10–12], adversarial learning [13] and recurrent and multi-stage networks [14,15]. Most deep learning methods still lack sufficient interpretability and are not fully integrated with the physical structures inside general rain patterns. There are methods to fit rain patterns and thus identify to remove them by combining convolution and dictionary learning where two sub-steps of M-net and B-net algorithm iterations are proposed to make the network structure with white box interpretability [16]. The interpretability of the network is improved because the rain patterns are mostly white under the optical effect, but the mere removal of the rain patterns does not enable good recovery of the background image. The other part implements the rain removal task by filtering, for example, by using a random synthetic dataset to train a neural filtering network, which quickly completes the rain removal of a single image [17,18].

In summary, although the above methods have brought tremendous performance gains, it is difficult to remove all rain patterns and recover the structural information of the image in complex scenes due to an over-reliance on model learning capability, resulting in a large number of iterative optimization and subsequent refinement modules [16,19]. In addition, there are still differences between the synthesized dataset and the natural rainfall images, and it is hard to include all the natural rainfall conditions only using the synthesized dataset [20,21]. Fortunately, a prior structure reasonably regularizes and constrains the solution space, which not only helps to avoid unexpected image details being identified as rain patterns but also helps to alleviate overfitting problems in the network [22]. Therefore, to solve the above problem, we propose a channel decomposition-based rain removal network that combines a prior knowledge of rain patterns with the learning capability of neural networks. The network maintains the background image structure and performs image restoration efficiently. This network first removes the rainfall pattern using a residual channel prior (RCP), which is the result of the residual of the maximum and minimum channel values of the rainfall image. The decomposed rain-free background is then fused with the original input image using self-attentive features.

2  Framework Design

Currently, the traditional surveillance field is connected using a wired method, and the wired network covers all the cameras which transmit the monitoring images through the network to the cloud or server for storage and processing. This not only increases the load of the network but also makes it difficult to reduce the end-to-end time delay. As shown in Fig. 1, we consider a monitoring system with edge cloud collaboration; it contains a centralized cloud within the cloud layer, various edge servers and a mobile edge computing sever close to the camera end layer, and several cameras in the end layer. Images are captured by IoT devices deployed in the end layer to generate data. The data is then handed over to an inference server on the edge side (e.g., the traffic crossing) for image derain [23,24]. If new rain-free background features appear in the captured images, then the data is uploaded to the cloud server to optimize, train, and eventually update the new model library for all edge devices and deploy them to the edge side.

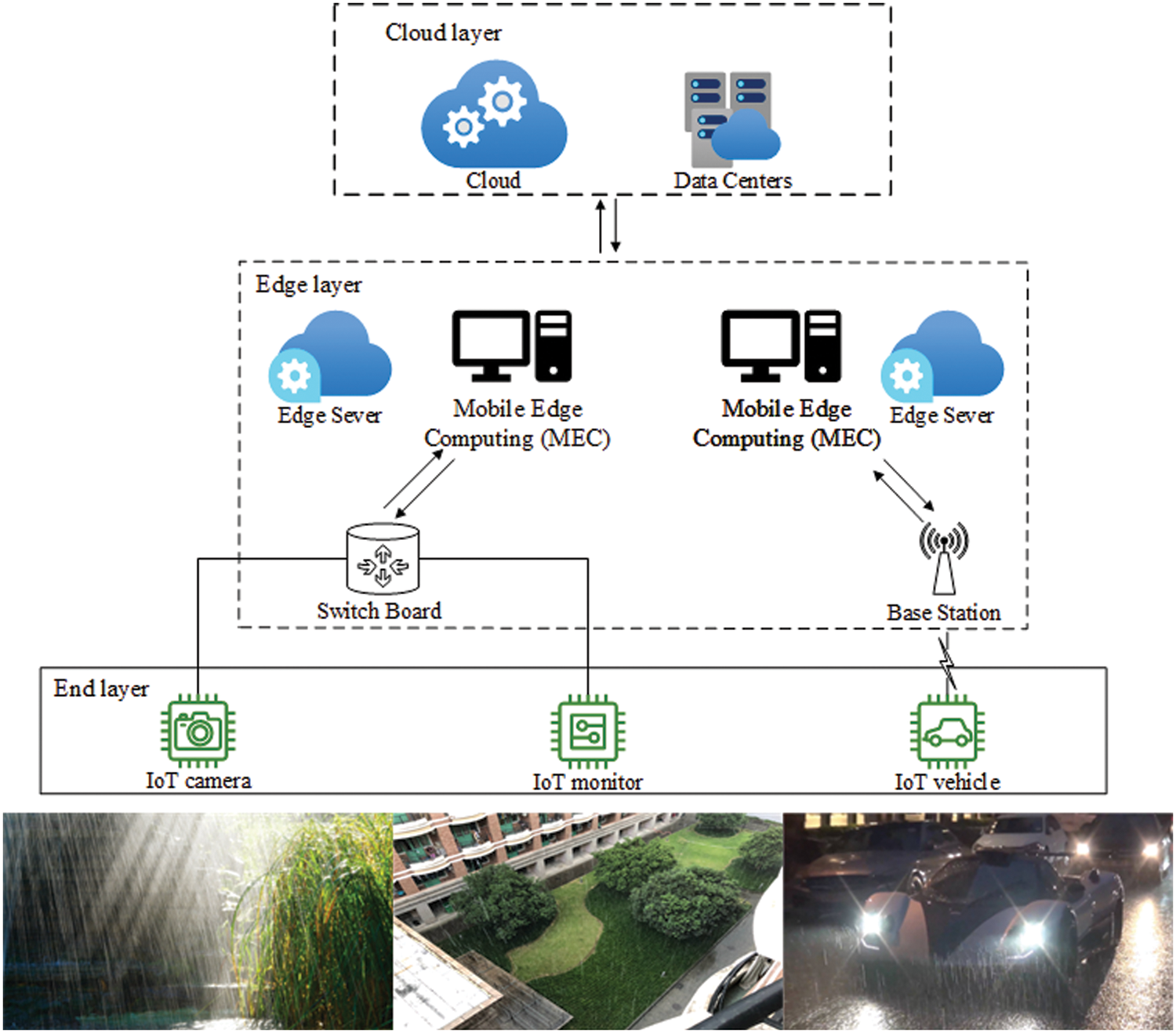
Figure 1: Image derain in edge computing

It has two benefits, providing proximity to data transmission and analysis at the edge; deploying work locally, which significantly reduces the reliance on and consumption of transmission resources while increasing the speed of local response [25]. On the cloud side, converged information governance is enabled by collecting data for second-round evaluation, processing and in-depth analysis. This ensures that the data simultaneously meets the needs of security and privacy aspects, but also takes advantage of the rapid iterative refreshing of the cloud services [26].

To address the problem of poor generalization ability of deep learning methods in realistic environments, this paper proposes an image derain network combining model-driven and data-driven sections (i.e., RCP combined U-Net network). As shown in Fig. 2, aiming to eliminate rain patterns, we first convert the input image color domain from Red, Green, Blue (RGB) to YCbCr color space. In fact, the Y channel is gray space, and the rest is color space. We assume by observation that the rain pattern is achromatic(colorless). Like the dark channel prior, the rain pattern is mainly concentrated on the Y channel after decomposition. We replace the Y component with the residual channel decomposition and then recombine it with Cb and Cr components, and finally transform it back to RGB color space to eliminate most of the rain patterns. This also brings the benefit of reducing the gap between the synthetic rain dataset and the real-world dataset.

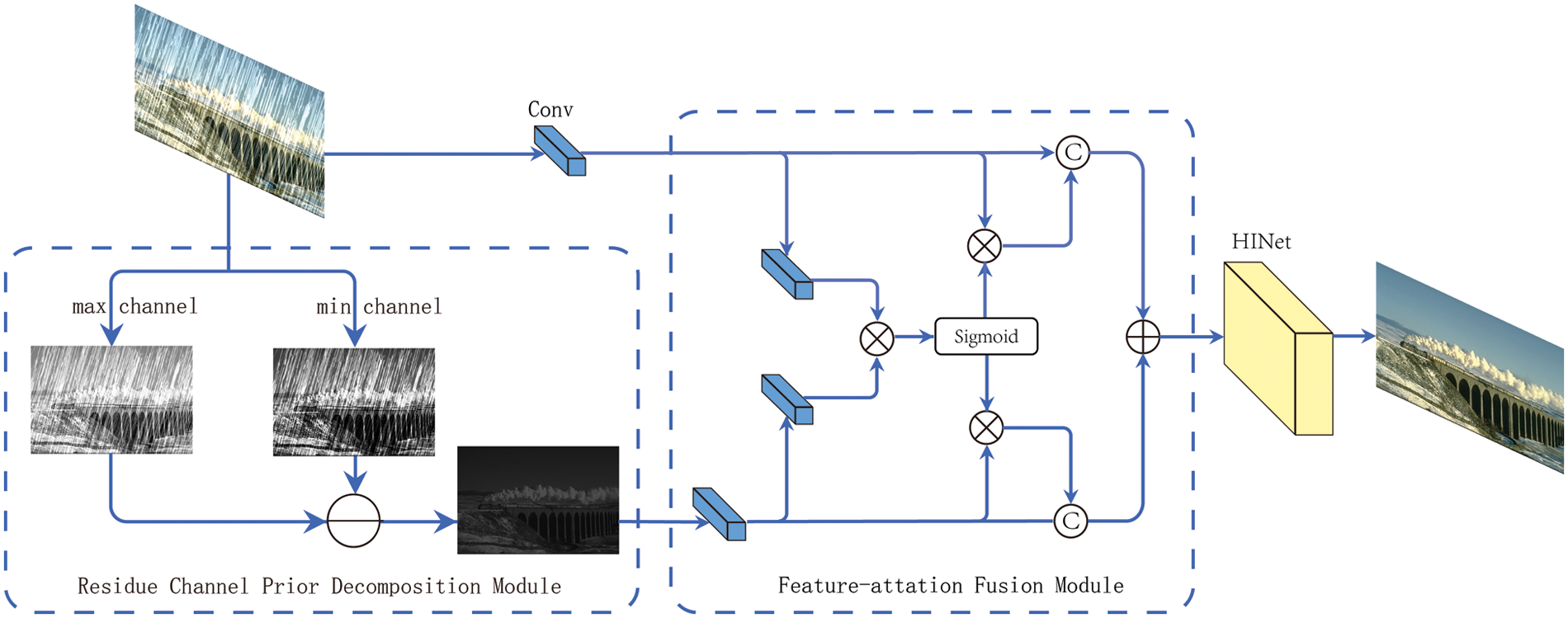
Figure 2: The proposed structure of model

Although the resulting residual channel image has complete structural information, the brightness of the image is reduced, and the clarity of the image deteriorates after processing. To better preserve the structural information of the background and produce a clearer image, this study first compared only the residual channel features with the original image features pixel by pixel, but the analysis showed that this method was not effective in achieving the derain effect because it destroys the originality of the input image and does not achieve a more effective derain result. Therefore, we propose an improved Feature-attention Fusion Module (FFM) that attempts to make more effective use of the feature information of the background, which can feed the a priori decomposition channel together with the original image into the feature attention module, recovering details that are reduced by the RCP module.

In terms of geometry, the rain patterns are distinctly linear, and a single rainfall pattern generally covers the image pixels in the longer direction. Using multiple convolution kernels for multi-scale convolution leads to an increase in the computational effort of the model and consumes more resources [27]. To solve this problem, a multi-stage network is chosen as the successor network in our paper. Theoretically, it outperforms the multi-scale convolution approach, which may produce boundary effects between patches [28].

3  Derain Based on Channel Decomposition

3.1 Residual Channel Prior Decomposition Module

This study transforms image derain into an image decomposition, where the rainfall-contaminated image is decomposed into a clean background layer and a rain streak layer:

I=B+∑in⁡Si(1)

where I is the observed input image, B represents the background image without the rain streaks, Si is the rain streaks layer, and n is a total number of layers of the rain pattern layer.

According to the paper [29], we assume a camera exposure time of T. The time elapsed when a raindrop passes through a pixel x is t. A color image with rain patterns is expressed as:

I~(x)=tβrs(x)Rα+(T−t)Bπ(2)

where I~(x)=(Ir,Ig,Ib)T is the light brightness’s color component, βrs is a constant for the coefficient of refraction, specular reflection and internal reflection from raindrops. ℛ=(Rr,Rg,Rb)T represents the light intensity of the RGB channel and R=Rr+Rg+Rb. ℬ=(Br,Bg,Bb)T represents background light intensity and B=Br+Bg+Bb. Define α=ℛ/R and π=ℬ/B the chromacities of ℛ and ℬ, respectively. Eq. (2) The first term is a rain-streak and the second term is the background.

To obtain a residual channel without rain streaks, we need to eliminate the optical chroma from the rain streak term, so we normalize it as follows:

I(x)=I~(x)α=Irs(x)i+Ibg(x)(3)

where i is a three-dimensional unit column vector, Irs=tβrs(x)R and Ibg=(T−t)Bπ/α vector division is calculated element by element. It is important to note that by normalizing the image, we remove not only the chromaticity of the light, as well as the color effect of spectral sensitivities.

Based on Eq. (3), we can calculate the formula for a given input image I without rain patterns as follows:

Ires(x)=IM(x)−Im(x)(4)

where IM(x)=max{Ir(x),Ig(x),Ib(x)} the maximum channel and Im(x)=min{Ir(x),Ig(x),Ib(x)} the minimum channel in Fig. 3, from the above formula, it can be derived Ires is the residual channel image of the input image I. As rain streaks appear optically mainly colorless, whose values in Eq. (3) are canceled in Eq. (4).

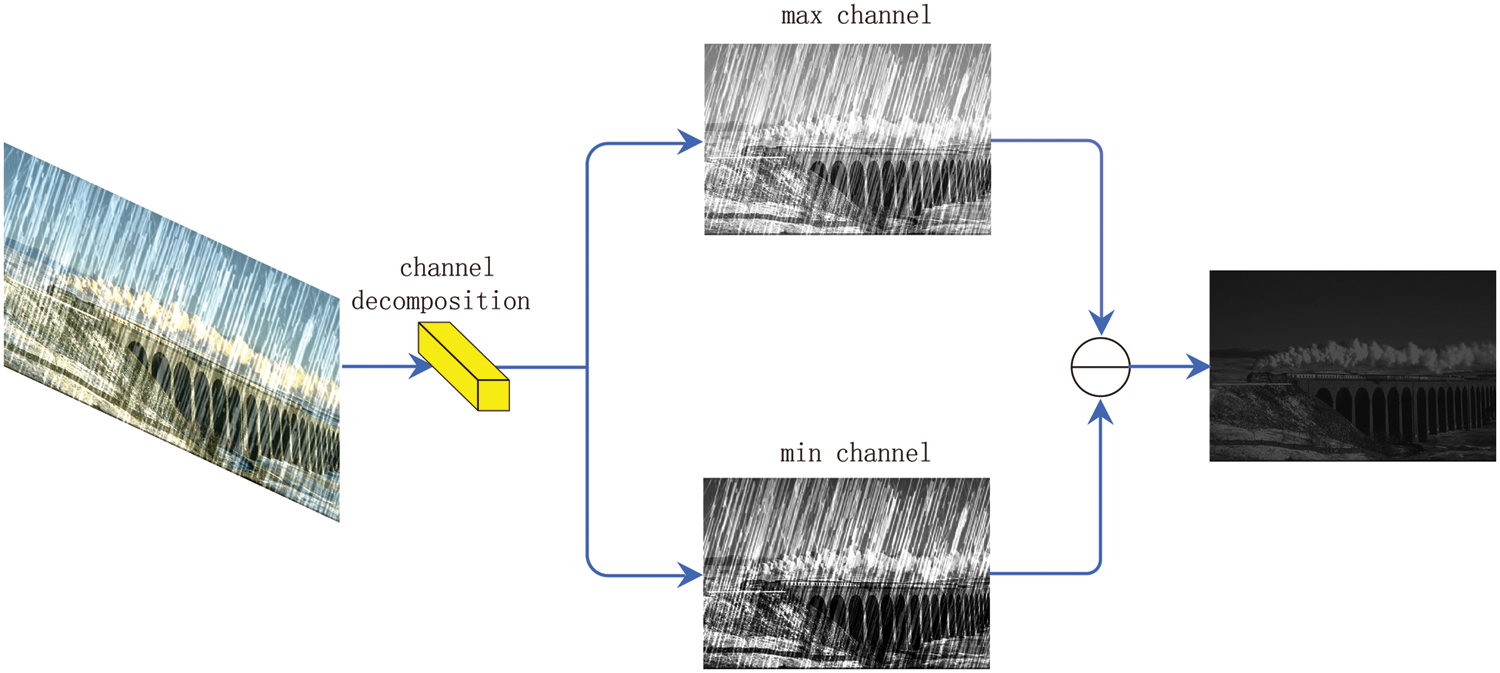
Figure 3: Residual channel decomposition module

Moreover, according to Li et al. [29]. The previous residual channel can still work if color constancy is not used. Because the predominantly gray atmospheric light is produced by cloudy skies in most cases, the appearance of the rain pattern is already colorless. Based on this observation, the residual channel prior can extract a more complete and accurate background and object structure. Therefore, we introduce the residual channel prior to the image derain model in this paper.

Combined with Fig. 4 we can observe that when the rainfall is slight, using the RCP can get a more precise rain-free background map, but in the face of severe image occlusion, this module still has shortcomings.

Figure 4: Comparison between the RCP of rainy images and ground truth

3.2 Feature-Attention Fusion Module, FFM

Although the use of RCP can eliminate most of the rain patterns, it also destroys the image information. Responding to the partial information disappearance problem, and we use an improved feature attention fusion module to recover the detailed information lost in residual decomposition by comparing the original rain map with the image processed and using the similarity of the features after convolution to fuse them.

As shown in Fig. 5, the input image Iin is convolved with the residual image Ires into a 3 * 3 convolution kernel:

Fin=Conv(Iin)(5)

Fres=Conv(Ires)(6)

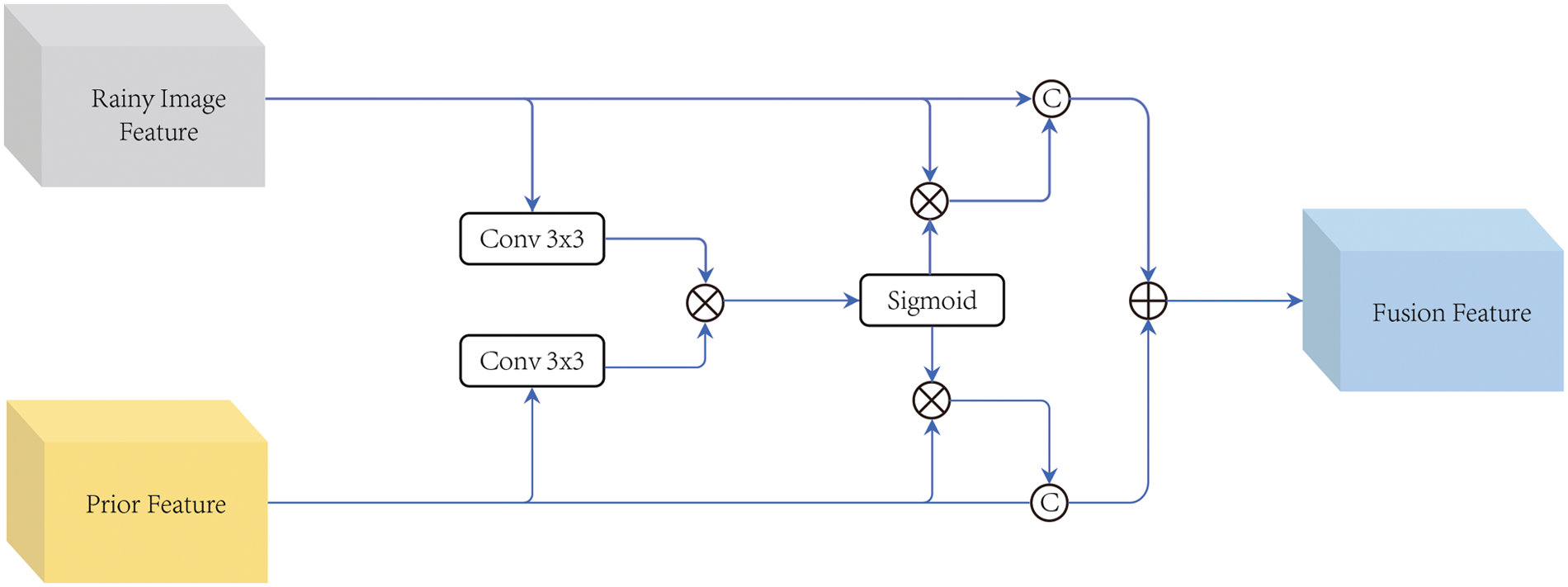
Figure 5: Feature-attention fusion module

In the next step, similarity mapping is obtained using element multiplication Fin⊗Fres to enhance the background information in the rain image. Because the background of the RCP is similar to the rain image, the location with significant difference in comparison with the input features is the rain streaks, so the similarity mapping can further enhance the structure of the a priori features.

M=Sigmoid(Fin⊗Fres)(7)

Fins=M⊗Iin(8)

Fress=M⊗Ires(9)

where M denotes the similarity map, Fins and Fress denotes the features activated by the input channel Fin and Fres, respectively.

Fout=Concat(Fin,Fins)+Concat(Fres,Fress)(10)

where Fout is the fusion feature in Fig. 5.

We concat the activated feature map with the original feature map. Finally, we add the activated feature map to the original feature map element by element to obtain the adjusted image. By exploiting the colorless property of the rain pattern, the masked background is recovered while retaining the background information after removing the rain pattern. More details are shown in Algorithm 1.

3.3 Loss Function

For the loss function, we utilize the Peak Signal-to-Noise Ratio (PSNR) as a loss function measure:

ℒoss=−∑i=12⁡PSNR((Ri+Xi),Y)(11)

Let Xi∈RN×C×H×W signifies the subnetwork’s input i, where N is the batch size of datasets, C is the number of channels, H and W represents the height and width of the image pixels, Ri∈RN×C×H×W denotes the final prediction of subnetwork i and Y∈RN×C×H×W is the ground truth.

4  Experiments

In this paper, we use BasicSR [30] based on the PyTorch framework for experiments. The code runs on a 3060 Nvidia graphics card with 12G memory, and to ensure the fairness of the experiments, we employ the same network training settings as HINet [20] does. The nets were trained with Adam optimizer, with initial learning rate at the same 2×10−4, using cosine annealing strategy learning rate with a minimum learning rate of 1×10−7. The evaluation methods include peak signal to noise ratio (PSNR) and structural similarity index (SSIM) of rain image processing results to the original image. The PSNR measures the overall image similarity and focuses on assessing the degree of distortion in image colors and smooth areas and is the most widely and commonly used objective metric for evaluating image quality. SSIM can better reflect the subjective perception of human eyes, and the SSIM value is equal to 1 when the content and structure of the two images are identical.

4.1 Synthetic Datasets

To validate the effectiveness of the proposed algorithm, we evaluate our method on several paired images datasets for the rain removal task, containing 13711 paired training sets with/without rain, and we evaluate the results on Test100 [31], Rain100L [19], Rain100H [19], Test1200 [13], Test2800 [11]. The comparison algorithm are DerainNet [10], Semi-supervised model (SEMI) [32], Density-aware image deraining method with multi-stream densely connected network (DID-MDN) [13], Multi-scale progressive fusion network (MSPFN) [33], Recurrent squeeze-and-excitation context aggregation net (RESCAN) [14], Multi-stage progressive image restoration net (MPRNet) [34] and HINet [20]. We show the effectiveness of our network on different datasets in Table 1.

It shows that the proposed method has an average decrease of 0.37 dB compared to SOTA in test sets. We believe this is due to the introduction of a priori domain knowledge, which makes the subsequent neural networks study fewer rain patterns, and the rain patterns generated in these synthetic datasets are a couple of fixed patterns, and thus partially underperform in similar scenes whereas the Test2800 has performed beyond HINet under the same training rounds.

To verify the effectiveness of the proposed network on the simulated scene data in this paper, we compare the trained obtained network effect with the current mainstream network for subjective visual effect, as shown in Fig. 6.

Figure 6: Image deraining results tested in the Rain100L datasets

The image resulting from the MSPFN-introduced multi-scale model (an algorithm with three sizes of convolution kernel to handle different size rain patterns) still has a portion of rain patterns remaining in larger pixels (e.g., sand image). MPRNet utilizes multi-stages (with different size of input image as small, medium and large) instead of multi-scales to guarantee the same effect with an increase in computational speed but there is a problem of over-smoothing the image, causing the loss of some detail information. HINet brings half-instance block and cross-stage feature fusion (CSFF) achieve the optimal result among the comparison algorithms, but there is a performance defect in the removal of rain patterns in smaller pixels. In detail, the desert on the left in the first set of images and the head of the bear on the right both have residual white rain patterns. Moreover, the combination of RCP and FFM has less deviation from the ground truth sand detail on the middle side of the first set of images and the bear’s abdomen in the second set.

4.2 Real-World Datasets

In this section, we added the comparison of the Natural Image Quality Evaluator (NIQE). In most tasks, PSNR and SSIM metrics can be used to demonstrate whether the image reconstruction task is more efficient. However, in super-resolution tasks, after the introduction of generative adversarial networks in recent years, it was found that a high PSNR or SSIM does not guarantee a better reconstruction quality, because in images with high PSNR or SSIM, the texture details of their images do not consistently match the visual habits of the human eye. NIQE is a reference-free image quality score that indicates the perceived image “naturalness”: the smaller the score, the better the perceived quality.

To test the generalization capability of the proposed module, we used the publicly paired test set by Wang et al. [35] (i.e., spatial attentive data, SPA-Data). It was created as a large-scale dataset consisting of 170 genuine rainfall recordings, 84 of which were captured using mobile phones and 86 of which were obtained via Storyblocks or YouTube. The films feature regular urban sights, suburban landscapes (such as streets and parks), and some outdoor locations (e.g., forests). Different acquisition parameters (exposure time and ISO parameters) were used in recording the rainfall scenes to generate 29,500 image pairs with/without rain. We use 1,000 pairs of testing datasets to evaluate performance. In this test, we use weights trained from synthetic datasets, without fine-tuning, to test the generalization ability of the trained network evaluated.

Based on the metrics in Table 2, it can be observed that the proposed module in this paper can enhance the performance of rain removal networks in complex scenes or real-world rain images. We conclude that addition of the RCP and FFM modules makes it possible to filter out most of the rain patterns before the images are fed into the subsequent network (e.g., Figs. 4b and 4e), and the proposed residual channel decomposition module can significantly enhance the regularization and constrained solution space of the network, removing the distinction between synthetic images and natural environment images, since it is challenging to encompass all real rainfall situations using only synthetic datasets. We are enabling the network to have better generalization ability with the same training dataset, which is a novel approach to enhance the generalization ability of rain removal without increasing the currently known dataset.

4.3 Ablation Study

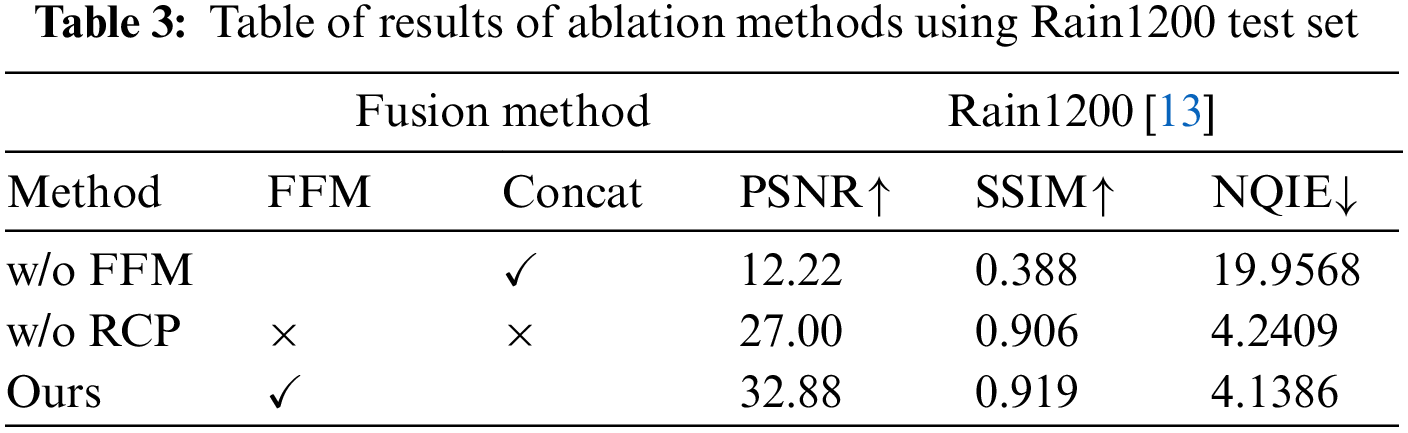
To demonstrate the effect of FFM on performance, we use the concat operation instead of FFM. The results are shown in Table 3. The network module with FFM achieves a significant performance improvement compared to the network without FFM, indicating that FFM is essential for reconstructing more explicit rain-free images, making the network capable of obtaining more helpful information.

5  Conclusion

With the rapid development of 5G network technology and sensor devices, the number of photos they capture is exploding. but photos are frequently affected by rainfall. Mobile edge computing is a way to optimize cloud computing systems by processing data at the network’s edge. To improve photo quality and processing speed, this study introduced a method of single image derain in edge computing. Specifically, we use the difference between the maximum and minimum values of the image Y channel to get the residual image with a priori feature information. Later, the fusion is performed by self-attention comparison with the original feature image. The feature concat nodes are adapted to enhance the image background information and effectively improve the network’s performance in a realistic environment. The experimental results of combining the above module with HINet show that adding this module increases the PSNR by 0.43 dB and decreases the NIQE by 0.06 in a natural environment (i.e., SPA-Data) and the generalization ability of the network image deraining is enhanced. The fusion experiments prove that the RCP and FFM modules are the most effective combination. In the future, we will work on further improving the multi-stage network into an end-to-end network to achieve the derain goal in real-time.

Acknowledgement: We are highly grateful to the Pytorch scientists, BasicSR and associated framework support. We also thank the anonymous reviewers for their comments and suggestions that improved this paper.

Funding Statement: This research is supported by the National Natural Science Foundation of China under Grant no. 41975183, and Grant no. 41875184 and Supported by a grant from State Key Laboratory of Resources and Environmental Information System.

Conflicts of Interest: The authors declare that they have no competing interests. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

1. K. Chandra, A. S. Marcano, S. Mumtaz, R. V. Prasad and H. L. Christiansen, “Unveiling capacity gains in ultradense networks: Using mm-wave NOMA,” IEEE Vehicular Technology Magazine, vol. 13, no. 2, pp. 75–83, 2018. [Google Scholar]

2. X. Xue, S. Jin, F. An, H. Zhang, J. Fan et al., “Shortwave radiation calculation for forest plots using airborne LiDAR data and computer graphics,” Plant Phenomics, pp. 1–21, 2022. https://doi.org/10.34133/2022/9856739 [Google Scholar] [PubMed] [CrossRef]

3. X. Lin, J. Wu, S. Mumtaz, S. Garg, J. Li et al., “Blockchain-based on-demand computing resource trading in IoV-assisted smart city,” IEEE Transactions on Emerging Topics in Computing, vol. 9, no. 3, pp. 1373–1385, 2021. [Google Scholar]

4. J. Li, Z. Zhou, J. Wu, J. Li, S. Mumtaz et al., “Decentralized on-demand energy supply for blockchain in internet of things: A microgrids approach,” IEEE Transactions on Computational Social Systems, vol. 6, no. 6, pp. 1395–1406, 2019. [Google Scholar]

5. Y. Li, R. T. Tan, X. Guo, J. Lu and M. S. Brown, “Rain streak removal using layer priors,” in Proc. IEEE(CVPR), Las Vegas, NV, USA, pp. 2736–2744, 2016. https://doi.org/10.1109/CVPR.2016.299 [Google Scholar] [CrossRef]

6. X. Hu, C. W. Fu, L. Zhu and P. A. Heng, “Depth-attentional features for single-image rain removal,” in Proc. IEEE/CVF, Long Beach, CA, USA, pp. 8014–8023, 2019. https://doi.org/10.1109/CVPR.2019.00821 [Google Scholar] [CrossRef]

7. Y. Luo, X. Yong and J. Hui, “Removing rain from a single image via discriminative sparse coding,” in Proc. IEEE, Boston, MA, USA, pp. 3397–3405, 2015. https://doi.org/10.1109/ICCV.2015.388 [Google Scholar] [CrossRef]

8. L. Zhu, C. W. Fu, D. Lischinski and P. A. Heng, “Joint bi-layer optimization for single-image rain streak removal,” in Proc. IEEE, Honolulu, HI, USA, pp. 2545–2553, 2017. https://doi.org/10.1109/ICCV.2017.276 [Google Scholar] [CrossRef]

9. L. W. Kang, C. W. Lin and Y. H. Fu, “Automatic single-image-based rain streaks removal via image decomposition,” IEEE Transactions on Image Processing, vol. 21, no. 4, pp. 1742–1755, 2011. [Google Scholar] [PubMed]

10. X. Fu, J. Huang, X. Ding, Y. Liao and J. Paisley, “Clearing the skies: A deep network architecture for single-image rain removal,” IEEE Transactions on Image Processing, vol. 26, no. 6, pp. 2944–2956, 2017. [Google Scholar]

11. X. Fu, J. Huang, D. Zeng, Y. Huang, X. Ding et al., “Removing rain from single images via a deep detail network,” in Proc. IEEE, Honolulu, HI, USA, pp. 3855–3863, 2017. https://doi.org/10.1109/CVPR.2017.186 [Google Scholar] [CrossRef]

12. C. Sun, C. Huang, H. Zhang, B. Chen, F. An et al., “Individual tree crown segmentation and crown width extraction from a heightmap derived from aerial laser scanning data using a deep learning framework,” Frontiers in Plant Science, vol. 13, pp. 1–23, 2022. [Google Scholar]

13. H. Zhang and V. M. Patel, “Density-aware single image de-raining using a multi-stream dense network,” in Proc. IEEE, Salt Lake City, UT, USA, pp. 695–704, 2018. https://doi.org/10.1109/CVPR.2018.00079 [Google Scholar] [CrossRef]

14. X. Li, J. Wu, Z. Lin, H. Liu and H. Zha, “Recurrent squeeze-and-excitation context aggregation net for single image deraining,” in Proc. ECCV, Munich, Germany, pp. 254–269, 2018. https://doi.org/10.1007/978-3-030-01234-2_16 [Google Scholar] [CrossRef]

15. D. Ren, W. Zuo, Q. Hu, P. Zhu and D. Meng, “Progressive image deraining networks: A better and simpler baseline,” in Proc. IEEE/CVF, Long Beach, CA, USA, pp. 3937–3946, 2019. https://doi.org/10.1109/CVPR.2019.00406 [Google Scholar] [CrossRef]

16. H. Wang, Q. Xie, Q. Zhao and D. Meng, “A model-driven deep neural network for single image rain removal,” in Proc. IEEE/CVF, Seattle, WA, USA, pp. 3103–3112, 2020. https://doi.org/10.1109/CVPR42600.2020.00317 [Google Scholar] [CrossRef]

17. Q. Guo, J. Sun, F. J. Xu, L. Ma, X. Xie et al., “EfficientDeRain: Learning pixel-wise dilation filtering for high-efficiency single-image deraining,” in Proc. AAAI, Vancouver, Online, Canada, 35, pp. 1487–1495, 2021. [Google Scholar]

18. Q. Guo, J. Sun, F. J. Xu, L. Ma, D. Lin et al., “Uncertainty-aware cascaded dilation filtering for high-efficiency deraining,” arXiv preprint, pp. 1–14, arXiv: 2201.02366, 2022. [Google Scholar]

19. W. Yang, R. T. Tan, J. Feng, J. Liu, Z. Guo et al., “Deep joint rain detection and removal from a single image,” in Proc. IEEE(CVPR), Honolulu, HI, USA, pp. 1357–1366, 2017. https://doi.org/10.1109/CVPR.2017.183 [Google Scholar] [CrossRef]

20. L. Chen, X. Lu, J. Zhang, X. Chu and C. Chen, “HINet: Half instance normalization network for image restoration,” in Proc. IEEE/CVF, Nashville, TN, USA, pp. 182–192, 2021. https://doi.org/10.1109/CVPRW53098.2021.00027 [Google Scholar] [CrossRef]

21. Z. Tu, H. Talebi, H. Zhang, F. Yang, P. Milanfar et al., “Maxim: Multi-axis MLP for image processing,” in Proc. IEEE/CVF, New Orleans, LA, USA, pp. 5769–5780, 2022. https://doi.org/10.1109/CVPR52688.2022.00568 [Google Scholar] [CrossRef]

22. H. Wang, Q. Xie, Q. Zhao, Y. Liang and D. Meng, “RCDNet: An interpretable rain convolutional dictionary network for single image deraining,” arXiv preprint, pp. 1–14, arXiv:2107.06808, 2021. [Google Scholar]

23. X. Xu, Q. Jiang, P. Zhang, X. Cao, M. Khosravi et al., “Game theory for distributed IoV task offloading with fuzzy neural network in edge computing,” IEEE Transactions on Fuzzy Systems, vol. 30, no. 11, pp. 4593–4604, 2022. [Google Scholar]

24. X. Xu, H. Tian, X. Zhang, L. Qi, Q. He et al., “DisCOV: Distributed COVID-19 detection on X-ray images with edge-cloud collaboration,” IEEE Transactions on Services Computing, vol. 15, no. 3, pp. 1206–1219, 2022. [Google Scholar]

25. W. Gu, F. Gao, R. Li and J. Zhang, “Learning universal network representation via link prediction by graph convolutional neural network,” Journal of Social Computing, vol. 2, no. 1, pp. 43–51, 2021. [Google Scholar]

26. L. Qi, W. Lin, X. Zhang, W. Dou, X. Xu et al., “A correlation graph based approach for personalized and compatible web APIs recommendation in mobile APP development,” IEEE Transactions on Knowledge and Data Engineering, pp. 1, 2022. https://doi.org/10.1109/TKDE.2022.3168611 [Google Scholar] [CrossRef]

27. Y. Liu, Z. Song, X. Xu, W. Rafique and X. Zhang, “Bidirectional GRU networks-based next POI category prediction for healthcare,” International Journal of Intelligent Systems, vol. 37, no. 7, pp. 4020–4040, 2021. [Google Scholar]

28. L. Yang, Y. Han, X. Chen, S. Song, J. Dai et al., “Resolution adaptive networks for efficient inference,” in Proc. IEEE/CVF, Seattle, WA, USA, pp. 2366–2375, 2020. https://doi.org/10.1109/cvpr42600.2020.00244 [Google Scholar] [CrossRef]

29. R. Li, R. T. Tan and L. F. Cheong, “Robust optical flow in rainy scenes,” in Proc. ECCV, Munich, Germany, pp. 288–304, 2018. https://doi.org/10.1007/978-3-030-01267-0_18 [Google Scholar] [CrossRef]

30. X. Wang, K. Yu, K. Chan, C. Dong and C. C. Loy, “BasicSR: Open source image and video restoration toolbox,” 2018. https://github.com/xinntao/BasicSR [Google Scholar]

31. H. Zhang, V. Sindagi and V. M. Patel, “Image de-raining using a conditional generative adversarial network,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 30, no. 11, pp. 3943–3956, 2019. [Google Scholar]

32. W. Wei, D. Meng, Q. Zhao, Z. Xu and Y. Wu, “Semi-supervised transfer learning for image rain removal,” in Proc. IEEE/CVF, Long Beach, CA, USA, pp. 3877–3886, 2019. https://doi.org/10.1109/CVPR.2019.00400 [Google Scholar] [CrossRef]

33. K. Jiang, Z. Wang, P. Yi, C. Chen, B. Huang et al., “Multi-scale progressive fusion network for single image deraining,” in Proc. IEEE/CVF, Seattle, WA, USA, pp. 8346–8355, 2020. https://doi.org/10.1109/CVPR42600.2020.00837 [Google Scholar] [CrossRef]

34. S. W. Zamir, A. Arora, S. Khan, M. Hayat, F. S. Khan et al., “Multi-stage progressive image restoration,” in Proc. IEEE/CVF, Nashville, TN, USA, pp. 14821–14831, 2021. https://doi.org/10.1109/CVPR46437.2021.01458 [Google Scholar] [CrossRef]

35. T. Wang, X. Yang, K. Xu, S. Chen, Q. Zhang et al., “Spatial attentive single-image deraining with a high quality real rain dataset,” in Proc. IEEE/CVF, Long Beach, CA, USA, pp. 12270–12279, 2019. https://doi.org/10.1109/CVPR.2019.01255 [Google Scholar] [CrossRef]