Instance Reweighting Adversarial Training Based on Confused Label

1  Introduction

Deep neural networks (DNNs) are powerful tools to solve real-world problems, such as image classification [1–5], speech recognition [6–8], and natural language processing [9–11]. Although DNNs show favorable performance, they have been substantiated to be highly vulnerable to being fooled by adversarial examples [12–15]. Here, adversarial examples are defined as the synthetic examples which are intentionally crafted by adding slightly perturbed noises to the natural origin examples [16–19]. The adversarial example attacks pose profound threats to many critical applications, such as medical diagnostics and self-driving cars [14,20,21].

Recently, many defense methods have been proposed to protect DNNs against adversarial examples, such as input/feature denoising [22–24], defensive distillation [25–27], and adversarial training (AT) [28–30]. Among them, AT is considered one of the most effective methods, which incorporates adversarial examples during the model training process [31,32]. Although AT improves the robustness of DNNs, it leads to a decline in prediction accuracy for natural data [33–35]. To address this issue, many works have been developed to find a trade-off between robustness and accuracy for improving the performance of AT. For instance, Zhang et al. [36] proposed a friendly adversarial training method (FAT), which can improve accuracy and maintain robustness by searching for friendly adversarial data to update the model. Wang et al. [37] proposed a once-for-all adversarial training (OAT), where the trained model could be adjusted among standards and robust accuracies at testing time. Zhang et al. [38] proposed a theoretically principled trade-off between robustness and accuracy (TRADES) to improve projected gradient descent (PGD) training via decoupling the minimax training objective into an accuracy term and a robustness regularization term. In addition to these methods, instance reweighted adversarial training [39] is regarded as the most promising method to improve the robustness and maintain the accuracy of DNNs. The main idea of instance reweighted adversarial training lies in the fact that the examples closer to the decision boundaries are much more vulnerable to being attacked and should be given larger weights. To characterize the closeness between the data and decision boundaries, Zhang et al. [40] proposed the least PGD steps (LPS) method, where LPS represents the shortest number of steps starting from natural data to make an adversarial variant of this natural data cross the class decision boundary. However, the values taken by LPS are discrete and affected by the adversarial examples [13,28]. Hence, Liu et al. [41] proposed the continuous and path-independent probability margin (PM) criterion, where PM is defined as the difference between the probability of the true label and the probability of the most misclassed catalog. Based on PM, they proposed a general AT training framework termed probabilistic margins for instance reweighting in adversarial training (MAIL-AT), which achieved state-of-the-art performance.

Although PM achieves favorable results in many applications, its performance is limited in the situation that the predictions of the adversarial examples have multiple confused labels (CLs), where a confused label (CL) is defined as the label whose prediction probability is higher than that of the ground truth label given a specific adversarial example. The reason for this crux lies in the fact that when adversarial examples yield multiple CLs, the PM method only considers the impact of the most CL while neglecting the impact of the other CLs. Yet, according to our observation, the example of having multiple CLs is closer to multi-classification decision boundaries and is supported to be more critical. To clearly illustrate this phenomenon, we research the following questions and raise our motivations:

(i) Whether there exist a number of adversarial examples having multiple CLs during the AT. If yes, how much impact do such adversarial examples have on AT?

(ii) Whether the PM criterion is the capability to distinguish the adversarial examples with multiple CLs and the ones with single CL. If not, how to improve this criterion?

For the first question, we train the ResNet-18 [1] model on CIFAR-10 using MAIL-AT. Starting from the 76th epoch of training, we divide the misclassified adversarial examples into two subsets: 1) a subset of misclassified examples with single CLs, termed Ssig, and 2) a subset of misclassified examples with multiple CLs, termed Smul. We explore different ways to retrain the same network and evaluate its robustness against white-box PGD-20 attacks on the test dataset. Fig. 1A shows the component of misclassified adversarial examples during AT. The blue bar represents the total number of misclassified examples, the orange bar represents the number of Ssig, and the green bar represents the number of Smul. We observe that there do exist numerous Smul in misclassified examples, and even the number of Smul is conspicuously larger than that of Ssig. Figs. 1C and 1D separately show a sketch regarding the output probability of a given misclassified adversarial examples from Ssig and Smul. Fig. 1B illustrates the impact of Ssig and Smul on the final robustness of the model. The blue curve represents the robustness of the model trained using both Ssig and Smul (as standard MAIL-AT does). The orange/green curve indicates the robustness of the model trained using the examples excluding the Ssig/Smul. From Fig. 1B, we can observe that if the example from Smul is not used for AT (the other examples are still used for AT), the final robustness of the model will drop drastically compared with the standard MAIL-AT (green curve). In contrast, the same operation using the examples excluding Ssig only slightly affects the final robustness (orange curve). This phenomenon implies that the impact of the examples with multiple CLs is more significant than the impact of the examples with single CL for the final robustness of the model. Accordingly, it is reasonable to assign greater weights for the examples having multiple CLs during AT.

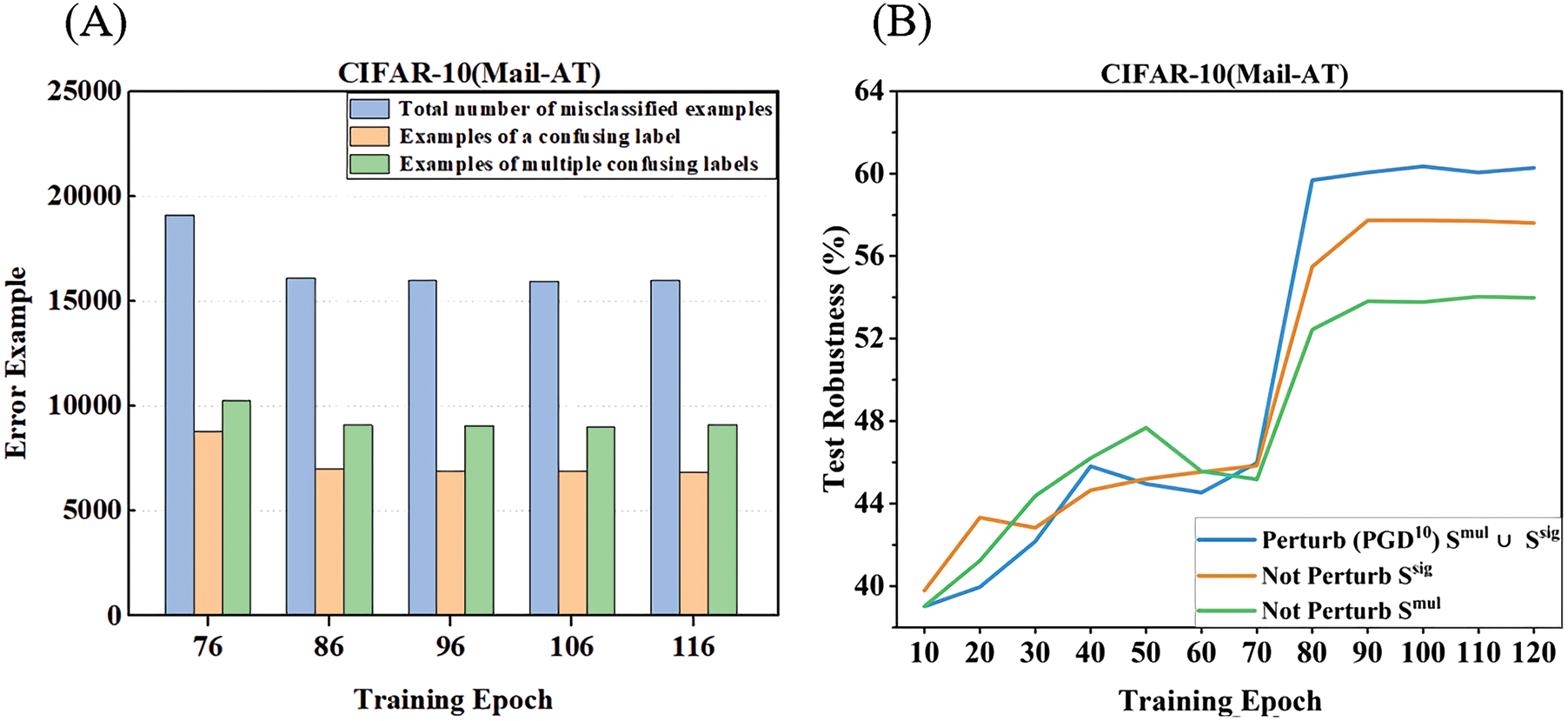
Figure 1: (A) shows the component of misclassified adversarial examples starting from the 76th epoch of AT. (B) shows the distinctive influence of misclassified examples with single CLs (Ssig) vs. misclassified examples with multiple CLs (Smul) on the final robustness of MAIL-AT. We test the robustness of different strategies on either a subset of examples: the blue curve represents the robustness of the model trained using both Ssig and Smul (as standard MAIL-AT does); the orange/green curve indicates the robustness of the model trained using the examples excluding the Ssig/Smul. (C) and (D) separately show a sketch regarding the output probability of a given misclassified adversarial examples from Ssig and Smul

For the second question, we draw a diagram to demonstrate the closeness between the example and the multi-classification decision boundary in Fig. 2. The solid circles represent the category center for a multi-classification task. The dotted pentagons represent the given examples: pentagon A stands for the example having single CL, and pentagon B stands for the example having multiple CLs. Then we use the PM method based on the adversarial variance to measure the closeness for A and B, where pu (u = i, j, k)is the probability that a data point belongs to the u-th class. Support the true labels of both A and B are class i. From the figure, we can find that the formalization closenesses of both A and B measured by the PM method are −0.2. Compared to A (a single CL example), B (a multiple CLs example) is much closer to the multi-classification decision boundary. That means the examples with multiple CLs are more critical than those with single CL. Nevertheless, the PM method is unreliable in differentiating these two types of examples since PM only considers the prediction probability of the most confused label. Hence, it is reasonable to incorporate all the CLs to formulate the closeness value for the misclassified examples. In our method (CL-PM), we evaluate the closeness by accumulating the probability differences of the whole CLs and ground truth label. Specifically, the closeness values derived by CL-PM for A and B are −0.2 and −0.3, which illustrates that our method is powerful to distinguish the examples having single CL and the ones having multiple CLs.

Figure 2: An illustration of PM and the proposed CL-PM, where pi, pj, and pk represent the probability that a data point belongs to the i-th, j-th, and k-th class, respectively. The solid circles denote the center of classes, and the dotted pentagons represent the misclassified adversarial examples: pentagons (A) and (B) stand for the example having single CL and the one having multiple CLs, respectively. The shaded area represents the other class. Support the true labels of (A) and (B) are i-th class, and the prediction probabilities of the labels from the shaded area are lower than those of the true label. As a special example, the closeness values regarding (A) and (B) calculated by the PM method are −0.2 (derived by pi − pj), while the closeness values regarding (A) and (B) calculated by the proposed CL-PM are −0.2 and −0.3 (derived by (pi − pj) + ( pi − pk))

According to the previous analysis, this paper proposed an improved criterion (CL-PM) to measure the closeness between the examples and the decision boundaries. Our method addresses the problem that PM is unreliable in distinguishing closeness between examples with single CL and those with multiple CLs. Specifically, we evaluate the closeness between the misclassified examples and the multi-classification margin by accumulating the probability differences of the CLs and ground truth label. Our main contributions are as follows:

■   We investigate the distinctive influence of the misclassified examples with single CL and those with multiple CLs for the final robustness of AT. We reveal that the manipulation of misclassified examples with multiple CLs has more impact on the final robustness of AT. Accordingly, the misclassified examples with multiple CLs should be given larger weights than those with single CL.

■   We proposed a new margin-aware criterion, CL-PM, to measure the closeness mentioned above. Based on CL-PM, we further propose confused-label instance-reweighted adversarial training (CLIRAT), which significantly enhances the performance of AT, especially when there exist numerous adversarial examples having multiple CLs.

■   Experiments demonstrated that CL-PM is more reliable in indicating the closeness regarding multiple misclassified categories, and CL-PM-based reweighting AT methods outperformed state-of-the-art counterparts.

2  Related Work

2.1 Adversarial Attacks

Given a clean example x with class label y and a target DNN model f (x; θ) with weight θ, the goal of an adversary is to find an adversarial example xadv that fools the network into making an incorrect prediction (e.g., f(xadv;θ)≠y), while remaining in the ϵ-ball centered at x (e.g., ||xadv−x||∞≤ϵ).

Fast Gradient Sign Method (FGSM) [17]. FGSM perturbs clean example x for one step by the amount of ϵ along the gradient direction:

xadv=x+ϵ⋅sign(∇xℓ(f(x;θ),y))(1)

Projected Gradient Descent (PGD) [28]. PGD perturbs standard example x for T steps with a smaller step size. After each step of perturbation, PGD projects the adversarial example back onto the ϵ-ball of x if it goes beyond the ϵ-ball:

xt+1adv=∏ϵ(xtadv+α⋅sign(∇xℓ(f(xtadv;θ),y)))(2)

where ∏ϵ(.) is the projection operation, and t is the number of iteration steps.

There are also other types of white-box attacks, including auto attack (AA) [42] and Carlini and Wagner (CW) [43]. AA can be viewed as an ensemble of several advanced attacks.

2.2 Adversarial Defenses

TRADES [38]. TRADES optimizes an upper bound of adversarial risk that is a trade-off between accuracy and robustness:

ℓ(θ)=1n∑i=1n{CE(f(xi;θ),yi)+β⋅maxKL(f(xi;θ)∥f(xiadv;θ))}(3)

where β > 0 is the trade-off parameter, CE is the cross-entropy loss, and KL denotes the Kullback-Leibler divergence.

MART [19]. Misclassification aware adversarial training (MART) incorporates an explicit differentiation of misclassified examples as a regularizer of adversarial risk.

ℓ(θ)=1n∑i=1n{BCE(f(xiadv;θ),yi)+λ⋅KL(f(xi;θ)∥f(xiadv;θ))⋅(1−fyi(xi;θ))}(4)

where fyi(xi;θ) denotes the yi−th element of output vector f(xi;θ), BCE(f(xi;θ),yi)=−log⁡(fyi(xiadv;θ))−log⁡(1−maxk≠yifk(xiadv;θ)) and λ is an adjustable scaling parameter that balances the two parts of the final loss.

3  The Proposed Method

In this section, we propose a new margin-aware criterion, called CL-PM, to measure the closeness between the data and decision boundaries. Based on CL-PM, we further propose confused-label instance-reweighted adversarial training (CLIRAT) to reweight adversarial examples during training based on confused label (CL).

3.1 Preliminary

For a K-classification problem, this deep classifier f (x; θ) predicts the label of an input data via f(x;θ)=argmaxkpk(x;θ), with pk(x,θ) being the predicted probability (softmax on logits) for the k-th class.

Inspired by the multi-classification margin in margin theory [44], PM is defined as the difference between two estimated class-posterior probabilities, e.g., such a probability of the true label minus the probability of the most CL given some natural data.

PM(x,y;θ)=py(x;θ)−maxj,j≠ypj(x;θ)(5)

Here, if PM is 0, the data point x is on the decision boundary between two classes; PM is positive, the data point x is much closer to the true label; PM is negative, and the data point x is much closer to the most confusing class. PM shares a negative correlation with data vulnerability: data with larger/smaller PMs are safer/riskier and should have smaller/larger weights.

Weight Assignment: Liu et al. [41] adopted the sigmoid function for weight assignment, which can be viewed as a softened sample selection operation of the form:

ωiunn=sigmoid(−γ(PMi−β))(6)

where β indicates how much data should have relatively large weights and γ ≥ 0 controls the smoothness around β.

3.2 Proposed CL-PM

From the previous section, we have learned that PM focuses on the difference between the probability of the true label and the probability of the most CL for given data. It cannot sufficiently distinguish the vulnerability of misclassified examples with the same PM values. Therefore, we propose a new margin-aware criterion called (CL-PM):

CL−PM(x,y;θ)={py(x;θ)−maxj,j≠ypj(x;θ),f(x;θ)=y∑j=1(py(x;θ)−pj(x;θ)),f(x;θ)≠y and py(x;θ)<pj(x;θ)(7)

where if the adversarial example is correctly classified, we use the probability of the true label minus the probability of the most CL to measure the robustness of the data. Similarly, if the adversarial example is misclassified, we measure the robustness of the data by accumulating the probability differences between CLs and ground truth label. Here, CL-PM is positive, indicating that data point x is closer to the true label, and CL-PM is negative, indicating that data point x will be closer to the confusing class. In Fig. 2, CL-PM for measuring the robustness of misclassified adversarial examples with only a CL is consistent with PM. However, it is slightly different in measuring the robustness of misclassified adversarial examples with multiple CLs. The difference is mainly reflected in the influence of other CLs on the true label.

3.3 Realization of CLIRAT

CL-PM is an improvement of the PM method, which also shares a negative correlation with the vulnerability of data: data with larger/smaller CL-PM are safer/riskier and should have smaller/larger weights. In Algorithm 1, CLIRAT reweights the loss of the adversarial data according to the CL-PM values of data (xiadv,yi) and then updates the model parameters by minimizing the sum of the reweighted losses.

4  Experiments

This section provides a comprehensive understanding of CLIRAT, including robustness and ablation studies to various white-box attacks on benchmark datasets.

Experimental settings and implementation details. (A) Dataset: We perform experiments on the CIFAR-10 [45] dataset, and the input images are normalized to [0, 1]. For generating the most adversarial data for updating the model, we set the perturbation budget ϵ = 8/255, and the PGD steps number K = 10 with step size α = 2/255. (B) Network Architectures: We mainly used ResNet-18 [1] and Wide ResNet (WRN-32-10) [46] models as classifiers for the following experiments. (C) Training Details: For the considered methods, networks were trained using mini-batch gradient descent with momentum 0.9, weight decay 3.5 × 10−3 (for ResNet-18)/7 × 10−4 (for WRN-32-10), batch size 128, and initial learning rate 0.01 (for ResNet-18)/0.1 (for WRN-32-10) which is divided by 10 at the 75th and 90th epoch. (D) White-box Attacks: We evaluate the robustness of the model according to the following attack methods, including PGD-20 [28], PGD-100 [28], CW [43], APGD CE attack (APGD) [42], and auto-attack (AA) [42].

4.1 Robustness Evaluation and Analysis

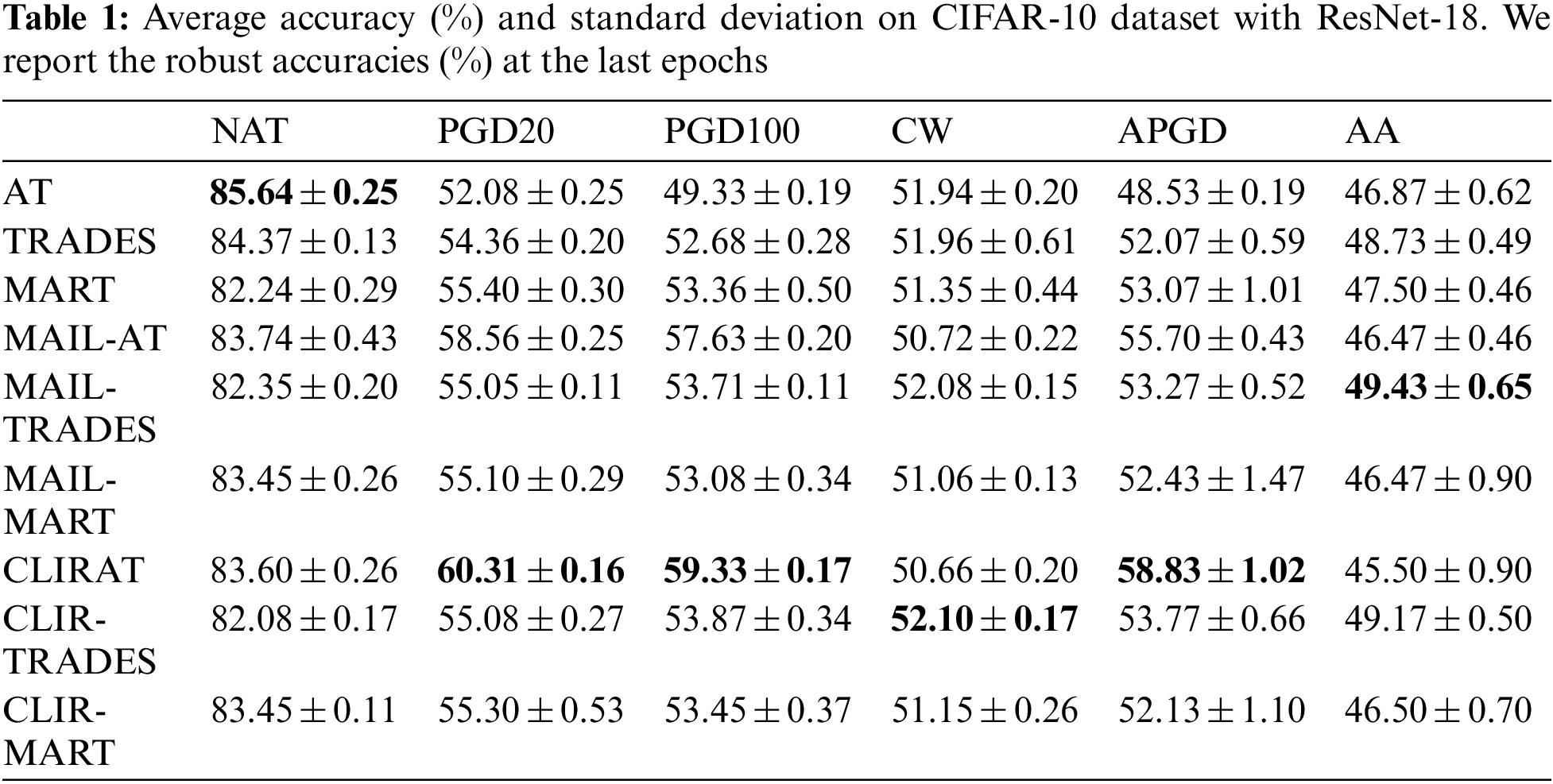
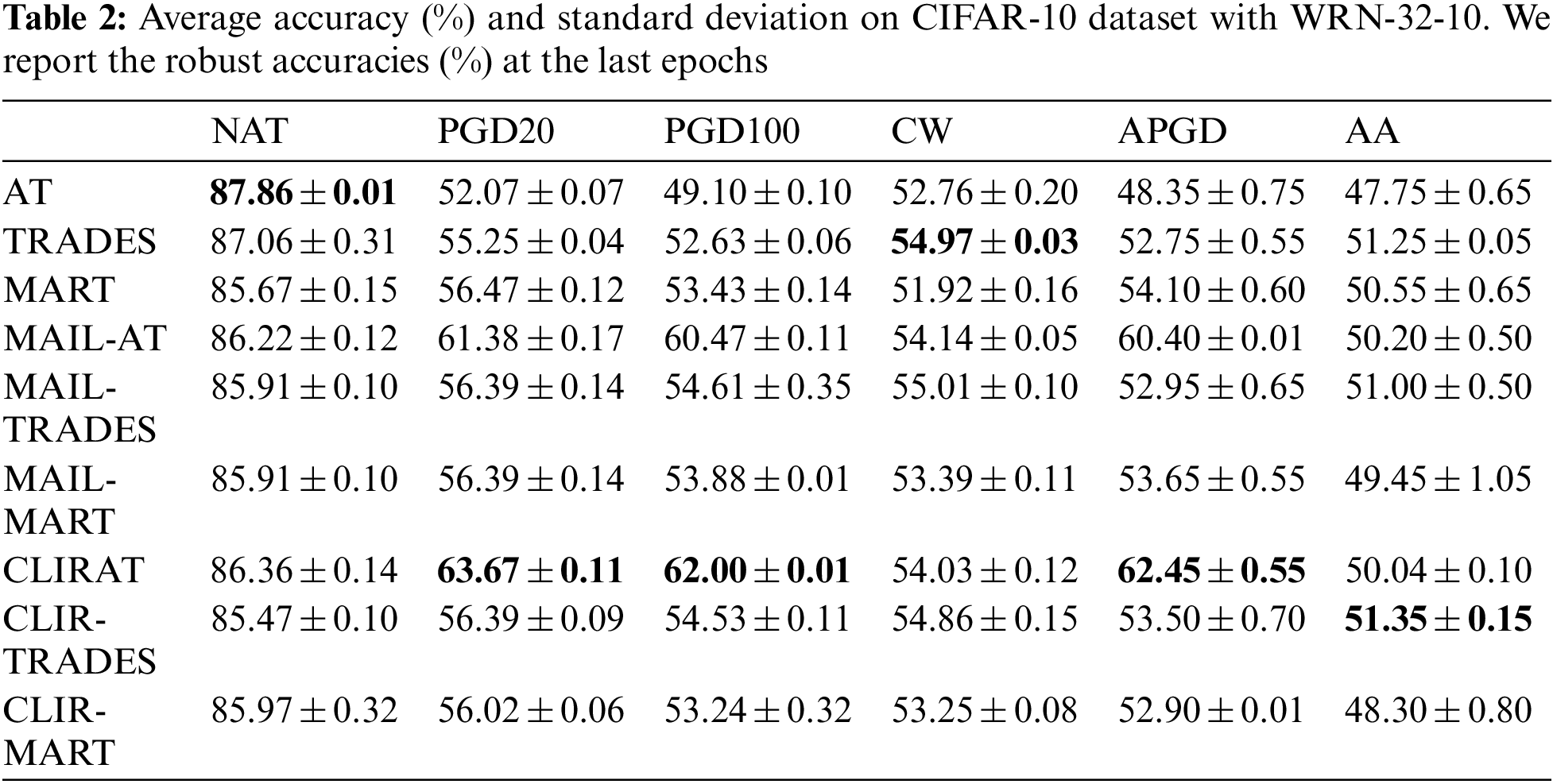
In this part, we evaluate the robustness of CLIRAT against various white-box attacks. Here, we adopted ResNet-18 as the backbone model and conducted experiments on the CIFAR-10 dataset. CLIRAT is a general method that is combined with existing methods such as AT [28], MART [19], and TRADES [38]. Specifically, MART and TRADES can be modified to CLIR-MART and CLIR-TRADES, respectively. In experiments, we set the slope and bias parameters to 10 and −0.5 in CLIRAT and 2 and 0 in both CLIR-MART and CLIR-TRADES. The trade-off parameter β was set to 6 in CLIR-MART and 5 in CLIR-TRADES.

Performance Evaluation. In Fig. 3, we conduct the standard AT, MAIL-AT, and CLIRAT using ResNet-18 [1] on the CIFAR-10 dataset. We use the reweighted objective function after the 75th epoch in the training process. In order to avoid the deep model is not fully learned in the initial training phase, and the geometric information is not obtained enough, which maybe accumulate the bias in erroneous weight assignment in the training. Therefore, until the 75th epoch, we fix ω to 1 regardless of the corresponding CL-PM value. In Fig. 3B, we can observe that the model trained by the CLIRAT method has dramatically improved the test robustness compared to the model trained by the MAIL-AT method. Figs. 3A and 3C also show that our improved CL-PM does not degrade other performances of the original method (e.g., PM). Fig. 5 provides more experimental details in terms of the performance evaluation. To further verify the effectiveness of the CL-PM method, we compare the performance of the standard AT, TRADES, MART, MAILAT, MAIL-TRADES, MAIL-MART, CLIRAT, CLIR-TRADES and CLIR-MART on the ResNet-18 and WRN-32-10 models respectively, and report the robust accuracies at the last epochs in Tables 1 and 2. In Table 1, we can observe that CLIRAT has significantly improved its performance in PGD and APGD attacks, and CLIR-MART and CLIR-TRADES also have slightly improved their robustness against PGD attacks. However, compared with the MAIL method, the adversarial robustness of CLIRAT, CLIR-MART, and CLIR-TRADES against CW and AA attacks is not significantly improved or slightly decreased, which may be related to the overfitting [47,48] of the model. In addition, the overall performance of the model trained with CLIR-TRADES/CLIR-MART is not much better than that of the model trained with MAIL-TRADES/MAIL-MART. In Table 2, we can find that the overall accuracy will also be improved when using the model with a large capacity. In a word, CLIRAT performs well on PGD-based methods, while CLIR-TRADES and CLIR-MART generally perform on CW and AA attacks. The experimental results also indicate that different optimization functions and model network capacity have unique effects on the CL-PM method, which means that the model’s performance may be further improved.

Figure 3: Comparisons of AT (red lines), MAIL-AT (green lines) and CLIRAT (blue lines) using ResNet-18 on the CIFAR-10 dataset. (A) shows the comparison of the standard accuracy of natural test data (NAT) of the model under three different training methods; Similarly, (B) shows the comparison of test robustness of the model under PGD-20, PGD-100 and APGD attacks; (C) shows the comparison of test robustness of the model under CW and AA attacks

4.2 Ablation Studies on CL-PM

In this part, we delve into CL-PM to investigate every component. We train ResNet-18 using CLIRAT with an L∞ threat model with ϵ = 8/255 for 120 epochs following the same setting in Section 4.1. The training attack is PGD-10 (step size 2/255), and the test attacks are the white-box attacks mentioned in Section 4.1 above.

Analysis of hyperparameters γ and β. Here we mainly study the effects of γ and β on the performance of CLIRAT. In the weight assignment function, β indicates how much data should have a relatively large weight, and γ ≥ 0 controls the smoothness around β. In the experiment, the hyperparameters γ and β of CLIRAT are 10 and −0.5, respectively. We always kept one of the hyperparameters unchanged during testing. Fig. 4 shows the results using different γ ∈ [7,13], β ∈ [−0.2, −0.7]. We can observe that properly adjusting the values of γ and β can increase the robustness of the model to PGD attacks, but the test robustness of NAT and AA, and CW attacks will tend to decrease. Therefore, the proper selection of hyperparameters during the experiment can improve the model’s overall performance.

Figure 4: Experiment of ablation of CIFAR-10 using CLIRAT

Figure 5: Comparisons of AT (red lines), MAIL-AT (green lines) and CLIRAT (blue lines) using ResNet-18 on the CIFAR-10 dataset

5  Conclusion

This paper proposes a new margin-aware criterion CL-PM to fill the gap that the PM method cannot distinguish the adversarial examples with multiple CLs and single CLs. Based on CL-PM, we proposed confused-label instance-reweighted adversarial training, which significantly enhances the robustness of AT without declining the prediction accuracy for the natural examples. Note that in our experiments, we observe that different loss functions have different impacts on the robustness of the model. Our future work mainly focuses on designing more powerful loss to improve the performance of instance-reweighted adversarial learning further.

Funding Statement: This work was supported by the National Natural Science Foundation of China (No. 62072127, No. 62002076, No. 61906049), Natural Science Foundation of Guangdong Province (No. 2023A1515011774, No. 2020A1515010423), Project 6142111180404 supported by CNKLSTISS, Science and Technology Program of Guangzhou, China (No. 202002030131), Guangdong basic and applied basic research fund joint fund Youth Fund (No. 2019A1515110213), Open Fund Project of Fujian Provincial Key Laboratory of Information Processing and Intelligent Control (Minjiang University) (No. MJUKF-IPIC202101), Scientific research project for Guangzhou University (No. RP2022003).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. K. M. He, X. Y. Zhang, S. Q. Ren and J. Sun, “Deep residual learning for image recognition,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, pp. 770–778, 2016. [Google Scholar]

2. T. X. Zheng, X. M. Wang, Y. X. Chen, F. J. Yu and J. Li, “Feature evolvable learning with image streams,” Intelligent Data Analysis, vol. 27, no. 4, pp. 1–11, 2023. [Google Scholar]

3. S. Ai, A. S. V. Koe and T. Huang, “Adversarial perturbation in remote sensing image recognition,” Applied Soft Computing, vol. 105, pp. 107252, 2021. [Google Scholar]

4. X. Zhang, F. Peng and M. Long, “Robust coverless image steganography based on dct and lda topic classification,” IEEE Transactions on Multimedia, vol. 20, no. 12, pp. 3223–3238, 2018. [Google Scholar]

5. X. H. Qin, S. Q. Tan, W. X. Tang, B. Li and J. W. Huang, “Image steganography based on iterative adversarial perturbations onto a synchronized-directions sub-image,” in ICASSP 2021–2021 IEEE Int. Conf. on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, pp. 2705–2709, 2021. [Google Scholar]

6. Y. S. Wang, X. J. Deng, S. B. Pu and Z. H. Huang, “Residual convolutional ctc networks for automatic speech recognition,” arXiv preprint arXiv:1702.07793, 2017. [Google Scholar]

7. A. Baevski, W. N. Hsu, A. Conneau and M. Auli, “Unsupervised speech recognition,” Advances in Neural Information Processing Systems, vol. 34, pp. 27826–27839, 2021. [Google Scholar]

8. T. Li, J. Li, X. F. Chen, Z. L. Liu, W. J. Lou et al., “Npmml: A framework for non-interactive privacy-preserving multi-party machine learning,” IEEE Transactions on Dependable and Secure Computing, vol. 18, no. 6, pp. 2969–2982, 2020. [Google Scholar]

9. J. Devlin, M. Chang, K. Lee and K. Toutanova, “Pre-training of deep bidirectional transformers for language understanding,” arXiv preprint arXiv:1810.04805, 2018. [Google Scholar]

10. Y. X. Jing, H. P. Wang, Y. Huang, L. Zhang, J. Xu et al., “A modeling language to describe massive data storage management in cyber-physical systems,” Journal of Parallel and Distributed Computing, vol. 103, pp. 113–120, 2017. [Google Scholar]

11. R. R. Ma, J. Y. Miao, L. F. Niu and P. Zhang, “Transformed l1 regularization for learning sparse deep neural networks,” Neural Networks, vol. 119, pp. 286–298, 2019. [Google Scholar] [PubMed]

12. H. L. Ren, T. Huang and H. Y. Yan, “Adversarial examples: Attacks and defenses in the physical world,” International Journal of Machine Learning and Cybernetics, vol. 12, no. 11, pp. 3325–3336, 2021. [Google Scholar]

13. H. Q. Chen, K. D. Lu, X. M. Wang and J. Li, “Generating transferable adversarial examples based on perceptually-aligned perturbation,” International Journal of Machine Learning and Cybernetics, vol. 12, no. 11, pp. 3295–3307, 2021. [Google Scholar]

14. X. M. Wang, J. Li, X. H. Kuang, Y. A. Tan and J. Li, “The security of machine learning in an adversarial setting: A survey,” Journal of Parallel and Distributed Computing, vol. 130, pp. 12–23, 2019. [Google Scholar]

15. X. H. Qin, B. Li, S. Q. Tan, W. X. Tang and J. W. Huang, “Gradually enhanced adversarial perturbations on color pixel vectors for image steganography,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 32, no. 8, pp. 5110–5123, 2022. [Google Scholar]

16. C. Szegedy, W. Zaremba, I. Sutskever, J. Bruna, D. Erhan et al., “Intriguing properties of neural networks,” arXiv preprint arXiv:1312.6199, 2013. [Google Scholar]

17. I. J. Goodfellow, J. Shlens and C. Szegedy, “Explaining and harnessing adversarial examples,” arXiv preprint arXiv:1412.6572, 2014. [Google Scholar]

18. X. J. Ma, B. Li, Y. S. Wang, S. M. Erfani, S. Wijewickrema et al., “Characterizing adversarial subspaces using local intrinsic dimensionality,” arXiv preprint arXiv:1801.02613, 2018. [Google Scholar]

19. Y. S. Wang, D. F. Zou, J. F. Yi, J. Bailey and X. J. Ma, “Improving adversarial robustness requires revisiting misclassified examples,” in Int. Conf. on Learning Representations, Addis Ababa, Ethiopia, 2019. [Google Scholar]

20. C. Badue, R. Guidolini, R. V. Carneiro, P. Azevedo, V. B. Cardoso et al., “Self-driving cars: A survey,” Expert Systems with Applications, vol. 165, pp. 113816, 2021. [Google Scholar]

21. S. Grigorescu, B. Trasnea, T. Cocias and G. Macesanu, “A survey of deep learning techniques for autonomous driving,” Journal of Field Robotics, vol. 37, no. 3, pp. 362–386, 2020. [Google Scholar]

22. C. H. Xie, Y. X. Wu, L. V. D. Maaten, A. L. Yuille and K. M. He, “Feature denoising for improving adversarial robustness,” in Proc. of the IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Long Beach, CA, USA, pp. 501–509, 2019. [Google Scholar]

23. R. T. Hou, S. Ai, Q. Chen, H. Y. Yan, T. Huang et al., “‘Similarity-based integrity protection for deep learning systems,” Information Sciences, vol. 601, pp. 255–267, 2022. [Google Scholar]

24. X. M. Wang, X. H. Kuang, J. Li, J. Li, X. F. Chen et al., “Oblivious transfer for privacy-preserving in vanet’s feature matching,” IEEE Transactions on Intelligent Transportation Systems, vol. 22, no. 7, pp. 4359–4366, 2020. [Google Scholar]

25. N. Papernot, P. McDaniel, X. Wu, S. Jha and A. Swami, “Distillation as a defense to adversarial perturbations against deep neural networks,” in 2016 IEEE Symp. on Security and Privacy (SP), San Jose, CA, USA, pp. 582–597, 2016. [Google Scholar]

26. M. Goldblum, L. Fowl, S. Feizi and T. Goldstein, “Adversarially robust distillation,” in Proc. of the AAAI Conf. on Artificial Intelligence, New York, NY, USA, vol. 34, pp. 3996–4003, 2020. [Google Scholar]

27. Y. Wang, W. Z. Meng, W. J. Li, J. Li, W. X. Liu et al., “A fog-based privacy-preserving approach for distributed signature-based intrusion detection,” Journal of Parallel and Distributed Computing, vol. 122, pp. 26–35, 2018. [Google Scholar]

28. A. Madry, A. Makelov, L. Schmidt, D. Tsipras and A. Vladu, “Towards deep learning models resistant to adversarial attacks,” arXiv preprint arXiv:1706.06083, 2017. [Google Scholar]

29. X. M. Wang, J. Li, Q. Liu, W. P. Zhao, Z. Y. Li et al., “Generative adversarial training for supervised and semi-supervised learning,” Frontiers in Neurorobotics, vol. 16, pp. 859610, 2022. [Google Scholar] [PubMed]

30. T. N. Chan, L. H. U, Y. Peng, B. Choi and J. L. Xu, “Fast network k-function-based spatial analysis,” Proceedings of the VLDB Endowment, vol. 15, no. 11, pp. 2853–2866, 2022. [Google Scholar]

31. X. Gou, L. B. Qing, Y. Wang and M. L. Xin, “Re-training and parameter sharing with the hash trick for compressing convolutional neural networks,” in Int. Conf. on Machine Learning for Cyber Security, Guangzhou, China, vol. 12486, pp. 402–416, 2020. [Google Scholar]

32. X. F. Du, J. F. Zhang, B. Han, T. L. Liu, Y. Rong et al., “Learning diverse-structured networks for adversarial robustness,” in Int. Conf. on Machine Learning, Virtual Event, vol. 139, pp. 2880–2891, 2021. [Google Scholar]

33. D. Tsipras, S. Santurkar, L. Engstrom, A. Turner and A. Madry, “Robustness may be at odds with accuracy,” arXiv preprint arXiv:1805.12152, 2018. [Google Scholar]

34. X. Xie, X. Y. Jiang, W. R. Wang, B. Wang, T. C. Wan et al., “Research and application of intrusion detection method based on hierarchical features,” Concurrency and Computation: Practice and Experience, vol. 34, no. 16, pp. e5799, 2022. [Google Scholar]

35. D. X. Wu, Y. S. Wang, S. T. Xia, J. Bailey and X. J. Ma, “Skip connections matter: On the transferability of adversarial examples generated with resnets,” arXiv preprint arXiv:2002.05990, 2020. [Google Scholar]

36. J. F. Zhang, X. L. Xu, B. Han, G. Niu, L. Z. Cui et al., “Attacks which do not kill training make adversarial learning stronger,” in Int. Conf. on Machine Learning, Virtual Event, pp. 11278–11287, 2020. [Google Scholar]

37. H. T. Wang, T. L. Chen, S. P. Gui, T. K. Hu, J. Liu et al., “Once-for-all adversarial training: In-situ tradeoff between robustness and accuracy for free,” Advances in Neural Information Processing Systems, vol. 33, pp. 7449–7461, 2020. [Google Scholar]

38. H. Y. Zhang, Y. D. Yu, J. T. Jiao, E. Xing, L. El Ghaoui et al., “Theoretically principled trade-off between robustness and accuracy,” in Int. Conf. on Machine Learning, Long Beach, California, USA, pp. 7472–7482, 2019. [Google Scholar]

39. P. Lahoti, A. Beutel, J. Chen, K. Lee, F. Prost et al., “Fairness without demographics through adversarially reweighted learning,” Advances in Neural Information Processing Systems, vol. 33, pp. 728–740, 2020. [Google Scholar]

40. J. F. Zhang, J. N. Zhu, G. Niu, B. Han, M. Sugiyama et al., “Geometry-aware instance-reweighted adversarial training,” arXiv preprint arXiv:2010.01736, 2020. [Google Scholar]

41. F. Liu, B. Han, T. L. Liu, C. Gong, G. Niu et al., “Probabilistic margins for instance reweighting in adversarial training,” Advances in Neural Information Processing Systems, vol. 34, pp. 23258–23269, 2021. [Google Scholar]

42. F. Croce and M. Hein, “Reliable evaluation of adversarial robustness with an ensemble of diverse parameter-free attacks,” in Int. Conf. on Machine Learning, VirtualEvent, vol. 119, pp. 2206–2216, 2020. [Google Scholar]

43. N. Carlini and D. Wagner, “Towards evaluating the robustness of neural networks,” in 2017 IEEE Symp. on Security and Privacy (SP), San Jose, CA, USA, pp. 39–57, 2017. [Google Scholar]

44. V. Koltchinskii and D. Panchenko, “Empirical margin distributions and bounding the generalization error of combined classifiers,” The Annals of Statistics, vol. 30, no. 1, pp. 1–50, 2002. [Google Scholar]

45. A. Krizhevsky and G. Hinton, “Learning multiple layers of features from tiny images,” 2009. [Google Scholar]

46. S. Zagoruyko and N. Komodakis, “Wide residual networks,” arXiv preprint arXiv:1605.07146, 2016. [Google Scholar]

47. L. Rice, E. Wong and Z. Kolter, “Overfitting in adversarially robust deep learning,” in Int. Conf. on Machine Learning, Virtual Event, vol. 119, pp. 8093–8104, 2020. [Google Scholar]

48. T. Y. Pang, X. Yang, Y. P. Dong, H. Su and J. Zhu, “Bag of tricks for adversarial training,” arXiv preprint arXiv:2010.00467, 2020. [Google Scholar]