Fusing Supervised and Unsupervised Measures for Attribute Reduction

1  Introduction

In the era of big data, a large number of irrelevant and redundant attributes are usually generated in practical applications, which will bring a series of problems in data processing, such as over-fitting, high computing cost and insufficient classification performance. Attribute reduction [1–4] is one of the effective methods to deal with this problem in rough set theory [5]. As a process of deleting irrelevant attributes and preserving key attributes, attribute reduction can reduce computational complexity and time by eliminating the influence of irrelevant attributes and noise. The result of attribute reduction is called reduct. Reduct is a new data which is composed of key attributes. In certain criterion of evaluation, such reduct can achieve or go beyond the performance of raw data [6]. As a dimension reduction method, the attribute reduction based on rough set theory consists of three stages, which are data representation under rough set, construction of attribute evaluation constraints and selection of search strategy. In the first stage, raw data can be described as a triple set, they are samples, conditional attributes and decision attributes. In second stage, the constraint can be constructed by using some related measures of rough set in certain learning perspective. There are many related measures in rough set theory, such as approximation quality [7], conditional entropy [8], and decision error rate [9]. And the learning perspective can be usually divided into two parts, supervised learning and unsupervised learning. Different measures correspond to different constraints [10]. In the third stage, using suitable search strategy can obtain the reduct effectively. Serving as a criterion of evaluation, constraint controls the condition of terminating search. Naturally, it may be concluded that different constraints imply different reducts, and then different learning performances.

With a literature review, it is noticed that most studies about constraint based on either supervised perspective or unsupervised perspective have been extensively explored [11]. In other words, the measure based on only one perspective is used to form a constraint of attribute reduction, and then the qualified reduct can be sought out through such a constraint. For example, Jiang et al. [12] and Yuan et al. [13] have investigated attribute reductions with respect to supervised information granulation and the relative supervised measures, respectively; Yang et al. [14] have introduced a measure, called fuzzy complementary entropy, into the attribute reduction based on the unsupervised framework. Nevertheless, either supervised measure or unsupervised measure is considered, the measure based on single perspective may have some limitations as follows.

(1)   The measure based on single perspective neglects the diverse evaluations [15,16]. That is, it may not identify more confident attributes. The potential reason is that if a measure is fixed to perform attribute reduction, then within the iterations in searching reduct, only such a measure can assess the importance of candidate attributes, so it follows that immediate results of the evaluation may be invalidated if some other measures are further required.

(2)   The measure based on single perspective ignores the complex constraint [17]. It may not effectively terminate the process of attribute selection. For example, supposed that conditional entropy serves as a measure to evaluate attributes [18,19], a derived reduct is only equipped with the single characteristic required by such an evaluation, no other types of uncertainty characteristics and learning abilities have been fully considered.

To overcome the limitations mentioned above, a new measure is proposed, which is a fusion of measures defined in both supervised and unsupervised perspectives. Fig. 1 shows the flowchart of attribute reduction, the dotted box presents our main work. Approximation quality and conditional entropy are classical measures and have been widely accepted in the field of rough set. The former can be used to build a bridge between attributes and labels [20], while the latter can quantitatively characterize the uncertainty of the data itself [21]. In our study, approximation quality from a supervised perspective and conditional entropy from an unsupervised perspective are employed to fuse into a new measure. Through abundant comparative experiments, the superiorities of new measure can be summarized as: (1) it is equipped with the distinguishing characteristic of multiple perspectives [22–24]; (2) it has more complex constraints than measure based on single perspective [25] and then more appropriate attributes are selected [26]; (3) it can not only quantitatively describe the relationship between attributes and label [27], but also quantitatively describe the internal structure of data itself [28,29].

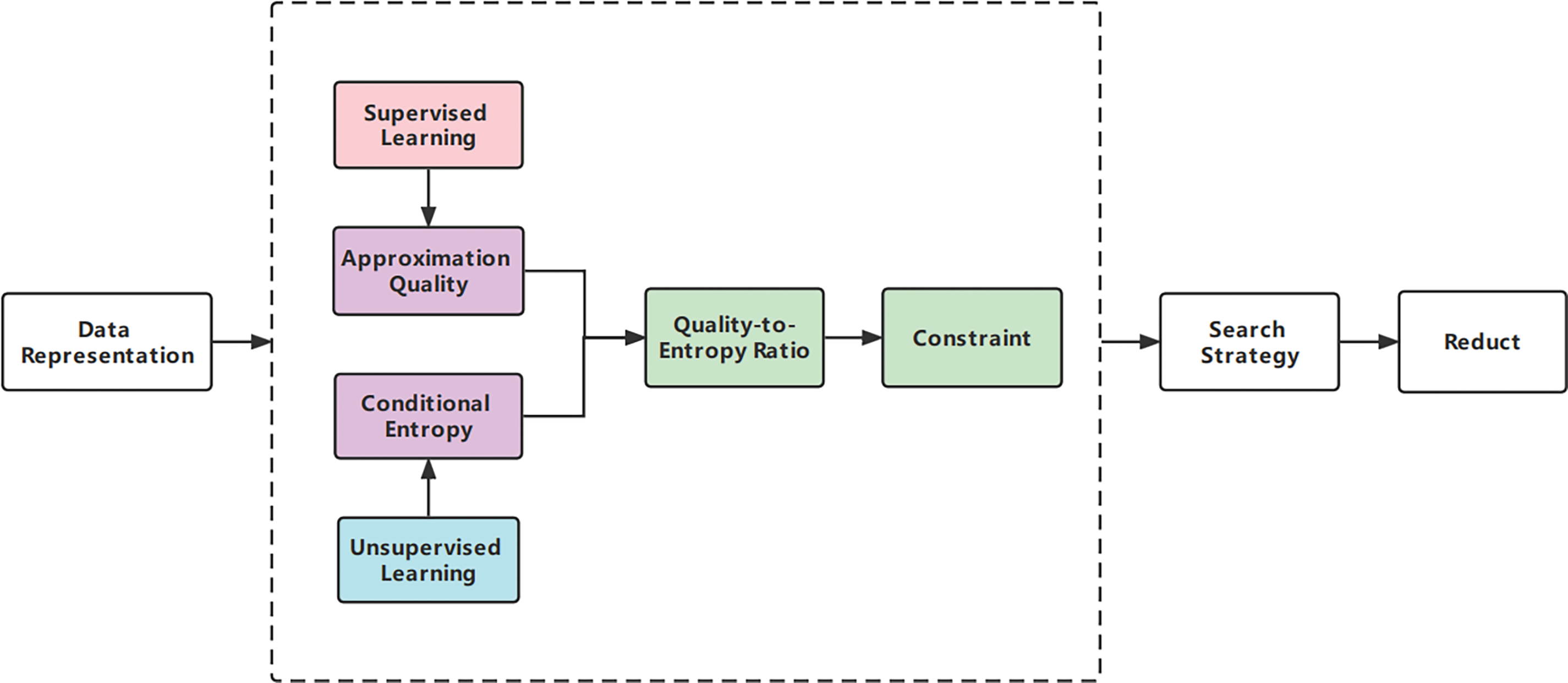
Figure 1: Fusing supervised and unsupervised measures for attribute reduction

The rest of this paper is organized as follows: Section 2 introduces the basic notions about the rough set, related measures, and attribute reduction. The proposed novel measure and searching process of solving reduct are elaborated in Section 3. Section 4 describes the comparative experimental results over 20 datasets and the corresponding analyses. The conclusions and future work are presented in Section 5.

2  Preliminary Knowledge

2.1 Neighborhood Rough Set

The neighborhood rough set was first proposed by Hu et al. [9,30], as an improvement of the conventional rough set. The most significant difference is that the neighborhood rough set is constructed by a neighborhood relation instead of an indiscernibility relation. Therefore, the superiorities of the neighborhood rough set are: (1) it can process data with complicated types; (2) it is equipped with the natural structure of multi-granularity if various radii are used.

Generally, a data can be represented by a triple DS=<U,AT,d>, where U is a set of finite samples, AT is a set of condition attributes, and d is a decision [30–32]. d records the labels of samples, ∀x∈U and ∀a∈AT, a(x) denotes the value of x over condition attribute a, and d(x) indicates the label of x. According to d, an equivalence relation over U can be obtained as Eq. (1).

IND(d)={(x,y)∈U×U:  d(x)=d(y)}(1)

Following IND(d), a partition U/IND(d)={X1,X2,…,Xq}(q≥2) over U can be induced. ∀Xk∈U/IND(d), Xk is regarded as the k-th decision class. Particularly, the decision class which contains sample x can also be expressed by [x]d.

Furthermore, suppose that A⊆AT, given a radius δ≥0, a neighborhood relation over U can be derived as:

NAδ={(x,y)∈U×U:  disA(x,y)≤δ}(2)

where disA is a distance function between samples x and y with respect to A.

In this study, Euclidean distance is applied, i.e., disA(x,y)=∑a∈A(a(x)−a(y))2. By NAδ, the neighborhood of sample x is then formed such that δA(x)={y∈U:  disA(x,y)≤δ}.

From the viewpoint of Granular Computing (GrC) [10,33,34], both the deriving of IND(d) and NAδ are information granulations. The most significant difference between such two information granulations is the inherent mechanism, i.e., the used binary relation. Following these results of information granulations, the definition of neighborhood lower and upper approximations, which are basic units of neighborhood rough set, have also been proposed by Cheng et al. [30].

Definition 1. Given a data DS=⟨U,AT,d⟩ and δ, ∀A⊆AT and ∀Xk∈U/IND(d), the neighborhood lower and upper approximations of Xk with respect to A are respectively defined as:

δA_(Xk)={x∈U:  δA(x)⊆Xk}(3)

δA¯(Xk)={x∈U:  δA(x)∩Xk≠∅}(4)

By the above definition, a neighborhood of Xk is obtained, i.e., a pair such that [δA_(Xk),δA¯(Xk)]. In addition, When the lower approximation is not equal to upper approximation, then the pair is called neighborhood rough set.

2.2 Supervised Attribute Reduction

As is well-known, a neighborhood rough set is frequently employed to execute the supervised learning tasks. Furthermore, in many supervised learning tasks, feature selection plays an important role in improving the generalization performance, decreasing the complexity of classifier, and so on. The superiority of attribute reduction is that it can be easily expanded with respect to different requirements in real-world applications. Therefore, various forms of attribute reduction have emerged in recent years. As far as the neighborhood rough set is concerned, the following two measures, approximation quality [30] and conditional entropy [8,19] can be used to further explore the forms of attribute reduction.

Definition 2. Given a data DS=⟨U,AT,d⟩ and δ, ∀A⊆AT, the approximation quality of d based on A is:

rA(d)=|⋃k=1qδA_(xk)||U|(5)

where |⋄| denotes the cardinality of the set ⋄.

Obviously, γA(d)∈[0,1] holds. Approximation quality reflects the percentage of the samples which belong to each decision class in lower approximation. Naturally, the higher the value of the approximation quality, the higher the degree of such belongingness.

Definition 3. Given a data DS=⟨U,AT,d⟩ and δ, ∀A⊆AT, the conditional entropy of d based on A is:

CEA(d)=−1|U|∑x∈U|δA(x)∩[x]d|log|δA(x)∩[x]d||δA(x)|(6)

It is proved that CEA(d)∈[0,|U|e] holds [8]. Conditional entropy reflects the discriminative ability of A relative to d. As the value of the conditional entropy descends, the discriminating ability of A relative to d becomes more and more powerful.

Definition 4. Given a data DS=⟨U,AT,d⟩ and a measure φ, Cφ is a constraint related to measure φ, ∀A⊆AT, A is regarded as a φ-reduct if and only if

(1)   φA(d) meets the constraint Cφ;

(2)   ∀A′⊂A, φA′(d) does not meet the constraint Cφ.

Without loss of generality, the constraint shown in Def. 4 is closely related to the used measure φ. Suppose that the measure φ is approximation quality shown in Def. 2, then the constraint Cγ is γA(d)≥γAT(d); if the form of measure φ is conditional entropy shown in Def. 3, then the constraint CCE is CEA(d)≤CEAT(d).

2.3 Unsupervised Attribute Reduction

It is well known that supervised attribute reduction relies heavily on the labels of samples, so it is time-consuming and costly to obtain labels of samples from many real-world tasks. However, unsupervised attribute reduction does not need to obtain such labels, this is why unsupervised attribute reduction has recently been paid much more attention to [14].

For unsupervised attribute reduction, if approximation quality or conditional entropy is still required to serve as a measure, the immediate problem is how to make labels for samples. As it has been pointed out by Qian et al. [35], a pseudo-label strategy can be introduced into the construction of a rough set model. The pseudo labels of samples are generated by using the information over condition attributes. Therefore, it is not difficult to present the following definitions of approximation quality and conditional entropy.

Definition 5. Given an unsupervised data IS=⟨U,AT⟩ and δ, ∀A⊆AT, the unsupervised approximation quality based on A is:

γA=1|A|∑a∈A(γA−{a}(da))(7)

where da is a pseudo-label decision which records the pseudo labels of samples by using condition attribute a.

A partition can also be obtained such that U/IND(da)={X1a,X2a,…,Xqa}. ∀Xka∈U/IND(da), Xka is the k-th decision class based on the pseudo-label decision da.

Similar to the approximation quality shown in Def. 2, γA∈[0,1] also holds. Nevertheless, different from Def. 2, the unsupervised approximation quality implies the correlation between a group of attributes and a single attribute. Although the unsupervised approximation quality is not strictly monotonic, it also possesses the property similar to that of Def. 2, i.e., the higher the value of unsupervised approximation quality, the higher the degree of such a correlation.

Definition 6. Given an unsupervised data IS=⟨U,AT⟩ and δ, ∀A⊆AT, the unsupervised conditional entropy based on A is:

CEA=1|A|∑a∈A(CEA−{a}(da))(8)

where da is a derived decision that records the pseudo labels of samples by using condition attribute a.

According to the definition of conditional entropy shown in Def. 3, CEA∈[0,|U|e] also holds. Note that the unsupervised conditional entropy also indicates the correlation between a set of attributes and a single attribute. Naturally, it possesses a property similar to that of Def. 3, i.e., the lower the value of unsupervised conditional entropy, the higher the degree of such a correlation.

Definition 7. Given an unsupervised data IS=⟨U,AT⟩ and a measure φ,Cφ is a constraint related to measure φ, ∀A⊆AT, A is regarded as a φ-reduct if and only if

(1)   φA meets the constraint Cφ;

(2)   ∀A′⊂AT, φA′ does not meet the constraint Cφ.

Without loss of generality, the constraint shown in Def. 7 is closely related to the used measure φ. Suppose that we serve unsupervised approximation quality as the form of measure φ, then the constraint Cγ is γA≥γAT ; if we serve unsupervised conditional entropy as the form of measure φ, then the constraint CCE is CEA≤CEAT.

3  Proposed Approach

Following Defs. 4 and 7, it is found that attribute reduction is closely related to the used measure. In other words, if different measures are employed then different results of reduct can be generated. From this viewpoint it can be concluded that the used measure is the key to deriving an expected reduct. Nevertheless, most previous measures based on single perspective may fall into the following limitations.

(1)   The measure based on single perspective ignores the diverse evaluations [15,16]. The less diverse evaluations, the identified attributes will be less confident. This is mainly because if a measure is fixed to perform attribute reduction, then in the iterations of seeking out reduct, only such a measure is applied to assess the importance of candidate attributes. It follows that such a result of evaluation may be invalidated [36] or ineffective for some other measures.

(2)   The measure based on single perspective ignores the complex constraint which is helpful in terminating the procedure of selecting attributes. For instance, given a form of attribute reduction that preserves the value of approximation quality in data, i.e., in Def. 4, the measure φ is γAT(d), such a derived reduct is only equipped with a single characteristic. Immediately, some other measures, such as conditional entropy and unsupervised related measures are not fully taken into account.

From the discussions above, a new measure is proposed to further solve such problems. Since both supervised and unsupervised cases have been presented in the above section, they will be introduced into our new proposed measure.

3.1 Quality-to-Entropy Ratio

Approximation quality and conditional entropy can be used to evaluate the importance of attributes. In Defs. 2 and 6, the relationships between such measures and the importance of attributes are revealed. And these two relationships are at opposite poles. To further unify the relationships, the format of ratio is employed to coordinate two relationships. Moreover, in order to enhance the relationship between conditional entropy and the importance of attributes, an exponential function is added to conditional entropy.

Definition 8. Given a data DS=⟨U,AT,d⟩ and δ, ∀A⊆AT, the quality-to-entropy ratio is:

κA(d)=γA(d)exp⁡(CEA)(9)

where γA(d) is the approximation quality of d based on A shown in Def. 2, CEA is the unsupervised conditional entropy based on A shown in Def. 6.

From the perspective of attribute reduction, conditional entropy is used to build a bridge between condition attributes and decisions [37]. It frequently reveals a learning relationship between samples and labels in data. In this study, unsupervised data can be labeled through a pseudo-label strategy, and then conditional entropy helps uncover the learning relationships among condition attributes. That is why we use unsupervised conditional entropy instead of unsupervised approximation quality in Eq. (9).

Furthermore, by the form of κA(d), it is observed that a higher value of approximation quality γA(d) and a lower value of unsupervised conditional entropy CEA, then a higher value of the quality-to-entropy ratio. It is also consistent with the previous objectives of attribute reductions related to measures γA(d) and CEA. That is, if approximation quality is employed, then a higher value of approximation quality is expected through adding qualified attributes or removing poor attributes; if conditional entropy is employed, then a lower value of approximation quality is expected through adding qualified attributes or removing low-quality attributes.

Theorem 1. Given a data DS=⟨U,AT,d⟩ and δ, ∀A⊆AT, κA(d)∈[0,1].

Proof. By the property of approximation quality, γA(d)∈[0,1] holds. By the property of conditional entropy, CEA∈[0,|U|e] holds. Immediately, exp⁡(CEA)∈[1,e|U|e] holds by the form of Eq. (9). In other words, κA(d) will get the minimal value 0 if γA(d)=0 and exp⁡(CEA)=e|U|e; κA(d) will get the maximal value 1 if γA(d)=1 and exp⁡(CEA)=1. □

Following Sections 2.1 and 2.2, it is known that the higher the value of the approximation quality, the more influential the discriminating performance of the condition attributes relative to decision d; the lower the value of the unsupervised conditional entropy, the stronger the discriminative power of the condition attributes relative to the pseudo labels. Since CEA is not strictly monotonically decreasing, we can conclude that exp⁡(CEA) is also not strictly monotonically decreasing. To sum up, the higher the value of the quality-to-entropy ratio, the stronger the discriminative power [38,39] of the condition attributes relative to decisions. Furthermore, it should be pointed out that our new measure does not possess the property of strict monotony. An illustrative example is elaborated below.

Example 1. For example, see Table 1. In Table 1, U={x1,x2,x3,x4} is the universe. Suppose that AT={a1,a2,a3,a4} is the set of condition attributes; d is the decision; da1,da2,da3 and da4represent the pseudo labels of samples based on four different condition attributes, respectively. They are obtained through using a learning approach. Additionally, the radius is given by 0.2.

Firstly, the corresponding partitions over U are:

U/IND(d)={X1,X2}={{x1,x2,x4},{x3}},

U/IND(da1)={X1a1,X2a1}={{x1,x4},{x2,x3}},

U/IND(da2)={X1a2,X2a2}={{x1,x2},{x3,x4}},

U/IND(da3)={X1a3,X2a3}={{x1,x2,x3},{x4}},

U/IND(da4)={X1a4,X2a4}={{x1,x3,x4},{x2}}.

By Eq. (9), κAT(d) is then calculated by the following results:

γAT(d)=|δAT_(X1)∪δAT_(X2)||U|=1,

CEAT=1|AT|(CEAT−{a1}(da1)+CEAT−{a2}(da2)+CEAT−{a3}(da3)+CEAT−{a4}(da4))=14(1+1+1+1)=1.

Therefore, κAT(d)=γAT(d)exp⁡(CEAT)=0.3679.

Presume that the condition attributes a1 is removed from data and then A={a2,a3,a4}. By Eq. (9), κA(d) is calculated by

γA(d)=|δA_(X1)∪δA_(X2)||U|=1,

CEA=1|A|(CEA−{a2}(da2)+CEA−{a3}(da3)+CEA−{a4}(da4))=13(1+0.5+0.5)=0.6667.

Therefore, κA(d)=γA(d)exp⁡(CEA)=1e0.6667=0.5134.

Though A⊆AT holds, κAT(d)<κA(d), such a case demonstrates that the new measure κ is not strictly monotonic with respect to the number of used condition attributes.

The quality-to-entropy ratio proposed above presents a form of attribute reduction as follows.

Definition 9. Given a data DS=⟨U,AT,d⟩ and ∀A⊆AT, A is regarded as a κ-reduct if and only if

κA(d)κAT(d)≥θ(10)

∀A′⊂A,     κA′(d)κAT(d)<θ(11)

where θ∈[0,1] is a threshold.

Following Def. 9, it is observed that as a minimal subset of attributes, κ-reduct improves the quality-to-entropy ratio. Immediately, an open problem is how to seek out such a reduct. Without loss of generality, it is frequently required to evaluate the significance or importance of attributes in AT [40,41]. The qualified attributes can be selected into the reduct pool, or low-quality attributes can be removed from the reduct pool. Based on the widely used greedy searching mechanism [42–44], the following definition presents a significant attribute in considering our proposed quality-to-entropy ratio.

Definition 10. Given a data DS=⟨U,AT,d⟩, ∀A⊆AT, ∀a∈AT−A, the significance with respect to quality-to-entropy ratio is defined as:

Sigκa(d)=κA⋃{a}(d)−κA(d)(12)

The above significance function shows: as the value rises, the condition attribute becomes more and more significant, and such an attribute is highly possible to be added to the reduct pool. For instance, if Sigκa1(d)<Sigκa2(d) where a1,a2∈AT−A, then κA⋃{a1}(d)<κA⋃{a2}(d). Such a result illustrates that: compared to a1, if a2 is selected into A, then the derived quality-to-entropy ratio will be higher.

The above interpretation is consistent with the semantic explanation of attribute reduction shown in Def. 9, i.e., a higher value of the quality-to-entropy ratio is expected.

3.2 Algorithm Description

Based on the significant function shown in Eq. (12), Algorithm 1 is designed to seek out a κ-reduct.

To simplify the discussion of the time complexity of Algorithm 1. Firstly, k-means clustering is employed to obtain the pseudo labels of samples. T is the iteration times of k-means, and k is the number of clusters, then the time complexity of producing pseudo labels is 𝒪(k⋅T⋅|U|⋅|AT|). Secondly, κA⋃{a}(d) is calculated at most (1+|AT|)⋅|AT|/2 times. Finally, the time complexity of Algorithm 1 is 𝒪(|U|2⋅|AT|3+k⋅T⋅|U|⋅|AT|).

4  Experimental Analysis

4.1 Data

To demonstrate the performance of our proposed strategy, 18 UCI datasets and 2 Yale face datasets have been employed in this study. Table 2 summarizes the detailed statistics of these data.

4.2 Configuration

All the experiments are carried out on a desktop computer with the Windows 10 operating system, Advanced Micro Devices (AMD) Ryzen 5 5500U with Radeon Graphics (2.10 GHz) and 32.00 GB memory. The programming environment is Matlab R2020a.

In this section, two groups of comparative experiments are designed and executed. For all the experiments, 20 different radii δ have been used, they are δ=0.02,0.04,…,0.40, increasing with the step of 0.02. Furthermore, k-means clustering [44] is adopted in the following experiments to generate the pseudo labels of samples, where the value of k is the same as the number of decision classes in the data.

Moreover, 10-fold cross-validation is used in the experiments, dividing the samples in U into ten groups [45–47]. They are U1,U2,…,and  U10. In the first round of calculation, the set U2∪⋯∪U10 is regarded as the training set for calculating reduct, andU1 is the set of testing samples; ⋯ ; in the last round of calculation, the set U1∪⋯∪U9 is regarded as the training set for calculating reduct, and U10 is the set of testing samples. Three classifiers are also employed to test the performances of derived reducts, they are Support Vector Machine (SVM) [48], Classification and Regression Tree (CART) [49] and K-Nearest Neighbor (KNN) [50].

4.3 Experiment (Group 1)

In the first group of the experiment, we will compare our proposed approach with previously supervised attribute reduction and unsupervised attribute reduction strategies. The supervised attribute reduction is based on the approximation quality [30], which is called Supervised Approximation Quality Reduct (SAQR). The unsupervised attribute reduction is based on the conditional entropy, which is called Unsupervised Conditional Entropy Reduct (UCER).

Since 20 different radii have been used to obtain reducts in our experiments, the mean values related to those 20 different reducts are presented in the following subsection.

4.3.1 Comparisons among Classification Stabilities

The classification stabilities [15] derived by different kinds of reducts are compared. Classification stability is used to test the stability of classification results if data perturbation (simulated by cross-validation) happens. Such a computation is based on the distribution of the classification results. The higher the value of classification stability, the better the ability to the data perturbation.

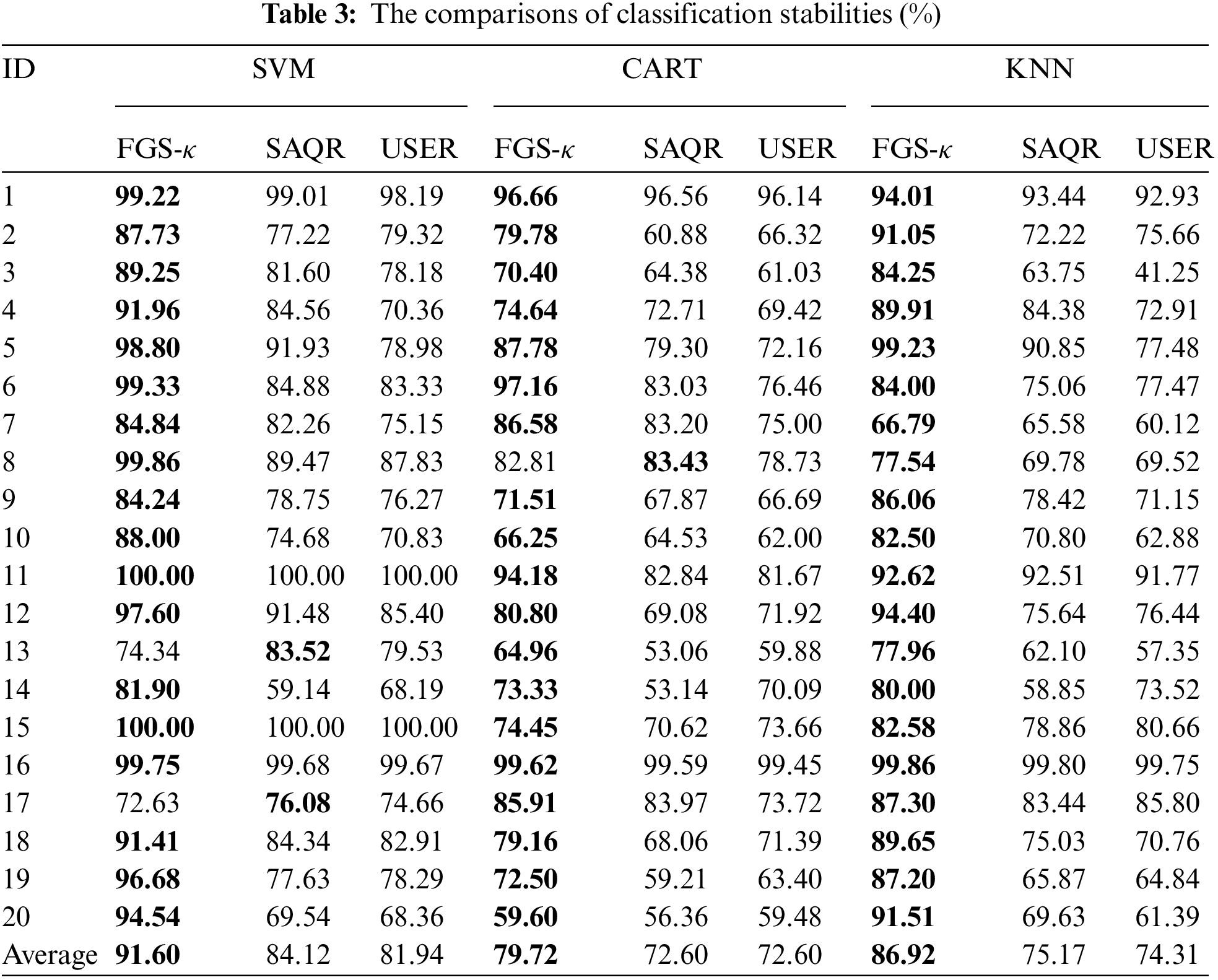
The following Table 3 reports the mean values of classification stabilities obtained over 20 datasets. A closer look at Table 3 reveals the following facts.

(1)   Whichever classifier is adopted, the classification stabilities related to κ-reducts are greater than those related to reducts derived by SAQR and UCER in most datasets. Take data “Drive-Face (ID:3)” as an example. Through the use of SVM, the classification stability of FGS-κ, SAQR and UCER are 89.25%, 81.60% and 78.18%, respectively. Through the use of CART, the classification stability of FGS-κ, SAQR and UCER are 70.40%, 64.38% and 61.03%, respectively. Through the use of KNN, the classification stability of FGS-κ, SAQR and UCER are 84.25%, 63.75% and 41.25%, respectively. From this point of view, it is concluded that by comparing with the single measure used in SAQR and UCER, the quality-to-entropy-based multiple measures in FGS-κ helps select attributes with superior data adaptability, i.e., the slight data perturbation in training data will not lead to more significant variation of the classification results.

(2)   From the perspective of the average values, the classification stability of FGS-κ is more remarkable than those related to both SAQR and USER. Through the use of SVM, the classification stability of FGS-κ is over 8.24% higher than others. Through the use of CART, the classification stability of FGS-κ is over 8.93% higher than others. Through the use of KNN, the classification stability of FGS-κ is over 13.50% higher than others.

From the discussions above, our new approach can select more critical attributes than other attribute reduction strategies, and these selected attributes are able to replace raw attributes to complete subsequent tasks.

4.3.2 Comparisons among Classification Accuracies

The classification accuracies corresponding to different results of reduct are compared. Table 4 reports the average values of classification accuracy obtained over 20 datasets.

A closer look at Table 4 reveals the following facts.

(1)   Whichever classifier is employed, the accuracies corresponding to κ-reducts are greater than those corresponding to both SQAR and USER. Take the dataset “Optical Recognition of Handwritten Digits (ID:10)” as an example. Through the use of SVM, the classification accuracy of κ-reduct, SAQR and UCER are 88.00%, 66.25% and 58.75%, respectively. Through the use of CART, the classification accuracy of κ-reduct, SAQR and UCER are 56.25%, 45.00% and 36.25%, respectively. Through the use of KNN, the classification accuracy of κ-reduct, SAQR and UCER are 78.75%, 58.75% and 63.75%, respectively. Because of this, it can be found that the attributes selected by our FGS-κ can also provide better learning performance.

(2)   Interestingly, compared to others, the κ-reducts derived from FGS-κ perform significantly better over high-dimensional datasets. Take the data “Yale face (64 × 64) (ID:20)” as an example, which possesses 4096 attributes. The classification accuracy of κ-reduct is 29.04% higher than the reduct derived from SAQR, and 36.58% higher than the reduct derived from USER. For “Connectionist Bench (Sonar, Mines vs. Rocks) (ID:1)”, which possesses 60 attributes. The classification accuracy of κ-reduct is 1.71% higher than the reduct derived from SAQR, and 0.38% higher than the reduct derived from USER.

(3)   From the perspective of the average values, the classification accuracies related to FGS-κ are also more significant than those of both SAQR and USER. Through the use of SVM, the classification accuracy of FGS-κ is over 13.74% higher than others. Through the use of CART, the classification accuracy of FGS-κ is over 8.33% higher than others. Through the use of KNN, the classification accuracy of FGS-κ is over 10.38% higher than others. Such an observation indicates that our proposed algorithm applies to several different classifiers.

4.4 Experiment (Group 2)

In this experiment, with respect to two measures addressed in this study, our proposed approach is compared with five other popular approaches, they are:

(1)   The novel rough set algorithm for fast adaptive attribute reduction in classification (FAAR) [51];

(2)   The multi-criterion neighborhood attribute reduction (MNAR) [17];

(3)   The robust attribute reduction based on rough sets (RARR) [52];

(4)   The attribute reduction algorithm based on fuzzy self-information (FSIR) [53];

(5)   The attribute reduction based on neighborhood self-information (NSIR) [54].

4.4.1 Comparisons among Classification Stabilities

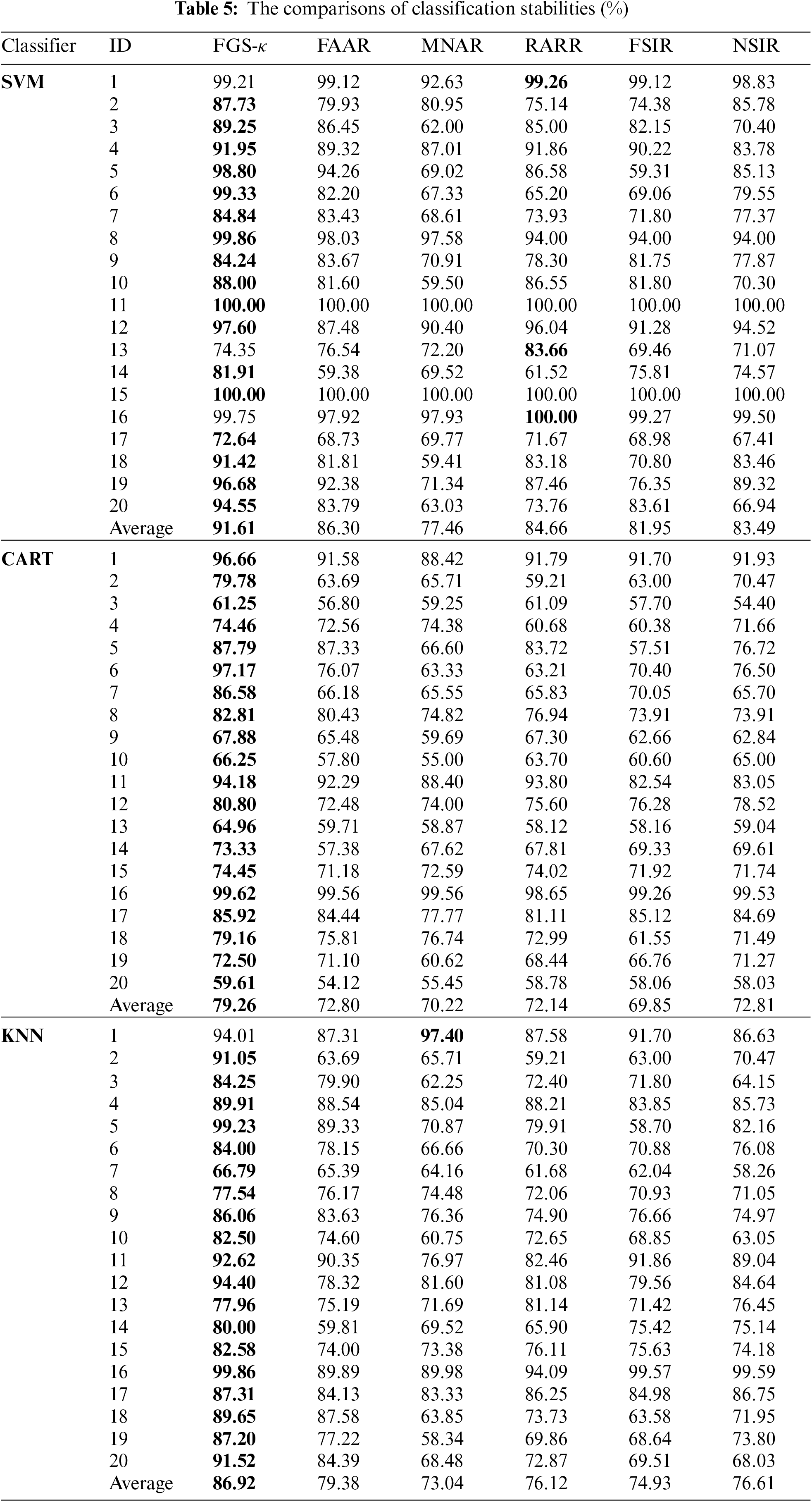
In this part, the classification stabilities derived from different kinds of reducts are compared. Table 5 shows the mean values of different classification stabilities obtained over 20 datasets. A closer look at Table 5 reveals the following facts.

(1)   Whichever classifier is chosen, the classification stabilities based on κ-reducts are more significant than others over most datasets. Take the dataset “Wisconsin Diagnostic Breast Cancer (ID:18)” as an example. Through the use of SVM, the classification stability of FGS-κ, FAAR, MNAR, RARR, FSIR and NSIR are 91.42%, 81.81%, 59.41%, 83.18%, 70.80% and 83.46%, respectively. Through the use of CART, the classification stability of FGS-κ, FAAR, MNAR, RARR, FSIR and NSIR are 79.16%, 75.81%, 76.74%, 72.99%, 61.55% and 71.49%, respectively. Through the use of KNN, the classification stability of FGS-κ, FAAR, MNAR, RARR, FSIR and NSIR are 89.65%, 87.58%, 63.85%, 73.73%, 63.58% and 71.95%, respectively.

(2)   From the perspective of the average values, the classification stability of FGS-κ is also greater than those related to FAAR, MNAR, RARR, FSIR and NSIR, respectively. Through the use of SVM, the classification stability of FGS-κ is over 5.87% higher than others. Through the use of CART, the classification stability of FGS-κ is over 8.21% higher than others. Through the use of KNN, the classification stability of FGS-κ is over 8.73% higher than others.

From the discussions above, our new approach is superior to state-of-the-art attribute reduction strategies in offering stable classification results from the discussions above.

4.4.2 Comparisons among Classification Accuracies

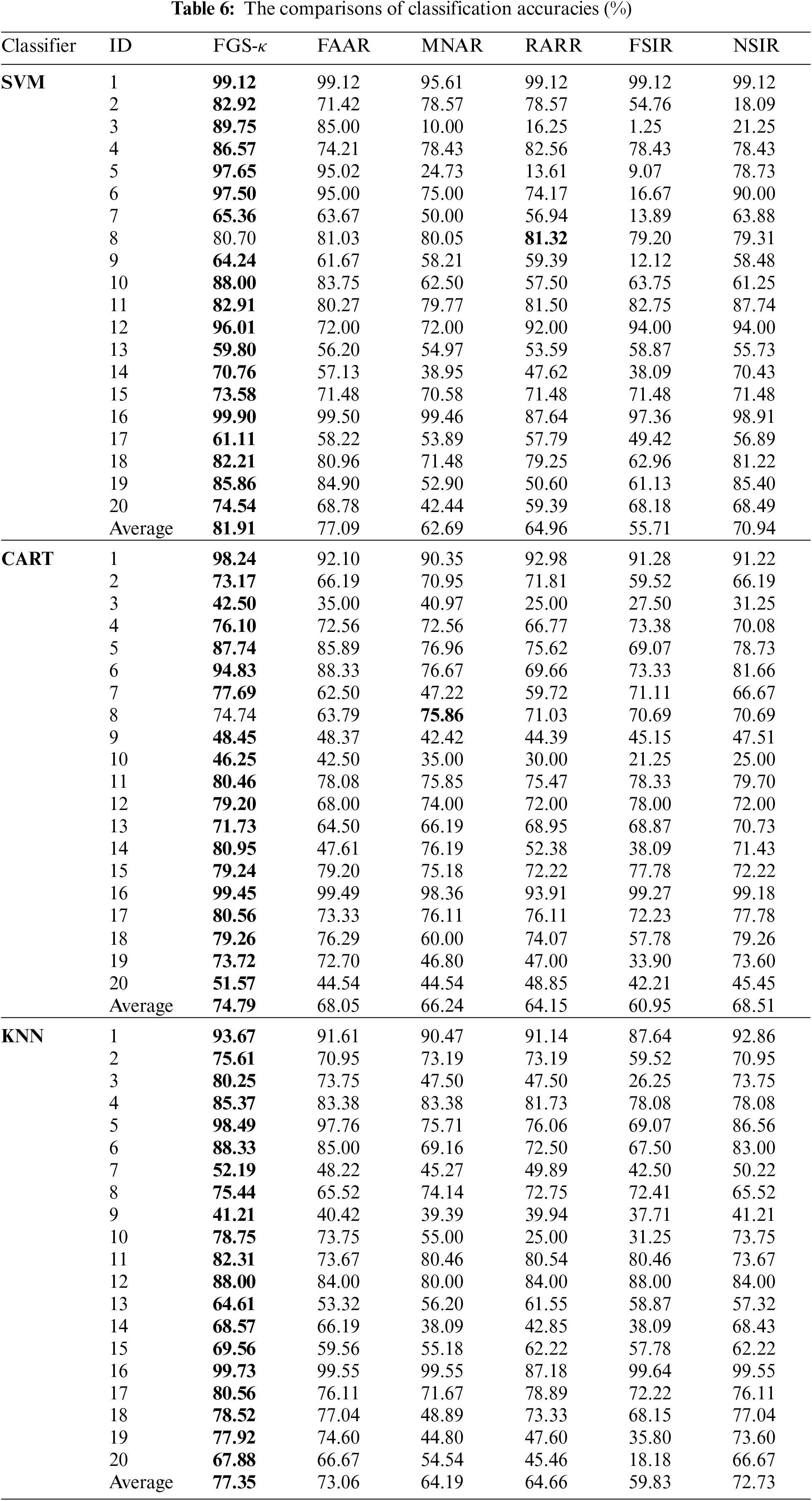
In this part, the classification accuracies based on different kinds of reducts are also compared. Different classification accuracies acquired by 20 datasets are shown in Table 6. A closer look at Table 6 reveals the following facts.

(1)   Whichever classifier is chosen, the classification accuracies based on κ-reducts are more significant than others over most datasets. Take the dataset “Ultrasonic Flowmeter Diagnostics-Meter D (ID:15)” as an example. By employing SVM, the classification accuracy of FGS-κ, FAAR, MNAR, RARR, FSIR and NSIR are 73.58%, 71.48%, 70.58%, 71.48%, 71.48% and 71.48%, respectively. By employing CART, the classification accuracy of FGS-κ, FAAR, MNAR, RARR, FSIR and NSIR are 79.24%, 79.20%, 75.18%, 72.22%, 77.78% and 72.22%, respectively. By employing KNN, the classification accuracy of FGS-κ, FAAR, MNAR, RARR, FSIR and NSIR are 69.56%, 59.56%, 55.18%, 62.22%, 57.78% and 62.22%, respectively.

(2)   From the perspective of the average values, the classification precision related to FGS-κ is also more significant than those of FAAR, MNAR, RARR, FSIR and NSIR. By employing SVM, the classification accuracy of FGS-κ is over 5.92% higher than others. By employing CART, the classification accuracy of FGS-κ is over 8.46% higher than others. By employing KNN, the classification accuracy of FGS-κ is over 5.61% higher than others.

From the discussions above, our new approach is superior to popular attribute reduction strategies in providing more precise classification results.

5  Conclusions and Future Work

In such a study, with a review of limitations derived from measures based on single perspective, a novel measure, called quality-to-entropy, is proposed. The superiorities of our research are: in the process of searching reduct, not only can the relationship between condition attributes and labels be characterized from the supervised perspective, but also the internal structure of data can be quantitatively described. More importantly, our new measure can be further introduced into other search strategies. Through extensive experiments, it has been demonstrated that the proposed measure helps select attributes with significantly superior classification performance.

Further investigations will be focused on the following aspects:

(1)   Our strategy is developed based on the neighborhood rough set. It can also be further introduced into other rough sets, e.g., fuzzy rough set [36,53,55] and decision-theoretic rough set [41].

(2)   Fused measures may increase time consumption for seeking out a reduct, accelerators [3,42] to reduce the corresponding elapsed time are then necessary.

Funding Statement: This work was supported by the National Natural Science Foundation of China (Grant Nos. 62006099, 62076111), the Key Research and Development Program of Zhenjiang-Social Development (Grant No. SH2018005), the Natural Science Foundation of Jiangsu Higher Education (Grant No. 17KJB520007), Industry-school Cooperative Education Program of the Ministry of Education (Grant No. 202101363034).

Conflicts of Interest: The authors declare that they have no conflicts of interest in reporting regarding the present study.

References

1. Z. H. Jiang, X. B. Yang, H. L. Yu, D. Liu, P. X. Wang et al., “Accelerator for multi-granularity attribute reduction,” Knowledge-Based Systems, vol. 177, pp. 145–158, 2019. [Google Scholar]

2. Y. Chen, X. B. Yang, J. H. Li, P. X. Wang and Y. H. Qian, “Fusing attribute reduction accelerators,” Information Sciences, vol. 587, pp. 354–370, 2022. [Google Scholar]

3. P. X. Wang and X. B. Yang, “Three-way clustering method based on stability theory,” IEEE Access, vol. 9, pp. 33944–33953, 2021. [Google Scholar]

4. Q. Chen, T. H. Xu and J. J. Chen, “Attribute reduction based on lift and random sampling,” Symmetry- Basel, vol. 14, no. 9, pp. 1828, 2022. [Google Scholar]

5. Z. Pawlak, “Rough sets,” International Journal of Computer and Information Sciences, vol. 11, no. 5, pp. 341–356, 1982. [Google Scholar]

6. X. B. Yang, Y. Qi, D. J. Yu, H. L. Yu and J. Y. Yang, “α-Dominance relation and rough sets in interval-valued information systems,” Information Sciences, vol. 294, pp. 334–347, 2015. [Google Scholar]

7. K. Y. Liu, X. B. Yang, H. L. Yu, H. Fujita, X. J. Chen et al., “Supervised information granulation strategy for attribute reduction,” International Journal of Machine Learning and Cybernetics, vol. 11, no. 9, pp. 2149–2163, 2020. [Google Scholar]

8. X. Zhang, C. L. Mei, D. G. Chen and J. H. Li, “Feature selection in mixed data: A method using a novel fuzzy rough set-based information entropy,” Pattern Recognition, vol. 56, pp. 1–15, 2016. [Google Scholar]

9. Q. H. Hu, W. Pedrycz, D. R. Yu and J. Lang, “Selecting discrete and continuous features based on neighborhood decision error minimization,” IEEE Transactions on Systems, Man, and Cybernetics, Part B(Cybernetics), vol. 40, no. 1, pp. 137–150, 2010. [Google Scholar]

10. Y. Chen, K. Y. Liu, J. J. Song, H. Fujita, X. B. Yang et al., “Attribute group for attribute reduction,” Information Sciences, vol. 535, no. 5, pp. 64–80, 2020. [Google Scholar]

11. K. Y. Liu, X. B. Yang, H. Fujita, D. Liu, X. Yang et al., “An efficient selector for multi-granularity attribute reduction,” Information Sciences, vol. 505, pp. 457–472, 2019. [Google Scholar]

12. Z. H. Jiang, K. Y. Liu, X. B. Yang, H. L. Yu, H. Fujita et al., “Accelerator for supervised neighborhood based attribute reduction,” International Journal of Approximate Reasoning, vol. 119, pp. 122–150, 2020. [Google Scholar]

13. Z. Yuan, H. M. Chen, T. R. Li, Z. Yu, B. B. Sang et al., “Unsupervised attribute reduction for mixed data based on fuzzy rough sets,” Information Sciences, vol. 572, no. 1, pp. 67–87, 2021. [Google Scholar]

14. X. B. Yang and Y. Y. Yao, “Ensemble selector for attribute reduction,” Applied Soft Computing, vol. 70, pp. 1–11, 2018. [Google Scholar]

15. Y. N. Chen, P. X. Wang, X. B. Yang and H. L. Yu, “BEE: Towards a robust attribute reduction,” International Journal of Machine Learning and Cybernetics, vol. 13, no. 12, pp. 3927–3962, 2022. [Google Scholar]

16. J. Z. Li, X. B. Yang, X. N. Song, J. H. Li, P. X. Wang et al., “Neighborhood attribute reduction: A multi-criterion approach,” International Journal of Machine Learning and Cybernetics, vol. 10, no. 4, pp. 731–742, 2019. [Google Scholar]

17. J. H. Dai, W. T. Wang, H. W. Tian and L. Liu, “Attribute selection based on a new conditional entropy for incomplete decision systems,” Knowledge-Based Systems, vol. 39, no. 1, pp. 207–213, 2013. [Google Scholar]

18. J. H. Dai, Q. Xu, W. T. Wang and H. W. Tian, “Conditional entropy for incomplete decision systems and its application in data mining,” International Journal of General Systems, vol. 41, no. 74, pp. 713–728, 2012. [Google Scholar]

19. Y. H. Qian, J. Y. Liang, W. Pedrycz and C. Y. Dang, “Positive approximation: An accelerator for attribute reduction in rough set theory,” Artificial Intelligence, vol. 174, no. 9–10, pp. 597–618, 2010. [Google Scholar]

20. W. Y. Li, H. M. Chen, T. R. Li, J. H. Wan and B. B. Sang, “Unsupervised feature selection via self-paced learning and low-redundant regularization,” Knowledge-Based Systems, vol. 240, no. 11, pp. 108150, 2022. [Google Scholar]

21. X. B. Yang, Y. Qi, H. L. Yu, X. N. Song and J. Y. Yang, “Updating multi-granulation rough approximations with increasing of granular structures,” Knowledge-Based Systems, vol. 64, pp. 59–69, 2014. [Google Scholar]

22. S. P. Xu, X. B. Yang, H. L. Yu, D. J. Yu and J. Y. Yang, “Multi-label learning with label-specific feature reduction,” Knowledge-Based Systems, vol. 104, pp. 52–61, 2016. [Google Scholar]

23. K. Y. Liu, T. R. Li, X. B. Yang, H. R. Ju, X. Yang et al., “Hierarchical neighborhood entropy based multi-granularity attribute reduction with application to gene prioritization,” International Journal of Approximate Reasoning, vol. 148, no. 3, pp. 57–67, 2022. [Google Scholar]

24. J. Qian, D. Q. Miao, Z. H. Zhang and W. Li, “Hybrid approaches to attribute reduction based on indiscernibility and discernibility relation,” International Journal of Approximate Reasoning, vol. 52, no. 2, pp. 212–230, 2011. [Google Scholar]

25. K. Y. Liu, X. B. Yang, H. L. Yu, J. S. Mi, P. X. Wang et al., “Rough set based semi-supervised feature selection via ensemble selector,” Knowledge-Based Systems, vol. 165, pp. 282–296, 2019. [Google Scholar]

26. X. B. Yang, M. Zhang, H. L. Dou and J. Y. Yang, “Neighborhood systems-based rough sets in incomplete information system,” Knowledge-Based Systems, vol. 24, no. 6, pp. 858–867, 2011. [Google Scholar]

27. Y. H. Qian, H. H. Cheng, J. T. Wang, J. Y. Liang, W. Pedrycz et al., “Grouping granular structures in human granulation intelligence,” Information Sciences, vol. 382–383, no. 6, pp. 150–169, 2017. [Google Scholar]

28. X. B. Yang, Y. H. Qian and J. Y. Yang, “On characterizing hierarchies of granulation structures via distances,” Fundamenta Informaticae, vol. 123, no. 3, pp. 365–380, 2013. [Google Scholar]

29. Q. H. Hu, D. R. Yu and Z. X. Xie, “Neighborhood classifiers,” Expert Systems with Applications, vol. 34, no. 2, pp. 866–876, 2008. [Google Scholar]

30. K. Cheng, S. Gao, W. L. Dong, X. B. Yang, Q. Wang et al., “Boosting label weighted extreme learning machine for classifying multi-label imbalanced data,” Neurocomputing, vol. 403, no. 8, pp. 360–370, 2020. [Google Scholar]

31. S. P. Xu, H. R. Ju, L. Shang, W. Pedrycz, X. B. Yang et al., “Label distribution learning: A local collaborative mechanism,” International Journal of Approximate Reasoning, vol. 121, no. 7, pp. 59–84, 2020. [Google Scholar]

32. Y. Chen, P. X. Wang, X. B. Yang, J. S. Mi and D. Liu, “Granular ball guided selector for attribute reduction,” Knowledge-Based Systems, vol. 229, pp. 107326, 2021. [Google Scholar]

33. X. B. Yang, S. P. Xu, H. L. Dou, X. N. Song, H. L. Yu et al., “Multi-granulation rough set: A multiset based strategy,” International Journal of Computational Intelligence Systems, vol. 10, no. 1, pp. 277–292, 2017. [Google Scholar]

34. X. B. Yang, S. C. Liang, H. L. Yu, S. Gao and Y. H. Qian, “Pseudo-label neighborhood rough set: Measures and attribute reductions,” International Journal of Approximate Reasoning, vol. 105, pp. 112–129, 2019. [Google Scholar]

35. Y. H. Qian, J. Y. Liang and W. Wei, “Consistency-preserving attribute reduction in fuzzy rough set framework,” International Journal of Machine Learning and Cybernetics, vol. 4, no. 4, pp. 287–299, 2013. [Google Scholar]

36. T. H. Xu, G. Y. Wang and J. Yang, “Finding strongly connected components of simple digraphs based on granulation strategy,” International Journal of Approximate Reasoning, vol. 118, no. 1, pp. 64–78, 2020. [Google Scholar]

37. Y. Y. Yao and Y. Zhao, “Discernibility matrix simplification for constructing attribute reducts,” Information Sciences, vol. 179, no. 7, pp. 867–882, 2009. [Google Scholar]

38. C. Z. Wang, Q. H. Hu, X. Z. Wang, D. G. Chen, Y. H. Qian et al., “Feature selection based on neighborhood discrimination index,” IEEE Transactions on Neural Networks and Learning Systems, vol. 29, no. 7, pp. 2986–2999, 2018. [Google Scholar] [PubMed]

39. X. S. Rao, K. Y. Liu, J. J. Song, X. B. Yang and Y. H. Qian, “Gaussian kernel fuzzy rough based attribute reduction: An acceleration approach,” Journal of Intelligent & Fuzzy Systems, vol. 39, no. 1, pp. 1–17, 2020. [Google Scholar]

40. J. J. Song, E. C. C. Tsang, D. G. Chen and X. B. Yang, “Minimal decision cost reduct in fuzzy decision-theoretic rough set model,” Knowledge-Based Systems, vol. 126, no. 1, pp. 104–112, 2017. [Google Scholar]

41. Y. H. Qian, J. Y. Liang, W. Pedrycz and C. Y. Dang, “An efficient accelerator for attribute reduction from incomplete data in rough set framework,” Pattern Recognition, vol. 44, no. 8, pp. 1658–1670, 2011. [Google Scholar]

42. X. S. Rao, X. B. Yang, X. Yang, X. J. Chen, D. Liu et al., “Quickly calculating reduct: An attribute relationship-based approach,” Knowledge-based Systems, vol. 200, pp. 106014, 2020. [Google Scholar]

43. Y. X. Liu, Z. C. Gong, K. Y. Liu, S. P. Xu, H. R. Ju et al., “A q-learning approach to attribute reduction,” Applied Intelligence, vol. 53, pp. 3750–3765, 2022. [Google Scholar]

44. P. X. Wang, H. Shi, X. B. Yang and J. S. Mi, “Three-way k-means: Integrating k-means and three-way decision,” International Journal of Machine Learning and Cybernetics, vol. 10, no. 10, pp. 2767–2777, 2019. [Google Scholar]

45. J. Ba, K. Y. Liu, H. R. Ju, S. P. Xu, T. H. Xu et al., “Triple-g: A new mgrs and attribute reduction,” International Journal of Machine Learning and Cybernetics, vol. 13, no. 2, pp. 337–356, 2022. [Google Scholar]

46. Z. C. Gong, Y. X. Liu, T. H. Xu, P. X. Wang and X. B. Yang, “Unsupervised attribute reduction: Improving effectiveness and efficiency,” International Journal of Machine Learning and Cybernetics, vol. 13, no. 11, pp. 3645–3662, 2022. [Google Scholar]

47. C. -C. Chang and C. -J. Lin, “LIBSVM: A library for support vector machines,” ACM Transactions on Intelligent Systems and Technology, vol. 2, no. 3, pp. 27, 2011. [Google Scholar]

48. M. Krzywinski and N. Altman, “Classification and regression trees,” Nature Methods, vol. 14, no. 8, pp. 755–756, 2017. [Google Scholar]

49. K. Fukunaga and P. M. Narendra, “A branch and bound algorithm for computing k-nearest neighbors,” IEEE Transactions on Computers, vol. 24, no. 7, pp. 750–753, 1975. [Google Scholar]

50. S. Y. Xia, H. Zhang, W. H. Li, G. Y. Wang, E. Giem et al., “GBNRS: A novel rough set algorithm for fast adaptive attribute reduction in classification,” IEEE Transactions on Knowledge and Data Engineering, vol. 34, no. 3, pp. 1231–1242, 2020. [Google Scholar]

51. L. J. Dong, D. G. Chen, N. L. Wang and Z. H. Lu, “Key energy-consumption feature selection of thermal power systems based on robust attribute reduction with rough sets,” Information Sciences, vol. 532, no. 5, pp. 61–71, 2020. [Google Scholar]

52. C. Z. Wang, Y. Huang, W. P. Ding and Z. H. Cao, “Attribute reduction with fuzzy rough self-information measures,” Information Sciences, vol. 549, no. 12, pp. 68–86, 2021. [Google Scholar]

53. C. Z. Wang, Y. Huang, M. W. Shao, Q. H. Hu and D. Chen, “Feature selection based on neighborhood self-information,” IEEE Transactions on Cybernetics, vol. 50, no. 9, pp. 4031–4042, 2020. [Google Scholar] [PubMed]

54. J. J. Song, X. B. Yang, X. N. Song, H. L. Yu and J. Y. Yang, “Hierarchies on fuzzy information granulations: A knowledge distance based lattice approach,” Journal of Intelligent & Fuzzy Systems, vol. 27, no. 3, pp. 1107–1117, 2014. [Google Scholar]

55. W. W. Yan, J. Ba, T. H. Xu, H. L. Yu, J. L. Shi et al., “Beam-influenced attribute selector for producing stable reduct,” Mathematics, vol. 10, no. 4, pp. 553, 2022. [Google Scholar]