Selection of Metaheuristic Algorithm to Design Wireless Sensor Network

1  Introduction

WSNs are ad hoc networks of widely scattered small wireless, affordable, and self-sufficient motes used for cooperative environment monitoring. Every sensor mote (network node) may gather sensory information, analyze it, and then broadcast the refined data to its associates via a wireless transmission medium. Monitoring, medical, pollution monitoring, medical diagnostics, and building automation are some of the applications for WSNs [1]. Obtaining complete coverage and extending the network lifespan are the two most crucial concerns facing wireless sensor networks. Artificial intelligence (AI) is playing vital role in dealing different kinds [2–5] of problems. When the coverage area is maximized, the deployed sensor nodes are keeping a close eye on the entire region of interest. The sensor field’s coverage has a direct impact on network performance since technology through AI determines how well the sensing zone can be monitored; as a result, it is regarded as a benchmark for WSN service quality. The type of monitoring of the sensing region is impacted by area coverage. The primary goal of the area coverage is to increase the sensing region’s detection rate. Rearranging the sensors would be a practical way to gain maximum coverage of the region. All these tasks should be done efficiently as one cannot increase the sensor’s lifetime or cannot provide additional Energy. Pieces of literature have been proposed to increase the sensor’s lifetime [1,6–14]. The proposed algorithm is helpful to improve the functioning time of the sensor by changing its arrangement. However, all these proposed algorithms have some limitations. The algorithm proposed by Huang is highly complex; for a huge dataset, it may block the channel. However, the algorithm proposed by [15] is less complicated but unable to identify node which has redundant data. Researchers recently implemented several bio-inspired metaheuristic swarm—based techniques to enhance the effectiveness of wireless sensor networks. These approaches include boosting network coverage, increasing network durability, routing mechanisms, sensor node dispersal, and so on. These metaheuristic processes are quite efficient in cracking a variety of optimization problems, particularly in the context of wireless sensor networks [16–18]. Efficiency in sensing and valuable information are both difficult under energy restrictions. The sensors must be spaced sufficiently apart to capture useful data, resulting in the least amount of overlapping in the sensing region [19]. Number of literatures has been proposed to enhance network’s lifetime. The proposed work compares six existing bio-inspired metaheuristic algorithm for increased network coverage based on optimized value of energy. The proposed wok also identifies how many cluster heads will be approximately required with increased network coverage. which algorithm best suites in form of optimized value of energy for given area. This piece of research will be helpful for those researchers who are going to apply wireless sensor networks for large network coverage with minimum value of energy.

2  Structure

2.1 Motivation

Several works have been proposed using NI Algorithms in WSN [20,14–18]. However, some covered optimal coverage in wireless sensor networks (WSNs) [21–23]. These works considered sensor deployment using the NI algorithm, which leads to optimal range [23]. NI algorithms’ mathematical, theoretical, and practical applications in WSNs for routing, gathering, analysis and localization were comprehensively discussed. None of them and the statements below offer a critical evaluation, especially on maximizing coverage range and minimizing energy.

2.2 Related Work

Different researchers uses wireless sensor networks for different applications [24–28]. Used modified particle swarm optimization (PSO) for distributed sonar placement. Optimized sensor deployment using PSO [24,29]. Projected virtual force PSO for dynamic sensor implementation [30]. Used conventional genetic algorithm (GA) for node placement in immobile WSNs [26]. Proposed network coverage with energy efficiency. Reference [31] genetic algorithm (GA) have better network coverage with improved sensing of useless information [32]. Used discrete test ant colony optimization (DT-ACO) toolbox for sensor deployment with hardware-based applications for WSNs. Reference [33] a proposed novel approach with three and transition concepts for sensor deployment [34]. For minimized redundant information sensing, a hybrid Improved Genetic Algorithm and Binary Ant Colony Approach (IGA-BACA) has been used.

PSO, GA, and ant colony optimizer (ACO) well address sensor deployment. Every new attempt toward this approach shows it improves results from previous. In continuation, this work compared six NI algorithms for optimal coverage. None of them offer a rigorous analysis, especially regarding maximizing coverage range while using minimal energy. Furthermore, it also identifies the required number of sensor nodes for given network coverage. moreover, if researcher is limited to design WSNs with limited number of sensor nodes. This piece of work will be helpful to pick algorithm which is giving optimal value of energy with increased network coverage and no larger percentage of sensor nodes. To determine the optimal optimization technique, the proposed work compares six currently used nature-inspired optimization algorithms. It is particularly applicable to applications that call for extensive network coverage with minimal energy consumption. Additionally, it offers comparison with identical sensor nodes but a larger coverage area.

2.3 Contributions

None of them provide a critical review, particularly of maximizing coverage range with optimized energy. The proposed work compares six existing nature-inspired optimization algorithms to find the best-fitted optimization algorithm. Especially it can be applied to applications where large network coverage is required with optimum energy requirement. Furthermore, it also provides comparison by no variations in sensor nodes but increased coverage area.

3  Literature Survey of NI Algorithms

Different researchers have compared different nature-inspired algorithms [6,35–39]. In [34] they Compared five evolutionary, i.e., genetic, ant colony, memetic, PSO, and shuffled frog leaping for continuous and discrete optimization [40,41]. Reviewed PSO and performed comparisons based on exploitation, exploration, source of inspiration, and communication model. In [42], they discussed bat, firefly, cuckoo search, genetic, and PSO and compared their results for discrete and continuous optimization problems. Research Paper [43] presented a detailed literature survey and comparison based on representation, operator, controlled parameter, and application area. Analyzed New challenges were investigated in [44] and search strategies in nature-inspired algorithms. In [45] performed a comparison of twelve algorithms based on contribution factors, evolutionary process, and application area. Matching performance, objective task, characteristics, and scope of usage. In [46] compared Bat, Cuckoo search, Killer herd, and firefly algorithms. In Research Paper presents state-of-art different NI for various real-world problems. In [47,48] guides how large search spaces can handle effectively and shows its reduction successfully. Papers analyze the performance of the selected NI optimization technique based on 52-bar steel truss and the analysis of nine recent bio-inspired algorithm its application and the research gap [48]. Investigated the performance of well-established algorithms for different optimization problems [49]. Compared different algorithms based on statistical parameters.

3.1 Classification of NI Algorithms

NI set of rules is classified into three major classes: bio-inspired, physics chemistry-based, and swarm intelligence algorithms, as shown in Fig. 1.

Figure 1: Types of nature-inspired algorithm

3.1.1 BIO-Inspired Computation

The Foundation of evolutionary computation is Darwin’s theory [49]. Its components are the individual population, which is evaluated through fitness function, parent selection mechanism having operators the crossover and mutation, etc.; an evolutionary algorithm is further classified into different classes. The literature survey is shown in Table 1.

3.1.2 Algorithms Founded on Physical and Chemical Science of Nature

Nature’s physical and chemical phenomena the resource of these algorithms like electrical charges, gravity, etc. Illustrations of these algorithms are simulated annealing SA [50], GSA (gravitational search) [51], and BBBC.

3.1.3 Inspired Algorithms (Swarm Intelligent)

These algorithms are a trace of inspiration for social insects, how they interact with each other and maintain social life like ants, cuckoos, bees, etc., make societies. Nature-inspired algorithms are gaining massive attention from researchers from every field. Fig. 2 shows class-wise percentages of NI algorithms.

Figure 2: Class-wise percentage of NI

3.2 The Theoretical and Mathematical Background of Compared Procedures

A recently huge number of NI algorithms have been established. This work draws a performance comparison between six NI algorithms Grey Wolf (GWO), Ant Lion (ALO), Sine Cosine Optimizer (SCO), Moth Flame (MFO), Dragonfly (DA), Whale Optimization (WOA) based on their optimum value. The following subsections provide a short introduction to these algorithms.

3.2.1 Ant Lion Optimizer (ALO)

The way ants hunt served as an inspiration for this. It adopts the antlion’s five-step hunting process. Building traps, taking a random trip, being stung by ants, and catching and rebuilding traps [58]. It can be mathematically modeled in the following steps of ants.

The haphazard walk of an ant can be analyzed through Eq. (1), where a least of random walk of ith adjustable.

A random walk can be represented as below stated equations is taken from [66]

Wn=∑k=1nyk(1)

where y_k is simple random movement of ant y_(k = +−)1.

Antlion’s Pit trapping: A mathematical model of this pit trapping is given by Eqs. (2) and (3).

git=antlionjt+gi(2)

hit=antlionjt+hi(3)

where is the minimum value at the t-the iteration. ht identifies the largest vector of the whole the variable quantity at the t-the repetition. gi is minimum and is maximum for i-th ant and antlions displays the location of the chosen i-th antlion fly at t-the repetition.

Sliding ants towards antlion: Antlion’s trap building is proportional to their fitness. This behavior 1 is shown in mathematical models (4) (5)

gt=gtI(4)

ht=htI(5)

Catching-prey and pit re-building: When an ant is in the antlion’s jaw by the time it reaches the bottom of the pit, the hunt has reached its conclusion.

It can be mathematically as Eq. (6) if fantt > fantliont

antliontj=anttj(6)

where t shows the current iteration, the position of jth is shown by antlion.

3.2.2 Moth Flame Optimizer (MFO)

It is a result of the navigation method of moths. It maintains a fixed angle concerning the moon, very feasible for traveling in a straight line [59]. This method was inspired by moth flying behavior. It flies at night by keeping a constant inclination toward the moon. The process of covering great distances in a straight line is incredibly inspirational. This algorithm finds a global optimum with the help of these equations [49]. In MFO = (X, Y, Z), X is a function that creates a arbitrary population while Y moves Moth around search space, and Z function rum iteratively until the Z return value is actual. In the end, Moth updates its position by following Eq. (7).

s(Mi,Gi)=Di.eaetcos(2πτ)+Gj(7)

where Di shows the remoteness of ith moth flame, Mi indicates ith Moth, Gj Indicates jth flame, and t is a arbitrary number, α denotes a fix to specify the logarithmic spiral’s shape.

3.2.3 Dragonfly Algorithm (DA)

It is a source of inspiration for social interaction of dragonflies routing, food-finding, and preventing enemies [65].

These two behaviors are based on 5 main factors of individuals in groups. These factors can be mathematically modeled in the given equations [56].

Separation:

Si=−∑k=1Ny−yk(8)

where yk is the recent position and Shows the position of the kth individual and y is the current position.

Alignment:

Ai=∑K=1NwK/N(9)

where wk Shows KT velocity of the individual, N is the amount of localities.

Cohesion:

Ci=∑K=1NyK−y/N(10)

where Y is position, N is the number of neighborhoods, and yk Is the position of the kT h individual.

Attraction toward food source:

Hi=y+−y(11)

where y is the current position of the individual and y+ Shows the food source position.

Distraction:

Hi=y−+y(12)

where y− Is the enemy’s position.

3.2.4 Whale Optimization (WOA)

It is an inspiration for the bubble net shooting approach of whales. The mathematical model of whale optimization consists of encircling prey, a bubble-net feeding mechanism, and a search for a target [54]. Encircling prey behavior is given by Eqs. (13) and (14). All equations are taken from [54].

H⇀=B⇀Z⇀∗t−Y→(t)(13)

Y→(t+1)=Y→∗(t)−E→.H→(14)

where t indicates the current iteration. E→ solution and B→ are constant vector, Z→ indicates the position vector, Y→ the best position trajectory of

Bubble net hunting mechanism: Humpback whales shrink the circle around prey by swimming in a spiral-shaped path. The given mathematical model with fifty percent probability chooses the shrinking process or spiral model as shown in Eq. (15) if ϕ < 0.5 and (16) if ϕ 0.5.

f(x)=Y→(t)−E→.H→(15)

f (x)=H→.eaetcos(2πτ)+Y→(t)(16)

where ϕ is the random number [0,1].

Prey Search: Humpback whales explore arbitrarily according to the location of other whales. The math-magical Eqs. (17) and (18) for this behavior is shown

H→=G→Y→ rand−Y→(17)

Y→(t+1)=Y→ rand−E→H→(18)

3.2.5 Grey Wolf Optimizer (GWO)

The Development of this algorithm is an inspiration by grey wolve’s hunting and leadership behavior [54].

It is founded on the hunting mechanism of grey wolves. The mathematical model of the Gray Wolf optimizer shows that Alpha α is the fittest solution. The 2nd and the 3rd best solution is represented by β and δ. The leftover answers are characterized by ω. Grey wolves surround prey during hunting.

Mathematical equations of hunting behavior [60] are shown in (19) and (20).

y→(t)=|D→.z→p(t)−z→(t)|(19)

z→(t+1)=zp→−B→.y→(20)

where t is the up-to-date iteration. y→ are constant vectors. Zp is the position vector of prey. z→ indicates the position vector of the grey wolf, B→. y→ are coefficients vetor. The vectors y→ and D→ can be calculated by Eqs. (21) and (22) [54].

y→=2b→.s→1−b→(21)

D→=2s→2(22)

3.2.6 Sine Cosine Algorithm (SCO)

It is developed by inspiring sine and cosine mathematical models [55]. Where Random solution updates its position based on these Eqs. (23) and (24) [55].

Yt+1=(Yt)+r1∗sin(r2)|(r3)(Pt)−(yt)|(23)

Yt+1=(Yt)+r1∗cos(r2)|(r3)(Pt)−(yt)|(24)

where Y t is the place in the ith element at the t-the iteration r1, r2, r3 are arbitrary numbers, and Pi is the place in the ith element.

4  Results and Discussion

4.1 Benchmark Functions and Experimental Setup

The test had been led on a laptop (intel core i5, 3 GHZ CPU, 3 MB cache, MATLAB 2020b). The analysis of six NI algorithms (Grey wolf, Ant lion, Dragon fly, Whale, Moth flame, Sine cosine optimizers) been done on the basis’s optimum of four composite benchmark functions. These benchmark functions offer significant variants in the form of shifting, rotation, and expansion. It provides excellent complexity among current benchmark functions.

Ackley’s Function

f(x,y)=−20 exp[−0.2.5(x2+y2)]−exp[0.5(cos 2(π)x+cos 2(π)y)]+e+20(25)

Sphere Function

f(x)=∑i=1nx2(26)

Rastrigin Function

f(x)=An+∑i=1n[xi2−Acos2(π)x1](27)

Griewank Function

1+14000∑i=1n2xi2−Πi=1ncosxii(28)

4.2 Proposed Methodology Framework

Fig. 3 shows framework of proposed method. Initiate nodes, expand the coverage area, and maintain the same number of nodes. Test each algorithm for the specified parameters. Compare them based on the optimum value of energy and select the algorithm that provides the best optimum value of energy with increased network coverage and no change in nodes.

Figure 3: Solution framework of proposed methodology

4.3 Experimental Results

Results are analyzed based on the different optimum values obtained. The minimum optimum value shows convergence on a small value near zero. The optimum energy value varies as the number of network coverage varies. Table 2 shows the optimum value concerning the number of network coverage and nodes. Whereas distance between nodes and cluster heads remained fixed.

4.4 Experimental Analysis

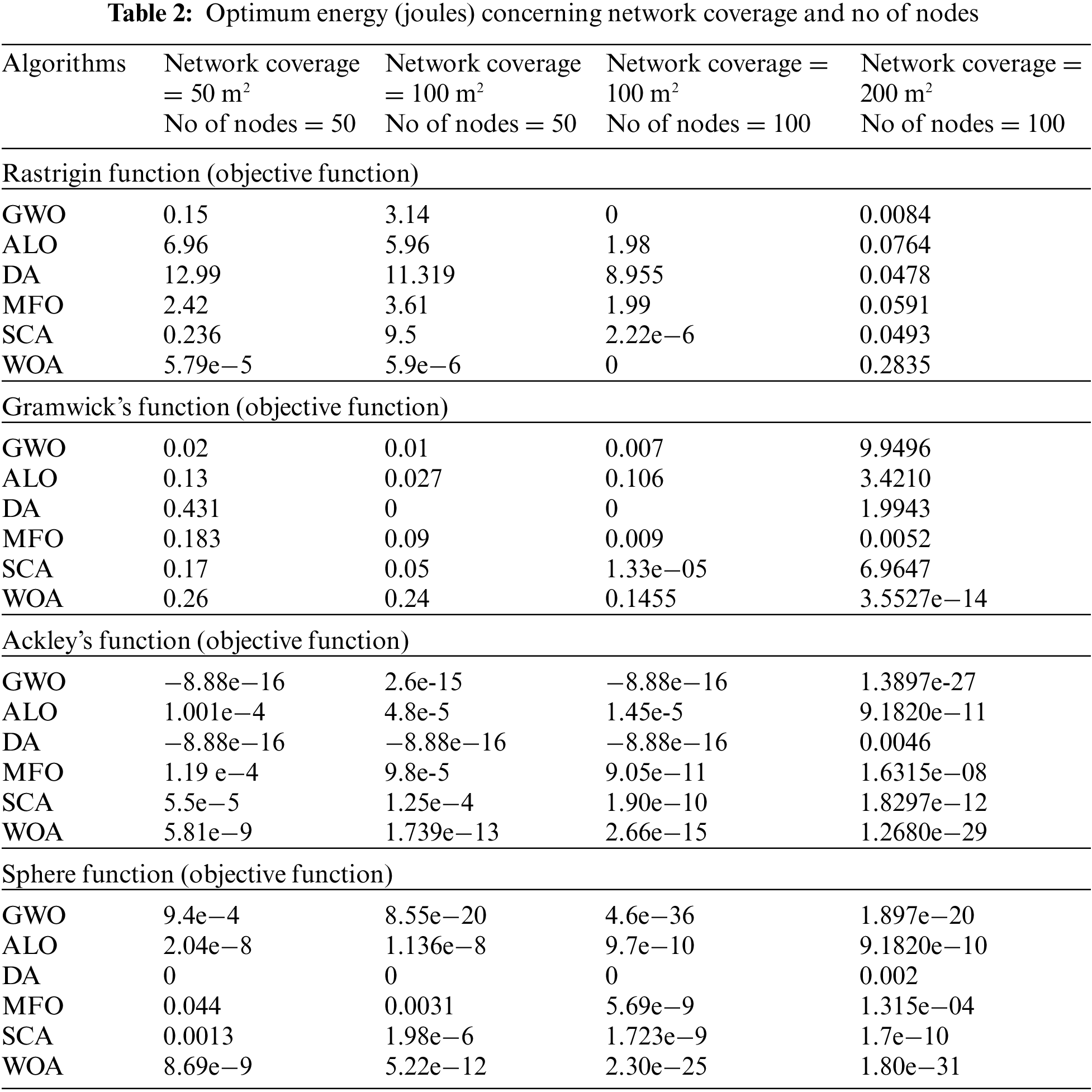
This part shows the effect of search agents and iterations on the objective function. Search agents = network coverage area, iterations = no of nodes. The testing has been performed on four composite benchmark functions. The size of the network coverage area varies from 50–200 m2; no nodes also followed the same. Among the methods for optimum value, as the network handling area increase without increasing the amount of nodes of WSNs, the optimum value does not converge to 0 or near zero. As the coverage area increases with an increased no of nodes, the algorithm’s global optimum improves for each test function. It converges to zero or near zero, but in all six algorithms, WOA performs better. It finds local optima for most benchmark functions with increased coverage area without increasing nodes.

The convergence curves of six compared algorithm for composite test function is illustrated in Figs. 4–7. These figures show that most algorithms show fast convergence on the given test functions with a large population with many iterations. Results show that most algorithms have balanced exploration and exploitation for a large population with many iterations.

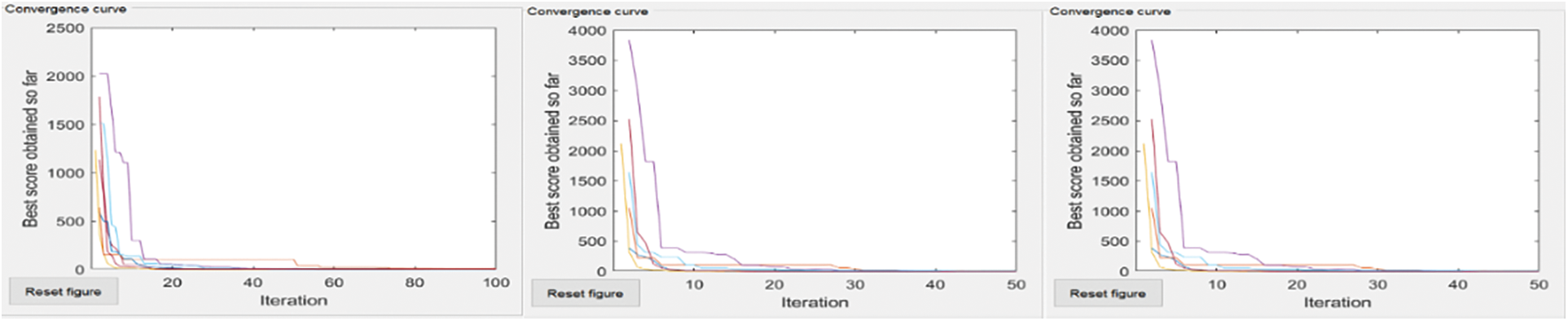
Figure 4: Rastrigim’s-Number of coverage area, no of nodes = 50, 50 and 100, 50 and 100, 100

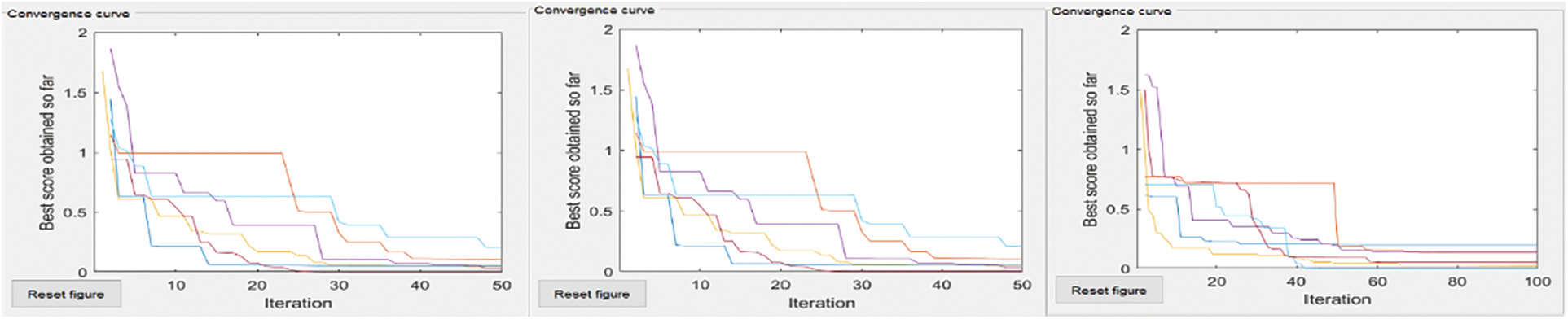
Figure 5: Griewank’s-coverage area, no of nodes = 50, 50 and 100, 50 and 100, 100

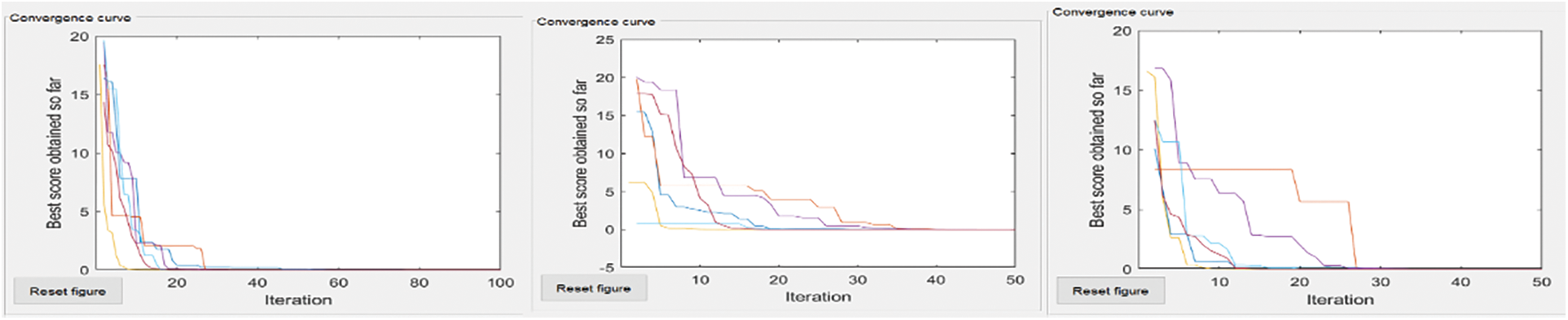
Figure 6: Ackley’s-coverage area, no of nodes = 50, 50 and 100, 50 and 100, 100

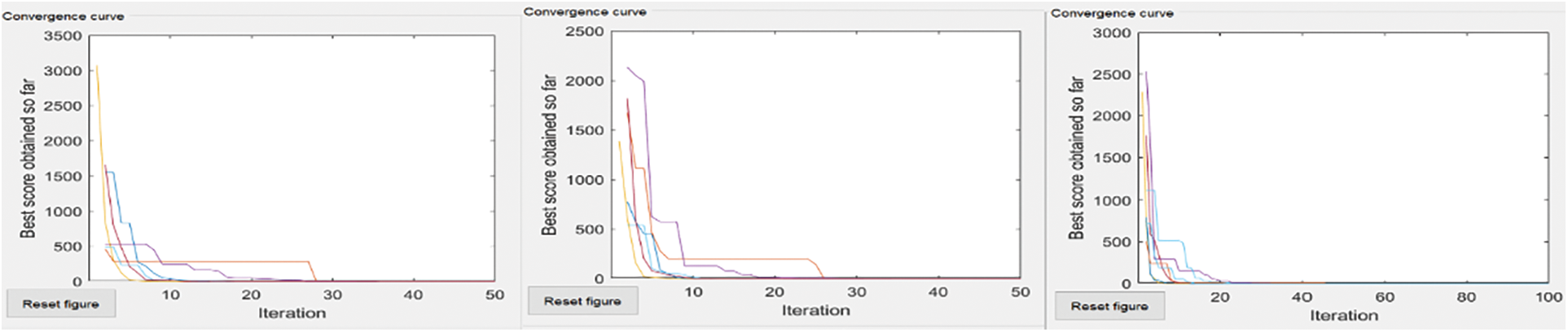
Figure 7: Sphere’s-coverage area, no of nodes = 50, 50 and 100, 50 and 100, 100

The extreme left convergence curve is of extensive network coverage with a few nodes. The middle has the same no of nodes but increased network coverage. The severe right convergence curve is slight in-network coverage with a small no of nodes.

Each curve shows that if coverage areas increase, then the global minimum does not converge to Most algorithms converge to a global minimum if the coverage area grows with increased nodes.

5  Conclusion

Nature-inspired algorithms are most efficient in producing an optimal solution for several optimization problems.

This paper compares six NI algorithms for optimal coverage in WSNs that are analyzed based on their objective function. This shows that increasing coverage area and a small number of nodes performance of algorithms becomes low. If the number of nodes increases with an improved coverage area, the algorithm gives fast convergence toward the global optimum. However, many algorithms analyzed did not perform well by growing coverage areas with small nodes. On the other hand, WOA (whale optimization algorithm) converges towards global optima for most of the benchmark functions among these six algorithms. To conclude, WOA can be chosen for optimal network coverage of WSNs without increasing nodes.

Acknowledgement: The authors would like to acknowledge Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R193), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Funding Statement:: Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R193), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. J. Yick, B. Mukherjee and D. Ghosal, “Wireless sensor network survey,” Computer Networks, vol. 52, no. 12, pp. 2292–2330, 2008. [Google Scholar]

2. S. Lee, Y. Ahn and H. Y. Kim, “Predicting concrete compressive strength using deep convolutional neural network based on image characteristics,” CMC-Computers, Materials & Continua, vol. 65, no. 1, pp. 1–17, 2020. [Google Scholar]

3. A. Gumaei, M. Al-Rakhami, H. Alsalman, S. M. M. Rahman and A. Alamri, “DL-HAR: Deep learning-based human activity recognition framework for edge computing,” CMC-Computers, Materials & Continua, vol. 65, no. 2, pp. 1033–1057, 2020. [Google Scholar]

4. F. N. Al-Wesabi, S. Alzahrani, F. A. M. Al-Yarimi, M. Abdul, M. M. Almazah et al., “A reliable NLP scheme for English text watermarking based on contents interrelationship,” Computer Systems Science & Engineering, vol. 37, no. 3, pp. 297–311, 2021. [Google Scholar]

5. D. Payne and J. Stern, “Wavelength-switched passively coupled single-mode optical network,” in Proc. IOOC-ECOC, Boston, MA, USA, pp. 585, 1985. [Google Scholar]

6. A. Singh, V. Kotiyal, S. Sharma, J. Nagar and C. -C. Lee, “A machine learning approach to predict the average localization error with applications to wireless sensor networks,” IEEE Access, vol. 8, pp. 208253–208263, 2020. [Google Scholar]

7. I. F. Akyildiz, W. Su, Y. Sankarasubramaniam and E. Cayirci, “Wireless sensor networks: A survey,” Computer Networks, vol. 38, no. 4, pp. 393–422, 2002. [Google Scholar]

8. L. M. Borges, F. J. Velez and A. S. Lebres, “Survey on the characterization and classification of wireless sensor network applications,” IEEE Communications Surveys & Tutorials, vol. 16, no. 4, pp. 1860–1890, 2014. [Google Scholar]

9. S. Lu, X. Huang, L. Cui, Z. Zhao and D. Li, “Design and implementation of of an ASIC-based sensor device for WSN applications,” IEEE Transactions on Consumer Electronics, vol. 55, no. 4, pp. 1959–1967, 2009. [Google Scholar]

10. S. Sharma, J. Singh, R. Kumar and A. Singh, “Throughput-save ratio optimization in wireless powered communication systems,” in 2017 Int. Conf. on Information, Communication, Instrumentation And Control (ICICIC), Indore, India, pp. 1–6, 2017. [Google Scholar]

11. R. Kumar and A. Singh, “Throughput optimization for wireless information and power transfer in communication network,” in 2018 Conf. On Signal Processing And Communication Engineering Systems (Spaces), Andhra Pradesh, India, pp. 1–5, 2018. [Google Scholar]

12. M. Imran, H. B. Hasbullah and A. M. Said, “Personality wireless sensor networks (PWSNs),” Arxiv Preprint Arxiv:1212.5543, 1212. [Google Scholar]

13. S. Sharma, R. Kumar, A. Singh and J. Singh, “Wireless information and power transfer using single and multiple path relays,” International Journal of Communication Systems, vol. 33, no. 14, pp. E4464, 2020. [Google Scholar]

14. E. A. E. H. Amor and S. A. Ghannouchi, “Applying data mining techniques to discover KPIs relationships in business process context,” in 2017 18th Int. Conf. on Parallel and Distributed Computing, Applications and Technologies (PDCAT), Andhra Pradesh India, pp. 230–237, 2017. [Google Scholar]

15. M. Cardei and D. -Z. Du, “Improving wireless sensor network lifetime through power aware organization,” Wireless Networks, vol. 11, no. 3, pp. 333–340, 2005. [Google Scholar]

16. A. Mehmood, M. M. Umar and H. Song, “ICMDS: Secure inter-cluster multiple-key distribution scheme for wireless sensor networks,” Ad Hoc Networks, vol. 55, no. 9, pp. 97–106, 2017. [Google Scholar]

17. K. Skiadopoulos, A. Tsipis, K. Giannakis, G. Koufoudakis, E. Christopoulou et al., “Synchronization of data measurements in wireless sensor networks for IoT applications,” Ad Hoc Networks, vol. 89, no. 4, pp. 47–57, 2019. [Google Scholar]

18. Z. Miao, X. Yuan, F. Zhou, X. Qiu, Y. Song et al., “Grey wolf optimizer with an enhanced hierarchy and its application to the wireless sensor network coverage optimization problem,” Applied Soft Computing, vol. 96, no. 3, pp. 106602, 2020. [Google Scholar]

19. X. Wang, G. Xing, Y. Zhang, C. Lu, R. Pless et al., “Integrated coverage and connectivity configuration in wireless sensor networks,” in Proc. of the 1st Int. Conf. On Embedded Networked Sensor Systems, Los Angles, USA, pp. 28–39, 2003. [Google Scholar]

20. C. -W. Tsai, T. -P. Hong and G. -N. Shiu, “Metaheuristics for the lifetime of WSN: A review,” IEEE Sensors Journal, vol. 16, no. 9, pp. 2812–2831, 2016. [Google Scholar]

21. A. J. Al-Mousawi, “Evolutionary intelligence in wireless sensor network: Routing, clustering, localization and coverage,” Wireless Networks, vol. 26, no. 8, pp. 5595–5621, 2020. [Google Scholar]

22. R. Nair, M. Ragab, O. A. Mujallid, K. A. Mohammad, R. F. Mansour et al., “Impact of wireless sensor data mining with hybrid deep learning for human activity recognition,” Wireless Communications and Mobile Computing, vol. 2022, no. 6, pp. 1–8, 2022. [Google Scholar]

23. R. F. Mansour, S. A. Alsuhibany, S. Abdel-Khalek, R. Alharbi, T. Vaiyapuri et al., “Energy aware fault tolerant clustering with routing protocol for improved survivability in wireless sensor networks,” Computer Networks, vol. 212, pp. 109049, 2022. [Google Scholar]

24. P. N. Ngatchou, W. L. Fox and M. A. El-Sharkawi, “Distributed sensor placement with sequential particle swarm optimization,” in Proc. 2005 IEEE Swarm Intelligence Symp., 2005. SIS 2005., California, USA, pp. 385–388, 2005. [Google Scholar]

25. J. Li, K. Li and W. Zhu, “Improving sensing coverage of wireless sensor networks by employing mobile robots,” in 2007 IEEE Int. Conf. on Robotics and Biomimetics (ROBIO), Xishhuangbanna, China, pp. 899–903, 2007. [Google Scholar]

26. X. Liu and D. He, “Ant colony optimization with greedy migration mechanism for node deployment in wireless sensor networks,” Journal of Network and Computer Applications, vol. 39, no. 1, pp. 310–318, 2014. [Google Scholar]

27. R. Eberhart and J. Kennedy, “Particle swarm optimization,” in Proc. of the IEEE Int. Conf. on Neural Networks, California, USA, pp. 1942–1948, 1995. [Google Scholar]

28. J. Wang, Y. Cao, B. Li, H. -J. Kim and S. Lee, “Particle swarm optimization-based clustering algorithm with mobile sink for WSNs,” Future Generation Computer Systems, vol. 76, no. 12, pp. 452–457, 2017. [Google Scholar]

29. A. P. Bhondekar, R. Vig, M. L. Singla, C. Ghanshyam, P. Kapur et al., “Genetic algorithm based node placement methodology for wireless sensor networks,” in Proc. of the Int. Multiconference of Engineers and Computer Scientists, Tsimshatsui, Kowloon, Hon Kong, pp. 18–20, 2009. [Google Scholar]

30. J. Jia, J. Chen, G. Chang and Z. Tan, “Energy efficient coverage control in wireless sensor networks based on multi-objective genetic algorithm,” Computers & Mathematics with Applications, vol. 57, no. 11–12, pp. 1756–1766, 2009. [Google Scholar]

31. D. Li, W. Liu, Z. Zhao and L. Cui, “Demonstration of a WSN application in relic protection and an optimized system deployment tool,” in 2008 Int. Conf. on Information Processing in Sensor Networks (IPSN 2008), Nashville, Tennessee, USA, pp. 541–542, 2008. [Google Scholar]

32. X. Liu, “Sensor deployment of wireless sensor networks based on ant colony optimization with three classes of ant transitions,” IEEE Communications Letters, vol. 16, no. 10, pp. 1604–1607, 2012. [Google Scholar]

33. A. Singh, S. Sharma, J. Singh and R. Kumar, “Mathematical modelling for reducing the sensing of redundant information in WSNs based on biologically inspired techniques,” Journal of Intelligent & Fuzzy Systems, vol. 37, no. 5, pp. 6829–6839, 2019. [Google Scholar]

34. S. K. Pal, C. Rai and A. P. Singh, “Comparative study of firefly algorithm and particle swarm optimization for noisy non-linear optimization problems,” International Journal of Intelligent Systems and Applications, vol. 4, no. 10, pp. 50, 2012. [Google Scholar]

35. J. J. Grefenstette, “Optimization of control parameters for genetic algorithms,” IEEE Transactions on Systems, Man, and Cybernetics, vol. 16, no. 1, pp. 122–128, 1986. [Google Scholar]

36. G. John, “Optimization of control parameters for genetic algorithms,” IEEE Transactions on Systems, Man, and Cybernetics, vol. 16, no. 1, pp. 122–128, 1986. [Google Scholar]

37. Y. Sun, W. Dong and Y. Chen, “An improved routing algorithm based on ant colony optimization in wireless sensor networks,” IEEE Communications Letters, vol. 21, no. 6, pp. 1317–1320, 2017. [Google Scholar]

38. Z. Michalewicz, R. Hinterding and M. Michalewicz, “Evolutionary algorithms,” In: Pedrycz, W. (Eds.Fuzzy Evolutionary Computation, Boston, MA: Springer, 1997. https://doi.org/10.1007/978-1-4615-6135-4_1 [Google Scholar] [CrossRef]

39. J. Kennedy, “Swarm intelligence,” In: Zomaya, A.Y. (Eds.Handbook of Nature-Inspired and Innovative Computing, Boston, MA: Springer, 2006. https://doi.org/10.1007/0-387-27705-6_6 [Google Scholar] [CrossRef]

40. N. Sureja, “New inspirations in nature: A survey,” International Journal of Computer Applications & Information Technology, vol. 1, pp. 21–24, 2012. [Google Scholar]

41. N. Nitesh Sureja, “New inspirations in nature: A survey,” International Journal of Computer Applications & Information Technology, vol. 1, no. 3, pp. 21–24, 2012. [Google Scholar]

42. S. Binitha and S. S. Sathya, “A survey of bio inspired optimization algorithms,” International Journal of Soft Computing and Engineering, vol. 2, pp. 137–151, 2012. [Google Scholar]

43. X. -S. Yang, “Nature-inspired mateheuristic algorithms: Success and new challenges,” Arxiv Preprint Arxiv:1211.6658, 2012. [Google Scholar]

44. P. Agarwal and S. Mehta, “Nature-inspired algorithms: State-of-art, problems and prospects,” International Journal of Computer Applications, vol. 100, no. 14, pp. 14–21, 2014. [Google Scholar]

45. P. Kaur and T. Kaur, “A comparative study of various metaheuristic algorithms,” International Journal of Computer Science and Information Technologies, vol. 5, no. 5, pp. 6701–6704, 2014. [Google Scholar]

46. A. Darwish, “Bio-inspired computing: Algorithms review, deep analysis, and the scope of applications,” Future Computing and Informatics Journal, vol. 3, no. 2, pp. 231–246, 2018. [Google Scholar]

47. T. M. Vala, V. N. Rajput, Z. W. Geem, K. S. Pandya and S. C. Vora, “Revisiting the performance of evolutionary algorithms,” Expert Systems with Applications, vol. 175, no. 4, pp. 114819, 2021. [Google Scholar]

48. J. Nondy and T. K. Gogoi, “Performance comparison of multi-objective evolutionary algorithms for exergetic and exergoenvironomic optimization of a benchmark combined heat and power system,” Energy, vol. 233, pp. 121135, 2021. [Google Scholar]

49. C. Darwin, On the Origin of Species, 1859. London: Routledge, 2016. [Google Scholar]

50. B. Attaran, A. Ghanbarzadeh and S. Moradi, “A novel evolutionary optimization algorithm inspired in the intelligent behaviour of the hunter spider,” International Journal of Computer Mathematics, vol. 98, no. 3, pp. 627–655, 2021. [Google Scholar]

51. E. Rashedi, E. Rashedi and H. Nezamabadi-Pour, “A comprehensive survey on gravitational search algorithm,” Swarm and Evolutionary Computation, vol. 41, no. 4, pp. 141–158, 2018. [Google Scholar]

52. V. Hayyolalam and A. A. P. Kazem, “Black widow optimization algorithm: A novel meta-heuristic approach for solving engineering optimization problems,” Engineering Applications of Artificial Intelligence, vol. 87, pp. 103249, 2020. [Google Scholar]

53. I. Aljarah, M. Mafarja, A. A. Heidari, H. Faris and S. Mirjalili, “Clustering analysis using a novel locality-informed grey wolf-inspired clustering approach,” Knowledge and Information Systems, vol. 62, no. 2, pp. 507–539, 2020. [Google Scholar]

54. H. Alsattar, A. Zaidan and B. Zaidan, “Novel meta-heuristic bald eagle search optimisation algorithm,” Artificial Intelligence Review, vol. 53, no. 3, pp. 2237–2264, 2020. [Google Scholar]

55. M. H. Sulaiman, Z. Mustaffa, M. M. Saari and H. Daniyal, “Barnacle’s mating optimizer: A new bio-inspired algorithm for solving engineering optimization problems,” Engineering Applications of Artificial Intelligence, vol. 87, pp. 103330, 2020. [Google Scholar]

56. M. F. F. Ab. Rashid, “Tiki-Taka algorithm: A novel metaheuristic inspired by football playing style,” Engineering Computations, vol. 38, no. 1, pp. 313–343, 2020. https://doi.org/10.1108/EC-03-2020-0137 [Google Scholar] [CrossRef]

57. N. Covic and B. Lacevic, “Wingsuit flying search—A novel global optimization algorithm,” IEEE Access, vol. 8, pp. 53883–53900, 2020. [Google Scholar]

58. S. Mirjalili, A. H. Gandomi, S. Z. Mirjalili, S. Saremi, H. Faris et al., “Salp swarm algorithm: A bio-inspired optimizer for engineering design problems,” Advances in Engineering Software, vol. 114, pp. 163–191, 2017. [Google Scholar]

59. S. Arora and S. Singh, “Butterfly optimization algorithm: A novel approach for global optimization,” Soft Computing, vol. 23, no. 3, pp. 715–734, 2019. [Google Scholar]

60. G. Dhiman and V. Kumar, “Spotted hyena optimizer: A novel bio-inspired based metaheuristic technique for engineering applications,” Advances in Engineering Software, vol. 114, no. 10, pp. 48–70, 2017. [Google Scholar]

61. M. E. Rahmani, A. A. Amine, R. M. Hamou, A. Rahmani, H. Menad et al., “A novel bio inspired algorithm based on echolocation mechanism of Bats for seismic hazards detection,” In: S. Chikhi, A. Amine, A. Chaoui, M. Kholladi, D. Saidouni (Eds.Modelling andImplementation of Complex Systems, pp. 77–89, Cham: Springer, 2016. [Google Scholar]

62. A. Kaveh, M. Seddighian and E. Ghanadpour, “Black hole mechanics optimization: A novel meta-heuristic algorithm,” Asian Journal of Civil Engineering, vol. 21, no. 7, pp. 1129–1149, 2020. [Google Scholar]

63. S. Mirjalili and A. Lewis, “The whale optimization algorithm,” Advances in Engineering Software, vol. 95, no. 12, pp. 51–67, 2016. [Google Scholar]

64. S. Mirjalili, “SCA: A sine cosine algorithm for solving optimization problems,” Knowledge-Based Systems, vol. 96, no. 63, pp. 120–133, 2016. [Google Scholar]

65. S. Mirjalili, “Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems,” Neural Computing and Applications, vol. 27, no. 4, pp. 1053–1073, 2016. [Google Scholar]

66. S. Mirjalili, “The ant lion optimizer,” Advances in Engineering Software, vol. 83, pp. 80–98, 2015. [Google Scholar]

67. S. Mirjalili, “Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm,” Knowledge-Based Systems, vol. 89, pp. 228–249, 2015. [Google Scholar]