Object Tracking Algorithm Based on Multi-Time-Space Perception and Instance-Specific Proposals

1  Introduction

Video object tracking [1–3] is an important research direction in computer vision and plays an essential role in artificial intelligence and big data applications. Firstly, the initialized object position is used as input, many candidate boxes are generated in the next frame, and the different representation features of the candidate boxes are extracted. Then, the candidate box is scored through a specific mechanism. Finally, the candidate box with the highest score is used as the prediction object, or multiple prediction results are fused to obtain a better result.

In the past few decades, many theories and algorithms about object detection and object tracking have been proposed. Video datasets used to test the algorithm’s performance are also emerging, and the performance and robustness of the algorithm are constantly improving. However, when dealing with the problem of object tracking in real application scenarios, unpredictable interference factors will appear at any time, such as the appearance change of the object, illumination variation, and occlusion, which will affect the effect of the algorithm and bring significant challenges to track. By improving the tracking performance of the tracking algorithm in complex scenes, such as object deformation, background interference, fast motion, and occlusion, and realizing the balance between real-time performance and robustness of the tracking algorithm, the needs of practical applications will be met.

Based on these aspects, researchers have conducted studies on the object appearance representation model and model update [4,5]. However, many problems still need to be addressed, such as the ability to effectively use different features to adapt to different environments. Therefore, how to optimize multi-feature coupling objective function and train an adaptive filter model are urgent problems to be solved.

In this study, starting with the optimization of the objective function of the multi-feature correlation filter (CF), a coupling correlation filter model based on the multi-time-space perception is designed, and the dual filter with adaptive environment weights is used to locate the object, which provide a reference for improving the tracking effect in a complex environment. The critical contributions of the proposed algorithm are summarized as follows:

•   The time-space information is established from the mask matrix and the neighborhood of the object by calculating the consistency of the object frames and the filter frames to improve the identification of the algorithm in complex scenes.

•   The constraint term of time-space perception is introduced to enhance the learning ability of the correlation filters to optimize the final tracking results. The objective function is optimized by the Lagrange function and iteratively calculated in a closed form to obtain an adaptive filter model.

•   A multi-time-space perception complementary scheme is proposed based on CF to locate the object by introducing adaptive position weights. The complementary scheme can adaptively and perfectly combine these advantages of different features and solve the long-term tracking in complex scenes, such as occlusion and background clutter.

•   When the tracking results fluctuate, the proposed scheme of instance-specific proposals is designed to reduce the risk of model drift effectively.

2  State of the Art

We will discuss the tracking methods related to this work in this section.

2.1 Tracking by Correlation Filters

Before the emergence of the object tracking algorithm based on CF, all tracking operations were completed in the time domain. The amount of data in matrix operation is large, and the calculation time of the algorithm is long. The object tracking algorithms based on CF [6,7] convert the tracking operations into the frequency domain, which can reduce the amount of calculation and ensure data integrity. Many domestic and foreign scholars have introduced CF into object tracking algorithms [8,9] and achieved excellent results in the latest open datasets and academic competitions. The trackers based on CF only need to extract features from the searching box once and generate many candidate samples through cyclic convolution operation. According to the convolution theorem, convolution calculation can be transformed into multiplication by elements in the frequency domain. The tracker can effectively learn from the training samples, which significantly reduces computational complexity. Bolme et al. introduce the CF into the tracking field for the first time and propose to use the minimum output sum of square error (MOSSE) filter to realize the tracking task. This algorithm can obtain faster-tracking speed while ensuring accuracy [10]. However, when the MOSSE filter is used for dense sampling, the tracking performance will degrade due to insufficient training samples. Based on the MOSSE algorithm, Danelljan et al. add a regular term in the construction of the objective function to alleviate the situation that the sample has zero frequency components in the frequency domain and build a scale pyramid to estimate the object scale [11]. Henriques et al. [12] propose the kernel correlation filter (KCF) algorithm, which significantly improves the object tracking speed by extracting the characteristics of the histogram of oriented gradient (HOG) and combining it with ridge regression and cyclic matrix. Hare et al. [13] design an adaptive object tracking algorithm (Struck) based on structured support vector machine (SVM), which omits the classification process and directly outputs the results. Liu et al. [14] use the locally sensitive histogram and super-pixel segmentation to represent the object appearance model and propose a CF model based on multi-feature fusion, which achieves good tracking results.

2.2 Tracking by Multi-Feature Objective Function Optimization

Karunasekera et al. [15] discuss the latest development trend and progress of tracking algorithm and compare the performance of the tracker based on CF and non-correlation filter, which provides an essential reference for the research of object tracking algorithm. The continuous convolution operators (C-COT) algorithm [16] uses the method of weighting different filter coefficients for regularization constraints, and the background region is allocated with low coefficients. Kim et al. design a tracking algorithm with channel and spatial reliability [17], which divides the candidate region into foreground and background and then performs spatial regularization processing. Ma et al. propose a boundary-constrained tracking algorithm [18], which only activates the coefficients of the object region and forces the coefficients of the corresponding background region in the filter to 0. Yuan et al. [19] propose a real-time tracking algorithm combining gradient feature and color feature with a complex ridge regression framework. Liu et al. [20] design a long-term tracking algorithm based on dual model fusion and carry out adaptive fusion of the sparse kernel correlation filter model and color model to realize long-term tracking. Liu et al. [21] fuse the scale-invariant feature transform (SIFT) feature and the color histogram feature for object matching, and mark the motion state of the object in each frame to achieve object tracking. The abovementioned algorithms don’t take into account the mathematical modeling of multi-feature objective function and the optimization of filter model and ignore the diversified advantages of multi-feature in different scenes.

2.3 Tracking by Region Proposals

The correlation filter is used to solve the long-time tracking, and the performance of the tracking algorithm is greatly improved with the help of the re-detection function [22,23]. A scale-driven convolutional neural network (SD-CNN) model is proposed in reference [24] to improve the object detection accuracy, which uses heads as the dominant and visible features to localize people in videos consisting of low-density to high-density crowds. Due to the complex and changeable traffic environment, the possible deformation of the object, and background interference, it is easy to cause tracking failure. Zhang et al. [25] propose a re-detection architecture based on the Siam network (SiamRPN), which uses the first frame annotation and the previous frame prediction for dual detection, and combines with the trajectory-based dynamic programming algorithm to model the complete history of the tracking object to achieve long-term object tracking. Pareek et al. [26] calculate the average value of all tracking results before the current frame and update the object template. With continuous tracking, the object template is constantly polluted, which eventually leads to tracking drift. When the object is blocked, the impact of this pollution will be more obvious. Shan et al. [27] design a sample pool based on high confidence and use the template in the reserved sample pool to train and update the model online. The algorithm can maintain certain robustness. Wang et al. [28] introduce the Kalman filter [29] to compensate for the position of the occluded part of the object, which plays well on the tracking benchmark. The above mentioned re-detection methods have less consideration for the effectiveness of the initial frame, and there are still unsatisfactory or inefficient solutions to different complex scenes.

Given the shortcomings of the abovementioned algorithms in the objective function modeling, the CF is optimized from the modeling method of coupling objective function. By looking for the coupling relationship between features, the tracking position is adaptively obtained according to the contribution of different features.

The remainder of this study is organized as follows. Section 3 describes the overall framework of the proposed algorithm, constructs the multi-time-space perception correlation filter and location prediction algorithm, and discusses the execution steps of the algorithm in detail. Section 4 verifies the tracking effect of the algorithm on the object tracking benchmark 2015 (OTB2015) and the temple color 128 (TC-128) and compares it with other compared algorithms through experiments in two aspects, namely, quantitative analysis and qualitative analysis. Section 5 summarizes the conclusions.

3  Methodology

A correlation filter tracking algorithm based on time-space perception is proposed by unified modeling of different feature objective functions and exploring the constraint relationship between objective functions. Based on the consistency of the object models of two adjacent frames, the objective function of multi-time-space perception coupling is constructed and optimized. The correlation filter models CF1 and CF2 corresponding to different features are obtained respectively (see Sections 3.2–3.3 for details). The position corresponding to the maximum response is calculated using the trained filter model and the final object position is estimated with dynamic weighting (see Section 3.4 for details). Given the loss of object tracking, a solution for instance-specific proposals (see Section 3.5 for details) is proposed to achieve continuous tracking. The algorithm model is shown in Fig. 1. The blue box represents the searching box, the red box represents the detecting result, and the green box represents the instance-specific proposals.

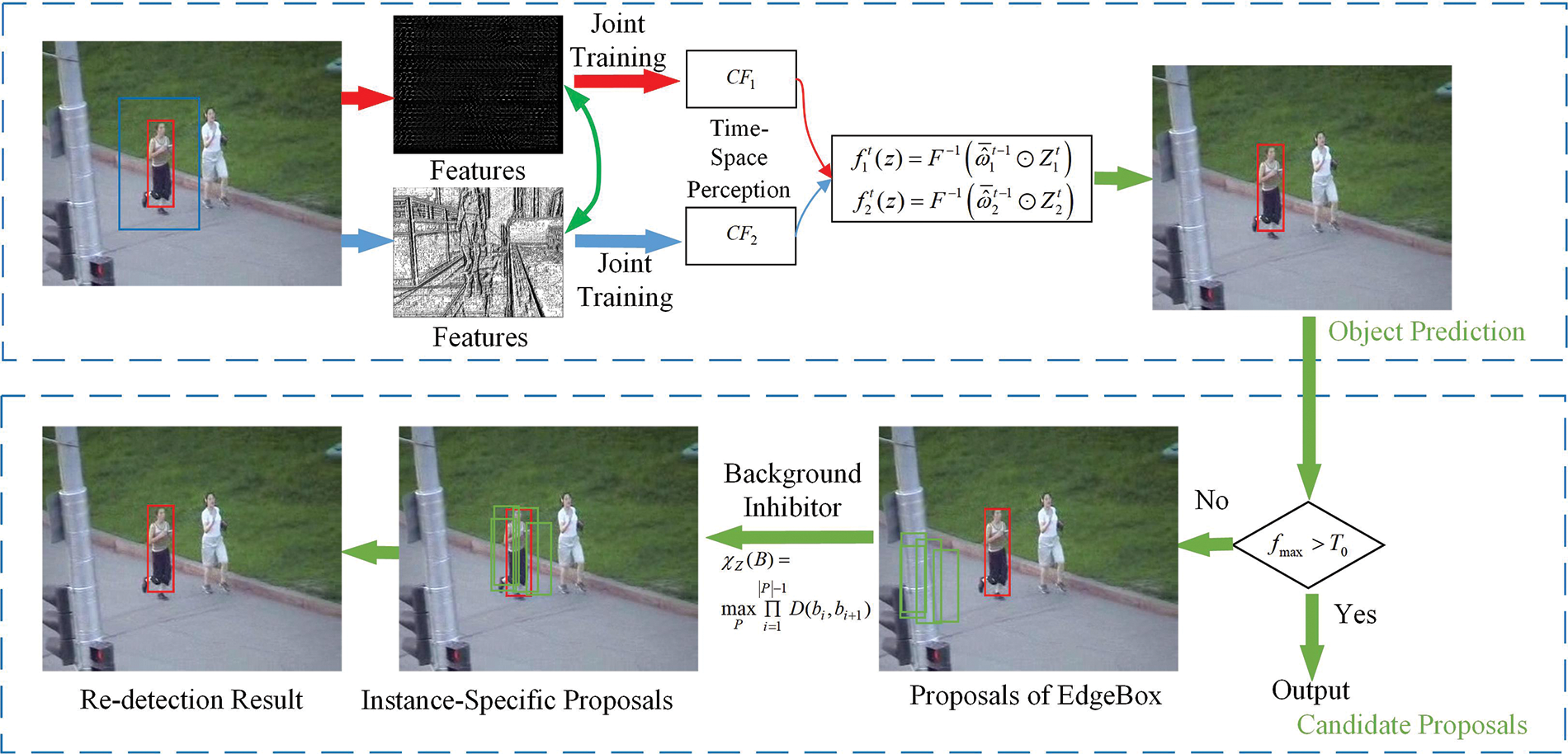
Figure 1: Algorithm model

3.1 Discriminative Correlation Filter Model

The discriminative correlation filter is a regularized least squares objective function to solve the filter ωt. The objective function [3] is as follows:

ω⌢t=argminωt‖ ∑d=1Dωtd∗xtd−y ‖2+λ∑d=1D‖ ωtd ‖2,(1)

where ωt is the correlation filter of the frame t, ωtd is the filter corresponding to each feature dimension, and xtd is the feature map corresponding to each feature of the input candidate box. d=1,2,⋯,D, D is the number of feature dimensions, with a value of 2. λ is the regularization coefficient that increases the generalization ability of the model, * is the relevant operation in the time domain, and y is the relevant expected output. We convert the objective function to the frequency domain and omit the subscript t, which can be expressed as:

ω^=argminω‖∑d=1Dω^¯d⊙x^d−y^‖+λ∑d=1D‖ω^d‖2.(2)

⊙ represents the point multiplication operation in the frequency domain, ω^,x^,and y^ are the Fourier transform of ω^,x^,and y^, respectively, and ω^¯ represents complex conjugation. The point multiplication in the frequency domain is the multiplication of each element. The process of optimizing Eq. (2) is to optimize the solution at the pixel level, as shown in Eqs. (3)–(6).

∂∂ω^¯ij{‖x^ijω^¯ij−y^ij‖2+λ‖ω^ij‖2}=0,(3)

∂∂ω^¯ij{(x^ijω^¯ij−y^ij)(x^ijω^¯ij−y^ij)¯+λω^ijω^¯ij}=0,(4)

∂∂ω^¯ij{x^ijω^¯ijx^¯ijω^ij−y^ijx^¯ijω^ij−x^ijω^¯ijy^¯ij+y^ijy^¯ij+λω^ijω^¯ij}=0,(5)

x^ijx^¯ijω^ij−x^ijy^¯ij+λω^ij=0, ω^ij=x^ijy^¯ijx^ijx^¯ij+λ,(6)

where i and j are the index of pixels, (i,j)∈{0,1,⋯,W−1}×{0,1,⋯,H−1}, W is the width of the candidate area, and H is the height of the candidate area. According to Eq. (7), the filter of each feature dimension is obtained, which is expressed as follows:

ω^l=x^ly^¯∑d=1Dx^dx^¯d+λ=AtlBt.(7)

The filter update strategy of the frame t+1 is shown as follows:

At+1l=(1−β)Atl+βx^tly^¯t,Bt+1=(1−β)Bt+β∑d=1Dx^tdx^¯td,(8)

where β is the learning rate, At+1l and Bt are the numerator and denominator of the filter ω^t+1l. When the model is updated, the update operation is carried out according to the numerator and denominator. Given a frame, its feature vector is expressed by z, and the filter response can be calculated by Eq. (9).

y=f(z)=F−1(∑d=1DA¯dzd/(B+λ))(9)

3.2 Proposed Multi-Time-Space Perception Objective Function Model

The correlation filter based on the HOG feature is robust in motion blur and illumination variation, but it is susceptible to object deformation. The texture feature is robust in similar background color and object deformation. Therefore, in order to solve the problems of similar background color, illumination variation, and object deformation in the long-term tracking process, the dual independent time-space perception filters used for object location are trained according to the HOG features and texture features, respectively.

According to Eq. (2), the objective functions of the HOG feature and texture feature are obtained respectively, as shown in Eqs. (10) and (11).

arg⁡minωhog‖∑d=1Dωhogd∗xhogd−yhog‖2+λ∑d=1D‖ωhogd‖2(10)

arg⁡minωtex‖∑d=1Dωtexd∗xtexd−ytex‖2+λ∑d=1D‖ωtexd‖2(11)

Subscripts hog and tex represent the HOG feature and texture feature of candidate regions, respectively. Generally, the object and background of the adjacent two frames change little or are similar in the object tracking in the real environment. So, the object models of the adjacent two frames will be the consistent; that the filter ωt+1 obtained from the frame t+1 is the same as the filter ωt obtained from the frame t, which are expressed by the following mathematical model:

arg minωhog‖ωt+1hog−ωthog‖2,(12)

arg minωtex‖ωt+1tex−ωttex‖2.(13)

The mask matrix M [4] is introduced into the filter to make it have a specific ability to perceive the background information in space. Combined with Eqs. (10)–(13), the objective function of multi-time-space perception coupling is constructed, and the proposed spatio-temporal perception constraint is shown in Eq. (14).

arg minωhog,ωtex‖∑d=1Dωhogd∗Mxhogd−yhog‖2+λ∑d=1D‖ωhogd‖2+‖∑d=1Dωtexd∗Mxtexd−ytex‖2+λ∑d=1D‖ωtexd‖2+ξ2‖ωhogt+1−ωhogt‖2+ζ2‖ωtext+1−ωtext‖2,(14)

where ξ and ζ are trade-off coefficients, which control the strength of the regularization term formed by the difference of filters between adjacent frames to prevent it from becoming more significant in the process of optimization solution. Otherwise, when the object is blocked, it will lead to tracking drift.

3.3 Optimization Process of the Proposed Objective Function

The objective function represented by Eq. (14) is optimized by constructing the Lagrange method, which is constructed by a Lagrange multiplier combined with certain constraints. Then, ADMM optimization [30] is iteratively updated in a closed form, and the constructed Lagrange function is as follows:

ℓ(ωhogt+1,ωtext+1,ρhogt+1,τhogt+1)=(‖ωhogt+1∗Mxhogt+1−yhogt+1‖2+λ‖ωhogt+1‖2)+(‖ωtext+1∗Mxtext+1−ytext+1‖2+λ‖ωtext+1‖2)+ξ2‖ωhogt+1−ωhogt‖2+ζ2‖ωtext+1−ωtext‖2+ρhogt+1(ωhogt+1−ωtext+1)+τhogt+12‖ωhogt+1−ωtext+1‖2.(15)

τhogt+1 and ρhogt+1 are Lagrange penalty parameters and multipliers, respectively. Eq. (15) is optimized and solved by optimizing the following objective functions:

arg minℓ(ωhogt+1,ωtext+1,ρhogt+1,τhogt+1).(16)

(1) Solution of ωhogt+1

Given ωtext+1, ρhogt+1, and τhogt+1, the variable ωhogt+1 is solved by optimizing the corresponding objective function, which is expressed as follows:

ωhogt+1=arg minωhogt+1(‖ωhogt+1∗Mxhogt+1−yhogt+1‖2+λ‖ωhogt+1‖2)+ξ2‖ωhogt+1−ωhogt‖2+ρhogt+1ωhogt+1+τhogt+12‖ωhogt+1−ωtext+1‖2.(17)

The closed solution is obtained in the form of a contraction threshold, which is expressed as follows:

ωhogt+1=F−1(x^hogt+1y^¯hogt+1+ρhogt+1+τhogt+12ω^hogt+1x^hogt+1x^¯hogt+1+(λ+ξ2+τhogt+12)I).(18)

(2) Solution of ωtext+1

Given ωhogt+1, ρhogt+1, and τhogt+1, the variable ωtext+1 is solved by optimizing the corresponding objective function, which is expressed as follows:

ωtext+1=arg minωtext+1(‖ωtext+1∗Mxtext+1−ytext+1‖2+λ‖ωtext+1‖2)+ζ2‖ωtext+1−ωtext‖2−ρhogt+1ωtext+1+τhogt+12‖ωhogt+1−ωtext+1‖2(19)

The closed solution is obtained in the form of a contraction threshold, which is expressed as follows:

ωtext+1=F−1(x^text+1y^¯hogt+1+ζ2ω^text+τhogt+12ω^text+1+ρhogt+1x^text+1x^¯text+1+(λ+ζ2+τhogt+12)I).(20)

(3) Solution of ρhogt+1 and τhogt+1

Given ωhogt+1 and ωtext+1, variables ρhogt+1 and τhogt+1 are updated as follows:

ρhogt+1=ρhogt+1+τhogt+1(ωhogt+1−ωtext+1).(21)

(4) Update the Lagrange multiplier

The updating method of the Lagrange multiplier ρhogt+1 is shown in Eq. (22), where ρ^t represents the Fourier transform of the Lagrange multiplier at the i-th iteration, ω^hogi+1 and ω^texi+1 denote the solution of the corresponding sub-problem at the i + 1-th iteration.

ρ^i+1=ρ^t+ω^hogi+1−ω^texi+1(22)

Repeating the above four steps to optimize, a set of optimal filters and spatial regularization weights can be obtained after convergence.

3.4 Proposed Object Location Estimation Model

On the premise that the position and size of the previous frame are known, the position of the current frame will be solved. The current frame represents the frame t, the object position of the frame t−1 is Pt−1=(xt−1,yt−1), and the scale is Slt−1n=(anWt−1,anHt−1). Regional samples are obtained by using the cyclic shift of the matrix. The scale of each candidate sample is Slt−1n and the regional samples named Xtpadding are expressed as follows:

Xtpadding={xt,yt|‖Pt−Pt−1‖<padding}.(23)

The candidate samples Zt are obtained by calculating the real rectangular box Dt−1 at the object position Pt−1=(xt−1,yt−1) with Xtpadding using Eq. (24).

Zt={Z:0.5<area(Dt−1∩Xtpadding)area(Dt−1∪Xtpadding)<0.9}(24)

According to the time-space perception correlation filter ωhogt−1 and ωtext−1 provided in the frame t−1, the correlation responses fhogt(z) and ftext(z) of the HOG feature zhogt and the texture feature ztext of the candidate samples Zt are calculated, respectively.

fhogt(z)=F−1(ω^¯hogt−1⊙Zhogt)(25)

ftext(z)=F−1(ω^¯text−1⊙Ztext)(26)

The corresponding maximum response values fhogmax and ftexmaxare obtained respectively according to Eqs. (25) and (26), which are expressed as follows:

fhogmax=arg maxn(fmax(Zt1),fmax(Zt2),⋯fmax(Ztn)),(27)

ftexmax=arg maxn(ftex(Zt1),ftex(Zt2),⋯ftex(Ztn)).(28)

The object position response diagram ffianl is calculated by Eq. (29) as follows :

ffinal=κhogfhogmax+κtexftexmax.(29)

where κhog and κtex are the object position weight coefficients estimated by the HOG feature and texture feature, respectively. The weight coefficients related to the maximum response values corresponding to different features are calculated as follows:

κhog=F(fhogmax)F(fhogmax)+F(ftexmax),(30)

κtex=F(ftexmax)F(fhogmax)+F(ftexmax).(31)

Different features have different abilities to distinguish objects and backgrounds in different tracking environments. The function F(x) is expressed as F(x)=11+exp⁡(−x) which can balance the interference of background to feature contribution.

3.5 Proposed Instance-Specific Proposals for Re-Detection

In a real environment, object tracking may be interfered with different factors, resulting in tracking failure. How to effectively restore retraining is also a significant problem when designing an object tracking algorithm. When g(⋅) defined as the maximum response of the filter is less than the threshold T0, the instance-specific proposals is started. The Edgebox [31] method is used to generate the candidate region of the whole image and calculate its reliability score. The candidate region with the highest confidence is the re-detection result. The candidate regions generated by the EdgeBox include two types, one is near the prediction object (represented by Bs), and the other is the whole image region (represented by Bh). B (B∈{Bs,Bh}) is a candidate bounding box in Bs or Bh, which is expressed as (x,y,w,h). (x,y) is the central coordinate of the bounding box and (w,h) is the width and height of the bounding box. The similarity of the two edge groups {Bi,Bj∈B} is determined by the average position expressed as (xi,xj) and the average direction expressed as (αi,αj). The similarity of edge boxes is represented by D(Bi,Bj)=|cos⁡(αi−αij)cos⁡(αj−αij)|2, where αij represents the direction deviation of two edge groups, which is obtained from the average position xi and xj.

The candidate boxes are searched in the whole image using the Edgebox algorithm, in which case the candidate boxes may contain background or other interfering objects. Noise suppression promotes the determination of the final object candidate box. The contour that intersects with the candidate region Z which includes the object does not belong to the object. When the candidate region is suppressed, the influence of the background is suppressed accordingly.

An inhibitory factor χZ(B) is designed, expressed as χZ(B)=maxP∏i=1|P|−1D(bi,bi+1). P with a length of |P| refers to the candidate box path which ends at b|P|. The response score of each boundary box g(bti) is recalculated after calculating all boundary suppression factors in candidate region Z.

According to the filter response score g(bti), N recommended areas with high scores are considered as object candidates. The Euclidean distance between the candidate boxes (bti, i=1,2,⋯N) of the current frame and the CF results (pt−1, (xt−1,yt−1)) is calculated as follows:

D(bti,pt−1)=exp⁡(−12σ2‖(xti,yti)−(xt−1,yt−1)‖2).(32)

σ is the diagonal length of the initial object size, and (xt,yt) indicates the object position predicted in the frame t. The re-detection result is selected as the optimal scheme by minimizing the joint weighting term of confidence and Euclidean distance:

arg mini,j βg(bti)+(1−β)D(bti,bt−j),g(bti)>T0.(33)

The object is blocked for a long time in the video sequence Jogging. Fig. 2 shows the candidate region recommendation results after the object reappears. The red boundary box represents the manually marked position, and the green boundary boxes represent the recommendation candidate regions. The regions generated by the Edgebox, as shown in Fig. 2a, stay near the object position when it is blocked. The proposed regions generated in this study, as shown in Fig. 2b, are around the object, which is more suitable for solving the problem of re-detection.

Figure 2: Region proposals

3.6 Model Update Scheme

When there is more than one similar object in the scene, the tracker treats the similar object as the background. If the maximum response value g(⋅) of the current frame is greater than the threshold T0, the object model is updated. Assuming the learning rate is γ, the updating strategy of the object model is expressed as follows:

ωt+1=(1−γ)ωt+1+γωt.(34)

3.7 Algorithm Flow

The response diagrams with different characteristics are calculated using the learned multi-space-time perception filter model to obtain the object location adaptive to the real environment. The main working steps of the proposed algorithm are shown as follows:

4  Result Analysis and Discussion

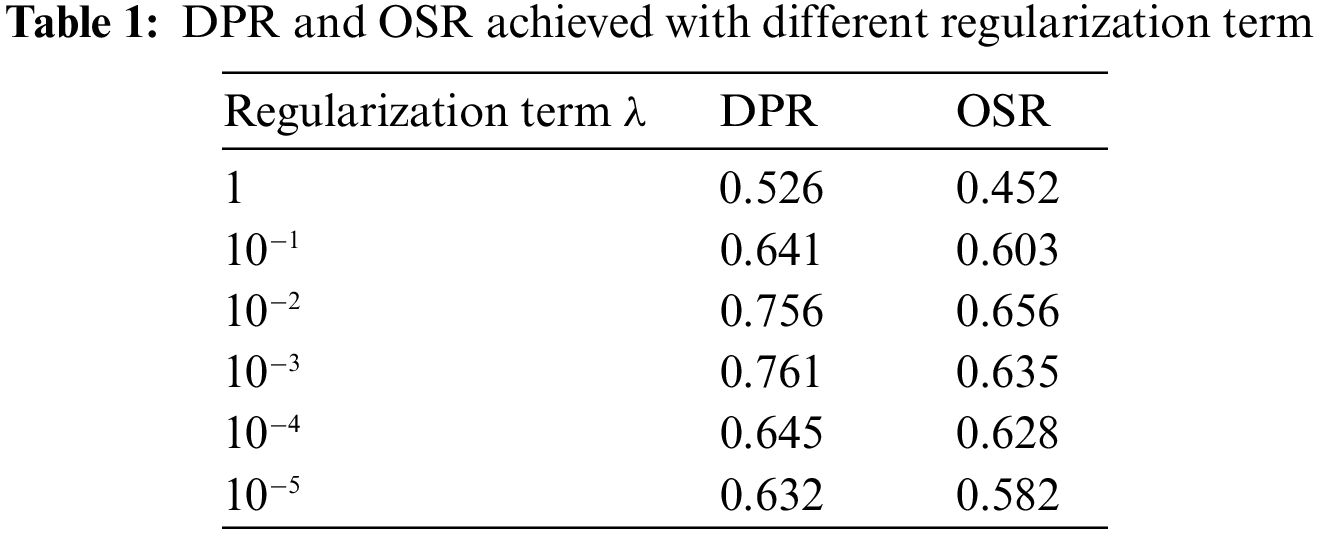
To evaluate the multi-time-space perception coupling tracking algorithm based on the correlation filter proposed in Section 3 comprehensively and objectively, a large number of experiments are carried out on the OTB2015 [32] benchmark, which contains 11 video challenge attributes, covering the complex scenes of various challenging factors contained in the real application environment. The sensitivity of the algorithm is analyzed by using the benchmark protocol and different parameter values, and the parameters with the best comprehensive tracking effect are selected. The parameter settings are as follows: the regularization parameter λ is 0.01, the object model update threshold T0 is 0.2, and the learning rate γ is 0.85. The proposed algorithm is compared with other four competing algorithms: KCF [12], C-COT [16], an unobtrusive multi-occupant detection (uMoDT) [9], and SiamRPN [25] from two aspects of quantitative analysis and qualitative analysis. The experimental simulation environment is MATLAB R2018b. The computer configuration are as follows: Intel Core i7-8550U CPU, 2.0 GHZ frequency, 8GB memory, and Windows 10 operating system.

The regularization term prevents model overfitting, and its value affects the tracking performance directly. If λ is too small, the regularization term is inactive. In contrast, if λ is too large, the regularization term dominates the overall error. The distance precision rate (DPR) and overlap success rate (OSR) achieved by the proposed tracker with different regularization terms are listed in Table 1. As the regularization term changes slowly, it is proved that the proposed multi-space-time perception model has strong stability while bringing performance gain.

4.1 Evaluating Indicator

The experiments in this study are mainly carried out on the OTB2015 and the TC-128 benchmarks. The algorithm is compared and analyzed with two evaluation indexes which are DPR and OSR.

(1) DPR

The center position error (CPE) is calculated by using the Euclidean distance between the center point of the object position and the center point of the manually marked object. As CPE decreases, the accuracy and stability of the algorithm increase. DPR refers to the percentage of video frames whose Euclidean distance are less than a given threshold. With different thresholds and different ratios, a curve is obtained. Generally, the threshold is set to 20 pixels.

(2) OSR

The overlap rate (OR) is calculated by using the predicted bounding box S1 estimated by the tracking algorithm and the ground-truth bounding box S2. As the OR increases, the success rate increases. The intersection and union of these two bounding boxes S1 and S2 are represented by ∩ and ∪, and Area(⋅) represents the area. The OR S is calculated using S=|Area(S1∩S2)|/|Area(S1∪S2)|. OSR represents the percentage of video frames whose OR scores are bigger than another given threshold.

4.2 Quantitative Analysis

The algorithms will be evaluated and analyzed on the OTB2015 and the TC-128 benchmarks.

4.2.1 Experiment on the OTB2015

(1) Comparison and analysis of DPR

The typical evaluation method is to initialize the object position in ground-truth for the tracking of subsequent frames, so as to calculate the accuracy and success rate of other frames. This evaluation standard is called one-pass evaluation (OPE). Fig. 3 shows the comparison results of CPE of different algorithms in different video sequences where the objects are disturbed by occlusion for a long time, motion blur, and scale variation. The results show that the uMoDT algorithm is prone to tracking loss when the background and foreground colors are similar. Although the SiamRPN algorithm achieves a good tracking effect, its efficiency is low due to the increase in re-location per frame. The CPE of the algorithm in this study maintains a low value, and its the maximum is only 23. The tracking window can converge to the object area and maintain good tracking results.

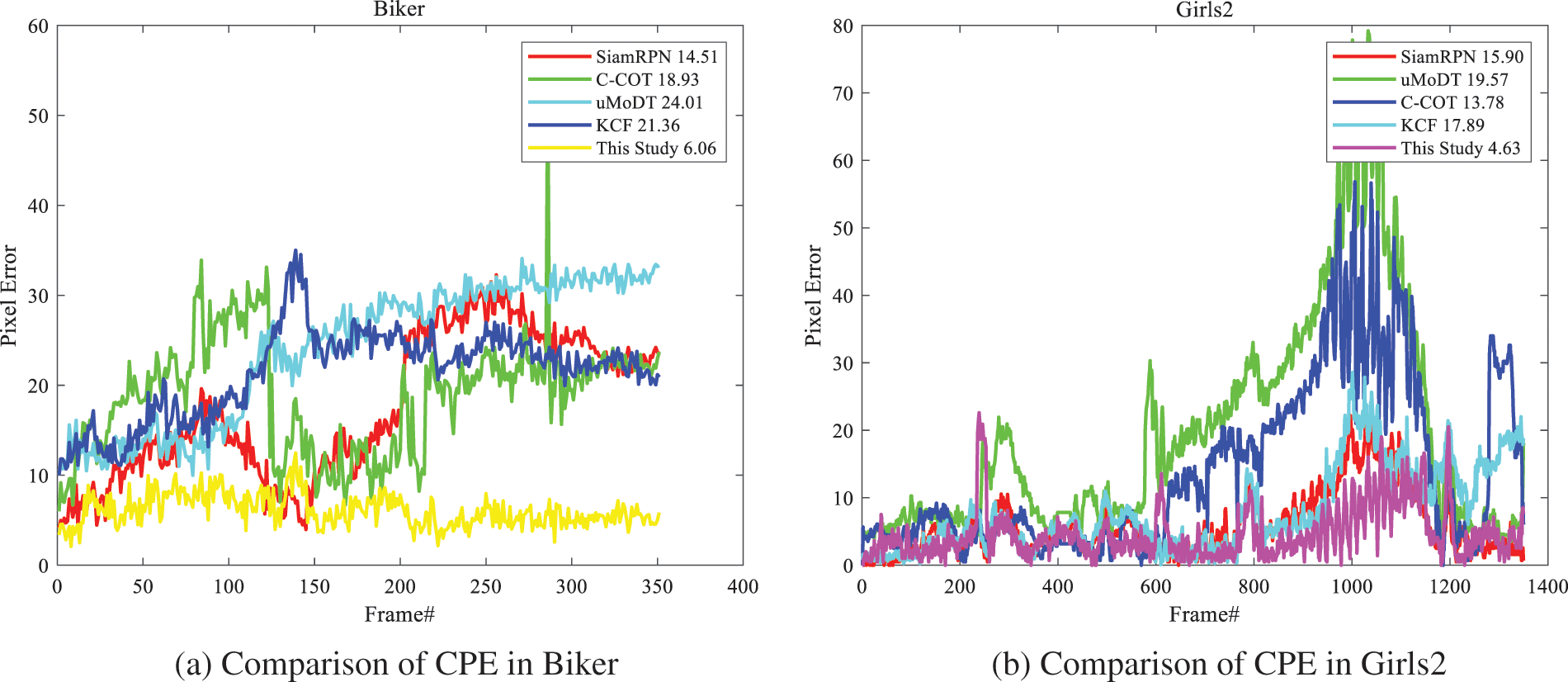
Figure 3: Comparison results of CPE in different test videos

The object in the video sequence Biker has the characteristics of motion blur, low resolution, and fast motion. The comparison results of the DPR of different algorithms in the video sequence Biker are shown in Fig. 4. Fig. 4a shows the maximum response curve of the algorithm in this study in each frame of the video sequence. The maximum response values are above 0.2, which meets the threshold conditions, and the object model is updated commonly. As can be seen from Fig. 4b, when the threshold is set to 8, the DPR obtained by the algorithm in this study is close to 1, indicating the effectiveness of the threshold setting. Otherwise, the tracking accuracy of KCF and uMoDT algorithms are very low, which are close to 0. The object is correctly tracked only in the first few frames of the video sequence. When the object leaves the line of sight, the tracking will drift. In the later tracking process, the object cannot be located.

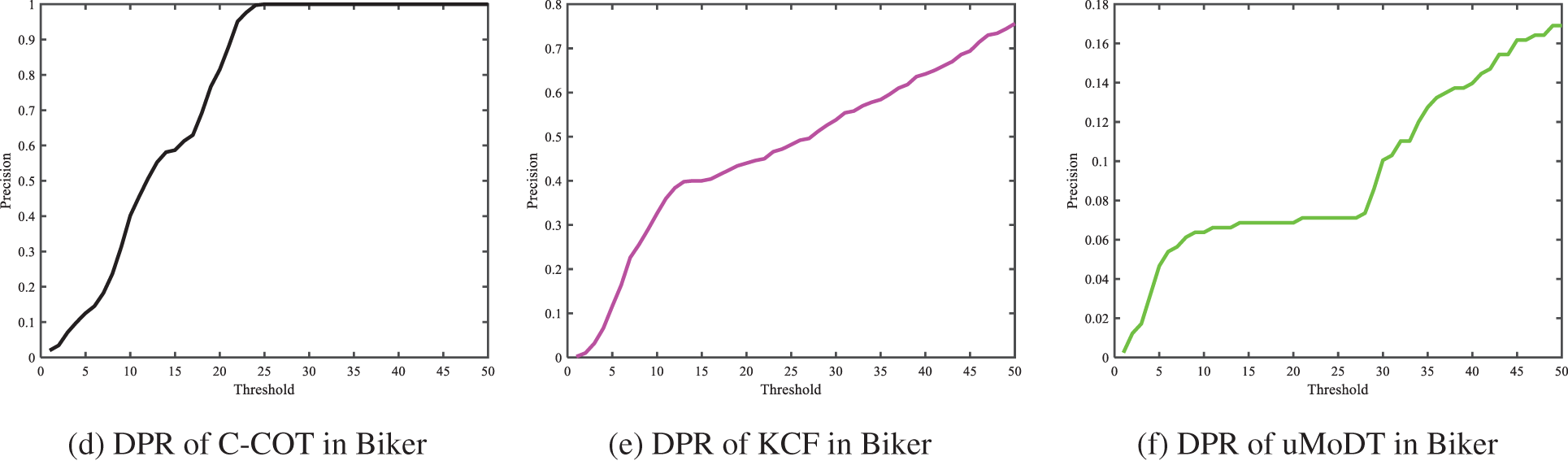
Figure 4: Comparison of DPR of different algorithms in Biker

Fig. 5 shows the complete statistical results of the DPR of the comparison algorithms on the OTB2015. The DPR of this study reaches 0.756, which is 19.6% higher than that of the second-ranked SiamRPN algorithm (0.608). Compared with the KCF tracker with a precision rate of 0.525, the performance is improved by more than 30.5%. In complex environments such as illumination variation and occlusion, the proposed algorithm achieves high accuracy and shows strong robustness. The proposed algorithm constructs an adaptive object function, which improves the tracking effect of the algorithm in various complex environments.

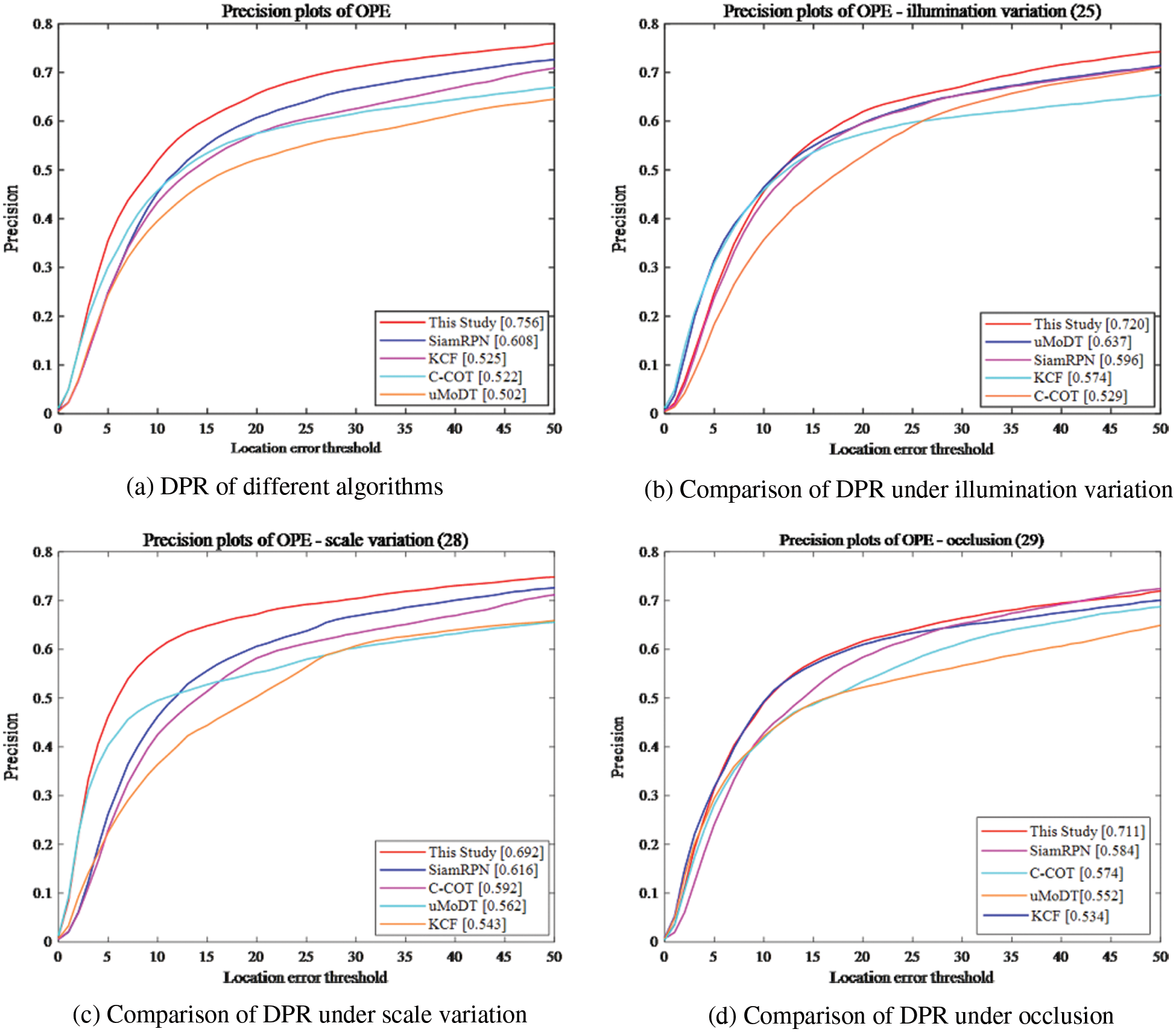
Figure 5: Comparison of DPR on the OTB2015

(2) Comparison and analysis of OSR

Fig. 6 shows the complete statistical results of the OSR of the comparison algorithms on the OTB2015. The OSR of this study reaches 0.656, which is 11.7% higher than that of the second-ranked SiamRPN algorithm (0.579). Compared with the KCF tracker whose accuracy is 0.516, the performance of the proposed algorithm is improved by more than 21.3%. In the video sequence where the object is occluded for a long time, the instance-specific proposal scheme designed in this study can better relocate the object and achieve a high success rate. Other comparison algorithms have poor performance in dealing with the problem that the object disappears for a long time.

Figure 6: Comparison of OSR on the OTB2015

Fig. 7 shows the comparison results of OR of different algorithms in video sequences Biker and Girls2. The average OR of the algorithm in this study are 0.70 and 0.82, respectively. The candidate region recommendation module is started since the object is out of view around frame 160, and the normal tracking mode is quickly restored. The OR of the uMoDT algorithm is only 0.25, and the robustness of this algorithm is weak in the scene of object disappearance.

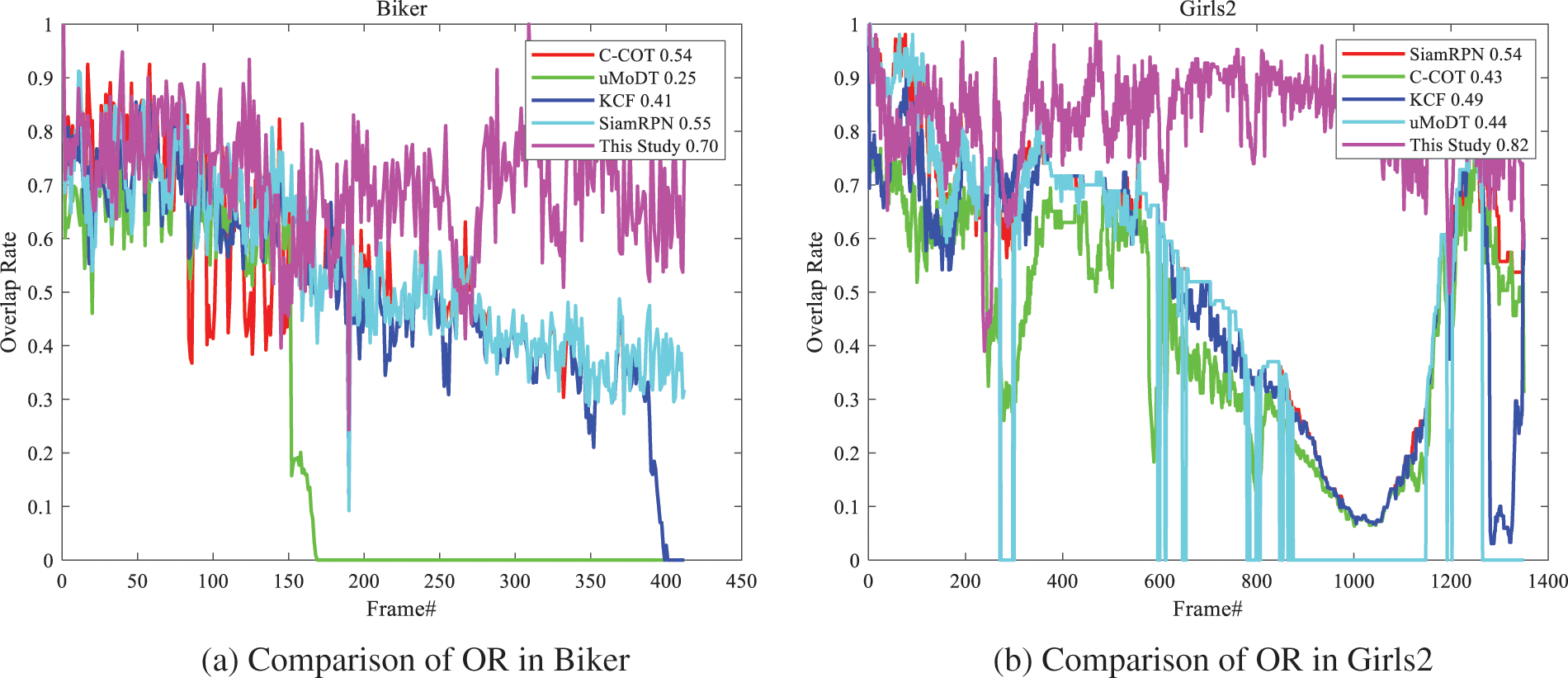
Figure 7: Comparison results of OR in different video sequences

(3) Performance analysis

The tracking speed described by FPS (frames per second) are shown in Table 2. Although the proposed tracker is not the fastest, it is better than other comparison trackers in the tracking accuracy. The proposed algorithm has a tracking speed of 60FPS, which can meet the real-time tracking requirements.

Fig. 8 shows the OSR and tracking speed between the proposed tracker and other comparison trackers on the OTB2015. The abscissa represents the tracking speed, and the ordinate represents the OSR. The results show that the proposed tracker achieves the highest tracking accuracy. However, the tracking speed needs to be improved. In the future study, we prepare to use the SVM to optimize the re-location module to improve the speed of the proposed algorithm.

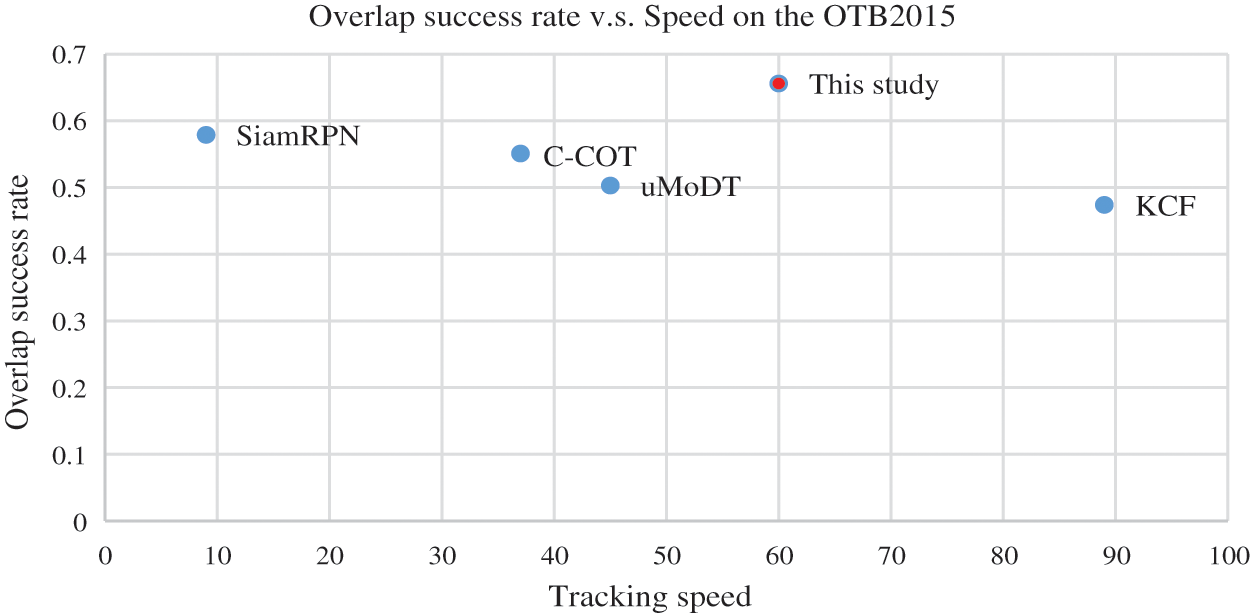
Figure 8: Comparison of the efficiency of different algorithms

4.2.2 Experiment on the TC-128

The comparisons with the state-of-the-art trackers on the TC-128 [33], including KCF [12], C-COT [16], uMoDT [9], and SiamRPN [25], are shown in Table 3. The first and second best values are highlighted in bold and underlined. It shows that the proposed tracking algorithm obtains the best performance with a DPR of 0.749 and an OSR of 0.637. Compared with uMoDT, the proposed algorithm achieves significant improvements, which shows the benefits of using the multi-time-space perception objective function model.

4.3 Qualitative Analysis

The comprehensive effects of the algorithms on all video sequences of the OTB2015 are analyzed and discussed in Section 4.2. The visualization results in all video sequences of the OTB2015 and the TC-128 benchmarks will be analyzed to more intuitively illustrate the accuracy of the proposed algorithm in this section. Fig. 9 shows the visual comparison results between the proposed algorithm and the other four competing algorithms (KCF, C-COT, uMoDT, and SiamRPN) in four typical video sequences, namely, Car2, Car4, Biker, and Girl2 with different complex environments.

Figure 9: Qualitative comparison of different algorithms in typical video sequences

The fast speed, low resolution, and significant background interference of the object in the video sequence Car2, as shown in Fig. 9a, lead to significant central position error and small overlap rate when the object changes lanes, but it can still ensure that the object is in the tracking box. When the object is gradually away from the line of sight, other comparison algorithms can also track the object correctly, but there are some deviations. It shows that these algorithms are robust in complex environment with low resolution and changing illumination. The speed of the tracking object in the video sequence Car4, as shown in Fig. 9b, is fast, and the illumination changes significantly, which leads to some errors in tracking when the object changes lanes, but there is no failure. The SiamRPN algorithm has different degrees of drift and even leads to tracking failure. The KCF algorithm drifts from 100 frames, and the overlap rate is 0. Around 450 frames, the overlap rate rises to 0.3, which still can’t meet the standard of accurate tracking. The resolution is low in the video sequence Biker, as shown in Fig. 9c, and the motion blur phenomenon occurs in the rapid movement of the object. When the object is gradually away from the line of sight, the proposed algorithm results deviate from the manual annotation, causing a central position error, which is close to the tracking effect of the C-COT algorithm and SiamRPN algorithm. Due to the rotation change of the object attitude, other comparison algorithms drift and fail. The object in Fig. 9d has deformation and rotation, and other comparison algorithms cannot accurately locate the object. However, the proposed tracker benefits from the robust object appearance representation model, which can locate the object accurately. The SiamRPN tracker performs well in deformation and fast-moving sequences (Car2), but fails to track in sequences where the object is occluded (Girls2). Other comparison algorithms can’t solve the problem of object tracking in complex scenes with both deformation and background interference. The qualitative analysis results show that the multi-time-space perception coupling model can adapt to the complex scenes such as background noise, illumination change, color similarity, and occlusion. The proposed algorithm has obvious advantages, which further verifies the effectiveness of the re-detection module.

4.4 Failure Cases

In the Gym video sequence of the OTB2015, the proposed approach performs poor in the presence of in-plane rotation. As the proposed algorithm uses instance-specific proposals with a small step size to generate scale proposals that consider the background regions as parts, the model is updated inaccurately in the rotation scene.

5  Conclusion

Starting with modeling the objective function, the filter model of multi-time-space perception is designed based on exploring the coupling relationship between different feature filter models and sparse constraints of different filter models. The following conclusions can be drawn:

(1) Considering the small changes between the object and background of two adjacent frames, the prediction accuracy can be improved by constructing a multi-time-space perception coupling objective function to train the object model, which is adaptively optimized according to the real environment.

(2) The mask matrix and the constraints term of time-space perception are introduced into the object function to enhance the learning ability of the CF to optimize the final tracking results.

(3) The maximum response is dynamically weighted to realize the object position estimation. In the optimization process, trade-off coefficients are added to balance the background interference on different feature contributions, which reduces the risk of tracking drift.

(4) Aiming at solving the tracking loss caused by severe occlusion of the object, the optimal instance-specific proposals are selected as the re-detection result by minimizing the weight of confidence and the Euclidean distance. In this way, the proposed algorithm can maintain high robustness and efficiency in the long-term tracking.

For the sensitive performance of a single filter model in complex scenes, the adaptive multi-time-space perception model designed in this study shows strong robustness in various complex scenes, which has a specific reference for the subsequent development of traffic event processing.

Funding Statement: This research was funded by the Basic Science Major Foundation (Natural Science) of the Jiangsu Higher Education Institutions of China (Grant: 22KJA520012), the Xuzhou Science and Technology Plan Project (Grant: KC21303, KC22305), and the sixth “333 project” of Jiangsu Province.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. J. P. Sun, E. J. Ding, B. Sun, L. Chen and M. K. Kerns, “Image salient object detection algorithm based on adaptive multi-feature template,” DYNA, vol. 95, no. 6, pp. 646–653, 2020. [Google Scholar]

2. D. Li, J. Bao, S. Yuan, H. Wang and W. Liu, “Image enhancement algorithm based on depth difference and illumination adjustment,” Scientific Programming, vol. 1, no. 1, pp. 1–10, 2021. [Google Scholar]

3. J. P. Sun, “Improved hierarchical convolutional features for robust visual object tracking,” Complexity, vol. 3, no. 3, pp. 1–16, 2021. [Google Scholar]

4. J. Tünnermann, C. Born and B. Mertsching, “Saliency from growing neural gas: Learning pre-attentional structures for a flexible attention system,” IEEE Transactions on Image Processing, vol. 28, no. 11, pp. 5296–5307, 2019. [Google Scholar]

5. D. Li, L. L. Bei, J. N. Bao, S. Z. Yuan and K. Huang, “Image contour detection based on improved level set in complex environment,” Wireless Networks, vol. 27, no. 7, pp. 4389–4402, 2021. [Google Scholar]

6. J. Akhtar and B. Bulent, “The delineation of tea gardens from high resolution digital orthoimages using mean-shift and supervised machine learning methods,” Geocarto International, vol. 36, no. 7, pp. 758–772, 2021. [Google Scholar]

7. M. Majd and R. Safabakhsh, “Correlational convolutional LSTM for human action recognition,” Neurocomputing, vol. 396, no. 1, pp. 224–229, 2020. [Google Scholar]

8. W. Howard, S. K. Nguang and J. W. Wen, “Robust video tracking algorithm: A multi-feature fusion approach,” IET Computer Vision, vol. 12, no. 5, pp. 640–650, 2018. [Google Scholar]

9. M. A. Razzaq, J. Medina, I. Cleland, C. Nugent, S. Lee et al., “An unobtrusive multi-occupant detection and tracking using robust kalman filter for real-time activity recognition,” Multimedia Systems, vol. 26, no. 5, pp. 553–569, 2020. [Google Scholar]

10. L. Meng and X. Yang, “A survey of object tracking algorithms,” Acta Automatica Sinica, vol. 45, no. 7, pp. 1244–1260, 2019. [Google Scholar]

11. Q. Y. Liu, Y. R. Wang, J. L. Zhang and M. H. Yin, “Research progress of visual tracking methods based on correlation filter,” Acta Automatica Sinica, vol. 45, no. 2, pp. 265–275, 2019. [Google Scholar]

12. J. F. Henriques, R. Caseiro, P. Martins and J. Batista, “High-speed tracking with kernelized correlation filters,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 37, no. 3, pp. 583–596, 2015. [Google Scholar] [PubMed]

13. S. Hare, A. Saffari and P. H. S. Torr, “Struck: Structured output tracking with kernels,” IEEE Transactions on Pattern Analysis & Machine Intelligence, vol. 38, no. 10, pp. 2096–2109, 2015. [Google Scholar]

14. M. H. Liu, C. S. Wang, Q. Hu, C. X. Wang and X. H. Cui, “Part-based object tracking based on multi collaborative model,” Journal of Software, vol. 31, no. 2, pp. 511–530, 2020. [Google Scholar]

15. H. Karunasekera, H. Wang and H. Zhang, “Multiple object tracking with attention to appearance, structure, motion and size,” IEEE Access, vol. 7, pp. 104423–104434, 2019. [Google Scholar]

16. S. Shen, S. Tian, L. Wang, A. Shen and X. Liu, “Improved C-COT based on feature channels confidence for visual tracking,” Journal of Advanced Mechanical Design Systems and Manufacturing, vol. 13, no. 5, pp. JAMDSM0096, 2019. [Google Scholar]

17. Y. Kim, W. Han, Y. H. Lee, C. G. Kim and K. J. Kim, “Object tracking and recognition based on reliability assessment of learning in mobile environments,” Wireless Personal Communications, vol. 94, no. 2, pp. 267–282, 2017. [Google Scholar]

18. C. Ma, J. B. Huang, X. K. Yang and M. Hsuan, “Robust visual tracking via hierarchical convolutional features,” Transactions on Pattern Analysis and Machine Intelligence, vol. 41, no. 11, pp. 2709–2723, 2019. [Google Scholar]

19. D. Yuan, X. M. Zhang, J. Q. Liu and D. H. Li, “A multiple feature fused model for visual object tracking via correlation filters,” Multimedia Tools and Applications, vol. 78, no. 19, pp. 27271–27290, 2019. [Google Scholar]

20. Q. L. Liu and Y. D. Liu, “Long-term object tracking algorithm based on self-adaptive fusion,” Journal of Chengdu University (Natural Science Edition), vol. 38, no. 3, pp. 281–286, 2019. [Google Scholar]

21. P. Z. Liu, X. H. Ruan, Z. Tian, W. J. Li and H. Qin, “A video tracking method based on object multi-feature fusion,” CAAI Transactions on Intelligent Systems, vol. 9, no. 3, pp. 319–324, 2014. [Google Scholar]

22. Z. Lai, E. Lu and W. Xie, “MAST: A memory-augmented self-supervised tracker,” in IEEE/CVF Conf. on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, United States, pp. 6478–6487, 2020. [Google Scholar]

23. P. Voigtlaender, J. Luiten and P. H. S. Torr, “Siam R-CNN: Visual tracking by re-detection,” in IEEE/CVF Conf. on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, United States, pp. 6577–6587, 2020. [Google Scholar]

24. S. Basalamah, S. D. Khan and H. Ullah, “Scale driven convolutional neural network model for people counting and localization in crowd scenes,” IEEE Access, vol. 7, pp. 71576–71584, 2019. [Google Scholar]

25. Z. L. Zhang and Y. X. Wang, “SiamRPN target tracking method based on kalman filter,” Intelligent Computer and Applications, vol. 10, no. 3, pp. 44–50, 2020. [Google Scholar]

26. A. Pareek and N. Arora, “Re-projected SURF features based mean-shift algorithm for visual tracking,” Procedia Computer Science, vol. 167, no. 4, pp. 1553–1560, 2020. [Google Scholar]

27. J. N. Shan and H. W. Ge, “A long-term object tracking algorithm based on deep learning and object detection,” CAAI Transactions on Intelligent Systems, vol. 16, no. 3, pp. 433–441, 2021. [Google Scholar]

28. P. Wang, J. G. Chen and M. M. Wang, “Improved target tracking algorithm based on kernelized correlation filter in complex scenarios,” Computer Engineering and Applications, vol. 57, no. 2, pp. 198–208, 2021. [Google Scholar]

29. J. P. Sun, E. J. Ding, B. Sun, Z. Y. Liu and K. L. Zhang, “Adaptive kernel correlation filter tracking algorithm in complex scenes,” IEEE Access, vol. 8, pp. 208179–208194, 2020. [Google Scholar]

30. S. Boyd, N. Parikh, E. Chu, B. Peleato and J. Eckstein, “Distributed optimization and statistical learning via the alternating direction method of multipliers,” Foundations & Trends in Machine Learning, vol. 3, no. 1, pp. 1–122, 2011. [Google Scholar]

31. H. Liu, Q. Y. Hu, B. Li and Y. Guo, “Robust long-term tracking via instance-specifific proposals,” IEEE Transactions on Instrumentation and Measurement, vol. 69, no. 4, pp. 950–962, 2020. [Google Scholar]

32. Y. Wu, J. Lim and M. H. Yang, “Object tracking benchmark,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 37, no. 9, pp. 1834–1848, 2015. [Google Scholar] [PubMed]

33. P. Liang, E. Blasch and H. Ling, “Encoding color information for visual tracking: Algorithms and benchmark,” IEEE Transactions Image Process, vol. 24, no. 12, pp. 5630–5644, 2015. [Google Scholar]