Docurity: A New Cryptographic Primitive for Collaborative Cloud Systems

1  Introduction

The advances of cloud, web, 6G, and beyond wireless network technologies brought a new era of office productivity applications. In recent years, collaborated cloud-based office suites such as Microsoft Office 365 and Google G Suite have been adopted by a significant number of office workers and the market is expected to grow continuously [1]. Such cloud-based systems allow users to work together on the same document stored in a cloud server at once, by which users can effectively collaborate with each other. On the other hand, the drastic shift to collaborative cloud-based platforms has raised concerns regarding the security of data stored in cloud servers [2].

There have been many studies on the security of cloud storage and dynamic data, most of them focused on storing data safely [3], the proof of integrity such as Provable Data Possession (PDP) [2,4–6], and Proof of Retrievability (PoR) [7–9]. With PDP techniques, users can verify the integrity of encrypted data on a cloud server without decryption. PoR techniques support not only checking integrity, but also a way to recover users’ data. However, the current security posture for protecting data used in cloud collaboration still has not been approached to the fundamental level—the data cannot be stored in encrypted form.

For protecting users’ data in a cloud server from various threats, the data should be stored securely, preventing disallowed access to it. To this end, as the bottom line, we need to keep data encrypted in a server. However, we currently cannot avoid the use of unencrypted data stored in cloud servers due to the dynamic nature of collaborative cloud-based systems—users’ data needs to be updated dynamically by multiple users at once—and the absence of a cryptographic primitive that is able to securely store and update ciphertext. Albeit, technically, the Electronic Code Book (ECB) mode of the Advanced Encryption Standard (AES) algorithm can be used to update ciphertext, the cryptological weakness of the mode hinders it to be used in practice for real-world systems [10]. Consequently, if we must use encrypted data for collaborative cloud-based applications, the best practical way to keep the security of the data seems to decrypt and re-encrypt the whole data every time when we update it.

In this work, our goal is to design, implement, and evaluate a new security primitive to securely store users’ data and enable encrypted data in collaborative cloud-based systems. To this end, we propose a novel mode of operation for AES, called Double Linked ECB (DL-ECB), based on the traditional ECB mode. The core idea of the DL-ECB mode is to insert “links” between data blocks and use two types of metadata for indexing bytes in ciphertext to update it. A link is a 1-byte-size random number, and we insert it in the first and the last byte of each plaintext block. To be specific, we put the same link into the first and the last byte of two successive blocks, and thus, it appears as if blocks are connected through links. By using the link with the metadata, we can update (modification, insertion, and deletion) ciphertext without decrypting it and improve the secrecy, overcoming the lack of diffusion of the ECB mode. Furthermore, the DL-ECB mode provides other advantages as follows: (1) Data blocks do not need to be linearly addressed in the virtual memory space because we manage each data block by using the double-linked list, by which we can conveniently insert and delete data blocks of ciphertext; and (2) We can verify the integrity of cipher text and check whether the blocks are out of order or not. To sum up, the DL-ECB mode can preserve the confidentiality, integrity, and auditability of users’ data used in collaborative cloud systems from adversaries who try to leak users’ data.

To demonstrate the effectiveness and performance of the DL-ECB mode, we implemented the prototype of the DL-ECB mode on top of the encryption and decryption functions of the AES algorithm and thoroughly evaluated the prototype. Our experimental results show that the DL-ECB mode has impressive performance as the first step towards the cryptographic primitive for collaborative cloud-based systems: In our evaluation, when it updates ciphertext, the DL-ECB mode is roughly 20 times faster than the others, even though the DL-ECB mode has the nonnegligible runtime overhead to encrypt and decrypt the whole data and storage overhead. We release the source code of our proof-of-concept implementation at https://github.com/ssu-csec/Docurity.

Contribution: The paper makes the following contributions:

•   We propose a novel mode of operation, DL-ECB, by which we can modify, insert, and delete the ciphertext based on changes in plaintext. Therefore, we can use encrypted data in collaborative cloud-based platforms.

•   We implement and evaluate the DL-ECB mode to demonstrate that the DL-ECB mode can preserve the confidentiality, integrity, and auditability of users’ data used in collaborative cloud systems from adversaries.

2  Background

In this section, to illustrate the problem that we are going to address in this paper, we first introduce collaborative cloud-based systems. Next, we discuss the Advanced Encryption Standard (AES), a variant of the Rijndael block cipher established by the U.S. National Institute of Standards and Technology (NIST) [11], and its modes of operation.

2.1 Collaborative Cloud-Based Systems

A collaborative cloud-based system is a platform where multiple users can work together on documents simultaneously [12]. To use a collaborative cloud-based system, data needs to be stored in a cloud server. At the same time, the data can be dynamically changed by users, and changes made by one user should be instantly reflected to the others so that they can always view identical data from different locations. Because of such very dynamic characteristics of cloud collaboration, data that multiple users are working together cannot be stored in encrypted form. In addition, to the best of our knowledge, there are no security primitives implemented and used in real-world systems that can dynamically update encrypted data. Therefore, data used in collaborative cloud-based systems have high-security risks because the data itself is unprotected information that is easily readable, and its integrity can be broken at any time. We analyze the security policies of two well-known collaborative cloud-based systems—Overleaf and Google docs editors.

2.1.1 Overleaf

Overleaf is a collaborative LaTex editing platform. It supports 256-bit Transport Layer Security (TLS) encryption for secure network connections and secure storage featuring electronic access cards, perimeter fencing, etc. However, Overleaf does not guarantee data privacy.

2.1.2 Google Docs Editors

Google docs editors are web-based office suites provided by Google within its Google Drive service, which include Google Slides, Docs, and so forth. Google docs editors store users’ data in their cloud server which provides security features like Overleaf. However, they also do not guarantee data privacy and they can access users’ data.

As such, currently, when users use cloud collaboration, their data is not secured because the data is not stored encrypted due to the absence of cryptographic primitives for updating encrypted data. Therefore, it is greatly important to design and implement a new cryptographic primitive for securing users’ data used in collaborative cloud-based systems.

2.2 Advanced Encryption Standard (AES)

Albeit asymmetric key cryptography algorithms provide strong security, we generally do not use them for protecting large data due to their high time and space complexity, but we rather use block cipher algorithms (i.e., symmetric key cryptography algorithms) [13]. Among the block cipher algorithms, Advanced Encryption Standard (AES) is the de facto standard block cipher algorithm established in 2001. The AES works with multiple modes of operation that can allow us to use the algorithm efficiently and strengthen the algorithm [14].

2.3 Modes of Operation of AES

We briefly introduce the AES modes of operation and discuss them. Encryption processes of all modes of operation explained below are in Fig. 1.

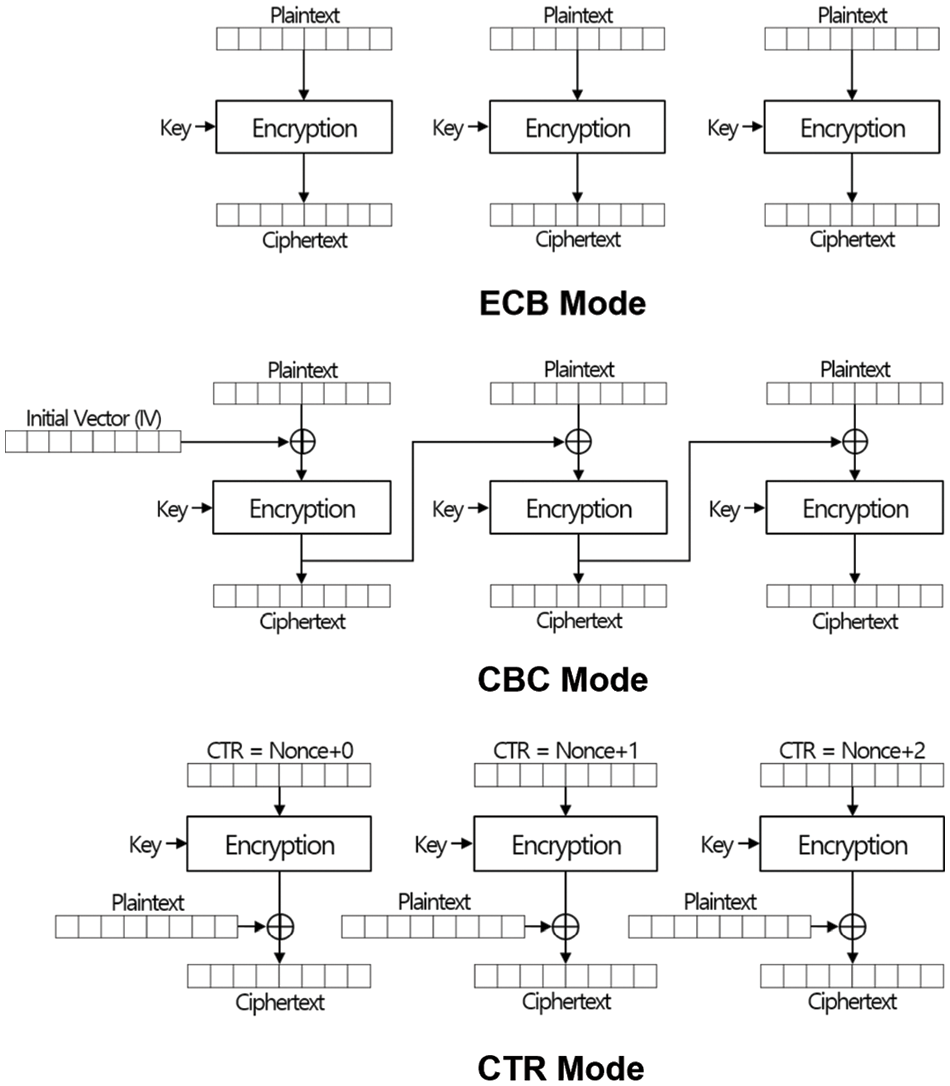
Figure 1: Encryption processes of the traditional modes of operation

2.3.1 Electronic Code Book (ECB) Mode

ECB Mode cuts the entire plaintext into blocks of a specific length and encrypts it using block cipher. The ECB mode operates on each block, and thus if an error occurs in a block or a block is inserted or deleted, it does not affect operations on the other blocks. Because the ECB mode does not use an initialization vector or block chaining (two identical blocks of plaintext will become two identical blocks of ciphertext with the same key), it is easy to implement, but cryptologically weak [15].

2.3.2 Cipher Block Chaining (CBC) Mode

CBC Mode encrypts a block of plaintext by using the previously encrypted block. It uses an initial vector for the first block that does not have a previous one. Hence, even if the same plaintext is encrypted with the same key, the ciphertext will be totally different as far as the initial vector is different. On the other hand, the same initial vector must be used to decrypt the ciphertext. The interlinkability of the CBC mode makes it cryptologically strong, but it is not possible to operate on blocks of plaintext in parallel and modify encrypted blocks.

2.3.3 Counter (CTR) Mode

CTR Mode uses a nonce, which is a random value of the block size for encryption and decryption processes to provide strong security16. With the CTR mode, parallel processing on multiple blocks is possible. Also, if we know the nonce, we can modify specific blocks of ciphertext, but we cannot change the order of blocks—insertion, and deletion of blocks is also not possible [16].

In summary, the modes of operation of AES are not able to dynamically and efficiently update encrypted data stored in a cloud server, which includes insertion, deletion, and modification of ciphertext blocks. In other words, currently, there is no mode of operation that can be used in collaborative cloud-based systems for protecting users’ data securely.

There exist other modes of operation like Output Feedback Mode (OFB) and Cipher Feedback mode (CFB). The previous block affects the next block like CBC in them. You can check the details in NIST Special Publication [17].

3  Design

In this section, we first show the goal and threat model of this work. We then, propose a new mode of operation for AES, called Double Linked ECB (DL-ECB), and demonstrate how we implement it for collaborative cloud-based systems.

3.1 Goal

In this work, we aim to design, implement, and evaluate a novel cryptographic primitive for protecting data used in collaborative cloud-based systems. To be specific, we focus on designing a new mode of operation of AES, de facto standard block cipher algorithm, to be practically adopted by real-world systems. This new cryptographic primitive, named Double Linked ECB (DL-ECB), enables encrypted data stored in a cloud server to be updated dynamically so that multiple users can work on the data at once as well as the data can be stored in a cloud server securely in encrypted form. Because previously used modes of operations are not capable of updating ciphertext (insertion, deletion, and modification of specific parts), we need to decrypt and re-encrypt the whole ciphertext to update it. However, with DL-ECB, the data always stays in a server in encrypted form, while users can efficiently update it at any time from the client side. Therefore, we can consider plaintext of users’ data cannot be revealed by anyone as far as the secret key is not leaked.

3.2 Threat Model

Our defensive goal is to preserve the confidentiality, integrity, and auditability of users’ data used in collaborative cloud systems from adversaries who try to leak users’ data. In this work, we assume that cloud servers can be compromised by exploiting vulnerabilities in the servers so that attackers can breach and obtain users’ data. Therefore, if users’ data was not encrypted, attackers can read all the data in a cloud server. Also, we consider that there can be an inside adversary who can access arbitrary data in a cloud server. Because inside adversaries can access any files in a cloud server, if users’ data is not encrypted, they can easily read arbitrary data created by users like the first threat scenario. We believe that assuming such worst-case scenarios allows us to develop as strong a defense as possible. We will present our approach to address the threat model in the rest of this paper.

3.3 Double Linked ECB (DL-ECB)

We designed a novel model of operation based on the ECB mode of which the clear drawback is weak security. However, because it operates on each block with the same key, the ECB mode is efficient and can work on multiple blocks of plaintext in parallel, and random reading is available. We focus on the atomicity and efficiency of the ECB mode because our goal is to provide a novel cryptographic primitive to collaborative cloud-based systems where several users very frequently update a document together.

First of all, we have to address the lack of diffusion of the ECB mode caused by the fact that the ECB mode encrypts identical blocks of plaintext into identical ciphertext blocks (and thus, it cannot hide data patterns). In order to provide enough diffusion, we insert random numbers, called link, into the first and the last byte of each block of plaintext so that different ciphertext can be generated even when the same data is encrypted with the same key. However, when we insert the random numbers, we put the same number into the first and the last byte of two successive blocks. For example, the last byte of the second block and the first byte of the third block have the same random number. By doing so, when we decrypt blocks of ciphertext, we can find errors in each block by comparing the link values with adjacent blocks’ ones, which in turn, also, allows us to verify the integrity of ciphertext. Consequently, inserting the link in each data block improves the security of the ECB mode and adds advantages. You can see the detail encryption process of DL-ECB in Fig. 3.

Figure 2: Data structure of DL-ECB: We use the double linked list for managing data blocks of DL-ECB. Each node contains each ciphertext block which has 16-byte size and the address of previous node and next node

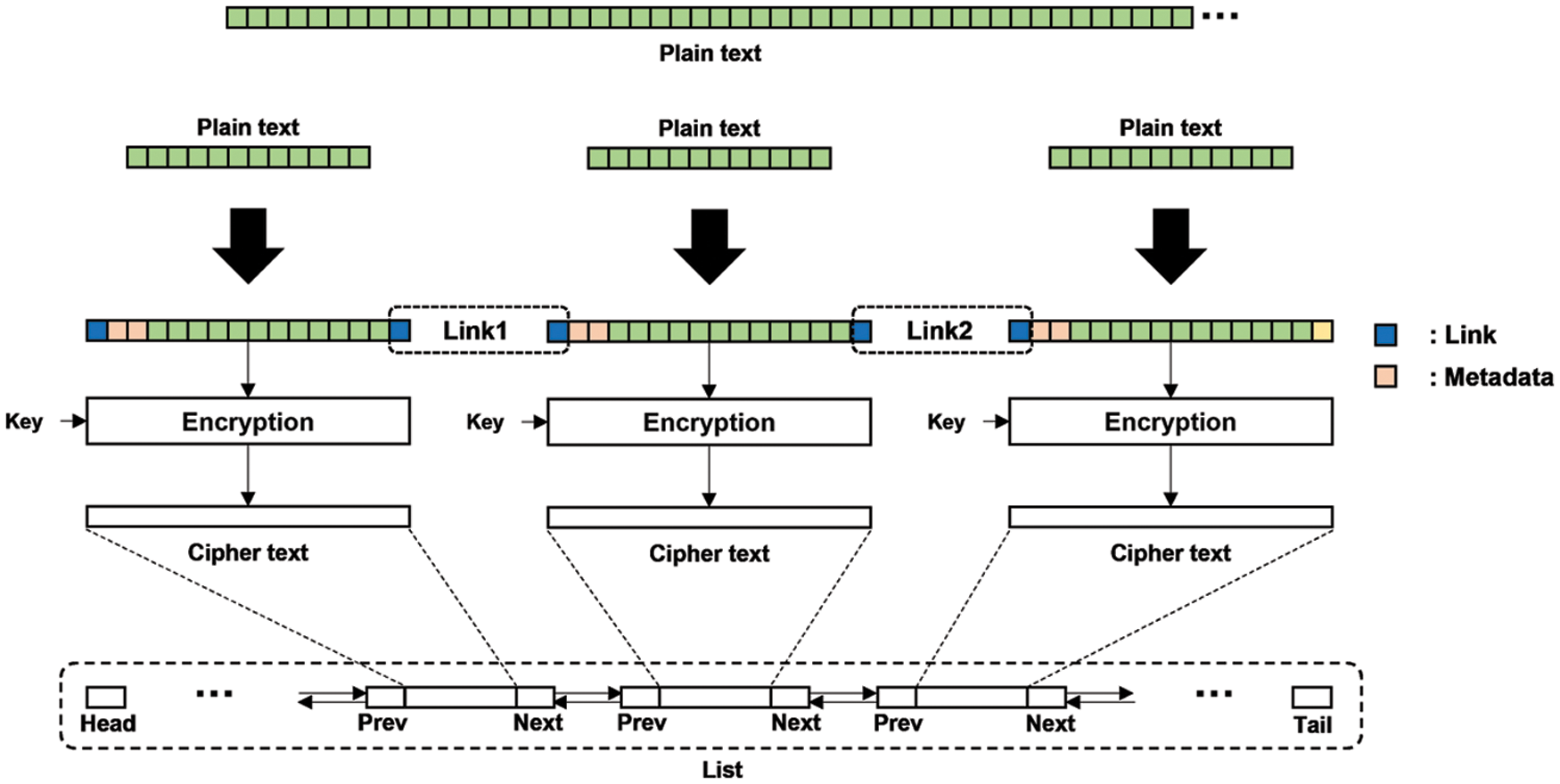
Figure 3: Encryption process of DL-ECB: Separate plaintext to the size per one block. Add a bitmap and links to the divided plaintext. Encrypt the data with AES. Make a node with the encrypted data

In addition, in DL-ECB mode, data blocks do not need to be linearly addressed in the virtual memory space because we manage each data block by using the “double linked list.” As in Fig. 2, adjacent data blocks are linked, pointing to each other. Hence, unlike existing modes of operation, we can conveniently insert and delete data blocks of ciphertext. This design enhances the security of the ECB mode and provides a way to check errors that can occur while updating ciphertext. Also, by using a double-linked list, we can save the search time of blocks. On the other hand, it increases the space complexity because we need to insert links in every block as well as the time complexity for additional computation processes. However, DL-ECB mode is the only mode of operation that can update ciphertext without needing to decrypt the whole blocks, and thus, we claim that it is more efficient to update the ciphertext than any other mode.

Next, to update ciphertext without decrypting it, we should be able to manage and pinpoint a specific byte to modify, insert, and delete. To this end, we use two types of metadata: Global metadata and a bitmap in each block. We will present our design of DL-ECB in detail in the rest of this section. We also, demonstrate how DL-ECB operates to dynamically update ciphertext.

3.4 Metadata of DL-ECB

We use two types of metadata data in the DL-ECB mode for finding the exact location (in a unit of byte) of data that are going to be updated in data blocks of ciphertext: Global metadata and a bitmap in a data block. We use the global metadata for finding which data block has user data that will be updated and use a bitmap of the data block for pinpointing the exact location of the data.

3.4.1 Global Metadata

In DL-ECB mode, we use the bitmap in each data block with global metadata that stores the number of valid bytes in data blocks. We note that invalid data does not only mean padded bytes for the encryption but also empty bytes that occurred by partial modifications such as insertion and deletion. Because the DL-ECB mode supports partial updates on ciphertext in an encrypted data block, there can be deleted bytes even in the middle of a data block. Each data block of the global metadata can represent how many bytes are valid in 12 data blocks and each byte in a data block of the global metadata has a value between 1 and 12 (because each data block used in the DL-ECB mode can have up to 12 bytes). When we want to insert data at the specific index of the plaintext, we cannot know which block contains the index with ciphertext because we do not know how many invalid bytes exist in each block. However, we can check the index of plaintext without decrypting all ciphertext with the global metadata. The global metadata is also encrypted by the DL-ECB mode without a bitmap so we can guarantee the confidentiality of global metadata.

3.4.2 Data Block and Bitmap

For using DL-ECB, we need to insert two links in the first and the last bytes of each block. Also, we need to put a bitmap right after the first byte where a link value is stored to find which byte in a block currently has valid data. The bitmap is used to pinpoint the exact byte of plaintext to modify it. Also, by using the bitmap, we can verify whether the data pointed from a user’s request for updating is valid or not. For matching each bitmap and plaintext, we set the bitmap size as 2 bytes so that we can handle it in bytes. In AES, the size of each data block is 16-byte, and thus, each data block can have 12-byte of plaintext. The size of a bitmap is two bytes, but the size of actual data that can be stored in each data block is 12 bytes. We, thus, do not use the first 4 bits of a bitmap—we simply set them to zero. Fig. 4 illustrates how the data block is designed for the DL-ECB mode.

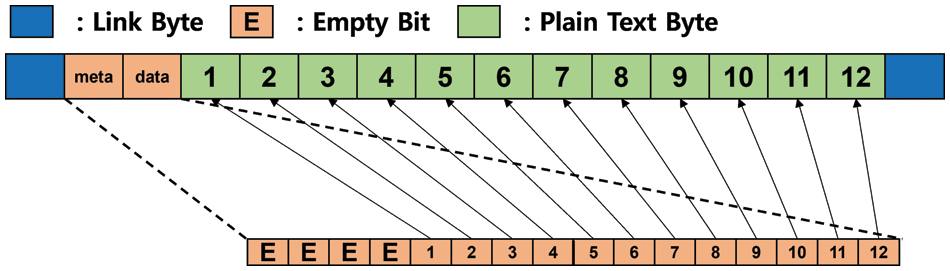
Figure 4: Block design and bitmap design

For indicating valid bytes in each block, we set each corresponding bit of a bitmap to 1. To be more specific, if the fifth bit of a bitmap is 1, the first byte has valid data, and vice versa. For example, if only the fifth byte does not have valid data and the other bytes have valid data, the ninth bit of a bitmap is 0 (also the unused first 4 bits are 0) and the other bits are all 1. Consequently, the bitmap of the data block is 0000111101111111. It is worth noting that, when we decrypt such data block, the invalid byte is stored as a blank character.

3.5 Operations of DL-ECB

3.5.1 Encryption

The DL-ECB’s encryption process consists of the following four steps: (1) Divide plaintext by 12-byte so that each block of plaintext can fit into a 16-byte block; (2) Generate links and a bitmap, then stores them in each data block; (3) Encrypt each block with the AES algorithm by using the secret key; and (4) Encapsulate each data block into a node of a linked list so that we can manage data blocks as we discussed in Section 3.3. Also, we should generate the global metadata for the encrypted plaintext and encrypt it. Algorithm 1 illustrates the encryption process.

3.5.2 Decryption

As Algorithm 3 demonstrates the decryption process, the DL-ECB mode consists of the following three steps: (1) Decrypt each block of ciphertext through the AES algorithm by using the secret key; (2) Verify whether or not adjacent blocks—linked each other in the double linked list—have correct link values that we inserted when encrypting a block (the first byte of a data block must be same as the last byte of a previous block); and (3) Check if a decrypted data block has an invalid data.

3.5.3 Insertion

When inserting new data into ciphertext, we first need to find the exact location where the data should be stored by using the global metadata after decrypting it. The insertion process can have the following two cases depending on the location where a new block should be stored: (1) When a new block of ciphertext needs to be stored between two blocks; and (2) When we must store a new ciphertext in the middle of an existing block. In the first case, we can insert new blocks by modifying links and the linked list as illustrated in Fig. 5. Therefore, if the number of inserted blocks is n, n + 2 blocks need to be modified. On the other hand, if we need to insert a new block in the middle of an existing one, we first decrypt the block where the new data should be inserted, and then, we concatenate the new data and re-encrypt the modified data. If the concatenated data is larger than 12 bytes (the maximum size of a data block), we should check the following block to check whether there is enough space to store new data. If so, we insert the remaining data (after inserting new data to the targeted block) in the next block, otherwise, we create a new data block. Fig. 6 demonstrates this process. Finally, after the insertion process is done, we update global metadata accordingly.

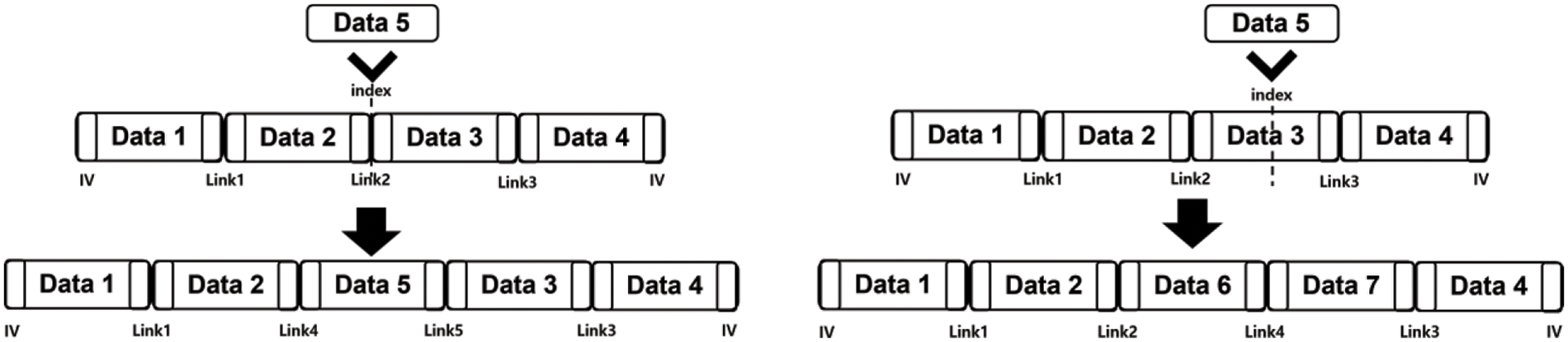
Figure 5: Inserting data between two blocks (left side) and inserting data in one block (right side)

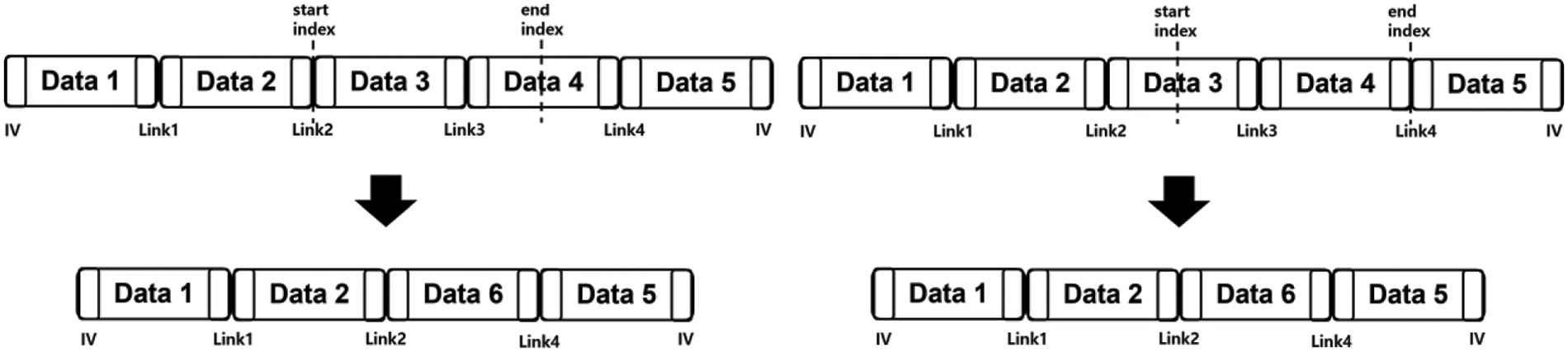
Figure 6: Deleting data from between two blocks to the middle of one block on the left side and deleting data from the middle of one block to between two blocks on the right side

3.5.4 Deletion

When deleting data from data blocks of cipher text, like the insertion process, we first find where the data is located by checking the global metadata. However, the deletion process can have four cases depending on the location of the first byte and the last byte of data that we are going to delete.

In the first and second cases, as in Fig. 6, the first byte or the last byte of data that we are going to delete is in the middle of a data block. In these cases, there must be remaining data of one data block. Therefore, we leave the data block where the remaining data is stored and change its link of it by using a link from a deleted block. The third case is when the first byte and the last byte of data that will be deleted are located at the first byte of one data block and the last byte of the same data block or another data block. In this case, we can simply delete data blocks of ciphertext as the left side of Fig. 7. The last case is when the first and the last indices are in the middle of data blocks as shown at the right side of Fig. 7. In this case, we decrypt two data blocks where the first and the last byte are located, and then, we merge remaining data from the blocks. Next, we should consider the size of the remaining data. If the remaining data is smaller than the size of a data block, we make a new data block and store the remaining data in it. We then insert this block between two adjacent blocks. When we insert the new data block, like in the third case, we can use links obtained from the blocks in which the first and the last indices are located. On the other hand, we generate blocks of more than two with the remaining data and link the blocks. Lastly, we insert the blocks between two adjacent blocks.

Figure 7: Deleting data from between two blocks to between two blocks on the left side and deleting data from the middle of one block to the middle of one block on the right side

4  Evaluation

In this section, we implement and evaluate the effectiveness and performance of the DL-ECB mode.

4.1 Security Analysis

The DL-ECB mode is designed based on the ECB mode for collaborative cloud-based systems, and thus, the security of the DL-ECB mode is guaranteed by its underlying scheme—AES algorithm [18]. However, the core idea of DL-ECB mode is the link that can add more confusion (a critical limitation of the ECB mode is the lack of diffusion) to improve the secrecy of ciphertext.

In addition, the DL-ECB mode can verify the integrity of ciphertext by using the link. We summarized these security properties as following two theorems with proofs.

Theorem 1. The proposed method is secure against a chosen-plaintext attack.

If the adversaries have a significant amount of plaintext and corresponding ciphertext, furthermore, if they can make the proposed method without the knowledge of how it works, the chosen-plaintext attack can occur. The adversaries can match each plaintext block and ciphertext block so when the ciphertext has any pattern, it is vulnerable to the attack.

Proof. By adding two random numbers of 1 byte (each data block has two link values), we can effectively prevent attacks that aimed to reveal plaintext encrypted by using the ECB mode such as the chosen plaintext attack. Consequently, even if adversaries can have all encrypted data blocks, we claim that confidentiality cannot be broken if the adversaries do not have the secret key or a polynomial time algorithm that can find ciphertext stored by the user with possible combinations of the secret key, plaintext, and links.

Theorem 2. The proposed method is secure against a poison attack.

With the poison attack, the adversaries try to change the data without any agreement from the user. If the adversaries succeed in changing some part of the ciphertext, users cannot notice that. Also, if the original data is not natural language, users cannot distinguish tainted data from the original data even after decrypting the data.

Proof. We recall that the link value of two adjacent blocks is the same. Therefore, even if ciphertext was somehow corrupted by adversaries and the ciphertext can be decrypted to validate plaintext, we can notice that the integrity of the ciphertext is broken by checking link values of two adjacent data blocks.

4.2 Runtime Performance on DL-ECB

Implementation and Experiment Setup. We implemented the proof-of-concept of the DL-ECB mode in C language by using the AES encryption and decryption functions implemented in Openssl v1.1.1. The prototype supports all operations as designed in this paper and consists of 908 SLoC. To benchmark the DL-ECB mode, we designed experiments as follows:

1.    Encryption and Decryption: We measured execution times of the encryption and decryption processes of the DL-ECB mode and the others, increasing the size of data.

2.    Insertion, Deletion, and Modification: We measured execution time for the insertion, deletion, and modification processes of the DL-ECB mode and the others, increasing the size of data that we insert, delete and modify to/from ciphertext. Also, we set the initial size of the ciphertext to be around 100 MB for the main graph of operations and then change the initial size and modification size for more experiments. The initial data size and modified data size are in each graph. When we performed these experiments with the other modes of operation, we measured execution times from when they start decrypting ciphertext to re-encrypt it because they do not support those operations.

We performed experiments for evaluating execution times of each operation of the DL-ECB mode on a workstation equipped with an Intel(R) Xeon(R) Gold 6230 CPU @ 2.10 GHz and 188 G RAM memory, running Ubuntu 20.04 LTS.

Figs. 8 and 9 demonstrate the evaluation results for each operation of the DL-ECB mode, comparing them with the execution times of the other modes of operation. As we discussed, the encryption and decryption processes of the DL-ECB mode are slower than the others as in Fig. 8. This is because of the DL-ECB mode’s additional operations using the global metadata and bitmaps.

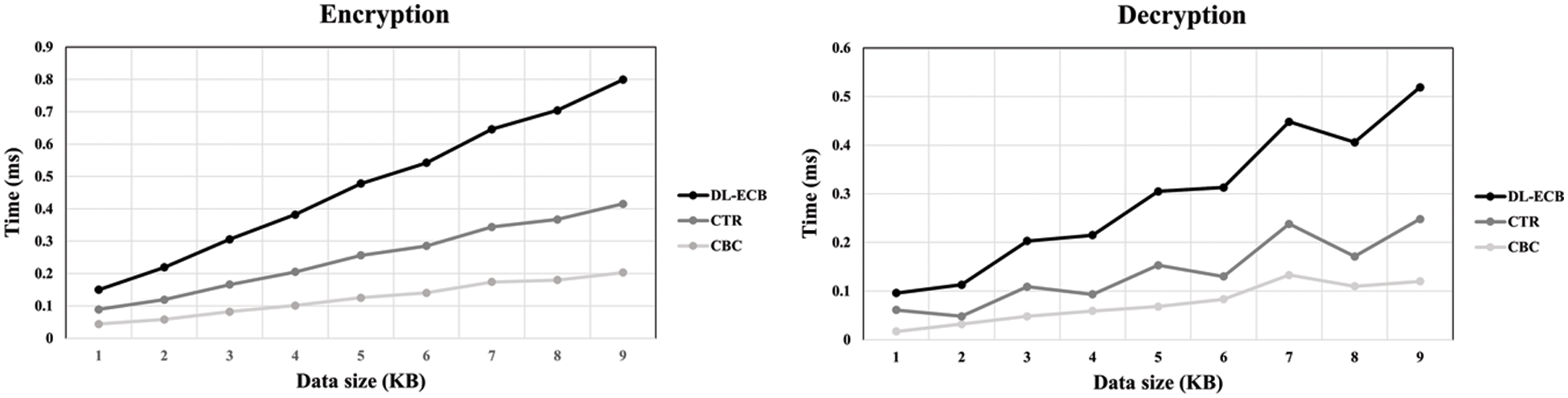
Figure 8: The graph shows the time spent on encryption on the left side and decryption on the right side depending on the data size. Each line shows the result of each mode of operations

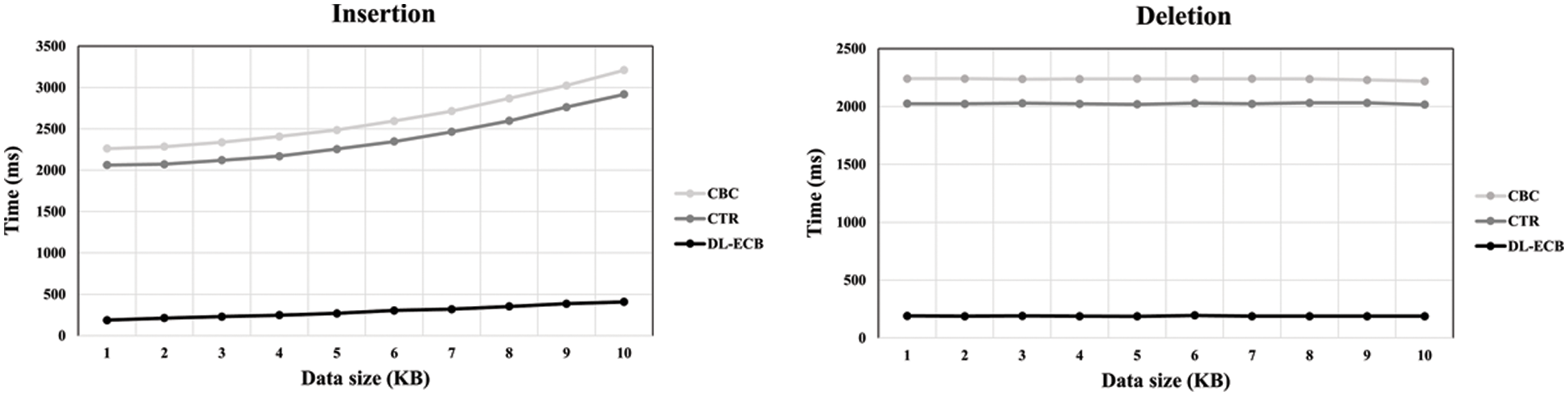
Figure 9: The graph shows the time spent on inserting data depending on the inserted data size on the left side and the deleted data size on the right side. Each line shows the result of each mode of operations

However, as illustrated in Fig. 9, when we update ciphertext, the DL-ECB mode showed the best performance among them: When it inserts or deletes ciphertext, the DL-ECB mode is at least 20 times faster than the others because the DL-ECB mode does not necessarily decrypt and re-encrypt all data blocks.

Figs. 10 to 12 demonstrate the evaluation results for each operation in different settings. Each title of the graph shows which operation is executed and what is the size of the initial data when the experiment is performed. In Fig. 10, we intend to show how inserted data with a significant size (5% of the initial data size) affects execution time. By comparing each side of Fig. 10, we can see the difference in the slopes of graphs, and the difference shows that regarding to the size of inserted data, the execution time for each operation is changed. On the left side of Fig. 10, we insert the data with 1 KB size each time to the same data. It means the existing data size is increased by 1 KB each time. That is why the execution time is increased according to the graph. CBC and CTR make steeper graphs than DL-ECB because they decrypt all data, insert the data and encrypt it again. On the other hand, DL-ECB only encrypts inserted data, and the size of the data is the same each time. The factor which affects the slope of the graph is the execution time to decrypt and encrypt global metadata. Therefore, the graph made by DL-ECB is an upward-sloping graph, but the gradient is gentle. Also, by comparing Figs. 10 and 11, we can see how the ratio of the initial data size and inserted data size affects the slope of the graph. For that, we choose 600 KB as the initial data size in Fig. 11. We insert also 1 KB of data in Fig. 11, but it is about 0.17% of the initial data size. Therefore, though we insert the data of the same size, we can see the difference on the left side of Figs. 10 and 11.

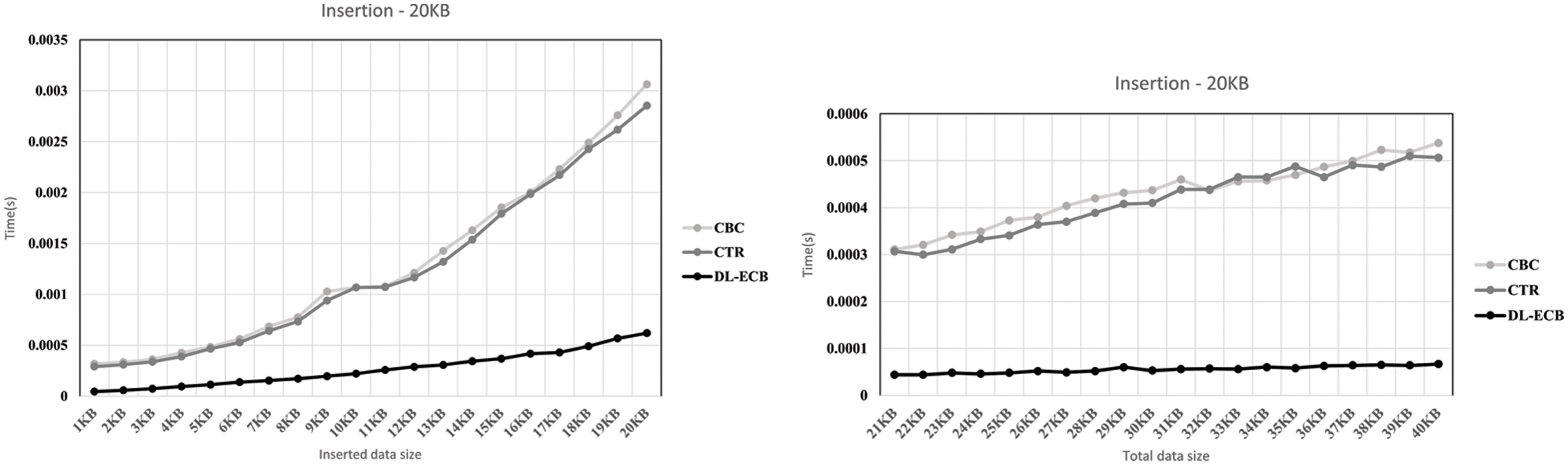
Figure 10: The result graph when the initial data is 20 KB. Inserted data is increased by 1 KB on the left side and inserted data is 1 KB on the right side. To show this, we make x-axis be the inserted data size and y-axis be the execution time

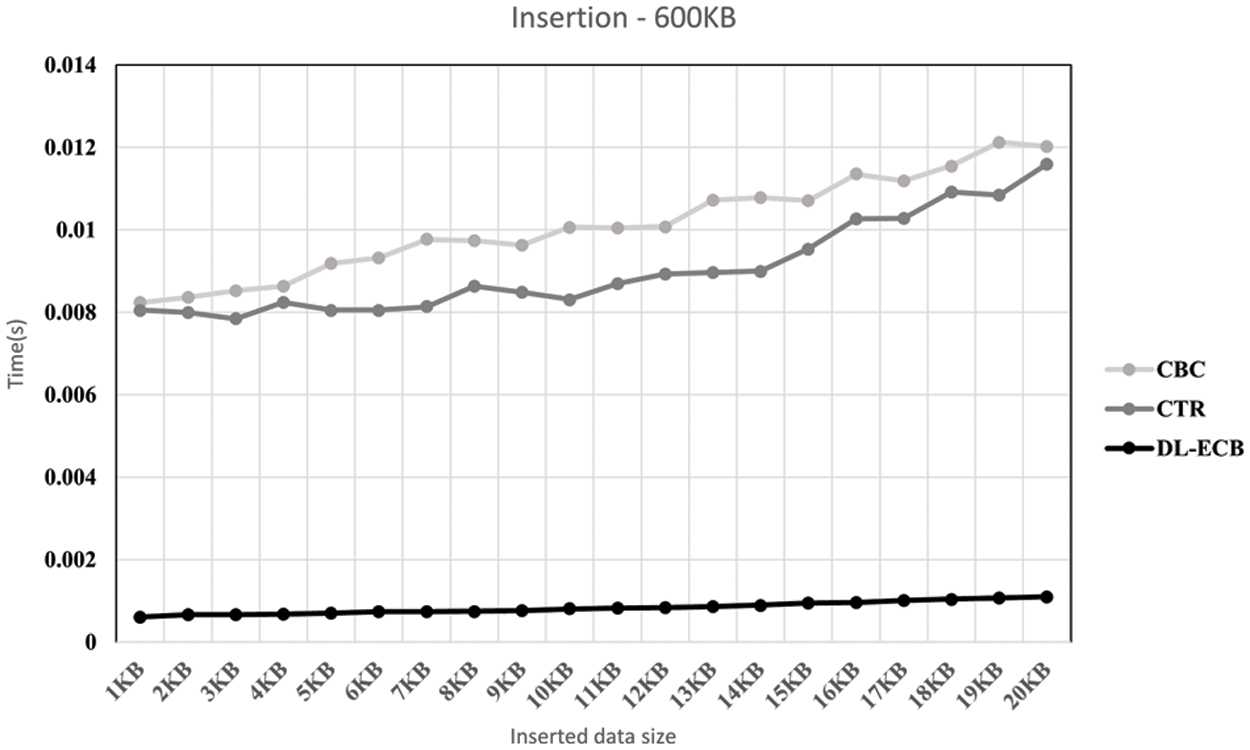
Figure 11: The result graph when the initial data is 600 KB and the data is deleted 20 times and 20 KB of the data is deleted in each time. To show this, we make x-axis be the inserted data size and y-axis be the execution time

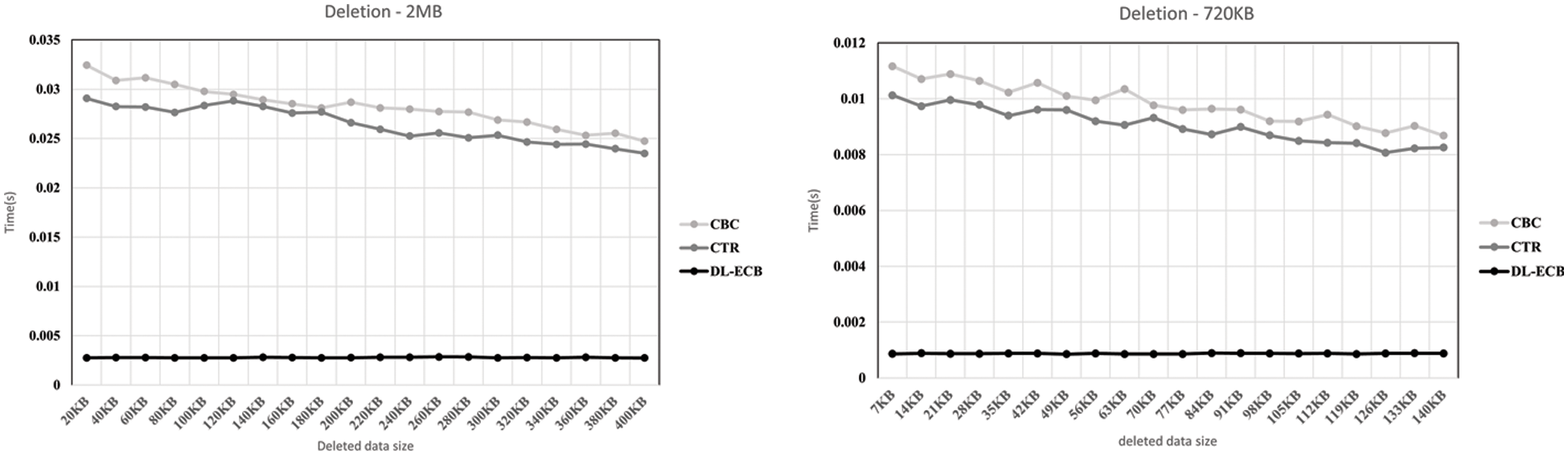
Figure 12: The result graph when the initial data is 2 MB and the data is deleted 20 times and 20 KB of the data is deleted in each time on the left side. The initial data is 720 KB and the data is deleted 20 times and 7 KB of the data is deleted in each time on the right side. To show this, we make x-axis be the inserted data size and y-axis be the execution time

Likewise, in deletion operation, we can see the differences. Fig. 12 have a similar setting about the ratio of initial data size and deleted data size, but we can see the difference in performance speed because they have different initial data sizes. Even though 2 MB and 720 KB are quite far, we can see a similar slope of the graph on CBC and CTR graphs. However, we can see an almost horizontal graph of DL-ECB. With DL-ECB, as explained in Section 3, we just delete corresponding blocks and modify the blocks containing the index. The factors which affect execution time are searching for time and global metadata dealing time. For the accuracy of experiments, we fixed the index so only global metadata dealing time affects the execution time.

Even though the DL-ECB mode has the nonnegligible overhead required to encrypt and decrypt the whole data, it showed overwhelming performance when updating ciphertext as the evaluation results demonstrate. Consequently, as the evaluation results indicate, we believe the DL-ECB mode shows impressive performance as the first step towards the cryptographic primitive for collaborative cloud-based systems.

4.3 Space Complexity of DL-ECB

The DL-ECB mode requires more space than the other modes of operation because of the global metadata, bitmaps, and links. In this section, we analyze the overhead storage that the DL-ECB mode uses.

Let the length of data be n, then the total length of encrypted data is ⌈n12⌉×16≈4n3 (when n is significantly big). Then, the length of plain global metadata is ⌈n12⌉ and encrypted global metadata is ⌈⌈n12⌉14⌉×16≈2n21 . Therefore, the space complexity required to use the DL-ECB mode is 4n3+2n21=10n7≈1.43n → overhead: 3n7≈0.43n . It shows that, when there is no invalid byte in all data blocks, the storage overhead is 43%. Albeit, the storage overhead is not negligible, the DL-ECB mode is the only mode of operation that can update ciphertext without decrypting the whole data, and thus can be used in collaborative cloud-based systems, storing data in a cloud server securely. In addition, as the evaluation results of the runtime performance showed, the DL-ECB mode is much faster than the others when it updates ciphertext.

5  Related Work

5.1 Dynamic Cloud Data

Most of the previous studies focused on protecting dynamic data, verifying the integrity of transmitted data over a network, and restoring data. There have been approaches for data integrity verification and restoration of dynamic cloud data because data can be corrupted while it is sent over the network to a cloud server. Among the approaches, Provable Data Possession (PDP) is a technique that allows us to check whether a file in the cloud is accessed or damaged by an adversary without decrypting the data [2,4–6]. In a study performed by Erway et al. [2], their method puts metadata based on the authenticated flip table, corrects it when data is updated and verifies the validity of the updated data through metadata verification. In another study, Huaqun Wang et al. proposed Identity-based Non-repudiable Dynamic Provable Data Possession (ID-NR-DPDP) [4]. ID-NR-DPDP uses the monotonic dynamic structure index logic table and Diffie-Hellman key exchange scheme based on the identity-based PDP [2] for the efficiency of cloud storage certificate management. While ID-DPDP [6] aimed to reduce the cost of I/O in the existing PDP by using probabilistic proofs of possession and metadata is maintained for minimizing network communication.

Like PDP, Proof of Retrievability (POR) was proposed to detect external access or damage to data and recover it. The biggest difference between PDP and POR is that POR adds a data recovery method. There have been many related studies on POR [7–9], they commonly use distributed storage for recovering data. High-Availability and Integrity Layer (HAIL) [7] encrypts the original data using a well-known error-correcting code and distributes the encoded data to a distributed storage server so that the corrupted data can be recovered using the other storage. Also, Ren et al. [8] proposed Aggregated Signature-Based Broadcast (ASBB) approach which divides the data into small blocks, stores them in distributed storage, and encodes each data block individually before outsourcing it. Then, based on the encoded data block for dynamic data, ASSB applies the data sequence for the dynamic operation using Range-Based 2–3 tree (rb23Tree) to prevent the cloud service provider from fixing blocks to pass the integrity check. Li et al. avoided heavy calculations on the server and user intervention was eliminated in the audit and preprocessing step by outsourcing tag generation for authentication rather than proceeding from the cloud server [9]. In this approach, Merkle Hash Tree (MHT) is used to store the value and location of the data block, and when data modification occurs, this tree is modified to make it easier for users to access the data they need. Bellare et al. proposed Message-Locked Encryption (MLE) as a new cryptographic primitive [19]. MLE is a symmetric encryption scheme in which the key used for encryption and decryption is itself derived from the message. Also, Keelveedhi et al. proposed DupLESS which leveraged MLE to support secure deduplication of ciphertext, and thus, users can upload encrypted data for cloud storage services such as Dropbox [3].

5.2 Modes of Operation of AES

Various studies have been conducted to overcome the limitations of the traditional modes of operation of AES. We review some of these studies and compare them with DL-ECB mode. Jutla proposed the Integrity Aware Parallelizable Mode (IAPM) [20] which supports parallel processing by dividing the data into blocks and enables it to operate individually. The encryption process uses a random value t to generate data S0~Sz which is one more than the number of blocks z. In the encryption process, S0~S(z−1) data are XORed with a plaintext block one by one, and then, all blocks are encrypted. Finally, S data is XORed again to the encrypted blocks. After encrypting all blocks, the checksum is generated by XORing all encrypted blocks, Sz data, and S0 data. This checksum is used for integrity verification. Like the CTR mode, the decryption operation is straightforward, and the key can be reused for each block because the result is different as the value of t changes. However, with IAPM, partial modifications are impossible when data is inserted or deleted. Also, users should share the data t for encryption and decryption. Based on the IAPM, Hawkes proposed an approach to support partial encryption and decryption with authentication IAPM [21]. However, it does not support partial modifications, and thus, is not capable of data insertion and deletion. Another study conducted by Rogaway et al. [22] was also based on IAPM, but it has a different sequential generator for S data. It proposed the Offset Code Book (OCB) mode, which supports parallelization, minimized initial vector, nearly optimal number of block cipher calls, and efficient offset calculations. However, it does not support any partial operation for inserting and deleting data in the DL-ECB mode. Also, the OCB mode used a nonce for generating S data though the nonce is shorter than the one used by the IAPM.

5.3 Searchable Symmetric Encryption Scheme

There exist other studies which are targeted at server-side adversaries. Among them, a notable encryption scheme, named Searchable Symmetric Encryption (SSE) scheme [23], allows one to efficiently search over a collection of encrypted documents or files without decrypting them. With SSE schemes, users can search for data on untrusted servers and the servers cannot access any data. Because of this nature, many applied technologies based on SSE have been studied. S. Kamara et al. suggested Dynamic SSE [24], which targeted dynamic data in cloud storage. For that, they constructed their method with a sublinear (and preferably optimal) search, adaptive security, compactness, and the ability to support the addition and deletion of files. In another study, Liesdonk et al. presented a novel symmetric searchable encryption scheme that offers to search at a constant time in the number of unique keywords stored on the server [25]. With these schemes, users can search their data on the cloud server without decryption. However, they still cannot modify their data without decryption.

6  Conclusion

In this work, we proposed, implemented, and evaluated a novel mode of operation, called DL-ECB, that can efficiently update ciphertext based on the change of plaintext. Since we do not need to decrypt all ciphertext to update it, DL-ECB is useful, especially for frequently modified dynamic data. From this property, DL-ECB can be applied to collaborative cloud-based applications. Our evaluation results showed that, with the DL-ECB mode, we can securely store our data encrypted in a cloud server and work on it with other collaborators. We believe that this new cryptographic primitive can benefit the security of data used in cloud collaboration.

As the use of collaborative cloud-based systems increases, security in the cloud server will become increasingly important. Therefore, we will improve the DL-ECB mode for enhancing usability and efficiency. To be specific, for usability, we plan to use the DL-ECB mode with a searchable encryption scheme so that it can provide stronger security. In addition, we will design a network protocol specified for the DL-ECB mode, by which we can manage ciphertext with multiple users in real time.

Funding Statement: This work was supported in part by the Mid-Career Researcher and Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science and ICT (MSIT), and Future Planning under Grant NRF2020R1A2C2014336 and Grant NRF2021R1F1A105611511.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Global Industry Analysts I, “Cloud Based Office Productivity Software-Global Market Trajectory & Analytics,” 2022. [Online]. Available: https://www.researchandmarkets.com/r/5rlywv. [Google Scholar]

2. C. C. Erway, A. Küpçü, C. Papamanthou and R. Tamassia, “Dynamic provable data possession,” ACM Transactions on Information and System Security, vol. 17, no. 15, pp. 1–29, 2015. [Google Scholar]

3. S. Keelveedhi, M. Bellare and T. Ristenpart, “DupLESS: Server-aided encryption for deduplicated storage,” in 22nd USENIX Security Symp. (USENIX security 13), Washington, D.C., USA, 2013. [Google Scholar]

4. F. Wang, L. Xu, H. Wang and Z. Chen, “Identity-based non-repudiable dynamic provable data possession in cloud storage,” Computers & Electrical Engineering, vol. 69, no. 3, pp. 521–533, 2018. [Google Scholar]

5. G. Ateniese, R. Burns, R. Curtmolab, J. Herring, L. Kissner et al., “Provable data possession at untrusted stores,” in Proc. of the 14th ACM Conf. on Computer and Communications Security, Alexandria, VA, USA, pp. 598–609, 2007. [Google Scholar]

6. H. Wang, “Identity-based distributed provable data possession in multicloud storage,” IEEE Transactions on Services Computing, vol. 8, no. 2, pp. 328–340, 2014. [Google Scholar]

7. K. D. Bowers, A. Juels and A. Oprea, “HAIL: A high-availability and integrity layer for cloud storage,” in Proc. of the 16th ACM Conf. on Computer and Communications Security, Chicago, IL, USA, pp. 187–198, 2009. [Google Scholar]

8. Z. Ren, L. Wang, Q. Wang and M. Xu, “Dynamic proofs of retrievability for coded cloud storage systems,” IEEE Transactions on Services Computing, vol. 11, no. 4, pp. 685–698, 2015. [Google Scholar]

9. J. Li, X. Tan, X. Chen, D. S. Wong and F. Xhafa, “Opor: Enabling proof of retrievability in cloud computing with resource-constrained devices,” IEEE Transactions on Cloud Computing, vol. 3, no. 2, pp. 195–205, 2014. [Google Scholar]

10. P. Patil, P. Narayankar, D. G. Narayan and S. M. Meena, “A comprehensive evaluation of cryptographic algorithms: DES, 3DES, AES, RSA and Blowfish,” Procedia Computer Science, vol. 78, pp. 617–624, 2016. [Google Scholar]

11. J. Nechvatal, E. Barker, L. Bassham, W. Burr, M. Dworkin et al., “Report on the development of the advanced encryption standard (AES),” Journal of Research of the National Institute of Standards and Technology, vol. 106, no. 3, pp. 511–577, 2001. [Google Scholar] [PubMed]

12. J. A. Añel, D. P. Montes and J. R. Iglesias, “Tools in the cloud,” in Cloud and Serverless Computing for Scientists, 1st ed., vol. 1. Cham: Springer, pp. 41–46, 2020. [Google Scholar]

13. S. Chandra, S. Paira, S. S. Alam and G. Sanyal, “A comparative survey of symmetric and asymmetric key cryptography,” in Int. Conf. on Electronics, Communication and Computational Engineering (ICECCE), Hosur, India, IEEE, pp. 83–93, 2014. [Google Scholar]

14. D. Blazhevski, A. Bozhinovski, B. Stojchevska and V. Pachovski, “Modes of operation of the AES algorithm,” in The 10th Conf. for Informatics and Information Technology, Bitola, Macedonia, 2013. [Google Scholar]

15. P. T. Tarigan, “Use of electronic code book (ECB) algorithm in file security,” Jurnal Info Sains: Informatika dan Sains, vol. 10, no. 1, pp. 19–23, 2020. [Google Scholar]

16. H. Lipmaa, P. Rogaway and D. Wagner, “CTR-mode encryption,” in First NIST Workshop on Modes of Operation, Baltimore, MD, USA, vol. 39, 2000. [Google Scholar]

17. Morris J. Dworkin, “Sp 800-38a 2001 edition. Recommendation for block cipher modes of operation: Methods and techniques,” in Technical Report. Gaithersburg, MD, USA: National Institute of Standards & Technology, 2001. [Google Scholar]

18. C. Paar and J. Pelzl, “The advanced encryption standard (AES),” in Understanding Cryptography, 1st ed., vol. 1. Berlin, Heidelberg: Springer, pp. 87–121, 2010. [Google Scholar]

19. M. Bellare, S. Keelveedhi and T. Ristenpart, “Message-locked encryption and secure deduplication,” in Annual Int. Conf. on the Theory and Applications of Cryptographic Techniques, Berlin, Heidelberg, Springer, pp. 296–312, 2013. [Google Scholar]

20. C. S. Jutla, “Encryption modes with almost free message integrity,” in Int. Conf. on the Theory and Applications of Cryptographic Techniques, Berlin, Heidelberg, Springer, pp. 529–544, 2001. [Google Scholar]

21. P. Hawkes and G. G. Rose, “A mode of operation with partial encryption and message integrity,” IACR Cryptology ePrint Archive, 2003. [Google Scholar]

22. P. Rogaway, M. Bellare and J. Black, “OCB: A block-cipher mode of operation for efficient authenticated encryption,” ACM Transactions on Information and System Security (TISSEC), vol. 6, no. 3, pp. 365–403, 2003. [Google Scholar]

23. R. Curtmola, J. Garay, S. Kamara and R. Ostrovsky, “Searchable symmetric encryption: Improved definitions and efficient constructions,” in Proc. of the 13th ACM Conf. on Computer and Communications Security, Alexandria, VA, USA, pp. 79–88, 2006. [Google Scholar]

24. S. Kamara, C. Papamanthou and T. Roeder, “Dynamic searchable symmetric encryption,” in Proc. of the 2012 ACM Conf. on Computer and Communications Security, Raleigh, NC, USA, 2012. [Google Scholar]

25. P. V. Liesdonk, S. Sedghi, J. Doumen, P. Hartel and W. Jonker, “Computationally efficient searchable symmetric encryption,” in Workshop on Secure Data Management, Berlin, Heidelberg, Springer, 2010. [Google Scholar]