Hand Gesture Recognition for Disabled People Using Bayesian Optimization with Transfer Learning

1  Introduction

People with speaking and hearing disabilities utilize various communication models, and sign language is a commonly employed mode of communication. Sign language enables people to communicate with human body language; every individual word has a collection of human actions defining a specific expression. Individuals who cannot hear or speak use sign language (SL) to express their opinions and interact with ordinary people or among them [1]. SL involves the movement of various parts, such as the mouth, hand, lips, and many others denoted as gestures. Such languages comprise certain broadly accepted SL, namely Indian Sign Language (ISL), American Sign Language (ASL), Sign language in japan (JSL), and so on [2]. But the difficulty faced by these people who were deaf and hard of hearing is that ordinary persons could not understand the sign they used to communicate as they did not have proper knowledge of various signs used for communication [3].

Hand gesture recognition (HGR) is one such most advanced field where artificial intelligence (AI) and computer vision (CV) has assisted in enhancing transmission with deaf people while also supporting gesture-related signalling system [4]. Sub-fields of HGR add physical exercise monitoring, SL recognition, human action recognition, pose and posture detection, detection of special signal language utilized in sports, and controlling smart home or supported living applications with HGR [5]. For the last few years, computer scientists have utilized various computational methods and algorithms to solve issues and ease our lives [6]. The usage of hand gestures (HGs) in various software applications had more contribution to enhancing human and computer communications. The development of the gesture recognition system serves an important play in the progression of human and computer communications, and the usage of HGs from several fields was rising more frequently [7]. The application of HGs is realized in games, cognitive development assessment, virtual and augmented reality, assisted living, etc. The expansion of HGR in various sectors has gained the interest of industry and also human-robot communication in the industrial and control of autonomous cars [8]. The ultimate purpose of this practical HGR application was to recognize and classify the gestures. Hand recognition was an approach that utilized various concepts and algorithms of numerous methods, such as NNs and image processing, for understanding hand movement [9]. Generally, there were countless applications of HGR. For instance, deaf people that cannot hear it could interact with their standard SL [10].

This article develops a new Bayesian Optimization with Deep Learning-Driven Hand Gesture Recognition Based Sign Language Communication (BODL-HGRSLC) for Disabled People. The BODL-HGRSLC technique aims to recognize the HGs for disabled people’s communication. The presented BODL-HGRSLC technique integrates the concepts of computer vision (CV) and DL models. In the presented BODL-HGRSLC technique, a deep convolutional neural network-based residual network (ResNet) model is applied for feature extraction. Besides, the presented BODL-HGRSLC model uses Bayesian optimization for the hyperparameter tuning process. At last, a bidirectional gated recurrent unit (BiGRU) model is exploited for the HGR procedure. A wide range of experiments was conducted to demonstrate the enhanced performance of the presented BODL-HGRSLC model.

2  Literature Review

Su et al. [11] examine a gesture detection approach with EMG signals dependent upon deep multi-parallel CNN that resolves the issue of which standard ML approaches can fall into too much helpful data in extracting features. The CNNs offer an effective manner for constraining the difficulty of FFNNs by weighted sharing and limiting local connections. The sophisticated extracting feature is that avoided, and HG is classified directly. A multi-parallel and multi-convolutional layer convolutional infrastructure were presented for classifying HG. Wang et al. [12] examine a deformable convolutional network (DCN) for optimizing the standard convolution kernels to obtain optimum performances of sEMG-based gesture detection. The DCN initially executes a standard convolutional layer for obtaining a lower-dimensional feature map and then utilizes a deformable convolution layer to obtain a higher-dimensional feature map. In addition, the authors present and relate two novel image representation approaches dependent upon standard extracting features that allow DL structures for extracting understood correlations betwixt distinct channels in the sparse multi-channel sEMG signals.

Mujahid et al. [13] examine a lightweight technique dependent upon YOLOv3 and DarkNet-53 are CNNs for gesture detection without another improvement of images, pre-processing, and image filtering. The presented technique obtained maximum accuracy even in difficult environments and effectively-identified gestures from lower-resolution picture mode. The presented technique has been estimated on the labelled dataset of HG in either Pascal VOC or YOLO format. Wong et al. [14] introduce an effectual, low-cost capacitive sensor device for HGR. Particularly, the authors planned a prototype of wearable capacitive sensor units for capturing the capacitance values in the electrodes located in finger phalanges. Several examines followed to provide further insights into sensing data. The authors implemented and related 2 ML approaches such as Error Correction Output Code SVMs (ECOC-SVM) and KNN classifications. In [15], an HGR model utilizing a single patchable six-axis IMU involved at the wrist using RNN was projected. The presented patchable IMU with soft procedure factors is worn from close contact with a human body, easily adjusting for skin deformation. So, signal distortion (that is, motion artefacts) created by vibration in the motion has been minimized. Besides, the patchable IMU is a wireless communication (for instance, Bluetooth) component for always sending the sensor signals to some processing devices.

Yang et al. [16] present an HGR technique dependent upon range-Doppler-angle paths and a reused LSTM (RLSTM) network utilizing a 77 GHz frequency modulated continuous wave (FMCW) multiple-input-multiple-output (MIMO) radar. To overcome the count of gesture interference, a gesture desktop was planned, and a potential HGR technique was followed to define whether it could be possible HG. Once the gesture ensues in the considered gesture desktop, the range-Doppler-angle paths were extracted by utilizing the multiple signal classification (MUSIC), discretized Fourier transform (DFT), and Kalman filtering (KF). Nasri et al. [17] examine an sEMG-controlled 3D game which leverages a DL-based structure for real-time gesture detection. The 3D game knowledge established in the case concentrated on rehabilitation movements, permitting persons with particular disabilities to utilize low-cost sEMG sensors to control the game experiences.

3  The Proposed Gesture Recognition Model

This article develops a new BODL-HGRSLC technique to recognize the HGs for disabled people’s communication. The presented BODL-HGRSLC technique integrates the concepts of CV and DL models. It encompasses ResNet feature extraction, BO hyperparameter tuning, and BiGRU recognition processes. Fig. 1 represents the block diagram of the BODL-HGRSLC system.

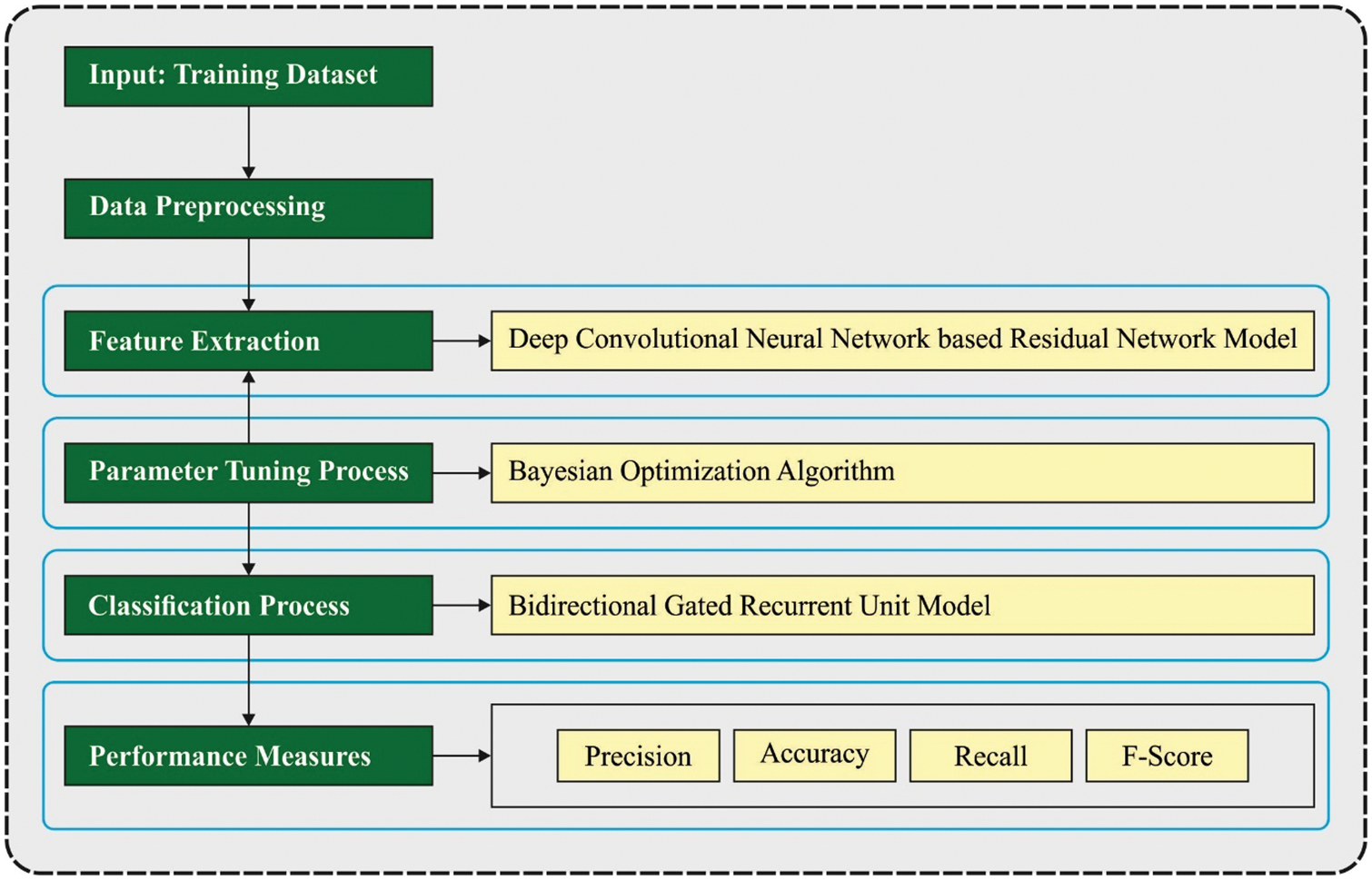
Figure 1: Block diagram of BODL-HGRSLC system

3.1 Module I: Feature Extraction

In the presented BODL-HGRSLC technique, the ResNet model is applied for feature extraction. A research worker demonstrates a DRL architecture. The study aims to facilitate network training that is deeper when compared to the former [18]. This presented architecture helps to address the degradation problem. Instead of expecting each small number of stacked layers to fit the mapping directly, researchers permitted this layer to fit a residual mapping.

The concept of ResNet is to construct a bypass connection; it connects the deep layer by bypassing the nonlinear conversion layer. The block output is the addition of this connection output and network stacked layer output as (1).

H(X)=F(X)+X (1)

Now, X represents the connection output, F(X) indicates the network stacked layer output, and H(X) represents the block output.

Researchers are trained in the ResNet model using ImageNet data; the test results were 3.57% errors in prediction. Each convolution filter has a stride of 2. The study used ResNet 50, where the global average pooling shapes (1, 2048) .

Next, the presented BODL-HGRSLC model uses Bayesian optimization (BO) for the hyperparameter tuning process. Generally, there exist two kinds of hyperparameter optimization techniques: automatic and manual search. Manual hyperparameter optimization is a challenging process to regenerate because it depends on various trial and error efforts [19]. Grid search isn’t adaptable for high dimensions. Random search servers are a greedy method, which settles for local optimal and therefore does not obtain global optimal. Other evolutionary optimized techniques need a broad range of trained cycles and could be noisy. From the above mentioned, the BO technique could resolve this constraint by proficiently defining the global optimization of the black box function of NNs, and it can be based on the Bayes theorem. BO technique is used to resolve computationally costly function to discover the extrema.

The major components in the optimized technique are given below:

•   The gaussian approach of f(x) .

•   The bayesian updating process is used to modify the Gaussian approach at every novel assessment of f(x) .

•   An acquisition function an (x) depends on the Gaussian approach of f that is maximized for determining the subsequent point χ for estimation.

This model determines where the function attains the optimum value, thereby maximizing the model’s accuracy and reducing loss. As already mentioned, the optimization aims at finding a minimal value of loss in the sampling point to unknown function f :

xopt=argxεD⁡min f(x), (2)

whereas D represents the searching domain of χ.

The fundamental probabilistic method for the f objective function is a Gaussian model prior with additional Gaussian noise in the observation that is thorough. The gaussian approach works in a way that anticipates output approximating input and therefore assumes a statistical algorithm.

P(M|E)∞P(E|M)P(M).  (3)

The above equation reflects the concept of the BO technique. By observing the sampling dataset E, P(M|E), the posterior probability of the M model is proportionate to the probability P(E|M) of detecting E provided model M multiplied with (M) prior probability. It is determined that Bayes optimization enhances unknown functions by merging the previous distribution according to the Gaussian model of the f(x) function with present sample data used to acquire the posterior function. Then, the posterior data for finding whereby the criterion values minimalize the f(x) function. This condition has characterized by an acquisition or utility function. Function a describes the next sampling point for maximizing the expected function. There is some widely employed acquisition function. In the study, we used the expected improvement (EI) function, as it assesses the expected quantity of improvement in the main function, which ignores the value that causes a rise in the objective function. EI evaluates the expectation of the degree of enhancement that point could attain while discovering the neighbourhood of the present optimal value. When xbest refers to the position of the low posterior mean and μQ(xbest) indicates the lowermost value of the posterior mean, then the expected development is

EI(x,  Q)=EQ[ max(0, μQ(xbest)−f(x))] (4)

In other words, when the development of function values is lesser than the expected values afterwards, the procedure is implemented, the present ideal value point might be the local optimum solution, and the process defines the optimal value point in another position. Searching the sampling areas include exploitation (sample from the highest value) and exploration (sample from the area of highest uncertainty) that assist in reducing the sampling count. At last, improve the performance although the function has more than one local maxima. Besides the sampling data, the BO technique depends on the previous distribution of function f, an essential part of the statistical inference of the posterior distribution of functions f.

The major steps in the optimization are given below:

•   For existing iterations t

•   Estimate yi=f(x) for determining the amount of points xi randomly taken within the parameter bound.

•   Upgrade the Gaussian f(x) approach to achieving posterior distribution over function (f|xi, yi for i=1, …t) .

•   Define the novel point χ that maximizes acquisition function (x) .

The process ends after the number of iterations limits or reaches a time. In the presented method, tuning the CNN architecture and hyperparameter can be accomplished using the BO technique.

3.2 Module II: Gesture Recognition

Finally, the BiGRU model is exploited for the HGR procedure. An RNN is effectively utilized for handling data series from distinct regions [20]. In RNN, assume that input series x=(x1, …, xT) , hidden vector series h=(h1, …, hT) , and resultant vector sequence y=(y1, …, yT) are derivative by the provided formulas:

hτ=Φ(Uxt+WWhτ−1+b)  (5)

yt=Vht+c  (6)

Assume that Φ is the activation function, and the popular activation function was commonly an element-wise application of sigmoid functions. U represents the input-hidden weighted matrixes, W indicates the hidden-hidden weight matrixes, Eq. (6) b indicates the hidden bias vector, V stands for the hidden-output weighted matrixes, and c implies the resultant bias vector. It can be difficult to capture the long-term dependences of RNN as the gradient inclines explode or vanish. Thus, in several types of research, workers have made every effort to develop a further difficult activation function for resolving the faults. The LSTM unit was primarily presented for the sample to capture the long-term dependencies. Recently, another variation of recurrent units, the GRU, is also developed that is simpler for calculating and taking optimum generalised efficiency than LSTM units. For LSTM, it allowed the utilization of the resultant gate to control the exposure of the number of memory contents.

ht=ottanh(ct) (7)

In Eq. (7), the resultant gate was demonstrated as 0t is computed as:

0t=σ(W0⋅[ht−1, xt, cl]+b0) (8)

In Eq. (8), the logistic function was represented as σ . The memory cell ct was conserved by adding some novel memory and removing (forgetting) present memory:

ct=ftct−1+iτc~+bc (9)

The c~t novel memory is provided as:

c~=tanh(Wc⋅[ht−1, xt]) (10)

The range to remove and add memory is measured by the input gate it and forget gate ft . The forget gate is computed by the following formula:

ft=σ(Wf⋅[ht−1, xt, ct−1]+bf) (11)

and it is computed as:

it=σ(Wi⋅[ht−1, xt, ct−1]+bi) (12)

In the formula, the matching bias vector was represented as b. Like the LSTM unit, GRU utilizes a gate to influence the data stream inside units, but there are no memory cells. The hr hidden layer (HL) is a linear combination of novel HLs h~t and earlier HL ht−1 :

ht=(1−zt)ht−1+zth~t (13)

In Eq. (13), the upgrade gate zt control that several its novel activation becomes upgrade. It can be computed as:

zt=σ(Wz⋅[ht−1, xt]) (14)

The h~t novel activation was computed as:

h~=tanh(Wh⋅[rt⊙ht−1, xt]) (15)

In Eq. (15), the forget gate rt is similar to the upgrade unit from the LSTM:

rl=σ(Wr⋅[ht−1, xt]) (16)

But the standard RNN activities the previous data, the bi-directional RNN (BRNN) procedure data in 2 directions. The y outcome of BRNN can be obtained with measured the hr→ forward hidden series and ht← backward series as follows:

h→t=Φ(WWχh→xt+Wh→h→h→t−1+bh→) (17)

ht←=Φ(Wxh←xtxh+Wh←h←h←t−1+bh←) (18)

yt=Wh→yh→t+Wh←​yh←​t−1+by (19)

Combining BRNN with GRU offers BIGRU, which is employed to access the long-term data series in 2 directions. While a fault analysis problem is commonly assumed a classifier problem, cross-entropy was modified as a loss function. The weighted cross entropy was defined as:

f(θ)=−∑n=1N⁡wn∑i=1M⁡yilog(y^i) (20)

In Eq. (20), θ stands for the NN parameter, N defines the instance number, the count of faults is demonstrated as M , the true label is referred to as yi , and the forecasted probability signifies y^i . Fig. 2 demonstrates the framework of the BiGRU technique.

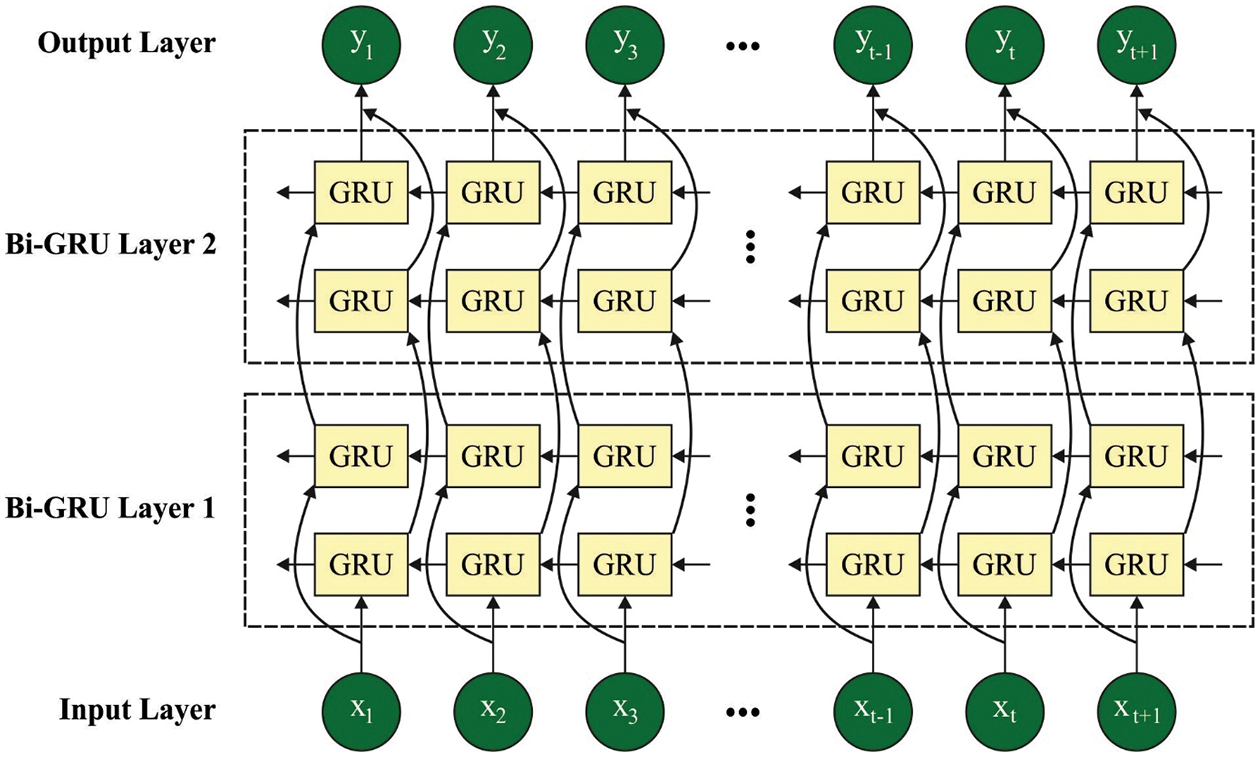
Figure 2: Architecture of BiGRU

4  Results Analysis

The experimental validation of the BODL-HGRSLC model is tested using a dataset comprising different hand gesture images. The parameter settings are learning rate: 0.01, dropout: 0.5, batch size: 5, epoch count: 50, and activation: ReLU. Fig. 3 demonstrates the sample images for alphabets A-Z.

Figure 3: Sample images for alphabets A-Z

The confusion matrix derived by the BODL-HGRSLC model on the entire dataset is depicted in Fig. 4. The figure indicates that the BODL-HGRSLC model has proficiently categorized 26 class labels.

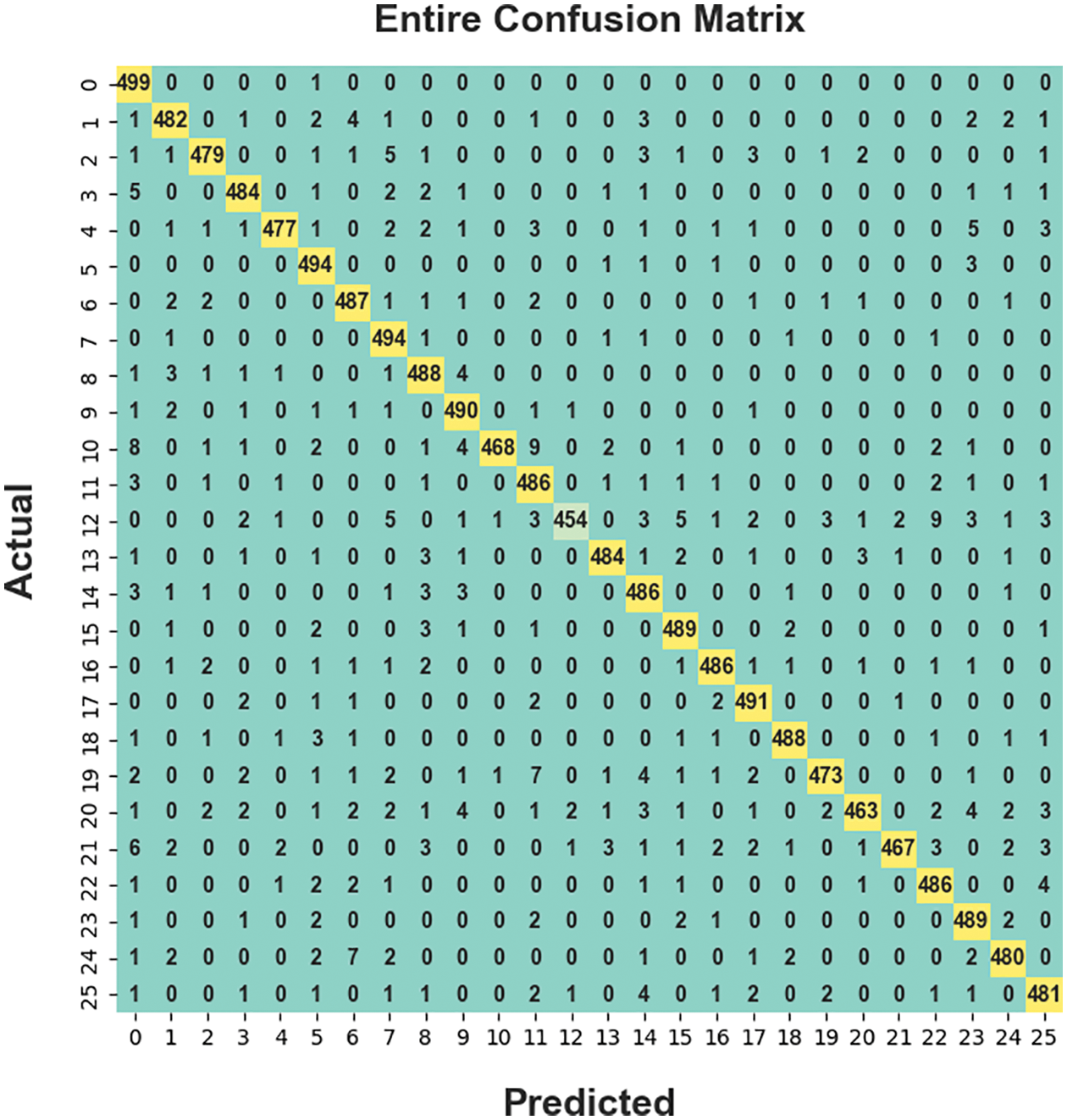
Figure 4: Confusion matrices of the BODL-HGRSLC approach under the Entire dataset

Table 1 and Fig. 5 demonstrate the overall gesture recognition outcomes of the BODL-HGRSLC model. The experimental results demonstrated that the BODL-HGRSLC model had effectively categorized all the hand gestures. For instance, in class ‘a’, the BODL-HGRSLC model has obtained accuy of 99.70%, precn of 92.92%, recal of 99.80%, and Fscore pf 96.24%. Meanwhile, in class ‘b’, the BODL-HGRSLC model has obtained accuy of 99.73%, precn of 96.59%, recal of 96.40%, and Fscore pf 96.50%. Eventually, in class ‘c’, the BODL-HGRSLC model obtained accuy of 99.75%, precn of 97.56%, recal of 95.80%, and Fscore pf 96.67%. Simultaneously, on class ‘d’, the BODL-HGRSLC model has obtained accuy of 99.75%, precn of 96.80%, recal of 96.80%, and Fscore pf 96.80%. Finally, in class ‘e’, the BODL-HGRSLC model has obtained accuy of 99.77%, precn of 98.55%, recal of 95.40%, and Fscore pf 96.95%.

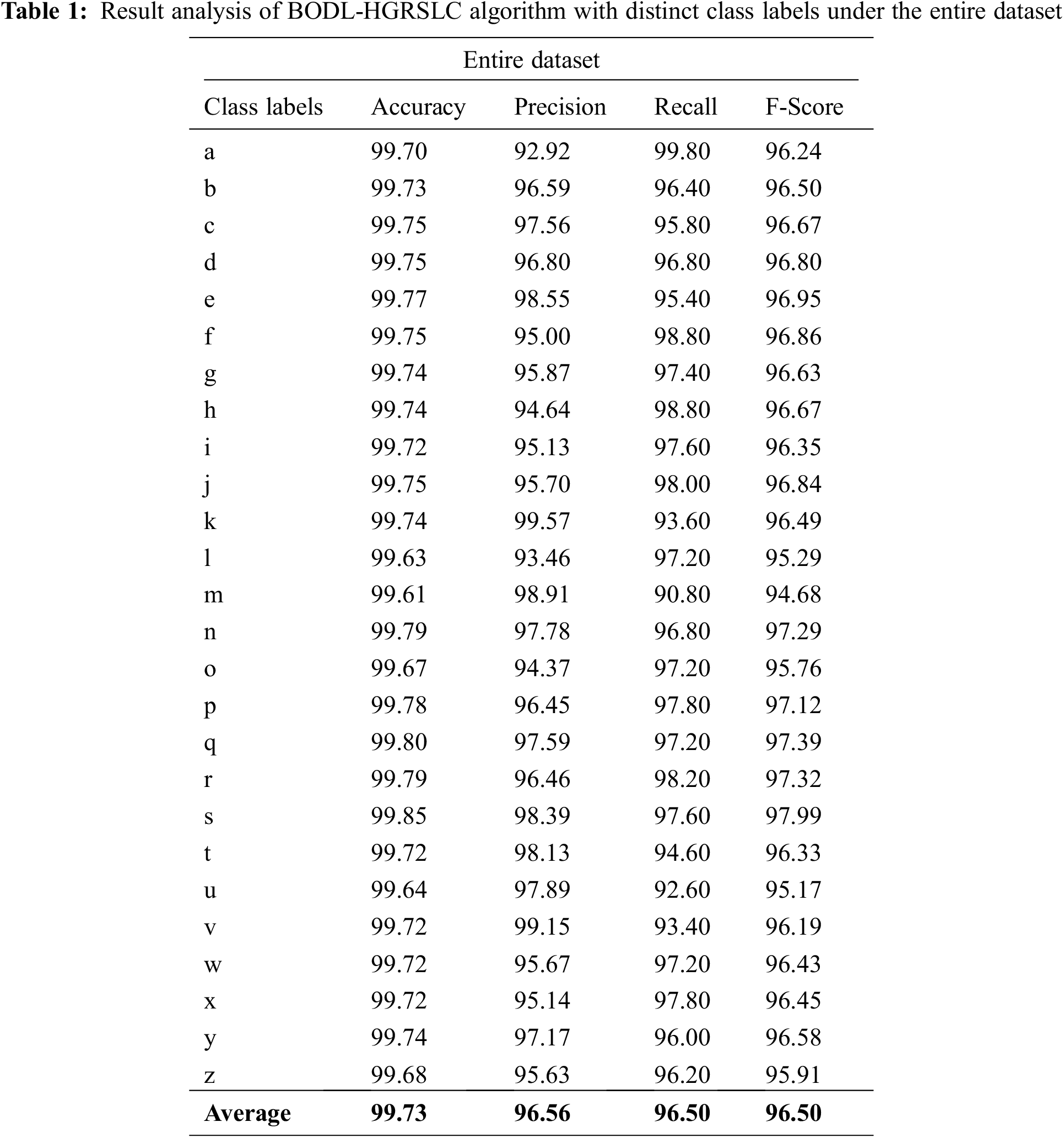
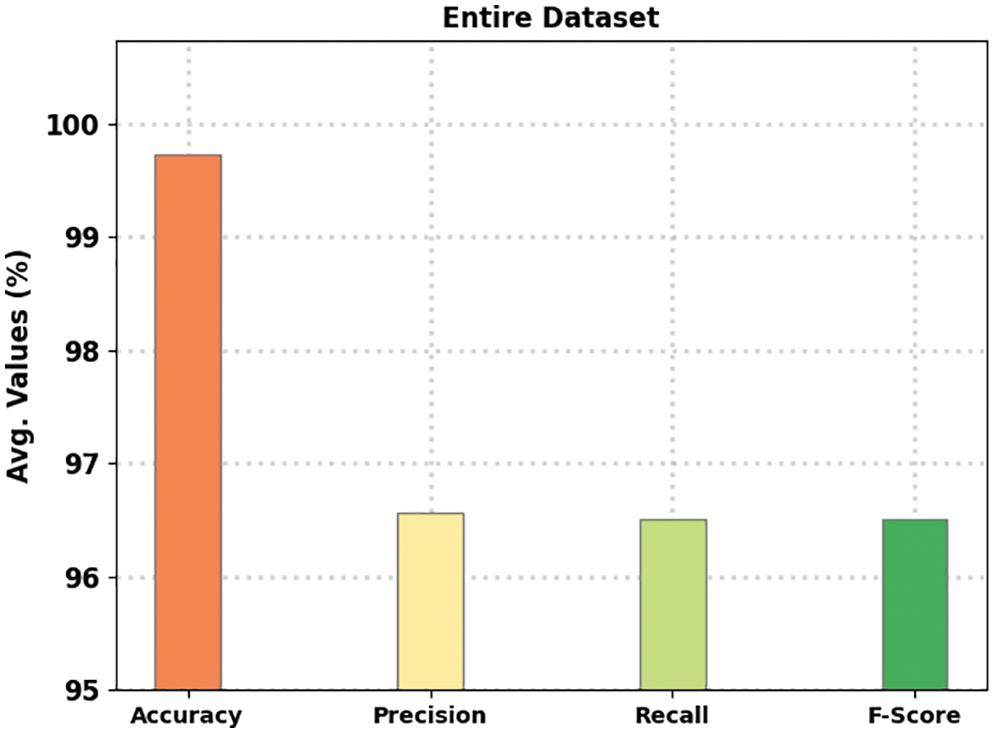
Figure 5: Average analysis of the BODL-HGRSLC algorithm under the entire dataset

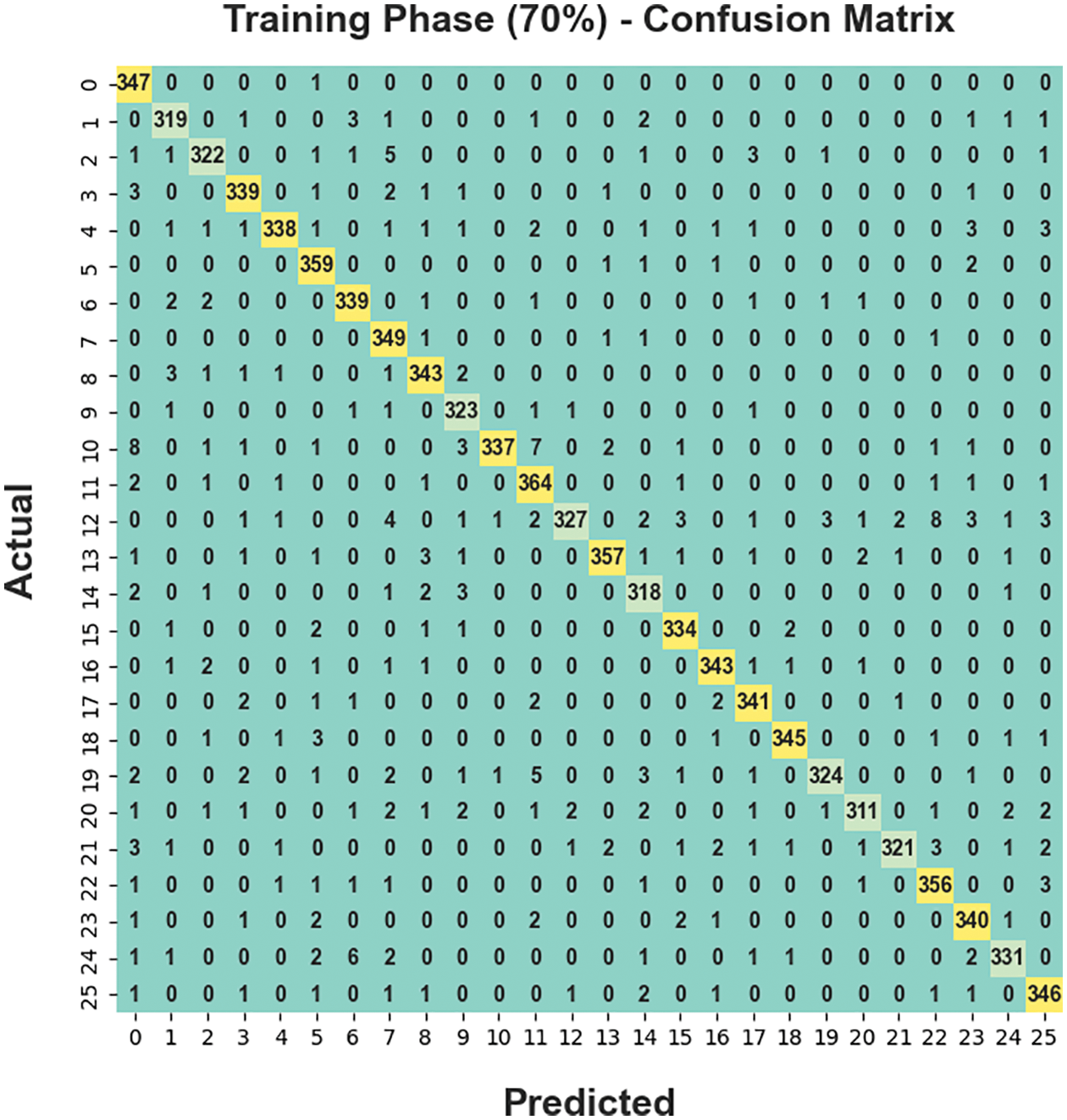
Figure 6: Confusion matrices of BODL-HGRSLC approach under 70% of TR dataset

Table 2 and Fig. 7 illustrate the complete gesture recognition outcomes of the BODL-HGRSLC method under 70% of TR dataset. The experimental outcomes manifested by the BODL-HGRSLC approach have effectively categorized all the hand gestures. For example, in class ‘a’, the BODL-HGRSLC technique has acquired accuy of 99.69%, precn of 92.78%, recal of 99.71%, and Fscore pf 96.12%. In the meantime, in class ‘b’, the BODL-HGRSLC approach has achieved accuy of 99.75%, precn of 96.37%, recal of 96.67%, and Fscore pf 96.52%. Parellerly, on class ‘c’, the BODL-HGRSLC method has attained accuy of 99.71%, precn 96.70%, recal of 95.55%, and Fscore pf 96.12%. At the same time, on class ‘d’, the BODL-HGRSLC algorithm has gained accuy of 99.75%, precn of 96.31%, recal of 97.13%, and Fscore pf 96.72%. At last, in-class ‘e’, the BODL-HGRSLC technique has reached accuy of 99.74%, precn of 98.626%, recal of 94.94%, and Fscore pf 96.94%.

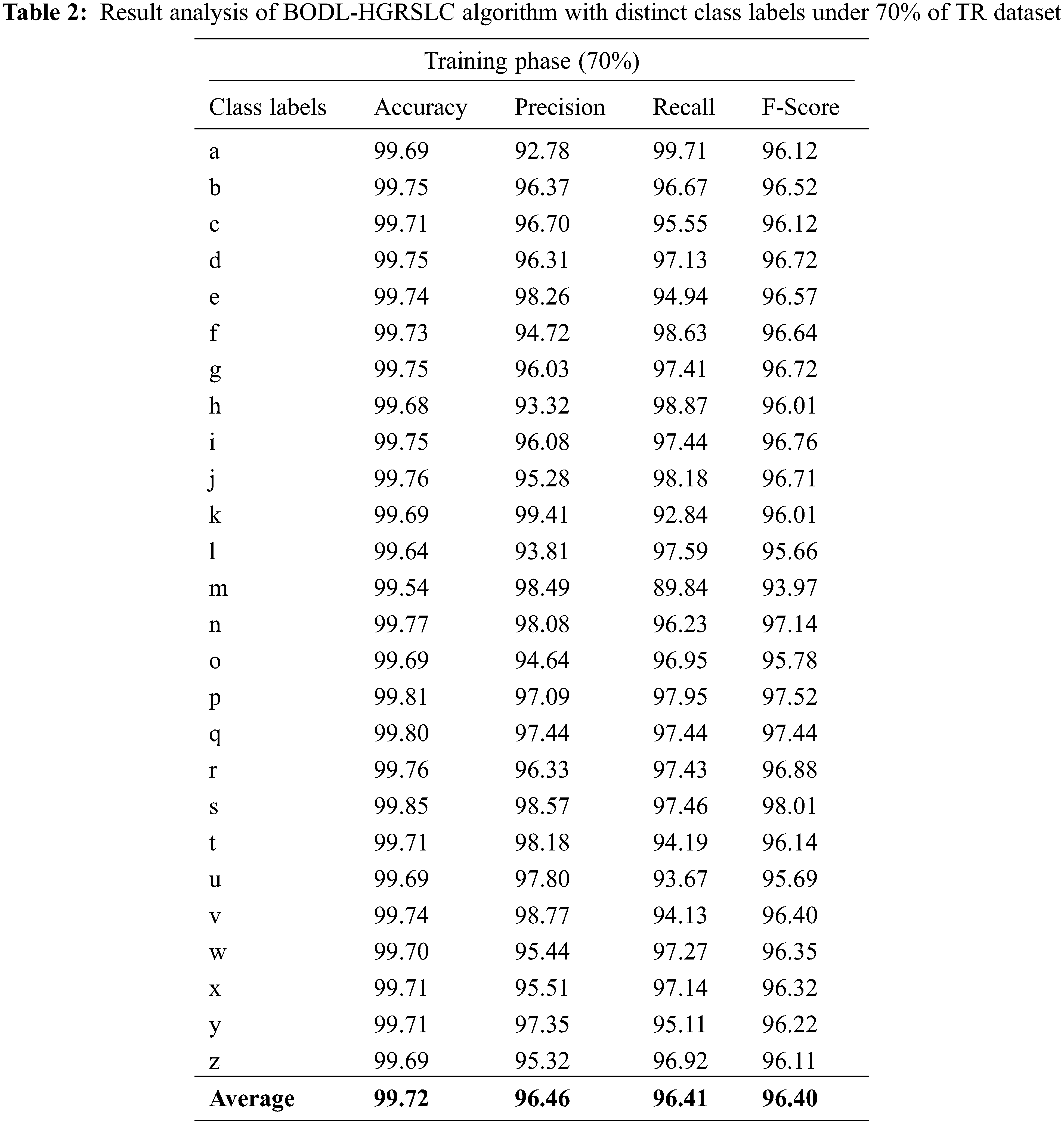
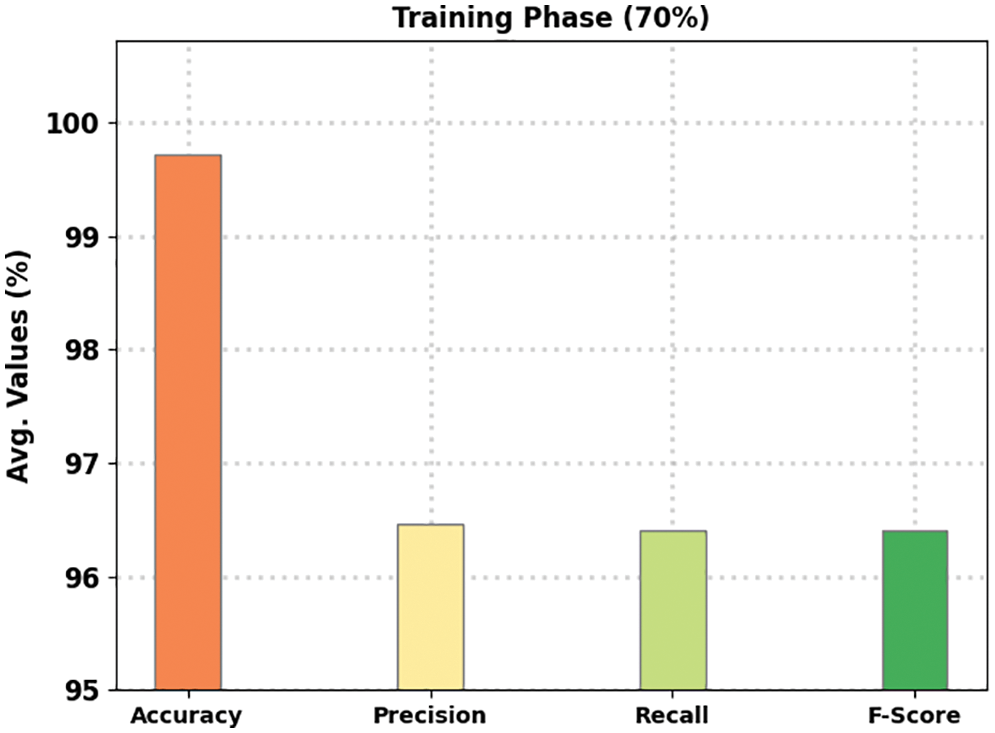
Figure 7: Average analysis of the BODL-HGRSLC algorithm under 70% of TR dataset

The confusion matrix derived by the BODL-HGRSLC method on 70% of TR dataset is shown in Fig. 6. The figure represents the BODL-HGRSLC algorithm has effectively classified 26 class labels.

The confusion matrix derived by the BODL-HGRSLC approach on 30% of TS dataset is displayed in Fig. 8. The figure denotes the BODL-HGRSLC methodology has proficiently categorized 26 class labels.

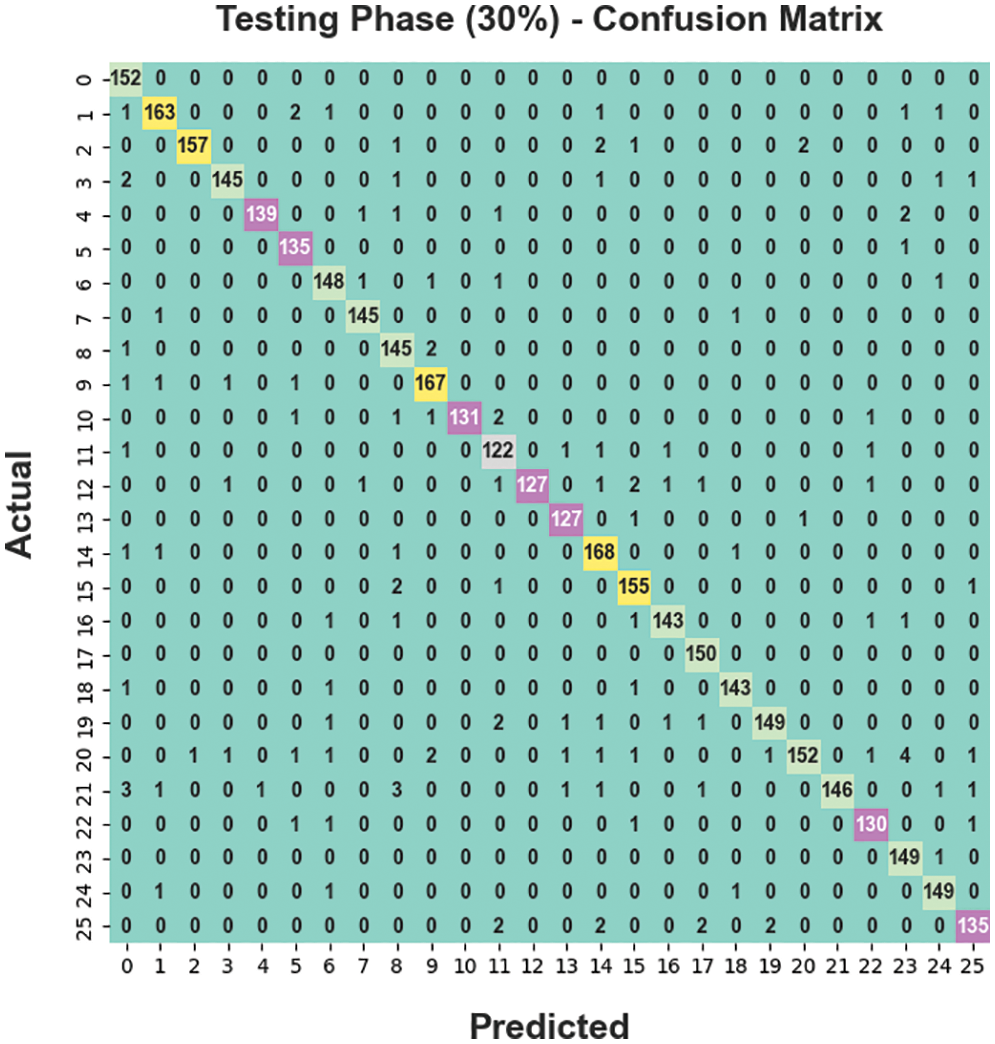
Figure 8: Confusion matrices of BODL-HGRSLC approach under 30% of TS dataset

Table 3 and Fig. 9 portray the overall gesture recognition outcomes of the BODL-HGRSLC model under 30% of TS dataset. The experimental outcomes of the BODL-HGRSLC method have effectively categorized all the hand gestures. For example, in class ‘a’, the BODL-HGRSLC approach has reached accuy of 99.72%, precn of 93.25%, recal of 100%, and Fscore pf 96.51%. In the meantime, in class ‘b’, the BODL-HGRSLC technique has reached accuy of 99.75%, precn of 96.37%, recal of 96.67%, and Fscore pf 96.52%. In Parallel, on class ‘c’, the BODL-HGRSLC method has attained accuy of 99.71%, precn 96.70%, recal of 95.55%, and Fscore pf 96.12%. Concurrently, on class ‘d’, the BODL-HGRSLC approach has attained accuy of 99.75%, precn of 96.31%, recal of 97.13%, and Fscore pf 96.72%. At last, in class ‘e’, the BODL-HGRSLC algorithm has acquired accuy of 99.74%, precn of 98.626%, recal of 94.94%, and Fscore pf 96.57%.

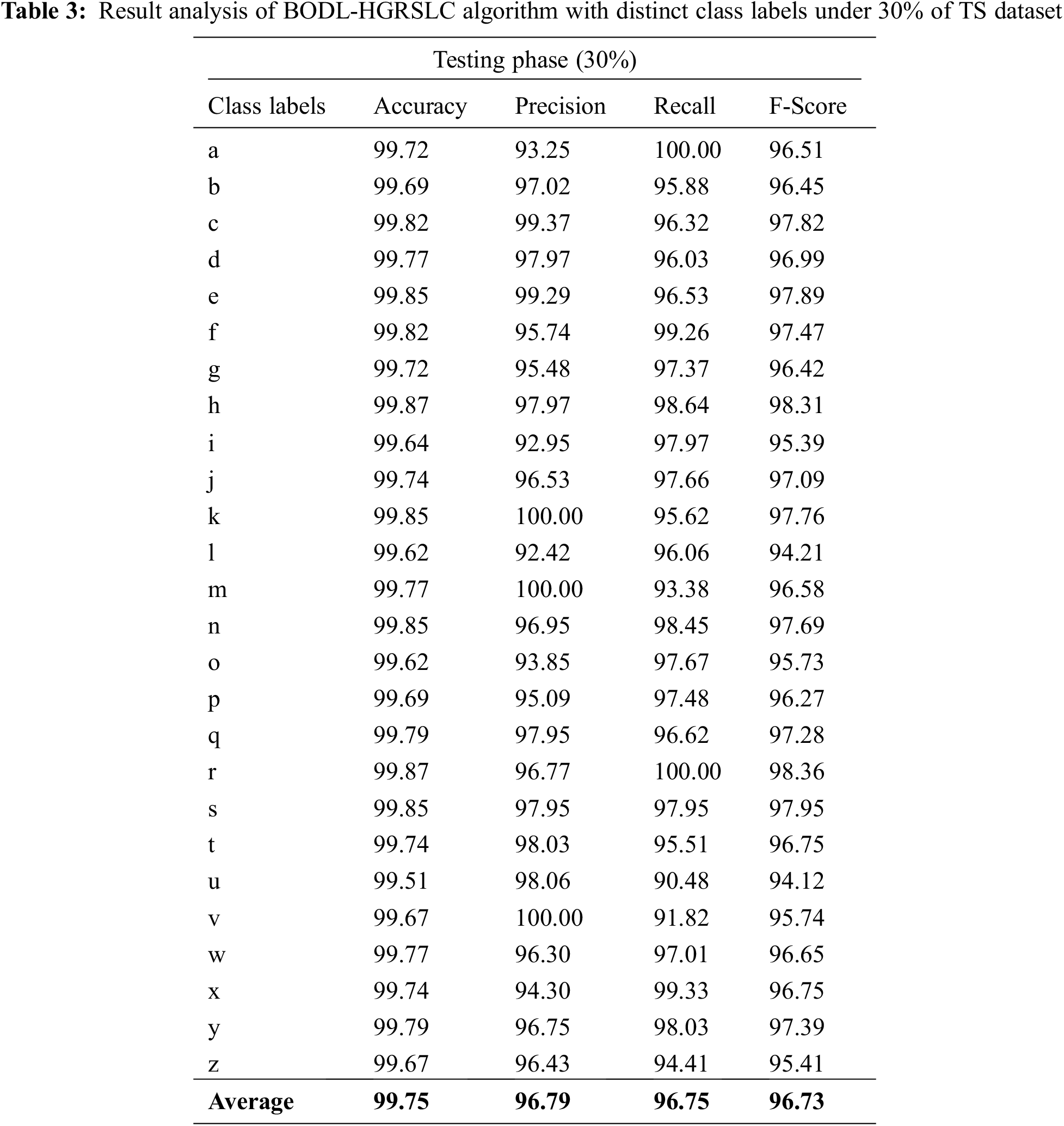
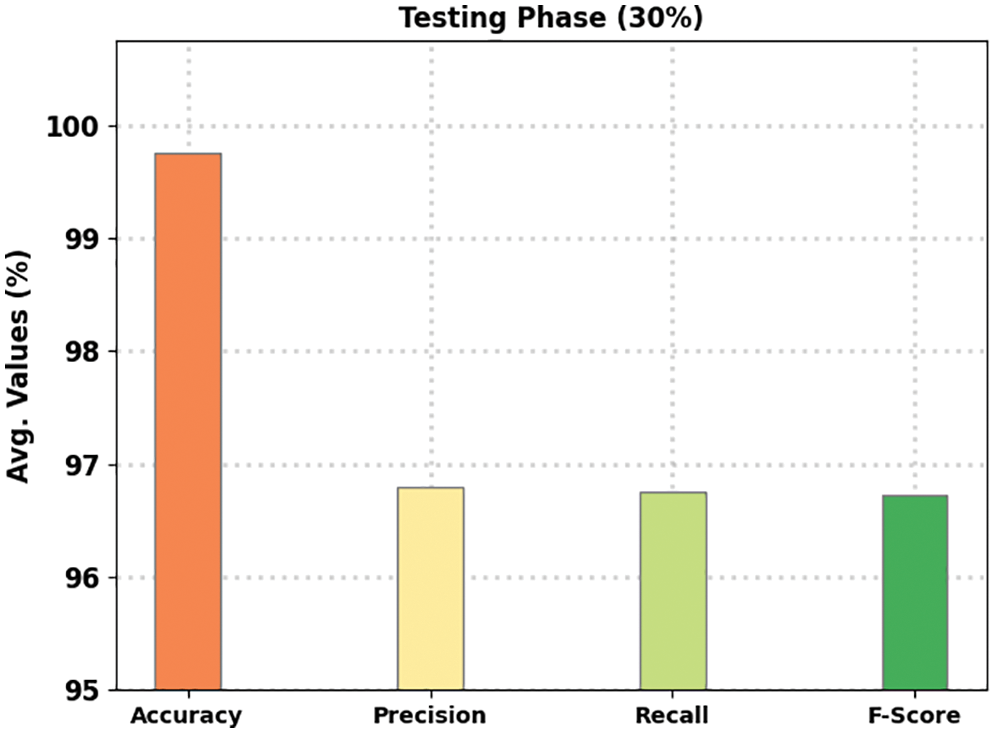
Figure 9: Average analysis of BODL-HGRSLC algorithm under 30% of TS dataset

The training accuracy (TRA) and validation accuracy (VLA) acquired by the BODL-HGRSLC approach on the test dataset is demonstrated in Fig. 10. The experimental result exhibited the BODL-HGRSLC method has attained maximal values of TRA and VLA. Seemingly the VLA is greater than TRA.

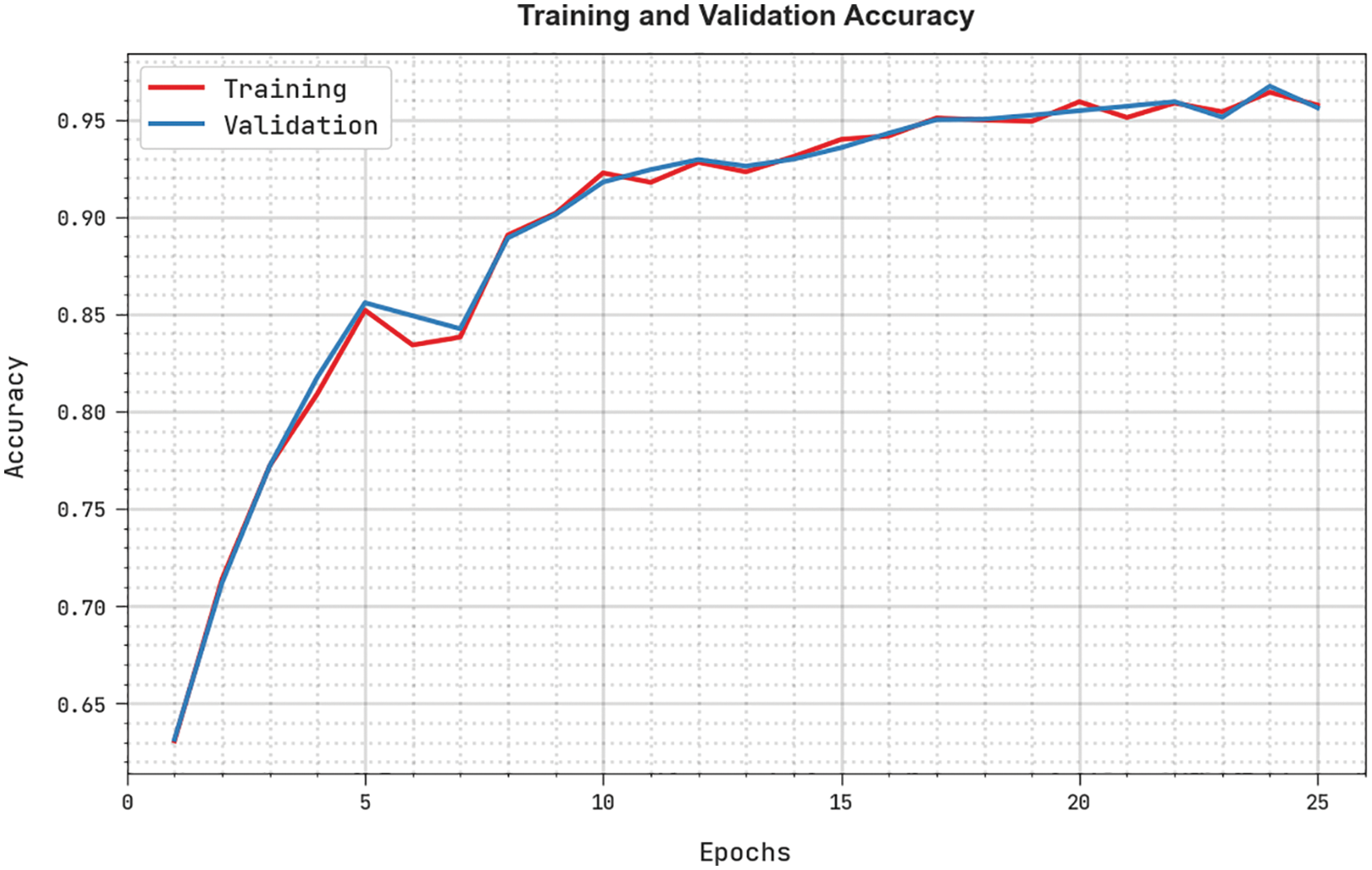
Figure 10: TRA and VLA analysis of the BODL-HGRSLC algorithm

The training loss (TRL) and validation loss (VLL) obtained by the BODL-HGRSLC algorithm on the test dataset are displayed in Fig. 11. The experimental outcome denoted the BODL-HGRSLC algorithm has outperformed minimal values of TRL and VLL. Particularly, the VLL is lesser than TRL.

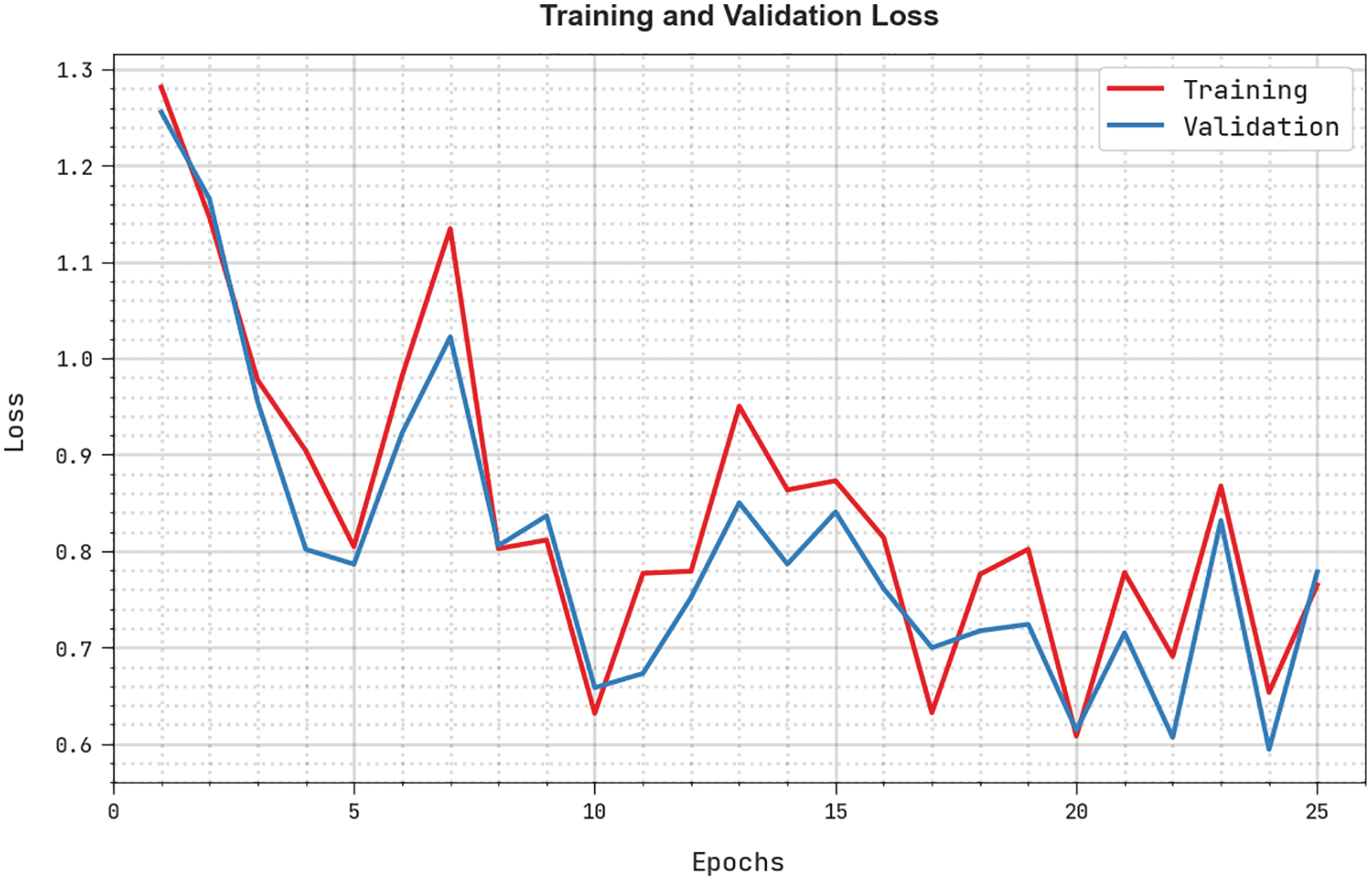
Figure 11: TRL and VLL analysis of the BODL-HGRSLC algorithm

A comprehensive accuy examination of the BODL-HGRSLC with recent models is given in Table 4 and Fig. 12 [21,22]. The results indicated that the k-NN and AlexNet models have failed to show effectual results. Following, the NB and CNN models have attained slightly enhanced performance. In line with this, the ANN and LSTM models have reached reasonable outcomes.

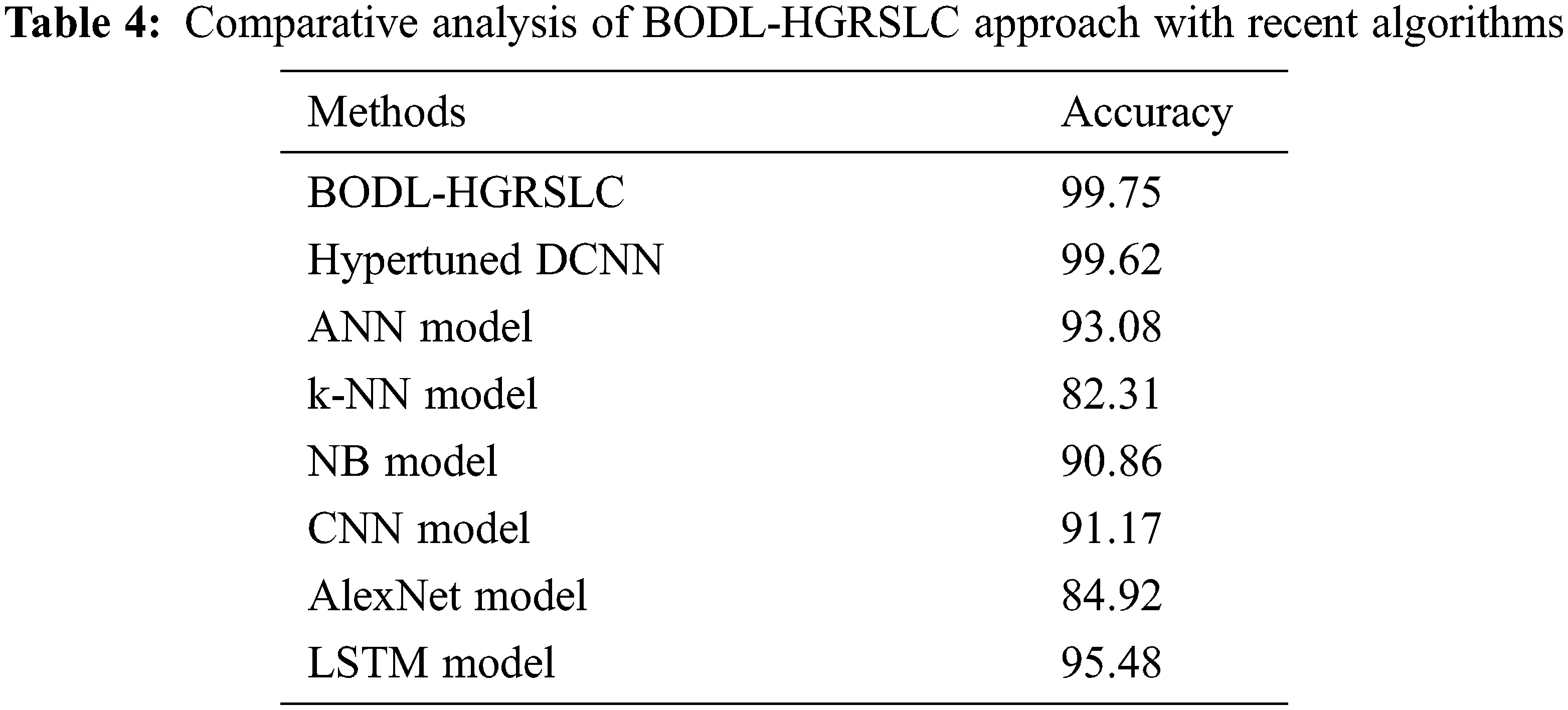
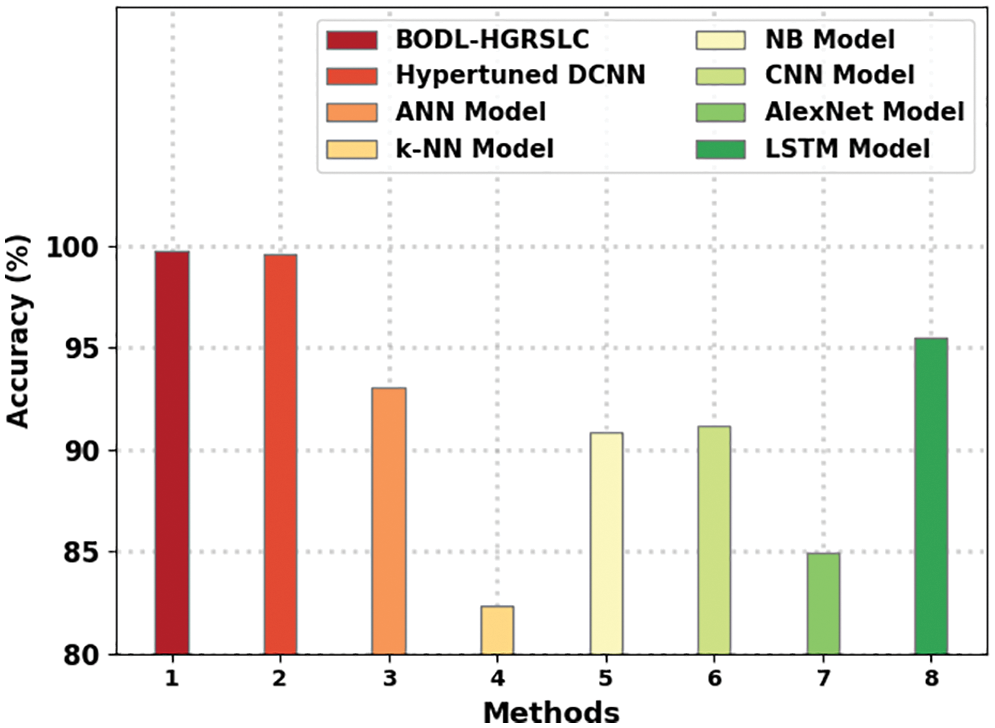
Figure 12: Comparative analysis of BODL-HGRSLC approach with recent algorithms

Though the hyperparameter-tuned DCNN model has gained near optimal accuy of 99.62%, the presented BODL-HGRSLC model has reached a higher accuy of 99.75%. Therefore, the experimental results confirmed the enhanced outcomes of the BODL-HGRSLC with a higher accuy of 99.75%. Thus, the BODL-HGRSLC can be employed as a productive approach for gesture recognition.

5  Conclusion

This article develops a new BODL-HGRSLC technique to recognize the HGs for disabled people’s communication. The presented BODL-HGRSLC technique integrates the concepts of CV and DL models. In the presented BODL-HGRSLC technique, the ResNet model is applied for feature extraction. Besides, the presented BODL-HGRSLC model uses Bayesian optimization for the hyperparameter tuning process. At last, the BiGRU model is exploited for the HGR procedure. A wide range of experiments was conducted to demonstrate the enhanced performance of the presented BODL-HGRSLC model. The comprehensive comparison study reported the improvements of the BODL-HGRSLC model over other DL models with maximum accuracy of 99.75%. In the future, an ensemble fusion of DL models can be derived to enhance the recognition outcomes.

Funding Statement: The authors extend their appreciation to the King Salman centre for Disability Research for funding this work through Research Group no KSRG-2022-017.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. L. Chen, J. Fu, Y. Wu, H. Li and B. Zheng, “Hand gesture recognition using compact CNN via surface electromyography signals,” Sensors, vol. 20, no. 3, pp. 672, 2020. [Google Scholar] [PubMed]

2. A. Moin, A. Zhou, A. Rahimi, A. Menon, S. Benatti et al., “A wearable biosensing system with in-sensor adaptive machine learning for hand gesture recognition,” Nature Electronics, vol. 4, no. 1, pp. 54–63, 2021. [Google Scholar]

3. S. Z. Gurbuz and M. G. Amin, “Radar-based human-motion recognition with deep learning: Promising applications for indoor monitoring,” IEEE Signal Processing Magazine, vol. 36, no. 4, pp. 16–28, 2019. [Google Scholar]

4. P. Wang, H. Liu, L. Wang and R. X. Gao, “Deep learning-based human motion recognition for predictive context-aware human-robot collaboration,” CIRP Annals, vol. 67, no. 1, pp. 17–20, 2018. [Google Scholar]

5. F. Wen, Z. Sun, T. He, Q. Shi, M. Zhu et al., “Machine learning glove using self-powered conductive superhydrophobic triboelectric textile for gesture recognition in VR/AR applications,” Advanced Science, vol. 7, no. 14, pp. 2000261, 2020. [Google Scholar] [PubMed]

6. U. Côté-Allard, C. L. Fall, A. Drouin, A. C. Lecours, C. Gosselin et al., “Deep learning for electromyographic hand gesture signal classification using transfer learning,” IEEE Transactions on Neural Systems and Rehabilitation Engineering, vol. 27, no. 4, pp. 760–771, 2019. [Google Scholar]

7. D. S. Breland, A. Dayal, A. Jha, P. K. Yalavarthy, O. J. Pandey et al., “Robust hand gestures recognition using a deep CNN and thermal images,” IEEE Sensors Journal, vol. 21, no. 23, pp. 26602–26614, 2021. [Google Scholar]

8. D. Tasmere, B. Ahmed and S. R. Das, “Real time hand gesture recognition in depth image using CNN,” International Journal of Computer Applications, vol. 174, no. 16, pp. 28–32, 2021. [Google Scholar]

9. C. S. Liang and H. Li-Wu, “Using deep learning technology to realize the automatic control program of robot arm based on hand gesture recognition,” International Journal of Engineering and Technology Innovation, vol. 11, no. 4, pp. 241, 2021. [Google Scholar]

10. A. Dayal, N. Paluru, L. R. Cenkeramaddi and P. K. Yalavarthy, “Design and implementation of deep learning based contactless authentication system using hand gestures,” Electronics, vol. 10, no. 2, pp. 182, 2021. [Google Scholar]

11. Z. Su, H. Liu, J. Qian, Z. Zhang and L. Zhang, “Hand gesture recognition based on semg signal and convolutional neural network,” International Journal of Pattern Recognition and Artificial Intelligence, vol. 35, no. 11, pp. 2151012, 2021. [Google Scholar]

12. H. Wang, Y. Zhang, C. Liu and H. Liu, “sEMG based hand gesture recognition with deformable convolutional network,” International Journal of Machine Learning and Cybernetics, vol. 13, no. 6, pp. 1729–1738, 2022. [Google Scholar]

13. A. Mujahid, M. J. Awan, A. Yasin, M. A. Mohammed, R. Damaševičius et al., “Real-time hand gesture recognition based on deep learning YOLOv3 model,” Applied Sciences, vol. 11, no. 9, pp. 4164, 2021. [Google Scholar]

14. W. K. Wong, F. H. Juwono and B. T. T. Khoo, “Multi-features capacitive hand gesture recognition sensor: A machine learning approach,” IEEE Sensors Journal, vol. 21, no. 6, pp. 8441–8450, 2021. [Google Scholar]

15. E. V. Añazco, S. J. Han, K. Kim, P. R. Lopez, T. S. Kim et al., “Hand gesture recognition using single patchable six-axis inertial measurement unit via recurrent neural networks,” Sensors, vol. 21, no. 4, pp. 1404, 2021. [Google Scholar]

16. Z. Yang and X. Zheng, “Hand gesture recognition based on trajectories features and computation-efficient reused LSTM network,” IEEE Sensors Journal, vol. 21, no. 15, pp. 16945–16960, 2021. [Google Scholar]

17. N. Nasri, S. Orts-Escolano and M. Cazorla, “An semg-controlled 3D game for rehabilitation therapies: Real-time time hand gesture recognition using deep learning techniques,” Sensors, vol. 20, no. 22, pp. 6451, 2020. [Google Scholar] [PubMed]

18. M. Hammad, P. Pławiak, K. Wang and U. R. Acharya, “ResNet-attention model for human authentication using ECG signals,” Expert Systems, vol. 38, no. 6, pp. e12547, 2021. [Google Scholar]

19. X. B. Jin, W. Z. Zheng, J. L. Kong, X. Y. Wang, Y. T. Bai et al., “Deep-learning forecasting method for electric power load via attention-based encoder-decoder with Bayesian optimization,” Energies, vol. 14, no. 6, pp. 1596, 2021. [Google Scholar]

20. Q. Zhou, C. Zhou and X. Wang, “Stock prediction based on bidirectional gated recurrent unit with convolutional neural network and feature selection,” Plos One, vol. 17, no. 2, pp. e0262501, 2022. [Google Scholar] [PubMed]

21. A. Mannan, A. Abbasi, A. Javed, A. Ahsan, T. Gadekallu et al., “Hypertuned deep convolutional neural network for sign language recognition,” Computational Intelligence and Neuroscience, vol. 2022, pp. 1–10, 2022. [Google Scholar]

22. A. Rahagiyanto, A. Basuki, R. Sigit, A. Anwar and M. Zikky, “Hand gesture classification for sign language using artificial neural network,” in 2017 21st Int. Computer Science and Engineering Conf. (ICSEC), Bangkok, Thailand, pp. 1–5, 2017. [Google Scholar]