Dual Image Cryptosystem Using Henon Map and Discrete Fourier Transform

1  Introduction

In the current age of multimedia and communication networks, security becomes an emergent and hot topic [1]. Now, many applications have exploited these advancements such as mobile smart phones, social media, military, and networking applications [2]. With these applications, huge amounts of bulky data like audio, image and videos are exchanged. So, there exists an emergent need to secure these applications from different types of security threats [3]. There are different solutions like data hiding and encryption techniques. Concerning encryption, conventional encryption algorithms are designed specially to manage only text data and cannot work properly with multimedia data like audio, images and videos due to their high correlation and redundancy [4–6]. Moreover, using such algorithms with different types of multimedia can degrade performance in terms of processing time and power consumption. So, other encryption methods are needed to satisfy such requirements [7]. Consequently, two main methods have been used to satisfy multimedia encryption requirements: data hiding and chaotic-based cryptosystems [8–11]. With data hiding, the classified data is concealed, where it cannot be seen and recognized by human vision. While chaotic-based image encryption utilizes Shannon rules [12] that employ confusion-diffusion operations depending on non-linearity theorems [13–16]. Chaotic-based encryption schemes may be employed in spatial and frequency domains [17–19]. Chaotic functions offer several merits like their sensitivity to the initial conditions, which results in secure cryptographic systems against parameter perturbation. Chaotic algorithms can utilize both discrete and continuous dynamical systems, whereas in the discrete system; different chaotic functions are employed iteratively [14], while the continuous system uses differential equations [15]. Many chaotic maps like Logistic, Tent, Baker and Henon maps can be used in different forms. They can be arranged in different forms like one-dimension (1D) [16], two-dimension (2D) [20], and three-dimensions (3D) [21]. Moreover, chaotic-based algorithms can be utilized either in time or frequency domains. In the time domain (spatial domain), the values of image pixels are used, while in the frequency domain; the values of image pixels are firstly transformed with the appropriate frequency transform domain and then, the encryption is applied to the transformed coefficients of the image pixels [22].

Hence, chaotic-based encryption algorithms are being used recently in image cryptography systems [23–27]. In [17], a colored image encryption scheme based on utilizing the Discrete Cosine Transform (DCT) with a chaotic baker map was presented. First, the three-color image components are transformed to the frequency domain with the DCT. Second, each color component is permutated with the chaotic baker map. Then, the cipherimage is finally obtained after performing the inverse DCT for each color component and combining them. In [28], a colored image cryptosystem based on utilizing dual 2D adjusted logistic sine chaotic map and 2D Henon chaotic map was introduced. With this scheme, each color channel is processed independently, where it goes through a confusion process using the 2D adjusted logistic sine chaotic map and then through a diffusion process using the 2D Henon chaotic mapping. After applying m-iteration for confusion and n-iteration for diffusion to each color channel, the three-color channels are combined to get the final encrypted image. The authors of [29] investigated the usage of chaotic mapping with different frequency domains. First, the plainimage is transformed using the chosen transform. Then, they apply baker chaotic mapping and the inverse of the chosen transform to obtain the final cipherimage. They studied different transforms including DCT, Discrete Sine Transform (DST), Discrete Wavelet Transform (DWT) and the Additive Wavelet Transform (AWT). In [30], an image cryptosystem based on 2D logistic chaotic mapping and 2D Fractional Fourier Transform (2D FrFT) was proposed. First, the colored plainimage is shuffled using 2D logistic chaotic mapping, where each color channel is processed independently. Second, the FrFT is applied to the shuffled image. Third, the 2D logistic chaotic mapping is applied again on the FrFT transformed image. Finally, the inverse FrFT is employed and the three-color channels are merged to obtain the final cipherimage. In [31], DWT transformation along with chaotic mapping was used for multiple-image encryption. First, all plainimages are decomposed and transformed with DWT and then the Arnold Cat chaotic mapping is used for scrambling. After that, each image is processed independently, where a robust chaotic map (RCM) is used to generate security keys used in the diffusion process. Finally, the cipher images are obtained. In [32], a dual-image cryptosystem based on chaotic mapping in DWT and Double Random Phase Encoding (DRPE) was presented. First, DWT is utilized to obtain approximate and detailed components from the plainimage. Second, the transformed image is encrypted using Baker chaotic mapping and then the inverse DWT is employed. For more security and to mitigate the correlation between pixels, the DPRE is employed.

The main contribution of the paper is to study the utilization of the chaotic henon map (CHM) in the Discrete Fourier Transform (DFT) to obtain secure images. The rest of the paper is structured as follows: Section 2 presents the mathematical background of the DFT and the CHM. Section 3 presents the proposed DFT-based CHM scheme. The obtained results are introduced and analyzed in Section 4. Section 5 lists the main conclusions of the paper.

2  Fundamental Knowledge

In this section, we will present the main information about the basic building blocks of the proposed DFT-based CHM encryption scheme. These include the DFT and the CHM. The discussion will start with the DFT followed by the CHM.

2.1 Discrete Fourier Transform (DFT)

The DFT may be considered an important transformation in digital signal processing. The DFT represents the digital image as a sufficient sequence of frequency samples in the frequency domain. The DFT transforms the digital image pixels into frequencies, where the image size does not change in both spatial or frequency domains. If we have an image f(a,b)  of size ( W X Z ), it can be expressed mathematically in the DFT as follows [33]:

D(u,v)=1WZ∑a=0W−1⁡∑b=0Z−1⁡f(a,b)e−2jπ(auW+bvZ). (1)

The image can be transformed back into the spatial domain by employing the inverse of the DFT as follows [33]:

f(a,b)=∑u=0W−1⁡∑y=0Z−1⁡D(u,v)e2jπ(auW+bvZ). (2)

2.2 Chaotic Henon Map (CHM)

In non-linear physics, chaotic henon mapping (CHM) represents a 2D nonlinear system that exhibits a chaotic-like randomized behaviour. So, this chaotic behaviour may be utilized efficiently for building a superior security system. The main idea of the CHM is to scramble or permutate image pixels to increase the confusion rate. The CHM can be mathematically expressed as follows [34]:

{Wn+1= 1−uWn2+ ZnZn+1= vWn. (3)

where, u and v define the main CHM parameters and in classical CHM, u=1.4 and v=0.3 , W and Z indicate the indices values after the iteration, and the iterations number is represented by n.

3  The Proposed DFT-based CHM Image Cryptography

This part provides the details of the proposed DFT-based CHM image cryptography. The proposed DFT-based CHM image cryptography has two procedures which are the encryption and decryption procedures. In the proposed DFT-based CHM image cryptography, the confusion is employed using the CHM while the diffusion is realized using the DFT. So, the proposed DFT-based CHM image cryptography achieves both confusion and diffusion characteristics.

3.1 DFT-based CHM Encryption Procedure

The encryption procedure of the proposed DFT-based CHM image cryptography starts firstly by applying the DFT transformation to the original plainimage to obtain its frequency coefficients. Then the coefficients of the DFT transformed image are then scrambled using the CHM and after that, the inverse DFT is applied to get the final DFT-based CHM encrypted image. As seen the proposed DFT-based CHM image cryptography scheme combines the confusion represented in CHM and the diffusion represented in the DFT. The main building block of the encryption procedure of the proposed DFT-based CHM image cryptography scheme is illustrated in Fig. 1.

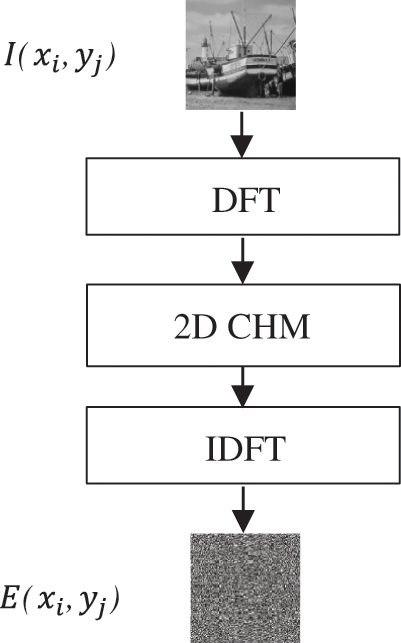
Figure 1: Encryption procedure of the proposed Discrete Fourier Transform (DFT)-based chaotic henon map (CHM) image cryptography

The encryption procedure of the proposed DFT-based CHM image cryptography can be listed as follows:

1. Apply the DFT on the original plainimage I (xi,yj) as follows.

E1(xi,yj)=DFT[I(xi,yj)]. (4)

2. The DFT coefficients of the original image are shuffled using the CHM.

E2(xi,yj)=CHM[E1(xi,yj)]=CHM[DFT[I(xi,yj)]]. (5)

3. Finally, apply the inverse DFT on CHM shuffled DFT coefficients.

E(xi,yj)=IDFT[E2(xi,yj)]=IDFT[CHM[DFT[I(xi,yj)]]]. (6)

4. Obtain the final encrypted image as E(xi,yj) .

3.2 DFT-based CHM Decryption Procedure

The decryption procedure of the proposed DFT-based CHM image cryptography starts firstly by applying the DFT transformation to the encrypted to obtain its frequency coefficients. Then the coefficients of the DFT transformed cipherimage is then inversely scrambled using the CHM and after that, the inverse DFT is applied to get the final decrypted. As seen the decryption procedure is the inverse of the encryption procedure. The main building block of the decryption procedure of the proposed DFT-based CHM image cryptography scheme is illustrated in Fig. 2.

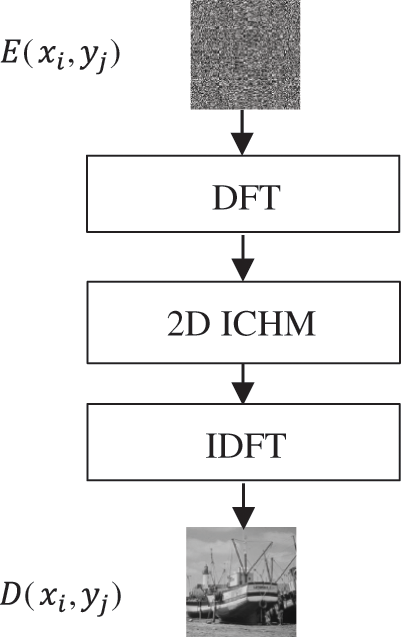
Figure 2: Decryption procedure of the proposed DFT-based CHM image cryptography

The decryption procedure of the proposed DFT-based CHM image cryptography can be listed as follows:

1. Apply the DFT on the encrypted image E(xi,yj) as follows.

D1(xi,yj)=DFT[E(xi,yj)] (7)

2. The DFT coefficients of the encrypted image are inversely shuffled using the CHM as follows.

D2(xi,yj)=I CHM[D1(xi,yj)]=I CHM[DFT[E(xi,yj)]] (8)

3. Finally, apply the inverse DFT on inverse CHM shuffled DFT coefficients.

D(xi,yj)=I DFT[D2(xi,yj)]=I DFT[I CHM[DFT[E(xi,yj)]]] (9)

4. Obtain the final decrypted image as D(xi,yj) .

4  Results and Discussions

This part investigates and tests the security of the proposed DFT-based CHM image cryptography system. This is done by employing a group of security tests that may include statistical tests in terms of histogram and correlation tests, information entropy analysis, differential tests in terms of NPCR and UACI, and noise immunity tests. Also, the proposed DFT-based CHM image cryptography system is compared with the CHM image cryptography system taking into account all of these above-mentioned tests. With the above-mentioned test experiments, four grayscale images of size 512 × 512 pixels are utilized as test plainimages. The four employed grayscale images include Girl, Boat, Peppers, and Baboon as depicted in Fig. 3.

Figure 3: Four gray scale test images

4.1 Visual Testing

Fig. 4 shows the encryption results of the four grayscale images for both the proposed DFT-based CHM image cryptography system and the CHM image cryptography system. The encryption outcomes demonstrate that the produced encrypted images using either the proposed DFT-based CHM image cryptography system or the CHM image cryptography system are different from their corresponding plainimages. These results demonstrate the superiority of the proposed DFT-based CHM image cryptography system and the CHM image cryptography system in hiding all the details of plainimages.

Figure 4: Visual ciphering outcomes of the proposed DFT-based CHM image cryptography system and the CHM image cryptography system using Girl, Boat, Baboon, and Peppers images

4.2 Statistical Measures

This subsection illustrates the statistical measures in terms of histogram testing and correlation coefficient measures.

4.2.1 Histogram Testing

Histogram testing is employed to examine the uniformity of the distributed gray levels in the encrypted images. For an efficient encryption algorithm, the histogram of the produced cipherimages must show a uniform distribution for all gray levels. The histograms outcomes of the tested four grayscale images for both the proposed DFT-based CHM image cryptography system and the CHM image cryptography system are illustrated in Fig. 5. It is firstly noted that the histogram produced by the CHM image cryptography system is the same as the histogram of the original plainimages. This can be interrupted as the CHM image cryptography system just performs a shuffling operation. On contrary, the histogram produced by the proposed DFT-based CHM image cryptography system is completely different from the histogram of their corresponding plainimages. These findings demonstrate the efficiency of the proposed DFT-based CHM image cryptography system in terms of histogram testing.

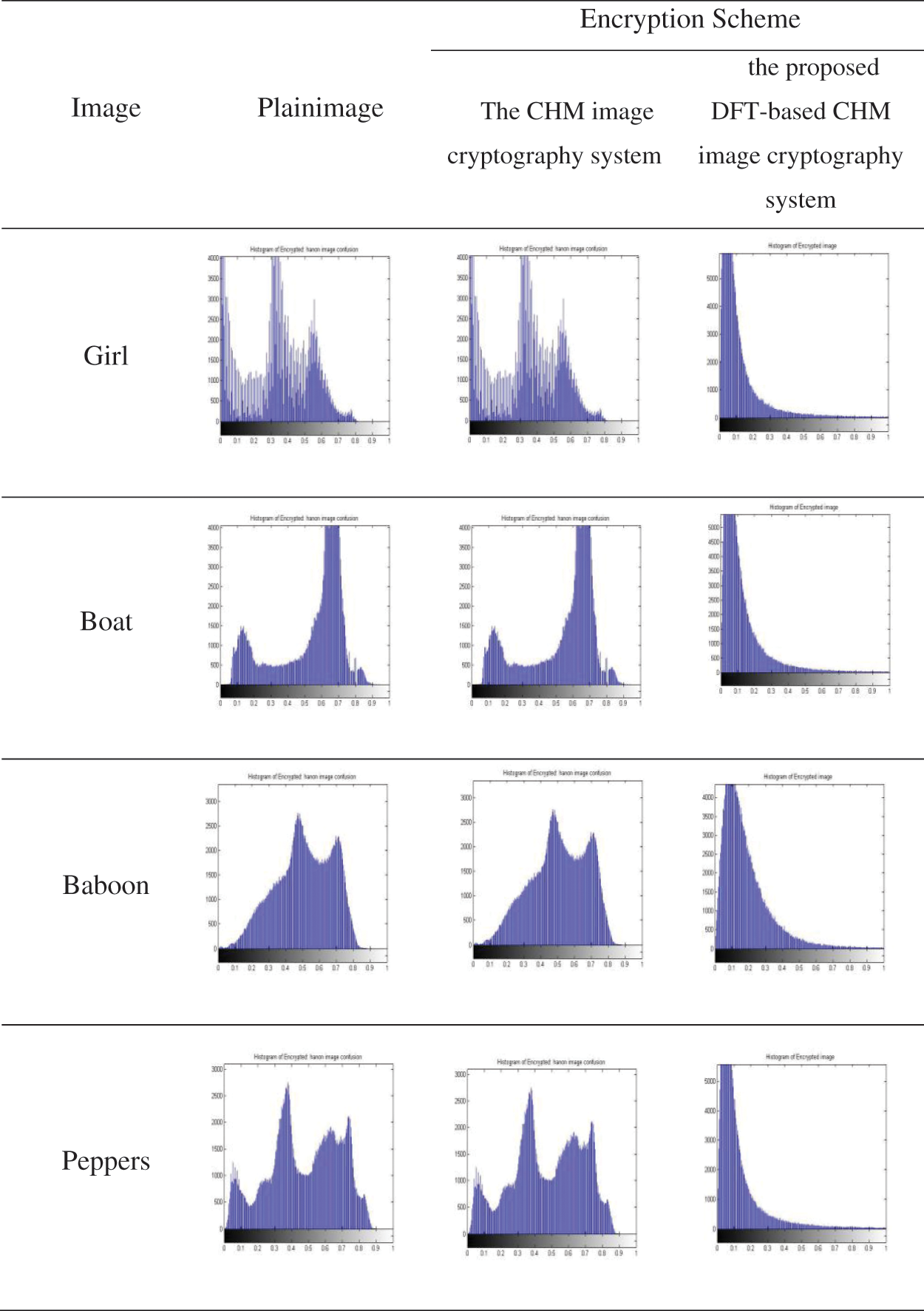
Figure 5: Histogram results of the proposed DFT-based CHM image cryptography system and the CHM image cryptography system using Girl, Boat, Baboon, and Peppers images

4.2.2 Correlation Coefficient Testing

The correlation coefficient testing is performed to test the similarity of the produced encrypted image to its corresponding plainimage. The correlation coefficient can be mathematically expressed as [28]:

r=E{(CI−E(CI))⋅(SI−E(SI))}E{[CI−E(CI)]2}E{[SI−E(SI)]2} (10)

where CI and SI represent the cipherimage and plainimage. An efficient cipher must produce a correlation coefficient that is very close to zero value. The resulted outcomes of the correlation coefficient of the proposed DFT-based CHM image cryptography system and the CHM image cryptography system using Girl, Boat, Baboon, and Peppers images are listed in Table 1. The resulted outcomes of correlation coefficient of the proposed DFT-based CHM image cryptography system and the CHM image cryptography system are very close to the zero value. These resulting outcomes of the correlation coefficient again prove the efficiency of the proposed DFT-based CHM image cryptography system.

4.3 Information Entropy Testing

The information entropy testing is performed to estimate the information amount of the produced encrypted image. An efficient cipher must produce a cipherimage that has information entropy neat 8. The information entropy can be mathematically expressed as [28]:

E(x)=∑i=12N−1⁡Y(xi)log21Y(xi) (11)

where E(x) represents the value of entropy value in bits. The resulting outcomes of E(x) for the proposed DFT-based CHM image cryptography system and the CHM image cryptography system using Girl, Boat, Baboon, and Peppers images are listed in Table 2.

The resulting outcomes of E(x) for the CHM image cryptography system are the same as their corresponding plainimages and this is because the CHM image cryptography system just performs a shuffling operation. On contrary, the resulting outcomes of E(x) for the proposed DFT-based CHM image cryptography system decreased but were still near to the E(x) values of their corresponding plainimages. These resulting outcomes of information entropy also prove the efficiency of the proposed DFT-based CHM image cryptography system.

4.4 Differential Analysis Testing

The differential analysis testing is employed in terms of the number of pixel change rate (NPCR) and unified average changing intensity (UACI) to measure the effect of changing just only 1-bit in the input plainimage.

The NPCR can be mathematically expressed as [28]:

NPCR (CI1,CI2)=∑i,j⁡S (Fi,Gj)M×100% (12)

where M represents the image total pixels number while S (Fi,Gj) can be expressed as []:

S (CI1,CI2)={0,CI 1(Fi,Gj)=CI 2(Fi,Gj)1,CI 1(Fi,Gj)≠CI 2(Fi,Gj) (13)

where CI 1(Fi,Gj) and CI 2(Fi,Gj) represent the two cipherimages CI1,CI2 .

The UACI metric can be mathematically expressed as [28]:

UACI (CI1,CI2)=1M[∑i,j|CI 1(Fi,Gj)−CI 2(Fi,Gj)|255]×100% (14)

Tables 3 and 4 list the resulting outcomes of both NPCR and UACI of the proposed DFT-based CHM image cryptography system and the CHM image cryptography system using Girl, Boat, Baboon, and Peppers images. The resulting outcomes of both NPCR and UACI demonstrate the high sensitivity of the proposed DFT-based CHM image cryptography system to just only 1-bit change and this again proves the efficiency of the proposed DFT-based CHM image cryptography system against differential attacks.

4.5 Noise Immunity Analysis

In this section, we test and measure the effect of additive white Gaussian noise (AWGN) noise on the decrypted images using the proposed DFT-based CHM image cryptography system. The measurement of noise immunity is based on three metrics which are the peak signal-to-noise ratio (PSNR), the structural similarity index metric (SSIM) and the Feature similarity index metric (FSIM) metric. An efficient cipher with good noise immunity should provide a PSNR equal to or more than 25 dB and SSIM and FSIM near 1.

The PSNR can be mathematically expressed as [28]:

PSNR(SI,CI)=10 log10(255)21MN∑i=0M−1⁡∑j=0N−1⁡[CI(xi,yj)−SI(xi,yj)]2 (15)

where SI(xi,yj) and CI(xi,yj) are the plainimage and its cipherimage.

The SSIM can be mathematically expressed as [28]:

SSIM (x,y|z)=(2z¯xz¯y+A1)(2σzxzy+A2)(z¯x2+z¯y2+A1)(σzx2+σzy2+A2) (16)

where z¯x , z¯y denote the mean of the regions x and y . A1 and A2 denote fixed values. σzxzy and σzx2 are the covariance and variance, respectively.

The FSIM can be mathematically expressed as [28]:

FSIM =∑x∈η⁡ZS(x).PC(x)∑x∈η⁡PC(x) (17)

where ZS(x) is the similarity among the decrypted and original images, η denotes the image time domain, and PC(x) is the phase congruency value.

Table 5 lists the resulting outcomes of PSNR with different SNR values of the proposed DFT-based CHM image cryptography system and the CHM image cryptography system using Girl, Boat, Baboon, and Peppers images. The resulting outcomes show high PSNR values that are more than 25 dB which demonstrates better immunity against AWGN. These PSNR results again prove the immunity of the proposed DFT-based CHM image cryptography system to AWGN.

Table 6 lists the resulting outcomes of SSIM with different SNR values of the proposed DFT-based CHM image cryptography system and the CHM image cryptography system using Girl, Boat, Baboon, and Peppers images. The resulting outcomes show high SSIM values that are very close to its ideal value of 1 which confirms better immunity against AWGN. These SSIM results again prove the efficiency of the proposed DFT-based CHM image cryptography system in reconstructing the deciphered image even in the existence of AWGN.

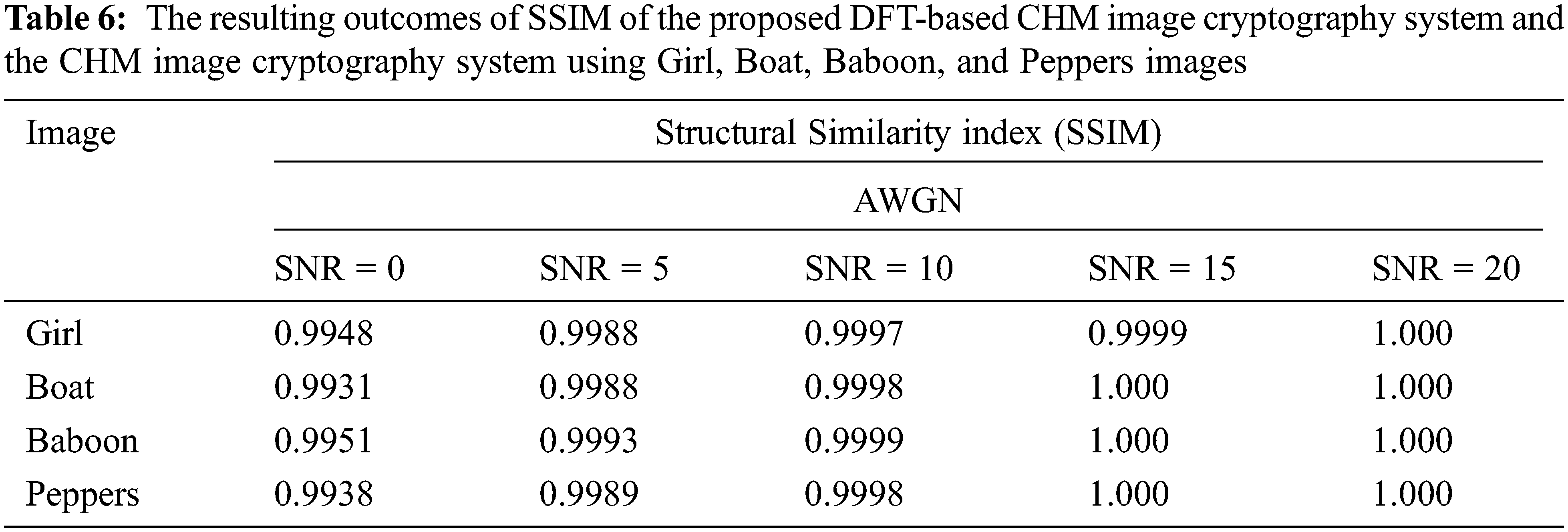
Table 7 lists the resulting outcomes of FSIM with different SNR values of the proposed DFT-based CHM image cryptography system and the CHM image cryptography system using Girl, Boat, Baboon, and Peppers images. The resulting outcomes show high FSIM values which prove better immunity against AWGN. These FSIM results confirm the superiority of the proposed DFT-based CHM image cryptography system in reconstructing the deciphered image even in the existence of AWGN.

5  Conclusion

This paper introduces an efficient DFT-based CHM image cryptography system. The proposed cipher is based on employing the CHM on DFT. The main advantage of the proposed DFT-based CHM image cryptography relies on achieving both confusion and diffusion characteristics. In the proposed DFT-based CHM image cryptography, the confusion is employed using the CHM while the diffusion is realized using the DFT. So, the proposed DFT-based CHM image cryptography achieves both confusion and diffusion characteristics. The cipher is investigated and compared with the CHM image cryptography system using a group of key performance metrics that may include statistical, entropy, differential, and noise immunity tests. The resulting outcomes prove and confirm the efficiency of the proposed DFT-based CHM image cryptography system. These findings support the utilization of the proposed DFT-based CHM image cryptography system in real-time applications.

Acknowledgement: The author would like to thank the Deanship of Scientific research, Taif University Researches Supporting Project number (TURSP-2020/216), Taif University, Taif, Saudi Arabia for supporting this scientific research work.

Funding Statement: This research was funded by Deanship of Scientific Research, Taif University Researches Supporting Project number (TURSP-2020/216), Taif University, Taif, Saudi Arabia.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. F. An and J. Liu, “Image encryption algorithm based on adaptive wavelet chaos,” Journal of Sensors, vol. 2019, pp. 1–12, 2019. [Google Scholar]

2. X. Wu and W. Sun, “High-capacity reversible data hiding in encrypted images by prediction error,” Signal Processing, vol. 104, no. 8, pp. 387–400, 2014. [Google Scholar]

3. D. Singh and S. Singh, “Effective self-embedding watermarking scheme for image tampered detection and localization with recovery capability,” Journal of Visual Communication and Image Representation, vol. 38, pp. 775–789, 2016. [Google Scholar]

4. J. Daemen and V. Rijmen, The Design of Rijndael: AES-The Advanced Encryption Standard. Berlin Heidelberg New York, USA: Springer Science & Business Media, 2002. [Google Scholar]

5. R. L. Rivest, “The RC5 encryption algorithm,” in Fast Software Encryption, Lecture Notes in Computer Science. Vol. 1008. Berlin, Heidelberg: Springer, pp. 86–96, 1995. [Google Scholar]

6. R. Rivest, M. Robshaw, R. Sidney and Y. L. Yin, The RC6 Block Cipher. San Mateo, USA: NIST AES Proposal, 1998. [Google Scholar]

7. J. Fridrich, “Symmetric ciphers based on two-dimensional chaotic maps,” International Journal of Bifurcation and Chaos, vol. 8, no. 06, pp. 1259–1284, 1998. [Google Scholar]

8. H. Yao, F. Mao, Z. Tang and C. Qin, “High-fidelity dual-image reversible data hiding via prediction-error shift,” Signal Processing, vol. 170, no. 3, pp. 107447, 2020. [Google Scholar]

9. L. Dong, J. Zhou, W. Sun, D. Yan and R. Wang, “First steps toward concealing the traces left by reversible image data hiding,” IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 67, no. 5, pp. 951–955, 2020. [Google Scholar]

10. A. Gutub and M. Al-Ghamdi, “Hiding shares by multimedia image steganography for optimized counting-based secret sharing,” Multimedia Tools and Applications, vol. 79, no. 13, pp. 1–35, 2020. [Google Scholar]

11. Z. Tang, H. Nie, C. M. Pun, H. Yao, C. Yu et al., “Color image reversible data hiding with double-layer embedding,” IEEE Access, vol. 8, pp. 6915–6926, 2020. [Google Scholar]

12. C. Shannon, “Communication theory of secrecy systems,” Bell System Technical Journal, vol. 28, no. 4, pp. 656–715, 1949. [Google Scholar]

13. J. M. Amigo, L. Kocarev and J. Szczepanski, “Theory and practice of chaotic cryptography,” Physics Letters A, vol. 366, no. 3, pp. 211–217, 2007. [Google Scholar]

14. M. S. Baptista, “Cryptography with chaos,” Physics Letters A, vol. 240, no. 1, pp. 50–54, 1998. [Google Scholar]

15. R. Matthews, “On the derivation of a “chaotic” encryption algorithm,” Cryptologia, vol. 13, no. 1, pp. 29–42, 1989. [Google Scholar]

16. C. Pak and L. Huang, “A new color image encryption using combination of the 1D chaotic map,” Signal Processing, vol. 138, no. 2, pp. 129–137, 2017. [Google Scholar]

17. H. Alhumyani, “Efficient image cipher based on baker map in the Discrete Cosine Transform,” Cybernetics and Information Technologies, vol. 20, no. 1, pp. 68–81, 2020. [Google Scholar]

18. X. Wu, D. Wang, J. Kurths and H. Kan, “A novel lossless color image encryption scheme using 2D DWT and 6D hyperchaotic system,” Information Sciences, vol. 349, no. 10, pp. 137–153, 2016. [Google Scholar]

19. Q. Lu, C. Zhu and X. Deng, “An efficient image encryption scheme based on the LSS chaotic map and single S-Box,” IEEE Access, vol. 8, pp. 25664–25678, 2020. [Google Scholar]

20. C. Han, “An image encryption algorithm based on modified logistic chaotic map,” Optik, vol. 181, no. 4, pp. 779–785, 2019. [Google Scholar]

21. M. L. Sahari and I. Boukemara, “A pseudo-random numbers generator based on a novel 3D chaotic map with an application to color image encryption,” Nonlinear Dynamics, vol. 94, no. 1, pp. 723–744, 2018. [Google Scholar]

22. H. Alhumyani, I. Alrube, A. Alsharif, A. Afifi, C. Amar et al., “Analytic beta-wavelet transform-based digital image watermarking for secure transmission,” CMC-Computers, Materials & Continua, vol. 70, no. 3, pp. 4657–4673, 2022. [Google Scholar]

23. M. Kumar, A. Saxena and S. S. Vuppala, “A survey on chaos based image encryption techniques,” in Multimedia Security Using Chaotic Maps: Principles and Methodologies. Cham: Springer, pp. 1–26, 2020. [Google Scholar]

24. K. A. Patro, M. P. Babu, K. P. Kumar and B. Acharya, “Dual-layer DNA-encoding-decoding operation based image encryption using one-dimensional chaotic map,” in Advances in Data and Information Sciences. Singapore: Springer, pp. 67–80, 2020. [Google Scholar]

25. S. Xiao, Z. Yu and Y. Deng, “Design and analysis of a novel chaos-based image encryption algorithm via switch control mechanism,” Security and Communication Networks, vol. 2020, pp. 1–12, 2020. [Google Scholar]

26. M. B. Farah, R. Guesmi, A. Kachouri and M. Samet, “A novel chaos based optical image encryption using fractional Fourier transform and DNA sequence operation,” Optics & Laser Technology, vol. 121, no. 7, pp. 105777, 2020. [Google Scholar]

27. M. Kalra, S. Katyal and R. Singh, “A tent map and logistic map based approach for chaos-based image encryption and decryption,” in Innovations in Computer Science and Engineering. Singapore: Springer, pp. 159–165, 2019. [Google Scholar]

28. H. Alhumyani, “Secure image cryptosystem based on henon map and adjusted sine logistic map,” Journal of Theoretical and Applied Information Technology, vol. 98, no. 16, pp. 3209–3221, 2020. [Google Scholar]

29. E. A. Naeem, M. M. Abd Elnaby and M. M. Hadhoud, “Chaotic image encryption in transform domains,” in 2009 Int. Conf. on Computer Engineering & Systems, Cairo, Egypt, pp. 71–76, 2009. [Google Scholar]

30. O. S. Faragallah, H. S. El-sayed, A. Afifi and W. El-Shafai, “Efficient and secure opto-cryptosystem for color images using 2D logistic-based fractional Fourier transform,” Optics and Lasers in Engineering, vol. 137, no. 6, pp. 106333, 2021. [Google Scholar]

31. C. L. Li, H. M. Li, F. D. Li, D. Q. Wei, X. B. Yang et al., “Multiple-image encryption by using robust chaotic map in wavelet transform domain,” Optik, vol. 171, no. 3, pp. 277–286, 2018. [Google Scholar]

32. R. Jain and J. B. Sharma, “Multi-domain image encryption using chaotic map with DRPE,” in Proc. Int. Conf. Adv. Inf. Commun. Technol. Comput. (AICTC), Bikaner, India, pp. 10–16, 2016. [Google Scholar]

33. H. S. El-Sayed, A. Afifi, M. A. AlZain and O. S. Faragallah, “An image cryptosystem using chaotic baker map in DFT,” in 2021 Int. Conf. of Women in Data Science at Taif University (WiDSTaif), Taif, Saudi Arabia, pp. 1–7, 2021. [Google Scholar]

34. R. Anandkumar and R. Kalpana, “Analyzing of chaos based encryption with Lorenz and Henon Map,” in 2018 2nd Int. Conf. on I-SMAC (IoT in Social, Mobile, Analytics and Cloud) (I-SMAC)I-SMAC (IoT in Social, Mobile, Analytics and Cloud) (I-SMAC), Palladam, India, pp. 204–208, 2018. [Google Scholar]