Deep Capsule Residual Networks for Better Diagnosis Rate in Medical Noisy Images

1  Introduction

Deep learning and machine learning have already impacted various branches such as health care, image vision system, and even industrial automation. Even though it was first greeted with much scepticism [1], in a short period, it has proved itself to be a keynote player in solving many health care problems, including the disease classification and prediction, treatment and recommendation system, and even more [2–4]. Deep learning methods have already achieved unprecedented performances in many processes ranging from low-level applications to medical image processing. Such as denoising, enhancement and reconstruction to more high-level image analysis such as segmentation, prediction and classification.

Medical Image denoising and Medical Diagnosis rate are perceived as the process of improvisation in which imaging devices constitute more noise to the medical images, which harms the diagnosis rate. Hence, denoising is considered a strenuous task to improve the diagnosis rate. Traditionally, medical image denoising employs the Gaussian distribution to analyse noises in medical images. However, the traditional method results in efficient controversies to visualize the process of physical symptoms in the treatment process. As a result, intelligent methodology for Medical Image denoising is considered a relatively challenging task compared with conventional techniques.

In the recent past, substantial growth in Medical Image denoising with increased diagnosis rate has become the real challenge among researchers. Existing approaches such as non-local self-similarity (NSS) [5], sparse coding [6], and filter-based methods [7–9] have been proposed for the removal of noises. However, they do not concentrate on the diagnosis rate. Recently, the usage of deep learning algorithms has gained more insight into light and provides a viable alternative to the abovementioned methods. However, the existing deep learning models have focused on an inadequate range of noise deviations and diagnosis rates in the medical images.

The paper proposes the novel ensembled Deep Capsule Residual Learning Model for removing noises in medical images to overcome the above problem. Additionally, this paper introduces the Capsule networks, which utilize the feature correlation and combines it with redefined residual learning models. Here, this capsule network leverages such a way that it can extract the depth-wise features using its dynamic attention routing algorithms. Also, this study proposes to refine the residual learning to learn the low-level features under different noise levels, which can aid in achieving a better diagnosis rate. To the best of our knowledge, this study is the first of its kind to implement the capsule with residual learning models. The main contribution of the paper are summarized as follows as

1.    Dynamic Capsule Residual Framework: Proposes the novel ensembled capsule network with a residual network that combines the in-depth features and low-level features that aid the better diagnosis of complex, noisy images.

2.    Extensive Experiments: Conducts extensive experimentation with the substantial multi-disciplinary images and compared with the other state of learning models under noisy environments. Also, the proposed method has combined different medical image analysis tasks to reveal the practicability in the real world.

The rest of the paper is organized as follows: Section 2 presents the related works proposed by more than one author. The dataset collection, noise model and proposed methodology are presented in Section 3. The experimentations, results, findings and analysis are presented in Section 4. Finally, the paper is concluded in Section 5 with future enhancement.

2  Related Works

Chen et al., introduced a strategy, Spatial Compound Denoising Convolutional Neural Networks (SC-DnCNN), which is the SC-based denoising information base age. Because the picture is typical for Full-field Optical Coherence Tomography (FF-OCT), the pictures need not bother with an enlistment interaction before SC which makes it better than the direct checking OCT toward producing the detailed picture. This method incorporates boisterous and moderately clear pictures as its preparation information, versatile spatial planning as indicated by the intensifying data set can be inserted, and the impact of the dot can be diminished. Note that this denoising CNN model would consider to some extent, spatial connection to recuperate a good picture after deduction in any event when a solitary picture with no compounding. Such a way has tantamount to the dependable SC technique to diminish the clamour. In the meantime, since the necessary number of pixel lines to acquire a decent picture quality is diminished, the greatest B-filter pace of this framework is fundamentally improved by taking on this calculation. That is the issue of tedious for intensifying strategies can stay away from by performing SC-DnCNN without time series pictures [10].

Klyuzhin et al., proposed K-Nearest Neighbor (KNN) based on Computer Tomography (CT) picture denoising. This system utilizes this information to develop a directed denoising framework that gains ideal planning from input elements to denoised voxel values. As info includes, this system utilizes a few general channels and the result of existing standard sound decrease channels, prominently non-straight dissemination plans. After highlight determination, these are planned to the denoised values by KNN and support vector relapse. The subsequent relapse denoising frameworks perform fundamentally better than non-straight dispersion plans, Gaussian smoothing, and middle separating in probes CT chest examines [11].

van Ginneken et al., give a system for sorting the best in class calculations utilized in Magnetic Resonance Image (MRI) denoising. The denoising methods are gathered into spatial and change areas in light of the picture model utilized for clinical picture handling. The proposed classification improves the complicated framework and helps issue definition and preliminary trial and error. A quantitative examination is completed utilizing a broad scope of assessment lists, showing denoising and underlying similitude in the reestablished pictures. This proposes the fitting assessment lists to be utilized in MR picture denoising and the best technique to denoise MR pictures with given commotion. The discoveries of the review are-1) Filtering techniques are less complex and powerful for taking out Gaussian commotion from homogeneous areas. The possible disadvantage of the technique is that they dispose of the little designs and the edge subtleties by obscuring the non-homogeneous areas [12].

Mishro et al., proposed to utilize 3D CNNs for portioning the neuronal microscopy pictures. In particular, this structure planned an original CNN engineering that accepts volumetric pictures as the information sources and their voxel-insightful division maps as the results. The created engineering permits us to prepare and anticipate utilizing huge microscopy pictures from start to finish. This structure assessed the presentation of this model on an assortment of testing 3D microscopy pictures from various organic entities. Results showed that the proposed strategies developed the following execution when combined with various remaking calculations [13].

Li et al., depict a group of picture denoising calculations appropriate to the Graphical Processing Unit (GPU). The calculations iteratively play out a bunch of free, equal 1D pixel-update subproblems. To match GPU memory restrictions, they play out these pixel refreshes set up and just store the uproarious information, denoised picture, and issue boundaries. The calculations can deal with a broad scope of edge-protecting harshness punishments, including differentiable raised punishments and anisotropic all-out variety. The two calculations utilize the majorize-limit structure to settle the 1D pixel update subproblem. Results from a huge 2D picture denoising issue and a 3D clinical imaging denoising issue exhibit that the proposed calculations join quickly as far as both emphasis and run-time [14].

McGaffin et al., introduced a feed-forward Denoising CNN (DnCNNs) to embrace the advancement in exceptionally profound engineering, learning calculation, and regularization technique into picture denoising. In particular, lingering learning and cluster standardization accelerate the preparation cycle and lift the denoising execution. Not the same as the current discriminative denoising models, which typically train a particular model for added substance white Gaussian commotion at a specific clamour level, this DnCNN model can deal with Gaussian denoising with obscure commotion level (i.e., blind Gaussian denoising). With the leftover learning procedure, DnCNN verifiably eliminates the idle clean picture in the hidden layers. This property requires us to prepare a solitary DnCNN model to handle a few general picture denoising undertakings, for example, Gaussian denoising, single picture super-goal, and JPEG picture deblocking. These broad trials show that this DnCNN model can not just display high viability in a few general picture denoising undertakings yet additionally be productively carried out by profiting from GPU figuring [15].

Lee et al., presented an image denoising approach called self-cooperative learning which depends on various domains. This framework comprises various functions to boost the process of learning. The experimental validations incorporated noise from the Electro-Magnetic (EM) devices and structural noise found from low-dose CTs. Finally, the results show that image quality is ultimately high when contrasted with existing frameworks. However, this framework’s downside is that it requires additional resources when tested under real-time scenarios [16].

Wang et al., developed a deep learning-based unsupervised denoising technique to ease the labelled data dependency and explore the insights into the denoising framework. This framework integrates the data-driven technique and domain knowledge. The iterative soft threshold algorithm is utilized to frame the network. Also, a loss function is designed for the network training implementation with a smooth penalty. This framework provides better results in terms of accuracy, but its limitation is that it leads to computational complexity [17].

3  Proposed Methodology

This proposed study presents a novel deep capsule network for addressing the problems in denoising the medical images, which can aid the high diagnosis rate. This section details the methodology of the proposed work. Fig. 1 shows the end-to-end framework for the proposed methodology. The proposed network is presented as an end-to-end deep learning architecture where the proposed network utilizes capsule networks with a residual learning framework.

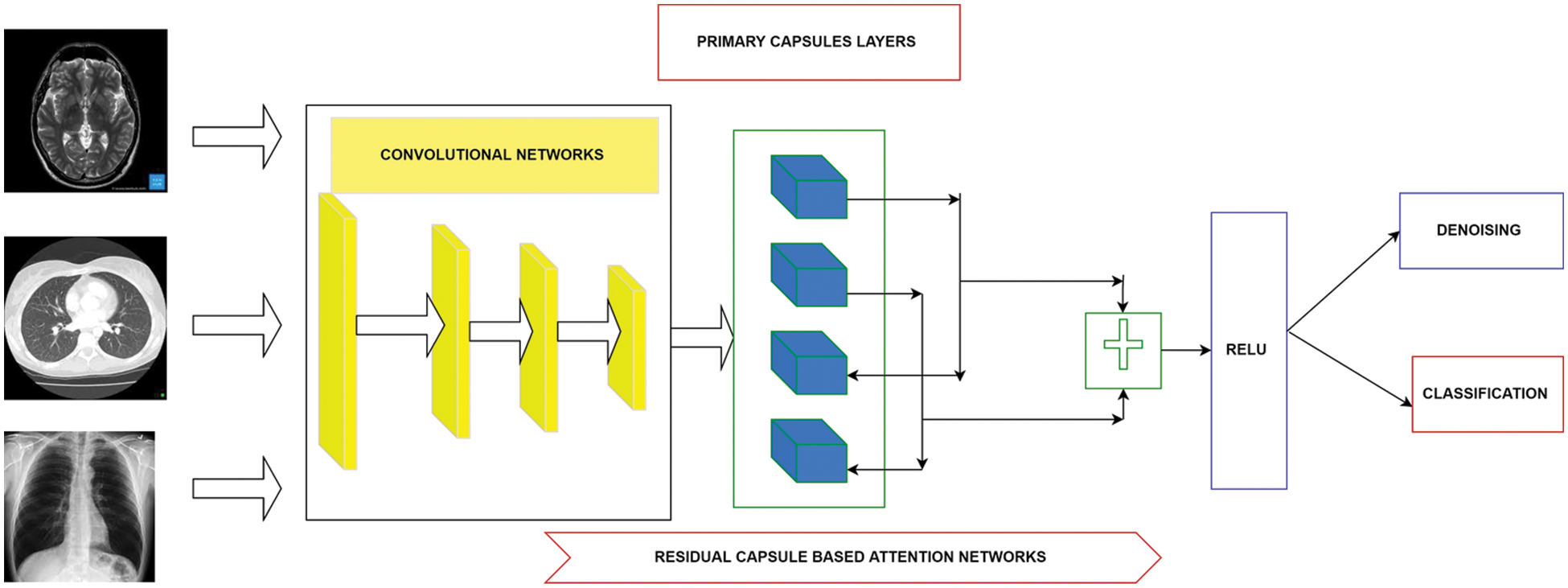
Figure 1: Overall proposed architecture used for denoising and high classification rate

3.1 Data Collection and Preparation

Data collection plays a vital role in training the deep learning model. For training purposes, collecting a sufficient amount of data samples is essential. Hence, a substantial amount of medical images are collected through different sources of modalities. The collected data were pre-processed and used for designing the model. The image samples collected from the different sources are categorized as shown In Fig. 2.

Figure 2: Overall dataset collection from the different image formats

Fig. 2 shows four different modalities of images such as brain Magnetic Resonance Images (MRIs), lung Computed Tomography (CT) scan images, Chest-X-ray images and Ultrasound Images were collected and used for the experimentation. This study collected nearly 500,332 medical images, where 80% of samples were used for model training and the rest of the 20% of data used for performance evaluation.

3.2 Noise Addicted Dataset Preparation

Despite having a significant number of image samples, collected datasets are not contaminated with the noises. Therefore, reference-noisy image pairs have to be formulated by adding artificial noises over the images. The final noise-addicted image is given as follows

C==N+Y (1)

Mathematically N is given as N = G(c|η, β) in which η, β is considered as mean, and variance and G(c) represents the Gaussian distribution of noise in input images Y.

3.3 Proposed Model Training

This section presents a novel deep learning method for addressing medical images denoising without sacrificing performance by learning from large-scale data samples. The proposed methodology involves the capsule networks with residual learning as the backbone.

The Capsule Network [17] have recently been proposed to address this limitation of existing Convolutional Neural Network (CNN) networks. Capsules are the groups of neurons that encode spatial information and the probability of an object being present. In the capsule network, corresponding to each entity in an image, there is a capsule which gives:

1.    Probability of Existence in entities

2.    Entities’ Instantiation parameters

The capsule network is sub-divided into three layers: a low capsule layer, a high capsule layer, and a classification layer. Global parameter sharing is performed to reduce the accumulation of errors, and an optimized dynamic routing algorithm is used to update the parameters iteratively. To encode the imperative spatial association between low- and high-level convolutional features within the image, the multiplication of the matrix of the input vectors with the weight matrix is calculated

Y(i.j)=Wi,j U(i,j)∗Sj (2)

The sum of the weighted input vectors is calculated to determine the current capsules and forward its output to the higher-level capsule.

S(j)=∑j⁡Y(i,j)∗D(j) (3)

Finally, non-linearity is applied using the squash function. While maintaining a direction of a vector, the squashing function maps it to a maximum length of one and a minimum length of 0.

G(j)=squash(S(j) (4)

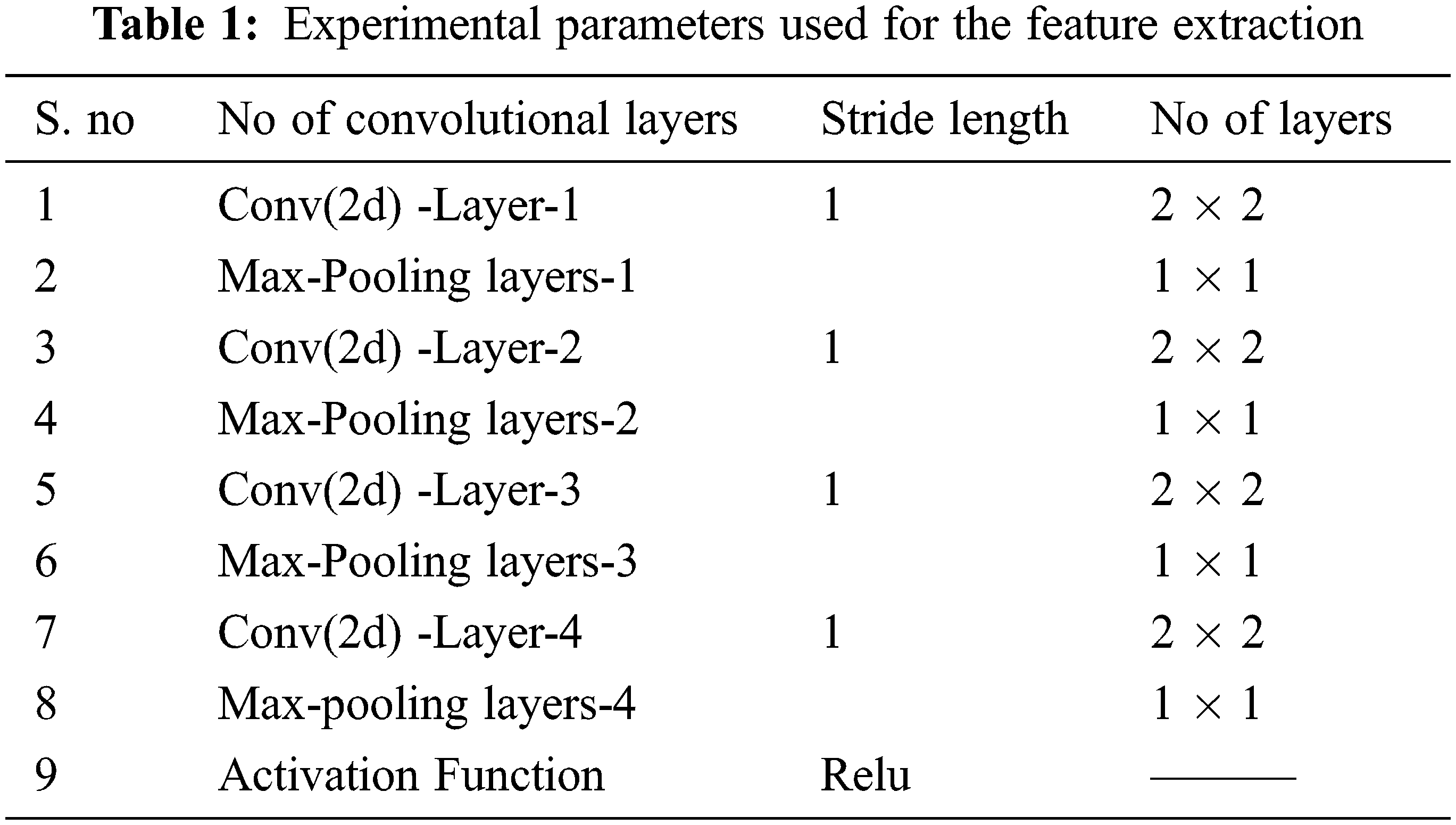
The capsule network can grab information in different positions and obtain the relationship between the features using the mathematical Eq. (2) for effective denoising and a high recognition rate. The convolution layers are implemented in the low capsule region and primary capsules in the high region. Table 1 presents the number of convolutional layers used for constructing the lower and primary capsule regions. The output weights are calculated using Eq. (3), passed to the high capsule region, while the squash function retains the original direction of the vector by compressing the length to (0, 1). In the next stage, the proposed model incorporates the dot product between similar capsules and outputs, using the self-attention routing. Finally, the output is updated, and this process continues for fixed iterations

3.4 Residual Learning to Capsule Networks

The residual learning is applied to the deep neural networks in which the skip connections are added to the networks’ output. Those skip functions do not contain the learning parameters but increase the performances of the final layers, which are replaced by the identity functions. In the proposed model, the skip functions are added after the routing process, which yields the best results in terms of denoising and a higher recognition rate.

However, the skip connection can backfire in denoising by delivering the lower-level capsules to the top levels. Hence the proposed network adopts the self-attention routing mechanism, which controls the propagation of trivial features by learning spatial features.

4  Implementation Details

The proposed architecture was designed as an end-to-end convolutional capsule residual network using Tensorflow as the backend and Keras as the frontend. Table 2 presents the experimental parameters used for building the proposed architecture.

All the experiments were conducted on an Intel I9 CPU clocked at 3.6 GHz and a RAM of 16 GB. Google Co-lab was exploited to train the proposed model.

5  Results and Discussion

The proposed model incorporates a unique evaluation strategy to investigate the superiority of its features over the other learning models by measuring two essential metrics: Peak-Signal-To-Noise Ratio (PSNR) and Structural-Similarity-Index-Metrics (SSIM). Such evaluation metrics are evaluated by comparing with the reconstructed images. The performance of the proposed model is compared with the other state-of-art learning models such as Block Matching and 3D (BM3D) filtering image denoising algorithm [18], Deep Residual Convolutional Neural Network (DRCNN) [19] and Densely Reversed Attention-based CNN (DRAN) [20] respectively to prove the superiority of the proposed model. Tables 3–5 show the proposed framework’s comparative analysis with the existing frameworks.

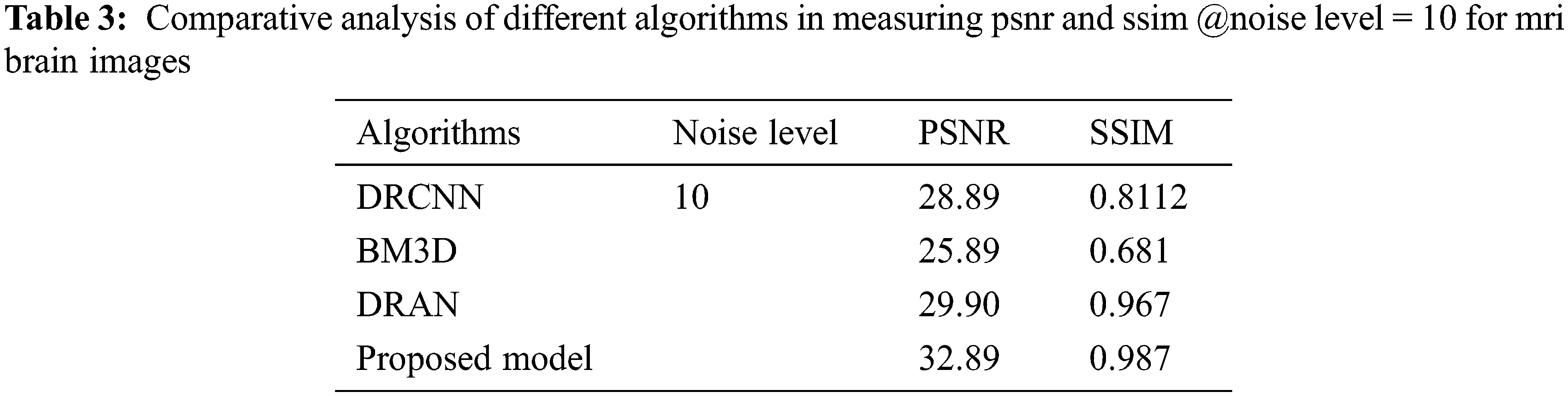
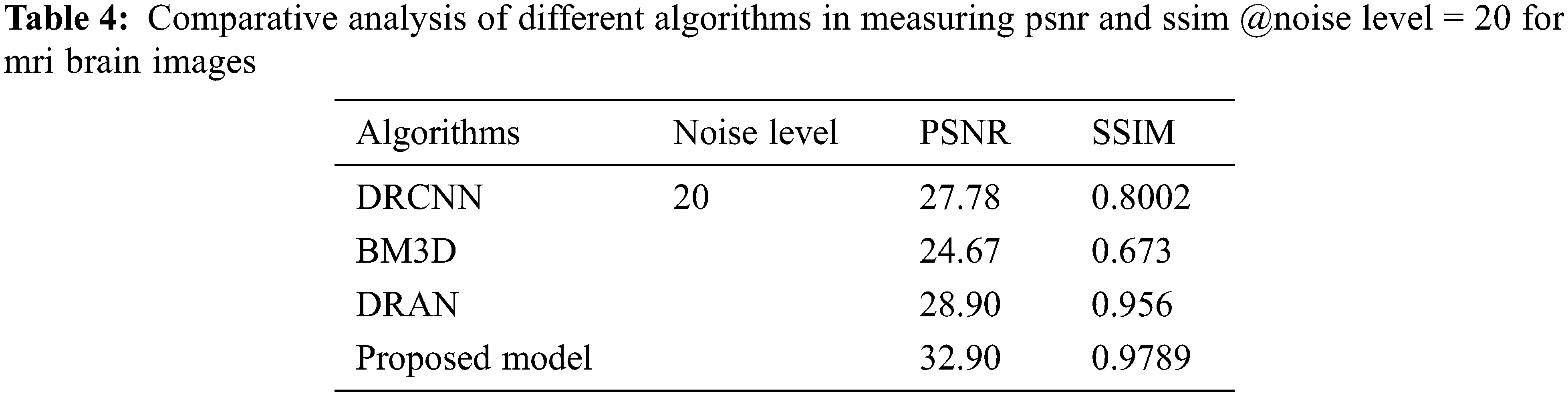
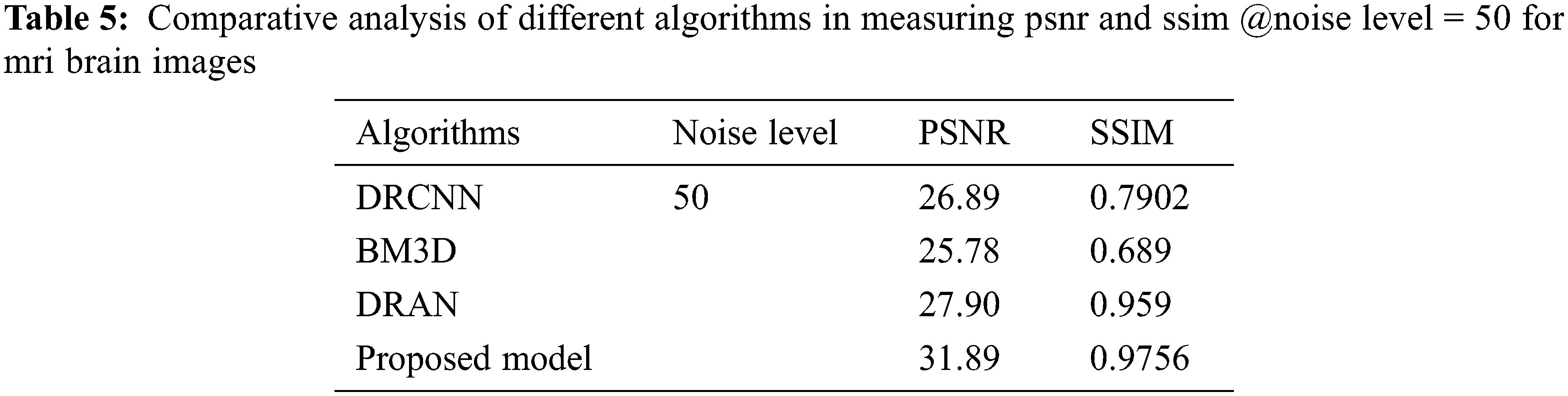
From Tables 3–5, it is evident that the proposed model, incorporating a capsule network with residual learning, outperformed the other learning models for MRI images. Though the proposed model and DRAN have produced a similar SSIM, the PSNR of the proposed model is better than DRAN under the increased distribution of noises.

From Tables 6 to 12, it is evident that the proposed model, which has incorporated a capsule network with residual learning, has outperformed the other learning models for CT lung images and Chest X-ray Images. Though the proposed model and DRAN have produced a similar SSIM, the PSNR of the proposed model is better than DRAN under the increased distribution of noises. The above tables show that the proposed model has better handled the different sources of images even in a noisier environment.

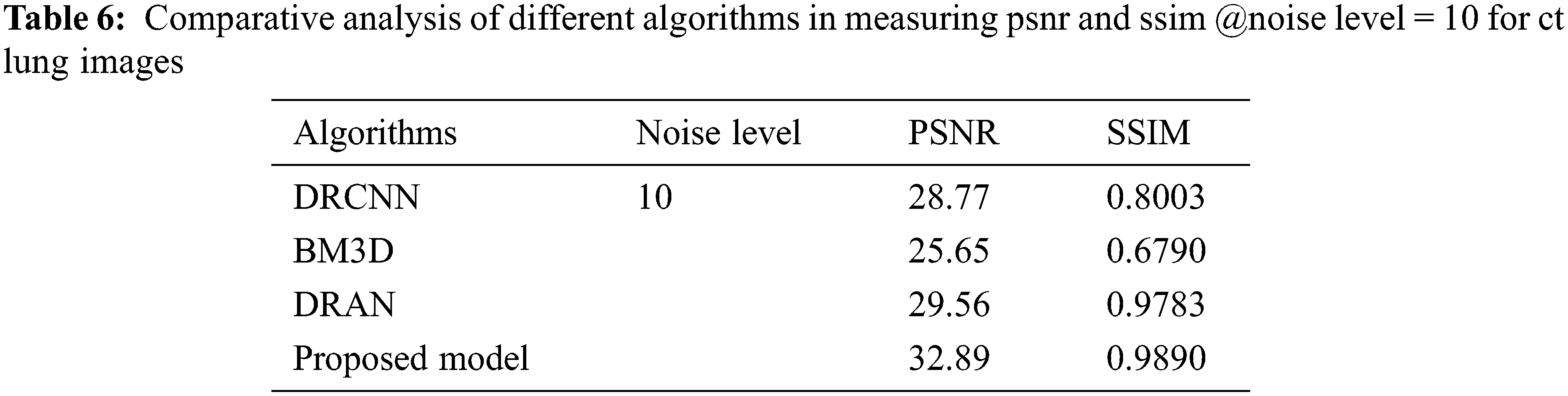
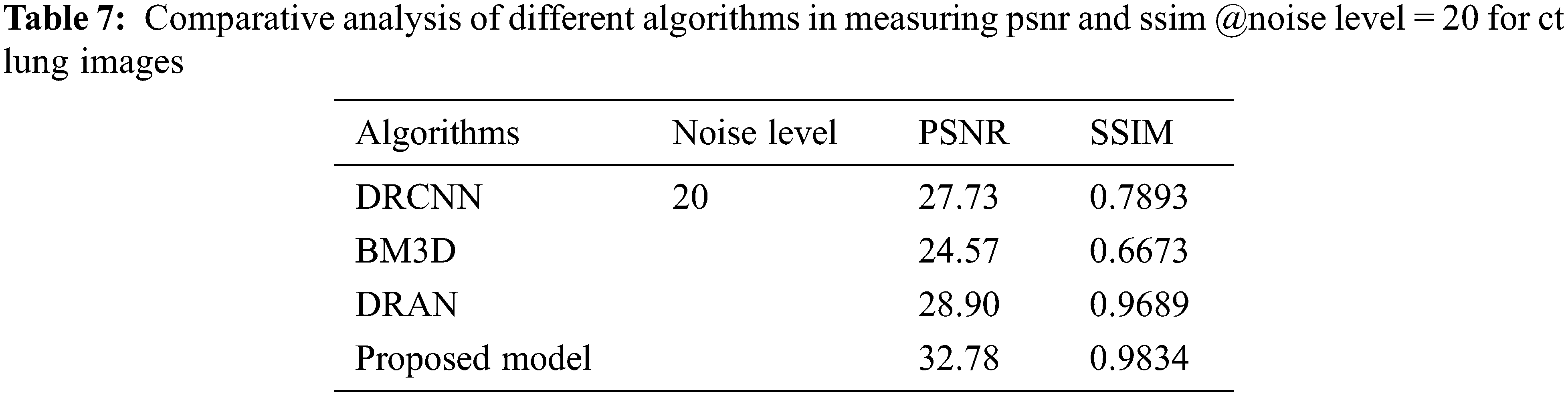
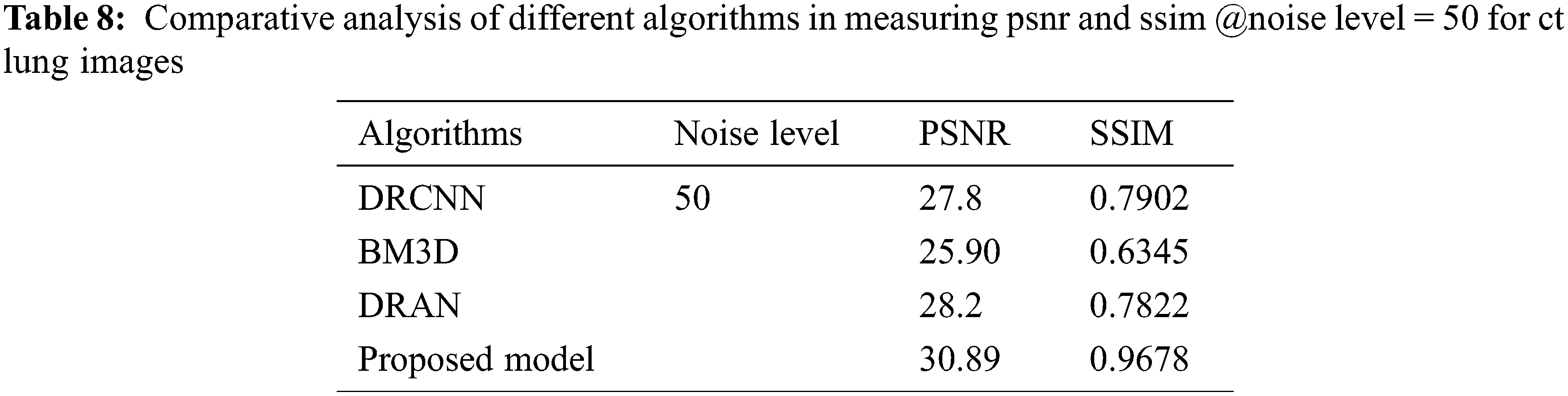
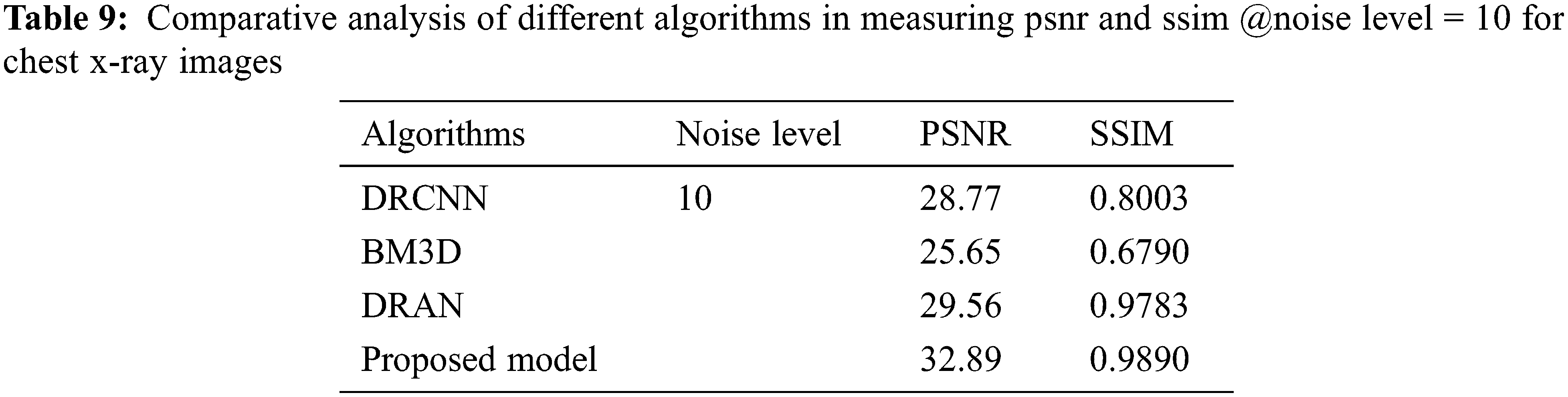
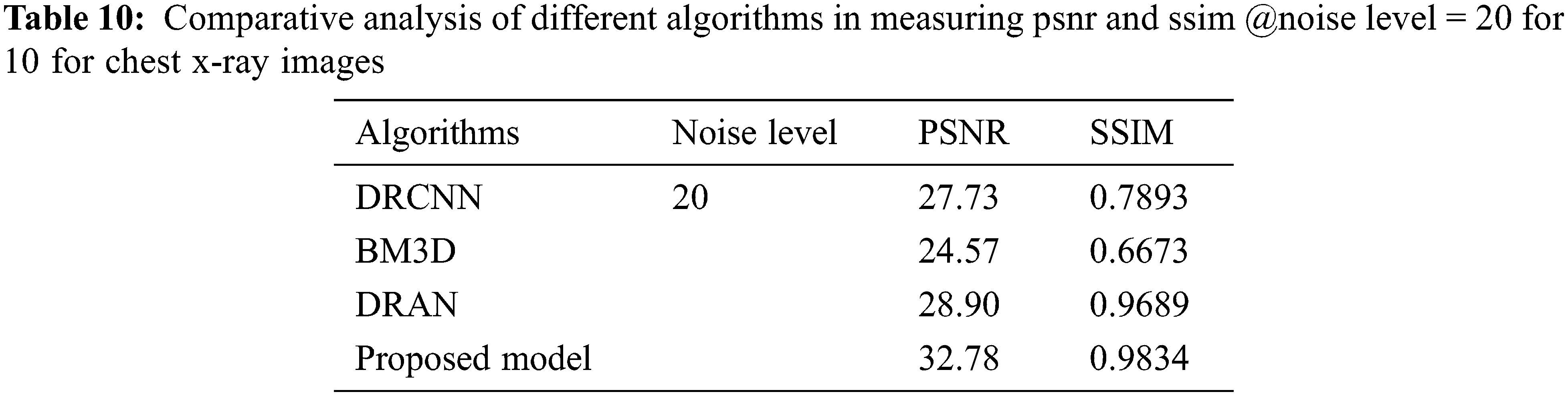
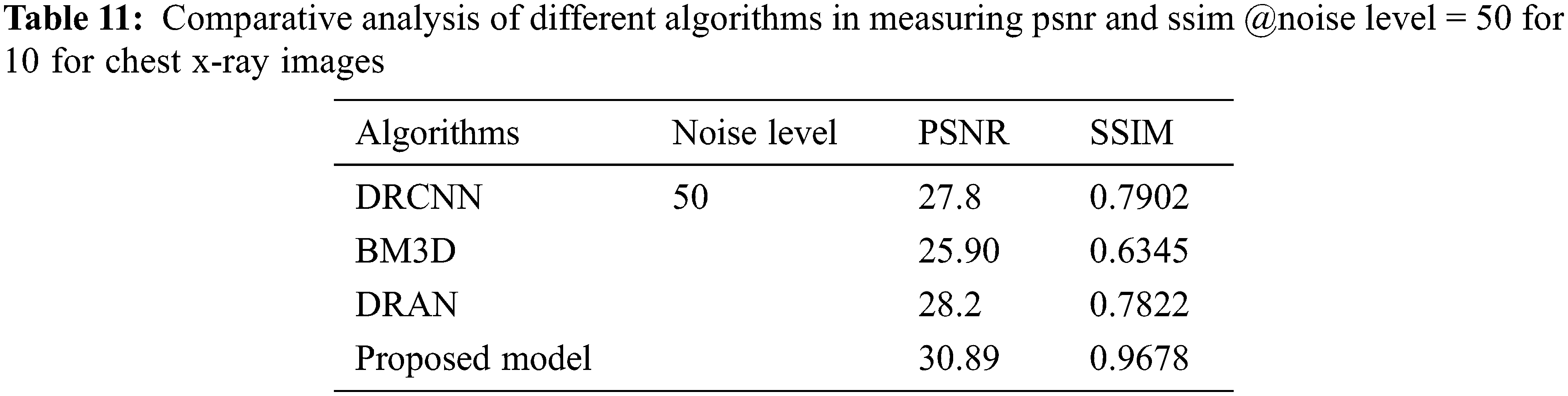
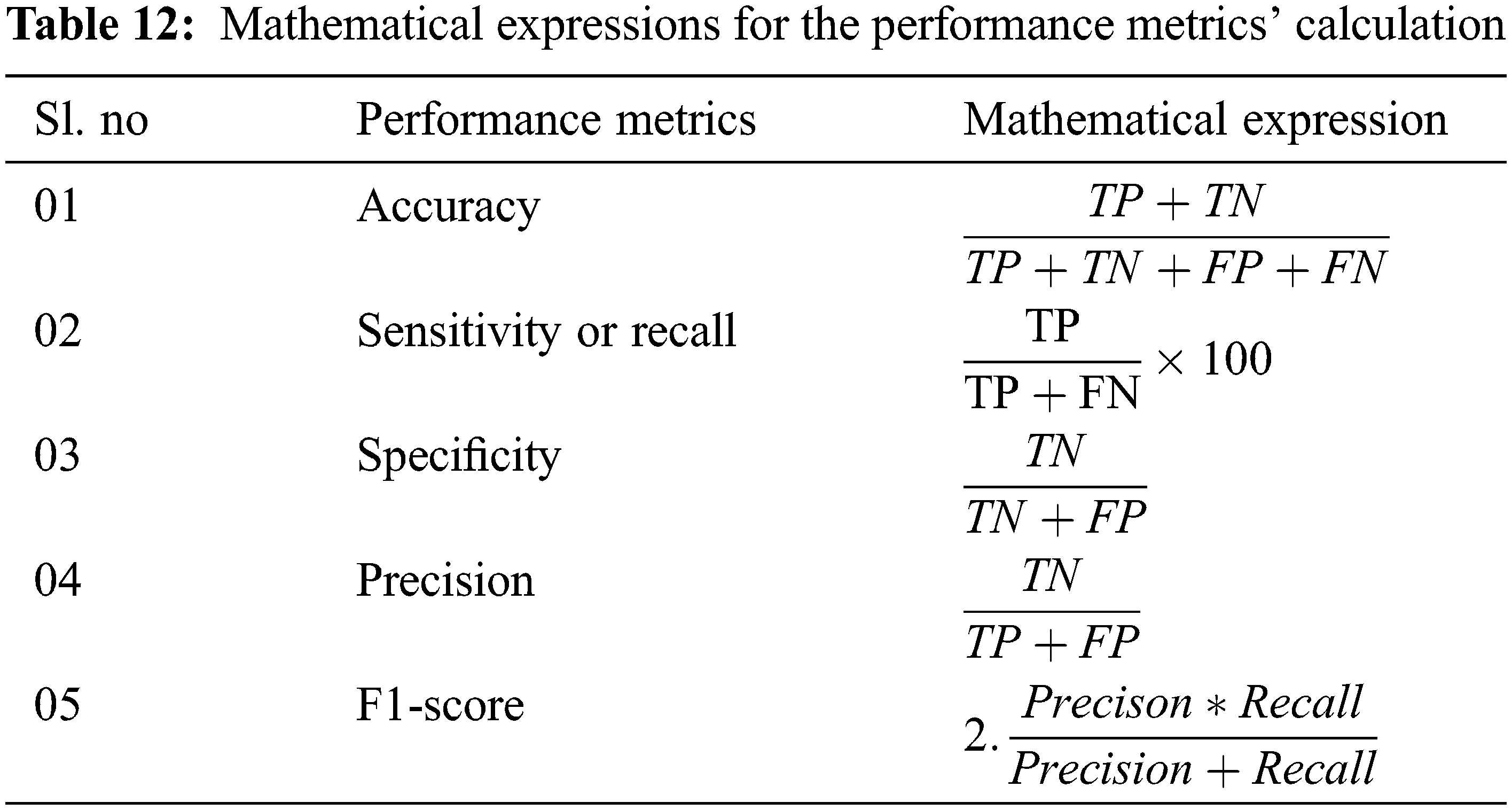
Additionally, the performance of the proposed model has been measured using the metrics mentioned in Table 12. The experimentation was done by adding the noise levels in the images with the abnormalities.

From Figs. 3–5, it is found that the proposed model has outperformed the other models in detecting the abnormalities in the different sources of the images. To summarize, integrating capsule networks with the residual networks has produced promising results in denoising and classification rate.

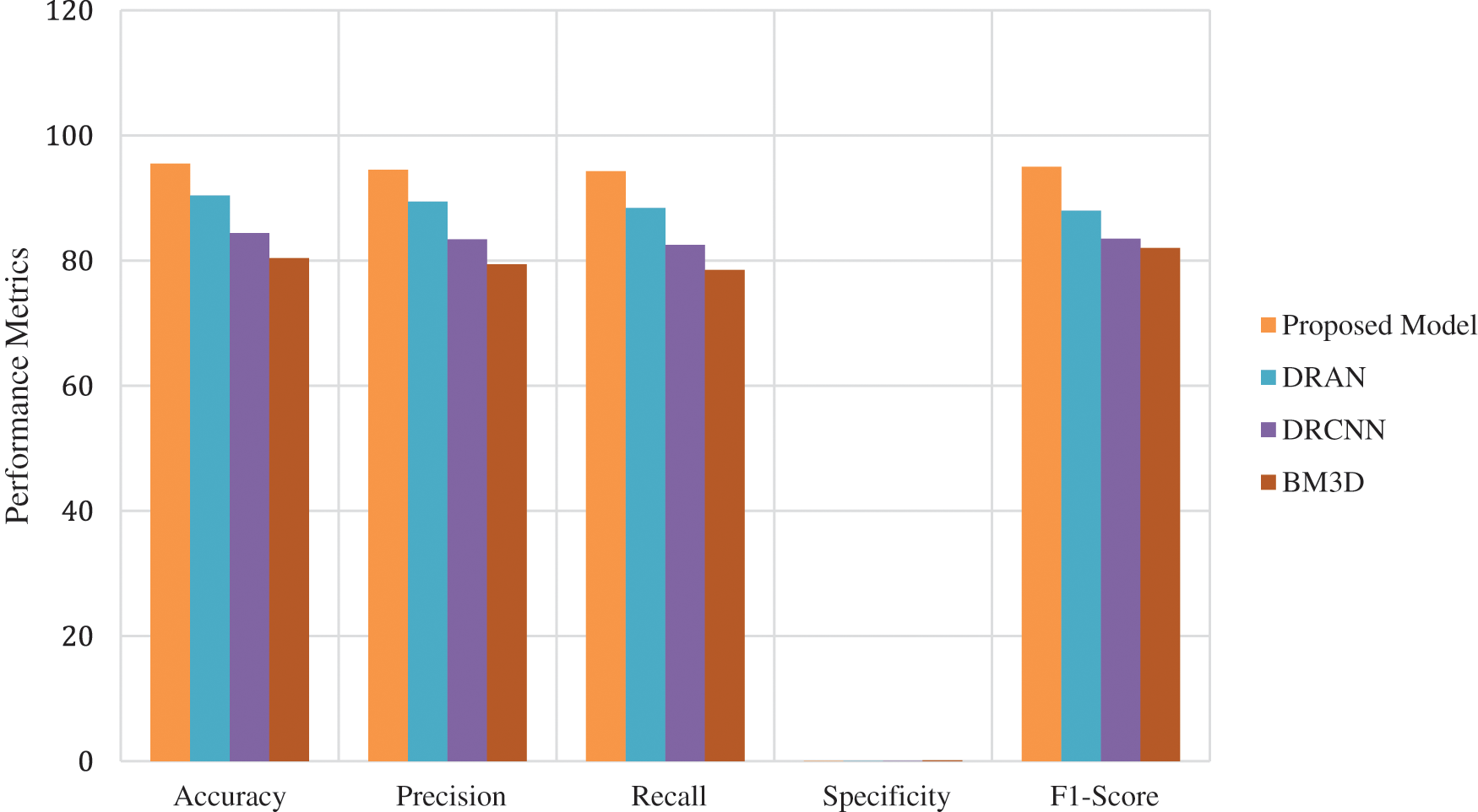
Figure 3: Average performance metrics of the different algorithms @different noise levels for mri brain images

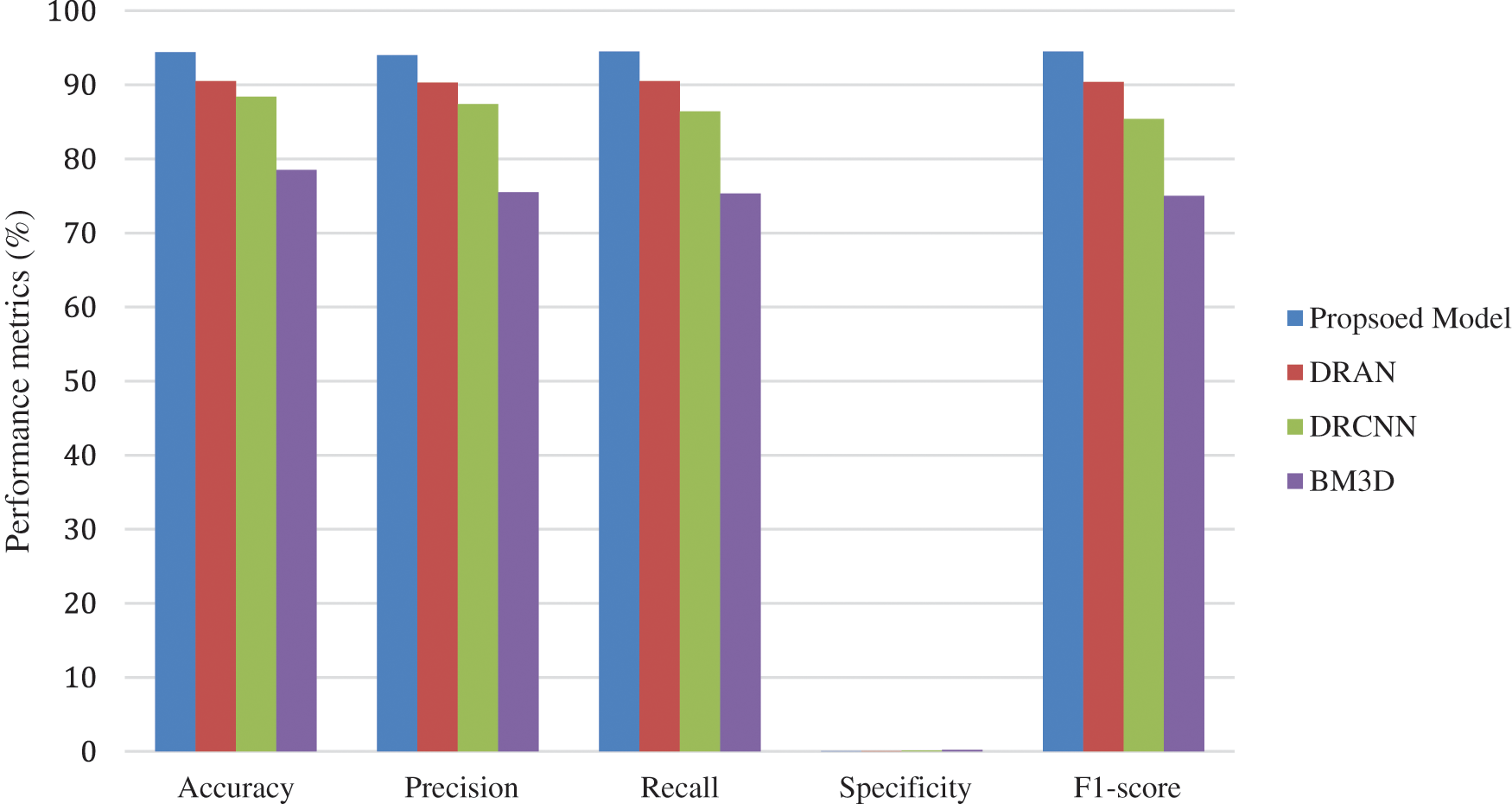
Figure 4: Average performance metrics of the different algorithms @different noise levels for ct lung images

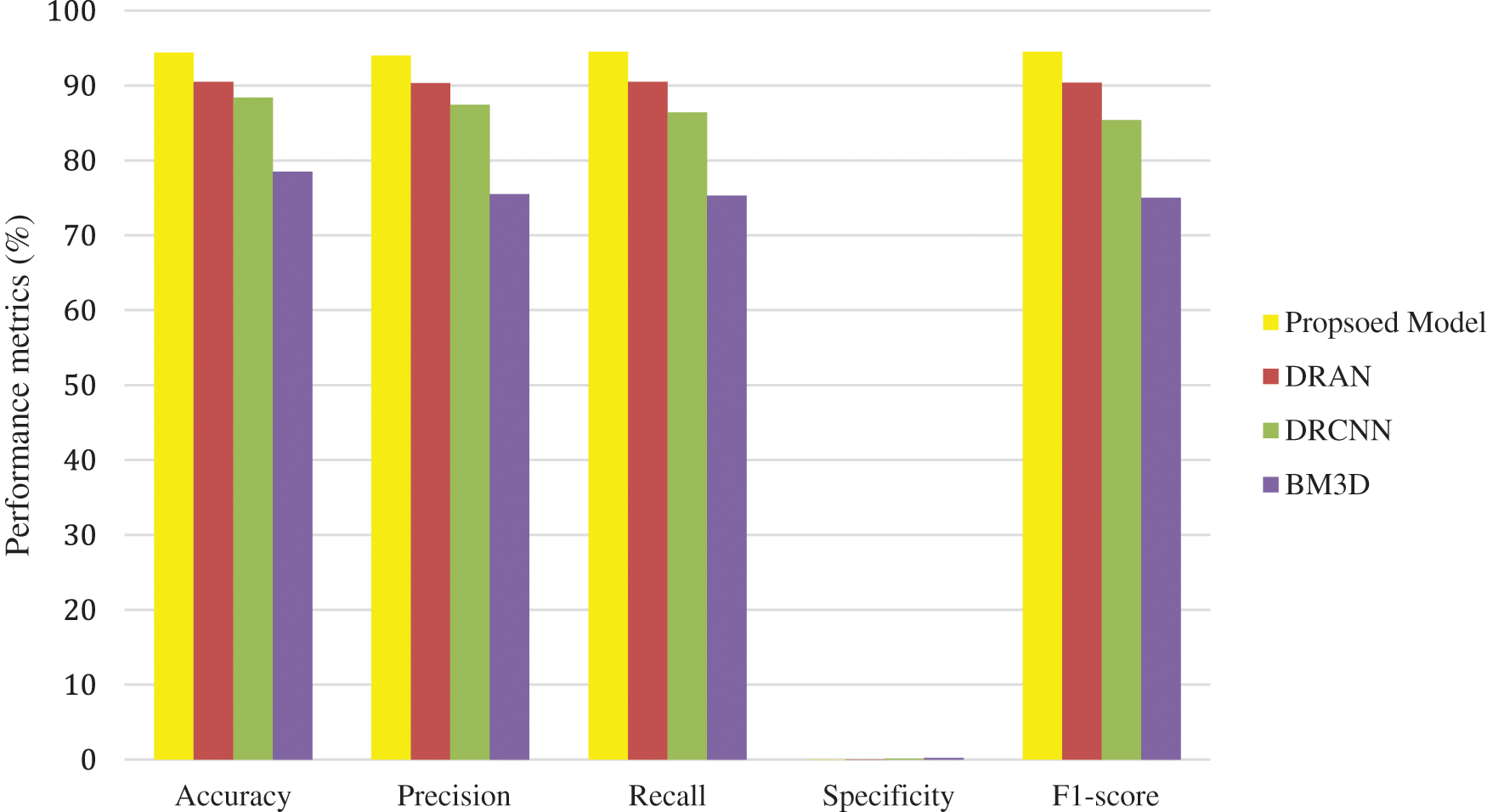
Figure 5: Average performance metrics of the different algorithms @different noise levels for chest X-ray images

6  Conclusion

This research work presented an end-to-end learning model that ensembles the capsule and residual networks to achieve better denoising and classification. The capsule network with an attention routing mechanism has been used to extract the spatial features used as an input to the residual learning. Notably, such a comprehensive hybrid combination has drastically improved the denoising performance and classification ratio. Extensive experimentation is carried out, and the results illustrate that the proposed model has outperformed the existing state-of-art models by the unmatchable margin while maintaining consistent performance even under noisy conditions. Soon, the proposed model has planned for improvisation by exploiting the self-adaptive learning algorithms suitable for real-time images.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare they have no conflicts of interest to report regarding the present study.

References

1. S. V. M. Sagheer and S. N. George, “A review on medical image denoising algorithms,” Biomedical Signal Processing and Control, vol. 61, no. 102036, pp. 1746–8094, 2020. [Google Scholar]

2. S. Kollem, K. R. L. Reddy and D. S. Rao, “A review of image denoising and segmentation methods based on medical images,” International Journal of Machine Learning and Computing, vol. 9, no. 3, pp. 288–295, 2019. [Google Scholar]

3. I. Rodrigues, J. Sanches and J. Bioucas-Dias, “Denoising of medical images corrupted by poisson noise,” in Proc. of IEEE Int. Conf. on Image Processing, San Diego, CA, USA, pp. 1756–1759, 2008. [Google Scholar]

4. M. S. Hansen and T. S. Sørensen, “Gadgetron: An open source framework for medical image reconstruction,” Magnetic Resonance in Medicine, vol. 69, no. 6, pp. 1768–1776, 2013. [Google Scholar] [PubMed]

5. M. Arsalan, R. A. Naqvi, D. S. Kim, P. H. Nguyen, M. Owais et al., “Irisdensenet: Robust iris segmentation using densely connected fully convolutional networks in the images by visible light and near-infrared light camera sensors,” Sensors, vol. 18, no. 5, pp. 1–30, 2018. [Google Scholar]

6. J. Ker, L. Wang, J. Rao and T. Lim, “Deep learning applications in medical image analysis,” IEEE Access, vol. 6, pp. 9375–9389, 2018. [Google Scholar]

7. J. Wang, Y. Guo, Y. Ying, Y. Liu and Q. Peng, “Fast non-local algorithm for image denoising,” in Proc. of the IEEE Int. Conf. on Image Processing, Atlanta, GA, USA, pp. 1429–1432, 2006. [Google Scholar]

8. M. Elad and M. Aharon, “Image denoising via sparse and redundant representations over learned dictionaries,” IEEE Transactions on Image Processing, vol. 15, no. 12, pp. 3736–3745, 2006. [Google Scholar] [PubMed]

9. A. Sameh Arif, S. Mansor and R. Logeswaran, “Combined bilateral and anisotropic-diffusion filters for medical image de-noising,” in Proc. of IEEE Student Conf. on Research and Development, Cyberjaya, Malaysia, pp. 420–424, 2011. [Google Scholar]

10. I. L. Chen, T. S. Ho and C. W. Lu, “Full field optical coherence tomography image denoising using deep learning with spatial compounding,” in Proc. IEEE Int. Symp. on Biomedical Imaging, Iowa City, IA, USA, pp. 1975–1978, 2020. https://doi.org/10.1109/ISBI45749.2020.9098452 [Google Scholar] [CrossRef]

11. I. S. Klyuzhin, J. C. Cheng, C. Bevington and V. Sossi, “Use of a tracer-specific deep artificial neural net to denoise dynamic pet images,” IEEE Transactions on Medical Imaging, vol. 39, no. 2, pp. 366–376, 2020. [Google Scholar] [PubMed]

12. B. van Ginneken and A. Mendrik, “Image denoising with k-nearest neighbor and support vector regression,” in Proc. of Int. Conf. on Pattern Recognition, Hong Kong, China, pp. 603–606, 2006. [Google Scholar]

13. P. K. Mishro, S. Agrawal, R. Panda and A. Abraham, “A survey on state-of-the-art denoising techniques for brain magnetic resonance images,” IEEE Reviews in Biomedical Engineering, vol. 15, pp. 184–199, 2022. [Google Scholar] [PubMed]

14. R. Li, T. Zeng, H. Peng and S. Ji, “Deep learning segmentation of optical microscopy images improves 3-d neuron reconstruction,” IEEE Transactions on Medical Imaging, vol. 36, no. 7, pp. 1533–1541, 2017. [Google Scholar] [PubMed]

15. M. G. McGaffin and J. A. Fessler, “Edge-preserving image denoising via group coordinate descent on the gpu,” IEEE Transactions on Image Processing, vol. 24, no. 4, pp. 1273–1281, 2015. [Google Scholar] [PubMed]

16. K. Lee and W. -K. Jeong, “Iscl: Interdependent self-cooperative learning for unpaired image denoising,” IEEE Transactions on Medical Imaging, vol. 40, no. 11, pp. 3238–3248, 2021. [Google Scholar] [PubMed]

17. F. Wang, B. Yang, Y. Wang and M. Wang, “Learning from noisy data: An unsupervised random denoising method for seismic data using model-based deep learning,” IEEE Transactions on Geoscience and Remote Sensing, vol. 60, pp. 1–14, 2022. [Google Scholar]

18. W. Jifara, F. Jiang and S. Rho, “Medical image denoising using convolutional neural network: A residual learning approach,” The Journal of Supercomputing, vol. 75, no. 2, pp. 704–718, 2019. [Google Scholar]

19. M. Siam, S. Valipour, M. Jagersand and N. Ray, “Convolutional gated recurrent networks for video segmentation,” in Proc. of IEEE Int. Conf. on Image Processing, Beijing, China, pp. 3090–3094, 2017. [Google Scholar]

20. Y. L. Chang, Z. Y. Liu, K. Y. Lee and W. Hsu, “Free-form video inpainting with 3d gated convolution and temporal patchgan,” in Proc. of IEEE/CVF Int. Conf. on Computer Vision, Seoul, Korea (Southpp. 9065–9074, 2019. [Google Scholar]