A Modified Firefly Optimization Algorithm-Based Fuzzy Packet Scheduler for MANET

1  Introduction

In Mobile ad hoc Networks (MANETs), a temporary network is constructed with a collection of randomly distributed wireless mobile nodes without depending on a centralized administration or an existing network infrastructure [1]. This temporary network represents a multi-hop network in which the process of communication is attained through the wireless channel that hops over different mobile nodes [2]. This MANET is useful in the applications of military operation, civilian operation (healthcare environmental monitoring, etc.) and disaster relief [3]. Multimedia and real-time applications necessitate the requirements of Quality of Service (QoS) with quantifying metrics for packet delivery ratio, end-to-end delay, and throughput. The overall network performance can be significantly improved through the utilization of scheduling algorithms that identify what packet or queue needs to be served sequentially [4]. Initially, First Come First Service (FCFS) packet scheduling is considered the default scheduling scheme for MANETs [5]. In our paper, we propose a Modified Firefly Optimization Algorithm (MFOA) to optimize a fuzzy inference system-based packet scheduling scheme. The fuzzy MFOA-optimized fuzzy scheduler is developed using Proto-C language in an OPNET modeller.

2  Related Work

Initially, a fuzzy-based priority scheduler was proposed by Gomathy et al. [6] for provisioning QoS and handling issues of frequent failures and dynamic mobility to sustain network performance. This fuzzy-based priority scheduler used the parameters of data rate and packet type for determining the priority of the packets. Then, another priority packet scheduling algorithm was proposed by Manoj et al. [7] for enhancing the performance in the congested network. It was proposed for handling the issues of the First Come First Serve (FCFS) scheduler, which may not completely be suitable for real-time applications. The next potential scheduling scheme was proposed by Gomathy et al. [8] with the merits of the Mamdani fuzzy inference-based scheduling mechanism that considered hop count and buffer size as the input to enhance the QoS of MANET. These two Mamdani fuzzy inference-based packet scheduling approaches did not utilize any kind of optimization algorithms for improving the fuzzy rules. Another priority scheduler based on network coding was proposed by Sun et al. [9] with fuzzy controllers for handling the process of multipath routing in MANETs. To prevent the problem inherent with the inference engine, a significant fuzzy packet scheduler based on the Mamdani inference engine was proposed by Sufian et al. [10] for attaining realistic and reliable wireless data propagation.

3  The Proposed Modified Firefly Optimization Algorithm Improved the Fuzzy Scheduler-Based Packet Scheduling (MFPA-FSPS) Mechanism

This proposed MFPA-FSPS Mechanism completely focuses on the utilization of the fuzzy logic concept to estimate the priority index of the packets. The proposed scheduler utilizes three parameters that include data rate, Signal-to-Noise Ratio (SNR) and queue length as input and the fuzzy logic integrates these parameters to determine the priority of the packet. The complete workflow of the proposed MFPA-FSPS Mechanism is presented in Fig. 1.

Figure 1: Workflow of the proposed MFPA-FSPS Scheme

The proposed MFPA-FSPS Scheme uses fuzzy logic as it is the potential to implement the preferences and experiences through membership rules and membership functions. This mathematical model adopts the merits of the Takagi–Sugeno–Kang (TSK) inference system that utilizes a complete rule base that envelops the entire rule base of the packet scheduling process. It utilizes the data-driven rule-based generation strategy that aids in supporting the characteristics of the TSK inference system. However, this TSK inference system lacks inheriting self-learning capabilities from the developed knowledge-based design for the packet scheduling process. Thus, Modified Firefly Optimization Algorithm (MFOA) is included to improve the self-learning capabilities of the TSK inference system.

3.1 Membership Functions Used in MFPA-FSPS Scheme

In this proposed scheduler, trapezoidal and triangular membership functions are utilized due to their low computational complexity and simplicity. The linguistic variables considered with the input variables of data rate, SNR and queue length are low (L), medium (M) and high (H). The membership function associated with input data rate, SNR and queue length is presented in Fig. 2.

Figure 2: (a) Degree of membership to SNR, (b) Degree of membership concerning data rate, (c) Degree of membership to Queue size in MFPA-FSPS

The 27 conditional rules, formulated with three input parameters (data rate, SNR and queue size), utilized for this proposed fuzzy MFPA-FSPS scheduler are presented in Fig. 3.

Figure 3: Fuzzy rule base and membership functions of input and output values

3.2 Takaki Sugeno-Kang Based Fuzzy Inference Engine

This proposed MFPA-FSPS scheduler utilizes the Takaki Sugeno-based Fuzzy inference engine for constructing the fuzzy index (priority index), which is useful for estimating the packet priority during the scheduling process with the added advantage of handling the uncertain data as depicted in Fig. 4.

Figure 4: Takaki Sugeno-based Fuzzy inference system used for packet priority estimation

Suppose a fuzzy rule based on the Takaki Sugeno-Kang (TSK) inference engine consists of n rules and each has k antecedents.

Rule 1: If a1 is L11 and ……and ak is Lk1

Then b=f(a1,a2,…..ank)k=α01+α11a1+…..+αk1ak............

Rule n: If a1 is L11 and ……and ak is Lkn

Then b=f(a1,a2,…..ank)k=αk1+αk1aa1+.....+αknak (1)

where α01 and αk1 highlights the constant parameters representing the linear functions related to the consequences rule.

This TSK inference engine facilitates the inference process through the following process.

Step 1: Calculate the firing strength associated with each rule that integrates the degree of similarity between the input and the antecedents of the fuzzy rule.

ηr=S(L1∗,L1r)∧....∧S(Lk∗,Lnl) (2)

where S(L1&,L1r) is the similarity degree determined between L1∗ and L1r with ∧ as the t-norm operator utilized as a minimum operator. This similarity degree is identified through

S(L1&,L1r)=max(min(μ(a1∗),μ(a1r) (3)

where, μ(a1∗) and μ(a1r) represents the membership degree considered value ‘ aij ’ inside a specific domain.

Step 2: Estimate the sub-output achieved through each rule based on the observation (L1∗,L2∗,......,Lk∗) .

f(a1∗,a2∗,.......ak∗)=α0+α1rRVal(L1∗)+.....+αNKRVal(L∗k) (4)

where Rval(Lk∗) represents the defuzzified value determined through the fuzzy sets based on the centre of an area associated with the membership function.

Step 3: The complete set of all sub-outputs estimated from the complete set of rules is integrated to generate the final output based on Eq. (5)

b=∑r=1n⁡ϖrf(a1,a2,......an)∑r=1n⁡ωr (5)

From Eq. (5), the firing strength is o when the input vector is not overlapping with the antecedents of the rules.

Finally, the output of the TSK fuzzy inference engine needs to be optimized before the process of defuzzification. In this proposed fuzzy scheduler, the process of optimization is achieved based on Modified Firefly Algorithm (MFOA)-based optimization as explained in the subsequent section.

3.3 Modified Firefly Algorithm (MFOA)-Based Optimization of a Fuzzy Inference Engine

Once the raw rule base is constructed, it needs to be potentially optimized for successful fine-tuning of the membership functions using a significant metaheuristic optimization algorithm. At this juncture, Modified Firefly Optimization Algorithm (MFOA) is utilized in this proposed scheduler for attaining rule base optimization. In particular, the Tidal force-improved firefly algorithm [11] is used in the rule base optimization of this proposed fuzzy scheduler. The primitive Firefly optimization algorithm (FOA) was proposed by Subahi et al. [12] based on the attractive flashing properties of the fireflies. This classical FOA algorithm utilizes the following three rules, (i) the fireflies’ brightness determines its fitness value on the optimizing search space, (ii) the increase in attraction and brightness of fireflies infers the shortest distance between two individual fireflies and (iii) The attraction of fireflies is completely based on their brightness, and they are attracted with one another independent of their sex. In the implementation, the function of attraction is monotonically decreased as expressed in Eq. (6).

β(r)=β0e−γdij2 (6)

where dij represents the distance visualized between any two individual fireflies with position xi and xj represented in Eq. (7)

dij=∑d=1D⁡(xi,d−xj,d)2 (7)

where, xi,d and xj,d represents the dimension of ith and jth fireflies’ spatial coordinate.

When a firefly moves towards another firefly based on the degree of attraction attributed to its brightness factor, the movement of the fireflies is modelled based on Eq. (8)

xiNEW=xiOLD+δ(rand−12)+(xiOLD−xj)β0e−γdij2 (8)

In this proposed scheduler, the FOA algorithm is improved based on the inclusion of the Tidal force formula to handle the basic algorithms’ shortcomings. The tidal force represents the force quantified in a scenario in which an object (Tidal water) completely depends on the impact of the gravitational impact of another two-object mass (Earth and Moon). The tidal force is inversely proportional to the square of the distance between two objects, while the gravitational attractive force is inversely proportional to the square of the distance from the objects. Thus, the tidal force ( TForce ) is determined based on the derivative of Newton’s Gravitational law presented in Eqs. (9) and (10)

TForce=GMMoonmobd2−GMMoonmob(d+Δr)2 (9)

TForce=GMMoonmob(d+Δr)2−GMMoonmobd2d2(d+Δr)2 (10)

where, G , M , m and d refer to the gravitational constant, the mass of the moon (r-radius of the moon), Mass of the object and distance between the objects.

In this proposed fuzzy scheduler, tidal force is included in the primitive firefly algorithm for obtaining the global minimum value with minimized generations. If the population is x=(x1,x2,.......xn) with ‘ n ’ number of individual solutions (number of rules in the raw ruleset) in the population, then each individual (each rule in the rule base) from the population is represented as x=(x11,x12,.......xnd) with ‘ d ’ as the number of variables or dimensional count used for the fitness evaluation. The fireflies’ computation is completely pairwise in every iteration. If any successive pair of fireflies (two fuzzy rules) is better than the other, then that superior fuzzy rule is used and the preceding fuzzy rule is not considered for decision making. To compute the tidal force in the MFOA algorithm, the distance between the pairwise fireflies is determined directly in the maximum number of feasible dimensions. At this juncture, the vector highlighting an individual firefly with ‘ d ’ number of dimensions is presented by

VFOA=[1x1,1,1x1,2.......,1x1,d] (11)

In this context, the lower and upper threshold of the distance between any fireflies (fuzzy rules comparison) in each ‘ d ’ dimension of operation is presented by

FL=Max(VFOA) (12)

FU=Min(VFOA) (13)

Then the tidal force in each ‘ d ’ dimension is determined based on Eq. (14)

β=(GMMoonmobFU2−GMMoonmobFL2) (14)

The tidal force and firefly algorithms are utilized mutually for sustaining the balance between exploitation and exploration.

3.4 Defuzzification Process

In this proposed scheduler, the centre of gravity (COG) is utilized for the process of Defuzzification Process. The TSK fuzzy consists of five points of output corresponding to output (very low (VL), low (L), medium (M), high (H) and very high (VH)), which is considered to be a constant. It is also identified that the output of the fuzzy inference process is a constant, on par with the fuzzy set considered during the evaluation of rules.

As a result, the proposed MFPA-FSPS Mechanism achieved the optimal process of packet scheduling through the parameters of data rate, SNR, and queue length as input. It adopted the concept of fuzzy logic and integrated them for estimating the priority of the packet depending on the Takaki Sugeno-based Fuzzy inference system. This adopted inference system played an anchor role in calculating the firing strength associated with each rule of inference, estimating the sub output attained for each possible formulated rule and determining the complete set of all sub-outputs from the defined collection of rules. However, the defined rules are optimized in the inference engine based on the merits of the modified firefly optimization algorithm. Finally, the optimized rules aided in determining the output of the TSK fuzzy inference engine through the aggregation of the fuzzy sets and the defuzzification process that was applied.

4  Simulation Results and Discussion

The proposed MFPA-FSPS mechanism, and the benchmarked schemes, are evaluated through OPNET modeller and verified using MATLAB fuzzy toolbox with different network loads of constant bit rate (CBR) and variable bit rate (VBR) data traffic. The simulation environment is modelled using Optimized Network Engineering Tools (OPNET) simulator with a network of 200 mobile nodes that are randomly distributed within a terrain area of 1000 × 1000 square meters. A channel capacity of 2 Mpbs is selected with each mobile node’s radio propagation range set to 250 m. The simulation experiments are conducted with multiple runs consisting of different seed values corresponding to each scenario and the data is collected and averaged over the simulation runs. In this simulation, each source mobile node is made to transmit data packets with CBR and VBR data traffic at a minimum rate of 20 packets/second to 60 packets/second.

The output membership functions for TSK are presented as follows: The randomization parameter of the firefly algorithm, fixed light absorption and attractiveness coefficient is set to 0.2, 1 and 1, respectively at the initial iteration. The two parameters are such that a tolerance of 10-4 and a maximum number of iterations of 3000 are used for halting the functions depending on the dimensions considered for evaluations. The complete experiments are run 50 times to prevent the influence of the initially set parameters during the evaluation process. In specific, the output membership functions for TSK refer to Type-1.

4.1 Performance of the Proposed MFPA-FSPS and the Existing Fuzzy Scheduling Schemes with CBR Data Traffic

The proposed MFPA-FSPS and the benchmarked DPSVAM, SVMPS and DPSF schemes are compared based on packet delivery ratio, throughput, end-to-end delay, and energy consumption with different CBR data traffic rates. Figs. 5 and 6 demonstrate the packet delivery ratio and throughput of the proposed MFPA-FSPS and the benchmarked DPSVAM, SVMPS and DPSF schemes with different CBR data traffic rates. The packet delivery ratio and throughput of the proposed MFPA-FSPS scheme, and the benchmarked schemes, are determined to decrease with an increase in the rate of CBR data traffic rate. However, the packet delivery rate and throughput of the network are considered to be significantly improved independent of the rate of CBR data traffic rate, since the utilized Sugeno inference engine is optimized through the inclusion of MFOA, which reduced the number of fuzzy rules contributed towards effective scheduling process. It further incorporated an adaptive fuzzy inference engine, which played an anchor role in eliminating frequent link breaks and issues introduced by the mobility of nodes. The packet delivery rate of the proposed MFPA-FSPS is determined to be improved by 18.21%, 15.32% and 13.84%, which is excellent compared to the benchmarked DPSVAM, SVMPS and DPSF schemes with different CBR data traffic rates. The throughput of the proposed MFPA-FSPS is also confirmed to be improved by 16,38%, 14.29% and 11.54%, superior to the benchmarked DPSVAM, SVMPS and DPSF schemes with different CBR data traffic rates.

Figure 5: Performance evaluation of MFPA-FSPS using packet delivery rate under different CBR data traffic

Figure 6: Performance evaluation of MFPA-FSPS using mean throughput under different CBR data traffic

Figs. 5 and 6 demonstrate the packet delivery ratio and throughput of the proposed MFPA-FSPS and the benchmarked DPSVAM, SVMPS and DPSF schemes with different CBR data traffic rates. The packet delivery ratio and throughput of the proposed MFPA-FSPS scheme and the bench-marked schemes are determined to decrease with an increase in the rate of CBR data traffic rate. However, the packet delivery rate and throughput of the network are significantly improved independent of the rate of CBR data traffic rate, since the utilized Sugeno inference engine is optimized through the inclusion of MFOA that reduced the number of fuzzy rules contributing toward an effective scheduling process. It further incorporated an adaptive fuzzy inference engine, which played an anchor role in eliminating frequent link breaks and issues introduced by the mobility of nodes. The packet delivery rate of the proposed MFPA-FSPS is determined to be improved by 18.21%, 15.32% and 13.84%, which is excellent when compared to the bench-marked DPSVAM, SVMPS and DPSF schemes with different CBR data traffic rates. The throughput of the proposed MFPA-FSPS is also confirmed to be improved by 16,38%, 14.29% and 11.54%, which is superior to the benchmarked DPSVAM, SVMPS and DPSF schemes with different CBR data traffic rates.

Figs. 7 and 8 present the end-to-end delay and energy consumption of the proposed MFPA-FSPS, and the benchmarked DPSVAM, SVMPS and DPSF schemes with different CBR data traffic rates. The end-to-end delay and energy consumption of the proposed MFPA-FSPS and the baselines approaches are systematically decreased with the respective increase in the CBR data traffic rate. This proposed MFPA-FSPS scheme is a predominantly accurate classification of packets priority such that the end-to-end delay also gets decreased since the packets waiting in the queue are reduced significantly based on precise estimation of packet classes. The energy consumption is also minimized as the packet drop of the mobile nodes is highly prevented by determining the classes of packets that need to be scheduled for the subsequent data dissemination process. Thus, the end-to-end delay in the proposed MFPA-FSPS is proved to be reduced by 16.74%, 14.38% and 12.84%, which is excellent compared to the benchmarked DPSVAM, SVMPS and DPSF schemes with different CBR data traffic rates. The energy consumptions of the proposed MFPA-FSPS are also identified to be minimized by 13.28%, 11.36% and 10.24%, a vast improvement when compared to the benchmarked DPSVAM, SVMPS and DPSF schemes with different CBR data traffic rates. These simulation results proved that the proposed MFPA-FSPS is capable of improving packet delivery rate by 23.84%, throughput by 18.94%, reducing end-end-delay by 20.74% and energy consumption by 19.62%, compared to the benchmarked schemes of CBR data traffic.

Figure 7: Performance evaluation of MFPA-FSPS using mean end-to-end delay under different CBR data traffic

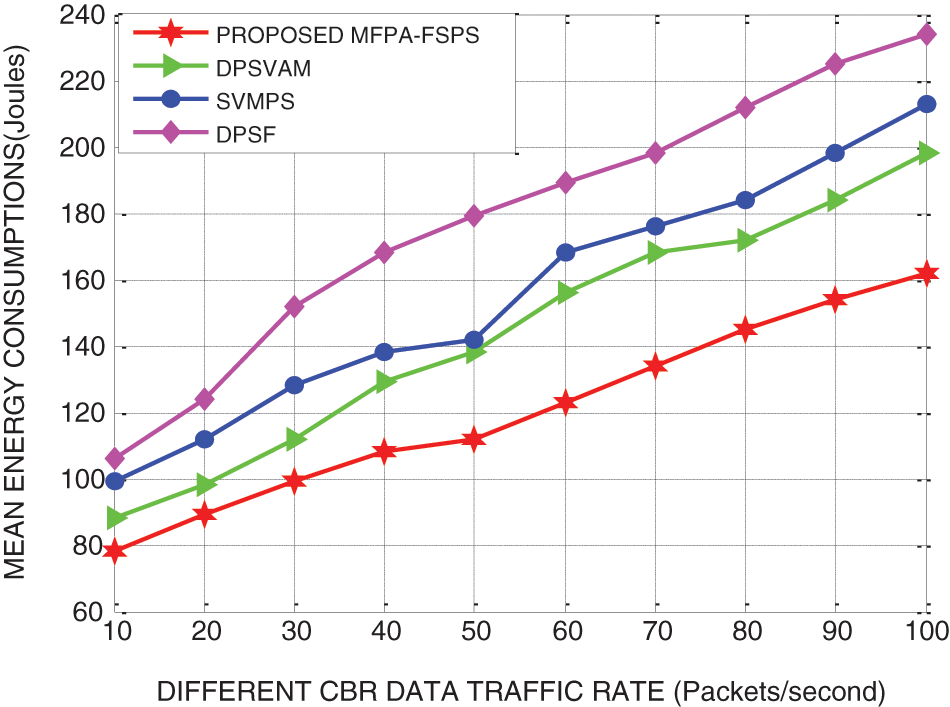
Figure 8: Performance evaluation of MFPA-FSPS using mean energy consumption under different CBR data traffic

4.2 Performance of the Proposed MFPA-FSPS and the Existing Fuzzy Scheduling Schemes with Respect to VBR Data Traffic

In the second part of the investigation, the proposed MFPA-FSPS, and the benchmarked DPSVAM, SVMPS and DPSF schemes are compared using packet delivery ratio, throughput, end-to-end delay and energy consumption with different VBR data traffic rates.

Figs. 9 and 10 depict the packet delivery ratio and throughput of the proposed MFPA-FSPS, and the benchmarked DPSVAM, SVMPS and DPSF schemes with different VBR data traffic rates. The proposed MFPA-FSPS scheme is estimated to sustain the packet delivery ratio and throughput independent of different VBR data traffic rates, since it incorporates a flexible and precise priority scheduling process that differentiates the packets entering a mobile node based on queue length, data rate and SNR. Further, the proposed MFPA-FSPS scheme is also capable of dynamically changing the rate of packet differentiation with the computationally less complex Sugeno fuzzy inference engine. The packet delivery rate of the proposed MFPA-FSPS is determined to have been improved by 14.86%, 12.68% and 9.32%, which is excellent when compared to the benchmarked DPSVAM, SVMPS and DPSF schemes with different VBR data traffic rates. The throughput of the proposed MFPA-FSPS is also confirmed to be improved by 13.28%, 11.84% and 9.32%, proving to be superior to the benchmarked DPSVAM, SVMPS and DPSF schemes with different VBR data traffic rates.

Figure 9: Performance evaluation of MFPA-FSPS using packet delivery rate under different VBR data traffic

Figure 10: Performance evaluation of MFPA-FSPS using mean throughput under different VBR data traffic

Figs. 11 and 12 plot the end-to-end delay and energy consumptions of the proposed MFPA-FSPS, and the benchmarked DPSVAM, SVMPS and DPSF schemes with different VBR data traffic rates. The proposed MFPA-FSPS reduces the end-to-end delay as the time incurred for optimizing the factors contributing to the estimation of packet priority is considerably reduced based on potential optimization attained through the MFOA algorithm with a respective increase in the VBR data rate. The energy consumption of mobile nodes also gets decreased as the possibility of unnecessary packet propagation is completely prevented based on the degree of accuracy introduced by the fuzzy inference approach. Thus, the end-to-end delay of the proposed MFPA-FSPS is identified to be minimized by 13.28%, 11.34% and 9.28%, superior to the baseline of the DPSVAM, SVMPS and DPSF schemes with different VBR data traffic rates. The energy consumptions of the proposed MFPA-FSPS are also identified to be minimized by 11.76%, 9.38% and 7.26%, as compared to the benchmarked DPSVAM, SVMPS and DPSF schemes with different VBR data traffic rates. These simulation results also confirmed that the proposed MFPA-FSPS is successful in improving packet delivery rate by 13.28%, throughput by 12.39%, reducing end-end-delay by 13.84% and energy consumptions by 12.62%, compared to the benchmarked schemes concerning VBR data traffic.

Figure 11: Performance evaluation of MFPA-FSPS using mean end-to-end delay under different VBR data traffic

Figure 12: Performance evaluation of MFPA-FSPS using mean energy consumption under different CBR/VBR data traffic

4.3 Performance Evaluation of Proposed MFPA-FSPS with and without Optimization Process

The packet delivery rate of the proposed MFPA-FSPS scheme with optimization under CBR data traffic was visualized to be increased by 21.38%, while an improvement of 15.68% only was identified without optimization. Further, the throughput of the proposed MFPA-FSPS algorithm with optimization under CBR data traffic was estimated to be improved by 18.27%, as opposed to 12.48% without optimization. End-to-end delay facilitated by the proposed MFPA-FSPS technique with CBR data traffic is reduced by 24.72%, while a reduction of 17.26% was determined without optimization. Moreover, the energy consumption enabled by the proposed MFPA-FSPS technique with CBR data traffic is considerably minimized by 19.38%, while a reduction of 13.26% was confirmed without optimization. In addition, the packet loss provisioned by the proposed MFPA-FSPS technique with CBR data traffic is also drastically minimized by 20.64%, while a reduction of 16.36% is observed without optimization. The packet delivery rate of the proposed MFPA-FSPS scheme with optimization under VBR data traffic was confirmed to have been increased by 15.64%, while an improvement of 11.21% only was observed without optimization. Throughput of the proposed MFPA-FSPS algorithm with optimization under VBR data traffic was identified to have been enhanced by 10.16%, while an improvement of 8.42% was determined without optimization. Furthermore, end-to-end delays facilitated by the proposed MFPA-FSPS technique with VBR data traffic were reduced by 19.43%, while a reduction of 15.12% was determined without optimization. The energy consumption enabled by the proposed MFPA-FSPS technique with VBR data traffic was considerably minimized by 16.34%, while a reduction of 10.64% was confirmed without optimization. In addition, the packet loss provisioned by the proposed MFPA-FSPS technique with VBR data traffic is also potentially minimized by 17.16%, while a reduction of 11.34% is visualized without optimization. As seen, there is a marked improvement both under CBR and VBR data traffic when the proposed MFPA-FSPS scheme with optimization is used.

4.4 Performance Evaluation by Including Mamdani and Sugeno Fuzzy Inference Engine Used in the Proposed MFPA-FSPS

The accuracy of the proposed MFPA-FSPS scheme with Sugeno fuzzy inference engine under CBR data traffic was identified to have improved by 11.21%, while Mamdani fuzzy inference engine if used, showed only an improvement of 7.32%. The precision of the proposed MFPA-FSPS approach with Sugeno fuzzy inference engine under CBR data traffic was identified to have improved by 13.65%, while Mamdani fuzzy inference engine if used, exhibited only an improvement of 9.42%. In addition, the recall of the proposed MFPA-FSPS approach with Sugeno fuzzy inference engine under CBR data traffic was confirmed to get enhanced by 12.68%, while Mamdani fuzzy inference, if used, exhibited only an improvement of 8.39%. This enhancement in performing the proposed MFPA-FSPS scheme with Sugeno fuzzy inference engine is mainly because of its potential ability in handling CBR data traffic packets and reduced computational complexity compared to the Mamdani fuzzy inference engine.

The accuracy of the proposed MFPA-FSPS scheme with Sugeno fuzzy inference engine under VBR data traffic was enhanced by 10.32%, while Mamdani fuzzy inference engine if used, showed only an improvement of 6.54%. The precision of the proposed MFPA-FSPS approach with Sugeno fuzzy inference engine under VBR data traffic was improved by 11.28%, while Mamdani fuzzy inference engine if used, exhibited only an improvement of 8.54%. In addition, the recall of the proposed MFPA-FSPS approach with Sugeno fuzzy inference engine under VBR data traffic was confirmed to be enhanced by 11.42%, while Mamdani fuzzy inference, if used, exhibited only an improvement of 7.28%. This improvement by the proposed MFPA-FSPS scheme with Sugeno fuzzy inference engine is mainly because of its adaptability in handling VBR data traffic packets.

4.5 Performance Comparison of Proposed MFPA-FSPS with the Existing Fuzzy Schedulers Based on Pause Time with CBR and VBR Data Traffic

In this section of the investigation, Tables 1 and 2 demonstrate the packet delivery rate, throughput, end-to-end delay and energy consumption with different pause times under the impact of CBR and VBR data traffic rates set to 30 packets/second.

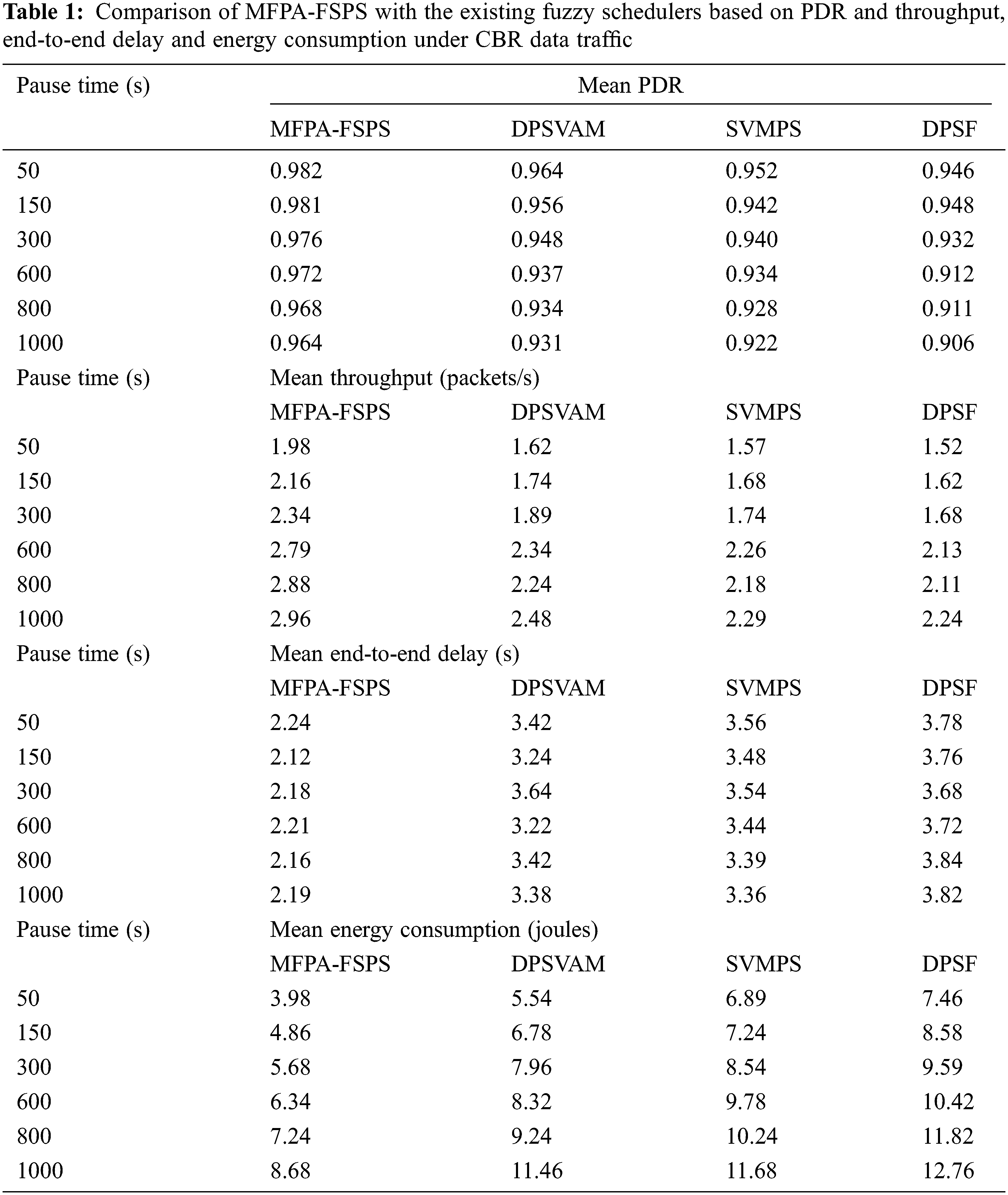
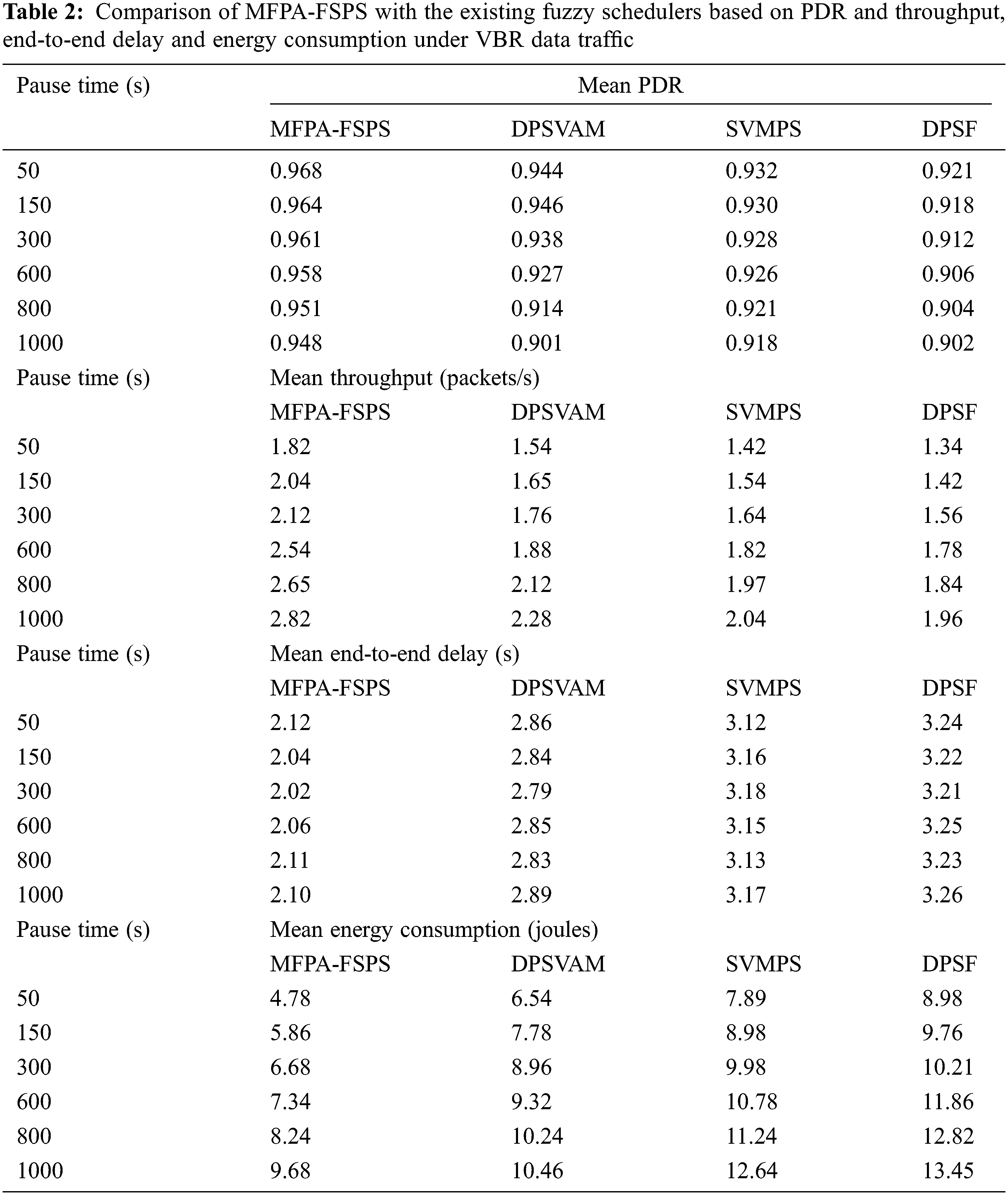
The packet delivery ratio of the proposed MFPA-FSPS scheme is identified to be improved by an average of 8.21% and 7.46% for the CBR and VBR data traffic. The throughput of the proposed MFPA-FSPS scheme gets enhanced, on average, by 7.42% and 6.21%, and the end-to-end delay in the proposed MFPA-FSPS scheme is systematically reduced, on average by 9.36% and 8.39%. In addition, the energy consumption of the proposed MFPA-FSPS scheme is inferred to be significantly minimized, on average by 8.42% and 7.38%. This superior performance of the proposed MFPA-FSPS scheme with different pause times is mainly achieved because of the diminished complexity of the Sugeno fuzzy inference engine used for the priority-based packet scheduling process. In addition, Table 3 presents the mean PDR, mean throughput, mean end-to-end delay and mean energy consumption of the proposed MFPA-FSPS scheme with the recently proposed approaches [11–18] considered for evaluation under an increasing number of packets. The mean PDR of the proposed MFPA-FSPS scheme is improved by 8.21%, 9.96% and 10.54%, which is better than the benchmarked FBRPS, ABOMLMDSS and APA schemes. The mean throughput of the proposed MFPA-FSPS scheme is improved by 7.94%, 8.76% and 9.42%, also better than the benchmarked FBRPS, ABOMLMDSS and APA schemes.

5  Conclusions

In this paper, MFPA-FSPS was contributed as an optimized fuzzy-based packet scheduling technique with the merits of Sugeno fuzzy inference engine possibly being fine-tuned by the MFOA optimization algorithm. The simulation results of the proposed MFPA-FSPS confirmed an improvement in packet delivery rate by 23.84%, throughput by 18.94%, reducing end-end-delay by 20.74% and energy consumption by 19.62%, compared to the benchmarked schemes with respect to CBR data traffic. The proposed MFPA-FSPS is also determined to enhance the packet delivery rate by 13.28%, throughput by 12.39%, reducing end-end-delay by 13.84% and energy consumption by 12.62%, compared to the benchmarked schemes with respect to VBR data traffic. The results also portrayed that the MFPA-FSPS approach with Sugeno fuzzy inference engine improved the accuracy by 6.32%, precision by 5.48% and recall by 7.38%, compared to the utilization of the Mamdani inference engine. The proposed MFPA-FSPS approach to optimization using MFOA confirmed an excellent performance on par with the proposed scheme without the inclusion of the optimization process.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. B. Sun, L. Li and C. Gui, “Fuzzy QoS controllers-based priority scheduler for mobile ad hoc networks,” in Proc. of the 2nd IEEE Asia Pacific Conf. on Mobile Technology, Applications and Systems, Guangzhou, China, pp. 5, 2005. [Google Scholar]

2. H. Joo, K. J. An and H. Song, “Urgency-based packet scheduling and routing algorithms for video transmission over MANETs,” in Proc. of IET Int. Communication Conf. on Wireless Mobile and Computing, Shanghai, China, pp. 403–408, 2011. [Google Scholar]

3. H. Luo, S. Lu and V. Bharghavan, “A new model for packet scheduling in multihop wireless networks,” in Proc. of the 6th Annual Int. Conf. on Mobile Computing and Networking, Boston, Massachusetts, USA, pp. 76–86, 2000. [Google Scholar]

4. A. Banerjee and P. Dutta, “Delay-efficient energy and velocity conscious non-preemptive scheduler (DEV-NS) for mobile ad hoc networks,” International Journal of Advanced Networking and Applications, vol. 5, no. 4, pp. 2002, 2014. [Google Scholar]

5. D. R. S. Victoria and S. S. Kumar, “Efficient bandwidth allocation for packet scheduling,” International Journal of Future Computer and Communication, vol. 1, no. 4, pp. 381–384, 2012. [Google Scholar]

6. C. Gomathy and S. Shanmugavel, “Supporting QoS in MANET by a fuzzy priority scheduler and performance analysis with multicast routing protocols,” EURASIP Journal on Wireless Communications and Networking, vol. 2005, no. 3, pp. 1–11, 2005. [Google Scholar]

7. K. Manoj, S. C. Sharma and L. Arya, “Fuzzy based QoS analysis in wireless ad hoc network for DSR protocol,” in Proc. of the IEEE Int. Advance Computing Conf., Patiala, India, pp. 1357–1361, 2009. [Google Scholar]

8. C. Gomathy and S. Shanmugavel, “Effect of packet scheduling and evaluation of fuzzy based priority scheduler on ad hoc network unicast communication,” in IEEE Int. Conf. on Signal Processing and Communications, Bangalore, India, pp. 506–510, 2004. [Google Scholar]

9. B. Sun, X. Lu, C. Gui and M. Luo, “Network coding-based priority-packet scheduler multipath routing in MANET using fuzzy controllers,” International Journal of Future Generation Communication and Networking, vol. 7, no. 2, pp. 137–148, 2014. [Google Scholar]

10. A. Sufian, A. Banerjee and P. Dutta, “FSNRP: Fuzzy-controlled priority scheduling of non-real-time data packets in mobile ad-hoc networks,” in Proc. of the IEEE Int. Conf. on Advanced Networks and Telecommunications Systems, Bhubaneswar, India, pp. 1–5, 2017. [Google Scholar]

11. M. Kashef and N. Moayeri, “Frame-based randomized scheduling of packets with random deadlines for multi-flow wireless networks,” Ad Hoc Networks, vol. 85, no. 3, pp. 11–18, 2019. [Google Scholar]

12. A. F. Subahi, Y. Alotaibi, O. I. Khalaf and F. Ajesh, “Packet drop battling mechanism for energy-aware detection in wireless networks,” Computers, Materials & Continua, vol. 66, no. 2, pp. 2077–2086, 2020. [Google Scholar]

13. K. Vijayalakshmi and R. Manikandan, “Minimum length minimum delay scheduling using Artificial Butterfly Optimization (ABO) algorithm in manet,” in IOP Conf. Series: Materials Science and Engineering, Kancheepuram, India, vol. 993, pp. 012053, 2020. [Google Scholar]

14. S. B. Sridhara, M. Ramesha and V. Patil, “Adaptive scheduling design for time-slotted channel hopping enabled mobile Ad hoc network,” International Journal of Advanced Computer Science and Applications, vol. 11, no. 3, pp. 272–277, 2020. [Google Scholar]

15. A. Yelghi and C. Köse, “A modified firefly algorithm for global minimum optimization,” Applied Soft Computing, vol. 62, no. December, pp. 29–44, 2018. [Google Scholar]

16. X. S. Yang, “Firefly algorithms for multimodal optimization,” in Proc. of the Int. Symp. on Stochastic Algorithms Springer, Berlin, Heidelberg, Germany, pp. 169–178, 2009. [Google Scholar]

17. X. R. Zhang, J. Zhou, W. Sun and S. K. Jha, “A lightweight CNN based on transfer learning for COVID-19 diagnosis,” Computers, Materials & Continua, vol. 72, no. 1, pp. 1123–1137, 2022. [Google Scholar]

18. X. R. Zhang, W. Z. Zhang, W. Sun, H. L. Wu, A. G. Song et al., “A real-time cutting model based on finite element ands order reduction,” Computer Systems Science and Engineering, vol. 43, no. 1, pp. 1–15, 2022. [Google Scholar]