Computing Connected Resolvability of Graphs Using Binary Enhanced Harris Hawks Optimization

1  Introduction

Recently, a connected resolving set of graphs has been introduced in [1]. Let G = (V, E) be a connected graph and d(u, v) be the shortest path between two vertices u, v ∈ V(G). An ordered vertex set B = {x1, x2,…, xk}⊆ V(G) is a resolving set of G if the representation

r(v|B)=(d(v,x1),d(v,x2),….,d(v,xk))

is unique for every v ∈ V(G). A resolving set B of G is connected if the subgraph B¯ induced by B is a nontrivial connected subgraph of G. Let |B| be the cardinality of B, the metric dimension and the connected metric dimension of G, denoted dim(G) and cdim(G), respectively, are defined as

dim(G) = min{|Bi|: Bi ⊆ 2v, Bi is a resolving set of G}, cdim(G) = min {|Bi|: Bi ⊆ 2v, Bi is a connected resolving set of G}.

Since every connected resolving set is a resolving set, dim(G) ≤ cdim (G) for all connected graphs G. To illustrate this notion, consider the graph G in Fig. 1.

Figure 1: A graph G with dim (G) = 3 and cdim (G) = 5

Example 1.1

The set B = {v1, v5, v8} is a minimum resolving set for G since the representations

r(v1|B) = (0, 2, 4), r(v2|B) = (1, 3, 5), r(v3|B) = (2, 2, 4), r(v4|B) = (1, 1, 3), r(v5|B) = (2, 0, 2), r(v6|B) = (3, 1, 1), r(v7|B) = (2, 2, 2), r(v8|B) = (4, 2, 0), r(v9|B) = (5, 3, 1), r(v10|B) = (4, 2, 2)

for the vertices of G are distinct. Thus, dim(G) = 3. The subgraph induced by B, B¯  = (B,E), E=∅ is disconnected. Thus, B is not a connected resolving set for G. Namely, no 3-element subset is a connected resolving set of G. On the other hand, the set B = {v1, v4, v5, v6, v8} is a connected resolving set since the representations

r(v1| B ) = (0, 1, 2, 3, 4), r(v2| B ) = (1, 2, 3, 4, 5), r(v3| B ) = ( 2, 1, 2, 3, 4), r(v4| B ) = (1, 0, 1, 2, 3), r(v5| B ) = (2, 1, 0, 1, 2), r(v6| B ) = (3, 2, 1, 0, 1), r(v7| B ) = (2, 1, 2, 1, 2), r(v8| B ) = (4, 3, 2, 1, 0), r(v9| B ) = (5, 4, 3, 2, 1), r(v10| B ) = (4, 3, 2, 1, 2). The set B  = {v1, v4, v5, v6, v8}

are distinct and the subgraph induced by B, B¯  = (B, E) = ({v1, v4, v5, v6, v8}, {{v1, v4},{{v4, v5},{{v5, v6},{v6, v8}) is a connected resolving set, hence cdim (G) = 5.

The metric dimension of several graphs is computed theoretically in the literature [2–19]. A few algorithms are proposed in the literature to compute the metric dimension of graphs heuristically. These are genetic algorithm [20], particle swarm optimization [21] and variable neighborhood search [22].

The connected metric dimension of some graphs is computed theoretically in [1,23]. In [1] it is proved that the connected metric dimension of the wheel graph Wn, n ≥ 7 is ⌊2n+25⌋+1 , the star graph K1,n−1, n ≥ 4 is n − 1. In [23], it is proved that the connected metric dimension of path graph Pn, n ≥ 2 is 2 and the complete graph Kn, n ≥ 3 is n − 1.

This study is the first attempt to compute the minimum connected resolving set of graphs heuristically. For this purpose, we use a binary version of an enhanced Harris Hawk Optimization (BEHHO) algorithm. The results of graphs that are computed theoretically are used for testing the proposed BEHHO algorithm. The proposed BEHHO algorithm is compared to competitive algorithms on the family of triangular snake graphs.

This paper is organized as follows: Section 2 presents the Harris Hawks optimizer. Section 3 presents the proposed BEHHO for determining the connected resolving set of a given graph. Computational results are presented in Section 4. Finally, the conclusion is stated in Section 5.

2  Harris Hawks Optimizer

The Harris hawk optimizer (HHO) is a swarm-based algorithm that simulates the cooperative manner and chasing behavior of harris [24,25]. The hawks try to hunt the prey by using several approaches (tracing, encircling and finally approaching and attacking). Hawks’ skillful tactic to hunt the escaping prey is known as “surprise pounce”. The mathematical model comprises three phases: exploration, the transition between exploration and exploitation; and exploitation (seeking and detecting prey). Based on the powerful characteristics of hawks in the exploration and exploitation processes of the search space, HHO is used to solve complex optimization tasks in a reasonable time [26]. The hawk’s position can be determined from Eq. (1) as follows:

X(t+1)={Xrand(t)−r1|Xrand(t)−2r2X(t)|q≥0.5(Xrabbit(t)−Xm(t))−r3(LB+r4(UB−LB))q<0.5 (1)

t is the current iteration, Xrabbit is the prey position, Xrand is the hawk which has been chosen randomly, q, r1, r2, r3 and r4 are random numbers in the range [0, 1], LB and UB refer to the lower bound and upper bound of variables respectively and Xm is the average position of hawks and can be calculated from Eq. (2) as follows:

Xm=1T∑i=1TXi(t) (2)

where T is the maximum number of iterations and Xi (t) refers to each hawk position. The transition from exploration to exploitation is the second stage. Hawks can use many exploitative behaviors depending on the prey’s escaping energy. In order to simulate the prey energy, the following energy is given:

E=2E0(1−tT) (3)

E0=2r−1 (4)

where Eo and E stand for the initial energy state and the prey’s escaping energy respectively. Eo was randomly chosen in [−1, 1]. Exploration occurs when the |E| ≥ 1 and exploitation occurs when |E| < 1.

The third stage is the exploitation phase in which hawks perform their surprise pounce. There are four situations to describe chasing tactics and astonishing attacks. Let r be a random number ∈ [0, 1].

•   Soft Besiege When both r and |E| ≥ 0.5, this behavior can be defined by the next Eq. (5)

X(t+1)=ΔX(t)−E|JXrabbit(t)−X(t)| (5)

ΔX(t)=Xrabbit(t)−X(t) (6)

where ΔX(t) is the distance between the current location and the prey position.

J=2(1−r5),wherer5∈[0,1] (7)

•   Hard Besiege When r ≥ 0.5 and |E| < 0.5. This behavior can be stated as follows:

X(t+1)=Xrabbit(t)−E|ΔX(t)|(8)

•   Soft Besiege with Rapid Dive When r < 0.5 and |E| ≥ 0.5. Then the prey has enough energy to escape from the attack. In order to describe this escaping pattern mathematically, Lévy fight (LF) is used as seen in Eq. (9).

LF(x)=0.01+u×σ|v|1β,σ=(Γ(1+β)×sin(πβ2)Γ(1+β2)×β×2(β−12))1β (9)

•   As a result, the hawk’s position can be determined from Eq. (10) as follows:

X(t+1)={ Xrabbit(t)−E| JXrabbit−X(t) |               F(Y) < F(X(t))Z=Y+S×LF(D)       F(Z)<F(X(t)) (10)

•   Hard Besiege with Rapid Dive IF both r and |E| < 0.5. Then, the prey has enough energy to escape.

X(t+1)={Xrabbit(t)−E|JXrabbit(t)−Xm(t)|F(Y)<F(X(t))Z=Y+S×LF(D)F(Z)<F(X(t)) (11)

3  Proposed Binary Enhanced Harris Hawk Optimization (BEHHO)

Several recent developments to improve the performance of the Harris hawk optimizer are proposed [27–29]. Here, a binary enhanced hawk optimizer (BEHHO) that combines classical HHO, chaotic local search (CLS) and opposition-based learning techniques (OBL) is used to determine the connected resolving set. In the OBL strategy, each individual fitness is calculated, compared to its corresponding opposite number and the better one is then used for the next iteration [30]. The opposite number x̄ is determined by the following Eq. (12) if x is a real number and x ∈ [lb, ub].

x=ub+lb−x (12)

where lb and ub stand for lower bound and upper bound.

Opposite vector If x = (x1, x2,…,xD) and x ∈ [lb, ub], then the following formula can be used to compute xi:

xi=lbi+ubi−xi (13)

if f( x¯ ) < f(x), then xi will insert the current solution.

Chaos is known as a random-like phenomenon that occurs in both deterministic and non-linear systems. It is quite susceptible to its starting state [31]. Chaos completes the search more quickly than ergodic search [32]. A large variety of sequences can be generated by only modifying their initial values. This work employs a logistic map to create the following chaotic sequence:

os+1=Cos(1−os) (14)

C = 4, os = rand (0, 1) and C1 ≠ 0.25, 0.5 and 0.75 are the initial parameters.

Chaos optimization allows for reasonable execution times on a small scale, but as the search space grows, these times become unacceptable [33]. The properties of a chaotic system can be used to create a search operator, which can subsequently be incorporated into metaheuristic algorithms. The solutions produced by CLS can be acquired by

Cs=(1−μ)×T+μC`l,i=1,2,3,…,n (15)

where Cs denotes the candidate solution and T denotes the target position μ is determined by the following equation.

μ=MaxIter−currIter+1Maxiter (16)

where the terms MaxIter and currIter stand for the maximum and current iterations, respectively. In order to maps C̀i into the domain

C`i=LB+Ci+(UB−LB) (17)

where the initial solution upper and lower bounds are denoted by UB and LB.

Several approaches have been proposed to convert continuous algorithms to binary ones [34]. These binarization methods can be divided into two categories: The first is known as the continuous-binary operator transformation, in which the original real operators of metaheuristic equations are redefined into binary operators [35]. While in the second group, which is known as two step binarization, the real operators are used without modifications, while the produced continuous solutions are converted into binary by using two extra steps. The first step uses a transfer function (TF) that aims to transform the continuous solution Rn into an intermediate probability vector [0, 1]n, where each element in this vector represents the probability of transforming the corresponding element in Rn to 1 or 0. In the second step, the intermediate solution is transformed into binary by applying various binarization methods [34].

xi,j={0rand≥0.51rand<0 (18)

The binary value of i-th agent in the j-th dimension is denoted by xi,j. A transfer function is used to be able to map continuous values to binary ones. In this study, the sigmoid function (S) is used as follows:

S=11+e−10xd (19)

where xd indicates the continuous-valued position at dimension d and S is the function output. The following equation is used to generate a binary value.

xi,j={1rand≥S0rand<S (20)

4  BEHHO for Connected Resolving Set Problem

When designing any optimizer, two fundamental components of the optimization problem should be considered; the solution representation and the evaluation function. The HHO algorithm was designed to solve continuous optimization problems, which is not appropriate for the connected resolving set problem. In the continuous version of HHO, hawks can move around the search space using position vectors within the continuous real domain. We convert the variables of EHHO to binary version by applying an S-shaped transfer function to transform the continuous variable into a binary one. In discrete binary search space, position updates require switching between 0 and 1.

The proposed algorithm deals with the connected resolving set problem as an optimization problem where it searches for the best solution, so each hawk can be represented as a one-dimensional vector xbinaryij = {xi1, xi2, xi3, …, xij}, xbinaryij is a binary valued position vector if j-th element of the vector has a value 1, it means that vertex j belongs to B. If every v ∈ V (G) has a distinct representation r(v|B), then B is a connected resolving set. The value of a binary valued position vector is produced by computing the value of S-shaped transfer function. In BEHHO algorithm, when a hawk is not feasible as a connected resolving set, that hawk is repaired by adding a vertex from V\B. This repairing is applied until that hawk becomes a connected resolving set.

The algorithm represents each solution (individual) in the population as a string of binary in which 1 means that the connected resolving set will be chosen, then the corresponding value will be “1” and if the connected resolving set is not selected, then the corresponding value will be “0”. Thus, the flowchart of the proposed BEHHO algorithm is displayed in Fig. 2 and the pseudo-code in Algorithm 1, respectively.

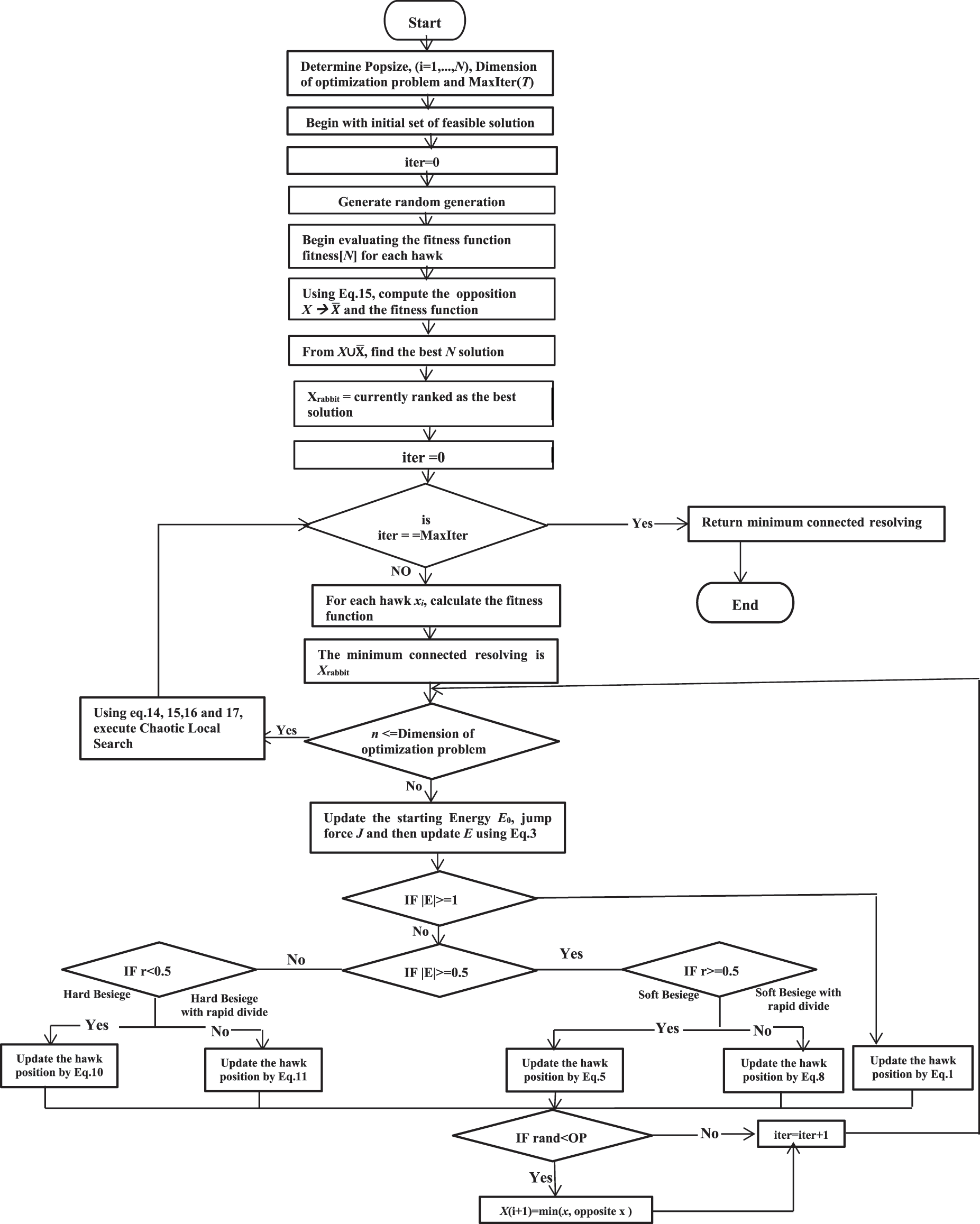
Figure 2: The flowchart of BEHHO

5  Experimental Results

The proposed BEHHO algorithm is compared to binary Harris Hawk Optimization (BHHO), binary opposition-based learning Harris Hawk Optimization (BOHHO), binary chaotic local search Harris Hawk Optimization (BCHHO) algorithms. The algorithms are applied to the star graph, wheel graph, the snake graphs instances: a triangular snake graph, a double triangular snake graph, a linear kC4-snake graph and a (2, n) C4-snake graph. The algorithms were run on the Windows 10 Ultimate 64-bit operating system; the processor was an Intel Core i7, 16 GB of RAM and the code was implemented in MATLAB 2021b. The parameter setting values are presented in Table 1.

All algorithms have been run 20 times for each instance and the results are summarized in Tables 2–7. The tabs are organized as follows:

- The first three columns contain the name of the test instance and the number of nodes and edges, respectively.

- The average execution time (t) used to reach the final algorithms for the first time is given.

- The iteration columns contain the average number of iterations for finishing algorithms.

In [1] Saenpholphat et al. computed the connected resolving set for a star graph and a complete graph only theoretically.

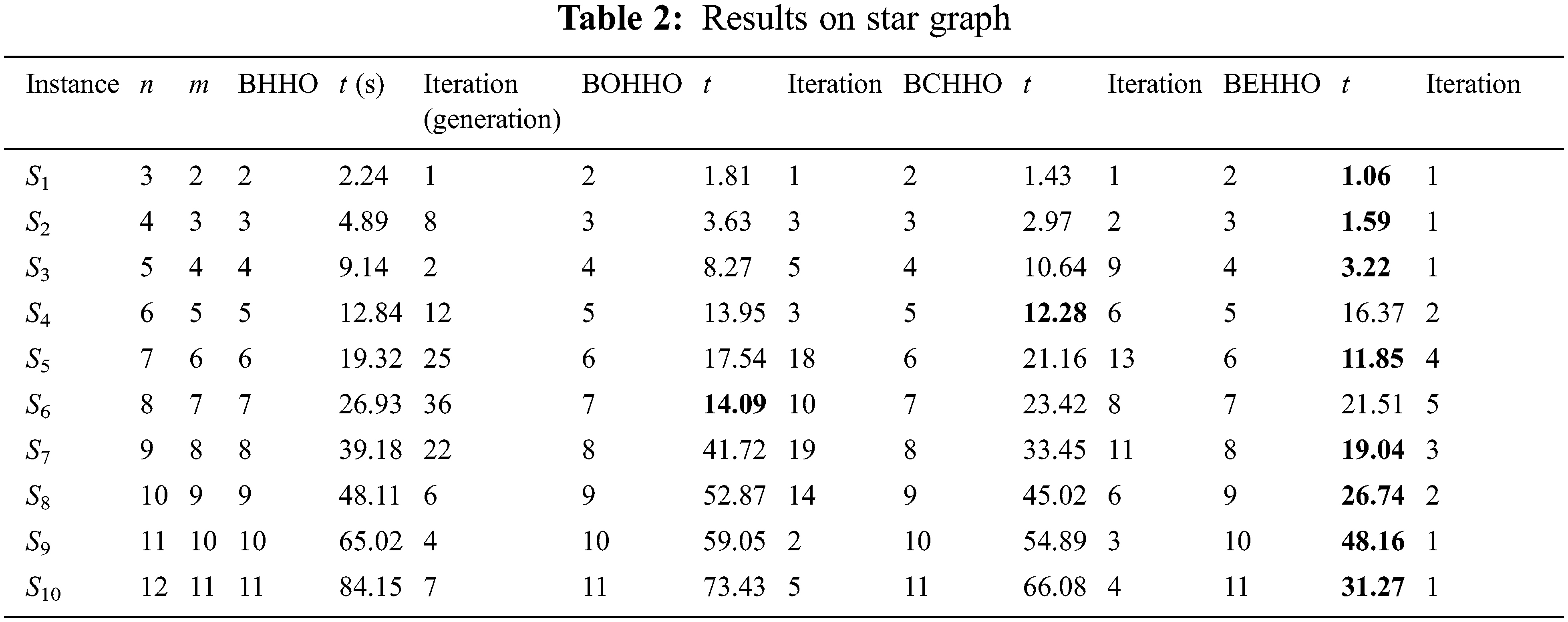
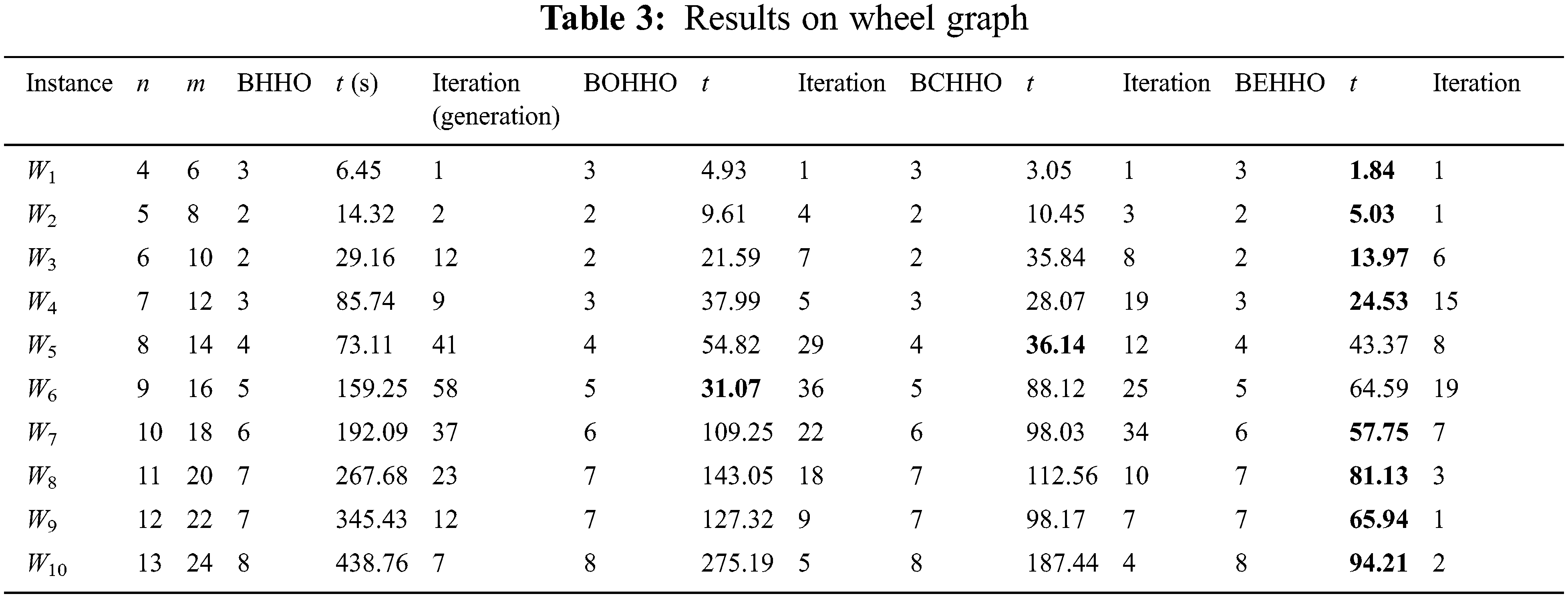
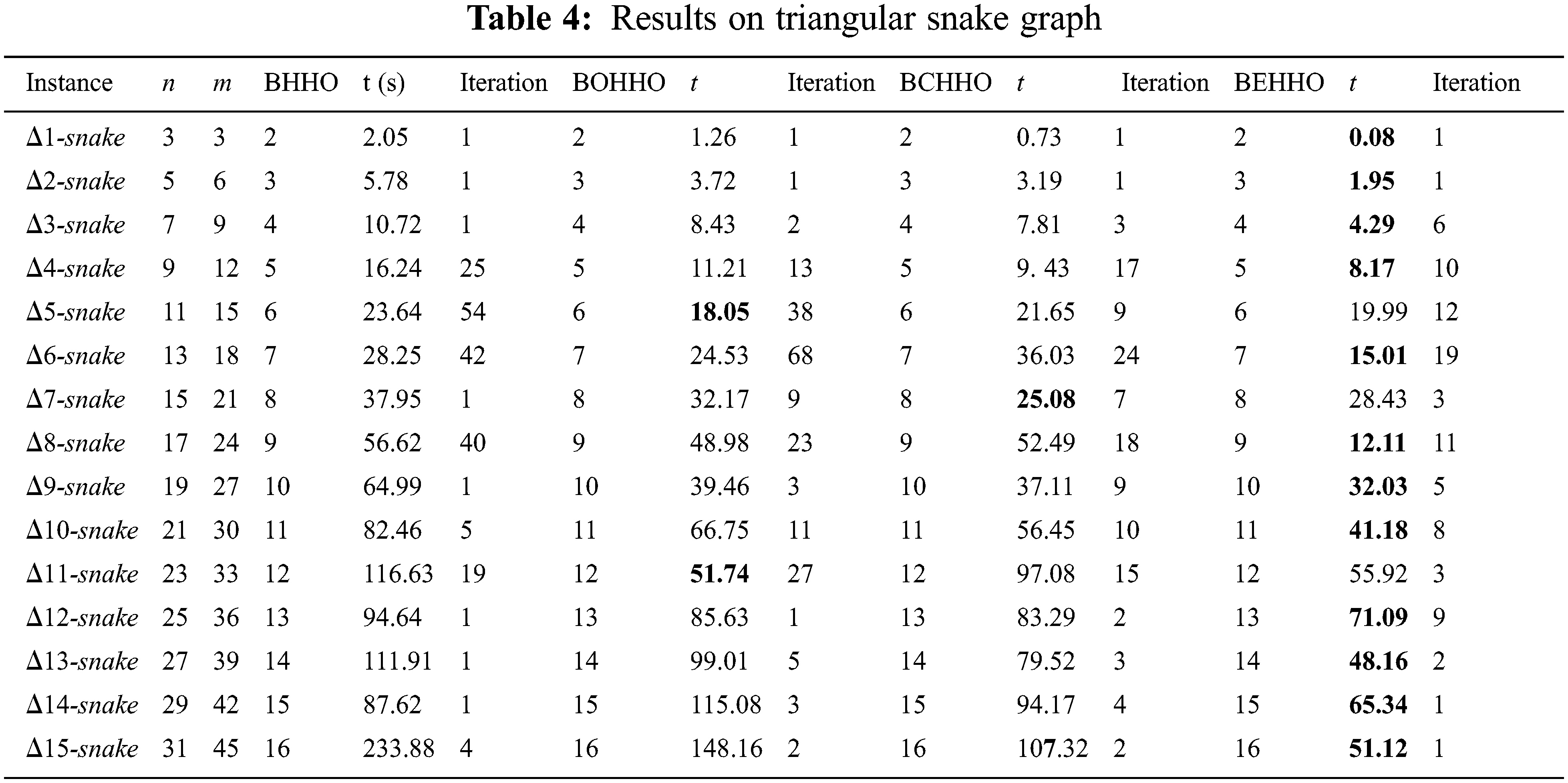
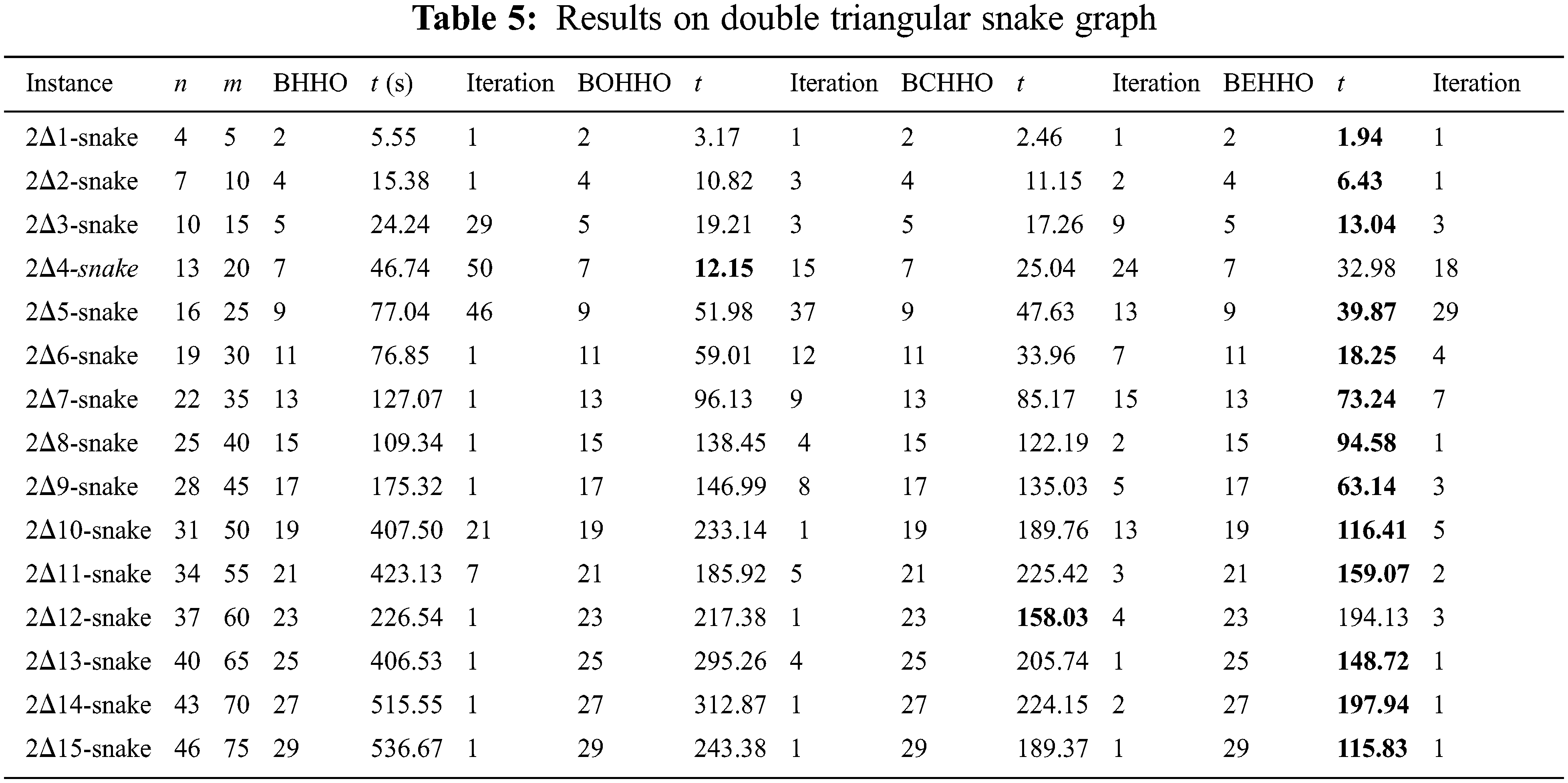
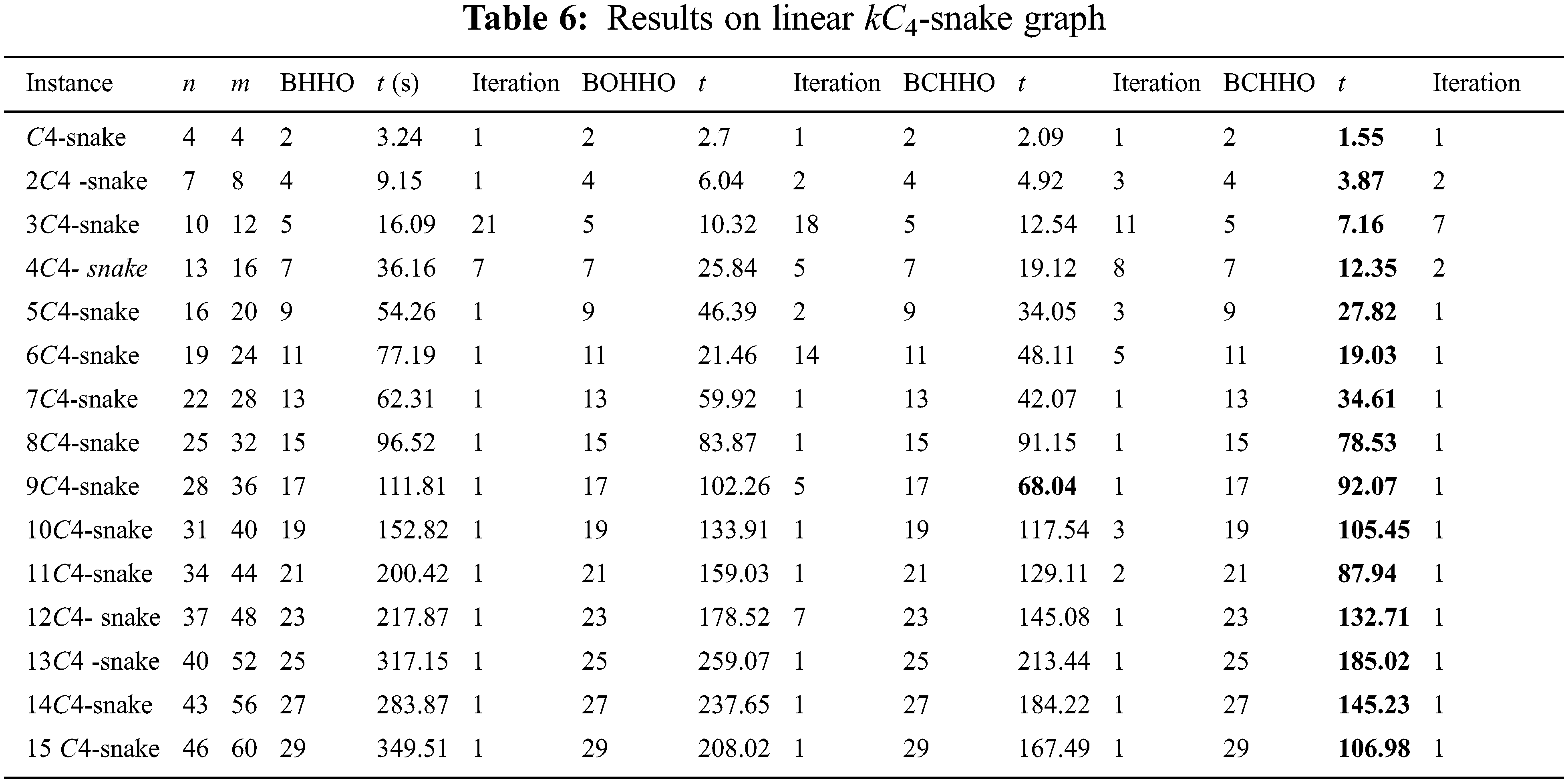
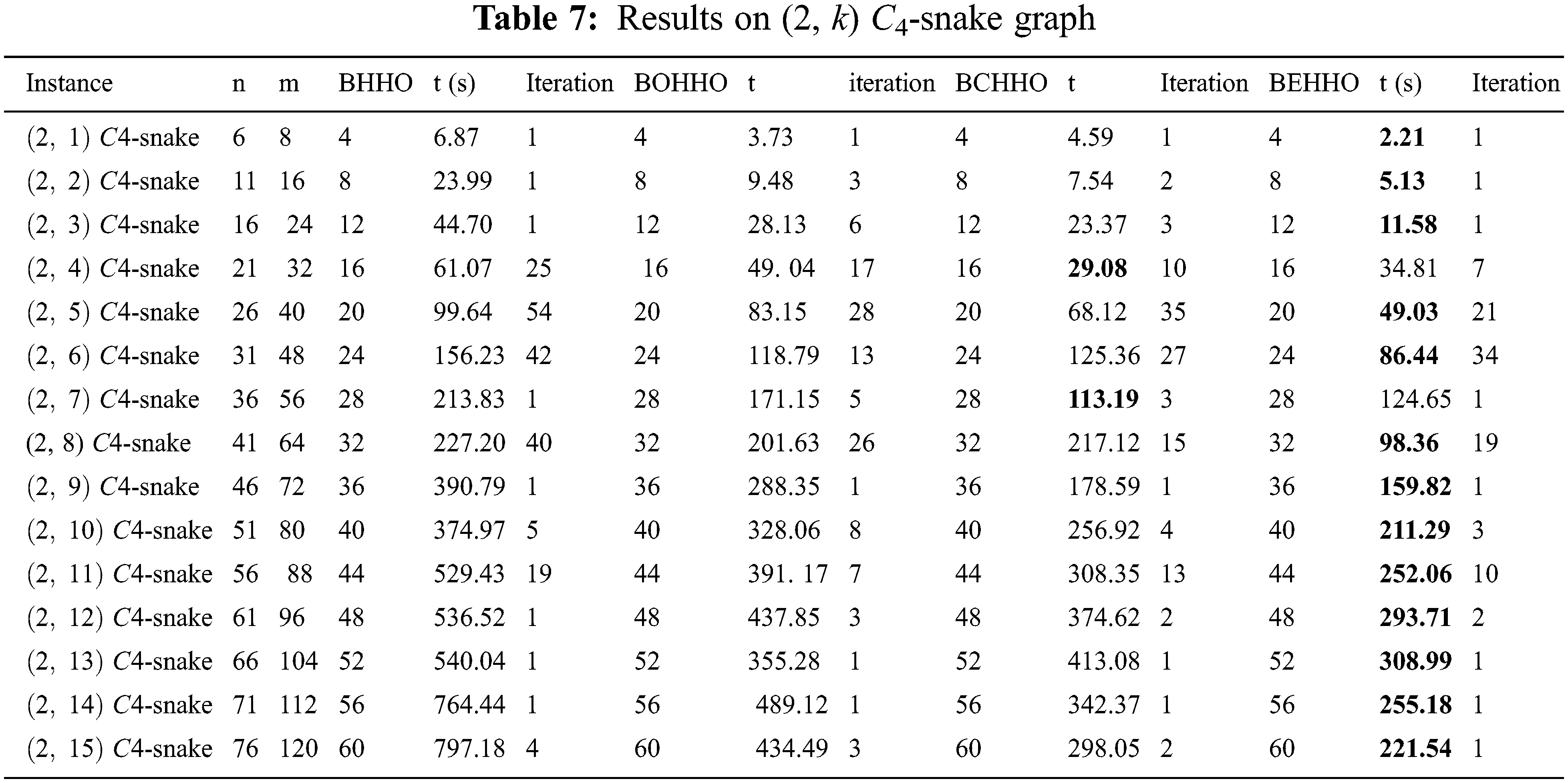
Tables 2–7 display the results for various graphs, which show that BEHHO can achieve the best optimal solution (known connected metric dimension) in a reasonable amount of time for the star graph, wheel graph, triangular snake graph, double triangular snake graph, linear kC4-snake graph and (2, n) C4-snake graph. It proves the correctness and superiority of BEHHO.

Experiments in this paper are performed on a subset of star graph instances with n ≤ 12 and m ≤ 11 in Table 2, wheel graph instances with n ≤ 13 and m ≤ 24 in Table 3, triangular snake graph instances with n ≤ 31 and m ≤ 45 in Table 4, double triangular snake graph instances with n ≤ 46 and m ≤ 75 in Table 5, linear kC4-snake graph instances with n ≤ 46 and m ≤ 60 in Table 6 and (2, n) C4-snake graph instances with n ≤ 76 and m ≤ 120 in Table 7.

6  Conclusion

In this paper, we presented a binary enhanced Harris Hawk Optimization BEHHO algorithm for solving the connected metric dimension problem. The proposed algorithm is compared to classical HHO, chaotic local search HHO, opposition-based learning HHO. Comparisons were performed on the graphs: star graph, wheel graph, triangular snake graph, double triangular snake graph, linear kC4-snake graph, and (2, n) C4-snake graph. Computational results confirm the superiority of the proposed BEHHO algorithm for solving connected metric dimension problem.

Funding Statement: The author(s) received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  V. Saenpholphat and P. Zhang, “Connected resolvability of graphs,” Czechoslovak Mathematical Journal, vol. 53, no. 4, pp. 827–840, 2003. [Google Scholar]

 2.  P. J. Slater, “Leaves of trees,” Congressus Numerantium, vol. 14, pp. 549–559, 1975. [Google Scholar]

 3.  F. Harary and R. A. Melter, “On the metric dimension of a graph,” Ars Combinatoria, vol. 2, pp. 191–195, 1976. [Google Scholar]

 4.  M. Imran, F. Bashir, A. Q. Baig, A. U. H. Bokhary, A. Riasat et al., “On metric dimension of flower graphs fn×m and convex polytopes,” Utilitas Mathematica, vol. 92, pp. 389–409, 2013. [Google Scholar]

 5.  M. Munir, A. R. Nizami, Z. Iqbal and H. Saeed, “Metric dimension of the mobius ladder,” Ars Combinatoria, vol. 135, pp. 249–256, 2017. [Google Scholar]

 6.  A. Borchert and S. Gosselin, “The metric dimension of circulant graphs and cayley hypergraphs,” Utilitas Mathematica, vol. 106, pp. 125–147, 2018. [Google Scholar]

 7.  P. Singh, S. Sharma, S. K. Sharma and V. K. Bhat, “Metric dimension and edge metric dimension of windmill graphs,” AIMS Mathematics, vol. 6, no. 9, pp. 9138–9153, 2021. [Google Scholar]

 8.  M. Imran, M. K. Siddiqui and R. Naeem, “On the metric dimension of generalized petersen multigraphs,” IEEE Access, vol. 6, pp. 74328–74338, 2018. [Google Scholar]

 9.  S. Nawaz, M. Ali, M. A. Khan and S. Khan, “Computing metric dimension of power of total graph,” IEEE Access, vol. 9, pp. 74550–74561, 2021. [Google Scholar]

10. M. Zayed, A. Ahmad, M. F. Nadeem and M. Azeem, “The comparative study of resolving parameters for a family of ladder networks,” AIMS Mathematics, vol. 7, no. 9, pp. 16569–16589, 2022. [Google Scholar]

11. A. Ahmad, M. Bača and S. Sultan, “Computing the metric dimension of kayak paddles graph and cycles with chord,” Proyecciones, vol. 39, pp. 287–300, 2020. [Google Scholar]

12. H. Alshehri, A. Ahmad, Y. Alqahtani and M. Azeem, “Vertex metric-based dimension of generalized perimantanes diamondoid structure,” IEEE Access, vol. 10, pp. 43320–43326, 2022. [Google Scholar]

13. B. Sooryanarayana, S. Kunikullaya and N. N. Swamy, “Metric dimension of generalized wheels,” Arab Journal of Mathematical Sciences, vol. 25, no. 2, pp. 131–144, 2019. [Google Scholar]

14. M. F. Nadeem, S. Qu, A. Ahmad and M. Azeem, “Metric dimension of some generalized families of toeplitz graphs,” Mathematical Problems in Engineering, vol. 2022, pp. 1–10, 2022. [Google Scholar]

15. A. N. Koam, A. Ahmad, M. S. Alatawi, M. F. Nadeem and M. Azeem, “Computation of metric-based resolvability of quartz without pendant nodes,” IEEE Access, vol. 9, pp. 151834–151840, 2021. [Google Scholar]

16. M. F. Nadeem, A. Shabbir and M. Azeem, “On metric dimension and fault tolerant metric dimension of some chemical structures,” Polycyclic Aromatic Compounds, vol. 2, pp. 1–13, 2021. [Google Scholar]

17. A. N. Koam, A. Ahmad, M. A. Asim and M. Azeem, “Computation of vertex and edge resolvability of benzenoid tripod structure,” Journal of King Saud University-Science, vol. 34, no. 6, pp. 102–108, 2022. [Google Scholar]

18. A. Al Khabyah, M. K. Jamil, A. N. Koam, A. Javed and M. Azeem, “Partition dimension of COVID antiviral drug structures,” Mathematical Biosciences and Engineering, vol. 19, no. 10, pp. 10078–10095, 2022. [Google Scholar]

19. M. Azeem, M. Imran and M. F. Nadeem, “Sharp bounds on partition dimension of hexagonal möbius ladder,” Journal of King Saud University-Science, vol. 34, no. 2, pp. 101–107, 2022. [Google Scholar]

20. J. Kratica, V. Kovačević-Vujčić and M. Čangalović, “Computing the metric dimension of graphs by genetic algorithms,” Computational Optimization and Applications, vol. 44, no. 2, pp. 343–361, 2009. [Google Scholar]

21. D. T. Murdiansyah and A. Adiwijaya, “Computing the metric dimension of hypercube graphs by particle swarm optimization algorithms,” in Proc. of ICSCDM, Springer, Cham, pp. 171–178, 2016. [Google Scholar]

22. N. Mladenović, J. Kratica, V. Kovačević-Vujčić and M. Čangalović, “Variable neighborhood search for metric dimension and minimal doubly resolving set problems,” European Journal of Operational Research, vol. 220, no. 2, pp. 328–337, 2012. [Google Scholar]

23. L. Eroh, C. X. Kang and E. Yi, “The connected metric dimension at a vertex of a graph,” Theoretical Computer Science, vol. 806, pp. 53–69, 2020. [Google Scholar]

24. J. C. Bednarz, “Cooperative hunting Harris’ hawks,” Science, vol. 239, no. 4847, pp. 1525–1527, 1988. [Google Scholar]

25. A. A. Heidari, S. Mirjalili, H. Faris, I. Aljarah, M. Mafarja et al., “Harris hawks optimization: Algorithm and applications,” Future Generation Computer Systems, vol. 97, pp. 849–872, 2019. [Google Scholar]

26. A. G. Hussien, L. Abualigah, R. Abu Zitar, F. A. Hashim, M. Amin et al., “Recent advances in Harris hawks optimization: A comparative study and applications,” Electronics, vol. 11, no. 12, pp. 19–68, 2022. [Google Scholar]

27. A. G. Hussien and M. Amin, “A self-adaptive Harris hawks optimization algorithm with opposition-based learning and chaotic local search strategy for global optimization and feature selection,” International Journal of Machine Learning and Cybernetics, vol. 13, no. 2, pp. 309–336, 2022. [Google Scholar]

28. H. Gezici and H. Livatyalı, “Chaotic Harris hawks optimization algorithm,” Journal of Computational Design and Engineering, vol. 9, no. 1, pp. 216–245, 2022. [Google Scholar]

29. Y. Zhang, R. Liu, X. Wang, H. Chen and C. Li, “Boosted binary Harris hawks optimizer and feature selection,” Engineering with Computers, vol. 37, no. 4, pp. 3741–3770, 2021. [Google Scholar]

30. H. R. Tizhoosh, “Opposition-based learning: A new scheme for machine intelligence,” in Proc. of CIMCA-IAWTIC, Vienna, Austria, pp. 695–701, 2005. [Google Scholar]

31. B. Alatas, “Chaotic bee colony algorithms for global numerical optimization,” Expert Systems with Applications, vol. 37, no. 8, pp. 5682–5687, 2010. [Google Scholar]

32. L. dos Santos Coelho and V. C. Mariani, “Use of chaotic sequences in a biologically inspired algorithm for engineering design optimization,” Expert Systems with Applications, vol. 34, no. 3, pp. 1905–1913, 2008. [Google Scholar]

33. D. Jia, G. Zheng and M. K. Khan, “An effective memetic differential evolution algorithm based on chaotic local search,” Information Sciences, vol. 181, no. 15, pp. 3175–3187, 2011. [Google Scholar]

34. B. Crawford, R. Soto, G. Astorga, J. García, C. Castro et al., “Putting continuous metaheuristics to work in binary search spaces,” Complexity, vol. 2017, pp. 84–102, 2017. [Google Scholar]

35. F. Afshinmanesh, A. Marandi and A. Rahimi-Kian, “A novel binary particle swarm optimization method using artificial immune system,” in Proc. of ICCT, Eurocon, pp. 217–220, 2005. [Google Scholar]