Sensor-Based Gait Analysis for Parkinson’s Disease Prediction

1  Introduction

According to recent research studies, Parkinson’s disease is considered to be the second most common chronic neurodegenerative disease in the world. This particular disease can be characterized by primary motor dysfunctions such as tremors, stiffness, bradykinesia, and postural instability in elderly people [1]. In addition, some of the secondary motor symptoms such as micrographia, dysphagia, gait, speech, dystonia, and precision grip impairments may also worsen the life quality of people [2]. Nowadays clinicians show more emphasis on non-motor symptoms such as mood dysfunction, hyposmia, cognitive impairments, pain, and so on. Some of the described motor symptoms are not specific and they are not associated with Parkinson’s disease as well.

However, the assessment of non-motor symptoms is more crucial in clinical practice and has a direct impact on the progression of Parkinson’s disease [3]. Usually, the person affected by Parkinson’s disease could be above the age of sixty and may walk with a slower and shuffling gait speed. Progressively, there is a need to evaluate and monitor the increasing changes occurring in motor dysfunction using wearable sensors such as accelerometers, magnetometers, and gyroscopes. Spatio-temporal parameters such as gait velocity, cadence, time, distance, stride length, and step length are seemed to be the major descriptions of the gait cycle [4]. The severity of these Parkinson’s symptoms may vary considerably throughout the day which needs continuous monitoring and evaluation for a longer period. Moreover, prolonged stays in the hospital may lead to more financial costs, and also the evaluation could not imitate the real motor symptoms of patients with Parkinson on every day. Importantly, this type of increased burden and financial issues are the most challenging tasks to be considered among the biomarkers to effectively monitor and diagnose Parkinson’s patients with proper medical care [5].

To overcome the above limitations, various healthcare examinations are imposed by the clinicians to measure Parkinson’s disease symptoms without increasing the expenses and complexities. These types of early identification and diagnosis could overcome the complications of late clinical treatment which can alleviate the unwanted financial cost, social demand, family burden, etc. The current research studies have focused on developing computer-assisted technologies for Parkinson’s disease-related prediction, monitoring process, and diagnosis in the aspects of checking voice disorder, facial expression, handwriting dynamics, freezing-of-gait, and anxiety depression [6]. To check the voice disorder, speech processing and recognition are explored in the cloud-based framework to enable remote healthcare applications for Parkinson’s disease patients [7].

Facial emotion recognition is identified in Parkinson’s patients by analyzing the cognitive impairment and giving more preference to mouth and eye movement behaviors [8]. The facial expression and movement analysis rely mainly on a video-based system to keep track of the facial movements recorded in successive video frames over a specified period of time [9]. Handwriting dynamics are explored using machine learning techniques to assess various static and dynamic spiral tests conducted over the patients [10]. Preferably gait analysis is used to classify a Parkinson’s person easily from healthy persons based on gait pattern recognition by deploying sensors under the foot [11]. Similarly, the gait analysis can be done through the deployment of accelerometer sensors in the hip, knee, and ankle. The experimental analysis of human motion can be captured through the subsequent observation of the position, velocity, and acceleration of independent coordinates of the body base [12].

All the above healthcare systems help in improving the quality of life by providing classification, prediction, and rehabilitation monitoring on Parkinson’s patients. According to the recent research studies [13–15], the most important issues are highlighted for enhancing the healthcare systems; (a) insufficient prediction and prevention mechanisms for freezing of gait, (b) lack of consistent monitoring and validation of wearable sensor information, (c) lack of optimal placement of wearable sensor for continuous monitoring, (d) inappropriate feature selection scheme for supporting disease prediction and diagnosis, (e) lack of appropriate behavioral assessment scheme to identify the cognitive impairments of Parkinson patients.

Therefore, the proposed research study has focused on addressing the above-mentioned research issues to enhance the performance of the Parkinson’s disease prediction and diagnosis process. Since Parkinson’s disease is a progressive disorder, a proposed research study has aimed to offer symptomatic relief and slow down the progression of the disease among elderly people. The key contributions of this research study include; (a) the novel architecture of PDIDS to predict the various severity levels of Parkinson’s disease and choose an appropriate diagnosis method pertinent to levels; (b) a feature selection mechanism is applied to select the appropriate features during disease prediction; (c) a probabilistic classifier model is proposed for classification of various levels of Parkinson disease by improving the prediction time and accuracy. The rest of the research study is organized into five sections. The next section can give a complete literature survey on various feature selection mechanisms and classifier models. In Section 3, a detailed description of the proposed PDIDS architecture is given with the formulation of gait recognition, feature selection, and classification problems. Section 4 gives complete real-time experimentation and results of the proposed research study. The final section could explain the conclusion of the proposed research study and the future development of the Parkinson’s healthcare system.

2  Related Work

Many research studies exploit wearable sensors for promoting remote monitoring and diagnosis of Parkinson’s disease by effectively quantifying the motor symptoms [16,17]. To discriminate against Parkinson’s patients, a low-cost smartphone is used to practice the voice, gait, posture, and finger tapping exercises at least four times a day [18]. Moreover, several researchers have been dependent on machine learning and deep learning techniques in order to develop remote healthcare systems for robust prediction and diagnosis. In the machine learning context, a novel continuous wavelet transform-based complex plot was introduced during the gait analysis for the diagnosis of idiopathic Parkinson’s disease. During experimentation, an artificial neural network classifier model was explored along with the temporal features so as to recognize the severity stages of the disease [19].

A Gaussian neural network classifier was used in a recent research study for identifying Parkinson’s by detecting the freezing of gait information as a major symptom that can acquire the variation of knee angle or inter-foot distance [20]. Similarly, a rule-based processing classifier was used to differentiate the normal and abnormal freezing of gait patterns by processing the data observed from the sensor placed on the shank [21,22]. In particular, it can easily describe the freezing of gait with a short stride, tremor, and motor block to give a warning message for severe gait and near fall situations.

To further differentiate the Parkinson’s tremor from the essential tremor, a convolutional long and short-term memory network classifier was explored by learning both the postural and resting positions of hand tremor [23]. In order to classify the severity of Parkinson’s symptoms in a proper way, a Convolutional Neural Network classifier was employed with a tremor assessment system for processing the wearable sensor devices [24]. Apart from these techniques, a probabilistic classifier model was used along with the fisher discriminant ratio-based feature selection method to observe the gait patterns without any statistical errors [25]. Moreover, the discriminative feature selection helps in generating more accurate prediction results than the existing classifier models.

In a deep learning context, gait abnormal pattern detection was explored using the deep neural network-based framework and the wearable inertial sensors [26]. It helps to achieve more prediction accuracy and less loss function value than the existing convolution neural network-based classifier model. A temporal layer was introduced to model the sequential sensor data to learn the complete changes occurring due to the hidden unit present in the recurrent neural network classifier model [27,28]. This model requires the consistent update of current states which may be difficult to train and explore the sequence of long-time activities of sensor data.

In the case of deep neural networks, more hidden layers are presented than any other classifier model. It mainly helps in learning the human activities from a large amount of data [29]. A deep convolutional neural network classifier was used for the detection of freezing of gait patterns from the acceleration signals captured from various patients [30]. Mostly, gait activity recognition becomes more challenging due to problematic and imbalanced real-time datasets received from wearable sensors. For overcoming the challenges, an ensemble of deep long, and short-term memory network classifiers were used to combine the set of learners during the time of classification [31].

An active deep learning model was introduced to improve the accuracy and minimize the time during the recognition of human gait activities [32,33]. The major limitations of these machine and deep learning studies have included high-cost sensors installation and computational resources for gait analysis. Moreover, foot pressure sensor-based measurements cannot be sufficient to acquire the Parkinson’s gait pattern. There is a need to incorporate angular motions of the human body by placing the sensors in the joints of the knee, hip, and ankle pants. The study of healthy and Parkinson’s persons needs to be done in different walking styles to judge the deviation among two classes. Therefore, the proposed research study has planned for making gait analysis on human subjects by deploying tri-axial accelerometer sensors on the hip, knee, and ankle positions.

3  Architecture of Accelerometer Sensor Based Parkinson’s Disease Identification System

The proposed research study has introduced the layered architecture of ASPDIS as given in Fig. 1. It consists of a sensor and cloud computing layer to implement the accelerometer sensor-based gait analysis for real-time Parkinson’s disease-related prediction and treatment monitoring activity. For carrying out the process, tri-axial accelerometer sensors are placed on the hip, knee, and ankle location of the human body for observing various sequences of acceleration signals with respect to X , Y , and Z axes. These signals are periodically captured in the raspberry pi computing device and offloaded to remote the cloud servers available in the cloud computing layer for immediate processing and diagnosis. Also, the health status information will frequently be updated on the patient smartphone display device. After live observation of accelerating the data, the proposed healthcare service deployed in the cloud layer will apply the kernel-based support vector machine classifier model to analyze the gait patterns. Based on the previously trained medical data, the classifier can easily discriminate the patient with and without Parkinson’s disease. In the meantime, subsequent variations in health parameters are updated in the patient medical history to help the practitioner during future prediction and diagnosis. According to the severity level, the healthcare service will invoke the appropriate rehabilitation monitoring and assessment facilities for the patients. Furthermore, it can provide telemedicine suggestions and prescriptions to the appropriate patients based on the expert decisions available online. Accordingly, the formulation of gait cycle recognition and disease prediction using the proposed classifier is mathematically represented with the corresponding cycle-specific to parameters.

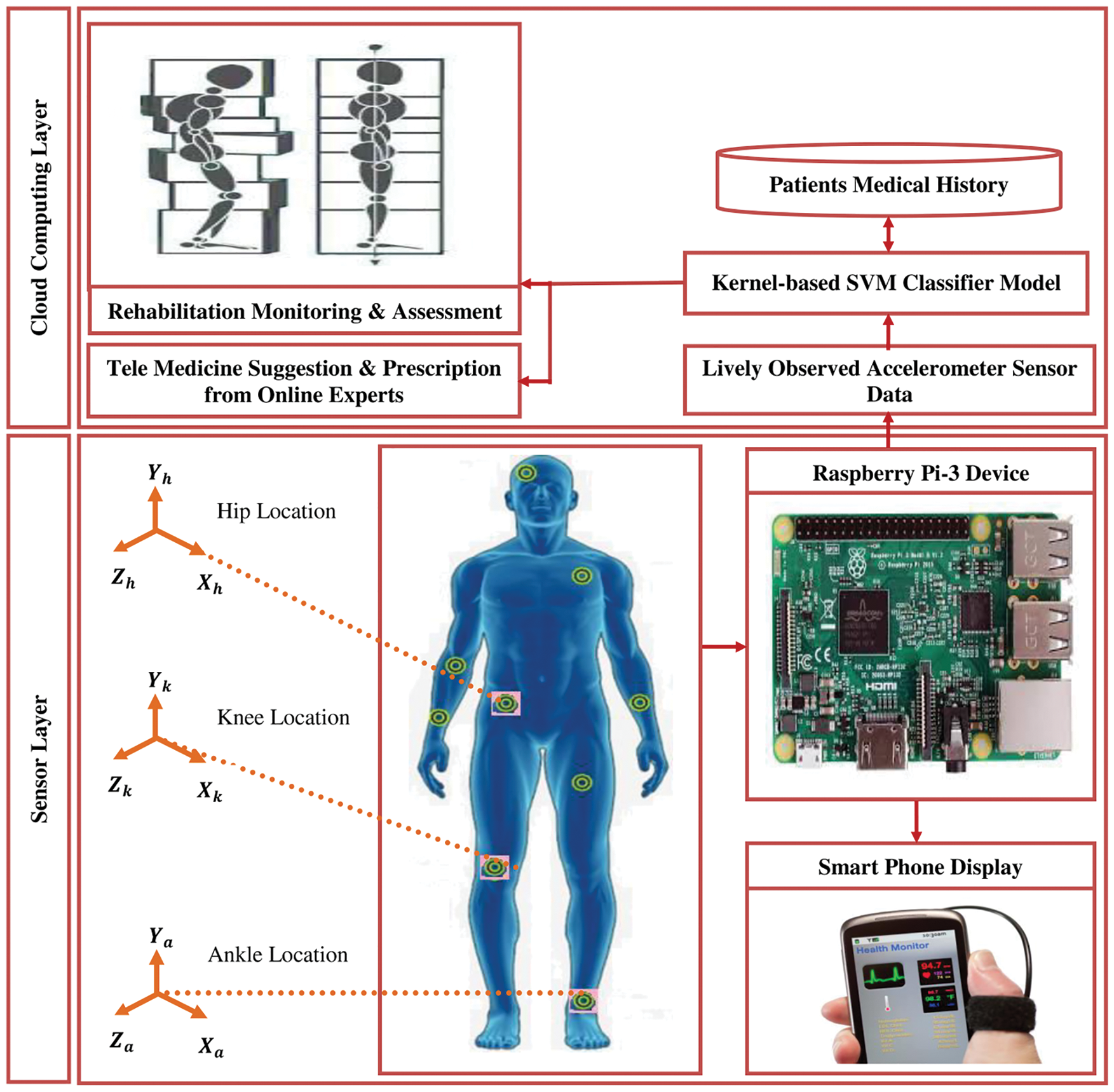
Figure 1: Architecture of ASPDIS

3.1 Formulation of Gait Cycle Recognition

A gait cycle specifies the time period of one of the foot contacts with the ground to the next foot. So, to get the complete gait cycle out of sensor data, the time of each gait event must be determined according to the maximum scale of interest Tmax . To measure the acceleration signals from the subject, a pbleal accelerometer sensor is fixed in the front of the center to represent the fixed belt. The orientation of acceleration axes X , Y , and Z represents the medial/lateral, superior/inferior, and anterior/posterior respective forward opens values of these axes correspond to the life, upward and forward opens elevations. It is important to consider the sequence of three-dimensional output signal points [xtytzt] the received from the tri-axial athe the ccelerometer sensors during gait monitoring process. Then, the gait event detection can be done through the measurement of normalized cross-correlation ( NCC ), anisobiphasicd biphasicity score ( BS ). The similarity between any two sequences with respect to time period T is characterized as a normalized cross-correlation function given by Eq. (1).

NCC(T)=∑t=1n⁡(x¯tx¯t+T+y¯ty¯t+T+z¯tz¯t+T)∑t=1n⁡(x¯t2+y¯t2+z¯t2)⋅∑t=1n⁡(x¯t+T2+y¯t+T2+z¯t+T2) (1)

Here, the average value of points x¯t and x¯t+T are computed from the base points as defined by Eqs. (2) and (3) respectively. Similarly, the average value of points y¯t , z¯t , y¯t+T and z¯t+T are also computed from the corresponding base points. These types of scalar quantity-based measurements provide a robust way of setting the coordinate system. Likewise, the mean value of the acceleration signal is observed to be high for dynamic activities such as hand movement and walking patterns. In case of low value of acceleration signal, static activities such as standing and sitting patterns are observed.

x¯t=xt−1n∑t=1n⁡xt (2)

x¯t+T=xt+T−1n∑t=1n⁡xt+T (3)

Next, the anisotropy measurement is defined in Eq. (4) to quantify the degree of time series data variation towards the positive or negative value. Finally, the biphasicity score BS of three-dimensional signal is given by the Eq. (5). The set of time functions characterizing the gait signal is given in the form of delta function such as f1(t)=cxδ(t) , f2(t)=cyδ(t) , and f3(t)=czδ(t) .

AN=∑t=1n⁡sgn(xt)∑t=1n⁡|sgn(xt)| (4)

BS=1−12|2cy−cx2cy+cx|m+12|2cz−cx2cz+cx|mm (5)

Let cx , cx , and cx denotes the corresponding cycles of axes X, Y, and Z.

The acceleration magnitude of the signal can be obtained through the filtering of component [ax(t)ay(t)az(t)] using the Eq. (6). In order to identify the human fall rotation, it is more sufficient to make transformations on x and y−axes in the two-dimensional coordinate as shown in Eq. (7).

ar(t)=[ax(t)2+ay(t)2+az(t)2]0.5 (6)

θ=tan−1(yvxv)×(180π) (7)

An integration of acceleration signals is explored to authenticate the subject during continuous monitoring and diagnosis using the Eq. (8).

I=arcsin⁡(azax(t)2+ay(t)2+az(t)2) (8)

where, t=1,2,…,k be the number of observations recorded at various time periods. Then, the absolute distance metric is measured to find the similarity score between the gait samples p and q as given by the Eq. (9).

dist(p,q)=∑i=1n⁡|pi−qi| (9)

The complexity of gait movement can be estimated in terms of signal spectrum energy as defined by the Eq. (10).

E(a(t))=∑t=1k⁡a(t)2k (10)

where, a(t) be the tth amplitude of the acceleration signal and k represents the number of spectrum lines. Further, the periodicity can be estimated as entropy measurement as expressed by the Eq. (11).

EN=−∑t=1k⁡p(t)log2(p(t)) (11)

Let p(t) denotes the probability of occurrence of amplitude spectrum a(t) of the respective acceleration signal. The lower of the entropy value represents the periodicity of the investigated signal. The range of acceleration signals can be represented as standard deviation as expressed by the Eq. (12). For estimating the dynamics of changes occurring in the acceleration signal, a kurtosis parameter is defined by the Eq. (13).

SD(a(t))=(1k−1)∑t=1k⁡(a(t)−a¯)2 (12)

k(a(t))=m4(a(t))SD(a(t))2−3 (13)

Let m4(⋅) be the fourth central movement. A ratio of maximum signal to the rms values gives the crest factor denoting the signal impulsiveness as expressed by the Eq. (14). Also, a correlation coefficient parameter is illustrated between the different pairs of the same accelerometer sensor as expressed by the Eq. (15).

kCF(a(t))=max(a(t))1k∑t=1k⁡(a(t))2 (14)

CC(a(t)il,a(t)jm)=a(t)ila(t)jm¯−ailajm¯SD(a(t)il)SD(a(t)jm) (15)

where i and j denotes the number of accelerometer sensors, and l=Parkinson′s and m=[xtytzt] denotes the various axes of accelerometer.

3.2 Parkinson Disease Prediction using Kernel-Support Vector Machine (SVM) Classifier Model

The classification of Parkinson disease is made with respect to acceleration signals received from various accelerometer sensors deployed on the hip, knee and ankle of the human body. In order to effectively assess the human gait analysis, the SVM classifier model is explored in this research study. It helps to classify the set of input parameters a={a1,a2,…,a1} into two classes yi∈{−1,+1} , where the vector ai=[xiyizi] . The kernel function φ(ai) helps to transform the input feature space ai into higher dimensional feature space where the linear clarification exists. A kernel SVM provides the optimal hyper-plane that can help to maximize the required margin among the positive and negative data points. Therefore, the kernel SVM can be formulated with appropriate decision surface as defined by the Eq. (16).

f(x)=wTx+b (16)

where, w be the highest dimensional coefficient vector and b be the offset. A weight factor w and offset value are defined together for hyper-plane separation as expressed by the Eq. (17). The kernel SVM classifier model tries to achieve the optimal hyper-plane by resolving the optimization problem given by the Eq. (18).

yi⋅(wTφ(ai)+b)≥1−ϵi;i=1,2,…,k (17)

Minw,b,ϵ12‖w‖2+C∑i=1k⁡ϵi (18)

Let C be the hyper parameter that controls the tradeoff between the classes margin and ϵi . The sample ai satisfies the conditions such as ϵi≥0 , yi⋅(wTφ(ai)+b)≥1−ϵi and ∀ai∈{1,2,…,m} . As a result, the optimization problem can be converted into a Lagrangian dual problem using multipliers α=(α1,α2,…,αn) as formulated by the Eq. (19).

Minw,b,ϵ∑i=1k∝i−12∑i=1k⁡∑j=1k∝i∝jyiyjxiTxj (19)

where, the parameter w and b can be determined with constraints such as ∝i≥0 , ∑i=1k∝iyi=0 , and i=1,2,…,k . Here, the unlabelled data samples can be classified according to the discriminant function given by Eq. (20).

C(X)=sgn(∑i=1k∝iyixiTx+b) (20)

As SVM addresses the non-linear data samples, the kernel function is used mostly to map the samples to the other space. There are four different kernel functions available such as liner, polynomial, radial basis and sigmoid for the classification of gait. Out of which, the radial basis function is used to map the lower dimensional data sample to the higher dimensional feature space. Therefore, the non-linear discriminate function using the kernel is expressed by the Eq. (21). In order to complete the transformation, the liner, polynomial, radial basis and sigmoid functions are explored in this study as defined by the Eqs. (22)–(25).

C(X)=sgn(∑i=1k∝iyik(x1,x2)+b) (21)

k(x1,x2)=⟨x1,x2⟩ (22)

k(x1,x2)=(⟨x1,x2⟩+b)d (23)

k(x1,x2)=e−yi‖x1−x2‖2 (24)

k(x1,x2)=tan⁡ h(yi⟨x1,x2⟩+b) (25)

The performance of the kernel-SVM classifier model is measured in terms of disease prediction time, prediction accuracy and Matthews’s correlation coefficient. Here, the prediction time represents the time of patient request submission to the ending response received from the healthcare system. Then, the classifier prediction accuracy denotes the ratio of properly classified Parkinson patients to the total number of patients observed as given by the Eq. (26).

CAcc=TP+TNTP+FP+TN+FN (26)

where, TP and TN indicates the amount of true positive and negative rate, FP and FN indicate the amount of false positive and negative rate. Finally, the Matthews’s correlation coefficient can be measured between the predicted and observed classification using confusion matrix as defined by the Eq. (27).

CMCC=TP×TN−FP×FN(TP+FP)(TP+FN)(TN+FP)(TN+FN) (27)

Let the value of CMCC could range from −1 to +1, where the value of +1 denotes the perfect, −1 denotes the disagreement and 0 denotes the unhealthy predictions of the specified classifiers.

4  Experimental Evaluations

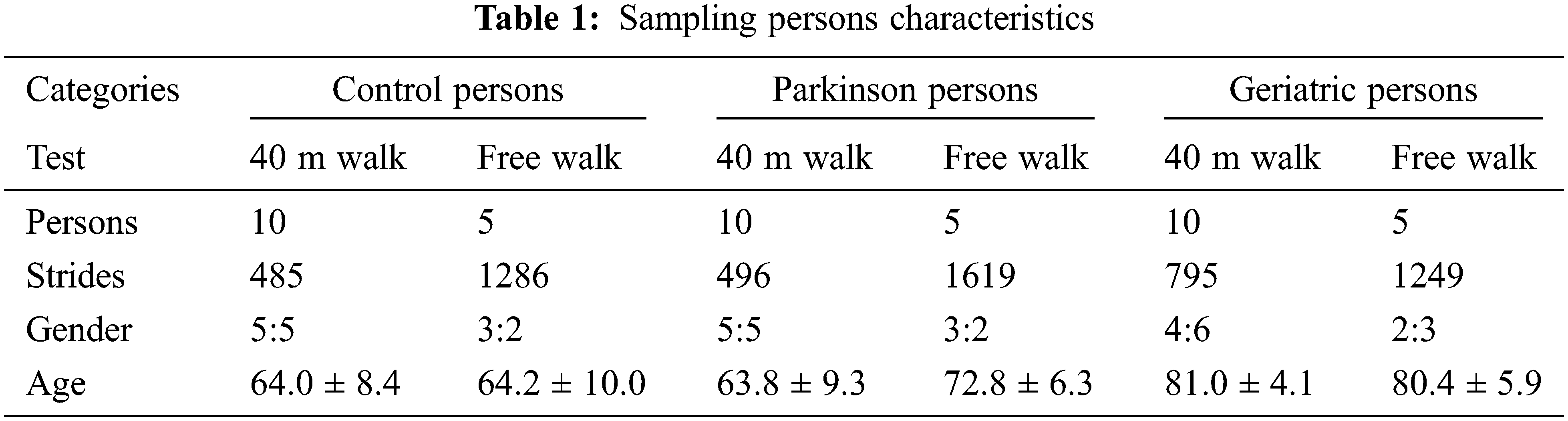
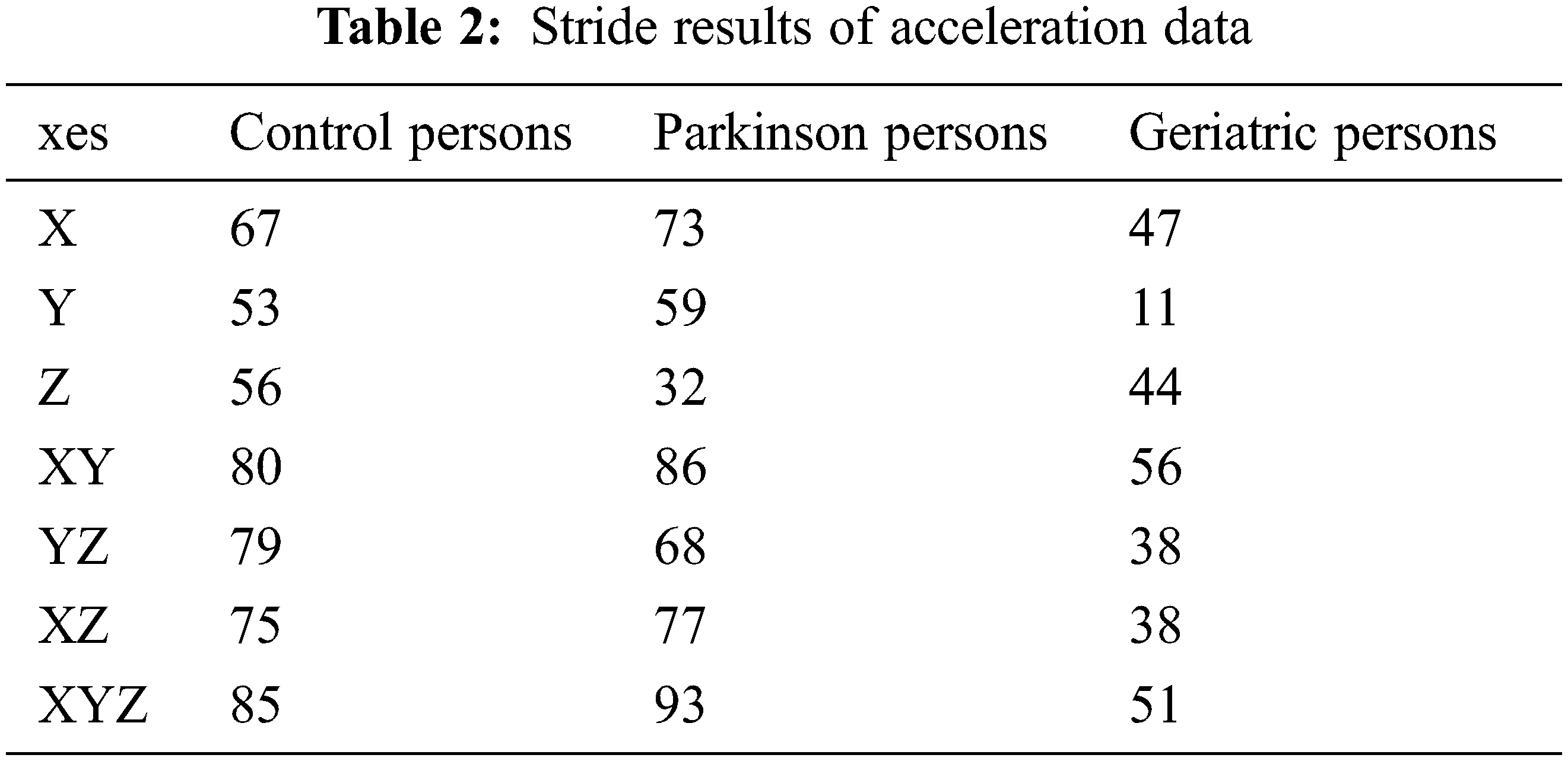
To assess the performance of the proposed classifier model against the existing classifiers, a benchmarking dataset is taken from the inertial sensor database [34,35]. It consists of forty-five persons, equally classified into control, Parkinson and geriatric persons with characteristics as given in Table 1. The persons were asked to present a 40-meter walk and free walk during the recording of the dataset at the sampling rate of 102.4 Hz. In case of 40-meter walk, the person was asked to walk four times 10 meter at the comfortable speed without any obstacle in the hospital environment. Afterwards, the persons were asked to turn 180 degrees along the transverse plane. In case of free walk, the persons were asked to walk for two minutes at a comfortable speed. During the first two minutes, the person was asked to walk straight for 20 meters twice the time. In next two minutes, the person was asked to climb the stairs for 30 s. To mimic the scenarios connecting the 20 meters walk and stair hiking, the persons were asked to perform sit-to-stand movement, walk straight, walk in the curves, and walk throughout the doors manually. In order to provide in-depth estimate, the most excellent performing axes of accelerometer sensor data are used as mentioned in Table 2.

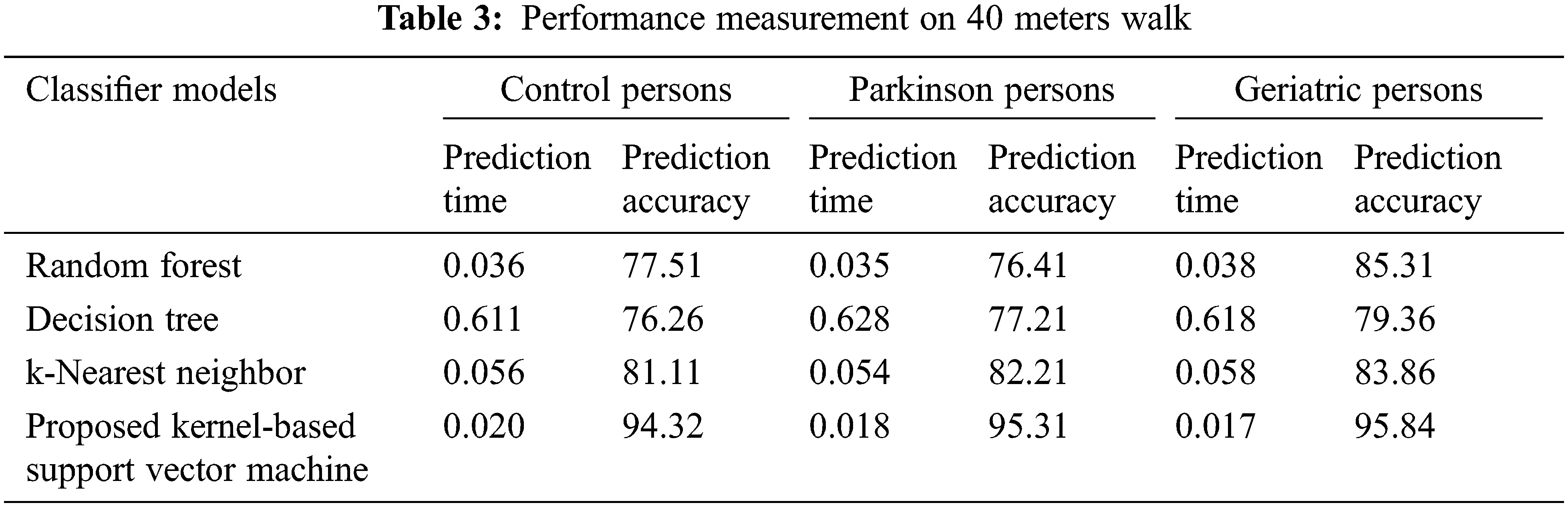
The performance metrics such as prediction time and accuracy were used to evaluate the proposed kernel-based support vector machine classifier model against the existing random forest, decision tree and k-nearest neighbor classifiers. The results of various classifier models were observed during the experimentation of persons in 40 meters walk as given in Table 3. It is more evident from the observed results, the proposed kernel-based support vector machine classifier model on 40 meters walk has obtained an average of 21.43%, 22.10% and 22.10% of less prediction time over the existing classifiers in the context of control, Parkinson and geriatric persons respectively. Then, the proposed kernel-based support vector machine classifier model on free walk has obtained an average prediction accuracy improvement of 16.02%, 16.70% and 12.99% over the existing classifiers in the context of control, Parkinson and geriatric persons respectively.

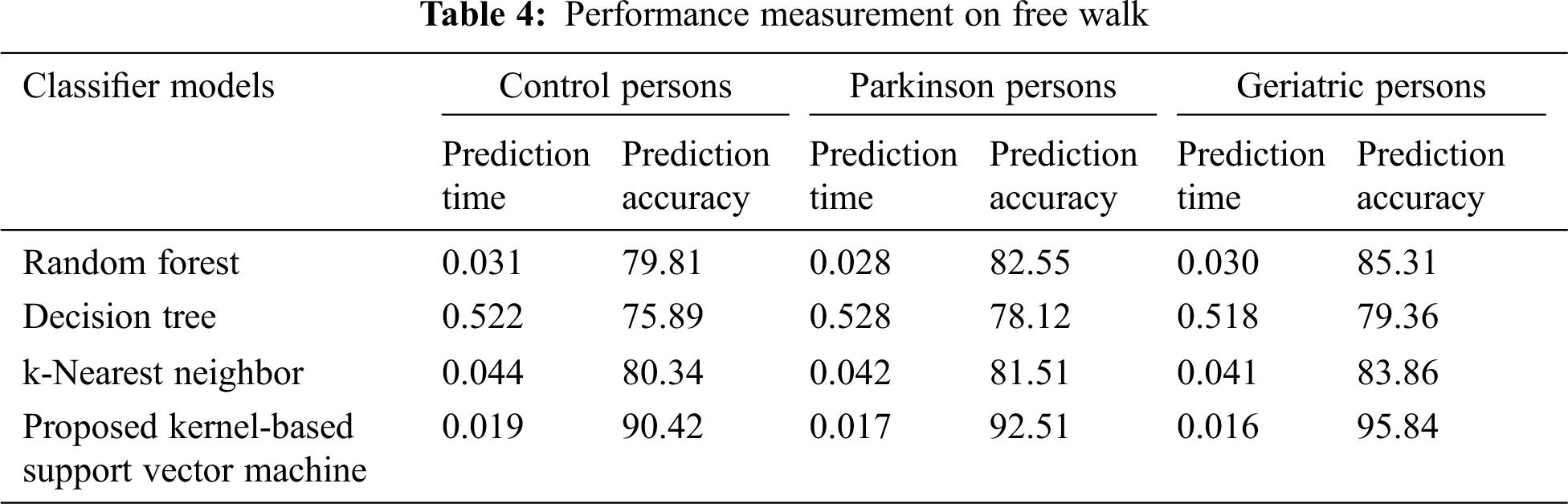
Similarly, the performance of various classifier models is observed during the free walk experimentation of persons as shown in Table 4. From the experimental results, it is distinctly understandable that the proposed classifier model has achieved very less average prediction time of 18%, 18.23% and 18.03% over the existing classifiers in the aspects of control, Parkinson and geriatric persons respectively. In addition, the proposed classifier model has achieved more prediction accuracy of 11.74%, 11.78% and 12.99% over the existing classifiers in terms of control, Parkinson and geriatric persons respectively. In both the cases of 40 meters walk and free walk, the proposed classifier model has outperformed the existing classifier models in the aspects of prediction time and prediction accuracy. In future, the research study can improve the healthcare system by providing a negotiation-based personalized diagnosis mechanism [36,37]. In addition, the research study can be extended to monitor and diagnose the remote patients by exploring real-time human tracking and activity identification mechanisms. Further, the detection methodology can be enhanced using deep learning algorithms for the improvement of prediction accuracy.

5  Conclusion

The proposed research study has developed the robust and efficient healthcare framework to validate the gait cycle observed from the accelerometer sensors. Therefore, the observed results have shown that the proposed ASPDIS provides more robust and accurate classification of persons with and without Parkinson disease. Moreover, the proposed kernel-based support vector machine classifier model can provide more computational efficiency and better prediction results while comparing to the existing classifier models. It can also provide consistent performance even with a smaller number of training samples used during the experimentation process. As a result, the proposed classifier has outperformed the others in terms of prediction time and accuracy. In addition, the proposed ASPDIS could be enhanced to perform well for the recognition of daily living activities of humans in the smart hospitals or homes. Still there is a lack in deploying the optimal number of accelerometer sensors over the human body to assess Parkinson disease motor symptoms. So, there is a need to identify the different combinations of sensor placements during the experimentation in order to dramatically improve the performance of the proposed ASPDIS. In future, freezing of gait and slowness of hand movements can be analyzed for the further improvement in the performance of healthcare systems. A personalized gait pattern analysis can be integrated with the healthcare system to detect and track the freezing of gait information in case of individuals with Parkinson disease.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  N. Amato, S. Caverzasio and S. Galati, “Clinical implication of high-density EEG sleep recordings in parkinson’s disease,” Journal of Neuroscience Methods, vol. 340, no. 1–2, pp. 108746, 2020. [Google Scholar]

 2.  C. Raza, R. Anjum and N. A. Shakeel, “Parkinson’s disease: Mechanisms, translational models and management strategies,” Life Sciences, vol. 226, no. 3, pp. 77–90, 2019. [Google Scholar]

 3.  A. Tetsuya, F. Huan, S. Kenji, N. Takao, K. Susumu et al., “Human behavioral assessments in current research of parkinson’s disease,” Neuroscience and Biobehavioral Reviews, vol. 68, pp. 741–772, 2016. [Google Scholar]

 4.  I. Thaıs Guerra, O. Gondim, C. Cassia Batista, M. Aurelio Benedetti, I. Muniz et al., “Portable accelerometers for the evaluation of spatio temporal gait parameters in people with parkinson’s disease: An integrative review,” Archives of Gerontology and Geriatrics, vol. 90, no. 104097, pp. 1–15, 2020. [Google Scholar]

 5.  Q. Wei Oung, H. Muthusamy, S. Nisha Basah, H. Lee and V. Vijean, “Empirical wavelet transform based features for classification of parkinson’s disease severity,” Journal Medical Systems, vol. 42, no. 29, pp. 1–17, 2018. [Google Scholar]

 6.  C. R. Pereira, D. R. Pereira, S. A. T. Weber, C. Hook, V. Hugo et al., “A survey on computer-assisted parkinson’s disease diagnosis,” Artificial Intelligence In Medicine, vol. 95, pp. 48–63, 2019. [Google Scholar]

 7.  K. Abdullah, M. Alhussein, K. Sailunaz and M. Saiful Islam, “Cloud based framework for parkinson’s disease diagnosis and monitoring system for remote healthcare applications,” Future Generation Computer Systems, vol. 66, pp. 36–47, 2017. [Google Scholar]

 8.  J. Waldthaler, C. Krüger-Zechlin, L. Stock, Z. Deeb and L. Timmermann, “New insights into facial emotion recognition in parkinson’s disease with and without mild cognitive impairment from visual scanning patterns,” Clinical Parkinsonism & Related Disorders, vol. 1, pp. 102–108, 2019. [Google Scholar]

 9.  B. Andrea, O. Silvia, E. Hugo Jair, G. Fabio, C. Massimo et al., “Analysis of facial expressions in parkinson’s disease through video-based automatic methods,” Journal of Neuroscience Methods, vol. 281, pp. 7–20, 2017. [Google Scholar]

10. I. Canturk, “Fuzzy recurrence plot based analysis of dynamic and static spiral tests of parkinson’s disease patients,” Neural Computing and Applications, vol. 33, no. 1, pp. 349–360, 2021. [Google Scholar]

11. W. Zeng, F. Liu, Q. Wang, Y. Wang, L. Ma et al., “Parkinson’s disease classification using gait analysis via deterministic learning,” Neuroscience Letters, vol. 633, no. 6, pp. 268–278, 2016. [Google Scholar]

12. F. Mouzo, U. Lugris, R. Pamies-Vila and J. Cuadrado, “Skeletal level control based forward dynamic analysis of acquired healthy and assisted gait motion,” Multibody System Dynamics, vol. 44, no. 1, pp. 1–29, 2018. [Google Scholar]

13. J. Goyal, P. Khandnor and T. Chand Aseri, “Classification, prediction, and monitoring of parkinson’s disease using computer assisted technologies: A comparative analysis,” Engineering Applications of Artificial Intelligence, vol. 96, no. 1.0.0, pp. 103955, 2020. [Google Scholar]

14. A. Mirelman, P. Bonato, R. Camicioli, T. D. Ellis, N. Giladi et al., “Gait impairments in parkinson’s disease,” The Lancet Neurology, vol. 18, no. 7, pp. 697–708, 2019. [Google Scholar]

15. A. Tetsuya, F. Huan, S. Kenji, N. Takao, K. Susumu et al., “Human behavioral assessments in current research of parkinson’s disease,” Neuroscience and Biobehavioral Reviews, vol. 68, no. 5, pp. 741–772, 2016. [Google Scholar]

16. X. Qian, H. Hao, Y. Chen and L. Luming, “Wake sleep identification based on body movement for parkinson’s disease patients,” Journal of Medical and Biological Engineering, vol. 35, no. 4, pp. 517–527, 2015. [Google Scholar]

17. A. Almogren, “An automated and intelligent parkinson diseasemonitoring system using wearable computing and cloud technology,” Cluster Computing, vol. 22, no. S1, pp. 2309–2316, 2019. [Google Scholar]

18. L. Borzì, M. Varrecchia, G. Olmo, C. Alberto Artusi, M. Fabbri et al., “Home monitoring of motor fluctuations in parkinson’s disease patients,” Journal of Reliable Intelligent Environments, vol. 5, no. 3, pp. 145–162, 2019. [Google Scholar]

19. M. Alafeef and M. Fraiwan, “On the diagnosis of idiopathic parkinson’s disease using continuous wavelet transform complex plot,” Journal of Ambient Intelligence and Humanized Computing, vol. 10, no. 7, pp. 2805–2815, 2019. [Google Scholar]

20. A. Saad, I. Zaarour, F. Guerin, P. Bejjani, M. Ayache et al., “Detection of freezing of gait for parkinson’s disease patients with multi sensor device and gaussian neural networks,” International Journal of Machine Learning and Cybernetics, vol. 8, no. 3, pp. 941–954, 2017. [Google Scholar]

21. D. Milica, D. Jovičić, S. Nenad, M. Saša, I. Radovanović et al., “Automatic identification and classification of freezing of gait episodes in parkinson’s disease patients,” IEEE Transactions on Neural Systems and Rehabilitation Engineering, vol. 22, no. 3, pp. 685–694, 2014. [Google Scholar]

22. A. Betul Oktay and A. Kocer, “Differential diagnosis of parkinson and essential tremor with convolutional LSTM networks,” Biomedical Signal Processing and Control, vol. 56, no. 1, pp. 101683, 2020. [Google Scholar]

23. H. Kim, W. Woo Lee, A. Kim, H. Lee, H. Young Park et al., “Wrist sensor based tremor severity quantification in Parkinson’s disease using convolutional neural network,” Computers in Biology and Medicine, vol. 95, no. 4, pp. 140–146, 2018. [Google Scholar]

24. A. Nandy, “Statistical methods for analysis of parkinson’s disease gait pattern and classification,” Multimedia Tools and Applications, vol. 78, no. 14, pp. 19697–19734, 2019. [Google Scholar]

25. J. Chakraborty and A. Nandy, “Discrete wavelet transform based data representation in deep neuralnetwork for gait abnormality detection,” Biomedical Signal Processing and Control, vol. 62, no. 102076, pp. 1–10, 2020. [Google Scholar]

26. H. Nweke, Y. Wah, M. Ali Garadi and U. Rita, “Deep learning algorithms for human activity recognition using mobile and wearable sensor networks: State of the art and research challenges,” Expert Systems With Applications, vol. 105, pp. 233–261, 2018. [Google Scholar]

27. J. Wang, Y. Chen, S. Hao, X. Peng and L. Hu, “Deep learning for sensor-based activity recognition: A survey,” Pattern Recognition Letters, vol. 119, no. c, pp. 3–11, 2019. [Google Scholar]

28. Y. Xia, J. Zhang, Q. Ye, N. Cheng, Y. Lu et al., “Evaluation of deep convolutional neural networks for detection offreezing of gait in parkinson’s disease patients,” Biomedical Signal Processing and Control, vol. 46, pp. 221–230, 2018. [Google Scholar]

29. Y. Guan and T. Plotz, “Ensembles of deep LSTM learners for activity recognition using wearables,” Proceedings of the ACM on Interactive, Mobile, Wearable and Ubiquitous Technologies, vol. 1, no. 2, pp. 1–28, 2017. [Google Scholar]

30. H. M. Sajjad Hossain, M. Abdullah, A. Hafiz Khan and N. Roy, “De active: Scaling activity recognition with active deep learning,” in Proc. ACM on Interactive, Mobile, Wearable and Ubiquitous Technologies, New York,United States, 2018. [Google Scholar]

31. J. Barth, C. Oberndorfer, C. Pasluosta, S. Schülein, H. Gassner et al., “Stride segmentation during free walk movements using multi dimensional subsequence dynamic time warping on inertial sensor data,” Sensors, vol. 15, no. 3, pp. 6419–6440, 2015. [Google Scholar]

32. A. Rampp, J. Barth, S. Schülein, K. Günter Gaßmann, J. Klucken et al., “Inertial sensor based stride parameter calculation from gait sequences in geriatric patients,” IEEE Transactions on Biomedical Engineering, vol. 62, no. 4, pp. 1089–1097, 2015. [Google Scholar]

33. R. Rajavel and T. Mala, “Agent based automated dynamic SLA negotiation framework in the cloud using the stochastic optimization approach,” Applied Soft Computing, vol. 101, no. 107040, pp. 1–20, 2021. [Google Scholar]

34. R. Rajavel, S. Ravichandran and G. R. Kanagachidambaresan, “Agent based cloud service negotiation architecture using similarity grouping approach,” International Journal of Wavelets, Multiresolution and Information Processing, vol. 18, no. 1, pp. 1941015, 2020. [Google Scholar]

35. R. Rajavel, “IoT-based smart healthcare video surveillance system using edge computing,” Journal of Ambient Intelligence and Humanized Computing, vol. 13, pp. 3195–3207, 2022. [Google Scholar]

36. W. Sun, G. Z. Dai, X. R. Zhang, X. Z. He and X. Chen, “TBE-Net: A three branch embedding network with part-aware ability and feature complementary learning for vehicle re identification,” IEEE Transactions on Intelligent Transportation Systems, vol. 23, no. 9, pp. 14557–14569, 2021. [Google Scholar]

37. W. Sun, L. Dai, X. R. Zhang, P. S. Chang, Z. He et al., “RSOD: Real time small object detection algorithm in UAV based traffic monitoring,” Applied Intelligence, vol. 52, pp. 8448–8463, 2022. [Google Scholar]