E-MOGWO Algorithm for Computation Offloading in Fog Computing

1  Introduction

Today’s devices have an array of sensors embedded to continuously monitor their surroundings in real-time. The internet of things (IoT) devices generally has inadequate battery power, computational capability, and memory capacity, which leads to poor performance and reduces the quality of service (QoS) for computational-intensive applications [1]. Cisco predicts that 500 billion IoT devices will be in use by 2025 [2]. The enormous increase in connected devices and their demands enforce a gigantic paucity in communication networks and computational resources [3]. Computation offloading (CO) is used to improve the performance of IoT devices by executing computation-intensive parts of the application on remote machines or servers [4]. For CO, the end devices send computational tasks to the remote server over resource-limited communication channels such as long-term evolution (LTE), wireless channels, 5G systems etc [5]. Then the remote server executes the tasks and returns the results to the IoT devices. Using this technique, the resource-intensive tasks are executed in coordination with the offloading server. Therefore, CO strategy design is critical for selecting the right offloading server. During offloading decisions, we have to deal with many questions such as when, what, why, and where to offload [6]. Suppose we choose the where factor, the target can be a fog or cloud layer. When we offload to the cloud, the task is completed, and the cloud server returns the results. However, new research indicates that offloading to the cloud is never a good idea when some delay-sensitive applications must be completed by a certain deadline. Moreover, cloud computing (CC) has higher communication costs and transmission delay [7]. For latency-sensitive tasks, the availability of computational resources via fog computing (FC) is advantageous [8]. It offers a distributed infrastructure, which results in faster response and lower latency to application requests [9]. The computational capability and resources of fog nodes are lesser compared to CC. Hence the offloading destination should be wisely selected based on different conflicting parameters like delay, energy consumption, computational time, throughput etc. Only properly offloaded tasks can result in a higher quality of experience and services. Developing a task offloading scheme in the FC environment is a little more difficult than in normal CC, where an IoT device simply selects whether or not to transmit a task to the cloud [10]. In FC, the number of offloading destinations increases in proportion to the number of fog nodes. Moreover, fog nodes have limited computing capabilities and resources compared to cloud resources [11]. Furthermore, earlier studies assumed single-user single fog node scenarios, single-user single with single cloud server scenarios, or multi fog server with single cloud server scenarios, which are impractical. Few studies have focussed on task offloading in multi-user, multi-fog, and cloud server scenarios.

The full potential of fog computing can be realized using the offloading technique. Moreover, the offloading problem is np hard, and its complexity increases with the number of tasks. In this article, we use the MOGWO technique for the CO problem. MOGWO is integrated with gravity reference points to enhance the performance further. The proposed strategy significantly contributes by identifying the best computing server for every task based on two QoS parameters, i.e., computational time and energy consumption.

The following is a summary of the paper’s main contribution:

•   We investigate a multiobjective CO problem for a heterogeneous multi-user, multi-fog server and cloud environment.

•   MOGWO algorithm is used to select the best offloading server on the basis of minimum energy consumption and computational time.

•   A gravity reference point method is also integrated with MOGWO to improve its performance as it has a better solution spread set.

•   Lastly, the simulation of the proposed model and comparison of results with two other multiobjective algorithms have been carried out in a three-layer architecture.

The rest of the article is as follows: Section 2 of this paper details the literature review related to CO using metaheuristic techniques. Section 3 goes over the system model in detail, including the computational and energy models and the problem definition. The proposed algorithm is described in Section 4. Section 5 describes the simulation’s findings, and Section 6 describes the paper’s conclusion.

2  Literature Review

Various studies have been conducted for CO problems in FC till now. Various authors published review papers [12–16] on task offloading in FC as a research direction. Many researchers use the queuing theory [17–19], game theory [20–22], dynamic programming and clustering techniques [18,23,24] to solve CO problems. It has been observed that each has separately investigated essential parameters, for example, delay, execution time, service time, communication cost, computational cost, quality of service and energy consumption etc. In reality, the offloading problem is multiobjective and np-hard. As a result, only some researchers have investigated meta-heuristic techniques for CO in FC. However, metaheuristic offloading techniques in FC are new and require extensive augmentation to maximize the QoS and end-user experience. These algorithms are motivated by natural, physical phenomena and animal behaviour [25]. Authors in [26] proposed two swarm intelligence-based schedulers named ant colony optimization (ACO) and particle swarm optimization (PSO) to efficiently balance the workload of IoT devices by taking into account response time and cost over fog nodes. Finally, the authors declared that ACO outperformed PSO and round-robin (RR) in case of response time. Authors in reference [27] proposed adaptive GA-PSO (Genetic algorithms and particle swarm optimization) to find near-optimal scheduling algorithms for scheduling resource-intensive components of an application. The authors combined genetic algorithm (GA) and PSO, where GA is used for exploration, and PSO is used for exploitation for optimal offloading with deadline constraints. GA was also used in [28] to improve response time and load balancing while finding the best destination for the offloaded task. Here queuing model is also utilized to calculate waiting time and service time. Authors in [29] also proposed a multiobjective optimization non-dominated sorting genetic algorithm that finds an optimal offloading approach for all workflow applications. Authors in [30] proposed a fruit-fly-based CO algorithm which improves resource allocation and offloading to gain nominal energy usage.

Most of the problems were either single objectives or converted to a single objective by assigning weight to the parameters. As a multiobjective problem, literature has no sufficient discussion to solve the offloading problem. Also, offloading is a multiobjective problem and its complexity increase with the number of tasks. Thus, developing a multiobjective grey wolf to solve the CO problem is an open issue.

3  System Model

We propose a three-layer system model in our proposed work: IoT devices layer, fog server (FS) layer, and cloud server (CS) layer. The FS layer is at the network’s edge and connects end devices with the cloud server. Suppose there are X IoT users U={U1,U2,U3,U4…Ux} . Each IoT user submits a T number of computation-intensive or resource-sensitive tasks. The task set in a time interval δt is represented as T={T1,T2,T3,…,Tx} . Here, we define Tx={Lx,Dx_in,Dx_o,τx} where Lx represents task length, Dx_in represents request size, Dx_o represents response size, τx represents the maximum delay a task can tolerate. It is also considered that there are M fog servers FS={FS1,FS2,FS3,FS4,…FSM} and N cloud servers CS={CS1,CS2,CS3,CS4,…CSN} . Let there are R computation servers deployed in an area S={S1,S2,S3,S4,…SR} where Rϵ{CS,FS} . FS have a higher computing capacity than IoT devices, but less than cloud servers CCIoTCPU<CCfogCPU<CCcloudCPU . We’ll utilize a binary version of CO in which a computational task is either calculated locally or submitted to a remote computing server for processing. A task cannot be divided and must be accomplished entirely on a single server. Our objective is to find the best computational server for tasks to be offloaded based on the multiobjective optimization problem.

3.1 Computation Model

This model is used to compute computational time, which is the time it takes to execute a task. It is determined by the computational capabilities of the remote server or local device and the communication medium’s latency. It is calculated using Eq. (1).

CTi,ju=ETi,ju+Li,jwherejϵS,iϵX (1)

Here CTi,ju represents the computational time of task i generated from device u and executed on device j. Here j can be the IoT device itself, or it can be a remote server belonging to set S. ETi,ju represents the execution time of task i, which is calculated as ETi,ju=Lx/CCjCPU .

The latency between end device i and the remote computing server j is calculated on the basis of the network’s bandwidth and distance.

Li,j=PDi,j+SDi,j∀(i,j) (2)

Here PDi,j denotes propagation delay and SDi,j denotes serialization delay. The PDi,j is the ratio of distance ( Di,j ) between device i and j and bandwidth ( BWi,j ) of the network i.e., Di,j/BWi,j . Where Di,j=(Xj−Xi)2+(Yj−Yi)2 in 2-D area (X,Y) . However, SDi,j is calculated by dividing the size of the task by the transmission rate i.e., Lx/Tr . Here we consider two cases for the calculation of computational time.

Case1: Local Execution

Here the task is processed at the end device itself, so the computational time is calculated using Eq. (3).

CTi,ju=ETi,ju (3)

The task is processed locally, so the latency ( Li,j=0 ) is zero.

Case 2: Remote Execution

The computational task is forwarded to the fog or cloud layer depending on the task’s latency and resource sensitivity. The computational time required to execute an application on a remote server is calculated using Eq. (4).

CTi,jr=ETi,ju+Li,j (4)

3.2 Energy Consumption Model

Two factors primarily determine the energy utilization: (i) computational energy, which is consumed when the device is busy in executing the task, while (ii) transmission energy is the energy consumed during to and fro transmission of the task to a remote computational server. The energy consumed during execution is calculated as follows:

Case1: Local Execution

The energy consumed when a task executes at a local device is calculated using Eq. (5).

ECi,ju=ETi,ju∗Erc (5)

where Erc represents the energy consumption rate while executing a task.

Case 2: Remote Execution

The energy consumed when a task executes at a remote device is calculated using Eq. (6).

ECi,jr=Dx_inTr∗Er_upc+Dx_oTr ∗ Er_downc+ETi,ju∗Erc (6)

ECi,jr represents energy consumption when a task executes at the remote device. In Eq. (6) Er_upc/Er_downc represents the rate of energy consumption for sending the request and receiving back the results.

3.3 Problem Definition

MinF(x)=(F1(x),F2(x)) (7)

where F1(x) refers computational time

F2(x) refers energy consumption

F1(x)=∑i=ox⁡(CTi,ju+CTi,jr)

F2(x)=∑i=ox⁡(ECi,ju+ECi,jr)

Subject to

C1:Tx,i,j=1,Tx,i,jϵ[0,1] // Constraint is used for binary offloading

4  MOGWO for Computation Offloading Problem

4.1 Multiobjective Optimization Problem

Multiobjective optimization (MOO), which was introduced by Vilfredo Pareto, determines the best solution values for multiple goals [19]. The MOO’s use is justified by the fact that complex equations are no longer required for problem-solving. Objective functions here are vectorized. The vector corresponding to an objective function is also a function of the solution vector. Moreover, multiple solutions exist corresponding to each function in the problem definition. The two techniques, i.e., Pareto technique and scalarization, are used for solving the MOO problem. However, these two techniques are different to each other. Suppose we consider different desired outcomes and performance matrices. The Pareto technique then gives a conciliation solution (trade-off) that may be represented as a Pareto front (PF) [31]. The scalarization technique produces a scalar function, which is then implemented using the fitness function. So, to tackle the described problem here, we employed the MOGWO approach.

4.2 GWO Algorithm

GWO is a nature-inspired meta-heuristic approach motivated by the grey wolf’s hunting style and social hierarchy [30]. Grey wolves live in packs of five to twelve members. Four rankings are assigned to wolves (α,β,δ,ω) in a particular pack. α wolf is the decision-makers about hunting, living places etc. The β,δ,ω wolves give feedback to the alpha wolf and aid in decision-making. The best candidate for an optimal solution is α . In contrast, β and δ are the second and third best solutions. Grey wolves hunt by encircling their victim and attacking it from all sides. The first phase of encircling the prey is represented using Eqs. (8) and (9)

D→=|Cv→.XP→(t)−XG→(t)| (8)

XG→(t+1)=|XP→(t)−Av→.D→| (9)

where D→ denotes distance-vector, X→P indicates the prey’s location, t represents the current iteration, X→G denotes the grey wolf’s location and Av→ , Cv→ represents the coefficient vectors calculated using Eqs. (10) and (11):

Av→=2.a→.r1→−a→(10)

Cv→=2.r2→(11)

where r1→andr2→ are random vectors with value between [0, 1]. The value of a→ decreases from 2 to 0 during the course of the experiment. Other wolves alter their positions based on α,β,andδ wolves. The hunting behaviour of grey wolves is simulated using Eqs. (12)–(18).

Dα→=|Cv1→.Xα→−XG→(t)| (12)

Dβ→=|Cv2→.Xβ→−XG→(t)| (13)

Dδ→=|Cv3→.Xδ→−XG→(t)| (14)

Position if we follow alpha, then

X1→=|Xα→−Av1→.Dα→| (15)

Position if we follow beta, then

X2→=|Xβ→−Av2→.Dβ→| (16)

Position if we follow delta, then

X3→=|Xδ→−Av3→.Dδ→| (17)

The final position of the wolf is calculated using Eq. (18).

XG→(t+1)=(X1→+X2→+X3→)/3 (18)

The final stage of attacking the prey has been formulated using the vector a→ . The value of a→ lies between [−a,a], and its value decreases from 2 to 0 during the iteration and is calculated using Eq. (19) as follows:

a→=2−t.2maxIter(19)

The maxIter represents the total number of iterations, t indicates the current iteration.

4.3 Multiobjective Grey Wolf Optimization Technique

The GWO approach was developed to tackle one optimization problem at a time. Because of this, it cannot be used to solve multiobjective problems directly. MOGWO was proposed in 2016 by Mirjalili et al. [32]. Although it has been used for a variety of real-world problems, it has yet to be utilized to offload issues in FC. It has good exploration and exploitation and has a faster convergence rate with fewer parameter tuning. Therefore MOGWO is used to solve CO problems in FC. Two new mechanisms were integrated into the original GWO. Initially, storage was utilized to store the solutions called archives. Then a leader selection strategy is utilized to select the first, second, and third leaders from the archive.

Here we assume that all IoT devices’ probable CO decisions create a single position for the grey wolf as follows:

Step 1: Randomly initialize the wolf population

GW=[GW1GW2GW3…GWn]=[GW1,1..GW1,dGW2,1..GW2,dGW3,1..GW3,d......GWn,1..GWn,d]

Here n represents the number of wolves, and d represents the dimension

Step 2: Calculate the objective function value of the wolf population. For each wolf, there are two objective functions to evaluate, i.e., F1 and F2 .

FW=[F1(GW1)F2(GW1)F1(GW2)F2(GW2)....F1(GWn)F2(GWn)]

FW=TimeEnergyGW120.7GW230.6GW330.7GW440.5GW550.45GW650.6

It can be clearly observed that GW1 dominate GW3 ; GW2 dominate GW3 and GW6 ; GW4 dominate GW6 ; and GW5 dominate GW6 . Here { GW1,GW2,GW4 , and GW5 } form a non-dominating set and are also called Pareto optimal front. However, no clear winner is identified. When two solutions have the same non-dominated rank, the one in a less crowded region is selected.

FW=TimeEnergyGW120.7GW230.6GW440.5GW550.45F1(GWmax)=5F1(GWmin)=2F2(GWmax)=0.7F2(GWmin)=0.45

The crowding degree (CD) of all the non-dominated solutions is computed using Eq. (20).

CDi=∑j=12fji+1−fji−1fjmax−fjmin (20)

where i denotes the ith solution, all the values are arranged in decreasing order of CD and represented as set St . The optimal solution is then chosen using the roulette wheel selection method. It does not ensure that the fittest solution will be chosen, but it does increase the probability that it will be chosen [33]. The probability of selection is calculated using Eq. (21).

P(Fi|St)=k−i+1∑j=1k⁡j (21)

where Fi is the destination function of the ith solution, St is the set of solutions, and k denotes the number of the St .

4.4 E-MOGWO for Computation Offloading in Fog Computing

Since the solution set of the gravity reference point technique is more evenly distributed, integrating it with MOGWO can boost its performance even more. E-MOGWO is a new hybrid method that combines the gravity reference point technique with MOGWO as shown in Fig. 1.

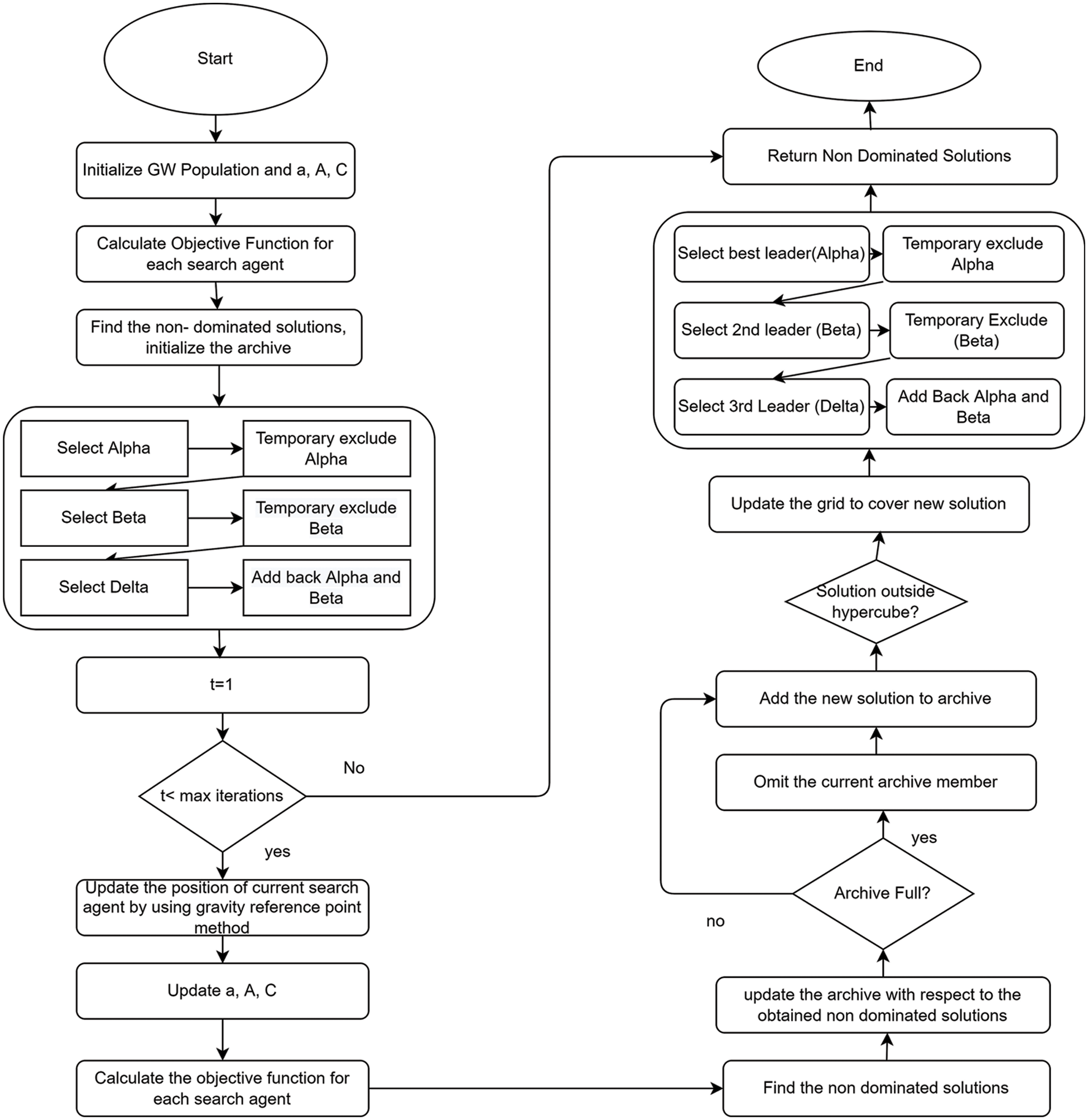
Figure 1: Flow chart of E-MOGWO

The weight coefficient increases when the gravity reference point is closer to the current solution. This work defines two functions of computational time and energy consumption usage. When F1(X) takes the min value, then the resultant solution is called X1 . When F2(X) takes the min value, then the resultant solution is called X2 . When X=X1 then F1(X) and F2(X) are calculated based on Eq. (7), known as CT1 and EC1 . When X=X2 The value corresponding to functions F1(X) and F2(X) are called CT2 and EC2 . Then compute the weight and distance parameter for each set as follows:

Calculate the energy consumption and computational time of the current solution, and then estimate the distance between X1,X2 and the current solution.

D1=(CT−CT1)2+(EC−EC1)2 (22)

D2=(CT−CT2)2+(EC−EC2)2 (23)

Compute the weight parameters

WT1=D1+D2−D1D1+D2=D2D1+D2 (24)

WT2=D1+D2−D2D1+D2=D1D1+D2 (25)

The current solution is updated using Eq. (28).

D1=|Cv→.X1→−X→(t)| (26)

D2=|Cv→.X2→−X→(t)| (27)

X→(t+1)=WT1∗|Xt→−Av→.D1→|+WT2∗|Xt→−A→v.Dα|→ (28)

5  Results and Analysis

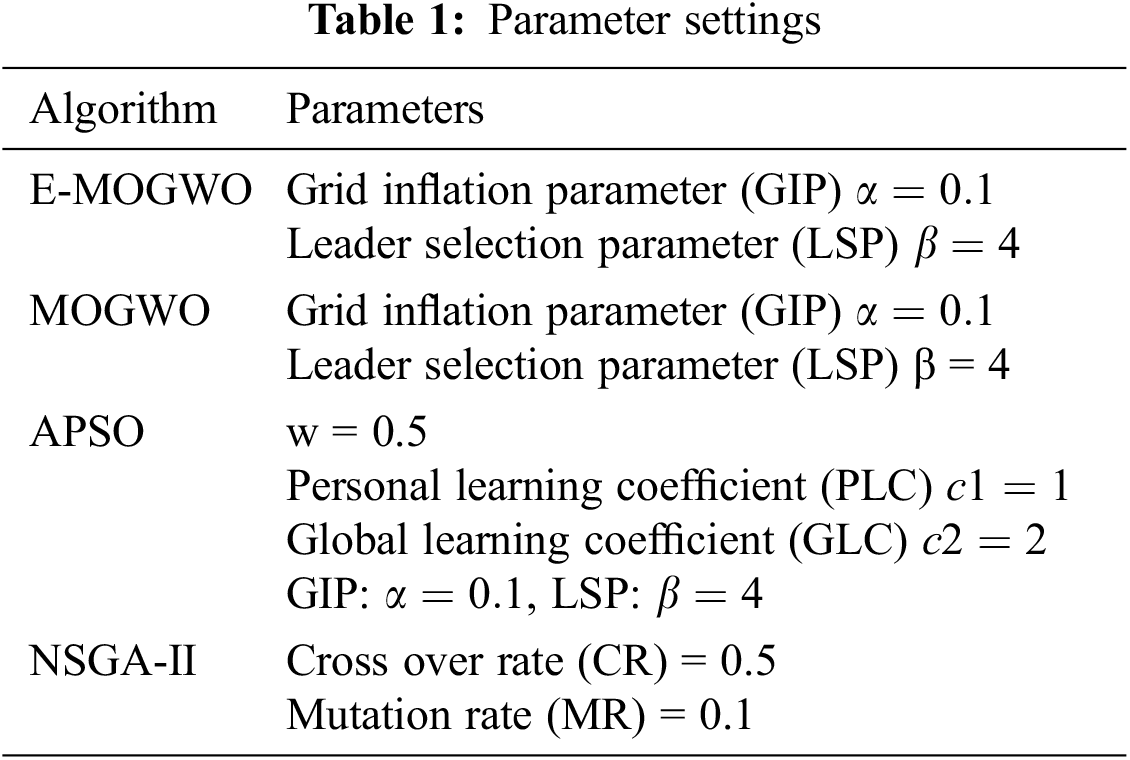
This part presents a simulation scenario for evaluating the proposed algorithm’s performance. The simulation has been performed using a pure edge simulator. All experiments are run on a system with an intel i5 processor, 8 GB RAM, 1TB hard disk and windows 10 operating system. The proposed E-MOGWO is compared with two multiobjective metaheuristic algorithms APSO [34] and NSGA-II [35]. The parameters of each algorithm are settled according to related references, as shown in Tab. 1. For the experiment, 100 search agents are investigated for 50 iterations. Each algorithm runs independently 50 times. The archive size of 50 is considered for all algorithms.

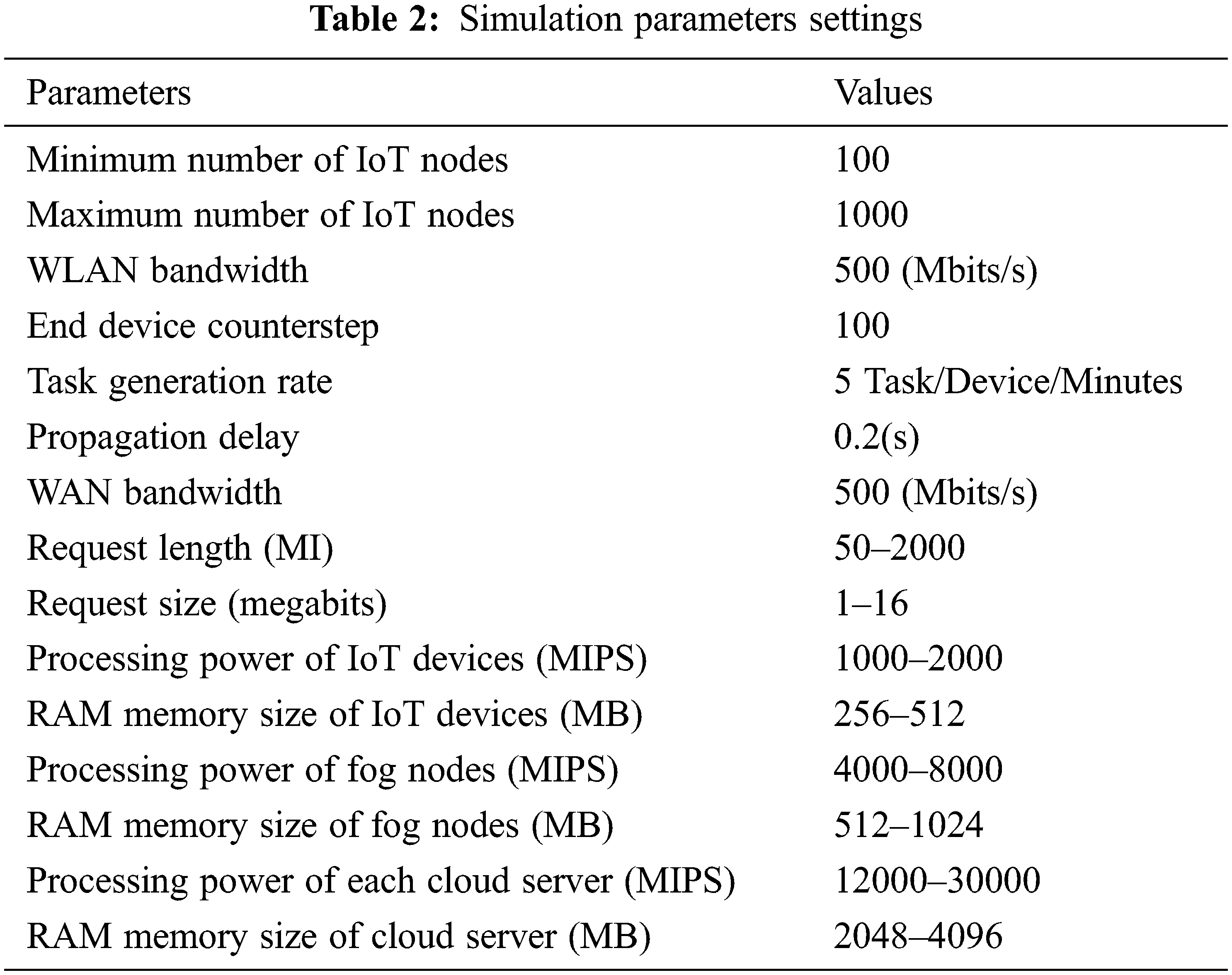
The simulator has been designed to simulate a three-layer system, i.e., IoT devices, fog server and cloud server. In the first layer, three different types of IoT applications of health, intelligent transport systems and augmentation reality are deployed on IoT devices. Each device generates a task according to deployed application and task generation rate. The experimental setup of IoT devices, fog nodes and cloud are shown in Tab. 2.

Comparison Analysis: To evaluate the proposed technique, We analyzed energy consumption, computational time, the overall percentage of successful tasks, and the number of tasks completed at each level (local, fog, cloud).

5.1 Computational Time

It is the time required to execute a task either on a local IoT device or a fog or cloud server. It is defined by both the time required to complete a task on the device and the time required to transmit the task to the remote server. A comparative analysis of computational time is represented using Fig. 2. The performance improvement rate (PIR) [36] has been calculated to determine the improvement of the proposed algorithm over the existing algorithm using Eq. (29).

PIR(%)=(∑old⁡Value−∑New⁡Value∑old⁡Value)∗100 (29)

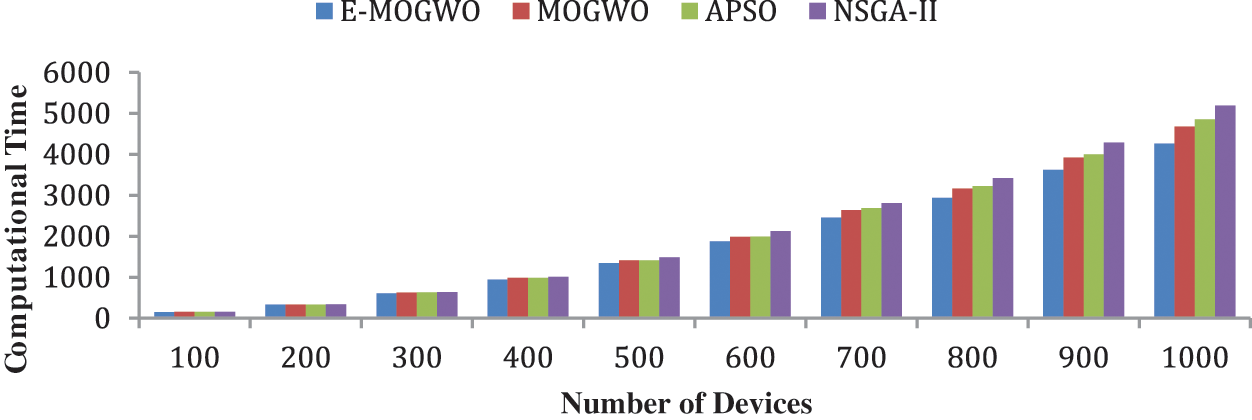
Figure 2: Comparison of computational time

E-MOGWO algorithm reduces computational time by 5.10% over MOGWO, 6.10% over APSO and 9.72% over NSGA-II, as presented in Tab. 3.

5.2 Energy Consumption

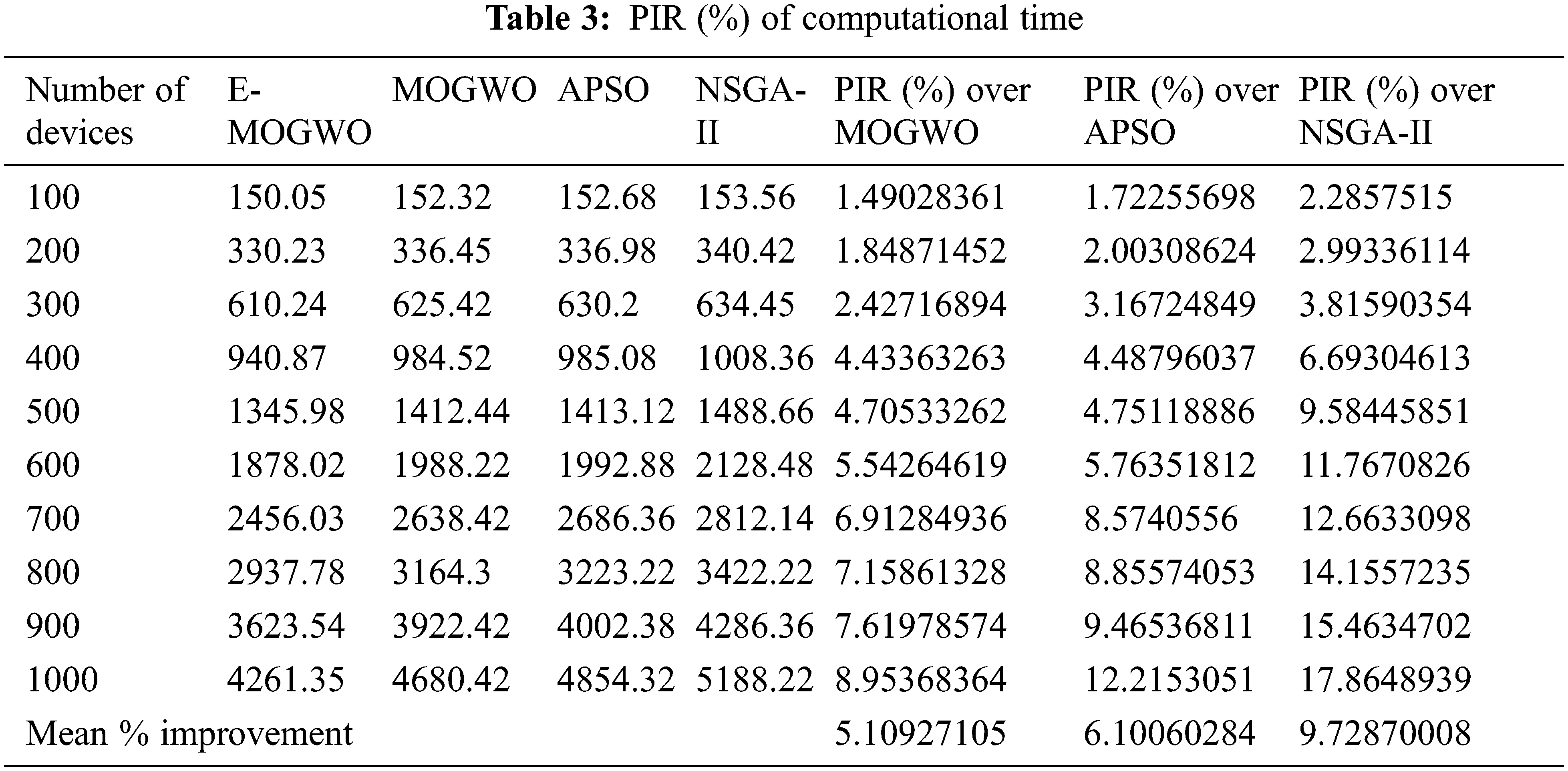
The total amount of energy used is the sum of computational and transmission energy. Most tasks in the simulation are handled at the fog layer or local device rather than the cloud layer. The cloud is only used for the most resource-intensive tasks. As fog nodes are deployed close to the end device, they assist in reducing transmission energy and total energy usage.

The proposed E-MOGWO algorithm significantly improved energy consumption over MOGWO, APSO and NSGA-II Algorithms. This algorithm reduces energy usage by 15.10% over MOGWO, 17.29% over APSO, and 21.91% over NSGA-II, respectively, as presented in Tab. 4. A comparative analysis of energy consumption is displayed in Fig. 3.

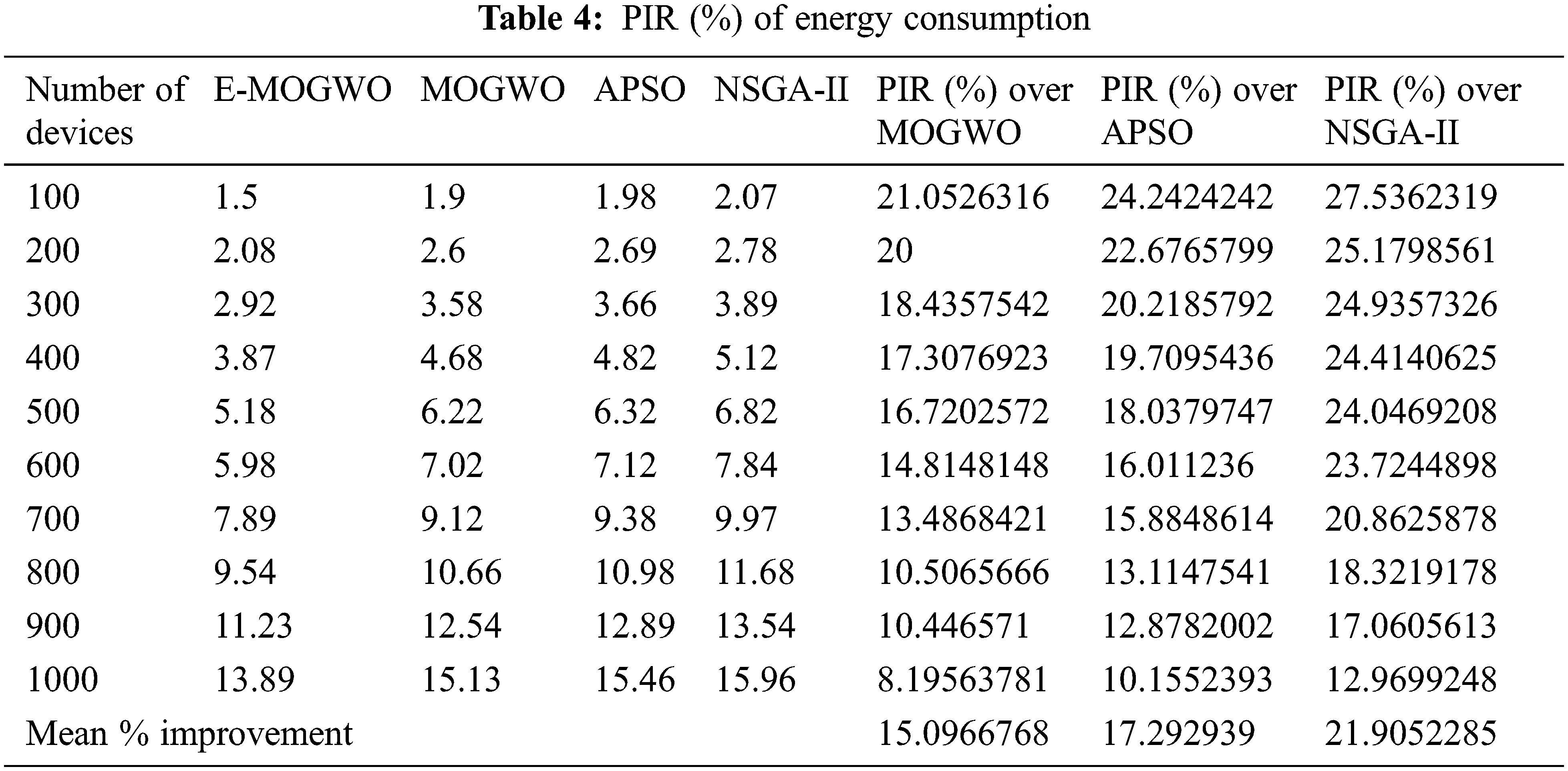
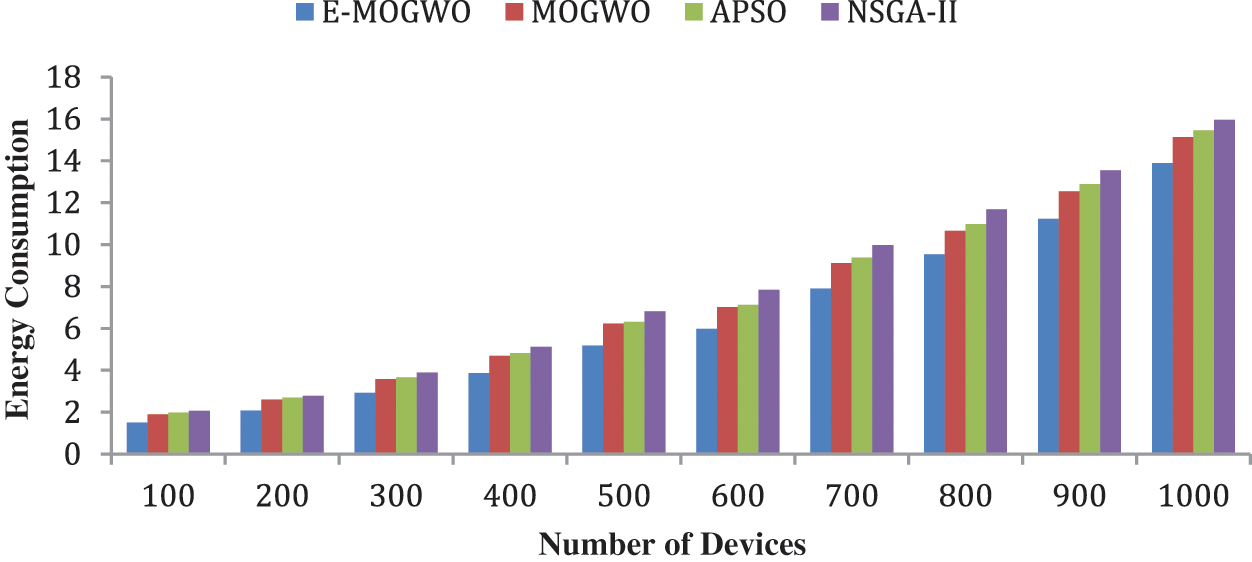
Figure 3: Comparison of energy consumption

5.3 Number of Tasks Successfully Executed

The analysis of the percentage of the number of tasks successfully executed using the various algorithms is presented in Fig. 4. The percentage of tasks successfully executed by E-MOGWO is 0.63% more than MOGWO, 1.06% more than APSO and 1.80% more than NSGA-II. A task may fail due to high delay, unavailability of resources and low remaining battery. The task failure rate in E-MOGWO is lower than in other algorithms. Fig. 5 shows the number of tasks executed at different levels either to the fog node, cloud node and IoT devices.

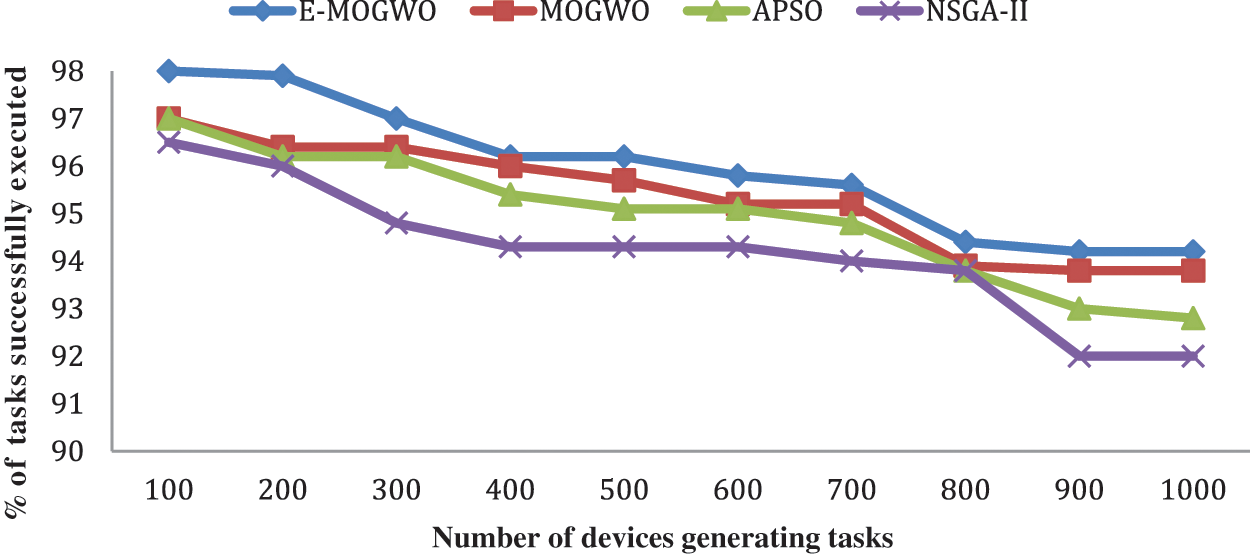
Figure 4: Comparison of percentage of tasks successfully executed

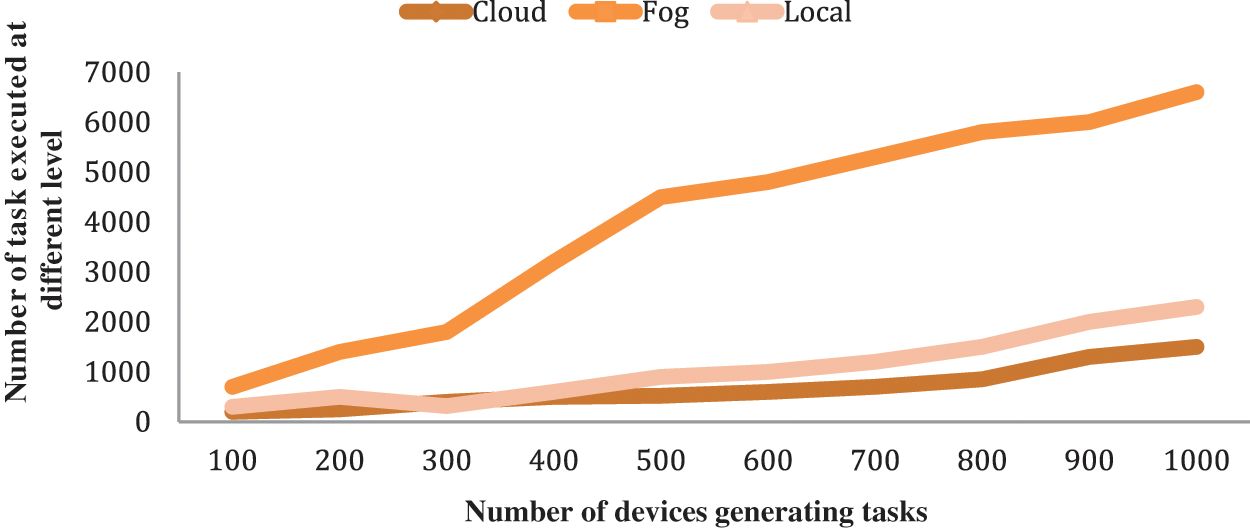
Figure 5: Number of tasks executed at different levels

E-MOGWO provides good results than other algorithms. Because this algorithm has a good balance between exploration and exploitation, which allows the escape of local optima stagnation. This method also has fewer parameters than others, which is advantageous. Moreover, it has only one position vector compared to APSO, which has two vectors, i.e., velocity and position. Hence it requires less memory space. Moreover, when the total number of iterations is finished, the obtained solutions are stored as non-dominated solutions set. These are chosen from the less crowded region of the solution space using a leader selection algorithm. APSO and NSGA-II, on the other hand, save previously discovered solutions, resulting in solution duplication and premature convergence due to the rapid loss of diversity. This can be avoided with a grid mechanism that removes the current solution from the archive when it fills up and replaces it with a better one. The computational complexity of E-MOGWO is O(MN2 ) where N is the population size, M is the number of objectives, and the complexity is the same as other well-known multiobjective algorithms.

6  Conclusion

A metaheuristic-based multiobjective offloading technique is proposed in this work. The optimal computing destination for each task is selected based on minimum energy consumption and minimum computational time. The E-MOGWO algorithm allocates delay-sensitive applications to local devices or fog nodes. In contrast, resource-sensitive applications are assigned to the fog or cloud layers. It decreases the energy consumption and processing time of offloaded applications, as specified in the results section. The simulation results showed that the proposed offloading approach reduces energy consumption by 15.10% over MOGWO, 17.29% over APSO, and 21.91% over NSGA-II, and reduces computational time by 5.10% over MOGWO, 6.10% over APSO and 9.72% over NSGA-II. In the future, we will be examining the alternative service level agreement constraints and other parameters to enhance the algorithm’s performance further.

Acknowledgement: Authors also acknowledge the CSE Department of Deenbandhu Chhotu Ram University of Science and Technology for providing various facilities in the research lab.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding this research work.

References

 1.  S. R. Hassan, I. Ahmad, J. Nebhen, A. U. Rehman, M. Shafiq et al., “Design of latency-aware IoT modules in heterogeneous fog-cloud computing networks,” Computers, Materials and Continua, vol. 70, no. 3, pp. 6057–6072, 2022. [Google Scholar]

 2.  W. Paper, “Prepare to succeed with the internet of things,” CISCO, White Paper, pp. 1–9, 2017. [Google Scholar]

 3.  M. G. R. Alam, M. M. Hassan, M. Zi. Uddin, A. Almogren and G. Fortino, “Autonomic computation offloading in mobile edge for IoT applications,” Future Generation Computer Systems, vol. 90, pp. 149–157, 2019. [Google Scholar]

 4.  J. Fang, J. Shi, S. Lu, M. Zhang and Z. Ye, “An efficient computation offloading strategy with mobile edge computing for IoT,” Micromachines, vol. 12, no. 2, pp. 204, 2021. [Google Scholar]

 5.  D. D. Lieira, M. S. Quessada, A. L. Cristiani, and R. I. Meneguette, “Algorithm for 5G resource management optimization in edge computing,” IEEE, vol. 19, no. 10, pp. 1772–1780, 2020. [Google Scholar]

 6.  J. Yadav and S. Sangwan, “Computation offloading in fog computing : Use cases, techniques & issues,” Turkish Journal of Qualitative Enquiry, vol. 12, no. 6, pp. 1480–1488, 2021. [Google Scholar]

 7.  X. Gao, S. Member, X. Huang, S. Member, S. Bian et al., “PORA : Predictive offloading and resource allocation in dynamic fog computing systems,” IEEE Internet of Things Journal, vol. 7, no. 1, pp. 72–87, 2019. [Google Scholar]

 8.  S. R. Hassan, I. Ahmad, S. Ahmad, A. Alfaify and M. Shafiq, “Remote pain monitoring using fog computing for e-healthcare: An efficient architecture,” Sensors (Switzerland), vol. 20, no. 22, pp. 1–21, 2020. [Google Scholar]

 9.  L. F. Bittencourt, J. D. Montes, R. Buyya, O. F. Rana and M. Parashar, “Mobility-aware application scheduling in fog computing,” IEEE Cloud Computing, vol. 4, no. 2, pp. 26–35, 2017. [Google Scholar]

10. K. Gasmi, S. Dilek, S. Tosun and S. Ozdemir, “A survey on computation offloading and service placement in fog computing-based IoT,” The Journal of Supercomputing, vol. 78, no. 2, 1983–2014, 2022. [Google Scholar]

11. G. Baranwal and D. P. Vidyarthi, “Computation offloading model for smart factory,” Journal of Ambient Intelligence and Humanized Computing, vol. 12, no. 8, pp. 8305–8318, 2021. [Google Scholar]

12. M. M. Alqarni, A. Cherif and E. Alkayal, “A survey of computational offloading in cloud/edge-based architectures: Strategies, optimization models and challenges,” KSII Transactions on Internet and Information Systems, vol. 15, no. 3, pp. 952–973, 2021. [Google Scholar]

13. R. C. Palacios, “A systematic literature review of fog computing,” in Proc. the Norwegian Conf. on Information Systems, Bergen, vol. 24, no. 1, pp. 28–30, 2016. [Google Scholar]

14. M. Aazam, S. Zeadally and K. A. Harras, “Offloading in fog computing for IoT: Review, enabling technologies, and research opportunities,” Future Generation Computer Systems, vol. 87, pp. 278–289, 2018. [Google Scholar]

15. A. Bhattacharya and P. De, “A survey of adaptation techniques in computation offloading,” Journal of Network and Computer Applications, vol. 78, pp. 97–115, 2017. [Google Scholar]

16. P. Habibi, M. Farhoudi, S. Kazemian, S. Khorsandi and A. Leon-Garcia, “Fog computing: A comprehensive architectural survey,” IEEE Access, vol. 8, pp. 69105–69133, 2020. [Google Scholar]

17. A. Yousefpour, G. Ishigaki, R. Gour and J. P. Jue, “On reducing IoT service delay via fog offloading,” IEEE Internet of Things Journal, vol. 5, no. 2, pp. 998–1010, 2018. [Google Scholar]

18. I. Ullah and H. Y. Youn, “Task classification and scheduling based on K-means clustering for edge computing,” Wireless Personal Communications, vol. 113, no. 4, pp. 2611–2624, 2020. [Google Scholar]

19. L. Liu, Z. Chang, X. Guo, S. Mao and T. Ristaniemi, “Multiobjective optimization for computation offloading in fog computing,” IEEE Internet of Things Journal, vol. 5, no. 1, pp. 283–294, 2018. [Google Scholar]

20. N. Shan, Y. Li and X. Cui, “A multilevel optimization framework for computation offloading in mobile edge computing,” Mathematical Problems in Engineering, vol. 2020, pp. 1523–1534, 2020. [Google Scholar]

21. Z. Xiong, S. Feng, W. Wang, D. Niyato, P. Wang et al., “Cloud/Fog computing resource management and pricing for blockchain networks,” IEEE Internet of Things Journal, vol. 6, no. 3, pp. 4585–4600, 2018. [Google Scholar]

22. H. S. Mansouri and V. W. S. Wong, “Hierarchical fog-cloud computing for IoT systems: A computation offloading game,” IEEE Internet of Things Journal, vol. 5, no. 4, pp. 3246–3257, 2018. [Google Scholar]

23. L. Dong, M. N. Satpute, J. Shan, B. Liu, Y. Yu et al., “Computation offloading for mobile-edge computing with multi-user,” in Proc. Int. Conf. on Distributed Computing Systems, Dallas, TX, USA, vol. 2019-July, pp. 841–850, 2019. [Google Scholar]

24. E. Balevi and R. D. Gitlin, “A clustering algorithm that maximizes throughput in 5G heterogeneous F-RAN networks,” in Proc. IEEE Int. Conf. on Communications, Kansas City, MO, USA, vol. 2018-May, 2018. [Google Scholar]

25. M. Kumar and S. Suman, “Scheduling in IaaS cloud computing environment using sailfish optimization algorithm,” Trends in Sciences, vol. 19, no. 10, pp. 4204, 2022. [Google Scholar]

26. M. K. Hussein and M. H. Mousa, “Efficient task offloading for IoT-based applications in fog computing using ant colony optimization,” IEEE Access, vol. 8, pp. 37191–37201, 2020. [Google Scholar]

27. R. Ezhilarasie, M. S. Reddy and A. Umamakeswari, “A new hybrid adaptive GA-PSO computation offloading algorithm for IoT and CPS context appplication,” Journal of Intelligent & Fuzzy Systems, vol. 36, no. 5, pp. 4105–4113, 2019. [Google Scholar]

28. S. A. Zakaryia, S. A. Ahmed and M. K. Hussein, “Evolutionary offloading in an edge environment,” Egyptian Informatics Journal, vol. 22, no. 3, pp. 257–267, 2020. [Google Scholar]

29. K. Peng, “An energy and cost-aware computation offloading method for workflow applications in mobile edge computing,” Eurasip Journal on Wireless Communications and Networking, vol. 2019, no. 1, pp. 207, 2019. [Google Scholar]

30. K. Lin, S. Pankaj and D. Wang, “Task offloading and resource allocation for edge-of-things computing on smart healthcare systems,” Computers and Electrical Engineering, vol. 72, pp. 348–360, 2018. [Google Scholar]

31. A. Khalili and S. M. Babamir, “Optimal scheduling workflows in cloud computing environment using pareto-based grey wolf optimizer,” Concurrency Computation, vol. 29, no. 11, pp. 1–11, 2017. [Google Scholar]

32. S. Mirjalili, S. Saremi, S. M. Mirjalili and L. D. S. Coelho, “Multiobjective grey wolf optimizer: A novel algorithm for multi-criterion optimization,” Expert Systems with Applications, vol. 47, pp. 106–119, 2016. [Google Scholar]

33. O. Shahryari, H. Pedram and V. Khajehvand, “Energy and task completion time trade-off for task offloading in fog-enabled IoT networks,” Pervasive and Mobile Computing, vol. 74, pp. 101395, 2021. [Google Scholar]

34. M. Adhikari, S. N. Srirama and T. Amgoth, “Application offloading strategy for hierarchical fog environment through swarm optimization,” IEEE Internet of Things Journal, vol. 7, no. 5, pp. 4317–4328, 2020. [Google Scholar]

35. M. Keshavarznejad, “Delay-aware optimization of energy consumption for task offloading in fog environments using metaheuristic algorithms,” Cluster Computing, vol. 24, no. 3, pp. 1825–1853, 2021. [Google Scholar]

36. M. Kumar and S. Sangwan, “Hybrid cuckoo search algorithm for scheduling in cloud computing,” Computers, Materials and Continua, vol. 71, no. 1, pp. 1641–1660, 2022. [Google Scholar]