Weighted PageRank Algorithm Search Engine Ranking Model for Web Pages

1  Introduction

The World Wide Web (WWW) is comprised of billions of web pages containing massive amounts of data. Users can use search engines to find useful information among the vast amount of data available. The current search engines, on the other hand, do not fully satisfy the demand for high-quality information search services. This creates difficulties in retrieving information, and several ranking systems are used to navigate through the search results. For ordering web pages, page rank algorithms are well recognised. Ranking algorithms have evolved into a useful tool for sorting and retrieving relevant web pages based on the user’s interests.

To make use of a wide range of data from the internet, time and money are required to collect and analyse data. Extracting useful information from web data and producing benefit content necessitates data extraction, transformation, and rework. Web crawlers have recently gained popularity as a method of extracting vital information from a website. Because their web crawling behaviour is similar to that of a spider crawling through a web, web crawlers are also known as web spiders. The web crawler regularly visits the web server, gathers vital information on every appended homepage, automates the process of following each link and gathering information, analyses the content of each online page, and attaches to each web page one by one to collect the data.

The Weighted Page Ranking (WPR) is a metric that measures how well web pages are ranked. Web structure and content mining techniques are combined in this manner. The importance of a page is determined by web structure mining, while the relevancy of a page is determined by web content mining. The number of pages that point to or are referred to by a page is defined as its popularity here. It can be computed using the page’s number of in links and out links. Relevancy refers to the page’s compatibility with the executed query. A page becomes more relevant if it is maximally matched to the query.

To address the issue of bias, this study suggests a new rating set of criteria based entirely on the PageRank (PR) set of rules, which is one of the most widely used weighted page ranking algorithms. To test the relationship between these various variables, we present weighted PageRank algorithms. In three separate studies, the Weighted Page Rank (WPR) model was utilised to compare the ranking scores of documents and pages based on one or more user preference criteria. The outcomes of the Weighted Page Rank model revealed that ranking based on a variety of criteria beat rankings based on a single criterion, and that some criteria had a greater impact on ranking outcomes than others. The model used the top 7 criteria for data acquisition and retrieving outcomes whereas totally disregarding the other metrics that could be significant with other needs and requirements. It included an evaluation of relevant related works with identifying the top page ranking factors and more towards achieving high application performance and obtaining the maximum mark for each page result.

1.1 Limitations of Weighted PageRank (WPR)

•   By utilising the web’s structure, the Weighted PageRank (WPR) algorithm delivers vital information about a particular query. While some pages may be irrelevant to a certain query, it nevertheless achieves the highest ranking due to the large number of inbound and outbound links.

•   The pages’ relevance to a certain query is less predetermined.

•   This method is primarily based on the number of inbound and outbound links.

1.2 Comparison of Weighted Page Rank and Page Rank

To evaluate the Weighted Page Rank (WPR) to the antique PageRank, they categorised the question end result pages into 4 organizations primarily based totally on their relevance to the furnished question. This is the way it works: Very Relevant Pages (RP) are pages that consist of crucial statistics on a selected topic.

•   Related Pages are pages that are relevant to a query but do not contain crucial information.

•   Weak Relevant Pages (WRP) are pages with query keywords but insufficient information.

•   Irrelevant Pages (IR) are those with no relevant content or query keywords.

On the basis of the user’s query, both PageRank and weighted PageRank (WPR) return rated pages in category order. As a result, users care about the amount of relevant sites in the resulting list, as well as their ranking. The Relevance Rule was used to determine the relevancy value of each page in the list of pages. As a result, Weighted Page Rank differs from PageRank.

2  Literature Survey

The Weighted Page Rank algorithm prioritises inbound and outbound connections, while the standard Page Rank algorithm prioritises link number. [1] It also looks at the most recent studies on how to incorporate user behaviour and interests into page rank algorithms to improve page rank algorithms. [2] Utilizing the suggested technique on various datasets, Average, median, and mid-range are a subset of basic weighting methods that produce more efficient weights when compared to the recently introduced sophisticated weighting methods. [3] Classifiers were created and trained in this research to categorise an unknown sample (web page of page adjustment). With classifier accuracy ranging from 54.59% to 69.67%, the findings imply that machine learning can be utilised to predict the degree of web page adaption to SEO recommendations. [4] Suggested a graph-based strategy for classifying communities into one of three categories, as well as identifying critical characteristics that determine degree compression. Iteratively merging vertices with degrees of 1 or 2 into higher-degree neighbours compresses a graph. The number of communities and initial community seeds in a compressed social network are determined by combining these two variables. [5] The author examines three different strategies in depth: centrality-based node ranking, PageRank algorithm, and HITS algorithm. These sample techniques’ most recent extensions and advancements, as well as a number of major application areas. Based on our evaluation of current literatures, we want to suggest some exciting new research possibilities. The conclusions of this research are both educational and valuable to academic and industry groups.

The suggested technique to detect malicious web pages makes use of a 30-parameter feature vector. The recommended deep learning model employs Adam Optimizer and a List smart approach to discriminate between bogus and legal websites. [6] The proposed method outperforms traditional machine learning algorithms such as Support Vector Machine (SVM), Adaboost, and AdaRank. [7] We created a model that combines BiLSTM and Efficient Net for detecting website defacement. The proposed approach takes care of the text content and page screenshot photos, two important components of web pages. The proposed version beats current tactics on maximum parameters, in line with experimental consequences on a dataset of over 96,000 internet pages. [8] In order to rank the top N influential nodes in a network, Weighted Mixed Degree Decomposition (WMDD) uses input metrics such underlying relationship strength, exhausted degree, and k-shell value. The SIR epidemic model is used to test the proposed technique on both simulated network and real-world datasets. A weight parameter outperforms existing approaches and enables more precise assessment of node influence. [9] The evaluation-based weighted PageRank (EWPR) algorithm was devised by him as a reputation ranking indicator. Two existing approaches are tested against the evaluation-based weighted PageRank algorithm using OpenStreetMap as an example. The findings suggest that the algorithms used to understand VGI contributors’ reputations may also be used to members of online sites and social networks. [10] The main characteristic of a measure of centrality for multiplex networks has been devised and validated using a real numerical example, with the key feature of taking into consideration both graph connections and a collection of data connected with the nodes included in each layer. The changes in conditions observed in each case from the most central city regions demonstrate the advantage and utility of the suggested strategy.

When the network is vast, ranking nodes in an uncertain graph takes a lengthy time due to the large number of alternative universes. Reference [11] We show that for highly rated nodes, the suggested method surpasses the s (avg) approach in terms of precision, and that it could be a viable substitute. In terms of sample size, the p (avg) technique outperforms the s-avg method by a factor of ten. Reference [12] Analyse, compare, and contrast the various centrality measurements employed in a city network. One of these indicators has the virtue of being able to cover a narrow range of values. A new metric has been proposed because this is inconvenient when working with massive data networks. Reference [13] It was suggested that a mechanism for detecting copied profiles be developed. The Hardtop platform is used to implement it. The first stage’s PageRank algorithm’s conclusion is utilised to rank the profiles in this technique. Our findings were positive, and we were able to precisely detect all duplicated profiles in several circumstances. The main point of this article is that it takes into account both the connectedness of the graphs and the data included in each layer linked with the nodes. The similarities and differences between the conditions as seen from the most central city regions in each example indicate the advantage and utility of the suggested method. Reference [14] Proposed the “pairwise link prediction” job, which is tasked with identifying which nodes are most likely to create a triangle with a given edge. The definition of an edge’s neighbourhood, which has a startlingly large impact on empirical performance, is a major divergence from our previous work. According to Diffusion-based algorithms, their results are more trustworthy and less vulnerable to the type of graphs used. Reference [15] An automatic extraction approach based on network topology coincidence degree is proposed to successfully overcome the above concerns. To classify web text content, a search engine, a web crawler, and a hypertext tag are utilized, followed by dimensionality reduction. Reference [16] The Modified Salp Swam Optimization takes all homogeneous rankings and combines them to get a better optimized rating for each web page. The accuracy and performance measure of the modified Salp Swarm algorithm reveal that it outperforms existing ranking algorithms. Reference [17,18] Searching with page ranking algorithms does not yield the required results. To address this issue, a novel meta search engine is proposed that use a similarity measurement function to identify the relevancy of a web page to a given query and a document clustering technique to organize the results into separate groups. Reference [19] presents a new way to organize search results and describe which page is more significant when PageRank produces a disagreement between pages with the same rank. So the user can quickly and simply obtain more relevant and important results.

3  Proposed System

This paper addresses the issue of bias by proposing a new ranking algorithm based on the PageRank (PR) algorithm, which is one of the most widely used page ranking algorithms We propose weighted PageRank (WPR) algorithms to test the relationship between these various measures. We propose weighted PageRank algorithms (WPR) to measure the relationship between these factors. The Weighted Page Rank method makes use of the web's structure to transmit crucial information about a query. Despite the fact that some sites may be irrelevant to a specific query, it receives the greatest priority ranking due to its massive quantity of in-links and out-links. The pages' relevance to a single query is less consistent. The number of connected in- and out-links is an important part of this strategy.

3.1 Collection of Web Documents

Consumers now have access to a huge amount of information on the internet. This type of web material is spread among several portal sites. Web information, on the other hand, can only be gained through the user’s own registration and effort. Additionally, the only portions of the search that can be utilised to find current information are the title and introduction of the online publication. We present a method for extracting title, content, author, writing time, and other data from web documents by automating the crawler and extracting it without requiring the user’s interaction. The following are some things to think about when implementing a theme-driven crawler: For starters, there is no uniform formal structure for web documents. Second, key website address connections are usually found on the home page. As a result, the number of links on a web site’s main page should be reduced when searching for the location of an online document. The crawler proposed in this research makes use of the portal site’s random access module to address the aforementioned concerns and maximise the effect of gathering online documents. The crawler collects website URLs via the modules call on a regular basis, limits the size of the search queue to the number of links on the main page, and checks links breadth-first. However, if the website’s main page is in frame format, you’ll need to put in more effort. Because frames do not include genuine connection is established, it is necessary to examine a page that makes up a frame in order to find a web page with a link.

3.2 Weighted Page Rank Algorithms

The proposed weighted page rank (WPR) algorithm contains set of rules, its works on both online and offline web sites and records, and it makes use of a variety of retrieval techniques to assist the indexing and statistics extraction methods provide more relevant outcomes to customers while addressing most of the issues that plagued previous web page rating algorithms. [1,19] The version used the top seven standards for indexing and retrieving results, while ignoring other standards that may be important with different wishes and requirements, according to a review and evaluation of numerous related works with determining the high point web page rating elements and in the direction of achieving high processing overall performance and obtaining the very best rating for each web page result.

Winin(v,u) is the weight of link(v,u) depending on the number of in links of page u and all citation sections of page v.

Winin(v,u)=Iv∑pε(R)v⁡Ip (1)

More significant (popular) internet pages obtain higher page rank ranks in the weighted page rank approach. The number of inbound and outgoing links on a website determines its popularity, and each website is assigned a proportional web page rank grade. Eqs. (1) and (2) can be used to compute the popularity of each page using the in and out weights Winin(v,u) and Winout(v,u) , respectively.

Winout(v,u)=Ou∑pε(R)v⁡Op (2)

The variables Ou and Op represent the number of outbound connections on page u and page p , respectively. The symbol (R) v stands for the reference page list of page v. Winout(v,u) is a type of (v,u) that is the weight of link(v,u) derived from the number of out links on page u and all of the pages v reference pages.

Tab. 1 displays the relevancy scores for the Web pages.“Relevant pages in this table reflect both irrelevant pages and relevant pages”.

3.2.1 The Calculation of Page Rank

Instead of sharing the rank value of a page evenly across it’s out link pages, the Weighted PageRank assigns large rank values to more significant pages. The number of inbound and outward connections is used to determine popularity, which is written as Winin(v,u) and Winout(v,u) correspondingly. In Weighted PageRank, the distribution of links is uneven. The formula used to calculate the weighted PageRank is as follows:

PR(U)=(1−d)+d∑vεB(U)⁡PR(V)Win(U,V)Wout(U,V) (3)

The number of in links on pages U and V were used to make the calculation, with d = damping factor to set value 0 to 1, Win(U,V) =Weighted of link (U,V) , and d = damping factor to set value 0 to 1.

Win(U,V)=Iu∑p∈R(V)⁡IP (4)

3.2.2 Relevancy Calculator

The relevance calculator estimates a page’s relevance on the fly based on two factors: one shows the likelihood that the query will be answered in the page, and the other represents the query’s maximum match to the page. Reference [2] The weighted web page rank approach assigns higher page rank ranks to more significant (popular) websites. The number of inbound and outgoing links on a website determines its popularity, and each website is assigned a proportional web page rank grade.

Probabilityweight(PWi)=YiN (5)

The number of query phrases in the supplied document is denoted by the variable Yi . Content weight refers to how much weight a web page’s content has in query keywords. The letter N stands for the total number of phrases in the question. To calculate this factor, multiply the total frequency of all query strings and the frequencies of the highest possible query strings.

The maximum number of strings is determined so that each string represents a logical word combination in its own right. This yields the Content Weight Eq. (6).

RelevenceWeight(Wi)=XiM (6)

The total of all possible meaningful query strings in order is Xi , while the sum of all possible meaningful question strings in order is M. Fig. 1 shows the weighted PageRank (WPR) algorithm.

Figure 1: The Weighted Page Rank (WPR) calculation algorithm

3.2.3 Relevancy Rule

The category and location of a page in the page list determines its relevance to a query. The relevancy value increases as the result improves. The category and position of a page-relevance, lists k are determined:

k=∑i∈R(V)⁡(n−i)×Wi (7)

where I is the ith web page withinside the end result web page-listing R(p) , n is the primary n pages picked from the listing R(p) , and Wi is the burden of the web page i .

3.2.4 Computation

In large networks, we offer an efficient technique for computing the proposed Weighted Page Rank (WPR). The power iteration approach is the most common way to calculate classical Page Rank. As is well known, power iteration is sluggish, particularly for large and dense networks. [6,9] As a result, more sophisticated algorithms are being created. When 6 = 1, the random surfer version of classical Page Rank is an irreducible Markov chain in which every country has a high-quality possibility of being visited from another area. Nodes in a community are thought of as states in a Markov chain in this context. To the proposed Weighted Page Rank (WPR), a similar argument can be made. Let M:=mij be the related Markov chain’s transition matrix for Weighted Page Rank.

mij={θwij/Sj(Out)+(1−θ)ajidj(Out),ifdj(Out)≠0;βi/∑iεV⁡βiifdj(Out)≠0; (8)

In other words, matrix M is non-negative and column stochastic. p=(∅(1),∅(2),…,∅(n))T is a column vector that contains each node's Weighted Page Rank (WPR). In Eq. (3) Where * β∗=β/||β||1 represents the normalisation of β .

p=γMP+(1−γ)B∗ (9)

B is a (n×n) matrix with the ith column when i=1,2,…,n If 6 = 0, M∗ is exactly beneficial and column stochastic. The normalised response of P is seen as a desk bound Markov chain associated to the chance transition matrix M∗ in the context of stochastic processes. The computation of P in a large community can be reduced to discovering the largest eigenvector of a large-scale matrix using the method described above.

4  Experimental Results

We used the Weighted Page Rank (WPR) and traditional PageRank (PR) algorithms to compare their findings in order to evaluate the Weighted Page Rank method.

Fig. 2 The two algorithms are used to calculate the page rank values for the web graph at d = 0.5. As we can discover from the preceding segment on the in-out weight primarily based entirely web page rank technique, our approach is faster than the authentic web page rank algorithm. It’s also worth noting that the website rankings produced with our method are identical to those obtained through the original page rank methodology. Despite the fact that the weighted page rank method is not the same as the original page rank algorithm, it nevertheless generates a ranking.

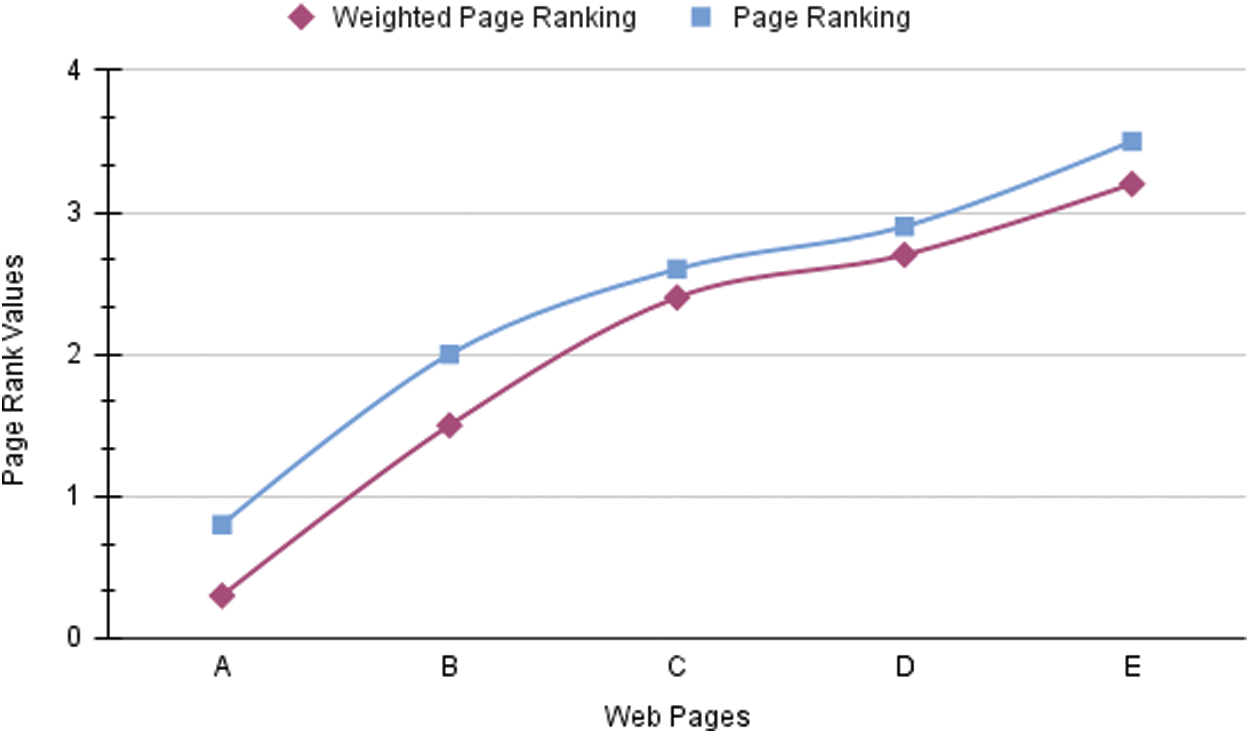
Figure 2: Page rank values for the web graph at d=0.5

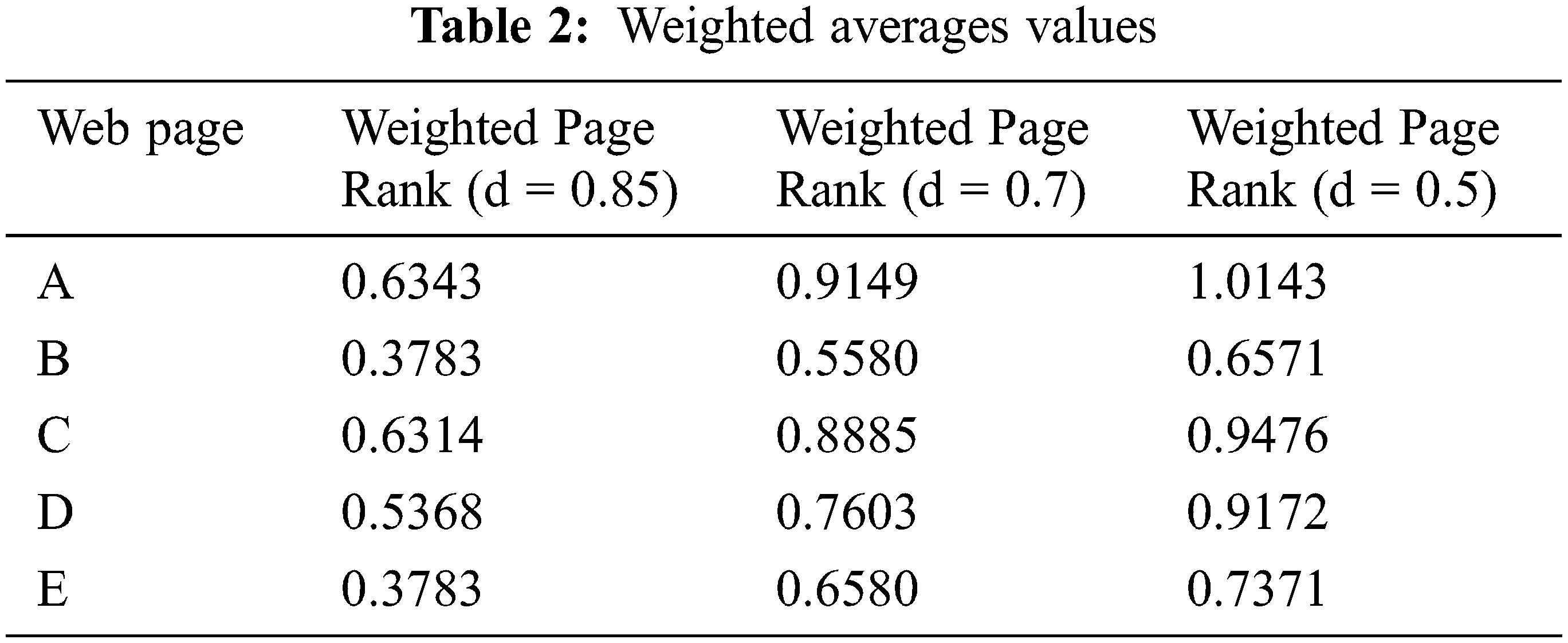
Tab. 2 Weighted averages values using our suggested weighted page rank algorithm. When computing the scores based on one or two rank parameters as well as numerous parameters, the final ranking scores are noticeably different. We use to determine the weighted page rankings after receiving the load matrix W. (G). Three uncommon damping element values, d = 0.85, d = 0.7, and d = 0.5, were used to determine the page ranks. Tab. 1 shows the ranges at which the web page ranks converge in each of the three circumstances.

Weighted Page Rank (WPR) generates higher relevancy values, implying that it outperforms PageRank. The performance is shown in Fig. 3. Furthermore, the following two points should be noted: Weighted Page Rank (WPR) identifies one relevant page inside the first ten pages, whereas no relevant page is detected within the first hundred pages.

Figure 3: Performance of page rank and Weighted Page Rank (WPR)

Fig. 4 depicts the time it took to identify the necessary pages in an experiment. When the number of links in a chain grows, the execution time increases slightly. We tested a variety of data sets from different web pages.

Figure 4: Execution time analysis

5  Conclusion

This work introduces the Weighted Page Rank (WPR) algorithm, which is a PageRank extension. Weighted Page Rank assigns rank scores to pages based on their popularity, taking both inbound and outbound links into account. In the current model of Weighted Page Rank (WPR), only the inside and outside hyperlinks of the pages within the reference web page listing are used to determine the rank rankings. In three separate studies, the Weighted Page Rank model was utilised to compare ranking scores of documents and pages based on one or more user preferences criteria. According to the Weighted Page Rank model, ranking results based on many criteria are preferable to ranking results based on a single criterion, and certain criteria have a bigger impact on ranking outcomes than others.

Acknowledgement: The author with a deep sense of gratitude would thank the supervisor for his guidance and constant support rendered during this research.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  H. Alghamdi and F. Alhaidari, “Extended user preference based weighted page ranking algorithm,” in 2021 National Computing Colleges Conf. (NCCC), Taif, Saudi Arabi, pp. 1–6, 2021. [Google Scholar]

 2.  F. Ghahramani, H. Tahayori and A. Visconti, “Effects of central tendency measures on term weighting in textual information retrieval,” Soft Computing, vol. 25, no. 11, pp. 7341–7378, 2021. [Google Scholar]

 3.  G. Matošević, J. Dobša and D. Mladenić, “Using machine learning for web page classification in search engine optimization,” Future Internet, vol. 13, no. 1, pp. 9, 2021. [Google Scholar]

 4.  X. Zhao, J. Liang and J. Wang, “A community detection algorithm based on graph compression for large-scale social networks,” Information Sciences, vol. 551, no. 3, pp. 358–372, 2021. [Google Scholar]

 5.  J. Q. Liu, X. R. Li and J. C. Dong, “A survey on network node ranking algorithms: Representative methods, extensions, and applications,” Science China Technological Sciences, vol. 64, no. 3, pp. 451–461, 2021. [Google Scholar]

 6.  J. Raeder, D. Larson, W. Li, E. L. Kepko and T. Fuller-Rowell, “OpenGGCM simulations for the THEMIS mission,” Space Science Reviews, vol. 141, no. 1, pp. 535–555, 2008. [Google Scholar]

 7.  T. H. Nguyen, X. D. Hoang and D. D. Nguyen, “Detecting website defacement attacks using web-page text and image features,” International Journal of Advanced Computer Science and Applications, vol. 12, no. 7, pp. 215–222, 2021. [Google Scholar]

 8.  S. Raamakirtinan and L. M. Jenila Livingston, “Identifying influential spreaders in complex networks based on weighted mixed degree decomposition method,” Wireless Personal Communications, vol. 80, no. 4, pp. 1–17, 2021. [Google Scholar]

 9.  D. Zhang, Y. Ge, A. Stein and W. B. Zhang, “Ranking of VGI contributor reputation using an evaluation-based weighted pagerank,” Transactions in GIS, vol. 25, no. 3, pp. 1439–1459, 2021. [Google Scholar]

10. L. Tortosa, J. F. Vicent and G. Yeghikyan, “An algorithm for ranking the nodes of multiplex networks with data based on the PageRank concept,” Applied Mathematics and Computation, vol. 392, no. 3, pp. 125676, 2021. [Google Scholar]

11. T. Fushimi, K. Saito, K. Ohara, M. Kimura and H. Motoda, “Efficient computing of PageRank scores on exact expected transition matrix of large uncertain graph,” in Proc. 2020 IEEE Int. Conf. on Big Data (Big Data), Atlanta, GA, USA, pp. 916–923, 2020. [Google Scholar]

12. M. Curado, L. Tortosa, J. F. Vicent and G. Yeghikyan, “Analysis and comparison of centrality measures applied to urban networks with data,” Journal of Computational Science, vol. 43, no. 3, pp. 101127, 2020. [Google Scholar]

13. M. Zare, S. H. Khasteh and S. Ghafouri, “Automatic ICA detection in online social networks with PageRank,” Peer-to-Peer Networking and Applications, vol. 13, no. 5, pp. 1297–1311, 2020. [Google Scholar]

14. H. Nassar, A. R. Benson and D. F. Gleich, “Neighborhood and PageRank methods for pairwise link prediction,” Social Network Analysis and Mining, vol. 10, no. 1, pp. 1–13, 2020. [Google Scholar]

15. Z. Shu and X. Li, “Automatic extraction of web page text information based on network topology coincidence degree,” Wireless Communications and Mobile Computing, vol. 2022, no. 3, pp. 1–10, 2022. [Google Scholar]

16. E. Manohar, E. Anandha Banu and D. Shalini Punithavathani, “Composite analysis of web pages in adaptive environment through Modified Salp Swarm algorithm to rank the web pages,” Journal of Ambient Intelligence and Humanized Computing, vol. 13, pp. 2585–2600, 2022. [Google Scholar]

17. J. Mor, N. Kumar and D. Rai, “Effective presentation of results using ranking & clustering in meta search engine,” Compusoft, vol. 7, no. 12, pp. 2957, 2018. [Google Scholar]

18. N. Kumar and R. Nath, “A meta search engine approach for organizing web search results using ranking and clustering,” International Journal of Computer (IJC), vol. 10, no. 1, pp. 1–7, 2013. [Google Scholar]

19. R. Nath and N. Kumar, “To overcome HITS rank similarity confliction of web pages using weight calculation and rank improvement,” in AIP Conf. Proc., American Institute of Physics, vol. 1414, pp. 77–80, 2011. [Google Scholar]