Efficient Hardware Design of a Secure Cancellable Biometric Cryptosystem

1  Introduction

With the large development of multimedia applications over Internet and mobile networks, it has become a must to introduce more secure access methods to serve users. Passwords and Personal Identification Numbers (PINs) have been used as traditional access methods to the Internet and the other networks. However, the keys and passwords are exposed to being stolen or even forgotten [1]. The good alternative to avoid the limitations of keys and passwords is to use biometrics. Biometric-based access methods do not require to remember passwords or save keys, as biometrics are always accompanying persons [2]. The main problem with the utilization of biometrics as access tools is the need to create databases to store the user biometrics. These databases may be vulnerable to attacks. A possible solution to eliminate the effect of attacks is to use cancellable biometrics. The idea of cancellable biometrics is to use distorted or encrypted versions of the biometric templates rather than the original biometric templates in the recognition process. The intended distortion is created through non-invertible transforms. On the other hand, strong encryption algorithms can be used to generate encrypted biometric templates to be stored in the databases for the recognition task. A good property that should be achieved in cancellable biometric systems is the pattern diversity with unlinkability between patterns to use different patterns for different applications [3]. These properties can be guaranteed through changing the initial parameters or keys of the used transforms or encryption algorithms [4].

In another classification of cancellable biometric schemes, they can be categorized into helper-data-based schemes and cancellable biometric transformation schemes. In the helper-data-based schemes, some auxiliary data are integrated with the original templates. These data make it possible to restore or renew the key or initial parameters during the authentication process. In [5], both feature extraction and a fuzzy vault algorithm were used for cancellable fingerprint recognition. In [6], a cancellable fingerprint recognition scheme was built through the utilization of an Error Correction Code (ECC) [6]. The coding schemes give better representations of the obtained features that are difficult to be reversed.

In [7–9], the robustness of biometric encryption has been improved by applying a hybrid biometric cryptosystem, which combines two or more template protection techniques in order to enhance the privacy of users. Traditional encryption algorithms can be used for encrypting biometric templates, but they have some difficulties in implementation, and they require much time. On the other hand, chaotic-based algorithms are simple in implementation and may be implemented with permutation operations only [10]. That is why chaotic encryption is more recommended for biometric encryption.

In [11], both piecewise and logistic maps have been combined for biometric encryption, leading to high unpredictability in a highly-complicated and long-length chaotic pseudo-random number generator. In [12], the chaotic behavior of the logistic map is used for building a projection matrix of the individual biometric. This scheme is non-invertible, which fulfills the revocability, diversity, and robustness to attacks. The authors of [13,14] presented a hybrid cryptosystem based on a 3D chaotic map that improves security and efficiency in the presence of various attacks. In [15], chaotic encryption has been used to generate cancellable iris codes. A modification of the logistic map has been incorporated to enlarge the keyspace, and hence privacy is increased. In real-time applications, many digital cryptographic algorithms based on chaotic maps have been introduced with the corresponding hardware to protect the transferred multimedia data from rapid attacks [16]. Prototyping of an algorithm with FPGA implementation enhances the credibility that the algorithm will work practically [17]. FPGA prototypes are used to test certain functions in real time. Furthermore, with the high speed of FPGA prototypes, a larger amount of data can be used, potentially revealing bugs that are not found in simulation models. Hardware implementation is increasingly important due to the computational complexity of the algorithms and the high throughput requirements [18].

Field Programmable Gate Arrays (FPGAs) can be used in biometric applications, particularly with embedded applications in which latency and power are critical. However, running an encryption algorithm on FPGA mostly results in frustration as most encryption algorithms are designed for serial processors. In order to effectively optimize the implementation with FPGA, it is typically important to convert the algorithm to a new one compatible with hardware design at both operational and application levels. In [19], a modern encryption scheme for digital images based on a chaotic system was presented and implemented on FPGA. The resulting design is robust and effective.

Many researchers discussed the problem of cancellable biometric recognition systems [1–22], where all of them have drawbacks in investigating the attack analysis and a shortage in using more recent datasets. In addition, the round errors on the hardware systems give lower evaluation metrics. This paper introduces an improved hybrid encryption algorithm with its FPGA implementation to create an efficient, more protected, cancellable biometric recognition system that is immune to fraudsters. The main contributions of this work are as follows:

a) Proposal of an efficient cancellable biometric recognition system using a 3D chaos cryptosystem.

b) Testing the performance of this cryptosystem on different biometric datasets.

c) Hardware implementation of the proposed cancellable biometric recognition system on the FPGA platform.

d) Estimation of security evaluation metrics for the proposed system.

The symbols and notation utilized throughout the whole paper are summarized in Tab. 1. The rest of this work is arranged as follows. An overview of the cancellable biometric recognition system and its implementation with the FPGA is provided in Section 2. A description of the authentication quality assessment metrics used is given in Section 3. Section 4 presents the results of simulation and cryptanalysis with a detailed performance comparison. Finally, Section 5 summarizes the concluding remarks.

2  Proposed Cryptosystem

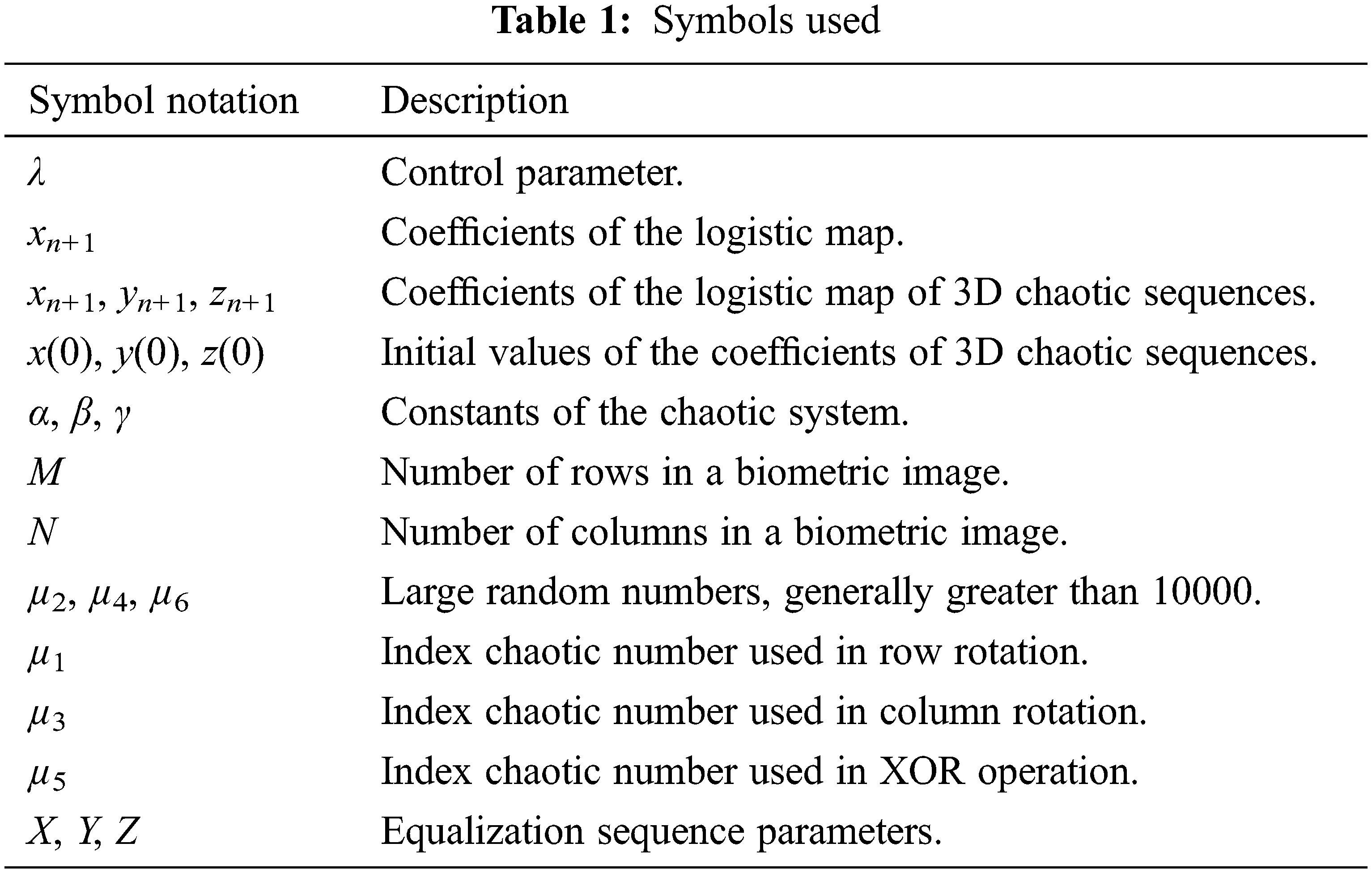
Fig. 1 shows the proposed hybrid cryptosystem based on 3D chaotic sequences. The framework of the suggested cryptosystem is represented in two cascaded stages: confusion and diffusion. In the confusion stage, the positions of pixels of the original biometric image are shuffled in row/column rotation. On the other hand, in the diffusion stage, the XOR operation is applied to change the values of the pixels.

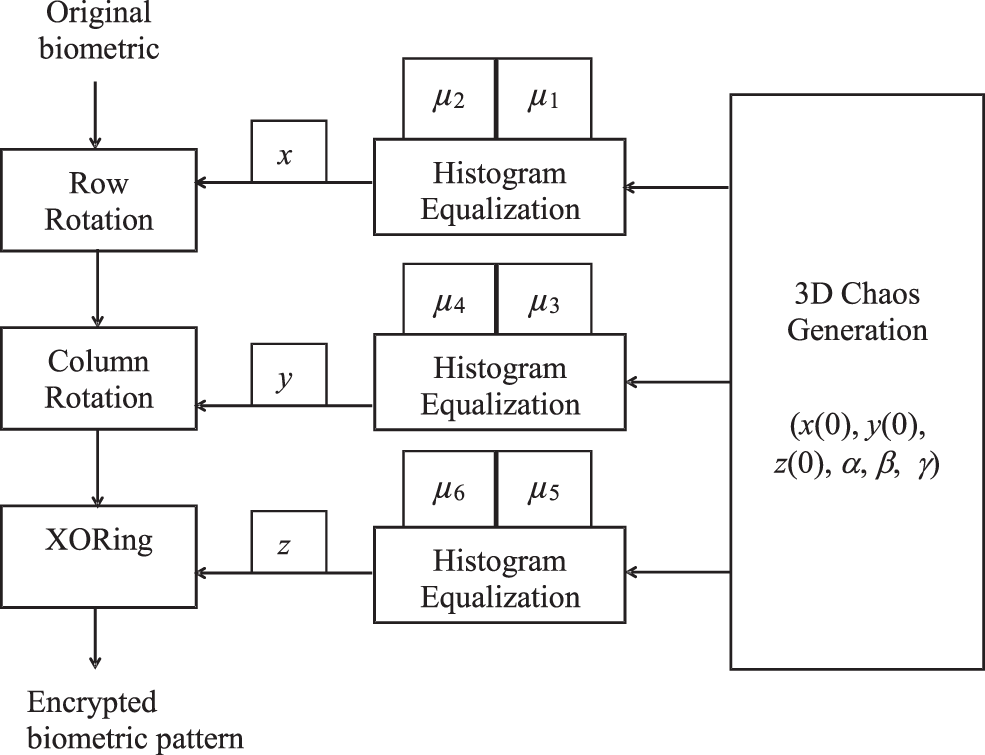
Figure 1: The proposed hybrid 3D chaotic cryptosystem

2.1 3D Chaos Generation

The logistic map is one of the simplest and most frequent chaotic algorithms for relocating and adjusting the gray values of biometric template pixels. The nonlinear chaotic logistic map generation is provided by:

xn+1=λxn(1−xn) (1)

The chaotic behaviour of the suggested model is achieved, when λ = 4. The 3D logistic map generation formulas [23] are given by:

xn+1=γxn(1−xn)+βyn2xn+αzn3 (2)

yn+1=γyn(1−yn)+βzn2yn+αxn3 (3)

zn+1=γzn(1−zn)+βxn2zn+αyn3 (4)

The coefficients in the above three sequences are generated in the range [0,1], and they depend on the values of x(0), y(0), and z(0). The efficient chaotic behavior is achieved, with 3.53 < γ < 3.81, 0 < β < 0.022, 0 < α < 0.015, x(0), y(0), z(0), γ, β, α, µ1, µ2, µ3, and µ4 as the security keys. The presence of cubic, quadratic coupling, and three constant parameters makes the 3D logistic map more complicated for better security. To achieve higher security, we need to equalize the biometric template histogram. So, if we have a biometric template with dimensions M × N, where M is the number of rows and N is the number of columns, then the biometric template histogram is equalized by the following formulas:

X=(integer(x×μ2))modN (5)

Y=(integer(y×μ4))modM (6)

Z=(integer(z×μ6))mod256 (7)

where µ2, µ4, and µ6 are large random numbers, generally greater than 10000. For simplicity, µ2, µ4, and µ6 are assumed to be equal.

2.2 Row Rotation

An efficient method for rotating the rows and columns for the permutation of the biometric template pixels is proposed. The row rotation of a biometric template is as follows:

a) The length of the generated chaotic sequence (X) is set equal to the size M.

b) A large random constant µ1 is considered as the initial index of X.

c) Depending on the value of X whether odd or even, the position of each pixel is rotated either to right or left, respectively.

2.3 Column Rotation

The same process applied in row rotation is used in column rotation, except that the rotation direction is taken vertically from up or down.

2.4 XOR Operation

The XOR operation, which essentially changes the grayscale pixel values, is the final stage in the proposed cryptosystem. The shuffled output biometric image is converted into a vector with size 1 × MN and XORed with the sequence Z to generate the encrypted biometric template.

3  FPGA Implementation

FPGA prototyping of an algorithm increases the confidence that it will function properly in practice. For example, we use FPGA prototypes to implement functions and run simulation scenarios at high speed. In addition, because FPGA prototypes run faster, it is possible to use larger datasets, potentially exposing bugs that a simulation model would not reveal.

The suggested cryptosystem is developed with built-in MATLAB Simulink blocks as well as certain user-defined features. All data utilized are described as fixed point data, and each block should even provide a Hardware Description Language (HDL) coder. In the simulation, the discrete-no continuous state solver and fixed-step solution types are chosen.

The schematic diagram of the proposed cryptosystem model is depicted in Figs. 2–6. The model, which is made up of four main subsystems, is revealed. The schematic diagram for producing a 3D chaotic sequence is shown in Fig. 2. Fig. 3 shows the equalization of the histogram of the obtained chaotic sequence. Fig. 4 displays the stage of confusion. Fig. 5 depicts the diffusion stage.

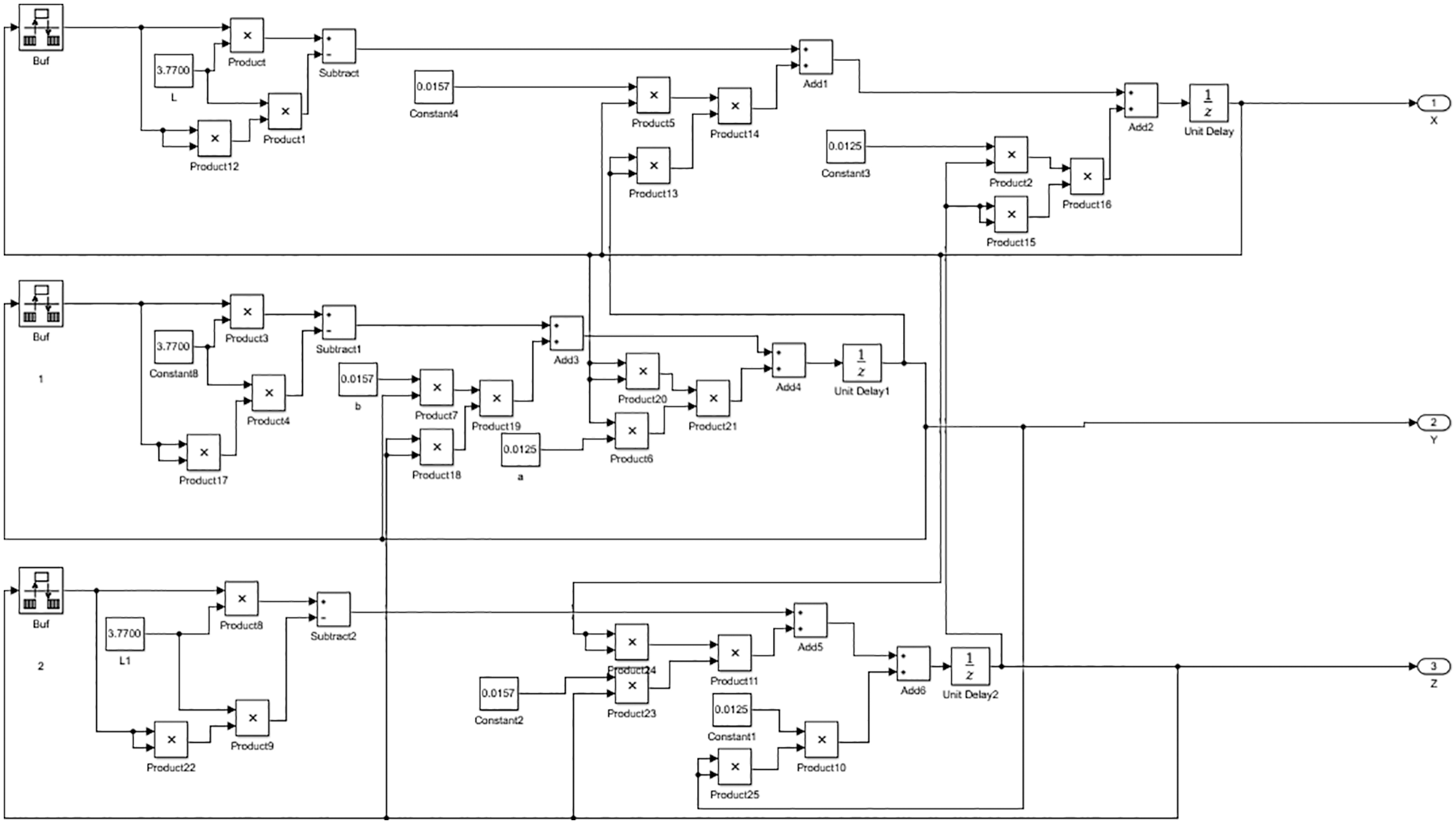
Figure 2: Key generation schematic view

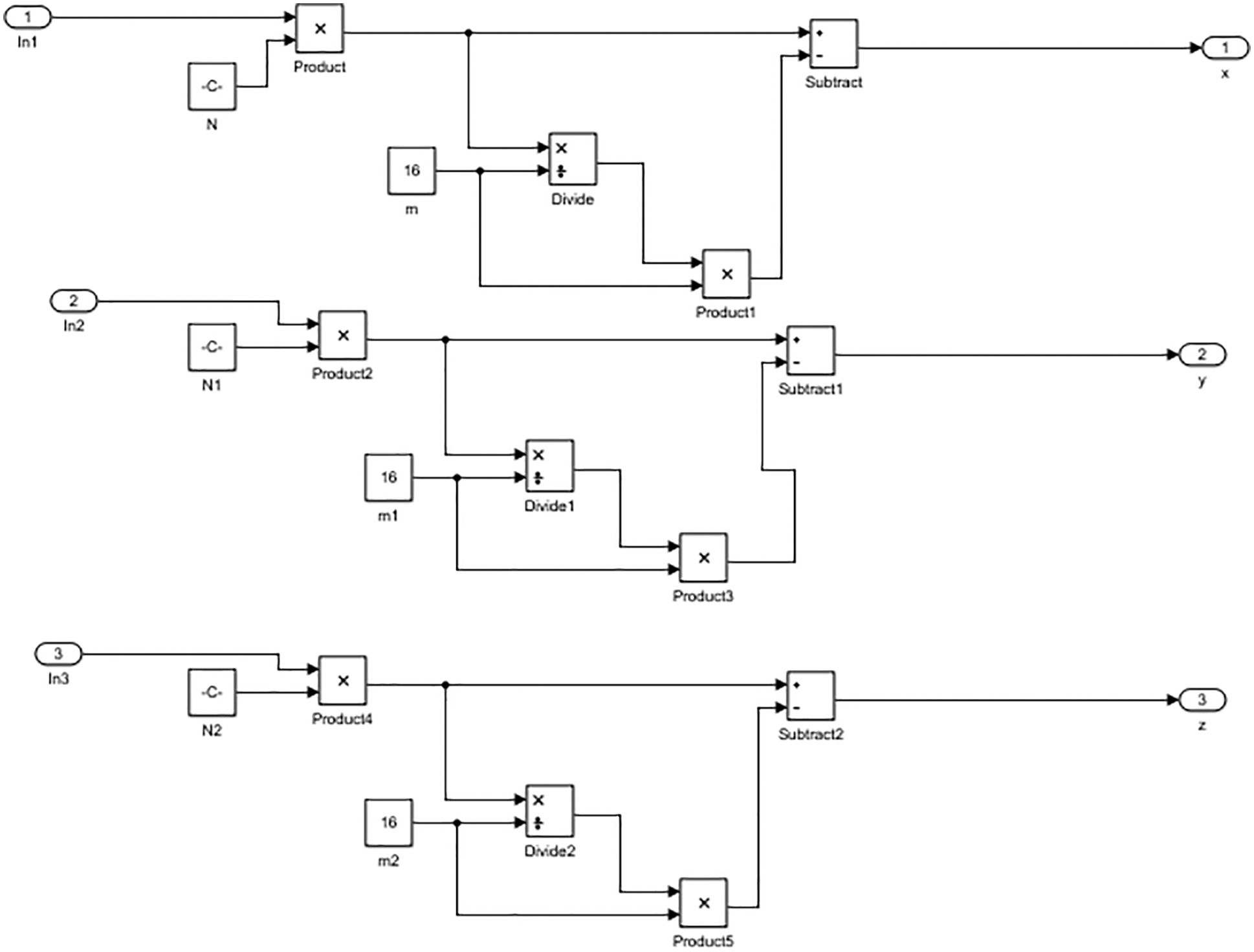
Figure 3: Histogram equalization schematic view

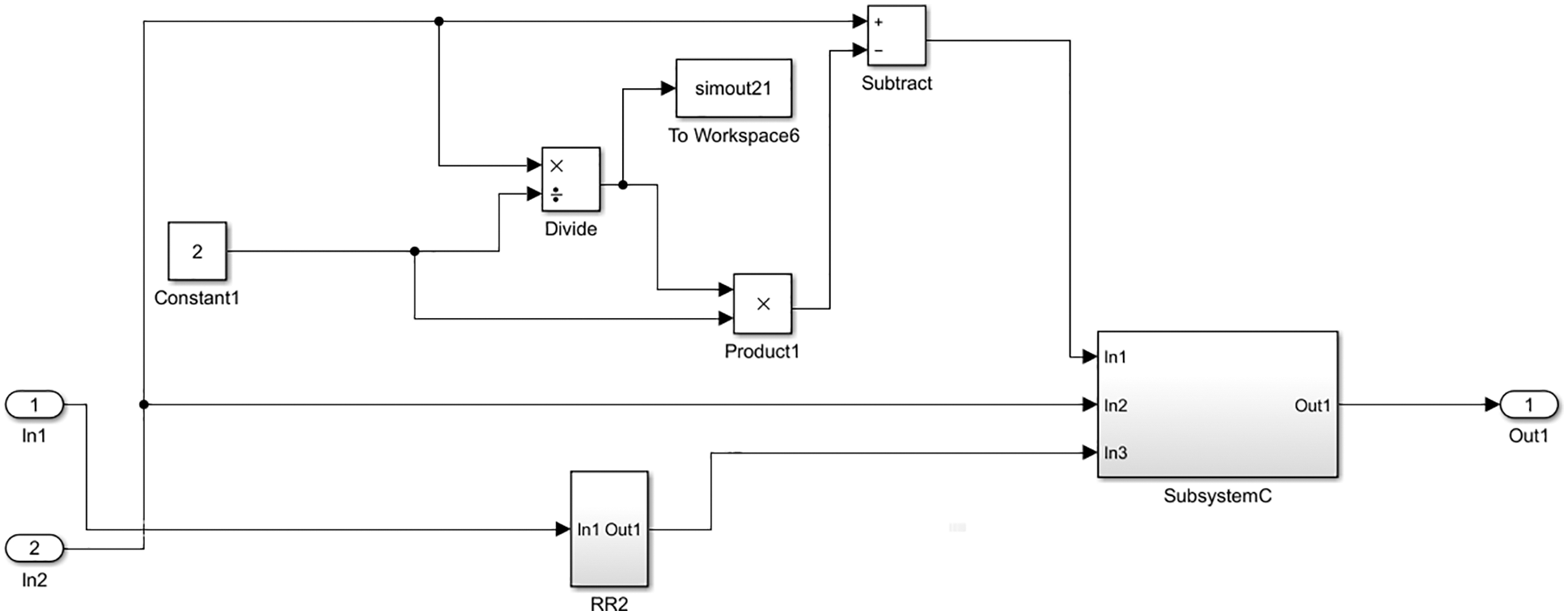
Figure 4: The Diffusion stage schematic view

Figure 5: The Confusion stage schematic view

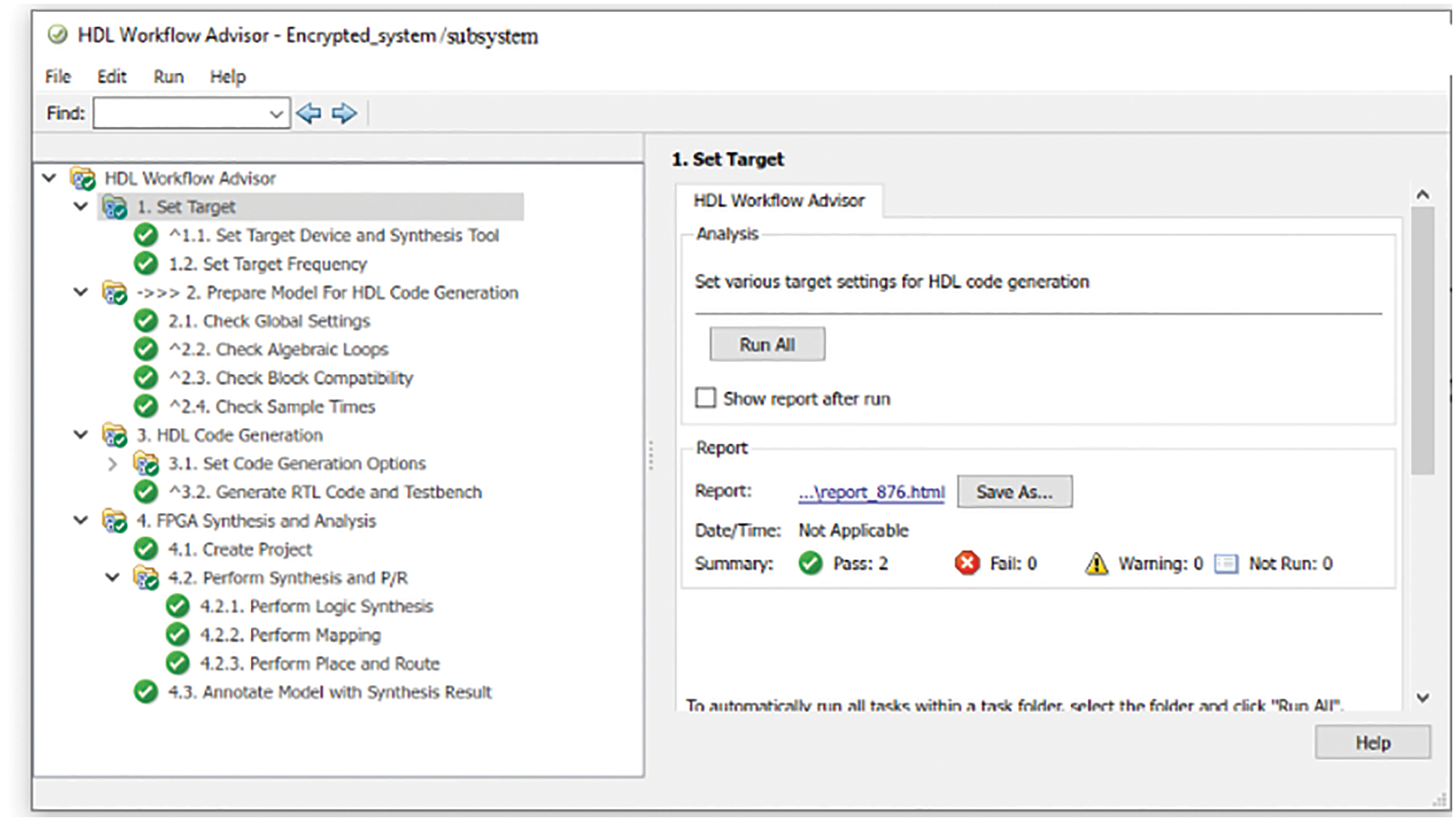
Figure 6: HDL workflow adviser

The HDL workflow advisor tool generates the HDL code in the second step, as shown in Fig. 6. It facilitates the Register-Transfer Level (RTL) code and the test-bench generation from the proposed algorithm, performs synthesis tasks by invoking a supported third-party synthesis tool, and annotates critical path information back to the system. It also sets a particular workflow and guides the designer through the tasks necessary for full deployment. Each task performs a distinct step of the workflow. Feedback is adopted on the results of each task. If the task fails, the HDL workflow advisor tool provides information on how to modify the model to complete the task. The HDL code is then simulated to produce the RTL with the Xilinx generator, providing a well-suited hardware design system. The developed model is then synthesized using ISE software with Xilinx FPGA technology, as shown in Figs. 7 and 8.

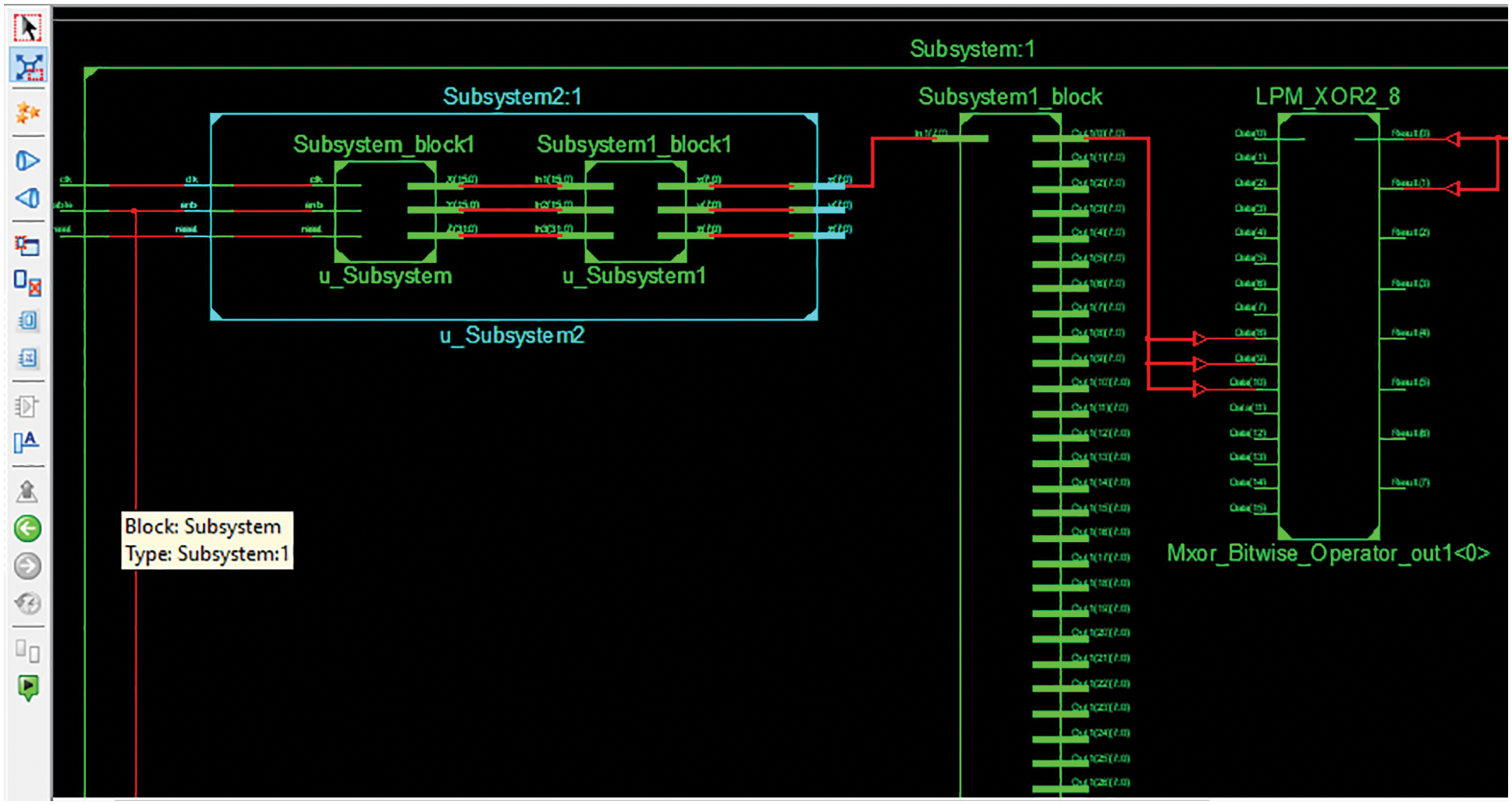
Figure 7: RTL schematic plot of diffusion and confusion stages

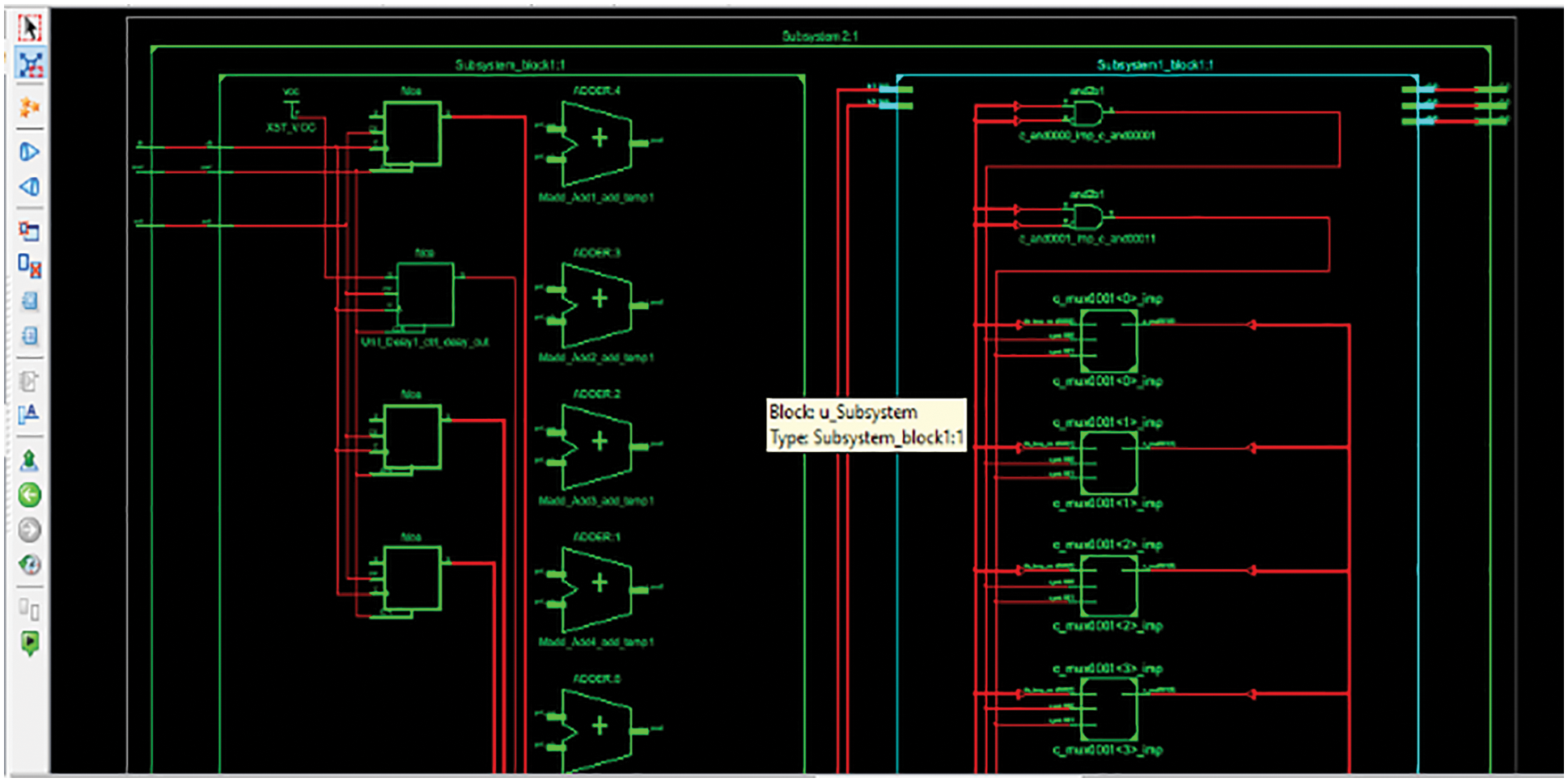
Figure 8: RTL schematic plot of 3D chaos generation

4  Authentication Evaluation Metrics

Biometric authentication is the process that ensures whether a particular template is or is not the same as one of the templates stored. A new biometric template is compared during the verification phase to the existing ones to confirm matching with the stored templates. The effectiveness of the cancellable biometric recognition system is determined by correlation analysis and Receiver Operating Characteristic (ROC) curve. If the tested individual correlation score exceeds a predefined level, access is granted. Generally, the correlation score of an authorized individual should frequently be larger than that of an unauthorized individual [24,25].

The classification process of genuine and imposter users is based on a statistical concept. Two distributions are created for genuine and imposter correlation scores. The intersection point of both distributions reflects the efficiency of the system through the so-called Equal Error Rate (EER). These two distributions can be used to estimate the ROC curve of the system. The ideal ROC curve that reflects a success rate of 100% has a corner at the top-left point. The roll-off shape below the top left corner represents the deviation from ideality.

5  Results and Security Analysis

5.1 Simulation Results

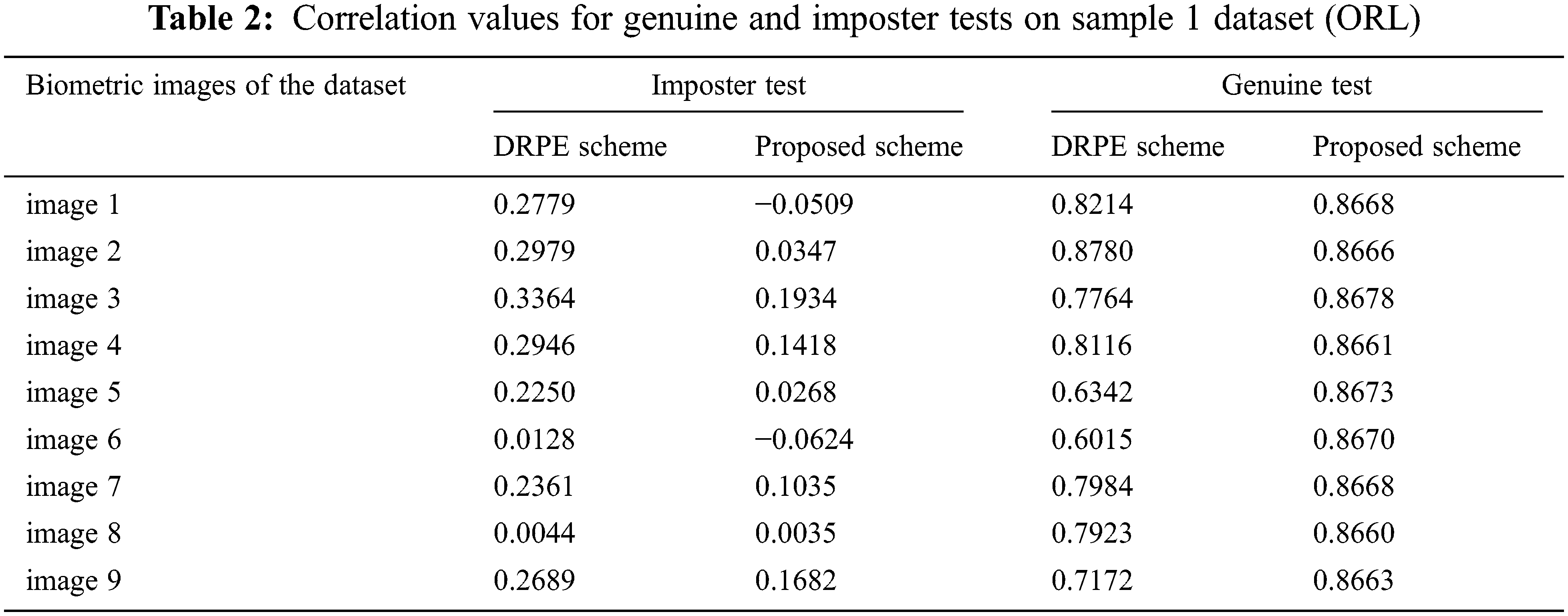
Different biometric samples of face and fingerprint datasets have been considered to examine the efficiency of the proposed cancellable biometric recognition system and its robustness, as shown in Figs. 9, 11, 13, 15, and 17. The images of faces are taken from the ORL [26], the two recent FERET [27], and the LFW [28] datasets, and the fingerprint images are taken from the FVC dataset [29]. We have run our simulation experiments on MATLAB R2016a environment using Win10, a 64-bit operating system with Intel core i5. The initial conditions for chaotic coefficients are selected to be x(1) = 0.2350; y(1) = 0.3500; z(1) = 0.7350. In addition, α(1) = 0.0125, β(1) = 0.015 and γ(1) = 3.7700. In this work, we have taken µ2 = µ4 = µ6 = 105, µ1 = 500, µ3 = 600, and µ5 = 700.

Figure 9: The examined sample 1 dataset (ORL)

Figure 10: Result of the proposed and the DRPE schemes on sample 1 dataset (ORL)

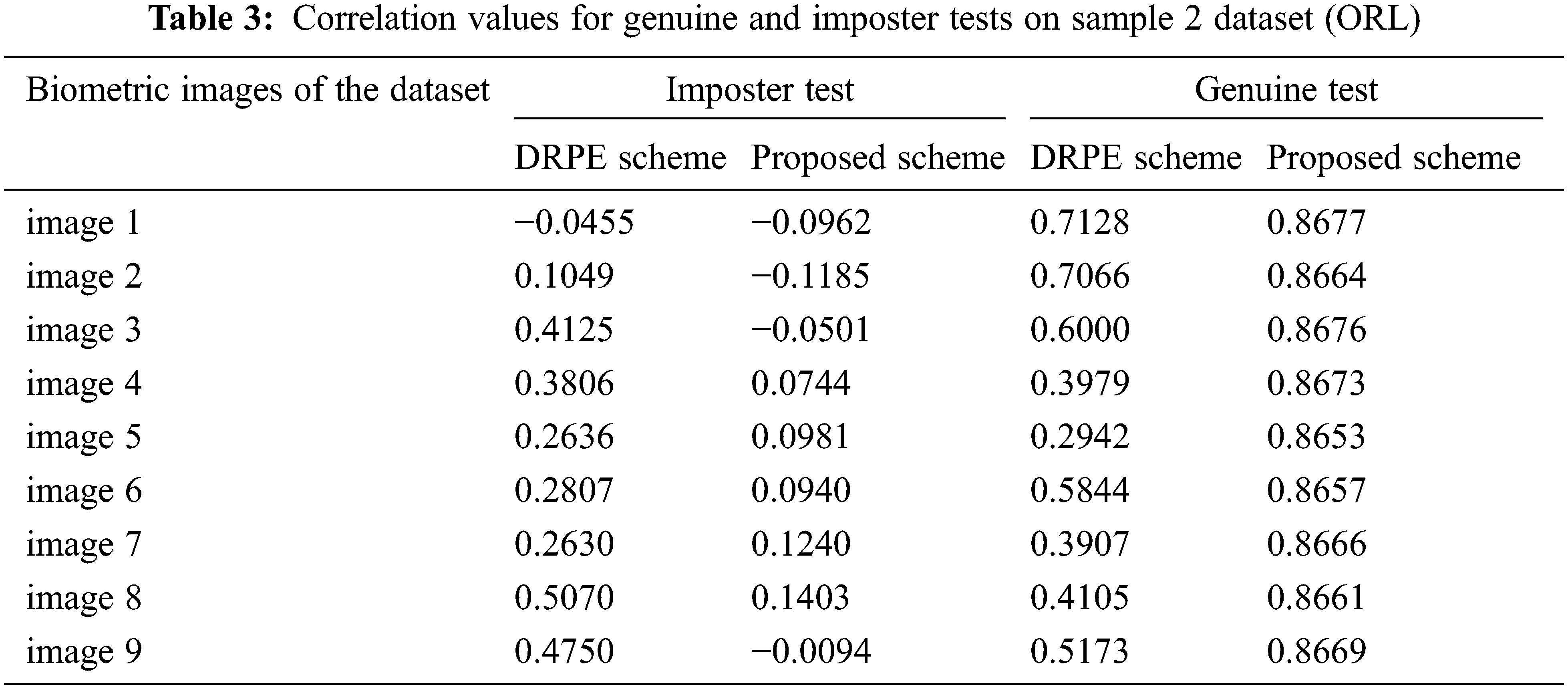
Figure 11: The examined sample 2 dataset (ORL)

Figure 12: Result of the proposed and DRPE schemes on sample 2 dataset (ORL)

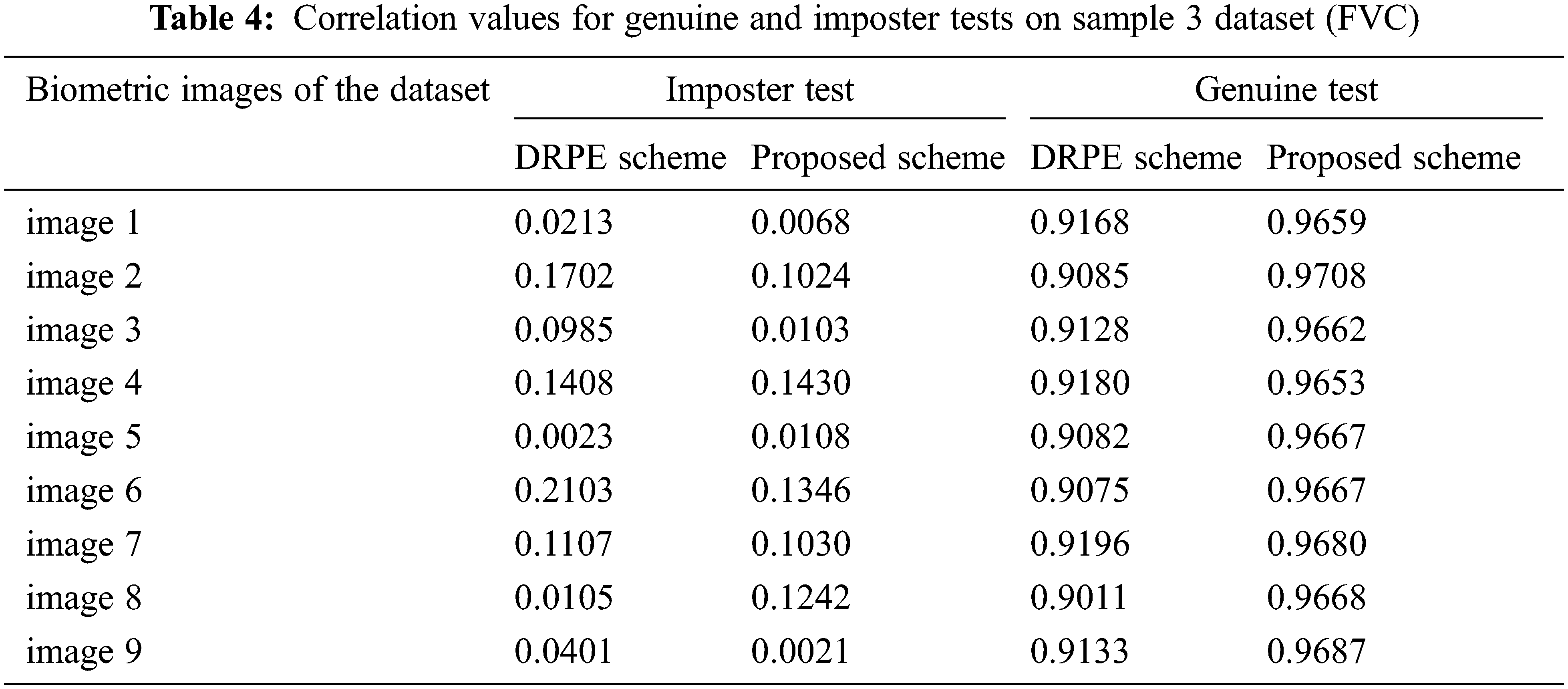
Figure 13: The examined sample 3 dataset (FVC)

Figure 14: Results of the proposed and DRPE schemes on the sample 3 dataset (FVC)

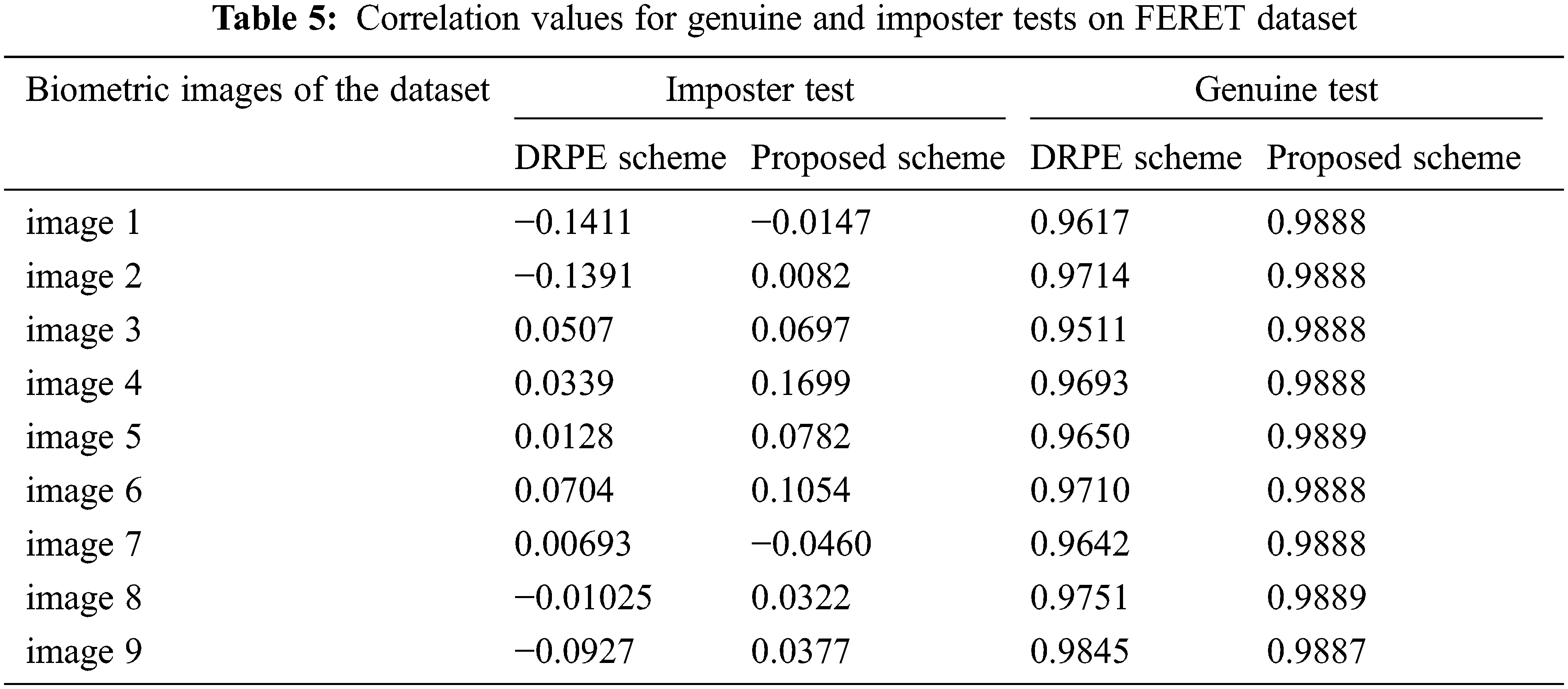
Figure 15: The examined images of the FERET dataset

Figure 16: Results of the proposed and DRPE schemes on the FERET dataset

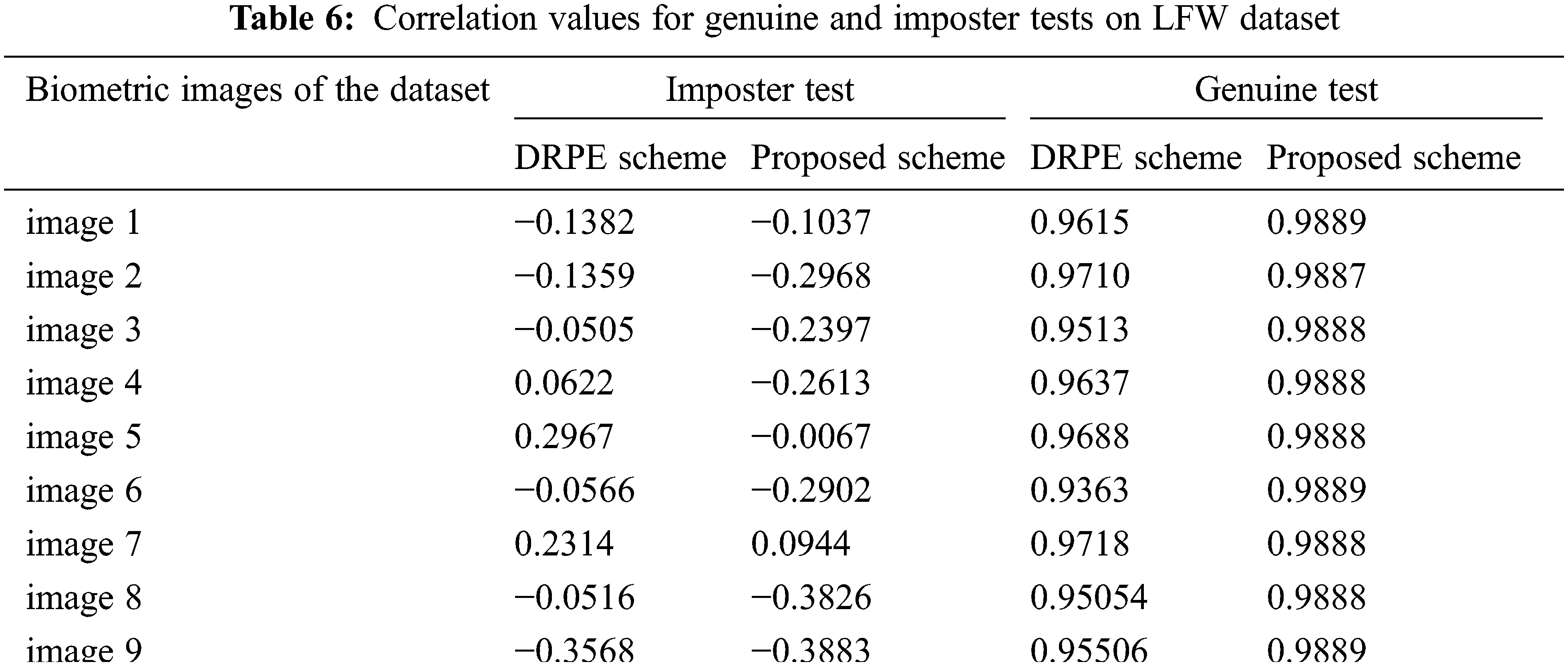
Figure 17: The examined images of the LFW dataset

All biometric patterns are of size 512 × 512. The results obtained from the proposed cryptosystem are compared to those achieved with the optical Double Random Phase Encoding (DRPE) [30,31].

Figs. 10, 12, 14, 16, and 18 show the simulation results of the encryption with the proposed 3D chaotic scheme compared to the state-of-the-art DRPE scheme for all examined biometric samples. It has been noticed that when compared to the standard DRPE scheme [30,31], the results of the suggested hybrid encryption strategy are more recommended for a highly-efficient cancellable biometric recognition scheme.

Figure 18: Results of the proposed and DRPE schemes on the LFW dataset

The Probability of True Distribution (PTD), Probability of False Distribution (PFD), and ROC curves for the proposed cancellable biometric system and that based on the DRPE scheme for all biometric samples examined are shown in Figs. 19–28. These curves reveal the threshold and error probability of the authentication process. The threshold value, which is used for discrimination, is determined at the intersection point between the PTD and PFD curves.

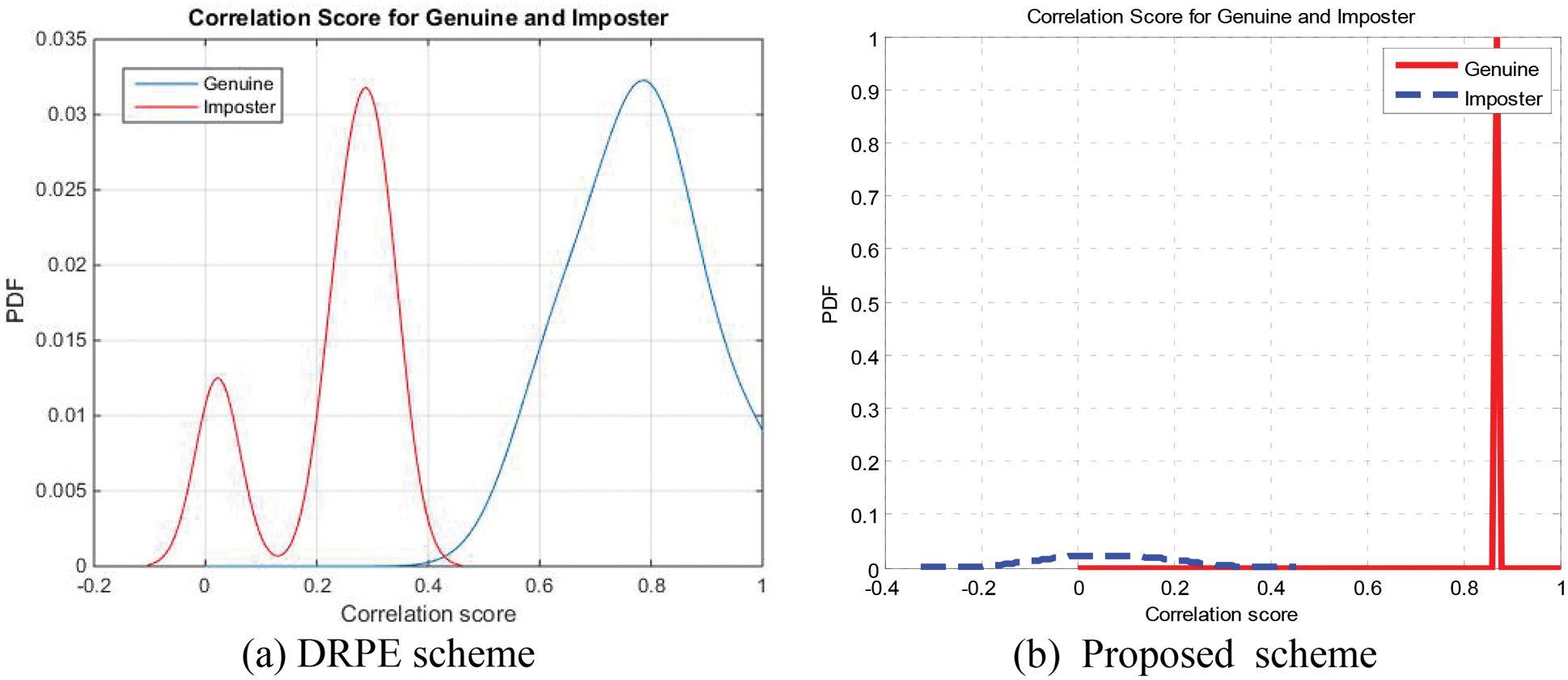
Figure 19: PTD and PFD curves on sample 1 for the cancellable biometric recognition systems based on the DRPE and the proposed schemes (ORL)

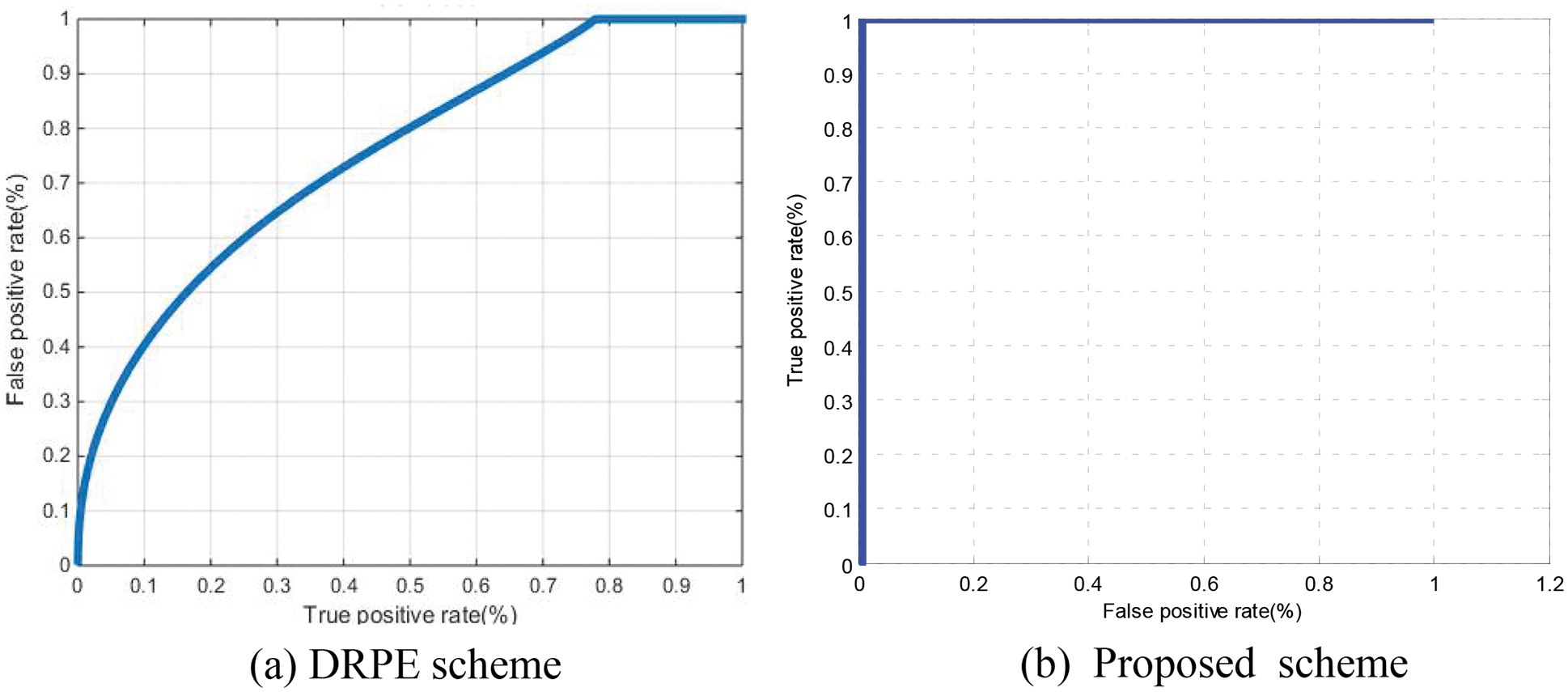
Figure 20: ROC curves on sample 1 for the cancellable biometric recognition systems based on the DRPE and the proposed schemes (ORL)

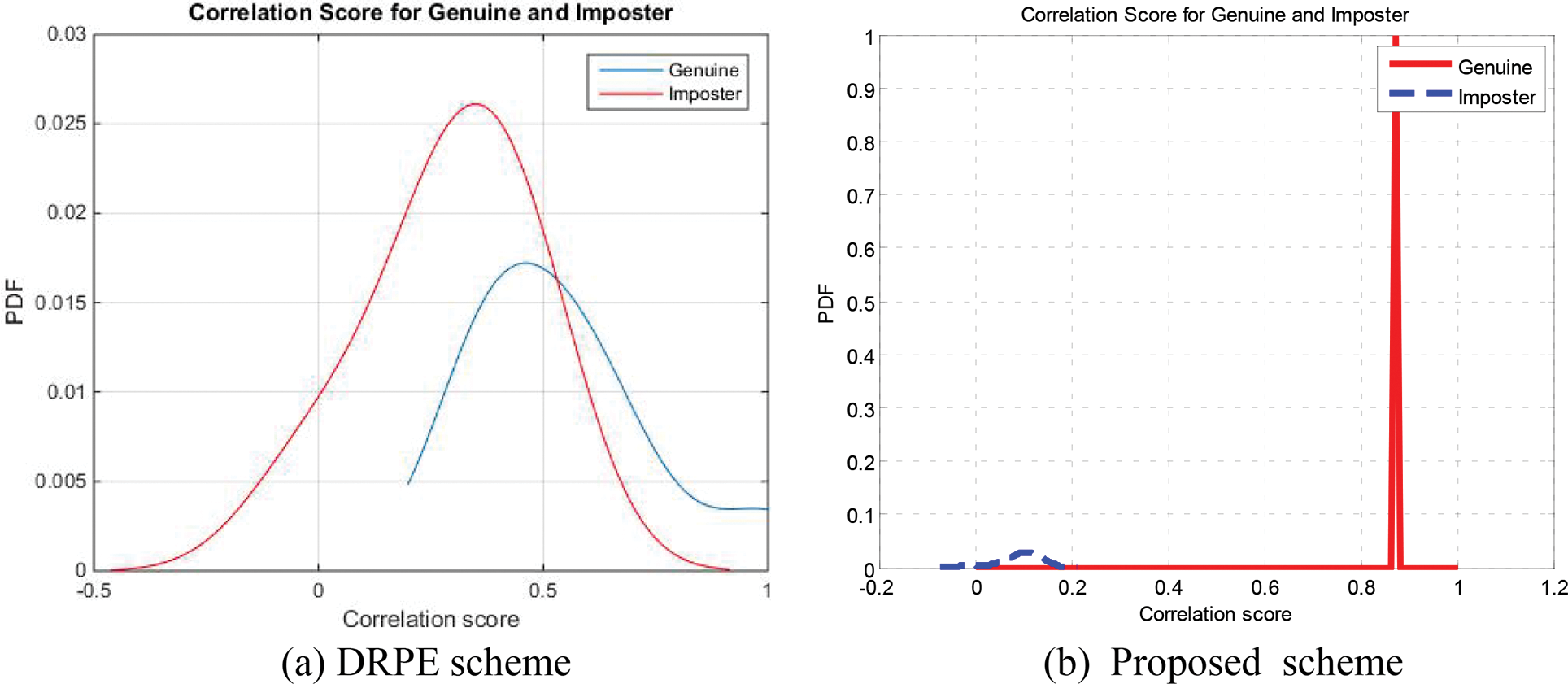
Figure 21: PTD and PFD curves on sample 2 for the cancellable biometric recognition systems based on the DRPE and the proposed schemes (ORL)

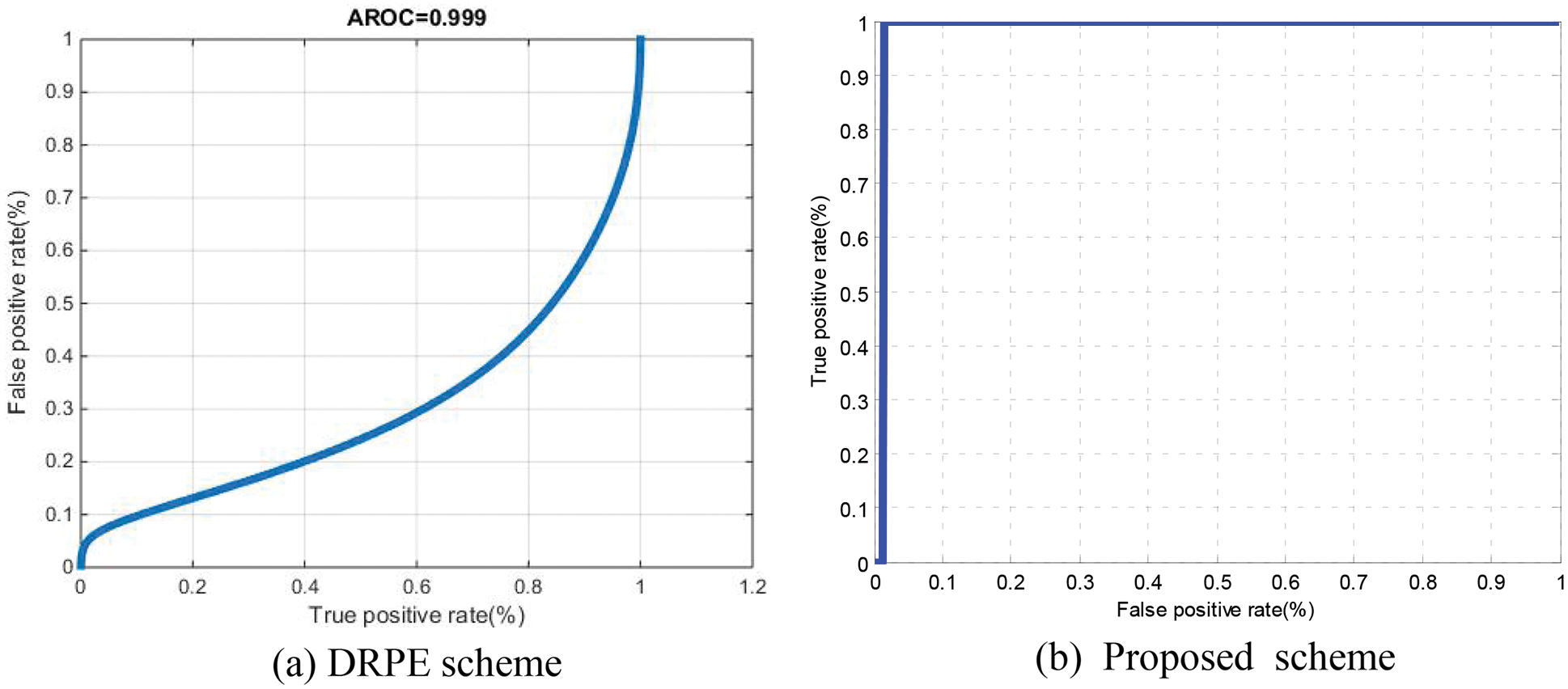
Figure 22: ROC curves on sample 2 for the cancellable biometric recognition systems based on the DRPE and the proposed schemes (ORL)

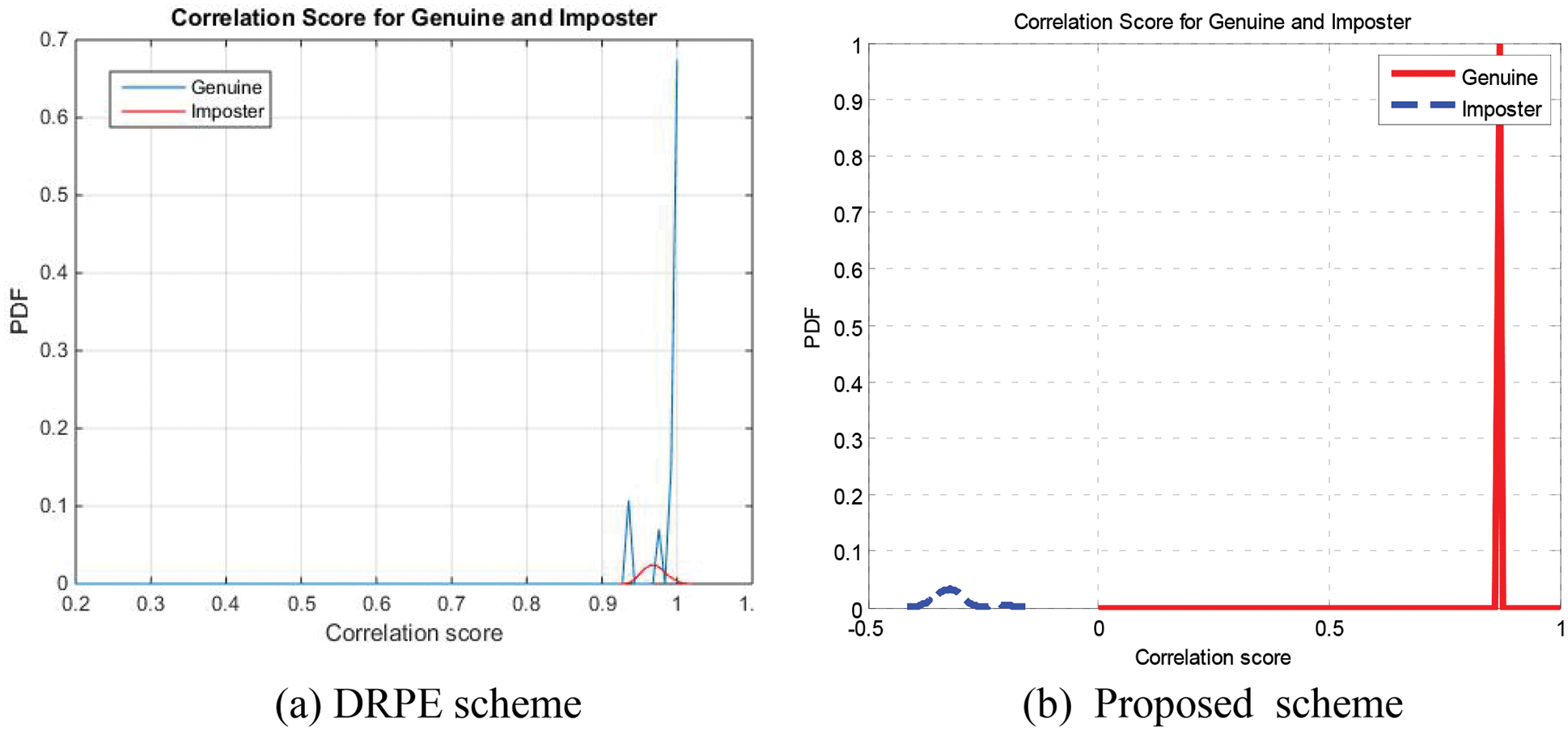
Figure 23: PTD and PFD curves on sample 3 for the cancellable biometric recognition systems based on the DRPE and the proposed schemes (FVC)

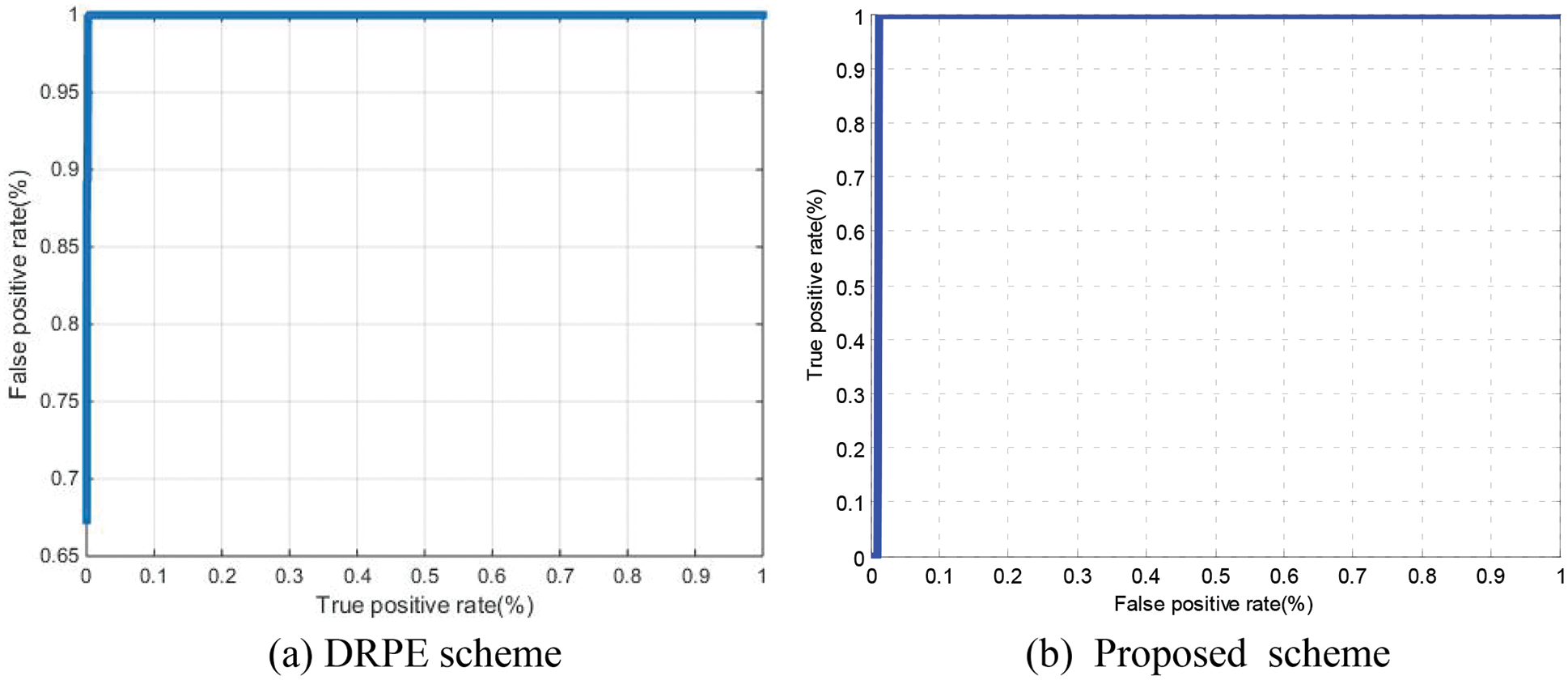
Figure 24: ROC curves of the cancellable biometric recognition systems based on the proposed and the DRPE schemes on sample 3 dataset (FVC)

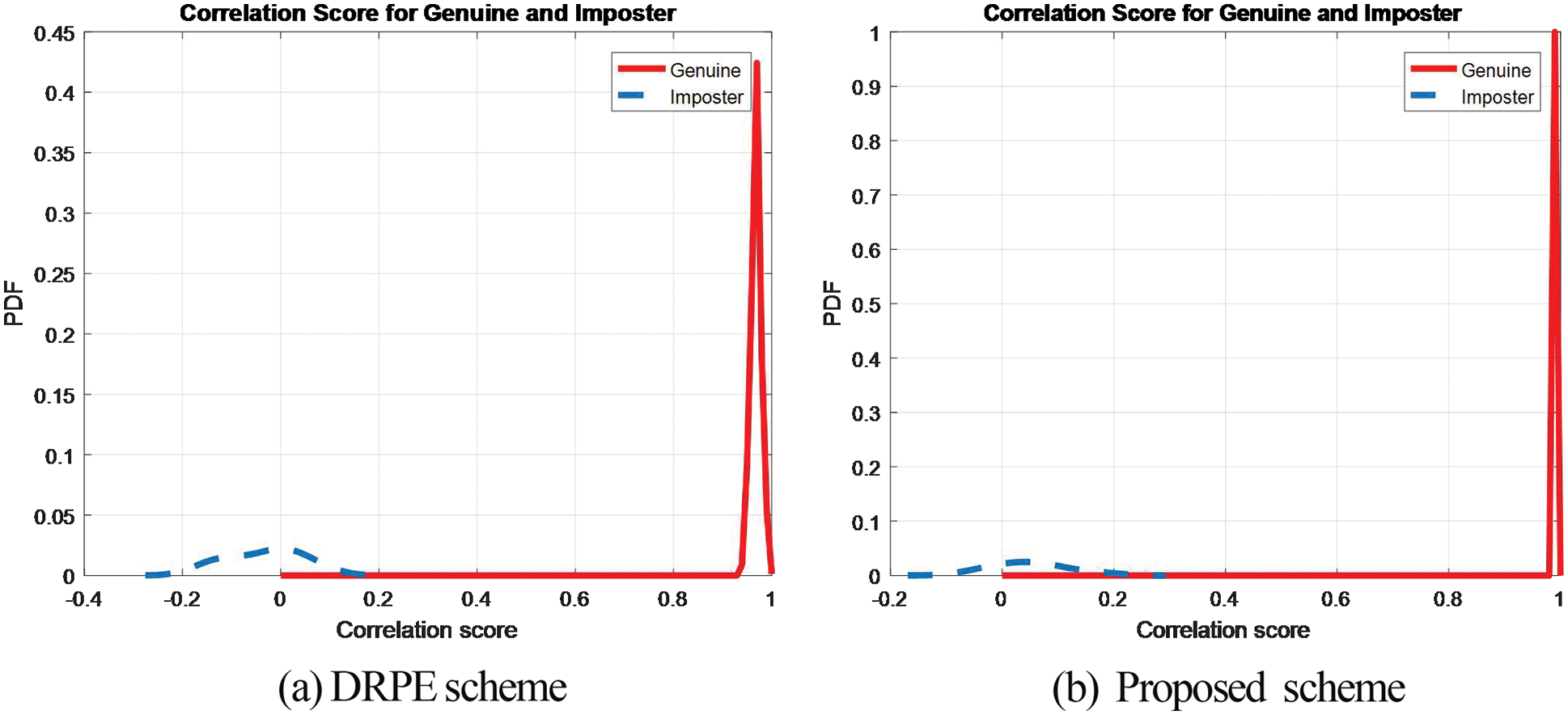
Figure 25: PTD and PFD of the cancellable biometric recognition systems based on the proposed and the DRPE schemes on FERET dataset

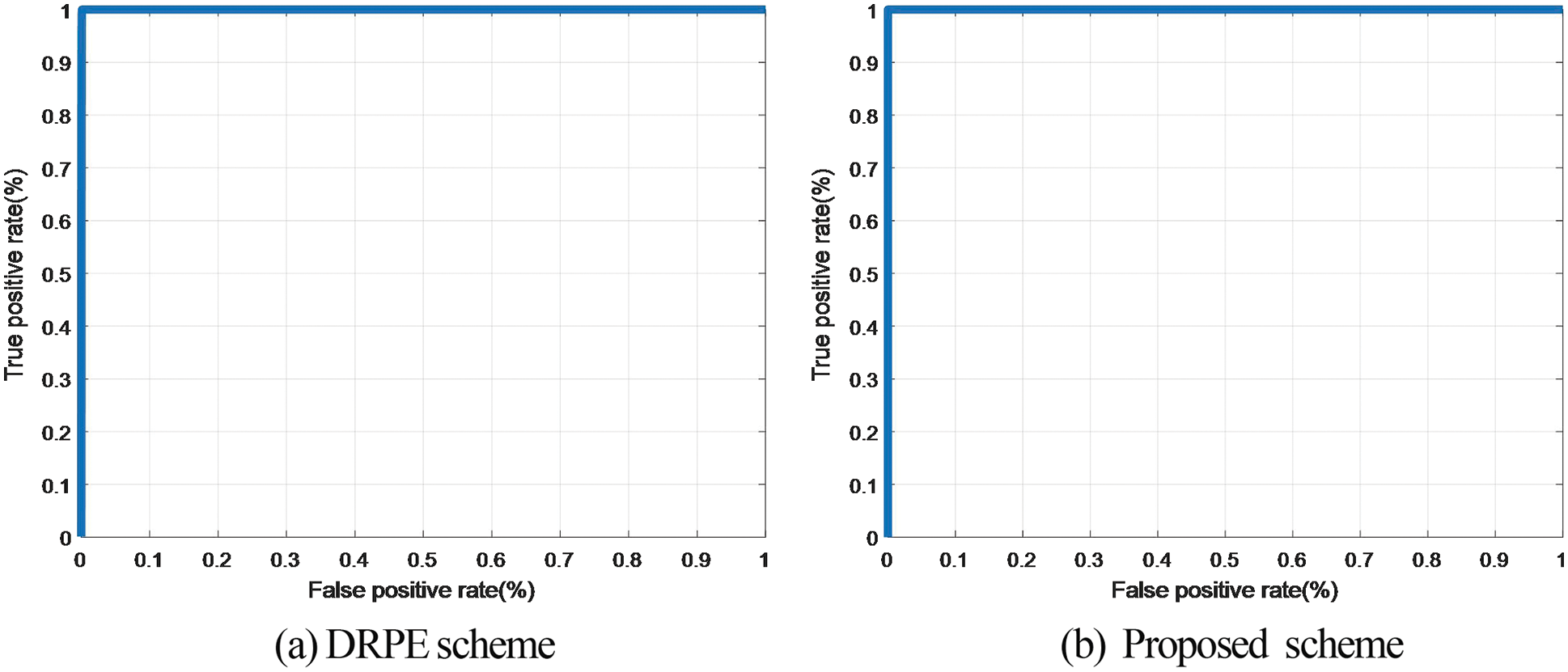
Figure 26: ROC curves of the cancellable biometric recognition systems based on the proposed and the DRPE schemes on FERET dataset

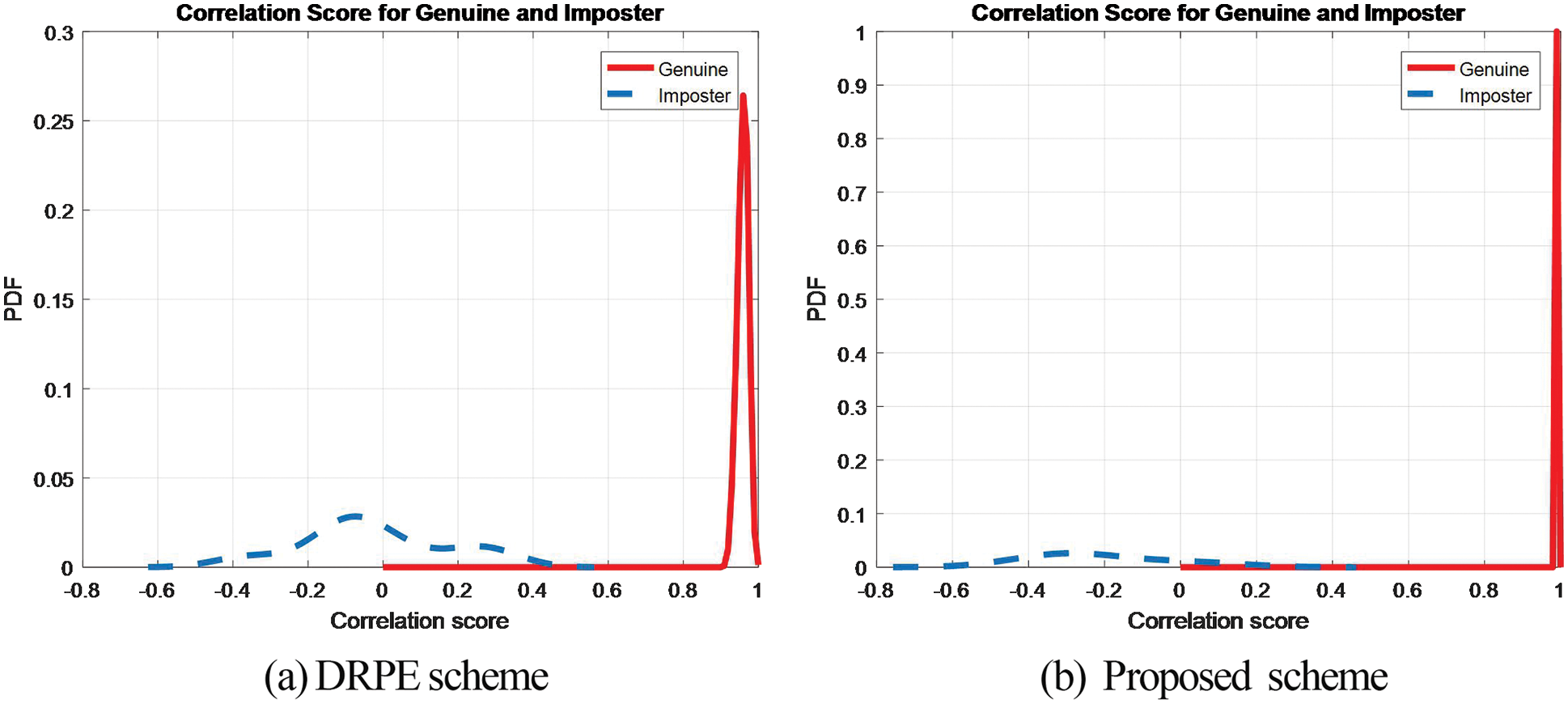
Figure 27: PTD and PFD of the cancellable biometric recognition systems based on the proposed and the DRPE schemes on LFW dataset

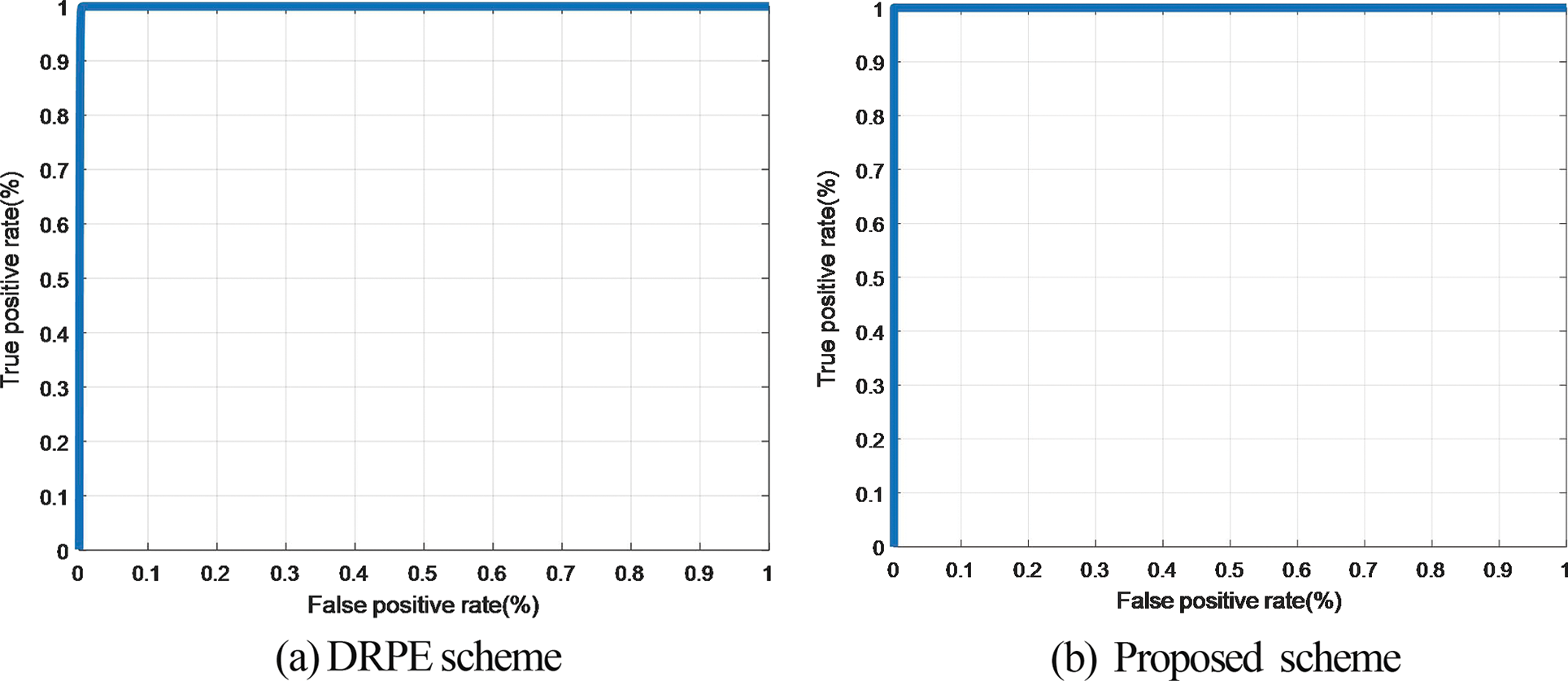
Figure 28: ROC curves of the cancellable biometric recognition systems based on the proposed and the DRPE schemes on LFW dataset

Figs. 29–33 show the histograms of all investigated biometric samples in order to compare between the proposed and the DRPE encryption schemes. The proposed scheme clearly produces almost flat and uniform histograms for all cases. Hence, a secure cancellable biometric system can be built upon the proposed encryption scheme. Tabs. 2–6 depict the correlation values for genuine and imposter tests with the proposed and the DRPE encryption schemes. The results reflect the superiority of the cancellable biometric system based on the proposed encryption scheme according to the genuine and imposter distributions.

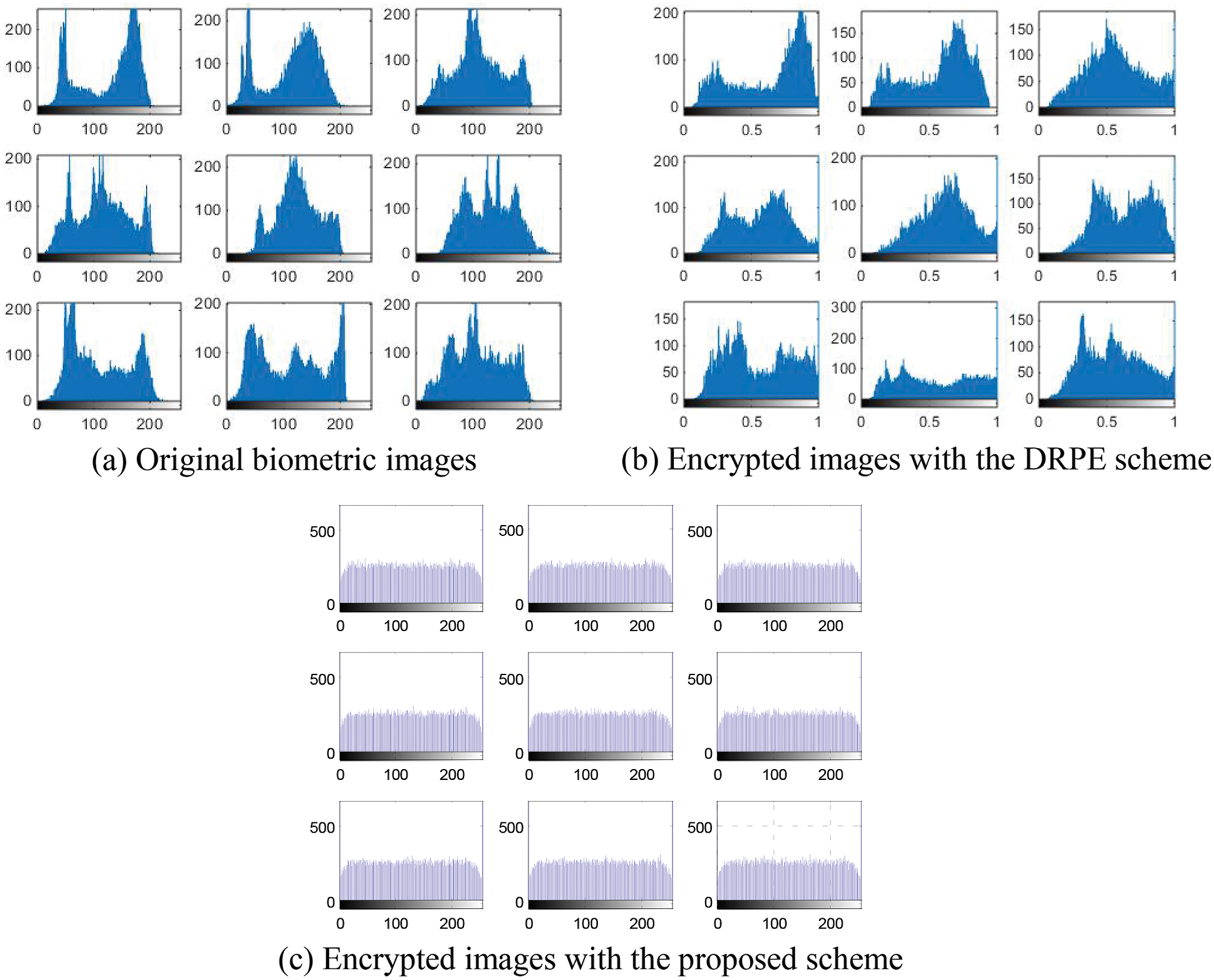
Figure 29: Histograms of original biometric images, encrypted images with the DRPE scheme and encrypted images with the proposed scheme on the ORL sample 1 dataset

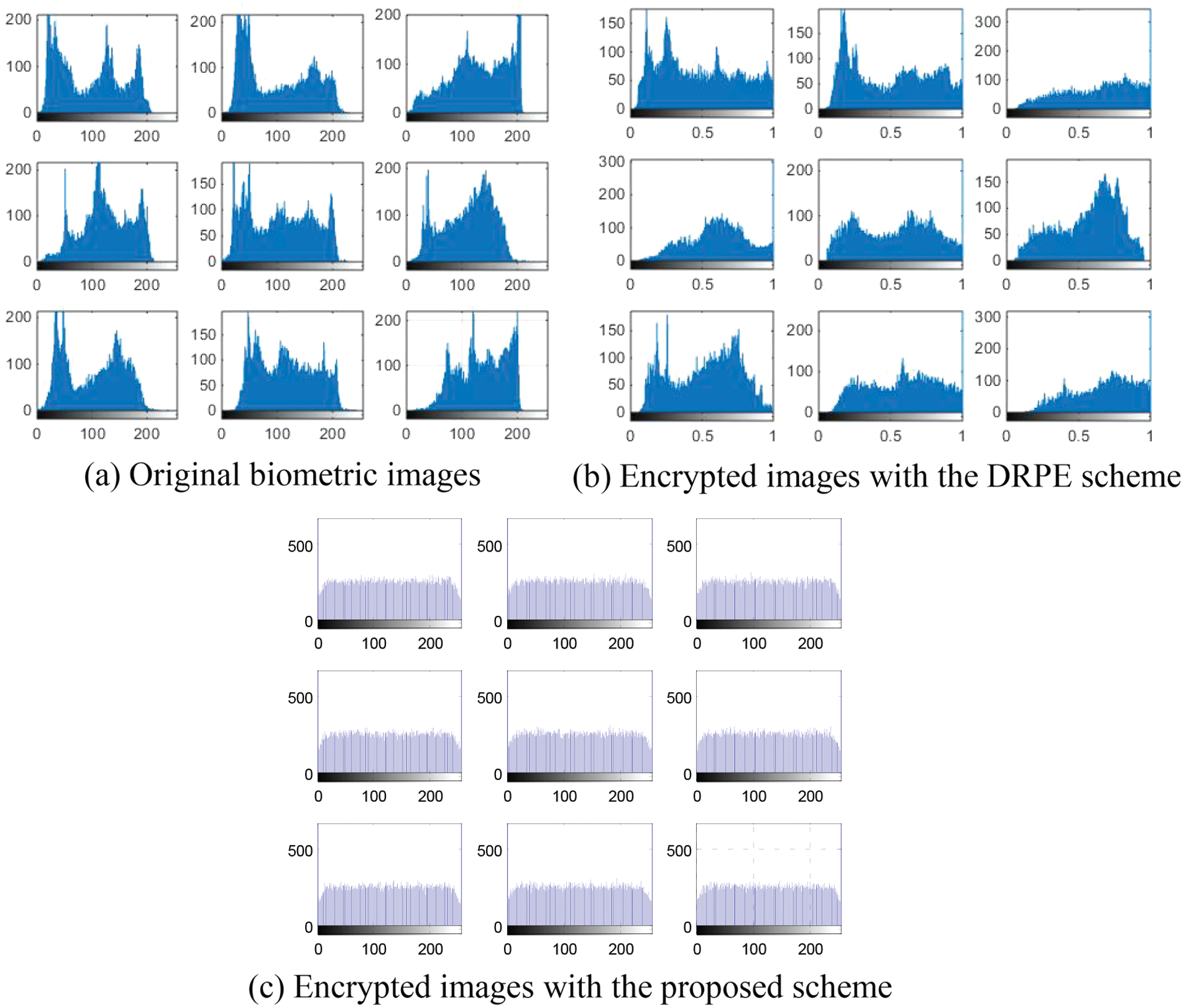
Figure 30: Histograms of original biometric images, encrypted images with the DRPE scheme and encrypted images with the proposed scheme on the ORL sample 2 dataset

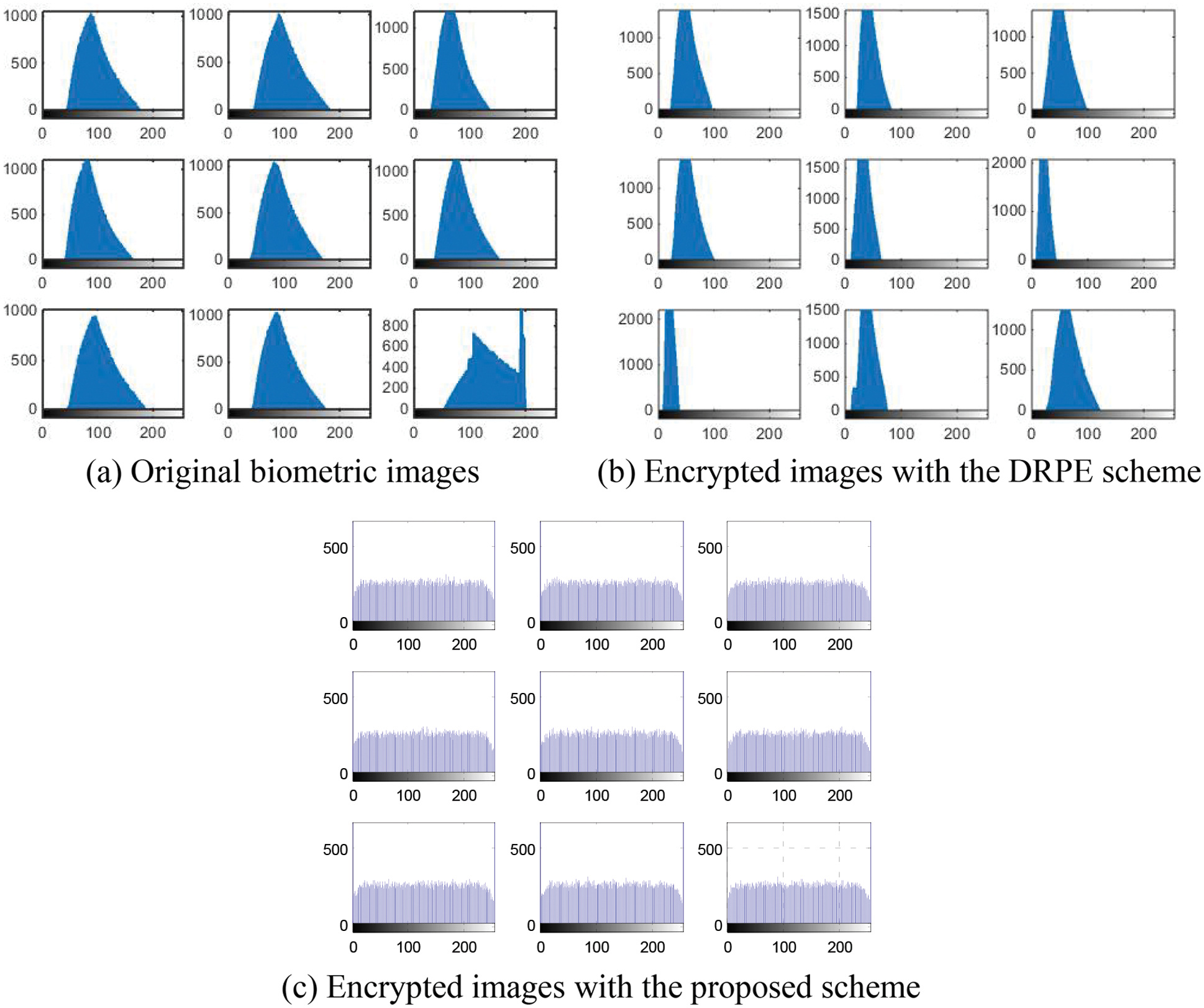
Figure 31: Histograms of original biometric images, encrypted images with the DRPE scheme and encrypted images with the proposed scheme on the FVC sample 3 dataset

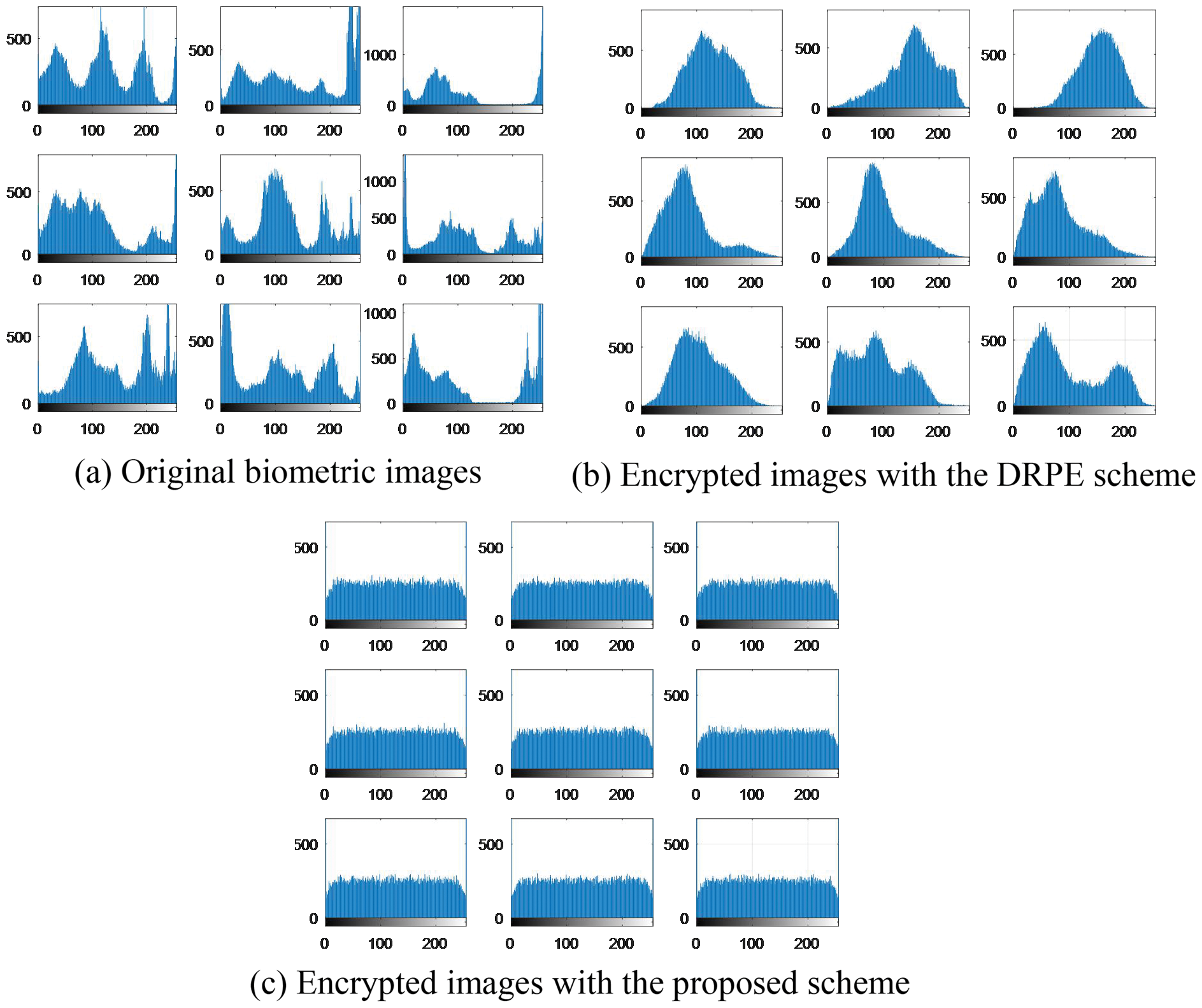
Figure 32: Histograms of original biometric images, encrypted images with the DRPE scheme and encrypted images with the proposed scheme on the FERET dataset

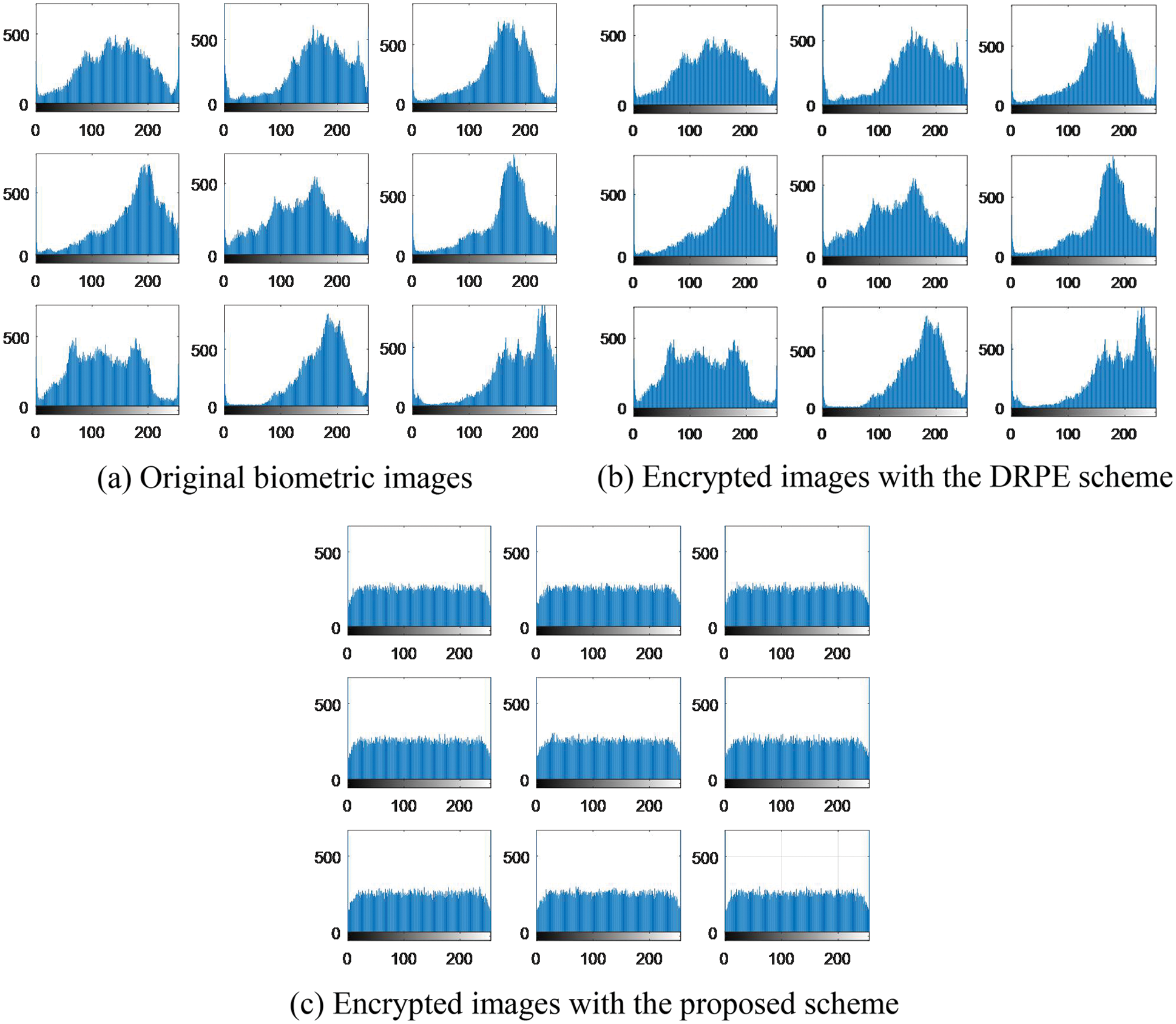
Figure 33: Histograms of original biometric images, encrypted images with the DRPE scheme and encrypted images with the proposed scheme on the LFW dataset

5.2 Experimental Results

FPGA tests on sample 1 and sample 2 have been implemented to check the system performance. Tab. 7 shows the results of the proposed design using a Virtex5 FPGA. Fig. 34 presents the simulation Xilinx results. Fig. 35 displays the encrypted outputs of the biometric images of sample 1 and sample 2 with the proposed scheme. The PTD, PFD, and ROC curves for the authentication stage of the proposed cancellable biometric recognition system on images of sample 1 and sample 2 are shown in Figs. 36 and 37. These curves reveal the threshold and error probability in the authentication process. The threshold value, which is used for discrimination, specifies the intersection between the PTD and PFD curves. It is clear that the implemented FPGA model of the proposed cancellable biometric recognition system succeeds in all experiments.

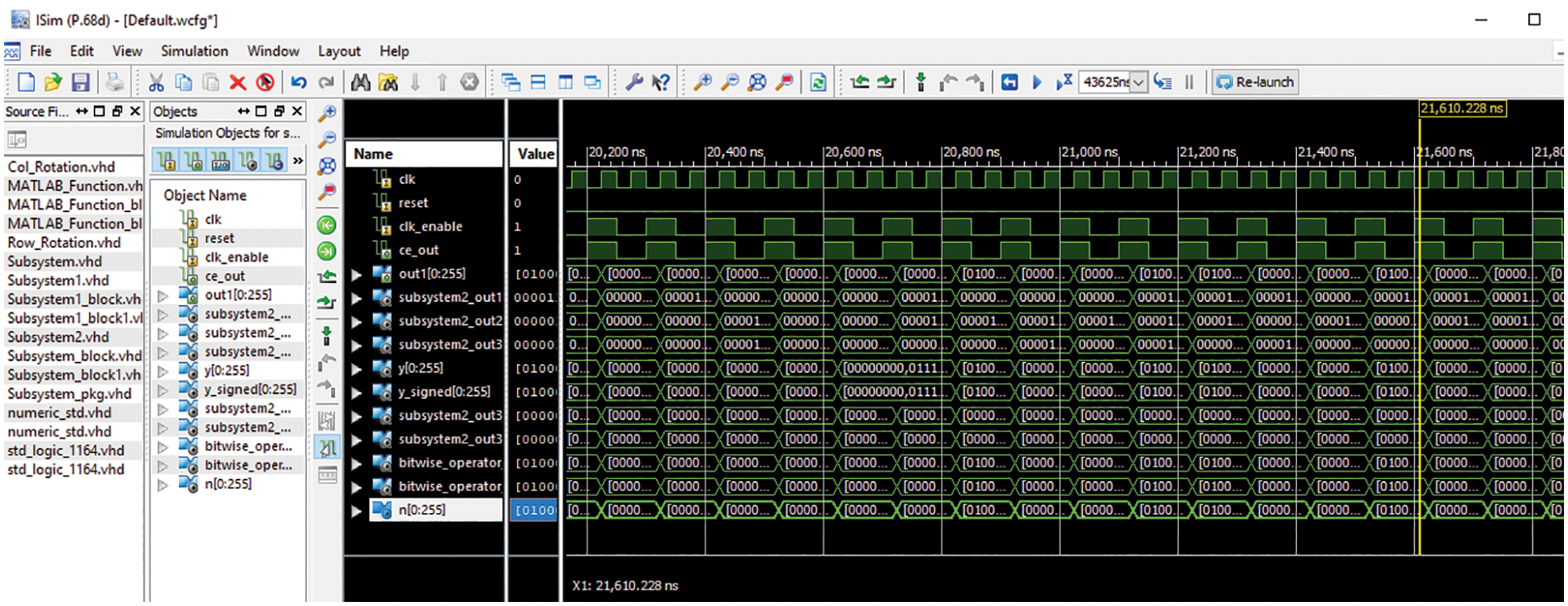
Figure 34: Simulated Xilinx output

Figure 35: FPGA outputs for face and fingerprint datasets

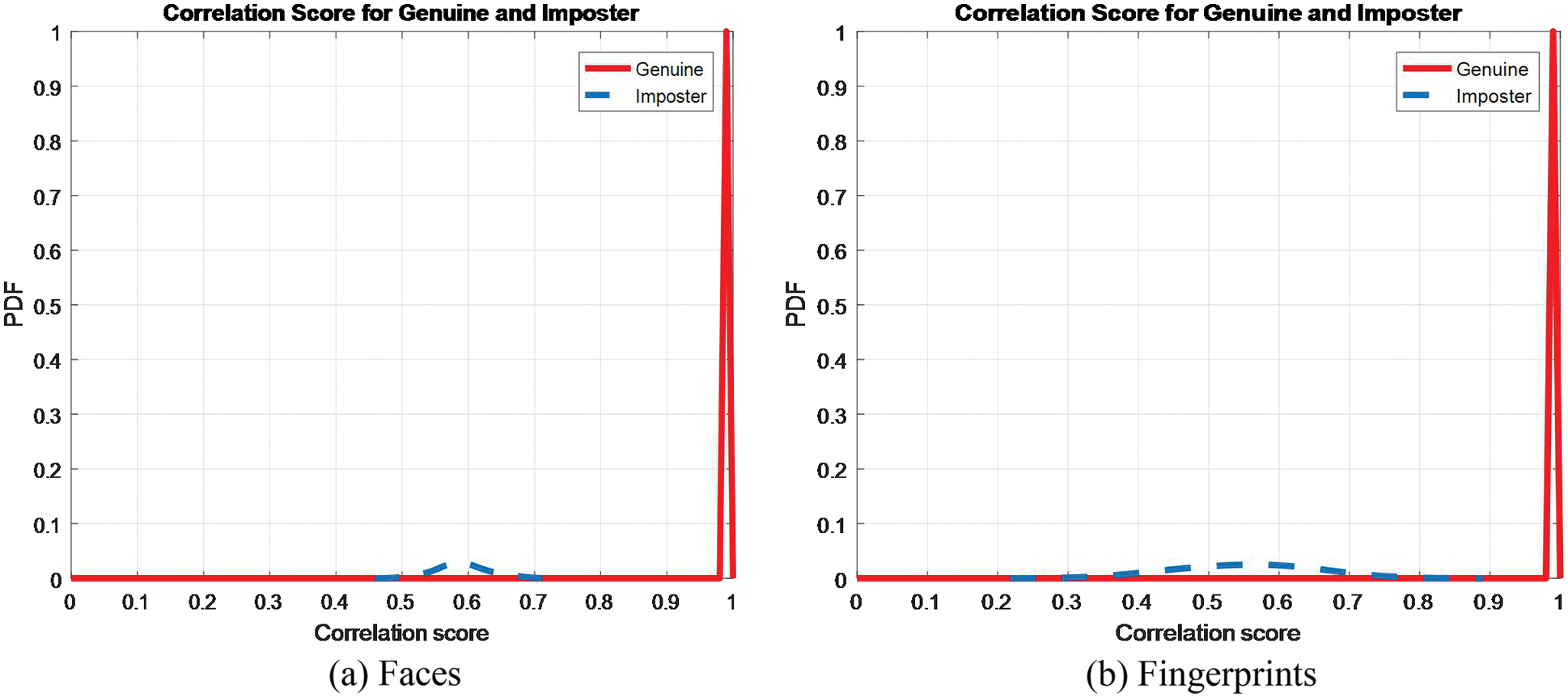
Figure 36: PTD and PFD curves of the proposed FPGA model on ORL and FVC datasets

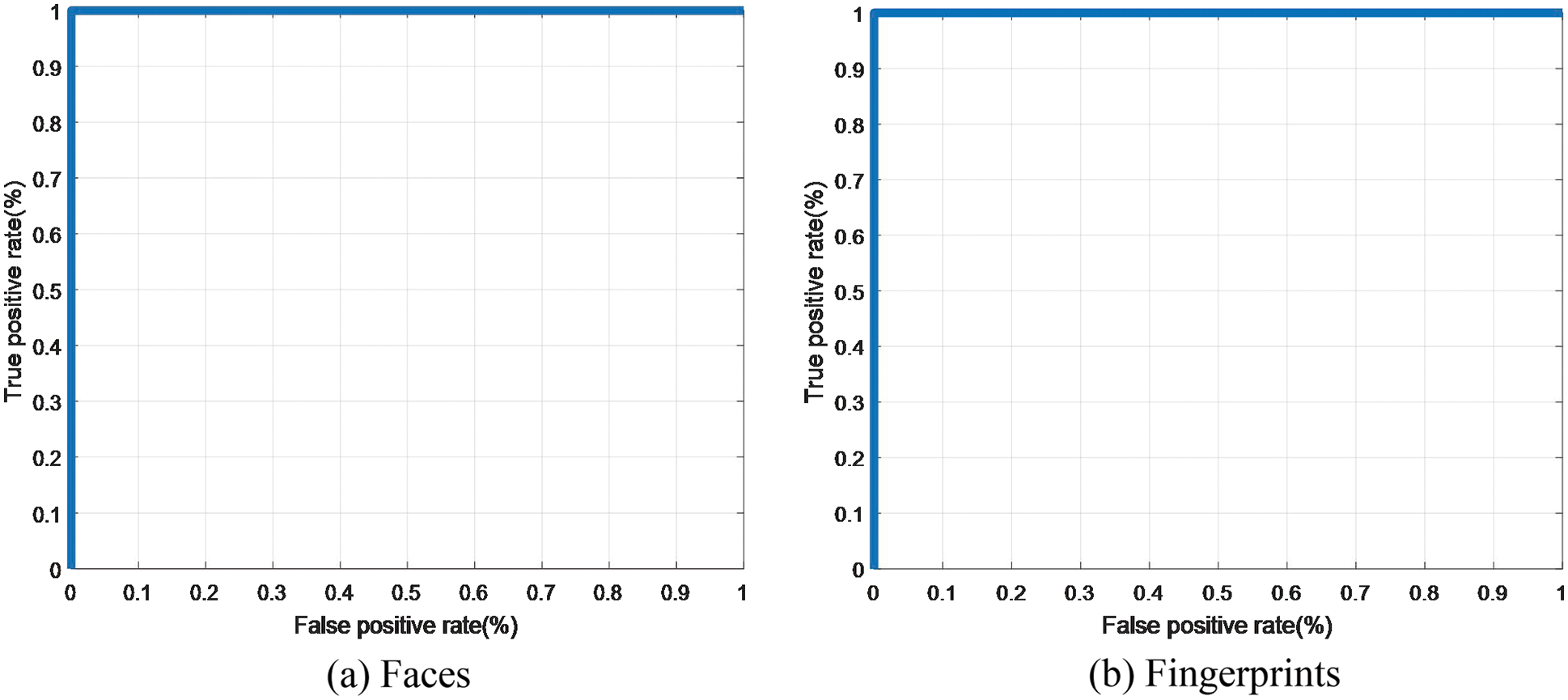
Figure 37: ROC curves of the proposed FPGA model on ORL and FVC datasets

6  Conclusions

This paper investigated a modern biometric-based security application, namely cancellable biometric recognition. The 3D chaotic logistic map is exploited for this purpose. It is used to scramble biometric traits, including faces and fingerprints, to generate the cancellable biometric traits. Through the proposed cryptosystem, the user privacy is maintained. In addition, the distinguishability of biometric traits is guaranteed. The proposed cancellable biometric recognition has been evaluated statistically based on EER and area under ROC curves (AROC). Three datasets have been utilized in the performance evaluation of the proposed system. Simulation results revealed EER values of 6.2460 × 10−13 and average AROC values of 0.9998 for the proposed cancellable biometric recognition system.

Acknowledgement: Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R66), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Funding Statement: Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R66), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  A. Algarni, G. El Banby, S. Ismail, W. El-Shafai, F. El-Samie et al., “Discrete transforms and matrix rotation based cancelable face and fingerprint recognition for biometric security application,” Entropy, vol. 22, no. 12, pp. 1–24, 2020. [Google Scholar]

 2.  A. Alarifi, M. Amoon, M. Aly and W. El-Shafai, “Optical PTFT asymmetric cryptosystem based secure and efficient cancelable biometric recognition system,” IEEE Access, vol. 8, pp. 221246–221268, 2020. [Google Scholar]

 3.  L. A. Abou elazm, S. Ibrahim, M. Egila, H. Shawky, M. Elsaid, W. El-Shafa et al., “Cancelable face and fingerprint recognition based on the 3D jigsaw transform and optical encryption,” Multimedia Tools and Applications, vol. 3, pp. 1–26, 2020. [Google Scholar]

 4.  N. Soliman, M. Khalil, A. Algarni, S. Ismail, R. Marzouk et al., “Efficient HEVC steganography approach based on audio compression and encryption in QFFT domain for secure multimedia communication,” Multimedia Tools and Applications, vol. 5, pp. 1–35, 2020. [Google Scholar]

 5.  A. Alarifi, S. Sankar, T. Altameem, K. Jithin, M. Amoon et al., “Novel hybrid cryptosystem for secure streaming of high efficiency H. 265 compressed videos in IoT multimedia applications,” IEEE Access, vol. 8, pp. 128548–128573, 2020. [Google Scholar]

 6.  O. Faragallah, A. Afifi, W. El-Shafai, H. El-Sayed, E. Naeem et al., “Investigation of chaotic image encryption in spatial and FrFT domains for cybersecurity applications,” IEEE Access, vol. 8, pp. 42491–42503, 2020. [Google Scholar]

 7.  W. El-Shafai, S. El-Rabaie, M. El-Halawany and F. Abd El-Samie, “Encoder-independent decoder-dependent depth-assisted error concealment algorithm for wireless 3D video communication,” Multimedia Tools and Applications, vol. 77, no. 11, pp. 13145–13172, 2018. [Google Scholar]

 8.  W. El-Shafai, “Pixel-level matching based multi-hypothesis error concealment modes for wireless 3D H. 264/MVC communication,” 3D Research, vol. 6, no. 3, pp. 1–11, 2015. [Google Scholar]

 9.  H. El-Hoseny, W. Abd El-Rahman, W. El-Shafai, G. El-Banby, E. El-Rabaie et al., “Efficient multi-scale non-sub-sampled shearlet fusion system based on modified central force optimization and contrast enhancement,” Infrared Physics & Technology, vol. 10, no. 2, pp. 102–123, 2019. [Google Scholar]

10. H. Hammam, W. El-Shafai, E. Hassan, A. El-Azm, M. Dessouky et al., “Blind signal separation with noise reduction for efficient speaker identification,” International Journal of Speech Technology, vol. 4, no. 6, pp. 1–16, 2021. [Google Scholar]

11. N. El-Hag, A. Sedik, W. El-Shafai, H. El-Hoseny, A. Khalaf et al., “Classification of retinal images based on convolutional neural network,” Microscopy Research and Technique, vol. 84, no. 3, pp. 394–414, 2021. [Google Scholar]

12. W. El-Shafai, F. Mohamed, H. Elkamchouchi, M. Abd-Elnaby and A. ElShafee, “Efficient and secure cancelable biometric authentication framework based on genetic encryption algorithm,” IEEE Access, vol. 9, pp. 1–25, 2021. [Google Scholar]

13. W. El-Shafai, I. Almomani and A. Alkhayer, “Optical bit-plane-based 3D-JST cryptography algorithm with cascaded 2D-FrFT encryption for efficient and secure HEVC communication,” IEEE Access, vol. 9, pp. 35004–35026, 2021. [Google Scholar]

14. A. Canuto, F. Pintro and J. Xavier-Junior, “Investigating fusion approaches in multi-biometric cancelable recognition,” Expert Systems with Applications, vol. 40, no. 6, pp. 1971–1980, 2013. [Google Scholar]

15. M. Sandhya and M. Prasad, “Securing fingerprint templates using fused structures,” IET Biometrics, vol. 6, no. 3, pp. 173–182, 2017. [Google Scholar]

16. M. Barrero, E. Maiorana, J. Galbally, P. Campisi and J. Fierrez, “Multi-biometric template protection based on Homomorphic encryption,” Pattern Recognition, vol. 67, no. 10, pp. 149–163, 2017. [Google Scholar]

17. Y. Lai, Z. Jin, A. Teoh, B. Goi, W. Yap et al., “Cancelable iris template generation based on indexing-first-one hashing,” Pattern Recognition, vol. 64, no. 1, pp. 105–117, 2017. [Google Scholar]

18. S. Umer, B. Dhara and B. Chanda, “A novel cancelable iris recognition system based on feature learning techniques,” Information Sciences, vol. 406, no. 407, pp. 102–118, 2017. [Google Scholar]

19. S. El-Khamy, M. Hadhoud, M. Dessouky, B. Salam and F. Abd El-Samie, “Blind multichannel reconstruction of high-resolution images using wavelet fusion,” Journal of Applied Optics, vol. 44, no. 34, pp. 7349–7356, 2005. [Google Scholar]

20. O. Faragallah, H. El-sayed, A. Afifi and W. El-Shafai, “Efficient and secure opto-cryptosystem for color images using 2D logistic-based fractional Fourier transform,” Optics and Lasers in Engineering, vol. 137, no. 6, pp. 1–15, 2021. [Google Scholar]

21. W. El-Shafai, E. El-Rabaie, M. El-Halawany and F. Abd El-Samie, “Efficient multi-level security for robust 3D color-plus-depth HEVC,” Multimedia Tools and Applications, vol. 77, no. 23, pp. 30911–30937, 2018. [Google Scholar]

22. K. Al-Afandy, W. El-Shafai, E. El-Rabaie, F. Abd El-Samie, O. Faragallah et al., “Robust hybrid watermarking techniques for different color imaging systems,” Multimedia Tools and Applications, vol. 77, no. 19, pp. 25709–25759, 2018. [Google Scholar]

23. W. El-Shafai, S. El-Rabaie, M. El-Halawany and F. Abd El-Samie, “Security of 3D-HEVC transmission based on fusion and watermarking techniques,” Multimedia Tools and Applications, vol. 78, no. 19, pp. 27211–27244, 2019. [Google Scholar]

24. W. El-Shafai, S. El-Rabaie, M. El-Halawany and F. Abd El-Samie, “Efficient hybrid watermarking schemes for robust and secure 3D-MVC communication,” International Journal of Communication Systems, vol. 31, no. 4, pp. 1–23, 2018. [Google Scholar]

25. ORL database, 2021. [Online]. Available: https://www.cl.cam.ac.uk/research/dtg/attarchive/facedatabase.html. [Google Scholar]

26. Fingerprint verification competition, (FVC2000 DB1:secure desktop scanner by keytronic2021. [Online]. Available: http://bias.csr.unibo.it/fvc2000/databases.asp. [Google Scholar]

27. CASIA-IrisV3 database, 2021. [Online]. Available: http://www.cbsr.ia.ac.cn/english/IrisDatabase.asp. [Google Scholar]

28. CASIA palm print image database, 2021. [Online]. Available: http://biometrics.idealtest.org/dbDetailForUser.do?id=5. [Google Scholar]

29. A. Mahmoud, W. El-Shafai, T. Taha, S. El-Rabaie, O. Zahran et al., “A statistical framework for breast tumor classification from ultrasonic images,” Multimedia Tools and Applications, vol. 80, no. 4, pp. 5977–5996, 2021. [Google Scholar]

30. O. Faragallah, M. AlZain, H. El-Sayed, J. Al-Amri, W. El-Shafai et al., “Secure color image cryptosystem based on chaotic logistic in the FrFT domain,” Multimedia Tools and Applications, vol. 79, no. 3, pp. 2495–2519, 2020. [Google Scholar]

31. O. Faragallah, M. Alzain, H. El-Sayed, J. Al-Amri, W. El-Shafai et al., “Block-based optical color image encryption based on double random phase encoding,” IEEE Access, vol. 7, pp. 4184–4194, 2018. [Google Scholar]