A New Sine-Ikeda Modulated Chaotic Key for Cybersecurity

1  Introduction

Recently, cryptographic systems have gained importance because of the broad usage of multimedia in various fields. Hence, it is essential to strengthen the security of multimedia content against illegitimate users. Recently, chaotic map-based security algorithms have gained much attention and are being widely used to conceal intelligible information that is present in images. Hence, it becomes essential to construct a chaotic map that offers excellent security. One of the primary reasons for emphasizing security in chaotic maps is the keyspace. The keyspace can be expanded by increasing the space of control parameter, initial value, or iteration time. The work presented here focuses on expanding the chaotic range of chaotic control parameters using a novel chaotic map and the development of a key generation algorithm to conceal information stored in the cloud.

In general, most prevailing image encryption techniques depend on chaotic maps [1–12]. In [13], the designed map exhibits chaos when the chaotic parameter varies from 0 to 1.7, so the keys expansion technique was additionally applied. In [14], the logistic map has been used as chaotic map. The adversary can very easily detect the keys due to the restricted chaotic range and the presence of blank windows in the bifurcation plot. In [15], the Lyapunov exponent value is very low which shows the presence of weak keys, and in some regions the Lyapunov exponent is negative. The negative Lyapunov exponent indicates the presence of blank windows in the bifurcation plot.

However, many encryption techniques are crypt analyzed due to inadequate key space and weak keys. For instance, [16] deals with a cryptanalysis scheme on a logistic map based on a limited choice of logistic parameters. In [17], it has been pointed out that the presence of weak keys in chaotic maps causes security issues in cryptosystems. Recently, in [18], cryptanalysis has been performed by locating the elementary value of the logistic map related to the notion of reduced key space. New chaotic equations [19,20] have been developed based upon which encryption algorithms have been proposed. These chaotic expressions require little iteration to satisfy the property of sensitive dependence on initial conditions. Furthermore, the proposed 2D chaotic maps in [21–26] exhibit hyperchaotic properties for a subset of chaotic parameters but are not chaotic outside of this subset.

In this article, we propose a Sine Ikeda modulated map and a key generation algorithm to improve the security of images stored in the cloud. The designed map provides sufficient keyspace, optimum sensitivity to initial conditions and hyperchaotic behavior throughout the chaotic range. The proposed algorithm behaves like a one-time pad and offers considerable security. Moreover, the randomness of the key generated has been tested using the standard NIST test, and the results are found to be excellent. The designed chaotic key can be used to secure stored medical images, military-related images, intelligent transportation images [27,28] and so on.

The subsequent sections are framed as follows. Section 2 describes the basic and Sine Ikeda modulated maps. Section 3 describes the designed key generation algorithm. In Section 4, performance analysis for the chaotic maps and the key generation algorithm has been performed and Section 5 concludes the article.

2  Description of the Chaotic Map

An Ikeda map [29] is a 2D iterative chaotic map that was first used in optics to model light passing around an optical cavity consisting of a nonlinear dielectric medium, and is described mathematically in parametric form as follows:

xn+1=1+α(xncosφn−ynsinφn) (1)

yn+1=α(xnsinφn+yncosφn) (2)

φn=β−γ/(1+xn2+yn2) (3)

This map acts chaotic for values  0.5≤α≤0.95 , β=0.4   and   γ=6 .

2.1 Proposed Chaotic Map

The proposed chaotic map (Sine Ikeda modulated map) has been constructed by adding sine and Ikeda maps. The chaotic region of the map is stretched over a wide range. Thus, the keyspace of the designed map is expanded. Moreover, the total number of chaotic parameters and the sensitivity of the map to initial conditions increase compared to the Ikeda map. The proposed chaotic map can be defined mathematically as follows:

xn+1=1+α(xncosφn−ynsinφn)+μsin(πxn) (4)

yn+1=α(xnsinφn+yncosφn)+μsin(πyn) (5)

φn=β−γ/(1+xn2+yn2) (6)

The control parameters μ,α  and γ act chaotic when   0≤μ<∞ , 0≤α≤1.18 and 0≤γ<∞  and the parameter  β=0.4 . The state space plot helps us to visualize the dynamics of the chaotic map. Fig. 1 shows the state space plot of the Ikeda and the Sine Ikeda modulated map for  α=0.95,  γ=6 and  μ=10 .

Figure 1: 2D state space plot of the (a) Ikeda and (b) Sine Ikeda modulated map

The chaotic nature of the proposed map can be proved mathematically by using Schwarzian derivative, considering the Eqs. (4) and (5) separately.

Definition: The Schwarzian derivative [30] of the differentiable function f at point z=(xn,yn) is given by,

Sfz=U−32(V)2 (7)

where U=d3f(Z)/dZ3df(Z)/dZ and V=(d2f(Z)/dZ2df(Z)/dZ)2

Theorem: The map f(X,Y)∈C3  shows the period–doubling bifurcation route to chaos when the Schwarzian derivative  (Sfz) is negative for X,Y≥0.

The evidence of the concept is in [31]. The designed map in Eqs. (4) and (5) meets the condition  Sfz<0 , as (V)2 in Eqs. (4) and (5) are much larger than U for all values of  X,Y≥0 .

2.2 Sensitivity of the Designed Map

The most important property of the chaotic map is its sensitive dependence on the initial conditions. Fig. 2a shows a time series plot of two Sine Ikeda modulated maps with one-digit variation in their initial conditions. The first map (x1) is plotted with the initial condition   x0=1.8888887 , and the second map (x2) is plotted with the initial condition  x0=1.8888888 . Even though, the two maps initially occupy closer points, they take different paths from the second iteration. This outcome shows that the designed map is highly sensitive to the initial conditions. Fig. 2b exhibits the difference between maps x1 and x2. Figs. 2c and 2d show the time series plot of two Ikeda maps with one-digit variation in initial conditions and the difference between the two Ikeda maps. Comparing Figs. 2b and 2d, takes approximately thirty-five iterations, whereas Fig. 2b takes only two iterations for the two maps to diverge. This outcome shows that the designed map is extremely sensitive to initial conditions.

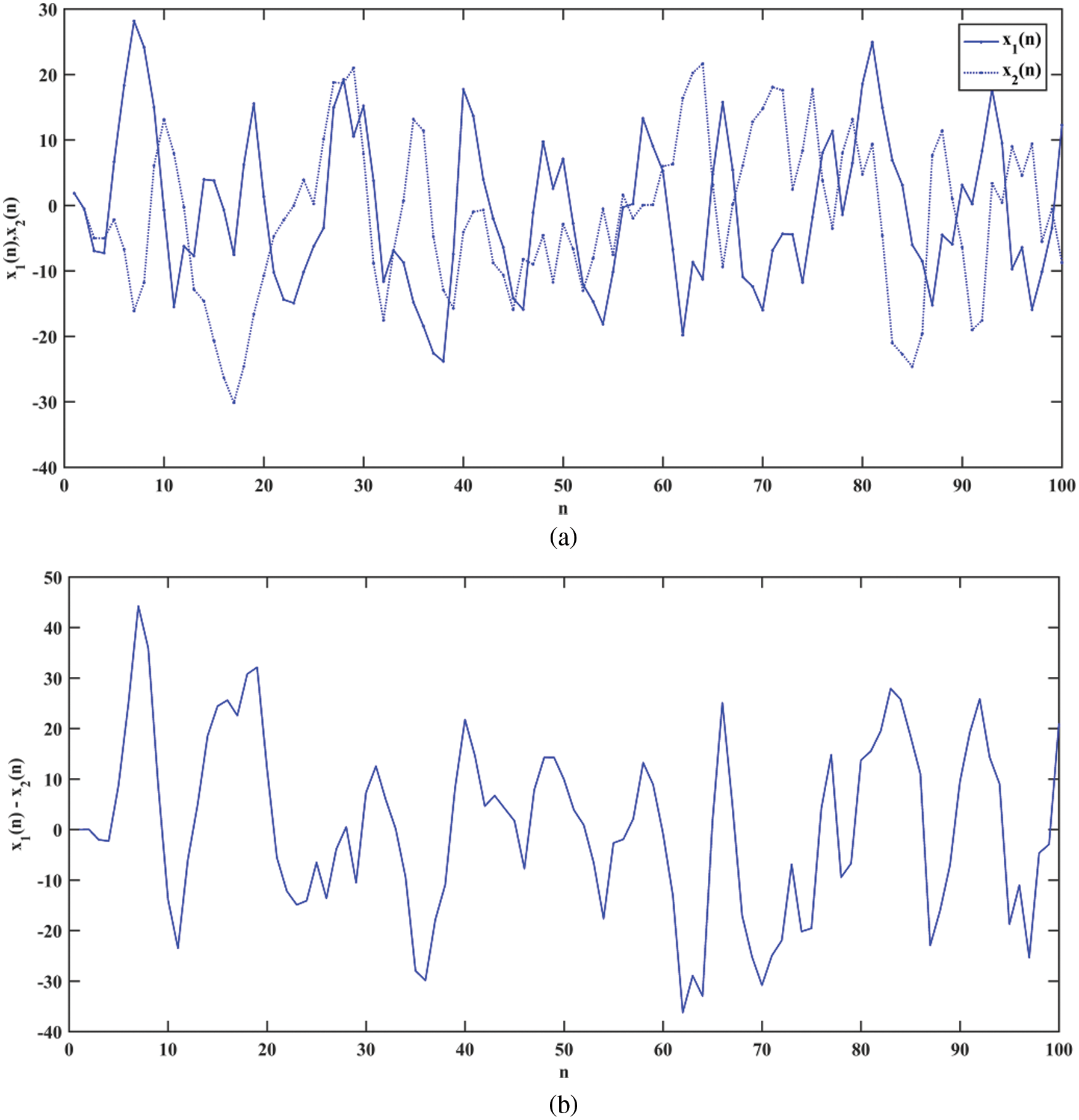
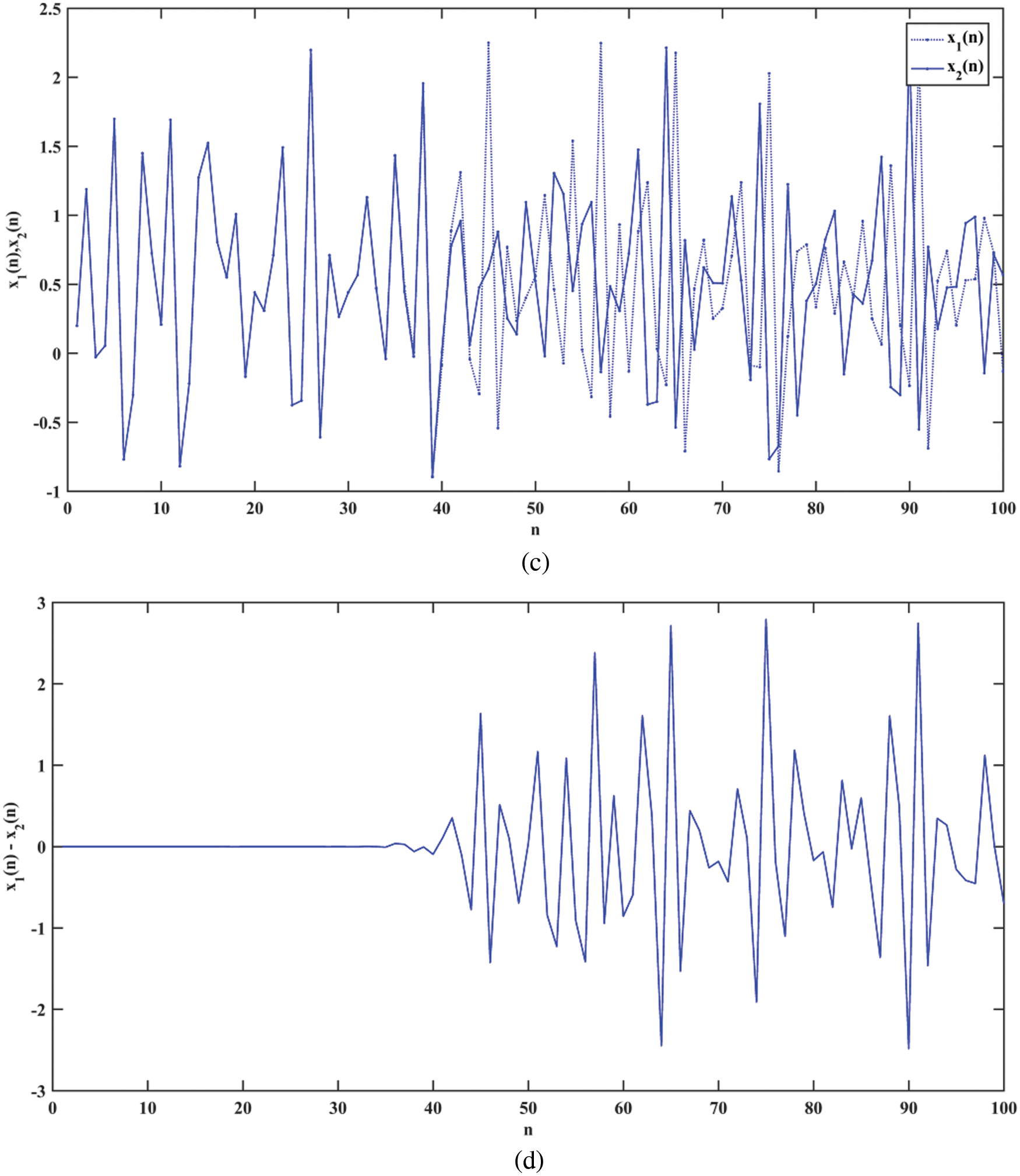
Figure 2: Plot of (a) Proposed map with a one-digit change in initial conditions (b) The difference between them (c) Ikeda maps with a one-digit change (d) The difference between them

3  Key Generation

The algorithm for key generation using the designed chaotic map is stated below in this section.

Step 1: Generate L sequences of x and y using the Eqs. (4)–(6) by choosing random control parameters μ,α  and γ . In this work, α=0.95,  γ=6 and  μ=10 and the initial seed keys as x0=1.8888887 and y0=0.9234567 have been chosen.

Step 2: Calculate the harmonic means of the generated sequences using the formula hx=L1x1+1x2+1x3+…1xL

Step 3: Take the harmonic means hx and hy and use it as a seed key for x0 and y0 .

Step 4: Use the generated seed key and new values of random control parameters μ,α  and γ to generate a new set of sequences of x and y using the Eqs. (4)–(6).

Step 5: The generated set of sequences of x and y are then represented as a matrix as the dimension of the image to be concealed.

The key generated can be made more secure by randomly changing the control parameter values after each iteration. Thus, the adversary cannot detect the keys, even using phase plots. The key provided to each image to be encrypted can also be changed by providing the initial seed key as the harmonic mean derived from the image. This acts as a one-time pad, and the adversary cannot hack the key from the image.

4  Performance Analysis

In this segment, the bifurcation diagram of the Sine Ikeda modulated map, the Lyapunov exponent and the bifurcation entropy, which are the most important characteristics of the chaotic systems, are analyzed. The parameters used for analysis are  x1=0.2 ,  y1=0.8 , γ=6 ,  α=1.18 , and  β=0.4 .

4.1 Bifurcation Diagram

The bifurcation diagram illustrates the change in qualitative behavior of the map as the chaotic control parameters are varied. Fig. 3 shows the bifurcation structure of the Ikeda and the Sine Ikeda modulated maps. The bifurcation structure of the Ikeda map has blank windows, but the Sine Ikeda modulated map shows no sign of any blank windows. The blank windows do not exhibit chaos. Moreover, the proposed map exhibits bifurcations over a large chaotic parameter range compared to the state-of-the-art techniques. As a result, when compared to other chaotic maps, the Sine Ikeda modulated map is better suited for cryptographic systems.

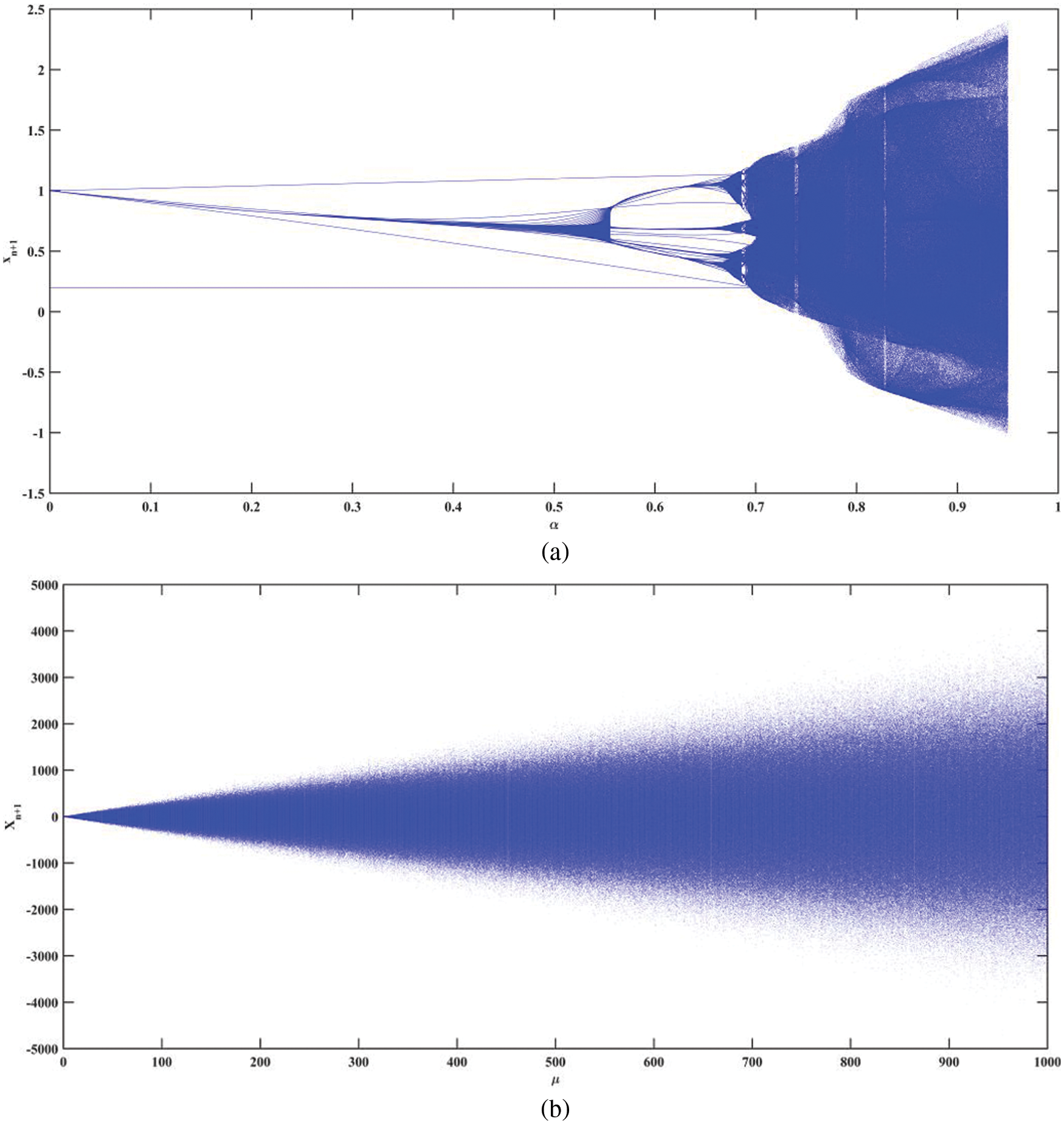
Figure 3: Bifurcation plot of (a) The Ikeda map and (b) The Sine Ikeda modulated map

4.2 Lyapunov Exponent

The characteristics of discrete chaotic maps are determined using a tool termed the Lyapunov exponent. A positive Lyapunov exponent signifies the presence of chaos. The Lyapunov exponents are calculated using the Jacobian matrix-based method that is described in [32]. Using (4), (5) and (6), the derivatives and the Jacobian matrix (J) can be written as:

∂xn+1∂xn=α[costn−2xn2(β−tn)sintn−2xnyn(β−tn)costn]+μπcosπxn (8)

∂xn+1∂yn=α[−sintn−2xnyn(β−tn)sintn−2yn2(β−tn)costn (9)

∂yn+1∂xn=α[sintn+2xn2(β−tn)costn−2xnyn(β−tn)sintn (10)

∂yn+1∂yn=α[costn+2xnyn(β−tn)costn−2yn2(β−tn)sintn]+μπcosπyn (11)

J=[∂xn+1∂xn∂xn+1∂yn∂yn+1∂xn∂yn+1∂yn] (12)

Similarly, the Jacobian matrix of the Ikeda map is computed using Eqs. (1)–(3). Fig. 4 provides the Lyapunov exponent plot of the Ikeda, and the Sine Ikeda modulated map. The Lyapunov exponent of the Sine Ikeda modulated map is more positive compared to the Ikeda map. Therefore, the Sine Ikeda modulated map outperforms the basic Ikeda map in terms of the Lyapunov exponent. Furthermore, the Lyapunov exponent value is much larger than the existing chaotic map, which indicates that the proposed map is highly sensitive to initial conditions. Additionally, the two Lyapunov exponent values (LE1 and LE2) are positive in the proposed map, which shows that the Sine Ikeda modulated map exhibits hyperchaotic behavior. The Ikeda map exhibits chaotic behavior because only one Lyapunov exponent is positive. Also, existing 2D maps exhibit hyperchaotic behavior for very few values of the chaotic parameter. Therefore, compared to the Ikeda map and the existing 2D maps, it is very difficult to predict the output of the proposed map because of the hyperchaotic property. Hence, the proposed chaotic map exhibits the desirable characteristics of a cryptographic system.

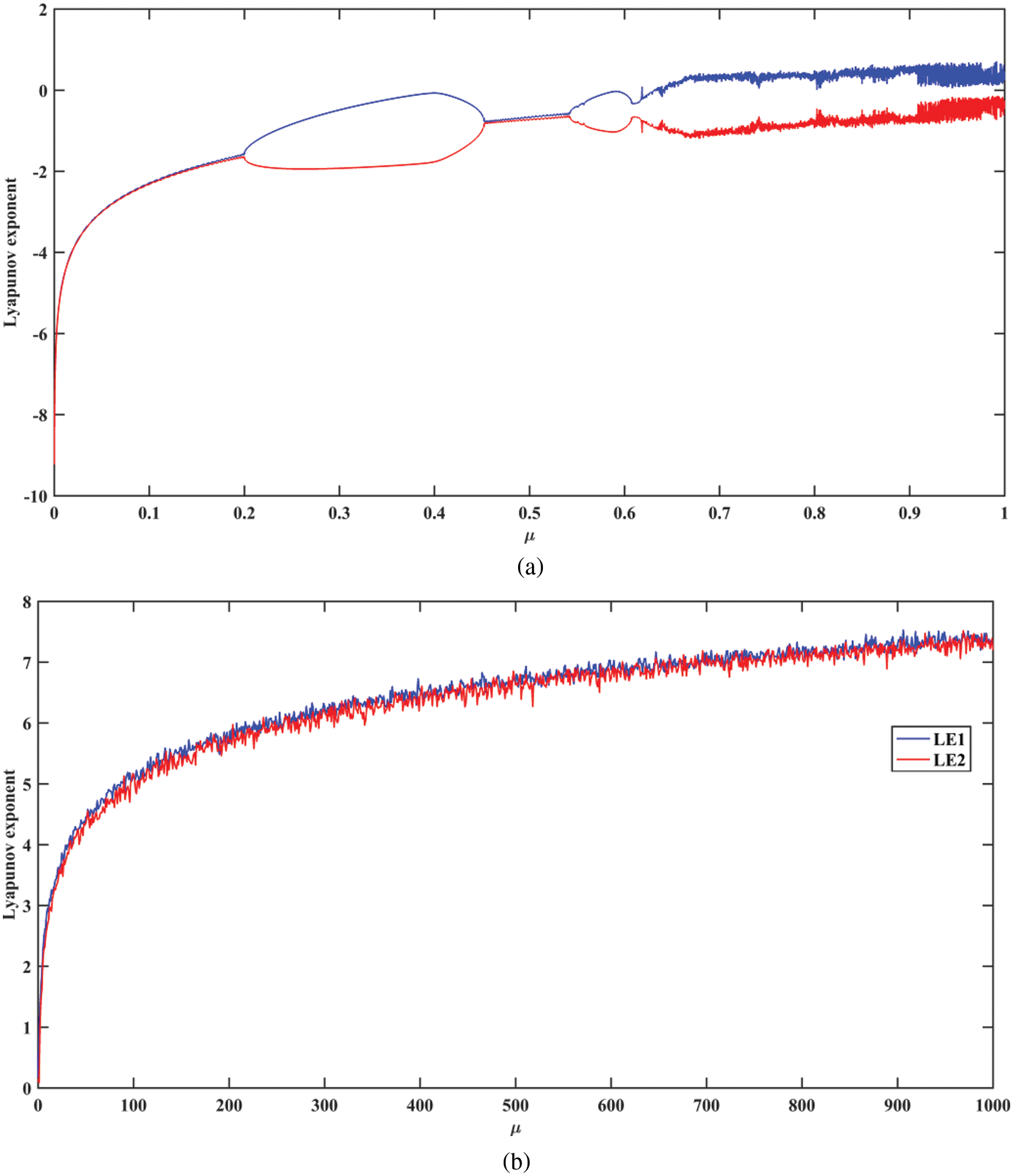
Figure 4: The plots of Lyapunov exponent for (a) The Ikeda map and (b) The Sine Ikeda modulated map

4.3 Bifurcation Entropy

The bifurcation entropy specifies the measure of uncertainty present in the bifurcation structure. Fig. 5 shows the plot of the bifurcation entropy of the Ikeda map and the Sine Ikeda modulated map for 256 samples. The bifurcation entropy of the Ikeda map is maximal for very few values of the chaotic parameter, but the bifurcation entropy of the Sine Ikeda modulated map is always at its peak after some initial iteration. Also, the bifurcation entropy is zero for a few values of the chaotic parameter in the case of the Ikeda map, but the bifurcation entropy is non-zero and is greater than four in the case of the proposed map. Therefore, the Sine Ikeda modulated map outperforms other maps when used in cryptographic systems.

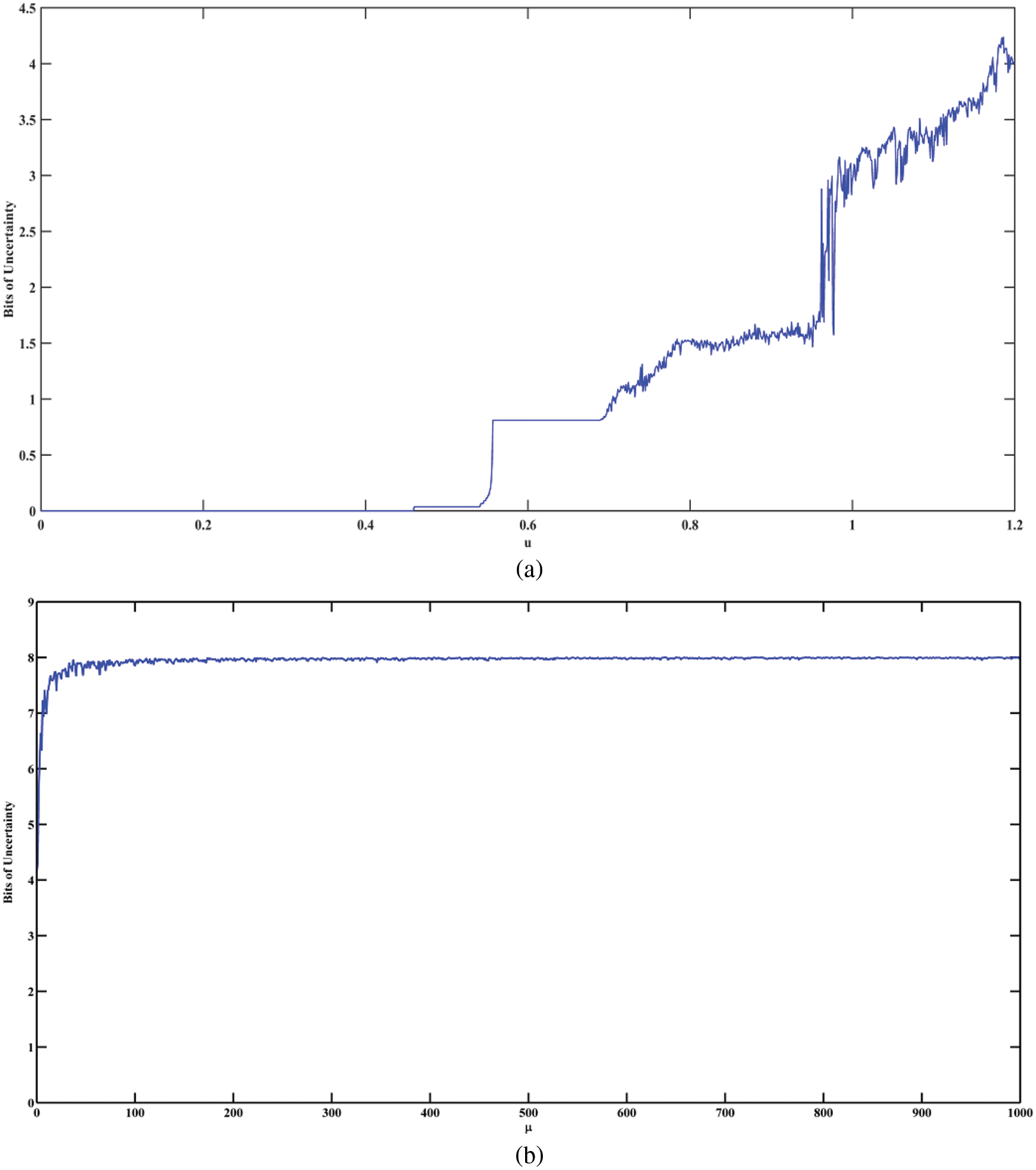
Figure 5: The plots of bifurcation entropy for (a) The Ikeda map and (b) The proposed map

4.4 NIST Test for the Randomness of the Designed Chaotic key

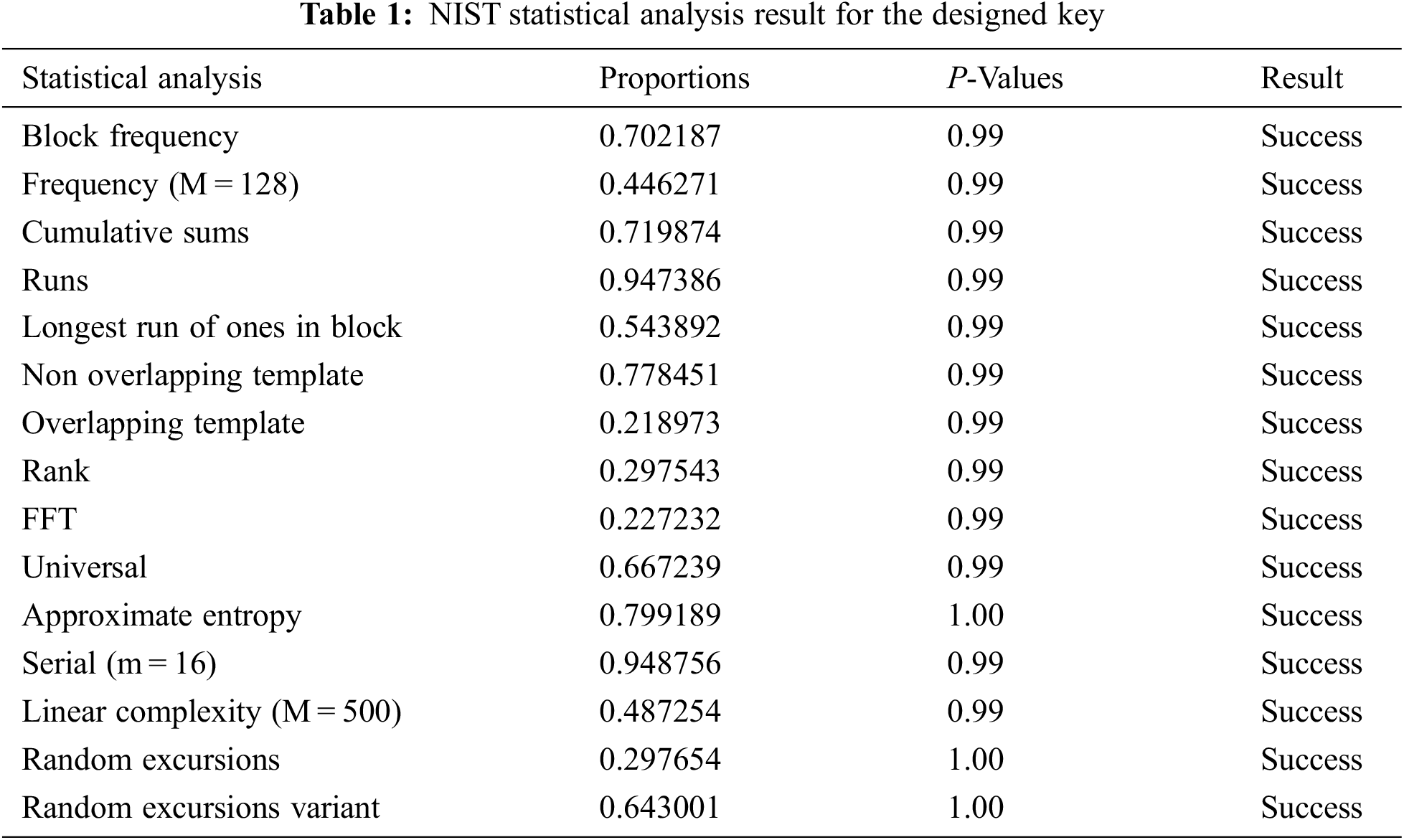
The randomness of the keys generated using the proposed sine-modulated Ikeda is verified using the NIST statistical test suite SP 800-22 [33]. First, the keys generated were represented in binary form and tested using hundred samples of ten lakh bit length keys, and their significance level is 0.001. In Tab. 1, all the P-values are greater than the significant value and have passed the test. Fifteen test results demonstrate that the designed sine-modulated Ikeda map has enough randomness to be used in cryptographic systems.

4.5 Comparison of the Existing Technique with the Designed Chaotic Map-Based Key

In this section, the designed chaotic map has been compared with the existing techniques in terms of sensitive dependence on initial conditions, average cycle length, maximum Lyapunov exponent, and approximate entropy. Tab. 2 shows the comparison of the existing chaotic map-based key with that of the proposed key.

The first parameter from the table shows the number of iterations required for the chaotic maps to change their paths with a one-digit change in the initial condition. The initial conditions for all maps are assumed to be the same. The proposed chaotic map requires only two iterations compared to the existing map. This outcome shows that the sensitive dependence on the initial conditions is high compared to that of the existing 2D maps, which is the desirable characteristic of a chaotic key.

The second parameter is the cycle length. The cycle length of the chaotic map is important to decide on the dynamical degradation of the chaotic map. Also, Fig. 6 shows the comparison plot for different precisions. From Tab. 2 and Fig. 6, it could be inferred that the cycle length is larger compared to the existing technique. Therefore, the proposed map can be applied to the cryptographic system.

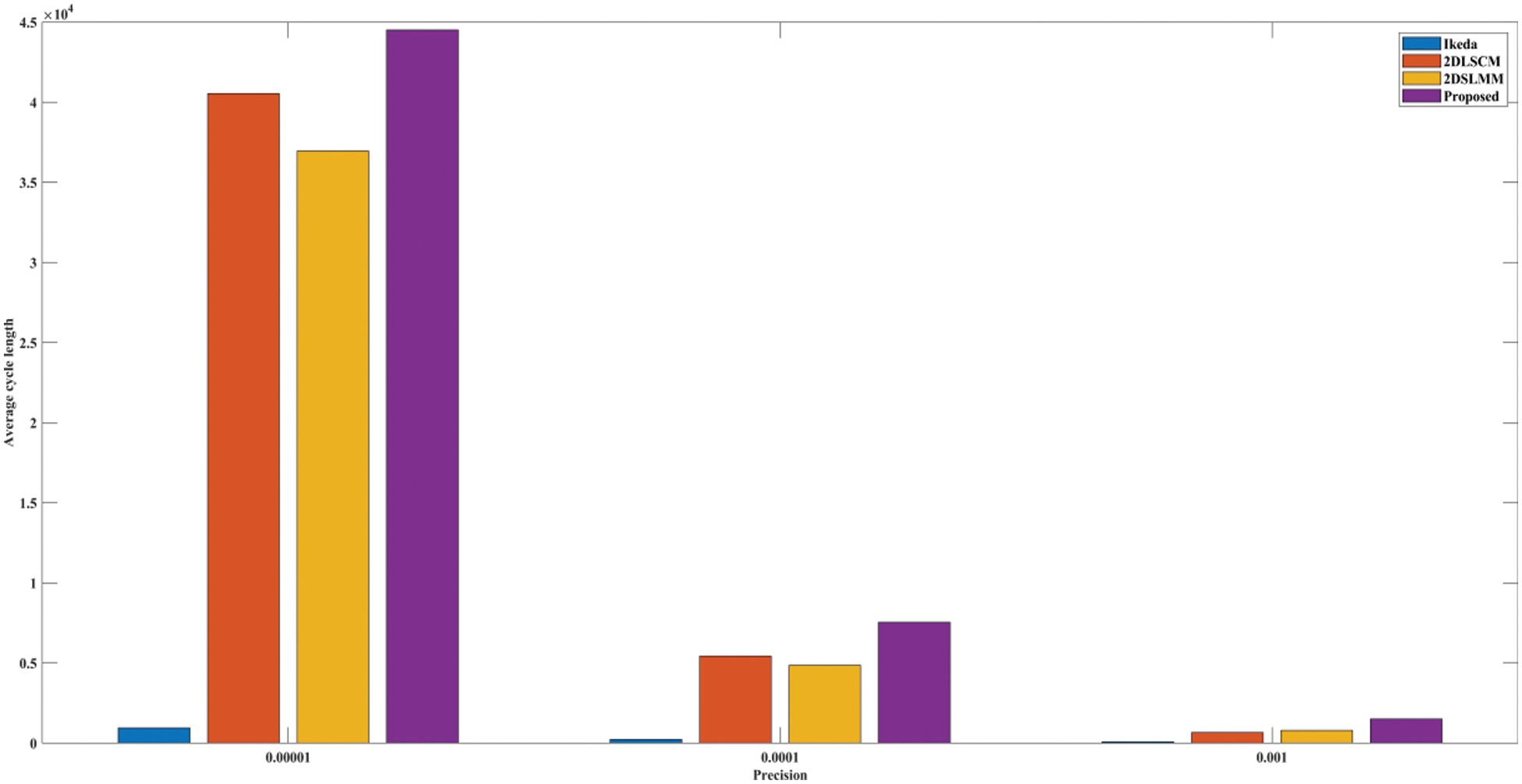
Figure 6: The plots of average cycle length vs. precision for different chaotic maps

The last parameter listed in the table is the approximate entropy of the key generated. The entropy is used to measure the randomness of the key. The maximum entropy for an eight-bit key is 8. It can be inferred from the above table that the designed map has an entropy close to 8 compared to the existing technique. As a result, an attacker will find it difficult to decode and interpret the keys.

5  Conclusions

In this article, a novel chaotic map has been designed that exhibits chaos over a wide range of the chaotic parameters so that the keyspace is increased. The proposed map has excellent sensitivity to the initial conditions. The absence of the blank window in the bifurcation plot of the designed map reduces the possibility of an exhaustive search attack. The increased number of chaotic parameters further enhances the security of cryptographic systems. Furthermore, the uncertainty and the Lyapunov exponent in the chaotic region are maximal and exhibit hyper-chaotic properties compared to the existing maps. Also, NIST test results show that the designed chaotic map provides excellent randomness; this outcome enhances its applications in cybersecurity.

Funding Statement: The author received no specific funding for this study.

Conflicts of Interest: The author declares that they have no conflicts of interest to report regarding the present study.

References

 1.  G. Jakimoski and L. Kocarev, “Chaos and cryptography: Block encryption ciphers based on chaotic maps,” IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, vol. 48, no. 2, pp. 163–169, 2001. [Google Scholar]

 2.  A. Belazi, A. A. Abd El-Latif and S. Belghith, “A novel image encryption scheme based on substitution-permutation network and chaos,” Signal Processing, vol. 128, no. 1, pp. 155–170, 2016. [Google Scholar]

 3.  W. Liu, K. Sun and C. Zhu, “A fast image encryption algorithm based on chaotic map,” Optics and Lasers in Engineering, vol. 84, no. 1, pp. 26–36, 2016. [Google Scholar]

 4.  Y. Abanda1 and A. Tiedeu, “Image encryption by chaos mixing,” IET Image Processing, vol. 10, no. 10, pp. 742–750, 2016. [Google Scholar]

 5.  W. Zhang, K. Wong, H. Yu and Z. Zhu, “An image encryption scheme using reverse 2-dimensional chaotic map and dependent diffusion,” Communications in Nonlinear Science and Numerical Simulation, vol. 18, no. 8, pp. 2066–2080, 2013. [Google Scholar]

 6.  N. K. Pareek, V. Patidar and K. K. Sud, “Image encryption using chaotic logistic map,” Image and Vision Computing, vol. 24, no. 9, pp. 926–934, 2006. [Google Scholar]

 7.  X. Yi, C. H. Tan and C. K. Siew, “A new block cipher based on chaotic tent maps,” IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, vol. 49, no. 12, pp. 1826–1829, 2002. [Google Scholar]

 8.  L. Kocarev and G. Jakimoski, “Logistic map as a block encryption algorithm,” Physics Letters A, vol. 289, no. 4–5, pp. 199–206, 2001. [Google Scholar]

 9.  G. Zhou, D. Zhang, Y. Liu, Y. Yuan and Q. Liu, “A novel image encryption algorithm based on chaos and line map,” Neurocomputing, vol. 169, no. 1, pp. 150–157, 2015. [Google Scholar]

10. K. Wong, B. S. -H. Kwok and W. -S. Law, “A fast image encryption scheme based on chaotic standard map,” Physics Letters A, vol. 372, no. 15, pp. 2645–2652, 2008. [Google Scholar]

11. H. Gao, Y. Zhang, S. Liang and D. Li, “A new chaotic algorithm for image encryption,” Chaos Solitons and Fractals, vol. 29, no. 2, pp. 393–399, 2006. [Google Scholar]

12. A. Ali, M. Masud, A. Rehman, C. Chen, A. Mehmood et al., “An effective blockchain based secure searchable encryption system,” Intelligent Automation & Soft Computing, vol. 33, no. 2, pp. 1183–1195, 2022. [Google Scholar]

13. S. De, J. Bhaumik and D. Giri, “A secure image encryption scheme based on three different chaotic maps,” Multimedia Tools and Applications, vol. 81, no. 4, pp. 5485–5514, 2022. [Google Scholar]

14. A. Elghandour, A. Salah and A. Karawia, “A new cryptographic algorithm via a two-dimensional chaotic map,” Ain Shams Engineering Journal, vol. 13, no. 1, pp. 101489, 2022. [Google Scholar]

15. O. Al-Hazaimeh, M. Al-Jamal, M. Bawaneh, N. Alhindawi and B. Hamdoni, “A new image encryption scheme using dual chaotic map synchronization,” The International Arab Journal of Information Technology, vol. 18, no. 1, pp. 95–102, 2021. [Google Scholar]

16. C. Li, S. Li, G. Chen and W. A. Halang, “Cryptanalysis of an image encryption scheme based on a compound chaotic sequence,” Image and Vision Computing, vol. 27, no. 8, pp. 1035–1039, 2009. [Google Scholar]

17. B. Wang, X. Wei and Q. Zhang, “Cryptanalysis of an image cryptosystem based on logistic map,” Optik, vol. 124, no. 14, pp. 1773–1776, 2013. [Google Scholar]

18. G. Alvarez, F. Montoya, M. Romera and G. Pastor, “Cryptanalysis of a discrete chaotic cryptosystem using external key,” Physics Letters A, vol. 319, no. 3–4, pp. 334–339, 2003. [Google Scholar]

19. Y. Zhang, D. Xiao, Y. Shu and J. Li, “A novel image encryption scheme based on a linear hyperbolic chaotic system of partial differential equations,” Signal Processing: Image Communication, vol. 28, no. 3, pp. 292–300, 2013. [Google Scholar]

20. M. T. Saleh and M. Haeri, “Chaos in the APFM nonlinear adaptive filter,” Signal Processing, vol. 89, no. 5, pp. 697–702, 2009. [Google Scholar]

21. X. -Y. Wang, Y. -Q. Zhang and Y. -Y. Zha, “A novel image encryption scheme based on 2-D logistic map and DNA sequence operations,” Nonlinear Dynamics, vol. 82, no. 1, pp. 1269–1280, 2015. [Google Scholar]

22. Z. Hua, F. Jin, B. Xu and H. Huang, “2D logistic–sine-coupling map for image encryption,” Signal Processing, vol. 149, no. 1, pp. 148–161, 2018. [Google Scholar]

23. Z. Hua, Y. Zhou, C. -M. Pun and C. L. Philip, “2D sine logistic modulation map for image encryption,” Information Sciences, vol. 297, no. 1, pp. 80–94, 2015. [Google Scholar]

24. H. Jiang, Y. Liu, Z. Wei and L. Zhang, “A new class of two-dimensional chaotic maps with closed curve fixed points,” International Journal of Bifurcation and Chaos, vol. 29, no. 7, pp. 1950094, 2019. [Google Scholar]

25. F. Hadjabi, A. Ouannas, N. Shawagfeh, A. -A. Khennaoui and G. Grassi, “On two-dimensional fractional chaotic maps with symmetries,” Symmetry, vol. 12, no. 5, pp. 1–13, 2020. [Google Scholar]

26. A. Elghandour, A. Salah and A. R. Karawia, “A new cryptographic algorithm via a two-dimensional chaotic map,” Ain Shams Engineering Journal, vol. 13, no. 1, pp. 101489, 2021. [Google Scholar]

27. W. Sun, X. Chen, X. R. Zhang, G. Z. Dai, P. S. Chang et al., “A multi-feature earning model with enhanced local attention for vehicle re-identification,” Computers, Materials & Continua, vol. 69, no. 3, pp. 3549–3560, 2021. [Google Scholar]

28. W. Sun, G. C. Zhang, X. R. Zhang, X. Zhang and N. N. Ge, “Fine-grained vehicle type classification using lightweight convolutional neural network with feature optimization and joint learning strategy,” Multimedia Tools and Applications, vol. 80, no. 20, pp. 30803–30816, 2021. [Google Scholar]

29. A. Kathleen, S. Tim and J. A. Yorke, Chaos: An Introduction to Dynamical Systems, Springer-Verlag, New York: Springer, 1997. [Online]. Available: https://link.springer.com/book/10.1007/b97589. [Google Scholar]

30. S. Hanis and R. Amutha, “A fast double-keyed authenticated image encryption scheme using an improved chaotic map and a butterfly-like structure,” Nonlinear Dynamics, vol. 95, no. 1, pp. 421–432, 2019. [Google Scholar]

31. G. Hacibekiroglu, M. Caglar and Y. Polatoglu, “The higher order schwarzian derivative: Its applications for chaotic behavior and new invariant sufficient condition for chaos,” Nonlinear Analysis: Real World Applications, vol. 10, no. 3, pp. 1270–1275, 2009. [Google Scholar]

32. G. Benettin, L. Galgani, A. Giorgilli and J. -M. Strelcyn, “Lyapunov characteristic exponents for smooth dynamical systems and for Hamiltonian systems: A method for computing all of them,” Meccanica, vol. 15, no. 1, pp. 9–20, 1980. [Google Scholar]

33. L. Bassham, A. Rukhin, J. Soto, J. Nechvatal, M. Smid et al., “A statistical test suite for random and pseudorandom number generators for cryptographic applications,” in Special Publication (NIST SPNational Institute of Standards and Technology, Gaithersburg, MD, USA, 2010 [online]. https://tsapps.nist.gov/publication/get_pdf.cfm?pub_id=906762. [Google Scholar]