Temperature Control Design with Differential Evolution Based Improved Adaptive-Fuzzy-PID Techniques

1  Introduction

CSTR is highly non linear and the reaction that occurs inside the reactor may be exothermic or endothermic in nature. The reactor is generally combined with an outer jacket in order to control the temperature parameter. During exothermic reactor evolution of heat is removed by the use of coolant stream during exothermic reaction whereas on endothermic heating medium is passed through jacket or coil for maintaining the reaction temperature. The exothermic or endothermic reactions are involved in the reactor, the temperature of the mixture varies with respect to time. This can be overcome by using a suitable controller which adapts to nonlinearity present in the process. Since model reference adaptive controller has the capability to adapt to the change in variation due to disturbance or any environmental conditions [1]. Nowadays, in industry, the control of chemical reactants is a vital task. Mostly, the chemical process is non-linear in nature and this nonlinearity affects the stability of the system. Conventional controller may not perform well in the case of variation in process dynamics due to the changes in environmental condition or due to the disturbances as it has fixed parameter coefficients. Adaptive controller has an ability to adjust its parameters automatically in order to compensate for the variations in the characteristic behaviour. The proposed work deals with application of Modified MRAC scheme to CSTR process in which MIT Rule is used along with Normalized Algorithm (Modified MIT Rule). Since the MIT Rule has some limitation of sensitivity to large or small changes in gamma (gain), it does not guarantee stability and convergences rate depends on gamma. To overcome this drawback, Modified MIT Rule is used. This gives better performance but still it will have high oscillation and overshoots. To reduce this, conventional PID controller, intelligent controller and Differential Evolution Algorithm based PID and Fuzzy is used in MRAC. The comparative analysis is made for MRAC, incorporation of PID and Fuzzy in MRAC, and optimization of PID and Fuzzy using DE in MRAC.

2  Literature Survey

The literature survey of various techniques employed for improving the performance of transient response of the CSTR process and the review is made on each process and their limitation is also discussed. Swarnkar et al. [2] proposed a GA based modified MRAC to tune the parameters in which it is adding PID controller with MRAC and it provides better transient response. Brijendra et al. [3] proposed a customized MIT Rule for II order system. Since MIT is sensitive to large and small deviations in amplitude of desired input signal, adaptation gain is important and depends on the signal levels.To reduce the sensitivity they have used MIT along with Normalization algorithm. Zuperl et al., [4] gave an idea of how the performance of temperature controlling system would work with respect to classical PID and fuzzy logic control and comparison is done. Upadhy et al. [5] gave an idea of how the fuzzy controller is used to maintain the speed of DC motor. It provides better response compared to the normal controller. Cheng-Hung et al. [6] gave a clear idea about how to identify the model for CSTR process by using mathematical concept and have used MRAC controller to maintain the temperature of the reactor constant and provides the result for both Conventional PID and MRAC controller and conveys that MRAC is superior to conventional controller even without parameter change. Brest et al., [7] used the concept of Model Reference Adaptive Control of velocity control systems which does not attain acceptable performance over the extensive range of speed requirement, especially at low speed and there is no calculated rule to direct designers to choose the adaptation gains [8]. The fuzzy based model reference adaptive control will maintain the acceptable response inspite of the inputs.

From the literature survey it is observed that MRAC controller is to be used to maintain non-linear systems with the ability to adapt to change in variation due to environment or by load changes. But use of MRAC can control the system with large oscillation and overshoots with increase of adaptation gain as 5. This is to be reduced depending upon the constraint [9]. In case to reach the steady state soon, PID controller can be used along with DE, to provide optimal PID values. DE is used along with fuzzy to optimize the fuzzy membership function parameter. The nonlinear system used is CSTR and controlling parameter is temperature which is slow process in nature therefore the overshoot problem and settling time is to be taken into account.

3  Mathematical Modeling of the Plant

CSTR is highly nonlinear feature in nature and usually has wide operating ranges and the real time setup is shown in Fig. 1.

Figure 1: CSTR plant –Real time set up

The CSTR runs at steady state and is mixed. Due to this process, the CSTR is modeled to have less variation in concentration, temperature in the vessel. Since the temperature and concentration are same all around in the reaction tank, they are the equal at the outlet point [10]. Thus the temperature and concentration at the outlet are modeled as being the same as those inside the reactor. The mathematical expression for the system is represented by mass and energy balances equations. The assumptions are made to find the simplified differential equation form of reactor and given below: (Source: George Stephanopoulos 1990). [11–13]

a) Correct mixing in the process reactor and jacket

b) Steady value of volume reactor and jacket

Mass balance equation is given as,

VdCAdt=CA(Fi−F)+CAiFi−CAiF−rAV (1)

where, CA is the outlet concentration of reactor A in the reactor and rA is the reaction rate per unit volume. The Arrhenius equation is used for the reaction rate. The first- order reaction rate results in the corresponding equation,

rA=K0exp(−ERT)CA (2)

where, ko is the constant rate of reaction, E is the activation energy, R is the constant of gas, T is the temperature of reactor (R, Rankine or K, Kelvin).

The energy balance equation is given as,

dTdt=FiV(Ti−T)+JK0exp(−ERT)CA−QρCpV (3)

The Eqs. (1) and (3) contain non-linear functions of T and CA. They are joined and it is impossible to solve single equation alone. In the following section, state representation models are obtained. [14–16]

The transfer function of plant and the model are obtained from above Eqs. (1) and (3).

Transferfunctionofplantis,Gp(s)=2.23s+16.87s2+3.085s+1.485 (4)

Transferfunctionofmodelis,Gm(s)=5.37s2+3.19s+5.37 (5)

Thus the model obtained should provide desired response for the process which tells about how the PID parameters are adjusted to the variation in the process due to change in set point by using MRAC.

3.1 Controller Design

The block diagram of adaptive PID controller for CSTR plant is shown in Fig. 2. The input and output details are given below.

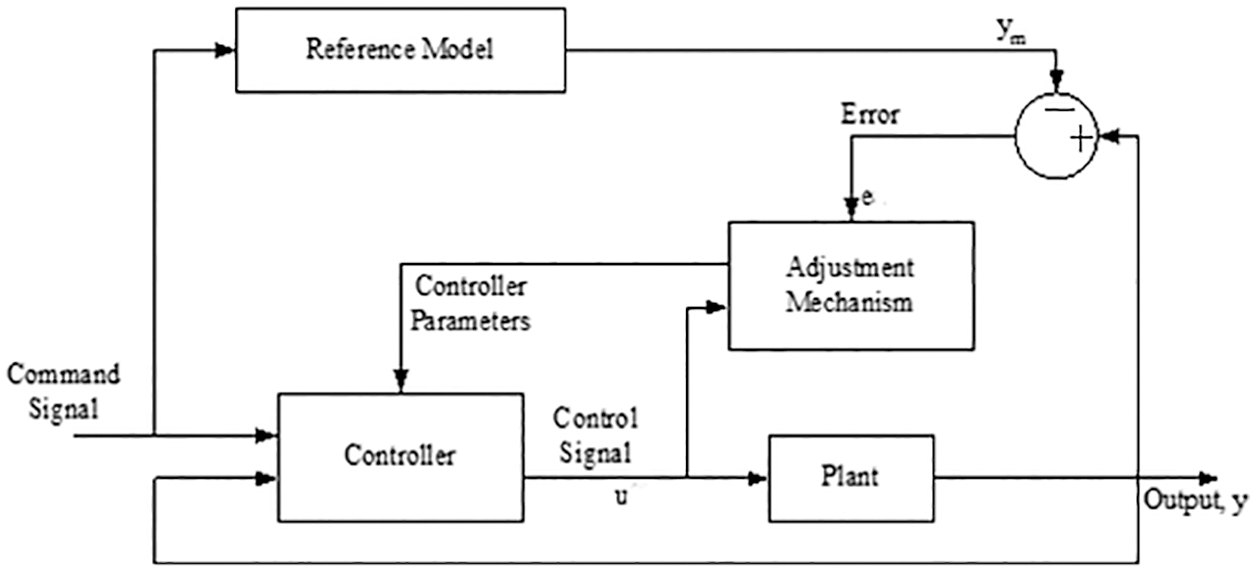
Figure 2: Block diagram of adaptive PID controller

Command Signal (Input) is the set value of Temperature, Output, ‘y’ is the process variable such as Actual Temperature of CSTR, ‘Ym’ is the reference transfer function, ‘U’ is the control signal or controller output to the CSTR process, ‘e’ is the error values to the adaptation mechanism and acts as an input to the controller, Controller parameters are Kp, Ti, Td present in the controller.

3.2 Modified MRAC Algorithm

The basic idea in adjusting controller parameters in MRAC is commonly known as the gradient approach. Thus, the gradient method of MRAC is often called the MIT rule. The MIT rule performs well when the adaptation gain γ is small. The size of γ is dependent on the value of the reference signal and the gain of the system. Moreover, the convergence rate critically depends on the γ . This is why we also have the normalized MIT rule. The rule is shown below.

dθdt=−γ∂J∂θ=−γ∂e∂θ (6)

The derivative ∂e∂θ is the sensitivity derivative of the system.

As MIT rule does not guarantee stability, it is imperative for people to modify it. As mentioned above, MIT rule let the users decide the critical parameter, which determines the rate of decrease of the cost function [17,18]. Thus it is possible to obtain a modified rule in which the rate of decrease of converge neither depends on gamma ( γ ), nor the value of the command signal. One successful way is to normalize and replace the MIT rule and it is shown in Eq. (7)

dθdt=−γe∂e∂θα+(∂e∂θ)T(∂e∂θ) (7)

In the above equation, the existence of the parameter α is introduced in case of division by zero. It is a small constant to prevent very low value of the denominator which can lead to instability in adaptation mechanism. Eq. (7) is called the normalized MIT rule which makes the adjustment rate dθdt not to depend totally on gamma ( γ ). Thus the stability of MRAC algorithm is guaranteed. Therefore, the controller parameter is adjusted by adjusting mechanism for which error between plant and model is given as input. It is used to control the manipulated variable this makes the response of the model to be followed by the plant which in turn makes inside temperature of the plant to be maintained as same as that of set point. From the response it is inferred that larger gain value makes the system to produce unstable response. To resolve this problem a small modification is done in MRAC (i.e., Normalized algorithm is used) which produces satisfactory result. [19–25]

3.3 Modified MRAC Using PID

The response of modified MRAC still has high oscillation, overshoot and long settling time. These can be reduced by tuning adaptive controller parameter using PID controller [26,27]. Therefore in the proposed work, PID controller is incorporated with MRAC which improves the transient characteristics of the plant response. The parameters are obtained by basic Ziegler Nichols Method. Error signals are taken as an input to the PID Controller. Tuning is done with PID controller. There is always a steady state error in proportional control. The error will decrease with increasing gain, but the tendency towards oscillation will also increase. The strength of integral action increases with decreasing integral time, Ti. The parameters K and Ti are chosen so that the closed-loop system is oscillatory. Damping increases with increasing derivative time, but decreases again when derivative time becomes too large.

3.4 Tuning MRAC Using Fuzzy Logic Controller

The concept of tuning MRAC by incorporating Fuzzy Inference System which improves performances better compare to conventional controller. The response of modified MRAC –PID has large overshoot with respect to increase of adaptation gain. This is to be reduced by use of some intelligent techniques. Therefore, the Mamdani type fuzzy inference system is used to tune the MRAC controller in order to reduce the transient characteristics performance of the CSTR plant to maintain the temperature of the reactor constant throughout the time. In the proposed work the input to the fuzzy is error and change in error and output is the manipulated variable that is inlet coolant flow rate. The number of membership function framed is 7 for each and the membership function used is triangular. The number of rules framed is 49. The range for error, change in error and coolant flow rate is (-15 10), (0 20) and (–1 1) is given to the system.

3.5 Tuning of PID Controller Using DE

The schematic diagram of DE algorithm is shown in Fig. 3. The steps involved in the tuning of proposed method are given below. The input and output details are given below.

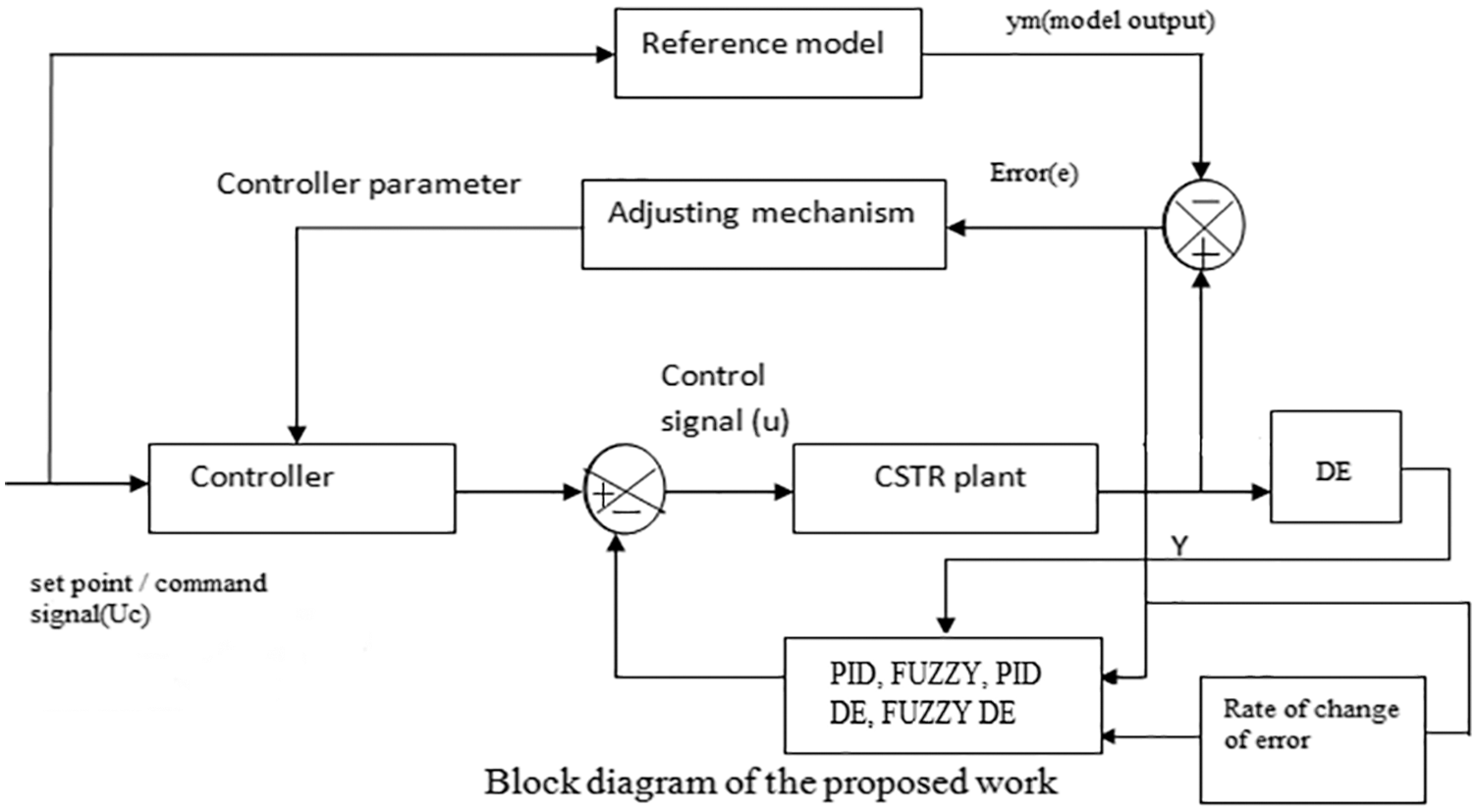
Figure 3: Proposed Block diagram of DE algorithm

Command Signal (Input) is the set value of Temperature, Output, ‘y’ is the process variable such as Actual Temperature of CSTR, ‘Ym’ is the reference transfer function, ‘U’ is the control signal or controller output to the CSTR process, ‘e’ is the error values to the adaptation mechanism and acts as an input to the controller, Controller parameters are Kp, Ti, Td present in the controller.

The steps involved in the tuning of proposed method are given below.

Step1: Setting DE optimization parameter

Step2: Initialize population size

Step3: Perform mutation and cross over operations. DE derived its name from the mutation operator it applies to mutate its individual. It generates the mutated individual for the principal parent. Then to complement the differential mutation search strategy, DE then uses a crossover operation, in which the mutated individual is mated with the principal parent and generates the offspring

Step4: Verify boundary constraints of the system

Step5: Selection process is made and is to ensure that the individuals given to the next generation are exactly with the best fitness values in the population

Step6: Repeat the steps 3 to 5 until new population completed

Step7: Repeat step 6 until fitness value converges and also met best solution till the end of generation.

The DE algorithm is used to get a optimal value for PID parameters. In the proposed work the number of population, crossover, mutation and generations used are 8, 0.7, 0.5 and 10. Total of 25 generations with a population size of 8 generated sufficient simulations. So, the initial population size chosen is 8. Crossover assists exploit and enhance the convergence. From empirical results and theoretical studies, all suggest a relatively higher probability pc for crossover in the range of 0.6 to 0.95, whereas the mutation probability pm is typically very low, around 0.1 to 0.5. First initialize P, I, D values. Normally, the PID values are initiated by applying Ziegler –Nichols tuning methods. The tuning values are 5.583, 0.4466 and 0.7274. Next is to reduce the transient characteristics since it calls the model response to read the overshoot and settling time value of current system and the start to evaluate the best member of the system up to 10th iteration since it is second order system. The fitness value is considered as the sum of overshoot and settling time. Next is the mutation here it replaces the low fitness population with the new vector and produce a new population with best fitness value. This process continues till the fitness values converges and met best solution till 10th iteration to get optimize values of P, I, D parameters.

3.6 Tuning of Fuzzy Using DE

The response obtained after tuning MRAC controller using has large overshoot with increase of adaptation gain 5. This is reduced by use of some optimization tool; therefore DE is used to optimize the value of fuzzy membership function structure. Due to excess running time the rules is reduced to 9 and the DE is used for 9 rules. Assume number of population, generation, mutation and crossover as 9,5,0,3 and 0.5. Initialize the value randomly by giving the default starting point as [–15 10 0 20 –1 1]. The search space range is given to search around that region to get best value, since lower and upper range for search space is [–20 5 –10 10 –1 0.5] and [–5 20 5 30 –0.5 1]. Next it reads the fuzzy membership function of current generation and get information of overshoot and settling time from the response using this it find best value. Then it goes for mutation and crossover from this it replaces the new vector population of best fitness to the lower fitness value. This process continues till it reaches 5th iteration. In each iteration, it finds best fitness value by using overshoot and settling time of that iteration. This makes the cost function to converge to make the global best. The result obtained using DE makes the fuzzy structure optimize and produces response with no overshoot and less settling time for increase of adaptation gain 5 compare to fuzzy at adaptation gain 5.

4  Results and Discussion

The result obtained using MRAC and incorporating different techniques like PID, PID+DE, Fuzzy and Fuzzy+DE with MRAC for improving the transient characteristics of CSTR plant are discussed here.

4.1 MRAC Controller

The set point given for system is 100 degree F. The reference model will produce the desired response that should track by the plant in order to maintain the particular temperature inside the reactor. To get a constant temperature of feed at outlet of the reactor MRAC controller is used in the system. The adaptation gain chosen is 5 for controller. The results obtain is shown in below Fig. 4.

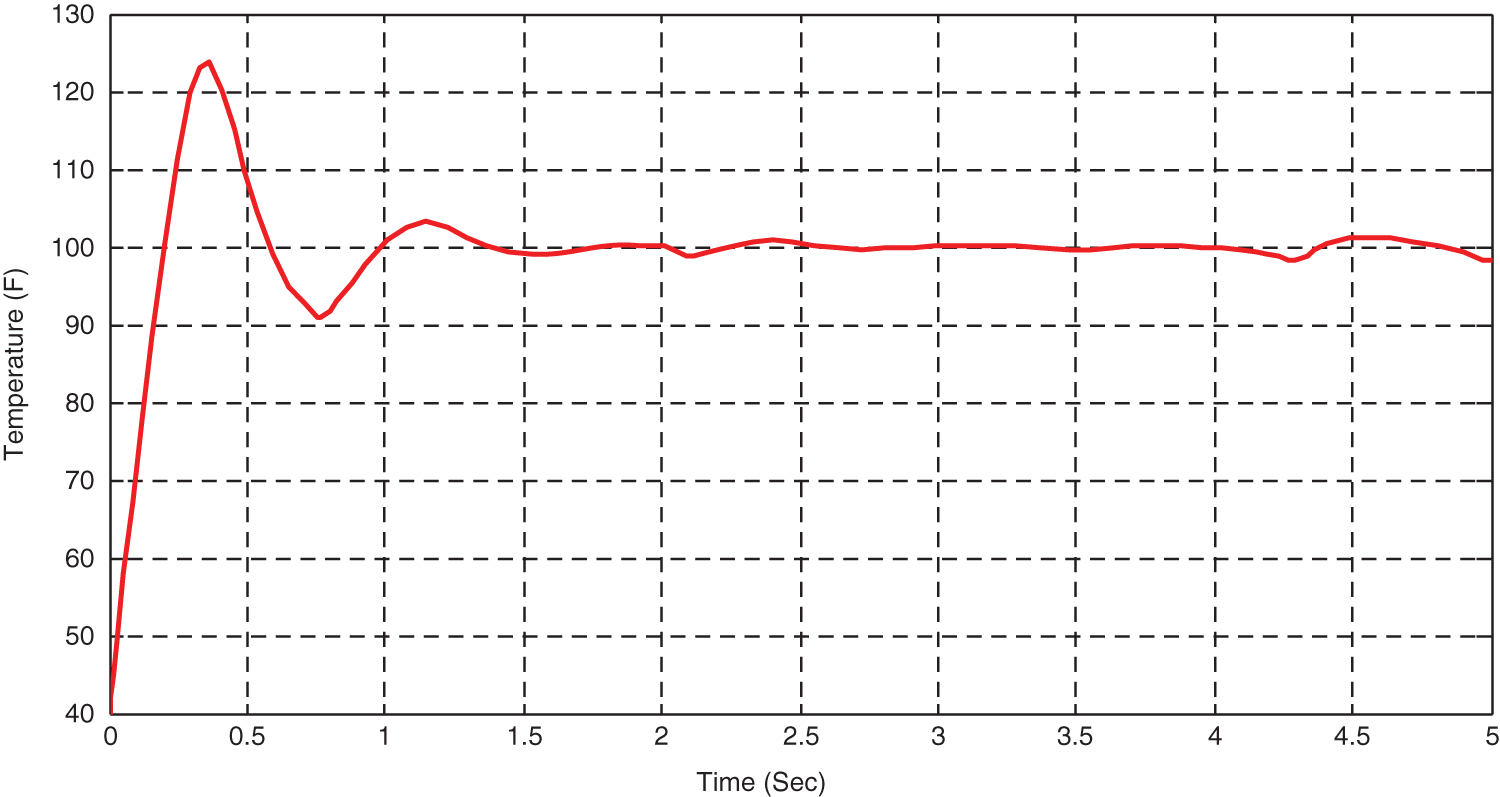
Figure 4: Response of Process variable using MRAC

The MRAC shows more oscillation and overshoots with respect to adaptation gain 5. The variation of manipulated variable and error signal response are shown in Figs. 5 and 6.

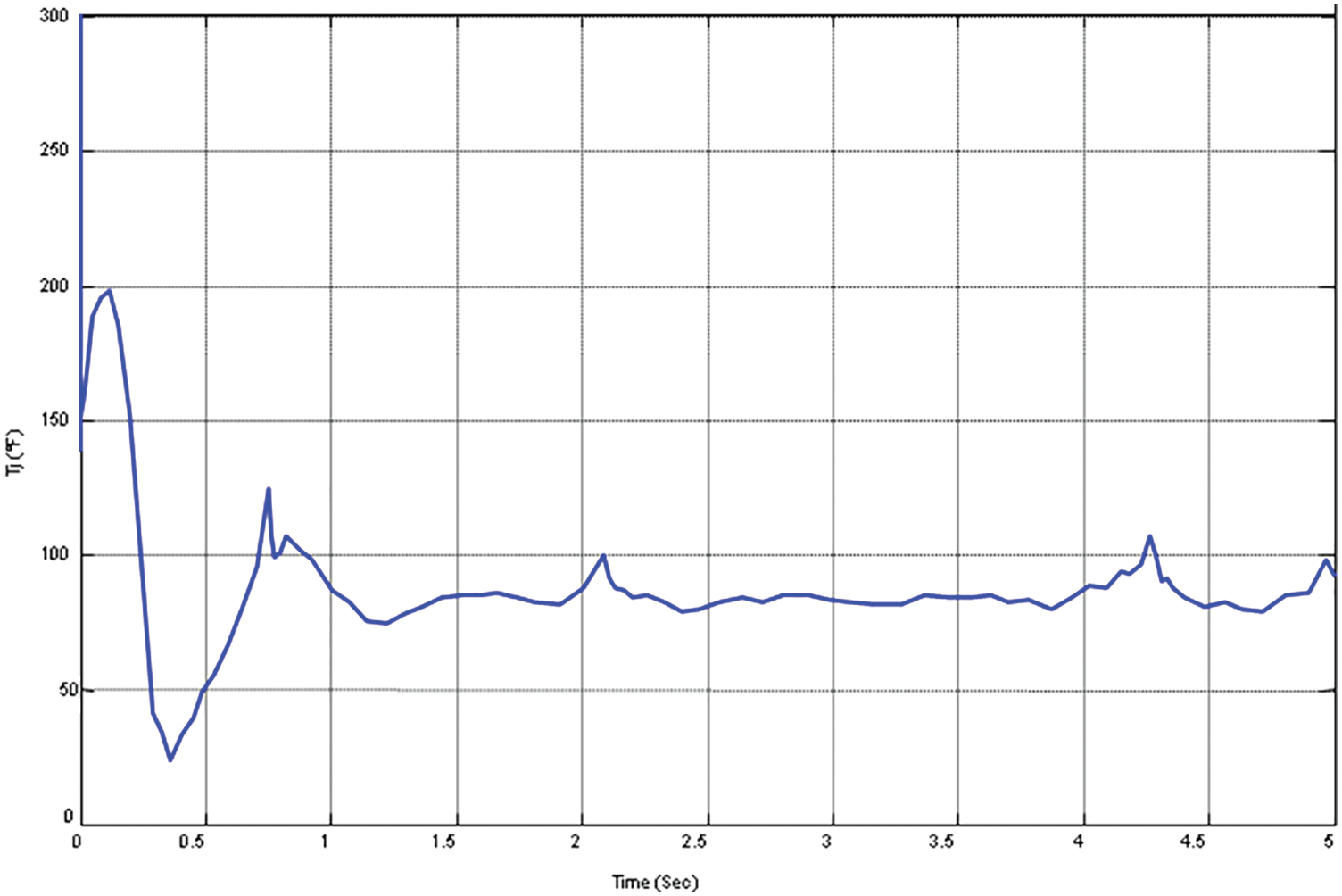
Figure 5: Variation of manipulated variable using MRAC

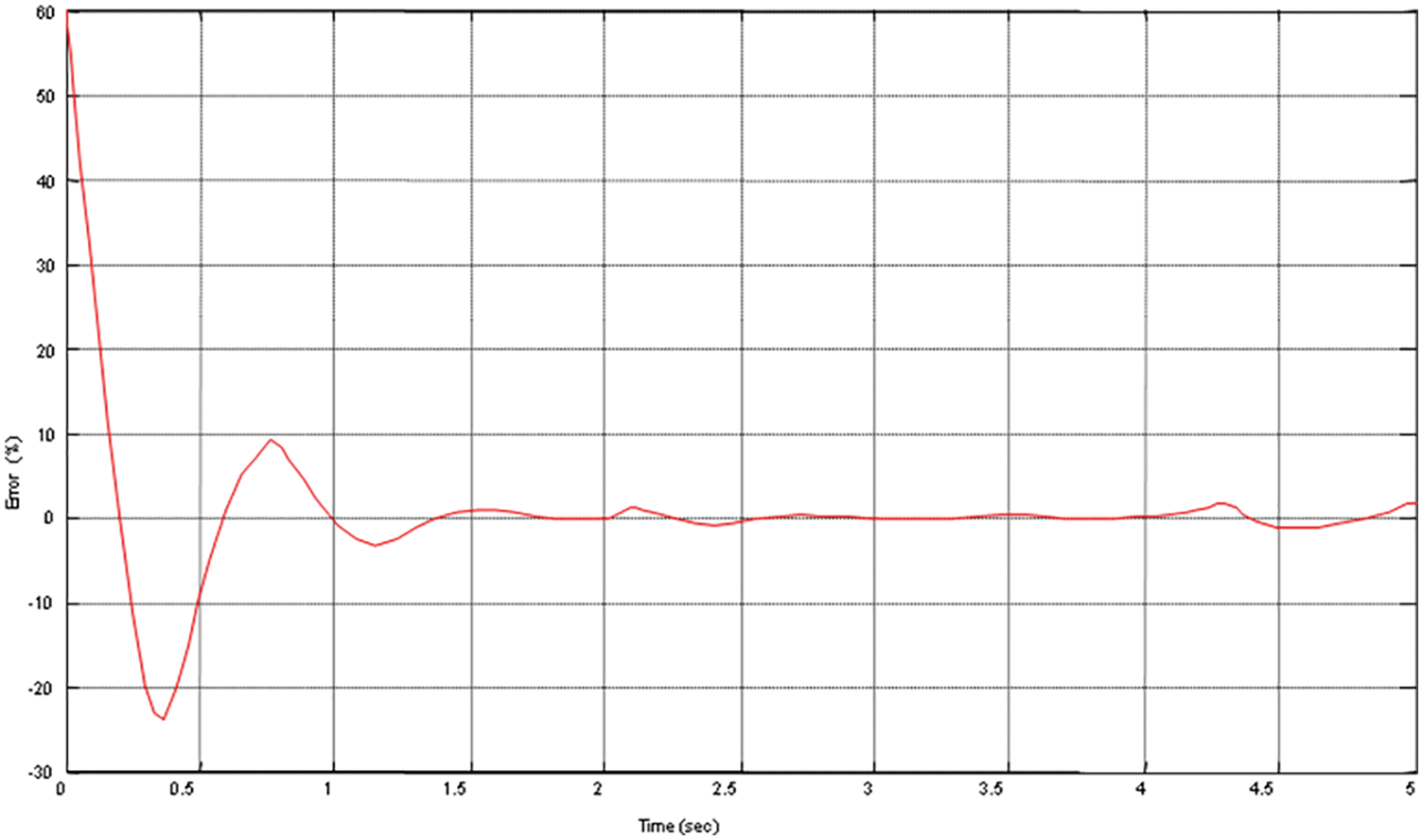
Figure 6: Variation of error signal using MRAC

It is from the responses that the response obtained using MRAC produces more overshoots and oscillation which needs to be reduced to prevent the system from damage therefore PID controller is incorporated with MRAC. The MRAC forces plant output to follow the desired response of reference model.

4.2 Incorporation of PID in MRAC

PID is to determine the control signal for controlling the temperature of CSTR process. The result obtained after incorporating PID with MRAC is shown in Fig. 7.

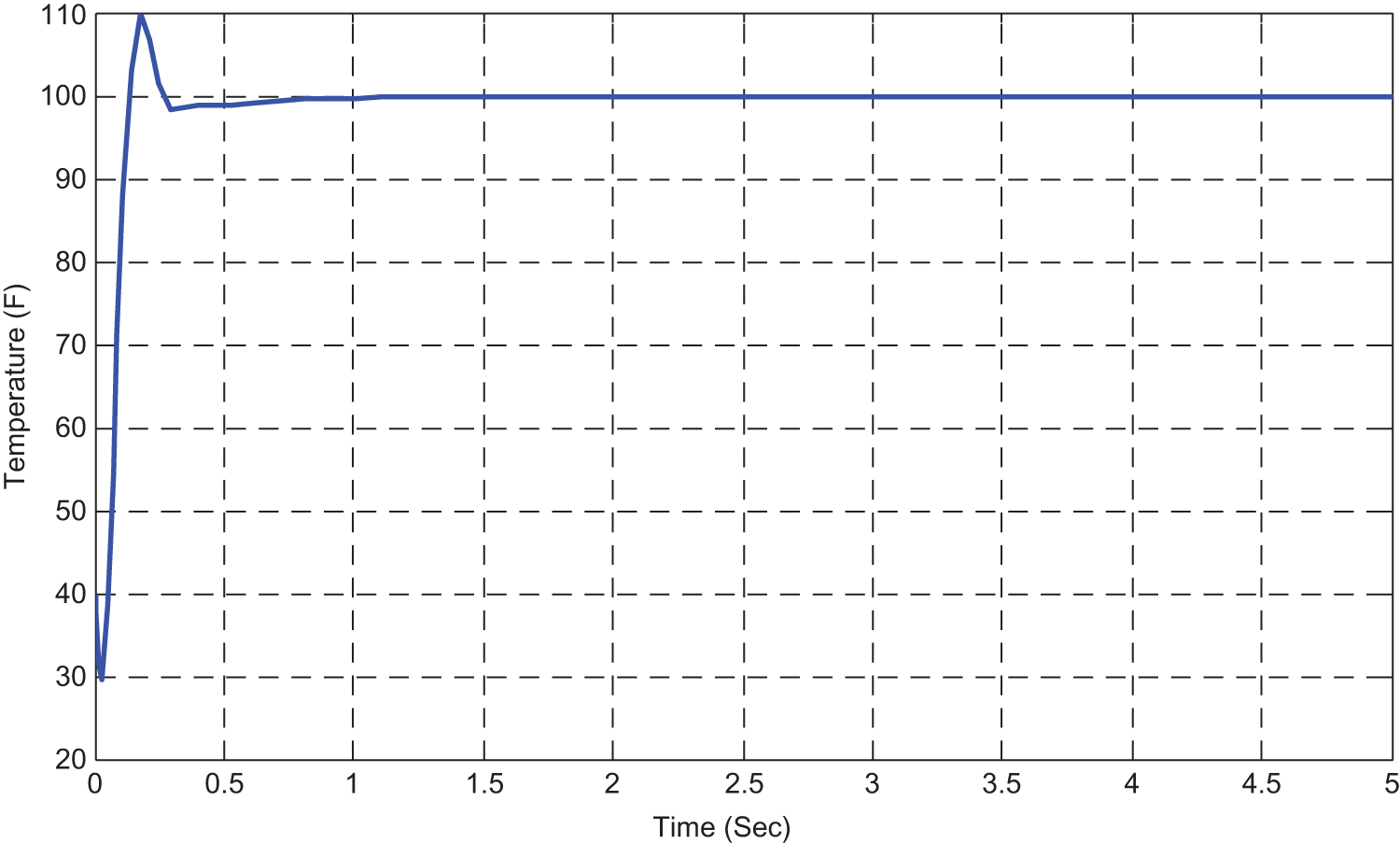
Figure 7: Response of process variable by incorporation of PID with MRAC

Usage of PID makes the system to reach the steady state soon and overshoot gets reduced. The variation of manipulated variable and error after incorporating PID is shown in Figs. 8 and 9.

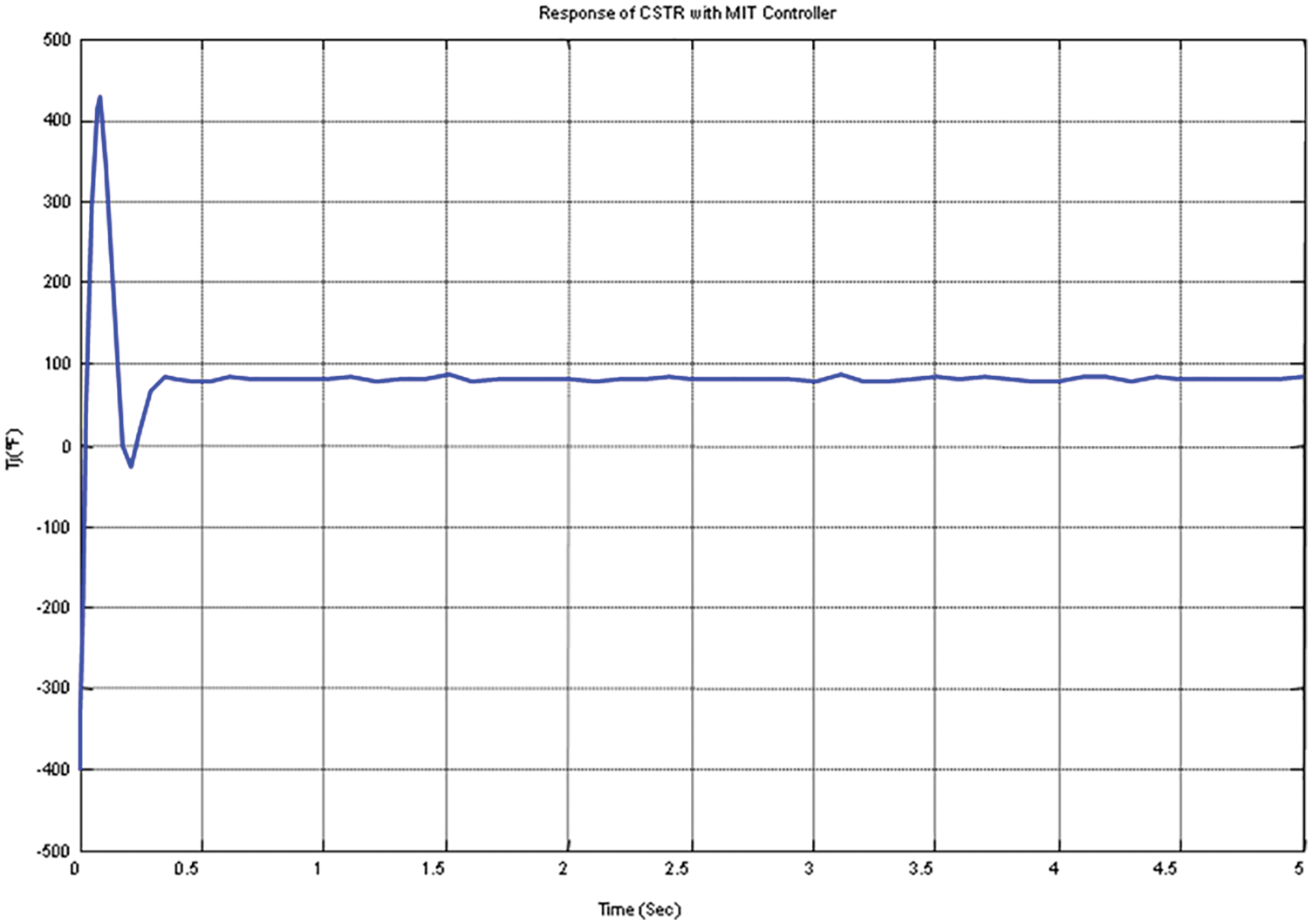
Figure 8: Variation of manipulated variable by incorporation of PID with MRAC

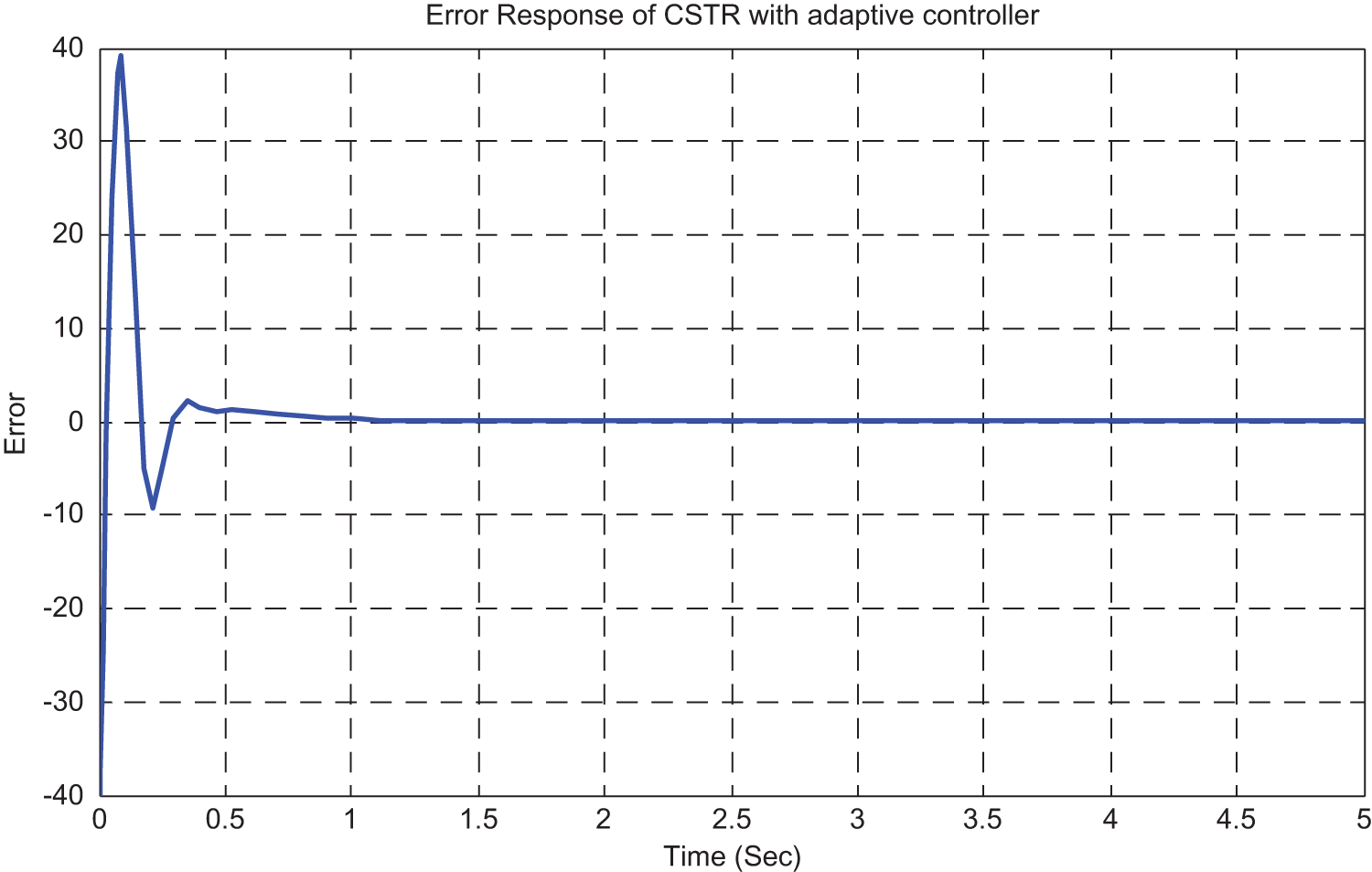
Figure 9: Variation of error signal by incorporation of PID with MRAC

Therefore, the PID controller is incorporated with MRAC and it is inferred that the transient characteristics of the plant response such as peak overshoot, settling time is improved when related to MRAC. The error-signal also gets reduced due to the incorporation of PID with MRAC and is shown in the Fig. 9.

4.3 Optimization of PID Using DE in MRAC

The values obtained with incorporation of PID in MRAC is optimized, may improve the response. Since DE algorithm is used to optimize the PID values the response obtained by use of DE for optimization of PID values are shown in Figs. 10–12.

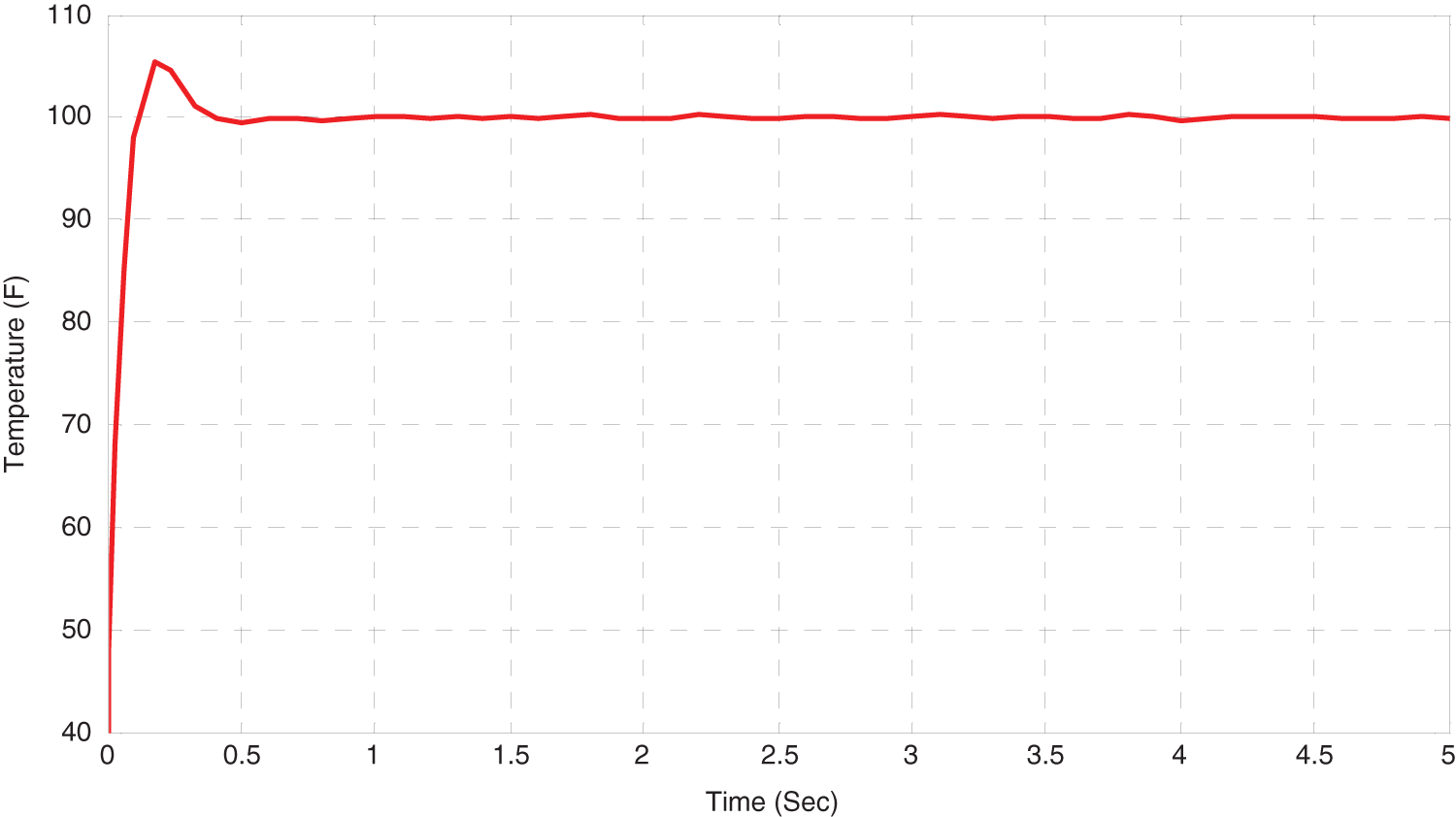
Figure 10: Response of process variable by optimization of PID using DE in MRAC

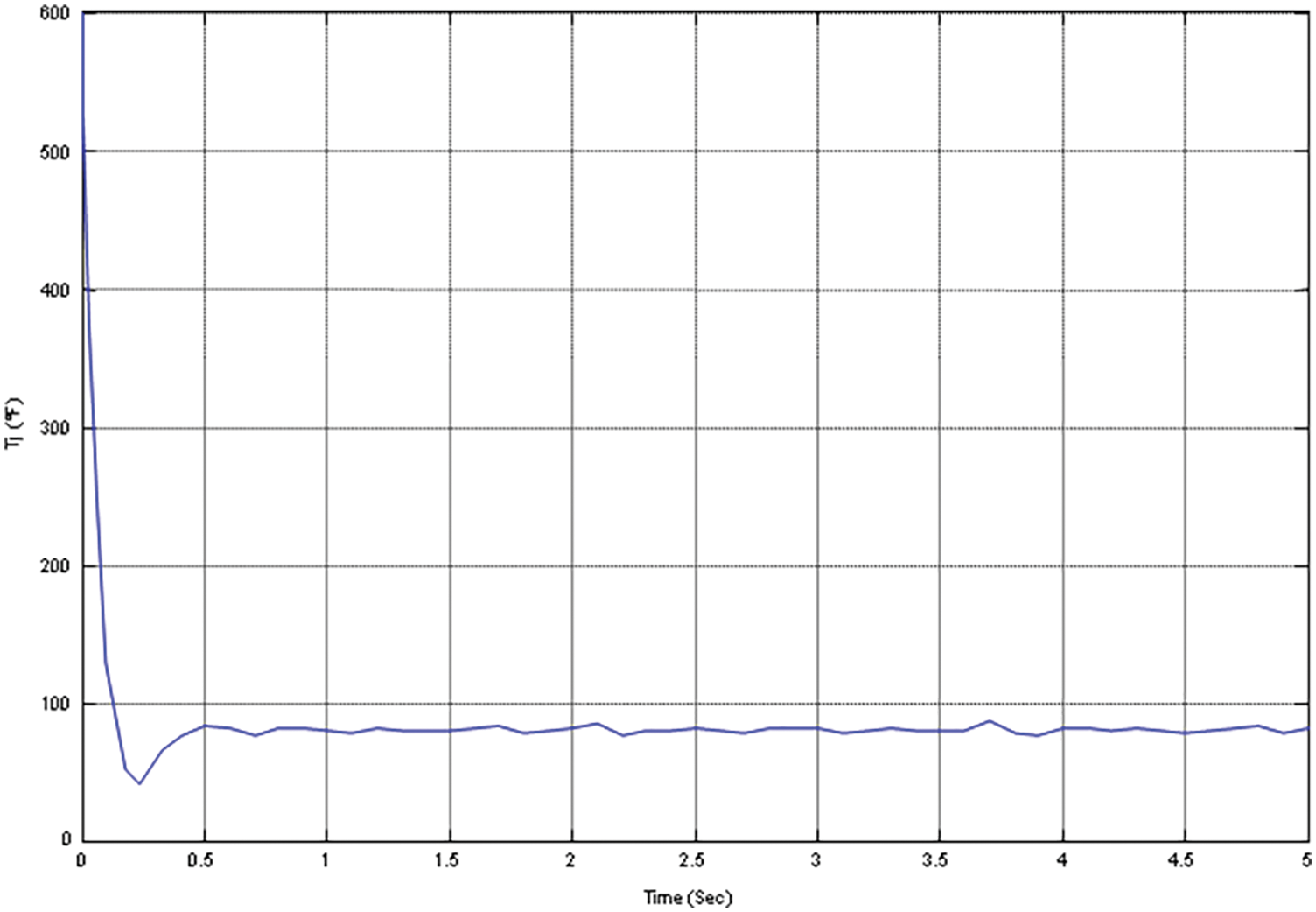
Figure 11: Variation of manipulated variable by optimization of PID using DE in MRAC

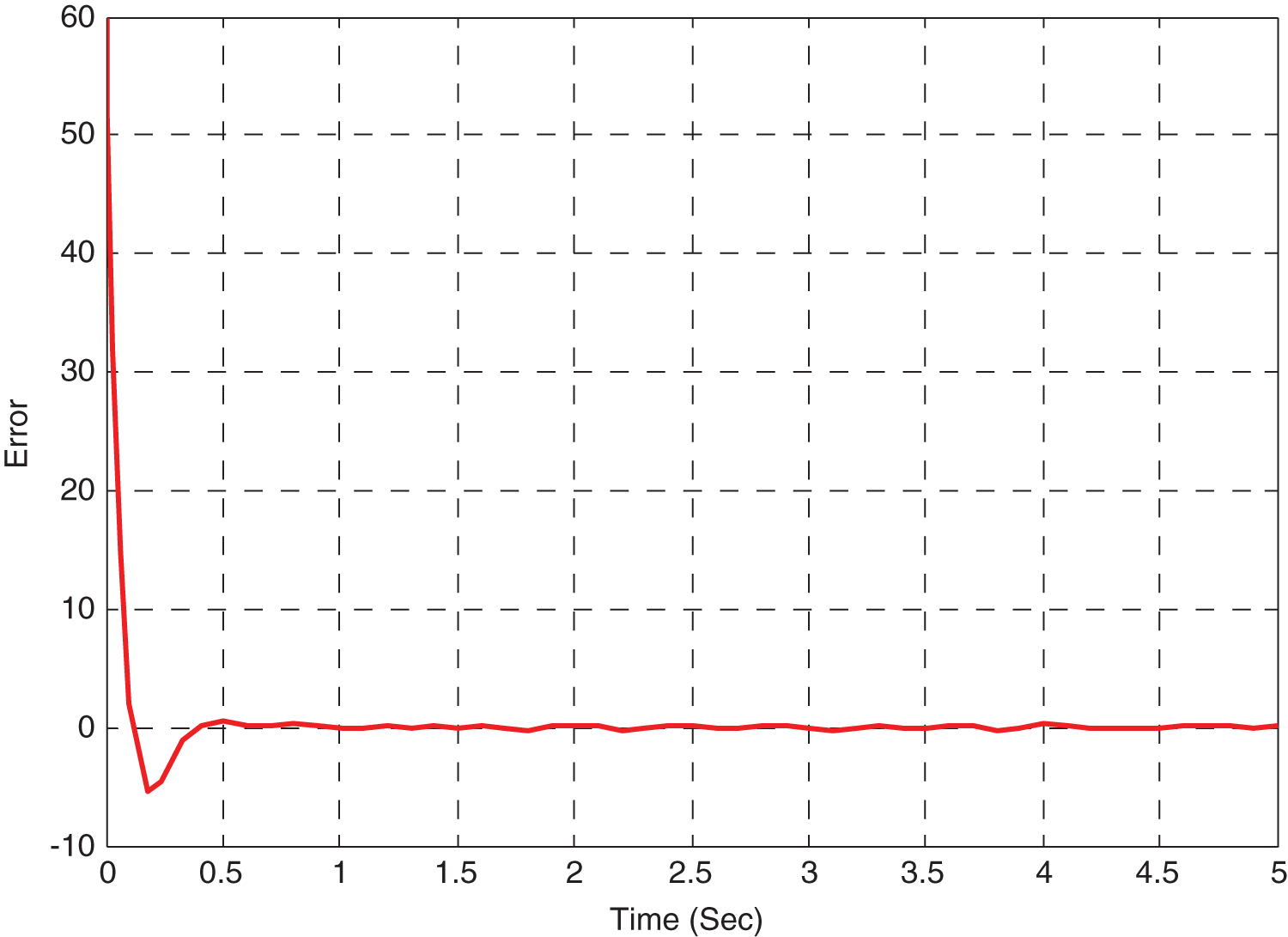
Figure 12: Variation of error signal by optimization of PID using DE in MRAC

The convergence rate obtained after optimization is shown in Fig. 13. The optimized value of PID after 10th iteration is shown in Tab. 1. The transient characteristic of MRAC, incorporation of PID with MRAC and optimization of PID with DE in MRAC are shown.

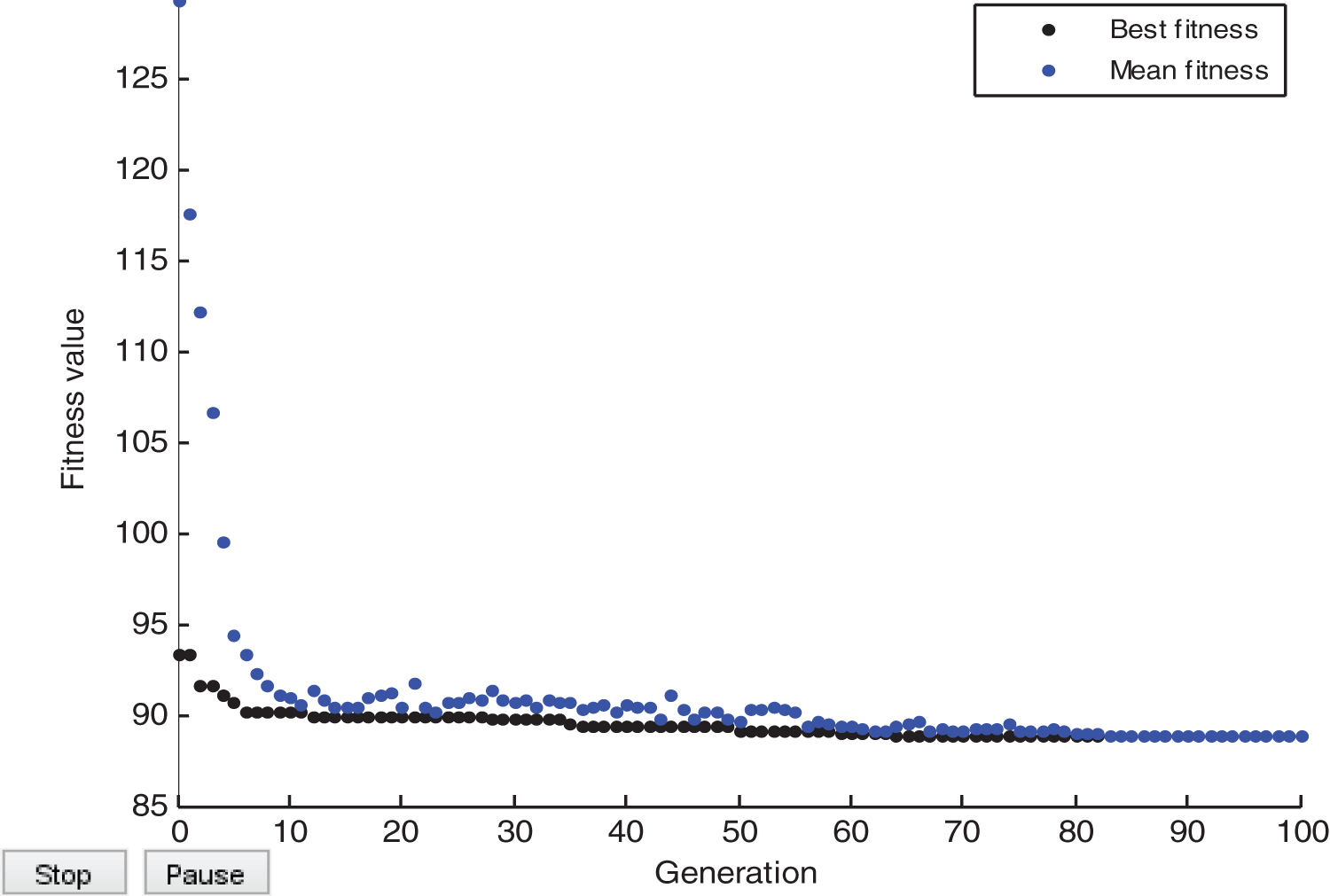
Figure 13: Convergence response of MRAC using DE optimized PID

4.4 Incorporation of Fuzzy in MRAC

The tuning of MRAC with the help of fuzzy which makes the system to improve its transient characteristic performance with the adaptation gain 5. Here the number of rules framed to tune the MRAC is 49 and number of inputs and output are 2 and 1. Membership function framed is triangular method is used for defuzzification techniques. The Figs. 14–17 represent the inputs, output of fuzzy controller and the Fig. 18 represents the rules framed for the tuning process. Where, Input 1 is Error, Input2 is rate of change of error and Output is coolant flow rate.

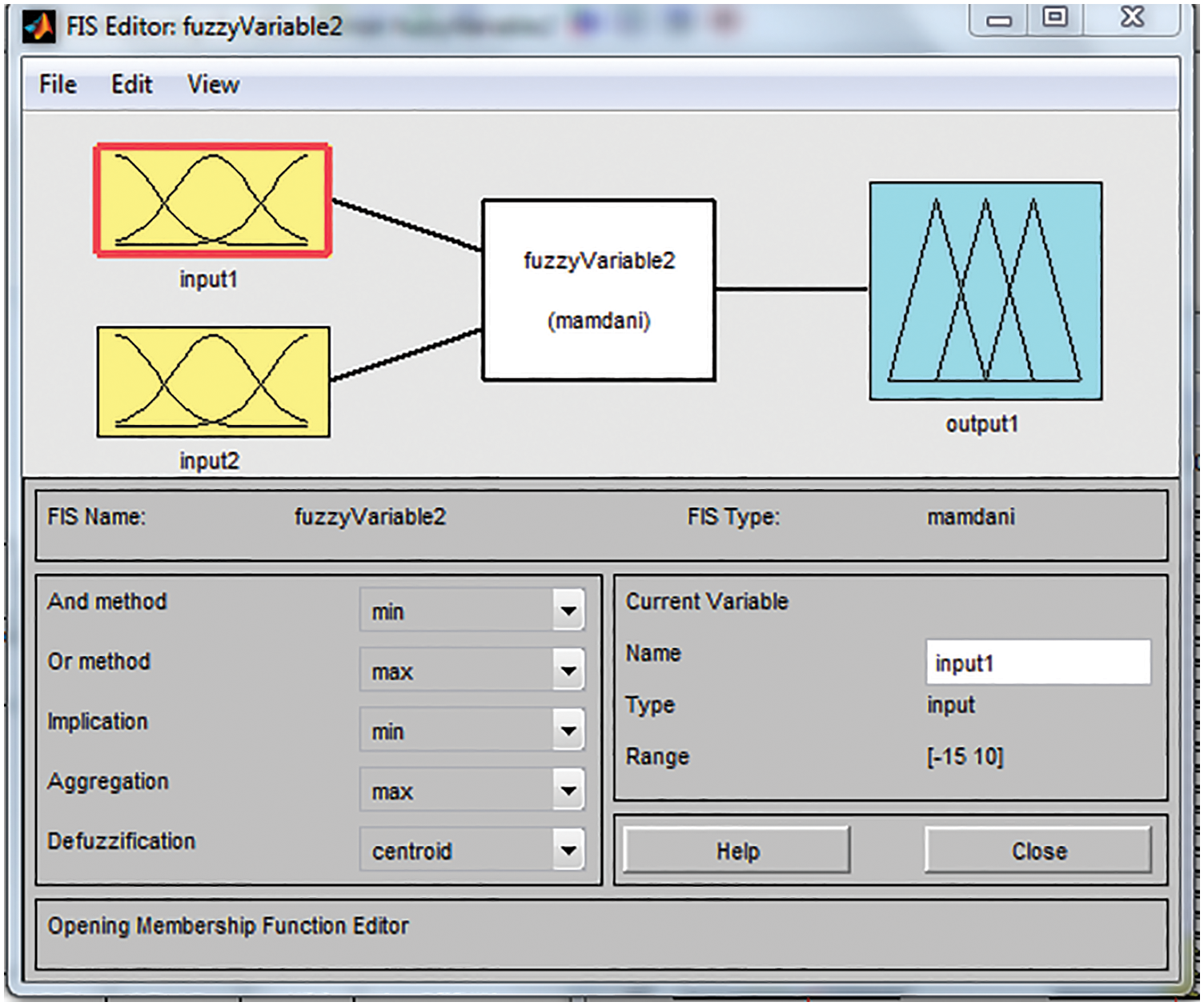
Figure 14: Fuzzy membership function editor tool

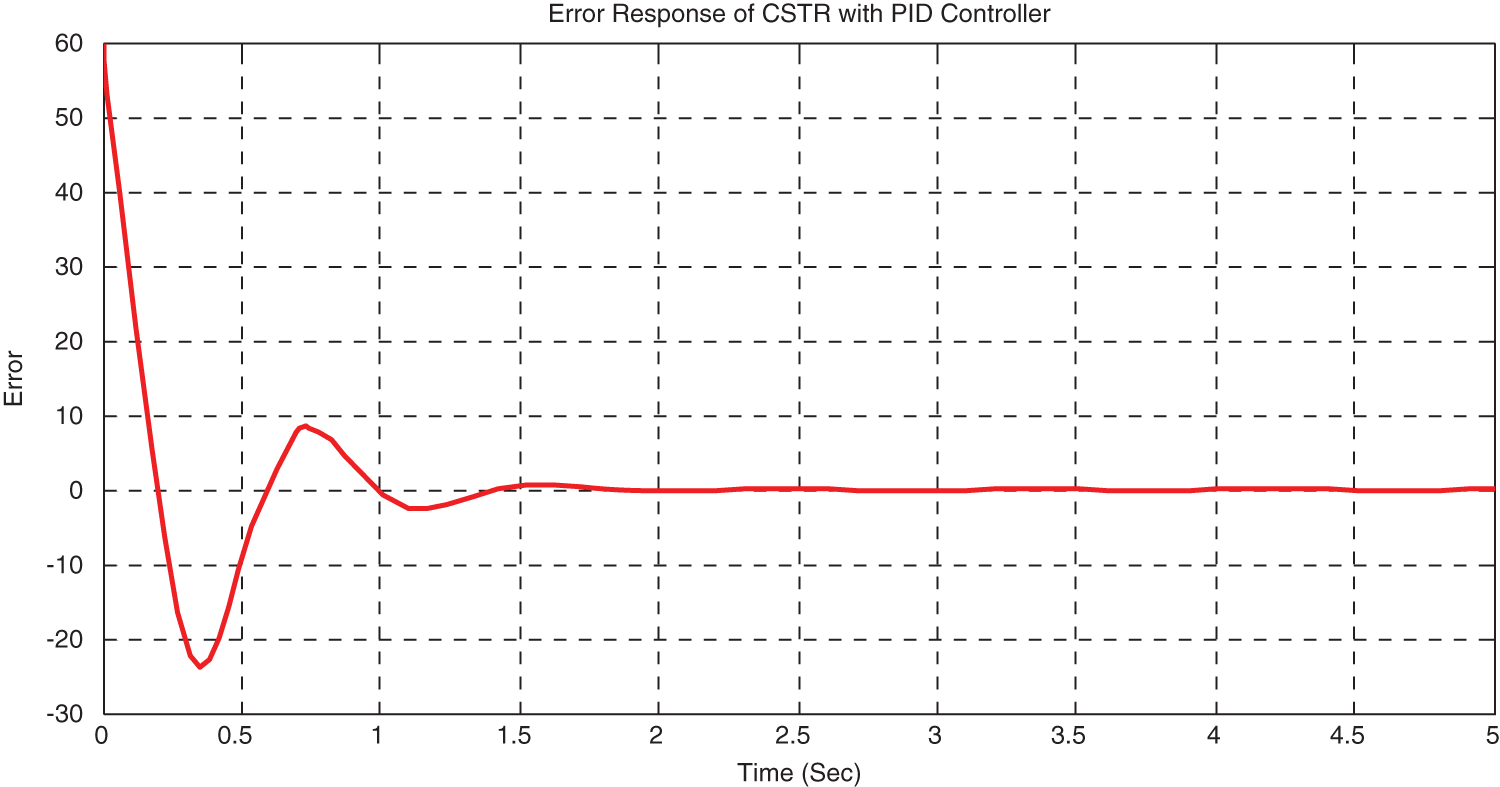
Figure 15: Error input to Fuzzy controller

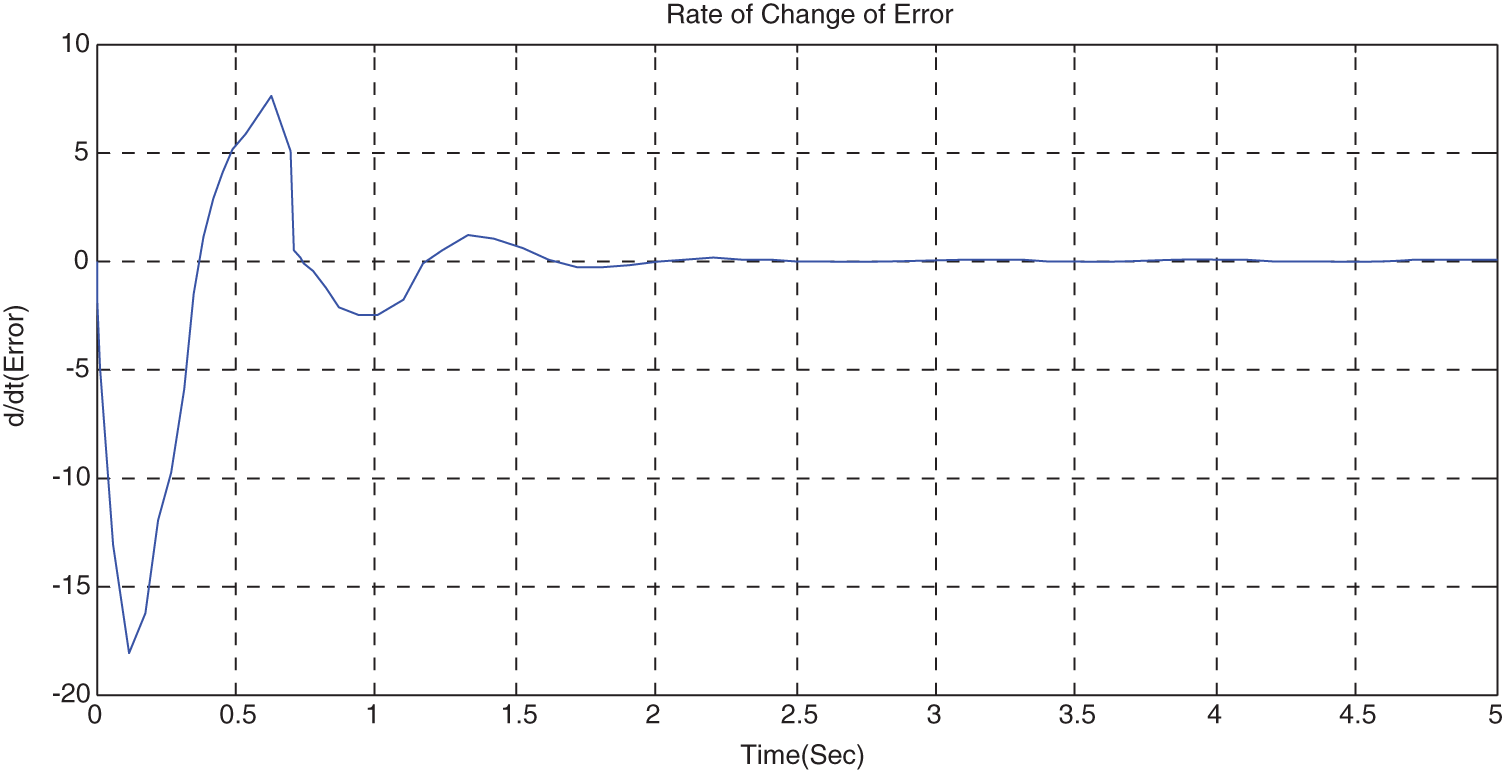
Figure 16: Rate of change error input to Fuzzy controller

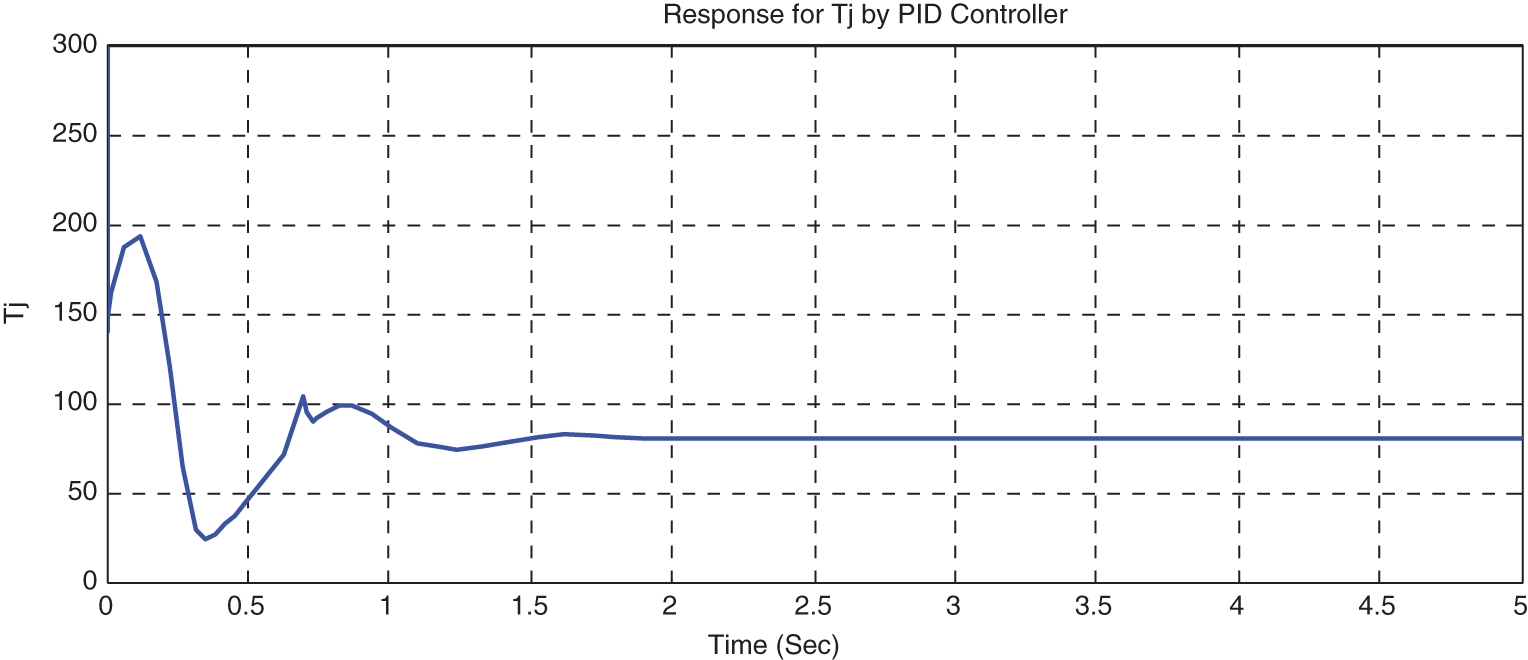
Figure 17: Fuzzy output

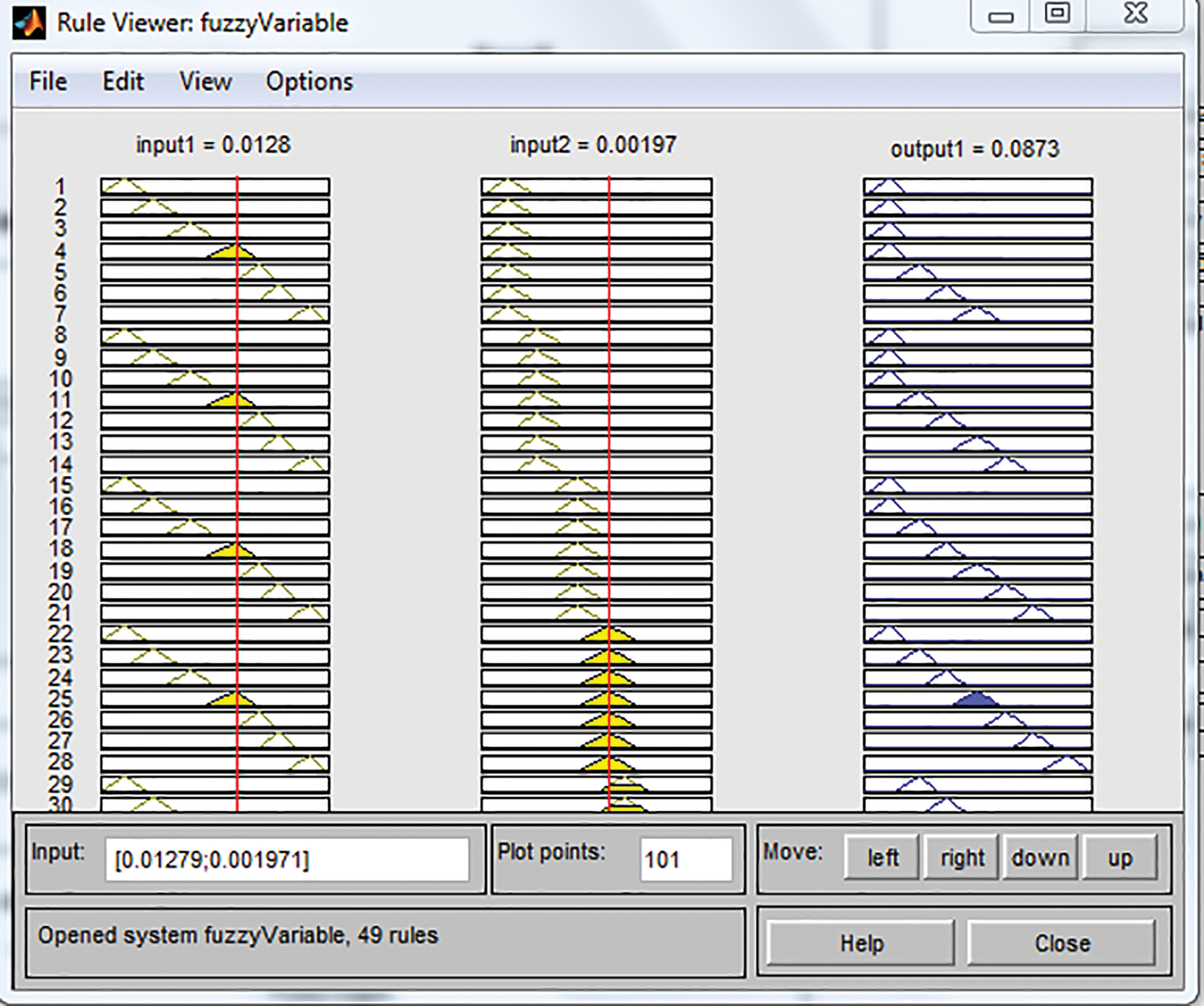
Figure 18: Fuzzy rule viewer

Membership function notation is represented by LN, MN, SN, Z, SP, MP and LP. [16,17]

Where, LN-large negative, MN-medium negative, SN-small negative, Z-zero, SP-small positive, MP-medium positive, LP-large positive.

The response obtained by the incorporation of Fuzzy in MRAC is shown in Figs. 19–21.

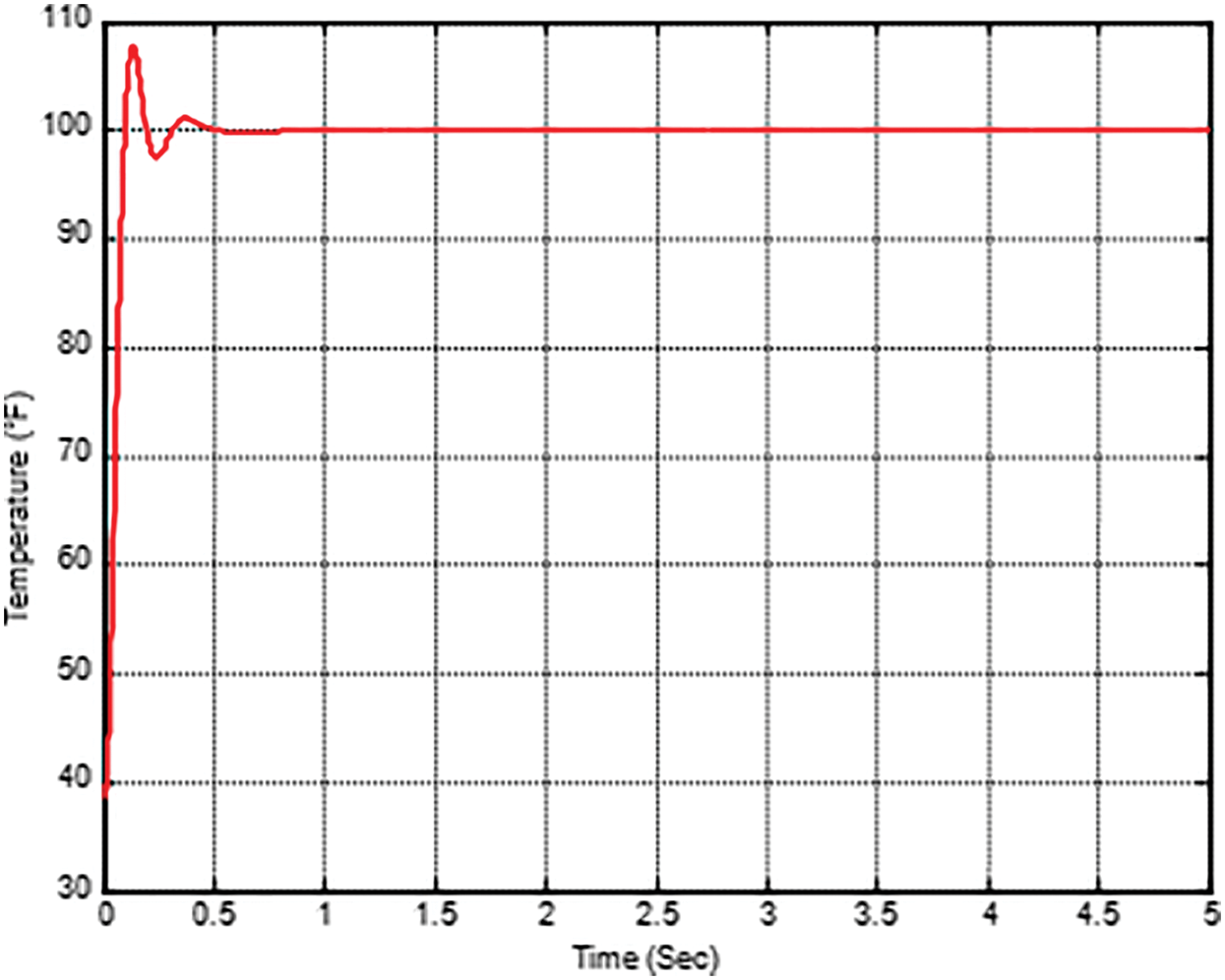
Figure 19: Response of process variable by incorporating Fuzzy in MRAC

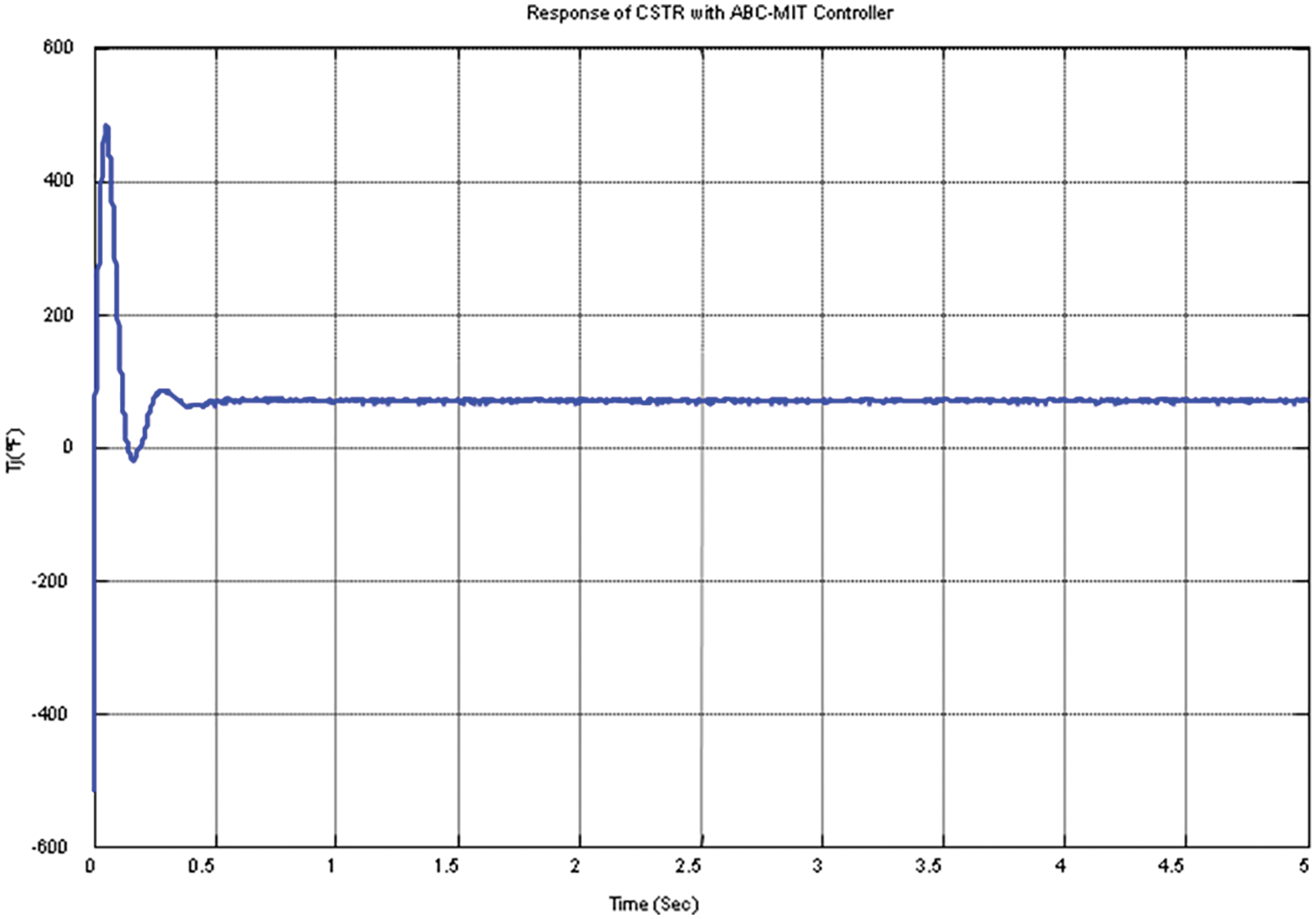
Figure 20: Response of manipulated variable by incorporating Fuzzy in PID

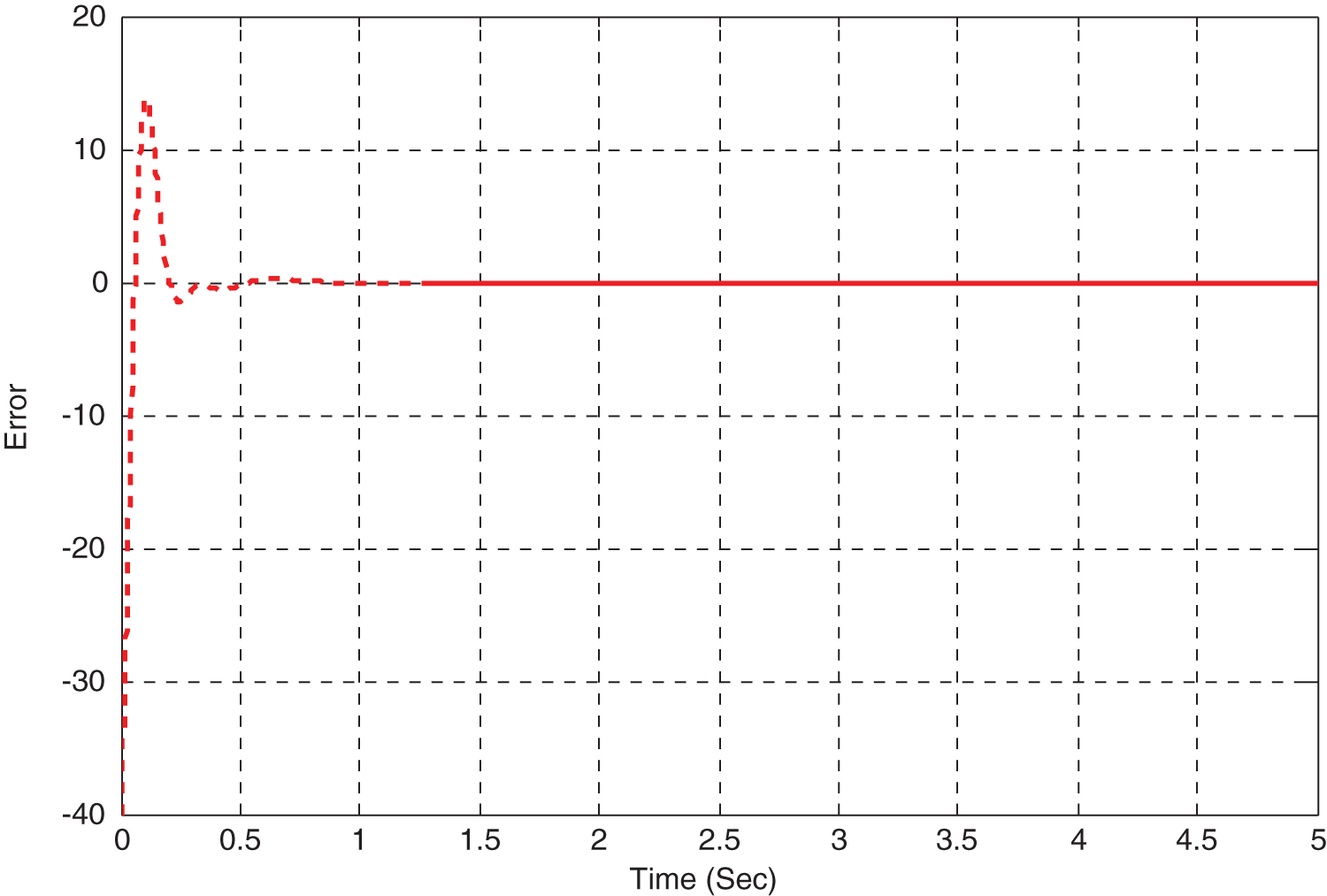
Figure 21: Response of error signal by incorporating Fuzzy in PID

The incorporation of Fuzzy in MRAC has an oscillation. The fuzzy range is fixed on trial and error basis, to get an optimal value have to use some optimization technique.

The result obtained by use of fuzzy has an oscillation and overshoot and it is to be reduced in order to meet the improved performance.

4.5 Optimization of Fuzzy Using DE in MRAC

The fuzzy structure is to be optimized with the help of DE. Here the number of rules framed is reduced due to time consumption problem so the rules framed are 9.The response of the system after the use of DE makes the overshoot zero and settling time to be less and is shown in below Figs. 22–24. The iteration is reduced further from 10th to 5th due to time consumption problem and therefore the time taken to settle will get increases by 20% (2.5seconds). Hence, the Fig. 25 shows the convergence rate of Fuzzy controller using DE for the iteration reduced from10 to 5.

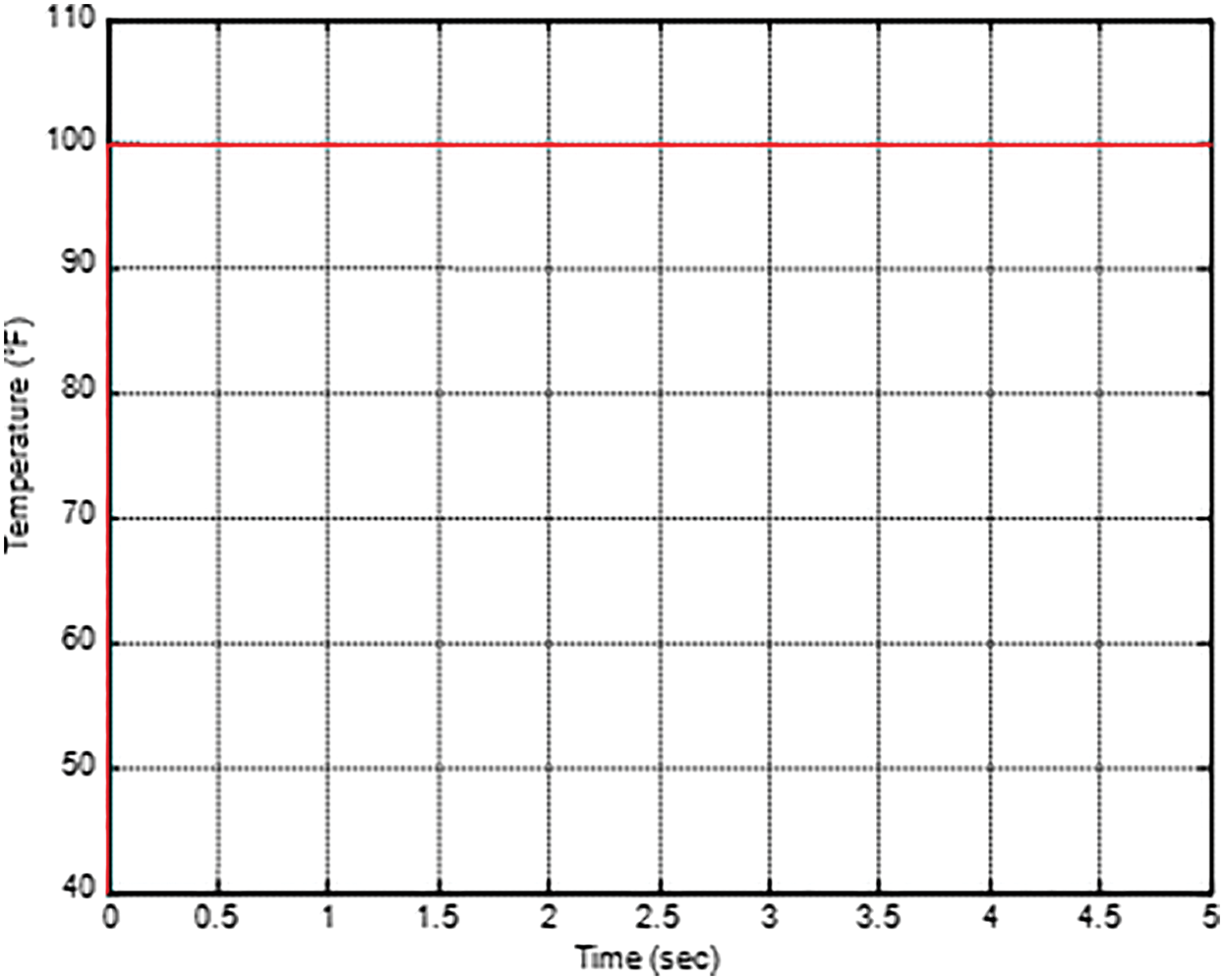
Figure 22: Response of process variable by optimization of Fuzzy using DE in MRAC

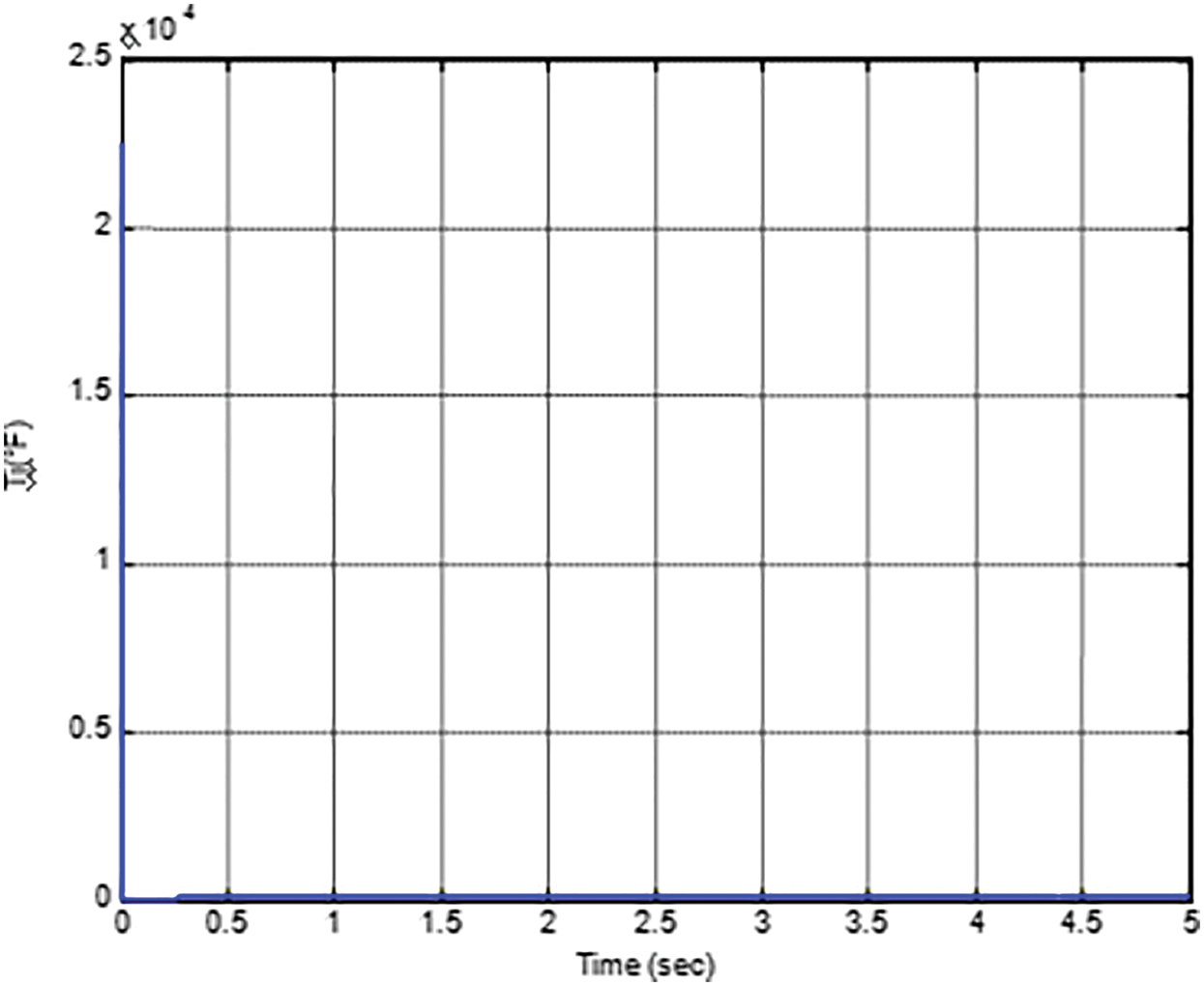
Figure 23: Response of manipulated variable by optimization of Fuzzy using DE in MRAC

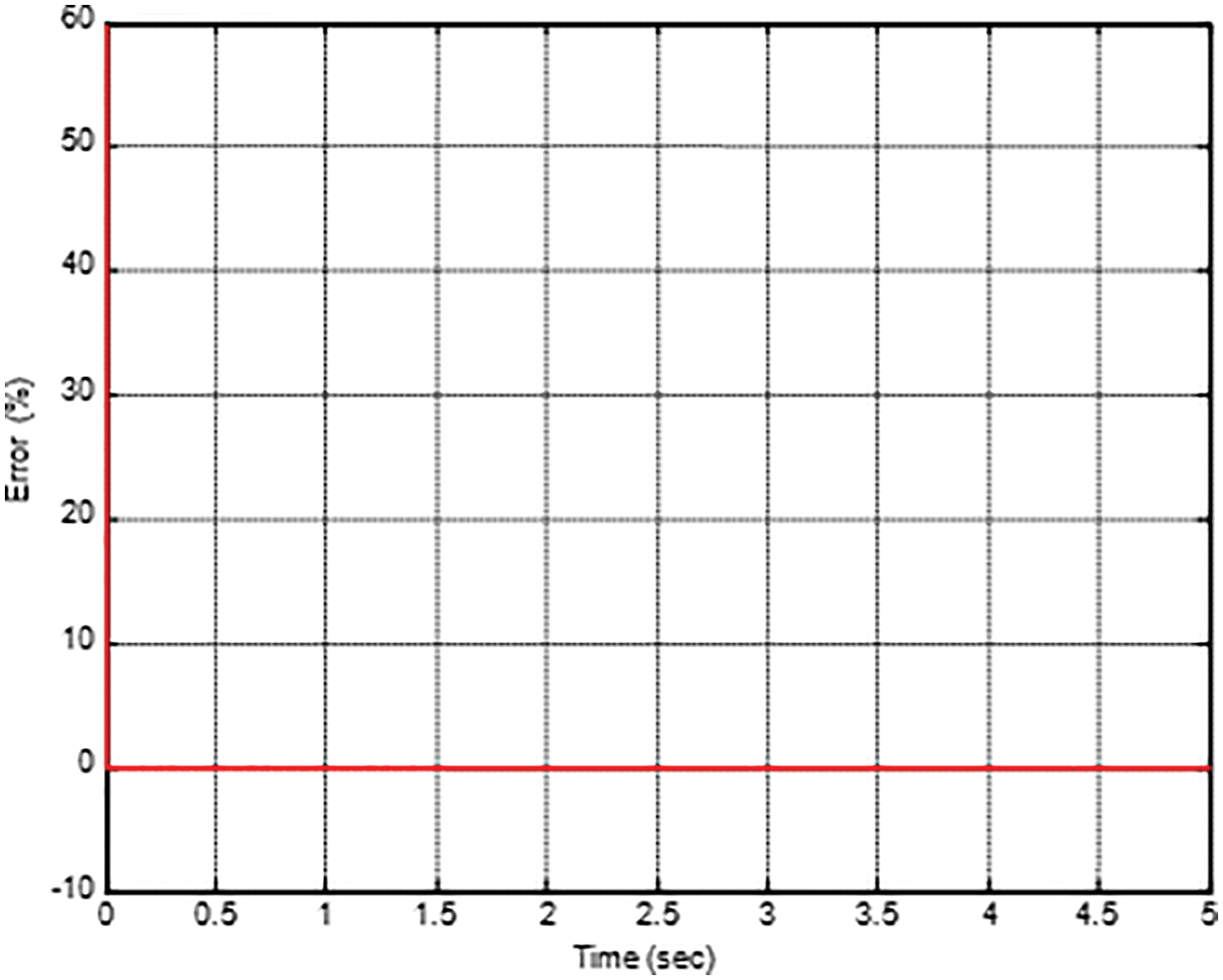
Figure 24: Response of error signal by optimization of Fuzzy using DE in MRAC

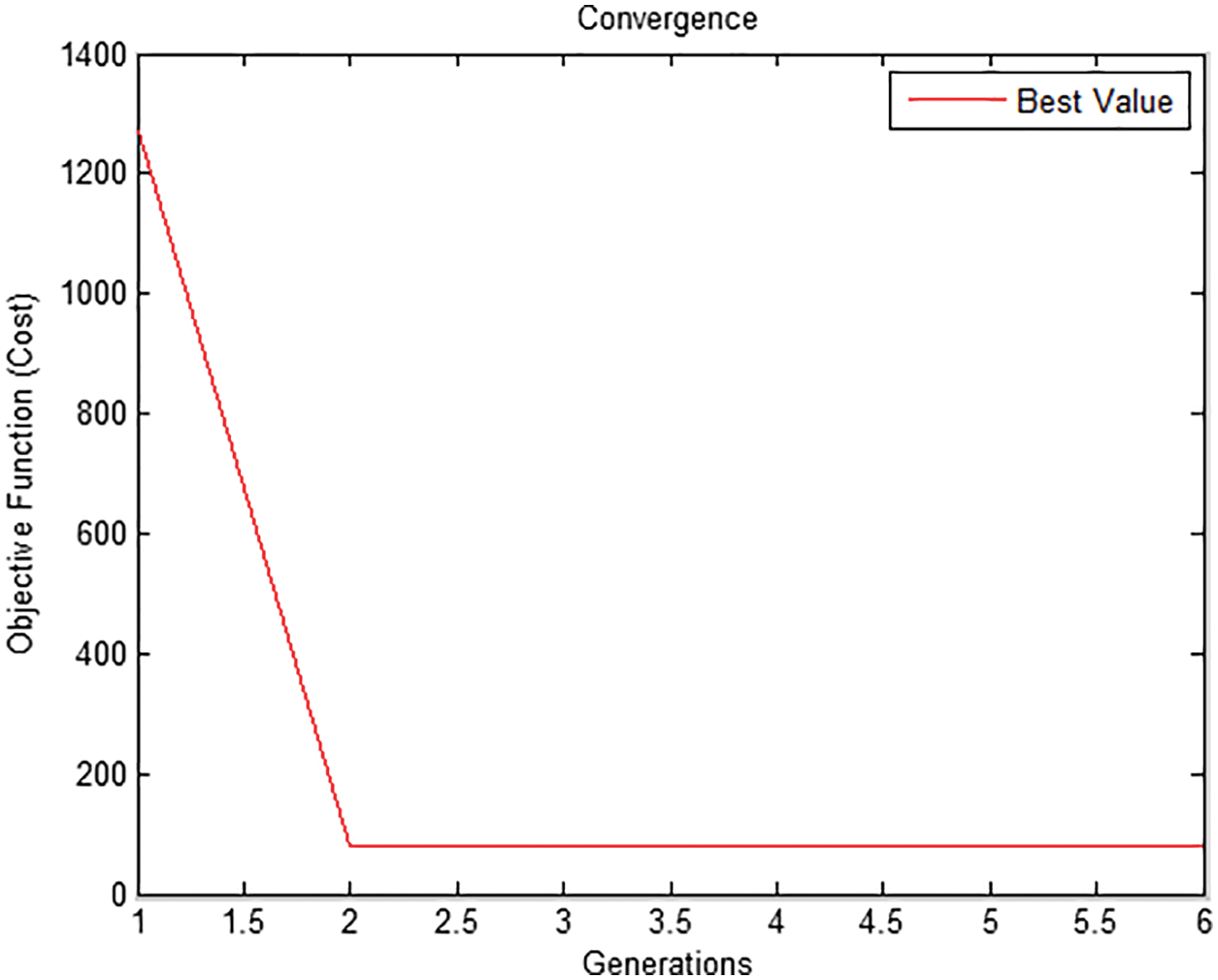
Figure 25: Convergence response of Fuzzy controller using DE

It is inferred from the fig. 24 that the optimization of Fuzzy by DE takes minimum time (2.5) to settle than PID controller and produce zero overshoot and no oscillation in the system. Also it is inferred from the Tab. 1 that Mean Square Criteria (MSE) gives better error (3.59) reduction compared to Integral of Absolute Squared Error (ITAE)

The PID values are obtained by Ziegler Nichols method shown in Tab. 2. It represents the gain values of PID controller and DE algorithm

The comparative analysis of MRAC, incorporation of PID, PID+DE, Fuzzy and Fuzzy+DE in MRAC are given in the Tab. 3.

It is inferred from the Tab. 3 that by using Fuzzy DE, the settling time is reduced by 80% (calculated based on 2.5 sec in MRAC and 20 sec in Fuzzy DE) when compared to conventional MRAC-PID. Also, by using Fuzzy DE, the overshoot is reduced by nearly 90% (calculated based on 16.2% in MRAC and 0.001% in Fuzzy DE) when compared to conventional MRAC-PID. The desired value to be maintained for settling time is 2 seconds, overshoot for 0.001 % and rise time is 5.2 seconds based on the real time applications carried out. The time domain parameters like settling time, rise time and overshoot listed above are calculated based on the standard expressions of second order system behavior for step change in input signal. Hence it is better to implement Fuzzy DE for the control of temperature in CSTR process.

5  Conclusion & Future Work

In chemical industries there is a problem of controlling the temperature of the liquid inside the chemical reactor due to the nature of exothermic and endothermic reaction. This makes the inside temperature of the plant to vary with time. This problem is reduced by designing the Modified Model Reference Adaptive Controller for CSTR process which controls the temperature of the plant by manipulating the coolant flow rate. This technique can be used for large gamma value as well as high set point using Normalization MRAC along with PID, FUZZY, PID+DE and FUZZY+DE which produces satisfactory result and the transient response characteristics of the CSTR plant is improved. From the result it is concluded that different techniques where used to improve the transient characteristics in which PID produce response with more overshoot and less time taken to settle, whereas fuzzy produce minimum overshoot and less time taken to settle. Depending upon our need either of the method can be used. For instance to make the system to reach the steady soon PID+DE can be used and in case of production from damage due to large overshoot Fuzzy +DE is used.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  K. Asan, G. Mohideena, D. Valarmathia, D. Devaraj and T. K. Radhakrishnan, “Real coded algorithms for system identification and tuning of a modified model reference adaptive controller for hybrid tank system,” Journal of Applied Mathematical Modeling, vol. 37, no. 8, pp. 3829–3847, 2020. [Google Scholar]

 2.  P. Swarnkar, S. Jain and R. K. Nema, “Effect of adaptation gain in model reference adaptive controller for II order system of CSTR process,” Engineering Technology and Applied Science Research, vol. 8, no. 3, pp. 70–75, 2019. [Google Scholar]

 3.  K. R. Brijendra and P. Maurya, “Fuzzy logic based temperature control of continuous stirred tank reactor,” International Journal of Engineering Trends and Technology, vol. 12, no. 2, pp. 109–112, 2014. [Google Scholar]

 4.  U. Zuperl, F. Cus and M. Milfelner, “Fuzzy control strategy for an adaptive force control in end-milling,” Journal of Materials Processing Technology, vol. 3, no. 6, pp. 1472–1478, 2005. [Google Scholar]

 5.  R. Upadhy and R. Singla, “Analysis of CSTR temperature control with adaptive and PID controller,” International Journal of Engineering and Technology, vol. 2, no. 5, pp. 637–643, 2010. [Google Scholar]

 6.  C. Cheng-Hung, C. Jian Lin and C. Teng Lin, “Nonlinear system control using adaptive neural fuzzy networks based on a modified differential evolution,” IEEE Transactions on Systems Man and Cybernetics, vol. 39, no. 4, pp. 459–473, 2017. [Google Scholar]

 7.  J. Brest, S. Greiner, B. Boskovic, M. Mernik and V. Zumer, “Self adapting control parameters in differential evolution: A comparative study on numerical benchmark problems,” IEEE Transactions on Evolutionary Computation, vol. 10, no. 6, pp. 646–657, 2018. [Google Scholar]

 8.  A. K. Qin, V. L. Huang and P. N. Suganthan, “Differential evolution algorithm with strategy adaptation for global numerical optimization,” IEEE Transactions on Evolutionary Computation, vol. 13, no. 2, pp. 398–417, 2009. [Google Scholar]

 9.  B. Vasu Murthy, Y. V. Pavan Kumar and U. V. Ratna Kumari, “Fuzzy logic intelligent controlling concepts in industrial furnance temperature process control,” IEEE International Conference on Advanced Communication Control and Computing Technologies, vol. 12, no. 1, pp. 353–358, 2012. [Google Scholar]

10. X. Wang, “Multi-core Implementation of F-16 flight surface control system using genetic algorithm based adaptive control algorithm,” IEEE Transactions on Aerospace and Electronics, vol. 7, no. 4, pp. 191–194, 2016. [Google Scholar]

11. Y. Liu, J. Zhao, M. Xia and H. Luo, “Model reference adaptive control-based speed control of brushless DC Motors with low-resolution hall-effect sensors,” IEEE Transactions on Power Electronics, vol. 29, no. 3, pp. 333–343, 2014. [Google Scholar]

12. Z. Zhang, C. Yaoming and D. Zhang, “Solving ordinary differential equations with adaptive differential evolution,” IEEE Access, vol. 8, pp. 128908–128922, 2020. [Google Scholar]

13. J. Vojtesk, R. Prokopb and P. Dostala, “Adaptive control of chemical reactor,” International Journal on Cybernetics and Informatics, vol. 61, no. 6, pp. 10–13, 2018. [Google Scholar]

14. K. J. Astrom and B. Wittenmark, Adaptive control, Hong Kong, 2nd (Eds.,). Pearson Education Asia, pp. 185– 225, 2001. [Google Scholar]

15. H. Madadum and Y. Becerikli, “A resource-efficient convolutional neural network accelerator using fine-grained logarithmic quantization,” Intelligent Automation & Soft Computing, vol. 33, no. 2, pp. 681–695, 2022. [Google Scholar]

16. S. Arun Kumar, S. Padma and S. Madhubalan, “Distribution network reconfiguration using hybrid optimization technique,” Intelligent Automation & Soft Computing, vol. 33, no. 2, pp. 777–789, 2022. [Google Scholar]

17. D. Nagendiran and S. P. Chokkalingam, “Real time brain tumor prediction using adaptive neuro- fuzzy technique,” Intelligent Automation & Soft Computing, vol. 33, no. 2, pp. 983–996, 2022. [Google Scholar]

18. M. Zuo and C. Guo, “A case learning-based differential evolution algorithm for global optimization of interplanetary trajectory design,” Applied Soft Computing, vol. 94, no. 2, pp. 106451, 2020. [Google Scholar]

19. B. Yu, “An improved dynamic maximum power point tracking method for PV application,” IEICE Electronics Express, vol. 11, no. 2, pp. 1–10, 2014. [Google Scholar]

20. S. Arun Kumar, S. Padma and S. Madhubalan, “Distribution network reconfiguration using hybrid optimization technique,” Intelligent Automation & Soft Computing, vol. 33, no. 2, pp. 777–789, 2022. [Google Scholar]

21. Pankaj Swarnkar, Automatic Control System, 3rd (Eds.,). New Delhi: Satya Prakashan, 2010. [Google Scholar]

22. H. Meisam and S. Abbas, “Sensor-less load and position estimation in linear reluctance actuator,” IEICE Electronics Express, vol. 11, no. 2, pp. 20130908–20130908, 2014. [Google Scholar]

23. S. Jain, V. K. Sharma and S. Kumar, “Robot path planning using differential evolution,” in Advances in Computing and Intelligent Systems, Singapore, Springer proceedings, pp. 531–537, 2020. [Google Scholar]

24. K. Keerthi and M. SivaSathyanarayana, “Fuzzy implementation of model reference adaptive control of DC drives,” International Journal of Engineering Science & Advanced Technology, vol. 2, no. 3, pp. 605–611, 2017. [Google Scholar]

25. L. Cui, C. Xu, G. Li, Z. Ming, Y. Feng et al., “A high accurate localization algorithm with DV-hop and differential evolution for wireless sensor network,” Applied Soft Computing, vol. 68, pp. 39–52, 2018. [Google Scholar]

26. C. Cao and N. Hovakimyan, “Design and analysis of a novel L1 adaptive control architecture with guaranteed transient performance,” IEEE Transactions on Automatic Control, vol. 53, no. 2, pp. 586–591, 2008. [Google Scholar]

27. F. Muhammad, Z. Aneela, S. Mirza, M. Sikander Mirza, M. Nasir Aslam et al., “Differential evolution based computation intelligence solver for elliptic partial differential equations,” Frontiers of Information Technology and Electronic Engineering, vol. 20, no. 10, pp. 1445–1456, 2019. [Google Scholar]