 Open Access
Open Access
ARTICLE
Design of Optical Filter Using Bald Eagle Search Optimization Algorithm
Research Scholar, Department of ECE, Sathyabama Institute of Science and Technology, Chennai, 600119, India
* Corresponding Author: L. Jegan Antony Marcilin. Email:
Intelligent Automation & Soft Computing 2023, 36(1), 1215-1226. https://doi.org/10.32604/iasc.2023.028764
Received 17 February 2022; Accepted 21 June 2022; Issue published 29 September 2022
Abstract
Controlled thermonuclear reactors require consistent monitoring of plasma in the toroidal chamber. Better working conditions of such machines can be monitored by analyzing its radiations. Various wavelengths such as 656.3, 486.1, 464.7 nm are quite significant which are used for health monitoring of thermonuclear machines. The optical thin film filters which work on constructive and destructive interference are the ideal choices. These filters are multilayered with a pair of high and low refractive index dielectric materials. Significantly high transmission index at the desired wavelength and relatively low transmission at the other wavelengths are desired. With this as the objective, it is necessary to design the filter. Various optimization techniques are used for identifying the suitable design of the filters. To choose the parameter combination that provides the most excellent performance, optimization of the design parameters is entailed. The goal of this work is to improve the optical band filter using the Bald eagle search optimization (BES) method. The ideal design is determined by assessing several characteristics such as thickness, refractive index, Full-Width at Half-Maximum (FWHM), and the impact of choosing optical properties, which increases transmission potential. Initially, an alternate multi-layer stack with 28, 30, and 32 layers is created by altering the thickness while keeping the dielectric substances high and low refractive indices constant. By adjusting the thickness of each layer, the BES algorithm achieves the best practical solution. The proposed method is implemented using MATLAB and the outcomes show the efficacy of the proposed technique. The transmittance, reflectance, and FWHM using the proposed BES are found to be 99.9356%, 0.065%, and 1.2 nm respectively.Keywords
Nomenclature
| Abbreviation | Description |
| BES | Bald Eagle Search algorithm |
| FWHM | Full-Width at Half-Maximum |
| GA | Genetic algorithm |
| PSO | Particle swarm optimization |
| GOA | Grasshopper optimization algorithm |
| ZnS | Zinc sulfide |
| TiO2 | Titanium dioxide |
| MgF2 | Magnesium fluoride |
| SiO2 | Silicon dioxide |
Optical filters are among the significant and sensible components, which are modeled and produced based on photonic crystals [1,2]. They assist the optical signal propagation with a definite level of frequency and avoid other frequencies from propagation [3]. Optical filters are normally featured with their frequency response that deliberates the change in phase angles and magnitude concerning frequency. Since they are believed to be time-invariant linear models, digital signal processing strategies can be utilized for the analysis of the effectiveness of the optical filters [4,5]. The similarity between the optical characteristics and the transmission line of multi-layer filters has been recognized for a long period. At about the same instance, several research works have applied the electrical filter synthesis strategy for the design of optical filters. The complexity of the strategy is the impractical index attained by evaluating the exact solutions of the layers using proportionate thickness, with the effectiveness being lost for variation in indices [6]. In comparison, the filter design by Seeley is more realistic. However, Liddell explored the major limitations of the Seeley filter design. In multilayer design, the measures of the prototype index profile attained must be practicable, and only some values match up to the practical grouping of materials. In addition, there is an issue of decline in the specified width of the pass-band. This is due to the ignorance of frequency change of phase shift in the equivalent quarter-wave stacks. The above-stated issue can be rectified by the proposed optimization strategy, named the BES optimization algorithm.
This work introduces the BES optimizer for the model and optimization of optical filters to improve transmission efficiency. Among the different stochastic optimization methods, nature-inspired, population-oriented methods are of particular interest since they mimic the behaviour of animals in order to solve real-world problems. The BES algorithm produces the optical thin film filter settings to provide the best results for structural applications. In summary, the BES method uses the design requirements and the transmittance pattern as data to determine the best layer thickness. By altering the thickness and number of layers with fixed refractive index, the suggested BES is utilized to optimize the optical filter characteristics in terms of reflectance, transmittance, and FWHM.
BES is a novel nature-inspired optimization technique that mimics the foraging strategy of bald eagles as they seek food. The searching procedure is partitioned into three sections. In the first step (selecting area), an eagle chooses the area with the most prey. The eagle goes within the designated area to look for prey in the second phase (scanning in area). The eagle hangs from the optimal location found in the second phase to decide the ideal place to attack in the third phase (snatching). Snatching begins at the best location, and all subsequent motions are geared toward it. This algorithm is examined using a two-part assessment framework: (1) describing the benchmark of the optimal solution to assess algorithm efficiency; and (2) evaluating algorithm efficiency to other computing approaches. The optimization findings show that the BES method outperforms other standard techniques algorithms.
The paper is organized in such a way that Section 1 offers a relatively short introduction to the study, Section 2 ponders the conventional systems of optical filter design with their restrictions, Sections 3 and 4 cope with determination and design methodology, respectively, Section 5 explains the concept of the suggested plan in optical filter design, Section 6 discuses the outcomes of the proposed strategy, and Section 7 elaborates the conclusion and future work.
This section describes the traditional techniques of optical filter design and its limitations.
Rabady et al. [1] employed the PSO approach to find the optimal optical filtering architecture globally. In terms of achieving the global optimum, the strategy surpassed the GA approach. The method’s disadvantage is that the result may settle at the local optimum solution and lack to obtain the global optimum. The article [7] discusses a proposed approach of optimizing optical parameters using GA and Taguchi to obtain an optical filter with good transmittance. The system’s key restriction is that it is very effective and is employed in live-streaming systems. However, the approach encounters convergent challenges and is thus less recommended. The author in [8] proposed a parallel pre-determined paradigm for optical filters. In the presence of real production constraints, this strategy provides a more rigorous and desirable option. Unfortunately, this technique is hampered by recurring difficulties. Reference [9] created a pattern of optical thin film based on the Fourier transform to provide a beginning populace, which is then optimized using GA. According to the findings, GA improves enhancement of optical thin film manufacturing. However, the approach that uses GA for design and optimization purposes requires a significant amount of computing time to get the desired outcome.
The challenges of the conventional techniques of optical filter model are discussed as,
■ The shortcomings of using the Grasshopper optimization algorithm (GOA) are tunstable speed of convergence, and unbalanced trade-off among exploration and exploitation operation [10].
■ The Monte Carlo method is less preferred due to the requirement of more time and computation to approximate the solution.
■ The GA method is computationally expensive and time consuming to perform the optimization process [11].
These are the limitations that act as inspiration for the improvement of the proposed method of optical filter design.
A multilayer optical band pass filter for the centre wavelength of 656.3, 486.1, 464.7 nm, and normal incidence in the visible range is designed. Different layers with high and low refractive index elements were used. For low and high refractive indices measurements, ‘structure configurations are chosen. Zinc sulphide and titanium dioxide have high refractive indexes, whereas magnesium fluoride and silicon dioxide have low refractive indexes. In the wavelength region 400 to 700 nm, an optical filter with good transmission is constructed. With three distinct substrate refractive indices, three variants of thickness restrictions are investigated. The design was created for 28, 30, or 32 layers, with refractive indices of the substrates of 1.5143, 1.5224, and 1.524, respectively. A computer program was established in MATLAB that takes the optical thin film filter settings as input and attempts to improve the reflectance and transmittance pattern by optimizing the criterion using the BES optimization method.
5 Proposed Bald Eagle Search Optimization Algorithm in Optical Filter Design
Thin-film optical interference filters are vital parts in a wide variety of uses, namely optical networks and science. These filtration must be developed preliminary site by deciding the appropriate combination of thicknesses for the thin film layer to provide the optimal filtering pattern. The BES method outperforms other standard techniques by creating a set of different thickness for the thin films stockpile with the finest spectrum analysis in aspects of filter sharpness and the reflection ratio in the passband to that in the stopbands. Because the BES technique has indeed demonstrated to be a potent optimization technique in a wide range of engineering systems, such as the configuration of multiple layer optical interference filtration systems, it has the prospects to be helpful for this problem by forecasting the ideal number of layers that can be used to acquire the optimal filtration spectroscopy that will ultimately be acquired.
Standard optimization algorithms exhibit the characteristics centered on the food-seeking features of the creatures. They depict the dynamic nature in handling the problems related to convergence nature. The suggested BES method tackles the convergence problem by utilizing the dynamic properties of Bald eagle search agents. This improves the algorithm’s capacity to achieve the ideal solution with a higher convergence speed than other optimization algorithms, which typically result in local best outcome. The computational cost of BES strategy is also less compared to the existing methods. The working principle of the BES algorithm comprises of three main phases of operations, such as the phase of selection, the phase of search, and the phase of prey. These stages are very important to acquire good results continuously and identify a round optimal solution. The proposed BES outperforms based on transmittance, reflectance, and FWHM when compared with various traditional methods. Initially, the relevant parameters of the BES algorithm are determined, which are then processed into training and test samples. Then, the fitness function is set, and fitness measure for each element is determined. The optimal parameters are obtained by optimizing the BES algorithm. The algorithmic steps of BES algorithm are stated as below,
Step 1: Parameter Initialization: Initialize the attributes of the optical thin film, like thickness, high and low refractive index, and layer quantity. Additionally, set the maximum iteration number.
Step 2: Initialization of Population:The number of bald eagle search agents is initialized on the basis of materials, like
where,
The optimal solutions of each bald eagle are saved in the manner of the above equation, which aids in determining the survival of the fittest throughout the whole group.
Step 3: Position Update: The location of bald eagles can be revised depending on three operations such as the phase of selection, the phase of the search, and the phase of prey.
Scenario 1: Phase of selection: The bald eagles initially select the search area in random and then explore the best position by evaluating the prey. The location at this stage is principally evaluated through a priori knowledge and location changing parameters that is expressed in Eq. (3) as below,
where,
Scenario 2: Phase of search: The spiral movement of the bald eagle search agents for searching its prey enhances the speed of search and evaluates the better dive capture location. The location based on this operation is expressed in Eqs. (4)–(8).
where,
Scenario 3: Phase of Prey: The bald eagle search agents dive from best location towards the target prey, and the others in the population go near the best location and attack them. The location at this phase of operation is formulated in Eqs. (9)–(13).
where,
Step 4: Sorting of solutions: The bald eagles are ordered according to their capacity measurements, and options with lower fitness values are ignored [17–20]. The best fitness metric is substituted with the current one. Or else, the prior option is still considered the best outcome [21,22].
Step 5: Stopping consition: The method is ended after completing the iteration number required to achieve the optimal outcome [23,24].
This section summarises the findings achieved when designing an optical thin film filter using the suggested BES model.
The method is tested in MATLAB 9.6 R2019a, a programme loaded in Windows 10 OS and 64-bit OS with 16 GB RAM, which provides an effective execution of the suggested model.
Reflectance and transmittance are the assessment indices used for the suggested method. The amount of flux transmission by the substrate is generalised with the amount of flux incident on the surface. The amount of flux reflecting by a material is defined as reflectance, which is generalised by the amount of flux incident on the layer. The term FWHM is the spectral bandwidth over which the bandpass filters transmit.
The GA, PSO, and GOA techniques are compared with the proposed BES optimization strategy to expose the efficacy of the proposed model in the design of optical filters.
6.4 Analysis in Terms of Reflectanceand Transmittance
This part explains the transmittance and reflectance assessment of the suggested approach. BES is used to vary the thickness while keeping the refractive index fixed. The number of Di-electric layers evaluated for each of the six Scenarios is shown in Tab. 1.
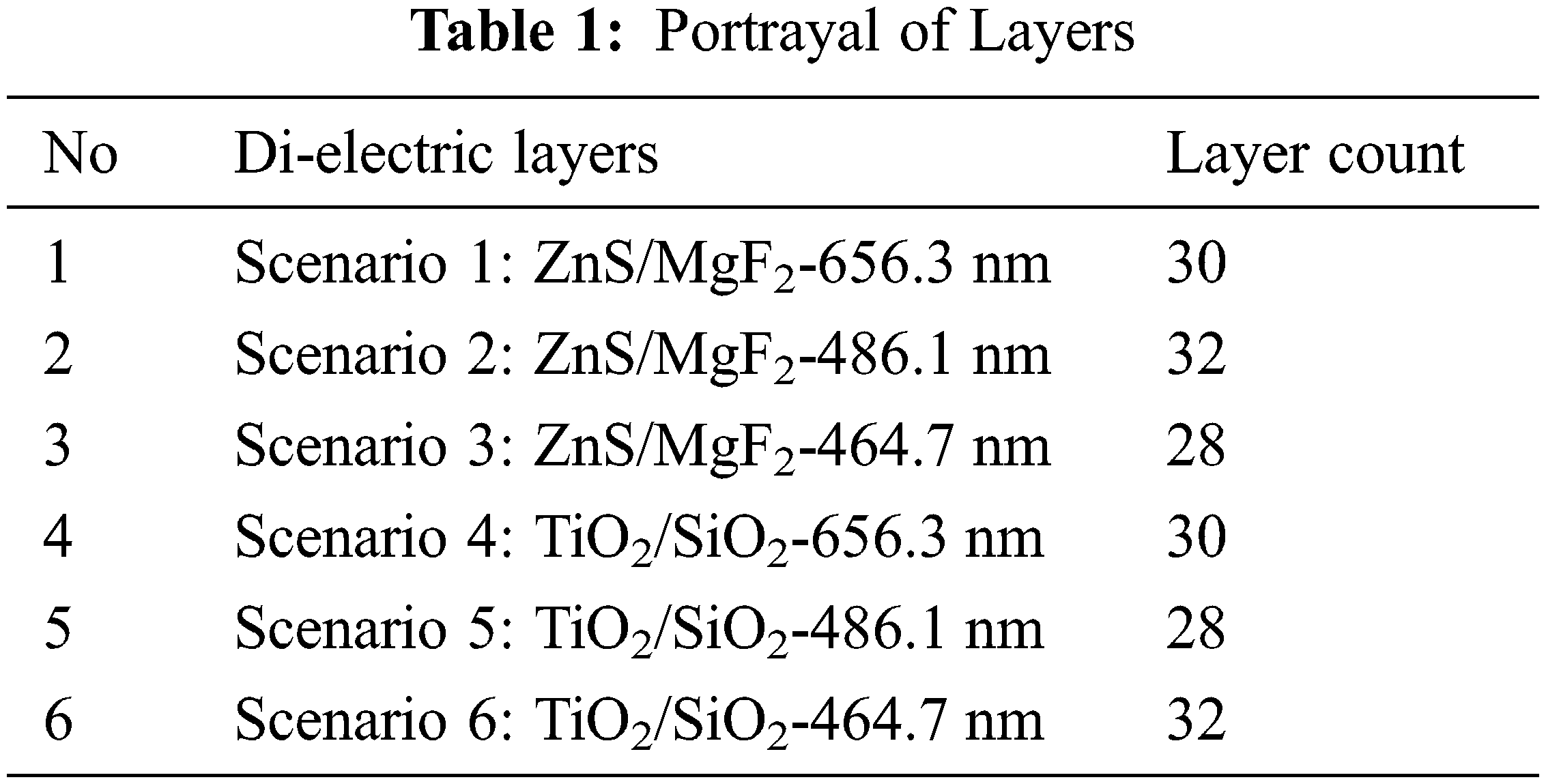
Scenario 1: In Scenario 1, the central wavelength = 656.3 nm,
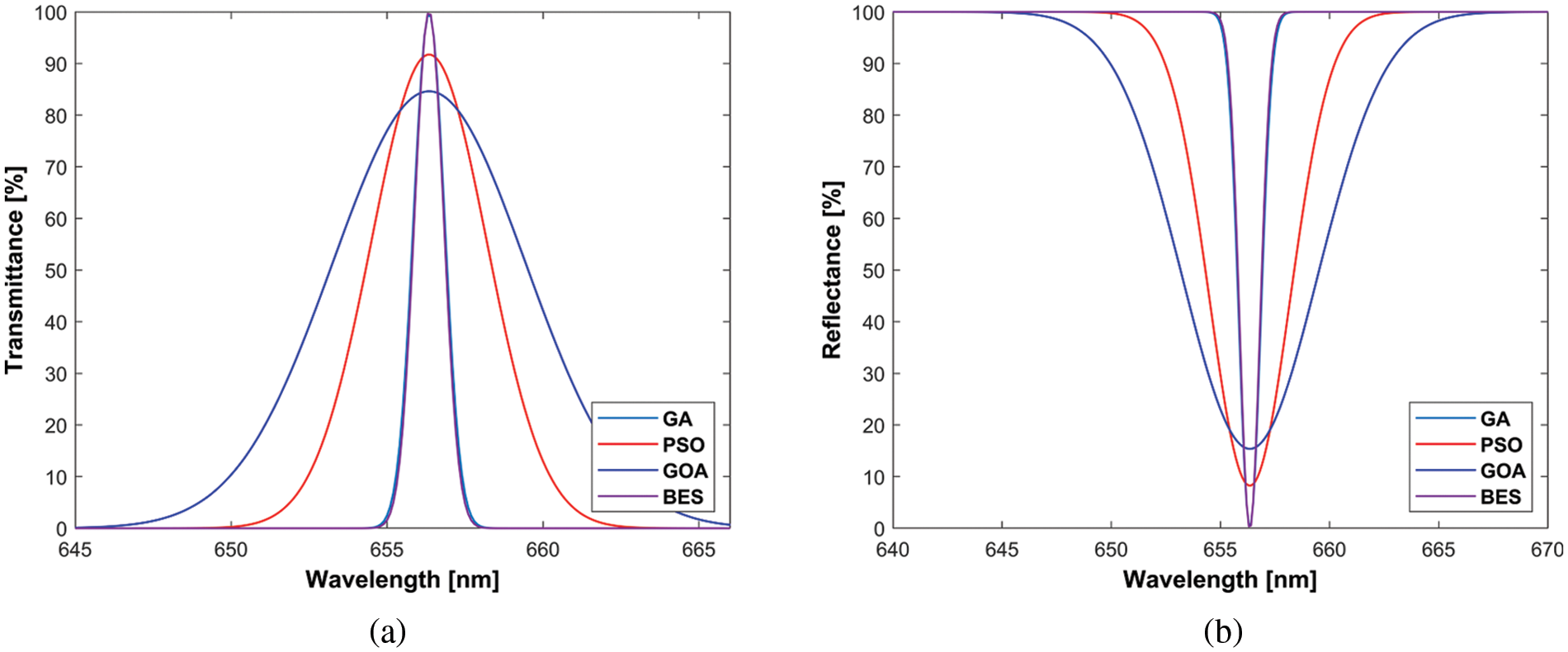
Figure 1: Scenario 1 (a) Transmittance, (b) Reflectance
Scenario 2: In Scenario 2, the central wavelength = 486.1 nm,

Figure 2: Scenario 2, (a) Transmittance, (b) Reflectance
Scenario 3: The centre wavelength in Scenario 3 is 464.7 nm,
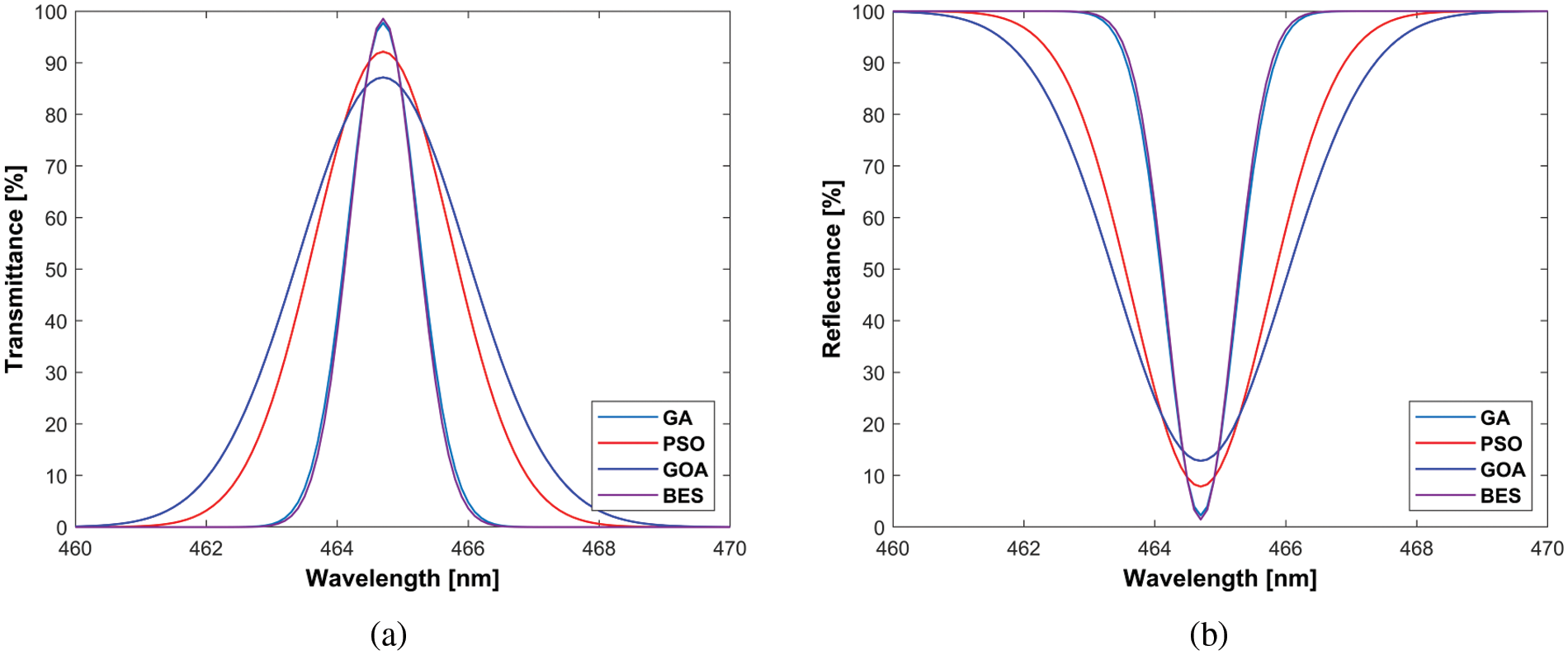
Figure 3: Scenario 3, (a) Transmittance, (b) Reflectance
Scenario 4: The centre wavelength in Scenario 4 is 656.3 nm, the high refractive index is 2.5709, the substrate (BK7 glass) is 1.5143 and the low refractive index is 1.5156, . Scenario 4’s transmittance and reflectance measurements are depicted in Fig. 4.
Figure 4: Scenario 4, (a) Transmittance, (b) Reflectance
Scenario 5: The centre wavelength in Scenario 5 is 486.1 nm, the high refractive index is 2.7346, substrate (BK7 glass) is 1.5224., and the low refractive index is 1.4631. Scenario 5’s transmittance and reflectance measurements are depicted in Fig. 5.
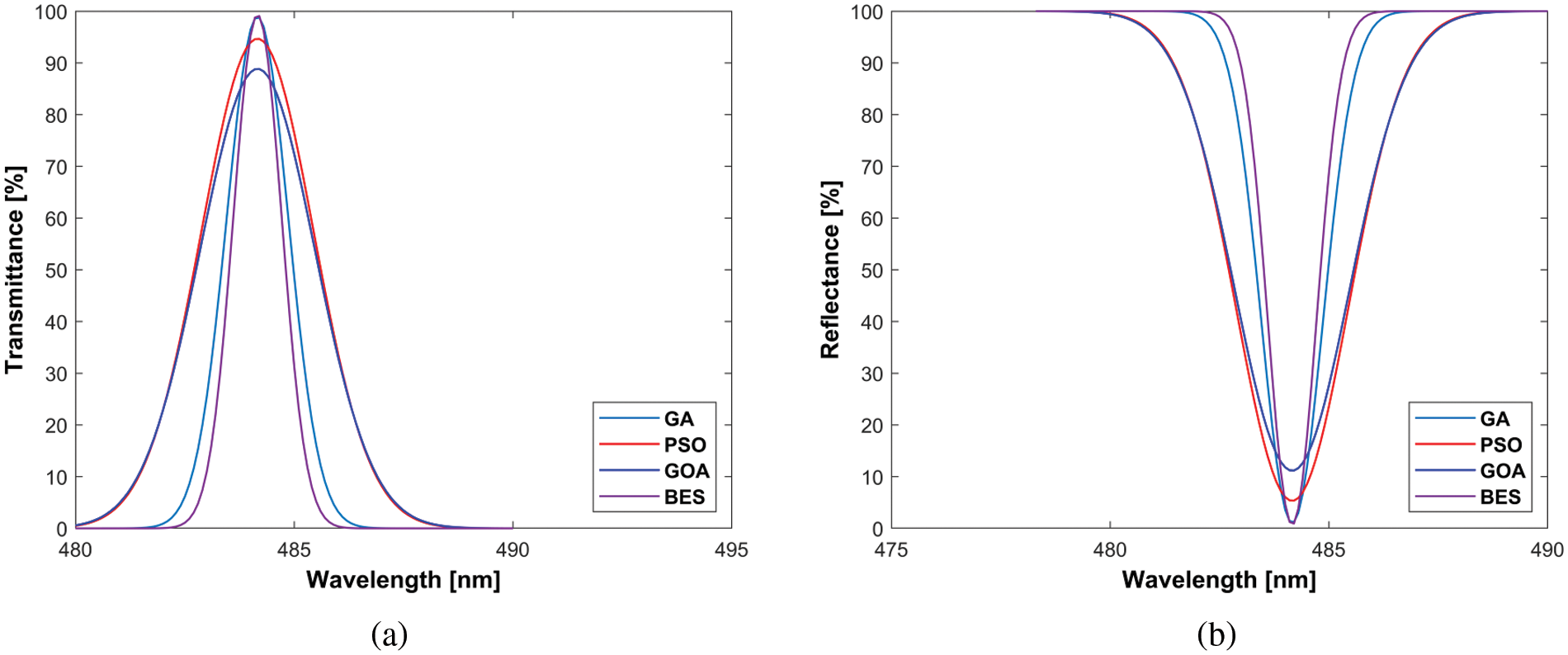
Figure 5: Scenario 5, (a) Transmittance, (b) Reflectance
Scenario 6: The central wavelength in Scenario 6 is 464.7 nm, the high refractive index is 2.7771, the low refractive index is 1.4645, and the BK7 glass substrate is 1.524. Scenario 6’s reflectance and transmittance measurements are depicted in Fig. 6.
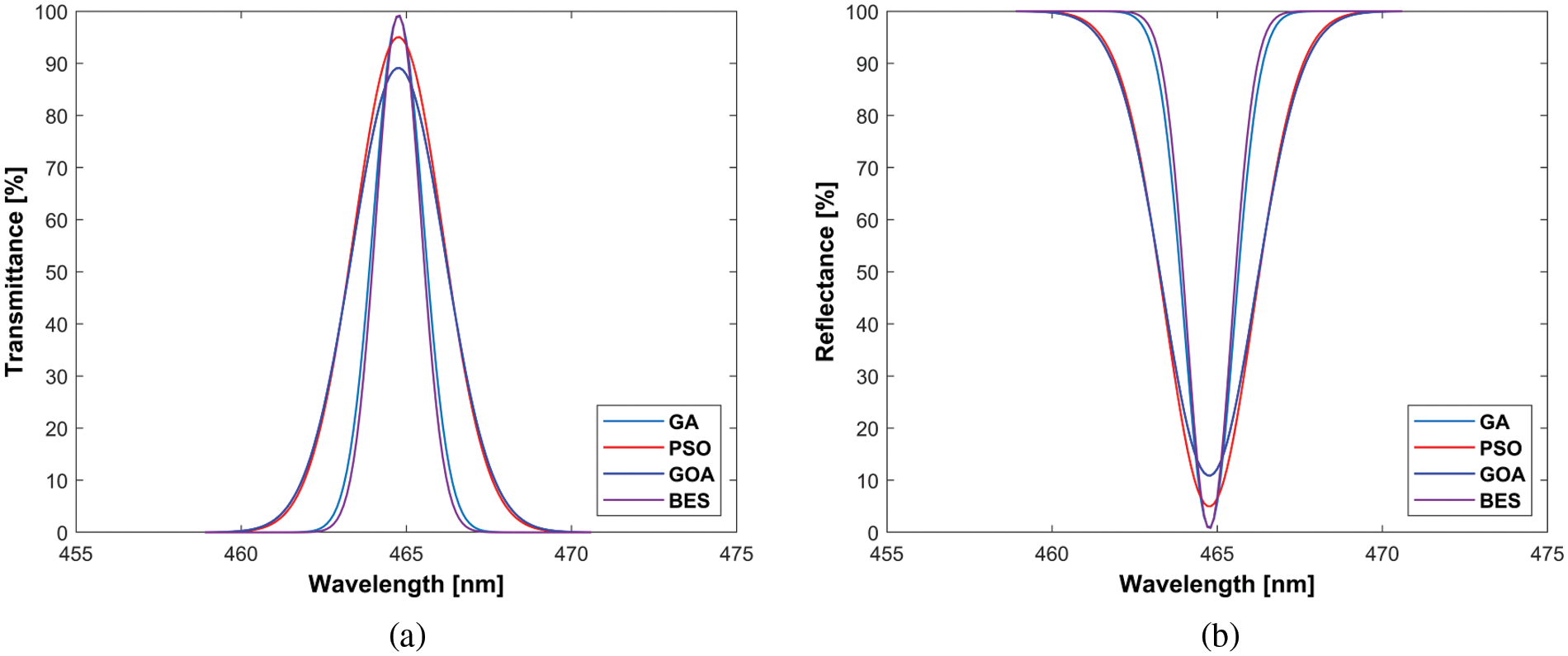
Figure 6: Scenario 6, (a) Transmittance, (b) Reflectance
From the results it is evident that the proposed BES-based optical filter design model is efficient in terms of transmittance, reflectance, and FWHM as compared with the existing GOA model.
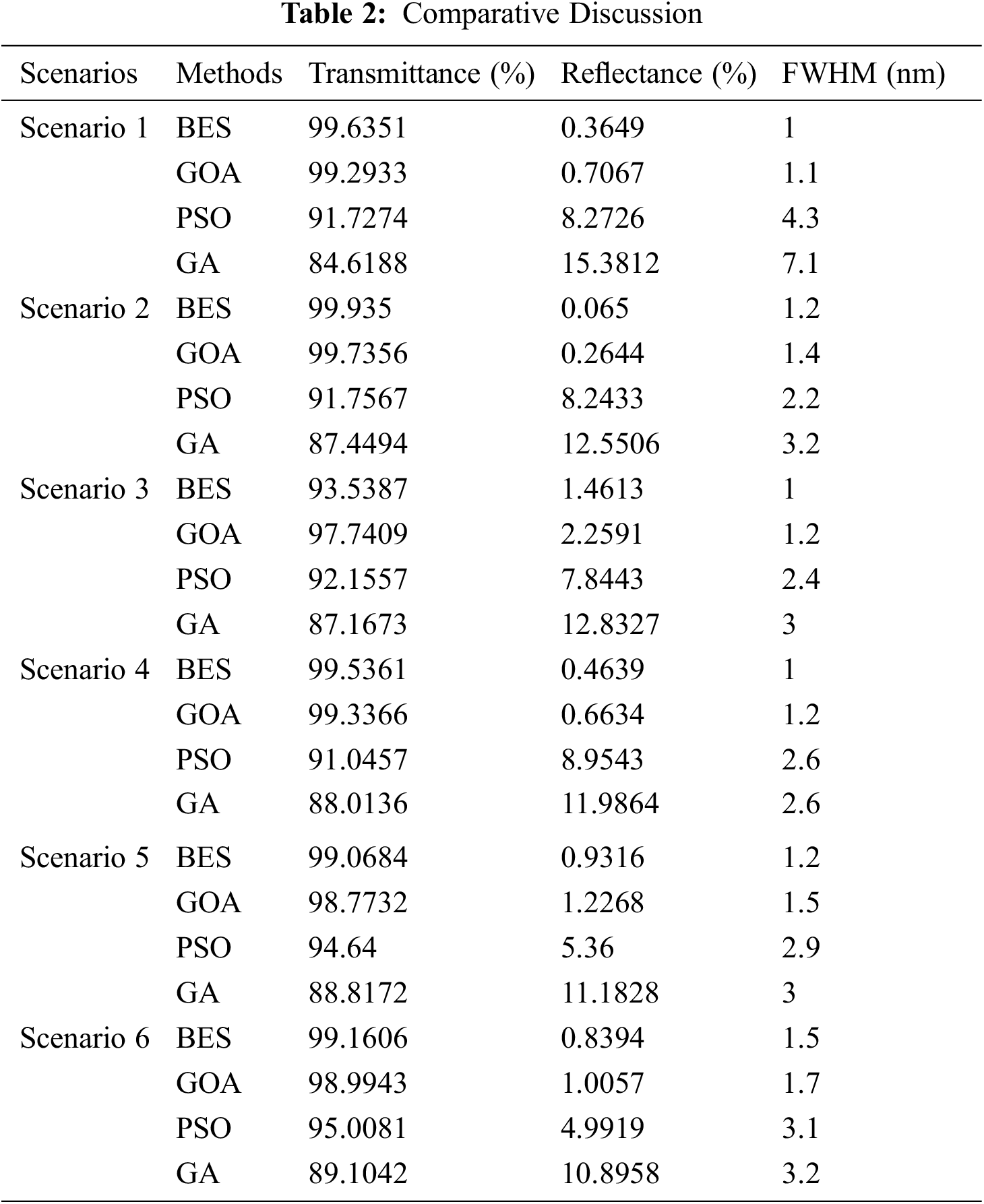
Tab. 2 shows the comparative discussion of the methods such as PSO, GA, GOA, and the proposed BES in terms of transmittance, reflectance, and FWHM. It is evident from the table that the proposed BES method achieves high transmittance, reduced reflectance and FWHM measure when compared to the conventional strategies and proved to show better performance in transmission applications.
An optimization-based strategy for the optimal model of an optical thin film filter is proposed in this work. The effects of optic restrictions like thickness, reflectance, and FWHM on model resolving convergence were investigated. BES has been applied to optimize the refractive index and thickness measurements in order to generate a design with an improved transmittance pattern. With a population size of 100 and thickness as the optimal parameter, the solution based on the fitness value with BES restraints was reached. As a consequence, the results reveal that using thickness as an optimum factor yielded better outcomes than using refractive indices. The results thus obtained using the proposed BES method are compared to the existing methods such as GA, PSO, and GOA and it is found that it outperformed the existing ones in terms of transmittance, reflectance, and FWHM. In the future, optical thin films will be created to deliver better results through the use of hybrid optimization tactics rather than single meta-heuristic optimization approaches. The ensuing work ceased with 2 different sets of di-electric materialswhere the Feasibility of modified BES algorithm for optimization is to be studied and it can be used for the distinct design of optical band pass filters.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. R. I. Rabady and A. Ababneh, “Global optimal design of optical multilayer thin-film filters using particle swarm optimization,” Optik, vol. 125, no. 1, pp. 548–553, 2014. [Google Scholar]
2. M. A. Kecebas, M. P. Menguc, A. Kosar and K. Sendur, “Passive radiative cooling design with broadband optical thin-film filter,” Journal of Quantitative Spectroscopy and Radiative Transfer, vol. 198, pp. 179–186, 2017. [Google Scholar]
3. M. S. Costa, V. Baptista, G. M. Ferreira, D. Lima, G. Minas et al., “Multilayer thin-film optical filters for reflectance-based malaria diagnostics,” Micromachines, vol. 12, no. 8, pp. 890, 2021. [Google Scholar]
4. H. A. Macleod, in Thin-Film Optical Filters, 3rd ed., Bristol, UK: J W Arrowsmith Ltd., pp. 1–667, 2001. [Google Scholar]
5. M. Tilsch, K. Hendrix and P. Verly, “Optical interference coatings design contest 2004,” Applied Optics, vol. 45, no. 7, pp. 1544–1554, 2006. [Google Scholar]
6. D. G. Li and A. C. Watson, “Genetic algorithms in optical thin film optimization design,” in Proc. ICCIMA, New Delhi, India, pp. 86–90, 1999. [Google Scholar]
7. S. Parinam, M. Kumar, N. Kumari, V. Karar and A. L. Sharma, “An improved optical parameter optimization approach using taguchi and genetic algorithm for high transmission optical filter design,” Optik, vol. 182, pp. 382–392, 2019. [Google Scholar]
8. P. Azunre, J. Jean, C. Rotschild, V. Bulovic, S. G. Johnson et al., “Guaranteed global optimization of thin-film optical systems,” New Journal of Physics, vol. 21, pp. 073050, 2019. [Google Scholar]
9. E. K. Ejigu and B. M. Lacquet, “The use of a genetic algorithm in optical thin film design and optimisation,” South African Journal of Science, vol. 106, no. 7, pp. 1–4, 2010. [Google Scholar]
10. S. Z. Mirjalili, S. Mirjalili, S. Saremi, H. Faris and I. Aljarah, “Grasshopper optimization algorithm for multi-objective optimization problems,” Applied Intelligence, vol. 48, pp. 805–820, 2018. [Google Scholar]
11. S. Parinam, A. L. Sharma, V. S. R. S. P. Kumar, M. Kumar, N. Kumari et al., “Optimization of optical parameters for the design of multilayer bandpass filter using genetic algorithm,” Materials Today: Proceedings, vol. 5, no. 2, pp. 5091–5096, 2018. [Google Scholar]
12. Y. Huang, H. Jiang, W. F. Wang, W. Wang and D. Sun, “Soil moisture content prediction model for tea plantations based on SVM optimised by the bald eagle search algorithm,” Cognitive Computation and Systems, vol. 3, no. 4, pp. 351–360, 2021. [Google Scholar]
13. L. Gao, F. Lemarchand and M. Lequime, “Exploitation of multiple incidences spectrometric measurements for thin film reverse engineering,” Optics Express, vol. 20, no. 14, pp. 15734–15751, 2012. [Google Scholar]
14. M. Niraula, J. W. Yoon and R. Magnusson, “Single-layer optical bandpass filter technology,” Optics Letters, vol. 40, no. 21, pp. 5062–5065, 2015. [Google Scholar]
15. J. Zhang, Y. Xie, X. Cheng, H. Jiao and Z. Wang, “Thin-film thickness-modulated designs for optical minus filter,” Applied Optics, vol. 52, no. 23, pp. 5788–5793, 2013. [Google Scholar]
16. I. Tariq, H. A. Alsattar, A. A. Zaidan, B. B. Zaidan, M. R. Abu Bakar et al., “MOGSABAT: A metaheuristic hybrid algorithm for solving multi-objective optimisation problems,” Neural Computing Applications, vol. 30, no. 2, pp. 1–15, 2020. [Google Scholar]
17. F. O. Sameer, M. R. Abu Bakar, A. A. Zaidan and B. B. Zaidan, “A new algorithm of modified binary particleswarm optimization based on the Gustafson–Kessel for credit risk assessment,” Neural Computing Applications, vol. 31, no. 2, pp. 337–346, 2019. [Google Scholar]
18. H. A. Alsattar, A. A. Zaidan and B. B. Zaidan, “Novel meta-heuristic bald eagle search optimisation algorithm,” Artificial Intelligence Review, vol. 53, no. 3, pp. 2237–64, 2020. [Google Scholar]
19. B. Birge, “PSOt-a particle swarm optimization toolbox for use with matlab,” in Proc. of the 2003 IEEE Swarm Intelligence Symp. SIS’03 (Cat. No.03EX706), Indianapolis, Indiana, USA, pp. 182–186, 2003. [Google Scholar]
20. D. M. Topasna and G. A. Topasna, “Numerical modeling of thin film optical filters,” Proceedings of the SPIE, vol. 9666, id. 96661P, pp. 1–10, 2009. [Google Scholar]
21. A. M. Mahdy and E. S. M. Youssef, “Numerical solution technique for solving isoperimetric variational problems,” International Journal of Modern Physics C, vol. 32, no. 1, pp. 2150002-1–2150002-14, 2021. [Google Scholar]
22. A. M. Mahdy, Y. A. E. Amer, M. S. Mohamed and E. Sobhy, “General fractional financial models of awareness with Caputo–Fabrizio derivative,” Advances in Mechanical Engineering, vol. 12, no. 11, pp. 1–9, 2020. [Google Scholar]
23. S. Pimenta, S. Cardaso, A. Miranda, P. DeBeule, E. M. S. Castanheira et al., “Design and fabrication of SiO2/TiO2 and MgO/TiO2 based high selective optical filters for diffuse reflectance and fluorescence signal extraction,” Biomedical Opticas Express, vol. 6, no. 8, pp. 3084–3098, 2015. [Google Scholar]
24. S. Naif Turki, “Optimization design of band pass filter in the infrared region,” International Journal of Emerging Trends of Technology in Computer Science (IJETTCS), vol. 4, no. 2, pp. 001–005, 2015. [Google Scholar]
APPENDIX A

Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools