A Novel ANFIS Based SMC with Fractional Order PID Controller

1  Introduction

Water level control is widely used in industry, particularly in petroleum refineries and chemical plants. Liquids must be pumped and collected in tanks before being pumped into the next tank in the petrochemical industries. The liquid is processed many times in the tanks using chemical to keep the water level under control. Generally, loop control exists in a few control loops of a process control system. Liquid level control in tanks, chemical combining, and reaction tanks is a common problem in industrial operations. Non-linearity is a key issue in process industries, and it is far more difficult to solve than linear ones. The nonlinear system performance is cannot be predicted based on the equations of the first degree and also the mathematical modelling not capable to give common solutions. Chemical industries, waste water treatment industries, power industries, fertilizer Controlling the flow rate of water level was essential in several sectors. It is important to control the liquid level in a spherical tank system, because non-linearity is caused by form change Compared with various conventional tank systems, the Spherical tank system has more merits such as product loss reduction, high strength, increased production, and inexpensive. To solve this problem the implementation of Backstepping Controller is based on an Adaptive Neuro-Fuzzy Inference System with FOPID controller for liquid level control in a nonlinear system is used.

Researchers proposed several attempting to control methods that are used to control the flow of liquid level. Elanaz et al. (2011) used Sliding Mode Control to investigate various methods for reducing the nonlinear problem and achieving fast transient response. This study uses Fuzzy logic to explain the mixed state feedback sliding-mode [1]. Govind and Arun (2017) focused on exploring the method of liquid level control using Sliding Mode Controller with FOPID applied for two tank hybrid system achieves maximum settling time reduction. This method conveys better closed loop performance than the existing method [2]. Mercy and Giriraj (2017) proposed the method for a nonlinear unstable process which uses the Particle Swarm Optimization method for sewage water treatment. This method performs well in time domain specifications, error minimization and external disturbance rejection [3]. Bharathi et al. (2014) presented the method to maintain the liquid level in a desired value by using Model-Based Controller and outperform overshoot reduction, better rise time, settling time, and error performance indices [4]. Sakthivel et al. (2013) A method for controlling a circular tank system's water level the proposed. This can be done by a Fuzzy logic controller which gives better set point tracking, overshoot, and rise time [5]. Ansari et al. (2016) identified important issue influencing the extent industries and control of nonlinear system using Iterative learning control [6]. From the literature, the Fuzzy logic controller cannot adapt for larger range of working environments. Because of the non-linearity, controlling the flow rate of liquid level in a circular container is a difficult operation exhibited because of the change in area of cross-section. Moreover, an ideal model with a conventional controller or an estimated model with a controller having robustness to model parameter uncertainties can efficiently control the liquid level [7,8]. Although most industrial processes are highly complex and nonlinear, linear methods are frequently sufficient to estimate a process in the region of a single operating point. Researchers have proposed a number of methods for controlling liquid levels. However, it does not produce superior results than the suggested system's regulating method. So ANFIS based SMC-FOPID is used.

As a result, the paper's significant contributions are as follows:

•   Creation of a mathematical formula for a spherical interacting tank system based on fundamental principles.

•   Dividing the complete working region of the Spherical Interaction Tank System into discrete time zones.

•   To design and implement the ANFIS based SMC with FOPID Spherical conversing tank structure controller.

•   Advantage of ANFIS based SMC with FOPID The method is less susceptible to liquid level management, has a during which, strong time-domain requirements, and better productivity indices [9].

•   Set point tracking performances under the set point for the desired level of liquid in an interacting circular tank system [10], as well as disruptions, are investigated to illustrate the enhanced algorithm's efficacy.

The paper is structured as follows; Section 1 describes the suggested new framework as well as the findings of several research papers, while Section 2 defines the concept, Section 3 presents the controller design and also it deals with ANFIS based SMC with FOPID controller. The acquired simulated findings and their explanation are presented in Section 4, and the paper is concluded in Section 5.

2  Process Description of Spherical Two-Tank Interacting System

In the last three decades, the control of spherical two-tank interacting liquid level system has concerned consideration of several researchers around the planet. This is the most significant trouble for the liquid level controlling system because of its non-linearity [11,12]. When there is an inlet and exit of liquid out of the tank accordingly, the major goal of a spherical Interaction two-tank design is to maintain an optimum amount of liquid in an interaction tank system [13]. Fig. 1 is a schematic design of a spherical two-tank interacting arrangement. In this arrangement, Tank 1 and Tank 2 are two identical circular interaction tanks, each with a height (H) of 40 cm and a radius (R) of 20 cm. A valve limitation with a P01 valve efficiency connects the two containers. Fin l and Fin 2 are the two input flows for Tank 1 and Tank 2, respectively. Fout 1 and Fout 2, respectively, are the drains for Tank 1 and Tank 2. Fin l’s inflow is regulated by a control valve [14]. The water level elevations in Tanks 1 and 2 are h0 and h1, respectively. Fluids flow from Tank 1 to Tank 2 when this MV 01 valve is opened.

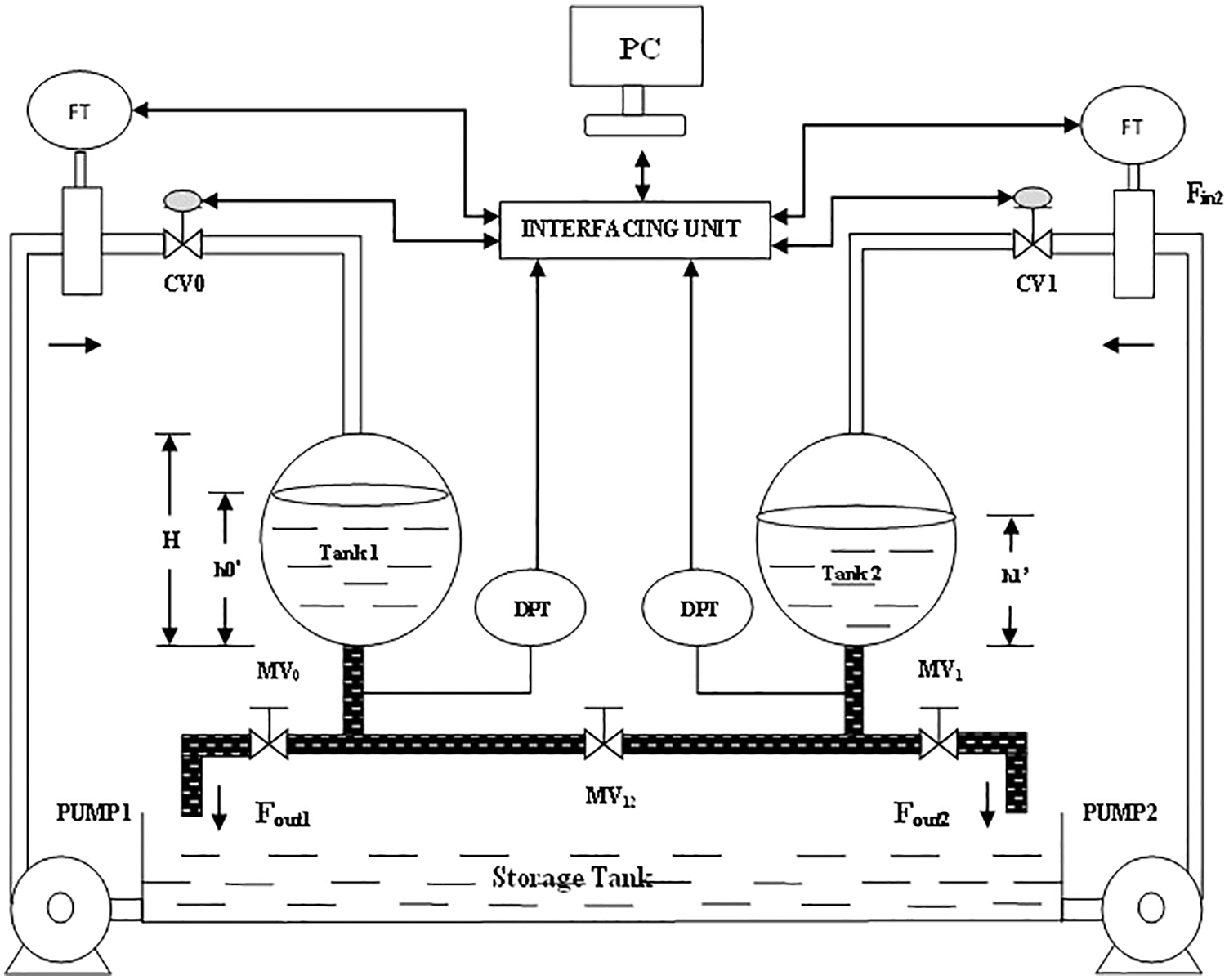
Figure 1: Schematic diagram for spherical two tank interacting system

To measure the water heights, differential pressure transmitters (DPT) are being used, and the output is used as feed to manage the level. Control valves CV0 and CV1 are used in this arrangement. In a storage tank, raw documents are stored. Magnetic Flow Transmitters (MFT) calculate the input flows F in 1 and F in 2 [15,16]. The DPT and MFT send current indications (4–20 mA), which are transferred thru the PC's interface unit. There are eight analogue input streams and two analogue output channels on the PC interface. Two pumps, PUMP l and PUMP 2 carry water from the basin to Tanks l and 2, correspondingly. In this case, the liquid level h1 in Tank2 will be used as a parameter. The flow of Tank 2 (Fin2) is kept continuous. The final control valve used in this technique is the throttle valve. controlling component that performs the necessary action to keep the liquid level in the Tank at a constant level 2. Fig. 1 demonstrates the simulation of a circular interacting system.

For Tank 1 the mass balance equation can be expressed as,

A0′(l0′)dl0′dp=Fin1−β01l0′−l1′ (1)

Linearization of above Eq. (1) written as,

A0′(l0′)d(∂l0′)dp=f0(Fin1)−f0(l0′−l1′) (2)

Apply partial differentiation in Eq. (2),

A0′(l0′)d(∂l0′)dp=(∂f0∂Fin1).∂Fin1−(∂f1∂l1′).∂l0′−(∂f1∂l1′)∂l1′ (3)

Eq. (3) can be rewritten as,

A0′(l0′)d(∂l0′)dp=∂Fin1−β012l0′−l1′∂l0′+β012l0′−l1′∂l1′ (4)

Apply Laplace transformation in Eq. (4),

∂h0′=∂Fin1+β012h0′−h1′∂l1A0′(l0′)s+β012l0′−l1′ (5)

For Tank 2 the mass balance equation can be expressed as,

A0′(l0′)dl1′dt=β01h0′−h1′−β1h1′ (6)

Linearization of above Eq. (6) as,

A1′(l1′)d(∂l1′)dp=f0(l0′,l1′)−f1(l2′) (7)

Apply partial differentiation in Eq. (7),

A1′(l1′)d(∂l1′)dp=(∂f0∂l0).∂l0′−(∂f0∂l1′).∂l1′−(∂f1∂l1′)∂l1′ (8)

Rearranging the above equation,

A1′(l1′)d(∂l1′)dp=β012l0′−l1′∂l0′−β012l0′−l1′∂l1′−β12l1′∂l1′ (9)

Applying Laplace transformation,

[A1′(l1′)z+β012l0′−l1′+β12l1′]∂l1′−β012l0′−l1′∂l0′ (10)

Substituting Eq. (5) in Eq. (10) we get,

[A1′(l1′)z+β012l0′−l1′+β12l1′]∂l1′=β012l0′−l1′[∂Fin1+β012l0′−l1∂l1′A0′(l0′)z+β01sl0′−l1′] (11)

Let us assume,

C0=12l0′−l1′,C1=12l1′,Q1=1β01C0,Q2=1β1C1

τ0=A(l0′)R0,τ1=A(l1′)Q1

Applying the above variables in (11) we get,

∂l1′∂Fin1=Q1τ0τ1s2+[τ0+τ1+A(l0′)R1]z+1 (12)

where, l-Height of spherical tank, Fin1 Maximum inflow to tank 1, β01 Valve co-efficient MV01, β1 Valve co-efficient MV1, Q is the Radius of spherical tank,

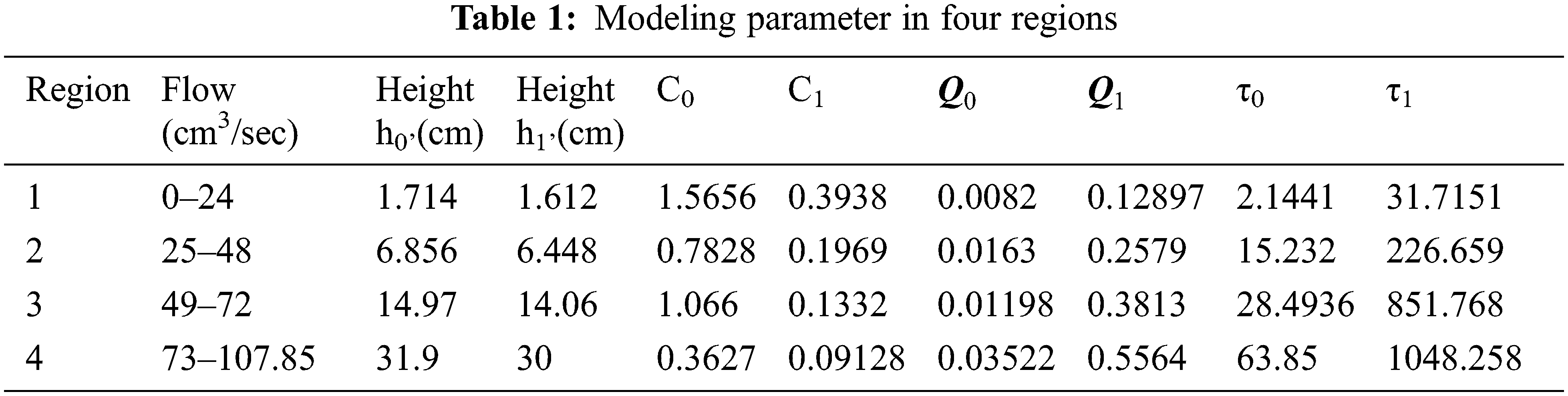
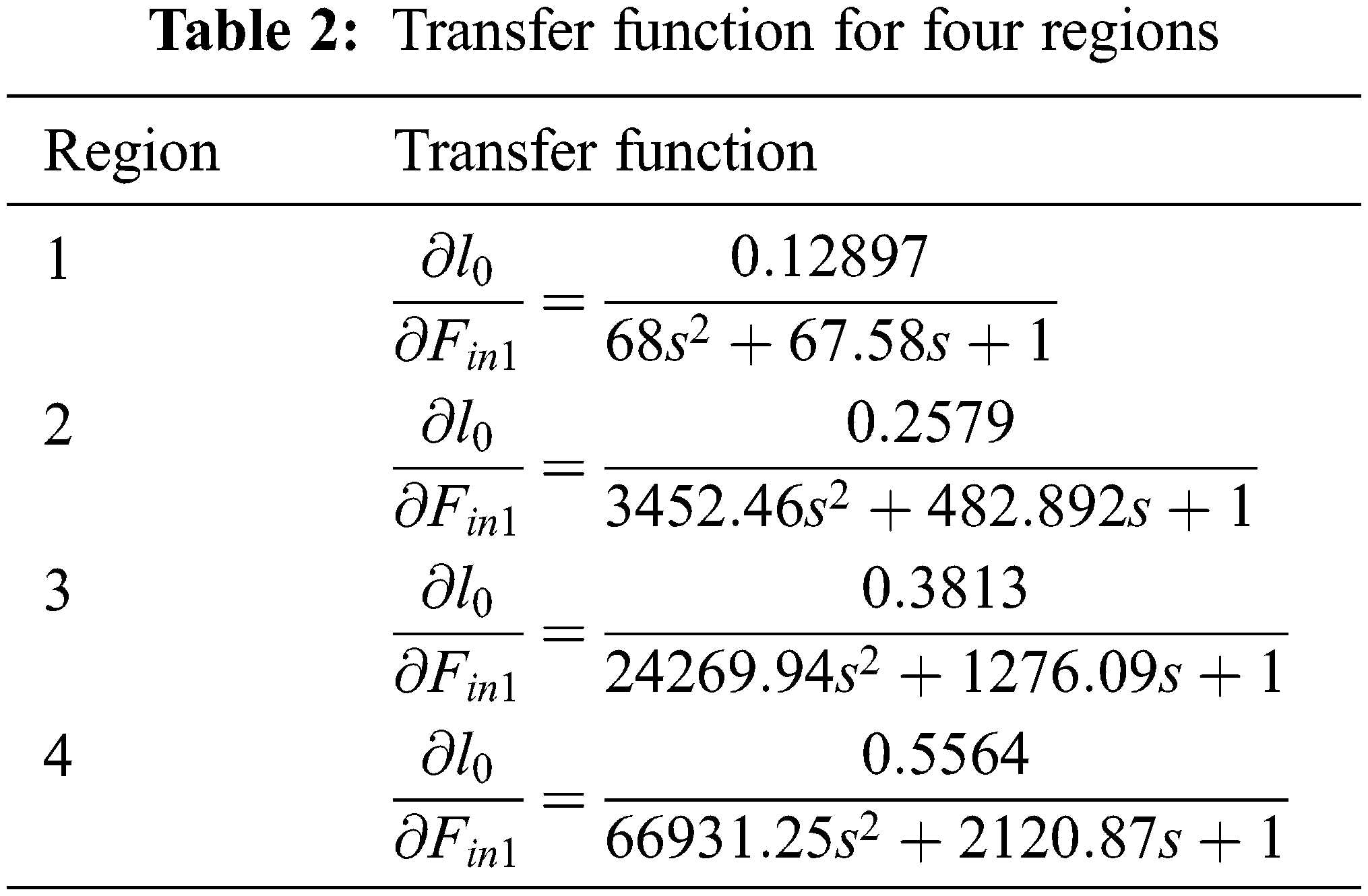
Substituting the modeling parameters in Eq. (12) Tab. 1 shows the modeling parameters. Tab. 2 shows the transfer functions for four regions.

3  Controller Design

Controllers are commonly applicable to control strategy in most of the industrial use.

3.1 PID Controller

This PID controllers are commonly applicable to control strategy in most industrial use. became an ordinary tool, which is commonly regarded as fundamental for achieving realistic control technique goals, as shown in Fig. 2, due to simplicity that permitted human adjustment and ability to effectively manage numerous nonlinear and partly unknown phenomena. 2. PID control is used in a significant number of practical feedback loops [17]. The discrepancy between desired set point u and a measured process variable y(t) is estimated by a Controller as a relative error e(t) (t). Let m(t) is the control signal denotes the sum of three terms.

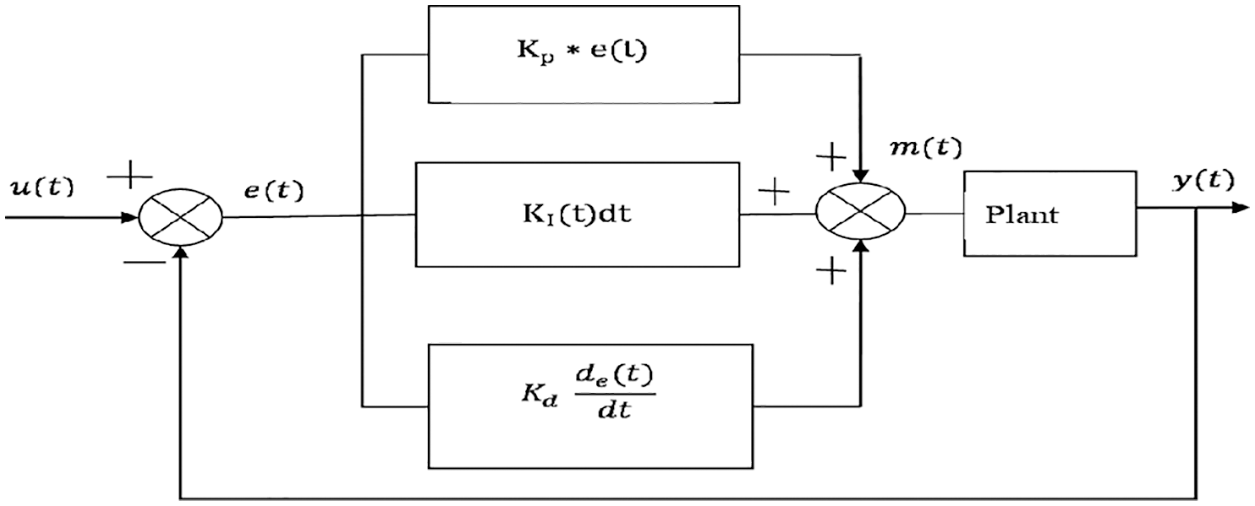
Figure 2: PID controller structure

3.2 FOPID Controller

Integral order computers have evolved into fractional computers. Sliding mode computers and adaptive controls are two different types of fundamental order controls. The example of the FOPID controlling transfer function is as follows

Gc(s)=u(s)e(s)=kp+kIs−λ+kDsμ (13)

Gc(s) stands for controller converter, (s) stands for error, and (s) stands for output. kp, kI, and kD are the gains for proportional, integral, and derivative terms, respectively. The term is the fractional component of integral parts and the percentage element of derivatives parts, as shown in Fig. 3. The FOPID circuit's time-frequency model is presented in,

u(t)=Kpe(t)+KiD−λe(t)+KdDμe(t) (14)

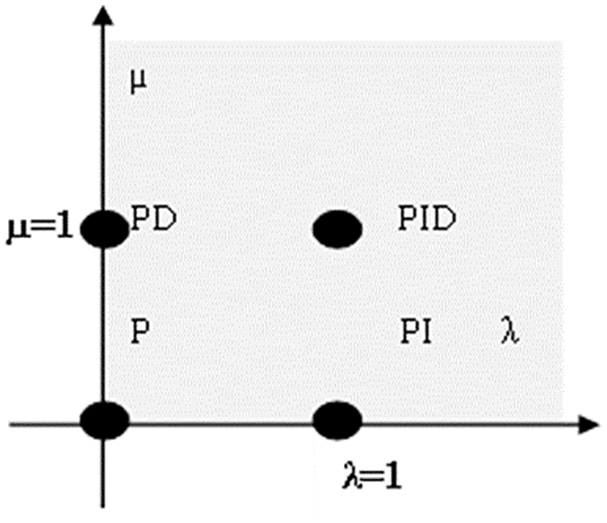
Figure 3: Normal form of FOPID controller

The FOPID controller is designed technique entails resolving five differential problems with five unknown factors, KP, KI, KD, λ. In comparison to the other difficulty of five nonlinear equations, the transfer function is quite important [18].

3.3 Adaptive Neuro-Fuzzy Inference System FOPID Controller for Spherical Tank System

The acronym ANFIS stands for Adaptive Neural Fuzzy Inference System. The modeling toolkit is a useful feature. ANFIS constructs an Inference System (FIS) with members from an output data collection. p value variables modified using a backpropagation neural process or grouping with a least squares technique. This enables fuzzy systems to study data that has been modelled. Fig. 4 depicts the layout of the ANFIS system. The circular nodes represent fixed nodes, whereas the square nodes represent nodes with characteristics that must be learned. The fuzzy set rule is utilised in the fuzzy set model [19]. This method is primarily used to reduce interpretability. The device's sloppy rule is given below

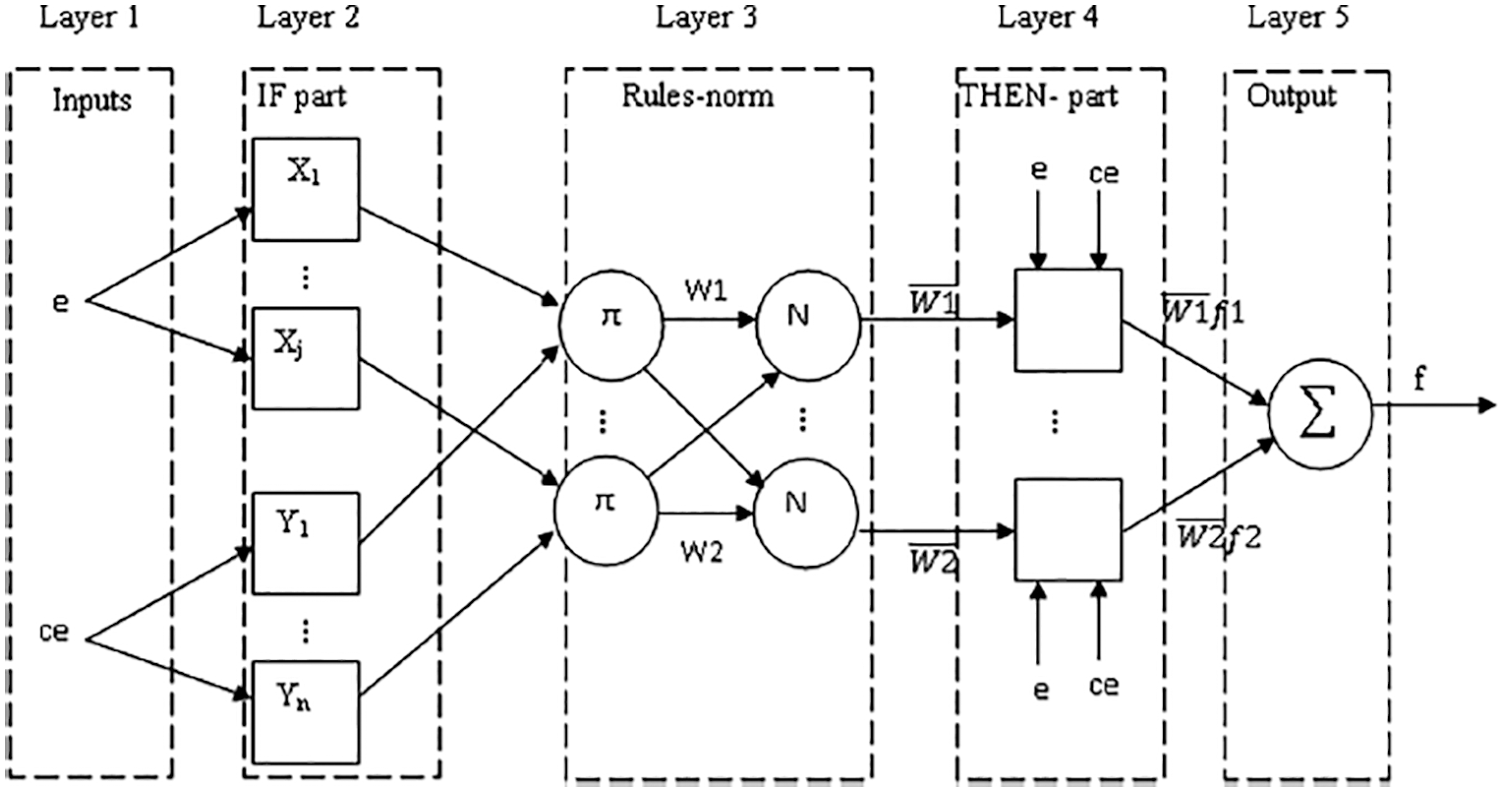
Figure 4: Adaptive neuro fuzzy inference system (ANFIS) architecture

Rules 1:

Input: If x = A1, y = B1,

Output: Z1 = p1 x + q1 y + r1,

Rules 2:

Input: If x = A2 and y = B2,

Output:Z2  = p2 x + q2 y + r2,

Ai, Bi (i = 1, 2) are fuzzy sets, while piqi, ri (i = 1, 2) are design parameters collected during the training process. It's a five-layer fuzzy neural net with feed forward. Each layer describes its own set of data. piqi, ri (i = 1, 2)

First layer: The first layer is the input layer which describes the input parameters of the specified controller and they are speed error and its variance ratio mentioned as x0, x1 correspondingly [20]. These inputs layer immediately presents the x0.

Second layer: The fuzzy layer, which checks the values of member functions, is the second layer. This received the input parameters from the first layer and corresponds to the fuzzy pairs of the corresponding values as just a member function. It also generates the MF factors, which determines the way in which the input parameters x0 are dependent on the fuzzy set [21], which serves as the third layer's input.

Third layer: The rule layer is the layer, in which each node performs pre-function comparison of fuzzy circumstances. Because the number of layers can be similar to the number of fuzzy rules, this analyses the excitability of each layer. Each node in the third layer calculates the normalized weights [22,23].

Fourth layer: This is the defuzzification layer, which is made up of consequent values ‘y’ from precondition inference. The fuzzy singletons that mention another class of parameters for the neural fuzzy network are used to value links across layers 1–3 and 1–4.

Fifth layer: This is the final layer, sometimes known as the output units. This implies that the average of all the inputs of layer four and turns the fuzzy classification results into crisp numbers [24].

The ANFIS controllers is made up of a few rules, the first of which is that it is primarily dependent on the shape learning and perfectly portioned algorithms. This individual's variable, the hybrid criterion, can be updated automatically. Update the structure and parameters of the ANFIS controller dynamically. Fig. 5 shows a simple block that demonstrates the ANFIS-based FOPID Controller.

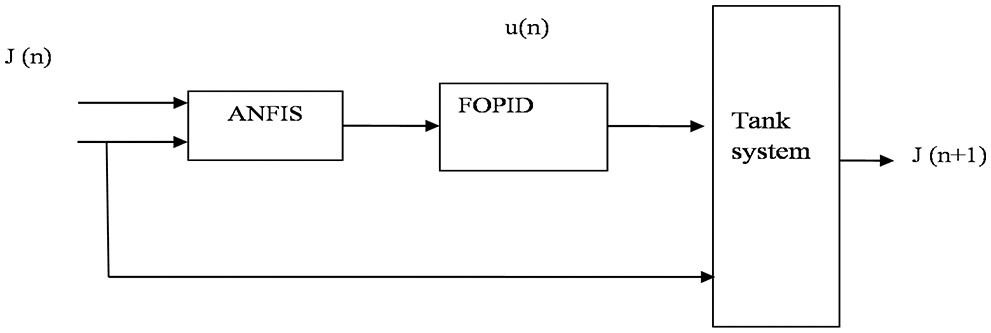
Figure 5: Structure of ANFIS based FOPID controller

3.4 SMC Controller

The Sliding Mode Controller is the most dominant technique for controlling the nonlinearity process in presence of external disturbances. The SMC is selected because of its stability and robustness in opposition to several categories of uncertainties such as external disturbances and modeling error. Sliding Mode Controller mainly consists of two stages named as design of a sliding face The next phase is to select the adequate gain of the controller in which the closed loop approach is stable on the slide face in order to achieve the desired level of network behavior, such as safety of the basis, when regulated to the surface.

3.5 FOPID-SMC Controller

The Sliding Mode Controller is a nonlinear regulator with a few advantages in terms of resilience and stability in the face of various uncertainties. When compared to conventional controllers, SMC is much simpler to integrate. Fig. 6 shows the FOPID-SMC schematic diagram. 6. The error (E) and process output (X) are input vectors in this Control system, while the modified variable (U) is the operator's output. The FOPID-SMC controller's theoretical equation is as follows:

Figure 6: Structure of FOPID with SMC controller

u(t)=KPE(t)+KI∫0t⁡E(t)dt+KDdE(t)dt

U=KSAT(u(t)Ω)

where, Ksat is the controller signal, u(t) is the correction factor and Ω is the boundary layer breadth.

3.6 Design of an ANFIS Based SMC with FOPID Controller

The plan of an Adaptive Neuro Fuzzy Inference System based Sliding Mode Control (ANFIS-SMC) using the stability criteria named as Lyapunov also applied sliding conditions. The ANFIS based advantages of a control algorithm over a standard controller include 0% steady-state error, superior set point tracking against parameter and external disruption, and reliability. Fig. 7 represents the Control Structure of the ANFIS based Sliding Mode Controller block diagram where the controller adapts its parameters (l) make use of the adaption law and to end with resultant controller input is send to the interacting tank system as its control input signal.

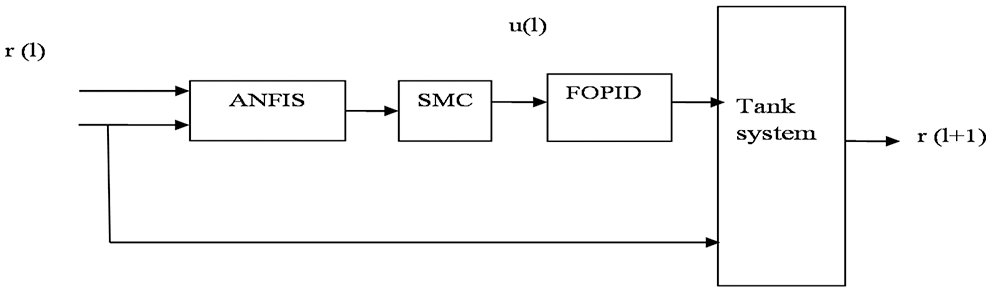
Figure 7: Block diagram for ANFIS based SMC with FOPID controller

4  Simulation Results and Discussion

The obtained result for liquid level control is described in this section. MATLAB software creates the ANFIS (Adaptive Neuro Fuzzy Inference System) controller based SMC with FOPID. In a Services also allow SMC controller, the error and change of error are used to build rules. The controller parameters specifications for the round storage tank are listed in Tab. 3. For control design, the Trapezoidal type input membership function is used. So far researches have not implemented ANFIS based SMC with FOPID on a spherical two tank interacting system. Henceforth a novel nonlinearity reducing technique, ANFIS based SMC with FOPID is used on the coupled spherical tank. The reservoir pressure in the tank is divided into four areas (0–107.85 cm). Each town's flow is controlled. The response of the ANFIS (Adaptive Neuro Fuzzy Inference System) controller is contrasted to that of the FOPID and Sliding Mode Controllers (SMC). Tab. 4 shows the parameters specifications used in the ANFIS based SMC-FOPID simulation.

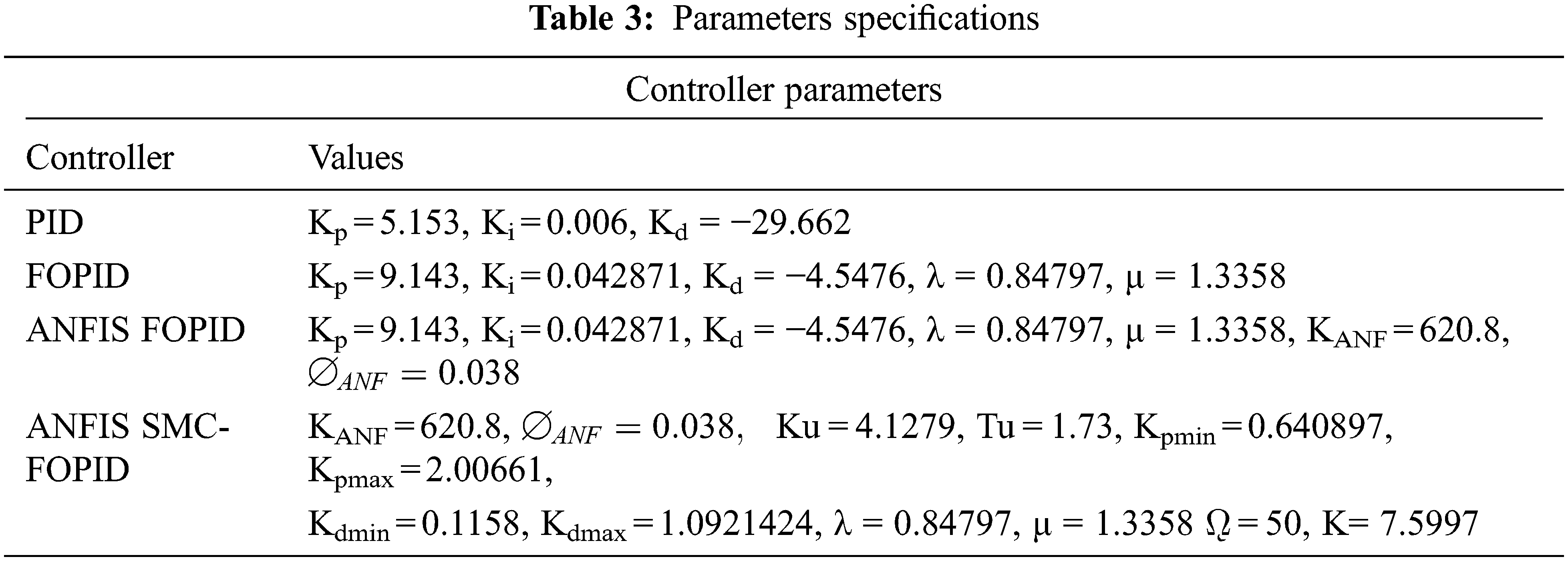
The output trajectories of the fuzzy FOPID controllers for a particular step input are shown in Fig. 8 for all areas. Tab. 5 shows the time domain and integral efficiency indexes. The amount of liquid in four sections is controlled using a fuzzy FOPID controller, and external disruptions are mitigated as well. In all areas, the time domain and integral performance indices are fluctuating. The performance of the fuzzy FOPID controller to that of the fuzzy Controller.

Figure 8: Output path of fuzzy FOPID controllers

In a fuzzy controller for a circular tank, the rising time is 1.328 milliseconds, the settling time is 0.054 milliseconds, the peak period is 0.081 milliseconds, and there is 0% overrun and underperform in R1. InR2, the rise of time is 3.938 milliseconds, the time constant is 2.057 milliseconds, the peak of time is 0.041 milliseconds, and there is neither overshoot or underperform. The peak amplitude in R3 is 9.5 milliseconds, the settling time is 4.27 milliseconds, the peak period is 0.121 milliseconds, and there is no overshoot or underperform. As shown in Fig. 9, R4 has a rise of time of 15.841 ms, a settlement time of 9.505 ms, a should be of 0.020 ms, and 0% overrun and underperform.

Figure 9: Output trajectories of fuzzy FOPID controller for destructive power avoidance

The ANFIS based SMC-FOPID controller is used for the spherical two tank interacting In R1, the rise time is 0.322 milliseconds, the system response is 0.001 milliseconds, the peak time is 0.003 milliseconds, and there is neither overshoot or undershoot. In R2, the rise time is 2.137 milliseconds, the settling time is 1.016 milliseconds, the peak time is 0.005 milliseconds, and there is neither overshoot or underperform. R3 has a rise time of 5.2 milliseconds, a settling time of 2.02 milliseconds, a peak time of 0.009 milliseconds, and no overshoot or underperform. The rise time in R4 is 10.8 milliseconds, the settling time is 5.8 milliseconds, the peak time is 0.008 milliseconds, and there is 0% overrun and undershoot. Tab. 6 shows that the ANFIS-based SMC with FOPID controller outperformed existing controls in terms of controlling liquid level in a connected circular two tank interaction system, as well as performance indices such as ITAE, IAE, and ISE. As demonstrated in Fig. 10, the R1 in the ANFIS-based Controllers provides the best efficiency for the other area.

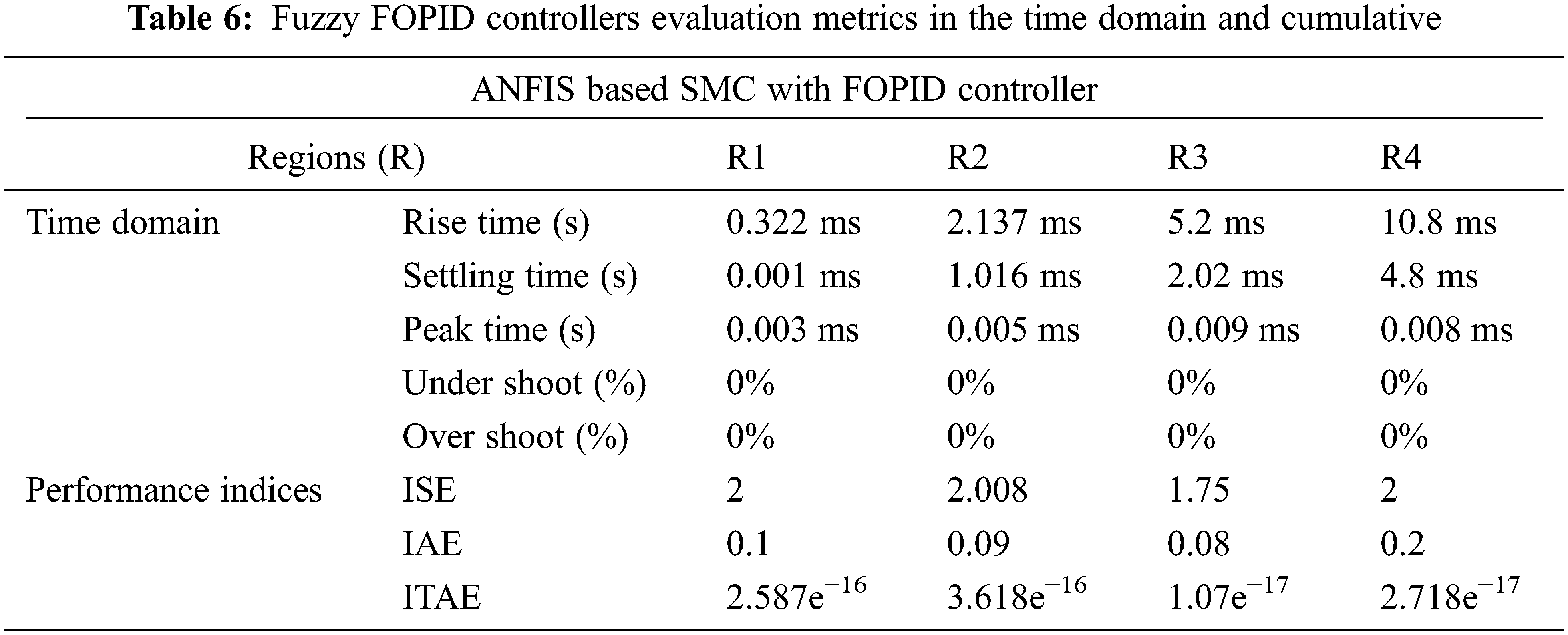
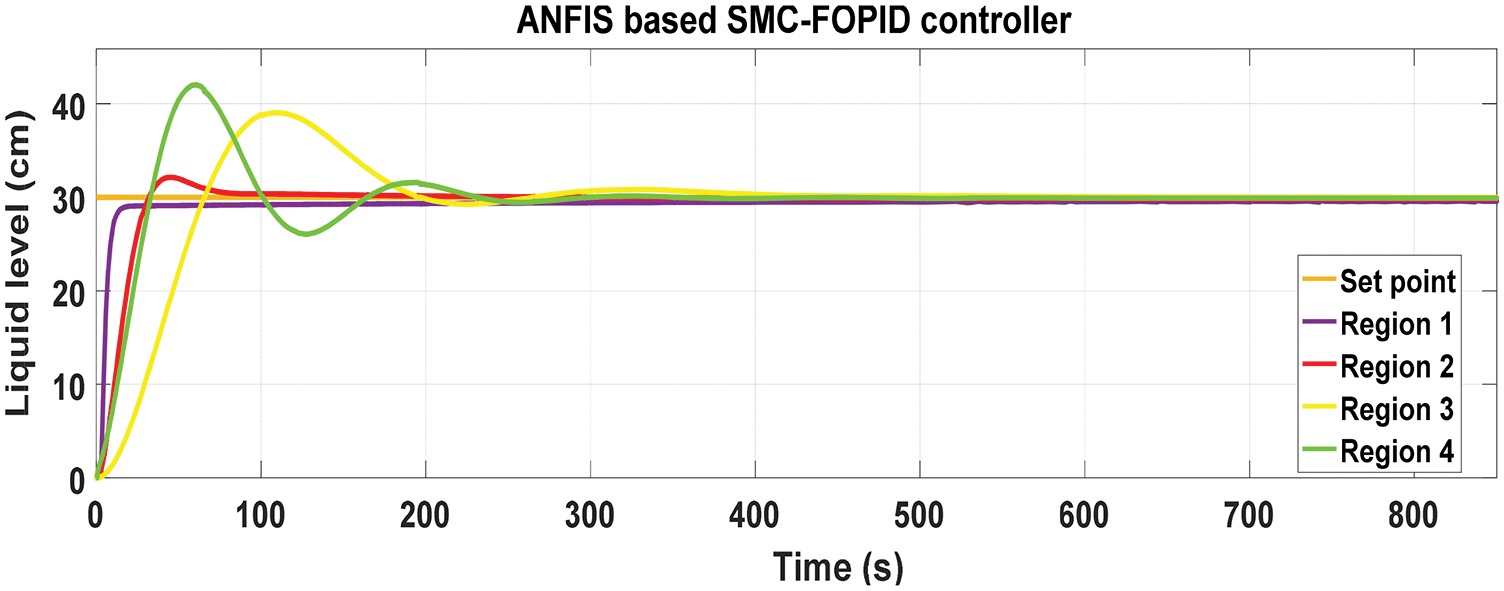
Figure 10: ANFIS based SMC-FOPID output trajectory

Fig. 11 shows the set point tracking performance of ANFIS based SMC with FOPID controller. In this spherical two tank interacting system ANFIS based SMC with FOPID In all areas, a microcontroller is employed to control the water level.

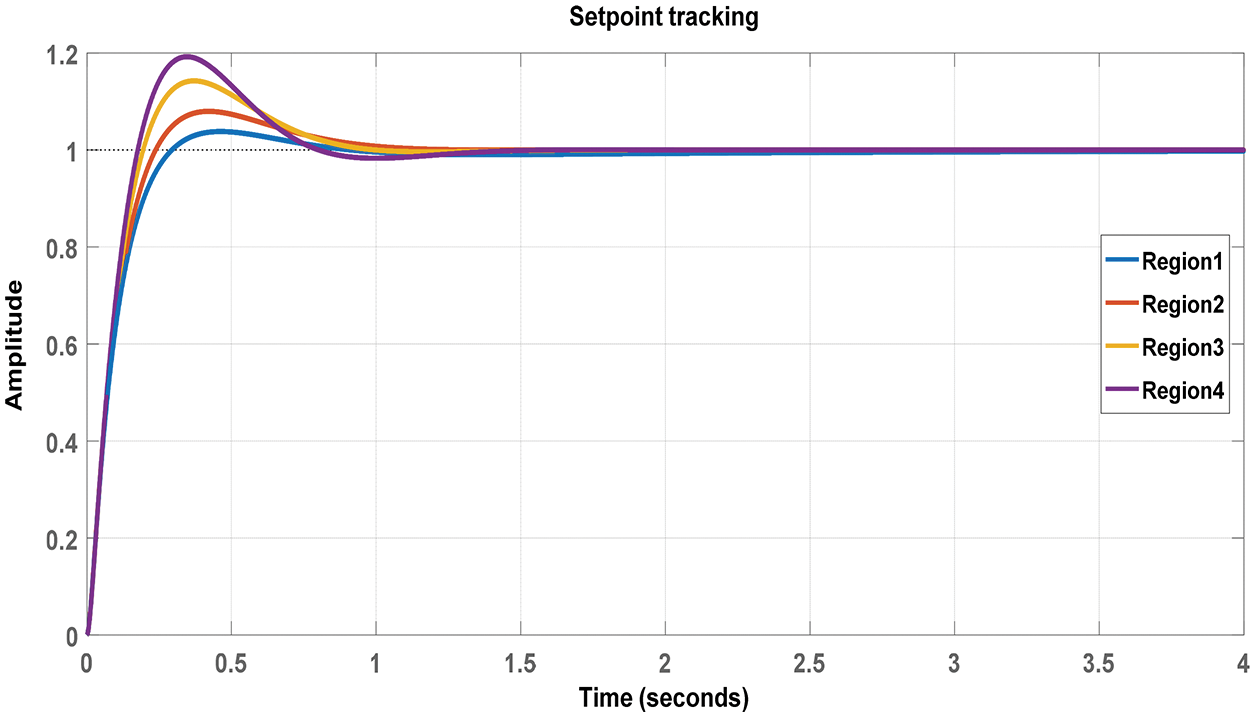
Figure 11: Set point tracking response for FOPID controller

ANFIS based SMC with FOPID For the spherical two tank, a microcontroller is used. interacting system for the error performance analysis. In this spherical tank system, four regions are divided, proposed the outside disruptions are also minimized by using a controller to control the liquid level in all zones and the external disturbance rejection capability of ANFIS based SMC-FOPID controller is shown in Fig. 12.

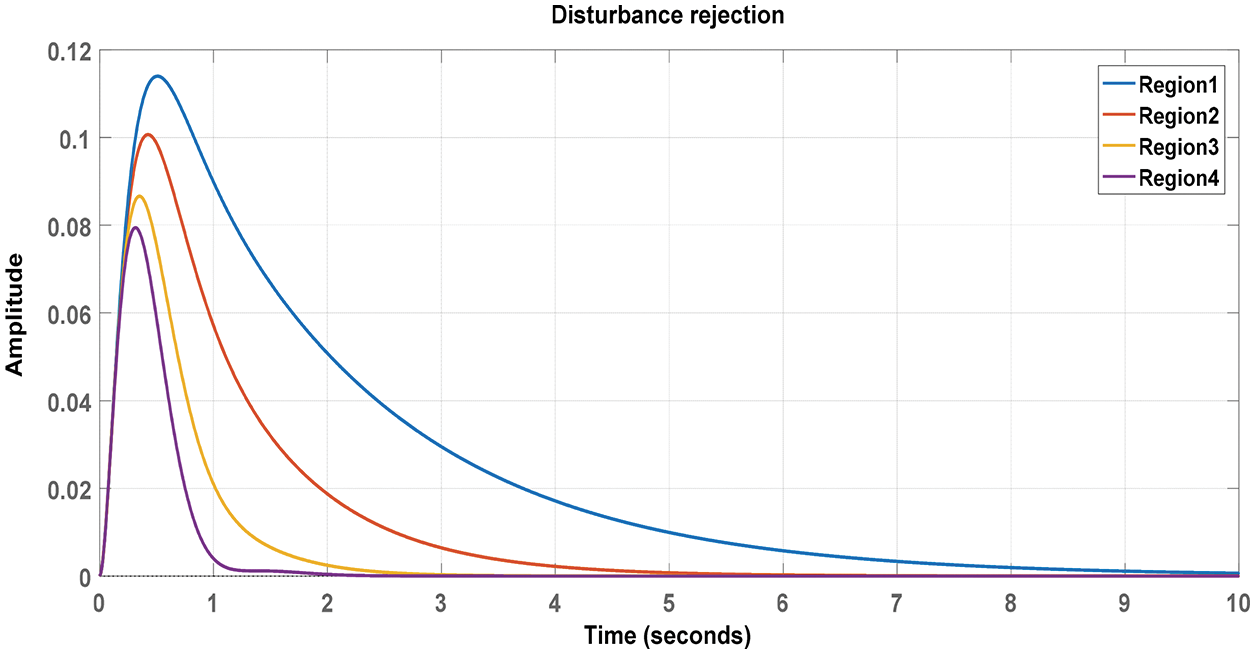
Figure 12: Disturbance rejection capability

Fig. 13 shows the FUZZY FOPID and ANFIS based SMC-FOPID set point tracking performance comparison. It is observed that the proposed ANFIS based SMC-FOPID approach conveys the With minimal residence time and simple linear error, the system reacts to the required level.

Figure 13: Set point tracking comparison

Fig. 14 shows the external disturbance rejection capability comparison between FUZZY FOPID and ANFIS based SMC with FOPID Controller. From this, the result shows ANFIS based SMC-FOPID provides a better reduction of external disturbance than the conventional technique. Tabs. 7 and 8 demonstrates the event comparison of PID, FOPID, ANFIS-FOPID, and ANFIS based SMC-FOPID Controller.

Figure 14: Disturbance rejection comparison

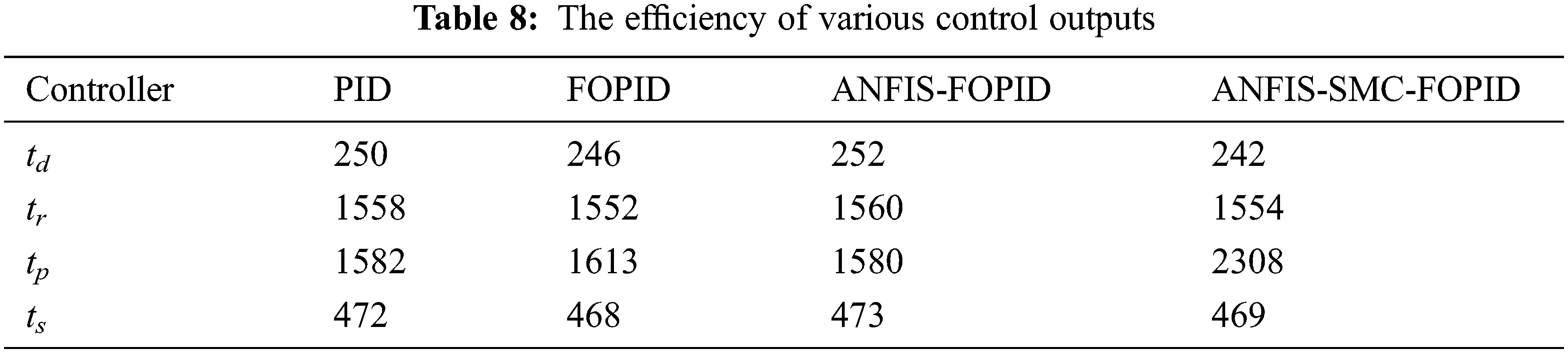
The performance evaluation of PID, FOPID, ANFIS-FOPID and ANFIS based SMC-FOPID Controller are analyzed as shown in Tab. 9.

From Tab. 9, ANFIS based SMC-FOPID Controller gives better chattering effect and disturbance rejection capability. Moreover, the time taken to reach the desired level is also less mentioned. Compared to other controlling techniques the proposed method provides a better result.

5  Conclusion

ANFIS-based Sliding Mode Controller with FOPID sliding surface is proposed and applied in this study to manage the water level of a spherical two functional systems. By integrating, the suggested ANFIS-based Sliding Mode Controller with FOPID sliding surface is realized. The closed-loop reaction of existing Fuzzy FOPID is proven to be sluggish in simulated tests. The ANFIS-based SMC with a FOPID has an oscillating response around the set-point value. The ANFIS-based SMC-FOPID has a stronger answer, which is studied in the construction. In comparison to other existing controllers in the research, the suggested ANFIS-based SMC with FOPID sliding surface provides Rise time, setpoint, peak time, steady flow error, and peak overrun are all improved time domains needs. Furthermore, when the predefined is adjusted to be above and below the threshold level, the suggested ANFIS based SMC with a FOPID sliding surface performs well in terms of managing. The suggested ANFIS-based SMC-FOPID controller's efficiency is highlighted in the efficiency index table. Furthermore, the suggested program's highly nonlinear effectiveness is examined.

Acknowledgement: The authors would like to thank Anna University and also we like to thank Anonymous reviewers for their so-called insights.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  E. Mirakhorli and M. Farrokhi, “Sliding-mode state-feedback control of non-minimum phase quadruple tank system using fuzzy logic,” IFAC Proceedings Volumes, vol. 44, no. 1, pp. 13546–13551, 2011. [Google Scholar]

 2.  J. Arunshankar and K. Govind, “Control of nonlinear two-tank hybrid system using sliding mode controller with fractional-order PI-D sliding surface,” Computers & Electrical Engineering, vol. 71, pp. 953–965, 2018. [Google Scholar]

 3.  D. Mercy and S. M. Girirajkumar, “Modeling and analysis of a real time spherical tank process for sewage treatment plant,” Applied Mathematics and Information Sciences, vol. 11, no. 5, pp. 1491–1498, 2017. [Google Scholar]

 4.  M. Bharathi, C. Selvakumar and A. Kalpana, “Model based controller design for a spherical tank,” IOSR Journal of Electrical and Electronics Engineering, vol. 9, no. 2, pp. 74–79, 2014. [Google Scholar]

 5.  G. Sakthivel, T. S. Anandhi and S. P. Natarajan, “Design of fuzzy logic controller for a spherical tank system and its real time implementation,” International Journal of Engineering Research and Applications, vol. 1, no. 3, pp. 934–940, 2011. [Google Scholar]

 6.  Y. Christy and D. D. Kumar, “Modeling and design of controllers for interacting two tank hybrid system (ITTHS),” International Journal of Engineering and Innovative Technology (IJEIT), vol. 3, no. 7, pp. 88–91, 2014. [Google Scholar]

 7.  M. A. Kafi, Y. Challal, D. Djenouri, M. Doudou, A. Bouabdallah et al., “A study of wireless sensor networks for urban traffic monitoring: applications and architectures,” Procedia Computer Science, vol. 19, pp. 617–626, 2013. [Google Scholar]

 8.  W. Sun, L. Dai, X. R. Zhang, P. S. Chang and X. Z. He, “RSOD: Real-time small object detection algorithm in UAV-based traffic monitoring,” Applied Intelligence, vol. 52, no. 8, pp. 1–16, 2021. [Google Scholar]

 9.  S. S. Prasad, B. Venkatesan and I. Thirunavukkarasu, “Performance analysis of two tank spherical interacting level control system with particle swarm optimization based PID controller,” International Journal of Advanced Engineering Technology, vol. 7, no. 2, pp. 0976–3945, 2016. [Google Scholar]

10. D. D. Kumar and B. Meenakshipriya, “Design and implementation of nonlinear system using gain scheduled PI controller,” Procedia Engineering, vol. 38, pp. 3105–3112, 2012. [Google Scholar]

11. M. K. Chakravarthi, V. K. Pannem and N. Venkatesan, “Real time implementation of gain scheduled controller design for higher order nonlinear system using LabVIEW,” International Journal of Engineering and Technology, vol. 6, no. 5, pp. 2031–2038, 2014. [Google Scholar]

12. A. H. Mary, A. H. Miry and M. H. Miry, “ANFIS based reinforcement learning strategy for control a nonlinear coupled tanks system,” Journal of Electrical Engineering & Technology, vol. 2021, pp. 1–9, 2021. [Google Scholar]

13. P. Chandrasekar and L. Ponnusamy, “Comparative study of controllers for a variable area MIMO interacting nonlinear system,” International Journal of Engineering and Technology, vol. 6, no. 1, pp. 227–235, 2014. [Google Scholar]

14. B. J. Parvat, V. K. Jadhav and N. N. Lokhande, “Design and implementation of sliding mode controller for level control,” in Proc. IOSR Journal of Electronics and Communication Engineering (IOSR-JECESecond Int. Conf. on Emerging Trends in Engineering, Jaysingpur, India, pp. 51–54, 2012. [Google Scholar]

15. F. A. Khadra and J. A. Qudeiri, “Second order sliding mode control of the coupled tanks system,” Mathematical Problems in Engineering, vol. 2015, no. 1, pp. 1–9, 2015. [Google Scholar]

16. K. Amuthambigaiyin Sundari and P. Maruthupandi, “Optimal design of PID controller for the analysis of two tank system using metaheuristic optimization algorithm,” Journal of Electrical Engineering & Technology, vol. 17, no. 1, pp. 627–640, 2022. [Google Scholar]

17. A. Sharma, “Modeling, simulation and intelligent control of coupled tank system,” International Journal of Latest Technology in Engineering, Management and Applied Sciences, vol. 7, pp. 69–77, 2018. [Google Scholar]

18. S. N. Engin, J. Kuvulmaz and V. E. Omurlu, “Modeling of a coupled industrial tank system with ANFIS,” in Proc. Mexican Int. Conf. on Artificial Intelligence, Springer, Berlin, Heidelberg, pp. 804–812, 2004. [Google Scholar]

19. R. Sivakumar, H. Muthu and R. Siddhardhan, “Design of ANFIS controller for quadruple-tank interacting system,” International Journal of Engineering Research and Applications, vol. 4, no. 4, pp. 152–157, 2014. [Google Scholar]

20. J. Merlin and K. Prabhu, “Fuzzy gain scheduled PI controller for a two-tank interacting conical tank system,” International Research Journal of Engineering and Technology, vol. 5, pp. 847–851, 2018. [Google Scholar]

21. K. Krishnapriya, M. R. Devi, U. Roshini and A. Jayachitra, “Analyzing the performance of interacting spherical tank system using internal model controller (IMC) and metaheurstic algorithm,” International Journal of Advanced Research in Computer and Communication Engineering, vol. 6, no. 4, pp. 36–42, 2017. [Google Scholar]

22. A. Senapati, A. Maitra, S. Batabyal and A. K. Kashyap, “Control and performance analysis of three tank flow control system using linear & non-linear controller,” International Journal of Innovative Research in Computer and Comunication Engineering, vol. 6, no. 1, pp. 329–340, 2018. [Google Scholar]

23. S. Nagarajan and B. Karthikeyan, “Control of interacting level process under sensor failure conditions using coactive adaptive neuro-fuzzy observer,” International Journal of New Technologies in Science and Engineering, vol. 2, no. 4, pp. 242–251, 2015. [Google Scholar]

24. G. Nandhinipriyanka, S. Ishwarya, S. Janakiraman, C. S. Thana and P. Vaishali, “Design of model reference adaptive controller for cylinder tank system,” International Journal of Pure and Applied Mathematics, vol. 118, no. 20, pp. 2007–2013, 2018. [Google Scholar]