Novel ARC-Fuzzy Coordinated Automatic Tracking Control of Four-Wheeled Mobile Robot

1  Introduction

Automation and robotics in manufacturing are becoming increasingly common due to rising demand, a shrinking supply of skilled workers and the need for more exact results. Wheeled mobile robots heavily influence industrial automation and outdoor [1] activities with skid-steering capabilities. In the Four-Wheeled Individual Driven (FWID) mobile robot, the differential velocities between inner and outer wheels create the steering effect on the robot’s center of gravity point ‘P’. A large volume of research papers has been presented on the trajectory control of two-wheel and car-like mobile robots with two-wheel steering. The variable wheel-ground contacts make it impossible to avoid lateral slides at high speeds. Hence, the trajectory tracking control of FWID skid steered mobile robots has become one of the hottest research topics in the robotics field.

Trajectory tracking control for mobile robots may be accomplished in two ways. 1) Kinematic control by controlling the speed of the driving wheel; and 2) Dynamic control by controlling the torque of actuators of the driving wheel. Real-time applications rely heavily on kinematic control [2] and feedback control systems [3]. The prior control approach assumed that the wheels of the mobile robot would never scuff. This leads to poor trajectory tracking resulting from controller performance that did not consider lateral skid [4,5]. Several control strategies were proposed that includes lateral skidding, to help mobile robots to achieve the tracking performance.

On the other hand, while the dynamics and uncertainties are taking into account the non-linearities of mobile robots are increased when analyzing the tracking performance of mobile robots. Developing a controller that can handle the model’s uncertainties and non-linearities becomes an immense challenge for the research community.

Over the past three decades, there has been a wide range of control approaches for wheeled mobile robots to deal with nonlinearities and model uncertainties. According to [6], wheel slip and accurate traction models of the wheeled mobile robot (WMR) are critical to their performances. The geometric and kinematic links between wheel slippage, the path following control and linear controllers employing robot localization coordinates are presented in [7] and [8,9]. For accurate vehicle velocity prediction, a dynamic model with actuator saturation and power constraints is proposed in [10] and [11]. In [12] and [13], a nonholonomic mobile robot’s kinematic and torque controllers are integrated. Finally, the lateral vehicle velocity of a mobile robot is indirectly controlled in [14] using a unique velocity prediction technique called model predictive control.

Additionally, [15] introduced sliding mode control with energy-efficient control allocation for robust tracking of mobile robots. Various other control strategies like, Network-based fuzzy decentralized sliding-mode control, adaptive control, robust control, adaptive robust control techniques, potential field control, neural network control, fuzzy control and adaptive fuzzy are also tried by many researchers. The smooth projection method suffers from the limitation that the internal parameter may still go unbounded. The variations of the σ-modification scheme suffers from the problem that requires prior information about the estimated parameter [16]. The limitations mentioned above can be mitigated by implementing the novel fuzzy parameter-adjusted adaptive robust control of the FWID mobile robot.

This article presents an adaptive robust control technique for coordinated control of FWID mobile robots using fuzzy parameter estimation. In contrast to [16], the proposed fuzzy parameter adaption technique generates model parameters concerning the tracking error. The coordinated adaptive robust control system generates a virtual control signal by combining adaptive and supervisory controls. Following that, the virtual control signal is subjected to the control allocation technique described in [17–19], which efficiently determines the torque on each wheel. Finally, the estimated torque shall be applied and regulated to the wheels. A unified dynamic model of the FWID mobile robot is developed for this research work using Newton-Euler mechanics [20]. A LabVIEW graphical interface has been designed to acquire the mobile robot’s odometry and voltage profile information.

The remaining part of this paper is organized as follows. Part 2 discusses adaptive robust control law design, fuzzy logic wheel slip control and fuzzy parameter estimation. Next, the hardware setup and the comparison of experimental results are presented in Part 3. Finally, part 4 presents the conclusion.

2  Design of Three-Tire ARC Control

The design process of the three-tire ARC law is split into the following parts:

1.    Dynamics modeling of FWID mobile robot.

2.    Deducing the control law for FWID mobile robot using the proposed three-tire ARC structure.

2.1 Dynamics Modeling of FWID Mobile Robot

The primary control challenges of FWID mobile robots are 1) over-actuated performance due to independent control of four wheels; 2) the influence of wheel dynamics. A standard solution to this problem is to define a new reference point at a fixed distance ‘D’ from ‘P’. The choices for output variables of the control system for the FWID mobile robot platform are given as

Zx=Xc+DcosϕZy=Yc+Dsinϕ (1)

By taking the first and second-time derivatives of Eq. (1), we can deduce the required dynamics of the FWID mobile robot Eq. (2).

M_z¨+ C_z˙=ut+dt+A_(2)

where,

M_=SMS−1,C_=SMS˙−1,ut=Su,dt=Sd,A_=SAt

S=[cosϕ−DsinϕsinϕDcosϕ]andAt=[mωvyJdv˙y]

2.2 Control Law Design

Uncertainties from the wheel ground interaction and over actuated response due to four-wheel individual driving are the principal challenges of this mobile robot. An adaptive robust control with a fuzzy-based parameter estimation technique is proposed to handle the challenges and to reduce the tracking error.

This proposed novel three-tier control structure illustrated in Fig. 1 is implemented as per the following sequence.

● Tier–I Estimation of virtual control law

● Tier–II Dynamic Control Allocation

● Tier–III Fuzzy wheel slip control

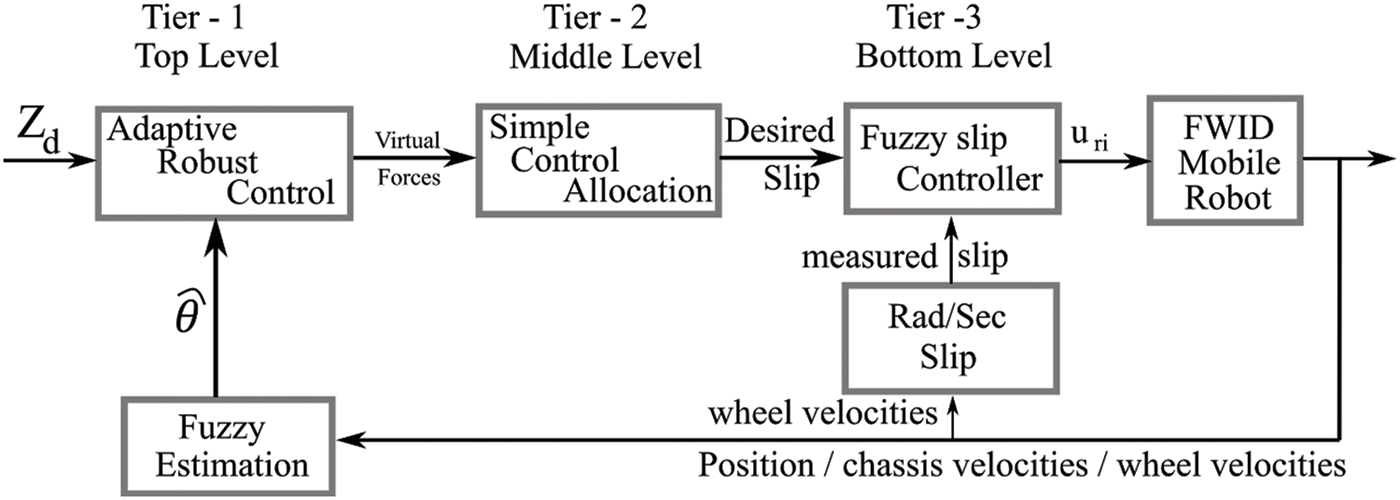
Figure 1: Three-tier adaptive robust control with fuzzy estimation

The proposed control law framework is schematically depicted in Fig. 1. This structure is integrated with adaptive robust control and dynamic control allocation to generate the required wheel slips.

2.2.1 Fuzzy - Parameter Estimation

The parameters θ are presented by θ^ and estimated using the Takagi Sugeno fuzzy model with the triangular membership function. The fuzzy linguistic variables for updating the different parameters are given in Tab. 1. The fuzzy system’s input is normalized between −1 and 1. Normalization of input data improves the fuzzy system’s effectiveness for handling a more comprehensive range of measurements. The type of fuzzy membership function and its fuzzification ranges are given in Tab. 2. The fuzzy membership functions are classified into nine classes, namely negative extra-large (NEL), negative large (NL), negative maximum(NM), negative small(NS), zero(Z), positive small(PS), positive maximum(PM), positive large(PL) and positive extra-large (PEL).

The parameters mass, inertia, longitudinal and lateral disturbances are adjusted about the angular velocity, linear velocity and the robot system’s position/orientation.

The estimated parameters are maintained within a specified range and satisfy the following properties.

Property 1:

θ∈Ω ≜ {θ:θmin≤θ≤θmax}

Property 2:

θ~≤0∀Γ

where Γ is the adaptation parameter for tuning the parameters.

2.2.2 Adaptive Robust Control Law

To address the trajectory tracking control, let e=z−zd be the trajectory error, z the actual trajectory and zd the desired trajectory. A switching function is given by Eq. (3).

Ps=e˙+Λe (3)

where, Λ is positive diagonal matrix as supervisory control feedback gain. By taking the first derivative of the switching function and using the second time derivative of output variables, we can form the error dynamics of the FWID mobile robot given in Eq. (4).

M_P′=−M_Z−¨dM_Λe′+C_Z˙−dt−A_]+ut+Δ~t (4)

Using the Lyapunov quadratic function and its derivative we can design the control.

V=12PsTM_Ps

V˙=PsTM_Ps′

V˙=PsT(−[M_Z−¨dM_Λe′+C_Z˙−dt−A_]+ut+Δ~t)

V˙=PsT[ut+ψ(Z,Z˙,t)θ+Δ~t] (5)

From the above Eq. (5), we can now form the adaptive robust control law

uv=T−1(ua+us)

ua=−ψ(Z,Z˙,t)θ^ (6)

where, adaptive model compensation law is ua,us is the feedback control law. It includes linear stabilizing feedback us1 and nonlinear robust feedback us2 compensating the effect of model uncertainties.

us2=−14ε[‖θmax−θmin‖2‖ψ‖2+δ2]e (7)

The chosen robust control should satisfy the below conditions:

1)    e(us2−ψ(Z,Z˙,t)θ~+Δ~t)≤ϵ1

2)    eus2≤0

where ϵ1 a design parameter. Finally, the virtual control law becomes as

uv=|uxuφ| (8)

2.2.3 Tier – II Dynamic Control Allocation

The ground-wheel interaction causes the production of the necessary driving forces for the mobile robot. By controlling the wheel slips, the driving forces on each wheel of the mobile robot are controlled. The desired tracking control entails the allocation of the driving forces, which are vital part of the robot control mechanism.

Since the vertical loads on the tyres ‘ Ni ’ plays vital role in force distribution on all four wheels and are estimated. The estimate of the normal forces on the tyres are given by Eq. (9)

Ni=mglrlf+lrwherei=1,2

Ni=mglflf+lrwherei=3,4 (9)

From the virtual control forces and the estimated parameters, the desired wheel slips are determined using the pseudo-matrix-based control law described. From the friction slip model, the friction on each wheel is calculated.

|ux uφ |=| Fx1+Fx2+Fx3+Fx4  −wFx1+wFx2−wFx3 +wFx4+lfFy1+lf Fy2− lrFy3− lrFy4  |

|uxuφ|+Nlf+lr|μ1lr−wμ1lrμ2lrwμ2lrμ3lf−wμ3lfμ4lfwμ4lf0μ1lflr0μ2lflr−μ3lflr0−μ4lflr||Sx1dSx2dSx3dSx4dSy1dSy2dSy3dSy4d| (10)

The linear equations given in Eq. (10) are solved at every iterations to find the required tyre slip force distribution. After estimating the lateral and longitudinal tyre slip forces, using the pseudo matrix approach, the resultant slip acting on the wheels are calculated. In the next level, the active control signals are generated using fuzzy logic control which attenuates the over actuation problems of the mobile robot’s actuators.

2.2.4 Tier – III Fuzzy Wheel Slip Control

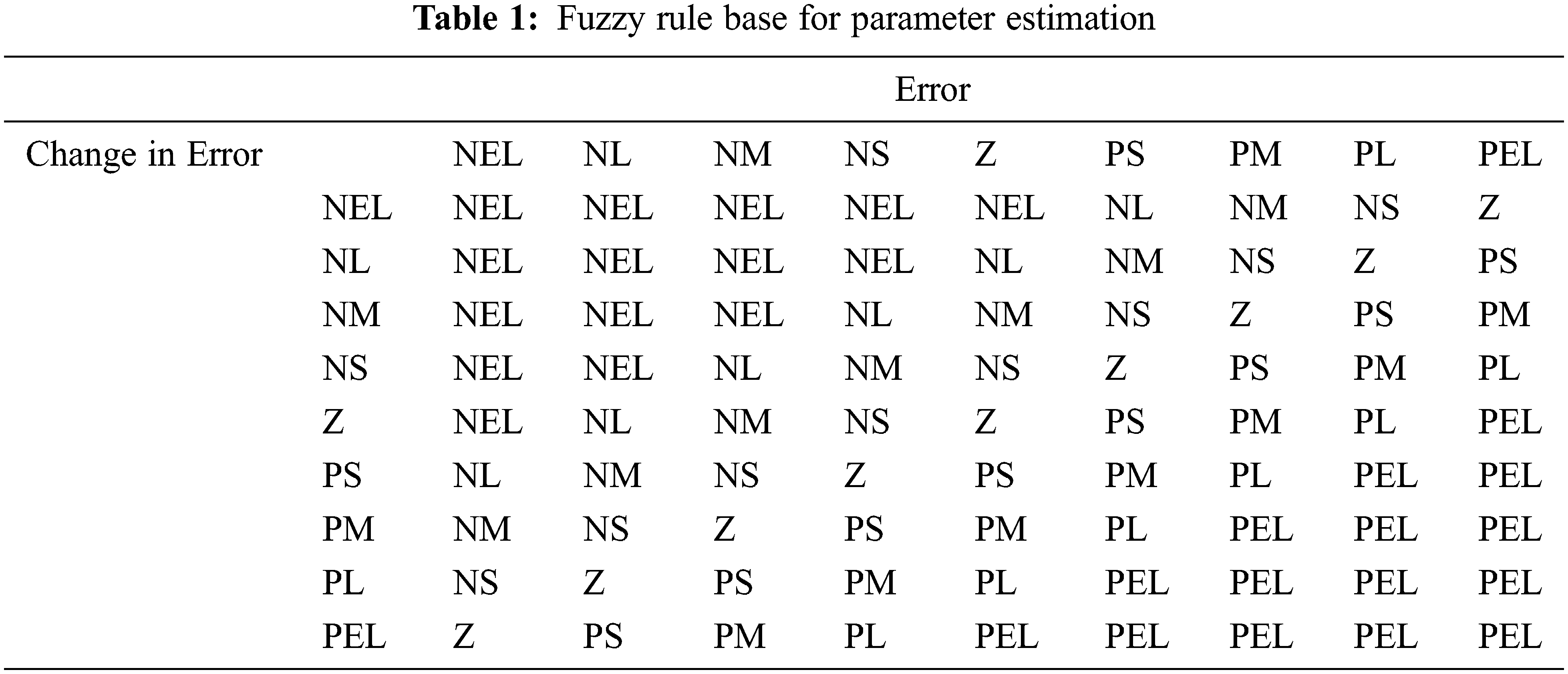
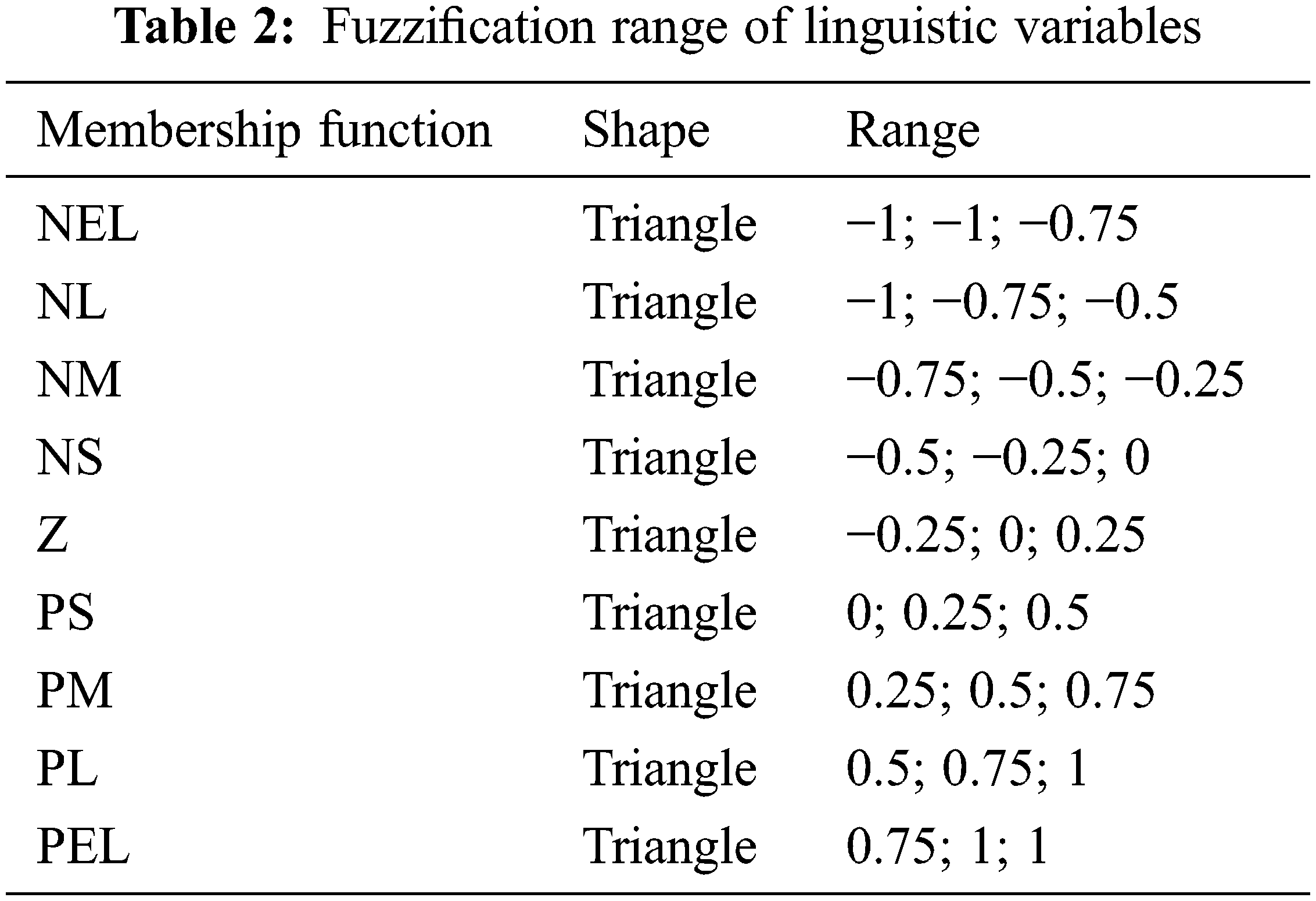
An approximate fuzzy model is established with four modules: the fuzzification interface, the rule base, the decision-making and the defuzzification. The normalized error slip and the rate of error slip construct the linguistic variables to the fuzzy system. Finally, the rule base and the decision-making logic provide a set of linguistic description rules mentioned in Tab. 1.

From the fuzzy system above, the desired value of actuating signals generated to the motors of the FWID mobile robot to track the trajectory with better accuracy. Therefore, the linear algebraic estimation of control allocation can change the inputs of actuators without changing the controllers.

3  Hardware Setup and Experimental Results

A simple FWID mobile robot set-up illustrated in Fig. 2 is the developed hardware model used to evaluate the performance of the proposed ARC-Fuzzy control technique. The position and orientation of the mobile robot were estimated from the quadrature encoder fitted on the coreless dc motor. The NI MyRIO executes the LabVIEW FPGA program to acquire the pulse count from the quadrature encoder on the motor and generates the PWM control signal according to the control allocation and the fuzzy slip control. The counted encoder pulses and the estimated duty pulses are exchanged between the NI MyRIO target and the host computer is accomplished by the shared variable concept. A pair of digilent motor adapters act as the interface between the NI MyRIO and the Faulhaber coreless motors [21] on the mobile robot.

Figure 2: Model of mobile robot

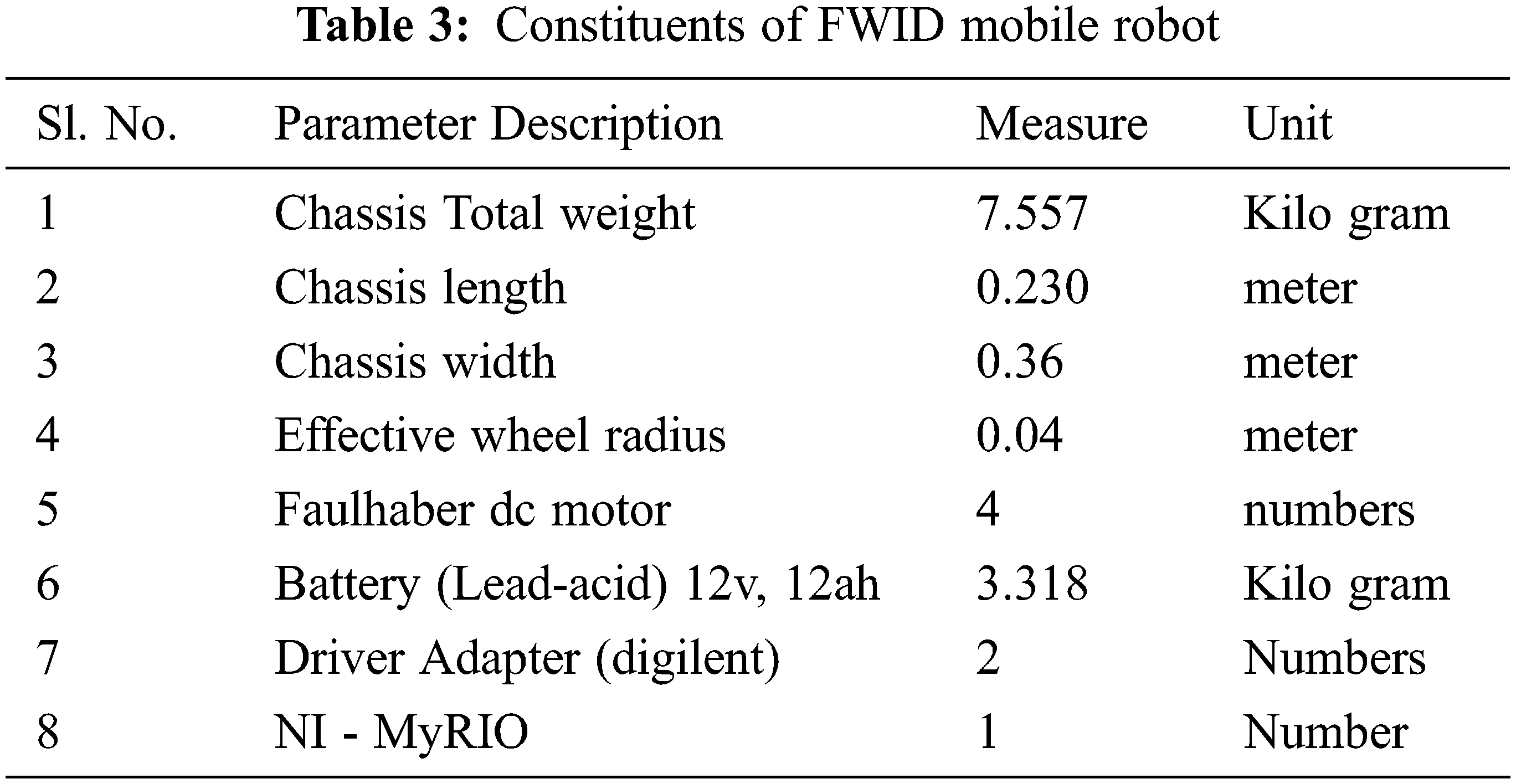
The basic constituents of mobile robots are available on the Tab. 3. The following parameters are completely describing the developed mobile robot: m = 7.557 kg, j = 0.0128 kgm2, lf = 0.115 m, lr = 0.115 m, w = 0.186 m, radius of wheel r = 0.04 m. The upper and lower limits of the robot model parameters are chosen as θmax = [8.2; 0.02; 0.2; 0.2] and θmin = [6.8; 0.01–0.2; −0.2].

The state machine concept and the control and simulation loop for controller implementation is used to develop the entire control logic.

3.1 Experimental Results

The performance of the proposed controller, a PID and a Fuzzy logic kinematic controller with simple motion tracking were compared. For the desired linear and angular velocities, the wheel velocities of the mobile robot to track the given trajectory tracking are computed by employing the LabVIEW robotics toolkit. The wheel angular velocities are given by

ωri=(vxd−ωd∗b)r,i=1,3

ωri=(vxd+ωd∗b)r,i=2,4 (11)

The kinematic control PID gains and the fuzzy control law adaptation parameters are carefully chosen as kp=0.25e+1,ki=0:023166e+1,kd=0.003+1,andλ=[0.005;0.005;0.005;0.005] to track the desired trajectory.

3.2 Proposed ARC with Fuzzy Parameter Estimation

Linear stabilizing feedback gain K = diag [0.50, 0.10] and nonlinear robust feedback are combined to form the robust feedback control law. The model parameters are estimated from the fuzzy system with the adaptation parameter Γ = diag [0.005, 0.005, 0.0002, 0.0002]. Finally, the adaptive compensation law is computed using the model parameters, regression matrix and the desired linear and angular velocities of the mobile robot. The tracking performances of the prototype mobile robot with different controllers are clearly presented in the next section.

The proposed pseudo matrix dynamic control allocation with fuzzy parameter estimation-based ARC control method is experimented on the two different trajectory models presented.

3.2.1 O Type Trajectory

The comparison between the suggested innovative ARC-Fuzzy controller’s tracking performance Vs Fuzzy, PID kinematic control and ARC-DP approaches are given in Fig. 3. This figure depicts the FWID mobile robot’s trajectory under various control methods. The Scheduled Performance Index (SPI) for various approaches are presented in Fig. 4.The associated angular velocities of the wheels are shown in Figs. 5 and 6. It was clearly observed that, all the implemented control techniques offer similar performance for the simple circular kind of trajectory model.

Figure 3: O Type trajectory

Figure 4: O type trajectory scheduled performance index

Figure 5: O type trajectory wheel velocity profile

Figure 6: O type trajectory wheel RPS - SPI

3.2.2 8 Type Trajectory

In this trajectory model, the wheeled mobile robot needs to change its direction of movement concerning the reference point. Hence, there is a sudden change in wheel velocities during the shifting of the trajectory segment. This sudden change causes the deviation in the trajectory tracking and is efficiently handled by ARC with Fuzzy parameter adaptation control.

The Figs. 7–10 show the comparative performance analyses of mobile robot’s in 8 type trajectory such as trajectory tracking, trajectory SPI performance, corresponding angular velocity profile of the wheels, and its RPS-SPI, respectively.

Figure 7: 8 Type trajectory

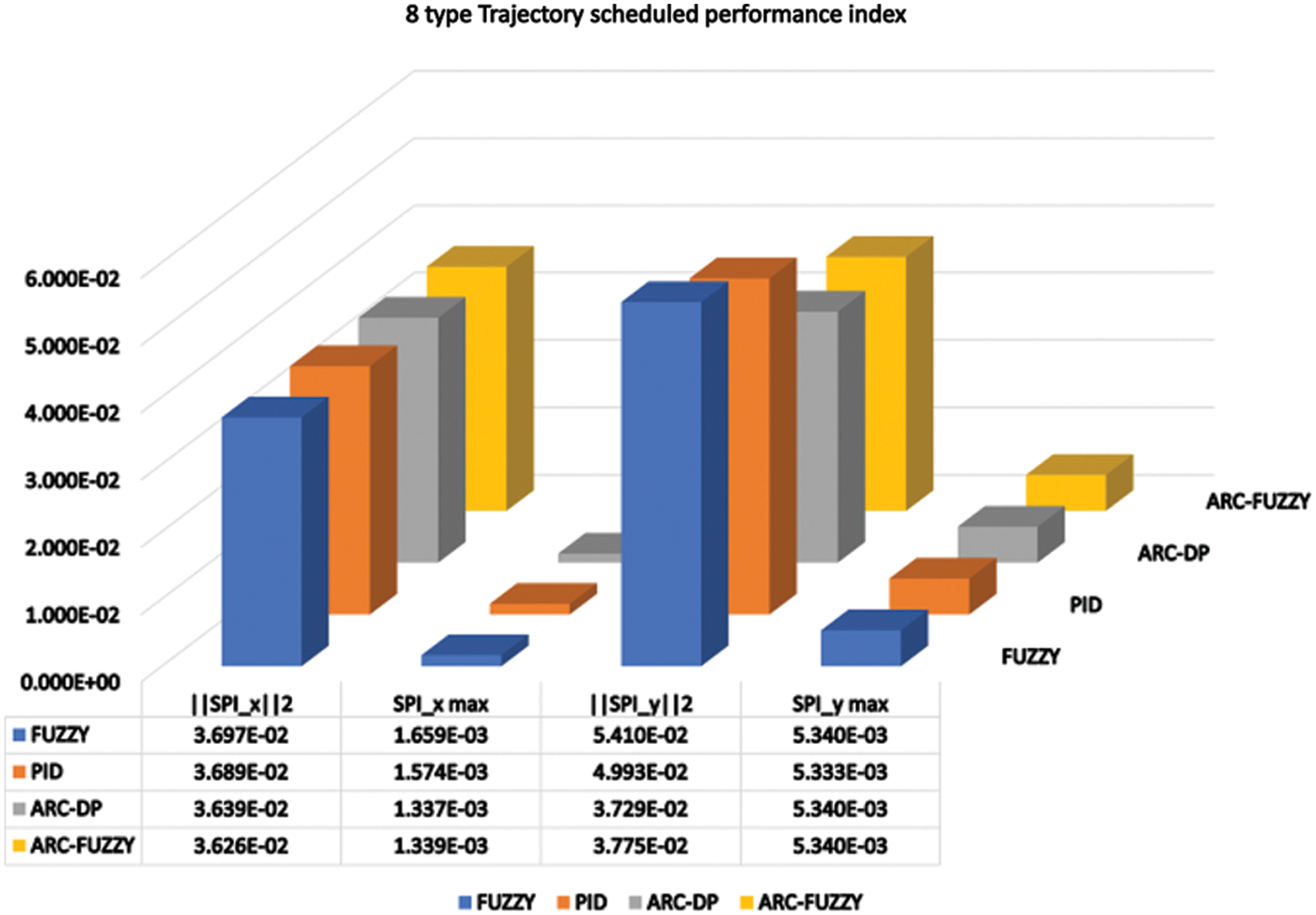
Figure 8: 8 Type trajectory scheduled performance index

Figure 9: 8 Type trajectory wheel velocity profile

Figure 10: 8 Type trajectory wheel RPS – SPI

Since, the 8 type trajectory is split into four components, there is a performance lag during the switching of trajectory from one portion to the next. The performance lag is effectively handled in the ARC with discrete projection and the proposed novel ARC-Fuzzy controller technique. However, the control inaccuracies of the conventional kinematic controls are reflected in the performances.

4  Conclusion

This paper investigates a fuzzy parameter adjusted adaptive robust control scheme for trajectory tracking of a four-wheel individually driven mobile robot system. First, a dynamical model of the four-wheeled mobile robot is developed to facilitate the fore mentioned investigation, covering the kinematics, dynamics and interactions among the wheels and ground. Then, the dynamic model is used to create a model-based fuzzy parameter adaptive robust control strategy. The top-level adaptive robust controller with fuzzy parameter estimation forms an adjustable model compensation, develops the adaptive control law and produces the virtual control forces when combined with the linear and robust nonlinear control laws. The linear algebraic mathematical-based control allocation forms the middle level of the control architecture. The over-actuated features are addressed at the intermediate level using a control allocation technique that calculates a reference slip for each wheel. Finally, the bottom level, the Takagi-Sugeno fuzzy model, acts as a wheel slip controller and generates the motor driving command for all four wheels of the mobile robot. This three-level fuzzy adaptive robust control scheme’s tracking performance has been compared to PID and fuzzy kinematic motion allocation approaches. The results show that, our proposed control method provides better tracking performances with less tracking error and SPI index compared to other approches.

Acknowledgement: The authors with a deep sense of gratitude would thank the supervisor for his guidance and constant support rendered during this research.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  J. Yi, D. Song, J. Zhang and Z. Goodwin, “Adaptive trajectory tracking control of skid-steered mobile robots,” in Proc. 2007 IEEE Int. Conf. on Robotics and Automation, Rome, Italy, pp. 2605–2610, pp. 10–14, 2007. [Google Scholar]

 2.  D. Pazderski and K. Kozłowski, “Trajectory tracking control of skid-steering robot – experimental validation,” IFAC Proceedings Volumes, vol. 41, no. 2, pp. 5377–5382, 2008. [Google Scholar]

 3.  M. Deng, A. Inoue, K. Sekiguchi and L. Jiang, “Two-wheeled mobile robot motion control in dynamic environments,” Robotics and Computer-Integrated Manufacturing, vol. 26, no. 3, pp. 268–272, 2010. [Google Scholar]

 4.  J. C. Ryu and S. K. Agrawal, “Differential flatness-based robust control of mobile robots in the presence of slip,” the International Journal of Robotics Research, vol. 30, no. 4, pp. 463–475, 2011. [Google Scholar]

 5.  S. J. Yoo, “Adaptive tracking control for a class of wheeled mobile robots with unknown skidding and slipping,” IET Control Theory & Applications, vol. 4, no. 10, pp. 2109–2119, 2010. [Google Scholar]

 6.  R. Balakrishna and A. Ghosal, “Modeling of slip for wheeled mobile robots,” IEEE Transactions on Robotics and Automation, vol. 11, no. 1, pp. 126–132, 1995. [Google Scholar]

 7.  J. Yi, H. Wang, J. Zhang, D. Song, S. Jayasuriya et al., “Kinematic modeling and analysis of skid-steered mobile robots with applications to low-cost inertial-measurement-unit-based motion estimation,” IEEE Transactions on Robotics, vol. 25, no. 5, pp. 1087–1097, 2009. [Google Scholar]

 8.  C. Hu, R. Wang and F. Yan, “Composite nonlinear feedback control for path following of four-wheel independently actuated autonomous ground vehicles,” IEEE Transactions on Intelligent Transportation Systems, vol. 17, no. 7, pp. 2063–2074, 2016. [Google Scholar]

 9.  D. Chwa, “Fuzzy adaptive tracking control of wheeled mobile robots with state-dependent kinematic and dynamic disturbances,” IEEE Transactions on Fuzzy Systems, vol. 20, no. 3, pp. 587–593, 2012. [Google Scholar]

10. W. Yu, O. Y. Chuy, E. G. Collins and P. Hollis, “Analysis and experimental verification for dynamic modeling of a skid-steered wheeled vehicle,” IEEE Transactions on Robotics, vol. 26, no. 2, pp. 340–353, 2010. [Google Scholar]

11. J. Kang, W. Kim, K. Yi, S. Jung and J. Lee, “Skid steering based driving control of a robotic vehicle with six in-wheel drives,” SAE International Journal of Passenger Cars-Mechanical Systems, vol. 3, no. 1, pp. 131–144, 2010. [Google Scholar]

12. R. Fierro and F. L. Lewis, “Control of a nonholonomic mobile robot: Backstepping kinematics into dynamics,” Journal of Robotic Systems, vol. 14, no. 3, pp. 149–163, 1997. [Google Scholar]

13. U. Kumar and N. Sukavanam, “Dynamic modeling and tracking control of a four-wheeled nonholonomic mobile robot,” in Proc. 13th National Conf. on Mechanics and Machines (NaCoMM07), IISc, Bangalore, India, pp. 127–134, 2007. [Google Scholar]

14. M. Jalali, E. Hashemi, A. Khajepour, S. ken Chen and B. Litkouhi, “Integrated model predictive control and velocity estimation of electric vehicles,” Mechatronics, vol. 46, pp. 84–100, 2017. [Google Scholar]

15. Y. Chen and J. Wang, “Adaptive energy-efficient control allocation for planar motion control of over-actuated electric ground vehicles,” IEEE Transactions on Control Systems Technology, vol. 22, no. 4, pp. 1362–1373, 2014. [Google Scholar]

16. M. Yue, P. Hu and W. Sun, “Path following of a class of non-holonomic mobile robot with underactuated vehicle body,” IET Control Theory Appl, vol. 4, no. 10, pp. 1898–1904, 2010. [Google Scholar]

17. Y. H. Kenta Maeda and H. Fujimoto, “Four-wheel driving-force distribution method for instantaneous or split slippery roads for electric vehicle with in-wheel motors,” in Proc. 12th IEEE Int. Workshop on Advanced Motion Control (AMC), Sarajevo, Bosnia and Herzegovina, pp. 1–6, 2012. [Google Scholar]

18. Y. Wang, H. Fujimoto and S. Hara, “Driving force distribution and control for ev with four in-wheel motors: A case study of acceleration on split-friction surfaces,” IEEE Transactions on Industrial Electronics, vol. 64, no. 4, pp. 3380–3388, 2017. [Google Scholar]

19. J. Zhang, W. Sun and H. Du, “Integrated motion control scheme for four-wheel-independent vehicles considering critical conditions,” IEEE Trans. Veh. Technol, vol. 68, no. 8, pp. 7488–7497, 2019. [Google Scholar]

20. Dhaouadi, A. A. Hatab, “Dynamic modelling of differential-drive mobile robots using lagrange and newton-euler methodologies: A unified framework,” Advances in Robotics A & Automation, vol. 2, pp. 1–7, no. 2, 2013. [Google Scholar]

21. https://www.faulhaber.com/fileadmin/Import/Media/EN_2342_CR_DFF.pdf. [Google Scholar]