Data Mining Approach Based on Hierarchical Gaussian Mixture Representation Model

1  Introduction

Data classification is an important topic of research. Numerous approaches for data classification have been presented in the literature. Recent applications such as computer vision and image processing have revealed that there are several accepted approach. These applications have encouraged hybrid discriminative characteristics. Generative learning also represents well reported research by authors [1,2]. They exhibit better performance when combined both generative and discriminative attributes. This is more important for applications that are based on classification of bags of vectors of extracted features [3]. In these instances, support vector machines (SVM) with typical kernels cannot be deployed. In our research, we propose Beta combination technique for bags of vectors.

SVMs are utilized in computer vision and machine learning problems. Support vector machine (SVM) is driven by statistical learning and utilizes nonlinear plotting of features to high-dimension space [4].

Finite combination represents [5–9] an influential and malleable statistical analysis for processing non-homogenous data that come from several populations. These models are utilized in studies of many central problems such as data mining. The linear model [10,11] is utilized in modeling the probabilistic observations. The linear transform can represent any arbitrary distribution with a finite component. The hyper-parameters of the linear model is powerfully estimated using optimum likelihood estimation technique. Although linear unbounded distribution is symmetric, the data in many applications are not symmetric.

Beta combination [3], and the Watson algorithm [8], have gained substantial attention as they deliver better representation abilities than linear ones for non-linear support data representation [12–16]. In the area of image processing, the normalized image bag-of-words modeling is bounded to [0,1]. In speech transmission, the frequency modeling of the predictive hyper-parameters is in the limit of [0, π].

To solve these challenges, the inverted Beta distribution (IBD) was proposed in [13]. IBD is more flexible than linear model where data distribution shape can be skewed. Meanwhile, the IBD can produce overfitting problems. Also, it is costly and slow for practical situations. To solve these situations, a Gaussian model for the inverted Beta distribution that is based on multiple bound approximation is proposed [14]. To assure convergence, we employ a Gaussian estimation using single bound approximation [17].

A Gaussian model is a probabilistic technique that defines data points as a finite Gaussian distribution with unidentified parameters. It usually utilizes k-means clustering to attain information about the covariance values of the data.

The non-linear data, which represents each combination component with several distributions, has enticed substantial attention. Cases of such representations were formerly considered in the research to embrace the combination of combinations of linear distributions [18–21], Combination of combinations of t-distributions [22], and combinations of linear distributions [23]. One negative side of these combination representation is the unbounded range of support between −∞ and +∞. Nevertheless, data representation cannot be performed in an unbounded fashion [3–8]. To tackle this situation, the combination of combinations of Beta distributions are utilized in [24] to represent bounded nonlinear data. Nevertheless, this technique is utilized for 1-D data only. Also, Gaussian approximation model has been utilized to train the representation hyper-parameters, which face divergence of the solution of the proposed technique [17,18].

Therefore, in this paper, we introduce a new finite combination to represent the probability density function of nonlinear data. Our technique varies from those models described above. First, a combination of combinations of Beta stochastic distributions is utilized to represent the univariate data; we solve this problem by defining a new combination representation that constitute inverted multi-dimensional non-negative data. The second phase is the novel approximation model proposed to optimize the hyper-parameters. The proposed model is utilized in the applications of Handwritten Arabic Text classification and facial expression recognition. The performance of the new model is tested and validated using real data valuations.

This paper is structured as follows. In Section 2, we introduce the proposed model. In Section 3, a novel learning technique is proposed. Experiments on hand written Arabic data and facial expression dataset are performed in Section 4. At the end, conclusions are depicted in Section 5.

2  Model Description

In this section, we are describing the Beta combination and the proposed hierarchical nonparametric method that are based on the two-hyper-parameter Poisson combination.

2.1 Beta Combination Representation

For a k random vector Z→=(Z1,…,Zk) , a k-dimension Beta distribution is depicted as follows:

β(Z→)=a0+∑k=1∞(ak+bn)+∏k=1K(μk)αkZkαk−1e−μkZkψ(αk) (1)

where {αd,μd} is the Beta vector, αd represents the shape and μd represents the location. ψ is the Beta function [13]. The vector Z→ has a finite Beta combination with n factors.

Prob(Z→|α)=Prob(Z→|μ→)=1m∑j=1Mπjβ(Z→|α→)∗μ (2)

The pair {α,μ} represents the Beta hyper-parameters of to the mth combination hyper-parameter represented by the vector M as depicted below:

M→=(M1,…,Mm) where the following constraint 0≤Mm≤1 holds.

2.2 The Hierarchical Beta Combination Representation Model: HBC

The hierarchical Beta process (HBC) is a nonparametric Gaussian process that represents grouped data and permits sharing components. Data is organized into combination groups that are linked using association rules. HBC is a Beta process ( β ) for group data [17]. It is significant that βeta is employed in deep learning for nonparametric cases [18]. The βeta process is defined as a priory probability pdf. This creates an infinite combination employing the Poisson-Kingman partition-breaking process [19]. For the hierarchical Beta process (HBC), the βetas for all data groups have a Beta distribution (B-dis). For a data set S that is partitioned into K groups that are related to the βeta Gj . Therefore, the HBC becomes an indexed βetas Fj representing part of base distribution F0 with base V and hyper-parameter r :

F0∼β(r,V) and

Fh∼β(r,F0)i∈{1,…,K} (3)

The hierarchical β process is modeled by the Poisson-Kingman partition-breaking computation [19,20]. The universal metric F0 is modeled by B−dis−dis(r,V) and it can be depicted as:

Wsk∼B−dis(1,r) (4)

where {Wk} is the Poisson-Kingman partition-breaking that satisfies ∑k=1∞Wk=1 . F0 is the base βeta distribution as depicted in Eq. (3).

Now, we present the latent hyper-parameter Ejtl to compute a pointer, where Ejtl∈{0,1} (to designate the group-level ejt which the grain will maps to) note that Ejtk=1 , if ejt maps to the GLl (universal-level grain) else, Ejtl=0 . Also, we can compute ejt=GLlEjtl . The pointer W→=(Wjt1,Wjt2,…) is represented by the following probability distribution:

p(E→∣W→)=∏j=1N∏t=1∞∏l=1∞WlEjtl (5)

where, W is function of W′ as depicted to Eq. (4). Therefore, the pointer p(W→) can be formulated as:

p(E→∣W′→)=∏j=1N∏t=1∞∏l=1∞[Wl′∏s=1k−1(1−Ws′)]Ejtl (6)

As defined in Eq. (4), the W′s are defined from Beta stochastic distribution and their computation is determined as

prob(W′→)=∑k=1NB(1,yk)+Wk′ (7)

The definition of the HBC representation links each point Dji→ with a parameter Pji (here i defines the location j ) where Dji→ and Pj→=(Pj1,Pj2,…) are statistically distributed using H(Pji) and Uj . In this situation, the probability functions are depicted as:

Pji∣Uj∼UjDji∣Pji∼H(Pji) (8)

H(Pji) is defined as the conditional probability distribution function of Dji given Pji . The prior distribution V defines the distribution function for Pji . This scenery of the Hierarchical Beta process (HBC) combination representation) shows an essential part and certifies that each computed group is linked with a combination representation, and the constituents of the combination are communal among various groups.

Pji is computed according to Uj and is defined by the rate rjt with probability ot . We then present another pointer variable Γjit∈{0,1} for Pji as

prob(Γ→∣o→)=∏j=1∞∏i=1∞∏t=1∞ojtΓjit (9)

That is, the pointer Γ→jit is utilized to define which constituent Pji fits in. Γ→jit is set to 1 if Pji is linked with constituent t (with grain rjt ); else, Γ→jitissetto0 . Therefore, we can define Pji=rjtΓ→jit . As γjt maps to γXk , we then can write

Pji=rγjtΓ→jit=XkWjtkΓ→jit (10)

The distribution of o′ is computed as:

prob(o′→)=∏j=1M∏t=1∞β(1,λxjt)=∏j=1M∏k=1∞xjt(1−ojt′)xjt−1 (11)

2.3 Hierarchical Two-Hyper-Parameter Poisson Process Mixture Model (HyperP)

Hyper-Parameter Poisson process (HyperP) is a two level parameter addition to the B-dis that allows exhibiting of tailed probability distributions. It can model hierarchical representations and delivers a refined method to group data in unknown number of groups. It is defined by an extra reduction hyper-parameter ya along with the concentration parameter yb , that sustains the conditions 0<ya<1 and yb>−ya . Analogous to B-dis, the instance defined from HyperP is linked to a probability H [25,26] Hierarchical Poisson-Kingman partitions process (HProcc) is proposed with the base HyperP metric is computed from HyperP. Precisely, HProcc computes the universal metric U0 and the group distribution function Uj (that is Uj has the equivalent base U0 which follows a HyperP process). This produces the HProcc to be appropriate for compound spatial data representation. The Poisson-Kingman partition process depicts the base metric as follows:

U0=∑k=1∞ηkΛkηk′∼β(1−ya,yb+kya)Λk∼V (12)

where {Λk} is a random variable taken from V . The random variables ψ represent the Poisson-Kingman partition-breaking scores that satisfy ∑k=1∞ψk=1 . The Poisson-Kingman partition-breaking score for the group HyperP Uj is computed as:

Uj=∑t=1∞djtψjtdjt=djt′∏s=1t−1(1−djs′)djs′∼β(1−μa,μb+tμa)ψjt∼U0 (13)

{djts} are the Poisson-Kingman partition-breaking weights ( ∑t=1∞djt=1 ). ψjt is the grain HyperP with U0 distribution. Then, a universal pointer I and a group pointer T are defined. T is utilized to map Pji to group grain ψjt and the pointer I is utilized to map the grain Pji to base-level grain.

3  Model Training

Spectral modeling [23,24] is a deterministic estimation model that is utilized to estimate the posterior probability value. In this paper, we present a spectral training platform of the hierarchical infinite Beta combination data representations. We employ a spectral training inference model called the factorial estimation [27], which offers operative updates.

We employed block difference feature extraction, which is performed as follows [25–28]:

1.    An image is partitioned into blocks.

2.    Spectral, and shape features are selected using a multi-scale technique

3.    Harris points is utilized to choose blocks in the training phase;

4.    An index image is computed by optimizing the spectral distances to the training centroid.

We employ this model to factorize Γ(Θ) , of on HBC and HProcc combinations, into mutually exclusive factors. Then, we apply an approximation model as defined in [28] to approximate the spectral factors into universal truncation value T and group level G as depicted below:

Ut(G)=1,∑t=1tUt(G)=1,Ut(G)=0whent>T (14)

Where, T and G will be minimized in the training process. The estimated posterior set of vectors X will be factorized as follows:

U(r)=U(X1→,X2→,X3→,X4→,X5→,X6→)=U(X1→)U(X→2)U(X3→)U(X4→)U(X5→)U(X6→) (15)

where the matching hyper-parameters in the previous equations can be computed using the spectral techniques of both HBC and HProcc as depicted in the following Algorithms.

4  Experiments

The experiment investigation depicts that the performance of the proposed models based on HBC combination and HProcc combination representations with Beta stochastic distributions. Therefore, we are comparing them with data mining representations employing Arabic hand written classification. In all cases in the experiments, the universal truncation parameter K:UT and the group parameter T: GT are set to 100 and 30. For HBC combination, we define the hyper-parameters of y as 0.13and λ as 0.13. The hyper-parameters of HProcc combination ya , yb , μa and μb are initialized to (0.4, 0.13, 0.4, 0.13). The hyper-factors of Beta stochastic distribution are sampled from previous data.

4.1 Arabic Hand Written Classification

In this research, we are interested in classifying Arabic hand written images. Divergent from regular images which has objects, Arabic hand written images are superior case that do not contain a precise shape. Arabic hand written pattern is defined in a content analysis paradigm. It is defined in deciphering compound deep spatial learning process. Arabic hand written classification includes image classification and segmentation [27–34]. The objective of our model is to classify Arabic hand written images utilizing the proposed hierarchical processes of infinite combinations and by integrating different feature maps (to mine pertinent features from text images).

4.1.1 Experiment Methodology

For Arabic hand written classification application, our model extracts the attributes from the text and represents them utilizing both HBC and HProcc. Each text image I:Imj is deliberated as an image group and is linked to the infinite combination representation G:Gmj . in the second step, each vector Y:Ymji of Imj is produced from Gmj , where Gmj denotes spatial data. We produce a universal terminology set to use it in all Gm0 (universal infinite representation). It is important to construct the spatial terminology set as part of the representations and thus, the magnitude of the terminology set (i.e., count of instances) is concluded from the input using the nonlinear Gaussian representations [35]. The scale-invariant feature transform parameters and the bag of words representation are used here to compute the statistics of the spatial words from each Arabic text. For the block difference, they are computed the block difference features and then converting them using the vector model proposed in [36]. The computed descriptors realize true discrimination from the resolution. It should be noted that each Arabic text image is modeled by a multi vector [37].

4.1.2 Dataset

The proposed Arabic hand written hierarchical classification HBC and HProcc Beta combinations are performed on two public datasets. The first dataset is ARABTex and found in [38] and has 230 Arabic hand written classes with 300 images each. The second public dataset ARD [39] has 400 classes with 230 images per class. Some Arabic hand written data is depicted in Fig. 1. We employ a k-fold cross-testing method to split the datasets to learn the model accuracy. The testing procedure is based on averaging the performance measures over 100 runs.

Figure 1: Arabic hand written samples in different classes for datasets (a) ARABTex [38], (b) ARD [39]

The accuracy validation of the proposed models (HBC and HProcc) are tested with respect to previous models namely infinite combination of linear distribution (IC-LD) [40], infinite combination of generalized linear distribution (ICG-LD) [23], infinite combination of linear distribution (ICM-LD) [17], hierarchical combination of linear regression (HC-LR) [41], hierarchical hyper-parameter Poisson combination of linear regression (HHP-LR) [33], Beta combination of generalized linear regression (BCG-LR) [13], and Two-hyper-parameter Poisson combination of generalized linear regression (THPG-LR [40].) Tab. 1 depicts the mean accuracy computation of Arabic hand written classification using different techniques for the Arabic hand written-datasets using Scale-Invariant Feature Transform features. While, Tab. 2 depicts the mean accuracy computation of Arabic hand written classification using different techniques for the Arabic hand written-datasets using Local binary patterns. Tab. 3 depicts the mean accuracy computation of Arabic hand written classification using different techniques for the Arabic hand written-datasets using block difference features.

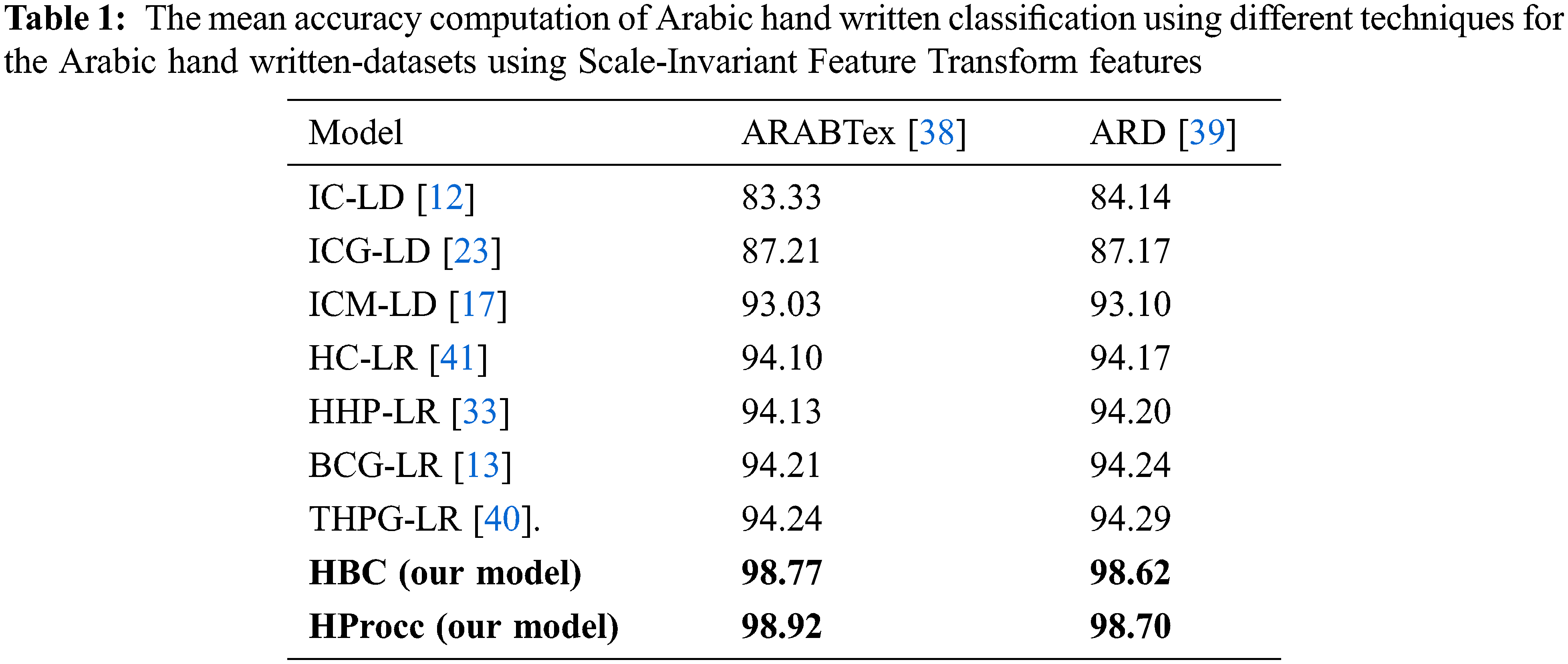
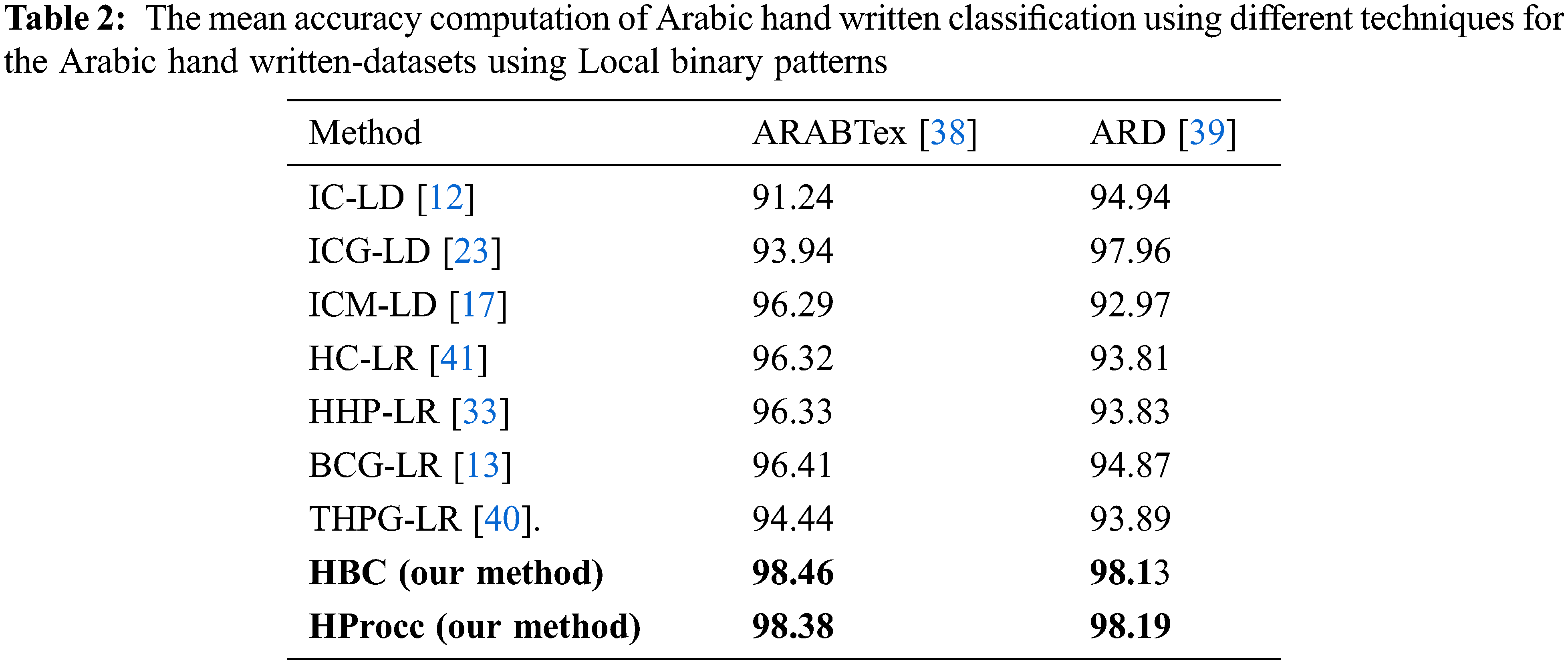
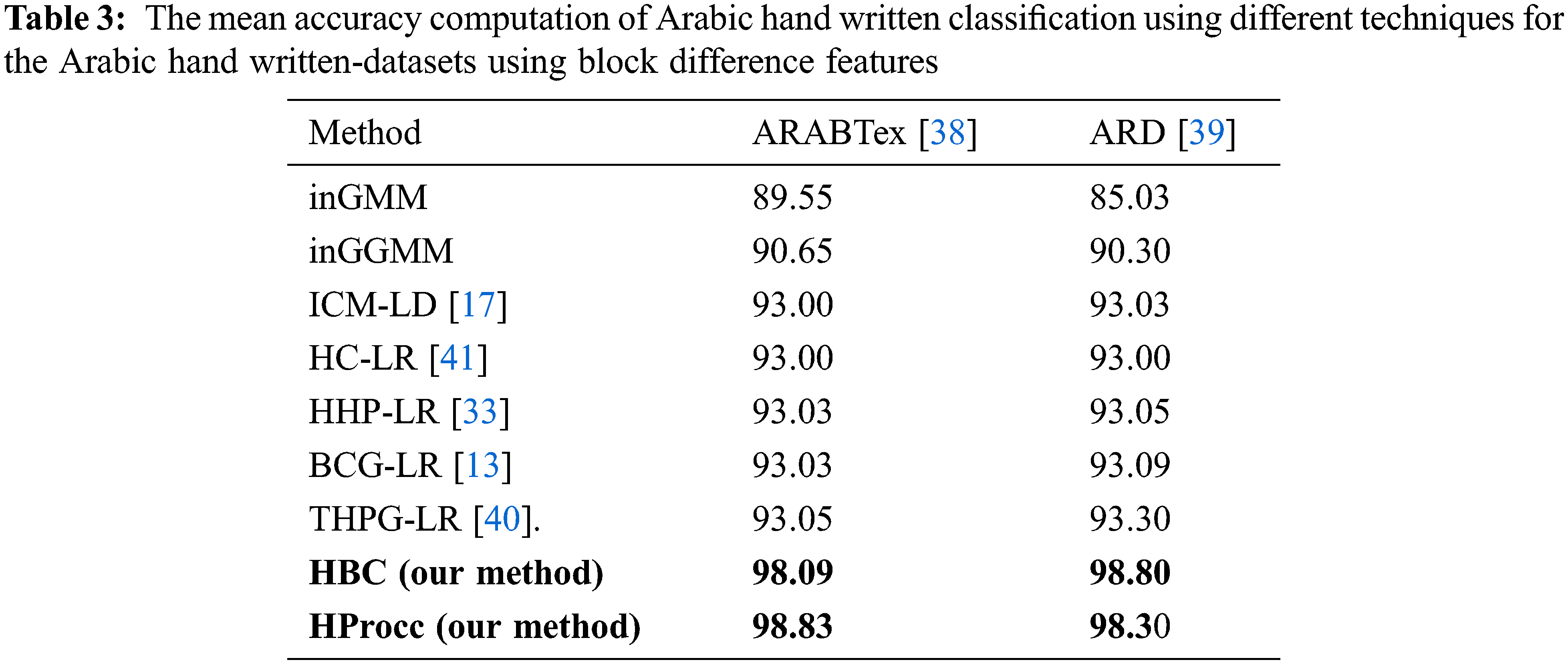
We executed all models for 100 runs and computed the mean prediction accuracy. The experiments prove that the proposed HBC and HProcc models can realize superior accuracy for the two public datasets in terms of the Arabic hand written prediction accuracy. The comparison of these performance results using the t-test depict that our model outperforms the rest of models in a significant datamining terms. Precisely, results depict the superiority of our technique for Arabic hand written and prediction aptitudes which exceed HC-LR [41], BCG-LR [13], HHP-LR [33], and THPG-LR [40]. In contradiction, the least accuracy is realized in the infinite linear combination method. The proposed models outperform the other models using Scale-Invariant Feature Extraction Transform, Local binary patterns and block difference extraction models. Therefore, these experiments approve the worth of our proposed models. Due to the efficiency of block difference feature extraction method for labelling the predicted Arabic hand written text images, we also discover that block difference technique realizes better performance compared with other feature extraction methods. It displays the qualities of block difference method which can reflect all probable details in text images at various resolutions. The HProcc combination model attains better results compared to HBC combination model for all tests. This can be explicated by the impact of the HProcc combination representation and its higher generalization aptitude and higher aptitude to represent tailed distribution.

4.2 Facial Expression Classification

Spatial classification is an important research area for facial expression classification [39–45] and image recognition [45–50]. In this research, we are concentrating on human facial expression classification (HFE) through a set of video frames. In fact, classifying facial expressions is used to detect and investigate various human facial expression. HFE is one the important automated visual recognition topics in research where expression identification can be valuable for monitoring various situations, especially in surveillance applications [51–53]. Accurate classification of facial expression is essential by utilizing effective automated techniques to tackle difficult settings such as bad illumination.

We accomplish the classification of facial expressions utilizing the proposed model HBC and HProcc. Our procedure is defined as following:

•   The model extracts the three dimensional scale-invariant feature transform from the dataset.

•   The extracted 3D features are then represented as spatial bag-of-words representation using C-means technique [39].

•   A probabilistic Semantic indexing [41] is used to build a vector.

Each video frame Ij defines a group that is linked to an infinite combination representation Groupj . Therefore, we assume that each scale-invariant feature transforms 3D feature vector into the infinite combination representation Groupj . Spatial words define the combination constituents of Groupj . Also, a universal terminology set is produced and pooled among all the groups of the universal-representation Group0 of the hierarchical representation. This venue confirms the applicability of the drive of the hierarchical combination representation. It is eminent that the construction of the spatial terminology is used as apart of the hierarchical combination representations. This phase is developed out distinctly using the C-means technique. It is also considered that the producing of the spatial terminology set is part of our hierarchical combination representations and this phase is not executed distinctly through C-means. Indeed, it is according to the features of the nonparametric representation that the count of constituents in the universal-level combination representation can be inferred from the data.

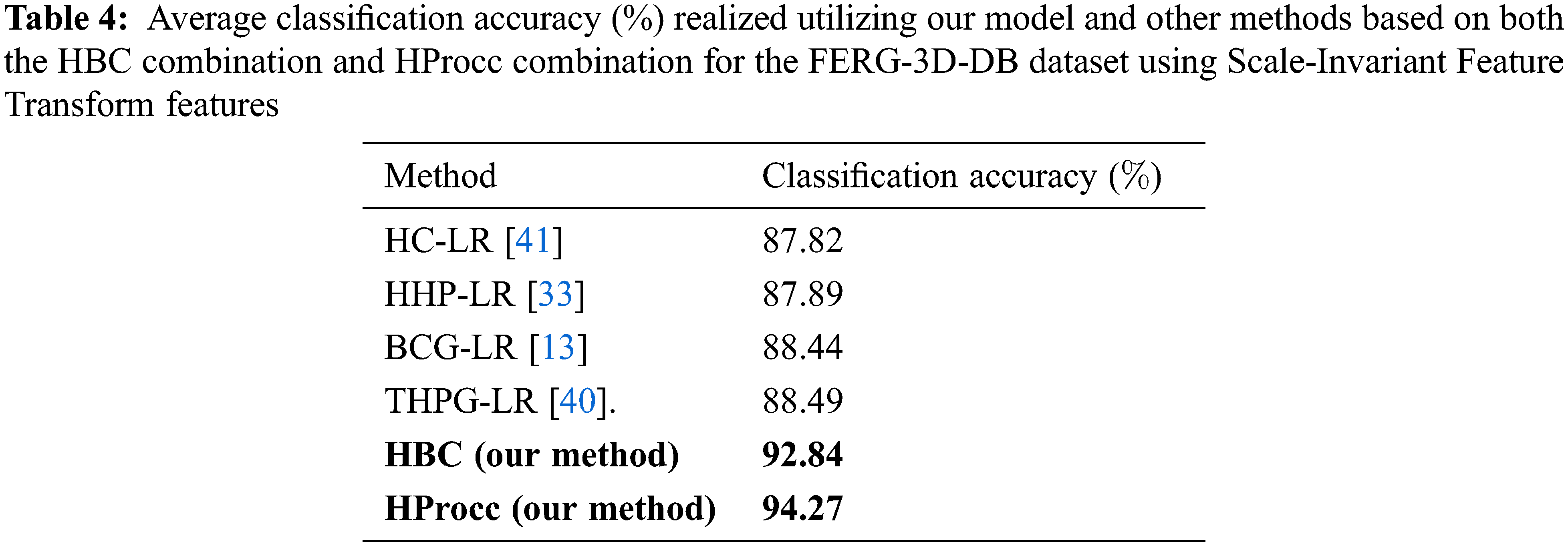
We piloted our experiments of facial expression classification using a public dataset (FERG-3D-DB) found in [41] with Calm, happy, sad, angry, fearful, surprise, disgust, and neutral expressions. FERG-3D-DB dataset encloses 3910 video frames of various facial expression categorized into 8 classes. We split the dataset into three subsets to train, validate and test. The results are depicted in Tab. 4, where Average classification accuracy (%) are realized utilizing our model and other methods based on both the HBC combination and HProcc combination. Tab. 5 depicts average classification accuracy (%) realized for our model and other methods based on both the HBC combination and HProcc combination for the FERG-3D-DB using Local binary patterns. While, Tab. 6 shows the average classification accuracy (%) realized utilizing our model and other methods based on both the HBC combination and HProcc combination for the FERG-3D-DB using block difference features.

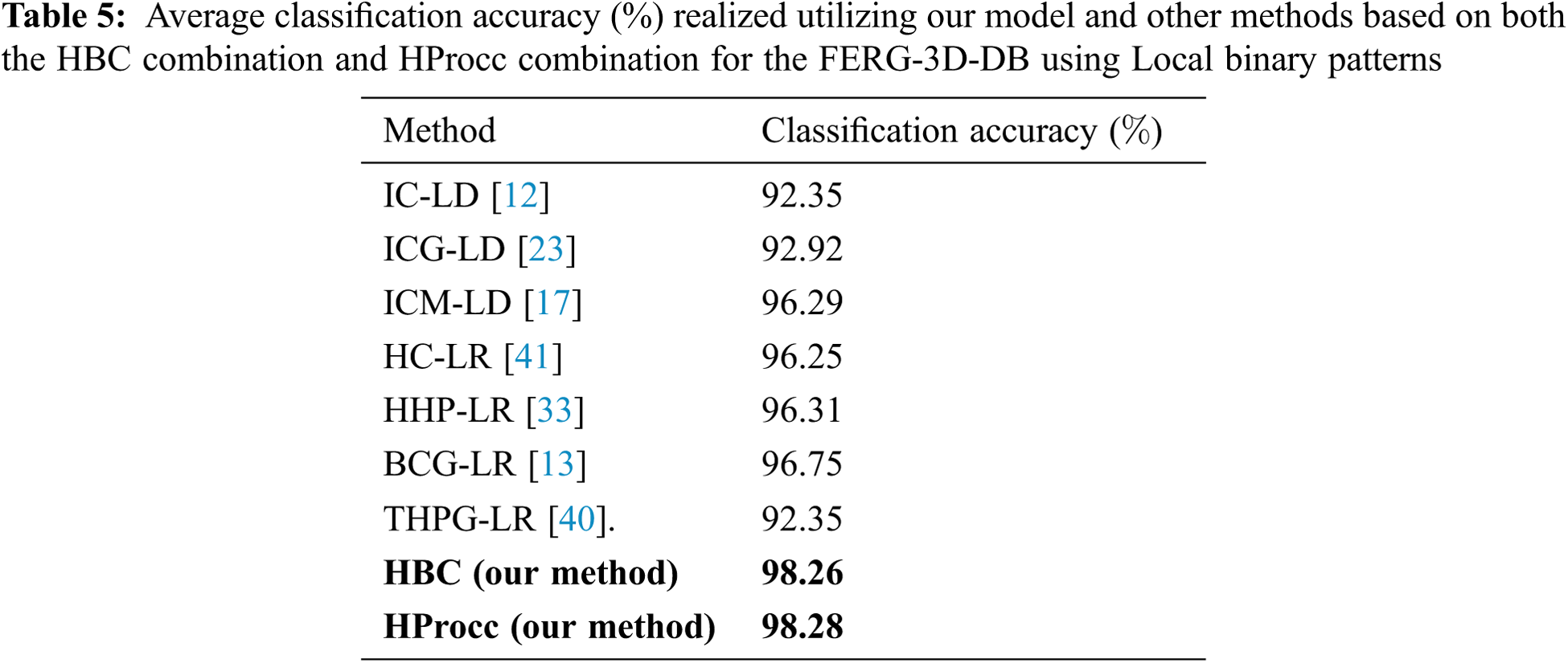
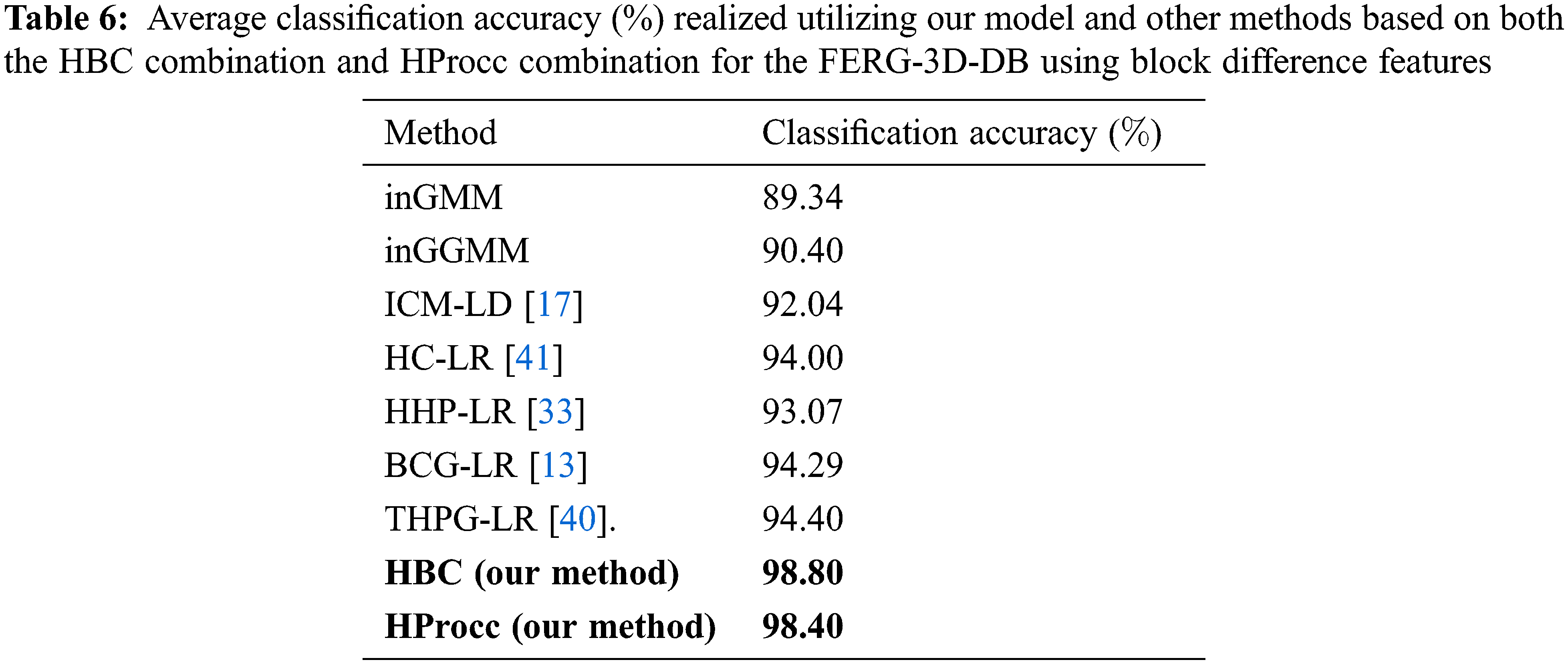
The average specificity and sensitivity accuracy of our model and of representations based on HBC combination and HProcc combination are depicted in Tab. 7.

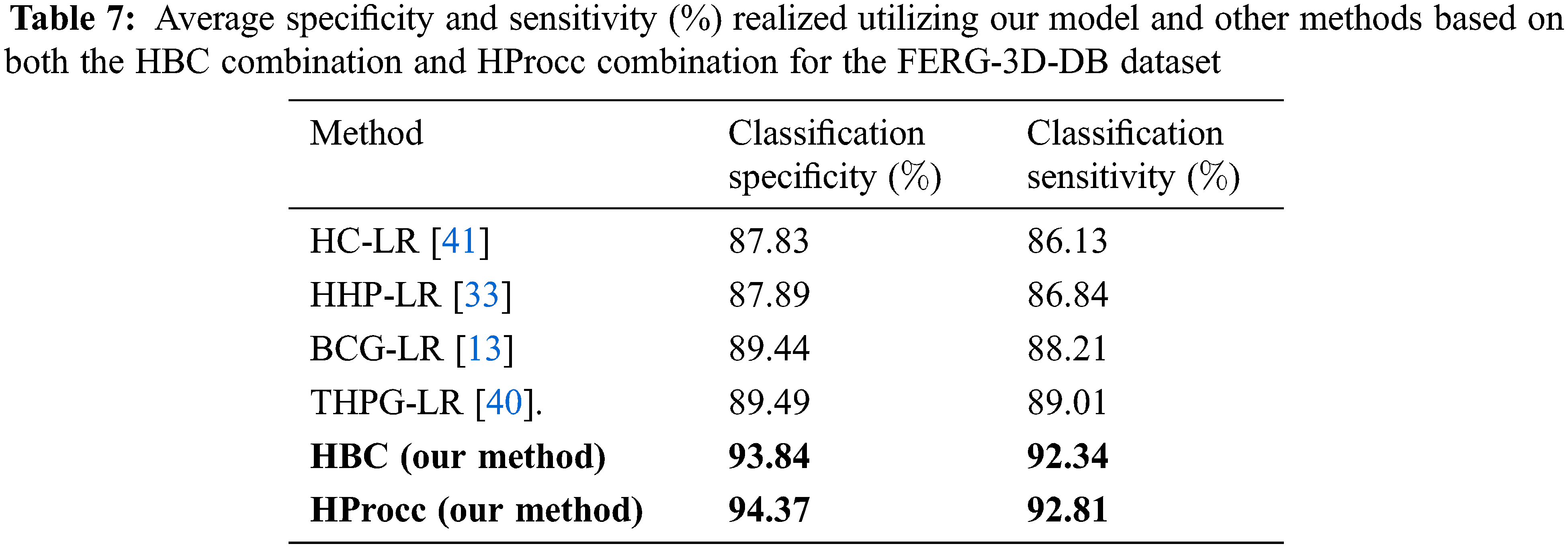
As depicted in Tab. 7, the proposed models are attaining the greatest classification in terms of specificity and sensitivity across all compared models. For 200 experiments, we have an average value < 0.028 and consequently, the enhancement in performance among our model and other methods are more significant using t-test. Also, we compared our methods with other combination representation models namely (HC-LR [41]), hierarchical Two-hyper-parameter Poisson process combination of linear distribution (HHP-LR [33]), Hierarchical Beta Process combination of generalized linear distribution (BCG-LR [13]), and hierarchical Two-hyper-parameter Poisson process combination of generalized linear distribution (THPG-LR) [40], from the literature. We can deduce that our representations can deliver more discrimination score than the other compared models. Obviously, these results approve the efficiency of our model for facial expressions classification compared to other hyper-parameter processes based on linear dissemination. Another observation is that our proposed HProcc method performs better than HBC for this particular facial expression application and this validates the utilizing of hierarchical hyper-parameter Poisson method over Beta procedure [53–55].

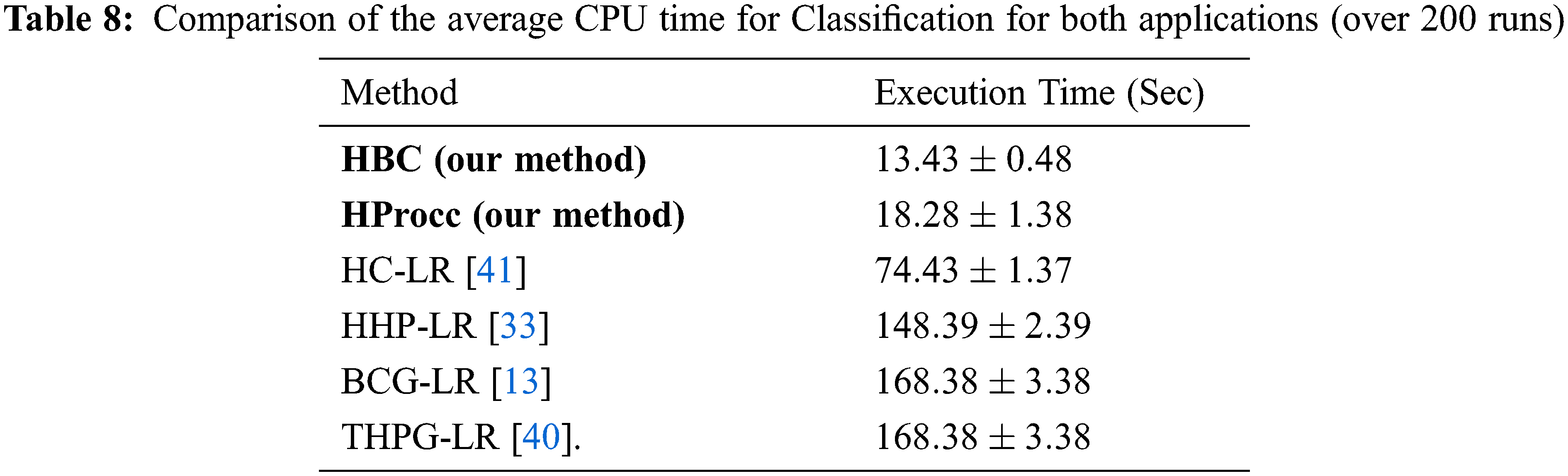
In Tab. 8, average execution time for classification in both applications is depicted. The experiment is done over 200 runs. Our models require less CPU time for classification which makes it suitable for real time applications.

5  Conclusions

In this article, we proposed two hierarchical non-parametric models using Beta and Two-hyper parameters Poisson processes. The Beta process is employed because of its bounded data representation capability. Infinite Gaussian mixture process is a model that computes the Gaussian mixture parameters with order. This process is a probability density distribution with adequate training data that can converge to the input density curve. Both models are trained utilizing spectral inference which has a robust valuation of convergence by presenting a Bayesian stochastic model. A significant property of our proposed model is that it does not require the determination of the count of combination beforehand. We performed out experiments on Arabic hand written categorization and face expression classification to validate the performance of our techniques which can be utilized more for several computer vision and pattern classification problems. The proposed HProcc combination model outperforms other model for all tests by an average of 9% in accuracy and recall. This is due to the impact of the HProcc combination and generalization features.

Acknowledgement: We would like to thank Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R113), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Funding Statement: This research was funded by Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R113), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  J. W. Lau and P. J. Green, “Bayesian represent-based clustering procedures,” Journal of Computational and Graphical Statistics, vol. 16, no. 3, pp. 326–338, 2007. [Google Scholar]

 2.  T. Singh, N. Saxena and M. Khurana, “Data clustering using moth-flame optimization technique,” Sensors, vol. 21, no. 12, pp. 4086, 2021. [Google Scholar]

 3.  J. L. Andrews, P. D. McNicholas and S. Subedi, “Model-based classification via combinations of t-distributions,” Computational Data Analysis, vol. 33, no. 1, pp. 320–329, 2021. [Google Scholar]

 4.  W. Fan, N. Bouguila, J. X. Du and X. Liu, “Axially symmetric data clustering through Beta process combination represents of Watson distributions,” IEEE Transaction of Neural Networks Learning Systems, vol. 30, no. 6, pp. 1683–1694, 2019. [Google Scholar]

 5.  W. Fan, H. Sallay and N. Bouguila, “Online learning of hierarchical two-hyper-parameter Poisson process combination of generalized Beta distributions with feature selection,” IEEE Transaction of Neural Networks Learning Systems, vol. 28, no. 9, pp. 2048–2061, 2017. [Google Scholar]

 6.  S. N. MacEachern and P. Müller, “Estimating Beta process representation,” Journal of Computational and Graphical Statistics, vol. 7, no. 2, pp. 223–238, 2019. [Google Scholar]

 7.  Y. W. Teh, M. I. Jordan, M. J. Beal and D. M. Blei, “Hierarchical Beta processes,” Journal of the American data mining association, vol. 101, no. 476, pp. 1366–1381, 2019. [Google Scholar]

 8.  J. Sethuraman, “A constructive definition of Beta priors,” Statistica Sinica, vol. 2, no. 3, pp. 639, 1994. [Google Scholar]

 9.  D. M. Blei and M. I. Jordan, “Spectral inference for Beta process combinations,” Bayesian Analysis, vol. 1, no. 1, pp. 121–143, 2019. [Google Scholar]

10. Y. W. Teh and D. M. Blei, “Sharing clusters among related groups: Hierarchical Beta processes,” in Proc. Graphical Statistics, New York, NY, USA, pp. 621–632, 2019. [Google Scholar]

11. C. Wang, J. W. Paisley and D. M. Blei, “Online spectral inference for the hierarchical Beta process,” Proc. of The Fourteenth International Conference On Artificial Intelligence and Statistics, vol. 13, pp. 732–760, 2011. [Google Scholar]

12. J. Pitman and M. Yor, “The two-hyper-parameter Poisson- Beta distribution derived from a stable subordinator,” Annals of Probability, vol. 23, no. 2, pp. 833–900, 1997. [Google Scholar]

13. H. Attias, “A spectral bayesian framework for graphical represents, Advances in neural information processing systems, 12(1–2):209–213, 2020. [Google Scholar]

14. Z. Song, S. Ali, N. Bouguila and W. Fan, “Nonparametric hierarchical combination represents based on asymmetric Gaussian distribution,” Digital Signal Processing, vol. 106, no. 1, pp. 102829, 2020. [Google Scholar]

15. W. Fan, H. Sallay, N. Bouguila and S. Bourouis, “Spectral learning of hierarchical infinite generalized Beta combination represents and applications,” Soft Computing, vol. 20, no. 3, pp. 979–990, 2016. [Google Scholar]

16. Y. Huang, F. Zhou and J. Gilles, “Empirical curve let based fully convolutional network for supervised Arabic hand written image segmentation,” Neuro Computing, vol. 349, no. 1, pp. 31–43, 2019. [Google Scholar]

17. Q. Zhang, J. Lin, Y. Tao, W. Li and Y. Shi, “Salient object detection via color and Arabic hand written cues,” Neuro Computing, vol. 243, pp. 33–48, 2020. [Google Scholar]

18. W. Fan and N. Bouguila, “Online facial expression classification based on finite Beta-liouville combination represents,” in in Proc. of International Conference On Computer and Robot Vision, London, England, pp. 37–44, 2019. [Google Scholar]

19. G. Zhao and M. Pietikainen, “Dynamic Arabic hand written classification using local binary patterns with an application to facial expressions,” IEEE Transactional of Pattern Analysis and Machine Intelligence, vol. 29, no. 6, pp. 913–928, 2019. [Google Scholar]

20. A. Badoual, M. Unser and A. Depeursinge, “Arabic hand written-driven parametric snakes for semi-automatic image segmentation,” Computer Vision Image Underset, vol. 188, no. 3, pp. 102793, 2019. [Google Scholar]

21. Y. Zheng and K. Chen, “A general represent for multiphase Arabic hand written segmentation and its applications to retinal image analysis,” Biomedical Signal Processing Control, vol. 8, no. 4, pp. 374–381, 2021. [Google Scholar]

22. E. Hayman, B.-dis Caputo, M. Fritz and J. O. Eklundh, “On the significance of real-world conditions for material classification,” in Proc. Computer Vision - ECCV 2004, 8th European Conf. on Computer Vision, Prague, Czech Republic, pp. 233–266, 2004. [Google Scholar]

23. J. Zhang, M. Marszalek, S. Lazebnik and C. Schmid, “Local features and kernels for classification of Arabic hand written and object categories: A comprehensive study,” International Journal of Computer Vision, vol. 73, no. 2, pp. 213–238, 2017. [Google Scholar]

24. H. Ishwaran and L. F. James, “Gibbs sampling methods for Poisson-Kingman partition-breaking priors,” Journal of the American Data Mining Association, vol. 96, no. 433, pp. 161–173, 2021. [Google Scholar]

25. Z. Guo, L. Zhang and D. Zhang, “A completed modeling of local binary pattern operator for Arabic hand written classification,” IEEE Transaction of Image Processing, vol. 19, no. 6, pp. 1637–1663, 2019. [Google Scholar]

26. P. D. McNicholas, “Model-based clustering,” Journal of Classification, vol. 33, no. 3, pp. 331–373, 2016. [Google Scholar]

27. X. Liu, H. Fu and Y. Jia, “Linear combination modeling and learning of neighboring characters for multilingual text extraction in images,” Pattern Recognition, vol. 41, no. 2, pp. 484–493, 2018. [Google Scholar]

28. V. Kumar, D. Kumar, M. Kaur, D. Singh, S. A. Idris et al., “A novel binary seagull optimizer and its application to feature selection problem,” IEEE Access, vol. 9, no. 1, pp. 103481–103496, 2021. [Google Scholar]

29. A. Aggarwal, V. Sharma, A. Trivedi, M. Yadav, C. Agrawal et al., “Two-way feature extraction using sequential and multimodal approach for hateful meme classification,” Complexity, vol. 2021, no. 1, pp. 1–7, 2021. [Google Scholar]

30. A. Almulihi, F. Alharithi, S. Bourouis, R. Alroobaea, Y. Pawar et al., “Oil spill detection in SAR images using online extended spectral learning of Beta process combinations of Beta distributions,” Remote Sensing, vol. 13, no. 1, pp. 2991, 2021. [Google Scholar]

31. H. C. Li, V. A. Krylov, P. Z. Fan, J. Zerubia and W. J. Emery, “Unsupervised learning of generalized Beta combination represent with application in data mining modeling of high-resolution SAR images,” IEEE Transaction of Geoscience Remote Sensing, vol. 34, no. 4, pp. 2133–2170, 2019. [Google Scholar]

32. P. Dollár, V. Rabaud, G. Cottrell and S. Belongie, “Behavior classification via sparse spatial-temporal features,” in Proc. of IEEE Int. Workshop on Spatial Surveillance and Performance Evaluation of Tracking and Surveillance, Paris, France, pp. 63–72, 2020. [Google Scholar]

33. S. Bourouis, H. Sallay and N. Bouguila, “A competitive generalized Beta combination represent for medical image diagnosis,” IEEE Access, vol. 9, pp. 13727–13736, 2021. [Google Scholar]

34. R. Alroobaea, S. Rubaiee, S. Bourouis, N. Bouguila and A. Alsufyani, “Bayesian inference framework for bounded generalized Gaussian-based combination represent and its application to handwritten images classification,” International Journal of Imaging Systems, vol. 30, no. 1, pp. 18–30, 2020. [Google Scholar]

35. C. Beckmann, M. Woolrich and S. Smith, “Linear/Beta combination modelling of ICA/GLM spatial maps,” Neuroimage, vol. 19, no. 2, pp. 178–189, 2021. [Google Scholar]

36. S. Bourouis, R. Alroobaea, S. Rubaiee, M. Andejany, F. M. Almansour et al., “Markov chain monte carlo-based bayesian inference for learning finite and infinite inverted Beta-liouville combination represents,” IEEE Access, vol. 9, no. 1, pp. 71170–71183, 2021. [Google Scholar]

37. R. Mehta and K. O. Egiazarian, “Arabic hand written classification using dense micro-block difference,” IEEE Transaction of Image Processing, vol. 23, no. 4, pp. 1604–1616, 2016. [Google Scholar]

38. M. Aneja and B. Deepali, “Learning to generate 3D stylized character expressions from humans,” in Proc. of IEEE Winter Conf. on Applications of Computer Vision (WACV), Venice, Italy, pp. 451–459, 2018. [Google Scholar]

39. P. Scovanner, S. Ali and M. Shah, “A 3-dimensional sift descriptor and its application to action classification,” in Proc. of the 13th ACM Int. Conf. On Multimedia, Cairo, Egypt, pp. 337–360, 2019. [Google Scholar]

40. F. Najar, S. Bourouis, N. Bouguila and S. Belghith, “Unsupervised learning of finite full covariance generalized Gaussian combination represents for human activity classification,” Multimodal Tools Application, vol. 78, no. 13, pp. 18669–18691, 2019. [Google Scholar]

41. D. G. Lowe, “Distinctive image features from scale-invariant keypoints,” International Journal of Computer Vision, vol. 60, no. 2, pp. 91–110, 2020. [Google Scholar]

42. R. Zhu, F. Dornaika and Y. Ruichek, “Learning a discriminant graph-based embedding with feature selection for image categorization,” Neural Networks, vol. 11, no. 2, pp. 33–46, 2019. [Google Scholar]

43. H. Zhou and S. Zhou, “Scene categorization towards urban tunnel traffic by image quality assessment,” Journal of Computer Vision, vol. 6, no. 3, pp. 145–153, 2019. [Google Scholar]

44. F. S. Alharithi, A. H. Almulihi, S. Bourouis, R. Alroobaea and N. Bouguila, “Discriminative learning approach based on flexible combination represent for medical data categorization and classification,” Sensors, vol. 21, no. 1, pp. 24–30, 2021. [Google Scholar]

45. M. Vrigkas, C. Nikou and I. A. Kakadiaris, “A review of human activity classification methods,” Frontiers in Robotics and AI, vol. 2, no. 1, pp. 28–36, 2019. [Google Scholar]

46. C. Schuldt, I. Laptev and B.-dis Caputo, “Classifing human facial expression: A local SVM approach,” in Proc. of the 17th Int. Conf., Riyadh, KSA, vol.3, pp. 32–36, 2019. [Google Scholar]

47. S. Lazebnik, C. Schmid and J. Ponce, “A sparse Arabic hand written representation using local affine regions,” Journal of Computer Patterns, vol. 27, no. 8, pp. 1263–1278, 2020. [Google Scholar]

48. F. Najar, S. Bourouis, N. Bouguila and S. Belghith, “A new hybrid discriminative/generative represent using the full-covariance generalized gaussian combination represents,” Soft Computing, vol. 24, no. 14, pp. 10611–10628, 2020. [Google Scholar]

49. G. Csurka, C. Dance, L. Fan, J. Willamowski and C. Bray, “Spatial categorization with bags of keypoints,” Computer Vision, vol. 1, no. 2, pp. 123–132, 2018. [Google Scholar]

50. A. Bosch, A. Zisserman and X. Muñoz, “Scene classification via pLSA,” Computer Robotics, vol. 2, no. 3, pp. 317–330, 2018. [Google Scholar]

51. S.-F. Wong and R. Cipolla, “Extracting spatiotemporal interest points using universal information,” Computer Vision, vol. 3, no. 2, pp. 110–118, 2017. [Google Scholar]

52. W. Fan and N. Bouguila, “Spectral learning for Beta process combinations of Beta distributions and applications,” Multimedia Tools and Applications, vol. 70, no. 3, pp. 1683–1702, 2014. [Google Scholar]

53. Y. Xu, H. Ji and C. Fermüller, “Viewpoint invariant Arabic hand written description using fractal analysis,” Journal of Computer Vision, vol. 3, no. 1, pp. 83–100, 2019. [Google Scholar]

54. W. Sun, G. C. Zhang, X. R. Zhang, X. Zhang and N. N. Ge, “Fine-grained vehicle type classification using lightweight convolutional neural network with feature optimization and joint learning strategy,” Multimedia Tools and Applications, vol. 80, no. 20, pp. 30803–30816, 2021. [Google Scholar]

55. W. Sun, X. Chen, X. R. Zhang, G. Z. Dai, P. S. Chang et al., “A multi-feature learning model with enhanced local attention for vehicle re-identification,” Computers, Materials & Continua, vol. 69, no. 3, pp. 3549–3561, 2021. [Google Scholar]