Intention Estimation of Adversarial Spatial Target Based on Fuzzy Inference

1  Introduction

Suppose there are two confrontational space objects in a three-dimensional space, and consider one of them as an observer which needs to use real-time data measurement to identify the intent of the other target then make decisions in a very short time. Through the 1v1 intention estimation, this method can be further extended to 1vN, Nv1, and NvN situations [1–3]. Therefore, it is very important to study the target intention estimation in the 1v1 situation.

This algorithm is based on fuzzy mathematics theory for theoretical guidance of intention estimation [4]. Combined with the mathematical model of conditional probabilities [5–8], the probabilities of target intention can be effectively and quickly given. This algorithm divides the intention of the target object into 3 categories: offensive intention, escape intention, and unclear intention. Offensive intention means that the target will perform aggressive behaviors on the observer, including but not limited to fast approaching, adjusting the attack distance, and target locking. The intention to escape means that the target is in fear or there is an escape report after detecting opponent. Unclear intention means that the target’s behavior is uncertain, and it is likely to be in a hovering and wandering operation. It should be pointed out that the unclear intention does not mean the intention to attack, nor the intention to escape. Unclear intention belongs to the same level of intentions as offensive intention and escape intention.

The main solution in this paper is to calculate the distance, speed, relative heading angle, altitude difference, steering trend and other information between the two space objects [9,10], and according to the concept of membership function in fuzzy mathematics [11,12], calculate the fuzzy membership of each feature then determine the type of each feature [13]. Finally, the data is fused to give a credible instantaneous probability of intent. At the same time, based on the obtained instantaneous probabilities of intention estimation, the sequential storage operation is performed. Useful values are extracted from the recorded instantaneous probabilities of intention estimation [14,15], then the intention estimation probability based on the weighted historical probabilities is further deduced [16]. The weight value distribution of weighted historical probability data is based on the time distance as an indicator, the nearest time period is used as a high weight value, a relatively long time period is assigned a low weight value [17], eventually a smooth and historically based probability result is reached.

2  Target Feature Calculation Method

According to the relationship between the intention of space objects and the state of motion, this paper selects relative heading angle, distance, height difference, distance change rate, turning trend and other data as calculation parameters.

2.1 Calculation of Relative Heading Angle

The relative heading angle is defined as shown in the Fig. 1.

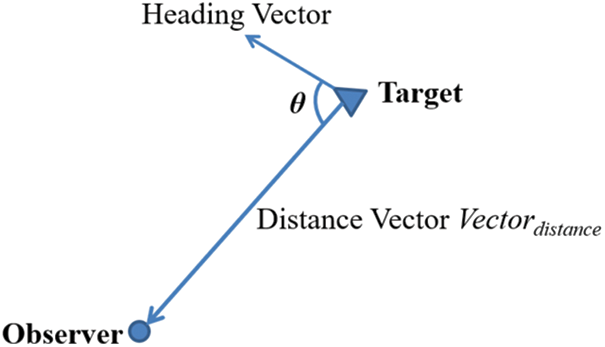
Figure 1: Definition of relative heading angle

From the speed formula Eq. (1):

v=ΔdΔt (1)

This equation is very basic. v denotes velocity, d and t stand for distance and time, respectively.

Further deduce the speed formula in all directions:

veast=ΔlΔt⋅π180⋅R⋅cos⁡b (2)

vnorth=ΔbΔt⋅π180⋅R (3)

vup=ΔhΔt (4)

veast represents the velocity with the coordinates in the true east direction as the positive direction in the three-dimensional coordinate system. The same goes for vnorth. vup represents the velocity from the center of the earth to the direction of observer as the positive direction in the three-dimensional coordinate system. This coordinate system represents the navigation coordinate system, and this coordinate method is also called the North-East Coordinate System. π is the ratio of pi. R is the radius of the earth (it is assumed here that the earth is approximately a standard sphere). l, b, h represent the longitude, latitude, and altitude where space objects are. Through the calculation of these three velocities, this paper can describe the velocity of each component in the north-east navigation coordinate system of a certain place, which can be used to further calculate the speed direction, judge the movement and predict the movement of the object. Special attention should be paid to: the speed here should have error tolerance, because the measurement of the target often has deviations [18]. In this paper, the measurement accuracy is achieved by increasing the time interval of the measurement. Take five seconds as a time interval as the sampling standard here, that is, Δt=5s .

Secondly, calculate the connection vector between the two space objects. Based on the existing latitude and longitude position information, a coordinate system with the observer as the origin, north and east as the positive direction is calculated. The distance vector can be obtained by the following Eq. (5).

vectordistance=(2πR(l1−l2)180,2πR(b1−b2)180,h1−h2) (5)

where vectordistance represents the vector of distance between the target and the observer. l1 , b1 , h1 are longitude, latitude and altitude of the observer, and l2 , b2 , h2 are the position information of longitude, latitude and altitude of the target. Then the following operation is performed.

v→t=(veast,vnorth,vup) (6)

cos⁡θ=vectordistance⋅v→t|vectordistance|⋅|v→t| (7)

Define v→t as the velocity vector of the target. cos⁡θ represents the cosine of the angle θ which between the target heading vector and the distance vector vectordistance of both objects. This formula is based on the calculation formula of the angle between vectors in three-dimensional space.

2.2 Algorithm of Distance Between Two Sides

2.2.1 When the Two Space Objects Are Far Apart

According to the cosine formula of the angle between two points in three-dimensional space:

OA→⋅OB→=|OA→|⋅|OB→|⋅cosα (8)

OA, OB are vectors with the origin of two points as the starting point. α is the angle between the two vectors. cosα represents the cosine of the angle α .

The arc length formula of a circle:

l=πRα180 (9)

l represents the arc length, R represents the radius, π represents the circumference of the circle, and α represents the angle corresponding to the arc length.

After further bringing in the latitude and longitude for conversion, the following formula is obtained:

d=πR180⋅arccos(cosb1⋅cosb2⋅cos⁡(l1−l2)+sin⁡b1⋅sinb2) (10)

d represents the distance between the two points of space objects. b1 and l1 represent the latitude and longitude of observer. b2 and l2 represent the latitude and longitude of target.

2.2.2 When the Two Space Objects Is Relatively Close

According to the distance formula in three-dimensional space:

d2=(x1−x2)2+(y1−y2)2+(z1−z2)2 (11)

d represents the distance between two objects. x1, y1, z1 represent the xyz axis coordinates of the object 1 in the space rectangular coordinate system, and x2, y2, z2 represent the xyz axis coordinates of the object 2 in the space rectangular coordinate system. Combined with the currently known conversion formula of latitude and longitude into the geocentric coordinate system, the authors can get the exact distance between observer and the target when the two objects are relatively close.

2.3 Algorithm for Height Difference Between the Two Sides

This algorithm is relatively simple, and only needs to calculate the difference from H. It should be noted that the height of observer is the guideline. A difference greater than 0 means that the target is above observer, and a difference of less than 0 means observer is below the target.

△H=H1−H2 (12)

H1 is the height of target, H2 is the height of observer.

2.4 Algorithm of Distance Change Rate

Distance information plays an important role in judging the intention of the target. This paper mainly considers the impact of distance changes on the estimation of target intentions, respectively considering when the target is getting closer or farther away from the observer, or the distance between the two objects keeps changing. Therefore, when constructing the fuzzy distance, it is divided into 3 fuzzy subsets, which are described by fuzzy variables. For the changes of distance, a new variable is defined to characterize it, that is, the rate of change of distance.

Δd=(d1−d2)(d1+d2)/2 (13)

Where ∆d is the calculated rate of change of distance. d1 represents the distance of the target at time 1. d2 represents the distance of the target at time 2. The membership function is an algorithmic equation that categorizes different values into the three fuzzy subsets above, and the membership function u(x) of ∆d is shown in the following Tab. 1:

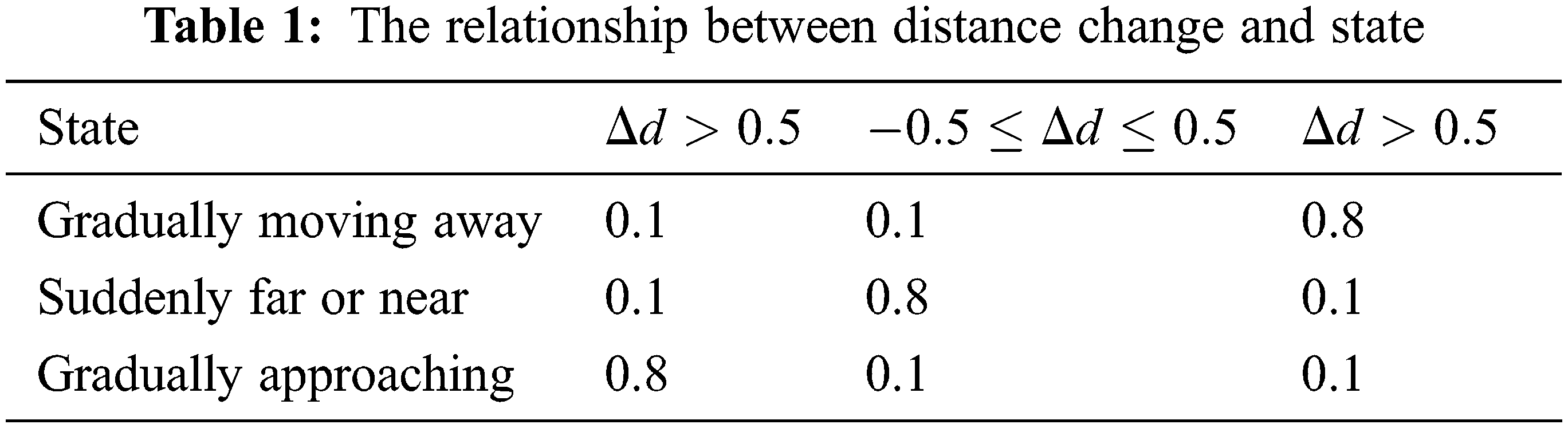
The membership function figure is shown below. Fig. 2 is a graphical representation of table above.

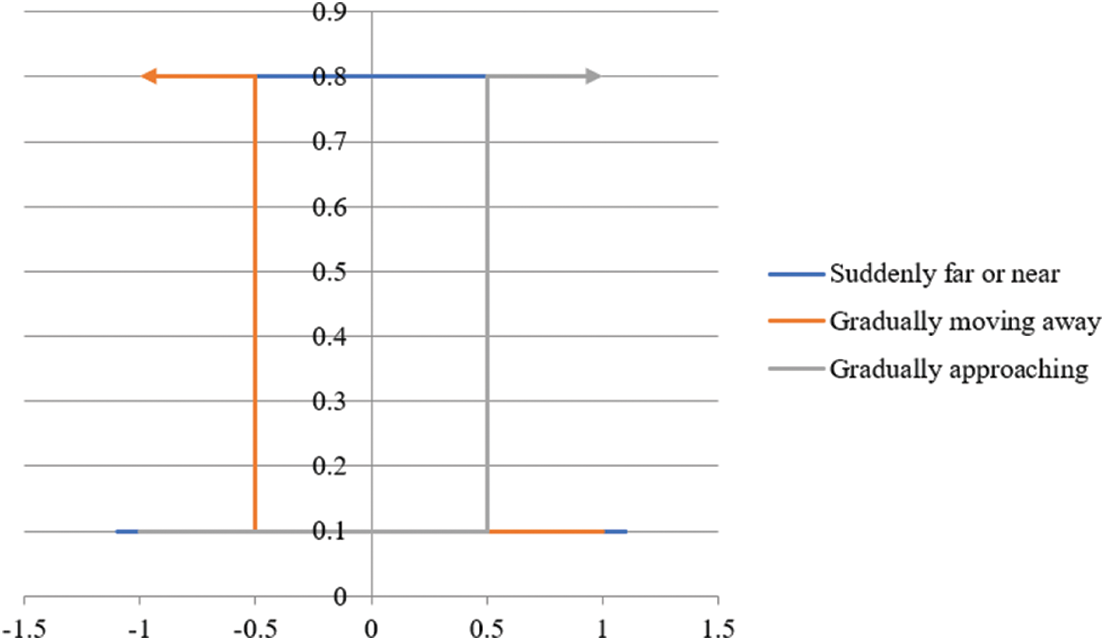
Figure 2: The membership function of distance change rate

2.5 Algorithm to Get Target Turning Trend Through Latitude and Longitude Height

The turning trend of the space target can reflect its intention to a certain extent. For example, when the target is approaching, the direction of movement will turn to the observer, and when retreating, it will deviate from the observer. Therefore, the target turning trend can be used as one of the parameters of intention inference to make the basis of intention estimation more abundant and sufficient.

In order to get the target turning trend, this paper starts from the curvature of the target trajectory. When the height is not considered, the target trajectory appears as a straight-line segment and a curved segment on the plane. What is needed in real-time intention estimation is the shape of the trajectory that the target’s current motion will produce, that is, the target is moving in a straight line or a curve. There are methods proposed to quantize and encode the turning at each moment, then select the trajectory sequence within a certain period of time, and finally identify based on the probability model [19,20]. However, the time range of the quantized trajectory of this method is difficult to determine and the calculation amount is large, which is not suitable for high-speed moving targets. This paper directly uses the target trajectory sampling points to calculate the curvature, uses the vector cross product to determine the direction, and combines the two to obtain the steering parameters. Therefore, the target turning trend can be expressed by the curvature of the target trajectory.

The curvature is expressed as follow Eq. (14):

Curv=2sin⁡(α)Distance (14)

Curv represents the curvature of the target. α represents the angle formed between the coordinate point at time t1, the coordinate point at time t2, and the coordinate point at time t3 in space. Use the angle cosine formula to combine the existing latitude and longitude height-geocentric coordinate system conversion function, here expressed as LBHtoXYZ, then calculate the cosine and sine.

cos⁡(α)=(LBHtoXYZ(t1)−LBHtoXYZ(t2))⋅(LBHtoXYZ(t2)−LBHtoXYZ(t3))|LBHtoXYZ(t1)−LBHtoXYZ(t2)|⋅|LBHtoXYZ(t2)−LBHtoXYZ(t3)| (15)

sin⁡(α)=1−{(LBHtoXYZ(t1)−LBHtoXYZ(t2))⋅(LBHtoXYZ(t2)−LBHtoXYZ(t3))|LBHtoXYZ(t1)−LBHtoXYZ(t2)|⋅|LBHtoXYZ(t2)−LBHtoXYZ(t3)|}2 (16)

cos⁡(α),sin⁡(α) represent the cosine and sine values corresponding to the angle of α. The magnitude of curvature reflects the degree of curvature of the curve, and the direction of curvature needs to be represented by curvature symbols. In this algorithm, if the left is positive, the curvature sign can be determined by the plane vector cross product. The specific method is as Eq. (17).

sign(Curv)=sign((LBHtoXYZ(t1)−LBHtoXYZ(t2))×(LBHtoXYZ(t2)−LBHtoXYZ(t3))) (17)

It should be noted that considering the influence of sampling error, the calculation between t1 and t2 should satisfy:

t1−t2=5s (18)

The above illustrates that the interval between t1 and t2 should meet the condition of 5 s. The velocity and distance are calculated by the position information separated by 5 s, which can calculate the speed more accurately and reduce the speed error.

The cross-product operation is defined as follows: AB=(x1,y1) , AC=(x2,y2) , AB×AC=x1y2−x2y1 .

When using this method to calculate the curvature, the measurement error of the track point will cause the fluctuation of the curvature, especially in the straight-line movement, the curvature sign will change repeatedly [21]. In order to reduce the random error, the sampling points in the sliding time window can be used to calculate the average curvature, and a threshold value can be set at the same time. When the curvature is less than the threshold value, the curvature is considered to be 0, and the target moves approximately in a straight line.

3  Fuzzy Deduction and Probability Deduction

When using fuzzy inference for target intent estimation, it is necessary to construct a fuzzy inference system from two aspects: fuzzy inference model and fuzzy inference rule. Different types of targets have different behavior patterns, and corresponding models and rules need to be established according to actual conditions.

3.1 Fuzzy Inference Model

This paper adopts the Mamdani fuzzy inference model with multiple inputs and single output [22,23]. The inputs are the position information status of the target observed by the sensors: longitude, latitude, altitude, and the 5 parameters obtained by further statistics and calculations using the target’s position information: speed, height, distance, relative heading angle and steering trend. The output is the target’s probability of intention: attack, escape, unclear. The three situations have different probabilities. The membership functions of inputs and outputs are shown in the Fig. 3.

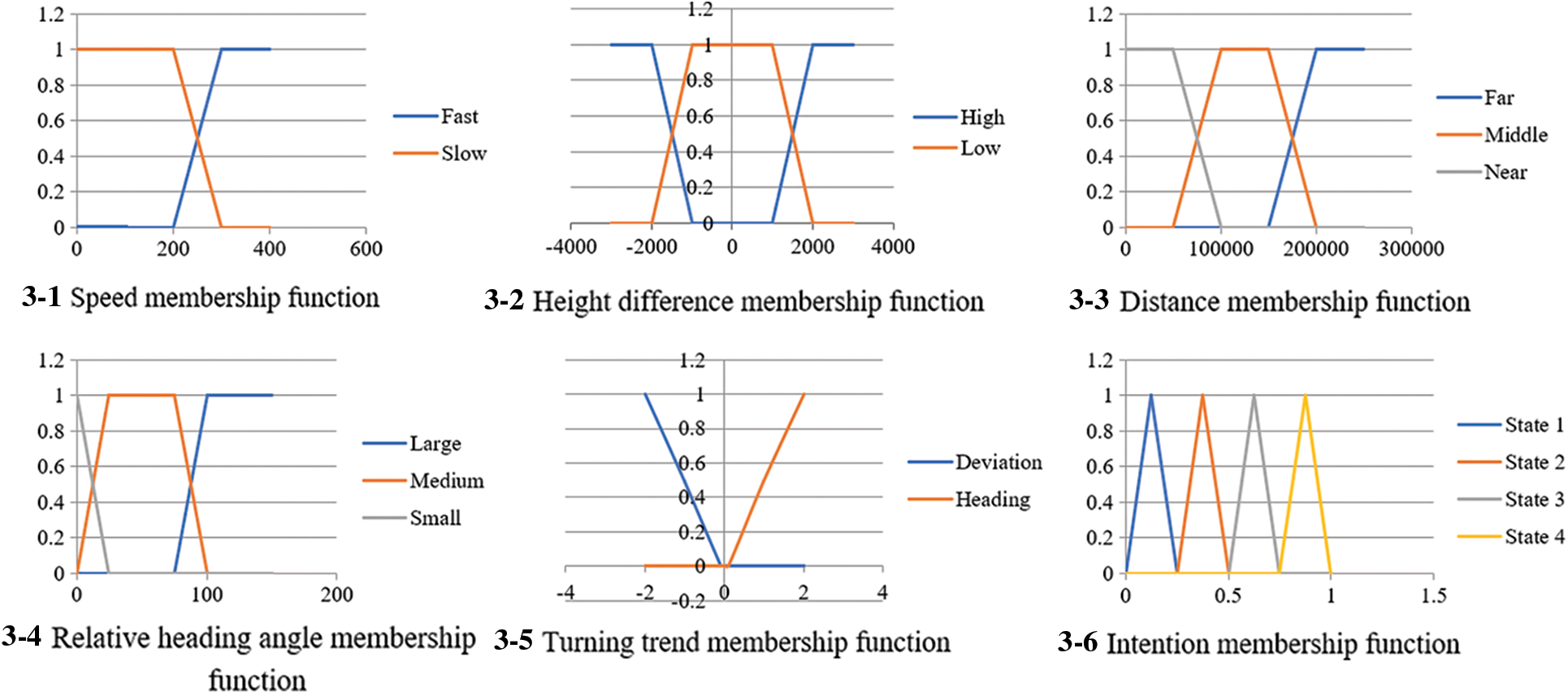
Figure 3: Images of some important membership functions

In Fig. 3-1, it represents the membership type of velocity. The abscissa represents the size of the target speed, and the ordinate represents the degree of fuzzy membership at a certain speed. The orange line indicates the degree of membership which belongs to the fuzzy feature of slow. The blue line indicates the degree of membership which belongs to the fuzzy feature of being fast. The two lines cross when the speed is equal to 250. When the target speed is less than 250, its speed is classified as slow. Similarly, when the target speed is greater than 250, its speed is classified as fast.

In Fig. 3-2, the abscissa denotes the height difference between the target and observer, which means the value obtained by subtracting the height of the target from the height of the observer. The value range of the abscissa is not necessarily greater than zero. The ordinate indicates the degree of fuzzy membership within a certain height difference. The orange line represents the degree of membership which belongs to the fuzzy feature of low membership. The blue line represents the degree of membership which belongs to the fuzzy feature of being high. The two lines cross when the height difference is −1500 and +1500, respectively.

In Fig. 3-3, the abscissa represents the straight-line distance between the target and the observer. The ordinate represents the degree of fuzzy membership at a certain distance. The gray line denotes the degree of membership belonging to the fuzzy feature of being close. The orange line indicates the degree of membership which belongs to the fuzzy feature of middle distance. The blue line indicates the degree of membership belonging to the fuzzy feature of being far away. The orange line and the gray line cross at a distance of 75,000, and the blue line and the orange line cross at a distance of 175,000.

In Fig. 3-4, the abscissa represents the relative heading angle of the target, and the ordinate represents the degree of fuzzy membership corresponding to a certain relative heading angle. The gray line indicates the degree of membership which belongs to the fuzzy feature of small angle. The orange line indicates the degree of membership belonging to the fuzzy feature of middle angle. The blue line indicates the degree of membership belongs to the fuzzy feature of large angle. The gray line and the orange line cross when the relative heading angle is equal to 12.5 degrees, the blue line and the orange line cross when the relative heading angle is equal to 87.5 degrees.

In Fig. 3-5, the abscissa represents the turning trend size of the target, and it can be greater than zero or less than zero. The ordinate represents the magnitude of the corresponding fuzzy membership within a certain turning trend. The blue line indicates the degree of fuzzy membership corresponding to the fuzzy feature of deviation. The orange line indicates the degree of fuzzy membership in a certain turning trend is classified as the fuzzy feature of heading. When the turning trend tends to zero, neither deviation nor heading can be indicated. At the same time, it is necessary to leave a little redundancy when the turning trend tends to 0, so when the turning trend is greater than 0.1, it can be determined the membership feature is belongs to heading. In the same way, when the turning trend is less than −0.1, it can be determined that the turning trend belongs to the fuzzy feature of deviation.

In Fig. 3-6, the abscissa of intention membership indicates the value of different states. The ordinate is the degree of membership of different states corresponding to different values. It can be seen that when the value is [0, 0.25], the intention belongs to state 1. When the value is [0.25, 0.5], the intention belongs to state 2. When the value is [0.5, 0.75], the intention belongs to state 3. When the value is [0.75, 1], the intention belongs to state 4.

3.2 Fuzzy Inference Rules

After the inputs and outputs are determined, the corresponding rules need to be formulated to perform fuzzy inference. For the fuzzy reasoning model in 3.1, the fuzzy rules are as shown in the Tabs. 2 and 3. At this point, the construction of the fuzzy inference system is completed. As long as the location and mobile information of the target is obtained in real time, the intent of the target can be inferred. It should be noted that the selection of membership functions and the formulation of fuzzy rules need to conform to objective facts [24]. Therefore, designing with reference to expert knowledge and experience can make the fuzzy inference system more accurately reflect the actual situation.

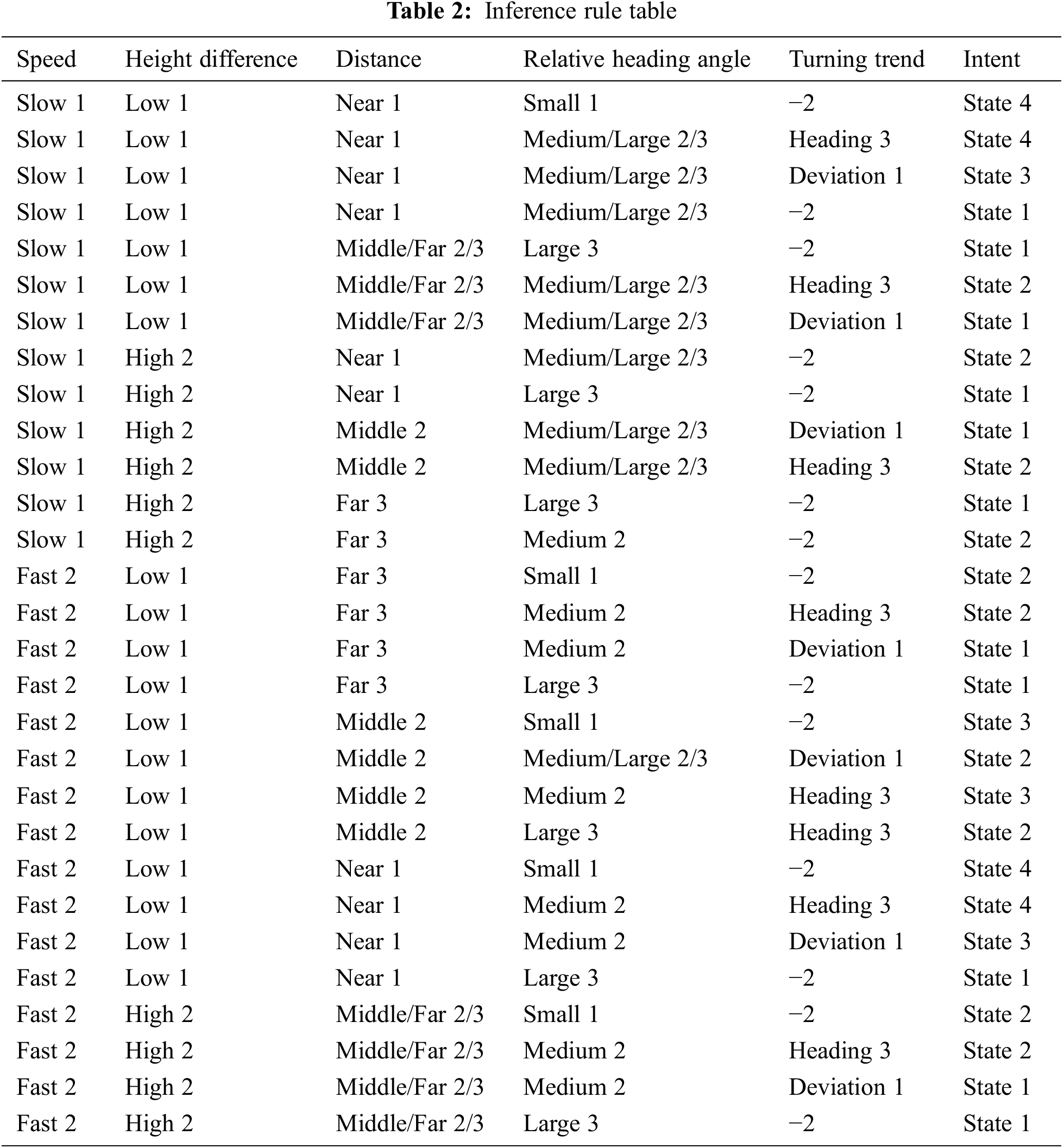
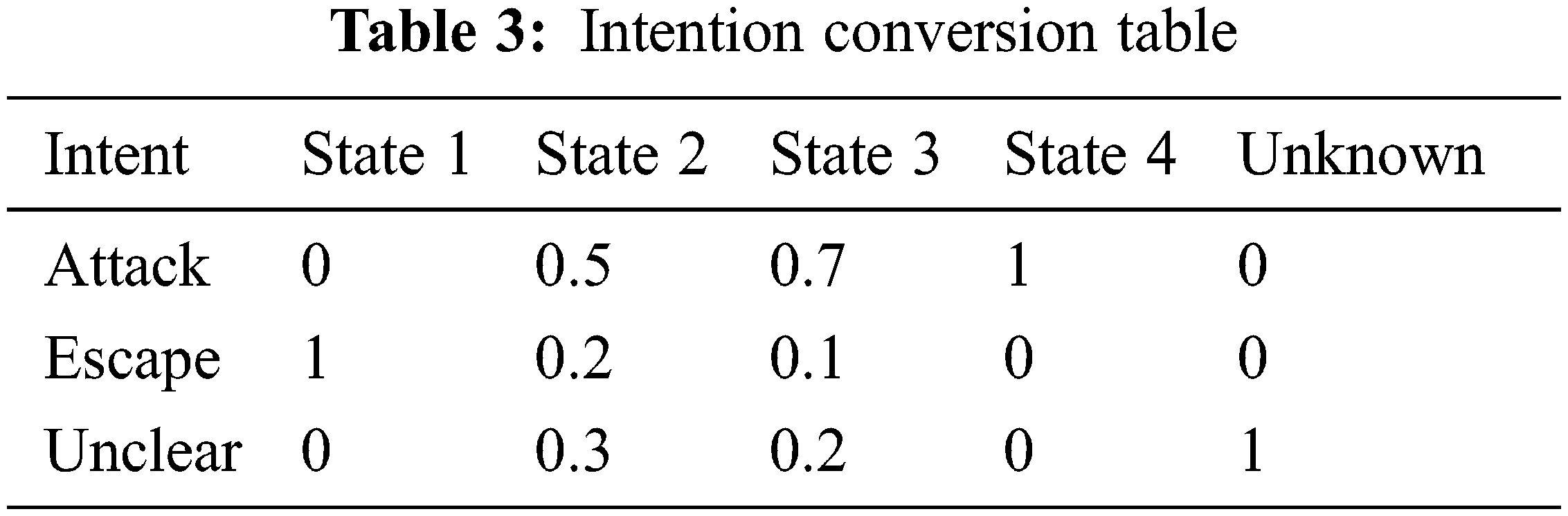
3.3 Update of Real-Time Intention Estimation Based on Historical Data

After obtaining the instantaneous intent probabilities, if only the instantaneous intent estimation probabilities are given each time, there are still many shortcomings, such as: probabilistic volatility, inaccurate probabilities, the probability change is not smooth enough, and so on. This paper solves this problem by using a sliding time window to store historical data.

The instantaneous probability data obtained in Section 2.4 can be stored in a sequential storage, and then performing weighting operations to obtain the update of the real-time intention estimation based on historical data. The size of historical probability data can be customized according to its own storage capacity. In this algorithm, it chooses to store nearly 4 minutes of historical probability data, and adopts a weighting method to perform the final weighted probability output. Since the data measured in the most recent time period has higher timeliness, the probability of the most recent intention needs to be given a higher weight value. And for the probability of an earlier intention, a lower weight value is given. Therefore, for the probability of being closer to the current time, a higher weight value is adopted; for the probability of an earlier time, a lower weight value is adopted. The distribution is shown in the following Tab. 4:

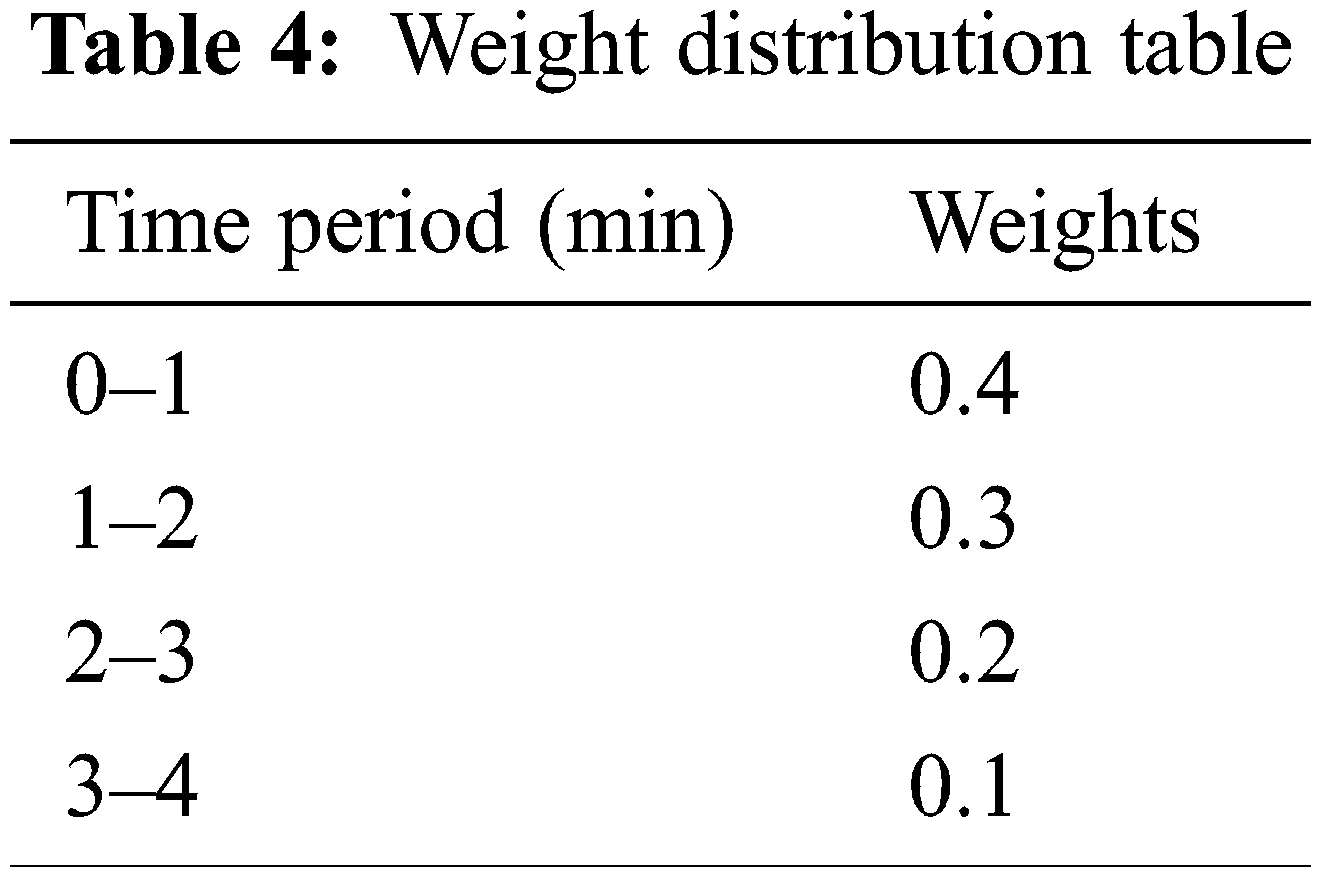
Define event A as attack, E as escape, and U as unclear. Define time T1, T2, T3, T4 as four different time periods. Perform a weighted sum:

μ(A)=0.4⋅∑i=01⁡P(A,Ti)+0.3⋅∑i=12⁡P(A,Ti)+0.2⋅∑i=23⁡P(A,Ti)+0.1⋅∑i=34⁡P(A,Ti) (19)

μ(E)=0.4⋅∑i=01⁡P(E,Ti)+0.3⋅∑i=12⁡P(E,Ti)+0.2⋅∑i=23⁡P(E,Ti)+0.1⋅∑i=34⁡P(E,Ti) (20)

μ(U)=0.4⋅∑i=01⁡P(U,Ti)+0.3⋅∑i=12⁡P(U,Ti)+0.2⋅∑i=23⁡P(U,Ti)+0.1⋅∑i=34⁡P(U,Ti) (21)

P(A,Ti) stands for the probability of the target’s attack intention in the time period Ti. P(E,Ti) stands for the probability of the target’s escape intention in the time period Ti. P(U,Ti) stands for the probability of the unclear intention of the target in the time period Ti. μ(A) represents the weighted sum of the probability of offensive intention. μ(E) represents the weighted sum of the probability of escape intention. μ(U) represents the weighted sum of the probability of unclear intention.

P(A)=μ(A)μ(A)+μ(E)+μ(U)⋅100% (22)

P(E)=μ(E)μ(A)+μ(E)+μ(U)⋅100% (23)

P(U)=μ(U)μ(A)+μ(E)+μ(U)⋅100% (24)

where P(A) represents the probability of the target’s intentional attack, which is the operation of normalizing the weighted sum. P(E) represents the probability that the target intends to escape. P(U) represents the probability that the intention of the target is unclear. The idea of this algorithm is to first obtain the sum of the weighted historical probabilities of each intent, and then standardize the sum of each weighted probability to obtain the estimated probability with a value range of (0,1). The process is shown in the Fig. 4.

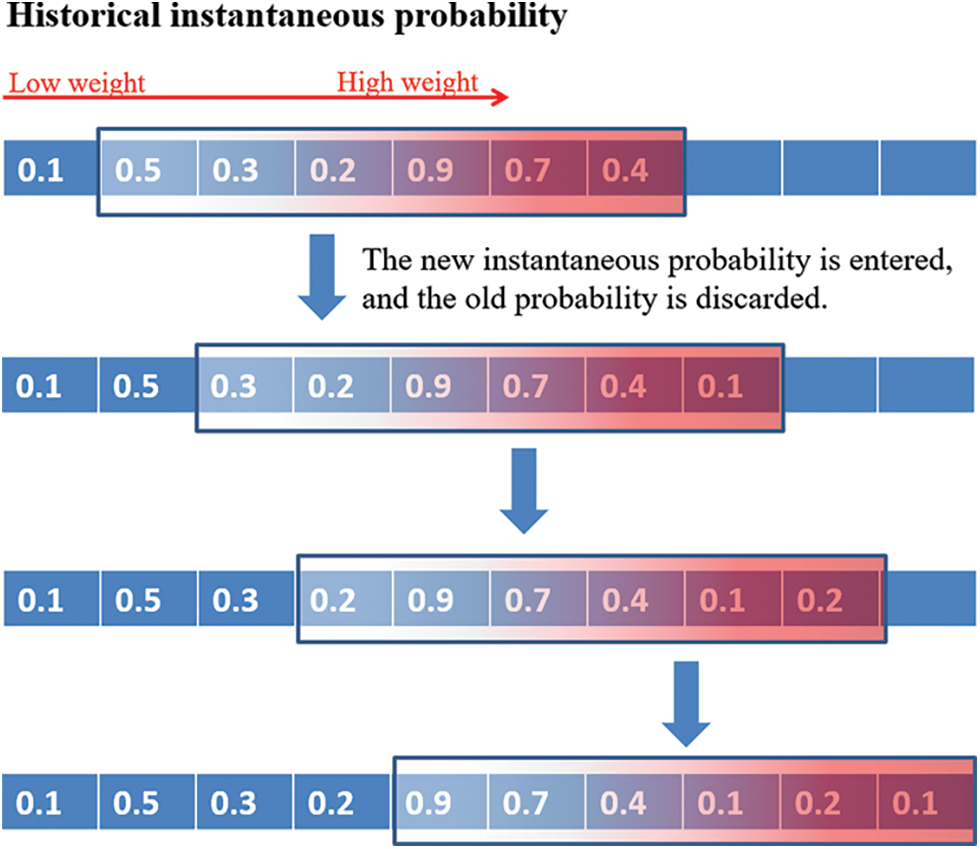
Figure 4: Schematic diagram of historical probability weighting algorithm

4  Experiment

Based on the above algorithm, the simulation experiment is adopted to verify effect, and the 1v1 intention estimation method can be extended to the NvN situation to verify the reliability of the algorithm.

The process is shown in the Fig. 5, where the experiment sets 3 space moving objects as observers and 8 space moving objects as the targets. First, each observer performs a 1v1 intention estimation for each target at the same time (blue solid line), and then the three observers transmit the calculated intention probability to each other (orange dashed line), finally output the targets’ intention.

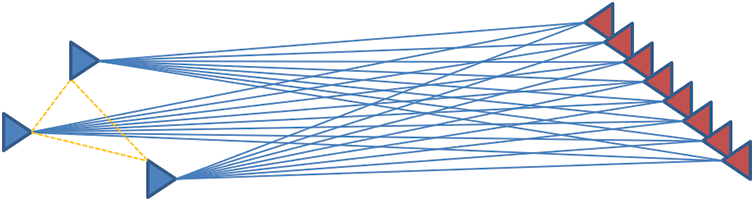
Figure 5: Schematic diagram of experimental model

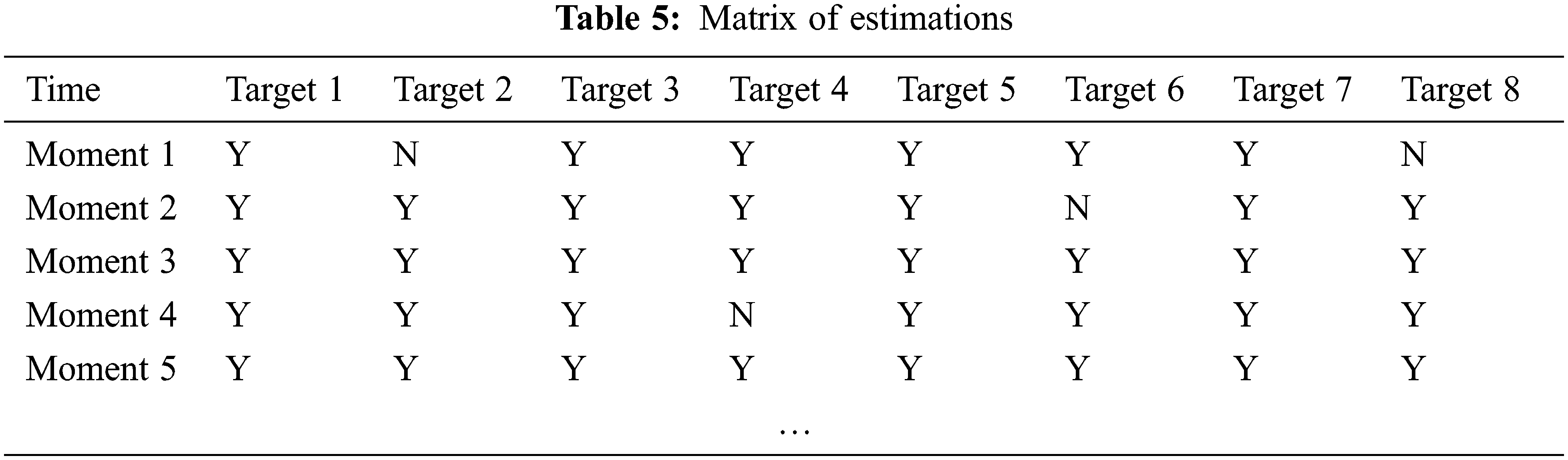
The intent estimations are compared with the subsequent real actions of the targets, and a matrix is output to indicate whether the prediction is correct, as shown in the Tab. 5. The matrix indicates the correctness of the target intent estimation at a certain moment (Y means correct, N means wrong). The line represents the moment. The column represents the target object number.

After checking for a few moments, the following Tab. 6 shows the accuracy of target intention estimation for 500,000 samples.

In summary, the simulation results show that the method in this paper basically conforms to the hypothesis and the method is effective.

5  Conclusion

This paper proposes a method of estimating intention characteristics of space targets. Based on this, combined with the movement state information obtained from the observation, the fuzzy inferencing method is also used to study the problem of target intent estimation. This method can effectively estimate the combat intention of the space target, thereby providing a reliable basis for situation analysis and command decision-making. And it can estimate the intent of the target without a large amount of statistical data. The result shows that this method could estimate intention of the target efficiently. This research can be used in drone control, flight navigation, military fields, etc. The advantage of this method is that it can achieve a better prediction effect without a lot of data training, and the results can be generated in real time, which is convenient for timely decision-making and rapid response. In addition, the deployment of this method requires no additional hardware, requires low computing power, and can be deployed quickly and without cost. Although the method in this paper does not require a probability model, it still needs to formulate corresponding membership functions and fuzzy rules for different goals based on experience and knowledge. Reasonable determination of the membership function and fuzzy rules is the key to this method, and it is also an important issue to be solved in the follow-up.

Acknowledgement: Special thanks to School of Information and Software Engineering and the members of the Information of Physics Computation Center for their help and support for this research. The authors would also like to thank everyone from the Institute of Logistics Science and Technology for their technical support.

Funding Statement: Project supported by the National Key R&D Program of China, Grant No. 2018YFA0306703 and J2019-V-0001-0092.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Y. Demiris, “Prediction of intent in robotics and multi-agent systems,” Cognitive Processing, vol. 8, no. 3, pp. 151–158, 2007. [Google Scholar]

 2.  M. Fanaswala and V. Krishnamurthy, “Detection of anomalous trajectory patterns in target tracking via stochastic context-free grammars and reciprocal process models,” Selected Topics in Signal Processing, vol. 7, no. 1, pp. 76–90, 2013. [Google Scholar]

 3.  A. Wang, V. Krishnamurthy and B. Balaji, “Intent inference and syntactic tracking with GMTI measurements,” IEEE Transactions on Aerospace & Electronic Systems, vol. 47, no. 4, pp. 2824–2843, 2011. [Google Scholar]

 4.  F. Chen, Z. Wang, S. Yang and Y. Tian, “A study on speech recognition for design intent of geometric modeling using HMM and its application,” Applied Mechanics & Materials, vol. 433, no. 35, pp. 420–425, 2013. [Google Scholar]

 5.  A. Attaallah and R. A. Khan, “Estimating usable-security through hesitant fuzzy linguistic term sets based technique,” Computers, Materials & Continua, vol. 70, no. 3, pp. 5683–5705, 2022. [Google Scholar]

 6.  W. Sung and S. Hsiao, “Employing a fuzzy approach for monitoring fish pond culture environment,” Intelligent Automation & Soft Computing, vol. 31, no. 2, pp. 987–1006, 2022. [Google Scholar]

 7.  X. Pang, Z. Han and Q. Wu, “Fuzzy automata system with application to target recognition based on image processing,” Computers & Mathematics with Applications: An International Journal, vol. 61, no. 5, pp. 1267–1277, 2011. [Google Scholar]

 8.  L. Lee and S. Chen, “Fuzzy interpolative reasoning for sparse fuzzy rule-based systems based on the ranking values of fuzzy sets,” Expert Systems with Applications, vol. 35, no. 3, pp. 850–864, 2008. [Google Scholar]

 9.  M. Luo and R. Zhao, “Fuzzy reasoning algorithms based on similarity,” Journal of Intelligent and Fuzzy Systems, vol. 34, no. 1, pp. 213–219, 2018. [Google Scholar]

10. G. P. Ramalingam, R. Arockia and S. Gopalakrishnan, “Optimized fuzzy enabled semi-supervised intrusion detection system for attack prediction,” Intelligent Automation & Soft Computing, vol. 32, no. 3, pp. 1479–1492, 2022. [Google Scholar]

11. S. Chen and L. Lee, “Fuzzy interpolative reasoning for sparse fuzzy rule-based systems based on interval type-2 fuzzy sets,” Expert Systems with Applications, vol. 38, no. 8, pp. 9947–9957, 2011. [Google Scholar]

12. E. Trillas, “Fuzzy sets in approximate reasoning, part 1: Inference with possibility distributions,” Fuzzy Sets and Systems, vol. 123, no. 3, pp. 405–406, 2011. [Google Scholar]

13. X. Liu, X. Song, W. Gao, L. Zou and L. L. Romero, “A decision making approach based on hesitant fuzzy linguistic-valued credibility reasoning,” Journal of Universal Computer Science, vol. 27, no. 1, pp. 40–64, 2021. [Google Scholar]

14. A. Sarkheyli-Hgele and D. Sffker, “Integration of case-based reasoning and fuzzy approaches for real-time applications in dynamic environments: Current status and future directions,” Artificial Intelligence Review, vol. 53, no. 3, pp. 1943–1974, 2020. [Google Scholar]

15. L. Hong, W. Wang and X. Liu, “Universal approximation of fuzzy relation models by semi-tensor product,” IEEE Transactions on Fuzzy Systems, vol. 1, no. 1, pp. 99, 2019. [Google Scholar]

16. X. Wang, Z. Xu and X. Gou, “A novel plausible reasoning based on intuitionistic fuzzy propositional logic and its application in decision making,” Fuzzy Optimization and Decision Making, vol. 19, no. 3, pp. 251–274, 2020. [Google Scholar]

17. Z. Zhang, D. Wang and X. Gao, “Imperfect premise matching controller design for interval type-2 fuzzy systems under network environments,” Intelligent Automation & Soft Computing, vol. 27, no. 1, pp. 173–189, 2021. [Google Scholar]

18. S. I. Kwak, C. Gang, I. S. Kim, G. H. Jo and C. J. Hwang, “A study of a modeling method of t-s fuzzy system based on moving fuzzy reasoning and its application,” Computer Science, vol. 1511, no. 24, pp. 32–38, 2015. [Google Scholar]

19. X. Qiao, Y. Li, B. Chang and X. Wang, “Modeling on risk analysis of emergency based on fuzzy evidential reasoning,” Systems Engineering-Theory & Practice, vol. 35, no. 56, pp. 2657–2666, 2015. [Google Scholar]

20. H. Espitia, J. Soriano, I. Machón and H. López, “Design methodology for the implementation of fuzzy inference systems based on boolean relations,” Electronics, vol. 8, no. 11, pp. 1243, 2019. [Google Scholar]

21. Y. Jin, W. Cao, M. Wu and Y. Yuan, “Accurate fuzzy predictive models through complexity reduction based on decision of needed fuzzy rules,” Neurocomputing, vol. 323, no. 7, pp. 344–351, 2018. [Google Scholar]

22. L. Chao, T. Chen and Z. Yuan, “Long-term prediction of time series based on stepwise linear division algorithm and time-variant zonary fuzzy information granules,” International Journal of Approximate Reasoning, vol. 108, no. 5, pp. 38–61, 2019. [Google Scholar]

23. H. Seki and H. Ishii, “On the infimum and supremum of fuzzy inference by single input type fuzzy inference,” IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, vol. 92, no. 1, pp. 611–617, 2009. [Google Scholar]

24. S. Fan, W. Zhang and X. Wei, “Fuzzy inference based on fuzzy concept lattice,” Fuzzy Sets & Systems, vol. 157, no. 24, pp. 3177–3187, 2006. [Google Scholar]