Robust Symmetry Prediction with Multi-Modal Feature Fusion for Partial Shapes

1  Introduction

Detecting the symmetry of 3D objects is a critical and fundamental problem for many computer vision applications. In geometric processing, finding symmetries in geometric data, such as point clouds, polygon meshes and voxels, could help numerous applications take advantage of symmetry information to solve their tasks or improve the algorithms, e.g., shape matching [1], segmentation [2], completion [3], etc. Among all the symmetry types, the most common and important one is planar reflective symmetry. Traditional planar symmetry detection methods are usually based on the observation that all points on the shape will coincide with the original shape after mirror transformation along the symmetry plane. e.g., a shape can be aligned to the principal axes, then planes formed by pairs of principal axes can be checked to see if they are symmetry planes. Recently, deep learning-based methods leverage a neural network to extract global features of the shape, which is used to capture possible symmetry [4,5].

However, these methods are all symmetry detection on complete 3D shapes. But the shape of an object captured in real-world applications is often incomplete due to the limited sensor resolution, single viewpoint, and occlusion, in this case, the above basic assumption for complete 3D shape will be broken.

For this reason, we propose to directly perform symmetry detection from partially observed objects/point clouds. A common application scenario is estimating symmetries of 3D shapes based on a single-view RGB-D image. Due to partial observations and object occlusion, it poses special challenges that are beyond the reach of geometric detection. For example, missing global geometric information leads to crucial difficulty to find local symmetry correspondences which are supported by mirror transformation. So, we try to dig out more potential information through the deep neural network, just as humans can infer symmetrical information through a large amount of learned knowledge when they see a new object.

In this work, we propose a learning approach for symmetry prediction based on a single RGB-D image. Trying to transform an incomplete shape into a complete shape is our main motivation. Our method consists of two modules, i.e., the multi-modal feature fusion module and the detection-by-reconstruction module. We build a channel-transformer network (CTN) to extract cross-fusion features from the RGB-D as the multi-modal feature fusion module. Then, our self-reconstruction network based on a 3D variational auto-encoder (3D-VAE) takes the cross-modal features as input, followed by a prediction symmetry network to detect the symmetry. Fig. 1 shows the pipeline of our method. Thanks to our reconstruction network, our detection network is trained in an unsupervised manner without any symmetry annotations. Extensive experiments on several benchmarks demonstrate the effectiveness of our method. To summarize, our main contribution is three-fold:

•   We propose a channel-transformer network for single-view RGB-D images to extract multimodal features.

•   We use a 3D-VAE network to perform the self-reconstruction, replacing the MLPs with 3D CNN in the latent layer.

•   We propose an end-to-end multi-feature network for symmetry prediction.

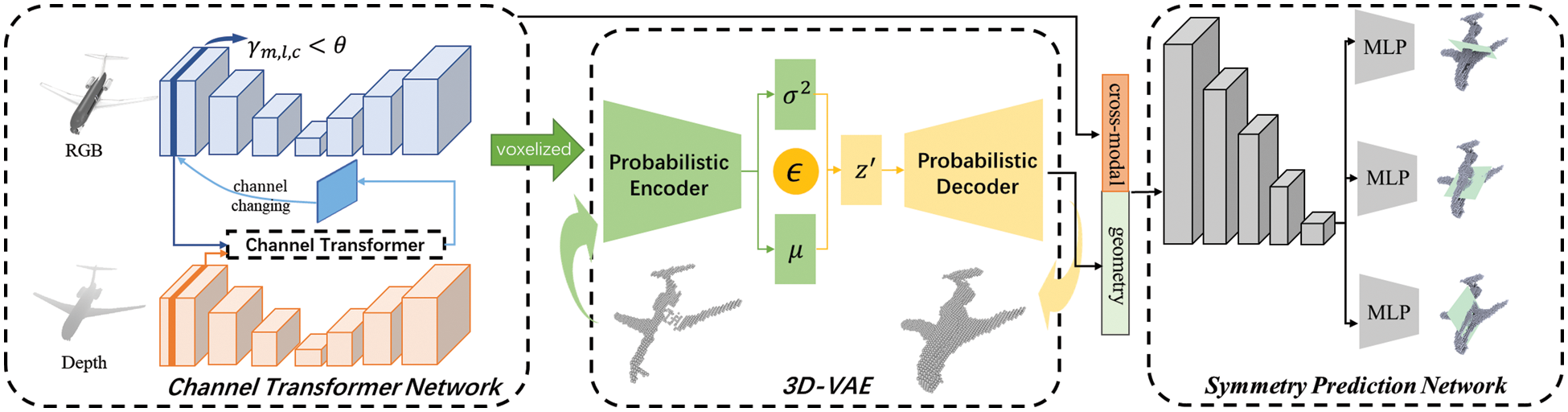
Figure 1: The architecture of our pipeline. At first, taking a RGB image and a depth image as input, cross-model features are extracted by the CTN and followed by the self-reconstruction network based on 3D-VAE. Then, aggregating the cross-features and enhanced geometric features to predict symmetry through the symmetry prediction network

2  Related Work

2.1 Multimodal Fusion

Multimodal fusion can take advantage of data obtained from different sources/structures for classification or regression, so it becomes a central problem in machine learning [6]. A variety of works have been done towards deep multimodal fusion [7]. A simpler way is to use the aggregation-based method, which employs a certain operation (e.g., averaging [8], concatenation [9,10], and self-attention [11]) to combine multimodal sub-networks into a single network. Or use alignment-based fusion [12,13], which adopts a regulation loss to align the embedding of all sub-networks while keeping full propagation for each of them. But the aggregation-based fusion is prone to underestimating the intra-modal propagation once the multimodal sub-networks have been aggregated. And the alignment-based fusion always delivers ineffective inter-modal fusion owing to the weak message exchanging by solely training the alignment loss. To balance the two methods, [14] proposed a channel exchanging method which is parameter-free and could dynamically exchange channels between sub-networks of different modalities. But by judging the parameter of BN layer approaches zero or not to exchange the channel directly would lead to no information attention between the corresponding channels, which may result in information faulting. So, our method opts to optimize the feature handling process, which includes attention mechanism between the corresponding channels.

2.2 Learning-based Symmetry Detection

In pattern recognition and computer vision literature, there exists a significant number of papers dedicated to finding symmetries in images [15], two-dimensional [16–18], and three-dimensional shapes [19–21]. For symmetry detection of 3D shapes, we usually use the Euclidean distance between points to measure the symmetry of a shape, and the planar reflective symmetry is the most fundamental one. Early methods [22] used some entropy features to help find the reflective symmetry or create different metrics to detect intrinsic symmetry [23]. Most recently, deep learning has been adopted for the task of 3D symmetry detection. In [24] utilize structured random forests to detect curved reflectional symmetries. In [25] develop an unsupervised deep learning approach for effective real-time global planar reflective symmetry detection, which demonstrates excellent results. However, just like PRS-Net proposed by Gao et al. [25], most of the work is aimed at the symmetry detection of complete 3D shapes, and they are not applicable to incomplete 3D shapes. Up to now, the existing works for incomplete 3D shapes mainly focus on learning-based shape descriptors [26], which makes it difficult to detect symmetry directly if the shape is seriously missing (e.g., rendered RGB-D). Our network aims to utilize the generate model to reconstruct the global geometric features of incomplete 3D shapes as much as possible, which is helpful to detect symmetry.

3  Method

The symmetry of a 3D object is easily measurable when its shape is complete. Global geometric features take enough information for conventional symmetry detection pipelines to find the positive symmetry plane. However, shapes captured in real-world applications are often incomplete due to the limited sensor resolution, single viewpoint, and occlusion. So, we take a single RGB-D image as input, to predict the symmetry of the incomplete shape.

As shown in Fig. 1, our solution consists of three major components. 1) Given an RGB-D image, a channel transformer network (CTN) extracts cross-modal features by fusing information from the RGB image and the depth image. 2) A self-reconstruction network (3D-VAE) predicts the complete geometric shape based on voxelized cross-modal features. 3) A symmetry prediction network, taking the cross-modal features from the CTN and the enhanced geometric features from 3D-VAE as multi-features input.

3.1 Channel-Transformer Network for RGB-D Images

Traditional methods often treat an RGB-D image as a 4-channel feature, while literature [14] found that RGB and depth are two modal features, the RGB takes texture information, and the depth contributes contour information. So, aggregation-based methods [7,9,10] and alignment-based methods [12,13] process them separately, but internal feature communication is ignored.

Therefore, we set up two sub-networks to deal with RGB and depth respectively and propose Channel-Transformer Network (CTN) to achieve the internal feature communication. Instead of using aggregation, alignment, or channel-exchanging methods as before, CTN dynamically transforms the channels between sub-networks for fusion. Inspired by [14], we utilize the scaling factor (i.e., γ) of Batch-Normalization (BN) [27] as the importance measurement of each corresponding channel and use a transformer between the channels associated with close-to-zero factors of each modality. Such message transformer is self-adaptive, as it is dynamically controlled by the scaling factors that are determined by the training itself.

We conduct multi-modal fusion on RGB-D images corresponding to the same image content. In this scenario, all modalities are homogeneous in the sense that they are just different views of the same input. Thus, the parameters except BN layers of the CTN are shared with each other. By using private BNs, we can determine the channel importance for each individual modality, and by sharing convolutional filters, the corresponding channels among different modalities are embedded with the same mapping, which could yield promisingly expressive power.

Suppose we have the i-th input data of M (M = 2) modalities, x(i)={xm(i)∈RC×(H×W)}m=1M , where C denotes the number of channels, H and W denote the height and width of the feature map. We first process each modality with a 2D U-Net sub-network fm(x), which shares all parameters with each other including convolutional filters, except BN layers. The output of the sub-network is y.

ym=fm(xm){m=rgb,whentheinputisRGBm=d,whentheinputisdepth (1)

Prior to introducing the channel transformer process, we first review the BN layer [27], which is used widely in deep learning to eliminate covariate shift and improve generalization. We denote by xm,l the l-th layer feature maps of the m-th sub-network, and by xm,l,c the c-th channel. The BN layer performs a normalization of xm,l followed by an affine transformation, namely,

xm,l,c′=γm,l,cxm,l,c−μm,l,cσm,l,c2+ε+βm,l,c (2)

μm,l,c and σm,l,c compute the mean and the standard deviation, respectively, of all activations over all pixel locations (H and W) for the current mini-batch data; γm,l,c and βm,l,c are the trainable scaling factor and offset, respectively; ε is a small constant to avoid divisions by zero. The (l + 1)-th layer takes {xm,l,c′}c as input after a non-linear function.

The factor γm,l,c in Eq. (2) evaluates the correlation between the input xm,l,c and the output xm,l,c′ during training. The gradient of the loss w.r.t. xm,l,c will approach 0 if γm,l,c → 0, implying that xm,l,c will lose its influence on the final prediction and become redundant thereby. In other words, once the current channel xm,l,c becomes redundant due to γm,l,c → 0 at a certain training step, it will almost do henceforth.

Thus, we pick out the channels of small scaling factors and the corresponding ones of other sub-networks, which are fed into the CTN, and then we replace the channels with the features from the CTN. The CTN is presented in Fig. 2. To be specific, it contains three cross-attention layers, each followed by two AddNorm layers and one feed-forward layer [11,28]. Suppose X = xm,l,c and the corresponding channel of another sub-network is Y=xm′,l,c . The cross-attention layer of CTN is:

S=crossAttention(Q,K,V)=Softmax(QKT)V (3)

where Q = XWQ, K = YWK, V = YWV are the query vector, the key vector, and the value vector respectively. WQ, WK, WV are the learned weights. The AddNorm layer is:

Z=AddNorm(X)=LayerNorm(X+S) (4)

where LayerNorm(⋅) is the layer normalization operation. The output of CTN is the attention-aware denoised feature Z=xm,l,c′ .

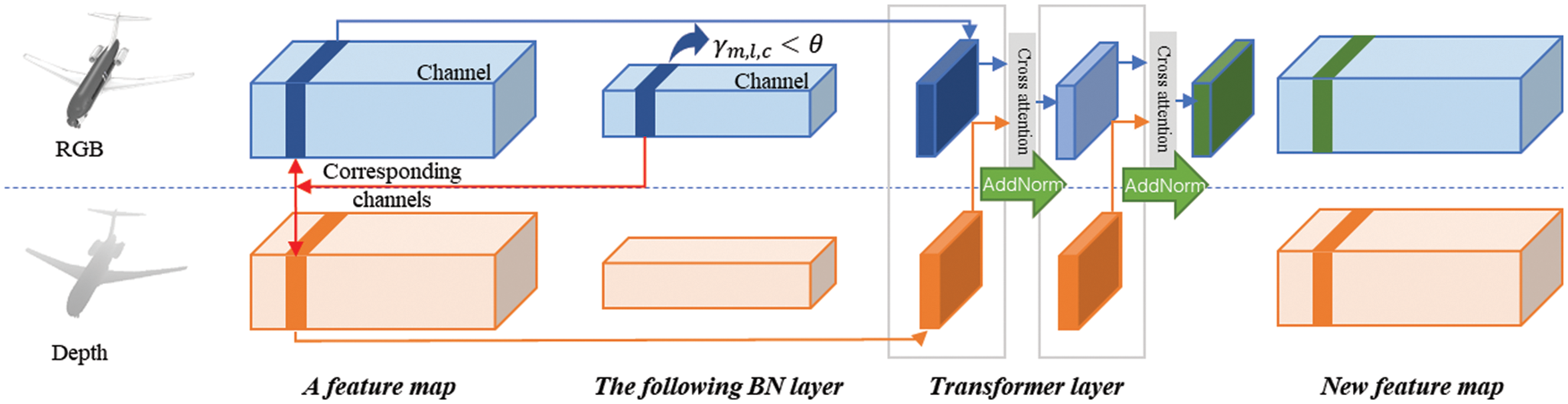
Figure 2: The framework of the CTN. If a channel in a BN layer has a small scaling factor (γm,l,c < θ), the corresponding channels in the feature map before the BN layer would be picked out from all sub-networks (as the red line shows in the figure). Then feed the features in these channels into the CTN to get new features

Thus,

xm,l,c′={γm,l,cxm,l,c−μm,l,cσm,l,c2+ε+βm,l,c,ifγm,l,c>θCTN(xm,l,c,xm′,l,c),else (5)

In a nutshell, if one channel of one modality has little impact on the final prediction, then we replace it with a new channel from the transformer network. We apply Eq. (5) for each modality before feeding them into the nonlinear activation followed by the convolutions in the next layer.

It is known in [29,30] that leveraging private BN layers is able to characterize the traits of different domains or modalities. In our method, specifically, different scaling factors (Eq. (2)) evaluate the importance of the channels of different modalities, and they should be decoupled. Except for BN layers, all sub-networks fm share all parameters with each other including convolutional filters.

Then we combine all the outputs via an aggregation operation followed by a global mapping. In formal, it computes the output by

y=f(x)=h(Agg(frgb(xrgb),fd(xd))) (6)

where h is the global network and Agg is the aggregation function. The aggregation can be implemented as averaging [4], concatenation [5,10], and self-attention [11], and we use concatenation here simply. To the end, we voxelized the point clouds together with their color features xrgb and depth features xd from CTN.

3.2 Voxel-Based 3D Variational Autoencoders

Due to partial observations, methods for symmetry prediction of complete shapes do not work anymore. Because missing global geometric information leads to crucial difficulty to find local symmetry correspondences which are supported by mirror transformation. In this situation, we use a generative network 3D Variable Autoencoders (3D-VAE) to reconstruct the complete 3D shape from an incomplete one, which provides enhanced geometric features for the following symmetry prediction network.

We take the cross-modal features from the CTN as input and reconstruct the corresponding complete shape, including more enhanced geometric features than the initial geometric features only from depth. As shown in Fig. 3, the 3D-VAE network consists of an encoder network, a latent layer, and a decoder network. We use an approximate 3D U-Net architecture to define the encoder and decoder network, except for the latent layer. Different from many other works [31,32], we design the latent layer as a 3D network to preserve global geometric features as much as possible. We encode the cross-modal features into an implicit space, which obeys the normal distribution (here we regress two parameters μ(i) and σ(i) to define the normal distribution), and then sample from the implicit space to reconstruct through the decoder network.

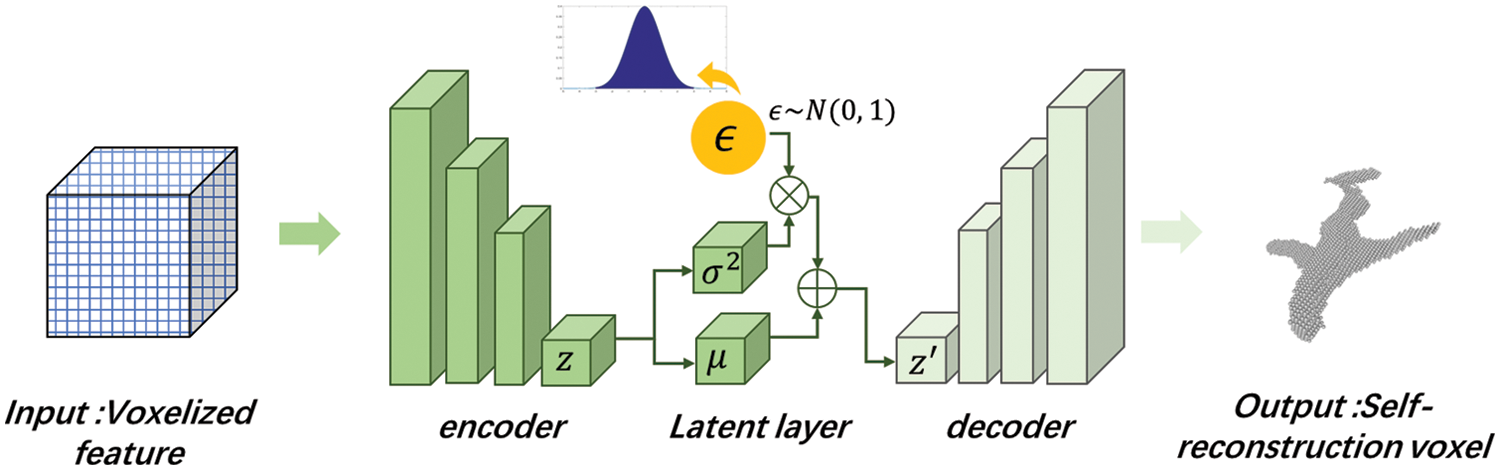
Figure 3: The 3D variational autoencoders

We use a 3D down-sampling network for the probabilistic encoder q∅(z|x) ((the approximation to the posterior of the generative model pθ(x,z) ) and where the parameters ∅ and θ are optimized jointly with the VAE algorithm.

Let the prior over the latent variables be the centered isotropic multivariate Gaussian pθ(z)=N(z;0,I) . We let q∅(z|xi) be a multivariate Gaussian (in case of real-valued data) or Bernoulli (in case of binary data) whose distribution parameters are computed from z with a 3D network (another 3D layer following the encoder network). In this case, we can let the variational approximate posterior be a multivariate Gaussian with a diagonal covariance structure:

logq∅(z|x)=logN(z;μ,σ2I) (7)

where the mean and standard deviation of the approximate posterior, μ and σ , are outputs of the last 3D layer following the encoder network, which consists of three 3D convolutional layers to the latent layer.

Then, we introduce the latent layer. All the outputs here are 3D matrices with one channel. We sample from the posterior z′∼q∅(z|x) using z′=μ+σ⊙ε where ε∼N(0,I) . With ⊙ we signify an element-wise product, and the z′ is the input of decoder network.

In this case, the KL divergence can be computed and differentiated:

Lμ,σ2=12∑i=1d⁡(μ(i)2+σ(i)2−logσ(i)2−1) (8)

The decoder network is a 3D up-sampling network for reconstruction, which has an identical, but inverted, architecture, and its weights are not tied to the encoders. The output of the decoder network is the result of the reconstruction, for which we use a specialized form of Binary Cross-Entropy (BCE). The standard BCE loss is:

Lrec=−tlog(o)−(1−t)log(1−o) (9)

where t is the target value in {0, 1} and o is the output of the network in {0, 1}at each output element. The derivative of the BCE with respect to o severely diminishes as o approaches t, which can result in vanishing gradients during training. Additionally, the standard BCE weights false positives and false negatives equally; because over 95% of the voxel grid in the training data is empty, the network can confidently plunge into a local optimum of the standard BCE by outputting all negatives:

Lrec=−γtlog(o)−(1−γ)(1−t)log(1−o) (10)

During training, we set γ to 0.95, strongly penalizing false negatives while reducing the penalty for false positives. Setting too high results in noisy reconstructions, while setting too low results in reconstructions which neglect salient object details and structure. Thus, the loss of the 3D VAE network is defined as

L=Lrec+wLμ,σ2 (11)

where w is the weight for balancing the reconstruction loss and the KL divergence.

It should be noted that the output of each element of the final layer can be interpreted as the predicted probability that a voxel is present at a given location. Down-sampling in the encoder network is accomplished via stridden convolutions (as opposed to pooling) in every second layer. Up-sampling in the decoder network is accomplished via fractionally stridden convolutions, in every second layer.

The network is initialized with Glorot Initialization [33], and all the output layers are Batch Normalized [27]. The variance and mean parameters of the latent layer are individually Batch Normalized, such that the output of the latent layer during training is still stochastic under the VAE parameterization trick.

3.3 Multi-feature for Symmetry Prediction Network

In this section, we propose the symmetry prediction network by combining the cross-modal features from CTN and geometric features from 3D-VAE. The overall network is presented in Fig. 4.

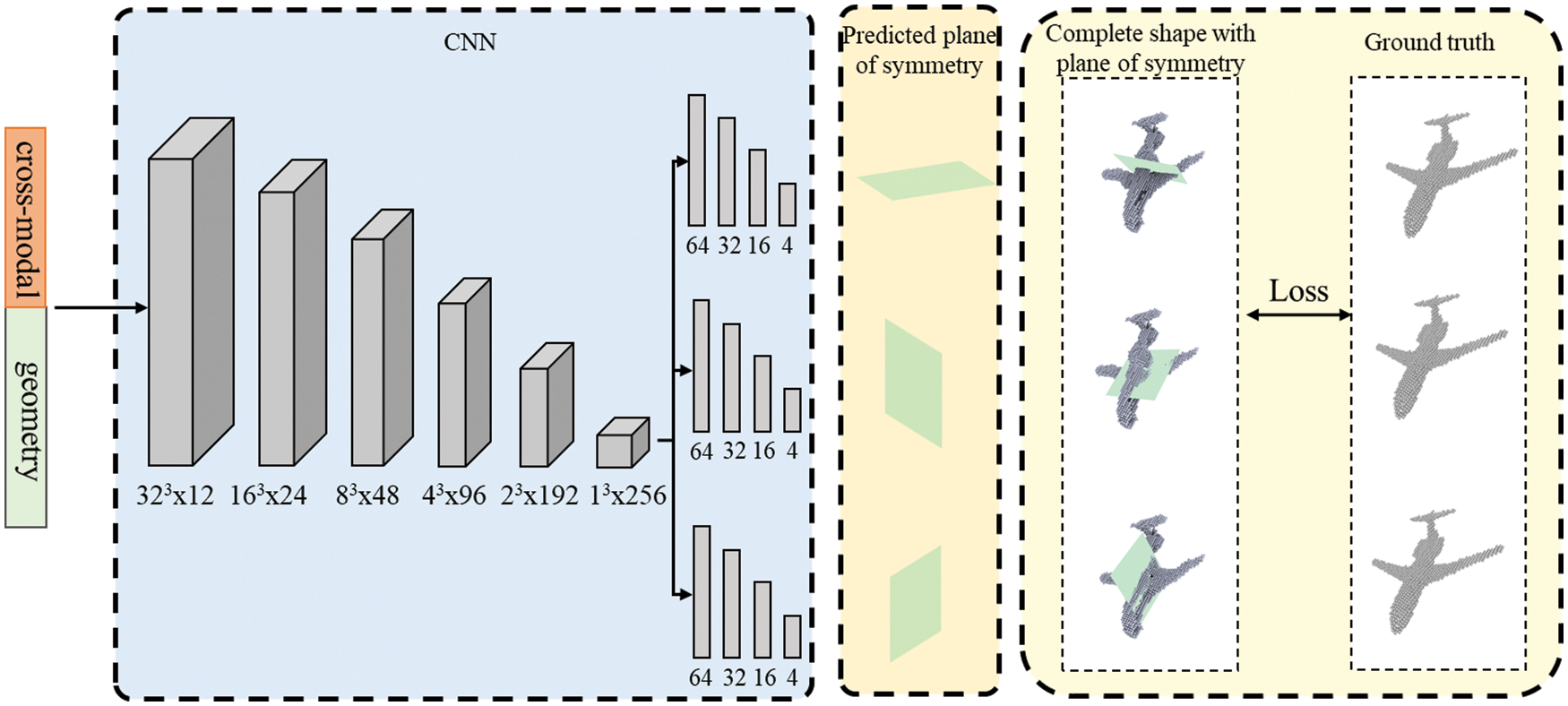
Figure 4: The architecture of the symmetry prediction network

Thanks to the 3D-VAE, we have a relatively complete shape and contain stronger geometric features than the initial depth, which gives us an opportunity to learn from some symmetry detection methods [34,35] that have been proved to be effective. Inspired by PRS-Net [25], we define a Convolutional Neural Network(CNN) to predict a fixed number (three in practice) of symmetry planes, which may not all be valid. Duplicated or invalid symmetry planes are removed in the validation stage.

From the above section, we get a variety of features, containing cross-modal features from the CTN, as well as enhanced geometric features from the 3D VAE. How do we aggregate these features to predict symmetry? A simple way is to directly use the self-reconstruction result from the 3D VAE, which is close to the complete shape. This has proved to be a valuable method, which can transform the symmetry detection of incomplete shape into the symmetry detection of complete shape, by providing global geometric features for the network. However, there are two problems. One is that the result of the VAE is only relatively complete, not absolutely complete, and it is inevitable to lose lots of detailed information through the multi-layer network and random sampling; Second, we do not make full use of the additional information we already have, such as color features and fine depth features from RGB-D, the former has rich texture information, while the latter contains a lot of contour details. Although there is only one view, it has been effectively extracted through the CTN.

Thus, we put these existing features into the corresponding voxel according to their respective characteristics as the final features of the voxel. Suppose that the cross-modal feature is Fc, coming from the CTN and are high-dimensional. The geometric features from 3D VAE are 0–1 feature, which is used to judge whether the voxel is or not the surface. Considering the dimensional consistency, we take the features of the previous layer of the last layer of VAE as the geometric features, Fg.

FA=concat(Fc,Fg) (12)

Then, we feed FA into the symmetry prediction network, which has six 3D convolution layers of kernel size 3, padding 1, and stride 1. After each 3D convolution, a max-pooling of kernel size 2 and leaky ReLU [36] activation is applied. These are followed by fully connected layers to predict the parameters of symmetry planes.

4  Results and Applications

4.1 Experimental Datasets

Our experiments are conducted on three public datasets: ShapeNet [37], YCB [38], ScanNet [39].

ShapeNet: We use the train set that contains 100000 training RGB-D images and split the test set into two subsets: holdout view and holdout instance.

YCB: We follow the original train/test split established in [38].

ScanNet: We use the train set that contain 13126 training RGB-D images and split the test set into two subsets: holdout view and holdout scene, we only test on holdout view.

4.2 Evaluation Metric

In order to determine whether a predicted symmetry is a true positive or a false positive, we compute a dense symmetry error from the difference between the predicted symmetry and the ground-truth symmetry. For a reflectional symmetry, we compute the dense symmetry error as:

εref=1N∑iN‖Tref(Pi)−T^ref(Pi)‖2ρ (13)

where Tref and T^ref are the symmetric transformation of the predicted symmetry and the ground-truth symmetry of a complete shape with points P = {Pi}, i[1, N] and ρ is the max distance from the points in P to the symmetric plane of T^ref .for rotational symmetry, we compute the dense symmetry error as:

εrot=1|Γ|1N∑γϵΓ⁡∑iN‖Trot,γ(Pi)−T^rot,γ(Pi)‖2ρ (14)

where Trot,γ is the rotational transformation of the predicted symmetry with a rotation angle of γ. The set of rotation angles is Γ = {κ ⋅ π/8}κ=1, …, 16, and ρ is the max distance from the points in P to the rotational axis of T^rot . We set the dense symmetry error threshold to be 0.25 for both reflectional and rotational symmetries.

4.3 Ablation Studies for Symmetry Prediction

To study the importance of each component of our method, we compare our full method against two variants. A specific part of the pipeline is taken out for each variant, as follows:

No 3D-VAE: Without the reconstruction part in our method, we predict symmetry only from the incomplete shape, which lacks a lot of geometric information.

No feature fusion for symmetry prediction: Without the aggregation of color features, depth features and geometric features, we use the result of 3D VAE to predict symmetry directly.

Fig. 5 shows the results of our ablation study, for reflectional symmetry detection. The full method outperforms the simpler variants in all cases. It can be seen that the self-reconstruction part (3D VAE) is crucial to our method, perhaps because it provides more geometric information for symmetry detection. In addition, by observing the results of using only geometric features and fusion features (color, depth, geometry), we can see that in most cases, more features are helpful to the final symmetry prediction, but not much, which indicates that the global geometric features are more important for symmetry detection.

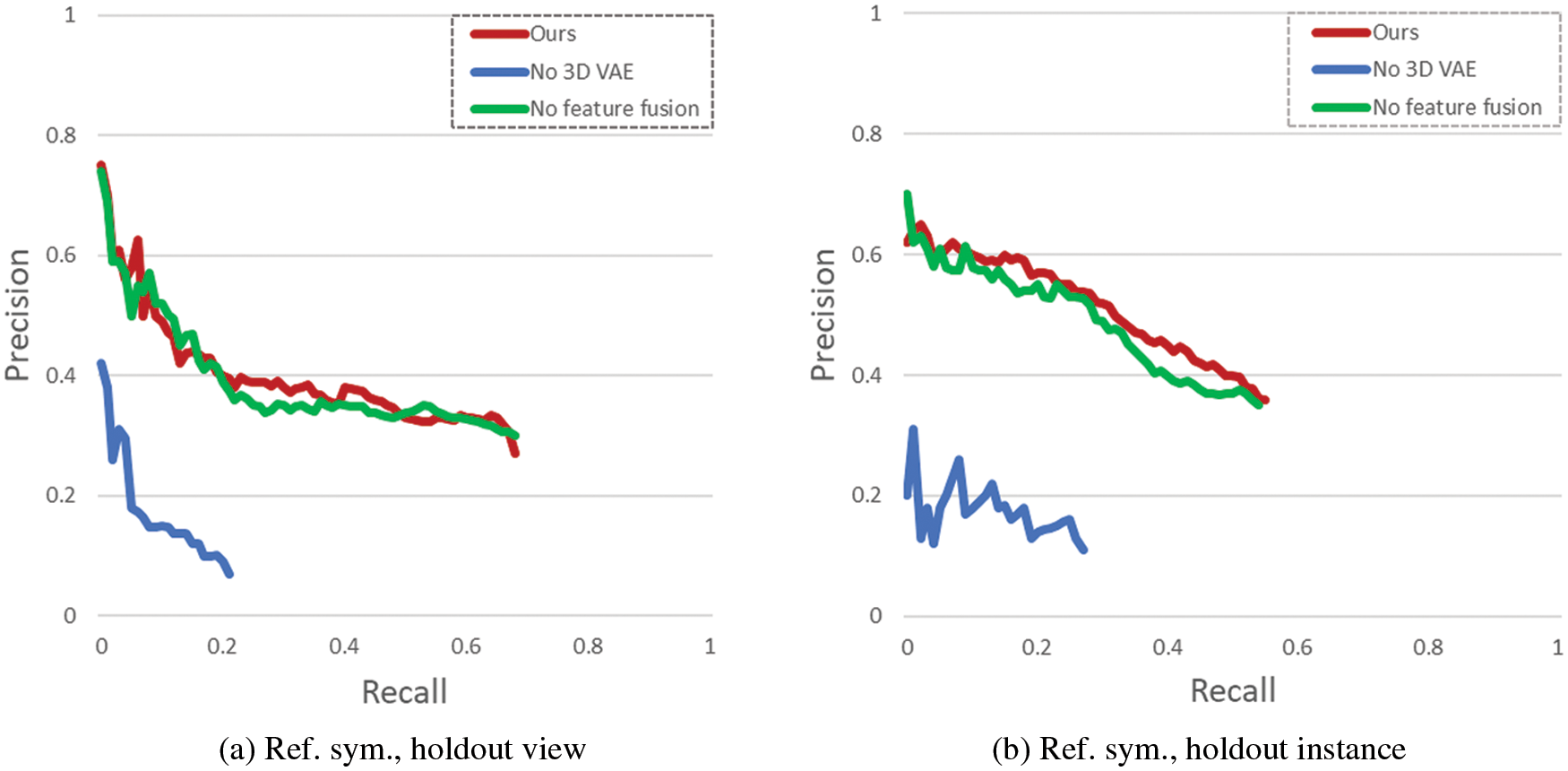
Figure 5: Ablation studies: comparison of symmetry prediction performance on two subsets of ShapeNet between our full proposed method (red) and its several variants (blue: without 3D VAE; green: without feature fusion)

4.4 Ablation Studies for Self-Reconstruction

To study the importance of the CTN to the 3D VAE, we compare our self-reconstruction results without some specific component: w/o independent network for color and depth, w/o channel transformer, w/o 3D latent layer. Without dependent networks for color and depth, we simply use a 3D U-Net to extract the RGB-D feature.

Tab. 1 shows the self-reconstruction accuracy of these ablation studies. It is worth noting that independent networks are very useful for feature extraction. Maybe it’s because color and depth are essentially different modal features. The former provides more detailed information, and the latter provides more contour information. If they are treated together, it may cause a waste of information. By analyzing the data in Tab. 1, we can see that the 3D CNN in the latent layer also makes some contribution to the final accuracy, which shows that the global information is also useful when fitting the two parameters of mean and variance.

4.5 Comparison to Baselines

We refer to the RGB-D Retrieval [40] and Geometric Fitting [41], to compare with our method. The comparisons are plotted in Fig. 6. It is obvious that our method achieves the best score over all the data subsets.

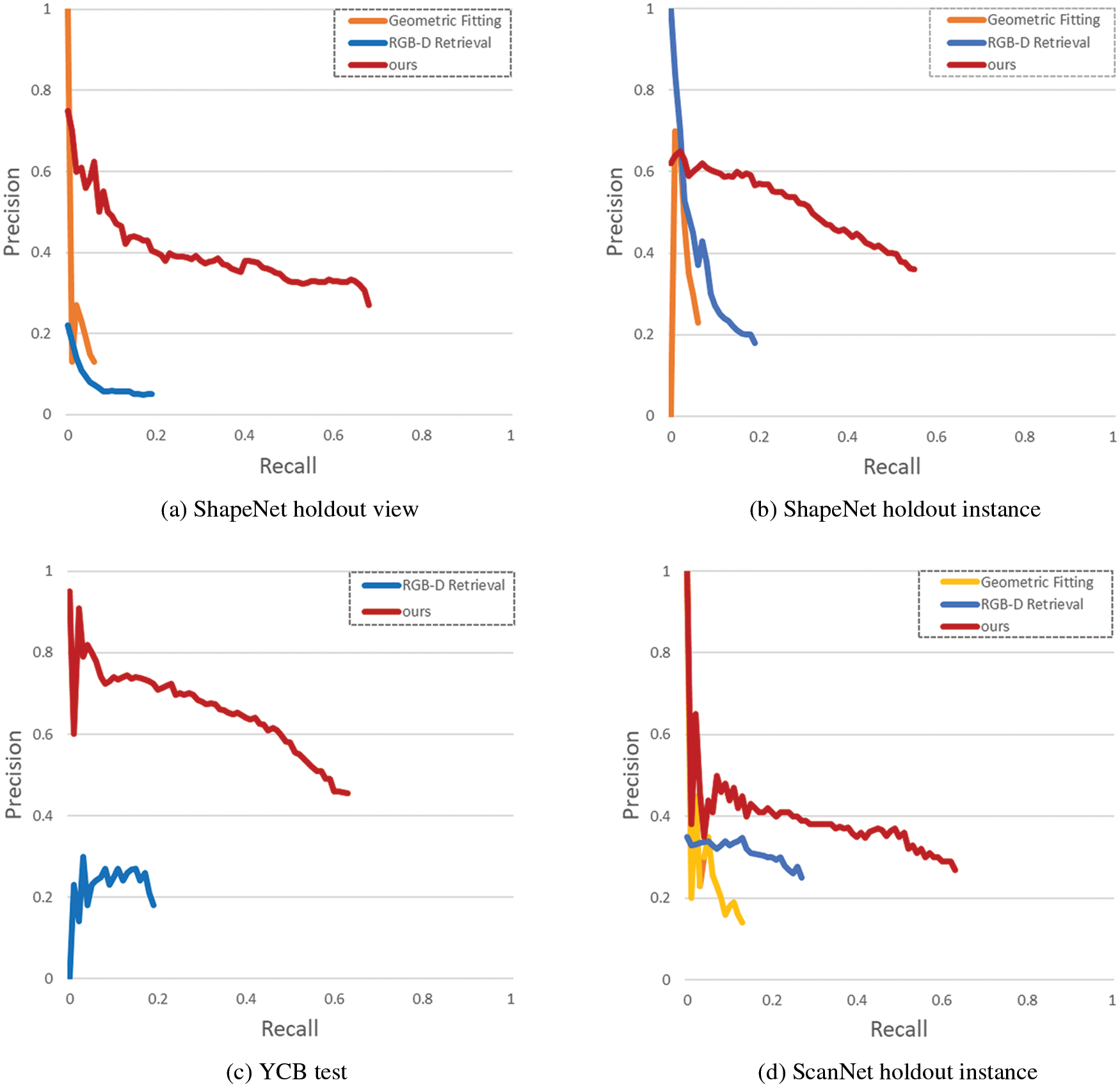
Figure 6: Comparisons with baselines on the performance of predicting reflectional symmetry

5  Conclusion

We have presented the robust symmetry prediction method, which benefits from global geometric features reconstructed from single RGB-D images. A channel-transformer network is designed to aggregate features from the color and the depth separately, which essentially helps feature fetching. The 3D-VAE network demonstrates a significant performance boost for global geometric features recovery. A limitation to our method is that we have not considered the rotational symmetry, which is also universal. An interesting future direction is to further utilize the detection-by-reconstruction module to help single view reconstruction target, which would help to preserve more geometry information through symmetry reflection, rather than deep learning networks.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  M. Kazhdan, T. Funkhouser and S. Rusinkiewicz, “Symmetry descriptors and 3D shape matching.” In Proceedings of the Symposium on Geometry Processing, pp. 115–123, 2004. [Google Scholar]

 2.  J. Podolak, P. Shilane, A. Golovinskiy, S. Rusinkiewicz and T. Funkhouser, “A planar-reflective symmetry transform for 3D shapes,” ACM Transactions on Graphics, vol. 25, no. 3, pp. 549–559, 2006. [Google Scholar]

 3.  P. Simari, E. Kalogerakis and K. Singh, “Folding meshes: Hierarchical mesh segmentation based on planar symmetry,” Symposium on Geometry Processing, vol. 256, pp. 111–119, 2006. [Google Scholar]

 4.  D. Lee, T. Kim, Y. Choi and M. Hong, “Volumetric object modeling using internal shape preserving constraint in unity 3D,” Intelligent Automation & Soft Computing, vol. 32, no. 3, pp. 1541–1556, 2022. [Google Scholar]

 5.  N. Lutsiv, T. Maksymyuk, M. Beshley, O. Lavriv, V. Andrushchak et al., “Deep semisupervised learning-based network anomaly detection in heterogeneous information systems,” Computers, Materials & Continua, vol. 70, no. 1, pp. 413–431, 2022. [Google Scholar]

 6.  W. Mehmood, A. W. Khan, W. Aslam, S. Ahmad, A. M. El-Sherbeeny et al., “Requirement design for software configuration and system modeling,” Intelligent Automation & Soft Computing, vol. 32, no. 1, pp. 441–454, 2022. [Google Scholar]

 7.  D. Ramachandram and G. W. Taylor, “Deep multimodal learning: A survey on recent advances and trends,” IEEE Signal Processing Magazine, vol. 34, no. 6, pp. 96–108, 2017. [Google Scholar]

 8.  C. Hazirbas, L. N. Ma, C. Domokos and D. Cremers, “FuseNet: Incorporating depth into semantic segmentation via fusion-based CNN architecture,” in Asian Conf. on Computer Vision, Asian Conference on Computer Vision (ACCVpp. 213–228, 2016. [Google Scholar]

 9.  J. Ngiam, A. Khosla, M. Kim, J. Nam, H. Lee et al., “Multimodal deep learning,” in Int. Conf. on Machine Learning, International Conference on Machine Learning, 2011. [Google Scholar]

10. J. Zeng, Y. Tong, Y. Huang, Q. Yan, W. X. Sun et al., “Deep surface normal estimationwith hierarchical RGB-D fusion,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 6153–6162, 2019. [Google Scholar]

11. S. Zhao, M. Hu, Z. Cai, Z. Zhang, T. Zhou et al., “Enhancing Chinese character representation with lattice-aligned attention,” IEEE Transactions on Neural Networks and Learning Systems, pp. 1–10, 2021. https://doi.org/10.1109/TNNLS.2021.3114378. [Google Scholar]

12. Y. H. Cheng, R. Cai, Z. W. Li, X. Zhao and K. Q. Huang, “Locality-sensitive deconvolution networks with gated fusion for RGB-D indoor semantic segmentation,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 3029–3037, 2017. [Google Scholar]

13. S. J. Song, J. Y. Liu, Y. H. Li and Z. M. Guo, “Modality compensation network: Cross-modal adaptation for action recognition,” IEEE Transactions on Image Processing, vol. 29, pp. 3957–3969, 2020. [Google Scholar]

14. Y. K. Wang, W. B. Huang, F. C. Sun, T. Y. Xu, Y. Rong et al., “Deep multimodal fusion by channel exchanging,” Neural Information Processing Systems, vol. 33, pp. 4835–4845, 2020. [Google Scholar]

15. G. Marola, “On the detection of axes of symmetry of symmetric and almost symmetric planner images,” Pattern Analysis and Machine Intelligence, vol. 11, no. 1, pp. 239–245, 1989. [Google Scholar]

16. J. Wolter, T. Woo and R. Volz, “Optimal algorithms for symmetry detection in two and three dimensions,” The Visual Computer, vol. 1, pp. 37–48, 1985. [Google Scholar]

17. M. J. Atallah, “On symmetry detection,” IEEE Transactions on Computers, vol. 34, no. 7, pp. 663–666, 1984. [Google Scholar]

18. H. Alt, K. Mehlhorn, H. Wagener and E. Welzl, “Congruence, similarity, and symmetries of geometric objects,” Discrete Comput. Geom, vol. 3, pp. 237–256, 1988. [Google Scholar]

19. C. Sun and J. Sherrah, “3D symmetry detection using the extended Gaussian image,” Pattern Analysis and Machine Intelligence, vol. 19, no. 2, pp. 164–168, 1997. [Google Scholar]

20. M. Kazhdan, B. Chazelle, D. Dobkin, T. Funkhouser and S. Rusinkiewicz, “A reflective symmetry descriptor for 3D models,” Algorithmica, vol. 38, no. 1, pp. 201–225, 2003. [Google Scholar]

21. N. J. Mitra, L. J. Guibas and M. Pauly, “Partial and approximate symmetry detection for 3D geometry,” in Special Interest Group on GRAPHics and Interactive Techniques, ACM Trans. on Graphics (Proc. SIGGRAPHvol. 25, no. 3, pp. 560–568, 2006. [Google Scholar]

22. B. Li, H. Johan, Y. Ye and Y. Lu, “Efficient 3D reflection symmetry detection: A view-based approach,” Graphical Models, vol. 83, pp. 2–14, 2016. [Google Scholar]

23. M. Ovsjanikov, J. Sun and L. Guibas, “Global intrinsic symmetries of shapes,” Computer Graphics Forum, vol. 27, no. 5, pp. 1341–1348, 2008. [Google Scholar]

24. C. L. Teo, C. Fermuller and Y. Aloimonos, “Detection and segmentation of 2D curved reflection symmetric structures,” in Proceedings of the IEEE International Conference on Computer Vision, pp. 1644–1652, 2015. [Google Scholar]

25. L. Gao, L. X. Zhang, H. Y. Meng, Y. H. Ren, Y. K. Lai et al., “PRS-net: Planar reflective symmetry detection net for 3D models,” IEEE Transactions on Visualization and Computer Graphics, vol. 27, no. 6, pp. 3007–3018, 2020. [Google Scholar]

26. H. B. Huang, E. Kalogerakis, S. Chaudhuri, D. Ceylan, V. G. Kim et al., “Learning local shape descriptors from part correspondences with multiview convolutional networks,” ACM Transactions on Graphics, vol. 37, no. 1, pp. 1–14, 2017. [Google Scholar]

27. S. Ioffe and C. Szegedy, “Batch normalization: Accelerating deep network training by reducing internal covariate shift,” in Int. Conf. on Machine Learning, International Conference on Machine Learning, pp. 448–456, 2015. [Google Scholar]

28. S. Zhao, M. Hu, Z. Cai and F. Liu, “Dynamic modeling cross-modal interactions in two-phase prediction for entity-relation extraction,” IEEE Transactions on Neural Networks and Learning Systems, 2021. pp. 1–10, 2021. https://doi.org/10.1109/TNNLS.2021.3104971. [Google Scholar]

29. W. G. Chang, T. You, S. Seo, S. Kwak and B. Han, “Domain-Specific Batch Normalization for Unsupervised Domain Adaptation,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 7354–7362, 2019. [Google Scholar]

30. Y. K. Wang, F. C. Sun, M. Lu and A. B. Yao, “Learning deep multimodal feature representation with asymmetric multi-layer fusion,” in Proceedings of the 28th ACM International Conference on Multimedia, pp. 3902–3910, 2020. [Google Scholar]

31. A. S. Almasoud, T. Abdalla, F. N. Al-Wesabi, A. Elsafi, M. A. Duhayyim et al., “Parkinson’s detection using RNN-graph-LSTM with optimization based on speech signals,” Computers, Materials & Continua, vol. 72, no. 1, pp. 871–886, 2022. [Google Scholar]

32. X. R. Zhang, X. Chen, W. Sun and X. Z. He, “Vehicle re-identification model based on optimized densenet121 with joint loss,” Computers, Materials & Continua, vol. 67, no. 3, pp. 3933–3948, 2021. [Google Scholar]

33. X. Glorot and Y. Bengio, “Understanding the difficulty of training deep feedforward neural networks,” in International Conference on Artificial Intelligence and Statistics, vol. 9, pp. 249–256, 2010. [Google Scholar]

34. C. Funk and Y. Liu, “Beyond planar symmetry: Modeling human perception of reflection and rotation symmetries in the wild,” in Proceedings of the IEEE International Conference on Computer Vision, pp. 793–803, 2017. [Google Scholar]

35. R. K. Vasudevan, O. Dyck, M. Ziatdinov, S. Jesse, N. Laanait et al., “Deep convolutional neural networks for symmetry detection,” Microscopy and Microanalysis, vol. 24, no. S1, pp. 112–113, 2018. [Google Scholar]

36. A. L. Maas, A. Y. Hannun and A. Y. Ng, “Rectifier nonlinearities improve neural network acoustic models,” International Conference on Machine Learning, vol. 30, no. 1, pp. 3–8, 2013. [Google Scholar]

37. A. X. Chang, T. Funkhouser, L. Guibas, P. Hanrahan, Q. X. Huang et al., “Shapenet: An information-rich 3D model repository,” arXiv preprint arXiv:1512.03012, 2015. [Google Scholar]

38. B. Calli, A. Singh, A. Walsman, S. Srinivasa, P. Abbeel et al., “The ycb object and model set: Towards common benchmarks for manipulation research,” in Indian Council of Agricultural Research, in International Conference on Advanced Robotics, pp. 510–517, 2015. [Google Scholar]

39. A. Dai, A. X. Chang, M. Savva, M. Halber, T. Funkhouser et al., “Scannet: Richly-annotated 3D reconstructions of indoor scenes,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 5828–5839, 2017. [Google Scholar]

40. A. Ecins, C. Fermüller and Y. Aloimonos, “Seeing behind the scene: Using symmetry to reason about objects in cluttered environments,” in 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems, pp. 7193–7200, 2018. [Google Scholar]

41. Y. Q. Yang, C. Feng, Y. R. Shen and D. Tian, “Foldingnet: Point cloud autoencoder via deep grid deformation,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 206–215, 2018. [Google Scholar]