An Optimal Algorithm for Secure Transactions in Bitcoin Based on Blockchain

1  Introduction

Since Satoshi Nakamoto proposed Bitcoin, a new decentralized digital currency based on blockchain technology in 2008 [1], and electronic cash technology has entered a new chapter of development [2]. The traditional electronic cash started in 1983. Blind and untraceable E-cash proposed by [3] is represented. Users realize transaction interaction through trusted central institutions, and use blind signature technology to protect user privacy. However, in the Bitcoin blockchain system, the public ledger reveals each transaction. All details from block reward transaction (coinbase transaction) to unspent transaction output (UTXO). As legal proof of user assets, blockchain ledger includes input transaction signature, denomination and output transaction address of each historical transaction, and the output transaction address can be regarded as the user identity of the Bitcoin system [4]. Research shows that the anonymity of electronic cash needs to achieve pseudonymity and unlinkability [5]. The Bit output transaction address of the Coin blockchain ledger is the Base58Check encoded string of the signature public key that has undergone a certain hash transformation, which has a certain degree of pseudonymity. However, because the transaction relationship is explicitly expressed in the blockchain, there is no difference between users. Therefore, the Bitcoin system is not anonymous and easily leaks user privacy [6].

A common attack method for user privacy in the Bitcoin system is de-anonymous attack [7–10], which includes three steps [11]. 1) generating a transaction graph according to the blockchain ledger; 2) converting the transaction graph according to the transaction content is an address graph; 3) the address graph is transformed into a user entity graph according to transaction habits in the sense of social engineering. These transaction habits include overlapping transaction inputs mean that multiple input transaction addresses are controlled by the same user entity and the only newly generated output address is likely to be a change address controlled by the user of the input transaction.

It should be pointed out that the anonymity discussed in this article only involves the protocol level of the blockchain ledger, and the de-anonymization attack against peer-to-peer (P2P) networks is not within the scope of this article. The privacy protection improvement measures of the chain ledger digital currency protocol layer include three aspects:

1)   Mixing. In order to break the interconnected relationship between transactions, reference [12] proposed the idea of CoinJoin in 2013. That is, several users execute the corresponding protocol and output the transaction of equal amount of Bitcoin to the newly generated address to confuse the connection relationship. There are many improvements and variants of the mixed currency protocol based on this idea [13–23]. Although, such research results break the connection between transaction entities, they only protect the privacy of user identity, and the mixed currency transaction amount is still exposed.

2)   Altcoins. Since the Bitcoin system is not perfect in many aspects such as privacy, transaction speed, scalability, etc., the altcoins based on blockchain technology have also received extensive attention from scholars, mainly including Monero Coin [24], ZeroCoin [25] and ZeroCash [26]. However, these alternative coins also have their own shortcomings. The basic idea of Monero is to confuse several transactions currently to be executed on the entire network at the same time, and the essence still draws on CoinJoin. However, the Monero analysis attack [27,28] shows that the design of non-mandatory currency mixing is not enough to force users to actively ensure transaction anonymity sets, and the proliferation effect of transactions with weak anonymity sets and even non-anonymous transactions will greatly weakened the overall anonymity of the system. The Monero cannot protect the privacy of the transaction amount without using RingCT. The ZeroCoin only protects the payer’s privacy and ZeroCash extends the content of privacy protection to the payer based on the payment amount and the payee to realize a fully anonymous blockchain system, but the efficiency of this scheme is low.

3)   Confidential transaction (CT). Maxwell first proposed the idea of encrypted transaction based on Pedersen commitment in 2015 [29]. The miners can use commitment homomorphism to affect the transaction value under the premise that the specific transaction amount is unknown. The sum of the input and output is verified. After that, the idea has been continuously improved and supplemented [30,31]. However, Pedersen promises that there is no “open commitment” operation in standard encrypted transactions and the payee still needs an additional communication channel to negotiate the transaction amount. The Dumb account scheme [32] uses non-interactive zero knowledge (NIZK) proof technology to verify the legitimacy of Paillier-based homomorphic ciphertext transactions, which conforms to the concept of CT and can directly decrypt ciphertext. If the text and public key are too long, the transaction efficiency will be extremely low. None of the above amount encryption schemes improve the unconnectivity of input and output, and still expose user privacy. Reference [33] combined the concepts of CT and CoinJoin in 2018, proposed a distributed ValueShuffle protocol that hides the transaction amount, which also cannot resist analysis attacks because there is no mandatory currency mixing requirement.

To sum up, this paper studies a fully anonymous blockchain scheme that realizes the privacy protection of the identity of the payee and the payment and the encryption of the transaction amount. It is systematically forced to embed the mixing operation into the whole block, which is resistant and consider the length of the ciphertext in the construction process of the scheme to avoid introducing too much transaction storage overhead and resulting in too few transactions in a single block.

This paper combines the ideas of currency mixing and encrypted transactions to realize a fully anonymous blockchain that protects the privacy of the payer, the payment amount and the payee. This paper uses the BGN06 encryption scheme [34]. Therefore, the year of the updated manuscript is used to refer to this scheme, that is, the BGN06 encryption scheme. The Pedersen-like promises homomorphism for transactions amount verification, and the transaction payee can directly decrypt the ciphertext without additional communication, which reduces the length of the ciphertext by half compared to the Dumb Account scheme. It uses the new NIZK proof technology BulletProof [35] to verify the positive range of the transaction amount, improving the original interval proof scheme using Borromean ring signature in CT implementation and MimbleWimble. Using the BGL03 one-way aggregated signature (OWAS) [36] and mixing technology to protect the user identity privacy, by deleting independent transactions public key of the signature and encryption scheme is used to increase the number of transactions stored in the block. In this scheme, miners are responsible for transaction verification, transaction packaging and transaction confusion, which conforms to the division of labor of the miner entity in the original blockchain system. The mixing scheme is embedded in the whole area block category can increase the size of the anonymity set and resist the analysis attacks. The Pedersen-like promises homomorphism for transactions amount verification, and the transaction payee can directly decrypt the ciphertext without additional communication, which reduces the length of the ciphertext by half compared to the Dumb Account scheme. It uses the new NIZK proof technology BulletProof to verify the positive range of the transaction amount, improving the original interval proof scheme using Borromean ring signature in CT implementation and MimbleWimbl. Using BGL03 one-way aggregated signature OWAS and mixing technology to protect the user identity privacy. By deleting independent transactions, the public key of the signature and encryption scheme is used to increase the number of transactions stored in the block. In this scheme, miners are responsible for transaction verification, packaging and confusion, which conforms to the division of labor of the miner entity in the original blockchain system. The mixing scheme is embedded in the whole area block category can increase the size of the anonymity set and resist analysis attacks.

There are five main contributions of this paper:

1)   In the original blockchain system, miners are responsible for verifying the legitimacy of transactions and blocks. Based on this feature, this paper makes appropriate modifications to add encrypted transaction ciphertext verification and transaction obfuscation functions for miners to achieve a fully anonymous blockchain.

2)   Combined with the homomorphic characteristics of the BGN06 encryption scheme, a four-step verification mechanism is proposed, which is in line with the real blockchain system transaction model to ensure that transaction initiators and verification miners cannot illegally increase or decrease their unspent transaction quotas. The payer is informed of the input transaction amount without additional communication channels.

3)   Use the BGL03 one-way aggregate signature scheme to aggregate the input transaction signatures of all transactions within the block, and systematically embed the currency mixing technology to the scope of the entire block to protect the privacy of the transaction user identity and resist analysis attacks on blockchain transaction data.

4)   The length of the ciphertext of the BGN06 encryption scheme used in this paper is half of the length of the Paillier ciphertext in the Dumb Account scheme under the same security. In order to further reduce the transaction storage overhead in the block, the miners package the transaction ciphertext to the block. During the block process, the encryption public key can be deleted and only the signature public key can be retained for the convenience of ownership proof. Comparing and evaluating this scheme compared with various privacy protection blockchain schemes, after quantitative analysis, it can be known that this blockchain system is implemented due to the transaction storage overhead introduced by the fully anonymous feature is reasonable.

5)   Compared with ZeroCash, the proposed scheme can also realize a fully anonymous blockchain system that protects the privacy of the payer, the payee’s identity and the transaction amount. However, this scheme does not require the trusted startup (Setup) stage in ZeroCash, it will not cause currency spamming due to the leakage of secret parameters and supports blockchain data pruning (Pruning) to avoid excessive storage overhead such as ciphertext data in ZeroCash.

2  Overview

This section describes the Bitcoin blockchain system and related cryptography in detail. In order to simplify the description and facilitate readers’ understanding, the introduction of the Bitcoin blockchain transaction structure in this section adopts the Pay-to-Public-Key (P2PK) structure, and omit some details that are not related to the idea of this article. This section specifies the symbols used in this article, analyzes the transaction structure, block structure and UTXO pool of the Bitcoin blockchain system, introduces the idea of CoinJoin and the concept of currency mixing, introduces BGL03 one-way aggregate signature scheme, BGN06 homomorphic encryption scheme and Pedersen commitment scheme, including BulletProof positive value interval verification and Pedersen commitment scheme equality verification, etc., the NIZK proof technology required by this scheme.

2.1 Symbol Definition

The user entities of the blockchain system are Alice, Bob, Carol, David, and miner Miner. Anti-collision hash function Hash, Large prime numbers p, q, q1 , q2 . Large composite number n=q1q2 . In the Bitcoin block chain system, the transaction is tx , and the block is denoted by block . The input and output of each transaction are TXin , TXout . The integer group of modulo p, q and n is expressed as Zp , Zq and Zn . The elliptic curve group used to aggregate the signatures and the bilinear map is denoted as G, G1 and e1:G×G→G1 , which is denoted as G2 for the BGN06 encryption scheme, G3 and e2:G2×G2→G3X . The random selection of elements from a set or group is expressed as x←RX . The transaction and its subscript index are expressed as the a-th input transaction initiated to the user’s public key address b is TXina,b , and generate the c-th output transaction initiated to the user’s public key address d, and TXtotal is the transaction initiating user’s ciphertext transaction encrypted by the miner’s verification public key. The TXcoinbase is the miner’s block reward transaction. The encrypted amount in the transaction is represented by v. The cryptography public and private keys are PK,SK . Ciphertext C, plaintext message M, and digital signature σ . The subscript i is the user index in the process of encryption and signature description, and the total number of users is k.

2.2 Bitcoin Blockchain System

The Bitcoin blockchain system includes two types of entities: users and miners. Users perform the transaction process, generate transactions and broadcast them. The miners receive a large number of transactions, check their authenticity, package and construct blocks, and then execute operations on the blocks. To demonstrate that the lawful block will be broadcast to the whole network and the UTXO pool will be updated after getting the lucky number (Nonce). Take Alice initiating a transaction to Bob as an example, Alice will broadcast the generated transaction, and it will be verified by the nearby miner Miner. The Miner packs several legal transactions to generate blocks, and broadcasts the legal blocks to the entire network, and adds an unspent output pointing to Bob’s address. The Bitcoin blockchain system architecture and transaction initiation and authentication based on the analysis of the above example process is shown in Fig. 1.

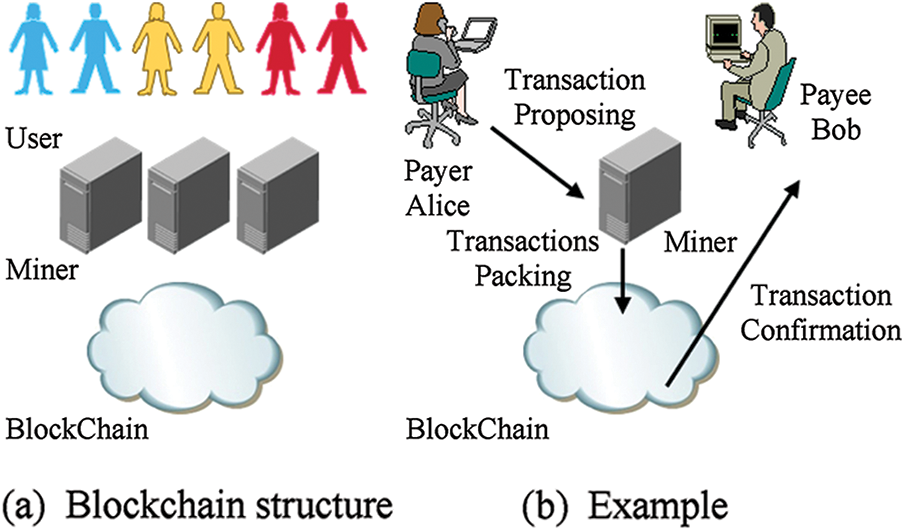
Figure 1: Blockchain system architecture

The transaction structure of the Bitcoin blockchain system includes information such as transaction ID, lock time, and input and output transactions. The transaction ID is the hash value of the transaction entity data. The lock time constrains the UTC time (International Standard Time) when the transaction takes effect. The current transaction’s amount derives from the preceding transaction’s output according to the input transaction. Depending on the amount, the output transaction links to multiple output addresses. To show ownership, the input transaction must also give a signature that corresponds to the public key address of the prior output transaction. The elliptic curve based digital signature algorithm uses the public key and signature of the Bitcoin blockchain system (ECDSA). After multiple hash conversions, the output address is the ECDSA public key. It’s worth mentioning that, the transaction can have many inputs and outputs, with the output address being the payer’s change address, allowing for the merging and splitting of funds in the Bitcoin system. The Bitcoin transaction structure is shown in Fig. 2.

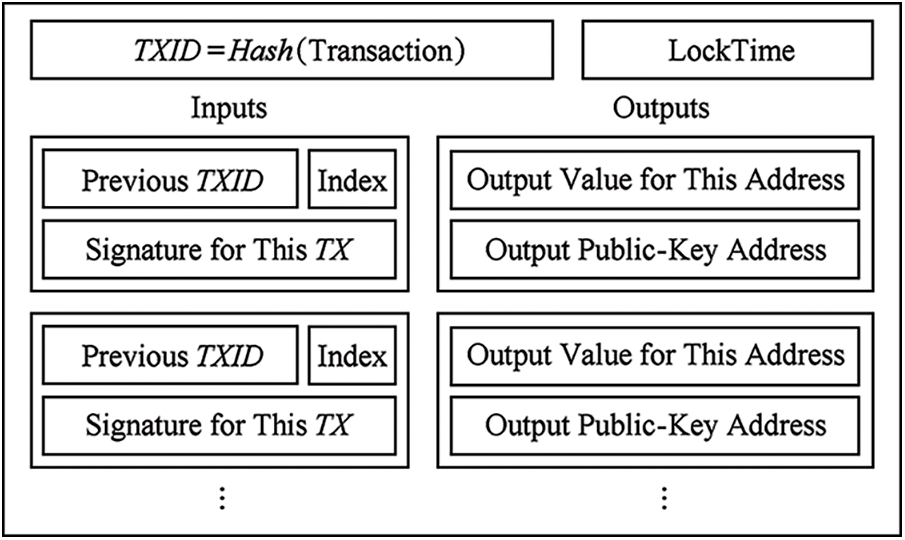
Figure 2: Block diagram of the bitcoin transaction

A Bitcoin block includes three parts: block information, block header and block body. The block information includes network magic number (as the identification code when the Bitcoin client parses block data), and block size. The Block header part includes the hash value of the current block, the hash value referring to the previous block, the Merkle tree root of the transaction in the block, the lucky number, the difficulty target and the timestamp Hash current block body and the previous block. The numerical result should satisfy the system difficulty goal. The Bitcoin blockchain structure is shown in Fig. 3.

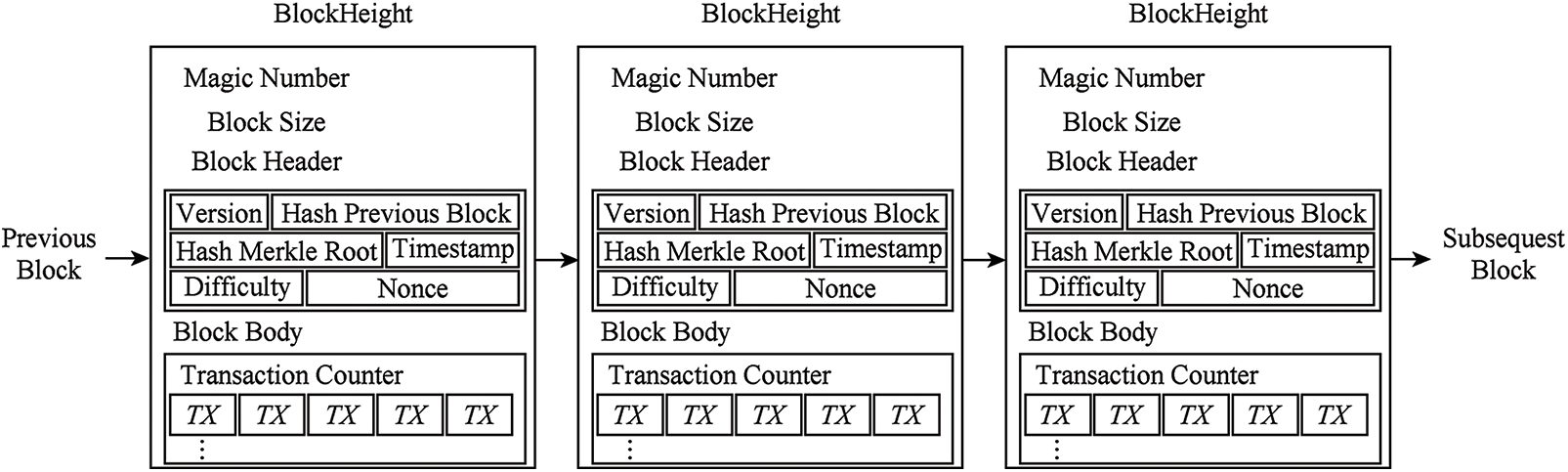
Figure 3: Illustration of the blockchain for bitcoin

All Bitcoin verified (Verified), confirmed and unspent transactions are deposited into the UTXO pool. The process of miners verifying whether a transaction is legal includes whether the input transaction is unspent. That is, in the UTXO pool is an input transaction. The sum of the input amount is equal to the sum of the output amount. The input and output amounts are both positive. The input transaction signature matches the public key of the previous output transaction. As shown in Fig. 4, the above process is described in detail with an example. The block contains a transaction that pays Alice’s address 2 bitcoins. Alice pays 1 bitcoin to Bob and Carol in the first transaction in block 1. Bob pays 1 bitcoin to the first transaction in block 2 to David. The miners receive the transaction initiated by Alice. First, they find in the previous UTXO hash value and the index of the transaction referenced by someone who paid Alice 2 bitcoins, and then verify whether the input and output are equal, the amount is positive and the value is fair. The key signature matches, and finally several legal transactions are packaged into blocks and subsequent operations are performed. The transaction verification process initiated by the miner for Bob is similar. The hash value of the referenced input transaction is found in the UTXO pool, which is the first block in block 1 transaction, and confirmed that the output amount 1 of its index 1 is equal to the current output amount 1. Also, it confirmed that its output public key address matches PKBob current transaction signature σBob .

Figure 4: Hash transactions illustrations of bitcoin blockchain

2.3 Mixing and CoinJoin

The CoinJoin transaction in the Bitcoin blockchain system contains several pairs of inputs and outputs with equal amounts, disrupting the original input-output relationship through various types of protocols. When the transaction initiator verifies that his output address exists in the output list, he signs the CoinJoin transaction. When all transaction initiators sign the transaction, the transaction takes effect and is broadcast to miners. The essence of CoinJoin is to destroy the input-output relationship, making the de-anonymization attack invalid. That is, to realize the privacy of the payer and the payee. Several CoinJoin variant uses the mixing fee to prevent the DoS and Sybil attacks. The mixing fee also serves as a motivation to increase the anonymity set. If a transaction is mixed with a weak anonymity set or even a non-anonymous transaction, its true anonymity set cannot achieve the claimed anonymity set. Therefore, the adversary can de-anonymize it through the proliferation effect. That is, the anonymity of CoinJoin depends on the size of the anonymity set. In addition, the CoinJoin also has an important defect, that is, the mixing service cannot encrypt the amount of participating coins. It is required that the transactions that participate in the mixing must be transactions of the same amount.

2.4 BGL03 One-Way Aggregate Signature

This section gives the definition of BGL03 one-way aggregated signature with reference to [36]. It includes five algorithms, that is, key generation, signature, verification, aggregation and aggregation verification. The length of the aggregated signature of the independent signature before aggregation is equivalent. The aggregation entity can be completely different from the signing entity. The aggregation algorithm only needs to obtain the individual signature/message pair and public key of the participating signing users to generate the aggregated signature. The aggregated verification algorithm only needs to aggregate the signature, aggregate the user public key and the message set to verify the validity of the aggregated signature. It should be emphasized that the underlying requirement of the aggregated signature is that the messages signed during the aggregation process should be different from each other.

The specific steps are as follows:

1)   Parameter convention. Large prime number p, elliptic curve group is G sum G1 , group G generator is g, and bilinear map e1:G×G→G1 ;

2)   The generation of keys. The i-th user private key is a random number xi←RZp , the public key is v PKi=gxi∈G , and the total number of users is k;

3)   Signature. The message to be signed is Mi∈{ 0,1]∗ , the hash transform is Hi=Hash(Mi)∈G , and the signature σi=Hixi∈G ;

4)   Verification. Whether e1(PK=gxi,Hi)=e1(g,σi=Hixi) is established;

5)   Aggregation. The Mi are required to be different, and the aggregation result is a signature σ=∏i=1k⁡σi=∏i=1k⁡(Hi)xi=∏i=1k⁡(Hased(Mi))xi

6)   Aggregate verification. Verify that the equation holds ∏i=1k⁡e(vi=g1xi,hi)=e(g1,σ=∏i=1k⁡σi=∏i=1k⁡hixi) .

The security of the above aggregated signature scheme relies on the random oracle model, which requires the assumption of a Gap Diffie-Hellman Group (GDH) where the decisional Diffie-Hellman (DDH) problem is easy but the computational Diffie-Hellman (CDH) problem is difficult, and bilinear mapped preimages are different groups (co-GDH) [36]. In addition, the uni-directionality of the aggregated signature scheme is reflected in the difficulty of extracting independent signature individuals from aggregated signatures, which can be reduced to solving the CDH problem [37].

2.5 BGN06 Encryption Scheme and Pedersen Commitment Scheme

This section introduces the BGN06 homomorphic encryption scheme and the Pedersen commitment scheme [38].

a)   BGN06 homomorphic encryption scheme

1.    Key generation. User i’s private key is a large prime number q1i , select a random element gi,ui←RG2i , hi=q1i -order subgroup generator of uiq2i and Gi bilinear mapping e2i:G2i×G2i→G3i ; the public key is PKi=(ni=q1iq2i,G2i,G3i,e2i,gi,hi) .

2.    Encryption. The plaintext requires Mi∈0,q2i , select the random number ri←RZni , and the ciphertext is Ci=giMihiri∈G2i .

3.    Decryption. Calculate the ciphertext q1i power to get Ci=(giMihiri)q1i=giMiq1ihiriq1i=giMiq1iuiq2iq1iri=giMiq1iuinri=giMiq1i1ri=giMiq1i=g^iMi . The plaintext can be solved by using Pollard’s Lambda method in [39]. The above decryption process relies on the characteristics of cyclic groups, and the method of solving discrete logarithms is time-consuming O(q2i) .

4.    Homomorphism. The multiplication operation of the ciphertext field is equal to the addition of the plaintext field, that is C=g1M1+M2h1r1;C1C2=g1M1h1r1g1M2h1r2=g1M1+M2h1r1+r2 .

Therefore, the homomorphism requires encryption with the same public key, and the random number of the blinding factor affects the shape of the ciphertext. It should be emphasized that, if the elliptic curve is specified in advance, the group parameter n and the group G2 generator g can determine the 2 group parameters, and the group parameter 3 and the bilinear map e2 are used for ciphertext addition homomorphism. This property does not need to be used in this fully anonymous blockchain scheme, so the deleted public key can be retained as PK=(ni,gi,hi) .

b)   Pedersen Commitment Scheme

The Pedersen commitment scheme is similar to the ciphertext form of the BGN06 encryption scheme. Both transform the secret on the number field group to the elliptic curve group, and prevent the secret from leaking through a random blinding factor. It should be emphasized that in BGN06 encryption scheme, the element h is no longer a random group element, but a generator G2 of the q1 -order subgroup of 2, and is used as part of the public key. Therefore, the BGN06 encryption scheme endows the Pedersen commitment scheme with “unblinding” or “solution commitment”, which is in line with the feature that the payee in the blockchain transaction can directly confirm to receive the transaction amount through the ciphertext, without relying on an additional amount transmission channel.

2.6 Zero-Knowledge Proof

The zero-knowledge proof required by this scheme is used by the transaction initiator (payer) to verify the legitimacy of the transaction to the transaction verifier (miner), including the proof of commitment content equality and the proof of interval. All proof processes are non-interactive, that is, the proof content contains the transaction content broadcast by the transaction initiator.

2.6.1 Proof of Promise Equality

Reference [40] introduces the commitment equality proof protocol as the prover Prover wants to prove to the verifier that the commitments E and F are commitments to the same plaintext M value. For the security parameters t,l,s1 and s2 , the commitment random numbers are respectively are r1 and r2 , the elements g1 and h1 in the group modulo n1 , and the elements g2 and h2 in the group modulo n2 , the commitment values are respectively:

E=g1Mh1r1mod n1 (1)

F=g2Mh2r2mod n2 (2)

where,

r1∈[−2s1n1+1,ss1n1−1] (3)

r2∈[−2s2n2+1,ss2n2−1]

Step 1. Prover selects random numbers ω,η1,η2 and calculates:

W1=g1ωh1η1modn1 (4)

W2=g2ωh2η1modn2 (5)

where,

ω∈[1,2l+tb−1] (6)

η1∈[1,2l+t+s1n1−1] (7)

η2∈[1,2l+t+s2n2−1] (8)

Step 2. Prover computes y=H(W1||W2) .

Step 3. Prover calculation:

D=ω+yM,D1=η1+yr1,D2=η2+yr2 (9)

The above D, D1 , D2∈Z ; and send the proof π=(y,D,D1,D2) to verifier (including commitments E and F );

Step 4. Verifier verifies that the equation holds:

y=H(g1Dh1DE−ymod n1g2Dh2D2F−ymodn2) (10)

2.6.2 Interval Proof

Due to space limitations, this paper will not repeat the proof process of the scheme. It should be emphasized that the BulletProof interval proof scheme is based on the Borromean based on the original CT scheme. The interval proof scheme of ring signature and the interval proof scheme in Dumb Account scheme have improved efficiency.

3  Proposed Methodology

The totally anonymous blockchain system based on aggregated signatures and encrypted transactions is described in depth in this section. The fully anonymous blockchain system protects the data privacy of users during the transaction process, including three types of data such as payer identity, transaction amount, and payee identity. Therefore, this scheme has the full anonymity feature analogous to the ZeroCash scheme. This section details the initial parameters of the scheme in turn, the miners’ verification process for the legitimacy of encrypted transactions, and the miners’ aggregation of all transactions in a block packaging process of signature. It introduces the construction of fully anonymous blockchain and UTXO pool. The idea of equivalence proof in this section, the idea of aggregate signature, and the corresponding BGN06 encryption scheme of this scheme is made according to the actual situation.

3.1 Protocol for System Parameters

The cryptographic tools that this fully anonymous blockchain system relies on include the BGN06 encryption scheme and the BGL03 one-way aggregate signature, so the initial parameters of these two schemes need to be agreed. The content includes the BGN06 encryption scheme, composite order elliptic curve, prime order elliptic curve of BGL03 one-way aggregate signature scheme, large prime p, group G sum G1 , group G generator g, and bilinear map e1:G×G→G1 .

3.2 Miner Transaction Verification

The essence of miner transaction verification is to verify whether the transaction generated by the transaction initiator (payer) is legal including the proof of ownership of the input transaction by the payer (the signature conforms to the public key of the previous transaction output), the sum of the transaction input is equal to the sum of the output and all the amounts satisfy the positive value. For the convenience of description, this section temporarily ignores the consideration of transaction fees, but this scheme supports the transaction initiator to explicitly pay the transaction fee to the miner’s decryptable account. The essence of verifying the transaction is to ensure the transaction initiator can only perform transaction operations on his own amount, and cannot create or maliciously destroy the transaction amount out of thin air. This section describes the process of transaction verification by miners, including the four-step verification transaction input and output in Section 3.2.1. In Section 3.2.2, we introduce the use of BulletProof to verify the amount range and signature verification.

3.2.1 Four-Step Verification of Input and Output and Equality

The essence of transaction verification is to ensure that the transaction initiator cannot cheat. Therefore, the process of transaction verification includes the correct interpretation of the transaction amount owned by the transaction initiator and the correct distribution of the transaction output amount. Without loss of generality, this section uses multiple inputs, a multi-output transaction is used as an example to describe the four-step verification process.

1)   Key generation. This scheme uses the BGN06 encryption scheme to realize transaction encryption. The user entity b of the blockchain system can freely generate a public and private key pair (PKb, SKb), and miners share the same public key PKminer. It is worth emphasizing that the user’s public key is his own payment address, and the user’s private key can decrypt his own ciphertext and generate a signature of the ownership certificate. While miners can only verify the legitimacy of the ciphertext. The above private key includes the encryption of the BGN06 encryption scheme. The private key and the signature private key of the BGL03 aggregate signature scheme, that is, the private key is SKb = (q1b, xb); the public key is PKb = (nb, gb, hb, gxb), an integer nb satisfies nb = q1bq2b, random element gb,ub←RG2 , hb=q1b -order subgroup generator of 2b . The miner does not have the private key for decryption, and the encryption public key is PKminer=(nminer,gminer,hminer) .

2)   Transaction generation.

PRNc,d,TXoutc,d←TXcreate(TXina,b) (11)

Among them, TXina,b represent several input transaction ciphertexts encrypted with PKb, subscript a represents the serial number of the input ciphertext; TXoutc,d represent several output transaction ciphertexts encrypted with PKd, and the subscript c represents the output ciphertext serial number. The transaction input and output are both BGN06 ciphertexts of the amount va,b,vc,d requiring va,b,vc,d∈[0,vtotal] , the input transaction ciphertext is

TXina,b=gbva,bhbra,bmod nb (12)

Note that, the blinded random numbers for different transactions are different here. Similarly, the output transaction ciphertext for the amount vc,d is for each transaction output, the transaction initiator generates a pseudo-random number PRNc,d .

For example, input and output transactions can be

TXin1,1,TXin2,1,TXin1,2,TXin2,2,TXin3,2,TXout1,3TXout2,3,TXout3,3,TXout1,4,TXout2,4 (13)

That is, the input of the transaction generator is the transaction TXin1,1,TXin2,1 encrypted with the public key PK1, and the transaction TXin1,2 , TXin2,2 , TXin3,2 encrypted with the public key PK2. The transaction output are transactions TXout1,3 , TXout2,3 , TXout3,3 encrypted with PK3, and transactions TXout1,4 , TXout2,4 encrypted with public key PK4.

3)   Transaction verification. Miners verify transactions for transaction initiators:

TXVerify(TXina,b,TXin′a,b,TXoutc,d,TXoutc.d′,TXtotal,σb,PKd,π1,π2,π3,π4,π5)→0,1 (14)

Among them, TXina,b′,TXoutc.d′,TXtotal is the transaction ciphertext encrypted by the transaction initiator with the miner’s public key PKminer, σb provides the transaction initiator with a signature for ownership proof, and the signed content is (PRNc, d, TXoutc, d). PKd is the public key address used by the transaction payee for signature verification. The π1,π2,π3, π4,π5 are the NIZK proofs in the verification process. The specific contents of the proofs areas follow. π1 is the transaction initiator prove to the verification miner that the correct commitment content is equivalent to decrypt the transaction input that it owns. π2 is the correct commitment content equality proof for the sum of the input of the current transaction initiated. π3 is the commitment to the sum of the input and output of the currently initiated transaction proof of content equality. π4 is the proof of the correct commitment content for encrypting the output transaction, and π5 is the correct construction of the output ciphertext for the current transaction. That is, the commitment interval proof that all input and output amounts are positive ciphertext. It should be emphasized that the miner is used to verify the public key encrypted transaction ciphertext, the same one-step verification random number rin,rout,rtotal can be used in the same transaction, but the one-step verification random number for different transactions should be different to improve the security of the verification ciphertext. The above uses The verification ciphertext for verifying that the sum of the input and output amounts is equal and preventing the transaction initiator from cheating is:

TXina,b′=gminerva,b,hminerrinmodnminer (15)

∏T⁡Xina,b′=gminer∑a,bvhminer∑inrmod nminer (16)

TXoutc,d′=gminervc,dhminerrinmod nminer (17)

∏T⁡Xoutc,d′=gminer∑c,dvhminer∑outrmod nminer (18)

TXtotal=gminervtotalhminerrtotalmod nminer (19)

As the examples in this section describe, TXina,b′,TXoutc,d′,σb are:

TXin1,1′,TXin2,1′,TXin1,2′,TXin2,2′,TXin3,2′,TXout1,3′,TXout2,3′,TXout3,3′,TXout1,4′,TXout2,4′,σ1,σ2 (20)

Refer to Section 2.6 for the equal secret verification process, and the four-step verification is:

1)   Use a number of proofs π1 to verify whether TXina,b are the same TXina,b′ secret commitment, that is, verify whether the transaction initiator cheats the decryption of the transaction input owned by himself.

2)   Use the proof π1 to verify the commitment of whether it is the same secret as TXtotal . The homomorphic property of the BGN06 ciphertext is used to verify whether the transaction initiator is cheating by summing the transaction input.

3)   Use the proof π3 to verify the commitment of whether it is the same secret as TXtotal. The homomorphic property of the BGN06 ciphertext is used to verify whether the transaction initiator is cheating by summing the transaction output.

4)   Use several proofs π4 to verify whether TXoutc,d are the same secret commitments, that is, verify whether the transaction initiator cheated on the encryption of the transaction output.

3.2.2 Four-Step Verification of Input and Output and Equality

The π5 is the proof used by BulletProof to verify the positive value of the transaction amount. Since the BGN06 encryption scheme is essentially for the amount on n, the negative value modulo n is calculated to be positive, which can make malicious transaction initiators out or maliciously destroy the transaction output amount. It should be emphasized that since the verification process includes the input and output summation equality verification, the interval proof does not need to separately verify whether the upper limit of each transaction amount is less than the sum of the input or output.

The signature verification process of a single transaction is the same as that of the traditional Bitcoin blockchain system. That is, to verify whether the σb of the current transaction matches the signature verification public key in the previous transaction PKd .

3.3 Miner Package Transaction

After verifying several legal transactions, miners need to package legal transactions into blocks and perform workload proof to obtain block rewards. The underlying requirement here is that all transactions are confirmed transactions, so there is no reference to an unverified transaction. All transactions will remove intermediate proofs and only include:

TXina,b(PRNc,d,TXoutc,d),σb,PKd (21)

Since the BGL03 one-way aggregated signature scheme requires that the aggregated signature messages are completely different, there may be transactions TXoutc,d that pay the same public key of the payee and have the same amount in the same block. Therefore, miners need to quantify the value of each output transaction. The pseudo-random numbers PRNc,d are verified to ensure that the blocks (PRNc,d,TXoutc,d) are completely different, and transactions with the same pseudo-random number and transaction output ciphertext pair can be delayed until subsequent block processing.

The miners randomly arrange the contents of several transactions with pseudo-random numbers, including the coinbase transaction TX coinbase without input, and aggregate the signature σ=σb , then the signature and transaction contents in the block are

σ,TX=(TX1,TX2,…,TXi,…),TXi=[TXcoinbase,TXina,b,(PRNc,d,TXoutc,d),PKd]i (22)

It should be emphasized that in order to reduce the space occupied by secondary information in the block and maximize the number of transactions in the block, the transaction output public key included in the block only needs to include the transaction payee’s signature public key to use it. For transaction ownership proof, it does not need to include the encryption public key.

3.4 Blockchain and UTXO Pool Construction

In order to verify the reference of the previous transaction to match the content of the one-way aggregated signature, the structure of the UTXO pool also needs to be modified appropriately. The UTXO structure of the original Bitcoin blockchain system is: hashTX,[Index ], which is now changed to hashBlock,H(PGNc,d,TXoutc,d) . This is because the index referenced by the original transaction is for different transaction outputs in a single transaction, while the input index in the fully anonymous blockchain is for all the blocks in the block that obfuscate the transaction order. The index of the transaction output. Therefore, for the example of the original blockchain and UTXO pool structure in Section 2.2, Fig. 4 can be correspondingly modified to Fig. 5.

Figure 5: Proposed framework

4  Experimental Results and Evaluation

This section details the efficiency and function comparison between the proposed and other schemes. First, it demonstrates the security and anonymity of the proposed scheme. Secondly, it details the length of the public key, the length of the ciphertext, and the transaction storage overhead in the block introduced by the function improvement and compared with the references. Finally, the comparison and improvement of the proposed scheme and various blockchain privacy protection improvement schemes in terms of function and efficiency are described in detail.

4.1 Security and Anonymity

The proposed scheme is based on the BGN06 public key encryption scheme and the BGL03 aggregated signature scheme. The security of the BGN06 ciphertext is based on the difficult problem of subgroup determination. Judging whether an element of a random group belongs to the prime order subgroup of the composite order group in polynomial time. The CDH difficulty problem on the co-GDH group determines the security of the BGL03 aggregate signature.

It passes four-step equality verification and BulletProof positive value verification. During the transaction creation process, the transaction initiator cannot deceive the encrypted value, nor can he produce coins out of thin air or intentionally destroy coins. The miners without the private key of the encryption scheme receive the input transaction password. The text cannot be decrypted correctly, but only to verify whether the transaction is legal, so miners cannot mint or destroy coins. It should be emphasized that the proof of ownership of the transaction amount in this scheme cannot only rely on the ability to decrypt the ciphertext and abandon signature verification, because in addition to encryption addition, decrypting the legal ciphertext cannot verify the user’s identity. However, in order to expand the number of transactions that may be accommodated in a block, the encrypted public key of the transaction payee might be erased from the data on the chain. Based on the BGN06 encryption scheme Ciphertext transactions conform to the concept of encrypted transactions and ensure the privacy of user transaction amounts. The miners randomly arrange legal transactions when packaging transactions, which confuses the relationship between transaction users and ensures the privacy of recipients and payers. Therefore, this blockchain solution is completely anonymous. In addition, the block data of this scheme can support public verification, it only needs to verify whether the aggregated signature, all transaction ciphertexts and pseudo-random numbers in the block, and the output public key satisfy:

∏⁡e1(PKc,d,H(PNGc,d,TXoutc,d))=e1(g,σ) (23)

4.2 Efficiency Comparison

4.2.1 Public Key and Ciphertext Length

The selection of cryptographic security parameters must guarantee that the modulus based on the big integer decomposition scheme is 2048 b (256 B), and the security parameter based on the elliptic curve scheme is 256 b, according to the development of the existing hardware system (32 B) [41]. Furthermore, the 256 b encoding point on the elliptic curve may be represented by 33 B encoding. As a result, the BGN06 encryption algorithm employs 256 B to represent the huge composite number, and 32 B to represent the BGL03 aggregate signature’s elliptic curve.

As mentioned in Section 2.5, if the elliptic curve on which the encryption scheme is based is prioritized in the system parameter agreement, group G2 can be determined by group parameter nb and group generator gb . The group G2 and bilinear mapping e2 is deleted because the ciphertext addition homomorphism is not required. Therefore, the public key length of this scheme is |PKb|=|nb|+|gb|+|hb|+|gxb| . However, this approach deletes the public key of the BGN06 encrypted transaction provided in the block transaction output address after the miner validates that the transaction is legitimate in order to expand the number of transactions that may be accommodated in the block |PKb′|=|gxb| . The large composite number nb , so the ciphertext length of this scheme is |nb| , which is 256 B [42].

The original Bitcoin blockchain architecture, regardless of P2PKH, requires 8 B space to represent the output amount and 33 B to represent the ECDSA public key. The public key implemented by the standard encrypted transaction, its structure includes the scan key version, traditional address version, scanning key, traditional address, and Base58Check encoding for the above content. The scanning key is essentially an elliptic curve-based Diffie-Hellman (ECDH) negotiated key, and the same random number seed is negotiated for generating the same blinding factor. Regardless of the version number and P2PKH transformation, the length of the ECDH key is 33 B, and the length of the ECDSA public key is 33 B, totaling 66 B. In addition, the ciphertext uses Pedersen in the form of commitment, the dedication length of ciphertext is 33 B and it is a point on the elliptic curve. The ValueShuffle protocol needs to use a distributed negotiation algorithm to mix coins and negotiate the sum of random blinding factors, so although blindness needs to be added in the distributed negotiation process. However, the basic encryption transaction public key and ciphertext length are the same as the original scheme.

The Paillier ciphertext needed by the Dumb Account system requires a length representation of 512 B if the same security is assumed (big integer decomposition demands a large composite number of 256 B) (modulo n2 group). The public key for encryption is a huge composite number and group generator with a length of 256 + 256 = 512 B. When you add in the ECDSA signature public key, the overall length of the public key is 512 + 33 = 545 B.

4.2.2 Transaction and Block Size

This system, in contrast to the original Bitcoin blockchain concept, transforms the amount stored in plaintext to ciphertext on the modulo n group, resulting in a commensurate increase in transaction size (block). The signatures of all transactions in the block are aggregated into one signature due to the use of the BGL03 aggregated signature scheme, and the public key of the BGN06 encryption scheme is deleted during the transaction inclusion process, reducing the size of the transaction in the block from the other direction. The challenge of blockchain growth is now academic. As a result, in this work and other references, this section quantifies the number of transactions that may be supported in a single block.

For the original Bitcoin blockchain system, the average block size in the past year is 644.2 kB, including 1 682 transactions [43]. Deducting about 100 B of block headers and related information, it can be calculated that the size of each transaction is about It is 392 B. Among them, the data at the head and tail of the transaction that has nothing to do with input and output is 8 B, regardless of the P2PKH condition or the amount of transaction input and output counters, each input contains 32 B to reference the hash value of the previous transaction, 4 B index, 64 B ECDSA signature and 4 B serial number of each output contains 33 B ECDSA public key and 8 B amount. Therefore, if the input and output are considered equal, there are about 2.649 input and output on average. Considering the limit case is a single input, 6.832 output or single output, 3.299 inputs. Calculate the number of transactions contained in each scheme block using the above transaction input and output data, as well as the public key and ciphertext length of each scheme in Section 4.2.1. When the limit input and output, equal input and output, the result is as indicated in Tab. 1.

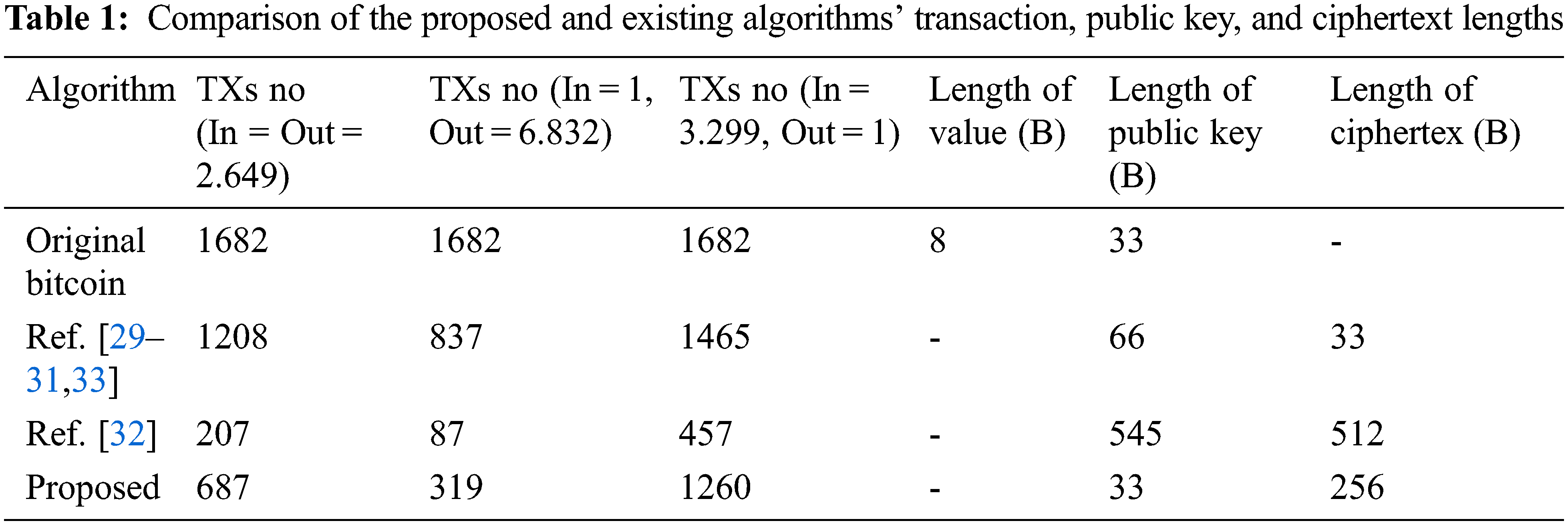
A detailed analysis of the evaluation data of the transaction storage cost of encrypted transaction ciphertext in the block in Tab. 1 shows that the size of the ciphertext of BGN06 still significantly affects the transaction capacity. The ciphertext security of BGN06 is based on the subgroup determination on the composite order bilinear group premise of this problem is that it is difficult to decompose the composite order, so a too small modulus n cannot be selected. It should be emphasized that although this scheme has no advantage in the ciphertext length achieved by a normal encrypted transaction, the standard encrypted transaction Pedersen promises that there is no “uncommitment” phase. That is, during the execution of the transaction, the user needs to add a second channel of communication to advise the payee of the transaction amount, which not only increases the communication overhead, but also easily leaks user privacy, and the payee is unable to verify if the transaction amount reported by the payer was received. In contrast, the BGN06 ciphertext of this scheme supports the decryption of the payee’s private key, and supports the payee to obtain the transaction amount directly through the transaction information, which is in line with the actual transaction scenario, and based on the comparison Dumb Account scheme of Paillier ciphertext [32], the transaction storage overhead introduced by the function improvement is reasonable.

4.3 Comparison of Characteristic

There is a bootstrap stage in the centralized or distributed currency mixing scheme that needs to negotiate the currency mixing object in advance. That is, the currency mixing process is not compulsory for the user. Although the bulletin board can be used to match mixed currency users, once a weak anonymity set or a non-anonymous mixed currency object appears, its proliferation effect will affect the privacy protection effect of the whole network, even if the ring is used Monero with the signature scheme embedded currency mixing service is also not immune. Therefore, the OWAS scheme, ZeroCoin and other schemes that force currency mixing into the transaction system can guarantee the anonymity set. The size is large enough to resist such analysis attacks. In contrast, none of the encrypted transaction-based schemes protect the user privacy, and Pedersen promises that transaction ciphertexts require additional communication channels to transmit transaction amount. If the transaction payee cannot directly decrypt the transaction ciphertext, it cannot verify whether the transaction amount claimed by the payer has been received, and the validity of the input and output will not be verified until the next time the transaction is spent. Although the ValueShuffle scheme combines the encrypted transactions and distributed currency mixing achieve full anonymity, but non-systematic embedded currency mixing is not resistant to analytical attacks.

To sum up, this scheme achieves full anonymity compared with several partial blockchain privacy protection improvement schemes, and improves the block transaction capacity compared with the Dumb Account scheme. Compared with the full anonymous scheme ZeroCash, the system parameters of the proposed scheme do not expose sensitive information related to encrypted transactions, and there is no risk of currency over-issuance due to the leakage of initialization information. Compared with the ValueShuffle scheme, it is resistant to analysis attacks, and the user identity anonymity set is covered. The proposed scheme can also support blockchain pruning similar to MimbleWimble, and the pruned blockchain only needs to retain the aggregated transaction signatures, further reducing the size of the pruned blockchain. The proposed scheme specific function comparison with the above-mentioned related studies is shown in Tab. 2.

5  Discussion

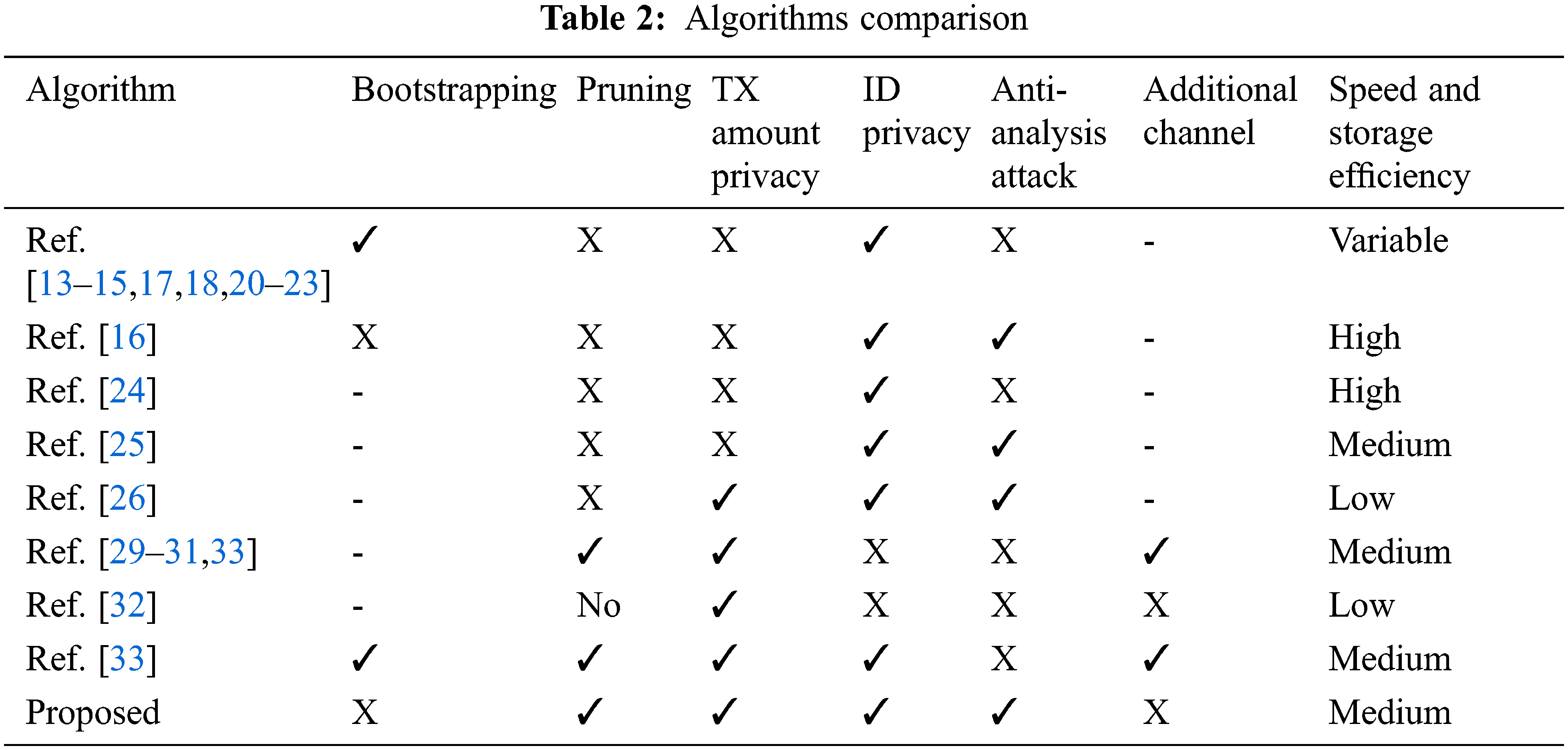
The currency mixing technology is based on the idea of CoinJoin proposed by Maxwell in 2013. A CoinJoin transaction confuses the output addresses set by several transaction initiators, and requires that the amount of mixed bitcoins is equal and public. This idea improves the degree of anonymity which depends on the number of users participating in the mixing. That is, there are many improvements and variants of the mixing protocol based on this idea, including a scheme that combines the idea of fair exchange between two parties. It relies on several intermediaries and is compatible with the Bitcoin system fair exchange scheme. The Blind signing contract fair exchange scheme relies on smart contracts. The systemic currency mixing scheme based on one-way aggregated signatures and combining the currency mixing center with miners. The introduction of a trusted third party Mixcoin scheme and its variant Blindcoin scheme [18] that uses blind signatures to improve the anonymity. The Xim scheme is for pairing the mixed currency users based on the CoinSwap idea, and compatible with the current Bitcoin system’s Tumblebit scheme. The CoinShuffle is a point-to-point centerless currency mixing protocol based on cryptography and a variant CoinShuffle++ scheme introduced by DC-net. However, although the above research results break the connection between transaction entities, internal and external non-connectivity, currency mixing efficiency, anti-stealing, anti-denial of service (DoS) attack, anti-Sybil attack and other aspects has been improved, but the essence only protects the identity privacy of the payer and the payee, and the CoinJoin transaction still exposes the transaction amount and needs to negotiate the mixed currency object in advance in the bootstrapping stage. It may affect the privacy protection effect of the entire network due to the proliferation effect caused by weak anonymity sets or non-anonymous currency mixing objects.

In addition, altcoins such as Monero, ZeroCoin, and ZeroCash still have certain problems while introducing improved features. The Monero transactions contain multiple inputs, which are verifiable using the ring signature technology. The ownership of the input transaction does not expose the signature entity. Its basic idea is similar to the concept of CoinJoin mixing currency, but the Monero analysis attack can trace the origin of about 88% of the transaction data. About 62% of the transaction input in the whole network vulnerable to the “chain reaction” based analysis attacks to expose the user identities. In addition, the Monero transactions do not enforce the protection of transaction amount privacy. The ZeroCoin system based on zero-knowledge proof technology introduces the “non-connectivity” idea of “chips” expands the scope of currency mixing to all “chips” that can be spent on the entire network. When minting coins (Mint), ZK technology is used to prove that the payer holds the same amount of Bitcoin, which can be obtained independently on the premise of not revealing the payer’s privacy. The ZK technology is also used to verify the legitimacy of “chips” when redeeming and record a list of all historically spent chips. However, the ZeroCoin does not protect the transaction amount and the privacy of the payee, and is relative to Bitcoin currency system maintains the unspent transaction output, and the cost of maintaining the exchanged chip ledger is relatively high. The ZeroCash extends the privacy protection content to the payer, payment amount and the payee on the basis of ZeroCoin. However, the problems include the need for a trusted third party to generate global parameters, the underlying zero-knowledge concise non-interactive knowledge proof technology relies on non-falsifiable cryptographic assumptions, and the overall implementation efficiency of the scheme is relatively low.

The encrypted transactions based on the Pedersen commitments uses ECDH to negotiate the same random number seed without knowing the specific transaction amount, generate the same blinding factor based on this, and utilizes the commitment homomorphism to verify the legitimacy of the transaction. Although the MimbleWimble scheme that supports CT and blockchain pruning greatly increases the size of UTXO, the size of the blockchain data body tends to be stable after pruning. It should be emphasized that the above schemes do not protect the user privacy, and additional channels are required to transmit the transaction amount. The Dumb Account scheme implements encrypted transactions through Paillier homomorphic ciphertext, and the transaction payee can directly decrypt the input ciphertext. However, its ciphertext security is based on the decomposition of large integers, the modulo n2 group requires at least 4096 b ciphertext under the current computing power conditions to ensure security, too long ciphertext and public key lengths will result in each block can only accommodate a small number of transactions. Although the ValueShuffle scheme combines encrypted transactions and distributed currency mixing to achieve full anonymity, the non-systematic embedded currency mixing is not resistant to analysis attacks.

6  Conclusion

This paper uses the BGN06 homomorphic encryption scheme and the BGL03 one-way aggregated signature scheme to perfectly combine the whole-block systematic currency mixing with the encrypted transaction technology to construct a fully anonymous blockchain. Combined with the equivalent proof of Pedersen-like commitment, using four-steps verification scheme ensures that the transaction initiators and verification miners cannot create coins out of thin air or maliciously destroy coins, and miners can only verify whether the transaction is legal but cannot know or obtain the transaction amount. Compared with the standard encrypted transaction scheme, the proposed scheme does not need to use additional channels to send transactions to the recipient for informing the transaction amount. Compared with the Dumb Account scheme, the encrypted ciphertext storage overhead is smaller, and compared with ValueShuffle, it avoids additional communication channels between users who mix coins. Quantitative analysis shows that the proposed scheme introduces the area due to the improvement of functions. The block transaction capacity overhead is reasonable. Reference [44] proposes that converting the BGN06 scheme to a prime order group can further reduce the length of the ciphertext while maintaining the same security. On this basis, the follow-up work will continue to study the full anonymity and support extended blockchain system.

Acknowledgement: The authors would like to thank the editors and reviewers for their review and recommendations. And the Researchers Supporting Project for supporting this work by Project No: (No. RSP-2021/395), King Saud University, Riyadh, Saudi Arabia.

Funding Statement: This work was supported by the Researchers Supporting Project (No. RSP-2021/395), King Saud University, Riyadh, Saudi Arabia.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  E. Zaghloul, T. Li, M. Mutka and J. Ren, “Bitcoin and blockchain,” IEEE Internet of Things Journal, vol. 7, no. 10, pp. 10288–10313, 2020. [Google Scholar]

 2.  J. Zhang, R. Tian, Y. Cao, X. Yuan, Z. Yu et al., “A hybrid model for central bank digital currency based on blockchain,” IEEE Access, vol. 9, pp. 53589–53601, 2021. [Google Scholar]

 3.  R. Borgas and F. Sebe, “A digital paradigm with valued and no-valued e-coins,” Applied Sciences, vol. 11, no. 21, pp. 1–18, 2021. [Google Scholar]

 4.  F. Tschorsch and B. Scheuermann, “Bitcoin and beyond: A technical survey on decentralized digital currencies,” IEEE Communications Surveys & Tutorials, vol. 18, no. 3, pp. 2084–2123, 2016. [Google Scholar]

 5.  R. Wu, K. Ishfaq, S. Hussain, F. Asmi, A. Siddiqui et al., “Investigating e-retailers intentions to adopt cryptocurrency considering the mediation of technostress and technology involvement,” Sustainability Journal, vol. 14, no. 2, pp. 1–19, 2022. [Google Scholar]

 6.  R. Saia, A. Podda, L. Pompianu, D. Recupero and G. Fenu, “A blockchain-based distributed paradigm to secure localization services,” Sensors Journal, vol. 21, no. 20, pp. 1–15, 2021. [Google Scholar]

 7.  M. Ober, S. Katzenbeisser and K. Hamachar, “Structure and anonymity of the bitcoin transaction graph,” Future Internet Journal, vol. 5, no. 2, pp. 1–19, 2013. [Google Scholar]

 8.  N. Sapkota and K. Grobys, “Asset market equilibria in cryptocurrency markets: Evidence from a study of privacy and non-privacy coins,” Journal of International Financial Markets, Institutions and Money, vol. 74, no. 8, pp. 1649–1658, 2021. [Google Scholar]

 9.  A. Aysan, H. Demirtas and M. Sarac, “The ascent bitcoin: Bibliometric analysis of bitcoin research,” Journal of Risk and Financial Management, vol. 14, no. 9, pp. 1–14, 2021. [Google Scholar]

10. A. Motamed and B. Bahrak, “Quantitative analysis of cryptocurrencies transaction graph,” Applied Network Science Journal, vol. 131, no. 4, pp. 875–886, 2019. [Google Scholar]

11. M. Conti, E. Kumar, C. Lal and S. Ruj, “A survey on security and privacy issues of bitcoin,” IEEE Communications Surveys & Tutorials, vol. 20, no. 4, pp. 3416–3452, 2018. [Google Scholar]

12. Q. Wang, X. Li and Y. Yu, “Anonymity for bitcoin from secure escrow address,” IEEE Access, vol. 6, pp. 12336–12341, 2017. [Google Scholar]

13. L. Kristoufek, “What are the main drivers of the bitcoin prices? Evidence from wavelet coherence analysis,” PloS One Journal, vol. 10, no. 4, pp. 1–13, 2015. [Google Scholar]

14. D. W. Jaya, J. Liu and R. Steinfeld, “Anonymizing bitcoin transaction,” in Int. 20th Conf. on Financial Cryptography and Data Security, Berling, Germany, pp. 271–283, 2016. [Google Scholar]

15. E. Heilman, F. Baldimtsi and S. Goldberg, “Blindly signed contracts: Anonymous on-blockchain and off-bloclchain bitcoin transactions,” in Int. Conf. on Financial Cryptography and Data Security, Berlin, Germany, pp. 43–60, 2016. [Google Scholar]

16. A. Saxena, J. Misra and A. Dhar, “Increasing anonymitiy in bitcoin,” in IEEE 18th Int. Conf. on Financial Cryptography and Data Security, Belin, Germany, pp. 122–139, 2014. [Google Scholar]

17. J. Bonneau, A. Narayan and A. Miller, “Mixicoin: Anonymity for bitcoin with accountable mixes,” in IEEE 18th Int. Conf. on Financial Cryptography and Data Security, Berlin, Germany, pp. 486–504, 2014. [Google Scholar]

18. L. Valenta and B. Rowan, “Blindcoin: Blinded, accountable mixes for bitcoin,” in IEEE 19th Int. Conf. on Financial Cryptography and Data Security, Berlin, Germany, pp. 112–125, 2015. [Google Scholar]

19. G. Bissias, A. Ozisik and B. Levine, “Sybil-resistant mixing for bitcoin,” in IEEE 13th Workshop on Privacy in the Electronic Society, New York, USA, pp. 149–158, 2014. [Google Scholar]

20. Z. Zhang, W. Li, H. Liu and J. Liu, “A refined analysis of zcash anonymity,” IEEE Access, vol. 8, pp. 31845–31853, 2020. [Google Scholar]

21. Y. Chen, J. Wu, Y. Hsieh and C. Hsuh, “An oracle-based on-chain privacy,” Computers Journal, vol. 9, no. 3, pp. 1–16, 2020. [Google Scholar]

22. T. Ruffing, P. Moreno and A. Kate, “CoinShuffle: Practical decentralized coin mixing for bitcoin,” in IEEE 19th Int. Conf. on European Symp. on Research in Computer Security, Berlin, German, pp. 345–364, 2014. [Google Scholar]

23. Y. Liu, X. Liu, C. Tang, J. Wang and L. Zhang, “Unlinkable coin mixing scheme for transaction privacy enhancement of bitcoin,” IEEE Access, vol. 6, pp. 23261–23270, 2018. [Google Scholar]

24. N. Amarasinghe, X. Boyen and M. Kague, “The cryptographic complexity of anonymous coins: A systematic exploration,” Cryptography Journal, vol. 5, no. 1, pp. 1–17, 2021. [Google Scholar]

25. I. Miers, C. Garman and M. Green, “Zerocoin: Anonymous distributed e-cash from bitcoin,” in IEEE 34th Int. Symp. on Security and Privacy, Los Angeles, USA, pp. 397–411, 2013. [Google Scholar]

26. E. B. Sassan, A. Chiesa and C. Garman, “Zerocash: Decentralized anonymous payments from bitcoin,” in IEEE 3rd Int. Symp. on Security and Privacy, New York, USA, pp. 459–474, 2014. [Google Scholar]

27. A. Kumar, C. Fischer and S. Tople, “A traceability analysis of moneros blockchain,” in IEEE 22nd Int. Conf. on European Symp. on Research in Computer Security, Berlin, Germany, pp. 153–173, 2017. [Google Scholar]

28. A. Z. Junejo, M. A. Hashmani and M. Memon, “Empirical evaluation of privacy efficiency in blockchain networks: Review and open challenges,” Applied Sciences, vol. 11, no. 15, pp. 1–18, 2021. [Google Scholar]

29. K. Qureshi, L. Shahzad, A. Abdelmaboud, T. Eisa, B. Alamri et al., “A blockchain-based efficient, secure and anonymous conditional privacy-preserving and authentication scheme for the internet of vehicles,” Applied Sciences Journal, vol. 12, no. 1, pp. 1–18, 2022. [Google Scholar]

30. J. Alupotha, X. Boyen and M. Mckague, “Aggregable confidential transactions for efficient quantum-safe cryptocurrencies,” IEEE Access, pp. 17722–17747, 2022. [Google Scholar]

31. A. Silveria, G. Betarte, M. Cristia and C. Luna, “A formal analysis of the mimblewimble cryptocurrency protocol,” Sensors Journal, vol. 21, no. 17, pp. 1–18, 2021. [Google Scholar]

32. Q. Wang, B. Qin, J. Hu and F. Xiao, “Preserving transaction privacy in bitcoin,” Future Generation Computer Systems, vol. 107, no. 3, pp. 793–804, 2020. [Google Scholar]

33. T. Ruffing and P. Sanchez, “ValueShuffle: Mixing confidential transactions for comprehensive transaction privacy in bitcoin,” in IEEE 21st Int. Conf. on Financial Cryptography and Data Security,¸ Berlin, Germany, pp. 133–154, 2017. [Google Scholar]

34. D. Boneh, J. Goh and K. Nissim, “Evaluating 2-DNF formulas on ciphertexts,” in IEEE 2nd Int. Conf. on Theory of Cryptography, Ottawa, Canada, pp. 325–341, 2005. [Google Scholar]

35. B. Bunz, J. Bootle, D. Boneh, A. Poelstra, P. Wuille et al., “Bulletproofs: Short proofs for confidential transactions and more,” IEEE Symposium on Security and Privacy (ISP), San Francisco, USA, pp. 969–975, 2018. [Google Scholar]

36. D. Boneh, C. Gentry and B. Lynn, “Aggregate and verifiably encrypted signatures from bilinear maps,” in Proc. of the 22nd Int. Conf. on Theory and Applications of Cryptographic Techniques, Glasgow, UK, pp. 416–432, 2003. [Google Scholar]

37. J. Coron and D. Naccache, “K-Element aggregate extraction assumption is equivalent to the diffie-hellman assumption,” in Proc. of the 22nd Int. Conf. on Theory and Applications of Cryptographic Techniques, Glasgow, UK, pp. 129–140, 1991. [Google Scholar]

38. T. Pedersen, “Non-incentive and information-theoretic secure verifiable secret sharing,” in Proc. of the 11th Advances in Cryptography, Sydney, Australia, pp. 129–140, 1991. [Google Scholar]

39. P. Shukla, A. Khare, M. Rizvi, S. Stalin and S. Kumar, “Applied cryptography using chaos function for fast digital logic based systems in ubiquitous computing,” Entropy Journal, vol. 17, no. 3, pp. 1–19, 2015. [Google Scholar]

40. O. Ersoy, T. Pedersen, K. Kaya, A. Selcuk and E. Anarim, “A crt-based verifiable secret sharing scheme secure against unbounded adversaries,” Security and Communication Networks, vol. 9, no. 7, pp. 4416–4427, 2016. [Google Scholar]

41. I. Hernanez, T. Ashur and V. Rijmen, “Analysis and recommendations for MAC and key lengths in delayed disclosure GNSS authentication protocols,” IEEE Transactions on Aerospace and Electronic Systems, vol. 57, no. 3, pp. 1827–1839, 2021. [Google Scholar]

42. E. Tijan, S. Aksentijevic, K. Ivanic and M. Jardas, “Blockchain technology implementation in logistics,” Sustainability Journal, vol. 11, no. 4, pp. 1–15, 2019. [Google Scholar]

43. C. G. Akcora, Y. R. Gel and M. Kantarcioglu, “Blockchain networks: Data structure of bitcoin, monero, zcash, ethereum, ripple, and lota,” WIREs Data Mining and Knowledge Discovery, vol. 12, no. 1, pp. 2271–2288, 2022. [Google Scholar]

44. Y. Tseng, Z. Liu and R. Tso, “Practical inner product encryption with constant private key,” Applied Sciences Journal, vol. 10, no. 23, pp. 1–16, 2020. [Google Scholar]