Blockchain-Based Privacy-Preserving Public Auditing for Group Shared Data

1  Introduction

Number of companies and developers turning to cloud service has been growing rapidly in recent years [1,2]. Other than individual users, these enterprise and corporate customers usually work in groups, sharing data with each other. What is more, this exchange of data may sometimes occur among entities across various domains for co-operated research, making use of cloud storage service.

One of the most compelling topics for cloud data is its integrity. Group sharing makes it even more complicate. One group member, which we call it data owner, generates some dataset and uploads it to cloud. The others can access the data and make use of it, which are called data users. To data users, they cannot ensure whether data corruption is due to hardware/software failure, human errors of data owner or some malicious attacks. What makes things even worse, cloud service providers may conceal corruptions from users [3], to avoid their responsibilities and maintain business reputation. Thus, group data sharing brings in more variables for trust between members. A method for group data verification is much needed.

There has been a few of works focusing on checking data correctness in cloud storage. An intuitive approach easy to call up is to retrieve the datasets from cloud and verify some kind of signatures (e.g., RSA) or collision-resistant hash values (MD5, SHA-256, etc.). Even though this method and some improved works [4,5] fulfill the basic demands of data verification, it seems more and more unaffordable since the scale of cloud data has become too large in past few years [6,7]. So, a new idea has been proposed: data owners compute specially designed digital signatures (called “tags”) for their data partitioned into blocks, and verifiers check the integrity of cloud data using tags and some intermediate results based on data blocks, which are offered by cloud storage. This method is called Provable Data Possession (PDP) [8].

Quite a few following works [9–12] paid attention to the topic of employing independent verifier (neither data owner nor cloud service provider) to execute the process of integrity proof verification, which is called public verification, or public auditing. Choosing public auditing may have various reasons, but there are two main ones: on one hand, most users turn to cloud service to save time and money, which means that they may have no enough computation and storage source in local devices, even no enough cryptographic knowledge necessary for executing PDP verification; on the other hand, private verification is a kind of unilateral verification. If user comes up with a negative result “the data is corrupted”, cloud service may dispute it. Public verification can solve these two problems. Wang et al. [9] proposed a privacy-preserving solution which ensured that public verifiers cannot infer the original content of challenged data blocks. In other words, it enables zero-knowledge integrity proving. This point is especially important when public verifier is Third Party Auditor (TPA), or any other data user to whom the owner has not decided to disclose the data. Based on this work, some researchers [13–18] continued to improve various aspects including application scenarios and security. Unfortunately, few works notice the significant difference between personal data and group shared data.

The most striking feature of group data is its sharing among multiple users. Although the basic public auditing scheme can be extended to group scenario, there exists an often-ignored privacy issue involved in data sharing, which we call it identity privacy. To illustrate what is identity privacy, we take an instance as follows. Alice and Bob work together in the same group, relying on cloud service to share data. The shared data is organized following some certain pattern, such as blocks or records. Alice generates a data block mi and becomes its owner. She signs the block with her private key and generates a tag necessary for data auditing. The data user, Bob, wants to make sure whether the data block is intact before downloading it. He challenges the block and authorizes a public verifier to check the integrity proof from cloud. Then, according to the basic auditing scheme, the verifier should use the public key of data owner for proof verification. What is more, if Bob modifies a data block, he should resign the block and upload the new tag. Next time, public verifiers will use his public key to check the integrity of this block. It can be easily inferred that a public verifier is able to obtain the information about the ownership correlation between data blocks and group members. Furthermore, as time goes on, a public verifier will eventually learn the details of which data block is accessed and modified by a certain user, since public keys reveal identities of group members. Finally, the ownership and behavior of group members, a necessary part of privacy, are undoubtedly leaked to public verifiers.

This privacy leaking may bring in unpredictable consequences. Considering a scenario of data assets transaction, Alice and Bob are two entities exchanging their data. Bob wants to know whether the data he will buy is intact. Due to the specificity of data assets, Alice needs a convincing integrity verification scheme that does not require Bob to download the challenged data blocks. It seems that the best way is to turn to a public verifier. However, those auditing schemes with no identity privacy preserving, will reveal valuable information of this transaction: who at which time tries to access whose data.

Wang et al. focused on group auditing and proposed a series of schemes [19,20] to solve the problem. They firstly proposed Knox [19], a group data auditing scheme based on group signatures. Knox relies on a “group manager” to control key generation and signature tracking for all users. It is no doubt that this centralized administrator will raise concerns about key and privacy disclosure. To remedy this defect, again the same authors proposed Oruta [20], using ring signature in the process of generating tags, in order to hide the identity of data owner from public verifier. Thus, we can say this scheme has enabled anonymous data auditing.

However, Oruta ignored an important issue in group data sharing: how to prevent members from malicious activities. Anonymous auditing brings another serious problem, that group members may deny some harmful or incorrect data they uploaded. What is more, when some member quit group, there needs solution to dispose of its data blocks. Since the identities of data owners are kept in secret, we need a convincing mechanism to make sure the quit member is indeed the data owner, not just on one side of the story.

Recently, blockchain-based PDP schemes draw attention of researchers. Han et al. [21] noticed the risk brought by untrusted TPA, but they made a mistake in the smart contract design that allowed CSP to perform replay attacks. Yuan et al. [22] introduced identity-based cryptography into blockchain-based PDP scheme, to avoid the complex certificate management caused by the public key infrastructure. Li et al. [23] tried to add cryptocurrencies to PDP scheme to promote TPA to be more active. And work [24] made some fine attempts in cloud-edge computation scenario. These works proved that blockchain-based PDP is practical, but lacked a full-featured solution to solve the problem of group data auditing.

To solve aforementioned problems, we design a novel blockchain-based anonymous public auditing scheme for group shared data. We choose ring signature for block tag construction to achieve fully privacy-preserving data auditing, and smart contracts to reduce manual intervention and possible repudiation. We utilize distributed ledger to store block tags for better reliability, and more impartial verification.

Contribution. 1) We introduce a construction of blockchain-based PDP scheme, which enables anonymous integrity verification via smart contract. 2) We propose a novel linkable ring signature tag generation method to protect identity privacy. 3) We analyze the security of our proposed scheme and evaluate its performance.

2  Problem Statement

In this section, we firstly describe the framework of cloud-chain integrated auditing system and its security model. Then aiming at the requirements for low performance devices network and security threat, we propose design goals to instruct the following scheme construction. Finally, we give the description of some preliminaries.

2.1 System Model

A system model of blockchain-based group data auditing is shown in Fig. 1. There are three kinds of entities and a blockchain network involved in group data auditing: a group of users, cloud service provider and public verifiers. Different from the work of [14], our scheme does not need to divide users into the original one and newcomers. All the users work in one group and each of them is allowed to access the shared data. Public verifier, role often taken by third-party auditor, can also be any other entities that have no interests involved in data to be audited. Cloud service provider offers storage for shared data, but not like previous works, it does not store meta data used for verification. Distributed ledger of blockchain network take over this duty instead. All of the three entities join in blockchain network and manage shared data via smart contracts.

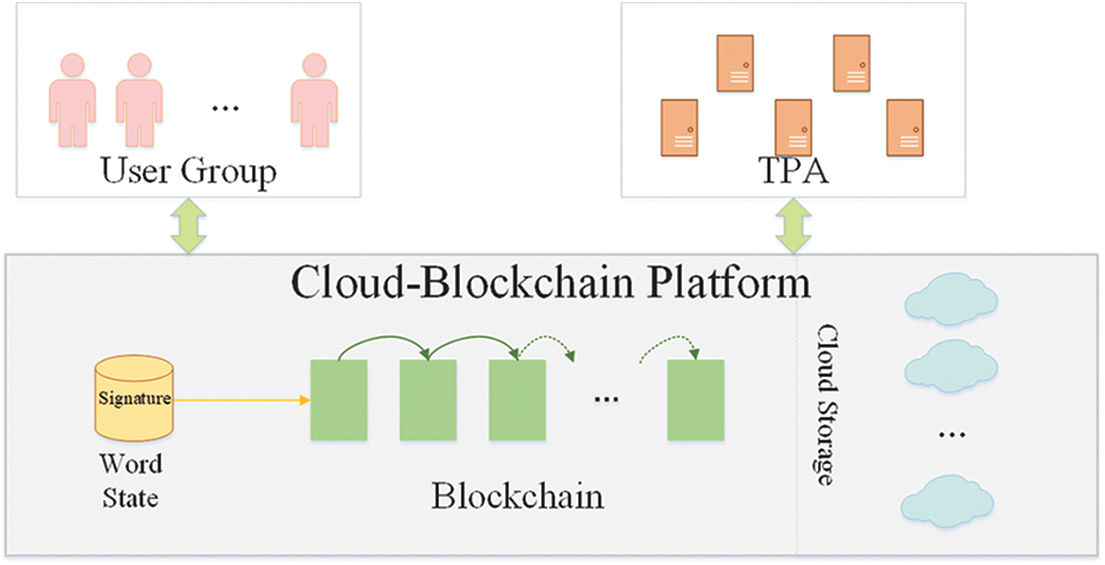
Figure 1: Tag generation time

The process of data auditing scheme in blockchain network is as follows. A group member send an auditing request to cloud service provider by invoking functions defined in smart contracts. The public verifier, playing the role of endorsement node in blockchain network, validate the request, including whether challenged data exists. After auditing request is accepted by blockchain network, cloud service provider compute integrity proof and send it by invoking smart contracts. The submission of integrity proof is wrapped as some kind of blockchain transaction, thus its verification can be naturally imbedded in the process of endorsement. Once public verifiers verify the integrity, they attach their endorsement to the proof, promoting the whole network accept it. In this way, the challenge-response PDP scheme has been transformed into the execution process of smart contracts.

2.2 Threat Model

Except the most basic threats of data corruption as in single user scenario, we also notice that there are other risks particularly lying in the situation of group data auditing.

Collusion Attack. Multiple-user structure of group members bring in new risks rooted in interactions among different entities. Entities participating in data auditing may collude to achieve certain purpose. For instance, data user may collude with verifiers to repudiate cloud storage or data owner, slandering the status of data stored in cloud. On the contrary, cloud service provider and public verifiers can also be complicit in concealing data corruption. Furthermore, data owner may speak on the side of cloud service provider, trying to disprove the adverse verification results made by verifiers and get users to accept its data.

Privacy Leakage. First of all, the owner-member relationship of cloud data is a kind of privacy to the group. Secondly, the identity of user who sends integrity auditing request, including meta data updating caused by data dynamics, should also be considered as secret and confidential information. Two aspects are both indispensable. Without proper identity shielding, a public verifier who engage in auditing work for the same group for a long time, can easily collect enough information to form activity records of every group member. These records can reveal which member accesses and modifies what kind of data at which time, and is able to allow a malicious attacker to distinguish valuable targets.

2.3 Design Goals

Taking aforementioned key points into account, we plan to design a blockchain-based PDP scheme with following features:

1)   Public Auditing: A public verifier is able check data integrity without retrieving any or part of the original content from cloud storage.

2)   Non-repudiation: The final decision on integrity verification is impartial and authentic. That is to say, the possibility of successful arbitrary manipulation of auditing results via collusion attack is negligible.

3)   Identity Unforgeability: Valid meta data can only be generated by group member, using correct private and public keys. Any external or internal parties trying impersonate some group member cannot pass the integrity verification.

4)   Privacy-Preserving: Public verifier cannot reveal owner identity of the data blocks it checks, or the identity of group member who requires the auditing.

3  A New Ring Signature Scheme

On the basis of previous works [9], we found that tags, the most important component of meta data for data integrity verification, are essentially various digital signatures that all have the property of zero-knowledge in common. The reason that most previous schemes failed to support privacy-preserving group auditing is the signature schemes adopted have no corresponding mechanism. Therefore, we choose ring signatures to protect ownership privacy and sensitive activity information for user group.

Unfortunately, most ring signature schemes are not suited for directly used in public verification. Because these schemes are usually designed for message authentication, whose key difference from those for public verifiable PDP is the absence of support for blockless verifiability. Directly sending data blocks to auditors is not only inefficient for communication overhead, but also contrary to the purpose of privacy preserving.

Taking the aforementioned factors into consideration, we design a new linkable homomorphic authenticable ring signature (LHARS) scheme adapted to group shared data PDP. It is extended from a classic ring signature scheme [25]. In the following chapters, we will introduce how the new scheme supports properties necessary for privacy-preserving public PDP via some critical alteration.

3.1 Preliminary

Bilinear Maps

Let G1 and G2 be multiplicative cyclic groups of prime order q and g1,g2 be their generators respectively. Bilinear map e:G1×G2→GT holds properties as follows:

Bilinearity: for all u∈G1,v∈G2 , a,b∈Zq , there holds e(ua,vb)=e(u,v)ab .

Non-degeneracy: e(g1,g2)≠1 .

Computability: there exists an efficient algorithm for computing mapping e in polynomial time.

Security Assumptions

Our scheme is built on two important security assumptions as follows:

Computational Diffie-Hellman Assumption: Consider a cyclic group G of prime order q. Choose g as a random generator of G and random elements a,b from Zq . Given (g,ga,gb) , it is computationally intractable to compute value of gab .

Discrete Logarithm Assumption: Consider a cyclic group G of order q. For any random element a,b of G , an integer k∈Zq that solves the equation bk=a is termed a discrete logarithm. If q is a sufficiently large prime number, computing k in polynomial time is hard.

Linkable Ring Signature

Signature generated in blockchain network has been proved to be practical by work [26,27]. But not all kinds of digital signatures are proper to design a PDP scheme. Ring signature was firstly introduced in 2001, whose name comes from its ring-like structure of signature algorithm. Ring signature is a kind of digital signature that can be performed by any member in a set of users connected by shared keys. And verifiers can learn whether the signature comes from certain set of users by checking its validity. One of the most distinctive securities of ring signature is that it is highly computationally infeasible to determine the real signer identity. The member group used to sign ring signature can be easily set without additional setup, which makes the scheme well suited for ad hoc group.

High anonymity brings in another problem: for a user, how to prove a certain signature is signed by itself without breaking the anonymity? Linkable ring signature solves the problem. Linkability means, two signatures signed by the same user can be proved to have some kind of link, which is called the signatures are linked.

3.2 Constructions of LHARS

The construction of LHAR consists of three components: KeyGen, SigSign, SigVerify.

KeyGen is the setup phase of whole scheme and each member of group should invoke it to generate their own private and public keys. SigSign is the algorithm used by user to generate signature for data block, with user private/public keys and a ring extracted from all the public keys of group members. SigVerify helps a public verifier not only to check the integrity of a data block, but also whether its signature is signed by a group member. Algorithms of LHARS build the basis of privacy-preserving PDP for group shared data, which will be introduced in the next section.

KeyGen. Let G1 and G2 be multiplicative cyclic groups of prime order q and g1,g2 be their generators respectively. Let e:G1×G2→GT be bilinear map. Choose two different collision-resistant hash functions that fulfill H1:(0,1)∗→Zq and H2:(0,1)∗→G1 . The group chooses a private-public key pair for submission as π←Zq,ϱ=g2π .

For each user ui , pick random element xi←Zq as its own private key, and compute the public key following yi=g1xi .

SigSign. Denote the total number of current members in group as d. The public keys of group members are (y1,y2,…,yd) . For a data block m, owner uj computes ring signature in the following way:

1)   Pick (n−1) public keys randomly from all the group members to form a n-member key ring L=(y1,y2,…,yn),1≤j≤n .

2)   Compute h=H2(L) . And y~=hxj .

3)   Choose random element λ←Zq , and compute

cj+1=H1(L,y~,g1λ,hλ)

4)   For other ui,i≠j in ring L, pick random element si←Zq and compute

ci+1=H1(L,y~,g1siyici,hsiy~ci)

5)   Finally, compute

sj=λ−xici

t=(c1g1m)π

The whole signature for data block m is σ=(c1,s1,…,sn,y~,t) .

SigVerify. For a given data block m, corresponding ring L and signature σ=(c1,s1,…,sn,y~,t) , a public verifier checks the validity of signature as follows:

Reconstructs part of the signatures: when 1≤i≤n−1 , compute

zi′=g1siyici,zi′′=hsiy~ci,ci+1′=H1(L,y~,zi′,zi′′)

After that, compute c~1=H1(L,y~,zn′,zn′′) .

Then check the equation e(c~1g1m,ϱ)=e(t,g2) . If it holds, accept the signature; otherwise, reject.

3.3 Security of LHARS

Denition 1 (Unforgeability). Let RSO(L,m) be a signing oracle that accept any inputs as public keys L=(y1,y2,…,yn) and block m, produces ring signature σ which is checked by the signature verification algorithm SigVerify. Denote the verification as V(L,m,σ) . An LHARS signature scheme is unforgeable if, for any PPT (Probabilistic Polynomial-Time) adversary A with a chosen ring L, construct inequation

Pr(V(L,m,σ)=1;ARSO(L))≤ε(k)

For any polynomial ε , the inequation holds. That is to say, with sufficient large prime order, the probability of forging a LHARS signature is negligible.

Definition 2 (Signer Ambiguity). An LHARS signature scheme is signer ambiguous if for any PPT algorithm E , on inputs of any message m, any list L of n public keys, any set of t private keys S=(x^1,x^2,…,x^t) , as well as any valid signature σ on L and m signed by user uj , the probability of extracting user uj from σ is

Pr[E(L,m,S,σ)→uj]={ε(1n−t−1Q(k),1n−t+1Q(k)),x^j∉Sand0≤t<n−1>1−1Q(k),o.w.

for any polynomial Q(k) .

The formula above implies an important fact: if the private key of real signer has not been leaked, its identity is as safe as any other undisclosed member; key exposures of other members will not directly reveal the signer identity, but weaken its security.

Definition 3 (Linkability). Let L=(y1,y2,…,yn) be a list of n public keys, (m1,σ1),(m2,σ2) are two messages with valid signatures respectively generated on L. Denote the signers of σ1,σ2 are u1,u2 . An LHARS scheme is linkable if there exist a PPT algorithm F , that outputs 1/0 with probability

Pr[F(m1,m2,σ1,σ2)=0:u1=u2]≤ε(k)

Pr[F(m1,m2,σ1,σ2)=1:u1≠u2]≤ε(k)

for all sufficiently large k, u1,u2∈L .

4  Blockchain-Based Privacy-Preserving Public Auditing Scheme

4.1 Reliable Signature Storage

An issue that has not been addressed in the past is that, since signature on block is the main and unique evidence for integrity verification, how to ensure retrieving authentic block signature concerns the security of the whole public PDP scheme. In traditional PDP schemes [9], signatures are often stored in cloud storage. When checking integrity, the cloud service provider extracts signatures from its own storage. Unfortunately, just like any centralized solution, cloud signature storage also suffers from data corruption. What is more, encountered with verification failure result, cloud service provider may argue that this is only the consequence of corrupted signature.

To ensure the correctness of signatures and support data dynamics, previous works adopt Merkle Hash Tree (MHT) to manage the corresponding relationship between blocks and signatures. Maintaining the additional data structure brings in complex imbalance problem. Similarly, using MHT stored in cloud cannot determine whether it is the data block or the signature corrupted.

To solve this problem, we exploit a novel blockchain-based solution, which makes use of distributed ledger. Blockchain platforms such as Hyperledger Fabric offer two kinds of storage: one is the sequenced, tamper-resistant record of all the transactions in the past; the other is so-called world-state database that maintains the current state of digital asset. In our proposal, we define a signature as the “state” of responding block. The world-state storage keeps the signatures of every block in the form of key-value database. In our proposal, data operations are wrapped as transactions which lead to transitions of signatures. The sequenced records of blockchain transactions have immutability so that the states of blocks, as the results of such transitions, is also authentic. Tracing back a block to its credible operation records can help reconstruct its signature. In this way, we ensure that blockchain-based signature storage is reliable.

Discussion. Revisit the structure of an LHARS signature σ=(c1,s1,…,sn,y~,t) on block m. Consider that m is an element of Zq and σ contains n+2 elements of G1 , one element of G2 where G1,G2 are cyclic groups with order q. That is to say, the size of every LHARS ring signature is (n+3)×|q| bits. But a closer observation will reveal that the part (c1,s1,…,sn,y~) of signature only relies on the public key ring and random element λ chosen by signer so that different blocks uploaded in the same assignment can share the common part. Denote the number of blocks sharing the same (c1,s1,…,sn,y~) as kp , and the size of ring signatures can be reduced from kp(n+3)×|q| bits to (n+2+kp)×|q| bits.

4.2 Construction of Our Proposal

In this part, we will present our proposed new privacy-preserving group PDP scheme in details, not only the algorithms, but also the process of executing smart contracts. Our scheme consists of five modules: KeyGen, SigGen, Update, ProofGen, ProofVerify.

The relationship of different modules in blockchain-based group PDP scheme is shown in Fig. 2. Each member of group should invoke KeyGen to generate their own private and public keys. Before uploading a data block, data owner uses SigGen for generating ring signature (called “tags”). The algorithm of Update is the complement of SigGen, for deleting or adapting data blocks. The tags, used as evidence for checking integrity proof, are stored in blockchain ledger. ProofGen is algorithm operated by cloud service provider in order to generate aggregated signature proof in response to challenge. Public verifiers can check the correctness of proof by invoking ProofVerify. There are also request and informing modules in the figure, which are system service used by user and CSP provided by blockchain platform. And we omit their details in the following construction.

•   Basic Verification

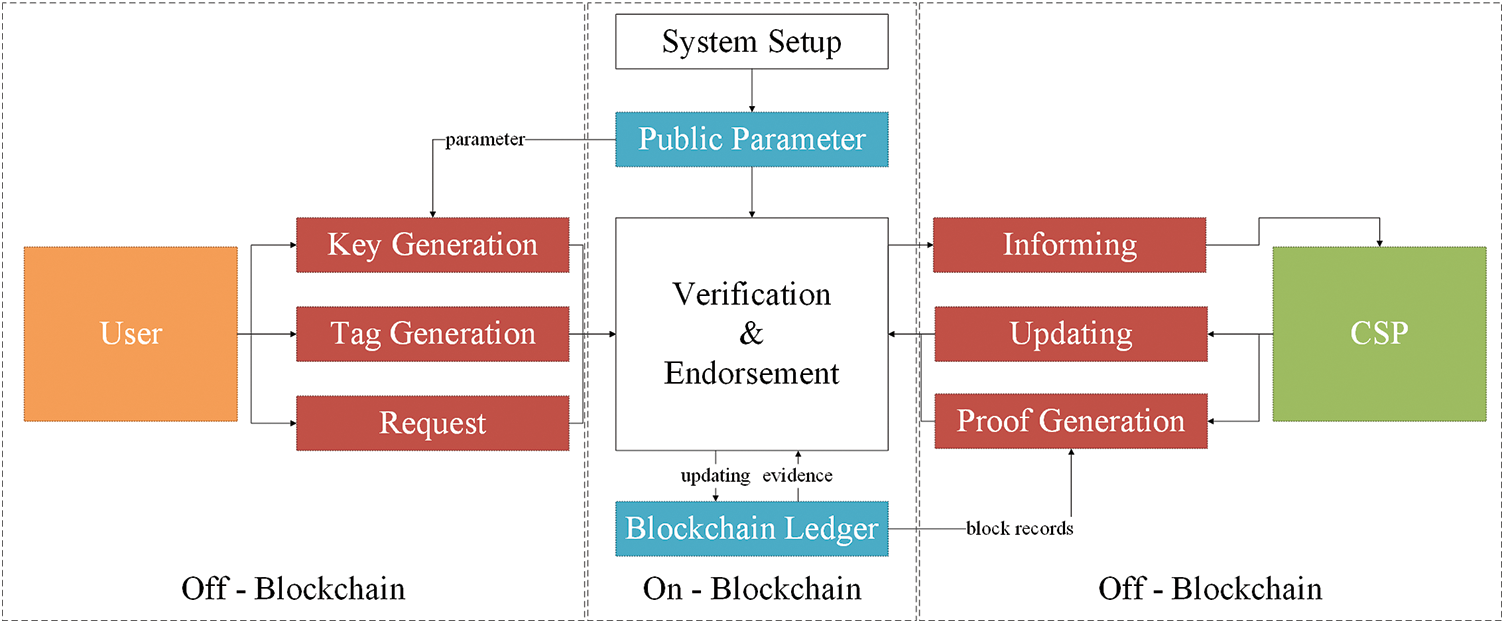
Figure 2: Modules of blockchain-based group PDP scheme

KeyGen. Let G1 and G2 be multiplicative cyclic groups of prime order q and g1,g2 be their generators respectively. Let e:G1×G1→G2 be bilinear map. Choose two different collision-resistant hash functions that fulfill H1:(0,1)∗→Zq and H2:(0,1)∗→G1 . The group chooses a private-public key pair for submission as π←Zq,ϱ=g2π

For each user ui , pick random element xi←Zq as its own private key, and compute the public key following yi=g1xi .

SigGen. Denote the total number of current members in group as d. The public keys of group members are (y1,y2,…,yd) . Given a data block m to be uploaded, its owner uj computes its ring signature in following way:

1)   Pick (n−1) users randomly from all the group members to form a n-member ring L=(u1,u2,…,un),1≤j≤n .

2)   Compute h=H2(L) . And y~=hxj .

3)   Choose random element λ←Zq , and compute

cj+1=H1(L,y~,g1λ,hλ)

4)   For other ui,i≠j in ring L, pick random element si←Zq and compute

ci+1=H1(L,y~,g1siyici,hsiy~ci)

5)   Finally, compute

sj=λ−xici

t=(c1g1m)π

Finally, the signature for data block m is σ=(c1,s1,…,sn,y~,t) .

ProofGen. Considering the case of challenging K blocks with indices (idx1,idx2,…,idxK),K≥1 , generate aggregated zero-knowledge proof. The procedures follow the steps below:

1)   Challenger picks K random element (γidx1,γidx2,…,γidxK) from Zq . Assemble the challenge {(idxk,γk)}1≤k≤K .

2)   Prover computes proof as follows:

According to the number of challenged blocks, choose random element r←Zq and compute R=g2r , in order to masking blocks.

Aggregate the blocks as

μ=γidxk⋅midxk+r

Then send (μ,R) as integrity proof.

ProofVerify. After receiving proof, public verifiers check the integrity in the following way:

For each data block midxk , verifier refers to its record and extracts corresponding ring Lk={yi,k}1≤k≤K .

Then it reconstructs part of the signatures: when 1≤i≤n−1 , compute

zi,k′=g1si,kyi,kci,k,zi,k′′=hsi,ky~ci,k,ci+1,k′=H1(Lk,y~,zi,k′,zi,k′′)

After that, compute c~1,k=H1(Lk,y~,zn,k′,zn,k′′) .

Finally, check the equation

e(∏k=1K⁡c~1,kγidxk⋅g1μ,ϱ)=e(R⋅∏k=1K⁡tidxkγidxk,g2) (1)

If it holds, accept the proof; otherwise, reject.

•   Enable Anonymous Dynamic Verification via Linkability

When we discuss how to “update” a block of group shared data, we can easily divide the scenarios into three cases: adding, deleting and modifying. Obviously, adding a block is in essence the same as uploading a new block, so the method of SigGen can be easily reused.

In cases of modifying, process of dealing with updated new block can also apply SigGen. However, either modifying or deleting has another factor to be considered: how to make sure whether users sending requests are indeed data owners? The authentication of ownership is indispensable for data security, or else any malicious members can arbitrarily change blocks of others. Taking that in account, we use linkability of our ring signature to identify whether the requestor is the real owner of data block.

Theorem X. (Linkability) Let L=(u1,u2,…,un) be a ring constitutive of n group members. Data tags based on ring signature are linkable if there exists a PPT algorithm F1 which outputs 1/0 with

Pr[F1(L,m,m′,σ,σ′)=0:u=u′]≤ε(k)

and

Pr[F1(L,m,m′,σ,σ′)=1:u≠u′]≤ε(k)

for all sufficiently large k, any u,u′∈(u1,u2,…,un) , any data block m,m′ and corresponding tags σ,σ′ . ε is some negligible function for sufficiently large k.

The algorithm F1 outputs 1 when it deems linkability existing in two tags, otherwise it outputs 0.

In our proposal, for two valid data tags σ,σ′ of block m,m′ , it is easy to construct F1 as judgement of whether σ=(c1,s1,…,sn,y~,t),σ′=(c1′,s1′,…,sn′,y~′,t′) holds y~=y~′ . Since σ,σ′ share the same ring L, y~=y~′=[H2(L)]xj generated by the same user uj must holds.

Modifying. Procedure of modifying a block can be seen as uploading a new block m′ to replace the original m. To prove ownership of original block m, data owner only needs to offer the new tag σ′ for checking whether y~=y~′ holds. In this way, we ensure data sovereignty of owners without adding too much extra computation and communication overhead.

Deleting. There is no new block to be uploaded in the case of deleting. Therefore, data owner needs to generate a temporary signature to prove its ownership. Data owner should choose a random message m′ and generate σ′ following the method in SigGen. If y~=y~′ holds and σ′ is a valid tag, the deleting request can be identified as coming from the real data owner.

ProofGen. When a group member tries to verify the integrity of some data blocks, there are two situations: a) the user wants to check some certain blocks; b) the user wants to learn the overall status of whole data blocks. No matter which situation, K blocks with indices (idx1,idx2,…,idxK),K≥1 will be picked out to be challenged. Thus, their procedures follow the same steps:

1)   Pick K random element (γidx1,γidx2,…,γidxK) from Zq . Assemble a challenge request {(idxk,γk)}1≤k≤K and send it to blockchain network.

2)   When cloud service provider receive challenge, it computes integrity proof as follows:

According to the number of challenged blocks, choose random element r←Zq and compute R=g2r , in order to masking blocks.

Aggregate the blocks as

μ=γidxk⋅midxk+r

Then send (μ,R) as integrity proof to blockchain network.

ProofVerify. After receiving proof, public verifiers check the integrity in the following way:

For each data block midxk , verifier refers to its own distributed ledger and extracts corresponding ring Lk={yi,k}1≤k≤K .

Then it reconstructs ring signatures of blocks: when 1≤i≤n−1 , compute

zi,k′=g1si,kyi,kci,k,zi,k′′=hsi,ky~ci,k,ci+1,k′=H1(Lk,y~,zi,k′,zi,k′′)

After that, compute c~1,k=H1(Lk,y~,zn,k′,zn,k′′) .

Finally, check the Eq. (1). If it holds, accept the proof; otherwise, reject.

5  Security and Performance Analysis

In this section, we evaluate the performance of our proposed scheme. We perform a simulation instance of the proposed scheme based on Hyperledger Fabric. The instance is deployed on a Virtual Private Server (VPS) with CentOS 8_x64 system, using 1 CPU core@3.8 GHz, 2048MB RAM and 55GB SSD. The smart contracts are implemented by JAVA, with Pairing-Based Cryptography library (jPBC@2.0.0) and Hyperledger Fabric SDK for JAVA (v1.4.1).

5.1 Security Analysis

In this part, we will discuss the security properties of our blockchain-based PDP scheme, including correctness, non-repudiation, unforeability and privacy preserving.

Theorem 3. (Correctness) The proposed scheme has the property of correctness. That is to say, when most auditors in blockchain network are honest, an integrity proof from CSP cannot pass verification unless the cloud holds correct data.

Proof. Firstly, we should prove that Eq. (1) holds, which builds the basis of ProofVerify. According to the preliminary knowledge, the right-hand side of Equation X can be deduced as follows:

e(g1μ⋅∏k=1K⁡c~1,kγidxk,ϱ)=e(∏k=1K⁡c~1,kγidxk⋅g1γidxk⋅midxk+r,g2π)=e(g1r∏k=1K⁡(c~1,k⋅g1midxk)γidxk,g2π)=e(R⋅∏k=1K⁡(c~1,k⋅g1midxk)π⋅γidxk,g2)=e(R⋅∏k=1K⁡tidxkγidxk,g2)

The last equation holds if and only if c~1,k=c1,k,k=1,…,K also holds. Thus, if a proof passes the checking of Eq. (1), we can ensure that both ownership (contained in c1,k ) and content (contained in midxk ) are correct.

Theorem 4. (Non-repudiation) When most auditors in blockchain network are honest, a minority of dishonest auditors control the end result of integrity verification.

Proof. We have proved the correctness of checking integrity proof above. That is to say, if an auditor is honest, it can always draw a correct result. Since we define the process of checking proof as the validation of blockchain transactions, the authenticity of final decision relies on the mechanism of how blockchain network works. Blockchain network is believed to be tamper-free within less than 51% collusion because more honest auditors will give impartial judgements. Thus, we can say that the proposed scheme can stand up to attacks from a minority of dishonest auditors.

Theorem 5. (Unforgeability) For any member in group or cloud service provider, forging meta data of another member is infeasible in polynomial time if and only if the DL assumption holds.

Proof. Let L=(y1,y2,…,yn) be a given ring of n group members. Assume a PPT adversary A , able to make at most qH times of queries to hash functions H1 and H2 as well as qS times to RSO , can forge ring signature σ with non-negligible probability as

Pr[A(L)→(m,σ):V(L,m,σ)=1]>1Q(k)

where Q is polynomial and k is the security parameter. RSO is a ring signature oracle which returns valid LHARS signatures upon queries of A .

Now we assume that A constructs a PPT simulator M to generate forged signature. Since π←Zq,ϱ=g2π are the common keys shared by group members, we suppose that M holds (π,ϱ) and simplify the problem as follows.

Ring Signing Oracle: Given any data block m, any public key list L=(y1,y2,…,yn) , the ring signing oracle RSO generate a signature. M simulates RSO to generate a signature without holding any secret keys of individual group members.

Without loss of generality, we assume that M randomly picks r←Zq and queries hash function to get h=H2(L) . Then compute y~=hr and chooses c1,…,cn,s1,…,sn . Back patch to

ci+1=H1(L,y~,g1siyici,hsiy~ci),1≤i≤n,n+1→1

Eventually A successfully forges (c1,…,cn,s1,…,sn,y~) and M performs rewind-simulation to generate (c1′,…,cn′,s1′,…,sn′,y~) . Denote the forgery signer of A is j, then M can obtain xj as follows:

cj+1=H1(L,y~,g1sjyjcj,hsjy~cj)

cj+1′=H1(L,y~,g1sj′yjcj′,hsj′y~cj′)

Remember y~=hr , then

sj+cjxj=sj′+cj′xj

sj+cjr=sj′+cj′r

Solve and obtain

xj=sj−sj′cj−cj′

According to Literature [25], the probability of M to achieve a solution is at least (1n(qH+nqS)Q(k))2 , which is non-negligible. Therefore, once A is able to forge signature with an advantage of 1Q(k) , M is able to solve Co-CDH problem with an advantage of (1n(qH+nqS)Q(k))2 . Desired contradiction. Theorem is proved.

Theorem 6. (Privacy Preserving) If and only if DDHP (Decisinal Diffie-Hellman Problem) is hard, in the random oracle model, the probability of distinguishing signer of an LHARS signature is at most 1n , where n is the size of ring list L.

Proof. For any g1,h∈G1 , and 1≤j≤n , the distribution of (c1,…,cn,s1,…,sn) is identical. Therefore, the probability of a PPT adversary A to distinguish cj,sj from (c1,…,cn,s1,…,sn) , in order to point out the signer uj , is at most 1n . Literature [25] gives further detailed explanation.

5.2 Performance Analysis

To evaluate the performance of our scheme, we firstly compare the security properties of our proposal with other two comparable works Knox [19] and Oruta [20]. As shown in Tab. 1, our scheme supports various important properties including public auditing, identity privacy protection, collusion attack resistance and traceability. Though the previous works realized three of them, but no one has successfully integrated all of these before. Thus, we can say our scheme is the most comprehensive work ever done.

To measure the practical performance of our scheme, we also deploy an instance on VPS, which has 1 CPU, 2GB memory and 2TB bandwidth. Based on platform provided by the open source blockchain project Hyperledger Fabric, we implement the chaincode via its SDK for JAVA. Fabric offers pluggable consensus services and editable endorsement policies, as well as necessary membership services and certificate authority management. We configure the benchmark test tool Hyperledger Caliper to evaluate the performance of our blockchain-based PDP scheme. Caliper enables users to write the test and network configuration, then launch an instance and execute required smart contracts defined in given chaincode automatically.

We implement every on-chain algorithm in our scheme, wrapped as functions. All the functions are contained in different scripts written in Node.js, in order to complete various tasks in PDP auditing. When someone wants to execute a certain smart contract, it just needs to run the scripts.

Tag generation time is shown in Fig. 3. The red line with dot “●” is the time for computing one tag of our proposal, while the green line with “▪” is that of Oruta and the purple line with “▲” is for Knox. We control the size of group/ring which is necessary for generating group/ring signatures. The result shows that Oruta is no doubt the highest one among three works, and our proposal is less than a half of Knox when the size of ring is between 2∼10. Knox, as a group signature solution, has stationary performance, since its signature generation does not rely on the size of group. Our scheme, based on ring signature, is also growing linearly. It must be noted that, although the computation cost of ring-based solutions depends on the size of ring, it will not be limitless. Ring signature just need to select a ring with “proper” size to hide the identity of signer. The ring size in our comparison ranges from 2 to 10, which we think is enough to cover most cases in practice.

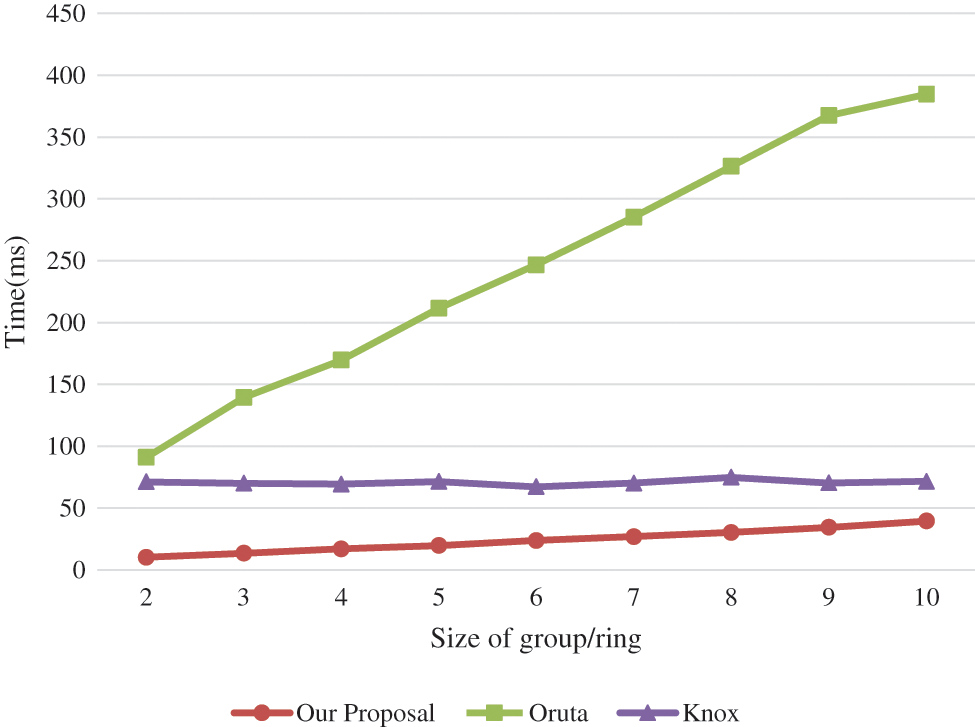
Figure 3: Computational cost for tag generation

Computational cost for integrity verification is shown in Fig. 4. The computing cost increases in member numbers. But the cost of per block is still very low. The red line with dot “●” is the time for computing one tag of our proposal, while the green line with “▪” is that of Oruta and the purple line with “▲” is for Knox. Since all the three schemes are based on bilinear pairing computation, there is no apparent difference in verification computation. There is a slight increase as the size of group/ring grows, but not very apparent. This is because bilinear pairings account for the bulk of the overhead.

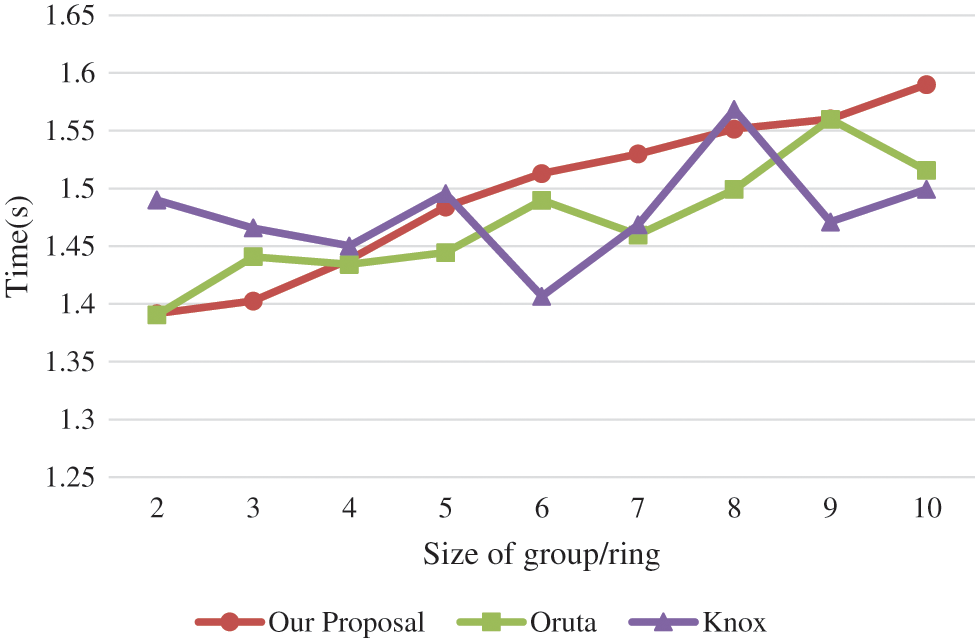
Figure 4: Computational cost for integrity verification

6  Conclusion

This paper focuses on exploring a blockchain-based PDP scheme for group shared data. We analyze the needs of group data auditing and find that resisting collusion attacks and identity privacy are the most important two issues. Blockchain network and smart contracts offer a potential solution of reliable outsourced computation, which makes tag generation and integrity verification free from collusion attack, and linkable ring signature provides support for anonymous data auditing. We design a novel method of LHARS scheme as well as a blockchain-based PDP scheme. Security analysis and performance evaluation prove that our scheme is both secure and efficient.

Funding Statement: The work is supported by the National Key Research and Development Program of China (No. 2018YFC1604002) and the National Natural Science Foundation of China (No. U1836204, No. U1936208, No. U1936216, No. 62002197).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  A. Rudniy, “Data warehouse design for big data in academia,” Computers, Materials & Continua, vol. 71, no. 1, pp. 979–992, 2022. [Google Scholar]

 2.  A. Berguiga and A. Harchay, “An IoT-based intrusion detection system approach for TCP syn attacks,” Computers, Materials & Continua, vol. 71, no. 2, pp. 3839–3851, 2022. [Google Scholar]

 3.  R. Jia, Y. Xin, B. Liu and Q. Qin, “Dynamic encryption and secure transmission of terminal data files,” Computers, Materials & Continua, vol. 71, no. 1, pp. 1221–1232, 2022. [Google Scholar]

 4.  M. Naor and G. N. Rothblum, “The complexity of online memory checking, ” Journal of the ACM, vol. 56, no. 1, pp. 1–46, 2009. [Google Scholar]

 5.  A. Oprea, M. K. Reiter and K. Yang, “Space-efficient block storage integrity,” in Proc. of 12th Annual Network and Distributed System Security Symposium (NDSS), San Diego, California, USA, 2005. [Google Scholar]

 6.  J. Almutairi and M. Aldossary, “Exploring and modelling IoT offloading policies in edge cloud environments,” Computer Systems Science and Engineering, vol. 41, no. 2, pp. 611–624, 2022. [Google Scholar]

 7.  L. Jiang and Z. Fu, “Privacy-preserving genetic algorithm outsourcing in cloud computing,” Journal of Cyber Security, vol. 2, no. 1, pp. 49–61, 2020. [Google Scholar]

 8.  G. Ateniese, R. Burns, R. Curtmola, J. Herring, L. Kissner et al., “Provable data possession at untrusted stores,” in Proc. of 14th ACM Conf. Computer and Communication Security (CCS ‘07), Alexandria, Virginia, USA, pp. 598–609, 2007. [Google Scholar]

 9.  Q. Wang, C. Wang, K. Ren, W. Lou and J. Li, “Enabling public auditability and data dynamics for storage security in cloud computing,” IEEE Transactions on Parallel and Distributed Systems, vol. 22, no. 5, pp. 847–859, 2011. [Google Scholar]

10. X. Tang, Y. Qi and Y. Huang, “Reputation audit in multi-cloud storage through integrity verification and data dynamics,” in Proc. of 2016 IEEE 9th Int. Conf. on Cloud Computing (CLOUD), San Francisco, California, USA, pp. 624–631, 2016. [Google Scholar]

11. Z. Mo, Y. A. Zhou, S. G. Chen and C. Z. Xu, “Enabling non-repudiable data possession verification in cloud storage systems,” in Proc. of 2014 IEEE 7th Int. Conf. on Cloud Computing (CLOUD), Anchorage, Alaska, USA, pp. 232–239, 2014. [Google Scholar]

12. H. Jin, H. Jiang and K. Zhou, “Dynamic and public auditing with fair arbitration for cloud data,” IEEE Transactions on Cloud Computing, vol. 6, no. 3, pp. 680–693, 2018. [Google Scholar]

13. C. Liu, R. Ranjan, C. Yang, X. Zhang, L. Wang et al., “MuR-DPA: Top-down levelled multi-replica merkle hash tree based secure public auditing for dynamic big data storage on cloud,” IEEE Transactions on Computers, vol. 64, no. 9, pp. 2609–2622, 2015. [Google Scholar]

14. Z. Mo, Y. A. Zhou and S. Chen, “A dynamic proof of retrievability (POR) scheme with O(log n) complexity,” in Proc. of 2012 IEEE Int. Conf. on Communications (ICC), Ottawa, Canada, pp. 912–916, 2012. [Google Scholar]

15. Y. Zhu, H. Wang, Z. Hu, G. J. Ahn, H. Hu et al., “Dynamic audit services for integrity verification of outsourced storages in clouds,” in Proc. of ACM Symp. on Applied Computing (SAC ‘11), TaiChung, Taiwan, pp. 1550–1557, 2011. [Google Scholar]

16. Y. Zhu, H. Hu, G. J. Ahn and M. Yu, “Cooperative provable data possession for integrity verification in multi-cloud storage,” IEEE Transactions on Parallel and Distributed Systems, vol. 23, no. 12, pp. 2231–2244, 2012. [Google Scholar]

17. K. Yang and X. Jia, “An efficient and secure dynamic auditing protocol for data storage in cloud computing,” IEEE Transactions on Parallel and Distributed Systems, vol. 24, no. 9, pp. 1717-1726, 2013. [Google Scholar]

18. H. Tian, Y. Chen, C. C. Chang, H. Jiang, Y. Huang et al., “Dynamic-hash-table based public auditing for secure cloud storage,” IEEE Transactions on Services Computing, vol. 10, no. 5, pp. 701–714, 2017. [Google Scholar]

19. B. Wang, B. Li and H. Li, “Knox: Privacy-preserving auditing for shared data with large groups in the cloud,” in Proc. of Int. Conf. on Applied Cryptography and Network Security, Berlin, Heidelberg, Springer, 2012. [Google Scholar]

20. B. Wang, B. Li and H. Li, “Oruta: Privacy-preserving public auditing for shared data in the cloud,” In IEEE Transactions on Cloud Computing, vol. 2, no. 1, pp. 43–56, 2014. [Google Scholar]

21. B. Han, H. Li and C. Wei, “Blockchain-based distributed data dntegrity auditing scheme,” in Proc. of 2021 IEEE 6th Int. Conf. on Big Data Analytics (ICBDA), Xiamen, China, pp. 143–149, 2021. [Google Scholar]

22. Y. Yuan, J. Zhang, W. Xu and Z. Li, “Identity-based public data integrity verification scheme in cloud storage system via blockchain,” the Journal of Supercomputing, vol. 78, pp. 8509–8530, 2022. [Google Scholar]

23. Y. Li, Y. Yu, R. Chen, X. Du and M. Guizani, “IntegrityChain: Provable data possession for decentralized storage,” IEEE Journal on Selected Areas in Communications, vol. 38, no. 6, pp. 1205–1217, 2020. [Google Scholar]

24. Q. Mei, H. Xiong, Y. C. Chen and C. M. Chen, “Blockchain-enabled privacy-preserving authentication mechanism for transportation CPS with cloud-edge computing,” IEEE Transactions on Engineering Management, in press, DOI 10.1109/TEM.2022.3159311. [Google Scholar]

25. J. K. Liu, V. K. Wei and D. S. Wong, “Linkable spontaneous anonymous group signature for ad hoc groups,” in Proc. of Australasian Conf. on Information Security and Privacy, Sydney, Australia, pp. 325–335, 2004. [Google Scholar]

26. C. Li, Y. Tian, X. Chen and J. Li, “An efficient anti-quantum lattice-based blind signature for blockchain-enabled systems,” Information Sciences, vol. 546, pp. 253–264, 2021. [Google Scholar]

27. C. Li, G. Xu, Y. Chen, H. Ahmad and J. Li, “A new anti-quantum proxy blind signature for blockchain-enabled internet of things,” Computer, Material & Continua, vol. 61, no. 2, pp. 711–726, 2019. [Google Scholar]