Evaluation of Codebook Design Using SCMA Scheme Based on A_n and D_n Lattices

1  Introduction

SCMA is a coding domain of Non-Orthogonal Multiple Access (NOMA), and its subclass has been investigated in further detail. The NOMA deals with orthogonal Resource Elements (REs) in a non-orthogonal manner to the users, with the same REs to many users being distributed to them in a non-orthogonal manner. In any system where the resource elements are shared, the system’s spectral efficiency improves, which in turn boosts the demand for mobile Internet [1–3]. Various NOMA approaches are grouped into three primary groups [4], each of which is described below. 1. NOMA with multiple domains, 2. NOMA with power domains, and 3. NOMA with code domains The SCMA is part of a revolutionary code-domain NOMA [5] system that was developed recently. The variance of the Low Density Signature has been especially addressed in this scheme, as well (LDS). In each RE, there is sharing among the active users inside or a subset of the establishing structure of sparse, similar to how LDS is structured. Multidimensional constellations (MdC) maps with incoming bits to distribute that information, however unlike Quadrature Amplitude Modulation (QAM), SCMA users disseminate that information using their pre-assigned REs, rather than QAM (QAM). SCMA transmits the varied symbols of REs, as opposed to LDS, which transmits the repetition of QAM symbols over the same symbols of REs. SCMA is a component of multidimensional constellations in each case (MdC). On a number of different levels, SCMA [6] and LDS are contrasted. It is thus possible to consider the LDS to be an SCMA special class whose repetition of QAM takes the MdC form. Because of its multidimensional constellation and contrast with Pattern division multiple access (PDMA), SCMA provides a feasible functioning, as illustrated in [7]. Another performance of sum-rate comparison is observed in the Power domain NOMA with SCMA [8], where it is demonstrated that the SCMA achieves the needed performance despite the larger complexity of the system in this case. There are several NOMA schemes research [9] that are carried out, and one of the studies discovered that code-domain NOMA has better resilience with higher accuracy for more connectivity than other NOMA schemes. It is very necessary to study a range of critical features with the Code-domain NOMA at purely SCMA because of the increased performance that it provides. In this manner, it follows one of the most compelling applications of SCMA uplink. The uplink systems service communications of the SCMA, in particular, will be addressed in more depth in this section [10–12].

Recent developments in 5G communication have sparked increased interest, owing to the fast advancement of mobile communication technology. 5G communication is extremely supportive of three main typical scenarios, which are enhanced Mobile Broadband (eMBB), massive Machine Type Communications (mMTC), and Ultra Reliable Low Latency Communications (uRLLC) [13,14]. These scenarios are enhanced Mobile Broadband (eMBB), massive Machine Type Communications (mMTC), and ultra reliable low latency communications (uRLLC). Smart city applications [15] and intelligent transportation systems [16] both rely on 5G communication, which is critical in both applications. The SCMA model is shown in Fig. 1 with all of the constituent blocks along with the relationships between each step. It is stated in this work that lattice theory-based codebook design is described with just minor modifications to achieve performance enhancement while still maintaining a low cost. Several ways may be used to locate the mother constellations, which will be used to determine the difference between the code word in that codebook design set. The constellation points with power variation can be found using a variety of approaches. When using the conventional lattice constellation in conjunction with mapping matrices, it is possible to generate the mother constellation. A rotational scheme is developed for this production of mapping matrices. From the above, it is possible to get the mother constellation by utilising ordinary lattice constellations, and the characteristics of matrices mapping with rotation constellation are explained in more detail. Together with the mother constellation and the matrices produced from the codebook sets, they provide a complete picture. Section 2 of this document has a more detailed organisation of the remainder of the work under the title contribution. Introduction to the system concept is provided in Section 3, and the suggested codebook architecture is discussed further in Section 4. A comparison is made between the BER performance of the Original Codebook (OCB) and the proposed codebook in Section 5.

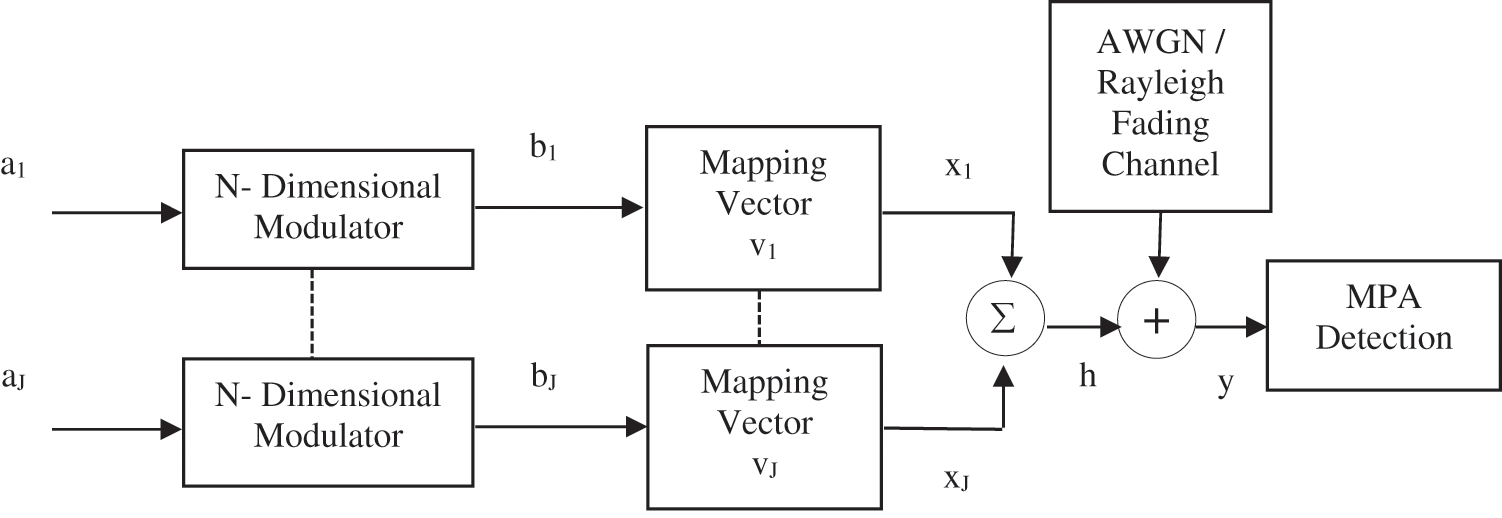
Figure 1: SCMA system model

2  Contributions

Recently, several works described that uplink channels, particularly unity rotations of the multidimensional constellation, which do not have an impact on the performance of sparse code systems due to random Rayleigh fading, were attributed between users in the same way that multi-dimensional constellations were attributed between users. Another point of contention is that the transmission of uplink ration, as well as the lower limit of Euclidean distance between the signals, govern the BER performance and communication dependability of the SCMA uplink system, according to certain sources. The appointment of above same between sparse users connected with Channel of Rayleigh fading has been thoroughly explored in past work, and it is possible that the performance may suffer as a result of the appointment.

With a multistage optimization approach, an efficient method for sparse code multiple access uplink system is sought. To construct a multidimensional mixture of the mother constellation, these subsets of 2D lattice constellation and its method must be combined. Following that, the mother constellation has been merged with the user of matrices mapping in order to build a new sparse codebook design that provides effective bit error rate performance for the user.

Specifically, it is discussed in this work how a sparse codebook design was carried out on the basis of lattice theory, with particular emphasis on the mother constellation approach, which aids in the differentiation of codewords.

The current research focuses on the development of matrices that include constellation rotation in conjunction with the mother constellation.

3  System Model

An uplink SCMA system with an overloading ratio has J users and K time-frequency resources, where λ = J/K. Prior to encoding, user j∈{1,⋯,J} is given as pre-allocated codebook as xj=[x1j,⋯,xMj] with size M=|xj| which can be expressed as,

xj=vjCj, (1)

where vj is a K×N(K>N) binary mapping matrix, with each column of vj containing only one element in addition to element 0. The code words that map into the resources occupied by jth user are represented by N-dimensional complex constellation Cj=[c1j,⋯,cMj] . In SCMA, the structure of J users sharing K resources can be represented by a K×J factor graph matrix F=[f1,⋯,fJ] containing REs and the user nodes (UNs).

The fj calculated by vj as

fj=diag(vjvjT), (2)

where Fkj=1 represents that the j th UN is linked to the k th RN. Fig. 2 shows that examples of factor graph F4×6 for J=6 users and K=4 resources with the connection relationship between UNs and REs, N=2 . During transmission, log2(M) bits of j th user are mapped into xmj picked out from the codebook xj . When all the users are sync the SCMA uplink system, it receives the signal y will be

y=∑j=1J⁡hjxmj+n, (3)

where xmj=[xmj1,⋯,xmjK]T indicates the K -dimensional complex codeword, and hj=[h1j,⋯,hKj]T is the gain of the channel j th user and the noise vector n=[n1,⋯,nK]T conforms with the complex Gaussian spread CN (0,σ2I) .

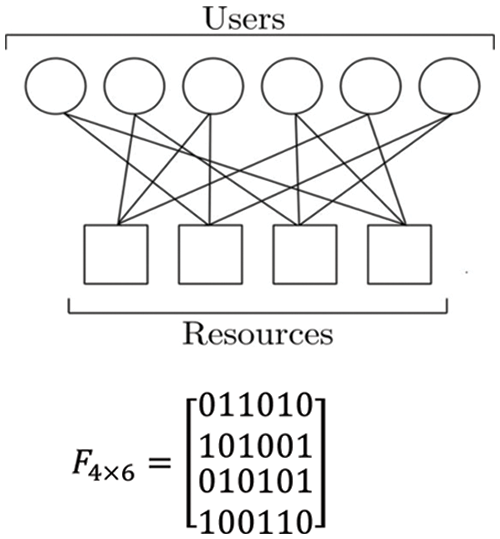
Figure 2: An example of the factor graph F4×6 for J=6 users and K=4 resources with the connection relationship between UNs and REs, N=2.

The following flow graph shown in Fig. 3 shows that the step-by-step process of codebook designs by the SCMA technique for the proposed system model. As the standard SCMA design is used in this research work, the implementation taken from the modified algorithm with the following graph.

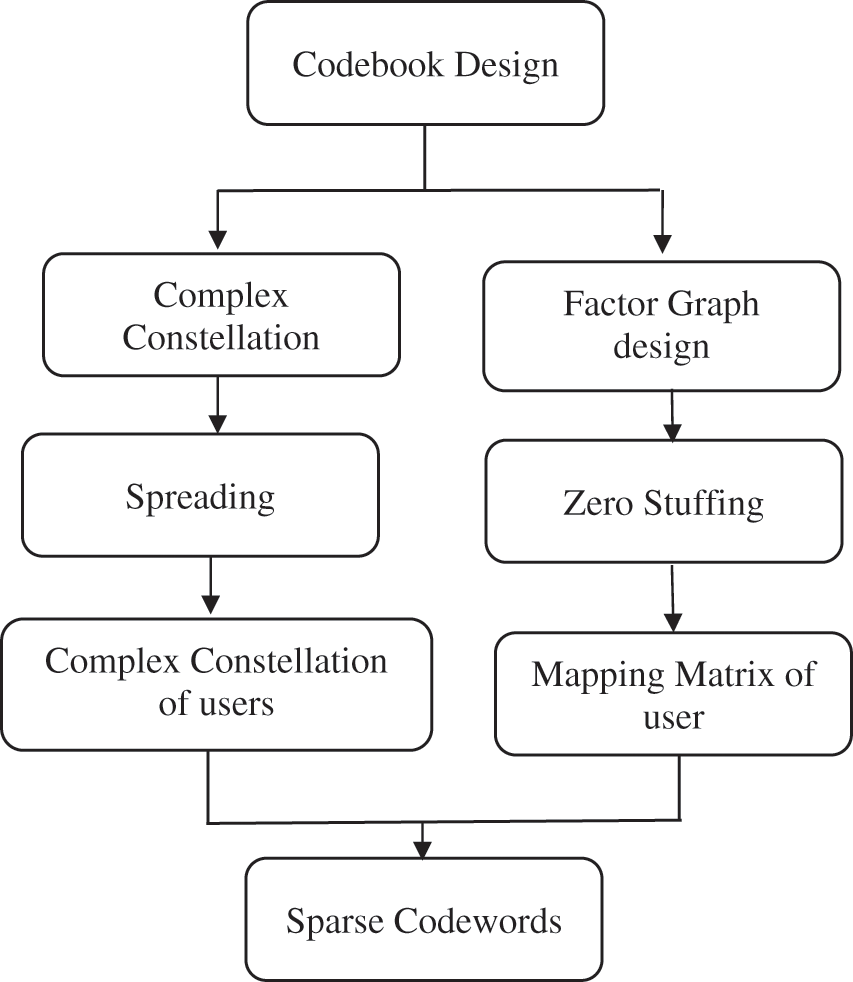
Figure 3: System flow graph of proposed codebook design technique

4  The proposed Codebook

To design SCMA codebook C∈CK×M×J , we designed complex mother constellation C∈CN×M from 2N -dimension real lattice codes such as An,Dn and formation of codebook for j th user Cj∈CK×M using complex mother constellation C , constellation rotation operation Δj∈CN×N and mapping matrices vj∈ZK×N .

A. Lattice Codes

In lattice n -dimensional Λn is a distinct additive subgroup of Rn . Whatever, the lattice was received by assuming that the integral manipulation of vector basis. From this vector basis assumed as column, the gives matrix G∈Rn×n is produced that Λn=GZn .

Take, for example, a lattice with a generator matrix G such that Gi is lower-triangular with diagonal elements that are prime powers. It is well-known that lattices such as A n, D n scaled by M satisfy these conditions, and the above-mentioned lattices demonstrated that these lattices have effective shaping advantages.

B. Formation of Mother Constellation from Lattice Codes

Obtain a real constellation R∈Rv×M with M points [pm]m=1M nearest coordinate origin of v=2N -dimension lattice codes,

R=[p1p2⋮pM]T=[p11p21p12p22⋯pM1⋯pM2⋮⋮p1vp2v⋱⋮⋯pMv] (4)

with average energy EavgR given by

Eavg=1M∑m=1M⁡‖pm2‖ (5)

Complex of the mother constellation C has fabricated through dimensional pairing of R . Because all columns in C contain non-zero elements of a code word in a set of codebooks, the mother constellation, with the most noticeable variation between columns [p1,…, pm] can be recognized. In this study, assumption of (n) represents, n th row of C variation, can be expressed [13,14]

Φ(n)=∑m=1M⁡(|cnm|2−Eavg),n∈[1,N]. (6)

Hence, the power variation maximized can be described like

argmax[pm]m=1M⁡(∑n=1N⁡Φ(n))s.t.cnm=pn1m+i∗pn2m, (7)

n1≠n2,n1,n2∈[1,v].

where I denotes the imaginary unit of measurement. Generally, the constellation dimension Ri is not more prominent, and this work made use of the exhaustive technique for Eq. (7) to get the N-dimensional complex multi-constellationC, which is not often seen.

C. Formation of SCMA Codebook from Mother Constellation

All of the components of the mother constellation code words are sent to and from the different resource nodes. Despite this, there exist d fusers that may be used to determine the location of each resource node. It is important to execute a similar constellation operation to the various users on the RN mentioned above in order to get the desired result. Constellation operations include permutation operations, constellation rotation operations, and complex conjugate operations, amongst others. Above and beyond full operations, the constellation rotation may be used to distinguish between distinct users. In order to identify the users of RN [16], the diagonal matrix _jas operation of the constellation is stated as follows: In order to differentiate the users of RN.

Δj=[eiθρ1u⋱eiθρNu], (8)

where ρn the position of element in n th column of K×N mapping matrix vj of j th user, θρnu denotes the rotation angle given by

θρnu=α(π2df),α=(ρn+u−N)mod(df),u=1,⋯,df, (9)

With different constellation operation ΔjN×N , the SCMA codebook differently identified the j th user can be expressed as

Cj=ΔjN×NCN×M. (10)

Steps to Perform The Proposed Technique

1.    Declare the resources of orthogonal, number of users and codewords number in each codebook

2.    Declare the number of frames in SCMA signals.

3.    Input signal with SCMA codebooks and estimate channel coefficients

4.    For following parameters find all values of SNR in Rayleigh channel

5.    i) Noise power

ii) Joint Encoding and Fading Channel propagation

Calculate the SCMA signal after fading channel to find the performance.

•   Define the 2-dimensional real mother constellation vector.

•   Convert the real value to complex.

•   Obtain the 2-dimensional complex user matrix, multiply the user specific value with 2-dimensional real mother constellation vector.

•   Multiply the above result with user defined mapping matrix to get codebook value for the user defined values.

D. Mother Constellation Generation

The minimal Euclidean distance, k, is normalised in the SCMA system’s mother constellation design, and it is envisaged as the system’s finding parameters. Increasing the low Euclidean distance, on the other hand, does not just result in an improvement in the execution. The energy variety of the codeword components, the low Euclidean distance of the mother constellation, and the energy diversity between the tones are all parameters of the mother constellation that influence the growing SCMA performance. In addition to improving bit error rate performance, the codeword parts should be spaced as far apart as possible in either energy or space, if possible.

E. Log MPA Decoding

Decoders for the Message Passing Algorithm (MPA) were designed to provide performance that was close to Maximum Likelihood while requiring the least amount of complexity. There are various exponential calculations in MPA that are used to figure out extrinsic data and the odds of receiving a signal from the outside world. Fig. 4 depicts a sketch of the SCMA block design, which includes a decoder for multiple access downlink, which is detailed in detail.

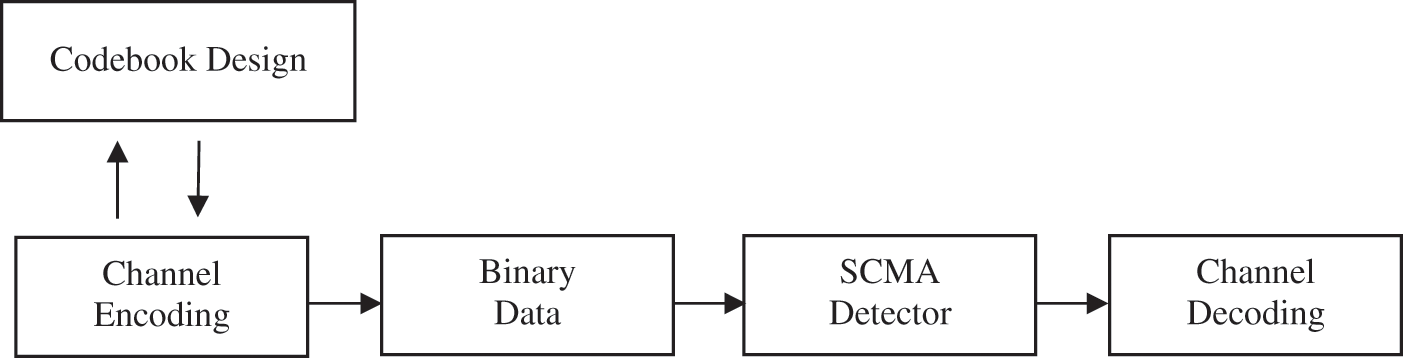
Figure 4: Outline view of SCMA block diagram decoder for downlink multiple access

The block diagram presented in Fig. 4 depicts the cascade stages of encoder, channel, and decoder, which process binary data from a codebook developed by SCMA and shown on a computer screen. The extrinsic information of computing in the logarithmic domain, which is a traditional method for overcoming this bottleneck, has been developed in advance, leading to the formulation of the log-MPA decoder. The MPA’s BER performance and complexity are compared to those of the log-MPA, and it is determined that employing log MPA with a small number of content authorising rounds produces a good trade-off between performance and complexity. We look at several techniques to determine the complexity of implementing MPA in 5G communication, including sparse codebook design with a small number of projections, clustered MPA (CMPA), which determines sub-graphs in MPA before running it, and it selected those exponential computations that are difficult to implement in MPA.

5  Simulation Results

The suggested method with OCB and Log-MPA employing multi-detector are compared based on the results of this research of performance assessment. A 4 and D 4 lattices are used in this simulation to create the mother constellation, which has N = 2 elements. Comparison of the BER of suggested design codebook and OCB schemes with different M when = 150 percent and OCB schemes with various M when = 200 percent is presented using Rayleigh channel.

5.1 Result and Discussions

The exponential message passing algorithm (MPA) with BER performance analysis is defined as Eb/N0 = 18 dB, and the rate of error is around 10-3 and 10-1 for permutation and SCMA schemes, respectively, based on the permutation and SCMA schemes. The simulation result, which contains the varied values obtained from the iterations carried out throughout the execution, is listed in Tabs. 1 and 2, respectively. The BER produced from the simulation reveals that it is falling, while EbN0 is increasing with the A4, B4, A8, and D8 lattices, as seen in the graph. The BER performance of SCMA in our suggested system is better for less than the Eb/N0 of the above-mentioned article, as shown by the results of the simulation Figs. 5 and 6.

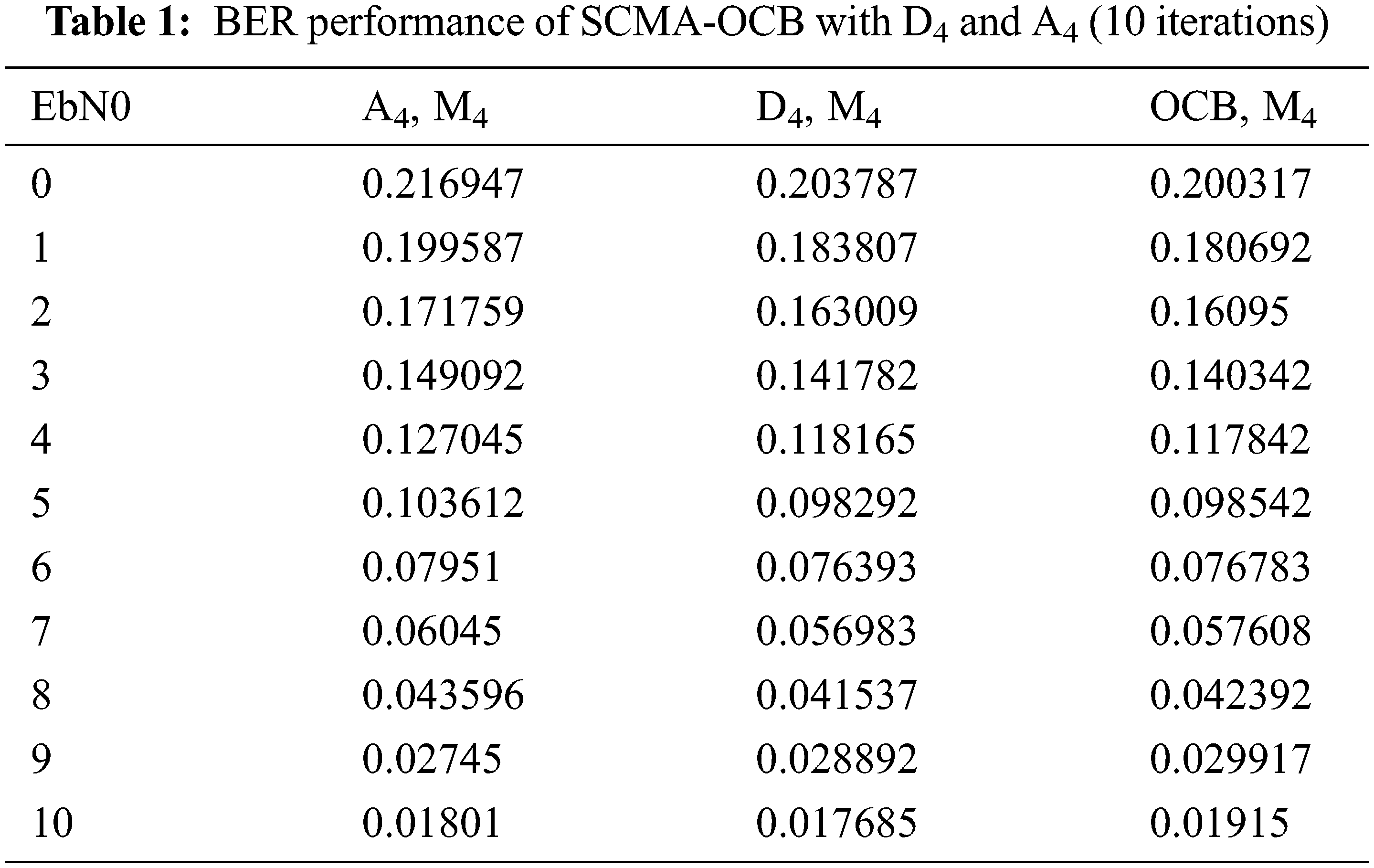
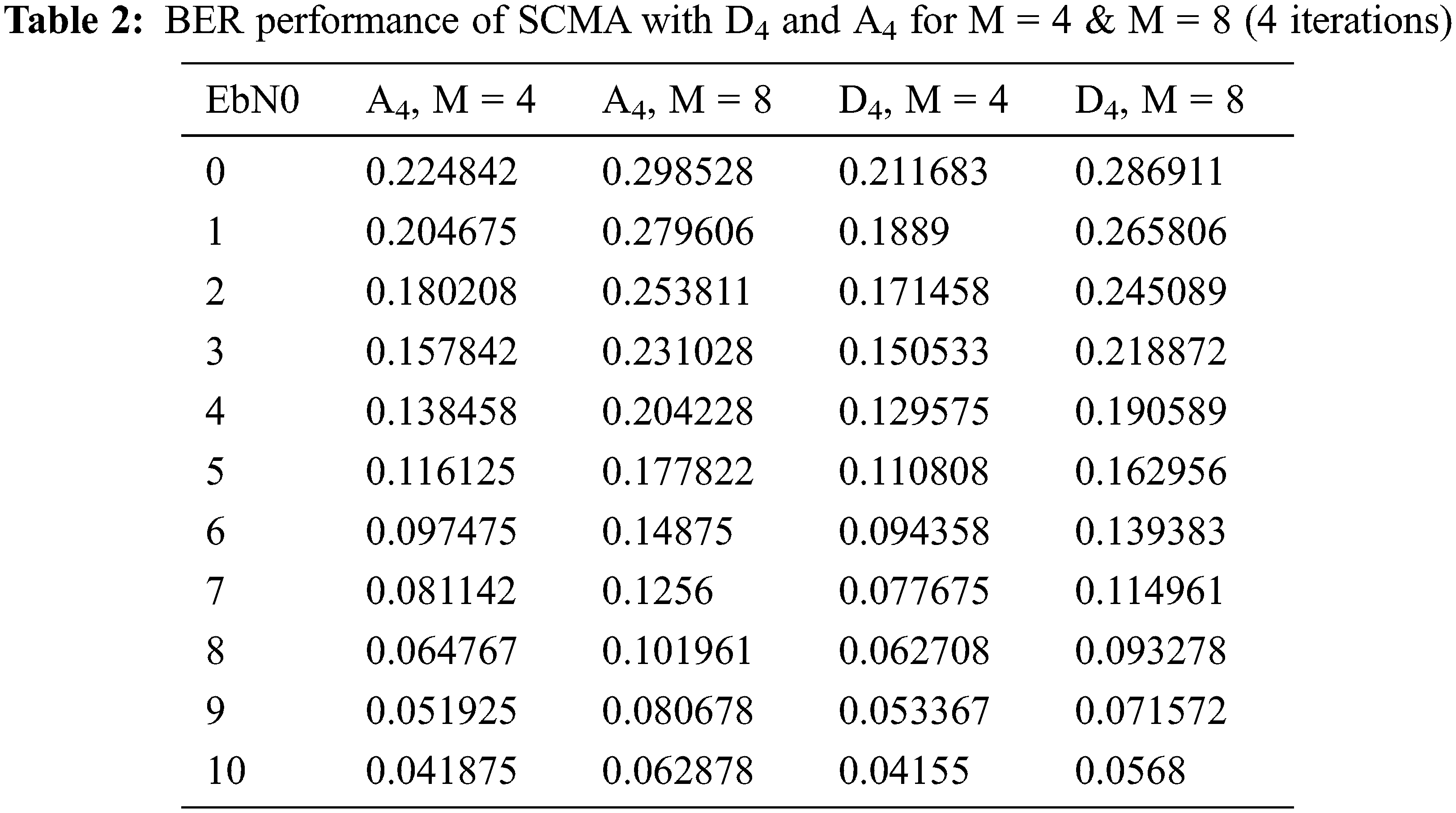
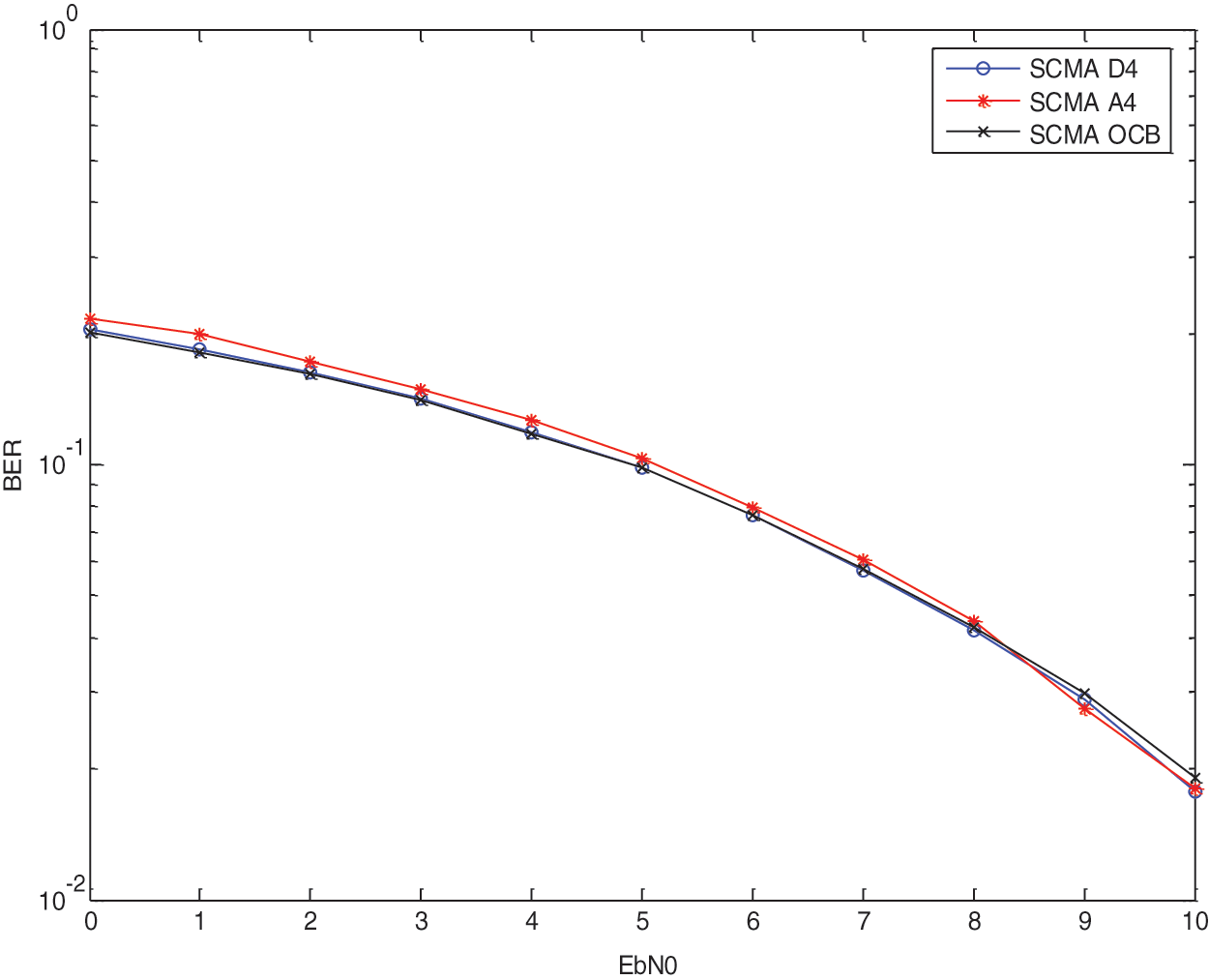
Figure 5: BER performance comparison with M = 4 and λ = 150%

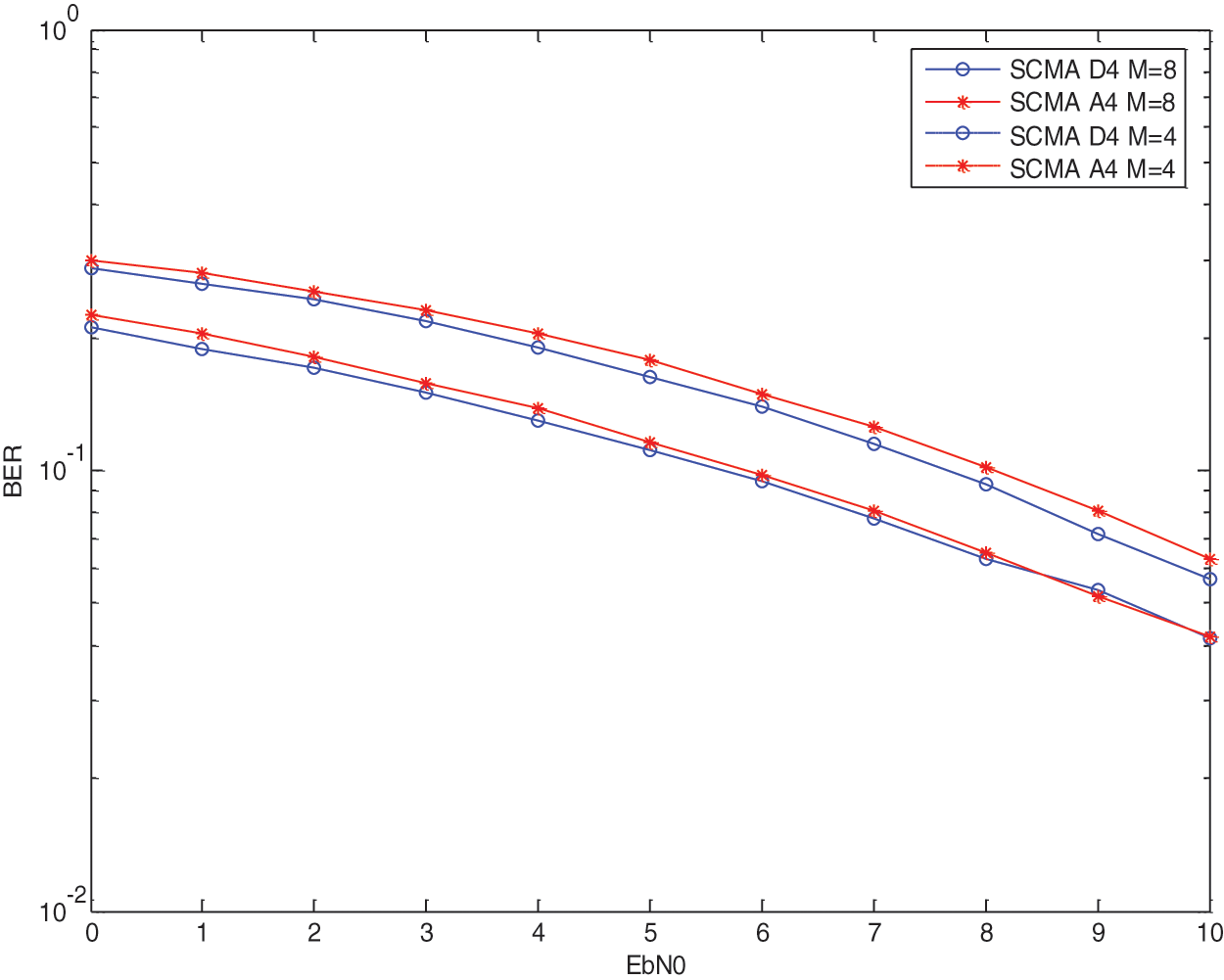
Figure 6: Comparison of BER performance A4andD4 with M = 4, M = 8 and λ = 150%

AWGN and Rayleigh fading channel performances are compared to one another, and AWGN is determined to be the superior of the two channels since it has the lowest bit error rate under log-MPA schemes. The performance of the Rayleigh fading channel is not up to the level of the other comparison channels, despite the fact that the difference between the two channels is minimal, and the BER of this channel has been influenced by this scheme. The different values produced from the simulation are tabulated in Tabs. 3 and 4 for the lattices A4 and D4 with the values of M = 4, M = 8, and are shown in the following table: Figs. 7 and 8 provide a comparison of the decrease in BER for the iterations that have been completed, respectively.

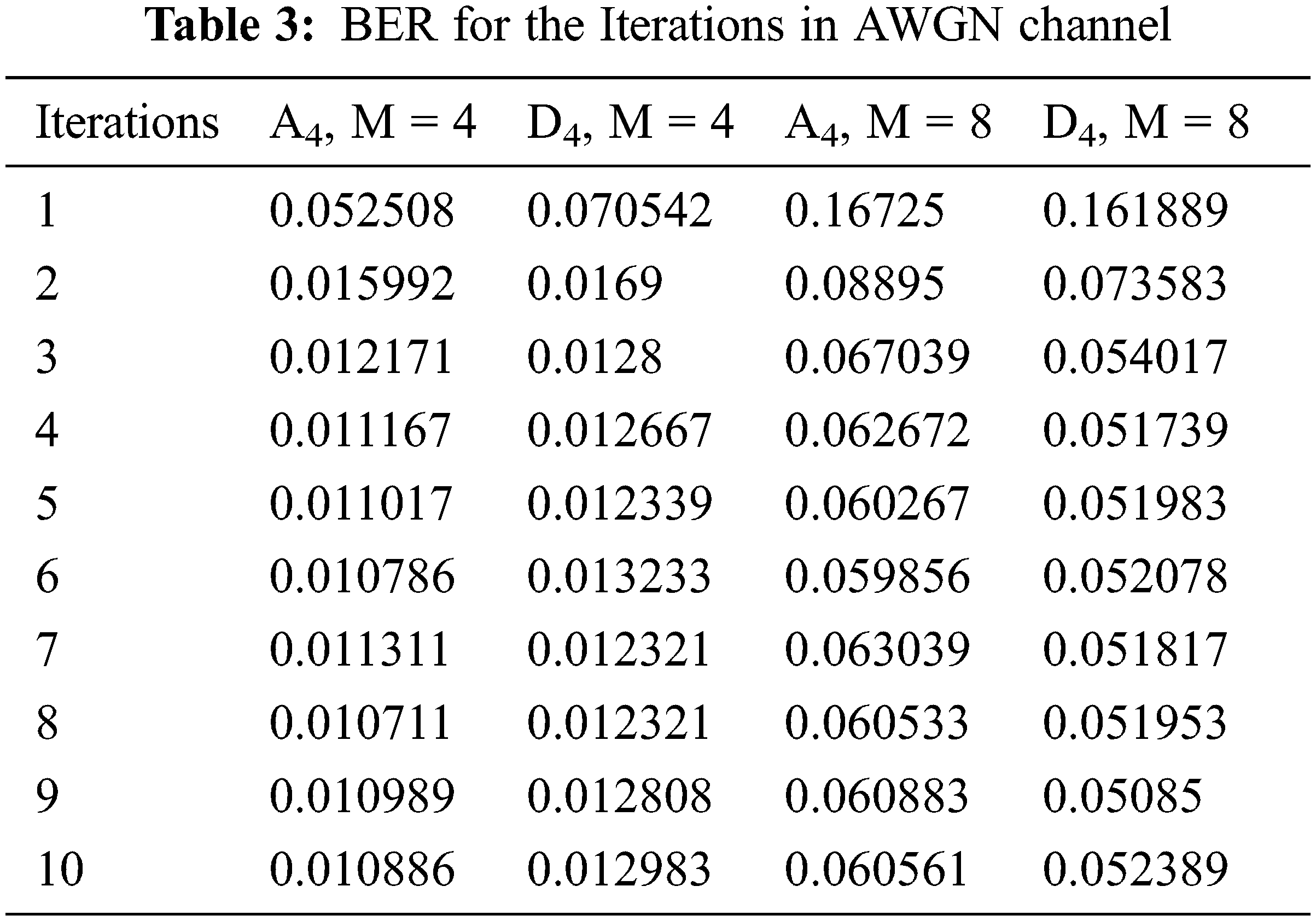
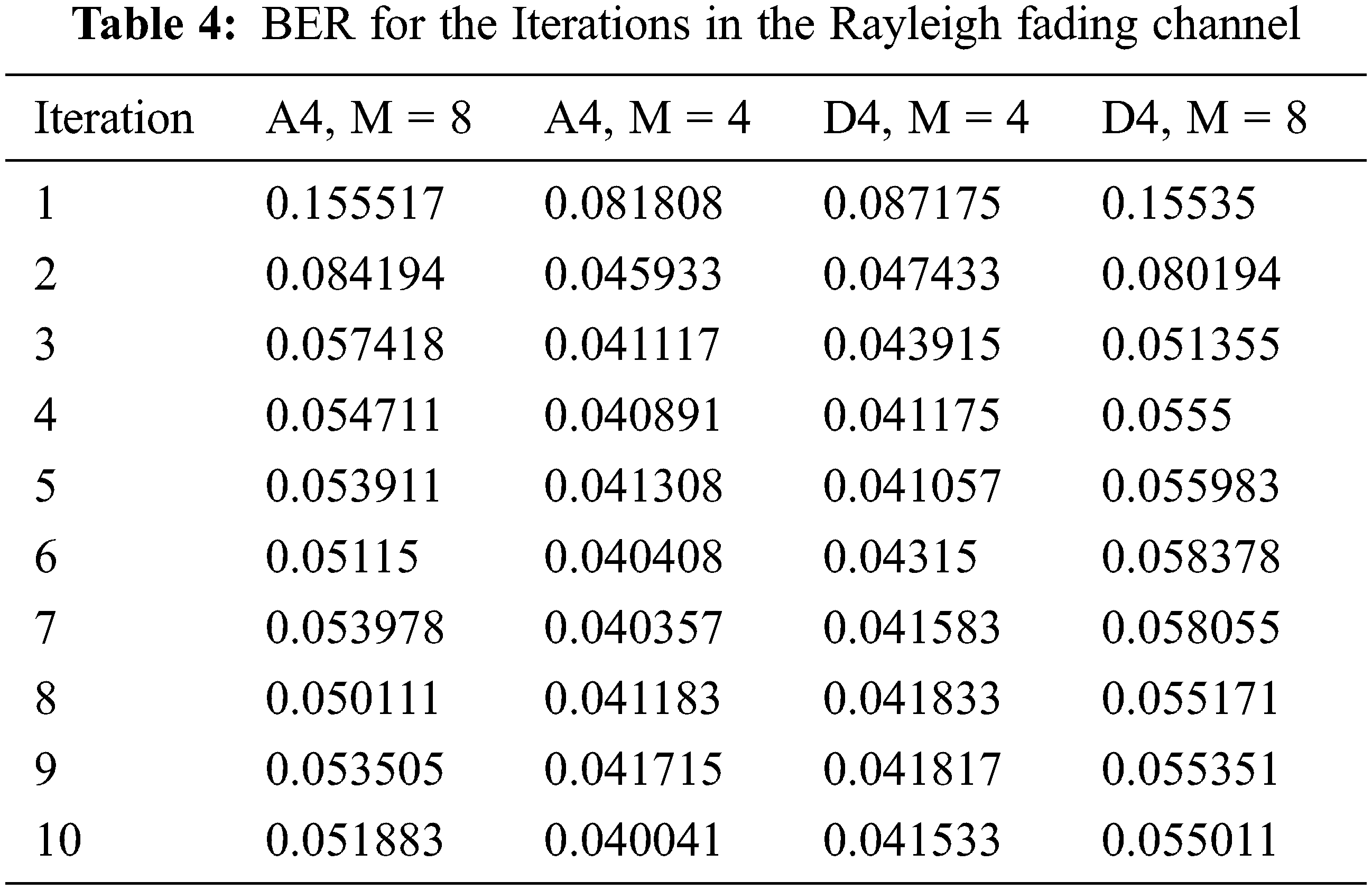
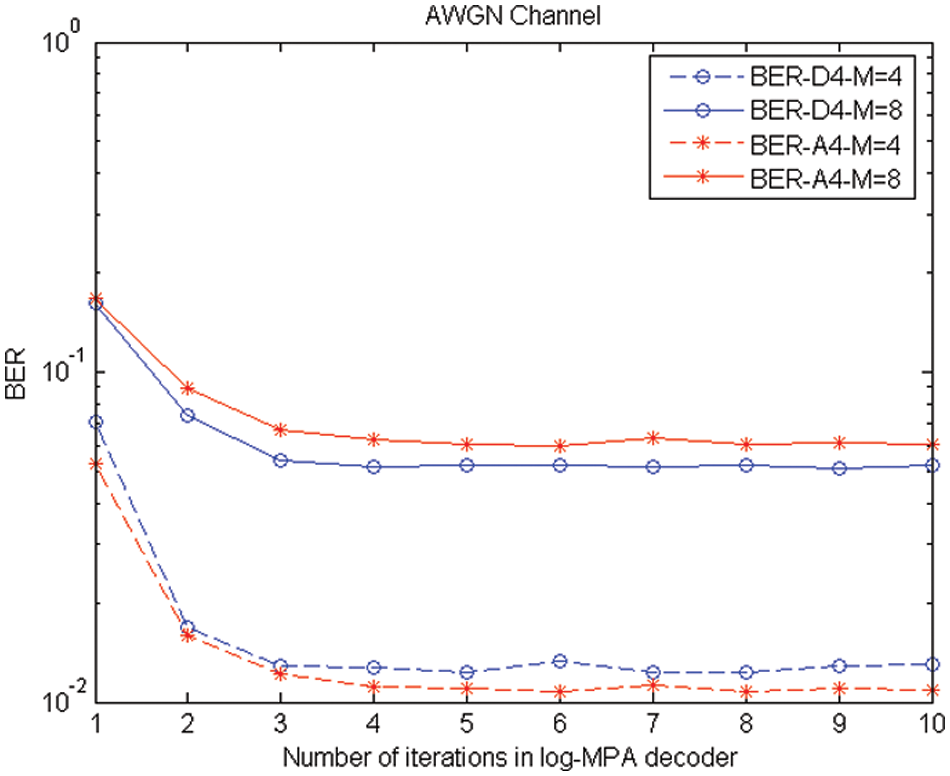
Figure 7: BER performance comparison of AWGN Channel

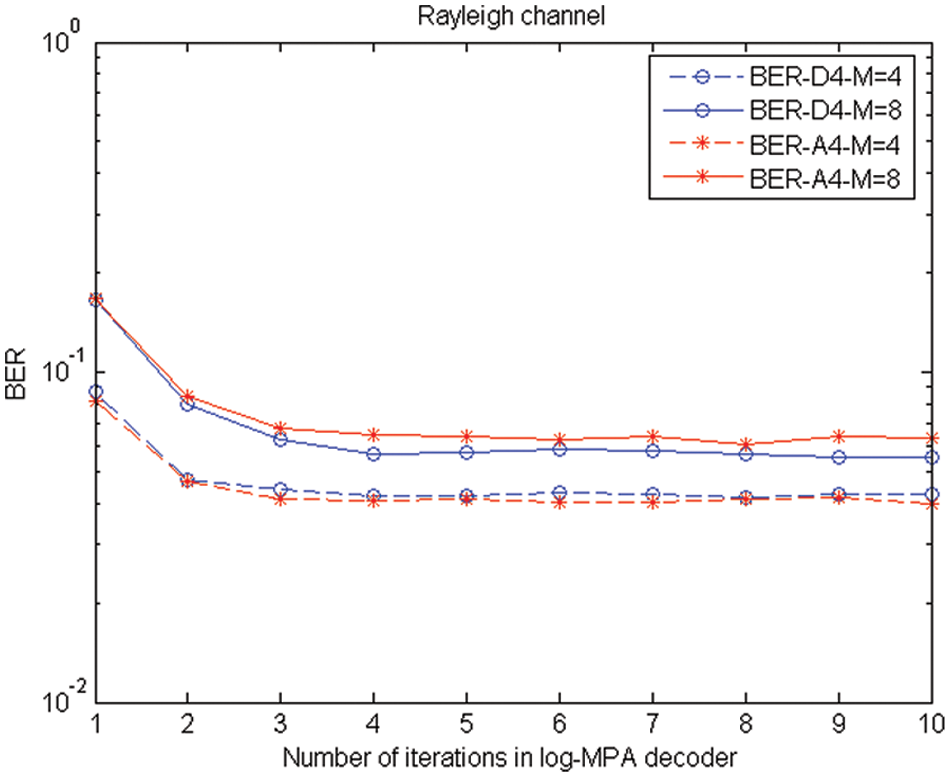
Figure 8: BER performance comparison of Rayleigh fading channel

According to the explanation above, AWGN produces positive outcomes. In this way, the SCMA approach with codebook design works better when used in conjunction with lattice, as presented in this unique design, which results in increased gain and stability for mobile communication applications.

6  Conclusion

The current work presents a unique codebook design SCMA that is reliant on lattice theory and is described in detail. As a result of the use of A n and D n lattice codes, it is possible to construct a literal constellation with M constellation directions and a high shaping gain. All users are familiar with the combination of a power-varying mother constellation with many dimensions, as well as with the mapping matrices created with the constellation rotation and the codebook sets that were formed with the constellation rotation. The simulation illustrates the comparison of the proposed codebook design scheme with the existing codebook design scheme. The size of the codebook and the overload ratio of SCMA systems have an influence on the BER performance of the system. Because of this, the SCMA approach is recommended for 5G communications in order to get greater performance in conjunction with lattice combination.

It will be possible to utilise different MPA in the decoder to distinguish the performance and raise the gain with the same approach in the future by using different MPA. To achieve this, an increase in the number of iterations may be proposed, and optimization of codebooks using the same approaches results in improved stability in the gain and complexity of the techniques used. The suggestions made throughout these rounds may have included experimenting with different approaches to boost the pace of execution.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  L. Yuanwei, Q. Zhijin, E. Maged, D. Zhiguo, N. Arumugam et al., “Non-orthogonal multiple access for 5G and beyond,” Proceedings of the IEEE, vol. 105, no. 12, pp. 2347–2381, 2017. [Google Scholar]

 2.  J. Wang, A. Jin, D. Shi, L. Wang, H. Shen et al., “Spectral efficiency improvement with 5G technologies: Results from field tests,” IEEE Journal on Selected Areas in Communications, vol. 35, no. 8, pp. 1867–1875, 2017. [Google Scholar]

 3.  P. Porambage, J. Okwuibe, M. Liyanage, M. Ylianttila and T. Taleb, “Survey on multi-access edge computing for Internet of Things realization,” IEEE Communications Surveys & Tutorials, vol. 20, no. 4, pp. 2961–2991, 2018. [Google Scholar]

 4.  Y. Cai, Z. Qin, F. Cui, G. Ye Li and J. A. McCann, “Modulation and multiple access for 5G networks,” IEEE Communications Surveys & Tutorials, vol. 20, no. 1, pp. 629–646, 2018. [Google Scholar]

 5.  W. Fan and C. Wen, “Low complexity iterative receiver design for sparse code multiple access,” IEEE Transactions on Communications, vol. 65, no. 2, pp. 621–634, 2017. [Google Scholar]

 6.  M. Vameghestahbanati, I. D. Marsland, R. H. Gohary and H. Yanikomeroglu, “Multidimensional constellations for uplink SCMA systems—A comparative study,” IEEE Communications Surveys & Tutorials, vol. 21, no. 3, pp. 2169–2194, 2019. [Google Scholar]

 7.  B. Wang, K. Wang, Z. Lu, T. Xie and J. Quan, “Comparison study of nonorthogonal multiple access schemes for 5G,” in Proc. IEEE Int. Symp. on Broadband Multimedia Systems and Broadcasting, Ghent, Belgium, pp. 1–5, 2015. [Google Scholar]

 8.  M. Moltafet, N. M. Yamchi, M. R. Javan and P. Azmi, “Comparison study between PD-NOMA and SCMA,” IEEE Transactions on Vehicular Technology, vol. 67, no. 2, pp. 1830–1834, 2018. [Google Scholar]

 9.  Z. Wu, K. Lu, C. Jiang and X. Shao, “Comprehensive study and comparison on 5G NOMA schemes,” IEEE Access, vol. 6, pp. 18511–18519, 2018. [Google Scholar]

10. Y. Yuan, Z. Yuan, G. Yu, C. H. Hwang, P. K. Liao et al., “Non-orthogonal transmission technology in LTE evolution,” IEEE Communications Magazine, vol. 54, no. 7, pp. 68–74, 2016. [Google Scholar]

11. Y. Chen, A. Bayesteh, Y. Wu, B. Ren, S. Kang et al., “Towards the standardization of non-orthogonal multiple access for next generation wireless networks,” IEEE Communication Magazine, vol. 56, no. 3, pp. 19–27, 2018. [Google Scholar]

12. M. Beko and R. Dinis, “Designing good multi-dimensional constellations,” IEEE Wireless Communications Letters, vol. 1, no. 3, pp. 221–224, 2012. [Google Scholar]

13. Y. Zhou, Q. Yu, W. Meng and C. Li, “SCMA codebook design based on constellation rotation,” in IEEE Int. Conf. on Communications (ICC), Paris, France, pp. 1–6, 2017. [Google Scholar]

14. H. Yaoyue, P. Zhiwen, L. Nan and Y. Xiaohu, “Multidimensional constellation design for spatial modulated SCMA systems,” IEEE Transactions on Vehicular Technology, vol. 70, no. 9, pp. 8795–8810, 2021. [Google Scholar]

15. F. Zhu, Y. Ren, Q. Wang and J. Xia, “Preservation mechanism of network electronic records based on broadcast- storage network in urban construction,” Journal of New Media, vol. 1, no. 1, pp. 27–34, 2019. [Google Scholar]

16. X. R. Zhang, X. Chen, W. Sun and X. Z. He, “Vehicle re-identification model based on optimized densenet121 with joint loss,” Computers, Materials & Continua, vol. 67, no. 3, pp. 3933–3948, 2021. [Google Scholar]