Breakdown Voltage Prediction by Utilizing the Behavior of Natural Ester for Transformer Applications

1  Introduction

Oil-filled transformers are inevitably a part of the power system network, used to step up or step down voltages. The reliable function of the transformer depends on the significant tasks of insulations such as solid and liquid [1]. But the reliability is stipulated by the breakdown strength of the liquid insulation [2]. Any slight change in the breakdown strength of the liquid insulation deteriorates enforce stress on the solid insulation [3]. The breakdown strength is mainly affected by adding water content to the oil or generating polar compounds due to an ionization reaction [4]. This leads to the weakening of the insulation capabilities of solid insulation. Such a process reduces the tensile strength of the solid insulation and increases the rate of polymerization reaction [5]. Hence, the breakdown voltage of the liquid insulation must be high and must not show a propensity to water molecules and the ionization process. Naturally, ester oils are slower to water saturation and possess high breakdown strength than mineral oil [6]. When such insulating oils are subjected to accelerated aging at high temperatures, the oils show inconsistent responses in their breakdown strength as the day progresses. As a result of the unpredictable behavior of oil, the transformer may be exposed to early failures and wear-out failures.

The use of petroleum-based MO as power transformer liquid insulation infers the importance of NE as a potential substitute for MO [7,8]. Researchers over two decades frequently address the dielectric and environmental factors to replace the MO with environmentally friendly insulating fluid [9]. The dielectric properties of the MO are poorer than the silicone-based fluids and NE. Also, the depletion of petroleum resources and ample availability of natural resources indicates that there must be a replacement sooner [10]. The development of NE for transformer applications includes MO, silicone-based oils, and various ester-based industry-grade insulating fluids. The dielectric capability of MO is inferior to silicone fluids and ester-based insulating fluids. Several efforts were taken to investigate the performance of the NE is attributed for recent years, from 2015 [11–13].

The dielectric performance of the NE against the MO and silicone-based insulating fluids reported by researchers specify several possibilities to investigate edible and non-edible NE available in the market [14,15]. The dielectric condition of the liquid insulation is assessed by measuring the breakdown voltage. It is essential to understand the behavior of the liquid insulation under room temperature and pressure (RTP) [16,17]. Moreover, the presence of the impurities such as moisture, dust, and ionic substances weakens the dielectric strength of the liquid insulation [18]. Therefore, it is imperative to measure the breakdown strength of the liquid insulation before conducting any other test. In addition to the survival of NE, the prediction plays a significant role in determining correlation and effects on aging. In that addition, the reliability of the NE is of reliable importance to state the alarming probability. The condition of the survival of these NE is used to investigate the survival rate of the NE over MO under the HVAC test. The tested oils are studied under different electrode geometry to understand their electric field distribution and leakage current characteristics. The breakdown voltages and the leakage currents are used to develop mathematical functions using an exponential function. Heat-tolerant NE NE1, NE2, and NE3 are used for investigation, subjected to HVAC under various electrode geometry. Equally, the electric field distribution of the liquid insulation under different geometry is integral to ensure that the electric field distribution varies according to the electrode shape [19,20].

The electric field distribution varies in the edges of the axially symmetrical electrodes than the electrode that is radially decreased by curvature [21]. The electric field distribution in two-dimensional space is analyzed using a partial differential equation using a finite element model [22]. The survival function of the sample is used to determine the survival rate of the oil under test [23]. The survival function tells us how the liquid insulation survives the leakage currents caused during the breakdown [24]. In other words, the survival function is the product of a continuous random variable over time [25]. Such behavior is empirically generated as a hazard function, and failure probability [26] is evaluated using the Weibull model. The fitted model is converted into a nonparametric model to see what a bathtub curve for the sample looks like. This enables us to understand the different stages of the hazard rate of an oil sample along with the breakdown strength probabilities. Hence analyzing the NE behavior under HVAC with other electrodes geometry and developing the survival function helps propose the NE as a suitable environmental-friendly substitute to petroleum-based mineral oil. In our investigation, the base oils (NE1, NE2, and NE3) were collected from the local markets of Kovilpatti, Tamilnadu, India. The oils were taken to the Liquid Dielectrics laboratory of the National Engineering College for processing and testing.

2  Recent Literature Study

Currently, Artificial Neural Network (ANN) studies are employed in various fields and applications [27,28]. ANN provides an unsupervised control over the variables; the complexity of the network structure in the non-linear domain and confidence interval of the predicted results are challenging to obtain. On the other hand, fuzzy predictions are like human reasonings and use simple mathematics for non-linear systems involving complex and straightforward solutions. The complex solution to determine the critical status of the power transformer by combining the dielectric characteristics under electrical, mechanical, and thermal. The results indicate a higher accuracy in classifying the transformer’s necessary quality and current prevailing conditions [29]. Further studies in the later years to predict the health index of the transformer are assessed using the fuzzy diagnostic vector that has an accuracy of 98.13% for the fault conditions [30]. To design the high voltage devices, fuzzy logic models were developed to evaluate the breakdown voltage conditions. The study came up with predictions that provide the insulation barrier between the air and rod-plane. The results suggest using a dielectric barrier to increase the breakdown voltage [31]. Further, in later studies, to improve the reliability of sensing fault’s severity by integrating multiple attributes of the power transformer [32]. Later multi-attribute studies of power transformers were conducted using fuzzy logic. The system uses a concentration of dissolved gases, test results of the transformer oil, and the paper insulation test results. The results suggest that integrating multiple attributes provides accurate results with a limited number of inputs and fuzzy rules [33]. Recently a real-time fuzzy-based system model to monitor the condition of the power transformer was developed. The study used the rule-based model to correlate the outcome and predict insulation lifetime. Studies prove that the thermal aged synthetic ester increases the dissipation factor or dielectric loss of insulation [34]. Based on the above literature, in our research, two dielectric properties, kinematic viscosity and water content (moisture), are the input variables. The output variable is the breakdown voltage. A set of rules relating to the relations between the input and output variables is developed, and the model is trained. Mamdani model is used to train the rules and predict the breakdown voltage. The model is employed to produce a surface model plot showing the relationships between the input and output variables. This correlation between the variables is used to interpret the interdependence effects on the overall quality of the natural ester. The different literature leading to the selection of fuzzy systems is given in below Tab. 1.

3  Test Methodology

The HVAC test procedure is carried out using the below setup in Fig. 1, consisting of a coupling capacitor, H.V. testing transformer TEO 100/20 with a rated voltage is 2 × 0.22/100/0.22 kV, and an oil-test chamber. The setup is controlled by a control panel arrangement that can sense the leakage current using the Rogowski sensor connected to the ground electrode. The geometry of the test electrodes is classified into S-S, P-P, PL-PL, and R-R as presented in Fig. 2 by keeping the distance between the electrode as 1, 2, and 3 cm. The electrodes are made of stainless steel. Generally, the various factors that affect the breakdown voltage are nearby earthed objects, atmospheric conditions like humidity and temperature, and irradiation. Here, the oil is placed in a closed chamber without the space for the atmospheric air to enter and oxidize the oil. The primary voltage of the H.V. testing transformer is varied slowly until the breakdown occurs in the oil under the test. The events before the study of liquid insulation are presented in Fig. 3. The H.V. end is coupled to the capacity voltage divider used to record the applied voltage during the test.

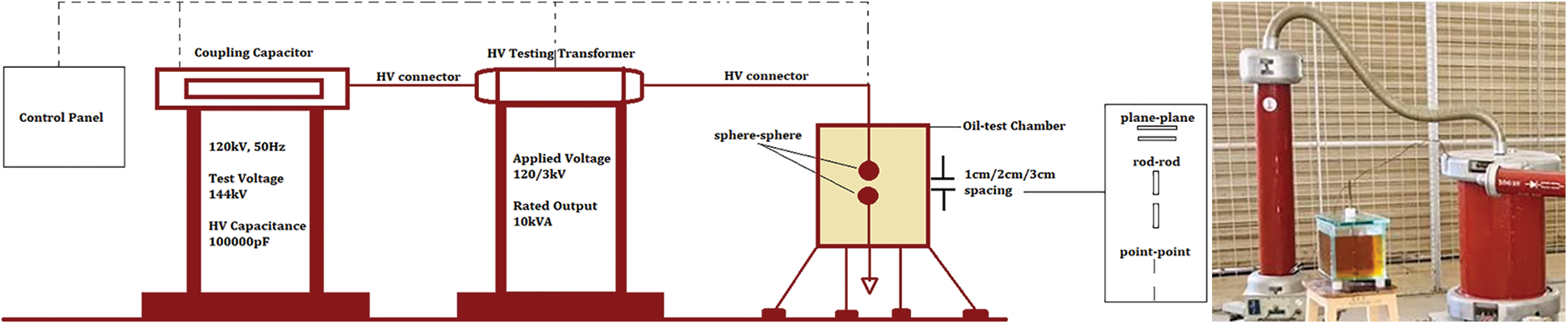
Figure 1: Experimental setup for HVAC test under different electrode configuration

Figure 2: Different configuration of electrodes a) Point-Point, b) Rod-Rod, c) Plane-Plane, and d) Sphere-Sphere

Figure 3: Events of failure of liquid insulation a) Flashover, b) Breakdown and c) post-breakdown

4  Results and Discussion

The breakdown strength of the NE under different electrodes and electrode gap spacing is presented in Tab. 2. The breakdown voltage has a linear relationship with the gap spacing like that of gaseous breakdown; according to the hypothesis of Pachen’s law, the breakdown voltage is a function of the pressure of the gas and the distance between electrodes. Here, the breakdown voltage event had a close connection with the leakage current measured before the inception of the breakdown process. The NE performs well in every electrode geometry. Also, the performance of the NE not only depends on the molecular stability but also on the geometry of the electrode used for the test. The leakage current shows how the electrode geometry affects the breakdown strength of NE. The S-S electrode geometry shows better field distribution with very low leakage current magnitude, followed by PL-PL. However, the edge effect of the PL-PL geometry shows higher leakage than the S-S geometry. On the other hand, R-R and P-P show very high leakage currents due to uneven field distribution and gathering of space charges near the pointed edges.

The primary cause of the leakage is caused due to capacitive leakage. At power frequency (50 Hz), the liquid does not experience a change in the capacitive component, but the resistive component causes leakage current. This randomly ionizes the free electrons and gathers them between the electrodes. This results in the formation of an electron bridge between the electrodes and leads to the breakdown of the liquid insulation. The voltage and leakage current functions are used to develop the exponential function in Eq. (1) with the 95% confidence interval

f(x)=a∗exp(b∗x) (1)

The exponential function determines the exponential growth in the leakage current with the rise in the voltage. The function f(x) is the leakage current function that will vary with every change in the voltage function ‘x.’ Here, breakdown voltage and leakage current are exponentially related. Tab. 3 displays the parameters of the exponential function and its correlation with the electrode geometry. The correlation of the exponential function from Tab. 3. Proves that the S-S geometry has the highest voltage acceptance with significantly less leakage current, followed by PL-PL, R-R, and P-P.

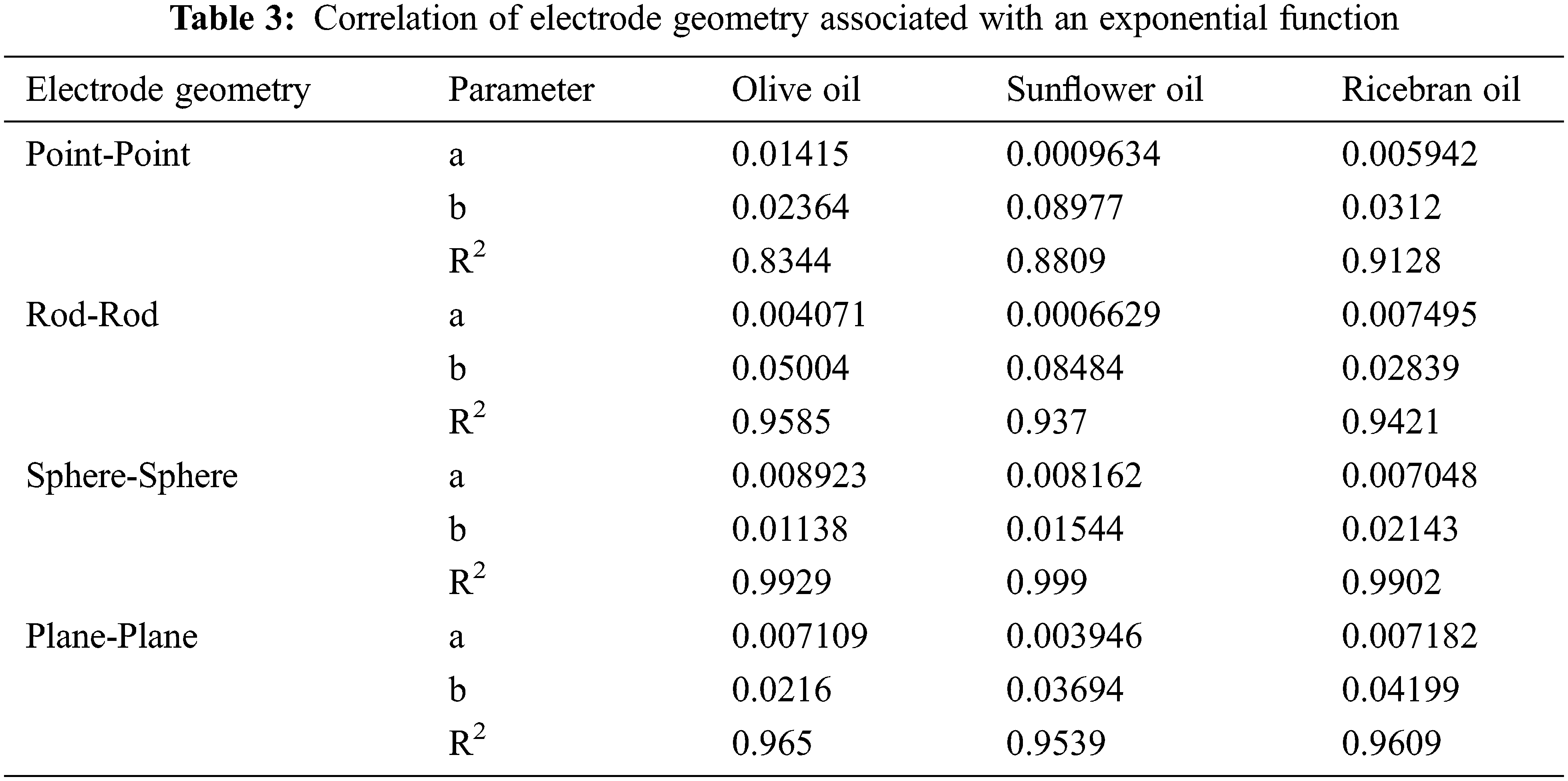
The exponential distribution shows the correlation between the breakdown voltage and the leakage current for various electrode geometry. It clearly shows that R2 is close to 1 for the S-S electrode; following that, R2 begins to reduce for the PL-PL, R-R, and P-P electrodes.

5  Prediction of Dielectric Properties Using Fuzzy Logic

The design is focused on the effect of kinematic viscosity and water content of the natural esters on its breakdown voltage. The input variables of the fuzzy logic controller are the kinematic viscosity and water content, and the output variable, breakdown voltage measured according to the standards of IEC [35] and ASTM [36–41]. The fuzzy logic controllers for NE1, NE2, and NE3 are shown in Fig. 4. The Fuzzy Inference System (FIS) model is based on the Mamdani model, a rule-specific to predicting the output variable by the correlation shown in Fig. 5.

Figure 4: The correlation between the input variables (A, B) and output variable (C) of FIS

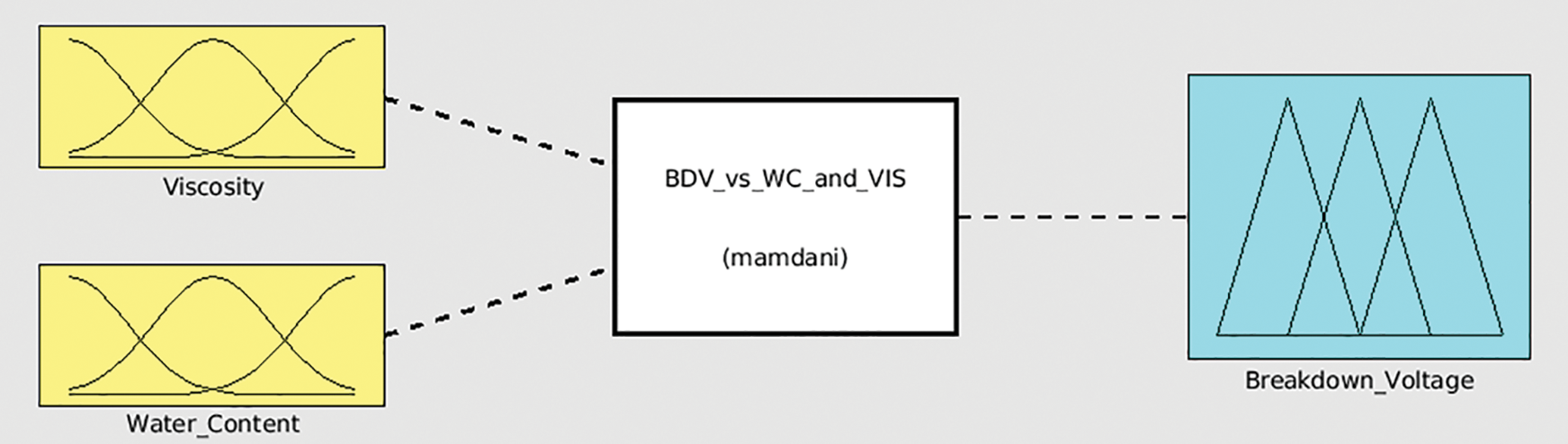
Figure 5: Design of fuzzy inference system to predict the breakdown voltage for highly viscous natural ester (NE1), and moderately viscous natural esters (NE2, NE3)

The rules associated with the input and output variables are loaded in the FIS with 15 rules and trained to predict the desired results, as shown in Fig. 6. For highly viscous ester (NE1), changing the water content does not affect the breakdown voltage (output variable); however, when reduced to 20.5 cSt, the kinematic viscosity significantly affects the breakdown voltage—the rate of reduction at 17% as shown in Fig. 6.

Figure 6: Rule viewer showing the breakdown voltage by changing the input variables, kinematic viscosity, and water content, (a) NE1 (high viscous), (b) NE2 and NE3 (moderate viscous)

The 3D surface model plot for the high viscous natural ester (NE1) is shown in Fig. 7. The changes can be seen from the posterior section of the surface plot along the axis of breakdown voltage with the effect of changing the kinematic viscosity and not the water content. This is clear evidence of no significant impact of water content over breakdown voltage of high viscous ester (NE1). Moreover, the Water content in NE1 has not significantly affected the breakdown voltage. The same effect is also spotted in the pattern of moderate viscosity (NE2 and NE3). The water content has not shown any detrimental effects on the breakdown voltage of natural esters (NE1 and NE3). Only after reducing the kinematic viscosity below the moderate level a significant improvement in the breakdown voltage is observed at 23%. The 3D surface model plot for the moderate viscous natural esters (NE2 and NE3) also shows the kinematic viscosity effect on the breakdown voltage. Hence from the predictions, it is concluded that natural esters do not get affected by the changes in the moisture. But the kinematic viscosity significantly affects the oil’s dielectric breakdown voltage.

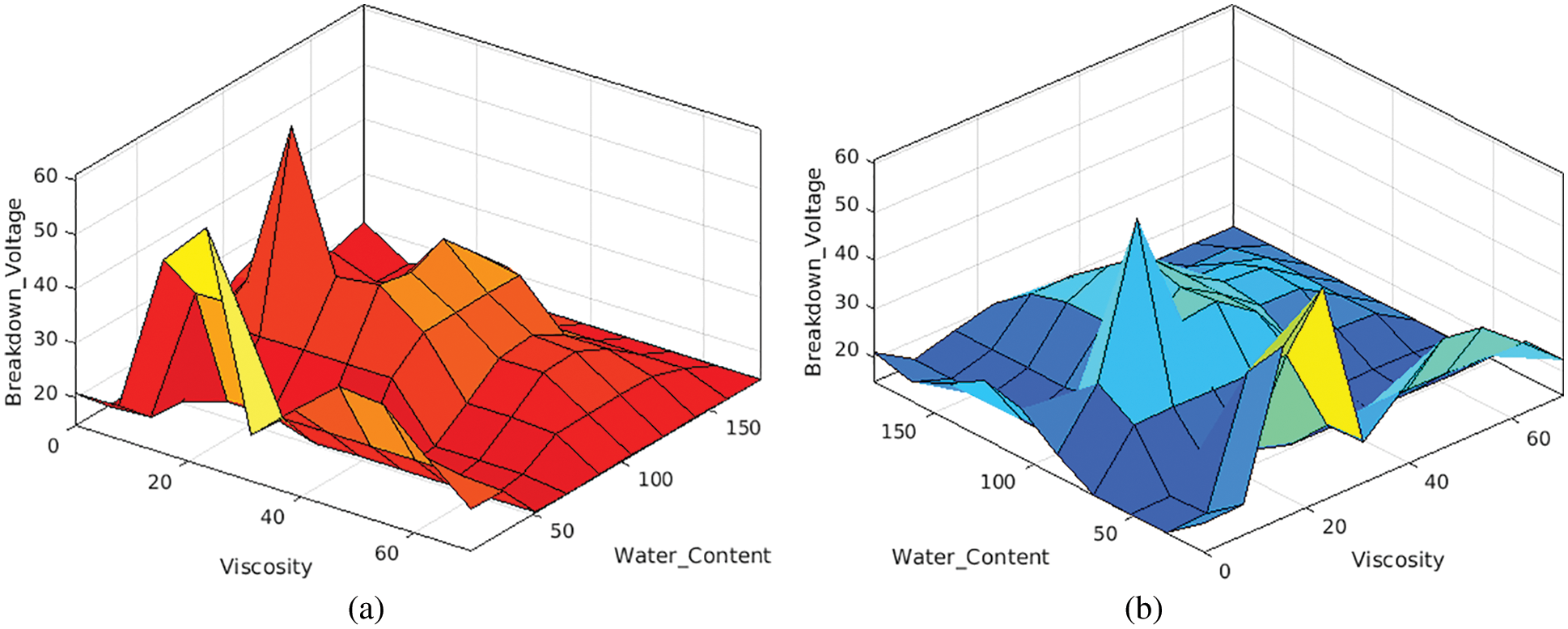
Figure 7: Surface model plot of the input variable and output variables, a) for higher viscosity (NE1), for moderate viscosity (NE2 and NE3)

6  Field Element Distribution Analysis Using Pde Tool

Electric field distribution between the electrode’s geometry is analyzed by applying the electric potential between the h.v. Electrode and l.v. Electrode. The design of the various electrode geometry is performed using the Partial Differential Equation (PDE) tool available in the software MATLAB R2020b. The PDE tool is used to solve any finite element using piecewise linear elements in 2D space by specifying all the boundary conditions and PDE coefficients. The axes scales are distributed even for maintaining the dimension of shapes of the various electrodes from Fig. 8. The distances between the electrodes are usually 1, 2, and 3 cm. The permittivity of the space is typically the permittivity of the natural ester used for the test.

Figure 8: showing the PDE tool in MATLAB R2020b with equal axes

Step 1: The first step of the design of the electrode geometry is by selecting the PDE tool in the MATLAB R2020b and specifying the axes of the design space. Then the procedure is performed using the draw option of the PDE tool, followed by the positioning of the shapes drawn according to the shape of the electrode used for the test. The shapes are covered using the formula bar of the drawing window to create the electrode boundary within the workspace, as shown in Fig. 9.

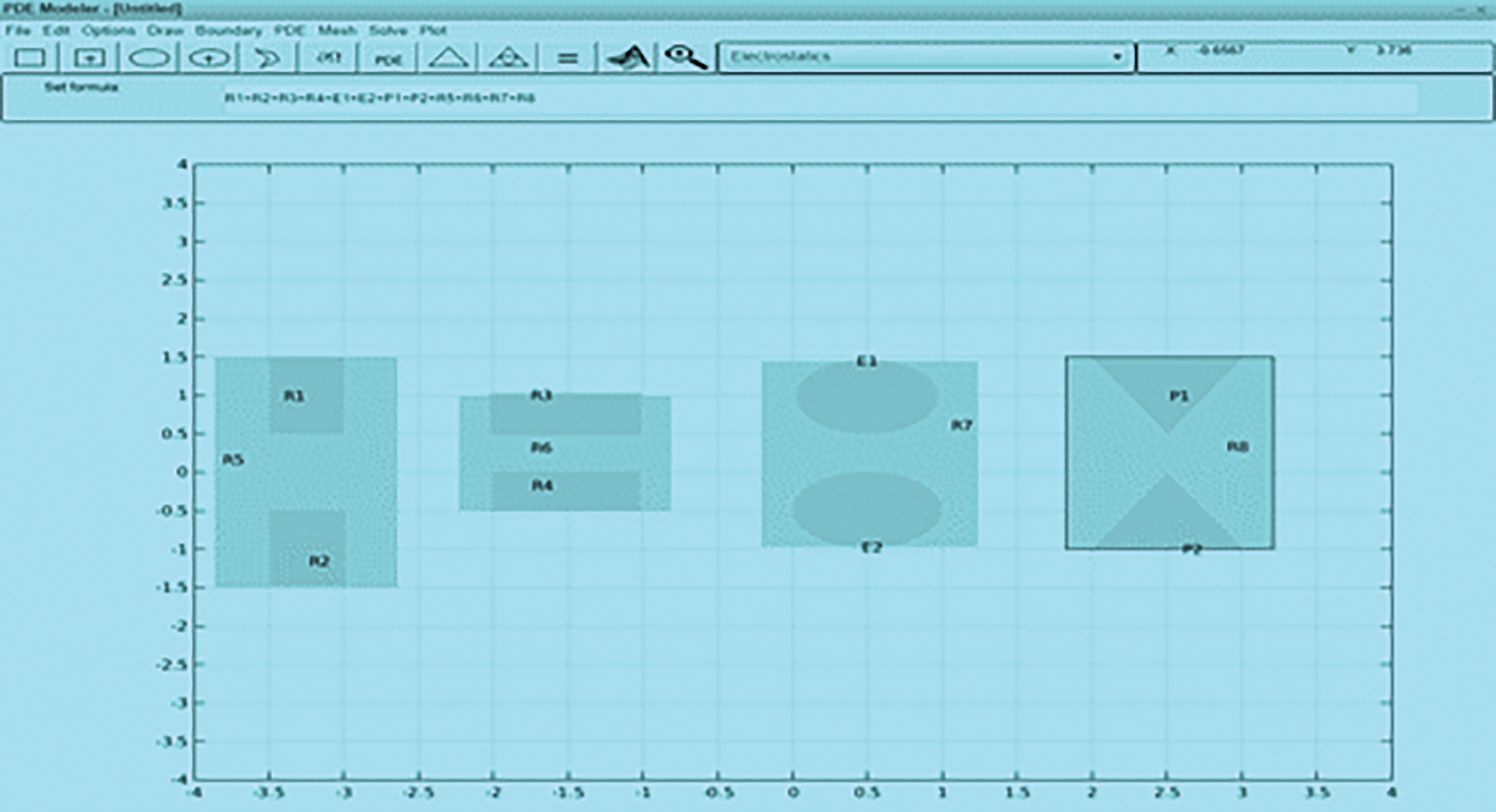
Figure 9: Design of electrode geometry for different shapes in 2-D plane

Step 2: Next step is to apply the boundary conditions of the subdomains one by one, which is usually the electric potential measured during the HVAC test. The boundary conditions from Fig. 10 are provided using Dirichlet’s condition. This says that the function converges, equal to the function, wherever the function is continuous.

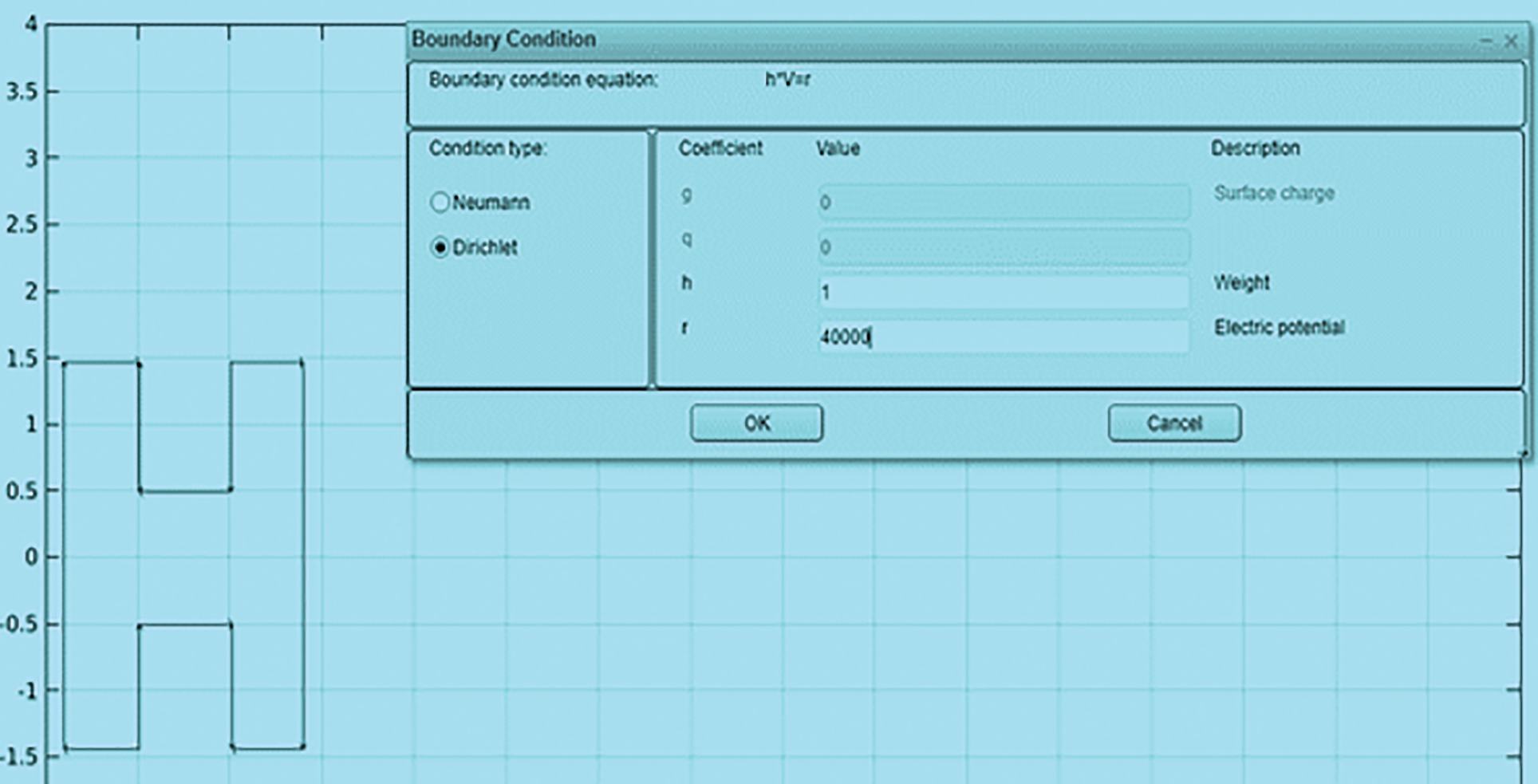
Figure 10: Specification of Dirichlet boundary conditions for the design in the 2-D plane

Step 3: The process is followed by creating the PDE model and applying the permittivity of the natural ester in the workspace between the two electrodes. The permittivity (ξ) of the natural esters used for testing is approximately 2.1 at 30°C. The space charge density (σ) is the distribution of charge per unit area represented as C-m-2 in a two-dimensional space in Fig. 11. Here, the space charge density is assumed to be 1 C-m-2.

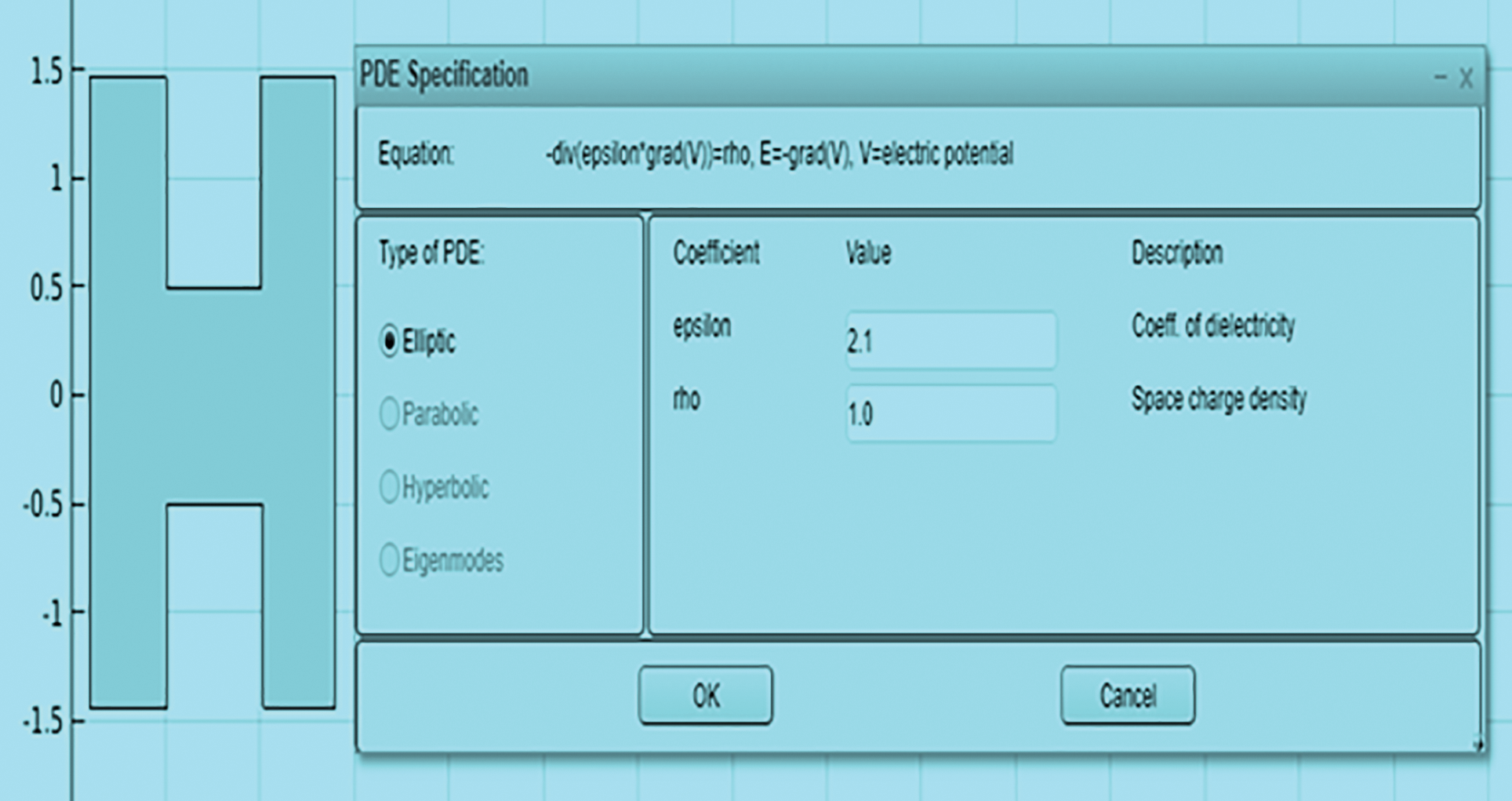
Figure 11: PDE specification showing the setup of permittivity and space charge for 2-D plane

Step 4: The next step is to generate the model’s mesh and then select solve the model. The required potential and field distribution is caused in separate windows used for the analysis shown in Fig. 12. The field distribution is governed by uniform and non-uniform patterns. Eqs. (2) and (3) computed the electric field at any point. Here the RI represents the distance between any point charge in the space and the electric field at the new point. And are the absolute and relative permittivity of the free space and the medium, and dq is the amount of distributed charge.

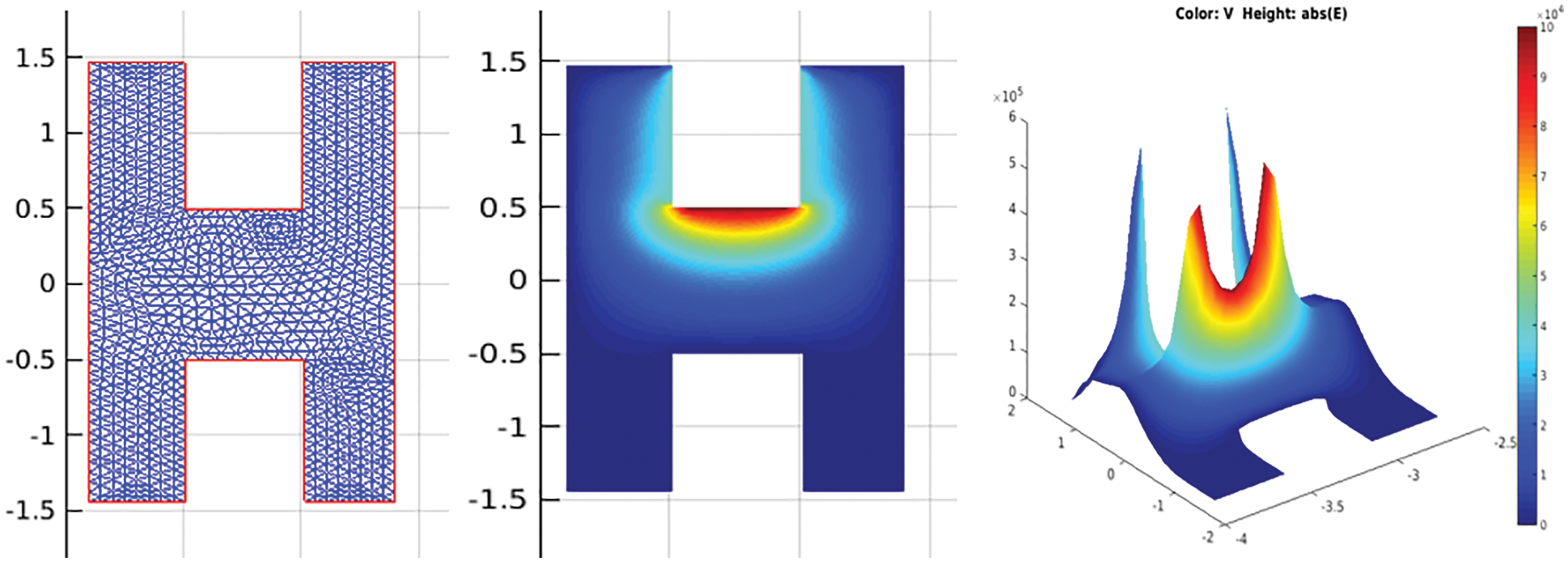
Figure 12: Model with generated mesh, distribution of electric potential, and electric field

The field distribution of the model gives a lot of information about how the field varies for the sphere-sphere, plane-plane, rod-rod, and point-point electrodes. Moreover, the field distribution model of the sphere-sphere electrode displays the uniform field between the H.V. and L.V. electrodes. This property is because of the contour reduction from end to end of the spheres. This is one of the reasons why the sphere-sphere electrode configuration gives the highest breakdown strength with a low leakage current. This kind of field distribution model enables low energy between the electrodes and does not cause ionization which is the main reason for the initiation of the streamer.

E(r)=14πξ0ξr∑i=1nqir12 (2)

E(r)=14πξ0ξr∑i=1n⁡∫dqr2r¯ (3)

The plane electrodes show similar electric field distribution to the sphere electrodes. But somehow, the field on the edges of the electrodes is irregular and supervises the initiation of the ionization. This tends to increase the magnitude of the leakage current to higher than the sphere-sphere configuration. On the other hand, the rod-rod electrodes and point-point electrodes show poor field distribution, and the field lines or charges are completely aligned or accumulated towards the center of the two electrodes or at the edges of the two electrodes. This strong field causes high leakage currents causing ionization and electron avalanche; electrons establish a bridge between the two electrodes and initiate breakdown. The result is the reduction of the breakdown strength of the dielectric fluid.

6.1 Electric Field Distribution

6.2 Survival Analysis of Natural Esters for the Leakage Current

The association between the HVAC test and the electrode configuration at which the natural ester is tested indicates the dielectric strength of the natural ester. Unlike other insulating oils, the natural esters have strong antioxidant content to slow ionization and streamer. This ultimately reduces the leakage currents between the electrodes during the breakdown. This also ensures that natural esters tested under various electrode configurations show temperament against electric stress. Significantly, the gap spacing effect on the natural esters is used to determine the exponential function and the correlation between the electric potential and the leakage current from Tab. 3. The survival function is the function that estimates the survival rate of the product of the measured quantity. This function is also called as reliability function and complementary cumulative distribution function. The survival function S(t) is given by Eq. (4), which states that the continuous random variable ‘T’ survives over the time ‘t.’

S(t)=P({T.t})=1−F(t) (4)

The survival rate of the natural ester according to the leakage current is determined by using the exponential function displayed in Eq. (1). The survival rate of the natural esters, according to the breakdown voltage data, shows that natural esters with high antioxidants reveal the highest survival rate when generalized using the exponential function. On the other hand, Tab. 3 also indicates that the sphere-sphere configuration has the highest correlation when all the natural esters are subjected to the HVAC test. The survival function is used to understand the survival rates of the NE under different electrode configurations. Fig. 13 shows the survival function of the NE1 for S-S, PL-PL, R-R, and P-P. The NE1 in the S-S electrode geometry produces less than 20 mA leakage current. It indicates that the lesser the leakage current higher the survival rate—the leakage current increases with the PL-PL, R-R, and P-P electrode geometry. There is an inflection for S-S and PL-PL at less than 16 mA, below which the sample has a 60% survival probability. There is also an inflection for the R-R and P-P at less than 48 mA, below which the sample has only 20% probability. At a 90% survival probability scale, the NE1 shows 14.5 mA for the S-S, 14 mA for the PL-PL, 14.5 mA for the R-R, and 34.5 mA for the P-P electrode geometry. The R-R has the highest leakage current range according to the exponential function. Whereas S-S and PL-PL show the least leakage current with the highest survival rate, S-S shows perfect field distribution among all the electrode configurations. The survival probability for the NE2 under different electrode configurations is shown in Fig. 14. There is a clear indication of inflection at 90% survival probability which shows a leakage current of 20 mA. The S-S electrode geometry also has the least leakage current than other electrodes in the order PL-PL, R-R, and P-P.

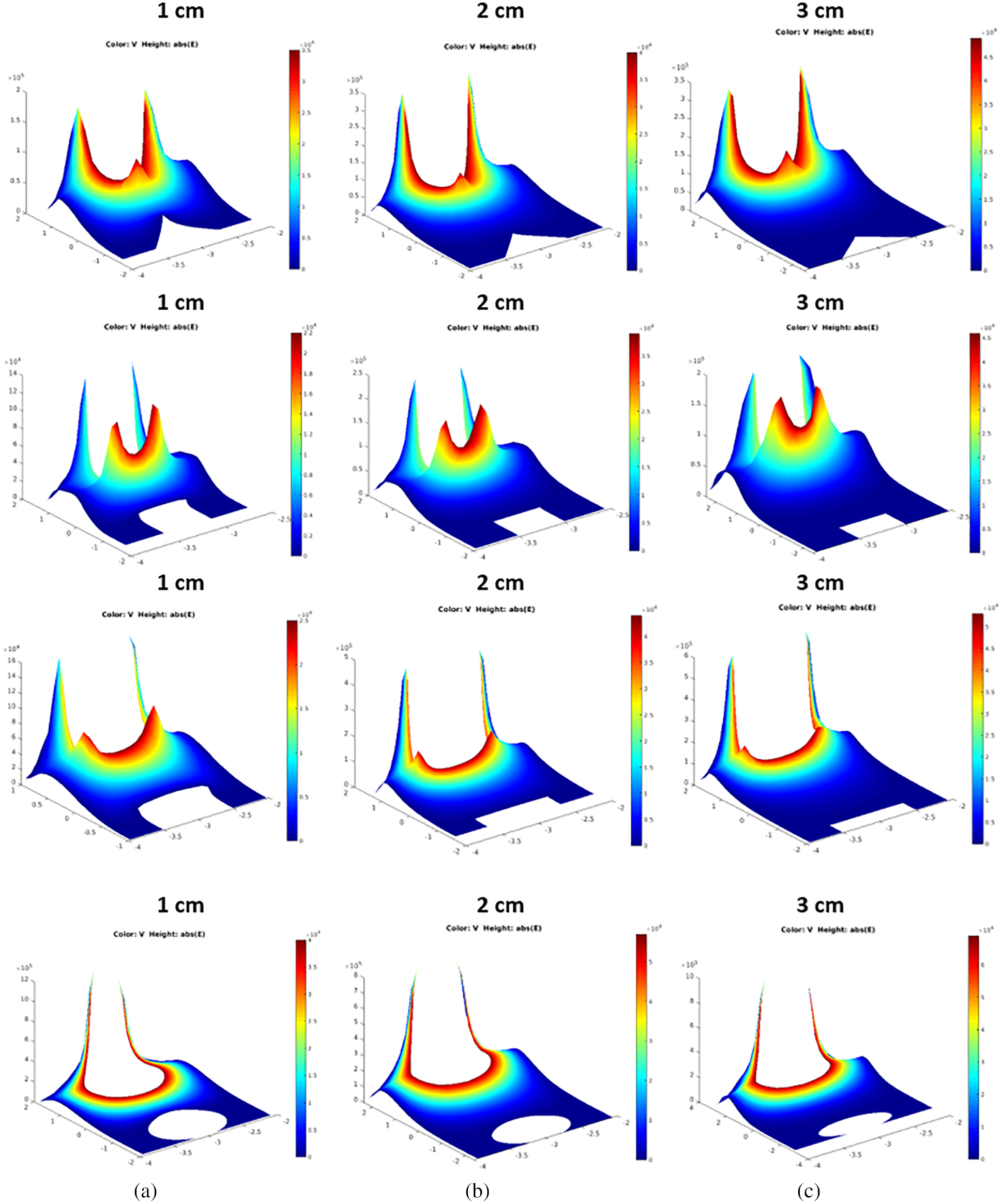
Figure 13: Distribution of electric field in Olive Oil (NE1) for the different electrode configurations, showing how the field is influential according to the geometry of electrodes. a) Point-Point, b) Rod-Rod, c) Plane-Plane, and Sphere-Sphere for gap spacing 1, 2, and 3 cm

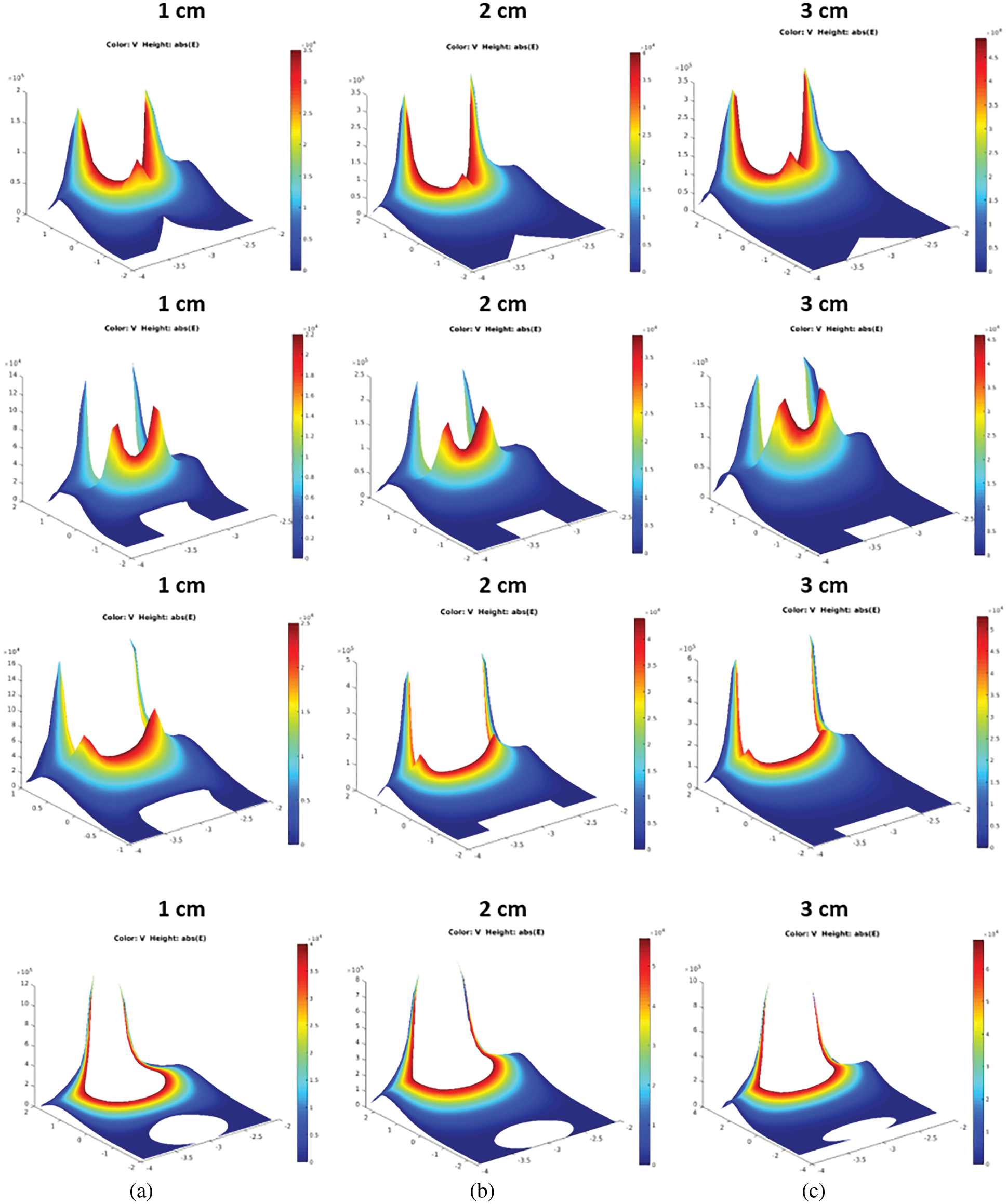
Figure 14: Distribution of electric field in Sunflower Oil (NE2) for the different electrode configurations, showing how the field is influential according to the geometry of electrodes a) Point-Point, b) Rod-Rod, c) Plane-Plane, and Sphere-Sphere for gap spacing 1, 2, and 3 cm

According to the exponential function, the R-R has a wider leakage current range from 20 to 140 mA. The R-R and P-P show poor electric field distribution and lead to a rise in the leakage current. The NE2 establishes a perfect electric field distribution between the electrodes for S-S geometry. But for the NE3, the survival probability from Fig. 15 shows closer inflection for the PL-PL and R-R. The S-S has a distinct survival curve with less than 35 mA, the same for PL-PL. The P-P shows the highest leakage current of 100 mA.

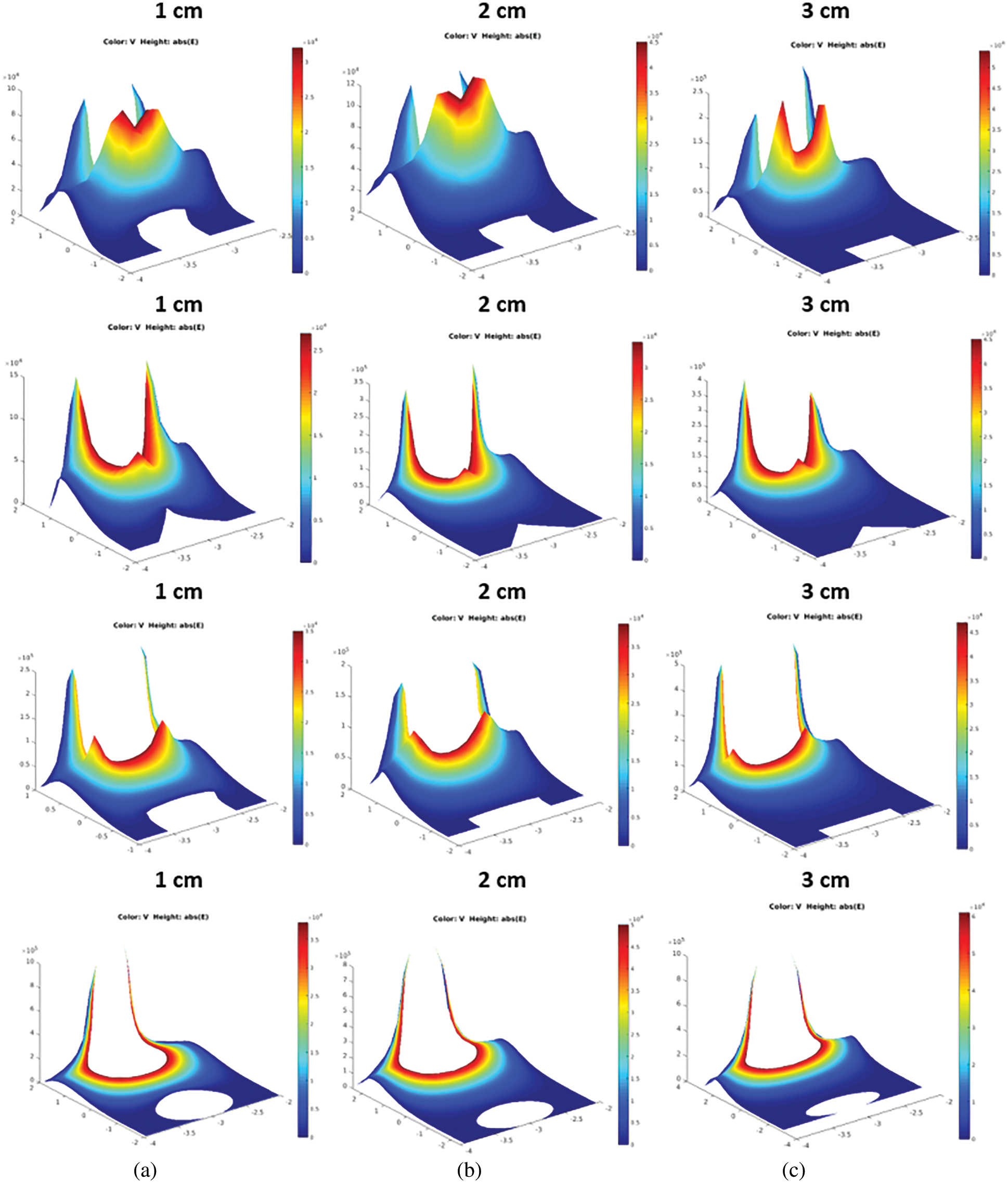
Figure 15: Distribution of electric field in Ricebran Oil (NE2) for the different electrode configurations, showing how the field is influential according to the geometry of electrodes a) Point-Point, b) Rod-Rod, c) Plane-Plane, and Sphere-Sphere for gap spacing 1, 2, and 3 cm

From the survival probability of NE3 in Figs. 16 and 17. It is seen that the leakage current under the S-S electrode configuration and PL-PL electrodes are below 30 mA. The field distribution of the NE3 under R-R and P-P electrodes is experiencing more significant stress, which can be seen from the leakage current characteristics in Fig. 18.

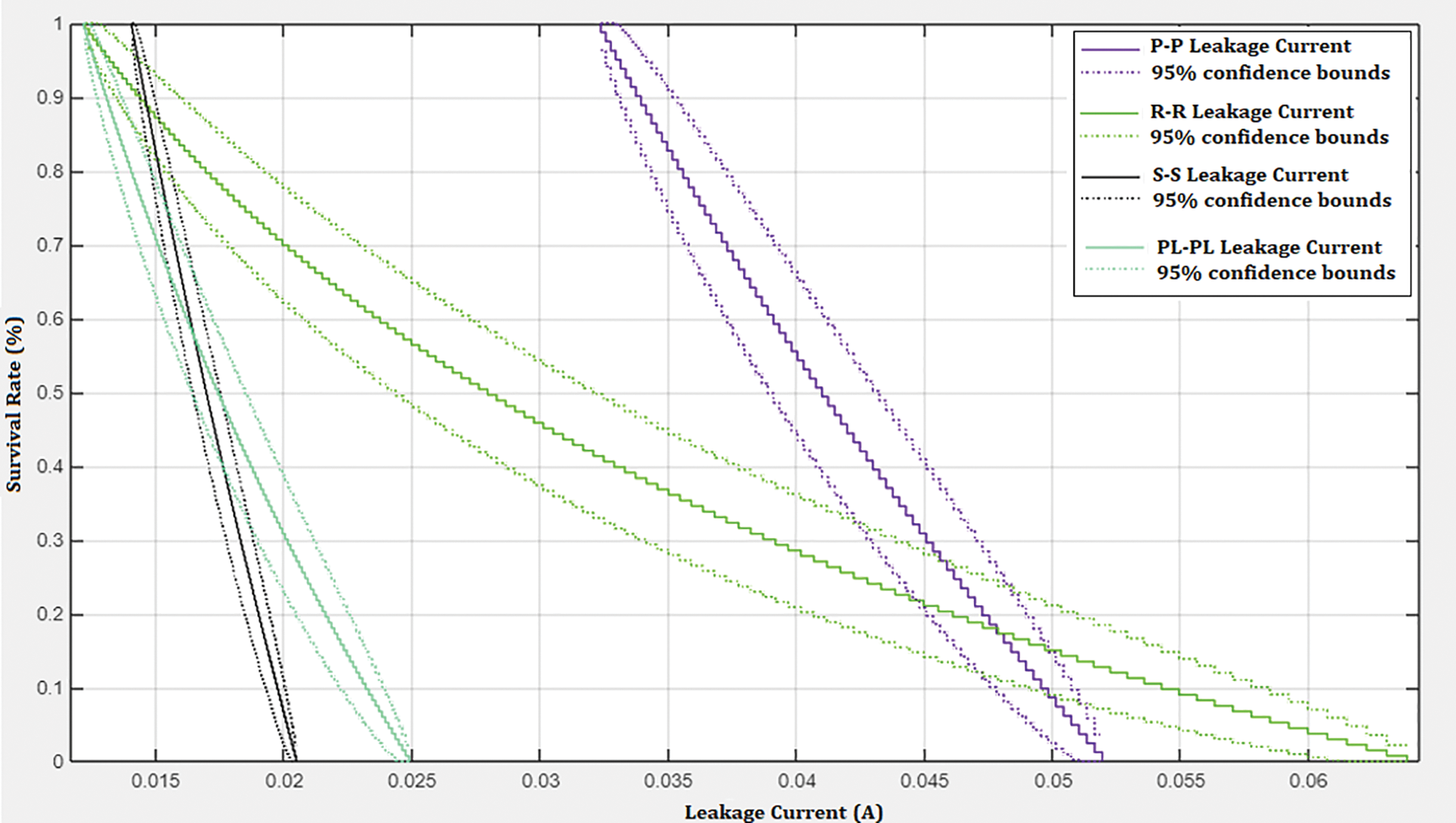
Figure 16: Survival function of the leakage current of NE1 under different electrode configurations

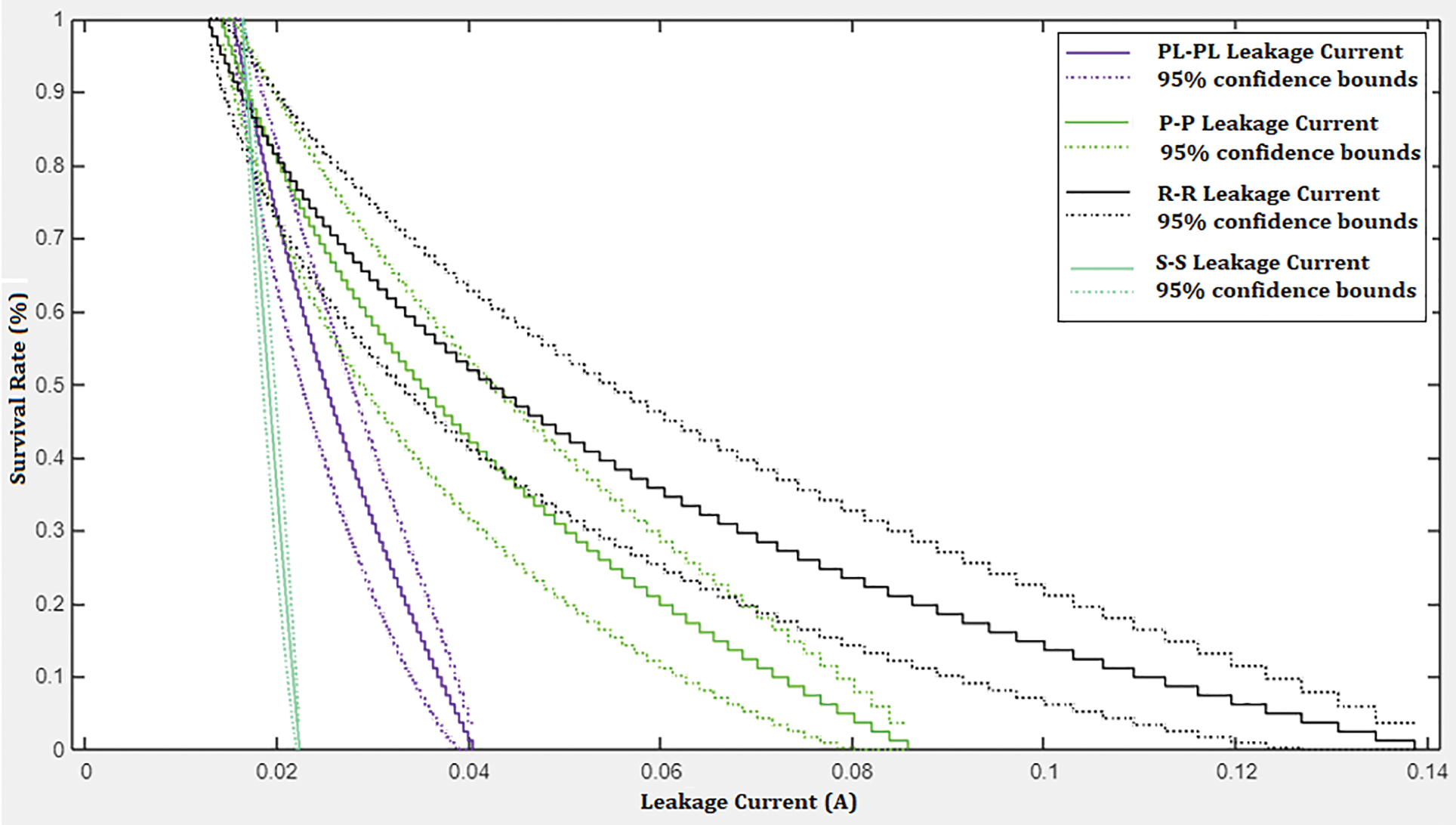
Figure 17: Survival function of the leakage current of NE2 under different electrode configurations

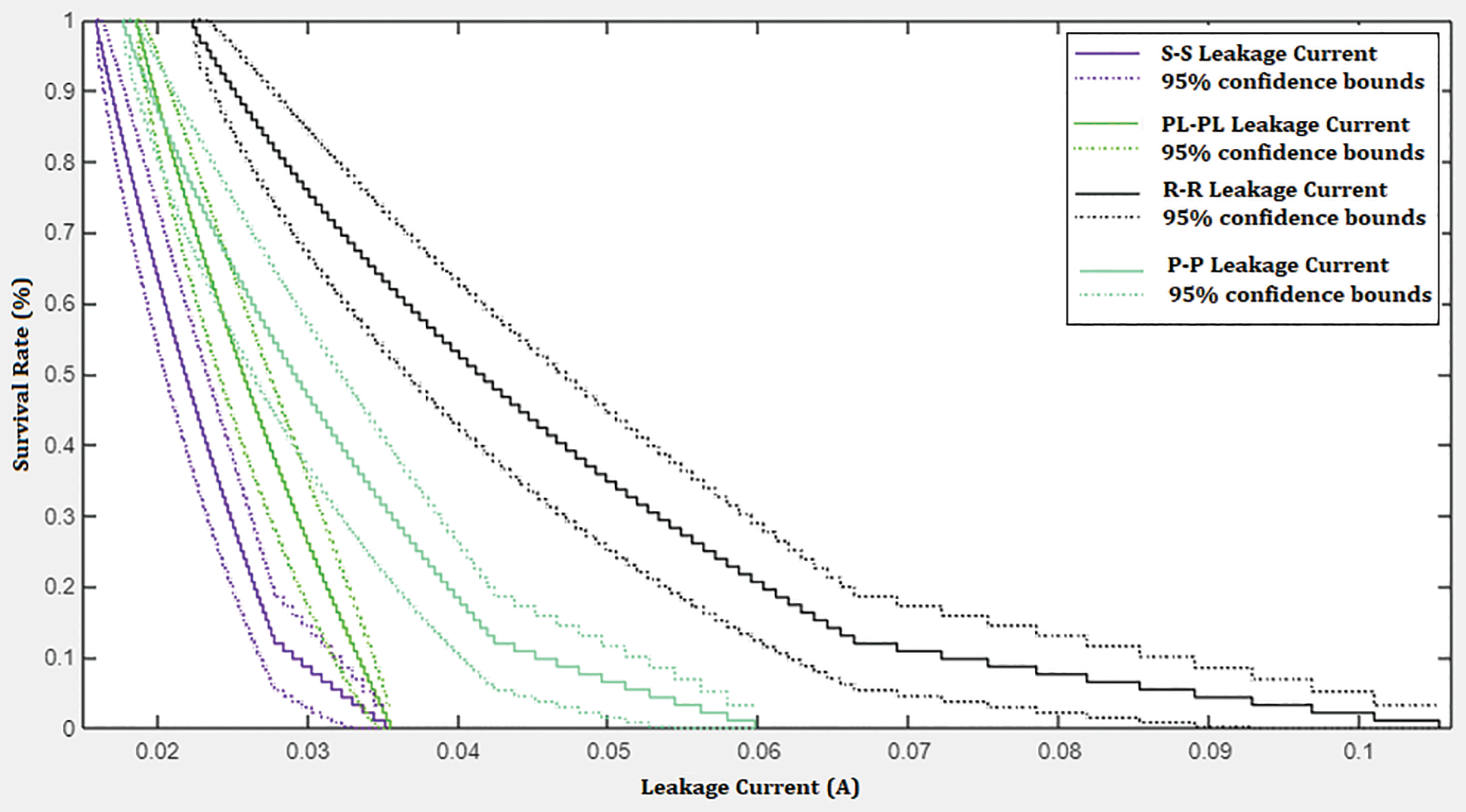
Figure 18: Survival function of the leakage current of NE3 under different electrode configuration

The R-R shows 60 mA, and P-P shows 105 mA, higher than NE1 but lesser than NE2. At 60% survival probability, NE3 shows 40 mA as the maximum leakage current caused by the P-P electrodes, followed by R-R with 29 mA, PL-PL with 26 mA, and S-S with 22 mA. Above the 60% probability of survival of the leakage current caused by the NE3 under R-R and P-P shows hazard. But S-S and PL-PL offer the highest survival rate due to the significantly lower magnitude of the leakage current caused during the breakdown.

According to the exponential function, the R-R has a wider leakage current range from 20 to 140 mA. The R-R and P-P show poor electric field distribution and lead to a rise in the leakage current. The NE2 establishes a perfect electric field distribution between the electrodes for S-S geometry. But for the NE3, the survival probability from Fig. 15 shows closer inflection for the PL-PL and R-R. The S-S has a distinct survival curve with less than 35 mA, the same for PL-PL. The P-P shows the highest leakage current of 100 mA.

7  Conclusion

From the above test results, it is conferred that fuzzy-based correlation studies of the dielectric properties of natural esters help predict the exact changes in the characteristics. Fuzzy is accurate and efficient in determining the conditions of the transformer insulating system by the standards. In addition to correlation and prediction studies, the HVAC test validates the breakdown strength of NE1, NE2, and NE3 by measuring the leakage current during the breakdown process. The development of an exponential function model to determine the survival function of the proposed NE indicates that the Sphere-Sphere electrode geometry has the least leakage current with the highest survival probability. The leakage current increases for the other shapes of the electrodes showing the liquid insulation experiences differential fields within the enclosure of the transformer system. Moreover, the electric field distribution is viewable through the PDE design of the electrode geometry for various shapes and electric potential. Upon analysis, it is concluded that the proposed natural esters are suitable to tolerate electrical stresses under various shapes of the electrode configuration. However, the better the Rogowski electrode better the dielectric strength of the liquid insulation. Over and above that, a higher level of moisture present in the natural esters does not affect the breakdown voltage of the oil. But in the FIS of natural esters with higher (NE1) and moderate (NE2 and NE3) kinematic viscosity, any small change (reduction) could significantly propel the breakdown voltage irrespective of the changes in the water content. Hence, the FIS will be significantly used in the future to determine the aging effects of natural esters under accelerated conditions and normal conditions, and incipient faults and gassing tendency studies on the natural esters

Acknowledgement: With a deep sense of gratitude, the authors would thank the supervisor for his guidance and constant support during this research.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

Reference

 1.  R. Raymon, P. S. Pakianathan, M. P. E. Rajamani and R. Karthik, “Enhancing the critical characteristics of natural esters with antioxidants for power transformer applications,” IEEE Transactions on Dielectrics and Electrical Insulation, vol. 20, no. 3, pp. 899–912, 2013. [Google Scholar]

 2.  J. Amalanathan, R. Sarathi, N. Harid and H. Griffiths, “Investigation on flow electrification of ester-based TiO2 nanofluids,” IEEE Transactions on Dielectrics and Electrical Insulation, vol. 27, no. 5, pp. 1492–1500, 2020. [Google Scholar]

 3.  R. A. Raj, R. Samikannu, A. Yahya and M. Mosalaosi, “Comparison of ageing characteristics of superior insulating fluids with mineral oil for power transformer application,” IEEE Access, vol. 8, pp. 141111–141122, 2020. [Google Scholar]

 4.  R. A. Raj, R. Samikannu, A. Yahya and M. Mosalaosi, “Investigation of survival/hazard rate of natural ester treated with Al2O3 nanoparticle for power transformer liquid dielectric,” Energies, vol. 14, no. 5, pp. 1510, 2021. [Google Scholar]

 5.  R. A. Raj, R. Samikannu, A. Yahya and M. Mosalaosi, “An overview of potential liquid insulation in power transformer,” International Journal on Energy Conversion, vol. 8, no. 4, pp. 126–140, 2020. [Google Scholar]

 6.  I. Fernandez, A. Ortiz, F. Delgado, C. Renedo and S. Perez, “Comparative evaluation of alternative fluids for power transformers,” Electric Power Systems Research, vol. 98, pp. 58–69, 2013. [Google Scholar]

 7.  E. O. Aluyor and M. O. Jesu, “Biodegradation of mineral oils–A review,” African Journal of Biotechnology, vol. 8, no. 6, pp. 915–920, 2009. [Google Scholar]

 8.  U. M. Rao, I. Fofana, T. Jaya, E. M. R. Celis, J. Jalbert et al., “Alternative dielectric fluids for transformer insulation system: Progress, challenges, and future prospects,” IEEE Access, vol. 7, pp. 184552–184571, 2019. [Google Scholar]

 9.  I. Fofana, “50 years in the development of insulating liquids,” IEEE Electrical Insulation Magazine, vol. 29, no. 5, pp. 13–25, 2013. [Google Scholar]

10. K. M. A. Islam, S. R. P. Primandari and Z. Yaakob, “Non-edible vegetable oils as renewable resources for biodiesel production: South-East Asia perspective,” Advances in Biofuels and Bioenergy, vol. 3, pp. 201–215, 2018. [Google Scholar]

11. J. R. Albert, A. Sharma, B. Rajani, A. Mishra, A. Saxena et al., “Investigation on load harmonic reduction through solar-power utilization in intermittent SSFI using particle swarm, genetic, and modified firefly optimization algorithms,” Journal of Intelligent and Fuzzy System, vol. 42, no. 4, pp. 4117–4133, 2021. [Google Scholar]

12. T. Mariprasath and V. Kirubakaran, “A critical review on the characteristics of alternating liquid dielectrics and feasibility study on pongamia pinnata oil as liquid dielectrics,” Renewable and Sustainable Energy Reviews, vol. 65, pp. 784–799, 2016. [Google Scholar]

13. J. Tokunaga, M. Nikaido, H. Koide and T. Hikosaka, “Palm fatty acid ester as biodegradable dielectric fluid in transformers: A review,” IEEE Electrical Insulation Magazine, vol. 35, no. 2, pp. 34–46, 2019. [Google Scholar]

14. M. Bakrutheen, M. W. Iruthayarajan and A. Narayani, “Influence of ultrasonic waves on viscosity of edible natural esters based liquid insulation,” IEEE Transactions on Dielectrics and Electrical Insulation, vol. 25, no. 5, pp. 1628–1635, 2018. [Google Scholar]

15. J. R. Albert and A. A. Stonier, “Design and development of symmetrical super-lift DC–AC converter using firefly algorithm for solar-photovoltaic applications,” IET Circuits Devices System, vol. 14, no. 3, pp. 261–269, 2020. [Google Scholar]

16. T. Mariprasath, V. Kirubakaran and D. K. Kumar, “Feasibility analysis of karanja oil as alternate liquid dielectrics for distribution transformers,” International Transactions on Electrical Energy Systems, vol. 27, no. 8, pp. 1–6, 2017. [Google Scholar]

17. R. A. Raj, R. Samikannu, A. Yahya and M. Mosalaosi, “Performance evaluation of natural esters and dielectric correlation assessment using artificial neural network (ANN),” Journal of Advanced Dielectrics, vol. 10, no. 5, pp. 1–10, 2020. [Google Scholar]

18. R. A. Raj, R. Samikannu, A. Yahya and M. Mosalaosi, “Enhancement of dielectric properties of baobab oil and mongongo oil using cost-effective additive for power transformer insulating fluids,” Environmental Technology & Innovation, vol. 20, pp. 1–13, 2020. [Google Scholar]

19. I. S. Kwon, S. J. Kim, M. Asif and B. W. Lee, “Evaluation of electric field and space charge dynamics in dielectric under DC voltage with superimposed switching impulse,” Energies, vol. 12, no. 10, pp. 1–15, 2019. [Google Scholar]

20. S. K. Ramaraju, T. Kaliannan, S. A. Joseph, U. Kumaravel, J. R. Albert et al., “Design and experimental investigation on VL-MLI intended for half height (HH) method to improve power quality using modified particle swarm optimization (MPSO) algorithm,” Journal of Intelligent & Fuzzy Systems, vol. 1, pp. 1–18, 2021. [Google Scholar]

21. V. K. S. Vijayakumar and A. V. S. James, “Hybrid cluster made content forwarding and light weight sign encryption IoT based named data network using African buffalo optimization algorithm,” Journal of Intelligent & Fuzzy Systems, vol. 1, pp. 1–15, 2022. [Google Scholar]

22. N. Sunthrasakaran, N. A. M. Jamail, Q. E. Kamarudin and S. Gunabalan, “Analysis of electric field and current density for different electrode configuration of XLPE insulation,” International Journal of Engineering & Technology, vol. 7, no. 3.36, pp. 127–133, 2018. [Google Scholar]

23. M. Bakrutheen, M. W. Iruthayarajan and A. Narayani, “Statistical failure reliability analysis on edible and non-edible natural esters based liquid insulation for the applications in high voltage transformers,” IEEE Transactions on Dielectrics and Electrical Insulation, vol. 25, no. 5, pp. 1579–1586, 2018. [Google Scholar]

24. R. Palanisamy, V. Govindaraj, S. Siddhan and J. R. Albert, “Experimental investigation and comparative harmonic optimization of AMLI incorporate modified genetic algorithm using for power quality improvement,” Journal of Intelligent & Fuzzy Systems, vol. 2, pp. 1–14, 2022. [Google Scholar]

25. D. Q. Nykamp, “The idea of a probability density function,” Math Insight, vol. 3, pp. 22–39, 2020. [Google Scholar]

26. P. Krishna, P. Bhupendra and K. Dinesh, “Leakage current prediction of composite insulator using artificial neural network,” International Journal of Recent Technology and Engineering (IJRTE), vol. 8, no. 2, pp. 1–9, 2019. [Google Scholar]

27. A. J. Renoald and M. Dhivya, “Analysis on super lift multilevel DC/AC inverters using photovoltaic energy with AC module application,” International Journal for Scientific Research & Development, vol. 5, no. 2, pp. 479–481, 2017. [Google Scholar]

28. J. R. Albert, “Design and investigation of solar PV fed single-source voltage-lift multilevel inverter using intelligent controllers,” Journal of Control, Automation and Electrical Systems, vol. 33, pp. 1–26, 2022. [Google Scholar]

29. R. M. A. Velasquez and J. V. M. Lara, “Principal components analysis and adaptive decision system based on fuzzy logic for power transformer,” Fuzzy Information and Engineering, vol. 9, no. 4, pp. 493–514, 2017. [Google Scholar]

30. C. Gnanavel, P. Muruganantham and K. Vanchinathan, “Experimental validation and integration of solar PV fed modular multilevel inverter (MMI) and flywheel storage system,” in Proc. 2021 IEEE Mysore Sub Section Int. Conf. (MysuruConIEEE, Hassan, India, pp. 147–153, 2021. [Google Scholar]

31. R. A. Prasojo, H. Gumilang, N. U. Maulidevi and B. A. Soedjarno, “A fuzzy logic model for power transformer faults’ severity determination based on gas level, gas rate, and dissolved gas analysis interpretation,” Energies, vol. 13, no. 4, pp. 1009, 2020. [Google Scholar]

32. J. R. Albert, T. Kaliannan, G. Singaram, F. I. R. E. Sehar, M. Periasamy et al., “Remote diagnosis using variable fractional order with reinforcement controller for solar-MPPT intelligent system, in Photovoltaic Systems, 1st ed., Taylor and Francis Group, Boca Raton, Florida: CRC Press, vol. 1, pp. 45–64, 2022. [Google Scholar]

33. S. A. Wani, A. J. Amalanathan and R. Sarathi, “Fuzzy based condition monitoring tool for real-time analysis of synthetic ester fluid as transformer insulant,” IEEE Access, vol. 10, pp. 18055–18064, 2022. [Google Scholar]

34. A. J. Renoald, V. Hemalatha, R. Punitha, M. Sasikala and M. B. E. Sasikala, “Solar roadways-the future rebuilding infrastructure and economy,” International Journal of Electrical and Electronics Research, vol. 4, no. 2, pp. 14–19, 2016. [Google Scholar]

35. D. R. Ramji, C. A. Palagan, A. Nithya, A. Appathurai and E. J. Alex, “Soft computing-based color image demosaicing for medical image processing,” Multimedia Tools and Applications, vol. 79, no. 15, pp. 10047–10063, 2020. [Google Scholar]

36. M. Vanitha, N. Narmadhai and M. Karthik, “Investigation of critical characteristics of mineral oil with activated carbon,” Circuits and Systems, vol. 7, no. 9, pp. 2521–2529, 2016. [Google Scholar]

37. T. Kaliannan, J. R. Albert, D. M. Begam and P. Madhumathi, “Power quality improvement in modular multilevel inverter using for different multicarrier PWM,” European Journal of Electrical Engineering and Computer Science, vol. 5, no. 2, pp. 19–27, 2021. [Google Scholar]

38. A. J. Renoald, D. M. Begam and B. Nishapriya, “Micro grid connected solar PV employment using for battery energy storage system,” Journal of Xidian University, vol. 15, no. 3, pp. 85–97, 2021. [Google Scholar]

39. M. Dhivya and A. J. Renoald, “Fuzzy grammar based hybrid split-capacitors and split inductors applied in positive output luo-converters,” International Journal of Scientific Research in Science, Engineering and Technology (IJSRSET), vol. 3, no. 1, pp. 327–332, 2017. [Google Scholar]

40. J. R. Albert and D. S. Vanaja, “Solar energy assessment in various regions of Indian Sub-continent,” Solar Cells: Theory, Materials and Recent Advances, vol. 51, pp. 12–23, 2021. [Google Scholar]

41. M. Murugesan, K. Kaliannan, S. Balraj, K. Singaram, T. Kaliannan et al., “A hybrid deep learning model for effective segmentation and classification of lung nodules from CT images,” Journal of Intelligent & Fuzzy Systems, vol. 43, no. 3, pp. 1–13, 2021. [Google Scholar]