Improved Rat Swarm Based Multihop Routing Protocol for Wireless Sensor Networks

1  Introduction

In recent years, wireless sensor network (WSN) has gained considerable interest. Because of the small size, self-organization, and low-cost sensors, WSN has been adapted in various applications, namely environmental monitoring, military, crime prevention, vehicular movements, health care services, and so on [1]. The nodes in the WSN are able to sense, process, and, as the name reveals, wireless communication. Usually, WSN is employed to detect ecological events including landslide, forest free, volcanic, and tsunami activities, virtual fences (geo-fences), and deploying country’s border surveillance [2]. The sensors in this network collected data and transmitted it to a centralized node known as sink node. Generally, sensors are limited irreplaceable (or non-rechargeable) batteries, categorized by the low storage, short transmission range, and, processing capacity; therefore, it transmits the gathered data to a reliable station. Amongst each abovementioned limitation, the energy utilization of nodes has often been the major problem in WSN. It can be resolved by presenting energy-aware routing algorithm and conducting effective clustering methods for reducing transmissions among sensors even though new improvement is still most valuable [3]. Technologically, there are different criteria to gauge the consistency of WSN including lifespan of the network. Network lifetime (NLT) is defined as the duration from utilizing the network to dying the initial sensors, where the loss of coverage occurs, or the network might partition. Fig. 1 demonstrates the overview of WSN.

Figure 1: Overview of WSN

Since sensors are provided with non-rechargeable batteries, designing an energy-effective routing method to extend lifetime of the network is a major problem in WSN. Several routing approaches were introduced for reducing the energy utilization of WSN. Amongst them, the clustering system has better scalability and flexibility, and consider the most efficient solution. In multihop routing, the source node employs other nodes as relay nodes in transmitting data packets to a distention node outside its broadcast range. Therefore, multihop routing extends the transmission coverage of nodes and improve the energy efficacy of node requiring shorter distance transmissions [4].

Several studies employed the multihop methods to design routing protocol for WSN aims at striking an effective balance amongst distinct QoS necessities, namely delay, reliability, and energy efficiency. Swarm intelligence-based routing protocol is developed for reducing the energy utilization in the whole network. For N sensors, there are completely 2N – 1 routes. Therefore, routing is considered an optimization problem and Evolutionary Algorithm (EA) has been effectively applied for solving it [5].

This study presents an improved rat swarm optimization based energy aware multihop routing (IRSO-EAMHR) protocol for WSN. The major intention of the IRSO-EAMHR approach is for determining optimal routes to base station (BS) in the clustered WSN. At the initial stage, a weighted clustering process is performed to group the nodes into clusters and select cluster heads (CHs). Besides, the IRSO-EAMHR methodology derive a fitness function containing three input parameters (residual energy (RE), distance, and node degree (ND)) for routing process. The design of IRSO algorithm with the inclusion of Levy movement concepts into the traditional RSO algorithm for multihop route selection process illustrates the novelty of the work. The experimental result analysis of the IRSO-EAMHR approach is carried out and the outcomes are inspected under several aspects.

2  Related Works

Haseeb et al. [6] introduced an energy-aware and secured multihop routing (ESMR) approach with a secret sharing system for increasing the accuracy of energy efficacy with multihop data security against malevolent action. Firstly, the network area is classified into inner and outer regions according to the node position. Moreover, in all the zones, several clusters are made according to node neighborhood vicinity. Next, the data communication from CHs in all the zones to the sink node is protected by the presented method. Elhoseny et al. [7] presented a swarm based clustering and multihop routing method for WSN. Firstly, enhanced particle swarm optimization (PSO) was utilized for selecting the CH and organize the cluster effectively. Followed by, the grey wolf optimizer (GWO) based routing method occurs for choosing the optimum path from the system. The study integrates PSO–GWO technique for the routing and clustering procedures that results in maximal network lifetime and energy efficacy.

The authors in [8] presented a multiobjective multihop routing (MOMHR) method for optimum data routing to enhance NLT. Initially, the K-means system wase employed for splitting the node into k clusters. Then, the artificial bee colony (ABC) optimization technique is employed for obtaining the optimum CH within the cluster. At last, the multihop routing protocols find a multihop route with minimal transmission cost from the nodes to the BS. Adnan et al. [9] employed a fuzzy logic (FL)-based cluster protocol (unequal clustering) with multihop communication for NLT prolongation, energy consumption minimization, and load balancing. The protocols form unequal cluster with CH being chosen by FL with competition radius. Input variables are concentration, RE, and Node distance to BS.

The authors in [10] presented a PSO based uneven dynamic clustering multihop routing protocol (PUDCRP). In the presented technique, the distributing of clusters changes vigorously as soon as node fails. It is utilized to define the area where the candidate CH node was situated. The adoptive clustering technique-based node distribution generates the cluster distributing better that balances the energy usage of network more efficiently. Rezaeipanah et al. [11] presented a clustering-based multihop routing method. During the presented approach, an integration of two techniques, such as Open-Source Development Model Algorithm (ODMA) and K-means algorithm, are applied for Genetic Algorithm, and clustering is employed for multihop routing. The authors in [12] proposed a hybrid metaheuristic approach-based cluster with multihop routing (HMA-CMHR) approach for WSN. The proposed approach integrates distinct stages namely clustering, node initialization, data transmission, and routing. Initially, the presented approach employs QHSA based cluster method for electing an optimum set of CHs. Next, the improved cuckoo search (ICS) technique-based routing method is applied for optimum election of route.

3  System Model

3.1 Network Model

Consider a network where an amount of homogeneous sensor nodes (SNs) are arbitrarily utilized from the region and BS was placed outside of network region. Some assumptions are made. 1) Each SN and BS is assumed that static after utilization. 2) SNs are joined as a single CH inside their imparting range. 3) The BS has no energy restriction. 4) The wireless connection has symmetric and bi-directional. 5) Primarily, each SN comprises a similar count of energy.

3.2 Energy Model

Assume that nodes are distributed uniformly in M∗M area. When there is cluster k , afterward the average is N/K nodes per cluster. The region involved by all clusters are approximately M2/K . The needed squared distance in the nodes to CH is provided as [13]:

E[dtoCH2]=ρ(x,y)dxdy (1)

It can be considered that this region is a circle with radius R=(MπK) and ρ(r,θ) is constant for r and θ , thus Eq. (1) is simplified into:

E[dtoCH2]=ρ∫θ=02π⁡∫r=0MπK⁡r3∂r∂θ=ρ2πM4K2 (2)

When the density of nodes has been uniform throughout the cluster region, afterward the diameter D=2MπK and

E[dtoCH2]=12πM2K (3)

The average distance amongst CH node to BS :

DtoBs=∫A⁡x2+y21A∂A=0.765M2 (4)

DtoBS=0.755M2 (5)

Initially, it is assumed every cluster are equivalent in size, thus the radius is R , and the region of all the clusters is MK , thus the radius of clusters are R=MπK , At this point, the diameter of clusters or distances among 2 CH is D=2MπK .

ETX(l,d)={lEelec+l∈fSd2,ifd≤dolEelec+l ∈amp d4,ifd≥do (6)

whereas Elec indicates the energy depleted per bit for operating the electronic circuitry, ∈fs and ∈amp depicts the energy utilization by free space and multi-fading channels, d stands for the distance amongst sending as well as receiving and do signifies the threshold broadcast distance. The threshold distance do is provided as formulating the formula to d=d0

lEelec+l∈fsdo2=lEelec+l ∈amp do4

d0=∈fs∈amp (7)

For obtaining 1-bit message, the radio utilizes:

ERX(l,d)=lEelec (8)

Therefore, the entire energy utilization is obtained:

Et=l(2NSEelec+NS∈fsdtoCH2+NSEDA+k∈fsD2+∈mpkdtoBS4) (9)

For determining the optimum amount of clusters, it can be differentiated Eq. (9) with k and placed the value 0.

Kopt=MdtoBS2NS2π∈fs∈mp (10)

where M refers the side of utilization region, thus region A=M∗Mm2 . Elec implies the energy utilized from transmit/receive 1-bit, dependent upon coding and modulation. ∈fs defines free space loss as co-efficient. Ns demonstrates the sensing node and EDA represents the aggregation energy.

4  The Proposed Model

In this study, a novel IRSO-EAMHR approach was developed to optimum selection of routes to BS from the energy efficient WSN. An important aim of the IRSO-EAMHR algorithm is to maximize energy efficiency and NLT in WSN. The IRSO-EAMHR system initially performed weight clustering process to the selective of CHs and cluster construction. In addition, an optimal set of routes are chosen by the use of IRSO algorithm with fitness function. Fig. 2 depicts the overall block diagram of IRSO-EAMHR technique. The detailed working of the clustering and routing modules are elaborated in the following.

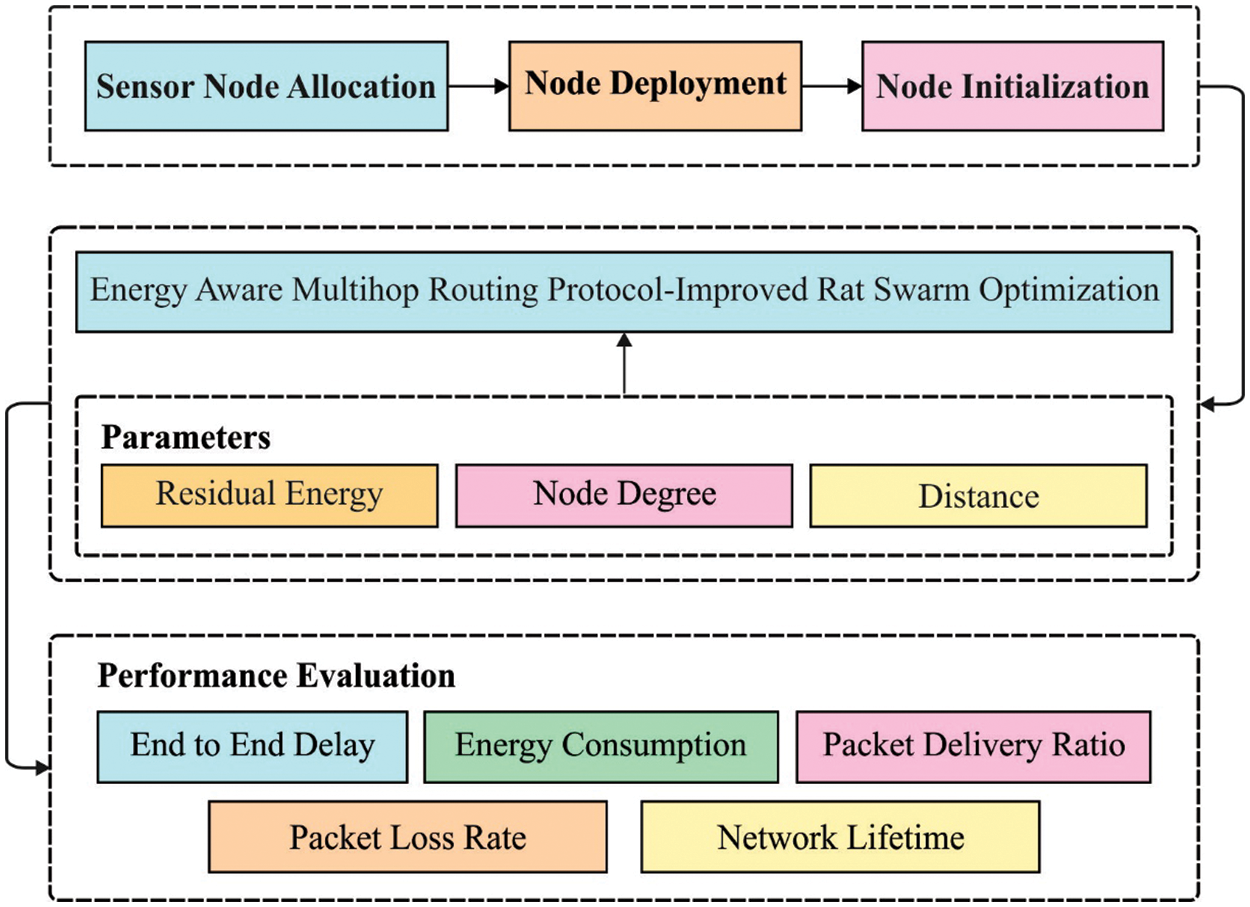
Figure 2: Block diagram of IRSO-EAMHR technique

4.1 CH Selection Process

At the initial stage, a weighted clustering process gets executed to choose CHs. It uses three parameters such as RE, distance, and ND. For every node in WSN, the probability of selecting CHs Pi can be determined using Eq. (11):

Pi=w1∗Eri+w2∗Di+w3∗NDi (11)

where w1 , w2 and w3 are defined as coefficients of the system, therefore

w1+w2+w3=1 (12)

4.2 Overview of IRSO Algorithm

RSO is a novel meta-heuristic technique which is simulated by the attacking and following performances of rats. The rats are regional animals which live from swarms of both male and female. During this technique, the following and aggressive performances of rats are mathematical processes for performing optimized [14]. Related to the other population based optimized approaches, the RSO begins with a group of arbitrary solutions that imply the rat place from the searching space. The arbitrary set was estimated frequently by main function and enhanced dependent upon the following and aggressive performances of rats. During the original version of RSO approach, primary places of eligible solutions (rat places) are defined arbitrarily from the searching space as follows:

xi=ximin+rand×(ximax−ximin),i=1,2,…,N, (13)

where ximin and ximax represents the lower as well as upper bounds to the ith variable correspondingly, and N represents the entire amount of agents. Usually, the rats are subsequent the bait from the group with its social painful behavior. In the mathematical model, for describing this efficiency of rats, it can be considered that highest searching agent is the data of bait placements. So, the other searching agents are updating their places interms of the maximum searching agent attained until now. The succeeding formula is suggested to present the attack procedure of rats utilizing bait and take the upgrade next place of rats [15]:

P→i(x+1)=|P→r(x)−P→|, (14)

where P→i(x+1)=|P→i(x)−P→)| depicts the upgraded places of ith rats and P→r(x) refers the optimal solution establish so far. During the aforementioned formula, P→ is attained utilizing the subsequent formula:

P→=A×P→i(x)+C×(P→r(x)−P→i(x)), (15)

where P→i(x) demonstrates the places of ith rat, and parameters A and C are computed as follows:

A=R−x×(RItermax),x=1,2,3,…,Itermax, (16)

C=2×rand. (17)

At this point, the parameter R refers the arbitrary number in 1 and 5, and C represents the arbitrary number amongst zero and two. x denotes the present iteration of optimized procedure and Itermax stands for the maximal count of iterations. Eq. (8) upgrades the places of searching agents and saved the optimum solutions.

For improving the performance of the RSO technique, the IRSO system has been derived by the utilize of Levy movement model. Levy movement [16] is an arbitrary searching path interchanging among short and irregularly long walks succeeding the Levy distribution. The position update formulation of the Levy movement can be defined as follows:

xij(t+1)=xij(t)×Levy(d), (18)

Levy(β)=0.01×(r1×σ)|r2|β−1 (19)

σ=((Γ(1+β)×sin⁡(πβ2))(Γ(1+β2)×β×2(β−12)))β−1 (20)

i denotes ith individuals and j indicates the number of individuals. Γ(β)=(β−1)!. t implies present algebra. d denotes dimension of optimized objects, r1, r2∈ rand ( 0,1).β indicate the partial real constant. Once the fitness value is judged as good or bad depending upon the recently produced individual position vector, the original individual in the RSO algorithm will be substituted by the best.

4.3 Process Involved in IRSO-EAMHR Technique

The process of determining optimal paths using proposed model involves the design of fitness functions using different parameters such as RE, distance, and ND. The goal of the proposed model is to identify optimal routes in WSN as follow that the network lifetime and energy efficiency is enhanced. The RE of the CHs is significant for route selection. An important parameter Fresm is related to Ech−n˙ and Ncl , defining RE and ND of CHs i correspondingly. It can be mathematically formulated as follows.

Fresm=∑i=1Ncl⁡Ech−ri (21)

Intercluster distance, i.e., distance from CHs to BS is employed and the CHs with lower distance to BS can be chosen for data transmission. Then, the Fdistm can be represented using Eq. (22):

Fdistm=∑i=1Ncld(CHifoMS)d(avgCHi to MS) (22)

where Ncl denotes number of CHs , d(CHi to MS) and d(avgCHi to MS) denotes distance average distance from CHs to BS, correspondingly [17]. Minimum value of Fdistm represents that the present CHi is a candidate to be the succeeding relay node to BS. ND in a cluster is the final parameter involved in the fitness function. The higher ND indicated the possibility of consuming more energy in the cluster which needs to be reduced. Therefore, the Fcmm can be represented using Eq. (23).

Fcmm=∑i=1Ncl⁡Ncm(i). (23)

where Ncm(i) denotes number of CMs that exist for the CH node i. At last, the fitness variables are integrated to derive the objective function, Fobjm as given below.

Fobjm=φ∗Fresm+γ∗Fdisfm+δ∗Fcmm (24)

where φ, γ and δ represent weighting coefficients, i.e., (φ+γ+δ=1) . Also, the value of Fobjm needs to be low so that optimal routes can be identified and network efficiency can be improved.

5  Experimental Analysis

This section inspects the experimental validation of the IRSO-EAMHR method using MATLAB tool. The results are assessed under several aspects and measures. Tab. 1 and Fig. 3 offer a comparative energy consumption (ECN) assessment of the IRSO-EAMHR model with recent models such as fully distributed energy aware multi-level clustering and routing (FDE), Energy-Efficient Optimal Multi-path Routing Protocol (EEOMPRP), Wolf optimization for multi-path routing protocol (WOMPR), CoAP congestion control for the internet of things (CoAP-IOT), and Collision-Aware Routing Using Multi-Objective Seagull Optimization Algorithm (CAR-MOSOA)under distinct nodes [18–22]. The results indicated that the IRSO-EAMHR model has resulted in effectual outcome with lower ECN over the other algorithms under distinct count of nodes. For sample, with 100 nodes, the IRSO-EAMHR approach has obtained minimal ECN of 0.52 J whereas the FDE, EEOMPRP, WOMPR, CoAP-IOT, and CAR-MOSOA techniques have obtained maximum ECN of 1.14 J, 1.39 J, 8.43 J, 11.27 J, and 0.70 J correspondingly. In addition, with 400 nodes, the IRSO-EAMHR model has obtainable a reduced ECN of 26.83 J whereas the FDE, EEOMPRP, WOMPR, CoAP-IOT, and CAR-MOSOA techniques have accomplished increased ECN of 42.13 J, 47.85 J, 44.01 J, 41.17 J, and 32.56 J respectively.

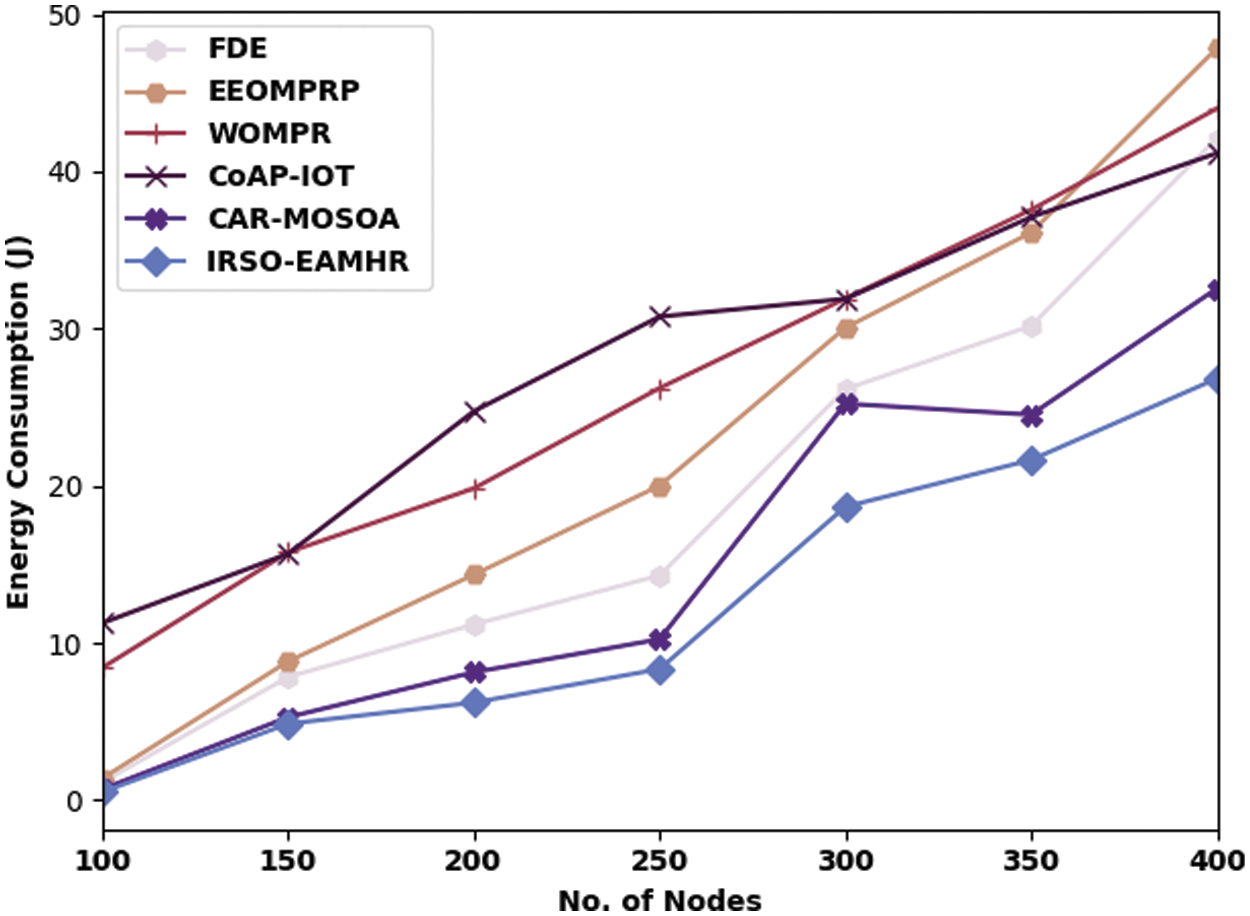
Figure 3: ECM analysis of IRSO-EAMHR technique with existing approaches

Tab. 2 and Fig. 4 demonstrate a comparative end to end delay (ETED) valuation of the IRSO-EAMHR model with existing techniques under several nodes. The figure demonstrated that the IRSO-EAMHR approach has accomplished reasonable performance with least ETED over the other algorithms under distinct count of nodes. For sample, with 100 nodes, the IRSO-EAMHR methodology has exhibited lower ETED of 3541 ms whereas the FDE, EEOMPRP, WOMPR, CoAP-IOT, and CAR-MOSOA techniques have accomplished higher ETED of 8070 ms, 10474 ms, 8365 ms, 11857 ms, and 4800 ms respectively. Eventually, with 400 nodes, the IRSO-EAMHR model has reached minimal ETED of 24255 ms whereas the FDE, EEOMPRP, WOMPR, CoAP-IOT, and CAR-MOSOA techniques have obtained increased ETED of 40501 ms, 50429 ms, 44229 ms, 54160 ms, and 29395 ms respectively.

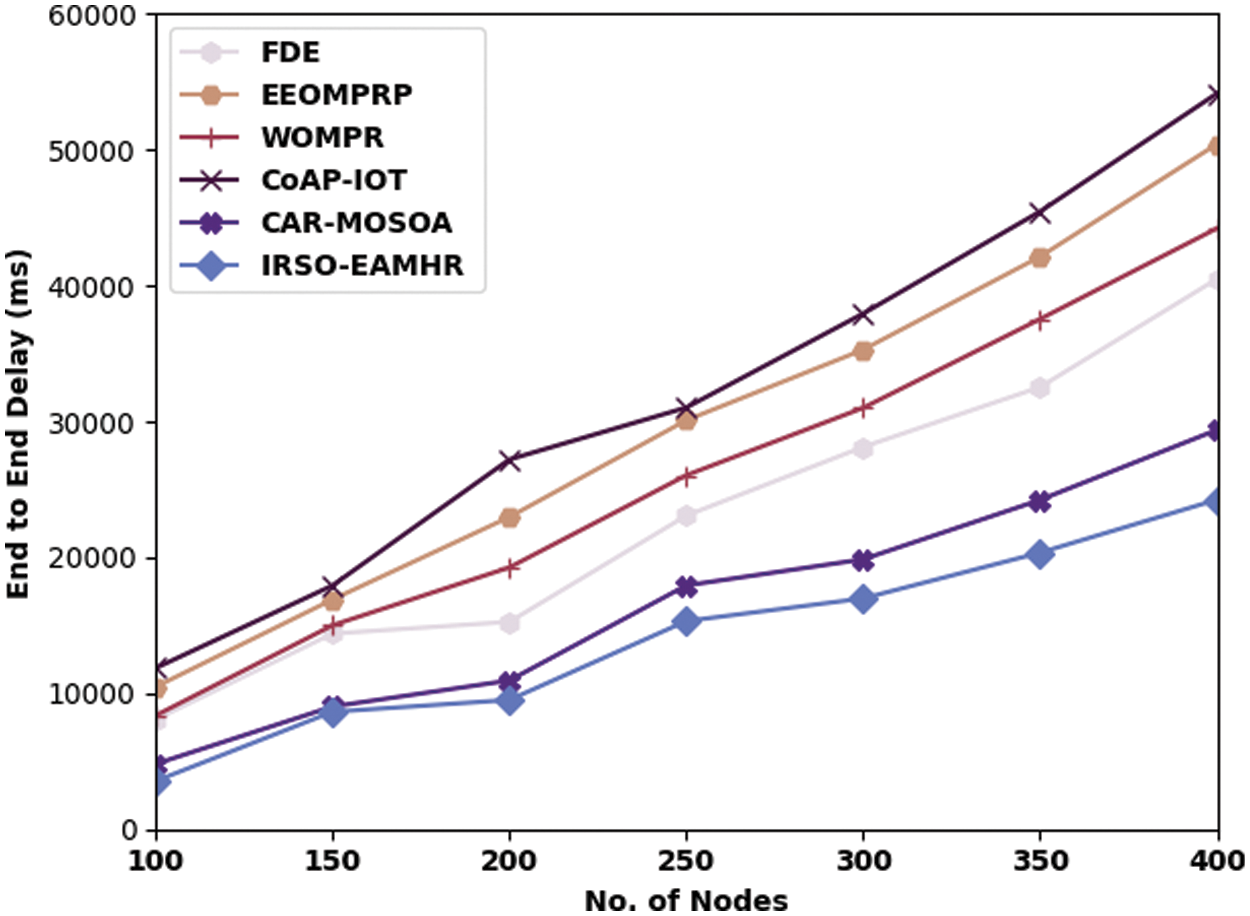
Figure 4: ETED analysis of IRSO-EAMHR technique with existing approaches

A detailed packet delivery ratio (PDR) examination of the IRSO-EAMHR model with recent methods is performed in Tab. 3 and Fig. 5. The experimental values implied that the IRSO-EAMHR model has exhibited effectual outcomes with higher values of PDR under all nodes. For instance, with 100 nodes, the IRSO-EAMHR system has accomplished increased PDR of 85.64% but the FDE, EEOMPRP, WOMPR, CoAP-IOT, and CAR-MOSOA techniques have reached minimal PDR of 80.68%, 70.34%, 72.82%, 67.86%, and 84.18% respectively. Similarly, with 400 nodes, the IRSO-EAMHR model has reached improved PDR of 98.54% whereas the FDE, EEOMPRP, WOMPR, CoAP-IOT, and CAR-MOSOA techniques have resulted in decreased PDR of 94.12%, 88.64%, 92.86%, 88.70%, and 96.09% respectively.

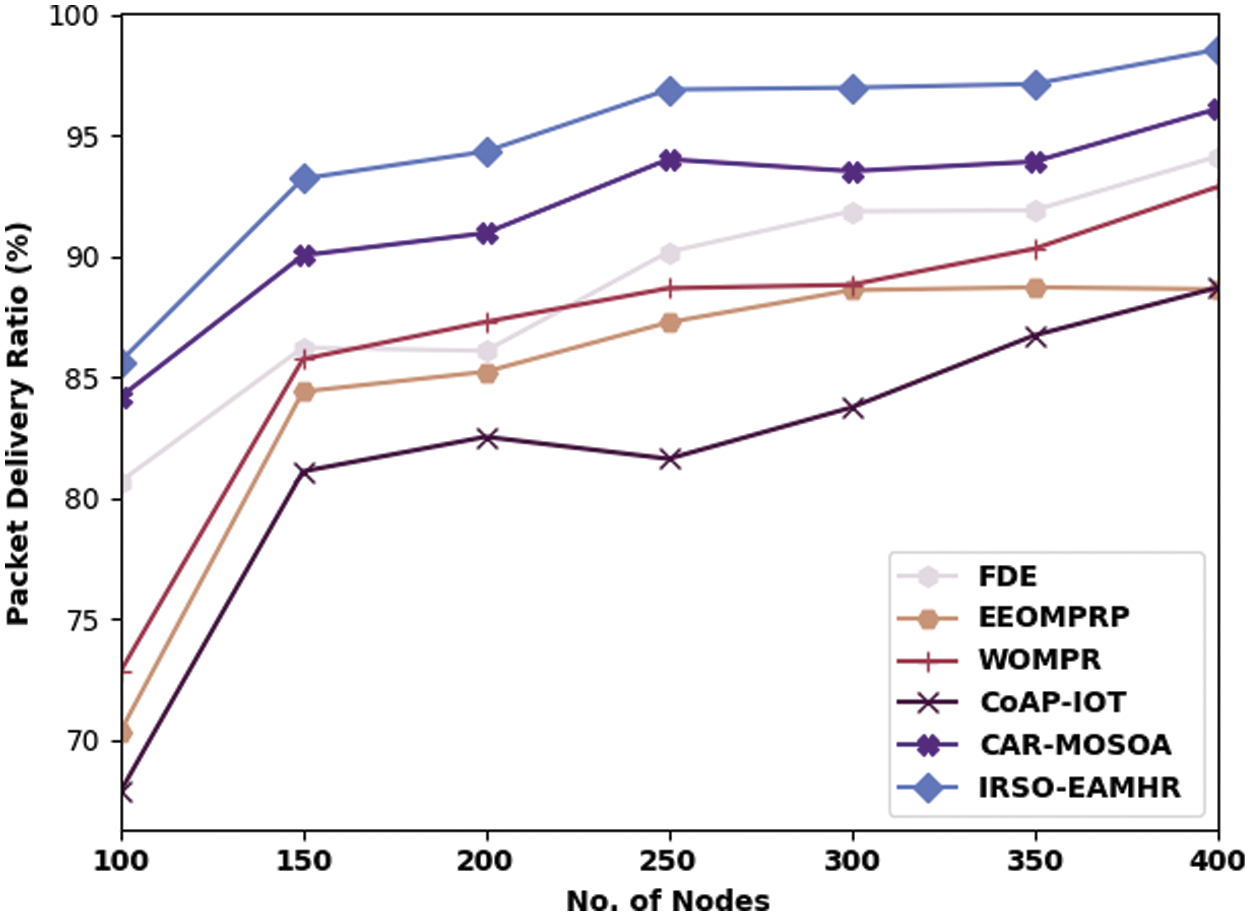
Figure 5: PDR analysis of IRSO-EAMHR technique with existing approaches

Tab. 4 and Fig. 6 illustrate an extensive packet loss rate (PLR) examination of the IRSO-EAMHR model with recent models under various nodes. The figure reported that the IRSO-EAMHR technique has led to supreme performance with minimal PLR over the other techniques under distinct count of nodes. For instance, with 100 nodes, the IRSO-EAMHR algorithm has gained minimal PLR of 14.36% whereas the FDE, EEOMPRP, WOMPR, CoAP-IOT, and CAR-MOSOA techniques have obtained maximum PLR of 19.32%, 29.66%, 27.18%, 32.14%, and 15.82% respectively. Followed by, with 400 nodes, the IRSO-EAMHR model has offered decreased PLR of 1.46% whereas the FDE, EEOMPRP, WOMPR, CoAP-IOT, and CAR-MOSOA techniques have demonstrated increased PLR of 5.88%, 11.36%, 7.14%, 11.30%, and 3.19% respectively.

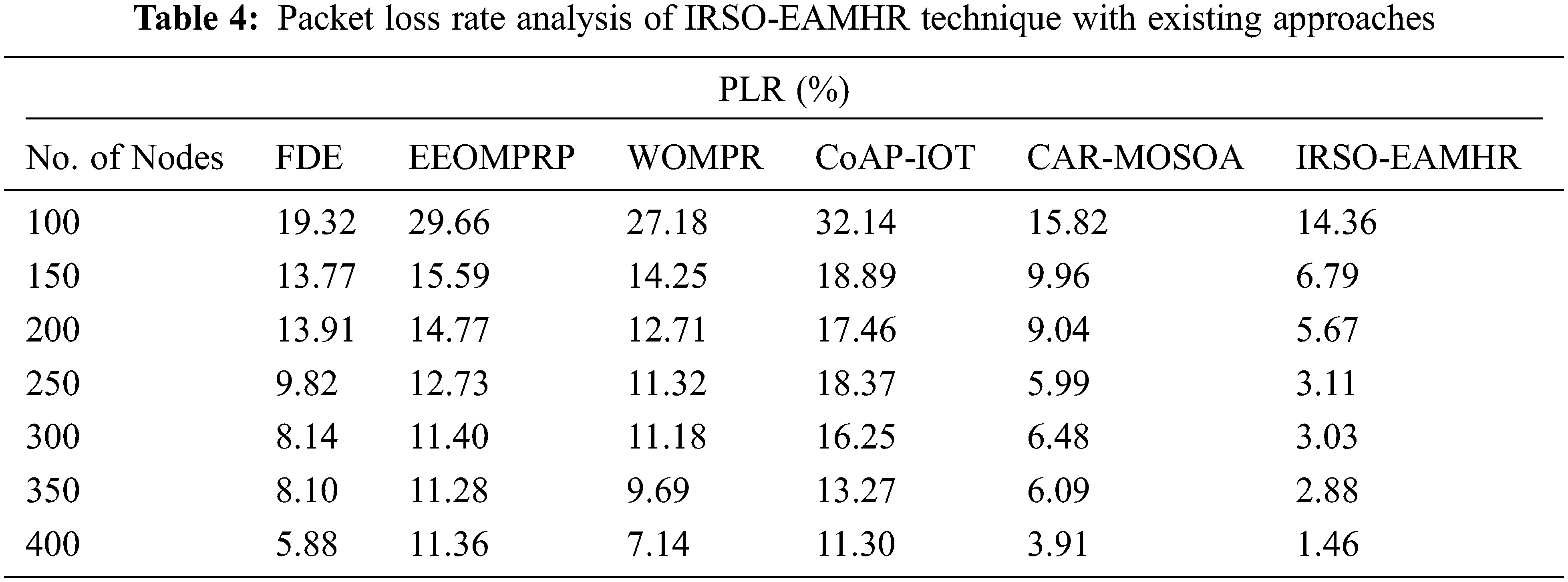
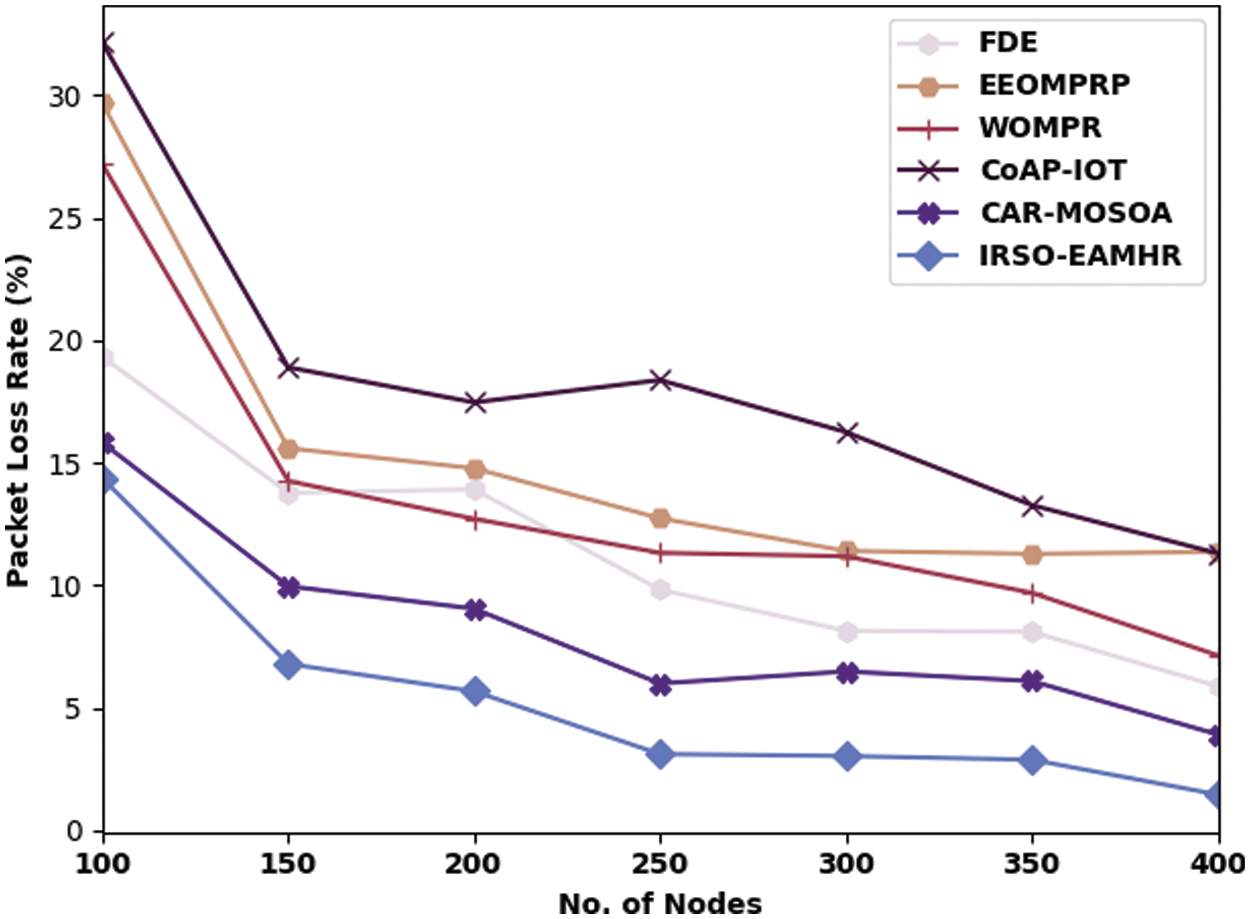
Figure 6: PLR analysis of IRSO-EAMHR technique with existing approaches

A thorough NLT inspection of the IRSO-EAMHR model with recent methods is performed in Tab. 5 and Fig. 7. The investigational values inferred that the IRSO-EAMHR method has shown capable outcomes with higher values of NLT under all nodes. For sample, with 100 nodes, the IRSO-EAMHR approach has gained superior NLT of 28.81 min whereas the FDE, EEOMPRP, WOMPR, CoAP-IOT, and CAR-MOSOA techniques have led to inferior NLT of 21.38 min, 20.00 min, 20.03 min, 18.05 min, and 23.17 min respectively. Meanwhile, with 400 nodes, the IRSO-EAMHR model has accomplished increased NLT of 22.19 min whereas the FDE, EEOMPRP, WOMPR, CoAP-IOT, and CAR-MOSOA techniques have accomplished reduced NLT of 17.93 min, 14.17 min, 16.90 min, 13.12 min, and 17.80 min respectively. From the above mentioned tables and figures, it can be ensured that the IRSO-EAMHR model has been initiate that effective routing protocol for WSN.

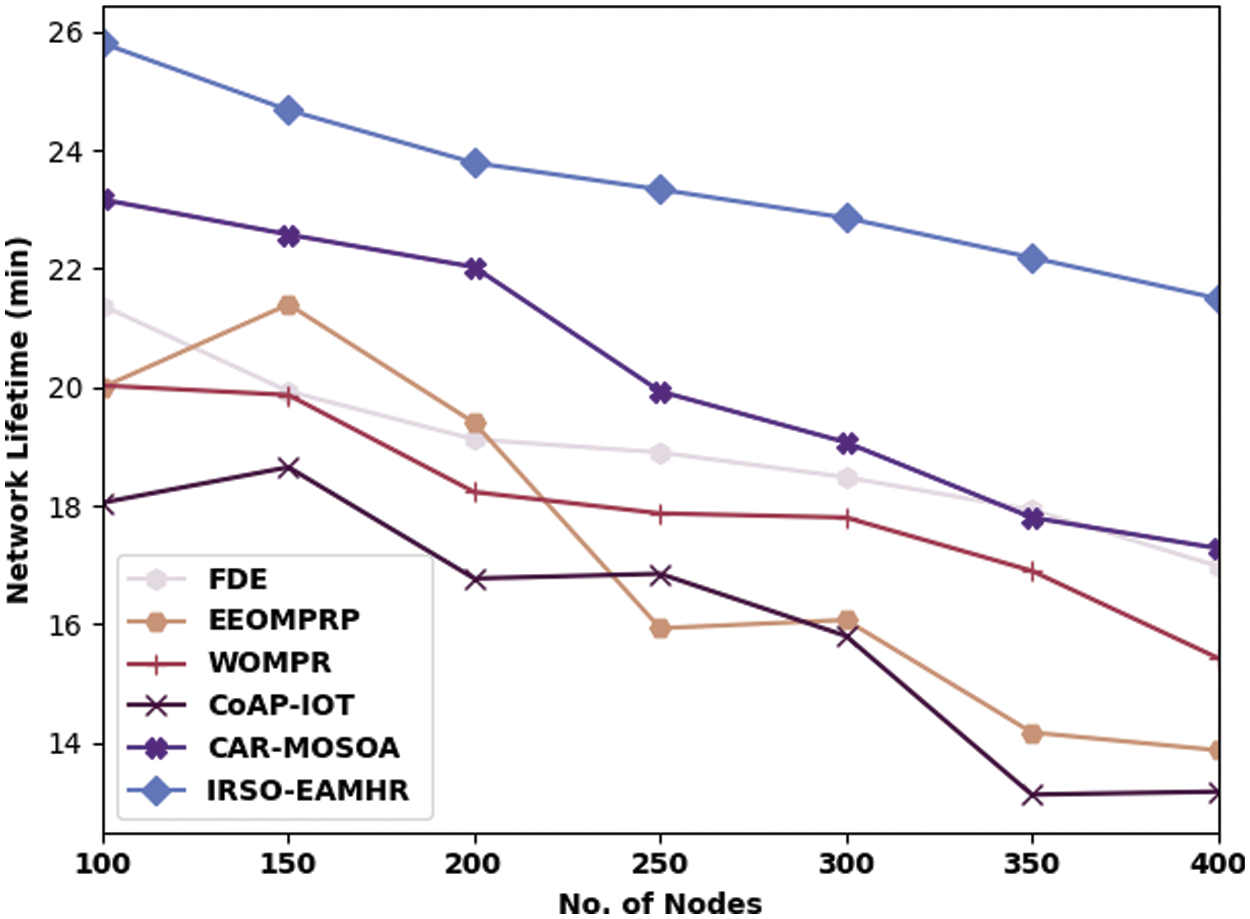
Figure 7: NLT analysis of IRSO-EAMHR technique with existing approaches

6  Conclusion

In this study, a new IRSO-EAMHR algorithm was developed for optimal selection of routes to BS in the energy efficient WSN. An important aim of the IRSO-EAMHR approach is to maximize energy efficiency and NLT in WSN. The IRSO-EAMHR system initially performed weight clustering process for the selective of CHs and cluster construction. In addition, an optimal set of routes are chosen by the use of IRSO algorithm with fitness function. The design of IRSO algorithm with the inclusion of the Levy movement concept into the traditional RSO algorithm helps to improve its efficacy. The experimental result analysis of the IRSO-EAMHR technique is carried out and the outcomes are examined in different aspects. The simulation outcomes demonstrate the promising performance of the IRSO-EAMHR technique over the recent state of art approaches. In future, data aggregation approaches are derived to further improve energy efficiency of WSN.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  S. Arjunan and P. Sujatha, “Lifetime maximization of wireless sensor network using fuzzy based unequal clustering and ACO based routing hybrid protocol,” Applied Intelligence, vol. 48, no. 8, pp. 2229–2246, 2018. [Google Scholar]

 2.  S. Famila, A. Jawahar, A. Sariga and K. Shankar, “Improved artificial bee colony optimization based clustering algorithm for SMART sensor environments,” Peer to Peer Networking and Applications, vol. 13, no. 4, pp. 1071–1079, 2020. [Google Scholar]

 3.  S. Arjunan and P. Sujatha, “Corrigendum to A survey on unequal clustering protocols in wireless sensor networks,” Journal of King Saud University - Computer and Information Sciences, vol. 33, no. 1, pp. 118, 2021. [Google Scholar]

 4.  A. Sun, K. Zhu, J. Du and H. Cao, “PSO-based K-means algorithm for clustering routing in 5G WSN networks,” in 2021 IEEE Globecom Workshops (GC Workshops). Madrid, Spain, pp. 1–6, 2021. [Google Scholar]

 5.  S. Arjunan, S. Pothula and D. Ponnurangam, “F5N-based unequal clustering protocol (F5NUCP) for wireless sensor networks,” International Journal of Communication Systems, vol. 31, no. 17, pp. e3811, 2018. [Google Scholar]

 6.  K. Haseeb, N. Islam, A. Almogren, I. Ud Din, H. N. Almajed et al., “Secret sharing-based energy-aware and multi-hop routing protocol for IoT based WSNs,” IEEE Access, vol. 7, pp. 79980–79988, 2019. [Google Scholar]

 7.  W. Sun, G. Z. Dai, X. R. Zhang, X. Z. He and X. Chen, “TBE-Net: A three-branch embedding network with part-aware ability and feature complementary learning for vehicle re-identification,” IEEE Transactions on Intelligent Transportation Systems, pp. 1–13, 2021. https://doi.org/10.1109/TITS.2021.3130403. [Google Scholar]

 8.  W. Sun, L. Dai, X. R. Zhang, P. S. Chang and X. Z. He, “RSOD: Real-time small object detection algorithm in UAV-based traffic monitoring,” Applied Intelligence, vol. 92, no. 6, pp. 1–16, 2021. [Google Scholar]

 9.  J. Uthayakumar, T. Vengattaraman and P. Dhavachelvan, “A new lossless neighborhood indexing sequence (NIS) algorithm for data compression in wireless sensor networks,” Ad Hoc Networks, vol. 83, no. 2009, pp. 149–157, 2019. [Google Scholar]

10. D. Ruan and J. Huang, “A PSO-based uneven dynamic clustering multi-hop routing protocol for wireless sensor networks,” Sensors, vol. 19, no. 8, pp. 1835, 2019. [Google Scholar]

11. A. Rezaeipanah, P. Amiri, H. Nazari, M. Mojarad and H. Parvin, “An energy-aware hybrid approach for wireless sensor networks using re-clustering-based multi-hop routing,” Wireless Personal Communications, vol. 120, no. 4, pp. 3293–3314, 2021. [Google Scholar]

12. J. Huang, T. Li and Z. Shi, “An uneven annulus sector grid-based energy-efficient multi-hop routing protocol for wireless sensor networks,” Peer to Peer Networking and Applications, vol. 15, no. 1, pp. 559–575, 2022. [Google Scholar]

13. M. Adnan, L. Yang, T. Ahmad and Y. Tao, “An unequally clustered multi-hop routing protocol based on fuzzy logic for wireless sensor networks,” IEEE Access, vol. 9, pp. 38531–38545, 2021. [Google Scholar]

14. A. Toolabi Moghadam, M. Aghahadi, M. Eslami, S. Rashidi, B. Arandian et al., “Adaptive rat swarm optimization for optimum tuning of SVC and PSS in a power system,” International Transactions on Electrical Energy Systems, vol. 2022, pp. 1–13, 2022. [Google Scholar]

15. G. Dhiman, M. Garg, A. Nagar, V. Kumar and M. Dehghani, “A novel algorithm for global optimization: Rat swarm optimizer,” Journal of Ambient Intelligence and Humanized Computing, vol. 12, no. 8, pp. 8457–8482, 2021. [Google Scholar]

16. D. Mukherjee, S. Mallick and A. Rajan, “A levy flight motivated meta-heuristic approach for enhancing maximum loadability limit in practical power system,” Applied Soft Computing, vol. 114, pp. 108146, 2022. [Google Scholar]

17. S. Yalçın and E. Erdem, “TEO-MCRP: Thermal exchange optimization-based clustering routing protocol with a mobile sink for wireless sensor networks,” Journal of King Saud University - Computer and Information Sciences, vol. 46, no. 2, pp. S1319157822000192, 2022. [Google Scholar]

18. İ. Abasıkeleş-Turgut and G. Altan, “A fully distributed energy-aware multi-level clustering and routing for WSN-based IoT,” Transactions on Emerging Telecommunications Technologies, vol. 32, no. 12, pp. e3816, 2021. [Google Scholar]

19. K. Jaiswal and V. Anand, “EOMR: An energy-efficient optimal multi-path routing protocol to improve QoS in wireless sensor network for IoT applications,” Wireless Personal Communications, vol. 111, no. 4, pp. 2493–2515, 2020. [Google Scholar]

20. N. Chouhan and S. C. Jain, “Tunicate swarm grey wolf optimization for multi-path routing protocol in IoT assisted WSN networks,” Journal of Ambient Intelligence and Humanized Computing, vol. 25, no. 8, pp. 4887, 2020. [Google Scholar]

21. A. Betzler, C. Gomez, I. Demirkol and J. Paradells, “CoAP congestion control for the internet of things,” IEEE Communication Magazines, vol. 54, no. 7, pp. 154–160, 2016. [Google Scholar]

22. P. Jagannathan, S. Gurumoorthy, A. Stateczny, P. Divakarachar and J. Sengupta, “Collision-aware routing using multi-objective seagull optimization algorithm for WSN-based IoT,” Sensors, vol. 21, no. 24, pp. 8496, 2021. [Google Scholar]