New Preamble Sequence for WiMAX System with Improved Synchronization Accuracy

1  Introduction

WiMAX technology formulated based on IEEE802.16e standard accomplishes high throughput wireless broadband access as well as IP connectivity and promotes various compatible mobile applications. A rich set of features like OFDM based physical layer, hybrid automatic repeat request, adaptive modulation and coding, advanced encryption standard, extensible authentication protocol, outer coding, inner coding and interleaving are assimilated to ensure the quality of service [1]. High rate digital transmission in WiMAX is supported by OFDM. This multicarrier modulation scheme with orthogonal sub-carriers provides attractive robustness to multipath fading and implementation flexibility [2,3]. By adding multiple antenna facility to OFDM, the transmission reliability as well as capacity is further increased significantly [4–6]. Despite of all the above advantages, WiMAX system experiences shortcoming of sensitivity to frequency and time offsets. The mismatch between the sampling time at the transmitter and receiver as well as random propagation delays induces TO. At the same time, Doppler frequency in the channel and inconsistencies between oscillators generating the carrier frequency at the transmitter and receiver are the main reasons behind CFO. Since demodulation of an OFDM signal with offset error deteriorates system performance, proper estimation and compensation of CFO and TO are inevitable for the reliable signal reception [7–9]. Offset estimation in OFDM has been a subject of intensive research in the last decade. The various approaches suggested in the literature for offset estimation can be classified based on whether the estimation is based on pilot symbols/preamble sequences or by exploiting the intrinsic structure and statistical properties of OFDM symbols. Moose [10] introduced the repeated preamble structure with two identical symbols which detects the CFO by just measuring the deviation of phase between the two identical blocks. Schmidl and Cox then proposed an improved preamble based algorithm which is capable of computing both frequency and timing offsets with an enhanced acquisition range [11]. Preamble based method developed by Awoselia incorporated autocorrelation, cross correlation and threshold based detection to reduce the MSE and to attain enhanced reliability [12]. Hsieh and Wu suggested a Maximum Likelihood (ML) based method to compute the likelihood function for CFO estimation with reduced computational complexity and it is mainly targeted for communication standards with more than two preambles [13]. In [14], M. Morelli et al. presented a preamble based CFO estimation method for MIMO OFDM system. The technique used both ML estimation and correlation based approaches to estimate both integer frequency offset and fractional frequency offset. Rogozhnikov and Babur proposed a CFO estimation method utilizing a pilot sequence consisting of two repeated parts [15]. A rough estimation of the CFO is acquired in the first stage by computing the angle of correlation between the two halves of the pilot sequence. A reference sequence is generated in the second stage and the fine estimate is calculated from the coefficient of correlation between the reference signal and the received sequence. Many more preamble synchronization based papers are available in the literature.

It is revealed from the literature survey that performance optimality of preamble based synchronization methods requires mathematical sequences with excellent correlation properties. The synchronization requirements in IEEE 802.16e or WiMAX system are met through preamble based offset estimation. Even though the feasibility of improving synchronization accuracy is a hot topic of research, the scope of improving the synchronization amenability of a sequence by optimizing the correlation side lobes is not explored yet. Literature review shows that a lot of investigations has been done to identify and develop new sequences with improved correlation properties using complicated search algorithms. In this paper, a new method to enhance the correlation properties of a preamble sequence is proposed. The results show that the offset estimation accuracy in MIMO OFDM based wireless communication systems can be significantly enhanced by redesigning the preambles by using the proposed method. Our contributions in this paper are as follows.

(a) Proposed a new method to improve the Merit Factor (MF) of WiMAX sequence.

(b) A new sequence is developed by reconstructing the WiMAX sequence using the proposed MF enhancing algorithm.

The novelty of this work is that the scope for improving the synchronization accuracy by optimizing the significant properties of the preamble sequence is not yet seen in the literature. The rest of the paper is organized as follows. Section 2 is devoted to the WiMAX model based on OFDM physical layer and its signal representation. Section 3 briefly defines the preamble aided estimation of frequency and time offsets. In Section 4, a new method to improve the accuracy of offset estimation is proposed based on fine tuning correlation properties. The performance analysis of the proposed method is explored in Section 5 through results of simulations. Finally concluding remarks are provided in Section 6. The list of symbols used in this paper is provided in Tab. 1.

2  WiMAX OFDM Signal Model

A general block diagram of the WiMAX physical layer is depicted in Fig. 1. The input data stream is preprocessed by a randomizer, channel encoder and an interleaver. This processed data stream is then mapped onto constellation points by phase shift keying or quadrature amplitude modulation. Inverse Fast Fourier Transform (IFFT) operation provides a simple way to modulate the constellation mapped data symbols into N orthogonal subcarriers [2,3]. By allocating data to N different subcarriers, it is possible to split a higher bit rate stream to N number of lower bit rate streams and maintain channel delays as an insignificant fraction of the symbol duration. This minimizes the Inter Symbol Interference (ISI) to a great extent. Further, a Cyclic Prefix (CP) is affixed at the beginning of each OFDM symbol as guard samples to mitigate the deleterious effects of channel spread.

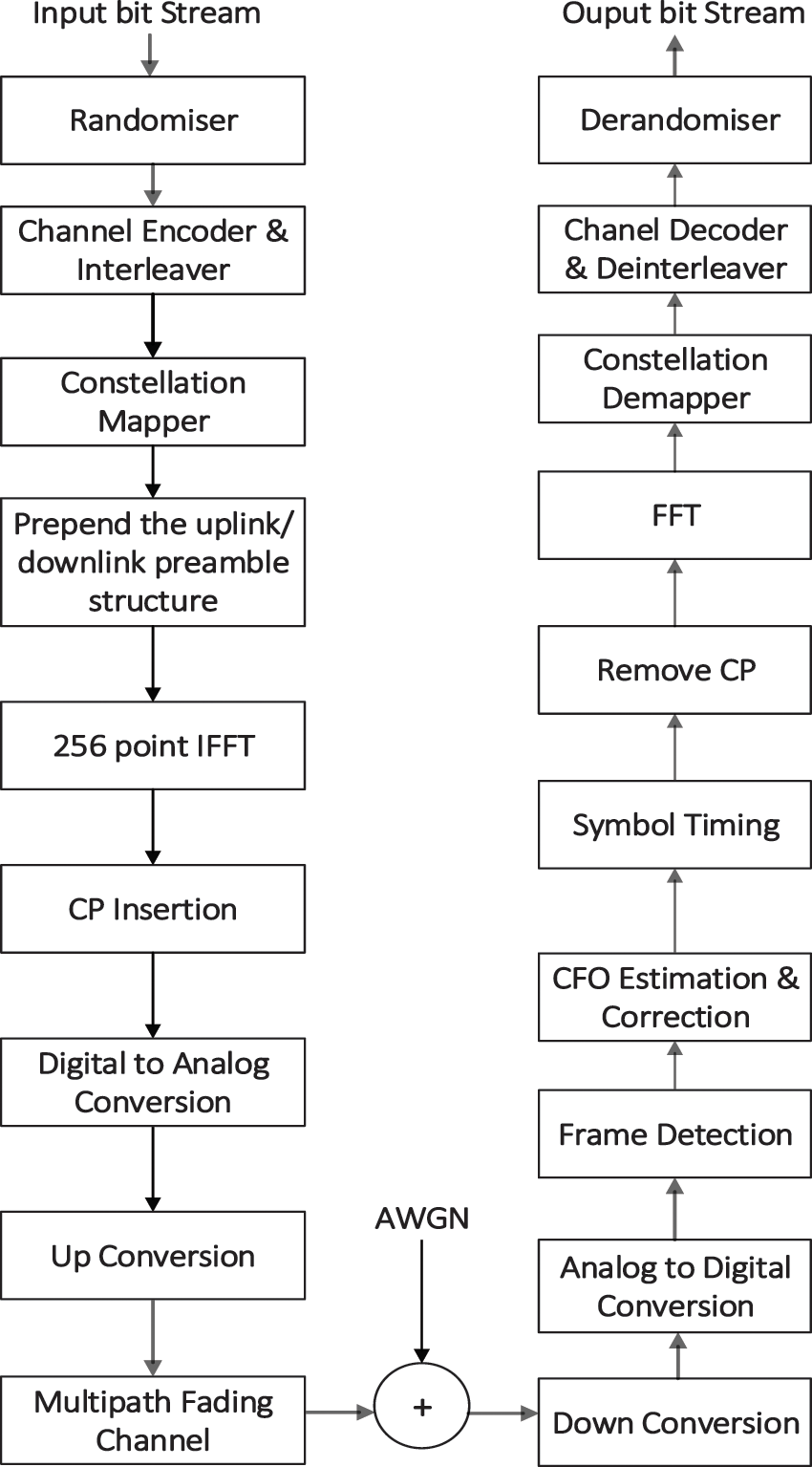
Figure 1: Block diagram of WiMAX physical layer

The transmitted OFDM samples can be mathematically modeled [16] as shown in Eq. (1)

s[n]=1N∑k=0N−1⁡Skexp⁡(j2πnkN),n=0,1….N−1 (1)

Sk is the frequency domain data symbol for the kth subcarrier, N is the number of subcarriers, k is the subcarrier index. At the receiver side, the demodulated signal from Fast Fourier Transform (FFT) processor can be represented by Eq. (2) and (3), where rl [n] is the nth sample of the lth OFDM symbol.

Rl[k]=∑n=0n−1⁡rl[n]e−j2ΠknNfork=0,1,...N−1 (2)

rl[n]=∑m=0M−1⁡hm[τ]sl[n−τm]+gl[n] (3)

In Eq. (3), hm τm and gl [n] represents Channel Impulse Response (CIR), delay of the mth path and Gaussian noise process.

The modulation/demodulation through IFFT/FFT processors makes the implementation of OFDM faster and less complex. Another key advantage of OFDM is the spectral efficiency attained through orthogonal subcarriers. As long as perfect synchronization is maintained between the transmitter and the receiver, these subcarriers remain orthogonal to each other. But the presence of CFO and TO destructs the orthogonality of subcarriers leading to the performance degradation of the system. The mismatch between sampling time at the transmitter and receiver as well as random propagation delays induces TO in the received signal. At the same time, the Doppler frequencies generated in the channel and the inconsistencies between oscillator generating carrier frequency at the base station and that at receiver produces CFO. Here the CFO and the TO are represented by ‘α’ and ‘µ’ respectively. The expression for the received signal samples effected by α and µ [17,18] is given in Eq. (4).

rl[n]=1N∑N=0N−1⁡Hl(k)Sl(k)ej2Π(k+α)(n=μ)N+G1(k) (4)

The TO causes the FFT window to shift away from its desired position and disturbs the demodulation process [19]. If the window is wrongly placed at a point prior to the actual position and after the CIR of previous the symbol is terminated, the received signal is distorted by a phase offset proportional to µ. The consequences will be more adverse if the symbol start is incorrectly selected at a point before the end of the previous CIR, leading to disorientation in the subcarrier orthogonality and Inter Carrier Interference (ICI). Moreover, the inclusion of samples from both the present and next OFDM symbols in the same FFT processing interval causes ISI also. Similarly, the presence of α brings about many troublesome effects in the received signal including ICI, phase distortion, amplitude degeneration and signal to noise ratio degradation [7,20].

3  Estimation of Frequency and Time offsets Using WiMAX Preamble

Synchronization is maintained in WiMAX by processing the sampled preamble sequence, where offsets are estimated mainly through a correlation operator and the data packet is compensated according to estimated offsets. The physical layer protocol data unit of both the Downlink (DL) and Uplink (UL) sub-frames start with a preamble. The structure of preamble in DL sub-frame consists of four times repetition of a sequence with 64 samples followed by two times repetition of a sequence with 128 samples and the UL sub-frame includes replication of a 128 sampled sequence only. The preamble for the UL and DL sub-frames can be mathematically represented by Eqs. (5) and (6).

Wd=[CW64W64W64W64CW128W128] (5)

Wu=[CW128W128] (6)

The standard WiMAX sequence is defined by the IEEE standard as given by Eqs. (7)–(9)

PW[k]={±1±j,k=−100,…−1,1,…+1000,otherwise (7)

W64[k]={2PW∗(k),kmod4=00,kmod4≠0 (8)

W128[k]={2PW∗(k),kmod2=00,kmod2≠0 (9)

The received signal is down converted to baseband and processed by an analog to digital converter. The preamble sequence extracted from the up/down sub-link frame is further processed to obtain estimates of CFO and TO. The procedure for CFO estimation from an uplink frame is provided by Eq. (10).

αW^=∠{∑k=0M−1⁡RW128(k)RW128(k+M)} (10)

TO can be detected from the correlation between the received preamble ‘RW128’ and a reference copy ‘FW128’ of the same sequence available at the synchronization unit of the receiver. The sample CM with the largest correlation magnitude is identified through Eq. (11) and its shift from the desired time index is estimated as the TO

CM=Max{∑k=0M−1⁡RW128(k)FW128(k)} (11)

4  Enhanced Synchronization Accuracy by Optimizing Merit Factor of Preamble

Judicious selection of mathematical sequence for the preamble structure is very important in preamble based synchronization systems [21]. Error-free offset detection and compensation stipulate sequences with good correlation properties for which autocorrelation side lobes must be minimal [22]. The quality of autocorrelation property of a sequence is generally evaluated using the parameters [23] Integrated Sidelobe Level (ISL) and MF. Let the preamble sequence inserted in the OFDM header represented by Eq. (12).

p=[p(1)p(2)…p(M)] (12)

Aperiodic autocorrelation function of the sequence p(m) can be represented by Eq. (13).

Ak=∑m=1M−k⁡p(m)p∗(m+k),0≤k≤M−1 (13)

The ISL and MF can be defined by Eqs. (14) and (15)

ISL=∑k=1M−1⁡|Ak|2 (14)

MF=|A0|2∑k=−(M−1)k≠0M−1⁡|Ak|2 (15)

The MF of a sequence can be enhanced by reducing the correlation side lobes and hence refining its ISL level. From [24], a quadratic approximation of ISL can be represented by Eq. (16)

ISL=‖P−arg⁡(P)‖2 (16)

P=U∗(p),whereU∗isaFFTmatrixofsize2MX2M (17)

Based on approximation in Eq. (16), the correlation side lobe amplitude can be reduced and the synchronization amenability of the sequence can be enhanced through the following steps given by Eqs. (18) to (24)

(i)d=[p(1)p(2)…p(M)0…0]NX1T,whereN=2M (18)

(ii)f=12M[e−jΩ1e−j2Ω1e−jΩ2⋮e−j2Ω2⋮e−jΩNe−j2ΩN⋯e−jNΩ1⋯⋮e−jNΩ2⋮⋯e−jNΩN]d (19)

(iii)Ωq=2πNq,q=1,2…M (20)

(iv)sq=ejarg(fq),q=1,2……N (21)

(v)s=[ejarg(f1)ejarg(f2)….ejarg(fN)]T (22)

(vi)i=1√2M[ejΩ1ej2Ω1ejΩ2⋮ej2Ω2⋮ejΩNej2ΩN⋯ejNΩ1⋯⋮ejNΩ2⋮⋯ejNΩN]s (23)

Redefinep(m)=ejarg(im),m=1,2….M (24)

The correlation sidelobes can be minimized by a phase modification process by repeating the above steps until the norm of difference between the sequences obtained in two consecutive iterations is less than a defined threshold σ. The value of σ is set at 10−3 after verifying that no further reduction in ISL is possible after that.

5  Results

The performance of a mathematical sequence employed in offset estimation strongly depends on its correlation properties. The merit of the Autocorrelation Function (ACF) is associated with its sidelobe pattern where we prefer minimum values for off-peaks of correlation or ACF sidelobes. WiMAX physical layer with a 256 subcarrier OFDM is simulated using MATLAB R2019a. A multipath Rayleigh fading channel with five paths is also simulated. The simulation parameters are as shown in Tab. 2.

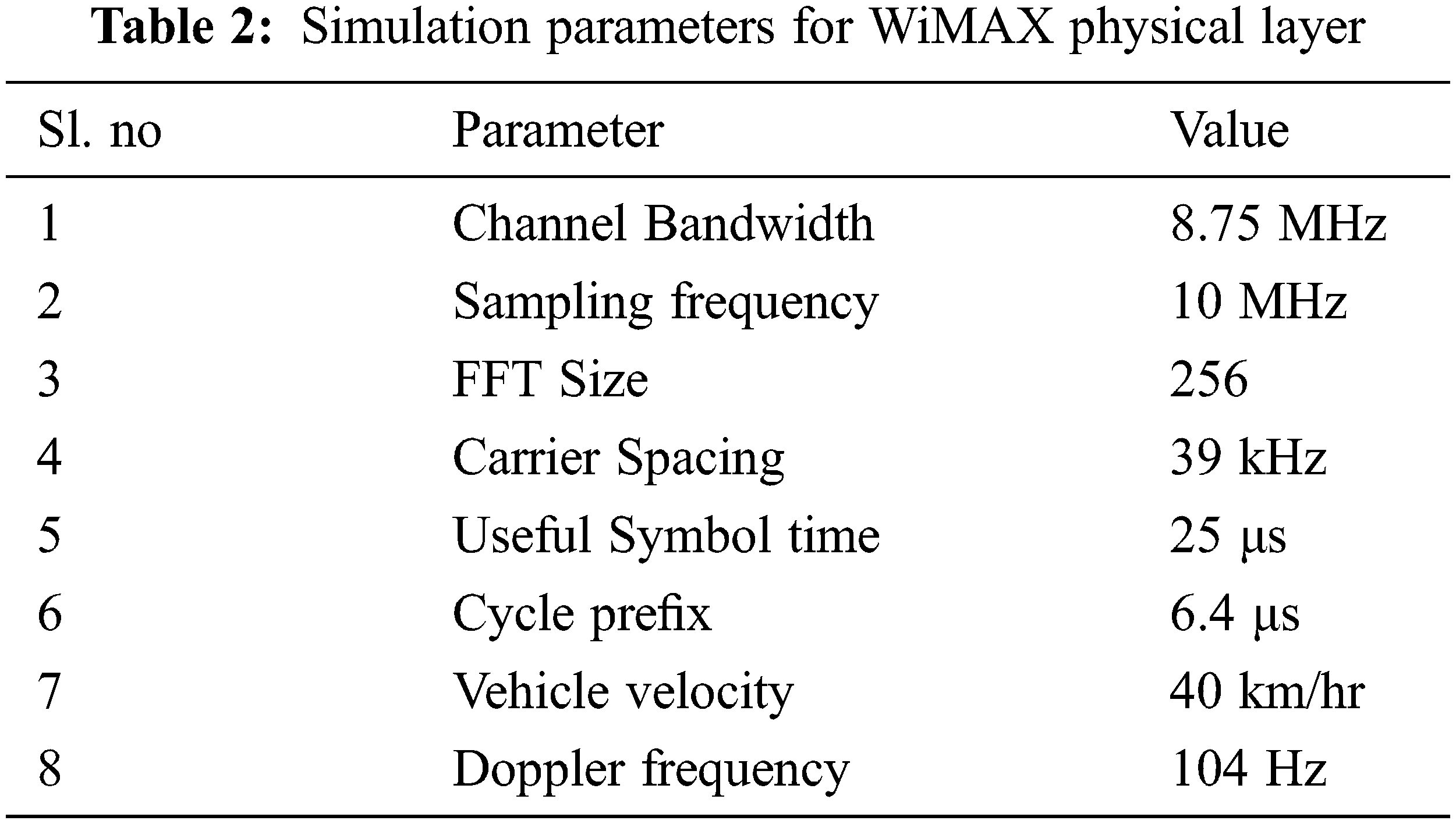
To conduct a comparative study on offset estimation performance of standard WiMAX sequence and MF enhanced sequences, a carrier frequency of 900 MHz is considered. Under the assumption that the user vehicle is moving at an angle 30° with respect to the base station antenna, Doppler frequency is computed as 104 Hz.

The MF and ISL of the WiMAX sequences W128 and W64 are enhanced and comparison with standard WiMAX sequence is provided in Tab. 3. Results show that the MF is increased by a factor of 54.25%.

Spectrum of MF enhanced new WiMAX preamble is compared with that of standard WiMAX preamble and is shown in Figs. 2 and 3. It is observed that spectrum of new preamble is more flat than standard one.

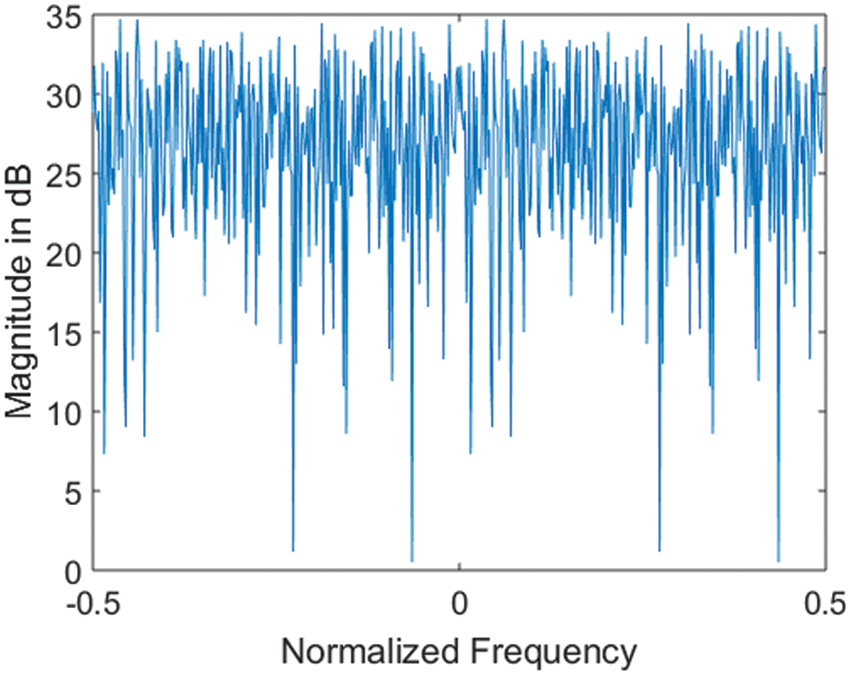
Figure 2: Spectrum of standard WiMAX preamble

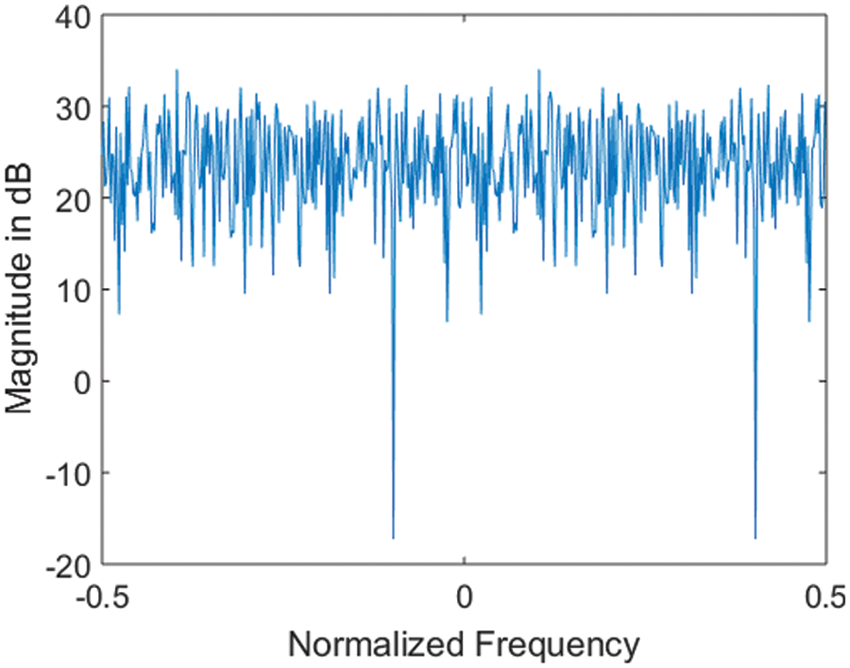
Figure 3: Spectrum of MF enhanced WiMAX preamble

The performance of the proposed preamble is evaluated in a Rayleigh fading channel through simulation in MATLAB R2019a and plotted the MSE curve for both standard WiMAX preamble and its MF enhanced version in Fig. 4. It is found that new sequence outperforms the standard WiMAX preamble.

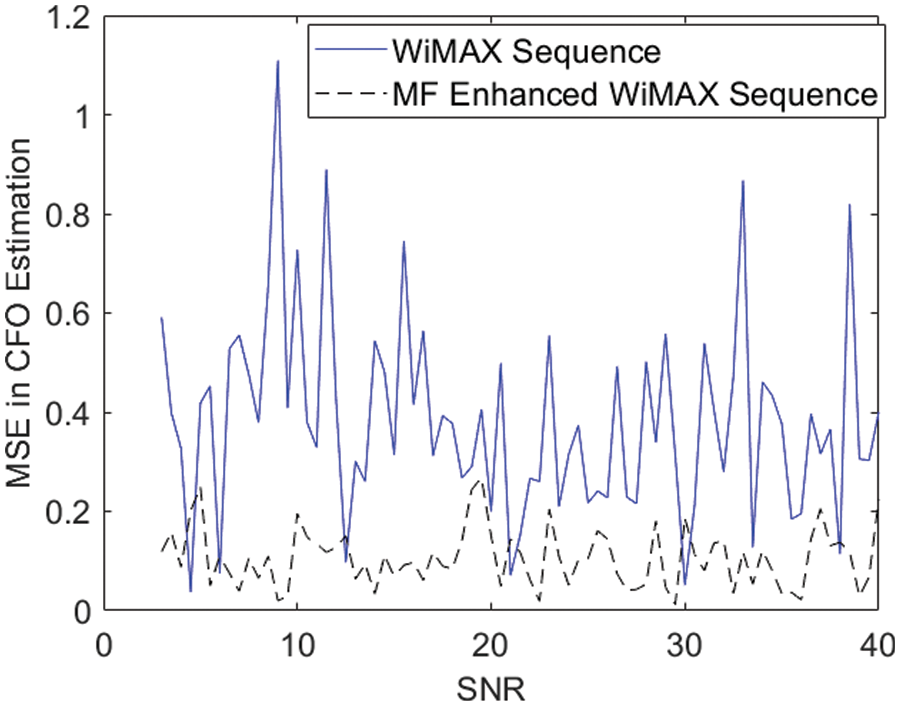
Figure 4: MSE plot of Standard WiMAX sequence and its MF enhanced version

From the Fig. 4, it is clear that offset estimation using new ISL minimized sequence is more reliable and stable.

The signal received after propagating through a Rayleigh fading channel with five taps and Doppler frequency 104 Hz was then simulated for various values of sample delays. Percentage error (e%) occurred in offset estimation is computed for 50 observations using both standard WiMAX and MF enhanced preambles.

The correlation between the received preamble and a reference copy of the same sequence available at the receiver is calculated. The index of the sample with largest correlation magnitude points out the timing offset. The error percentage in offset estimation using WiMAX and modified sequence is depicted in Fig. 5.

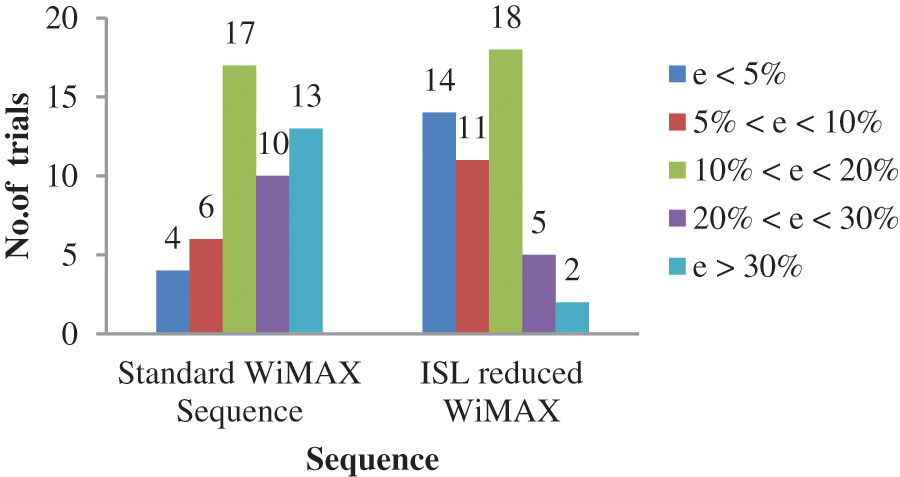
Figure 5: Comparison of standard WiMAX and MF enhanced sequences in a Rayleigh faded channel

Here 50 trials of offset estimation were observed using both standard and MF enhanced WiMAX sequences. It was noticed that when the standard WiMAX sequence was used in the preamble structure the number of observations with error less than 5%, between 5% to 10%, between 10% to 20%, between 20% to 30% and greater than 30% were 4,6,17,10 and 13 respectively. When the MF enhanced sequence was used the number of observations with error less than 5%, between 5% to 10%, between 10% to 20%, between 20% to 30% and greater than 30% were 14, 11, 18, 5 and 2 respectively. The comparison of error status reveals that accuracy in TO estimation can be significantly enhanced by the MF refining algorithm. Thus the goal of improved synchronization accuracy is accomplished by fine tuning the merit factor and hence enhancing the quality of the preamble sequences used for offset estimation.

The limitation of the modified sequence is that the MF is increased only up to 0.6712. The reason for this drawback is the very low MF of the standard WiMAX sequence and it can be corrected by completely replacing the WiMAX sequence by a high MF sequence and improving its properties by the proposed method.

6  Conclusion and Future Scope

The precise estimation of synchronization errors is a big challenge in WiMAX system. A novel method for improving the synchronization accuracy is proposed and a new preamble sequence with ameliorated sidelobe behavior is developed for WiMAX systems. It is verified that the new sequence is spectrally more compatible with reduced off-peaks in ACF and a MF improved by a factor of 54%. The results of the simulations reveal that the competency of the proposed preamble surpasses the existing WiMAX preamble. This work proposes a sound methodology for improving the synchronization accuracy in MIMO OFDM based communication systems. The above mentioned MF enhancing procedure can be applied not only in WiMAX sequence, but also in any other mathematical sequence that is suitable for a preamble structure. So the proposed algorithm for refining the MF can have a direct impact on all the MIMO OFDM wireless standards that uses the data aided synchronization. The synchronization accuracy can be further improved by identifying the mathematical sequences with MF higher than that of standard WiMAX sequence, processing it by proposed algorithm and replacing the WiMAX preamble by the new processed preamble. Applying a learning process to obtain a more accurate expression for the received preamble is another good direction for the future work. The scope for improving the precision of synchronization methods can be further explored by incorporating deep learning based neural networks or extreme learning machines in future.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  L. Kansal, G. S. Gaba, A. Sharma, G. Dhiman, M. Baz et al., “Performance analysis of WOFDM-WiMAX integrating diverse wavelets for 5G applications,” in Wireless Communications and Mobile Computing. Vol. 2021, Hindawi, pp. 1–14, 2021. [Google Scholar]

 2.  S. Weinstein and P. Ebert, “Data transmission by frequencydivision multiplexing using the discrete Fourier transform,” IEEE Transactions on Communication Technology, vol. 19, no. 5, pp. 628–634, 1971. [Google Scholar]

 3.  L. Cimini, “Analysis and simulation of a digital mobile channel using orthogonal frequency division multiplexing,” IEEE Transactions on Communications, vol. 33, no. 7, pp. 665–675, 1985. [Google Scholar]

 4.  G. J. Foschini and M. J. Gans, “On limits of wireless communications in a fading environment when using multiple antennas,” Wireless Personal Communications, vol. 6, no. 3, pp. 311–335, 1998. [Google Scholar]

 5.  A. Goldsmith, S. A. Jafar, N. Jindal and S. Vishwanath, “Capacity limits of MIMO channels,” IEEE Journal on Selected Areas in Communications, vol. 21, no. 5, pp. 684–702, 2003. [Google Scholar]

 6.  A. J. Paulraj, D. A. Gore, R. U. Nabar and H. Bolcskei, “An overview of MIMO communications-a key to gigabit wireless,” Proceedings of the IEEE, vol. 92, no. 2, pp. 198–218, 2004. [Google Scholar]

 7.  T. Pollet, M. V. Bladel and M. Moeneclaey, “BER sensitivity of OFDM systems to carrier frequency offset and Wiener phase noise,” IEEE Transactions on Communications, vol. 43, no. 2, pp. 191–193, 1995. [Google Scholar]

 8.  M. Speth, S. A. Fechtel, G. Fock and H. Meyr, “Optimum receiver design for wireless broad-band systems using OFDM,” IEEE Transactions on Communications, vol. 47, no. 11, pp. 1668–1677, 1999. [Google Scholar]

 9.  S. H. Ahn, D. H. Chong, T. H. Han, S. H. Kim and S. H. Yoon, “A novel OFDM integer frequency offset estimation scheme using differential combining,” The Journal of Korean Institute of Communications and Information Sciences, vol. 33, no. 8C, pp. 627–632, 2008. [Google Scholar]

10. P. H. Moose, “A technique for orthogonal frequency division multiplexing frequency offset correction,” IEEE Transactions on Communications, vol. 42, no. 10, pp. 2908–2914, 1994. [Google Scholar]

11. T. M. Schmidl and D. C. Cox, “Robust frequency and timing synchronization for OFDM,” IEEE Transactions on Communication, vol. 45, no. 12, pp. 1613–1621, 1997. [Google Scholar]

12. A. B. Awoseyila, C. Kasparis and B. G. Evans, “Robust time domain timing and frequency synchronization for OFDM systems,” IEEE Transactions on Consumer Electronics, vol. 55, no. 2, pp. 391–399, 2009. [Google Scholar]

13. H. T. Hsieh and W. R. Wu, “Maximum likelihood timing and carrier frequency offset estimation for OFDM systems with periodic preambles,” IEEE Transactions on Vehicular Technology, vol. 58, no. 8, pp. 4224–4237, 2009. [Google Scholar]

14. M. Morelli, M. Moretti and G. Imbarlina, “A practical scheme for frequency offset estimation in MIMO-OFDM systems,” “EURASIP Journal on Wireless Communications and Networking, vol. 2009, no. 1, pp. 1–9, 2009. [Google Scholar]

15. N. H. Cheng, K. C. Huang, Y. F. Chen and S. M. Tseng, “Maximum likelihood-based adaptive iteration algorithm design for joint CFO and channel estimation in MIMO-OFDM systems,” EURASIP Journal on Advances in Signal Processing, vol. 2021, no. 1, pp. 1–21, 2021. [Google Scholar]

16. E. Rogozhnikov and G. Babur, “Method for enhancing the accuracy of frequency offset estimation in OFDM modulation based communication systems,” Radio Electronics and Communications Systems, vol. 61, no. 8, pp. 342–349, 2018. [Google Scholar]

17. Y. S. Cho, J. Kim, W. Y. Yang and C. G. Kang, Synchronization for OFDM. In: MIMO-OFDM Wireless Communications with MATLAB. John Wiley & Sons (Asia) Pte Ltd., pp. 156–159, 2010. [Google Scholar]

18. Q. Ma, P. Yang, Y. Xiao, H. Bai and S. Li, “Error probability analysis of OFDM-IM with carrier frequency offset,” IEEE Communications Letters, vol. 20, no. 12, pp. 2434–2437, 2016. [Google Scholar]

19. Y. Mostofi and D. C. Cox, “Mathematical analysis of the impact of timing synchronization errors on the performance of an OFDM system,” IEEE Transactions on Communications, vol. 54, no. 2, pp. 226–230, 2006. [Google Scholar]

20. T. Wang, J. G. Proakis, E. Masry and J. R. Zeidler, “Performance degradation of OFDM systems due to Doppler spreading,” IEEE Transactions on Wireless Communications, vol. 5, no. 6, pp. 1422–1432, 2006. [Google Scholar]

21. K. Zheng, L. Huang, M. Chen and W. Wang, “Time and frequency synchronization for uplink OFDM-CDMA,” in Proc. of Int. Conf. on Communications, Circuits and Systems, Chengdu, China, pp. 349–353, 2004. [Google Scholar]

22. Z. Li, P. Li, X. Hao and X. Yan, “Optimal unimodular sequences design method for active sensing systems,” Mathematical Problems in Engineering, vol. 2018, no. 3, pp. 1–14, 2018. [Google Scholar]

23. M. Soltanalian and P. Stoica, “Computational design of sequences with good correlation properties,” IEEE Transactions on Signal Processing, vol. 60, no. 5, pp. 2180–2193, 2012. [Google Scholar]

24. P. Stoica, H. He and J. Li, “New algorithms for designing unimodular sequences with good correlation properties,” IEEE Transactions on Signal Processing, vol. 57, no. 4, pp. 1415–1425, 2009. [Google Scholar]