 Open Access
Open Access
ARTICLE
Efficient Expressive Attribute-Based Encryption with Keyword Search over Prime-Order Groups
1 School of Computer and Electronic Information, Nanjing Normal University, Nanjing, 210046, China
2 Graduate School of Science and Technology, University of Tsukuba Tsukuba, Ibaraki, 305-8577, Japan
* Corresponding Author: Yang Lu. Email:
Intelligent Automation & Soft Computing 2023, 35(3), 2737-2754. https://doi.org/10.32604/iasc.2023.028693
Received 15 February 2022; Accepted 05 May 2022; Issue published 17 August 2022
Abstract
Attribute-based encryption with keyword search (ABEKS) is a novel cryptographic paradigm that can be used to implement fine-grained access control and retrieve ciphertexts without disclosing the sensitive information. It is a perfect combination of attribute-based encryption (ABE) and public key encryption with keyword search (PEKS). Nevertheless, most of the existing ABEKS schemes have limited search capabilities and only support single or simple conjunctive keyword search. Due to the weak search capability and inaccurate search results, it is difficult to apply these schemes to practical applications. In this paper, an efficient expressive ABEKS (EABEKS) scheme supporting unbounded keyword universe over prime-order groups is designed, which supplies the expressive keyword search function supporting the logical connectives of “AND” and “OR”. The proposed scheme not only leads to low computation and communication costs, but also supports unbounded keyword universe. In the standard model, the scheme is proven to be secure under the chosen keyword attack and the chosen plaintext attack. The comparison analysis and experimental results show that it has better performance than the existing EABEKS schemes in the storage, computation and communication costs.Keywords
In recent years, the infrastructure of Internet has been upgraded greatly. Consequently, the cost of data transmission has been reduced. These favorable conditions make cloud storage appear. Compared with data sharing by other ways (e.g., email), cloud data sharing avoids the single point transmission of data and provides great convenience. Today, cloud storage has become an indispensable part of people’s life and work.
Although cloud storage has many advantages, it brings new challenges to data security. Data storage service is usually provided by some entities who are often thought to be honest-but-curious or even untrusted. Therefore, it is not advisable to upload data plaintexts directly to cloud because the outer adversary and the server in the cloud are able to easily achieve all information. How to protect data privacy has become the focus issue in cloud storage environment. Encryption is a necessary step to protect data privacy. But new problems arise after data encryption:
1. How to retrieve the data. Encryption ensures the security of data, but it is difficult for the data receiver to search specific files from cloud. It is not advisable to distinguish files by plaintext labels, because the plaintext labels describe the content of files and inevitably reveal private information.
2. How to access control. The receiver needs to access data files according to his/her authority, but simple encryption cannot achieve this requirement.
PEKS (public key encryption with keyword search), which was originally introduced by Boneh et al. in [1], can effectively handle the above first issue. To make the ciphertexts searchable, the data owner needs to attach a keyword ciphertext to a data ciphertext to create a searchable ciphertext. The data user needs to generate a searchable token of the search keyword for the storage server using his/her own private key, so that the server can execute a search algorithm to find all matching data ciphertexts. During ciphertext retrieval, no privacy information (either the data content or the search keyword) would be revealed to the server.
The PEKS scheme only allows single keyword search and may result in rough results that do not meet the users’ requirements because a data file is often related to several keywords. Therefore, the multi-keyword search function is extremely essential. In [2], Park et al. proposed the first PEKS scheme that can execute multi-keyword search, namely public key encryption with conjunctive keyword search (PECKS). But PECKS just implements simple conjunctive connection of multiple keywords. When a user wants to find the files attached with the keywords “important” or “urgent”, he/she has to search twice. To address this issue, some scholars [3,4] put forward more flexible multi-keyword search encryption method that supports expressive search predicates formed by the logical expression of “AND” and “OR”, namely expressive PEKS (EPEKS). As shown in Fig. 1 [5], an EPEKS system contains three parties: sender, receiver and storage server. The sender sends the server the ciphertexts attached with searchable encrypted labels, which are associated with a keyword set. The receiver generates the trapdoor based on the logical expression of keywords (shown as a logical tree in Fig. 1) and sends it to the storage server. Once receiving the trapdoor, the storage server executes a test algorithm to find the ciphertexts that match the trapdoor, and sends the receiver all matching ciphertexts finally.
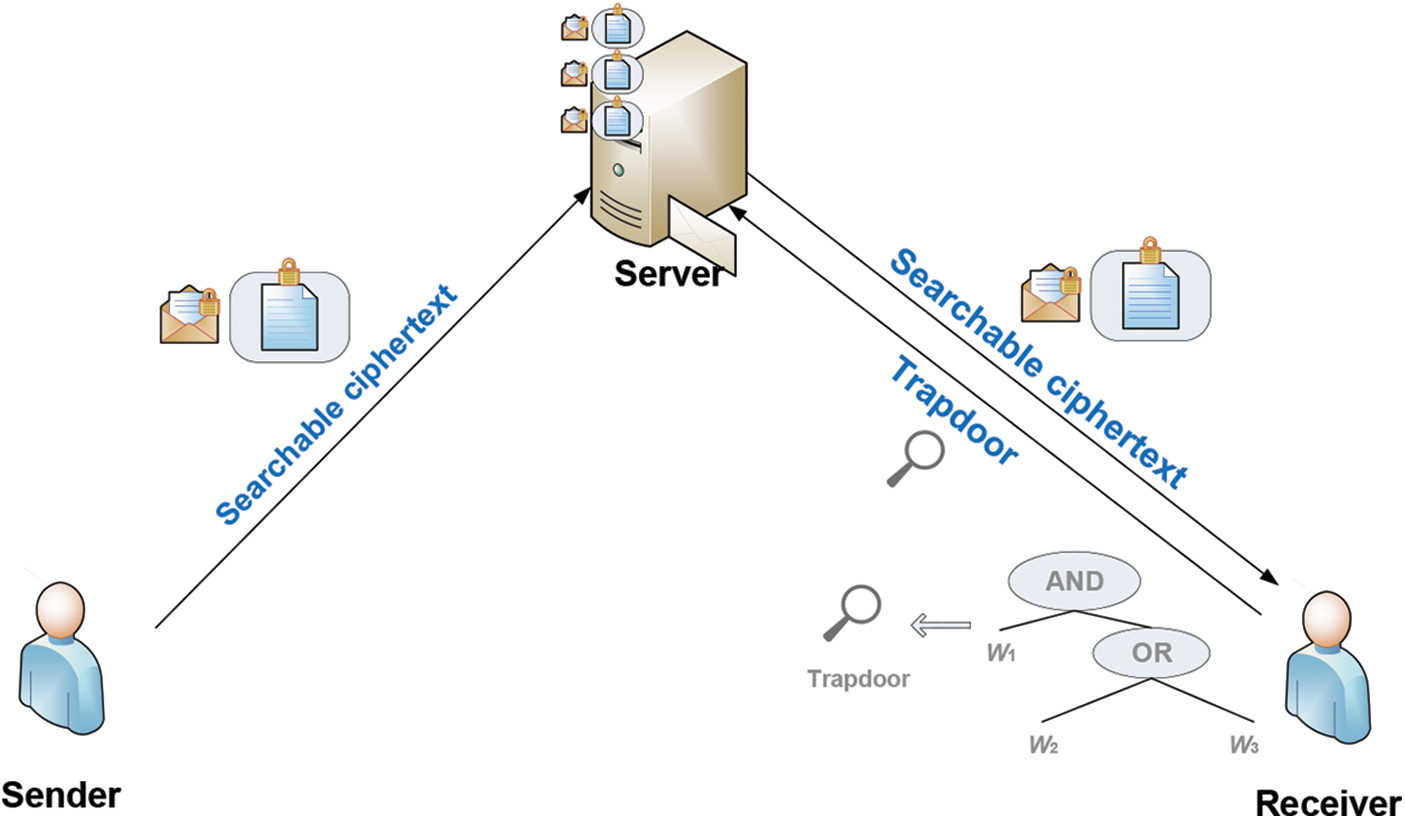
Figure 1: System framework of EPEKS
Attribute-based encryption (ABE) is a novel paradigm of public key cryptography. In ABE, only if the attribute set satisfies the given access structure, a user can recover the plaintext from a ciphertext correctly. Therefore, ABE has strong access control ability [6], which can be used to solve the second issue mentioned above. So far, many different ABE schemes have been proposed. Among them, the scheme which inserts the access structures into the users’ private keys is key-policy ABE (KP-ABE), while the scheme that inserts the access structures into the ciphertexts is ciphertext-policy ABE (CP-ABE). Attribute-based encryption with keyword search (ABEKS) was originally presented by Lai et al. in [3], which combines the functions of both PEKS and ABE. It simultaneously realizes the ciphertext retrieval and the fine-grained access control. Because ABEKS well meets the practical application requirements, it has become a hotspot of current research. In [7], Han et al. introduced the idea of expressive keyword search into ABEKS and put forward the first expressive ABEKS (EABEKS) scheme. Fig. 2 shows the system framework of a key-policy EABEKS scheme. In key-policy EABEKS, a trusted center (TC) is responsible for distributing a private key to every user according to the attribute-based access structure. The sender generates the searchable ciphertexts according to an attribute set and a keyword set, then sends the cloud server the ciphertexts. To retrieve ciphertexts on the server, the receiver needs requesting the trapdoor of the keyword-based search predicate from the TC and then sends the cloud server the trapdoor. After the server finishes searching operation, the ciphertexts matching the trapdoor are returned to the receiver. In a ciphertext-policy EABEKS system, the ciphertexts are associated with the attribute-based access structures, while the users’ private keys are produced according to their attributes.
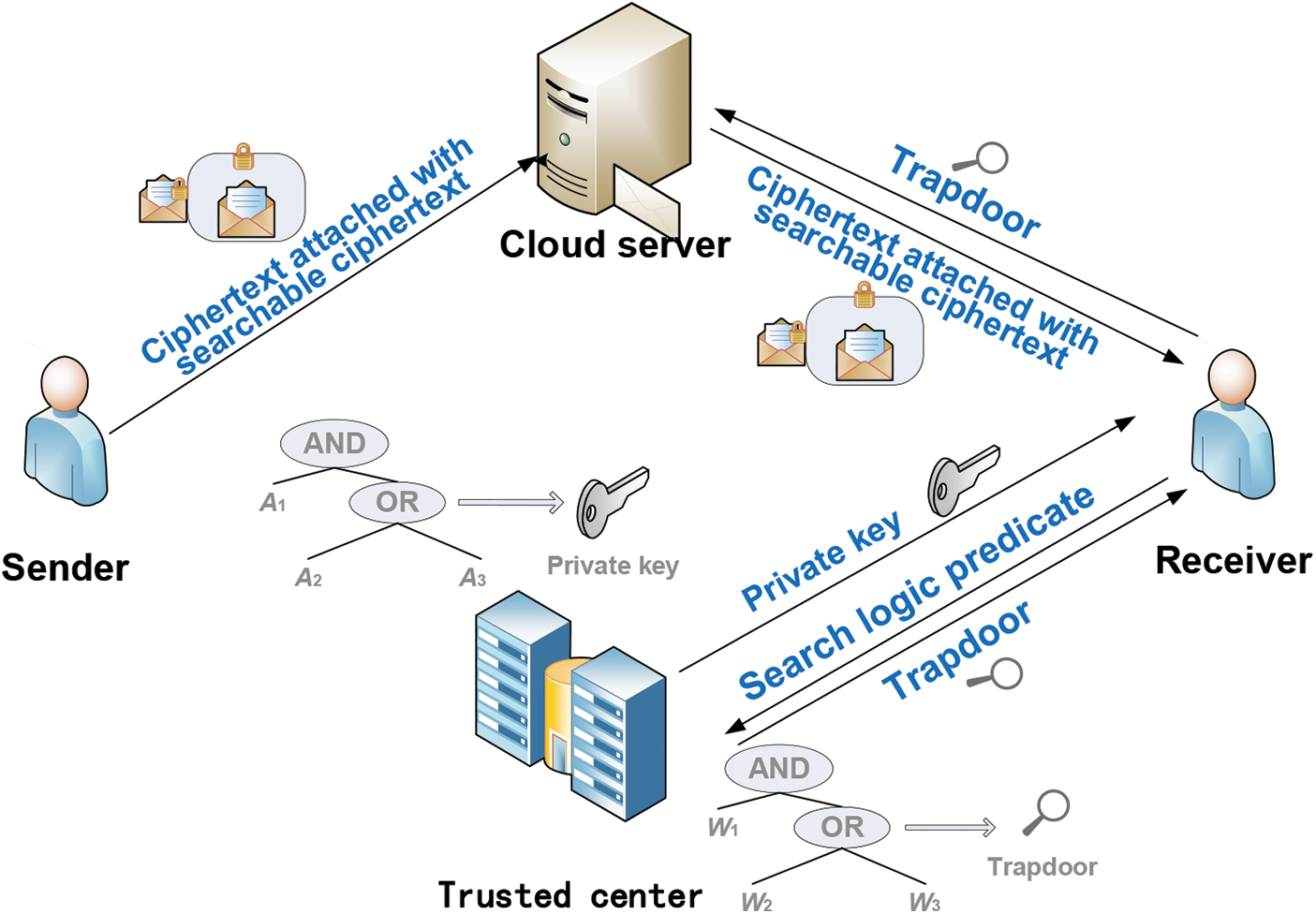
Figure 2: System framework of key-policy EABEKS
Song et al. [8] first proposed the definition of searchable encryption under the symmetric cryptosystem. The searchable encryption scheme under the public key system was presented by Boneh et al. [1], which also gave a general transformation from identity-based encryption (IBE) to PEKS. Since then, many improved schemes [9–22] involving security, performance, function were presented. After Park et al. [2] put forward a PECKS scheme which supports joint keyword search, many works [23–27] have been committed to reducing the computation cost and the trapdoor length. Lai et al. [3] firstly camp up with an EPEKS scheme that was constructed from the fully secure KP-ABE scheme presented in [28]. Later, Lv et al. [4] presented an EPEKS scheme supporting boolean logic combination of “AND”, “OR” and “NOT”. However, the above two schemes are based on the composite-order groups, which leads to low efficiency because the composite-order groups have longer elements and higher computation costs than the prime-order groups. In [29], Cui et al. inserted the linear secret sharing scheme (LSSS) structure into PEKS and constructed an EPEKS scheme over the prime-order groups. However, its efficiency is far from practical use. Therefore, the design of efficient and practical EPEKS schemes over the prime-order groups is still a problem worth studying.
The history of ABE was originated from 1984. In that year, the definition of identity-based signature (IBS) was put forward by Shamir [30]. Until 2001, the practical IBE scheme was presented by Boneh et al. [31] for the first time. Later, Sahai et al. [32] put forward a fuzzy IBE (FIBE) scheme that was considered as the rudiment of ABE. The KP-ABE scheme was first presented by Goval et al. [33]. The KP-ABE solution for the large universe was proposed by Lewko et al. [34], and the construction based on the prime-order group was implemented by Lewko [35]. The subsequent improved KP-ABE schemes can be reviewed in [36–39]. Bethencourt et al. [40] proposed the CP-ABE scheme for the first time. Subsequently, several improved schemes [41–43] were presented.
In [3], Lai et al. put forward a key-policy ABEKS scheme by combining KP-ABE with PEKS. At the same year, Wang et al. [44] also put forward an ABEKS scheme based on ciphertext-policy. After that, ABEKS quickly became a research hotspot and many schemes were designed, e.g., [44–49]. However, most of the existing ABEKS schemes have limited search capabilities and only support single or simple conjunctive keyword search. In [7], Han et al. showed a general transformation from KP-ABE to ciphertext-policy ABEKS and gave the first EABEKS scheme. Han et al.’s EABEKS scheme is based on the composite-order groups and thus suffers from poor efficiency. In [50], Meng et al. put forward a key-policy EABEKS scheme over the prime-order groups. However, the performance of Meng et al.’s scheme will deteriorate rapidly with the growth in the number of system keywords. Therefore, it cannot be applied to the applications with unbounded keyword universe.
Tab. 1 summarizes the characteristics of different frameworks of searchable public key encryption schemes mentioned above.

We present a novel EABEKS scheme over the prime-order groups that supports unbounded keyword universe. The proposed scheme can efficiently convert any monotonic boolean search predicate (expressed by the logical connectives “AND” and “OR”) into a LSSS matrix and hence supply the expressive keyword search function. Interestingly, its performance is independent on the sizes of both the system keyword universe and attribute universe. Therefore, the scheme is very suitable for the applications with large keyword or attribute universe. We believe that our EABEKS scheme is the first one that supports both unbounded keyword and attribute universes. The security proofs without the random model demonstrate that it is secure against chosen keyword attack and chosen plaintext attack. Compared with the existing EABEKS schemes, it has the merits of low storage, computation and communication costs.
2.1 Bilinear Map and Complexity Assumptions
Let G and GT be two groups of prime order p. The bilinear pairing is a bilinear map e: G × G → GT that possess the following properties:
1) Bilinearity: m, n ∈ G and x, y ∈
2) Non-degeneracy: m, n ∈ G, e(m, n) ≠ 1.
For the sake of simplicity, we call (p, G, GT, g, e) the bilinear groups, where g is the generator of the group G. The security of the proposed EABEKS scheme is based on the decisional (q-1) assumption and the decisional (q-2) assumption [5].
Definition 1. Let q be an integer and (p, G, GT, g, e) be the bilinear groups. The decisional (q-1) assumption is: given following elements
The decisional (q-1) assumption declares that for any PT adversary A, its advantage AdvA in working out the decisional (q-1) problem is negligible. The advantage AdvA in solving the decisional (q-1) problem is defined as
where S stands for the set of above-mentioned parameters.
Definition 2. Let q be an integer and (p, G, GT, g, e) be the bilinear groups. The decisional (q-2) assumption is: given following elements
The decisional (q-2) assumption declares that for any PT adversary A, its advantage AdvA in working out the decisional (q-2) problem is negligible. The advantage AdvA in solving the decisional (q-2) problem is defined as
where S stands for the set of above-mentioned parameters.
2.2 Access Structure and Linear Secret Sharing Scheme
Let the system attribute/keyword universe be U. The access structure
Definition 3. Let p be a prime and U be an universe of parties. A secret-sharing scheme Π is linear over
1) Every share of the parties forms a vector based on
2) MA is a l⊆n matrix which can generate each different shares. There exists mapping
A LSSS can be linearly reconstructed. Assuming that Π is a LSSS for the access policy
2.3 Framework of EABEKS and Security Definitions
The framework of an EABEKS scheme includes the following six algorithms:
1) Setup(f). A trusted central authority (TCA) runs the algorithm. It inputs a security parameter f, and produces the public parameters PP and a master secret key MSK. MSK is kept secret while PP is made public.
2) KeyGen(PP, MSK, AST). TCA runs the algorithm. It inputs PP, MSK and an attribute set AST, and returns a private key SKAST corresponding to AST.
3) Encrypt(PP, M,
4) Trapdoor(PP, MSK, P). TCA runs the algorithm. It inputs PP, MSK and a keyword search predicate P, and produces a search trapdoor TP of the predicate P.
5) Test(PP, TP, CT). This algorithm is executed by the server and takes PP, TP and CT as inputs. It outputs 1 if CT matches TP or 0 else.
6) Decrypt(PP, SKAST, CT). The receiver runs the algorithm which takes PP, SKAST and CT as inputs. If the attribute set AST encoded in SKAST meets the access structure
An EABEKS scheme should ensure that the keyword ciphertext and the message ciphertext are both indistinguishable. The security of an EABEKS scheme can be defined by the following two adversarial games which are executed between an adversary A and a challenger Ch .
The keyword ciphertext indistinguishability of the EABEKS scheme is defined by the following adversary game:
1) Init. A submits two different equal-size keyword sets WS0 and WS1.
2) Setup. Ch runs Setup algorithm to obtain PP and MSK. MSK is kept secret and PP is given to A.
3) Phase 1. A adaptively queries trapdoor TP of any search predicate P, but with the restriction that WS0 and WS1 do not satisfy P. Ch executes the algorithm Trapdoor(PP, MSK, P) and returns A the result.
4) Challenge. A submits an access structure
5) Phase 2. Consistent with Phase 1.
6) Guess. The adversary A outputs
Definition 4. An EABEKS scheme is indistinguishable against chosen keyword attack (IND-CKA) if any PT adversary’s advantage in the above game is negligible.
The message ciphertext indistinguishability of an EABEKS scheme is defined by the next game:
1) Init. A submits an access structure
2) Setup. Ch runs Setup algorithm to obtain PP and MSK. MSK is kept secret and PP is given to A.
3) Phase 1. A adaptively queries the SKAST of any attribute set AST, but with the restriction that AST does not satisfy
4) Challenge. A submits a keyword set WS and two message M0, M1 of same length. Ch selects a bit b ∈ {0, 1} randomly. Then, it executes the algorithm Encrypt(PP, Mb,
5) Phase 2. Consistent with Phase 1.
6) Guess. The adversary A outputs
Definition 5. An EABEKS scheme is indistinguishable against chosen plaintext attack (IND-CPA) if any PT adversary’s advantage in the above game is negligible.
The proposed EABEKS scheme is described as below:
1) Setup(f). The algorithm creates the bilinear groups (p, G, GT, g, e); picks four elements u, h, w, v ∈ G and two numbers α, β ∈
2) KeyGen(PP, MSK, AST). The algorithm chooses κ+1 numbers
3) Encrypt(PP, M,
4) Trapdoor(PP, MSK, P). The algorithm creates an access structure
5) Test(PP, TP, CT). Define I as the minimum subset satisfying
where
Obviously, if the keyword set WS is authorized, then
Thus, the test algorithm is correct.
6) Decrypt(PP, SKAST, CT). This algorithm computes
in which
If AST is an authorized set, then
Thence, the above Decrypt algorithm can correctly decrypt the ciphertext.
Next, we prove the security of the proposed scheme.
Theorem 1. If the (q-2) decisional assumption holds, then the proposed EABEKS scheme achieves the IND-CKA security in the standard model.
Proof. Assume that there exists a PT adversary A that has an advantage ε in breaking the IND-CKA security of our EABEKS scheme, then an algorithm B can be created to settle the decisional (q-2) problem with same advantage ε.
Suppose an instance of the decisional (q-1) problem is given to the algorithm B as follows.
1) Init. Algorithm B gets two keyword sets WS0 and WS1 given by A. Assume that both WS0 and WS1 contain k (k ≤ q) diverse keywords.
2) Setup. Algorithm B first selects β ∈ {0, 1} at random. Next, it randomly selects four integers
3) Phase 1. For every trapdoor query from adversary A, B first generates an access structure
For every row of MA, when ρ(τ) ∈ WSβ, MAτ
Under other circumstances, if ρ(τ) ∉ WSβ , B arbitrarily picks l elements
4) Challenge. A sends B a message M and an access structure. B runs the algorithm Encrypt to create CTM . Then B lets s = z and rτ = bτ for every τ ∈ [k], computes
5) Phase 2. Consistent with Phase 1.
6) Guess. Finally, the adversary A produces its guess
It is clear that if T = e(g, g)xyz, then the challenge ciphertext is legal and valid to A. Therefore, Pr[
This proves Theorem 1.
Theorem 2. If the (q-1) decisional assumption holds, then the proposed EABEKS scheme achieves the IND-CPA security in the standard model.
Proof. Assume that there exists a PT adversary A which has an advantage ε in breaking the IND-CPA security of our EABEKS scheme, then an algorithm B can be created to settle the decisional (q-1) problem with same advantage ε.
Suppose an instance of the decisional (q-1) problem is given to the algorithm B as follows.
1) Init. The algorithm B receives an access structure
2) Setup. B arbitrarily picks five numbers
3) Phase 1. For every query from adversary A, B replies with the corresponding private key. However, above queried attribute sets fail to match the access structure defined by AST. Since AST is not an authorized set, there is a vector
4) Challenge. A sends algorithm B two equal-length messages
B implicitly sets
Then, B sets
5) Phase 2. Consistent with Phase 1.
6) Guess. Finally, A produces its guess
It is clear that if T is equal to
This proves Theorem 2.
Next, we evaluate our scheme by comparing it with the previous EABEKS schemes in [7,50] in terms of property, security, computation cost, storage cost and communication cost. The symbols used in the comparisons are listed in Tab. 2.

Tab. 3 shows the properties and security of three compared EABEKS schemes. The scheme in [7] is built over the inefficient composite-order groups, while the scheme in [50] and ours are over the prime-order groups. The composite-order groups have longer elements and higher computation costs than the prime-order groups. Commonly, a cryptographic operation over the composite-order groups costs several times more than the same operation over the prime-order groups. Therefore, the scheme in [50] suffers from low performance. In addition, although the search expression ability of the schemes in [7,50] is the same as that of our scheme, they do not support unbounded system keyword universe. In our scheme, all performance parameters (including the communication cost and the computation cost) are independent on the number of keywords in the system keyword universe (as shown in Tabs. 4 and 5). For the scheme security, our scheme is strictly proven to achieve both the IND-CPA security and the IND-CKA security. The scheme in [7] only achieves the IND-CPA security, while the scheme in [50] only achieves the IND-CKA security.

Tabs. 4 and 5 show the communication/storage cost and the computation cost of three schemes. Because the scheme in [50] does not offer the message encryption function, the comparisons mainly consider the keyword search part of each scheme. As usually, the communication/storage cost of a parameter is measured by the size of the involved group elements. For example, the public parameter in our scheme includes five elements in the group G and two elements in the group GT. Therefore, the length of the public parameter is (5|G| + 2|GT|) bits. The computation cost of an algorithm is evaluated by the time costs of all involved cryptographic operations. For example, to produce a trapdoor, our scheme needs to calculate 5l exponentiations in G. Thus, the time cost of the trapdoor algorithm in our scheme is about 5lEx.


Since the scheme in [7] is based on the composite-order groups, its performance is far lower than that of the scheme in [50] and ours. Therefore, we only make the following comparisons between the scheme in [50] and ours. For the communication and storage overhead, it is easy to see that our scheme has obvious advantage on the sizes of the public parameter and the trapdoor. The size of a ciphertext in our scheme is longer than that in [50], when the ciphertext encrypts more than two keywords. However, the scheme in [50] is not independent on n (i.e., the number of the keywords in the system keyword universe). The size of the trapdoor in the scheme is related to n. Therefore, it is not suitable for the applications with large system keyword universe or unbounded system keyword universe.
To make a clear computation cost comparison, we simulate our scheme and the scheme in [50] by using the pairing-based cryptography library PBC-0.5.14 on a computer running Windows 7 (64 bit) with Intel Core i7 CPU (2.3 GHz) and 8 GB RAM. We implement the bilinear map based on the Type A bilinear pairing over a 512-bit elliptic curve.
Since the computation cost of the Encrypt algorithm and the Trapdoor algorithm in [50] is related to the total amount of attributes, we selected 100 keywords randomly to establish the keyword universe. Figs. 3–6 show the experimental results. We randomly choose 2~10 keywords to generate a search predicate and produce the trapdoor from the predicate. Actually, the number of keywords in a search query is usually no more than 10 in practice application. As shown in Fig. 3, to generate a trapdoor for 2, 4, 6, 8, 10 keywords in our scheme costs about 0.032 ms, 0.059 ms, 0.085 ms, 0.119 ms, and 0.162 ms, respectively, while that in scheme [50] is about 5.12 ms, 9.44 ms, 14.36 ms, 19.48 ms, and 24.6 ms, respectively. To evaluate the time cost of the encryption algorithm, we select different keyword sets containing 10–50 random keywords to generate the ciphertexts. The time cost of encryption for 10, 20, 30, 40, 50 keywords in our scheme is about 0.019 ms, 0.035 ms, 0.051 ms, 0.065 ms, and 0.079 ms, respectively, while that in the scheme [50] is about 0.0482 ms, 0.0485 ms, 0.049 ms, 0.0494 ms, and 0.0498 ms, respectively. Obviously, our scheme enjoys obvious advantage in the efficiency of the trapdoor algorithm. For the time cost of the encryption algorithm, our scheme becomes less efficient when the ciphertext contains more than 30 keywords. However, in practice, it is very seldom and even impossible to encrypt so many keywords in one ciphertext.
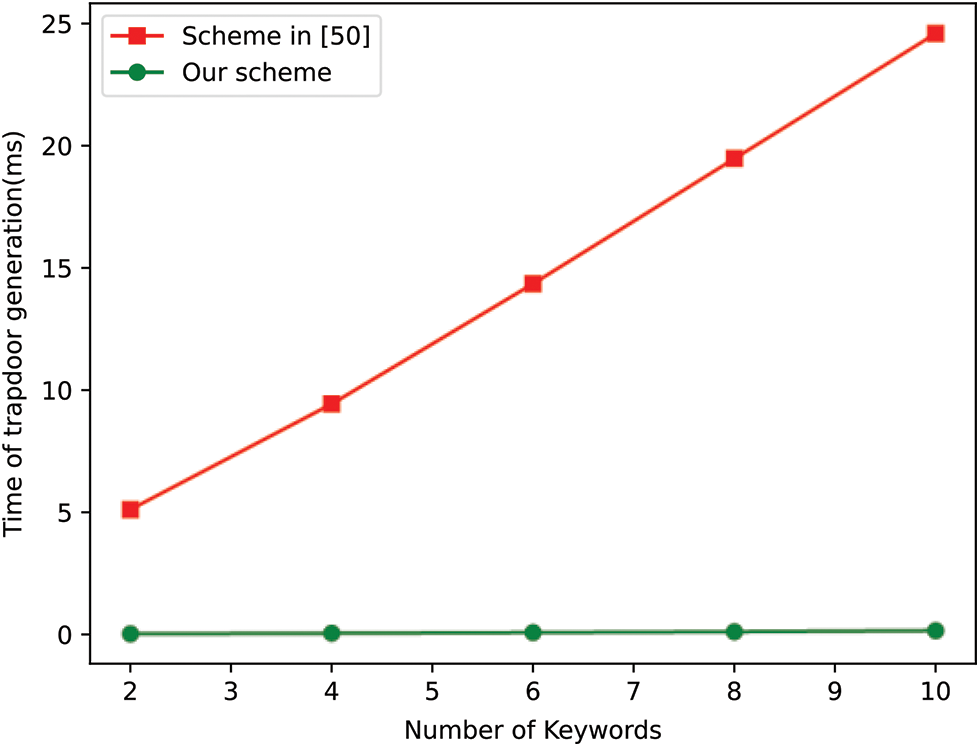
Figure 3: Computation cost of the Trapdoor algorithm
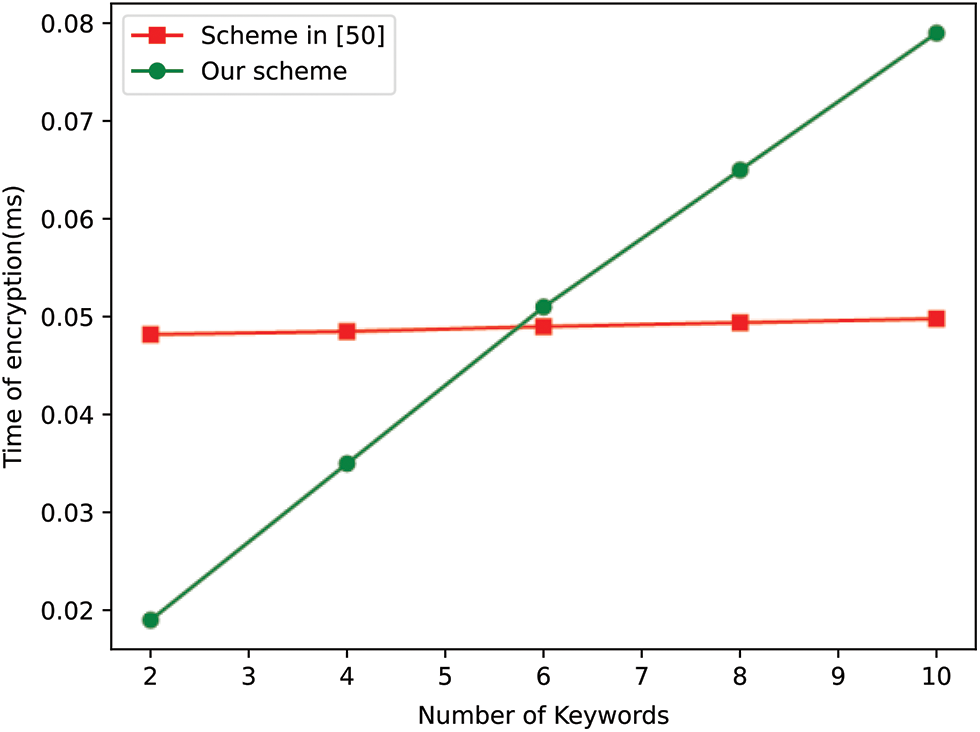
Figure 4: Computation cost of the Encryption algorithm
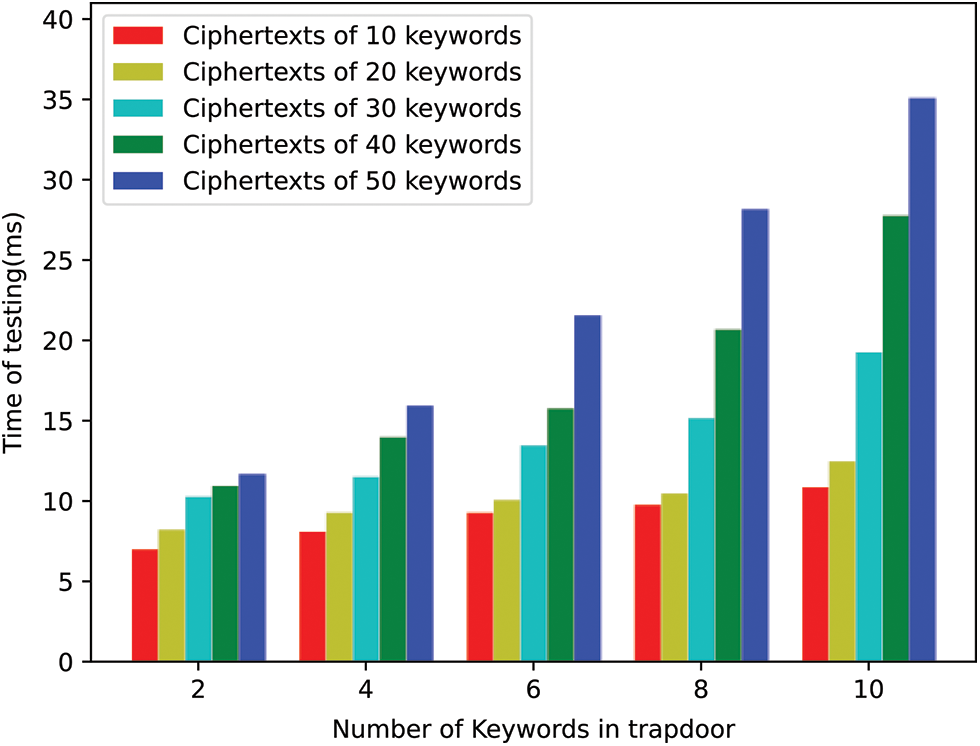
Figure 5: Computation cost of the Test algorithm in our scheme
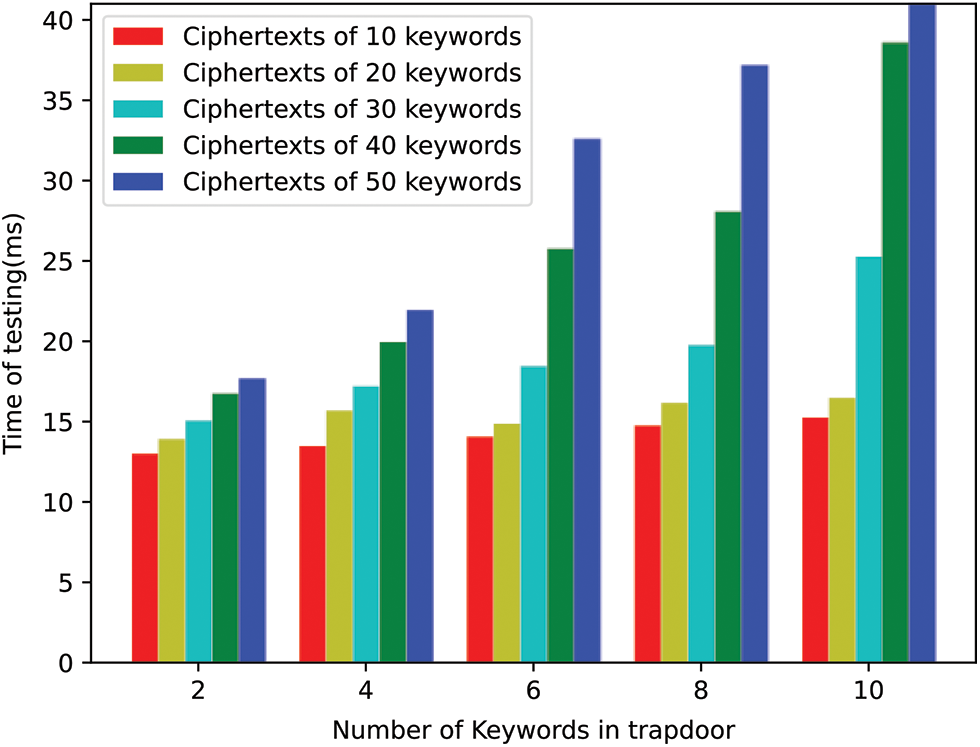
Figure 6: Computation cost of the Test algorithm in the scheme [50]
The time costs of the test algorithm in our scheme and [50] are shown in Figs. 5 and 6, respectively. In our experiment, the number of keywords in the trapdoor is set from 2 to 10, while the number of keywords in the ciphertext is set from 10 to 50. For example, when the ciphertext contains 20 keywords and the number of keywords in the trapdoor is from 2 to 10, the test algorithm of our scheme costs 8.245 ms, 9.311 ms, 10.1 ms, 10.5 ms and12.5 ms, respectively, while that in the scheme [50] is about 13.945 ms 15.711 ms, 14.9 ms, 16.2 ms, 16.5 ms, respectively. From Figs. 5 and 6, we can see that the time cost of the test algorithm in our scheme is lower than that in [50].
Overall, the experimental results show that our scheme has better computation efficiency than the scheme in [50].
In this paper, an efficient EABEKS scheme that supports unbounded attribute universe and keyword universe is proposed. The proposed scheme has the merits of expressive keyword search ability and fine-grained access control ability. The scheme is designed based on the efficient prime-order groups. In addition, its performance is independent on the sizes of system attribute universe and keyword universe. Therefore, it is very suitable for the applications with large system keyword/attribute universe. So far, all EABEKS constructions depend on the costly bilinear pairing. Therefore, to design a lightweight EABEKS scheme that does not use bilinear pairing and can be implemented on the resource-limited devices would be one of our future research works.
Funding Statement: This work was supported in part by the National Natural Science Foundation of China under Grant No. 61772009, the Natural Science Foundation of Jiangsu Province under Grant No. BK20181304.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. D. Boneh, G. Di Crescenzo, R. Ostrovsky and G. Persiano, “Public key encryption with keyword search,” in Proc. Int. Conf. on the Theory and Applications of Cryptographic Techniques, Interlaken, Switzerland, pp. 506–522, 2004. [Google Scholar]
2. D. J. Park, K. Kim and P. J. Lee, “Public key encryption with conjunctive field keyword search,” in Proc. the 5th Int. Conf. on Information Security Applications, Wuhan, China, pp. 73–86, 2005. [Google Scholar]
3. J. Lai, X. Zhou, R. H. Deng, Y. Li and K. Chen, “Expressive search on encrypted data,” in Proc. the 8th ACM SIGSAC Sym. on Information, Computer and Communications Security, Hangzhou, China, pp. 243–252, 2013. [Google Scholar]
4. Z. Lv, C. Hong, M. Zhang and D. Feng, “Expressive and secure searchable encryption in the public key setting,” in Proc. Int. Conf. on Information Security, Hong Kong, China, pp. 364–376, 2014. [Google Scholar]
5. C. Shen, Y. Lu and J. Li, “Expressive public-key encryption with keyword search: Generic construction from KP-ABE and an efficient scheme over prime-order groups,” IEEE Access, vol. 8, pp. 93–103, 2020. [Google Scholar]
6. Y. Rouselakis and B. Waters, “New constructions and proof methods for large universe attribute-based encryption,” in Proc. Proc. of the 2013 ACM SIGSAC Conf. on Computer & Communications Security, Berlin, Germany, pp. 463–474, 2013. [Google Scholar]
7. F. Han, J. Qin and H. Zhao, “A general transformation from KP-ABE to searchable encryption,” Future Generation Computer Systems, vol. 30, no. 3, pp. 107–115, 2014. [Google Scholar]
8. D. Song, D. Wagner and A. Perrig, “Practical techniques for searching on encrypted data,” in Proc. 2000 IEEE Sym. on Security and Privacy, Berkeley, California, USA, pp. 44–55, 2000. [Google Scholar]
9. R. Chen, M. Yi and G. Yang, “Dual-server public-key encryption with keyword search for secure cloud storage,” IEEE Transactions on Information Forensics & Security, vol. 11, no. 4, pp. 789–798, 2016. [Google Scholar]
10. L. Mei, C. Xu, L. Xu, X. Yu and C. Zuo, “Verifiable identity-based encryption with keyword search for IoT from lattice,” Computers, Materials & Continua, vol. 68, no. 2, pp. 2299–2314, 2021. [Google Scholar]
11. Y. Lu, J. Li and Y. Zhang, “Secure channel free certificate-based searchable encryption withstanding outside and inside keyword guessing attacks,” IEEE Transactions on Services Computing, vol. 14, no. 6, pp. 2041–2054, 2021. [Google Scholar]
12. Y. Lu, G. Wang and J. Li, “Keyword guessing attacks on a public key encryption with keyword search scheme without random oracle and its improvement,” Information Sciences, vol. 479, no. 4, pp. 270–276, 2019. [Google Scholar]
13. Y. Lu, J. Li and Y. Zhang, “SCF-PEPCKS: Secure channel free public key encryption with privacy-conserving keyword search,” IEEE Access, vol. 7, no. 1, pp. 40878–40892, 2019. [Google Scholar]
14. P. Xu, Q. Wu and W. Wang, “Generating searchable public-key ciphertexts with hidden structures for fast keyword search,” IEEE Transactions on Information Forensics and Security, vol. 10, no. 9, pp. 1993–2006, 2015. [Google Scholar]
15. K. Emura, L. Phong and Y. Watanabe, “Keyword revocable searchable encryption with trapdoor exposure resistance and re-generateability,” in Proc. 2015 IEEE Trustcom/BigDataSE/ISPA, Helsinki, Finland, pp. 167–174, 2015. [Google Scholar]
16. L. Li, C. Xu, X. Yu, B. Dou and C. Zuo, “Searchable encryption with access control on keywords in multi-user setting,” Journal of Cyber Security, vol. 2, no. 1, pp. 9–23, 2020. [Google Scholar]
17. L. Wu, B. Chen, K. Choo and D. He, “Efficient and secure searchable encryption protocol for cloud-based Internet of Things,” Journal of Parallel and Distributed Computing, vol. 111, no. 2, pp. 152–161, 2018. [Google Scholar]
18. M. Ma, D. He, N. Kumar, K. Choo and J. Chen, “Certificateless searchable public key encryption scheme for industrial internet of things,” IEEE Transactions on Industrial Informatics, vol. 14, no. 2, pp. 759–767, 2018. [Google Scholar]
19. M. Ali, C. Xu and A. Hussain, “Authorized attribute-based encryption multi-keywords search with policy updating,” Journal of New Media, vol. 2, no. 1, pp. 31–43, 2020. [Google Scholar]
20. B. Zhang and F. Zhang, “An efficient public key encryption with conjunctive-subset keywords search,” Journal of Network and Computer Applications, vol. 34, no. 1, pp. 262–267, 2011. [Google Scholar]
21. L. Xu, C. G. Xu, J. K. Liu, C. Zuo and P. Zhang, “Building a dynamic searchable encrypted medical database for multi-client,” Information Sciences, vol. 527, no. 3, pp. 394–405, 2020. [Google Scholar]
22. Q. Tang and L. Q. Chen, “Public key encryption with registered keyword search,” in Proc. the 6th European Conf. on Public Key Infrastructures, Services and Applications, Pisa, Tuscany, Italy, pp. 163–178, 2010. [Google Scholar]
23. P. Golle, J. Staddon and B. R. Waters, “Secure conjunctive keyword search over encrypted data,” in Proc. Int. Conf. on Applied Cryptography and Network Security, Yellow Mountain, China, pp. 31–45, 2004. [Google Scholar]
24. Z. Chen, C. Wu and D. Wang, “Conjunctive keywords searchable encryption with efficient pairing, constant ciphertext and short trapdoor,” in Proc. 2012 Pacific Asia Conf. on Intelligence and Security Informatics, Kuala Lumpur, Malaysia, pp. 176–189, 2012. [Google Scholar]
25. Y. H. Hwang and P. J. Lee, “Public key encryption with conjunctive keyword search and its extension to a multi-user system,” in Proc. Int. Conf. on Pairing-Based Cryptography, Tokyo, Japan, pp. 2–22, 2007. [Google Scholar]
26. L. Ballard, S. Kamara and F. Monrose, “Achieving efficient conjunctive keyword searches over encrypted data,” in Proc. Int. Conf. on Information & Communications Security, Beijing, China, pp. 414–426, 2005. [Google Scholar]
27. N. Cao, C. Wang and L. M., “Privacy-preserving multi-keyword ranked search over encrypted cloud data,” in Proc. 30th IEEE Int. Conf. on Computer Communications, Shanghai, China, pp. 829–837, 2011. [Google Scholar]
28. A. B. Lewko, T. Okamoto, A. Sahai, K. Takashima and B. Waters, “Fully secure functional encryption: attribute-based encryption and (hierarchical) inner product encryption,” in Proc. Annual Int. Conf. on the Theory and Applications of Cryptographic Techniques, Riviera, French, pp. 62–91, 2010. [Google Scholar]
29. H. Cui, Z. Wan, R. Deng, G. Wang and Y. Li, “Efficient and expressive keyword search over encrypted data in the cloud,” IEEE Transactions on Dependable & Secure Computing, vol. 15, no. 3, pp. 409–422, 2018. [Google Scholar]
30. A. Shamir, “Identity-based cryptosystems and signature schemes,” in Proc. CRYPTO 1984, vol. 196, pp. 47–53, 1984. [Google Scholar]
31. D. Boneh and M. Franklin, “Identity-based encryption from the weil pairing,” in Proc. Annual Int. Cryptology Conf., Santa Barbara, CA, USA, pp. 213–229, 2001. [Google Scholar]
32. A. Sahai and B. Waters, “Fuzzy identity based encryption,” in Proc. Annual Int. Conf. on the Theory and Applications of Cryptographic Techniques, Aarhus, Denmark, pp. 457–473, 2005. [Google Scholar]
33. V. Goyal, O. Pandey, A. Sahai and B. Waters, “Attribute-based encryption for fine-grained access control of encrypted data,” in Proc. the 13th ACM Conf. on Computer and Communications Security, Alexandria, VA, USA, pp. 89–98, 2006. [Google Scholar]
34. A. B. Lewko and B. Waters, “Unbounded HIBE and attribute-based encryption,” in Proc. 30th Annual Int. Conf. on Theory and Applications of Cryptographic Techniques: Advances in Cryptology, Tallinn, Estonia, pp. 547–567, 2011. [Google Scholar]
35. A. B. Lewko, “Tools for simulating features of composite order bilinear groups in the prime order setting,” in Proc. Int. Conf. on Theory & Applications of Cryptographic Techniques, Cambridge, UK, pp. 318–335, 2012. [Google Scholar]
36. N. Attrapadung, B. Libert and E. D. Panafieu, “Expressive key-policy attribute-based encryption with constant-size ciphertexts,” in Proc. Int. Workshop on Public Key Cryptography, Taormina, Italy, pp. 90–108, 2011. [Google Scholar]
37. J. Lai, R. H. Deng, Y. Li and J. Wang, “Fully secure key-policy attribute-based encryption with constant-size ciphertexts and fast decryption,” in Proc. the 9th ACM Sym. on Information, Computer and Communications Security, Kyoto, Japan, pp. 389, 2014. [Google Scholar]
38. Y. S. Rao and R. Dutta, “Computationally efficient expressive key-policy attribute based encryption schemes with constant-size ciphertext,” in Proc. Int. Conf. on Information and Communications Security, Beijing, China, pp. 246–362, 2013. [Google Scholar]
39. J. Kim, W. Susilo and F. Guo, “An efficient KP-ABE with short ciphertexts in prime ordergroups under standard assumption,” in Proc. 2017 ACM on Asia Conf. on Computer and Communications Security, Abu Dhabi, United Arab Emirates, pp. 823–834, 2017. [Google Scholar]
40. J. Bethencourt, A. Sahai and B. Waters, “Ciphertext-policy attribute-based encryption,” in Proc. IEEE Sym. on Security and Privacy, Berkeley, CA, USA, pp. 321–334, 2007. [Google Scholar]
41. B. Waters, “Ciphertext-policy attribute-based encryption: An expressive, efficient, and provably secure realization,” in Proc. Int. Workshop on Public Key Cryptography, Berlin, Germany, pp. 53–70, 2011. [Google Scholar]
42. L. Cheung and C. Newport, “Provably secure ciphertext policy ABE,” in Proc. 14th ACM Conf. on Computer and Communications Security, Virginia, USA, pp. 456–465, 2007. [Google Scholar]
43. L. Ibraimi, Q. Tang and P. Hartel, “Efficient and provable secure ciphertext-policy attribute-based encryption schemes,” in Proc. Int. Conf. on Information Security Practice and Experience, Berlin, Germany, pp. 1–12, 2009. [Google Scholar]
44. C. Wang, W. Li and L. Yuan, “A ciphertext-policy attribute-based encryption scheme supporting keyword search function,” in Proc. Int. Sym. on Cyberspace Safety and Security, Zhangjiajie, China, pp. 377–386, 2013. [Google Scholar]
45. T. Feng, H. Pei, R. Ma, Y. Tian and X. Feng, “Blockchain data privacy access control based on searchable attribute encryption,” Computers, Materials & Continua, vol. 66, no. 1, pp. 871–890, 2021. [Google Scholar]
46. H. Cui, R. Deng and J. Liu, “Attribute-based encryption with expressive and authorized keyword search,” in Proc. Australasian Conf. on Information Security and Privacy, Auckland, New Zealand, pp. 106–126, 2017. [Google Scholar]
47. J. Cui, H. Zhou, H. Zhong and Y. Xu, “Akser: Attribute-based keyword search with efficient revocation in cloud computing,” Information Sciences, no. 423, pp. 343–352, 2018. [Google Scholar]
48. Y. Miao, J. Ma, X. Liu, X. Li, Q. Jiang et al., “Attribute-based keyword search over hierarchical data in cloud computing,” IEEE Transactions on Services Computing, vol. 13, no. 6, pp. 985–998, 2020. [Google Scholar]
49. J. Li, M. Wang, Y. Lu, Y. Zhang and H. Wang, “ABKS-SKGA: Attribute-based keyword search secure against keyword guessing attack,” Computer Standard Interfaces, no. 74, pp. 103471, 2021. [Google Scholar]
50. R. Meng, Y. Zhou and J. Ning, “An efficient key-policy attribute-based searchable encryption in prime-order groups,” in Proc. Int. Conf. on Provable Security, Xi'an, China, pp. 39–56, 2017. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools