DOI:10.32604/iasc.2023.030100

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2023.030100 |  |
| Article |
An Efficient Allocation for Lung Transplantation Using Ant Colony Optimization
Biomedical Systems and Informatics Engineering Department, Hijjawi for Engineering Technology, Yarmouk University, Irbid, 21163, Jordan
*Corresponding Author: Lina M. K. Al-Ebbini. Email: Lebbini@yu.edu.jo
Received: 18 March 2022; Accepted: 20 April 2022
Abstract: A relationship between lung transplant success and many features of recipients’/donors has long been studied. However, modeling a robust model of a potential impact on organ transplant success has proved challenging. In this study, a hybrid feature selection model was developed based on ant colony optimization (ACO) and k-nearest neighbor (kNN) classifier to investigate the relationship between the most defining features of recipients/donors and lung transplant success using data from the United Network of Organ Sharing (UNOS). The proposed ACO-kNN approach explores the features space to identify the representative attributes and classify patients’ functional status (i.e., quality of life) after lung transplantation. The efficacy of the proposed model was verified using 3,684 records and 118 input features from the UNOS. The developed approach examined the reliability and validity of the lung allocation process. The results are promising regarding accuracy prediction to be 91.3% and low computational time, along with better decision capabilities, emphasizing the potential for automatic classification of the lung and other organs allocation processes. In addition, the proposed model recommends a new perspective on how medical experts and clinicians respond to uncertain and challenging lung allocation strategies. Having such ACO-kNN model, a medical professional can summarize information through the proposed method and make decisions for the upcoming transplants to allocate the donor organ.
Keywords: Ant colony optimization (ACO); lung transplantation; feature subset selection; quality of life (QoL)
Organ transplantation is the best handling method for patients with untreatable organ diseases. Many pre-transplant factors could increase post-transplant mortality, and organ transplantation can decrease immunity levels and initiate threatening infections leading to early graft failure and mortality [1–3]. However, organ transplantation should increase survivability and improve quality of life.
Transplant success represents a critical aspect of organ transplantation. The standard clinics for organ transplantation include misinterpretation, mortality, and graft failure [4,5]. Therefore, an appropriate method is necessary to aid clinicians in calculating survival and making decisions. For instance, using the most important predictive factors and substitutable transplants may promote accurate prognostic systems. Modeling an accurate prediction system coincides mainly two steps: first, selecting the most essential and representative donor/recipient demographic and characteristic data that guarantee transplant success to a high degree. Secondly, designing an optimal approach to establish a satisfying allocation strategy and validate the transplantation outcome [6]. The essential features to be clinically predicted are graft survival time and the functional status after transplantation (i.e., QoL). Meanwhile, their predictions represent a challenging problem.
It is worth mentioning that it is difficult for the patients to predict whether their durable quality of life is tolerable. Therefore, assessing the functional status after lung transplantation is a meaningful and helpful decision for patients outside the hospital after the transplantation process. Essentially, there is a particular emphasis on improving the expectation procedure of survival and QoL features [7].
In this setting, it has been reported by Rosso et al. that the lung allocation score (LAS) did not impact the long-lasting survival after transplantation [8]. Instead, LAS was characterized by a high prediction of graft impairment only in the first three days after transplantation. However, it has been stated by Bernhardt et al. that the current policies for organs allocation should be changed entirely to a broad discussion before implementation [9].
The development of soft computing techniques motivated researchers to apply different methods to enhance the automation process of organs allocation systems. These methods include Genetic Algorithms [10], Simulated Annealing [11], Harmony Search [12], and Ant Colony Optimization [13] in intelligent decision support systems (DSS). There are many attempts at developing an allocation system for lung transplantation. The authors in [14] conducted a scale named illness intrusiveness rating scale (IIRS) by assembling responses from different studies about QoL in lung, liver, heart, and renal transplants. The authors used exploratory and confirmatory factor analyses to identify the factor structure and then set it against patient groups of the various used transplants. Reference [15] presented data mining methods including neural networks, logistic regression, and decision trees to predict the survival of heart-lung transplants. The accuracy of the models ranged from 71% to 86%, considering 10-fold cross-validation.
Similarly, another study [16] proposed an integrated machine learning method in developing Cox survival models to analyze thoracic transplant procedures effectively. The UNOS dataset was used for survival time estimation to identify the optimum number of risk groups of thoracic recipients. Then, a Kaplan-Meier survival analysis was conducted to validate the identified risk groups. Other researchers [17] devised a structural equation modeling and decision tree construction procedure for lung transplant performance evaluation. The method was validated through the UNOS dataset, resulting in an R2 of 0.68. Two more studies ([18] and [19]) have analyzed QoL after lung transplantation. Reference [18] examined a fuzzy lung allocation system based on a real dataset from the UNOS to determine potential recipients for transplantation. This research has revealed that interpretation results have an R2 value of 83.2% and an overall accuracy of 82.1%.
On the other hand, another study [19] utilized a hybrid genetic algorithm-based feature selection model to predict QoL for patients undergoing a lung transplant. Using three classifiers, kNN, support vector machine (SVM), and artificial neural network (ANN), they found that SVM performance dominates the other two models in terms of accuracy. After optimizing parameters, the proposed models were applied to the UNOS dataset. The burden in that approach resides in that GA can become impractical due to the significant increase in computational time. However, many recent studies in medicine are focusing on lightweight decision-making systems [20,21].
Most lung allocation approaches do not have a noticeable mark between the essential and rest features. Considerably, identifying the unknown quality of life categories wants its intrinsic features to be predicted accurately. Therefore, introducing a robust feature decision-making approach for organs allocation is still a contest [22]. In lung transplantation, locating the faster and the most truthful result is still a confrontation as each technique has its restrictions.
This paper introduces an approach based on the ant colony optimization (ACO) technique to obtain an optimal threshold for classification. Many studies pointed out that GA performance in terms of speed is much slower than ACO [23]. However, it is the first work in lung allocation using ACO, which provides faster computational time compared to the GA [19] as provided in the literature. This investigation aims to develop automatic and fast recognition of the QoL for the lung allocation process. An expert algorithm has been developed to select discriminant features from the UNOS. The dataset has been preprocessed to remove undesirable features. Then, the optimal distinguishable features were explored using the ACO algorithm. As a final point, the kNN was used as a simple classifier for implementation and faster computational time. Other classifiers (e.g., ANN and SVM) were used to compare the accuracy and computational time, but kNN outperforms them. kNN used the resulted features from ACO to classify patients concerning the defined quality of life categories. The following sections give more detailed explanations about classifying QoL.
The scheme for an automatic allocation for lung transplantation has been constructed depending on machine learning. At first, a dataset from the UNOS since 1987 was involved in the proposed algorithm. The records include data related to heart, lung, and thoracic transplants. The patients were assigned unique identification numbers to track their information, considering confidentiality and security issues. The UNOS data is considered a complete source of information for research purposes in organ transplantation in the U.S. [24].
The raw dataset consists of 60,888 observations and 442 features. For assembling the features space, a few preprocessing steps were applied. This study focused only on lung transplantation, so any observation associated with the heart or simultaneous lung/heart transplants was omitted accordingly. However, most of the observations are related to heart and heart/lung transplants, and only 16,771 records are related to lung transplantation. In addition, any observation with an undetermined output value (i.e., missing class label of the output) was also excluded. Moreover, different cleaning stages were applied, such as removing unnecessary features (e.g., dates, addresses, identification numbers, and zip codes) and dropping highly correlated features.
Next, four steps of preprocessing were applied. Firstly, assertion values for features containing missing values. The average value was applied to continuous features, and the mode was applied to categorical features. Secondly, coding based on a medical dictionary was applied [25]. After that, some features were normalized because their large values might significantly hide the effect of other features with comparatively less significant values [26]. At this point, the Minmax law was applied as defined in Eq. (1).
Xn = the resulted normalized value, Xi = the old value for a particular feature, Xmin = the minimum value in that feature, and Xmax = the maximum value.
Finally, random undersampling (RUS) was applied since the dataset was imbalanced. In this setting, all records from the smaller class (i.e., class 2) were used; meanwhile, the bulk class records (i.e., class 1 and class 3) were randomly reduced until we reached the number of class 2 records [27]. However, the same dataset used in the literature is based on RUS. Therefore, RUS was conducted in this study for comparison and evaluation purposes with related works.
After the preparation process, the final data set produced 3,684 records and 118 inputs. The measured feature is the functional status after transplantation (FUNC-STAT-TRF) of the recipient, also known as recipient QoL. This feature is categorized into three classes: class 1 means independent (i.e., no limitation in mobility), class 2 means partially dependent (i.e., needing some assistance for daily activities), and class 3 means disabled (i.e., needing full assistance for daily activities).
The robust and relevant features are essential due to their significant effect on the classification process compared to irrelevant features. Subsequently, classification performance can be promoted by ignoring redundant and irrelevant features. For optimal feature decision-making, three prominent aspects should be considered: search mechanism, evaluation function, and search stopping criteria.
2.2 The Proposed Search Procedure
Several practical algorithms have been improved and applied as machine learning techniques in various fields. At this point, ACO has been used as an aspirant algorithm, representing a unique contribution in optimization problems such as routing optimization [28] and system fault detection [29]. In this paper, the idea of ACO resides in finding the optimal set of features in allocating a lung transplant.
As the fundamental part of any feature selection algorithm, the evaluation function evaluates the involved features, considering the robustness of subsets based on their capabilities for perception purposes. This study applies the wrapper technique [30] in its evaluation function. The wrapper methods denote the hypothesis domain that combines the evaluation function and learning algorithm. Various features are examined through a learning process. After several iterations, the optimal features are defined. Then, finding the accuracy of the obtained classification model is based on the test data set. A heuristic search algorithm should be applied to find optimal features in this setting because of the exponentially increased search space. It is worth mentioning that the heuristic search algorithm is conspicuous due to its tractability in the random examination.
Another principle in the ACO algorithm is the closure time in the search procedure. The algorithm wants to resolve the point where it should terminate searching within the feature space. There are many standard techniques: the first method sets the preferred number of selected features, and when this number is reached, the program closes. The second method is when the algorithm settles with a fixed accuracy, although the features change. The third possible principle is accomplishing a defined number of iterations after defining a determined subset of features. In this study, the third method was applied.
As a result of examining ants seeking and cooperative behavior, Darigo et al. presented the ACO method as a nature-inspired metaheuristic technique [31]. The structure is based on the thought described by ethologists about the environment used by ants since the ants employ pheromone paths to transfer information concerning the direct paths to food. Ants indirectly communicate with other ants through an odorous material called a pheromone to realize the direct food path from the destination to the source. Finding the food source allows the ant to drop an amount of pheromone on the route to make a guide while returning to the destination. Thus, a path is made by laying some pheromone on the ground. The memory structure is dynamic since it includes information regarding the efficacy of preceding selections based on the findings. This memory guides the assembly process of each ant. Therefore, the act of each ant is driven by the act of physical ants.
On the other hand, when another ant moves at random for exploration, it encounters the path assigned by other ants and can highly agree to follow it. Accordingly, that ant enforces the path by accumulating its pheromone. Thus, an autocatalytic practice occurred by which as more ants monitor a path, as more the path pays attention to be surveyed. Hence, choosing a route increases with the increasing number of ants who selected the same path. In selecting outstanding features, some adaptation is mandatory in the algorithm to make it appropriately work for QoL classification by representing optimal features.
Feature selection requires a functional search space in the ACO algorithm, including nodes (i.e., ants) and links (i.e., paths) symbolizing a feature search space. In the proposed approach, the number of used features in allocating a lung transplant is represented by the number of nodes, and the linking between the nodes affirms their reliance. A simulated pheromone is placed on the associated paths, and its amount changes with time.
Each ant selects its first node randomly penetrating the search space. The ant has the policy to determine the following link coupled to its link [32]. Accordingly, each ant forms a subset of features incrementally. Building subsets of features requires each ant to go through the features via a decision strategy to accomplish a solution. The motion is based on a probability expression containing pheromone value and heuristic information of features. Hence, the probability expression, as shown in Eq. (2), denotes the likelihood of selecting node j by ant k while going from node i as a present location at iteration t:
where,
(i) Pheromone initialization is the most critical step in the ACO program. The pheromone information of the search space is stored in the matrix (
(ii) Heuristic information: The efficiency of features is evaluated through heuristic information to achieve better discrimination. The heuristic desirability information, such as a correlation coefficient matrix, can highlight the independence among features. The correlation coefficient is a matrix calculated by the covariance of features divided by the corresponding standard deviations (σ) as shown in Eq. (3):
where Xi, Yi represents the features, and μXi, and μYi are their averages, respectively. The result of this equation is a value between −1 and + 1, which demonstrates the strength of the association between features. Indeed, as the resulting value is closed to 1, dependency increases, the sign implies the direction of the relationship, and the value 0 means no relationship. Eq. (4) explains the heuristic matrix (η):
Accordingly, the probability of dependency among features is represented by the absolute correlation matrix subtracted from 1. However, the absolute of Corr(X, Y) is used since only the amplitudes of features were added to the computation, and the orientation of features does not influence the calculation.
The quality of findings can be assessed using evaluation functions. In this study, the strength of discriminant features is assessed individually to find a specific subset capable of distinguishing the classes of QoL after lung transplantation. At this setting, a kNN classifier was applied to classify QoL concerning the produced subset of features by ACO, and then the misclassification should be computed. Therefore, an evaluation function such as γ(St) is used to reflect the error rate through two measures expanded by the classifier and the size of the present subset of features, as Eq. (5) shows:
where
Whereas the termination criterion has not yet been acquired, the (τ) matrix is updated over several iterations. Indeed, the pheromone value was updated for each feature subset made by each ant. The increase in the pheromone amount forcefully depends on the penalty of each subset. As
where,
where Q is a constant dictating how much all ants should put down pheromones [33]. The pheromone value,
2.3.5 Design of the ACO Algorithm
Implementing the ACO algorithm requires initializing the following parameters: number of iterations, the total number of used ants, the values of α and β parameters, initial pheromone, and evaporation rate. After several iterations, a better convergence has been achieved, obtaining the candidate values of ACO parameters. It has been observed that the evaporation rate significantly influences the fitness value. Tab. 1 shows the best values after several trial and error operations: the number of ants N = 118, the evaporation rate (ρ) and the initial pheromone (τo) are 0.5 and 0.2, respectively, the number of iterations is appropriate at T = 50, and α and β values are 1 and 3, respectively. It is worth mentioning that the ACO algorithm has been recurring for five consecutive times and 50 iterations each time. Thus, the algorithm was carried out for 250 iterations to avoid any bias and ensure the reliability of the features.

Fig. 1 shows the development process of the ACO that is applied to the space of the UNOS feature set to choose a subset of features. After initializing the ACO parameters, essential computations of the probability function and heuristic information are considered. Next, the first iteration executes the defined features subset because the pheromone path is similar for all features. After that, examination of the generated subsets using the evaluation function γ(St). The evaluation function finds the superiority of the chosen subset. In each iteration, the subsets are evaluated, allowing the pheromone value to be updated for the best features subset as a good reaction. This method of reaction is called a wrapper [34]. The interactivity of all features is evaluated using a classifier incorporated with the search algorithm to dictate the local best features in each round. Herein, the local paramount subset is kept for the next iteration. The updating function enhances the best subset by adding and evaporating the pheromone value for the produced subsets on other links. This process recurs through iterations yielding the best global subset. Fig. 2 summarizes the ACO steps of the algorithm. As explained in the following subsection, the classifier trains the dataset according to the global best features.
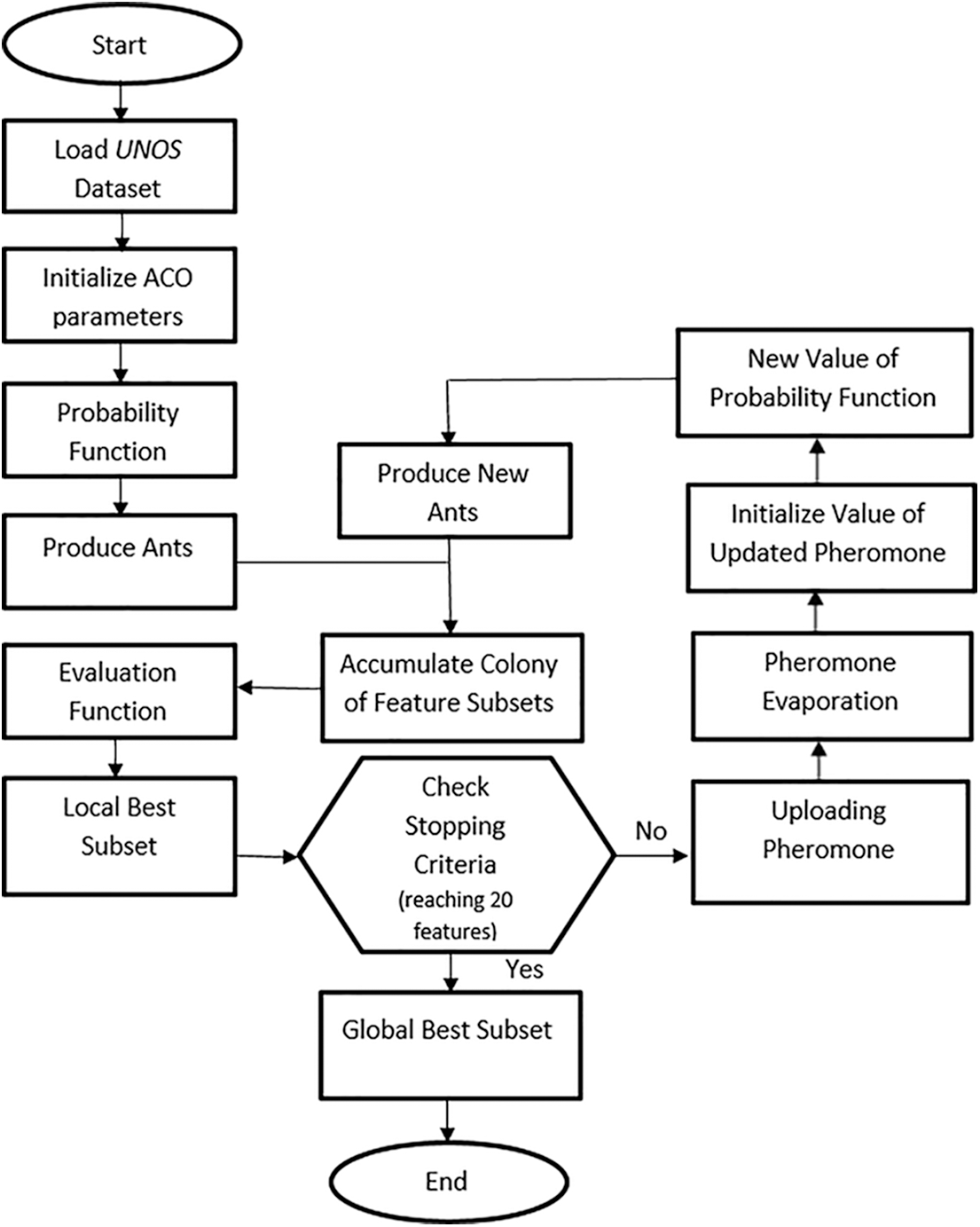
Figure 1: Flowchart of the ACO algorithm for allocation of lung transplantation

Figure 2: ACO steps for feature selection
2.4 Prediction Using kNN Classifier
The instant-based learning classifier (kNN) is a supervised and decision-based prediction learning method that can classify large-scale data into numerous classes. kNN is a simple and efficient data mining technique used for classifying observations based on their distance to other data points in a training dataset. kNN is an instance-based learner (also known as a lazy learner) where the training data is loaded into the model. Then, when a new observation needs to be classified, it looks for the defined k value of nearest neighbors, where the instance that should be classified is based on the majority vote. For example, if k is 5, then the classes of 5 nearest neighbors are determined. Distance functions measure similarity between records, and kNN calculates the distance between new and known data points [35]. The commonly used distance between two observations a = (a1,…, an) and b = (b1,…, bn) is the Euclidian distance as defined in Eq. (8).
The classification procedure for the allocation of lung transplantation is shown in Fig. 3. The number of neighbors (k) was set to 5 after several iterations. Fig. 4 shows the relationship between different odd values of k and the testing accuracy to evaluate the predictions. The kNN model has been trained using the resulting optimal features subset from the ACO using 10-fold cross-validation and repeats the process five times with different random samples to avoid any possible bias in verifying the robustness of the results. However, the kNN model was chosen due to its more straightforward implementation, computational efficiency, and analytical tractability than other potential model types such as ANN or SVM.
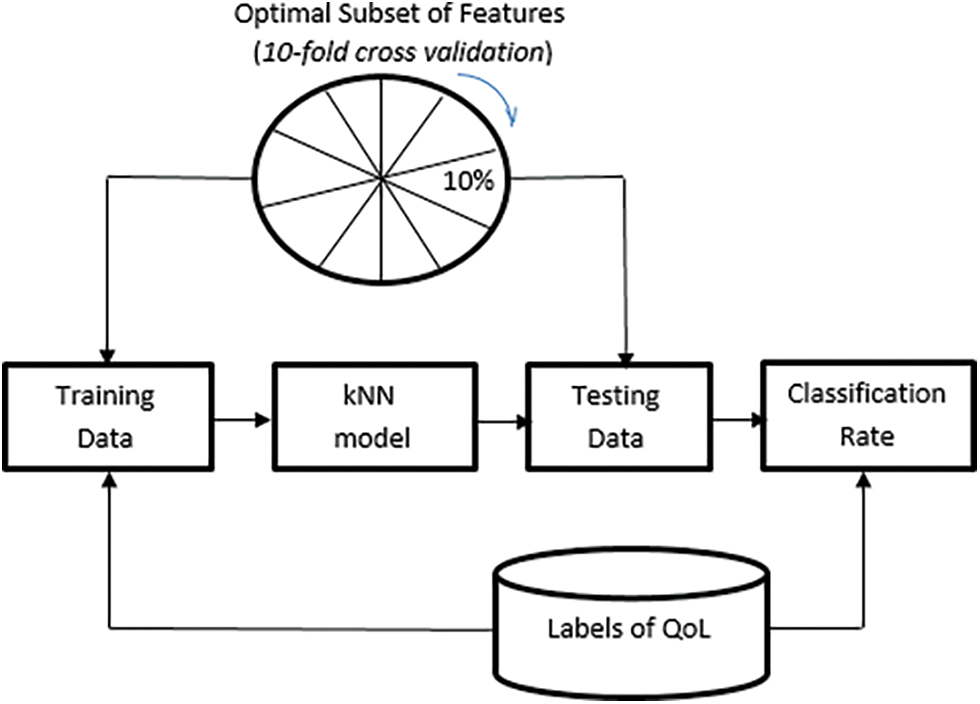
Figure 3: Representation of the QoL classification by kNN
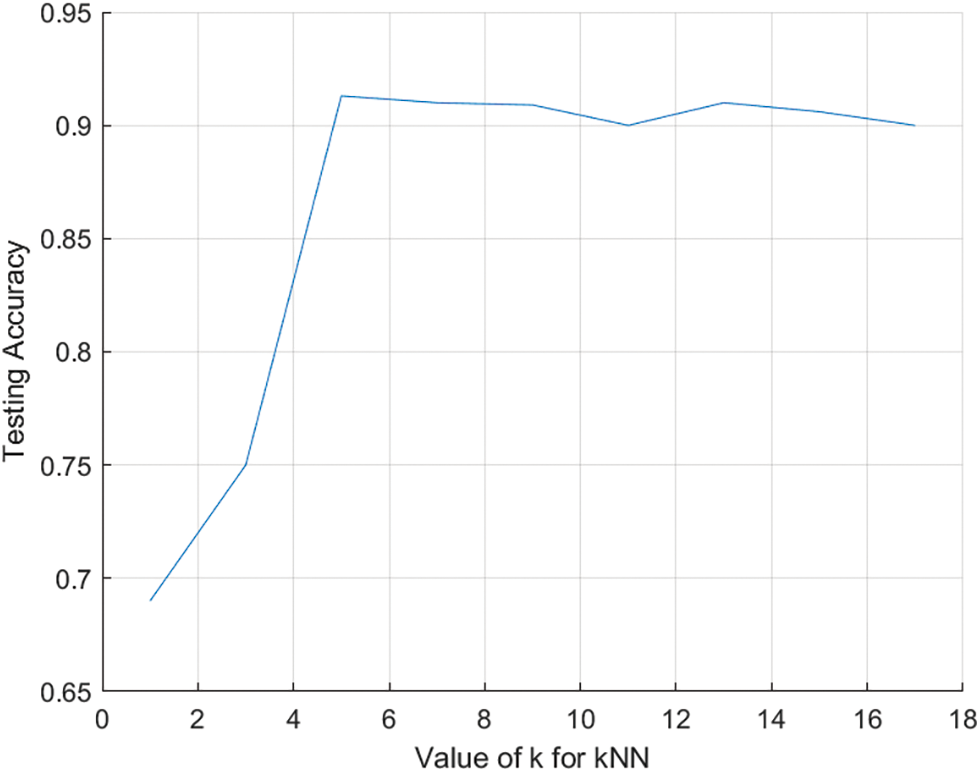
Figure 4: The relationship between k and testing accuracy
This section shows the performance evaluation of lung allocation based on the proposed ACO-kNN model. The UNOS dataset was used as a real-world medium-sized dataset. Extensive iterations have been tried to optimize the parameters of the ACO to get the best features subsets.
3.1 Feature Decision-Making Results
The ACO-kNN model for optimal features classifies all the processed UNOS dataset records. The ACO finds the most candidate features, and the kNN finds how the data is fitted for the trained data concerning the most important features. The stopping criterion in ACO was set to be twenty features after 50 iterations; thus, the most essential twenty features are derived by the proposed ACO algorithm. The accuracy (i.e., classification rate) is measured according to the average of the correctly classified records in the testing data through 10-fold cross-validation and five random repetitions. The accuracy of the features subset is the main factor in determining the quality of chosen features and the efficacy of the proposed model. The evaluation function γ(St) depends on the ongoing process of repetitions and iterations. As represented in Fig. 5, Y-axis denotes the fitness value γ(St) versus the number of iterations represented in the X-axis. The value of γ(St) fluctuates at the beginning of each repetition since the number of chosen features and the error rate change during the iterations. In addition, the value of γ(St) sharply decreases to converge to a steady level. Likewise, the convergence of all repetitions is approximately at the same level emphasizing the correctness of the globally gained subset and the ability of the algorithm to discover the optimal solution. Thus, the developed approach found the candidate features and disregarded the out-of-work features.
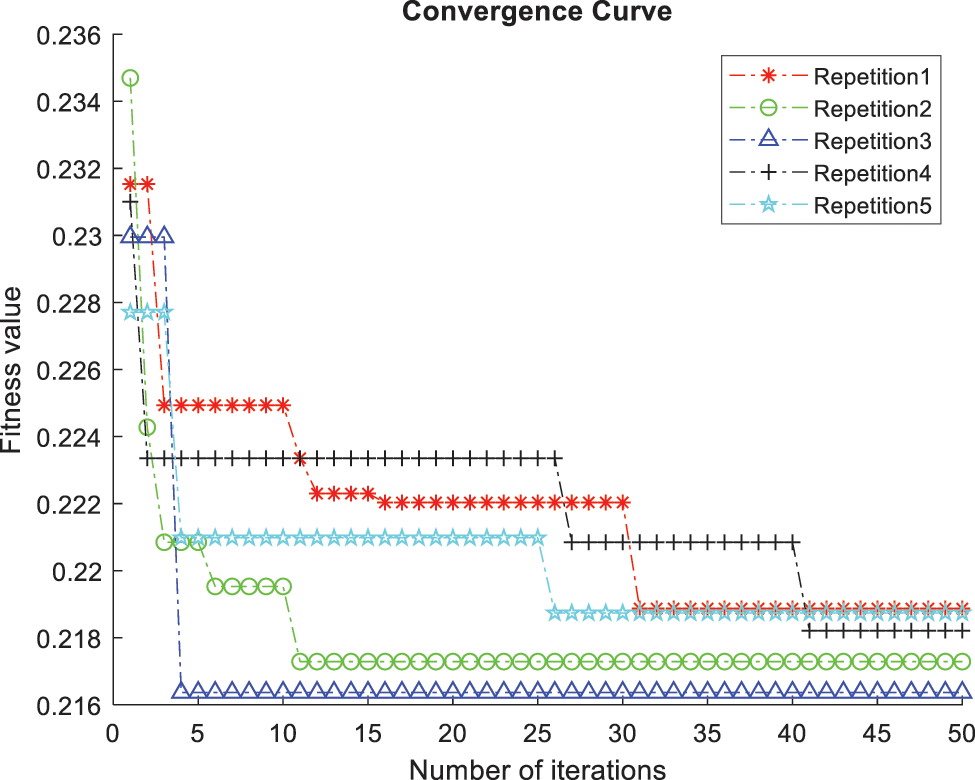
Figure 5: Comparison of convergence curves corresponding to five repetitions of the 10-fold kNN classifier
Tab. 2 demonstrates the results of the optimal subset of the UNOS dataset based on high classification accuracy. We considered five rounds validated ten times using the 10-fold cross-validation technique. The selected features in the third round were considered to achieve the highest accuracy, 91.3%. The features selection is made by considering the features with the best-fitted value as it improves the classification accuracy of the selected subset. Tab. 3 lists the names of the most candidate features selected by the third round.
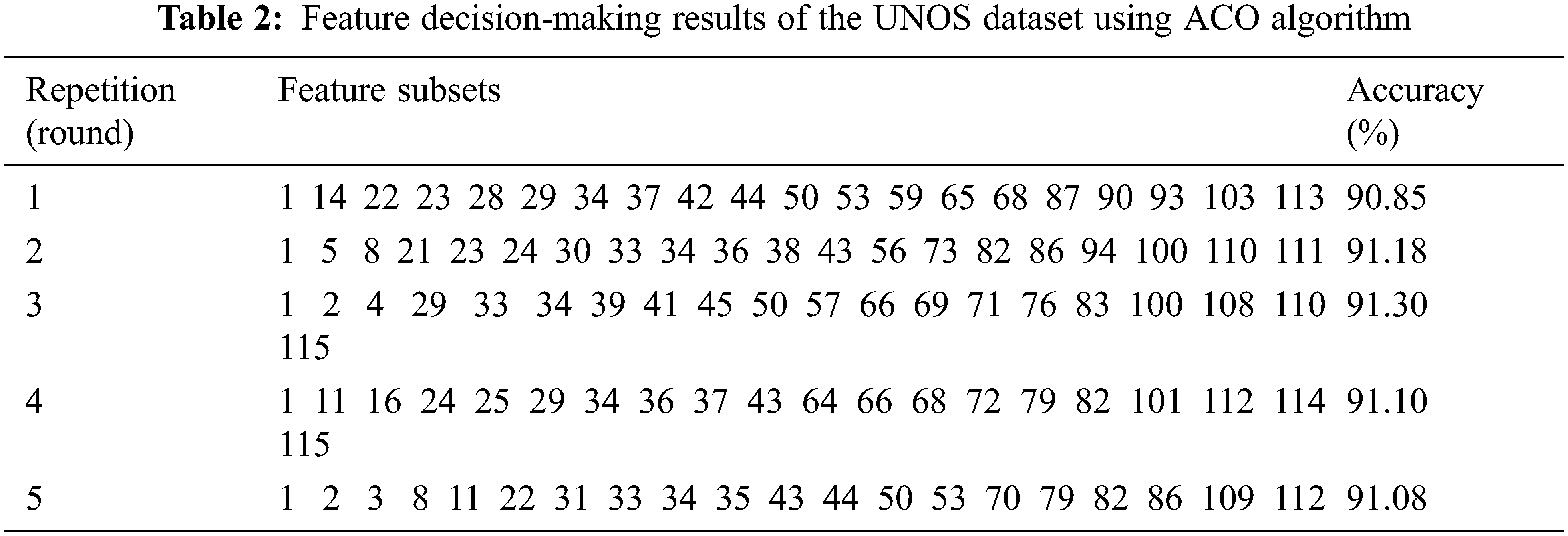
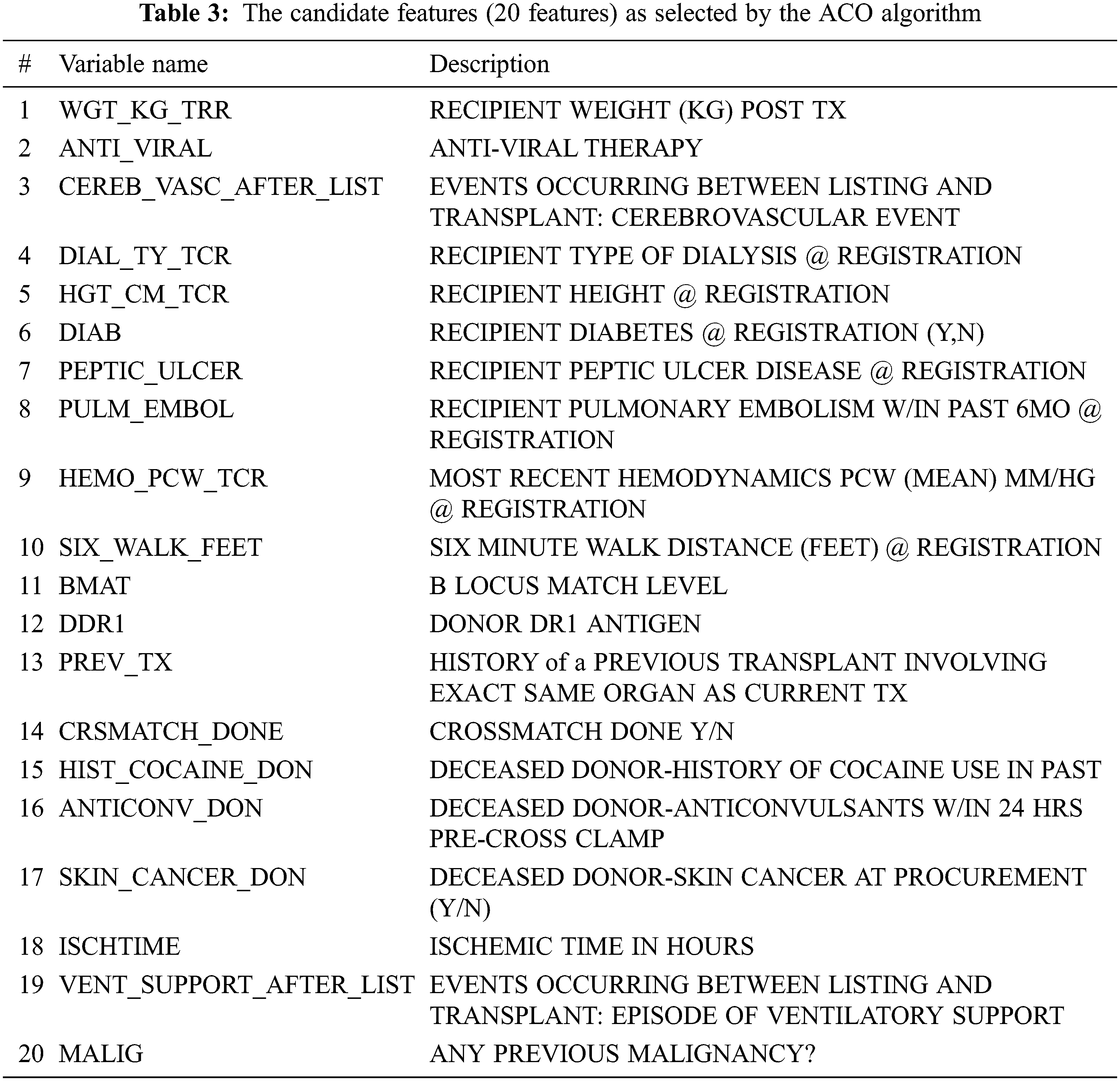
Essentially, the findings listed in Tab. 3 were consistent with medical studies. For instance, the ACO model found that the recipient weight after transplantation (WGT_KG_TRR) is an important feature that affects the functional status after transplantation. This finding is reconcilable with related studies [36–38] that support the findings in the proposed ACO-kNN model. These studies illustrated that the risk of death was increased in underweight recipients (i.e., their body mass index (BMI) is less than 18.5). Moreover, these studies showed that Kaplan-Meier modeling pointed out a significant effect of BMI on survival and QoL. Mortality is higher in obese, overweight, and underweight lung transplant patients than in normal-weight patients. In addition, this study found that the anti-viral therapy (ANTI_VIRAL) feature is essential to be considered in the lung allocation process, as also indicated in other studies [39–42]. By controlling anti-viral drugs, transplant patients can move to a situation where several medical complications can be reduced significantly and prevent viral diseases since the immunity level after lung transplantation is low. Other candidate features (CEREB_VASC_AFTER_LIST, DIAB, MALIG, PEPTIC_ULCER, ISCHTIME, VENT_SUPPORT_AFTER_LIST, and SIX_WALK_FEET) are listed in Tab. 3 are also mentioned by other researchers [43] as significant features affecting survival and QoL after lung transplantation. Other researchers highlighted the importance of considering (DIAL_TY_TCR) [44,45], (HGT_CM_TCR), (CRSMATCH_DONE) [46], (BMAT) [47], (DDR1) [48], and (PREV_TX) [49], which are important features in the proposed model as well as by the medical experts in the field of lung transplantation.
3.2 Comparison of Classification Results
The proposed model (ACO-kNN) identified the best contributing features and obtained good accuracy. Overall, an analysis of the selected features was conducted thoroughly and compared with the literature. Tab. 4 compares the proposed ACO-kNN model with the previous work. As mentioned earlier, the UNOS dataset is a standard dataset used by researchers to study the heart, lung, and thoracic allocation process to see whether their approaches work better and compare various other methods in the literature applying the same data. In this study, the comparison is limited to those using the same dataset to simplify the comparison competency. It has been demonstrated that the proposed ACO-kNN approach achieved one of the highest accuracies, to be 91.3%, and the least computational time (48 s on average) for classifying the functional status after lung transplantation. My last search in the allocation of lung transplantation [19] suffers from a high computational time of around 7 min on average and an accuracy of 95.3%, which is slightly higher than that in the proposed ACO-kNN. Overall, the resulting performance infers that the ACO algorithm is outstanding in selecting efficient features compared to the other methodologies considering a trade-off between accuracy and computational time. In other words, having a potential donor lung could make a fast decision for the recipient patient. Thus, ACO paves the way to consider the proposed model in the allocation process of other organs.
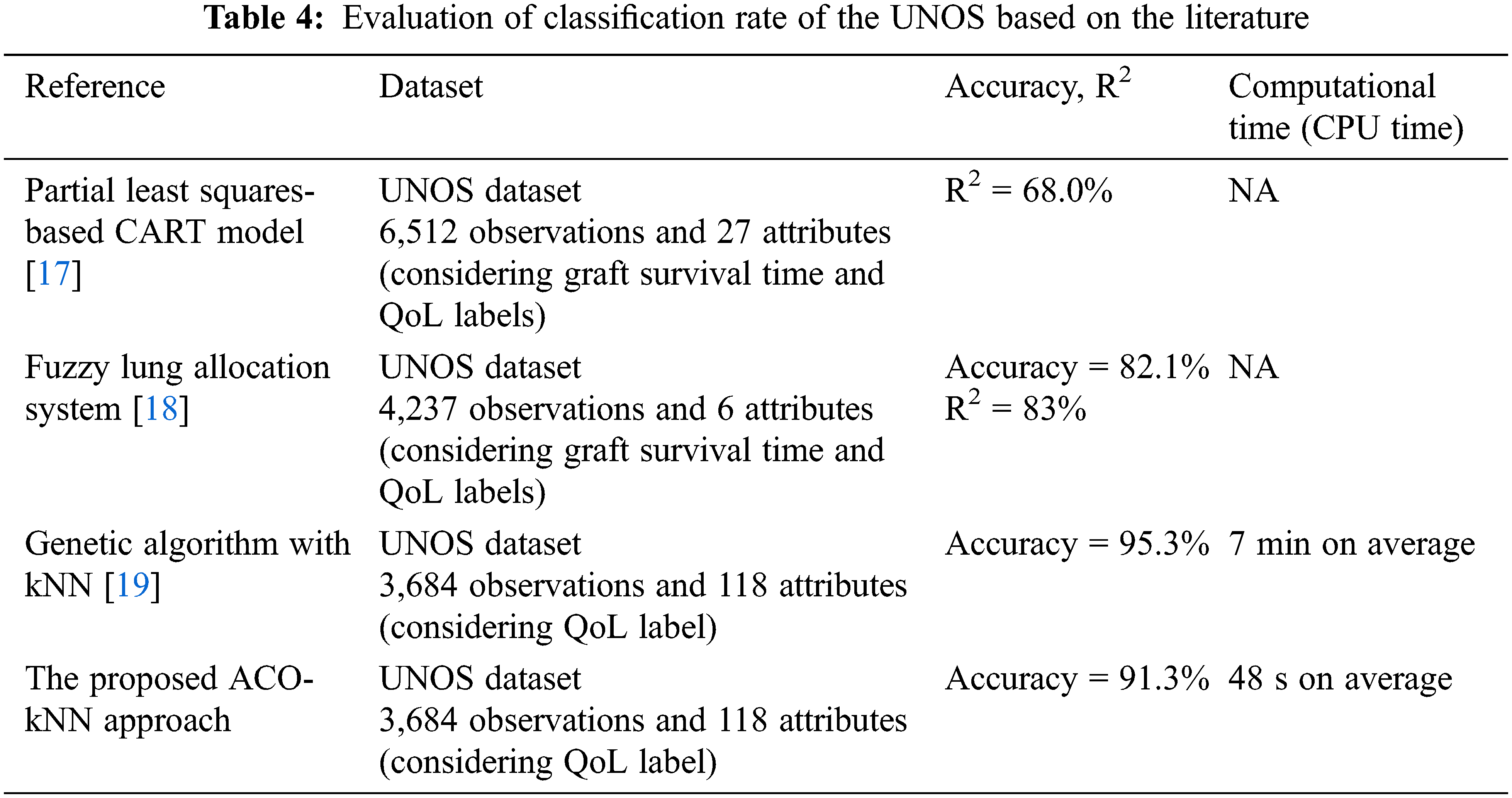
The lung allocation process is critical in lung transplantation. This paper introduced an innovative approach to using ACO for the lung allocation process. In the proposed ACO algorithm, essential features have been introduced. Then, an automated classifier based on kNN was used to classify QoL for the allocation of lung transplantation based on an optimal subset of features as an expert algorithm. From the perspective of the QoL classification application, the ACO-kNN algorithm has been developed to examine the quality of the selected features. The efficiency of the proposed method was evaluated against other similar research. The findings significantly improve QoL classification regarding the accuracy and computational time. The average accuracy was 91.3% by selecting the most essential 20 features, and the computational time did not exceed 48 s on average. Thus, the proposed method outperforms the achieved results in the literature in terms of QoL performance. In future work, this approach could be conducted to develop a reliable model for classifying different organs allocation, such as liver, kidney, and heart. In addition, ACO can deal with large data sizes returning optimal solutions.
Acknowledgement: The author would like to thank the Deanship of Scientific Research and Graduate Studies at Yarmouk University (Irbid, Jordan) for their support.
Funding Statement: The author received no specific funding for this study.
Conflicts of Interest: The author declares that she has no conflicts of interest to report regarding the present study.
1. K. A. Gillis, R. K. Patel and A. G. Jardine, “Cardiovascular complications after transplantation: treatment options in solid organ recipients,” Transplantation Reviews (Orlando, Fla.), vol. 28, no. 2, pp. 47–55, [in eng], 2014. [Google Scholar]
2. J. A. Fishman, “Infection in Solid-Organ Transplant Recipients,” New England Journal of Medicine, vol. 357, no. 25, pp. 2601–2614, 2007. [Google Scholar]
3. E. A. Engels, R. M. Pfeiffer, J. F. Fraumeni Jr Jr, B. L. Kasiske, A. K. Israni et al., “Spectrum of cancer risk among US solid organ transplant recipients,” Jama, vol. 306, no. 17, pp. 1891–1901, [in eng], 2011. [Google Scholar]
4. D. Hernández, A. Muriel and V. Abraira, “Current state of clinical end-points assessment in transplant: Key points,” Transplantation Reviews (Orlando, Fla.), vol. 30, no. 2, pp. 92–99, [in eng], 2016. [Google Scholar]
5. T. Dai, “Incentives in U.S. Healthcare Operations,” Decision Sciences, vol. 46, no. 2, pp. 455–463, 2015. [Google Scholar]
6. R. S. Lin, S. D. Horn, J. F. Hurdle and A. S. Goldfarb-Rumyantzev, “Single and multiple time-point prediction models in kidney transplant outcomes,” Journal of Biomedical Informatics, vol. 41, no. 6, pp. 944–952, [in eng], 2008. [Google Scholar]
7. J. P. Singer and L. G. Singer, “Quality of life in lung transplantation,” Seminars in Respiratory and Critical Care Medicine, vol. 34, no. 3, pp. 421–430, [in eng], 2013. [Google Scholar]
8. L. Rosso, A. Palleschi, D. Tosi, P. Mendogni, I. Righi et al., “Lung allocation score: A single-center simulation,” Transplantation Proceedings, vol. 48, no. 2, pp. 391–394, [in eng], 2016. [Google Scholar]
9. A. M. Bernhardt, A. Rahmel and H. Reichenspurner, “The unsolved problem of organ allocation in times of organ shortage: The German solution?,” The Journal of Heart and Lung Transplantation : the Official Publication of the International Society for Heart Transplantation, vol. 32, no. 11, pp. 1049–1051, [in eng], 2013. [Google Scholar]
10. K. Deep and M. Thakur, “A new mutation operator for real coded genetic algorithms,” Applied Mathematics and Computation, vol. 193, no. 1, pp. 211–230, 2007. [Google Scholar]
11. M. Gabere, Simulated annealing driven pattern search algorithms for global optimization, WIRe DSpace, South Africa, 2007. [Google Scholar]
12. G. Zong Woo, K. Joong Hoon and G. V. Loganathan, “A new heuristic optimization algorithm: Harmony search,” SIMULATION, vol. 76, no. 2, pp. 60–68, 2001. [Google Scholar]
13. M. Dorigo, M. Birattari and T. Stützle, “Ant colony optimization,” Computational Intelligence Magazine, IEEE, vol. 1, no. 4, pp. 28–39, 2006. [Google Scholar]
14. G. M. Devins, R. Dion, L. G. Pelletier, C. M. Shapiro, S. Abbey et al., “Structure of lifestyle disruptions in chronic disease: A confirmatory factor analysis of the illness intrusiveness ratings scale,” Medical Care, vol. 39, no. 10, pp. 1097–1104, 2001. [Google Scholar]
15. A. Oztekin, D. Delen and Z. Kong, “Predicting the graft survival for heart-lung transplantation patients: An integrated data mining methodology,” International Journal of Medical Informatics, vol. 78, no. 12, pp. e84–e96, 2009. [Google Scholar]
16. D. Delen, A. Oztekin and Z. J. Kong, “A machine learning-based approach to prognostic analysis of thoracic transplantations,” Artificial Intelligence in Medicine, vol. 49, no. 1, pp. 33–42, [in eng], 2010. [Google Scholar]
17. A. Oztekin, Z. J. Kong and D. Delen, “Development of a structural equation modeling-based decision tree methodology for the analysis of lung transplantations,” Decision Support Systems, vol. 51, no. 1, pp. 155–166, 2011. [Google Scholar]
18. L. Al-Ebbini, A. Oztekin and Y. Chen, “FLAS: Fuzzy lung allocation system for US-based transplantations,” European Journal of Operational Research, vol. 248, no. 3, pp. 1051–1065, 2016. [Google Scholar]
19. A. Oztekin, L. Al-Ebbini, Z. Sevkli and D. Delen, “A decision analytic approach to predicting quality of life for lung transplant recipients: A hybrid genetic algorithms-based methodology,” European Journal of Operational Research, vol. 266, no. 2, pp. 639–651, 2018. [Google Scholar]
20. W. Sun, G. Dai, X. Zhang, X. He and X. Chen, “TBE-Net: A three-branch embedding network with part-aware ability and feature complementary learning for vehicle re-identification,” IEEE Transactions on Intelligent Transportation Systems, pp. 1–13, 2021. https://dx.doi.org/10.1109/TITS.2021.3130403. [Google Scholar]
21. X. Zhang, J. Zhou, W. Sun and S. K. Jha, “A lightweight CNN based on transfer learning for COVID-19 diagnosis,” Computers Materials & Continua, vol. 72, no. 1, pp. 1123–1137, 2022. [Google Scholar]
22. H. R. Etheredge, “Assessing global organ donation policies: Opt-in vs opt-out,” Risk management and Healthcare Policy, vol. 14, pp. 1985–1998, [in eng], 2021. [Google Scholar]
23. N. B. Sariff and N. Buniyamin, “Comparative study of genetic algorithm and ant colony optimization algorithm performances for robot path planning in global static environments of different complexities,” in 2009 IEEE Int. Symp. on Computational Intelligence in Robotics and Automation-(CIRA), Daejeon, Korea (Southpp. 132–137, 2009. [Google Scholar]
24. S. A. Cupples and L. Ohler, Transplantation Nursing Secrets. Philadelphia, PA, USA, Hanley & Belfus, 2003. [Google Scholar]
25. R. Saran, B. Robinson, K. C. Abbott, L. Y. C. Agodoa, J. Bragg-Gresham et al., “US renal data system 2018 annual data report: Epidemiology of kidney disease in the United States,” American Journal of Kidney Diseases, vol. 73, no. 3 Suppl 1, pp. A7–A8, [in eng], 2019. [Google Scholar]
26. B. Ahmadi-Nedushan, “An optimized instance based learning algorithm for estimation of compressive strength of concrete,” Engineering Applications of Artificial Intelligence, vol. 25, no. 5, pp. 1073–1081, 2012. [Google Scholar]
27. J. F. Díez-Pastor, J. J. Rodríguez, C. García-Osorio and L. I. Kuncheva, “Random balance: Ensembles of variable priors classifiers for imbalanced data,” Knowledge-Based Systems, vol. 85, no. 1, pp. 96–111, 2015. [Google Scholar]
28. N. Nedjah, L. S. Junior and L. de Macedo Mourelle, “Congestion-aware ant colony based routing algorithms for efficient application execution on network-on-chip platform,” Expert Systems With Applications, vol. 40, no. 16, pp. 6661–6673, 2013. [Google Scholar]
29. X. L. Zhang, X. F. Chen and Z. J. He, “Fault diagnosis based on support vector machines with parameter optimization by an ant colony algorithm,” Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, vol. 224, no. 1, pp. 217–229, 2009. [Google Scholar]
30. Y. Saeys, I. Inza and P. Larrañaga, “A review of feature selection techniques in bioinformatics,” Bioinformatics, vol. 23, no. 19, pp. 2507–2517, 2007. [Google Scholar]
31. M. Dorigo, G. Di Caro and L. M. Gambardella, “Ant algorithms for discrete optimization,” Artificial Life, vol. 5, no. 2, pp. 137–172, 1999. [Google Scholar]
32. A. P. Engelbrecht, Computational Intelligence: An Introduction. CHICHESTER, United Kingdom, John Wiley & Sons, 2007. [Google Scholar]
33. B. Bullnheimer, R. Hartl and C. Strauss, “A new rank based version of the ant system: A computational study,” sfb report-Sonderforschungsbereich 010 “Adaptive Information Systems and Modelling in Economics and Management Science” Initiative 5 “Artificial Factory”, 1997. [Google Scholar]
34. R. Kohavi and G. H. John, “Wrappers for feature subset selection,” Artificial Intelligence, vol. 97, no. 1, pp. 273–324, 1997. [Google Scholar]
35. M. Kubat, Introduction to machine learning, Springer, New Mexico, USA, pp. 104–138, 1992. [Google Scholar]
36. M. Z. Molnar, C. P. Kovesdy, I. Mucsi, S. Bunnapradist, E. Streja et al., “Higher recipient body mass index is associated with post-transplant delayed kidney graft function,” Kidney International, vol. 80, no. 2, pp. 218–224, [in eng], 2011. [Google Scholar]
37. S. R. DiCecco and N. Francisco-Ziller, “Obesity and organ transplantation,” Nutrition in Clinical Practice, vol. 29, no. 2, pp. 171–191, 2014. [Google Scholar]
38. J. G. Allen, G. J. Arnaoutakis, E. S. Weiss, C. A. Merlo, J. V. Conte et al., “The impact of recipient body mass index on survival after lung transplantation,” The Journal of Heart and Lung Transplantation : the Official Publication of the International Society for Heart Transplantation, vol. 29, no. 9, pp. 1026–1033, [in eng], 2010. [Google Scholar]
39. P. D. Shah and J. F. McDyer, “Viral infections in lung transplant recipients,” Seminars in Respiratory and Critical Care Medicine, vol. 31, no. 2, pp. 243–254, [in eng], 2010. [Google Scholar]
40. M.-W. Welker and S. Zeuzem, “Pre- and post-transplant antiviral therapy (HBV, HCV),” Visceral Medicine, vol. 32, no. 2, pp. 105–109, [in eng], 2016. [Google Scholar]
41. I. P. Neuringer, “Posttransplant lymphoproliferative disease after lung transplantation,” Clinical and Developmental Immunology, vol. 2013, no. 6, pp. 430209, 2013. [Google Scholar]
42. T. Kotsimbos, T. J. Williams and G. P. Anderson, “Update on lung transplantation: Programmes, patients and prospects,” European Respiratory Review, vol. 21, no. 126, pp. 271–305, 2012. [Google Scholar]
43. L. Genao, H. E. Whitson, D. Zaas, L. L. Sanders and K. E. Schmader, “Functional status after lung transplantation in older adults in the post-allocation score era,” American Journal of Transplantation, vol. 13, no. 1, pp. 157–166, [in eng], 2013. [Google Scholar]
44. A. Osho, M. Mulvihill, N. Lamba, S. Hirji, B. Yerokun et al., “Is functional independence associated with improved long-term survival after lung transplantation?,” Annals of Thoracic Surgery, vol. 106, no. 1, pp. 79–84, [in eng], 2018. [Google Scholar]
45. A. Banga, M. Mohanka, J. Mullins, S. Bollineni, V. Kaza et al., “Interaction of pre-transplant recipient characteristics and renal function in lung transplant survival,” The Journal of Heart and Lung Transplantation : the Official Publication of the International Society for Heart Transplantation, [in eng], vol. 37, pp. 275–282, 2017. [Google Scholar]
46. J. B. Barnard, O. Davies, P. Curry, P. Catarino, J. Dunning et al., “Size matching in lung transplantation: An evidence-based review,” The Journal of Heart and Lung Transplantation : the Official Publication of the International Society for Heart Transplantation, vol. 32, no. 9, pp. 849–860, [in eng], 2013. [Google Scholar]
47. Y. Yamada, T. Langner, I. Inci, C. Benden, M. Schuurmans et al., “Impact of human leukocyte antigen mismatch on lung transplant outcome†,” Interactive CardioVascular and Thoracic Surgery, vol. 26, no. 5, pp. 859–864, 2018. [Google Scholar]
48. A. A. Zachary and M. S. Leffell, “HLA mismatching strategies for solid organ transplantation-A balancing act,” Frontiers in Immunology, vol. 7, pp. 575[in eng], 2016. [Google Scholar]
49. F. Venuta and D. Van Raemdonck, “History of lung transplantation,” Journal of Thoracic Diseases, vol. 9, no. 12, pp. 5458–5471, [in eng], 2017. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |