DOI:10.32604/iasc.2023.029489

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2023.029489 |  |
| Article |
An Improved Lifetime and Energy Consumption with Enhanced Clustering in WSNs
1Department of Electronics & Communication Engineering, Annamalai University, Chidambaram, 608002, India
2Department of Information Technology, Annamalai University, Chidambaram, 608002, Tamilnadu, India
*Corresponding Author: I. Adumbabu. Email: adumbabu401@gmail.com
Received: 04 March 2022; Accepted: 14 April 2022
Abstract: A wireless sensor network (WSN) is made up of sensor nodes that communicate via radio waves in order to conduct sensing functions. In WSN, the location of the base station is critical. Although base stations are fixed, they may move in response to data received from sensor nodes under specific conditions. Clustering is a highly efficient approach of minimising energy use. The issues of extending the life of WSNs and optimising their energy consumption have been addressed in this paper. It has been established that integrating mobile sinks into wireless sensor networks extends their longevity. Thus, this research proposes an optimal clustering and routing technique for optimising the energy usage and lifetime of WSNs. To minimise energy consumption, this research employs movable and stationary sink nodes. The K-Medoid clustering model is used to generate the initial number of nodes in the various clusters. After that, the cluster head is chosen using a hybrid Interval Type-2 Fuzzy technique that takes three aspects into account: residual energy, node centrality, and neighbourhood. A highly efficient backup cluster head (CH) collecting system can provide in significant energy savings while also prolonging the system’s life. Finally, better Reinforcement learning combined with a Genetic algorithm routing protocol is used to ensure effective data delivery. The suggested approach’s efficacy is evaluated in comparison to earlier approaches utilising residual node energy, delay or average delay, packet delivery ratio, throughput, network longevity, average energy consumption, and multiple alive nodes. In experiments, the proposed strategy outperforms existing strategies.
Keywords: Fuzzy logic; genetic algorithm; wireless sensor networks; routing; clustering; K-medoid clustering
Sensors are small electrical devices that are used to monitor or quantify changes occurring in real-time circumstances. They are frequently inexpensive, low-power devices capable of analysing and transmitting data to a base station. When sensor nodes are successfully deployed, they self-organize into a network called a WSN [1–3]. Wireless sensor networks are used in a variety of real-world applications due to their versatility. Processing is possible for commercial and real-time applications such as industrial applications, automation, retail, and transportation. Sensor nodes are powered by batteries, and because they consume less energy, their battery life varies based on the parameters. The sensor node’s performance may be diminished, which will have an effect on the system’s overall performance. As a result, energy consumption in WSN scenarios is more constrained [4,5]. While several measures have been taken in recent years to address the energy consumption issue in WSNs, communication difficulties such as network latency, traffic, end-to-end latency, scheduling, and routing must all be addressed [6,7].
Routing and clustering algorithms are two of the most energy-efficient techniques used in WSNs. Clustering is a technique for splitting a huge area into numerous smaller clusters [8,9]. Each cluster consists of numerous sensors referred to as cluster members, with one serving as the cluster head. Cluster members are responsible for detecting their environment, while the cluster leader collects data. Probabilistic algorithms, Quality of Service (QoS)-based routing protocols, negotiation-based routing protocols, query-based routing protocols, multipath, location-based routing protocols, hierarchical, hybrid, flat, reactive, and proactive routing protocols are just a few of the important routing protocols [10,11].
Numerous academics have concentrated on the clustering process to improve the energy efficiency of WSN. A multi-objective fuzzy clustering technique, an enhanced particle swarm optimization (PSO), and a fuzzy logic algorithm are used to construct clusters. The primary objective of these algorithms is to reduce network energy consumption. The Received Signal Strength Indicator (RSSI) is employed in the augmented ant colony optimization (ACO) approach for WSN route selection [12,13]. The distance is determined by summing the RSSI and transmit power values. The QoS-aware and heterogeneously clustered routing (QHCR) protocol conserves network energy by considering the starting expected transmission count, energy level, and minimal loss along the path. Data transmission is permitted in multi-hop communication based on the route metric. Away cluster head with Assistant Cluster head (ACH) is a routing approach that tries to extend the life of the network while simultaneously boosting its performance. To ensure effective routing, the following processes are recommended: network configuration, CH randomization, CH naturalisation, data scheduling, and free association [14,15].
Despite their widespread use, WSNs are limited by a variety of issues, including storage, transmission range, and battery power. As a result of these constraints, a routing algorithm must face and solve a variety of fascinating obstacles. The algorithm must be efficient in terms of both energy and scalability. Additionally, the energy resources of each sensor node must be efficiently managed [16,17]. Naturally, researchers choose to cluster sensor nodes to achieve the required scalability, high energy efficiency, and prolonged network lifetime in large-scale WSN situations. Any approach that relies on clustering begins by selecting CHs and clustering the remaining nodes [18]. In a cluster, nodes transfer data to their CH, which aggregates it and distributes it to the Base Station (BS) or to other CHs nearby. Cluster heads spend more energy on average than non-cluster head nodes. Due to pooled traffic relay, CHs located close the BS spend more energy than other nodes [19,20]. As a result, we provide a novel network model in this research that aims to minimise long-distance connections in order to enhance network longevity.
The following contributes significantly to the proposed methods:
a) Developing an efficient and energy-conscious clustering and routing protocol with the goal of extending the network’s life.
b) To create a wireless sensor network comprised of nodes.
c) To do clustering using the K-Medoid model.
d) Using the fuzzy approach, determine the cluster head.
e) To propose a new routing protocol based on enhanced reinforcement learning and a genetic algorithm for more efficient transmission.
Section 2 discusses the pertinent work. Section 3 discusses the proposed technique as well as the optimal cluster head selection and routing via the hybrid optimization algorithm. Section 4 discusses the findings and debates, and Section 5 finishes the work.
Numerous experts have worked on various aspects of energy-efficient routing in order to extend the network’s life. The following is a list of recent papers on the subject.
Anand et al. [21] proposed incorporating a Particle Swarm Optimization-Genetic Algorithm (PSO-GA) into WSNs to increase network longevity. The optimal cluster head employs a GA to collect data from the remaining nodes, taking energy and distance parameters into account. Additionally, the PSO technique is based on the determination of the optimal routing paths for all relay nodes transmitting data to the BS. By permitting and facilitating communication between the CH and drain, the proposed approach increases energy efficiency. Finally, the QoS of the WSNs is increased, extending the system’s life.
Panchal et al. [22] propose an Fuzzy C-Means Energy efficient hierarchical clustering and routing (FCM-EHCR) that is reliant on the cluster and grid centroid, the remaining node energy, and the respective Euclidean distances. By utilising a dynamic grid, energy-efficient routing, and cluster construction, this system optimises energy use. The fitness values of the nodes were used to assess if they could serve as the GH or CH. The packet routing techniques of all of the GHs are dictated by their Euclidean distances from one another and also by their residual energy. Additionally, they looked at energy consumption and discovered that the proposed approach is more efficient, results in more cluster formations, has a longer network lifetime, and provides better coverage.
Zachariah et al. [23] proposed a strategy for lowering the energy consumption and extending the life of WSNs in both heterogeneous and homogeneous environments. The authors demonstrated an efficient grouping and selection technique for cluster heads using cuckoo and Krill Herd. In terms of living nodes, they compared the proposed protocols to current protocols such as Energy Swarm Optimization-Low Energy efficient hierarchical Clustering and Routing (ESO-LEACH), Hybrid Harmony Search Algorithm Particle Swarm Optimization (HSAPSO), and Genetic algorithm based energy efficient clustering hierarchy (GAECH). Additionally, they assessed the efficacy of the recommended regimens.
Daneshvar et al. [24] pioneered a novel grouping technique that employs the Grey Wolf Optimizer (GWO) to choose Cluster Head (CHs). The alternatives are rated to help determine which Cluster heads to utilise based on their expected energy consumption and the current residual energy of each node. To improve energy efficiency, the suggested technique repeatedly applies the same clustering method. As a result, the protocol is able to conserve the energy required to recreate the clustering. Additionally, they devised a dual-hop routing algorithm for CHs located remote from the BS and demonstrated that this strategy ensures the least amount of energy and the most balanced utilisation when residual nodes interact via single-hop communication.
Thiagarajan [25] present a PSO-based energy-efficient clustering technique for WSNs. Routing nodes in a WSN is a difficult and complex problem. It is crucial for the network’s stability and long-term viability. The LEACH Protocol determines the longevity of a sensor network by correlating node energy consumption. Clustering was designed with the goal of decreasing intra-cluster distance while increasing network energy usage.
Mosavifard et al. [26] created a cluster-based two-level routing system. They improved packet delivery and reduced energy usage in the proposed technique by clustering, selecting backup cluster head (BCH) and Supporting Cluster Head (SCH), and dividing each cluster into four pieces. Two stages comprise the technique. The initial phase entails selecting CHs and BCHs, as well as grouping nodes. Each cluster is divided into four regions to facilitate intra-cluster routing, with nodes either directly communicating with CH or via the most appropriate node in their region. CHs are tiered according to their proximity to the BS to simplify inter-cluster routing [27–29]. Because CHs are stacked, the source CH chooses the next hop from the CHs in the top layer based on their residual energy and distance to the BS [30].
Khoshraftar et al. [31] proposed employing a GA to improve node grouping in WSNs, as well as to discover and optimise the ideal path and route of transition between nodes; the bee colony approach was adopted. The suggested technique divides a wireless sensor network into cells of varying sizes. For varying cell sizes, the normal mode determines cell area, compression, and energy consumption.
The proposed WSN system is composed of the following components: sensor nodes, cluster formation, cluster head, and routing. Energy efficiency is critical in WSNs. Through the use of routing systems, the efficient methodology of grouping and information collection is used to promote energy conservation. The WSN is composed of dynamic and static sinks. The position of the static sink is fixed. The mobile sink, on the other hand, may travel the network. The mobile sink concept is gaining traction as a technique of ensuring efficient data transmission and routing while conserving energy. The SNs can continue to function for an extended amount of time while still producing acceptable results. The flexibility path evaluation has an effect on the energy consumption of a moving sink with secured routes. Grouping is accomplished through the use of enhanced Electromagnetic (EM), which groups (Software-Defined Network) SNs with similar characteristics together. Clustering is very dependent on CH selection. For CH selection, the fuzzy approach is applied. The primary objective is to develop energy-aware sensor networks. CH is preferred over other SNs due to its lower energy consumption. A data transmission technology based on Reinforcement Learning and Genetic algorithms is used to facilitate data transmission. Total energy consumption is increased; as a result, the network’s life may be shortened. By addressing the aforementioned constraints of WSNs, the enhanced techniques may improve the performance of the suggested technique. The clustered WSN’s general architecture is depicted in Fig. 1.
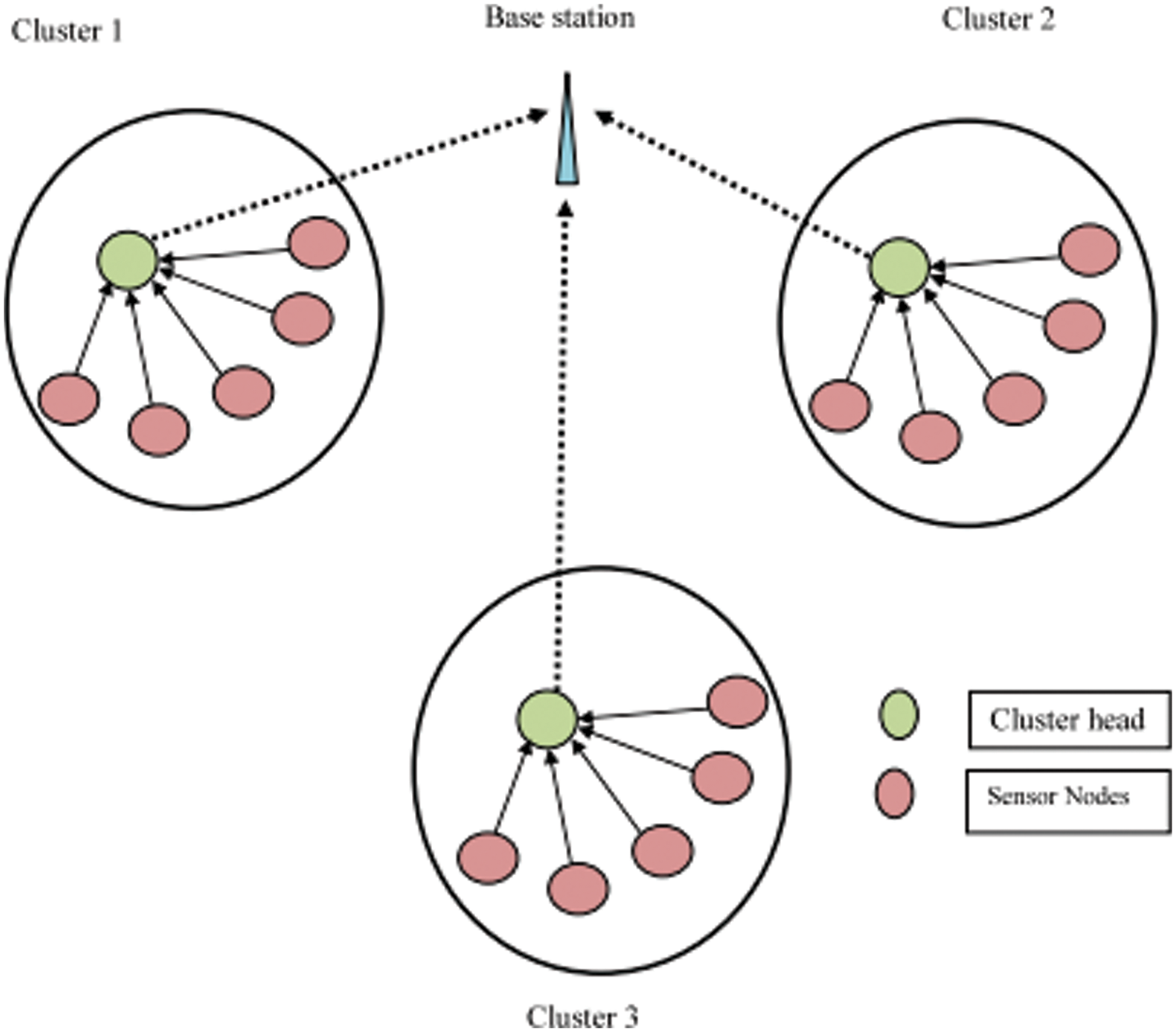
Figure 1: General architecture of clustered WSN
In recent years, scientists have concentrated their efforts on inventing novel methodologies and algorithms for energy conservation. A wireless sensor network(WSN) is composed of various layers, including hardware, application, and network. The majority of study has concentrated on the unique and specialised characteristics of energy dissipation in sensor networks. As a result, optimising the energy consumption of a single component may not assure that the energy consumption of the entire network is maximised. The study is limited to a single aspect of a WSN. The novel technique is being used to decrease the total amount of energy consumed by WSNs. The total amount of energy consumed can be used to balance energy consumption and extend the network’s life. By relocating the sink node, each node’s energy consumption is reduced.
WSNs are composed of a huge number of SNs. Two sink nodes have been deployed. Sinks are classified into two types: permanent and movable. The sensor network is designed in accordance with the following guidelines.
a) Following deployment, a large number of SNs are corrected. In two dimensions, the nodes are closely packed.
b) Each node should be roughly synced in terms of time in seconds.
c) Because each node lacks GPS antennae, they are unsuitable for location awareness.
d) Transceiver sensors modulate transmission power in order to achieve a wide range of transmission ranges. Each SN begins with a unique amount of energy. Despite this, CH nodes are quite energetic. Fig. 2 depicts the proposed structure.
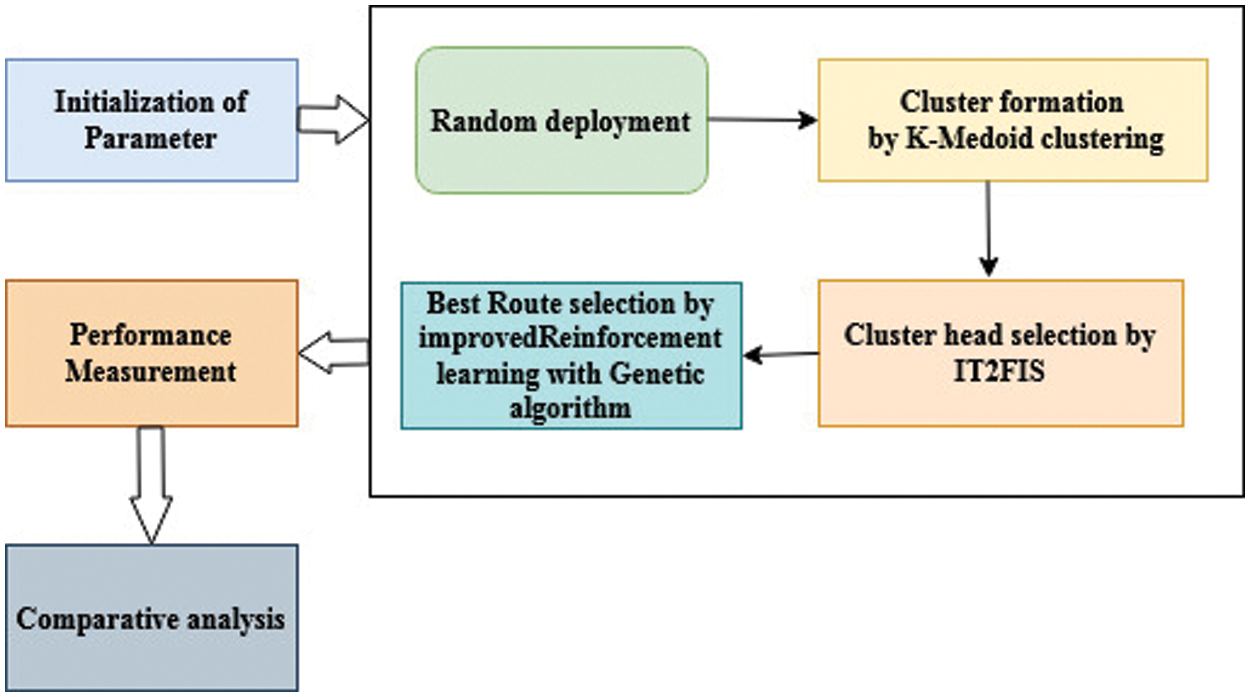
Figure 2: Block diagram of the proposed methodology
The information bits are transmitted between the receiver and transmitter via the radio model in WSN. The energy model is bipolar in nature, with one side dedicated to data transmission and the other for data reception. ‘d’ denotes the distance between the receiver and transmitter.
The following are the equations for transferring and receiving energy:
where
The free space model is denoted by d = 2 in Eqs. (1) and (2), whereas the multi-path model is represented by d = 4.
Where,
• The energy intended to transmit a data bit is denoted by Eelec.
• K represents the information bits and distance as ‘d’ between receiver and sender.
• Transmission energy is represented as Erans and the energy utilized to get data is represented as Ereceive.
• The amplification coefficient and amplification energy are represented as
3.4 Cluster Formation by K-Medoid Clustering Model
This research introduces K-medoid clustering, which utilises between 100 and 200 nodes to construct a full cluster. If a cluster node is denied, it will join another cluster node group nearby. If there are major disparities between the nodes they join and leave, they will join different networks.
Using K-Medoid clustering, the data items ‘k’ is picked inside a cluster. Numerous crucial characteristics about the nodes that come under the medoids of a cluster are incorporated within that cluster. The properties of the node will dictate which medoid it belongs to. The steps for clustering K-medoids are as follows:
Initializing: The K value is determined by the data node placements.
Selecting the Medoids The medoid value is the distance between the data points of two objects. As a result, the following formula may be used to compute the distance:
Clustering: The cluster is created using the medoid value that is closest to the object.
Medoid Update: The objective of each cluster is to keep the distance between the object and the cluster as small as feasible.
Nodes in Medoid: Clustering is accomplished by associating each element with the medoid. The distance between medoids and objects is determined by their separation. The collection of diverse nodes is analysed using the K-medoid technique.
3.5 Cluster Head Selection by Interval Type-2 Fuzzy C-Means (IT2FCM)
Choosing the optimal CH is a significant challenge for cluster formation in WSNs. The CH node collects and transmits data from all Sink Nodes (SNs) to the Base Station (BS). In the proposed protocol, CHs are selected using IT2FCM. Cluster head formation is predicted using node centrality, residual energy, and neighbourhood overlap. The input parameters are provided below.
a. Residual energy: CH will be selected from the most energetic nodes. Consider the initial energy of a node as Ei. E(t) denotes the energy consumed by the node following the t time period.
The mathematical equation for Eres at time t is:
b. Node centrality: This property indicates how central the chosen CH is in reference to its neighbours across the entire network.
At the end, both v and u have the same group of neighbours. NOVER will be number one at that time. If u and v have no mutual neighbours, NOVER will be 0. In this method, the NOVER value will be increased from 0 to 1.
IT2FLS is a version update of IT1FLS. The IT2FCM selects the optimal probability function for improved CH selection. IT2FCM is a Fuzzy C-Means algorithm extension that is more capable of dealing with uncertainty. The design of fuzzy membership requires the selection of a fuzzifier n. The two fuzzifier intervals [n1, n2] define the uncertainty footprint (FOU) for the IT2FLS membership function creation. The IT2FLS algorithm is divided into the following stages:
Initializing by setting up the fuzzy partition matrix
As a result, the fuzzy membership function matrix has an interval that tends to zero.
Fuzzy clusters compute the centroids
Eqs. (11) and (12) update the upper and lower fuzzy membership functions.
where termination criterion
The Gaussian membership functions (GMF) are chosen for the fuzzy system architecture. The GMF with variance and mean is expressed as:
IF-THEN rules are used to define fuzzy rules. The distance to the BS is the input to IT2FLS membership, while the node density and probability function are the outputs. As a result, the probability function is denoted by,
Here, the weights are represented as αnd and αq. Similarly, rnd and rq are used to denote the current levels. Similarly, Mnd and Mq are used to express node density values. Maximum, intermediate, and minimum values of membership functions (Mfns) are examined for node density. As a result, we used IT2FLS to choose cluster heads efficiently from each network node.
3.6 Hybrid Improved Reinforcement Learning with Genetic Algorithm
By lowering the computational cost, the combination method enhances the fitness of the optimization approach. As a result, performance is enhanced. Researchers are concentrating their efforts on various optimization techniques aimed at enhancing the network’s performance. Optimizing the hybrid method is an efficient way to reduce compilation time.
3.6.1 Improved Reinforcement Learning
Reinforcement learning was enabled by a finite Markov decision process (MDP) and discrete time (RL). Deep Q-Network (DQN) is a word used in this research to refer to an improved RL algorithm. Generally, the Q table keeps track of actions and states. Throughout the learning process, the values in the Q table are changed in line with Eq. (15). As a result, their behaviours and states are bound by certain circumstances.
where α = learning rate.
DQN agents may interact with the continuous environments since Deep Neural Network (DNN) can parameterize an approximate action-value function Q(s, a; θi). At the time step, et (agent’s experience) = (St, At, Rt, St + 1) is maintained in a replay memory pool D. DNNs can be trained using mini batches that are randomly taken from the memory pool, which ensures the system’s stability. The following is the DNN loss function:
where i = Target DNN parameters at the ith iteration; θi = Q-DNN parameters at the ith iteration.
QDNN parameters are upgraded in real-time. Target DNN is a forward network that is comparable to the Q-DNN architecture. The parameters are updated on a regular basis by simply extracting them from the Q-DNN parameters. This method of training may eliminate feedback loops and allow for rapid progress.
Selection, crossover, and mutation are the three genetic operations in GA. Selection is a process in which multiple individuals with superior fitness are picked from the entire group to birth a new generation. Following selection, hybridization and mutation are used to create a new population of the selected individuals. Crossover is a process in which two randomly chosen parents exchange segments of their DNA in order to create new individuals. It is possible to preserve genetic diversity between generations and to improve the GA population’s solution through mutation operation.
In the field of artificial intelligence, a genetic algorithm is a generic approach for selecting the optimal answer. To dynamically alter the population’s variety, a control function based on rough sets is introduced to the fitness value. Additionally, an RL mechanism was integrated into the mutation and crossover procedures in order to improve the accuracy and speed of convergence of the discretization approach by selecting the cross fragments and mutation sites.
a) Evolutionary operations: Each iteration determines the fitness of the current population, selects the optimal individual, and changes the global variable.
b) Selection Operator: Selection is based on an individual’s fitness level within a group. Fitter individuals are more likely to get chosen.
c) Crossover Operator: The crossover operation of a genetic algorithm entails exchanging genes between two matched chromosomes in order to generate two new individuals.
○ State: Using the aforementioned analysis, each characteristic will have a possibility of changing. A state is a collection of changing characteristics in a crossover operation.
○ Action: Since each state change requires one action, numerous actions must be specified, increasing computing complexity.
○ Reward: Set a reward for each state-action. The reward value is based on individual fitness change, which is used to assess the algorithm’s search for the best solution.
d) Mutation Operator: The mutation and cross operations have the identical state, action, and reward; the only difference is that the cross operation on the feature has been renamed a mutation. Each is equipped with a Q-table. After N iterations, the Q-tables for cross and mutation operations.
The preceding phase yields a solution, but it is not definitive; the method is repeated until the global optimum is obtained. When the optimal global solution is found, it is allocated to the learning rate of improved Reinforcement Learning.
4 Simulation Results and Discussions
This section includes simulation data generated in the Matlab environment for the purpose of evaluating the suggested approach’s performance in comparison to state-of-the-art approaches. The relevant findings were obtained in terms of the number of alive nodes, the average energy consumption, the network lifetime, the throughput, the packet delivery ratio, the delay or average delay, and the remaining node energy. Two tests were conducted: I with 100 nodes and (ii) with 200 nodes, with the number of rounds varied between 1000 and 5000. Tab. 1 illustrates the experimental parameter.

The nodes are initially distributed randomly around the network area. The K-Medoid clustering model assigns an appropriate number of groups to each SN. The remainder of the energy, NOVER, and NC is utilised to select CHs. CHs are chosen from SNs with a high energy, an excellent NOVER, and a near-NC. When a sink is fixed, the cluster head node gets data from SNs and transmits it to the BS via the cluster head node. Otherwise, the moveable sink traverses the network, collecting data from all CHs via an enhanced Reinforcement learning method. The proposed approach is compared to CREEP, CFSFDP, and EESCA. The system’s performance parameters such as the number of alive nodes, average energy consumption, delay or average delay, packet delivery ratio, throughput, network lifetime, and residual node energy are calculated using 100 and 200 nodes utilising the CREEP, CFSFDP, and EESCA techniques, respectively. Energy consumption is also calculated for movable and fixed sinks.
The following metrics are used to represent the suggested model.
A) Number of living nodes: The number of alive nodes in a network indicates the number of active nodes. A high number of active nodes improves the performance of the network.
B) Average energy consumption: This is the overall amount of energy consumed by nodes while receiving and transmitting data.
C) Network lifetime: The time period between the initiation and completion of a network action.
D) Throughput: The average number of packets received every round at the base station.
E) Packet delivery ratio: The ratio of packets received by a destination node (R1) to packets created by a source node (R2).
F) Time delay or average time delay: It is the sum of processing, queuing, and propagation delays.
G) Remaining energy in the node
4.2 Experiments with Varying Numbers of Sensor Nodes
According to Figs. 3 and 4, the number of living nodes does not decrease dramatically as the number of rounds increases. As illustrated in Figs. 5 and 6, the suggested method is more energy efficient than the CREEP, CFSFDP, and EESCA methods. Clustering enables cluster member nodes to connect with a nearby CH, resulting in decreased energy consumption.
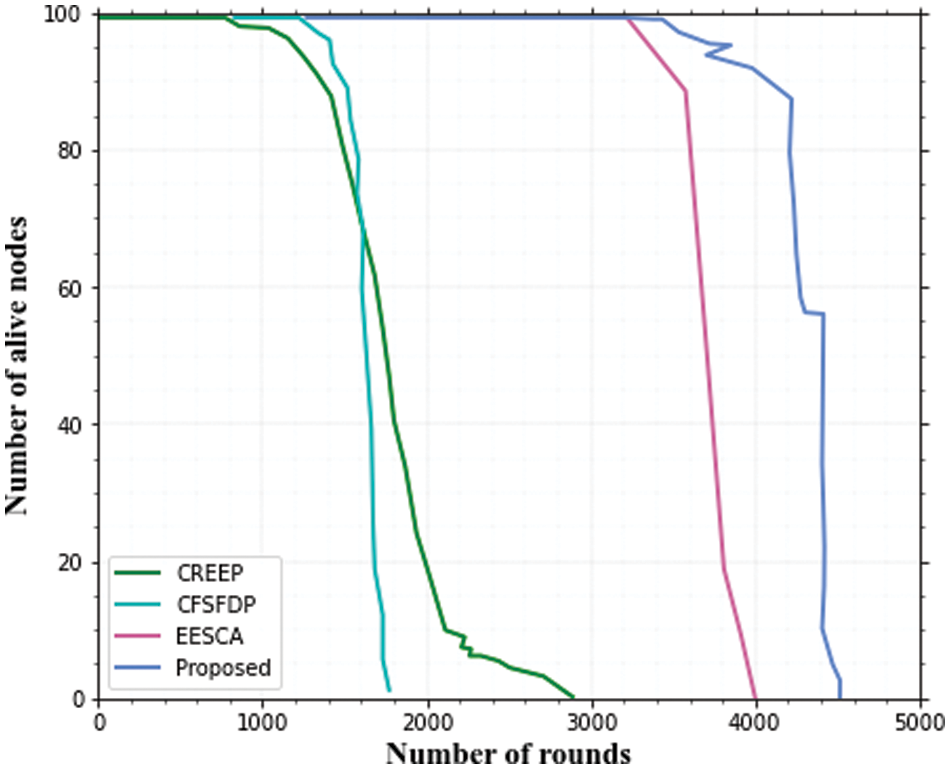
Figure 3: Alive nodes with 100 nodes

Figure 4: Alive nodes with 200

Figure 5: Energy consumption with 100 nodes

Figure 6: Energy consumption with 200 nodes
The Figs. 7 and 8 illustrate the suggested method’s network lifetime in terms of rounds. The alive nodes are evaluated for the 5000 rounds using their regular cycle numbers. Each round compares the proposed method to existing ways to determine how well the methods perform. The proposed method is compared to existing 100 and 200 node techniques.

Figure 7: Network lifetime with 100 nodes

Figure 8: Network lifetime with 200 nodes
Figs. 9 and 10 illustrate the throughput performance of the proposed technique and conventional systems. The graphic clearly displays how the developed technique has been expanded in terms of expressiveness. The proposed strategy outperformed existing approaches in terms of throughput. The greater the number of SN growths, the greater the throughput.

Figure 9: Throughput with 100 nodes

Figure 10: Throughput with 200 nodes
The simulation results for the packet delivery ratios of the three presented routing techniques, CREEP, CFSFDP, and EESCA, with 100 and 200 nodes, are shown in Figs. 11 and 12.

Figure 11: Packet delivery ratio with 100 nodes
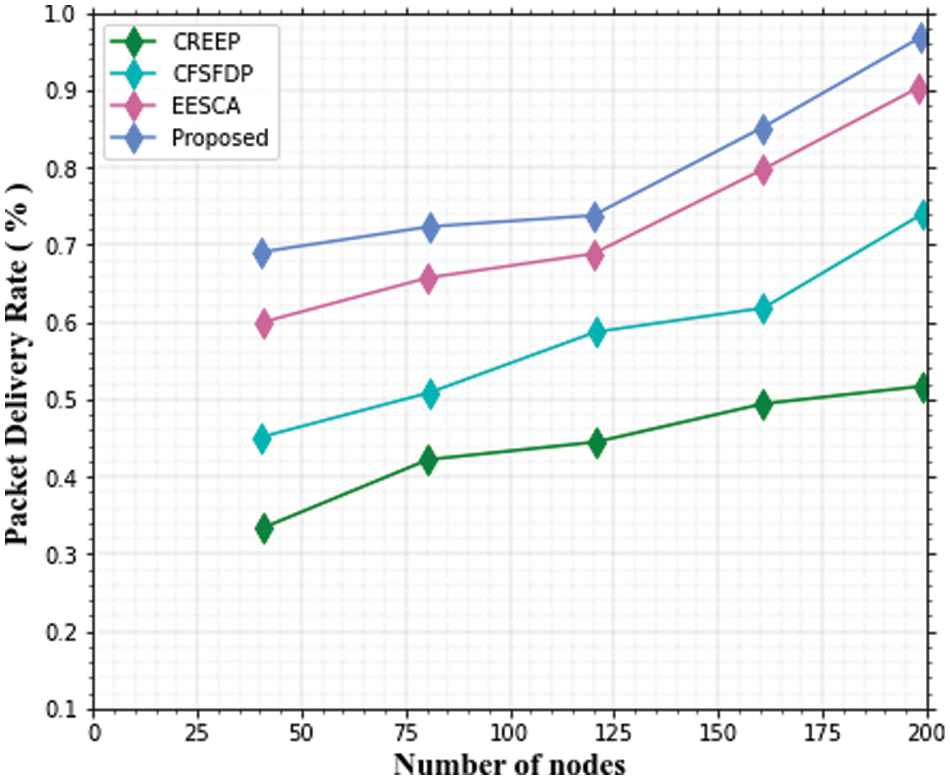
Figure 12: Packet delivery ratio with 200 nodes
As illustrated in Figs. 13 and 14, the proposed strategy has a shorter end-to-end latency than the CREEP, CFSFDP, and EESCA methods. Cluster nodes broadcast data to CH directly or via the node with the greatest result, increasing the likelihood of a reliable relay.

Figure 13: Comparison of end-to-end delay with 100 nodes

Figure 14: Comparison of end-to-end delay with 200 nodes
The network performance is studied in Figs. 15 and 16 using the residual energy of 100 and 200 nodes, respectively. The graph illustrates the total energy consumed by the nodes over a 5000-round period, and the performance is evaluated. The proposed protocol outlived the CREEP, CFSFDP, and EESCA protocols that were already in use. By lowering the network’s energy consumption, the proposed approach has demonstrated its superiority to conventional techniques.

Figure 15: Average residual energy with 100 nodes

Figure 16: Average residual energy with 200 nodes
The experimental results indicate that the suggested strategy outperforms established techniques. The effectiveness and efficiency of the proposed task are determined by the number of alive nodes, the average energy consumption, the throughput, the network lifetime, the delay or average delay packet delivery ratio, and the residual node energy.
For successful WSN routing, this approach mixes fuzzy clustering and enhanced reinforcement learning with a genetic algorithm. To begin, the nodes are grouped using the K-Medoid model of clustering. The optimal selection of Cluster heads from appropriate nodes is contingent on the neighbourhood overlap, node centrality, and residual energy of the nodes. The fuzzy idea is used to identify a more suitable CH node. The fuzzy if-then mapping rule is used in the fuzzy logic part that generates Cluster heads. Finally, better Reinforcement learning with a Genetic algorithm routing protocol is used to ensure effective data transport. Reinforcement learning is used to determine the quality of a connection in a routing route. Genetic algorithms determine the shortest path between the source and sink nodes. Routing is permitted via the nodes on the identified route. The simulation findings indicate that the suggested system outperforms alternative algorithms currently in use. Additionally, energy consumption is determined using a mobile and fixed sink.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. D. L. Reddy, C. Puttamadappa and H. N. Suresh, “Merged glowworm swarm with ant colony optimization for energy efficient clustering and routing in wireless sensor network,” Pervasive and Mobile Computing, vol. 71, pp. 101338, 2021. [Google Scholar]
2. S. Manikandan, S. Satpathy and S. Das, “An efficient technique for cloud storage using secured de-duplication algorithm,” Journal of Intelligent & Fuzzy Systems, vol. 41, no. 2, pp. 2969–2980, 2021. [Google Scholar]
3. S. Neelakandan, “Social media network owings to disruptions for effective learning,” Procedia Computer Science, vol. 172, no. 5, pp. 145–151, 2020. [Google Scholar]
4. N. Subramani and D. Paulraj, “A gradient boosted decision tree-based sentiment classification of twitter data,” International Journal of Wavelets, Multiresolution and Information Processing, vol. 18, no. 4, pp. 1–21, 2021. [Google Scholar]
5. A. Barzin, A. Sadegheih, H. K. Zare and M. Honarvar, “A hybrid swarm intelligence algorithm for clustering-based routing in wireless sensor networks,” Journal of Circuits, Systems and Computers, vol. 29, no. 10, pp. 2050163, 2020. [Google Scholar]
6. R. K. Yadav and R. P. Mahapatra, “Energy aware optimized clustering for hierarchical routing in wireless sensor network,” Computer Science Review, vol. 41, no. 2, pp. 100417, 2021. [Google Scholar]
7. H. Singh and D. Singh, “Hierarchical clustering and routing protocol to ensure scalability and reliability in large-scale wireless sensor networks,” The Journal of Supercomputing, vol. 77, no. 9, pp. 10165–10183, 2021. [Google Scholar]
8. S. Prithi and S. Sumathi, “Automata based hybrid PSO–GWO algorithm for secured energy efficient optimal routing in wireless sensor network,” Wireless Personal Communications, vol. 117, no. 2, pp. 545–559, 2021. [Google Scholar]
9. P. C. Rao, P. Lalwani, H. Banka and G. Rao, “Competitive swarm optimization based unequal clustering and routing algorithms (CSO-UCRA) for wireless sensor networks,” Multimedia Tools and Applications, vol. 80, no. 17, pp. 26093–26119, 2021. [Google Scholar]
10. D. K. Jain, P. Boyapati and J. Venkatesh, “An intelligent cognitive-inspired computing with big data analytics framework for sentiment analysis and classification,” Information Processing & Management, vol. 59, no. 1, pp. 1–15, 2022. [Google Scholar]
11. C. Ramalingam, “An efficient applications cloud interoperability framework using I-ANFIS,” Symmetry, vol. 13, no. 2, pp. 268, 2021. [Google Scholar]
12. G. B. Loganathan, I. H. Salih, A. Karthikayen, N. S. Kumar and U. Durairaj, “EERP: Intelligent cluster based energy enhanced routing protocol design over wireless sensor network environment,” International Journal of Modern Agriculture, vol. 10, no. 2, pp. 1725–1736, 2021. [Google Scholar]
13. P. Rawat and S. Chauhan, “Probability based cluster routing protocol for wireless sensor network,” Journal of Ambient Intelligence and Humanized Computing, vol. 12, no. 2, pp. 2065–2077, 2021. [Google Scholar]
14. T. Ravichandran, “An efficient resource selection and binding model for job scheduling in grid,” European Journal of Scientific Research, vol. 81, no. 4, pp. 450–458, 2012. [Google Scholar]
15. I. J. Jacob and P. E. Darney, “Artificial bee colony optimization algorithm for enhancing routing in wireless networks,” Journal of Artificial Intelligence, vol. 3, no. 1, pp. 62–71, 2021. [Google Scholar]
16. S. Janakiraman, “An energy proficient clustering inspired routing protocol using improved BKD-tree for enhanced node stability and network lifetime in wireless sensor networks,” International Journal of Communication Systems, vol. 33, no. 16, pp. e4575, 2021. [Google Scholar]
17. S. Neelakandan and D. Paulraj, “An automated exploring and learning model for data prediction using balanced CA-SVM,” Journal of Ambient Intelligence and Humanized Computing, vol. 12, no. 5, pp. 1–12, 2020. [Google Scholar]
18. P. Rawat, S. Chauhan and R. Priyadarshi, “A novel heterogeneous clustering protocol for lifetime maximization of wireless sensor network,” Wireless Personal Communications, vol. 117, no. 2, pp. 825–841, 2021. [Google Scholar]
19. I. E. Agbehadji, R. C. Millham, A. Abayomi, J. J. Jung, S. J. Fong et al., “Clustering algorithm based on nature-inspired approach for energy optimization in heterogeneous wireless sensor network,” Applied Soft Computing, vol. 104, pp. 107171, 2021. [Google Scholar]
20. R. K. Yadav and R. P. Mahapatra, “Hybrid metaheuristic algorithm for optimal cluster head selection in wireless sensor network,” Pervasive and Mobile Computing, vol. 79, pp. 101504, 2022. [Google Scholar]
21. V. Anand and S. Pandey, “New approach of GA–PSO based clustering and routing in wireless sensor networks,” International Journal of Communication Systems, vol. 33, no. 1, pp. e4571, 2020. [Google Scholar]
22. A. Panchal and R. K. Singh, “EHCR-FCM: Energy efficient hierarchical clustering and routing using fuzzy C-means for wireless sensor networks,” Telecommunication Systems, vol. 76, no. 2, pp. 251–263, 2021. [Google Scholar]
23. U. E. Zachariah and L. Kuppusamy, “A hybrid approach to energy efficient clustering and routing in wireless sensor networks,” Evolutionary Intelligence, vol. 15, pp. 493–605, 2022. [Google Scholar]
24. S. M. H. Daneshvar, P. A. A. Mohajer and S. M. Mazinani, “Energy-efficient routing in WSN: A centralized cluster-based approach via grey wolf optimizer,” IEEE Access, vol. 7, pp. 170019–170031, 2019. [Google Scholar]
25. R. Thiagarajan, “Energy consumption and network connectivity based on novel-LEACH-POS protocol networks,” Computer Communications, vol. 149, pp. 90–98, 2020. [Google Scholar]
26. A. Mosavifard and H. Barati, “An energy-aware clustering and two-level routing method in wireless sensor networks,” Computing, vol. 102, no. 7, pp. 1653–1671, 2020. [Google Scholar]
27. C. Pretty Diana Cyril, J. Rene Beulah, N. Subramani, P. Mohan, A. Harshavardhan et al., “An automated learning model for sentiment analysis and data classification of twitter data using balanced CA-SVM,” Concurrent Engineering: Research and Applications, vol. 29, no. 4, pp. 386–395, 2021. [Google Scholar]
28. B. Jaishankar, V. Santosh, S. P. Aditya Kumar, P. Ibrahim and N. Arulkumar, “Blockchain for securing healthcare data using squirrel search optimization algorithm,” Intelligent Automation & Soft Computing, vol. 32, no. 3, pp. 1815–1829, 2022. [Google Scholar]
29. P. V. Rajaram, “Intelligent deep learning based bidirectional long short term memory model for automated reply of e-mail client prototype,” Pattern Recognition Letters, vol. 152, no. 12, pp. 340–347, 2021. [Google Scholar]
30. S. Divyabharathi and S. Rahini, “Large scale optimization to minimize network traffic using MapReduce in big data applications,” in Int. Conf. on Computation of Power, Energy Information and Communication (ICCPEIC), India, pp. 193–199, April 2016. [Google Scholar]
31. K. Khoshraftar and B. Heidari, “A hybrid method based on clustering to improve the reliability of the wireless sensor networks,” Wireless Personal Communications, vol. 113, no. 2, pp. 1029–1049, 2020. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |