Intelligent Automation & Soft Computing DOI:10.32604/iasc.2023.029181
Article

An Optimized Method for Information System Transactions Based on Blockchain

Jazem Mutared Alanazi and Ahmad Ali AlZubi*

Computer Science Department, Community College, King Saud University, Riyadh, Saudi Arabia
*Corresponding Author: Ahmad Ali AlZubi. Email: aalzubi@ksu.edu.sa
Received: 26 February 2022; Accepted: 11 April 2022

Abstract: Accounting Information System (AIS), which is the foundation of any enterprise resource planning (ERP) system, is often built as centralized system. The technologies that allow the Internet-of-Value, which is built on five aspects that are network, algorithms, distributed ledger, transfers, and assets, are based on blockchain. Cryptography and consensus protocols boost the blockchain platform implementation, acting as a deterrent to cyber-attacks and hacks. Blockchain platforms foster innovation among supply chain participants, resulting in ecosystem development. Traditional business processes have been severely disrupted by blockchains since apps and transactions that previously required centralized structures or trusted third-parties to authenticate them may now function in a decentralized manner with the same level of assurance. Because a blockchain split in AIS may easily lead to double-spending attacks, reducing the likelihood of a split has become a very important and difficult research subject. Reduced block relay time between the nodes can minimize the block propagation time of all nodes, resulting in better Bitcoin performance. In this paper, three problems were addressed on transaction and block propagation mechanisms in order to reduce the likelihood of a split. A novel algorithm for blockchain is proposed to reduce the total propagation delay in AIS transactions. Numerical results reveal that, the proposed algorithm performs better and reduce the transaction delay in AIS as compared with existing methods.

Keywords: Information systems; internal control; blockchain; digital transactions

1  Introduction

Blockchain is an innovative application model of computer technologies such as distributed data storage, point-to-point transmission, consensus mechanism, and encryption algorithm in the Internet era. At present, the application of blockchain has been extended to the Internet of Things (IoTs), intelligent manufacturing, supply chain management, digital assets transactions, and many other fields [1]. The blockchain is derived from the underlying technology of Bitcoin. In 2008, a scholar under the pseudonym “Satoshi Nakamoto” proposed a digital currency called Bitcoin. The traditional currency system usually has a unified agency or an authoritative third-party as the central node to handle all transactions, and Bitcoin subverts this design, so that people who do not trust each other can directly use Bitcoin to conduct transactions without any authoritative intermediary coordination. Also, they can pay and maintain a distributed public ledger in the peer-to-peer network using consensus and incentive mechanisms, and the data in the ledger ensures the security and legitimacy through cryptographic algorithms [2–5].

A block is a data structure in Bitcoin used to record and confirm transactions. It is generated by some nodes in the blockchain network called miners, and the process of miners constructing blocks is called mining. A transaction after creation is broadcasted to the whole network, and miners then collect and verify these transactions, and store the legal transaction data in the local transaction pool. After the transaction reaches a certain number, the miners start to construct blocks with these transaction data. After successful mining, the miner will broadcast its constructed block to the whole network. The node that receives the block will verify and confirm the block, add the legal block data to the header, and continue outward propagation. The blockchain consist of many blocks connected end-to-end, and each block records the transaction data of the system for a period of time. When a block b is still being propagated, another conflicting block b′ finds and it is propagated. Thus, a blockchain split will be generated [6]. Among them, block b′ is generated by nodes in the network that do not know block b. Literature [7–8] found that when a blockchain split occurs at the same time, there may be transactions that spend the same bitcoin on blocks of different branches, which is easy for attackers to conduct double-spending.

Reference [9] gives the formula for calculating the blockchain split probability P :

PF≥1=1−(1−Pb)∫0∞⁡(1−f(t))dt (1)

Among them, f(t) is the percentage of nodes that receive the block after the block propagation time t ; F is a discrete random variable used to count the generation of other nodes that have not received the block when a block is being propagated and the number of conflicting blocks; Pb is the probability of mining a block per second, which is uniformly and randomly distributed on all nodes, the faster the block generation speed, the greater the Pb .

Because −Pb>−1 and ∫0∞⁡(1−f(t))dt≥1 , based on Bernoulli’s inequality, Eq. (1) can be enlarged and approximated as [10]

PF≥1≈Pb×∫0∞⁡(1−f(t))dt (2)

Eq. (2) shows that the fork generation probability P is approximately proportional to the block generation probability Pb . The faster the block generation speed, the greater the Pb , the greater the fork generation probability P , and the easier forks to appear. At the same time, the probability of fork generation P is inversely proportional to the speed of block propagation. The faster the block propagation speed, the larger the f(t) , the smaller the probability of fork generation P , and the less likely fork to appear. By reducing the block generation speed or increasing the block propagation speed to reduce the probability of blockchain forks, Bitcoin maintains the stability of the block generation speed by adjusting the difficulty target value, which becomes important for reducing the probability of blockchain forks.

The main contributions of this paper are as follows:

1) The optimal propagation path problem in the blockchain network is formally defined, and based on this, a novel algorithm for the optimal propagation path with low time and message complexities is proposed. By deploying the propagating path from source node has the lowest propagation delay;

2) An incremental update algorithm for the optimal propagation path is proposed when the change of the blockchain network topology leads to the need to delete edges and nodes, and insert them on the generated optimal propagation path. It reduces the required time and message complexities;

3) Examine the requirements that must be met for the incentive function to incentivize all nodes along the created optimum propagation path to propagate transactions and blocks. Define the reward fee sharing function, which is placed in the reasonable distribution of reward fees among all nodes on the propagation path, as the incentive function that meets the requirement. As a result, nodes are encouraged to propagate transactions and blocks so that they can eventually reach the whole network;

4) A method of signing the propagation path is proposed to ensure the security of the propagation path;

5)The time and message complexities of the optimal propagation path generation and maintenance algorithm are theoretically analyzed;

6) The number of messages and the delay of the proposed and existing methods under different network topologies, node scales and node degrees are compared.

2  Literature Review

At present, there are three main types of solutions to the blockchain fork problem. (1) Through the consensus algorithm [10–19], the system finally converges to a stable state with only one blockchain branch after the fork occurs, but this method does not reduce the probability of forking; (2) By specifying a special node to be responsible for the whole process of transaction and block verification and confirmation [20–24], or adding synchronization restrictions to increase the global scope of transaction and block verification and confirmation operations orderly [25], thereby avoiding the occurrence of forks, but reducing the decentralization characteristics of the blockchain network, and the additional synchronization limit will lead to a large synchronization overhead; (3) To reduce the likelihood of splits, optimize the blockchain network’s transaction and block propagation algorithms. The study on lowering the likelihood of forks in blockchain networks by improving block and transaction propagation methods falls into three categories: optimizing blockchain network structure, propagation behaviour of a single node, and pipelining the propagation process.

2.1 Optimization of Blockchain Network Topology

The blockchain network uses a peer-to-peer networking method to connect all nodes together. Each node in the network has equal status and is connected and interacted with each other in a flat topology. There is no central special node and hierarchical structure. It will undertake network routing, verify transactions and blocks, propagate it using the Gossip protocol, and discover new nodes [26]. Each node in the blockchain network randomly select neighbor nodes to establish connections. Thus, the propagation delay between adjacent nodes may be longer. At present, some research works optimize the topology of blockchain networks to speed up the propagation of transactions and blocks.

In order to minimize the number of routing hops between any two nodes, reference [26] connects each node in the network by constructing a star-shaped subgraph used as a central communication hub to reduce the number of nodes sending transactions and blocks and the number of routing hops between other nodes, thereby speeding up the propagation. Reference [27] implemented a connection pool that maintains 4000 open connections, which can connect to each node of the advertised address, and less than 4000 nodes can be reached each time. Therefore, only two routing hops is deployed between any two nodes connected to the central communication hub. Reference [28] proposed a blockchain network based on super nodes (BCBSN) clustering protocol. The goal of this protocol is to cluster based on the locality of nodes. In each cluster, a node is designated as the cluster head. Each common node is only connected to one cluster head node and that is connected to other cluster head nodes, which reduces the number of routing hops through which transactions and blocks are propagated. Experimental results show that the variation ranges of transaction and block propagation delay in BCBSN protocol increases with increasing the number of connected nodes. As the number of hops decreases through which transactions and blocks are propagated, the transaction and block propagation delay in BCBSN protocol increases. The magnitude of change is also reduced. The locality of nodes in the same cluster reduces the propagation delay of transactions and blocks. Reference [29] proposed a location based clustering (LBC) protocol. The goal of LBC protocol is to reduce the distance between adjacent nodes in the blockchain network by clustering nodes according to their locations, thereby reducing the propagation delay of adjacent nodes. The experimental results show that the distance based on the geographical location of nodes better defines the clustering structure, which optimizes the performance of transaction propagation. Compared with the BCBSN protocol, the LBC protocol can more effectively reduce the propagation delay of transactions and blocks, and the variation is smaller than that of the BCBSN protocol. Reference [30] proposed a bitcoin clustering based on ping time (BCBPT). The BCBPT protocol is based on the ping between nodes and deploy latency clusters nodes to reduce the propagation delay of adjacent nodes in a blockchain network. The experimental results show that compared with the LBC protocol, the BCBPT protocol better defines the clustering structure, enabling it to optimize the transactions and block propagation. The fundamental reason for its performance improvement is that the geographically adjacent nodes may be far apart on the physical network, and the use of ping delay can more accurately measure the physical distance between the nodes, thereby reducing the distance between adjacent nodes. The experimental results show that, the smaller the physical distance threshold is set, the smaller the propagation delay of transactions and blocks. Compared with the LBC protocol, the BCBPT protocol can more effectively reduce the propagation delay of transactions and blocks, and has less variation.

2.2 Optimization of Single Node Propagation Behavior

In order to avoid sending transactions and blocks to nodes that have already received from other nodes during the propagation process, the nodes do not directly forward the received transactions and blocks to neighboring nodes. But when they are completed after verification, the directory message-inv (inventory) is first send to the neighbor node to notify the availability of the transaction and block. The forwarding process of transactions and blocks on a single node is shown in Fig. 1. Among them, the inv message contains the set of hash values received and available by sending node A, and the getdata is a requesting message. Once node A completes the difficulty check and the verification of transactions and blocks, the node notifies its availability by sending an inv message to the neighbor node B. If B receives the inv message and finds that the transaction and block does not exist locally, it will send a message to node A using getdata message to request transactions and blocks. Then, node A sends transactions and blocks to node B. Among them, the difficulty check includes the node hashes of received block to verify the proof of work, and the calculated hash value is compared with the current difficulty target value. In this manner, each transaction and block generated is broadcasted from the source node to the entire network. The transactions and blocks are propagated every time they pass through and a node will have a propagation delay. The propagation delay consists of the transmission time, the difficulty checks time, the local verification time, and the block. It includes the transmission time of the inv, getdata, and transaction and block messages. Every transaction in the block needs to be verified when validating.

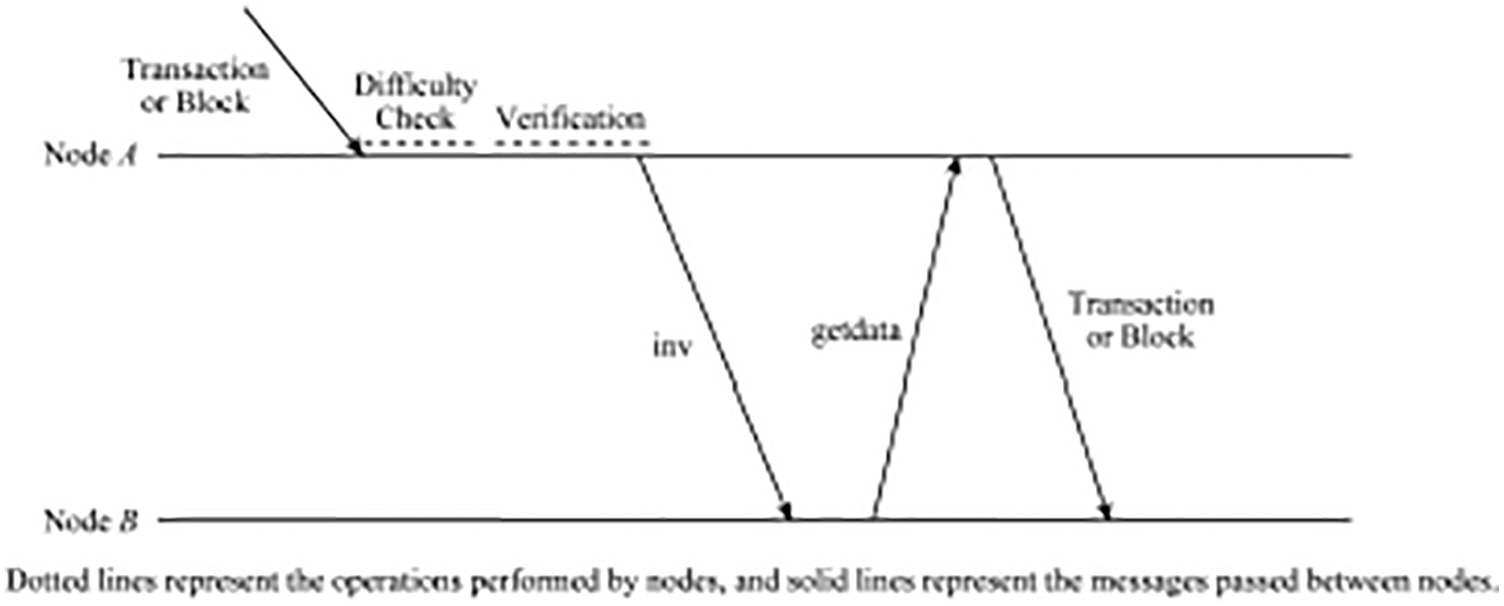
Figure 1: Propagation illustrations of nodes A and B

It can be seen that the main factor that causes the block propagation delay is the time it takes for nodes to verify the block before broadcasting it to the network. The block verification time is closely related to its size. Due to the propagation process, the nodes on each hop need to verify the block before forwarding it to the neighbor nodes. Therefore, the propagation delay is proportional to the length of the propagation path. The block verification process can be divided into two stages such as difficulty checking and block verification. The difficulty checking consist of nodes hash received block to verify the workload and compare the calculated hash value with the current difficulty target value. In addition, the node will also check the received block as the new block is a copy of the recently received old block, and deploys it as its predecessor to prove that the new block is not a resubmission. Therefore, verification is required for every transaction in a block. As long as the difficulty check has been completed, the block or transaction can be forwarded to the neighboring nodes before verification. Therefore, the authors in [31] proposes that the propagation behavior of each node can be changed to once the difficulty check is complete, the node sends an inv message instead of waiting for a longer transaction and block validation to complete before sending the inv message, and before validating the block or transaction, it can be forwarded to the neighboring nodes, as shown in Fig. 2. However, any changes to the propagation behavior of nodes in the network must be censored to reduce the possibility of being abused by attackers to damage the network. In particular, forwarding unverified transactions and blocks may allow an attacker to send any amount of data, which is immediately forwarded to some nodes in the network, resulting in a distributed denial of service (DDoS) attack. However, since generating an illegal block that passes the difficulty check and generating a valid block has equal difficulty, this change in node propagation behavior does not increase the risk of a DDoS. Although, this method accelerates the propagation of each hop along the propagation path, if implemented only on a single node that is not highly connected, the overall impact of propagation delay reduction is less.

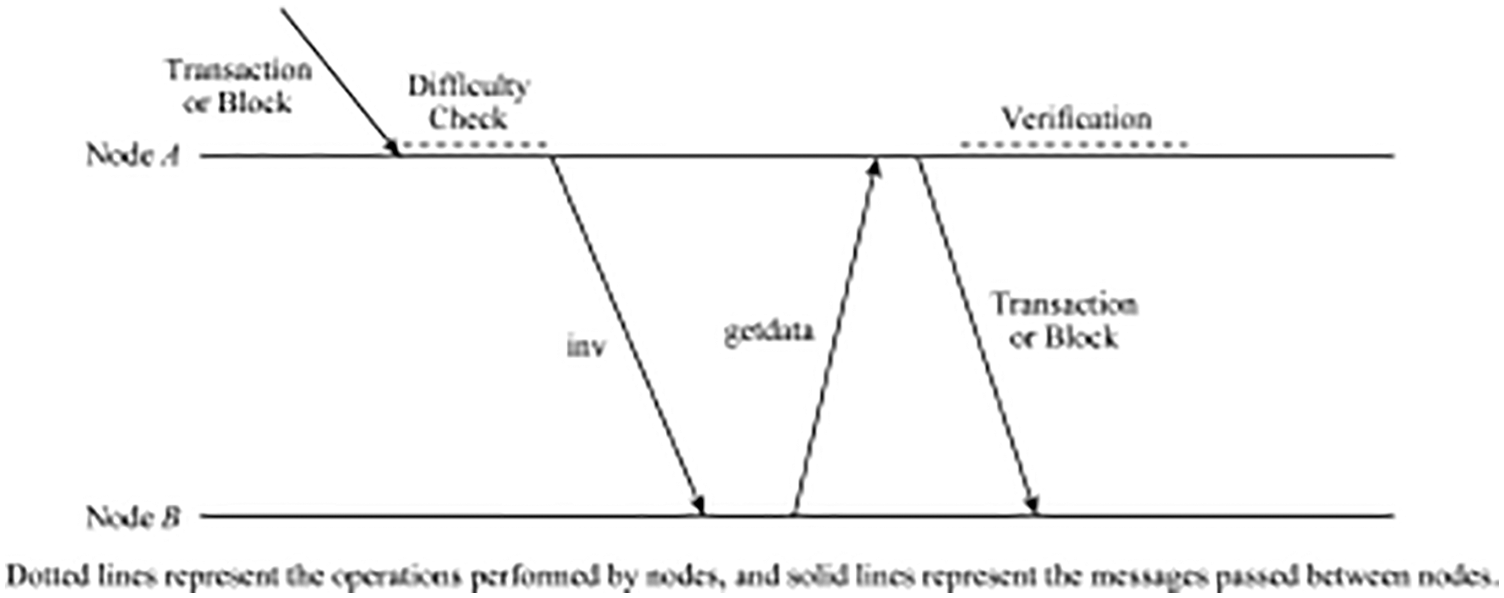
Figure 2: Propagation optimization

2.3 Propagation Pipelining

Reference [9] proposes a method to pipeline the process of block and transaction propagation. That is, once a node receives an inv message, it will immediately forward the message to the neighbor nodes without first difficulty checking and verification. As shown in Fig. 3, after node A receives the inv message, it immediately forwards it to neighbor node B. This method reduces the round-trip time (RTT) between neighbor nodes by announcing the availability of blocks or transactions in advance. The received getdata message will be queued until the block or transaction is received, and after the difficulty check has been completed, it is send to the requesting neighbor node. An attacker may announce any number of blocks or transactions without providing the requested block or transactions. The nodes that receive these spam announcements forward them to neighbors. Once a node detects that a neighbor is announcing a block or transaction that it cannot provide, the node revert to its original behavior after announcing is first validated before a block or transaction. Even though, this method causes nodes to forward inv messages that cannot provide blocks or transactions, since it size is small, it has little effect on the propagation delay. Although, this method speeds up the propagation per hop along the path is eliminated, but if implemented only on a single node that is not well-connected, it will have less effect on the reduction of overall propagation delay.

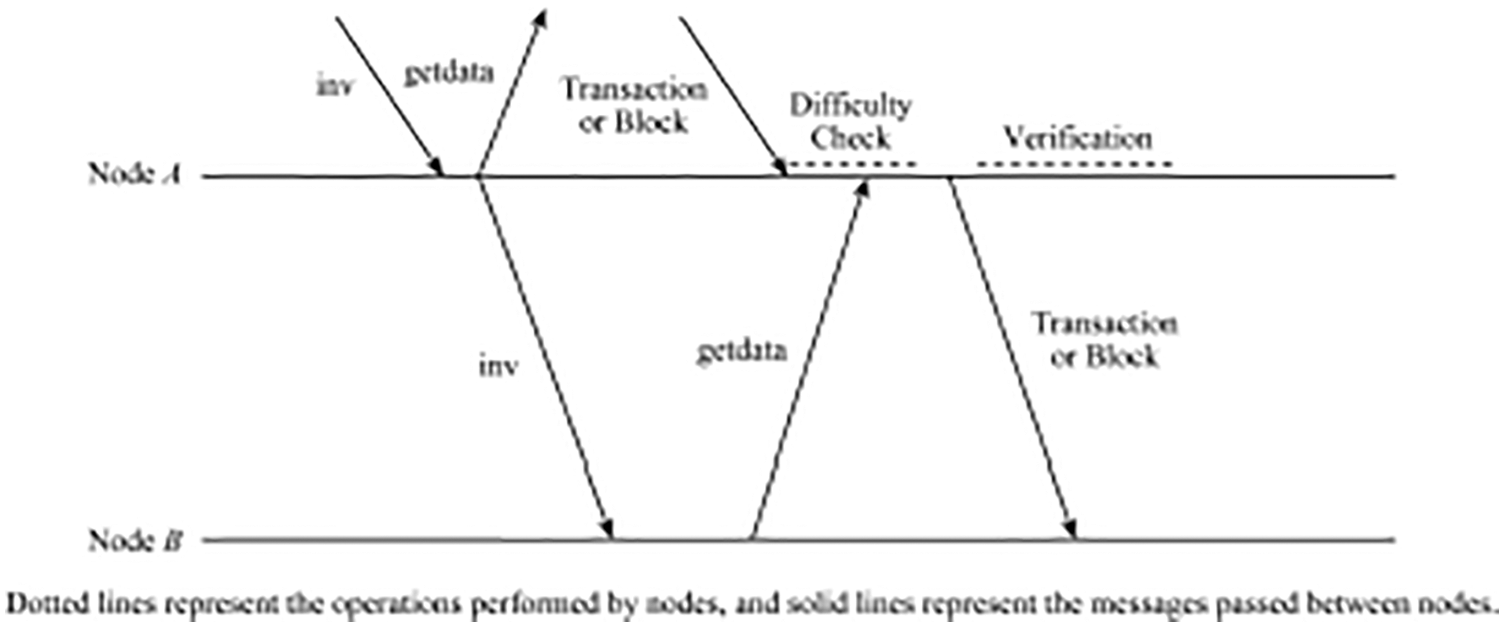
Figure 3: Instantaneous inv pass on process

To sum up, the existing literature have adopted three methods: optimizing the blockchain network topology, optimizing the propagation behavior of a single node, and pipelining the propagation process method to a certain extent. It accelerates the spread of transactions and blocks, but there are still three shortcomings:

1) It reduces the delay or the number of routing hops, but does not necessarily decrease the total propagation delay;

2) The Gossip protocol will cause loops, which will generate a large number of communication messages in the network;

3) Based on the premise that all nodes on the propagation channel will continue to transmit incoming transactions and blocks, some nodes may not decide.

Aiming at these three problems, this paper first generate and maintain the optimal propagation path with the minimum total propagation delay with low time and message complexities, and defines the excitation function that stimulates each node to propagate, so that the transactions and blocks are quickly propagated throughout the network with fewer generation of communication messages.

3  Optimal Propagation Path Incentive

Firstly, the optimal propagation path problem in the blockchain network is formally defined, and based on this, we study how to generate the optimal propagation path in a short time and with a small number of communication messages generated. Make transactions and blocks propagate along this path with the lowest total propagation delay, and study how to incrementally update the optimal propagation path when the blockchain network topology changes, making the required time and message complexities degrees are small. Further, we defined the incentive function that can motivate all nodes on the generated optimal path to flow.

3.1 Definition

When a node in the blockchain network generates a transaction or a block, the transaction and block need to be propagated. To enable them to be quickly propagated to other nodes, it is necessary to construct a starting node from the source node with optimal propagation path which minimizes the total propagation delay. The problem can be formalized as follows. Suppose a graph G=(V,E,W) represents the blockchain network, where V represents the set composed of all nodes, E represents the set of edges established between nodes in the blockchain network, and W represents the set of edge weights. The total number of nodes n=|V| , each edge e=(vi,vj|vi∈V,vj∈V,0≤i≤n−1,) have a weight wϵ , which represents the propagation delay from node vi to vj . The optimal propagation path problem is to find a spanning tree T=(V,E′)|E′⊆E of a graph G , and minimize the total propagation delay, that is, generate minimum spanning tree of graph G as ∑e∈T⁡we .

3.2 Optimal Propagation Path Generation

The communication model between nodes in a blockchain network is assumed to be a synchronous congestion model for distributed communication. Each node v in the graph G=(V,E,W) runs on a single processor, which is based on a synchronous loop O(log⁡n) messages for communication. Assume that all edges have weights of at most a polynomial of n or limit the message size to O(1) times the edge weights or the node identifier size. At the beginning of communication, each node v knows its unique node identifier, denoted by id(v) .

The improved Boruvka algorithm [32] is used to generate the optimal propagation path. After the algorithm is executed, each node v needs to know which edges belong to the minimum spanning tree. Assuming that the minimum spanning tree is unique, the only connected subtree of the minimum spanning tree is called a segment. If for each 1≤i≤h , Fi is a segment, and these segments are disconnected, and ⋃i=1h⁡V(Fi)=V , the set {F1,F2,…,Fh} is the minimum spanning tree forest. For parameters α and β , if the minimum spanning tree forest F contains at most α segments, and the maximum diameter of the segment is β , F can be called a (α,β) forest. Among them, the segment diameter of Fi is the node pair (u,v)|u,v∈V(Fi) , the diameter of the minimum spanning tree forest F is the maximum of the diameters of all its segments. If for each segment Fi∈F in the minimum spanning tree forest F , in the minimum spanning tree forest F′ , there is a fragment in all that contains fragment Fi , namely V(Fi)⊆V(Fi′) and E(Fi)⊆E(Fi′) , then the minimum spanning tree forest F′ is a roughening of the minimum spanning tree forest F . For a rooted tree T and a non-root node v in tree T , denote the parent of node v in tree T by πT(v) . For node v, use Fi′∈F′V(Fi′)E(Fi′),id(v) represents the identifier of node v .

For each fragment Fi , there is a designated root node rt(Fi) , and the identifier id(Fi) of Fi is set to the identifier id of the root node id(rt) . The generation process of the optimal propagation path is:

1) Construct an auxiliary breadth first search (BFS) tree τ for the graph G whose root node is rt . Each base segment Fi∈F has its assigned root node rFi . In the tree τ , each node v of is capable of routing messages from the root node rt of tree τ to the root node rFi of each base segment Fi , where each base segment belongs to a subtree τv of tree τ whose root node is v to compute its interval for each node v∈V(τ) , e.g. for each node pair (u,v) in V if they belong to the tree τ respectively, different branches of their intervals are disjoint. If a node with a longer interval is an ancestor of a node with a shorter interval in the tree τ , then their intervals are nested. Given these intervals, when node v needs to put the message is routed to the root node rFi of the base fragment Fi (where each node ∈V(τv) ), it will find the child node u of node v whose interval I(u) contains I(rFi) , and send the message to node u .

2) Considering the case when D≤n , where D is the diameter of the graph G , let it be assumed that j stages of k=n . The Boruvka algorithm have been executed, which starts from F0 and obtains the rough forest Fj(j=0,1,2,…) , then perform the next stage which is to construct a rough forest Fj+1 of Fj (also a rough forest of F ). Assume that each node v knows the identifier of its base fragment Fv , and that v belongs to identifiers of segments of Fj . For each neighbor u of v , assume that v knows the identifiers of Fv , while the root node rt is assumed to know the identifiers of all base segments, and at stage j(j=0,1,2,…) starts with rt knowing the identifiers of all fragments of Fj , and for each base fragment Fi∈F the root node knows the identifiers of the roughened fragments F^∈Fj . To ensure that the inductive base j=0 holds, after building the base minimum spanning tree forest, each node v updates its neighbor nodes with the identifier of Fv , and also performs the upward direction of |F0|≤n/k identifiers of the base segment on the BFS tree τ transformation. Compute the edge e(u,v) with minimum weight connecting the sum of nodes u∈V(F) on each base segment Fi∈F0 in parallel F^∈Fj fragment to roughen.

3) Send all O(n/k)=O(n) messages on the attached BFS tree τ to the root node rt of the tree τ , which is done through a pipelined convergent broadcast process. Where each intermediate node u of the tree τ sends its parent node πt(u) forwards the edges with the smallest weights on each segment, and these edges are initially stored on a certain node of the node set z of the subtree τu whose root node of the tree τ is u and F^∈Fj .

4) The root node rt calculates its minimum weight output edge locally for each fragment F^∈Fj and calculates the fragment graph locally, whose graph nodes are the fragments of Fj , the edges of the graph are the minimum weight output edges, and calculates the minimum spanning tree forest Fj+1 . For each base fragment Fi∈F , the root node rt knows the identifier of the fragment that roughened the base fragment, and knows that the identifier of the roughened fragment also roughened Fi . The root node rt total of |F| messages are sent on τ , and each message has the form where Fi is also roughened. Each message is appended with a target interval I(rt(Fi)), and along τ only from rt to Fi∈F,F^′∈Fj+1 path of rt(Fi) for routing.

5) The root node rFi of each base fragment Fi∈F broadcasts the identifier of the new (j+1) th layer fragment to all nodes in Fi . At the same time, each node v uses its new identifier id(F^′) of the fragment F^′∈Fj+1 at layer (j+1) updates its neighbors in G .

3.3 Optimal Propagation Path Updating

When the change of the blockchain network topology leads to the need to delete edges and nodes on the generated optimal propagation path, the node label-based update strategy can be deployed. As shown in Fig. 4, when deleting edge e(1,4) , the generated optimal propagation path becomes two different connected components. Labels 1 and 2 are assigned to node 1 and 4, respectively, and then node 1 assigns the connected component to which it belongs. Nodes 2, 3, and 5 are marked as 1, and node 4 marks both nodes 4 and 6 on its own connected components as 2. Run the optimal propagation path generation algorithm on the generated two new connected components, namely a new optimal propagation path can be generated. When multiple edges are deleted, a thread is created for each deleted edge, and the tag-based update algorithm is run separately. When the deleted node v is a leaf node, no update is required. If the deleted node v is a non-leaf node, it assigns different identifiers to its neighbor nodes. These neighbor nodes will initiate a marking process and use their identifiers to mark all nodes in the connected components to which they belong. If the deletion degree is d , the non-leaf node v will generate d different connected components, and run the optimal propagation path generation algorithm on these d connected components to generate a new optimal propagation path.

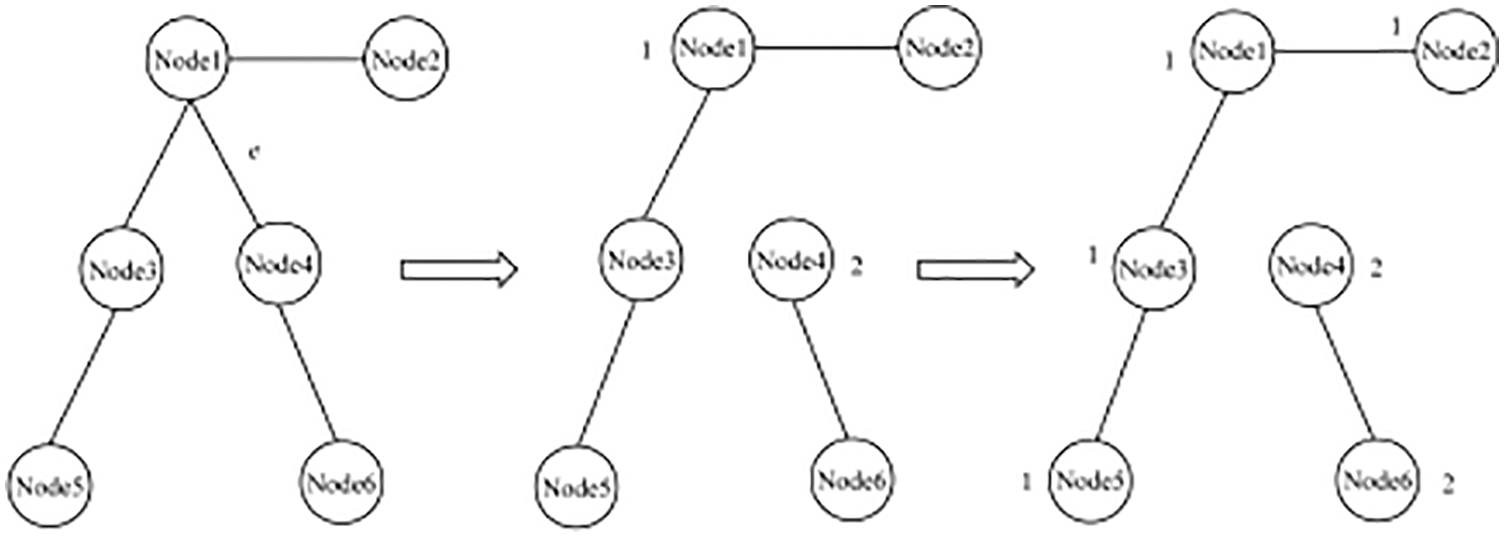
Figure 4: Pictorial illustration of removal of edge

When inserting an edge, we can find the common ancestor with the smallest identifier through the two nodes of the newly inserted edge, and then find the loop generated after the edge is inserted. Then delete the edge with the largest weight in the loop to get the new maximum weight optimal propagation path. As shown in Fig. 5, when inserting e(2,3) , first find the common ancestor of nodes 2 and 3 with the smallest identifier-node 1, and then find the cycle (1, 2, 3), since e(1,2) has the largest weight, after deleting the edge, a new optimal propagation path will be obtained. When a new node is inserted, the new node will be the same as some existing nodes in the blockchain network are connected, so some new edges will be generated. According to the order of the weights of these edges from small to large, the optimal propagation path update algorithm when inserting edges is executed in turn to complete the update when inserting new nodes.

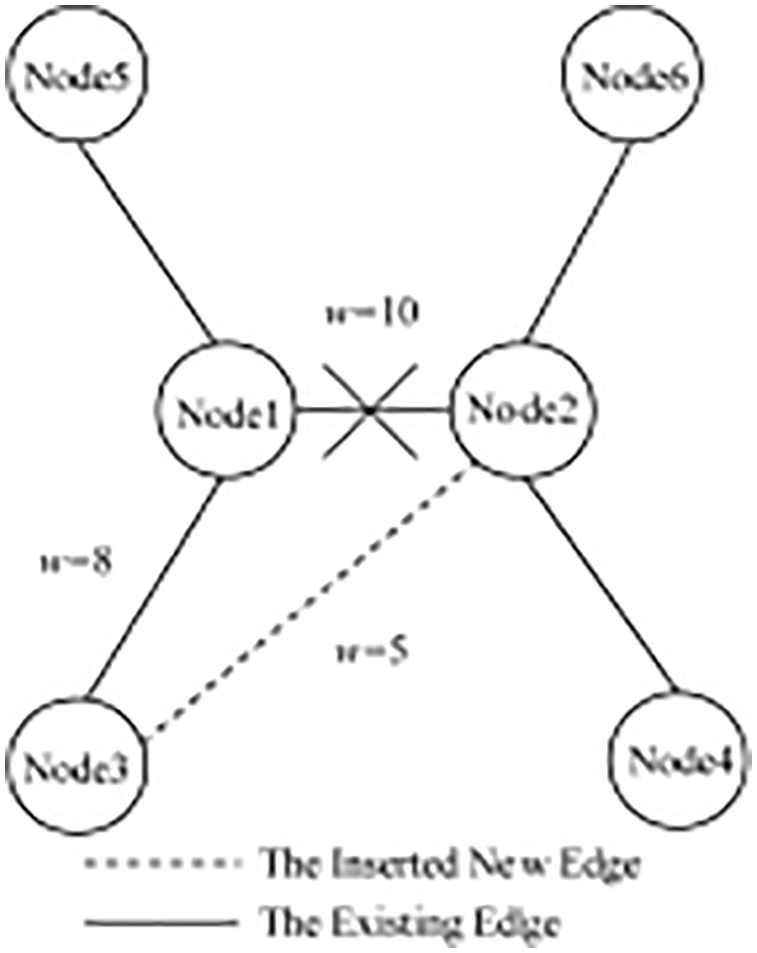
Figure 5: Pictorial illustration of inclusion of edge and update

3.4 Excitation Function

Consider the Sybil verification problem under 1-connected networks and other types of networks. Among them, k-connected network means that removing k −1 nodes will not make the network disconnected. A Sybil node is a fake node with the same neighbor nodes as the original node, it does not increase the network connectivity, nor does it increase the probability of a block owner. In order to not introduce Sybil nodes in a 1-connected network, the reward fee needs to be shared between the first propagation node and the block owner. Namely, makes it impossible to have a Sybil verification incentive mechanism in a 1-connected network. In a 2-connected network, there are multiple paths between any two nodes including the client and block owner nodes, and the nodes introduce Sybil by following the Sybil verification conditions. The Sybil verification condition can be expressed as

∀k≥1,∀s≥1,f[k]k≥∑i=0s⁡f[k+i]k+s (3)

Among them, f[i]k represents the reward fee shared by the i-th node (1≤i≤k) on the propagation path of k , where k represents the reward fee shared by the block owner. The reward fee shared by the Sybil node does not exceed the incentive of the block owner.

Transaction propagation decisions can be understood as simultaneous moves in a game where one party takes action without knowing the strategy of the other party. All nodes are assumed to be rational, and in deciding their respective actions, it is inferred that other parties will also act rationally. Some nodes will cooperate with each other. It is assumed that the neighbors who collude with each other have shared all information and act as a whole, that is, combined into a single node that can be regarded as a Sybil node. Through theoretical analysis, conclusions 1~3 can be obtained. Among them, NKT denotes the set of nodes that already know the transaction T; NKn,T represents the set of nodes that do not know the transaction T yet; NNKn,T represents the set of nodes seen from the perspective of node n that includes the node n itself and already knows the transaction T ; π(ni) represents the probability of node ni becoming the owner of the block, also known as the ability of node ni .

Conclusion 1. The propagation decision of a node has nothing to do with the probability of its neighbor nodes becoming the block owner, but is related to the relative probability that it knows the transaction relative to other nodes, and a rational node will propagate the transaction to all nodes or not to any node.

Conclusion 2. There is a node n∈NKt,NNKn,T≠ϕ , where the distance between n and the client node of transaction T(cT) is k if:

f[k]k+1f[k]k>π(n)π(NKn,T) (4)

That is, the ratio of the reward fee shared by the k-th node on the propagation path of length k + 1 to the reward fee shared by the block owner is greater than the ratio of the ability of node n to the ability of nodes that know transaction T . Then, all neighbors of node n will know that the transaction represents the set of nodes NKn,T that contain node n itself, as seen from node n ’s point of view, and that already know the transaction T .

Conclusion 3. For some constant C∈(0,1) , let f[k]k+1≥C×f[k]k will continue to expand until no more nodes NKT have n∈NKT neighbors in NNKT and the π(n)<C×π(NKn,T) fixed conditions f[k]k+1≥C×f[k]k are satisfied to support the block owner, we get:

∀k,f[k]k+1=C×f[k]k (5)

Eq. (5) shows that the reward fee shared by the k-th node on the propagation path of length k + 1 is a constant multiple of the reward fee shared by the block owner.

From conclusion 1, the probability of a neighbor node becoming a block owner does not have any effect on the decision of node’s propagation. Unless the reward fee received is reduced, which is caused by later actions such as increasing the path length, conclusion 1 will be satisfied. If the reward fee shared by the propagating node does not increase with the length of the path, then the propagating node will not be affected by any subsequent actions, which can be expressed as:

∀i<k,f[i]k≥f[i]k+1 (6)

Based on the above analysis, it can be concluded that an ideal incentive fee sharing function should satisfy the necessary conditions as follows:

1) The introduction of Sybil nodes into the network will not have any beneficial effect on the nodes on the propagation path;

2) There should be enough incentives for rational nodes to be willing to propagate transactions and blocks, and make transactions and blocks eventually reach the entire network.

Based on these two necessary conditions and Eqs. (3)–(6), it can be deduced that in an n-connected ( n≥2 ) network, if the total reward fee F is based on:

f[i]k={F×C(1−C)i−1,1≤i<kF×(1−C)k−1,i=k (7)

For sharing, each rational node whose probability of becoming a block owner is less than C will be motivated to propagate transactions and blocks without introducing Sybil nodes. The reward fee sharing function defined by Eq. (7) combines any transaction and total reward fee F generated by the block is allocated to k nodes on the propagation path. Among them, k is the length of the propagation path, that is, a total of k nodes participate in the verification and propagation of transactions and blocks. The total reward fee F includes verifying transactions, blocks, and propagating transactions and blocks. f[i]k represents the reward fee shared by node on the i(1≤i<k) propagation path; f[k]k represents the reward fee shared by the block owner, and satisfies ∑i=1k⁡f[i]k=F with a constant C chosen based on network connectivity.

4  Safety Assurance of Propagation Path

The optimal propagation path can be signed to ensure the security of the propagation path. M is used to represent the propagated transaction or block message. When node u propagates message M to node v , node u will get the corresponding reward and must first be ensured that node v cannot deny the fact that it received message M from node u . If node u only signs message M , node v can create a fake node w to sign message M once it receives the message, and declare that message M was sent from node w to node v . If node u encrypts message M , node v that receives message M cannot verify its authenticity. Thus, on each hop of the propagation path, based on the sending node’s private key signs the message M , the public key of the receiving node, and the reward fee x to be shared. Use u.pk and u.sk represent the public and secret keys of node u respectively, and the representations of the public and private keys of node v and node p are similar.

The way to sign the propagation path is shown in Fig. 6. Node p is the generating node of message M . Before node p forwards message M to node u , it first asks node u for its public key u.pk . Next, the message M , the public key u of the node u.pk and propagation cost x , that is, the reward fee x required by node p to share, use the private key p of node p.sk to sign. Finally, node p will sign the message Mp→u=(M,u.pk,x) is sent to node u . The message is passed to the public key of node u.pk is signed to be sent exclusively to node u , other nodes cannot receive it. Node u can only continue to propagate the received signed message Mp→u , but not the original message M . Assuming that node u continues to propagate the signed message Mp→u to node v , node u transmits the message Mp→u , and the public key v of node v . The reward fee x′ required to be shared by v.pk and node v , using the private key node u.sk to sign, the signed message is Mp→u→v=(Mp→u,v.pk,x′) . Only node v can receive the message, and can continue to propagate the message Mp→u→v to other nodes, and the process is similar to the process described by the message Mp→u . If there is no further propagation after propagation from node p to node v , and the total reward cost for propagating message M is 1. Then, the reward fee shared by node p is x , the reward fee shared by node u is x′ , and the reward fee shared by node v is 1−x−x′ .

Figure 6: Message transaction procedure

The propagation path is said to be safe if and only if the message M to be propagated starts to propagate from the source node p that generated it, and the sending node of each hop in the propagation process is the receiving node of the previous hop. The above method of signing the propagation path ensures that the sending node of each hop in the propagation process is the receiving node of the previous hop, thus ensuring the security of the propagation path.

5  Theoretical Analysis of Algorithms

5.1 Complexity Analysis of Optimal Propagation Path Generation Algorithm

In the proposed algorithm, the time complexity of each node v updating its neighbor nodes with the identifier of Fv is O(1) . The time complexity of the upward transition process is O(D+n/k) , and on each base segment Fi∈F0 , the connection nodes u∈V(F) and v∈V∖V(F^) are computed in parallel with the minimum time complexity of the process of the weighted edge e(u,v) is O(k) , sending all O(nk)=O(n) messages on the attached BFS tree τ to the root node of the tree τ . The time complexity of the pipelined broadcast process on rt is O(D+|Fj|) , and the time complexity of the process of locally computing the fragment graph is O(D+|F|) . The root of each base fragment Fi∈F process of node r(Fi) broadcasting the identifier id(F^′) of the new ( j+1 )-th layer fragment F^′∈Fj+1 to all nodes in Fi has a time complexity of O(k) , and each node v uses the time complexity of the process of updating its neighbor nodes in G with the identifier of its new (j+1) -th layer fragment is O(1) . For each j = 0, 1, 2, …, there is |Fj+1|≤12×|Fj| . Among them, Fj+1 and Fj are rough forests, and the number of stages l=O(log⁡n) . Therefore, its time complexity is

O(D+n/k)+O(k×log⁡n)+O((D+k+|F|×log⁡n))=O((D+k+nk)×log∗n)=O(n×log⁡n) (8)

The message complexity of constructing the minimum spanning tree forest F is O(|E|log⁡n+nlog⁡n×log∗n) , the message complexity of the calculation interval is O(D×nk+n) , and the message complexity of each subsequent stage is O(D×nk+|E|+n) . When D≤k , the total message complexity is O(|E|log⁡n+nlog⁡n×log∗n) . For D>n , when the parameter k=D , the time required to calculate (nk,O(k)) for the minimum spanning tree forest F=F0 is O(D×log∗n) , and the total number of messages generated is O(|E|log⁡n+nlog⁡n×log∗n) . For each j=0,1,2,…, the time required for the j th stage of the algorithm is O(D+k+|F|)=O(D+k+n/k)=O(D) , that is, the total time required for all stages is O(Dlog⁡n) . Therefore, the time complexity of the proposed algorithm is O((D+n)×log⁡n) . Since the number of messages generated in each stage is O(|E|+n+D×|F|) , that is, all l stages generate messages O((|E|+n)×log⁡n) , therefore, the message complexity of the proposed algorithm is O(|E|log⁡n+nlog⁡n×log∗n) .

5.2 Complexity Analysis of Optimal Propagation Path Maintenance Algorithm

When deleting edges and non-leaf nodes, the maintenance process includes the node labeling process and the process of regenerating the optimal propagation path. Each connected branch executes the labeling process in parallel. Among them, the time complexity of each connected branch labeling process is O(log⁡n) , and the time complexity of the optimal path generation algorithm is O((D+n)×log⁡n) . Therefore, when deleting edges and non-leaf nodes, the time complexity of the maintenance algorithm is O((D+n+1)×log⁡n) . The message complexity of the node labeling process is O(n) , and the message complexity of the optimal path generation algorithm is O(|E|log⁡n+nlog⁡n×log∗n) . Therefore, when deleting edges and non-leaf nodes, the maintenance algorithm message complexity is O(|E|log⁡n+nlog⁡n×log∗n+n) .

When inserting an edge, the time complexity and message complexity of the inserted edge are both O(1) . The time complexity and message complexity of the edge with the largest weight on the loop are both O(1) . Therefore, the time complexity and message complexity of the optimal propagation path maintenance algorithm when inserting edges are both O(log⁡n) . The process of inserting a node is equivalent to the process of inserting multiple edges. Therefore, the time complexity and message complexity of the maintenance algorithm when inserting a node are both O(log⁡n) .

6  Experiments and Results

6.1 Configuration

Peersim-1.0.5 [33] is used to generate three different blockchain network topologies: random graph, scale-free network graph based on Barabasi-Albert model, and small-world network graph based on Watts-Strogatz. Based on the event-driven method, the propagation mechanism based on the Gossip protocol in the blockchain network and the proposed optimal propagation path and incentive (OPPI) propagation mechanism are simulated. The number of nodes n is set to 10, 100, 1000, 10000 respectively. The propagation delay between nodes is set to an integer in the interval [1,100] that conforms to a uniform random distribution. The number of nodes are set to 2~8. The probability β of node reconnection in the small-world model graph is set to 0.8. The propagation efficiency is measured by the propagation delay spent.

6.2 Results

In order to make the experimental results look more intuitive, we take the logarithm of 10 for the number of communication messages and the propagation delay, respectively. Each experiment was performed 10 times respectively, and the average value of the 10 times was taken as the experimental result.

6.2.1 Number of Communication News

In order to observe the influence of the number of nodes on the number of messages, Figs. 7–9 compare the number of communication messages between Gossip and OPPI under different numbers of nodes when the network topology is different.

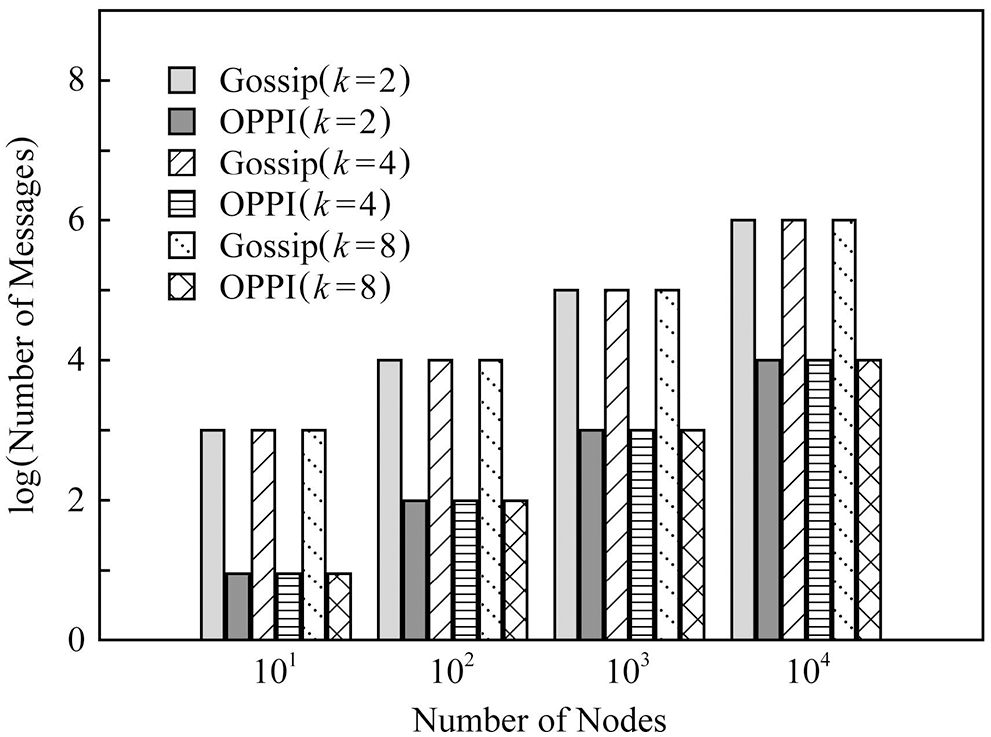
Figure 7: Evaluation of the proposed and existing algorithms under random graph

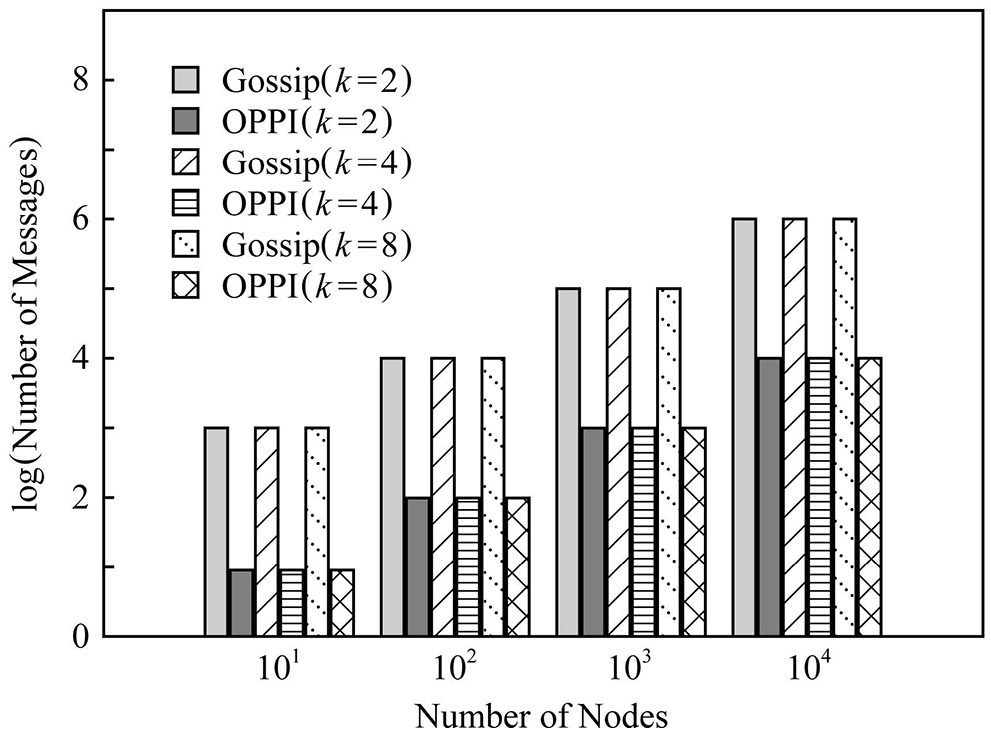
Figure 8: Evaluation of the proposed and existing algorithms under scale-free graph

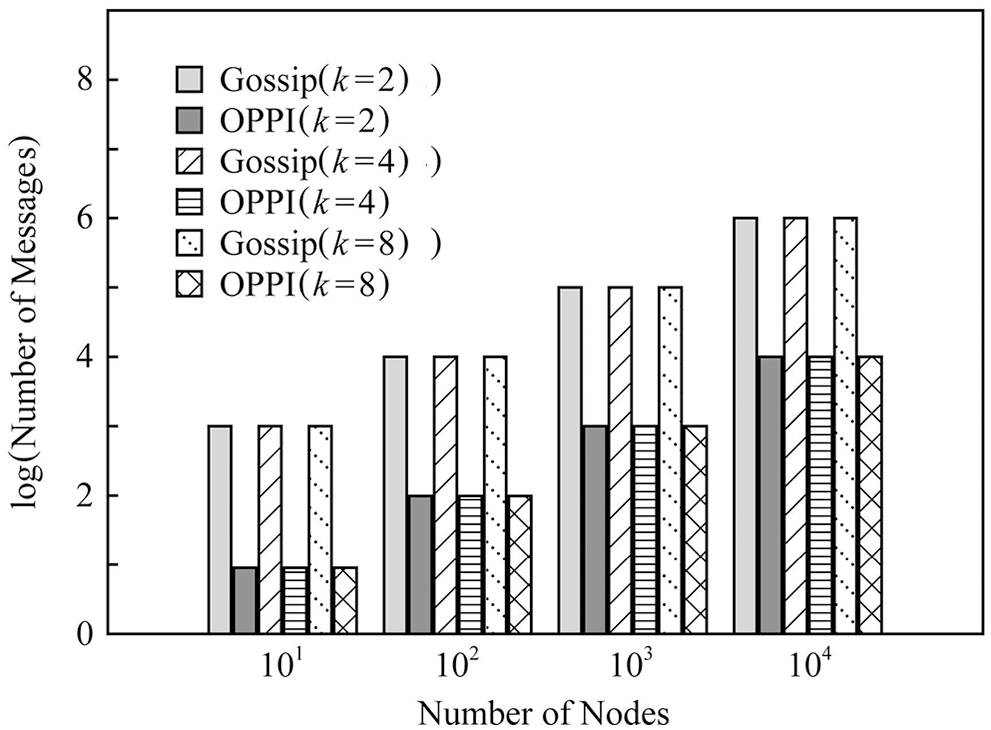
Figure 9: Evaluation of the proposed and existing algorithms under small-world graph

In order to observe the influence of node degree k on the number of messages, Fig. 10 compares the number of messages of Gossip and OPPI under different node degrees’ k when the number of nodes is 1000. In order to observe the influence of network topology on the number of messages, Fig. 11 compares the number of messages of Gossip and OPPI under different network topologies when the number of nodes is 1000.

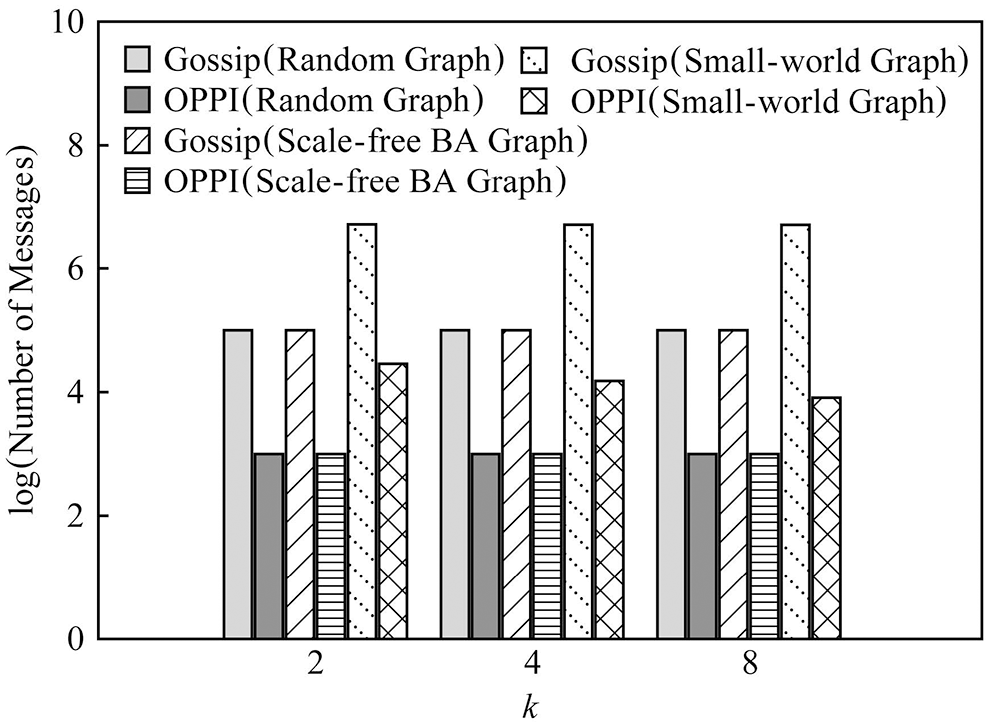
Figure 10: Evaluation of algorithms under different value of k and 1000 nodes

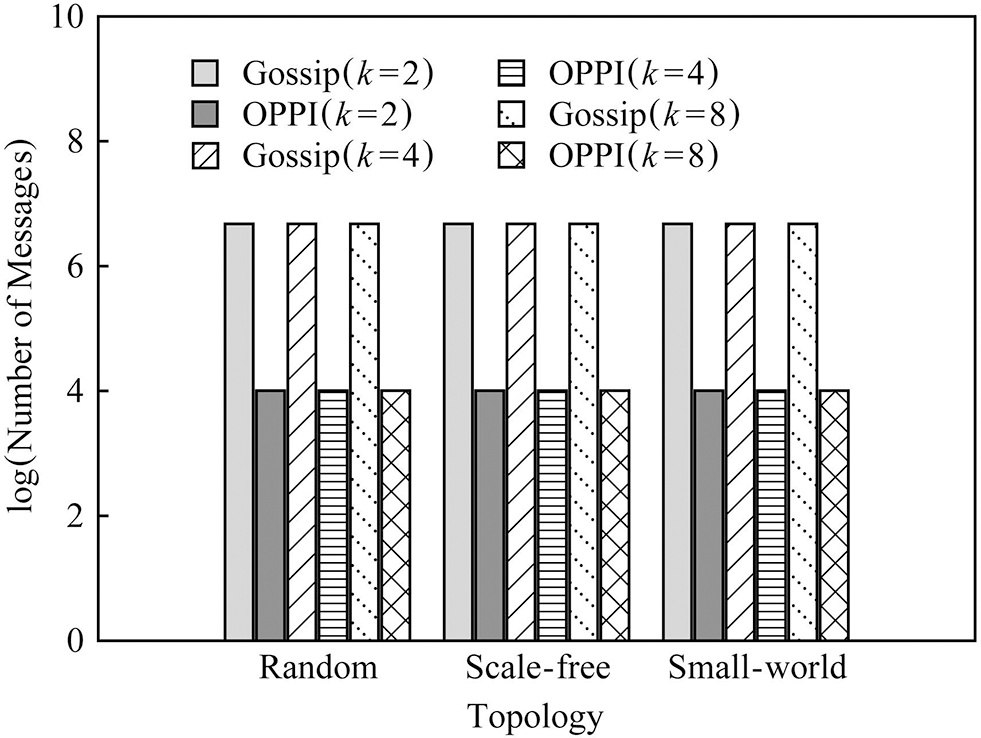
Figure 11: Messages comparison of the algorithms under different topology and 1000 nodes

The experimental results show that the number of messages generated by the propagation mechanism based on Gossip and the propagation mechanism based on OPPI increases approximately linearly with the increase of the number of nodes. The change of node degree k and network topology has almost no effect on the number of messages generated by these two propagation mechanisms. When the number of nodes, node degree k and network topology are the same, compared with the Gossip-based propagation mechanism, the proposed method reduces the number of messages by 99%~99.1%. This is because, in the Gossip protocol, the node will periodically randomly select neighbor nodes to forward the message, and the node that receives the message will also repeat this step, so it is inevitable that the message will be repeatedly sent to the same node, resulting in redundant messages. Moreover, since it is sent regularly, even the node that receives the message will receive repeated messages repeatedly, which aggravates the redundancy of the message. The number of messages generated by OPPI is O(n) , while the number of messages generated by Gossip is O(n2) . Therefore, compared with OPPI, the propagation mechanism based on Gossip will generate a large number of communication messages in the network.

6.2.2 Propagation Delay

In order to observe the effect of the number of nodes on the propagation delay, Figs. 12–14 compare the propagation delays of Gossip and OPPI under different numbers of nodes with different configurations

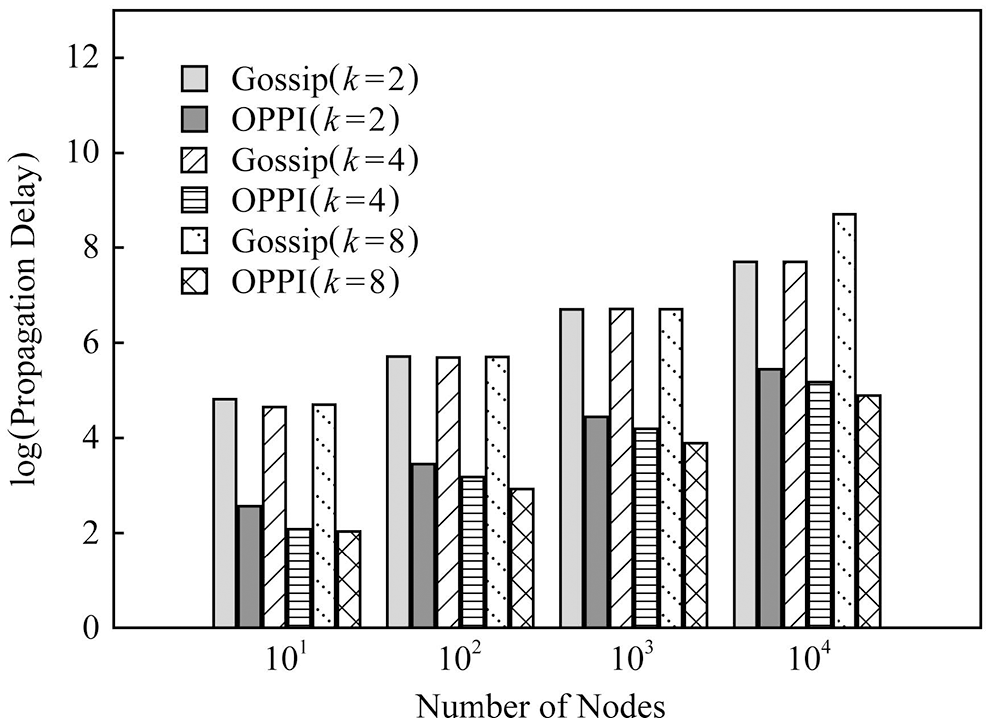
Figure 12: Random graph evaluation of delay

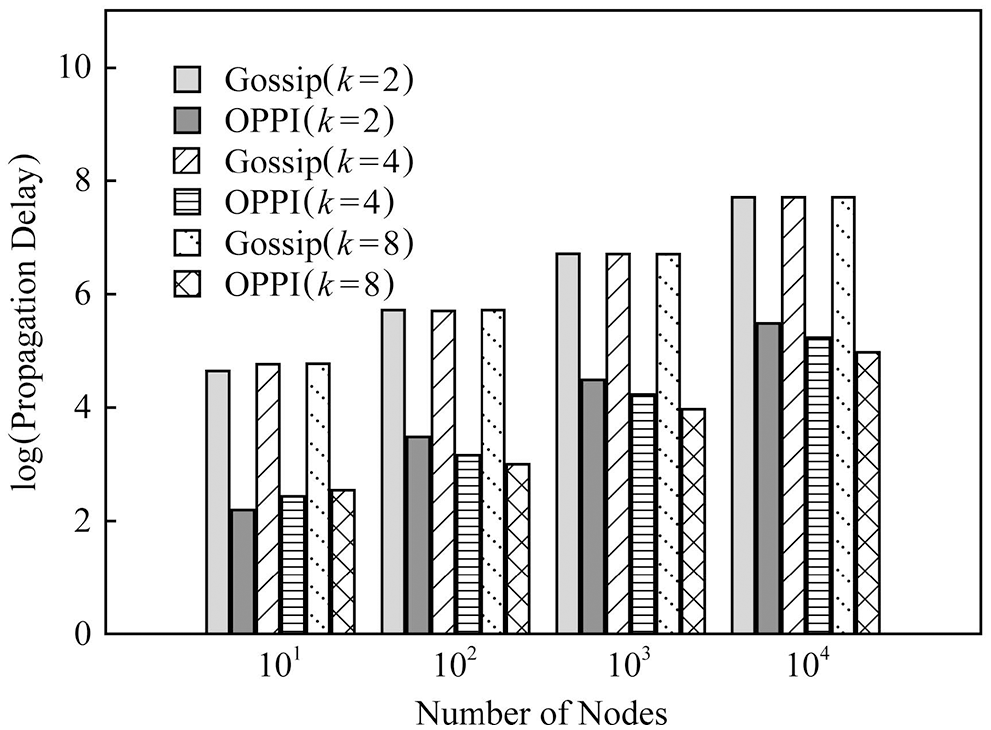
Figure 13: Scale-free graph evaluation of delay

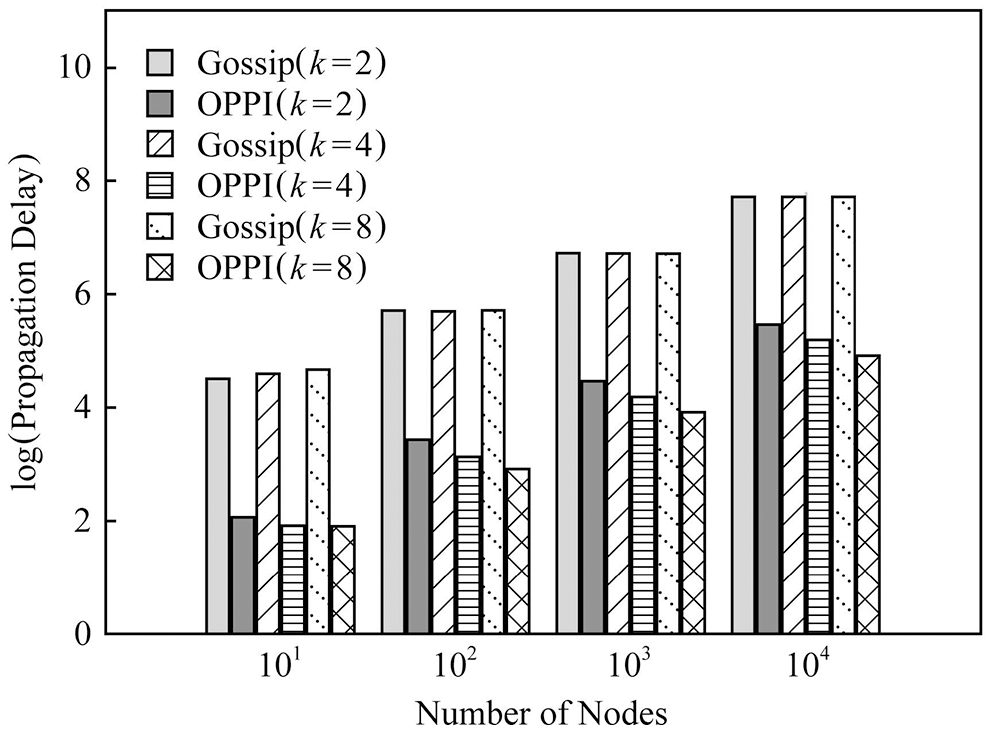
Figure 14: Small-world graph evaluation of delay

In order to observe the influence of node degree k on propagation delay, Fig. 15 compares the number of messages of Gossip and OPPI under different node degrees’ k when the number of nodes is 1000. In order to observe the influence of the network topology on the propagation delay, Fig. 16 compares the propagation delays of Gossip and OPPI under different network topologies when the number of nodes is 1000.

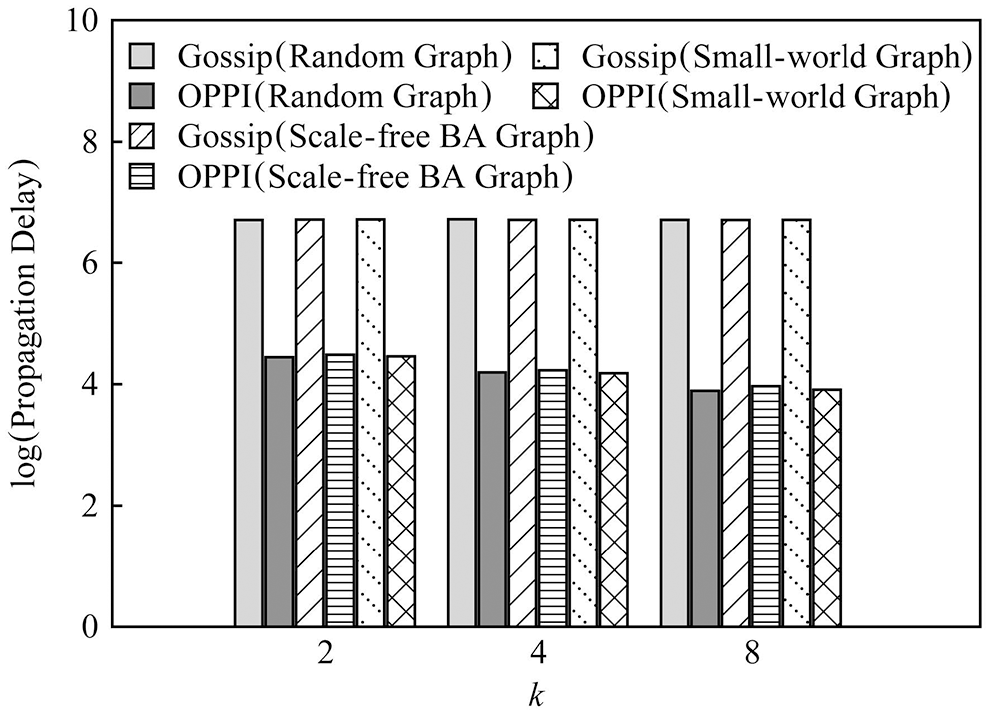
Figure 15: Delay evaluation under different k value and 1000 nodes

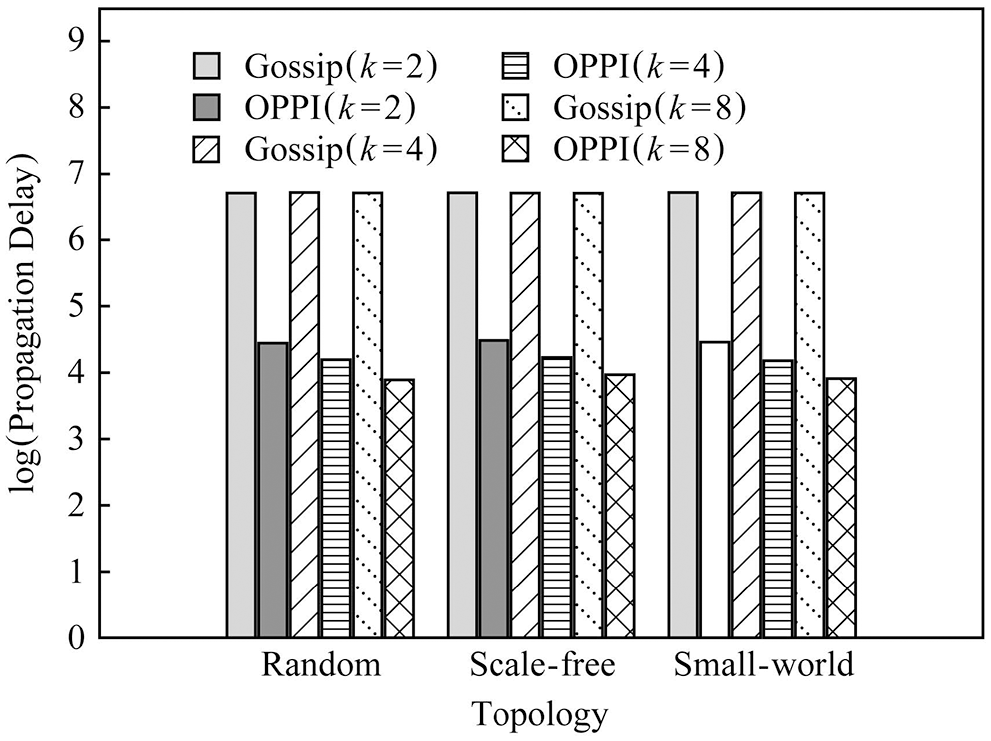
Figure 16: Delay evaluation under different topology value and 1000 nodes

The experimental results show that: with the increase of the number of nodes, the propagation delay of Gossip and OPPI increases approximately linearly. Changes in node degree k and network topology have little effect on the propagation delay of Gossip and OPPI. When the number of nodes, the node degree k and the network topology are the same, the propagation delay of OPPI is reduced by 99.4%~99.98% with respect to the traditional Gossip. This is because, the propagation delay of Gossip and OPPI is only related to the number of nodes, and transactions and blocks in OPPI are propagated along the propagation path with the smallest propagation delay, while Gossip randomly selects neighbor nodes to forward and generate loop, which increases the propagation delay.

The above experimental results show that the number of messages and propagation delay of Gossip and OPPI are closely related to the number of nodes. Compared with Gossip, the proposed algorithm has a significant effect on reducing the number of communication messages and propagation delay. A good balance has been achieved.

7  Conclusion

This paper first analyzes the quantitative relationship between the propagation speed of blocks in the blockchain and the probability of split. This paper analyzes and summarizes three problems existing in the existing research:

1) It only reduces the propagation delay or the number of routing hops between adjacent nodes, but does not reduce the total propagation delay;

2) The dissemination method creates a huge number of information messages;

3) It is assumed that there is continuous number of nodes in during transactions.

Aiming at these problems, an optimal algorithm in blockchain network is proposed. The experimental results indicate that, the proposed algorithm greatly reduces the number of messages and propagation delay as compared with existing algorithms. Among them, compared with Gossip, the number of messages of the proposed algorithm is reduced by 99%~99.1%, and the propagation delay is reduced by 99.4%~99.98%. The next step is to simulate the situation where some nodes on are unwilling to continue to flow the received transactions and evaluate the propagation coverage. The number of messages, delay and coverage of will be evaluated on real blockchain network.

Acknowledgement: The authors extend their appreciation to King Saud University for funding this work through the Researchers Supporting Project (No. RSP-2021/395), King Saud University, Riyadh, Saudi Arabia.

Funding Statement: This work was supported by the Researchers Supporting Project (No. RSP-2021/395), King Saud University, Riyadh, Saudi Arabia.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  F. Casino, T. Dasaklis and C. Patsakis, “A systematic literature review of blockchain-based applications: current status, classification and open issues,” Telematics and Informatics, vol. 36, no. 3, pp. 55–81, 2019. [Google Scholar]

 2.  A. Partida, S. Gerassis, R. Criado, M. Romance, E. Giraldez et al., “Modeling bitcoin plus ethereum as an open system of systems of public blockchain to improve their resilience against intentional risk,” Electronics Journal, vol. 11, no. 2, pp. 1–18, 2022. [Google Scholar]

 3.  T. A. Syed, A. Alzahrani, S. Jan, M. Siddiqui, A. Nadeem et al., “A comprehensive analysis of blockchain architecture and its applications: Problems and recommendations,” IEEE Access, vol. 7, pp. 176838–176869, 2019. [Google Scholar]

 4.  P. Shi, H. Wang, S. Yang, C. Chen and W. Yang, “Blockchain-based trusted data sharing among trusted stakeholders in IoT,” Journal of Software: Practice and Experience, vol. 51, no. 10, pp. 2051–2064, 2021. [Google Scholar]

 5.  D. Khan, L. Jung and M. Hashmani, “Systematic literature review of challenges in blockchain scalability,” Applied Sciences, vol. 11, no. 20, pp. 1–28, 2021. [Google Scholar]

 6.  G. Sladic, B. Milosavljevic, S. Nikolic, D. Sladic and A. Radulovic, “A blockchain solution for securing real property transactions: A case study of serbia,” International Journal of Geo-Information, vol. 10, no. 1, pp. 1–14, 2021. [Google Scholar]

 7.  T. Kuo, H. Kim and L. Machado, “Blockchain distributed ledger technologies for biomedical and health care applications,” Journal of the American Medical Informatics Association, vol. 24, no. 6, pp. 1211–1220, 2017. [Google Scholar]

 8.  N. Akbar, A. Muneer, N. Elhakim and S. Fati, “Distributed hybrid double-spending attack prevention mechanism for proof-of-work and proof-of-stake blockchain consensuses,” Future Internet Journal, vol. 13, no. 11, pp. 1–17, 2021. [Google Scholar]

 9.  J. Riposo, “Diffusion on the peer-to-peer network,” Journal of Risk and Financial Management, vol. 15, no. 2, pp. 1–15, 2022. [Google Scholar]

10. S. Idrees, M. Nowostawski, R. Jameel and A. Mourya, “Security aspects of blockchain technology intended for industrial applications,” Electronics Journal, vol. 10, no. 8, pp. 1–24, 2021. [Google Scholar]

11. S. Yonatana and Z. Aviv, “Bitcoin’s underlying incentives,” Communications of the ACM, vol. 61, no. 3, pp. 46–53, 2018. [Google Scholar]

12. V. Gramoli, “From blockchain consensus back to byzantine consensus,” Future Generation Computer Systems, vol. 107, no. 3, pp. 760–769, 2020. [Google Scholar]

13. D. Oyinloye, J. The, N. Jamil and M. Alawida, “Blockchain consensus: An overview of alternative protocols,” Symmetry Journal, vol. 13, no. 8, pp. 1–33, 2021. [Google Scholar]

14. Y. Fan, H. Wu and H. Paik, “DR-BFT: A consensus algorithm for blockchain-based multi-layer data integrity framework in dynamic edge computing system,” Future Generation Computer Systems, vol. 124, no. 8, pp. 33–48, 2021. [Google Scholar]

15. S. Zhang and H. Lee, “Analysis of the main consensus protocols of blockchain,” ICT Express, vol. 6, no. 2, pp. 93–97, 2020. [Google Scholar]

16. J. Hedman, T. Beaulieu and M. Karlstrom, “The tales of alphanumerical symbols in media: The case of bitcoin,” Journal of Theoretical and Applied Electronic Commerce Research, vol. 16, no. 7, pp. 1–19, 2021. [Google Scholar]

17. F. Franzoni, Z. Salleras and V. Daza, “AToM: Active topology monitoring for the bitcoin peer-to-peer network,” Peer-to-Peer Networking and Applications, vol. 15, no. 1, pp. 408–425, 2022. [Google Scholar]

18. S. Kushch, Y. Baryshev and S. Ranise, “Blockchain tree as solution for distributed storage of personal id data and document access control,” Sensors Journal, vol. 20, no. 13, pp. 1–28, 2020. [Google Scholar]

19. G. Karame, E. Androulaki and M. Roeschlin, “Misbehavior in bitcoin: A study of double-spending and accountability,” ACM Transactions on Information and Systems Security, vol. 18, no. 1, pp. 1–32, 2015. [Google Scholar]

20. A. A. AlZubi, “A new method oriented approach for forming multipath routing in cloud computing structure to accessing the protein folding information,” Journal of Medical Imaging and Health Informatics, vol. 8, no. 4, pp. 801–804, 2018. [Google Scholar]

21. A. Fornes, S. Hassan and J. Pavon, “Peer-to-peer system design trade-offs: a framework exploring the balance between blockchain and IPFS,” Applied Sciences, vol. 11, no. 21, pp. 1–28, 2021. [Google Scholar]

22. T. Wang, X. Bai, H. Wang, S. Liew and S. Zhang, “Game-theoretical analysis of mining strategy for bitcoin-ng blockchain protocol,” IEEE Systems Journal, vol. 15, no. 2, pp. 2708–2719, 2021. [Google Scholar]

23. K. Christodoulou, E. Losif, A. Inglezakis and M. Themistocleous, “Consensus crash testing: Exploring ripple’s decentralization degree in adversial environments,” Future Internet Journal, vol. 12, no. 3, pp. 1–16, 2020. [Google Scholar]

24. A. Emmanuelle, L. Thibaut and L. Romaric, “Safety analysis of bitcoin improvement protocols,” in IEEE 15th Int. Symp. on Network Computing and Applications, Washington DC, USA, pp. 318–325, 2016. [Google Scholar]

25. L. Thibaut, L. Romaric and A. Emmanuelle, “Handling bitcoin conflicts through a glimpse of structure,” in ACM Symp. on Applied Computing, New York, USA, pp. 444–449, 2017. [Google Scholar]

26. S. Boyd, A. Ghosh and B. Prabhakar, “Randomized gossip algorithms,” IEEE Transactions on Information Theory, vol. 52, no. 6, pp. 2508–2530, 2006. [Google Scholar]

27. A. A. AlZubi, “Identification of information systems threats sources: an analytical study,” Computer Networks and Internet Research Journal, vol. 10, no. 1, pp. 31–37, 2010. [Google Scholar]

28. F. Muntadher, O. Gareth and A. Mo, “A bitcoin model for evaluation of clustering to improve propagation delay in bitcoin network,” in IEEE Int. Conf. on Computational Science and Engineering, Ottawa, Canada, pp. 468–475, 2016. [Google Scholar]

29. F. Muntadher, O. Gareth and A. Mo, “Locality based approach to improve propagation delay on the bitcoin peer-to-peer network,” in IEEE Int. Symp. on Integrated Network Management, Los Angeles, USA, pp. 556–559, 2017. [Google Scholar]

30. F. Mutadher, O. Gareth and A. Mo, “Proximity awareness approach to enhance propagation delay on the bitcoin peer-to-peer network,” in IEEE 37th Int. Conf. on Distributed Computing Systems, Glasgow, UK, pp. 2411–2416, 2017. [Google Scholar]

31. P. Franti, T. Nenonen and M. Yuan, “Converting MST to TSP path by branch elimination,” Applied Sciences Journal, vol. 11, no. 1, pp. 1–15, 2021. [Google Scholar]

32. M. Chakraborty, S. Chowdhury, K. Chakraborty, R. Mehera and R. Pal, “Algorithms for generating all possible spanning trees of a simple undirected connected graph: An extensive review,” Complex and Intelligent Systems, vol. 5, no. 3, pp. 265–281, 2019. [Google Scholar]

33. I. Kazmi and S. Bukhari, “PeerSim: An efficient & scalable testbed for heterogeneous cluster-based P2P network protocols,” in IEEE UkSim 13th Int. Conf. on Computer Modeling and Simulation, Cambridge, UK, pp. 972–978, 2011. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.