DOI:10.32604/iasc.2023.029119

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2023.029119 |  |
| Article |
Abnormal Crowd Behavior Detection Using Optimized Pyramidal Lucas-Kanade Technique
1Department of Information Technology, Mepco Schlenk Engineering College, Sivakasi, 626005, India
2Department of Computer Science and Engineering, Mepco Schlenk Engineering College, Sivakasi, 626005, India
*Corresponding Author: G. Rajasekaran. Email: rajasekaran@mepcoeng.ac.in
Received: 25 February 2022; Accepted: 21 April 2022
Abstract: Abnormal behavior detection is challenging and one of the growing research areas in computer vision. The main aim of this research work is to focus on panic and escape behavior detections that occur during unexpected/uncertain events. In this work, Pyramidal Lucas Kanade algorithm is optimized using EMEHOs to achieve the objective. First stage, OPLKT-EMEHOs algorithm is used to generate the optical flow from MIIs. Second stage, the MIIs optical flow is applied as input to 3 layer CNN for detect the abnormal crowd behavior. University of Minnesota (UMN) dataset is used to evaluate the proposed system. The experimental result shows that the proposed method provides better classification accuracy by comparing with the existing methods. Proposed method provides 95.78% of precision, 90.67% of recall, 93.09% of f-measure and accuracy with 91.67%.
Keywords: Crowd behavior analysis; anomaly detection; Motion Information Image (MII); Enhanced Mutation Elephant Herding Optimization (EMEHO); Optimized Pyramidal Lucas-Kanade Technique (OPLKTs) algorithm
In the present world, video surveillance system is most essential to identify abnormal behavior in the crowd. There are huge number of unethical events are happening in many crowded places such as theft, explosions in the markets, subways, religion festivals, stadium.Studying videos has attracted interest in computer vision, and the areas being explored include object tracking/gait recognitions [1,2] and activity detections [3] which have promising futures. In addition, the study of crowded places is gaining popularity owing to large crowds in the markets, subways, religious festivals, public protests, and sporting events.
Studying crowd behaviors in public locations and specifically during public events has attracted much attention regarding safety controls, predicting potentially harmful situations, and preventing overcrowding (religious/sports events). These public safety concerns have culminated in the need to investigate crowd behaviors with high-level descriptions of people’s actions or interactions in crowds.
Growing concerns over public security/safety have resulted in explorations of Abnormal Event Detections (AEDs) in computer vision [4,5]. AEDs have issues due to frequent occlusions, excessive noises, congestions, dynamism/complexities, diversities of events, unpredictability, and reliance on contexts. Many challenges are involved in analyzing crowd behavior. Anomalies [6] in crowd recognition or characterizations, change in crowds [7–9]. These factors automatically identify changes or characterize crowd events through video sequences. Existing methods for analyzing crowd behaviors can be divided into two categories based on objects and holistic approaches [10–12].
Object-based techniques take crowds as a group of recognized and monitored objects to comprehend crowd behaviors. The significant disadvantages of these approaches lie in their unreliability of detecting objects or tracking their actions due to occlusions. In contrast, holistic approaches view crowds as a global unit and evaluate whole crowds to identify important information like applications of optical flows to frames and to identify crowd behaviors. Anomalies in the crowds can be detected in their event representations and anomaly measurements. AEDs can be identified using spatial-temporal information, where a one-class learning algorithm is used to learn normal samples. Few methods include Histograms of Optical Flows (HOFs), Histograms of Motion Directions (HMDs), spatial-temporal gradients, chaotic invariants, dynamic textures, sparse representations, and Behavior Entropies (BEs) [13].
In the field of computer vision, video surveillance has become a popular topic of study. Abnormal event identification is an important aim in this field that is gaining increasing attention. The goal of aberrant event detection is to identify activities that are unusual or irregular.
In the field of computer vision, video surveillance has become a popular topic of study. Abnormal event identification is an important aim in this field that is gaining increasing attention. The goal of aberrant event detection is to identify activities that are unusual or irregular.
Approaches based on optical flows for global/local crowd abnormalities are detailed in this section. Behavior Entropies were used to detect anomalous crowd behaviours [14]. Their scheme estimated BEs of pixels in images by taking into account behavior certainties of defined pixels. Their evaluation results suggested that their proposed technique could successfully capture crowd behavior dynamics. Patil et al. [15] suggested a novel framework for detecting global anomalies using Context Locations (CLs) and Motion-Rich Spatio-Temporal Volumes (MRSTVs) where the block-level features were extracted. Normal/abnormal motion characteristics were determined using a histogram of optical flow directions and features of motion magnitude by Spatio-Temporal Volume (STVs) for global feature descriptions. During the scheme’s training, single class Support Vector Machines (SVMs) learned normal behaviors from MRSTVs while identifying aberrant STVs from test data. Subsequently, their Spatio-temporal post-processing detected anomalous behaviors found in frames, thus minimizing false alarm rates. CLs were defined properly for identifying anomalous behaviors in unexpected locations. Using MRSTVs, their suggested approach neglected pixel-level feature extractions and background modeling, resulting in higher detection rates reducing computational complexities.
In Generative Adversarial Nets (GANs) used by Ravanbakhsh et al. [16], the internal representations of normal scenes were built with GANs where the frame’s related optical flow images were used. Ravanbakhsh et al. [17] suggested combining semantic information inherited from CNNs with low-level optical flow to measure local irregularities. The main advantage of their strategy was that it did not require fine tunings. Furthermore, they validated their approach on abnormal detection datasets, and their results revealed their suggested technique’s uniqueness.
Global Event Influences (GEIs), mid-level representations were proposed by Pan et al. [18] for detecting global anomalies in packed crowds. In GEIs, crowd movements with social-psychological features were combined to obtain better crowd descriptions. The study abstracted low-level crowd motion characteristics, including size, velocity, and disorders. Their scheme showed that it was robust in detecting anomalous occurrences within short times of event occurrences. Optical flows were also used by Colque et al. [19], where unique Spatio-temporal feature descriptors were assessed from the Histogram of Optical Flows (HOFs) in terms of their direction, amplitudes, and entropies. Their experimental findings showed that their suggested model could handle numerous abnormal occurrences in terms of detections.
Sparse Reconstruction Costs (SRCs) were explored by Cong et al. [20], where SRCs were used on normal bases for detecting abnormal occurrences. Their SRCs used normal dictionaries to quantify the testing samples’ normality based on collections of normal training samples, image sequences, or local Spatio-temporal patch collections. They introduced novel feature descriptors called Multi-scale Histogram of Optical Flows (MHOFs) for event representations where MHOFs concatenated different spatial or temporal structures. While estimating motions using optical flows, images were partitioned into basic units like two-dimensional image patches or three-dimensional Spatio-temporal bricks before extracting MHOFs from units. Motion histograms were built by concatenating optical flow directions and magnitudes at different scales. The experiments conducted on three benchmark datasets demonstrate the benefits of their suggested method compared to similar approaches.
Sparse Linear Models (SLMs) were suggested by Guo et al. [21] for the crowd’s features. They constructed statistical characterizations of sociality by assuming SLM distributions apriori. Initially, computed optical flows were used to extract motion information. Subsequently, sparse coding of input video’s motions produced SLMs. The scheme’s statistical characterizations of sociality were built with SLMs. Moreover, infinite Hidden Markov Models (iHMMs) were assessed if anomalous events were discovered. The anomalous detection tests on UMN and simulated datasets demonstrated promising results compared to other methods.
Hatimaz et al. [22] identified anomalous crowd behavior using optical flow characteristics. They analyzed surveillance videos and annotated semantically using web technologies. The multimedia metadata models generate interoperable metadata on aberrant crowd behaviors. The semantic search interfaces, based on crowd behavior, were used in identifications. Their proposed interface also displayed statistical data regarding crowd behavior and searched video segments. Extensive user evaluations of concept-based semantic searches allowed quick search/analysis of aberrant crowd behaviors.
Recent works on detection of abnormal crowd behaviors include Distribution of Magnitude of Optical Flows (DMOFs), Context Location (CL) and Motion-Rich Spatio-Temporal Volumes (MRSTVs), Generative Adversarial Nets (GANs), Temporal Convolution Neural Network Patterns (TCNNPs), Global Event Influence Models (GEIMs), Histograms of Optical Flow Orientations and magnitudes (HOFOs) [23], Improved Two-stream Inflated 3D ConvNet [24] and Discrete Cosine Transform (DCT) [25]. These works reported that approaches based on optical flows deliver better results while encountering global/local crowd abnormalities.
This research proposes detecting abnormal crowd events where the main contribution is in using the novel MIIs, which accurately represent and discriminate normal and abnormal events. Moreover, outputs of MIIs are inputs for CNNs, which learn and test MIIs data with promising results. People generally flee amidst unusual incidents where this is anomalous behavior, particularly in regions with motions. It increases the angle differences of computed optical flow vectors among previous and current frame’s pixel positions. Thus, the computed MIIs of frames form the inputs for CNNs, and aberrant crowd behaviors are learnt. CNNs classify input MIIs images in the testing phase. This work’s evaluations show better results than other similar approaches in their values of precisions, recalls, f-measures, and accuracy.
This work computes Optimizations using Pyramidal Lucas-Kanade Techniques (OPLKT) vectors from extracted video frames, generating MIIs that CNNs subsequently train to identify anomalous crowd events. In the initial stage, optical flow angle changes of current and prior frames are determined. Optical flow measurements will be noisy, resulting in angle differences. MIIs are formed by multiplying angle differences with the current frame’s optical flow magnitudes. Secondly, abnormal crowd events in surveillance footage are detected using CNNs. The usage of MIIs, CNNs results in learning about aberrant crowd behaviors. Finally, CNNs classifies input MII images in testing phases. Fig. 1 depicts the stages involved in the proposed system.
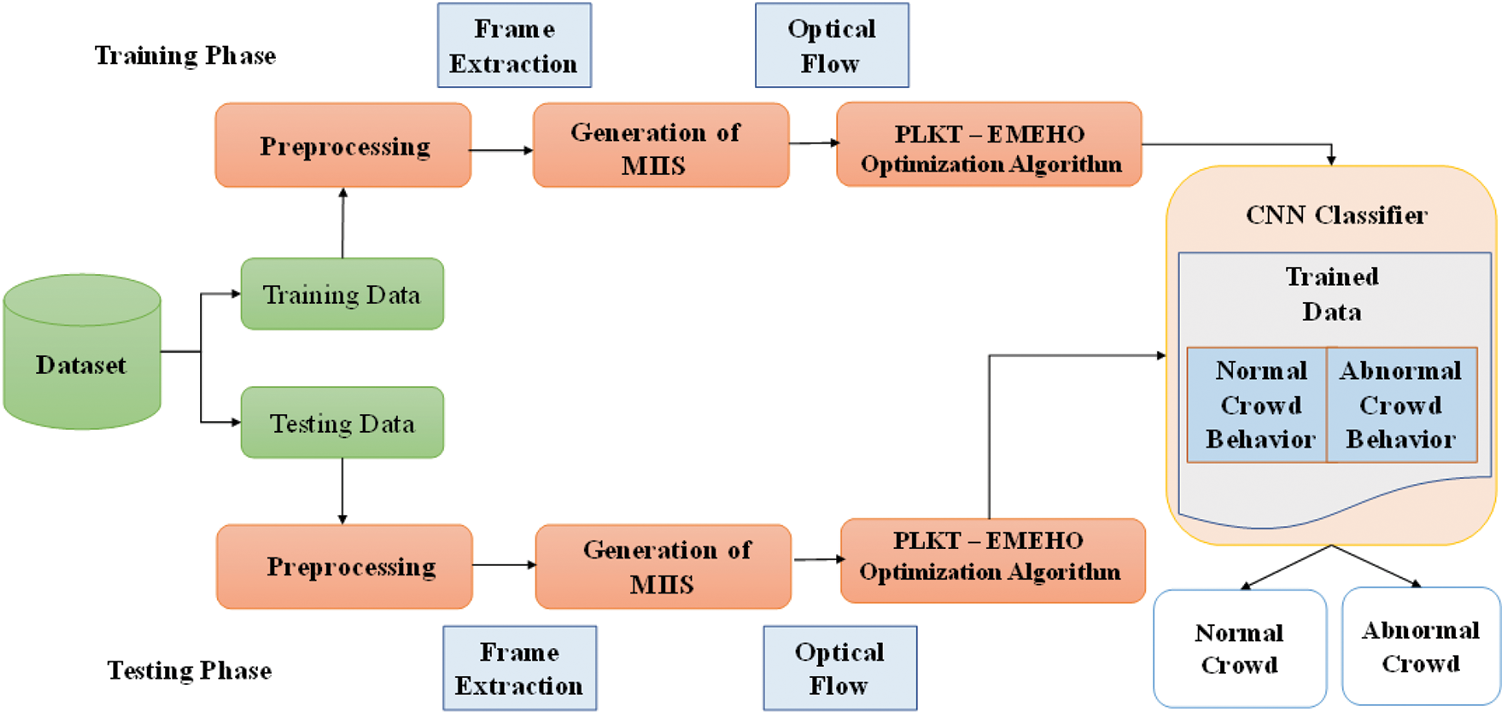
Figure 1: Flow diagram of the proposed system
Prior works combined optical flow characteristics with single class CNNs to identify anomalous crowd behaviors. The optical flow magnitude and optical flow angle difference information were combined [26], resulting in one-dimensional feature vectors. Feature vectors are extracted from frames for representing typical behaviors which are subsequently trained by using single class CNNs. When test frames deviated from normal frames, those frames were treated as abnormal. This work differs from prior works in unique MII representations that give visual impressions of crowd motions. MIIs are created based on optical flows. The generated MIIs are fed into CNNs for training and testing crowd behavior types, namely normal and abnormal. LKTs are then used to compute the optical flow of frames. During panic situations, people may run in opposite/same directions. Hence, MIIs need to be insensitive to the directional movements to retain the discriminations between normal and aberrant occurrences in frames. The proposed OPLKTs aim to align input images I into template frames T by computing warping transformations among frames for all pixels. In the following equation, p stands for warping vector in transformations. Assuming a two-vector, its translation can be depicted by Eq. (1),
Typical LKTs optimize warping parameters p by reducing the sum of squared differences between target intensities T(x) of pixels of T, and their corresponding intensities
where g(
where
where,
where H is the Hessian matrix’s Gauss-Newton approximation given by Eq. (7)
Integrating
EEHO is an Enhanced Elephant Herding Optimization algorithm which is used to improve the classification algorithm by finding suitable features related to the crowd dataset. To choose the independent optical flow from the generated MIIs to identify the abnormality. EMEHO choose best features to CNN architecture to improve the classification result.
Elephant Herding Optimizations (EHOs) are novel metaheuristic approaches for optimizations [28,29]. Explorations and exploitations can be achieved in Enhanced Mutation Elephant Herding Optimizations (EMEHOs) by updating clan and separating operators. In every generation, individuals (scale parameters of optical flows) with maximum fitness in clans
where
Elephants (j) in clans (i) have old positions (
where α-scale factor ∈ [0,1] influences clan matriarchs and new positions of elephants, β-scale factor ∈ [0,1] that determines elephant’s movement towards clan’s center, γ-scale factor ∈ [0,1] represents elephant’s random walks,
where r-uniform distribution’s randomly drawn vector
Addition of new mutation parameters for improving the clan updating operators where
where,
The separating operator of male elephants can be modeled according to Eq. (11).
Where

People panic and disperse when presented with an unexpected situation. In such scenario, we observe that the angle difference between optical flow vectors in consecutive frames increases at each pixel location, especially in motion areas. At each pixel point, the angle difference between two vectors is determined by Eq. (12):
where
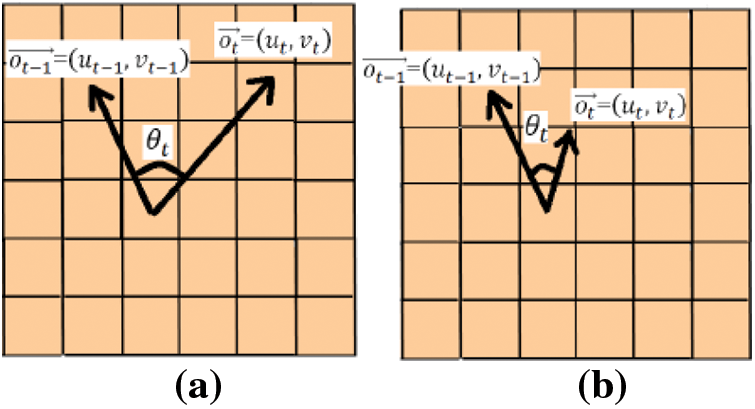
Figure 2: Optical flow angle difference observed behaviour in. (a) Abnormal and, (b) Normal situation
where
Figs. 3a and 3c images depict movement of people where they disperse in various directions. In Fig. 3b, everyone is traveling in the same direction (i.e., towards right). Irrespective of persons moving directions, they represent panic/escape. MIIs need to be invariant to directional motion while being discriminative for detecting normal/abnormal events. Fig. 3 depicts various examples of frames showing deviant behavior and their correlates. MIIs produced by deviant behaviors differ greatly from MIIs produced by regular behaviors (MIIs are scaled to a dimension of 75 * 75 as preparation for inputs into CNNs). Moreover, MIIs in Fig. 3 are also reversed for clarity.

Figure 3: (a) Abnormal behaviour sample 1, (b) Corresponding MIIs of sample 1 For CNNs, (c) Corresponding MIIs of sample 1-OPLKTs+CNNs, (d) Abnormal behaviour sample 2, (e) Corresponding MIIs of sample 2-CNNs, (f) Corresponding MIIs of sample 2-OPLKTs+CNNs
3.3 CNNs Training and Classifications
Here in our work, 2D CNNs are used to identify aberrant crowd behaviors, where CNNs are trained with MIIs for detecting normal and abnormal behaviors. The proposed architecture is illustrated in Fig. 4. MIIs are tested using University of Minnesota (UMN) datasets using CNN architectures with different convolution counts, channels, filter sizes, and pooling layers to predict accuracy. Fig. 5 depicts the design of CNNs where they get trained on MIIs for aberrant crowd behavior detection by including three convolution layers.
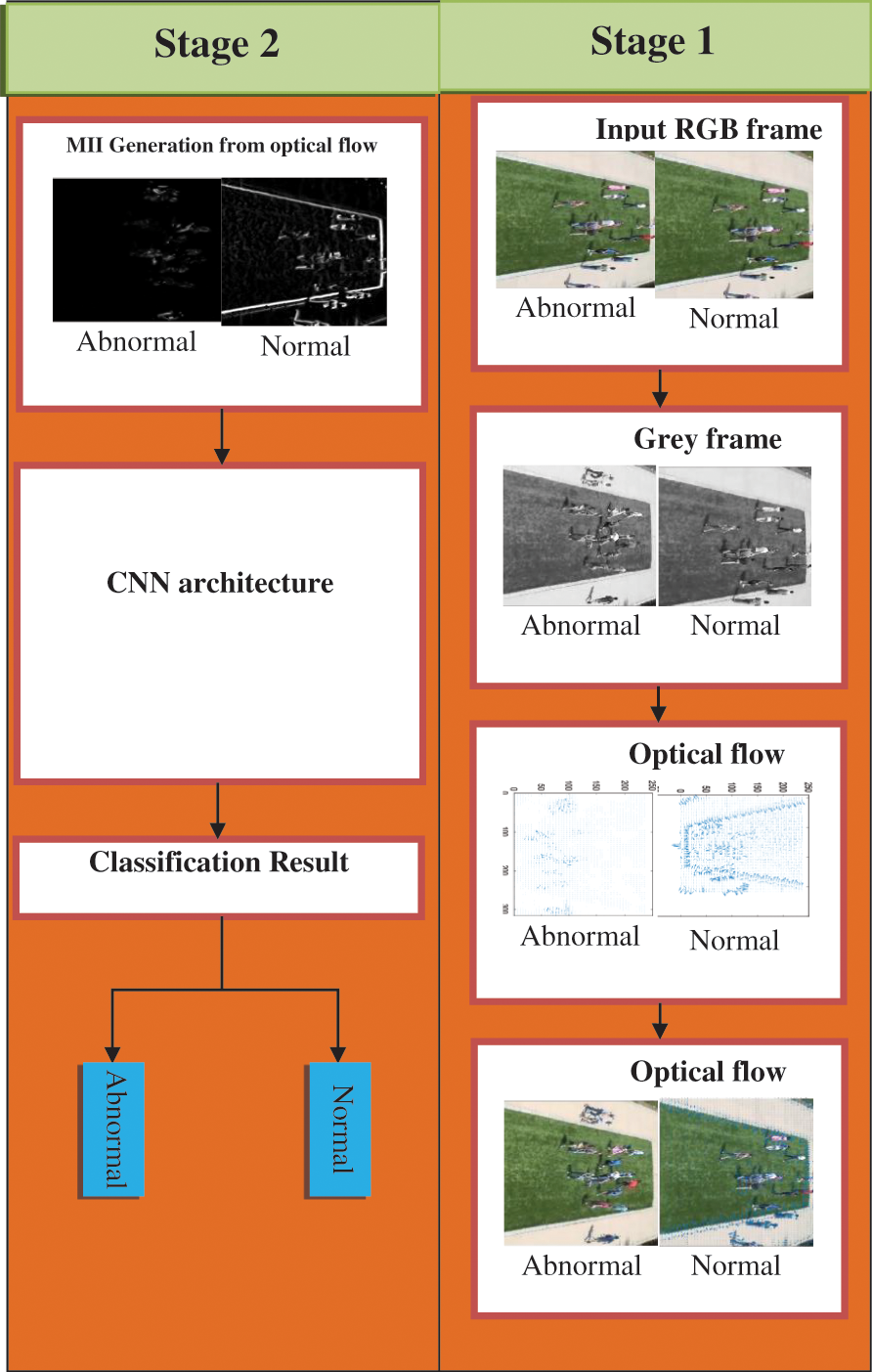
Figure 4: Proposed architecture

Figure 5: Proposed CNN architecture
It’s also worth noting that MIIs are fed to deep networks, used for image recognition. MII inputs are enlarged to 75 × 75 dimensions in the basic CNNs structure as depicted in Fig. 5. The first convolution layer employs 5 × 5 filter with 8-channel filters followed by batch normalization, Rectified Linear unit (ReLu) activations and a max pooling of 3 × 3. The second Convolution layer use 3 × 3 filters with 16 feature maps, followed by batch normalizations, ReLu activations, and 2 × 2 max poolings. The final convolution layer use 3 × 3 filters with 32 feature maps, followed by batch normalizations, ReLu activations and 2 × 2 max pooling. Pooling layers are used to reduce the dimension of the feature map, where pooling layer 1 used 3 × 3 stride and output of pooling layer 1 is 64 × 64, pooling layer 2 used 2 × 2 stride and output of pooling layer 2 is 32 × 32, pooling layer 3 used 2 × 2 stride and output of pooling layer 3 is 16 × 16.The fully connected layer with two nodes (normal/abnormal) use the softmax layer for predictions. The classification layer determines whether the input MII image was normal or abnormal. Stochastic gradient descent with momentum approach is utilized as a solution during training. The learning rate is set to 0.01, mini-batch size 50, with the number of epochs limited to 10. These values were determined empirically for obtaining the best results with the generated MIIs. The test frames in the UMN dataset were identified using 28/28 neighboring frames, implying a window size of 57 (including test frames), where each frame is labeled using CNNs classifier, and the most common class indicates the test frame’s behavior (normal or aberrant) [30,31].
4 Experimental Results and Discussion
Extensive experiments are carried out on the UMN datasets [32,33] consisting of 11 movies that depict typical and anomalous crowd behaviors.The result of pooling layer 3 is better than pooling layer 2. As pooling layer 3 dimensionality reduced to 16 × 16. If we add another pooling layer it reduces the dimension. Further, done to that the performance is not up to the mark.Therefore,in this work we have stopped at layer 3. This work is also compared with other global anomaly detection schemes, including BEMs, DMOFs, GANs and MHOFs, and Motion Information Images+Convolutional Neural Networks (MII+CNNs). These methods havebeen experimented in MATLAB R2016a. In this work, some standard statistical indices such as precision, recall, f-measure, and accuracy are used to evaluate the performance of the classification.
Precision refers to the ratio of positive samples which have been appropriately classified. Estimation of this metric can be formulated by Eq. (14),
Recall defines the positive samples that have been designated to the total number of positive samples. It is estimated by Eq. (15),
F-measure is referred to the harmonic mean of precision and recall. It is expressed below by Eq. (16),
Accuracy is a measure considered one of the widely-regarded metrics to analyze classification performance. This has been calculated in this work for crowd behavior detection by Eq. (17).
The symbols TP, TN, FP, and FN denote True Positive, True Negative, False Positive, and False Negative. The UMN dataset contains three distinct scenes (two outdoor scenes and one indoor scene). Tab. 1 shows the overall classification results compared to other methods with respect to metrics under three scenes. Tab. 2 illustrates the precision, recall, f-measure, and accuracy of six methods for this scenario. The proposed work (OPLKTs+CNNs) outperforms the other methods with an accuracy of 91.67%.
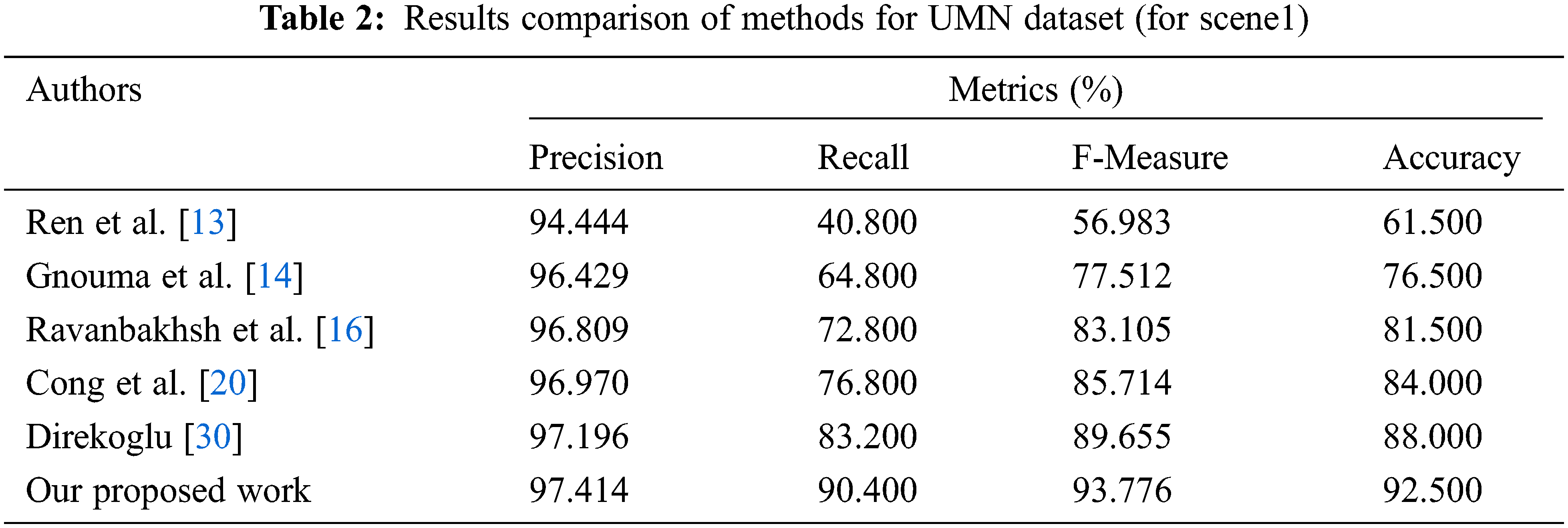
This work’s suggested technique yields the best results in the UMN dataset. Tabs. 2–4 depicts the accuracy comparisons of various approaches concerning scene 1, scene 2 and scene 3 respectively from the UMN dataset. The results demonstrate that the proposed technique achieves better precision when compared to other existing methods. From Tab. 5, it is inferred that the proposed OPLKT+CNN classifier has a better precision value of 95.78% when compared to BEM, DMOF, GANs, MHOF, and MII+CNNs gives a precision value of 94.23%, 94.45%, 94.89%, 95.25%, and 95.57%, respectively. In addition, the proposed classifier gives higher results than the other methods since optical flow is identified via the Enhanced Mutation Elephant Herding Optimization (EMEHO) algorithm. However, the proposed method can be improved by incorporating the concept of transfer learning [34] and parameter optimization in order to achieve the maximum accuracy of 100% which is limited by the number of layers used in the CNN architecture [35] and the parameter settings in EMEHO algorithm.
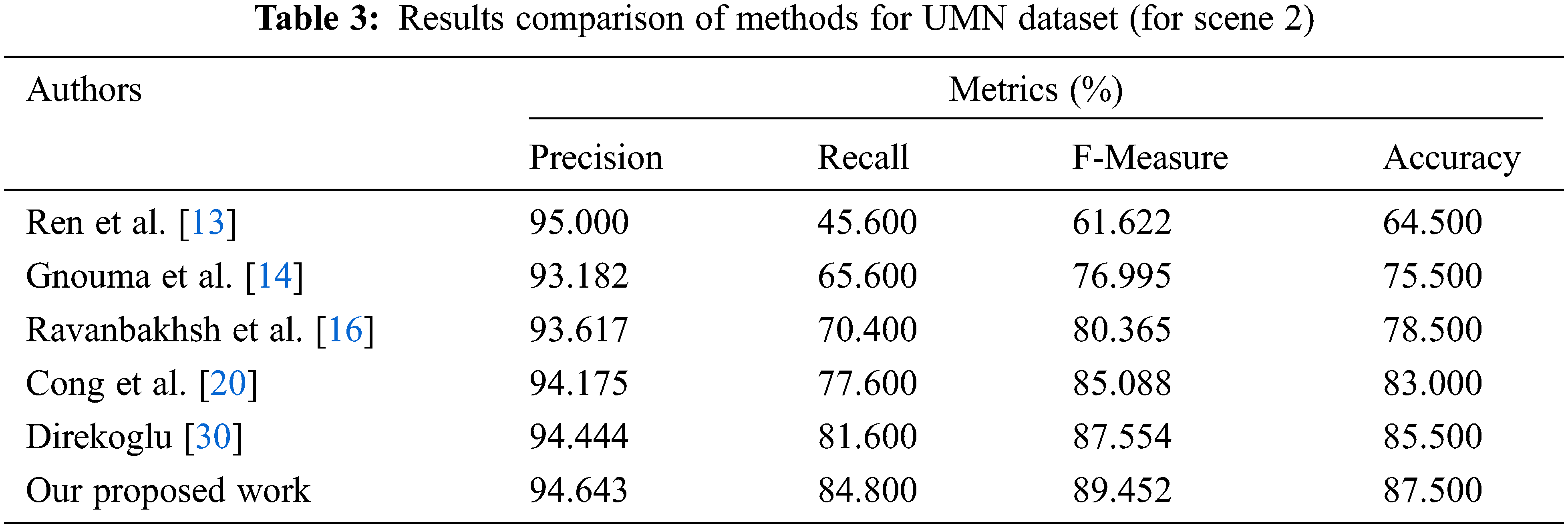
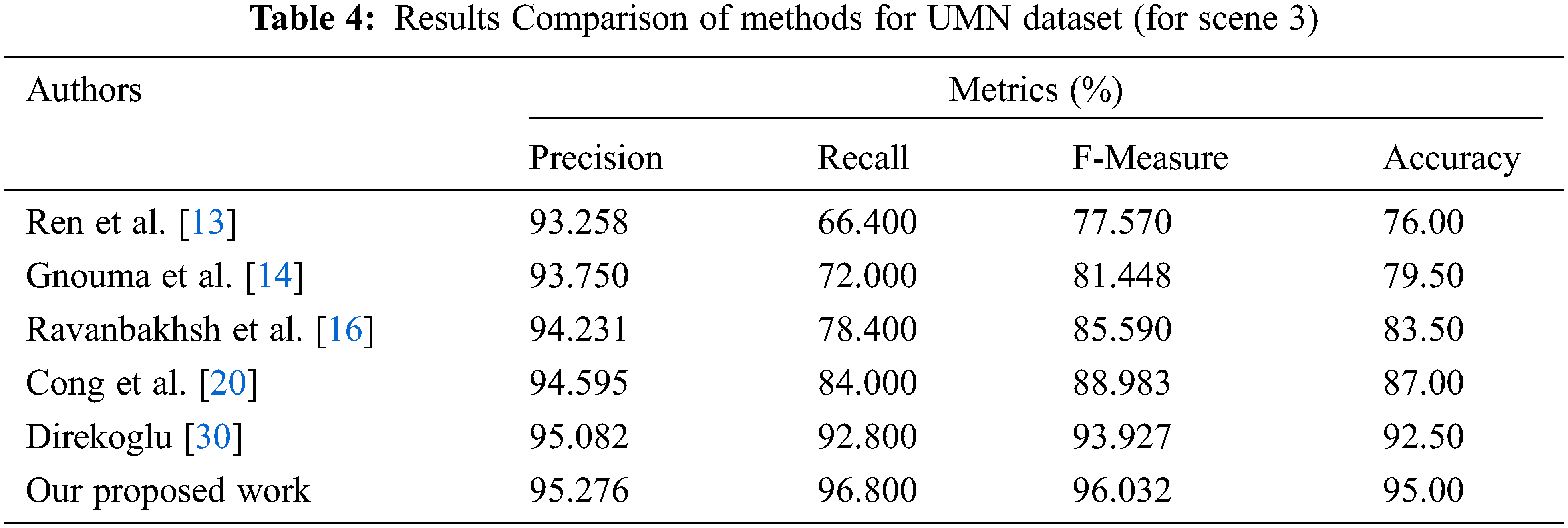
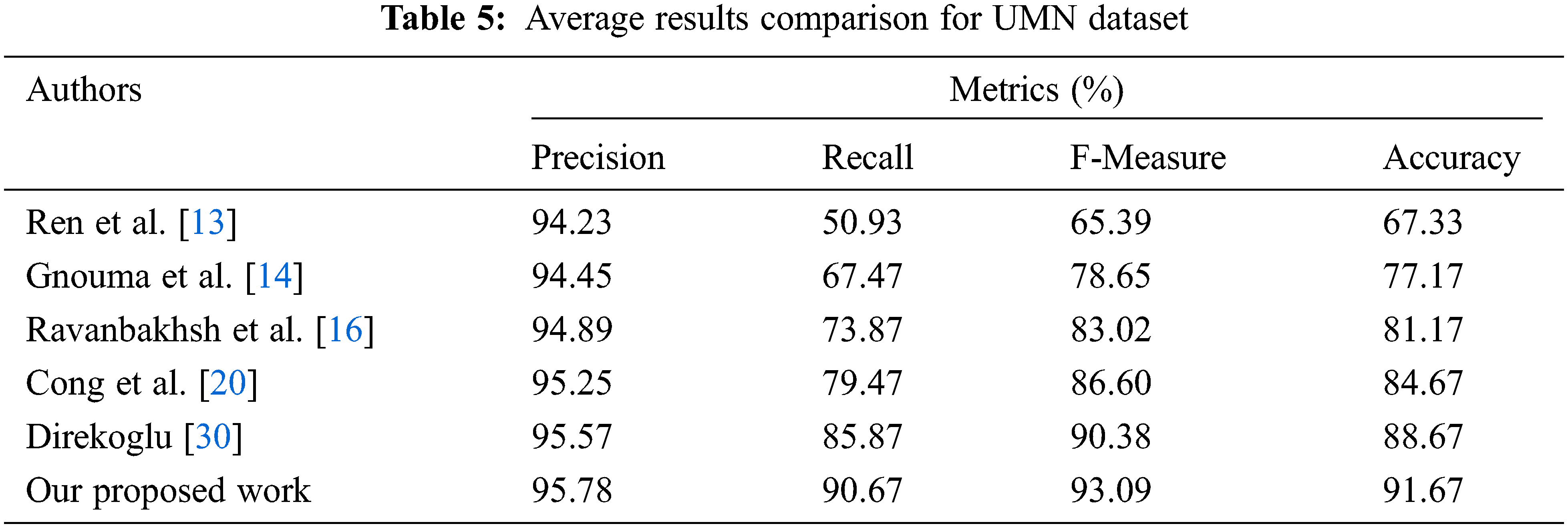
Tab. 5 shows the performance comparison results of different methods concerning recall. For example, the proposed OPLKT+CNN classifier gives a higher recall value of 90.67%, the other methods such as BEM, DMOF, GANs, MHOF, and MII+CNNs gives lesser recall value of 50.93%, 67.47%, 73.87%, 79.47%, and 85.87% respectively.
The F-measure results comparison of three different scenes under various methods are illustrated in Tab. 5. The proposed OPLKT+CNN classifier gives a higher f-measure value of 93.09%, the other methods such as BEM, DMOF, GANs, MHOF, and MII+CNNs gives a lesser value of 65.39%, 78.65%, 83.02%, 86.60%, and 90.38%, respectively.
Three different scenes with average accuracy results are compared with Behavior Detection methods, as illustrated in Fig. 6. The results prove that the proposed classifier gives higher accuracy than the other methods for all scenes. The proposed OPLKT+CNN classifier achieves accuracy value of 91.67%. The other methods such as BEM, DMOF, GANs, MHOF, and MII+CNNs give a lesser value of 67.33%, 77.17%, 81.17%, 84.67%, and 88.67%, respectively.
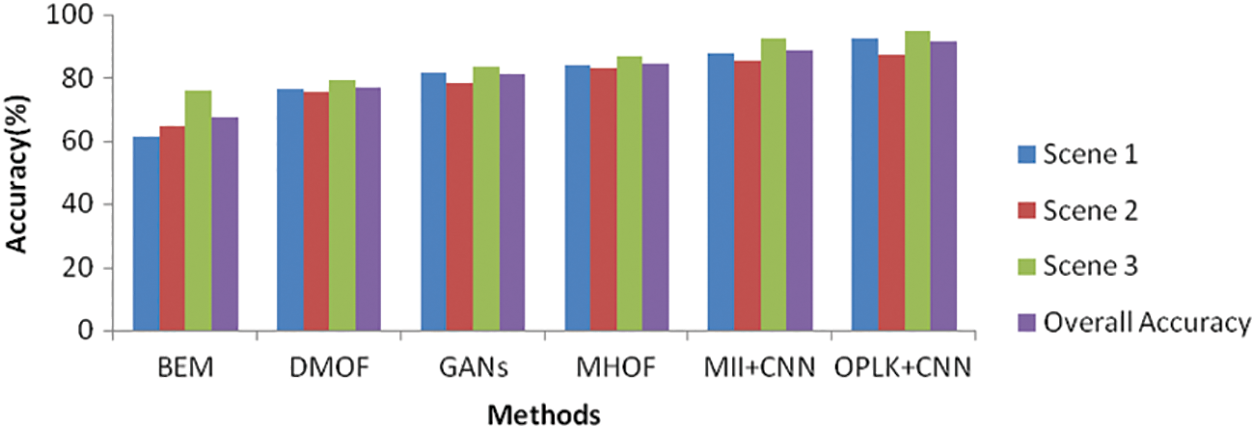
Figure 6: Accuracy comparison of scenes vs. methods
ROC results are compared to Behavior Detection methods and are illustrated in Fig. 7. The proposed OPLKT+CNN classifier gives a higher ROC value of 93.40%. The other methods, such as BEM, DMOF, GANs, MHOF, and MII+CNNs give a lesser value of 77.30%, 81.20%, 85.60%, 87.70%, and 91.20%, respectively at False Positive Rate of 100%.
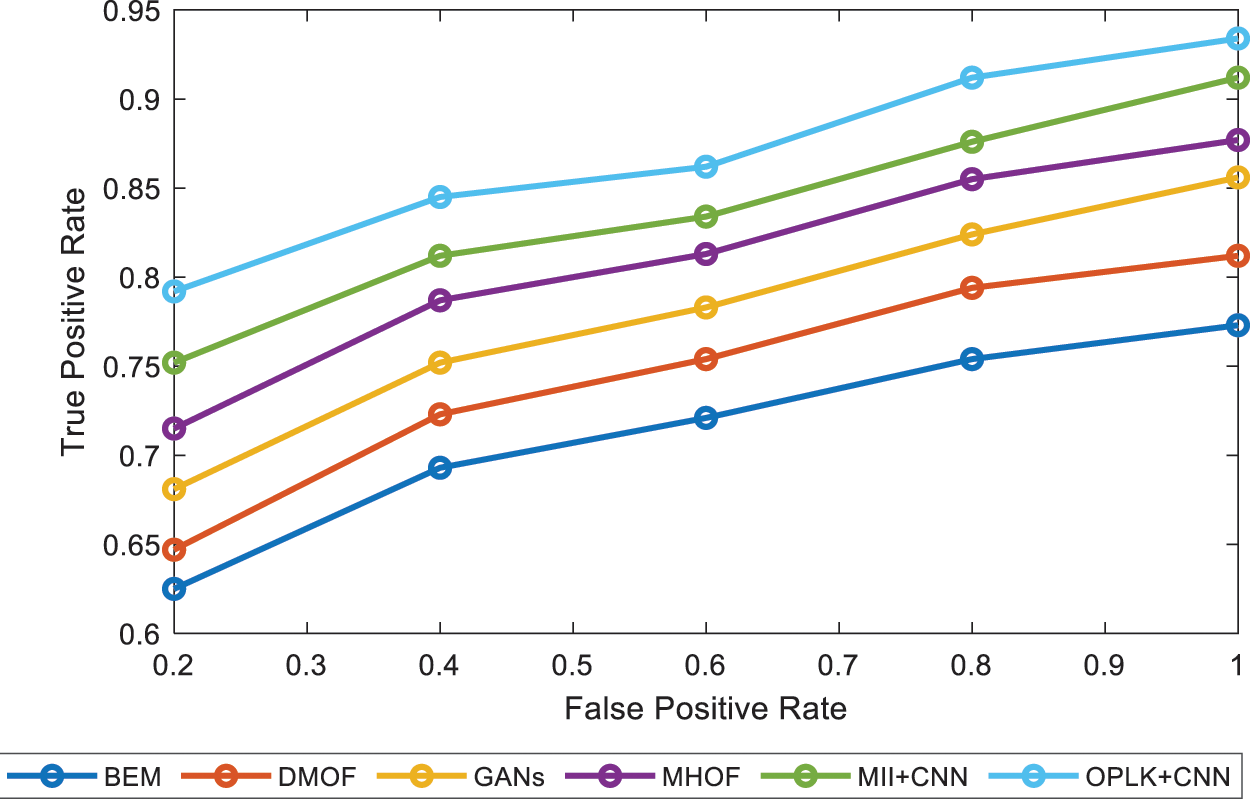
Figure 7: ROC curve comparison of different methods
The proposed system produced 91.67% accuracy. Compared to existing algorithms, the proposed system produced better accuracy. Here the input size is 75 × 75, due to that design convolution layer, pooling layer are limited to classify the crowd detection. We are working on this to achieve maximum accuracy by increasing the layers and varying the parameter values of optimization algorithms and CNN architecture.
Detecting unusual occurrences in cluttered environments is a critical and challenging job in computer vision. The focus of this work is on global anomalous crowd event identifications from surveillance recordings. The primary contribution is the development of novel MIIs generations based on OPLKTs, which then incorporated EMEHOs for optimizing scale parameters and enhancing EHOs with the application of a mutation function. MIIs are determined by angle differences between optical flow vectors in consecutive frames where specific minor optical flow measurements and angle differences could have altered observations. CNNs are used to learn normal and abnormal occurrences, and test samples are assigned to one of the two classes by CNNs. The architecture of CNNs in this work uses three convolutional layers for identifying aberrant crowd behavior using MIIs. Experiments are carried on using widely used UMN datasets where the proposed OPLKT+CNN framework achieves results better than the state-of-the-art methods. It indicates that it can effectively extract abnormal events from videos and is very effective. Furthermore, the proposed OPLKT+CNN classifier improves the accuracy value by 91.67 %. The research could focus more on human action recognition and crowd activity recognition in future work.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. D. Thapar, A. Nigam, D. Aggarwal and P. Agarwal, “VGR-net: A view invariant gait recognition network,” in Proc. of the IEEE Int. Conf. on Identity, Security, and Behavior Analysis (ISBA), Singapore, pp. 1–8, 2018. [Google Scholar]
2. Z. Y. Huang, L. Wang, X. Wang and T. Tan, “A comprehensive study on cross-view gait based human identification with deep CNNs,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 39, no. 2, pp. 209–226, 2017. [Google Scholar]
3. T. Wang, Y. Chen, M. Zhang, J. Chen and H. Snoussi, “Internal transfer learning for improving performance in human action recognition for small datasets,” IEEE Access, vol. 5, pp. 17627–17633, 2017. [Google Scholar]
4. M. Paul, S. M. Haque and S. Chakraborty, “Human detection in surveillance videos and its applications-A review,” EURASIP Journal on Advances in Signal Processing, vol. 5, pp. 1–16, 2013. [Google Scholar]
5. Z. Xu, X. Zeng, G. Ji and B. Sheng, “Improved anomaly detection in surveillance videos with multiple probabilistic models inference 2022,” Intelligent Automation & Soft Computing, vol. 31, no. 3, pp. 1703–1717, 2022. [Google Scholar]
6. H. Mousavi, S. Mohammadi, A. Perina, R. Chellali and V. Murino, “Analyzing tracklets for the detection of abnormal crowd behavior,” in Proc. of the IEEE Winter Conf. on Applications of Computer Vision(WACV), Waikoloa, HI, USA, pp. 148–155, 2015. [Google Scholar]
7. J. Shao, C. C. Loy and X. Wang, “Scene-independent group profiling in crowd,” in Proc. of the IEEE Conf. on Computer Vision Pattern Recognition(CVPR), Columbus, OH, USA, pp. 2227–2234, 2014. [Google Scholar]
8. H. Fradi and J.-L. Dugelay, “Sparse feature tracking for crowd change detection and event recognition,” in Proc. of the 22nd Int. Conf. on Pattern Recognition (ICPR), Stockholm, Sweden, pp. 4116–4121, 2014. [Google Scholar]
9. T. Li, H. Chang, M. Wang, B. Ni, R. Hong et al., “Crowded scene analysis: A survey,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 25, no. 3, pp. 367–386, 2015. [Google Scholar]
10. S. Wu, B. E. Moore and M. Shah, “Chaotic invariants of lagrangian particle trajectories for anomaly detection in crowded scenes,” in Proc. of the IEEE Computer Society Conf. on Computer Vision and Pattern Recognition, San Francisco, CA, USA, pp. 2054–2060, 2010. [Google Scholar]
11. W. Li, V. Mahadevan and N. Vasconcelos, “Anomaly detection and localization in crowded scenes,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 36, no. 1, pp. 18–32, 2013. [Google Scholar]
12. S. Arivazhagan, R. Newlin Shebiah and V. Sridevi, “Development of video analytic algorithm for anomaly detection in individual and crowd behavior,” International Journal of Applied Engineering Research, vol. 10, no. 1, pp. 754–758, 2015. [Google Scholar]
13. W. Ren, G. Li, J. Chen and H. Liang, “Abnormal crowd behavior detection using behavior entropy model,” in Proc. of the Int. Conf. on Wavelet Analysis and Pattern Recognition, Xi’an, China, pp. 212–221, 2012. [Google Scholar]
14. M. Gnouma, R. Ejbali and M. Zaied, “Abnormal events’ detection in crowded scenes,” Multimedia Tools and Applications, vol. 77, no. 19, pp. 24843–24864, 2018. [Google Scholar]
15. N. Patil and P. K. Biswas, “Global abnormal events detection in crowded scenes using context location and motion-rich spatio-temporal volumes,” IET Image Processing, vol. 12, no. 4, pp. 596–604, 2018. [Google Scholar]
16. M. Ravanbakhsh, M. Nabi, E. Sangineto, L. Marcenaro and C. Regazzonietal, “Abnormal event detection in videos using generative adversarial nets,” in Proc. of the IEEE Int. Conf. on Image Processing (ICIP), Beijing, China, pp. 1577–1581, 2017. [Google Scholar]
17. M. Ravanbakhsh, M. Nabi, H. Mousavi, E. Sangineto and N. Sebe, “Plug-and-play CNN for crowd motion analysis: An application in abnormal event detection,” in Proc. of the IEEE Winter Conf. on Applications of Computer Vision (WACV), Lake Tahoe, NV, USA, pp. 1689–1698, 2018. [Google Scholar]
18. L. Pan, H. Zhou, Y. Liu and M. Wang, “Global event influence model: Integrating crowd motion and social psychology for global anomaly detection in dense crowds,” Journal of Electronic Imaging, vol. 28, no. 2, pp. 1, 2019. [Google Scholar]
19. R. V. H. M. Colque, C. Caetano, C. Andrade and W. R. Schwartz, “Histograms of optical flow orientation and magnitude to detect anomalous events in videos,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 27, no. 3, pp. 673–682, 2017. [Google Scholar]
20. Y. Cong, J. Yuan and J. Liu, “Abnormal event detection in crowded scenes using sparse representation,” Pattern Recognition, vol. 46, no. 7, pp. 1851–1864, 2013. [Google Scholar]
21. C. Guo, H. Li, Z. He, X. Shu and X. Zhang, “Crowd abnormal event detection based on sparse coding,” International Journal of Humanoid Robotics, vol. 16, no. 4, pp. 1–14, 2019. [Google Scholar]
22. E. Hatirnaz, M. Sah and C. Direkoglu, “A novel framework and concept based semantic search Interface for abnormal crowd behaviour analysis in surveillance videos,” Multimedia Tools and Applications, vol. 79, no. 25-26, pp. 1–39, 2020. [Google Scholar]
23. V. J. Kok, M. K. Lim and C. S. Chan, “Crowd behavior analysis: A review where physics meets biology,” Neurocomputing, vol. 177, no. 5411, pp. 342–362, 2016. [Google Scholar]
24. L. Pan, L. Liu, M. Lin, S. Luo, C. Zhou et al., “An improved two-stream inflated 3D convnet for abnormal behavior detection,” Intelligent Automation & Soft Computing, vol. 29, no. 3, pp. 673–688, 2021. [Google Scholar]
25. A. Balasundaram, G. Dilip, M. Manickam, A. Sivaraman, K. Gurunathan et al., “Abnormality identification in video surveillance system using DCT,” Intelligent Automation & Soft Computing, vol. 32, no. 2, pp. 693–704, 2022. [Google Scholar]
26. C. Direkoglu, M. Sah and N. E. O'Connor, “Abnormal crowd behavior detection using novel optical flow-based features,” in Proc. of the 14th IEEE Int. Conf. on Advanced Video and Signal Based Surveillance (AVSS), Lecce, Italy, pp. 1–6, 2017. [Google Scholar]
27. Y. Ahmine, G. Caron, E. M. Mouaddib and F. Chouireb, “Adaptive lucas-kanade tracking,” Image and Vision Computing, vol. 88, pp. 1–8, 2019. [Google Scholar]
28. A. A. K. Ismaeel, I. A. Elshaarawy, E. H. Houssein, F. H. Ismail and A. E. Hassanien, “Enhanced elephant herding optimization for global optimization,” IEEE Access, vol. 7, pp. 34738–34752, 2019. [Google Scholar]
29. H. Singh, B. Singh and M. Kaur, “An improved elephant herding optimization for global optimization problems,” Engineering with Computers, pp. 1–33, 2021. http://dx.doi.org/10.1007/s00366-021-01471-y. [Google Scholar]
30. C. Direkoglu, “Abnormal crowd behavior detection using motion information images and convolutional neural networks,” IEEE Access, vol. 8, pp. 80408–80416, 2020. [Google Scholar]
31. R. Dubey and J. Agrawal, “An improved genetic algorithm for automated convolutional neural network design,” Intelligent Automation & Soft Computing, vol. 32, no. 2, pp. 747–763, 2022. [Google Scholar]
32. “University of Minnesota” Accessed: Feb 25, 2022. Available: http://mha.cs.umn.edu/movies/crowdactivityall. [Google Scholar]
33. “UMN-Dataset,” Available: https://www.crcv.ucf.edu/projects/Abnormal_Crowd/#UMN./. [Google Scholar]
34. X. R. Zhang, J. Zhou, W. Sun and S. K. Jha, “A light weight CNN based on transfer learning for COVID-19 diagnosis,” Computers, Materials & Continua, vol. 72, no. 1, pp. 1123–1137, 2022. [Google Scholar]
35. X. R. Zhang, X. Sun, W. Sun, T. Xu and P. P. Wang, “Deformation expression of soft tissue based on BP neural network,” Automation & Soft Computing, vol. 32, no. 2, pp. 1041–1053, 2022. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |